Identification of Both Distortion and Imbalance Sources in Electrical Installations: A Comparative Assessment
Abstract
:1. Introduction
1.1. The Scope of the Measurement
1.2. The Scope of the Non-Conformities
- -
- Voltage sag;
- -
- Voltage swell;
- -
- Flicker;
- -
- Frequency variations.
1.3. Identification of Distorting and Unbalancing Loads
2. Materials and Methods
3. Methods to Identify Distortion and Imbalanced Sources in Technical Literature
- -
- Traditionally, before the distributed generation made necessary the consideration of the microgrids, the distortion was assessed in the distribution systems. And the lines involved in these systems are designed to avoid the propagation of the imbalance.
- -
- The imbalance can be considered as distortion (multiple of three).
3.1. Algorithm to Calculate Thet3
3.2. Load Characterization Index and Unbalanced Current Ratio
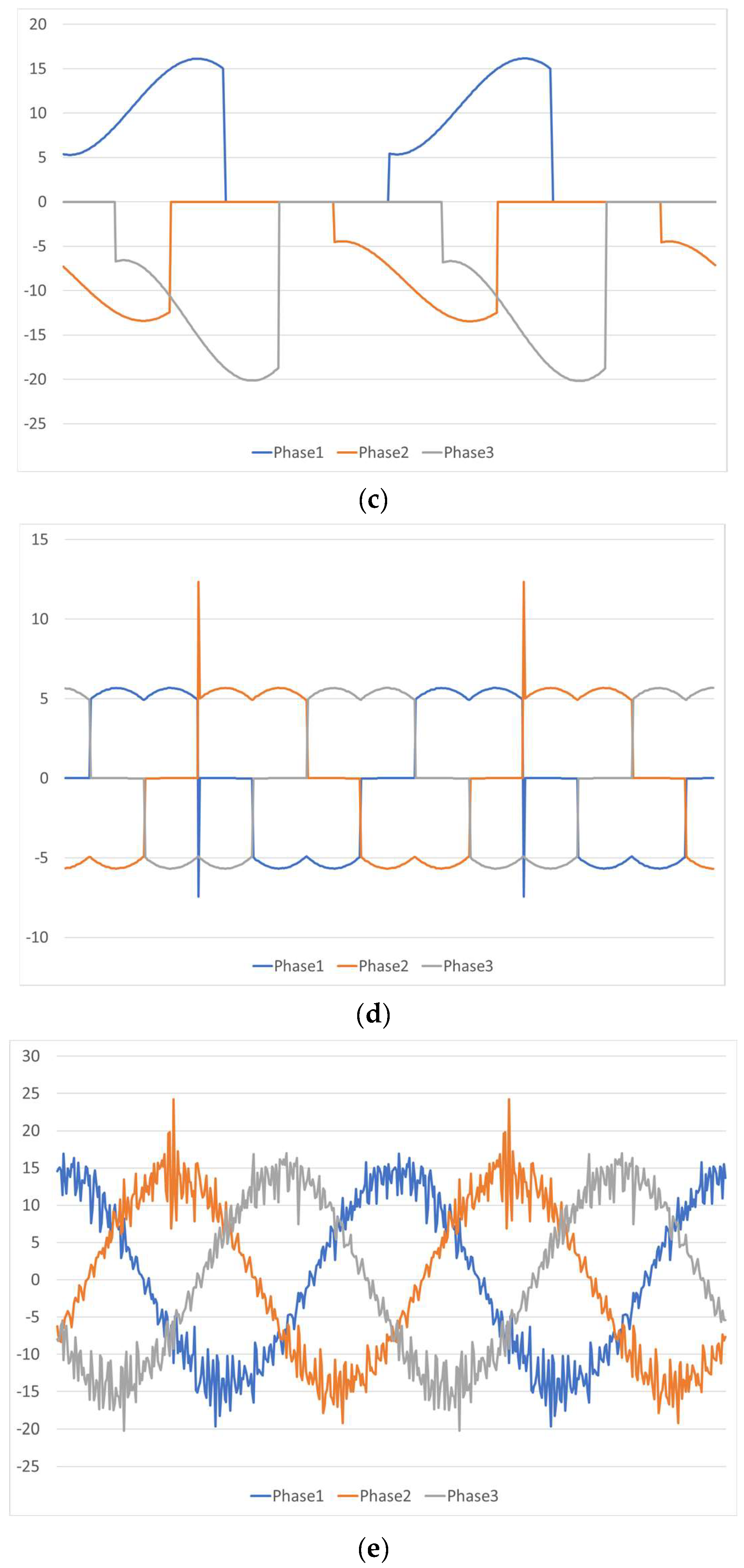
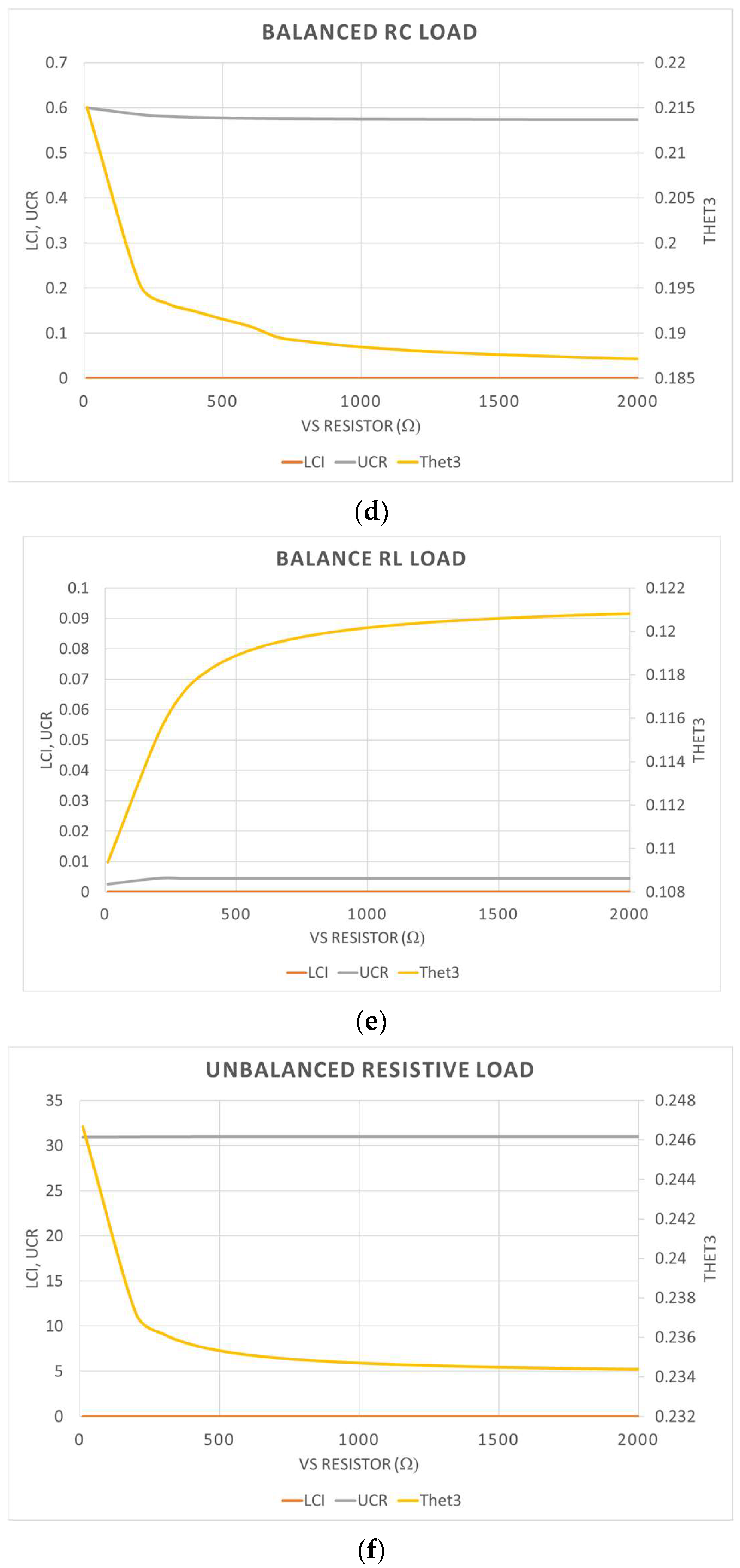
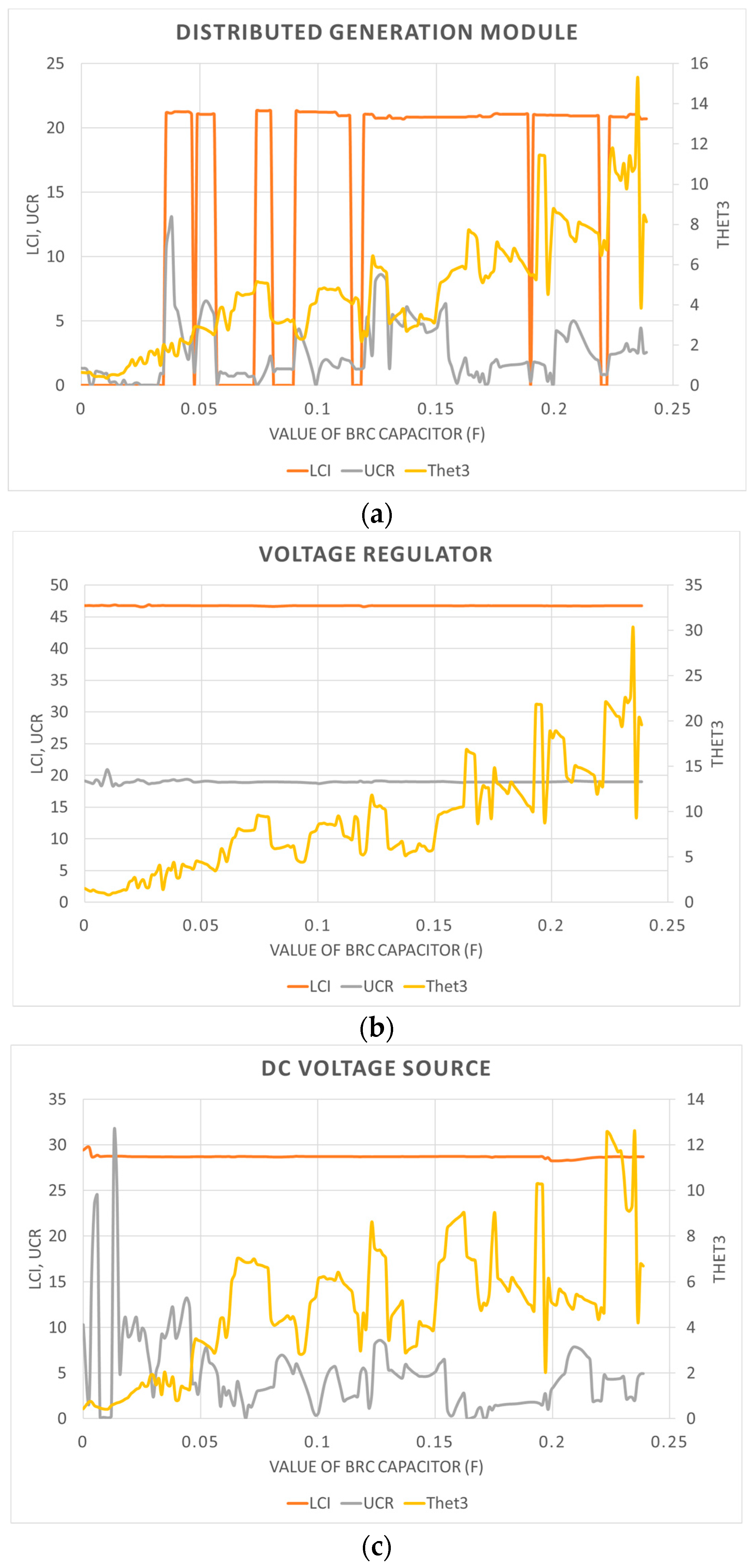
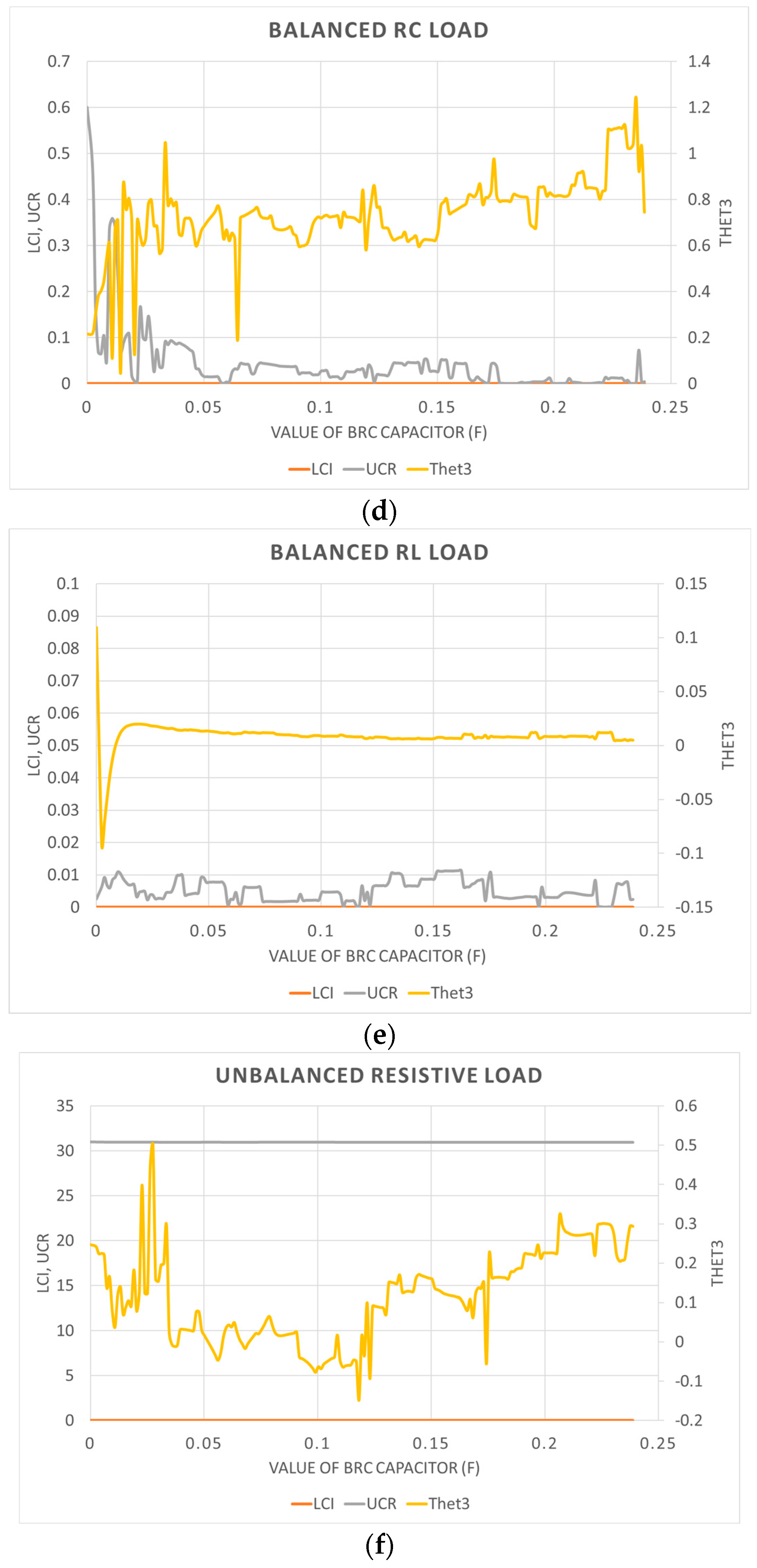
4. Results Obtained from the Application of Both Indices to a Simulation System
- -
- To assess different levels of the linear capacitive load, the value of the fifth load capacitor has been changed from 2.387 µF to 238.7 mF in 200 steps;
- -
- To assess the rectifier load with different weights in the global microgrid, the value of its resistor has been changed from 10 to 2000 in 20 steps.
- -
- It does not identify the unbalanced loads when they are linear; i.e., the value of this index assigned to the unbalanced resistive load is less than 1 in all the studied cases.
- -
- It identifies as the distortion source the capacitive linear load in some of the cases studied.
- -
- It identifies as distortion sources the voltage regulator in all the cases studied. However, it does not identify the DC voltage source as a distortion source (see Figure 6c). In addition, it cannot be corroborated if the index identifies the imbalance in the non-linear load because the value provided is higher than one without providing additional information.
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, K.; Wang, Y.; Yin, P.; Ni, J. Voltage sag source location technology based on corresponding sequence components. IET Gener. Transm. Distrib. 2015, 9, 820–827. [Google Scholar] [CrossRef]
- Kuwałek, P. Selective Identification and Localization of Voltage Fluctuation Sources in Power Grids. Energies 2021, 14, 6585. [Google Scholar] [CrossRef]
- Tee, W.; Yusoff, M.R.; Abdullah, A.R.; Yaakub, M.F. Voltage Variation Signals Source Identification and Diagnosis Method. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2019, 10, 170–180. [Google Scholar] [CrossRef]
- Muscas, C. Assessment of electric power quality: Indices for identifying disturbing loads. Eur. Trans. Electr. Power 1998, 8, 287–292. [Google Scholar] [CrossRef]
- Tanaka, T.; Akagi, H. A new method of harmonic power detection based on the instantaneous active power in three-phase circuits. IEEE Trans. Power Deliv. 1995, 10, 1737–1742. [Google Scholar] [CrossRef]
- Emanuel, A.E. On the assessment of harmonic pollution [of power systems]. IEEE Trans. Power Deliv. 1995, 10, 1693–1698. [Google Scholar] [CrossRef]
- Swart, P.H.; Case, M.J.; Van Wyk, J.D. On techniques for localization of sources producing distortion in electric power networks. Eur. Trans. Electr. Power 1994, 4, 485–489. [Google Scholar] [CrossRef]
- Swart, P.H.; van Wyk, J.D.; Case, M.J. On techniques for localization of sources producing distortion in three-phase networks. Eur. Trans. Electr. Power 1996, 6, 391–396. [Google Scholar] [CrossRef]
- Rens, A.P.J.; Swart, P.H. On techniques for the localisation of multiple distortion sources in three-phase networks: Time domain verification. Eur. Trans. Electr. Power 2001, 11, 317–322. [Google Scholar] [CrossRef]
- Farach, J.E.; Grady, W.M.; Arapostathis, A. An optimal procedure for placing sensors and estimating the locations of harmonic sources in power systems. IEEE Trans. Power Deliv. 1993, 8, 1303–1310. [Google Scholar] [CrossRef]
- Heydt, G.T. Identification of harmonic sources by a state estimation technique. IEEE Trans. Power Deliv. 1989, 4, 569–576. [Google Scholar] [CrossRef]
- Davis, E.J.; Emanuel, A.E.; Pileggi, D.J. Harmonic pollution metering: Theoretical considerations. IEEE Trans. Power Deliv. 2000, 15, 19–23. [Google Scholar] [CrossRef]
- Cristaldi, L.; Ferrero, A.; Salicone, S. A distributed system for electric power quality measurement. IEEE Trans. Instrum. Meas. 2002, 51, 776–781. [Google Scholar] [CrossRef]
- Sinvula, R.; Abo-Al-Ez, K.M.; Kahn, M.T. Harmonic Source Detection Methods: A Systematic Literature Review. IEEE Access 2019, 7, 74283–74299. [Google Scholar] [CrossRef]
- Safargholi, F.; Malekian, K.; Schufft, W. On the Dominant Harmonic Source Identification— Part I: Review of Methods. IEEE Trans. Power Deliv. 2018, 33, 1268–1277. [Google Scholar] [CrossRef]
- Safargholi, F.; Malekian, K.; Schufft, W. On the Dominant Harmonic Source Identification—Part II: Application and Interpretation of Methods. IEEE Trans. Power Deliv. 2018, 33, 1278–1287. [Google Scholar] [CrossRef]
- de Andrade, G.V., Jr.; Naidu, S.R.; Neri, M.G.G.; da Costa, E.G. Estimation of the Utility’s and Consumer’s Contribution to Harmonic Distortion. IEEE Trans. Instrum. Meas. 2009, 58, 3817–3823. [Google Scholar] [CrossRef]
- Pyzalski, T.; Lukomski, R.; Wilkosz, K. Utilization of the voltage rate to localization of harmonic sources in a power system. In Proceedings of the 12th IEEE Mediterranean Electrotechnical Conference (IEEE Cat. No.04CH37521), Dubrovnik, Croatia, 12–15 May 2004; IEEE: Dubrovnik, Croatia, 2004; Volume 3, pp. 1091–1094. [Google Scholar] [CrossRef]
- Thunberg, E.; Soder, L. A Norton approach to distribution network modeling for harmonic studies. IEEE Trans. Power Deliv. 1999, 14, 272–277. [Google Scholar] [CrossRef]
- Tsukamoto, M.; Ogawa, S.; Natsuda, Y.; Minowa, Y.; Nishimura, S. Advanced technology to identify harmonics characteristics and results of measuring. In Proceedings of the Ninth International Conference on Harmonics and Quality of Power. Proceedings (Cat. No. 00EX441), Orlando, FL, USA, 1–4 October 2000; Volume 1, pp. 341–346. [Google Scholar] [CrossRef]
- Chen, C.; Liu, X.; Koval, D.; Xu, W.; Tayjasanant, T. Critical impedance method—A new detecting harmonic sources method in distribution systems. IEEE Trans. Power Deliv. 2004, 19, 288–297. [Google Scholar] [CrossRef]
- Srinivasan, K. On separating customer and supply side harmonic contributions. IEEE Trans. Power Deliv. 1996, 11, 1003–1012. [Google Scholar] [CrossRef]
- Srinivasan, K.; Jutras, R. Conforming and non-conforming current for attributing steady state power quality problems. IEEE Trans. Power Deliv. 1998, 13, 212–217. [Google Scholar] [CrossRef]
- Dell’Aquila, A.; Marinelli, M.; Monopoli, V.G.; Zanchetta, P. New power-quality assessment criteria for supply systems under unbalanced and nonsinusoidal conditions. IEEE Trans. Power Deliv. 2004, 19, 1284–1290. [Google Scholar] [CrossRef]
- Locci, N.; Muscas, C.; Sulis, S. On the Measurement of Power Quality Indexes for Harmonic Distortion in the Presence of Capacitors. In Proceedings of the 2005 IEEE Instrumentationand Measurement Technology Conference Proceedings, Ottawa, ON, Canada, 16–19 May 2005; Volume 3, pp. 1600–1605. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; García-Triviño, P.; Fernández-Ramirez, L.M.; Jurado, F. Control strategies for DC networks: A systematic literature review. Renew. Sustain. Energy Rev. 2016, 58, 319–330. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. PRISMA Group Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med. 2009, 6, e1000097. [Google Scholar] [CrossRef] [PubMed]
- Zang, T.; He, Z.; Fu, L.; Wang, Y.; Qian, Q. Adaptive method for harmonic contribution assessment based on hierarchical K-means clustering and Bayesian partial least squares regression. IET Gener. Transm. Distrib. 2016, 10, 3220–3227. [Google Scholar] [CrossRef]
- Farhoodnea, M.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. An enhanced method for contribution assessment of utility and customer harmonic distortions in radial and weakly meshed distribution systems. Int. J. Electr. Power Energy Syst. 2012, 43, 222–229. [Google Scholar] [CrossRef]
- Nassif, A.B.; Yong, J.; Mazin, H.; Wang, X.; Xu, W. An Impedance-Based Approach for Identifying Interharmonic Sources. IEEE Trans. Power Deliv. 2011, 26, 333–340. [Google Scholar] [CrossRef]
- Farhoodnea, M.; Azah, M.; Shareef, H.; Jabbar Khan, R. An Improved Method for Determining Contribution of Utility and Customer Harmonic Distortions in a Power Distribution System. Int. J. Electr. Eng. Inform. 2010, 2, 204–215. [Google Scholar] [CrossRef]
- Park, J.-I.; Lee, H.; Yoon, M.; Park, C.-H. A Novel Method for Assessing the Contribution of Harmonic Sources to Voltage Distortion in Power Systems. IEEE Access 2020, 8, 76568–76579. [Google Scholar] [CrossRef]
- Safargholi, F.; Malekian, K. Relevant Factors for Evaluation of the Harmonic Responsibility of Utility and Customer. IEEE Trans. Power Deliv. 2021, 36, 124–134. [Google Scholar] [CrossRef]
- dos Santos, A.C.; Santos, I.N.; de Oliveira, J.C. Capacitor switching methodology for responsibility sharing of harmonic voltage distortions. Int. Trans. Electr. Energy Syst. 2019, 29, e12135. [Google Scholar] [CrossRef]
- Fernandes, R.A.S.; Oleskovicz, M.; Da Silva, I.N. Harmonic Source Location and Identification in Radial Distribution Feeders: An Approach Based on Particle Swarm Optimization Algorithm. IEEE Trans. Ind. Inform. 2022, 18, 3171–3179. [Google Scholar] [CrossRef]
- D’Antona, G.; Muscas, C.; Pegoraro, P.A.; Sulis, S. Harmonic source estimation in distribution systems. In Proceedings of the 2010 IEEE International Workshop on Applied Measurements for Power Systems, Aachen, Germany, 22–24 September 2010; pp. 59–63. [Google Scholar] [CrossRef]
- D’Antona, G.; Muscas, C.; Sulis, S. Localization of nonlinear loads in electric systems through harmonic source estimation. In Proceedings of the 2009 IEEE Instrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; pp. 390–395. [Google Scholar] [CrossRef]
- Carta, D.; Muscas, C.; Pegoraro, P.A.; Solinas, A.V.; Sulis, S. Compressive Sensing-Based Harmonic Sources Identification in Smart Grids. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Tang, K.; Shen, C. Method for detecting harmonic responsibility misjudgements based on waveform correlation analysis. IET Gener. Transm. Distrib. 2019, 13, 1545–1554. [Google Scholar] [CrossRef]
- Dağ, O.; Uçak, C.; Usta, Ö. Harmonic source location and meter placement optimization by impedance network approach. Electr. Eng. 2012, 94, 1–10. [Google Scholar] [CrossRef]
- Beites, L.F.; Alvarez, M.; Díaz, A. Sensor optimum location algorithm for estimating harmonic sources injection in electrical networks. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’14), Cordoba, Spain, 8–10 April 2014. [Google Scholar]
- Herrera, R.S.; Salmerón, P. Harmonic disturbance identification in electrical systems with capacitor banks. Electr. Power Syst. Res. 2012, 82, 18–26. [Google Scholar] [CrossRef]
- Moradifar, A.; Akbari Foroud, A.; Fouladi, M. Identification of multiple harmonic sources in power system containing inverter-based distribution generations using empirical mode decomposition. IET Gener. Transm. Distrib. 2019, 13, 1401–1413. [Google Scholar] [CrossRef]
- Safargholi, F.; Malekian, K.; Schufft, W. “Voltage-Current Ratio Difference” Concept for identifying the dominant harmonic source. Int. J. Electr. Power Energy Syst. 2020, 121, 106147. [Google Scholar] [CrossRef]
- Nath, S.; Sinha, P.; Goswami, S.K. A wavelet based novel method for the detection of harmonic sources in power systems. Int. J. Electr. Power Energy Syst. 2012, 40, 54–61. [Google Scholar] [CrossRef]
- Xu, F.; Yang, H.; Zhao, J.; Wang, Z.; Liu, Y. Study on Constraints for Harmonic Source Determination Using Active Power Direction. IEEE Trans. Power Deliv. 2018, 33, 2683–2692. [Google Scholar] [CrossRef]
- Wang, B.; Ma, G.; Xiong, J.; Zhang, H.; Zhang, L.; Li, Z. Several Sufficient Conditions for Harmonic Source Identification in Power Systems. IEEE Trans. Power Deliv. 2018, 33, 3105–3113. [Google Scholar] [CrossRef]
- Ferrero, A.; Prioli, M.; Salicone, S. Fuzzy Metrology-Sound Approach to the Identification of Sources Injecting Periodic Disturbances in Electric Networks. IEEE Trans. Instrum. Meas. 2011, 60, 3007–3017. [Google Scholar] [CrossRef]
- Moradifar, A.; Akbari Foroud, A.; Gorgani Firouzjah, K. Comprehensive identification of multiple harmonic sources using fuzzy logic and adjusted probabilistic neural network. Neural Comput. Appl. 2019, 31, 543–556. [Google Scholar] [CrossRef]
- Tian, M.; Wang, Y.; Li, J. Comprehensive Harmonic Responsibility Calculation Based on Different Weighting Methods. Energies 2019, 12, 4449. [Google Scholar] [CrossRef]
- Cataliotti, A.; Cosentino, V. A New Measurement Method for the Detection of Harmonic Sources in Power Systems Based on the Approach of the IEEE Std. 1459–2000. IEEE Trans. Power Deliv. 2010, 25, 332–340. [Google Scholar] [CrossRef]
- Stevanović, D.; Petković, P. A single-point method based on distortion power for the detection of harmonic sources in a power system. Metrol. Meas. Syst. 2014, 21, 3–14. [Google Scholar] [CrossRef]
- Karimzadeh, F.; Esmaeili, S.; Hosseinian, S.H. Method for determining utility and consumer harmonic contributions based on complex independent component analysis. IET Gener. Transm. Distrib. 2016, 10, 526–534. [Google Scholar] [CrossRef]
- Mohamed, A. Identification of Multiple Harmonic Sources in Power Systems Using Independent Component Analysis and Mutual Information. 2010. Available online: https://www.academia.edu/14323279/Identification_of_multiple_harmonic_sources_in_power_systems_using_independent_component_analysis_and_mutual_information (accessed on 10 December 2023).
- Du, Y.; Yang, H.; Ma, X. Multi-Harmonic Source Localization Based on Sparse Component Analysis and Minimum Conditional Entropy. Entropy 2020, 22, 65. [Google Scholar] [CrossRef] [PubMed]
- Saxena, D.; Bhaumik, S.; Singh, S.N. Identification of Multiple Harmonic Sources in Power System Using Optimally Placed Voltage Measurement Devices. IEEE Trans. Ind. Electron. 2014, 61, 2483–2492. [Google Scholar] [CrossRef]
- D’Antona, G.; Muscas, C.; Sulis, S. State Estimation for the Localization of Harmonic Sources in Electric Distribution Systems. In Proceedings of the 2008 IEEE Instrumentation and Measurement Technology Conference, Victoria, BC, Canada, 12–15 May 2008; pp. 865–869. [Google Scholar] [CrossRef]
- Martinez, R.; Castro, P.; Arroyo, A.; Manana, M.; Galan, N.; Moreno, F.S.; Bustamante, S.; Laso, A. Techniques to Locate the Origin of Power Quality Disturbances in a Power System: A Review. Sustainability 2022, 14, 7428. [Google Scholar] [CrossRef]
- Carta, D.; Muscas, C.; Pegoraro, P.A.; Sulis, S. Identification and Estimation of Harmonic Sources Based on Compressive Sensing. IEEE Trans. Instrum. Meas. 2019, 68, 95–104. [Google Scholar] [CrossRef]
- Ujile, A.; Ding, Z. A dynamic approach to identification of multiple harmonic sources in power distribution systems. Int. J. Electr. Power Energy Syst. 2016, 81, 175–183. [Google Scholar] [CrossRef]
- Ye, G.; Xiang, Y.; Cuk, V.; Cobben, J.F.G. Harmonic disturbance location by applying Bayesian inference. Electr. Power Syst. Res. 2016, 140, 886–894. [Google Scholar] [CrossRef]
- Sinha, P.; Goswami, S.K.; Nath, S. Wavelet-based technique for identification of harmonic source in distribution system. Int. Trans. Electr. Energy Syst. 2016, 26, 2552–2572. [Google Scholar] [CrossRef]
- Hamzah, N.; Mohamad, A.; Hussain, A. A New Method for Separating Utility and Customer Harmonic Contribution at The Point of Common Coupling. Int. Energy J. 2005, 6. Available online: http://www.rericjournal.ait.ac.th/index.php/reric/article/view/109 (accessed on 10 December 2023).
- Shojaie, M.; Mokhtari, H. A method for determination of harmonics responsibilities at the point of common coupling using data correlation analysis. IET Gener. Transm. Distrib. 2014, 8, 142–150. [Google Scholar] [CrossRef]
- de Matos, E.O.; Mota Soares, T.; Bezerra, U.H.; Tostes, M.E.; Manito, A.R.A.; Costa, B.C., Jr. Using linear and non-parametric regression models to describe the contribution of non-linear loads on the voltage harmonic distortions in the electrical grid. IET Gener. Transm. Distrib. 2016, 10, 1825–1832. [Google Scholar] [CrossRef]
- Melo, I.D.; Pereira, J.L.R.; Variz, A.M.; Garcia, P.A.N. Harmonic state estimation for distribution networks using phasor measurement units. Electr. Power Syst. Res. 2017, 147, 133–144. [Google Scholar] [CrossRef]
- Bentley, E.C.; Putrus, G.A.; McDonald, S.; Minns, P. Power quality disturbance source identification using self-organising maps. IET Gener. Transm. Distrib. 2010, 4, 1188–1196. [Google Scholar] [CrossRef]
- Sun, Y.; Xie, X.; Li, P. Unbalanced source identification at the point of evaluation in the distribution power systems. Int. Trans. Electr. Energy Syst. 2018, 28, e2460. [Google Scholar] [CrossRef]
- An Adjustment Scheme of Rewarding and Penalizing Electricity Charges Considering Unbalanced Responsibility–ProQuest. Available online: https://www.proquest.com/openview/fbedac51bae3ebfcecf61060517b0642/1?pq-origsite=gscholar&cbl=406310 (accessed on 10 December 2023).
- Herrera, R.S.; Vázquez, J.R. Identification of unbalanced loads in electric power systems. Int. Trans. Electr. Energy Syst. 2014, 24, 1232–1243. [Google Scholar] [CrossRef]
- Pérez Vallés, A.; Salmerón Revuelta, P. A new distributed measurement index for the identification of harmonic distortion and/or unbalance sources based on the IEEE Std. 1459 framework. Electr. Power Syst. Res. 2019, 172, 96–104. [Google Scholar] [CrossRef]
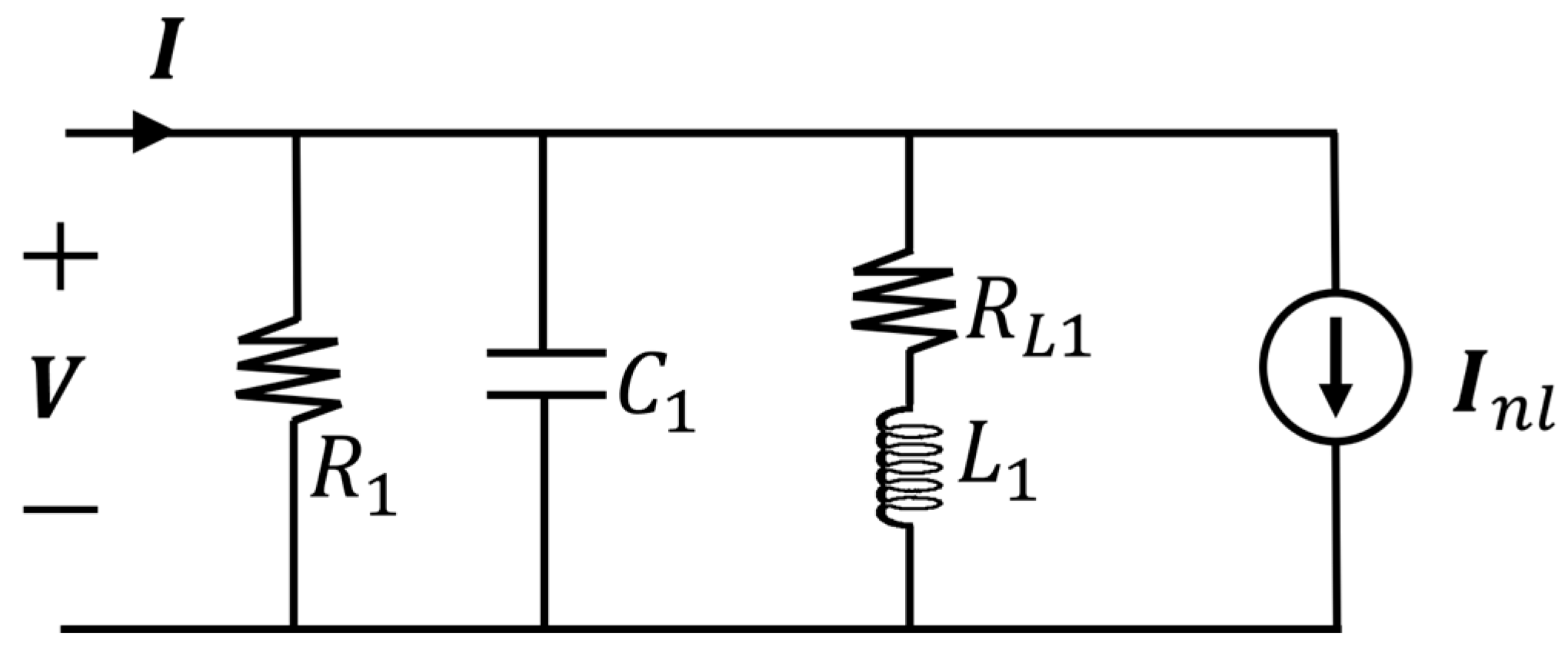
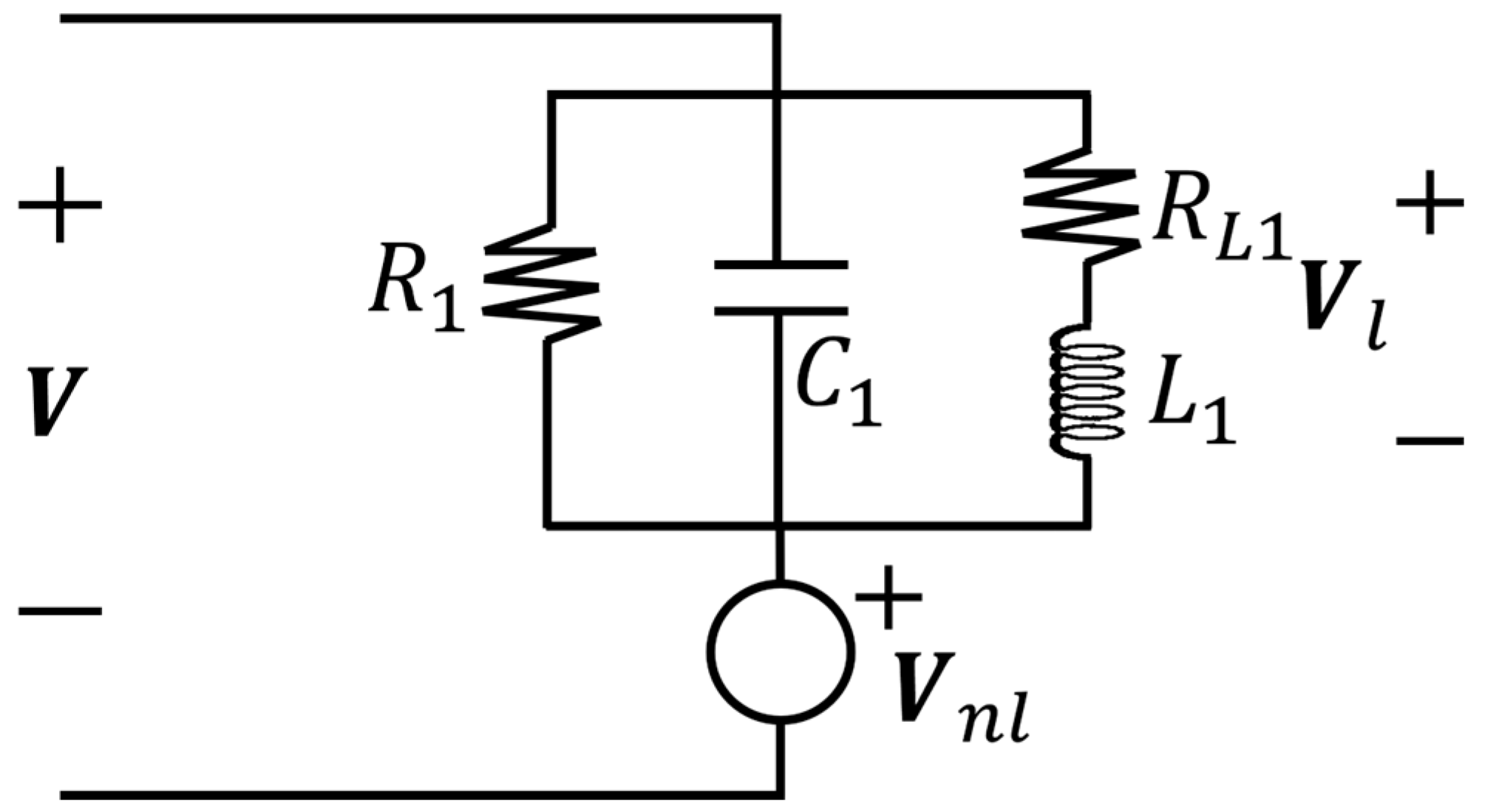
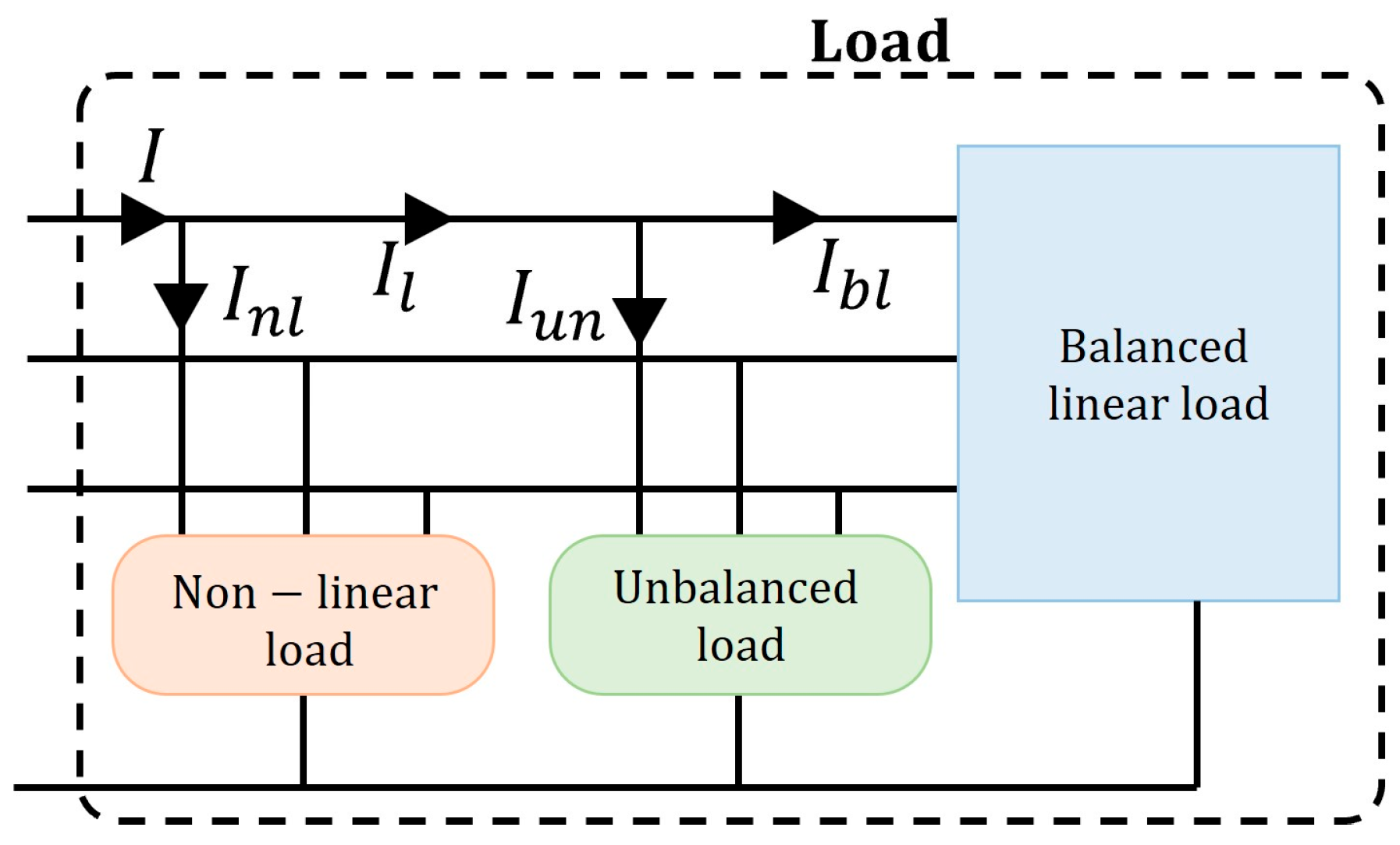

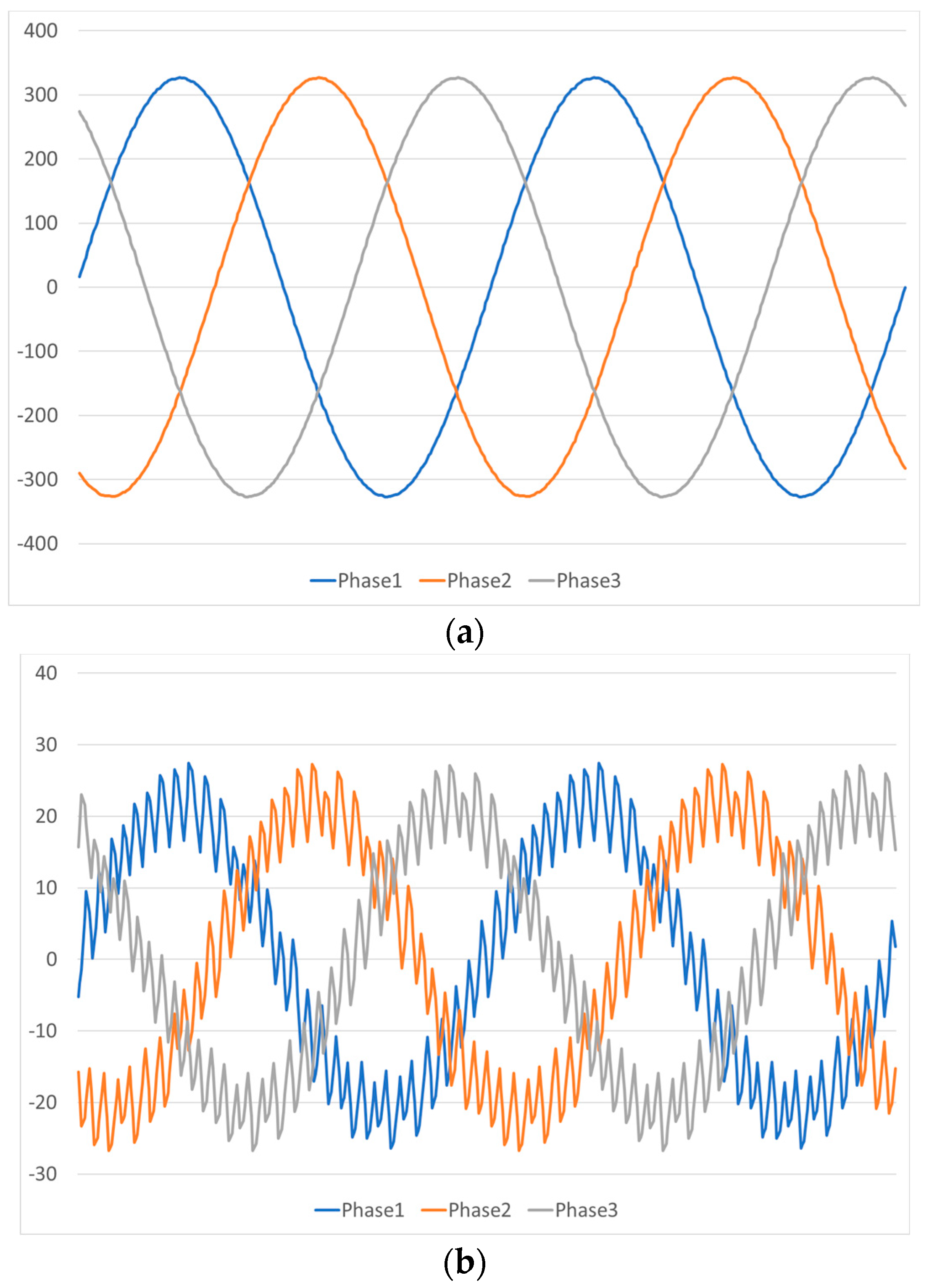


| Search | Keywords |
|---|---|
| 1 | Power quality & distortion sources identification & distortion sources detection |
| 2 | Power quality & harmonic sources identification & distortion sources detection |
| 3 | Power quality & imbalance sources identification & imbalance sources detection |
| 4 | Power quality & unbalance sources identification & unbalance sources detection |
| Distortion/Imbalance Identification | Method | Papers |
|---|---|---|
| Distortion | Norton equivalent | [28,29,30,31,32,33,34,35] |
| Measurer optimal location | [36,37,38,39,40,41] | |
| Current decomposition | [42,43,44] | |
| Active power direction | [45,46,47] | |
| Artificial intelligence | [48,49,50] | |
| IEEE Standard | [51,52] | |
| Independent component analysis | [53,54,55] | |
| Particle swarm | [35,56,57] | |
| Review | [14,15,58] | |
| State estimation | [59,60,61] | |
| Reactive power direction | [62,63] | |
| Data correlation | [64] | |
| Different weighting methods | [50] | |
| Power complex harmonic | [58] | |
| Regression method | [65] | |
| Safety barrier interior point method | [66] | |
| Self-organizing maps | [67] | |
| V/I ratio | [44] | |
| Imbalance | Unbalance factor | [68] |
| IEEE Standard | [69] | |
| Both | Current decomposition | [42,70] |
| IEEE Standard | [71] |
| Equipment | Acronym | Description | Values |
|---|---|---|---|
| 1 | DGM | Inverter injecting power to the PCC | |
| 2 | VR | Three regulators connected in star with inductive impedance on the right side (unbalanced) | Phase 1: R = 10 Ω, L = 0.1 H Phase 1: R = 12 Ω, L = 0.12 H Phase 3: R = 8 Ω, L = 0.08 H |
| 3 | DCVS | Three-phase rectifier with a capacitive impedance on the DC side | R = 100 Ω C = 0.2 µF |
| 4 | BRC | Three balanced capacitive loads (a resistor in parallel to a capacitor) connected in star | R = 26.67 Ω C = 1.19 mF |
| 5 | BRI | Three balanced inductive loads (a resistor in series to an inductance) connected in star | R = 6.67 Ω L = 21.22 mH |
| 6 | UR | Three unbalanced resistors connected in star | Phase 1: R = 80 Ω Phase 1: R = 64 Ω Phase 3: R = 160 Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Herrera, R.; Clavijo-Camacho, J.; Gómez-Ruiz, G.; Vázquez, J.R. Identification of Both Distortion and Imbalance Sources in Electrical Installations: A Comparative Assessment. Energies 2024, 17, 2536. https://doi.org/10.3390/en17112536
Sánchez-Herrera R, Clavijo-Camacho J, Gómez-Ruiz G, Vázquez JR. Identification of Both Distortion and Imbalance Sources in Electrical Installations: A Comparative Assessment. Energies. 2024; 17(11):2536. https://doi.org/10.3390/en17112536
Chicago/Turabian StyleSánchez-Herrera, Reyes, Jesús Clavijo-Camacho, Gabriel Gómez-Ruiz, and Jesús R. Vázquez. 2024. "Identification of Both Distortion and Imbalance Sources in Electrical Installations: A Comparative Assessment" Energies 17, no. 11: 2536. https://doi.org/10.3390/en17112536
APA StyleSánchez-Herrera, R., Clavijo-Camacho, J., Gómez-Ruiz, G., & Vázquez, J. R. (2024). Identification of Both Distortion and Imbalance Sources in Electrical Installations: A Comparative Assessment. Energies, 17(11), 2536. https://doi.org/10.3390/en17112536








