Improvement of Economic Integration of Renewable Energy Resources through Incentive-Based Demand Response Programs
Abstract
:1. Introduction
2. Methodology
2.1. Ellipsoidal Uncertainty
2.2. Proposed Robust IBDR
3. Test Cases and Discussion
3.1. WECC System Information
3.2. RER Expansion in WECC
3.2.1. Impact of RER Expansion on Market Price
- ■
- Condition 1: High load and low RER generation, which often happens in summertime around the peak hours. It is predictable that LMP will be significantly high during these periods. This condition may also occur during summer nights when there is low wind, while the need for electricity to control the temperature of business and domestic buildings is considerable.
- ■
- Condition 2: Low load and high RER generation that can occur during spring and fall when the weather is moderate. Therefore, the residential load is lower, and, at the same time, wind power is abundant. As RERs are supposed to generate as much as possible, the LMP reduces. In some cases, a negative LMP is allowed to be utilized for increasing the demand.
- ■
- Condition 3: The load and RER generation are both moderate. It is possible that this condition occurs at any time of year. However, it is more probable to occur during winter. In some areas, the average LMP increases after RER expansion, while in some other areas, the average LMP decreases. Therefore, a specific prediction towards LMP is impossible and it can be determined only through comprehensive analysis.
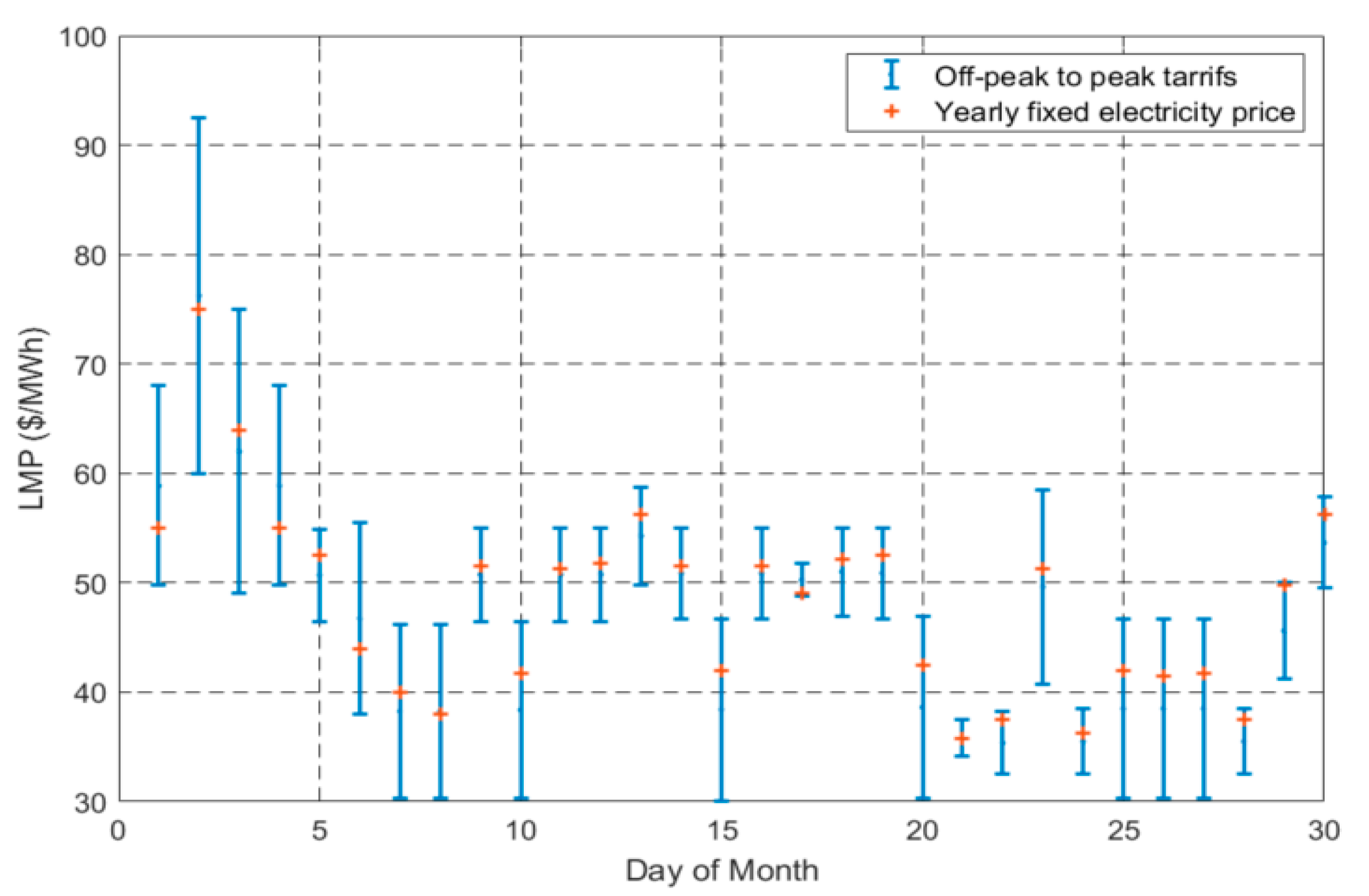
3.2.2. Effects of the Errors in Wind Forecast on the Electricity Price
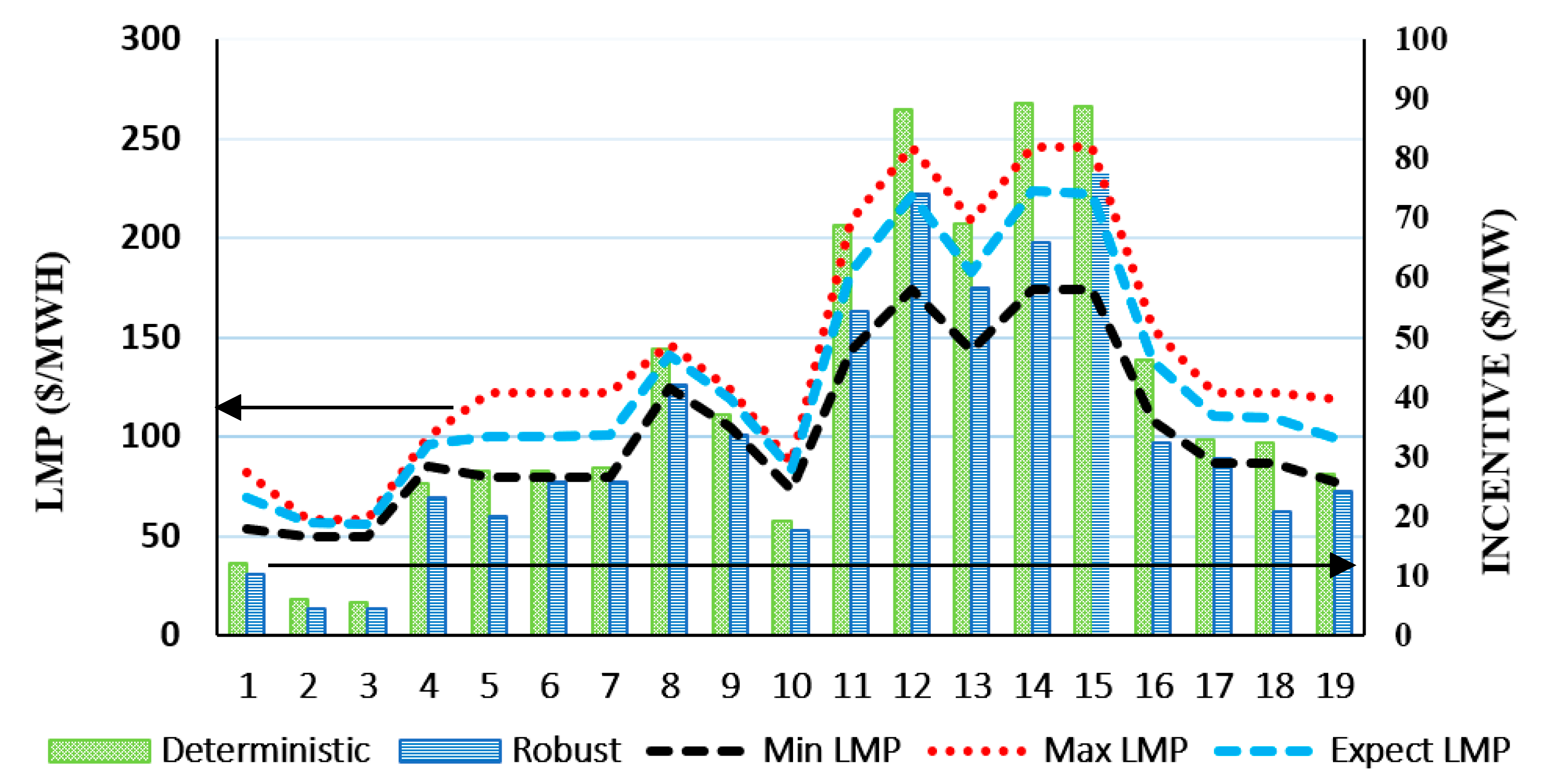
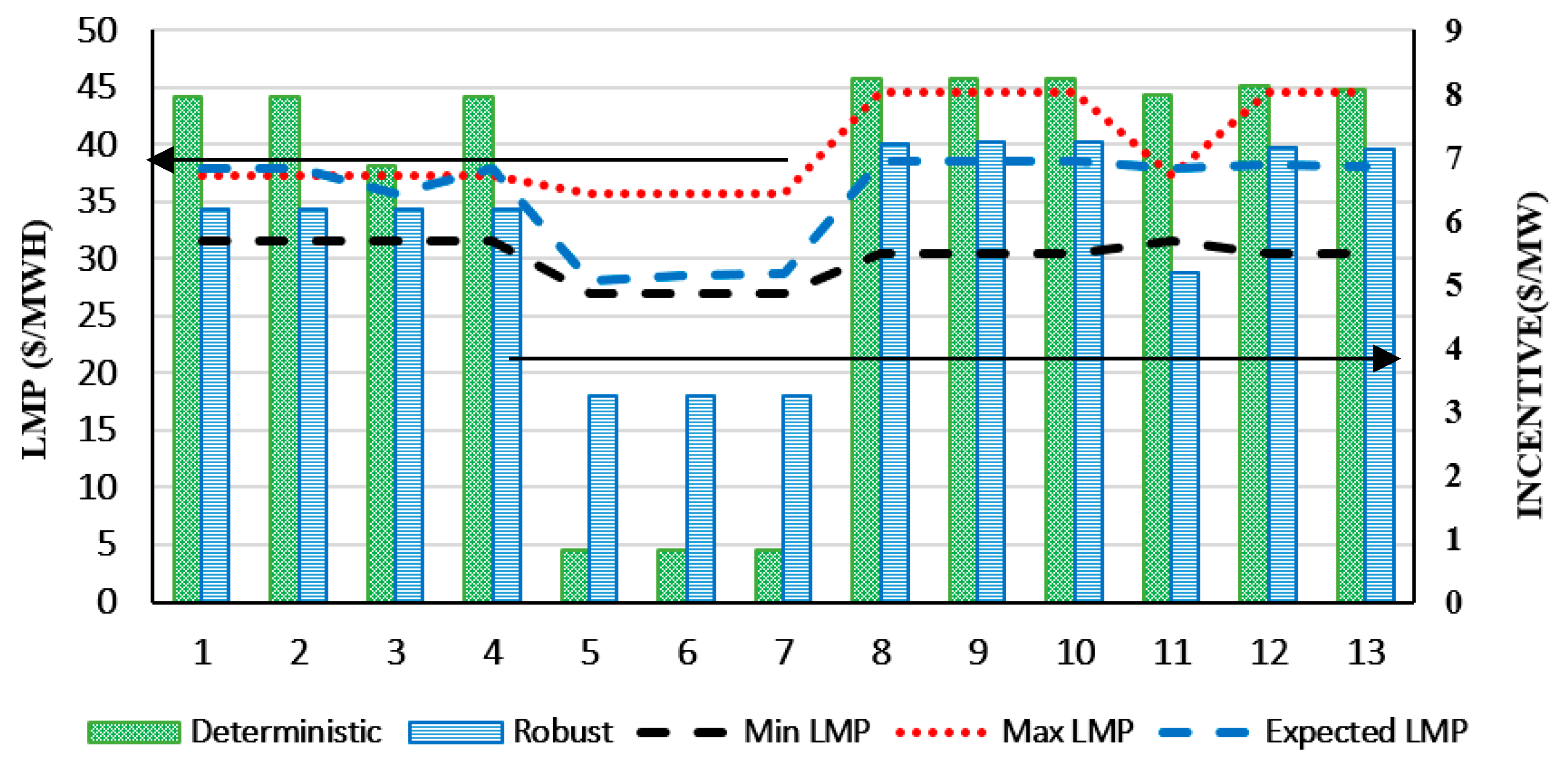
3.2.3. Comparison of Deterministic and Robust Program
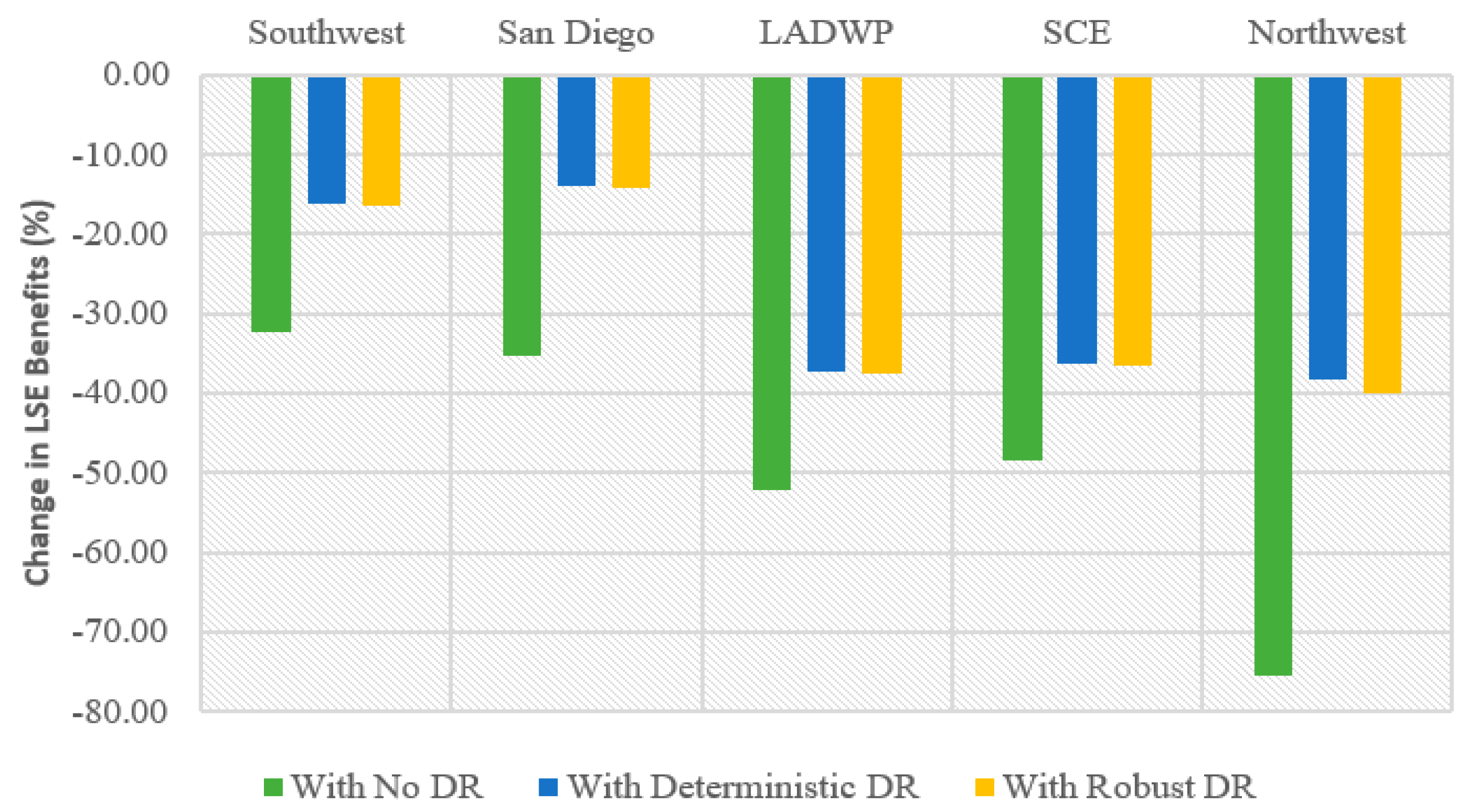
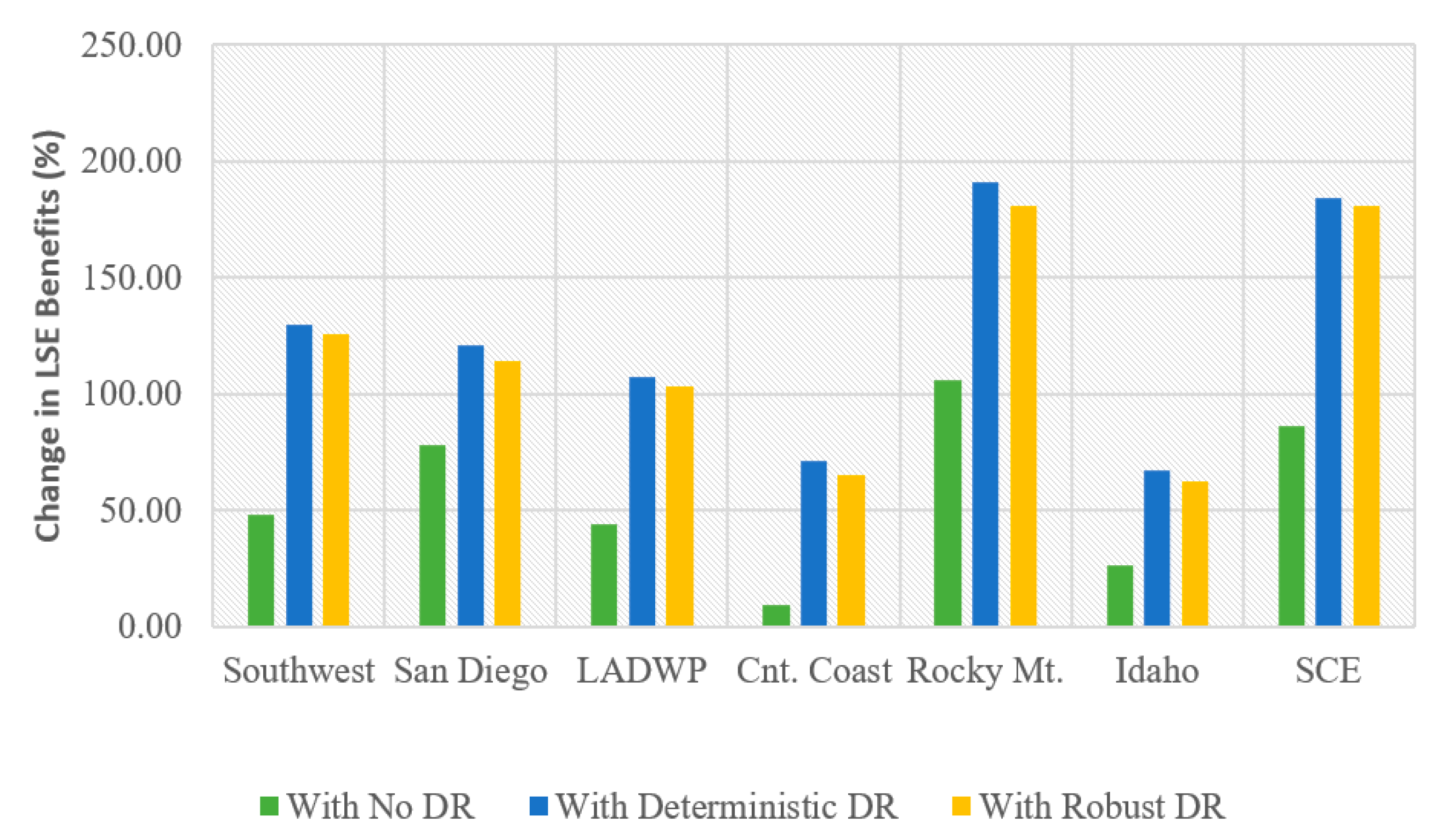
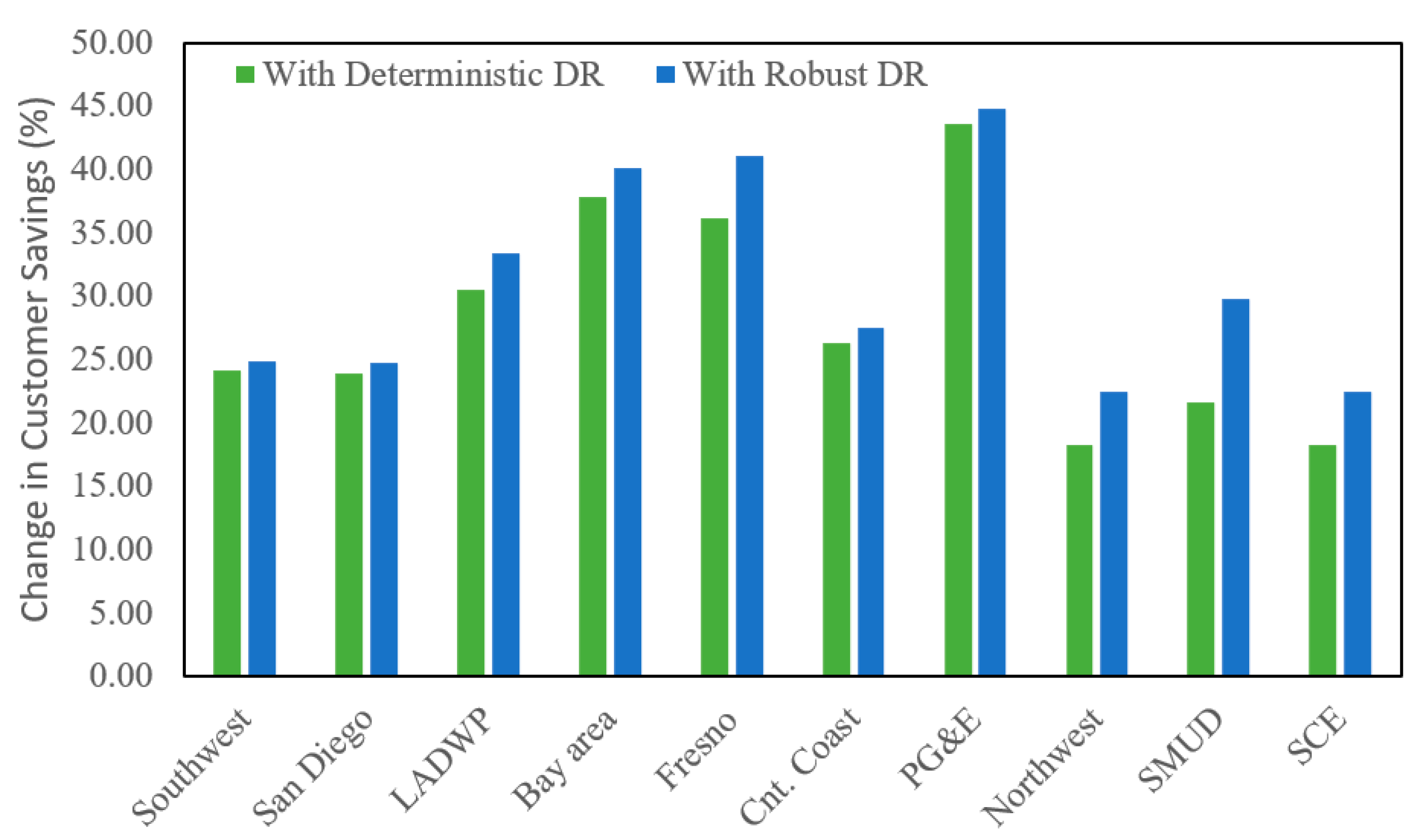
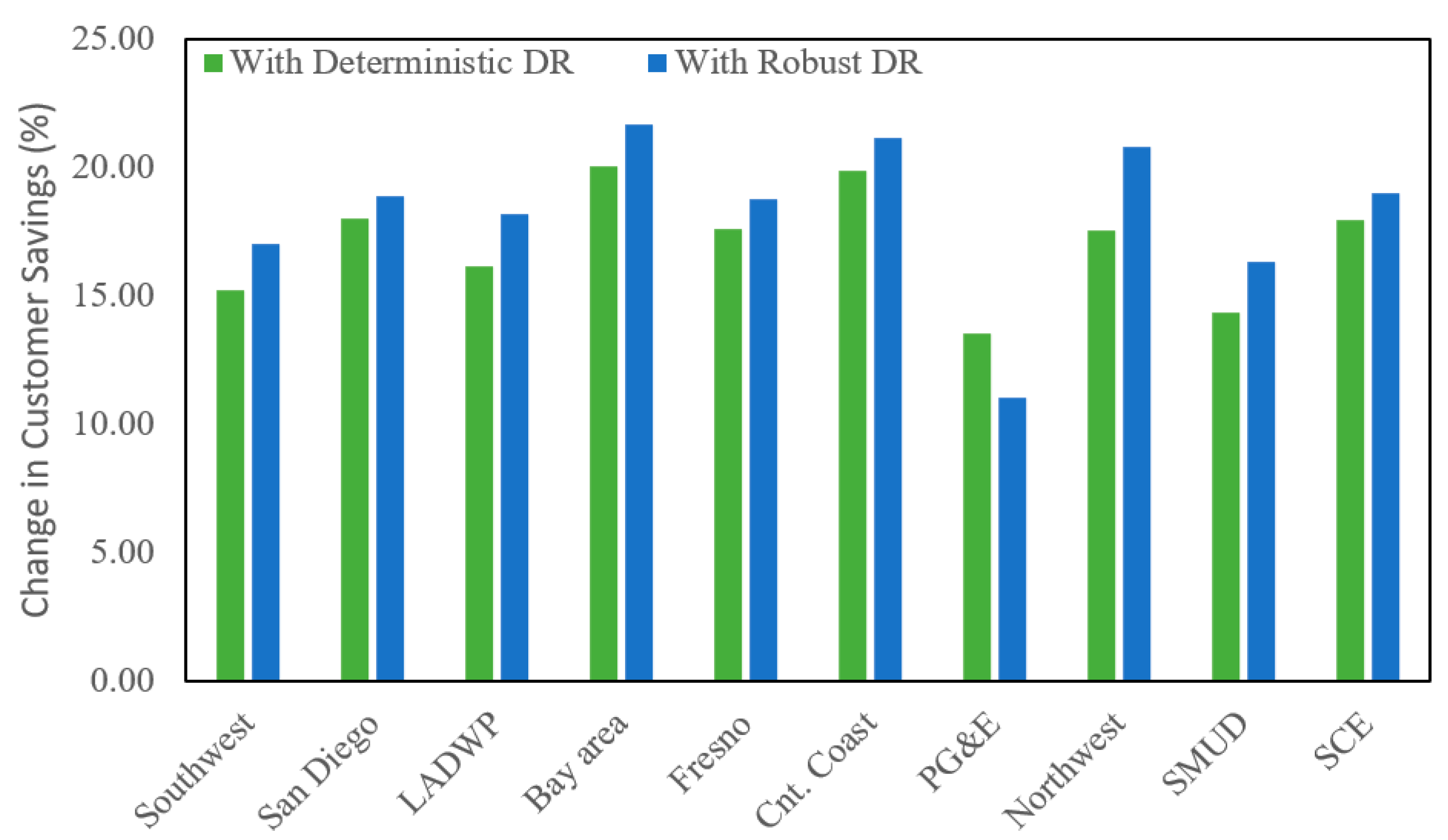
3.2.4. The Benefit of IBDR for Participants
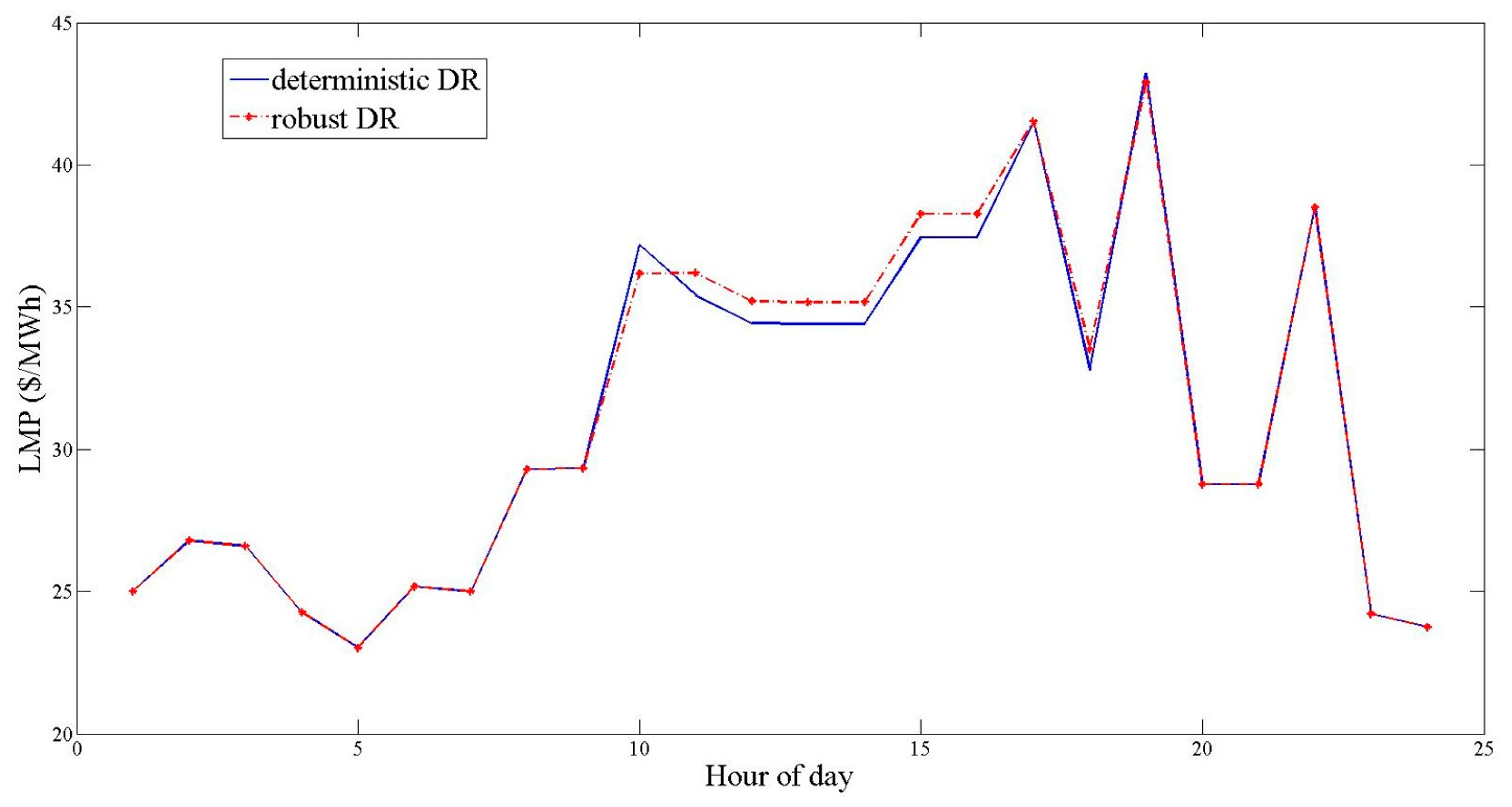
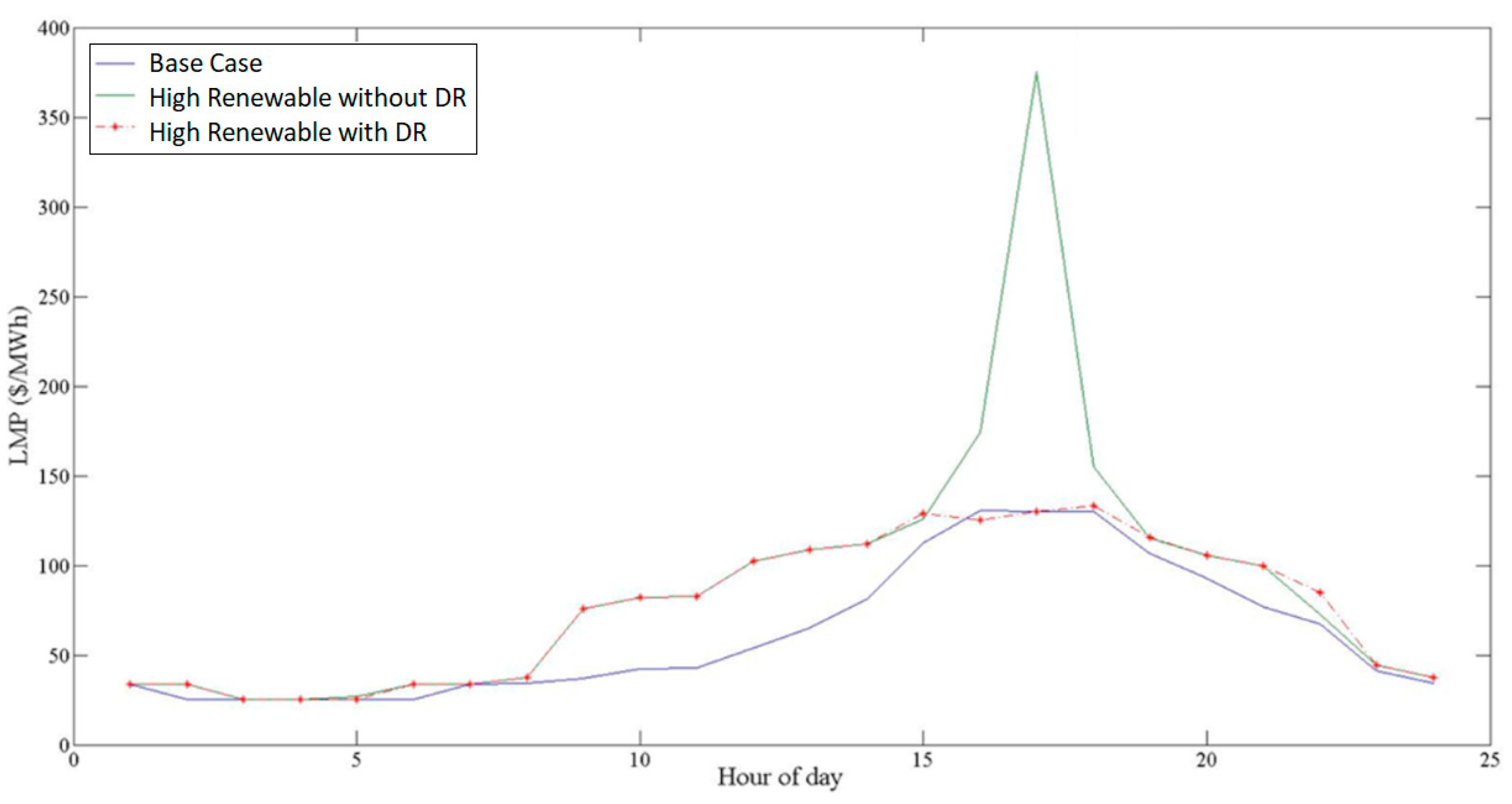
3.2.5. Effects of the Proposed IBDR on Electricity Price
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wigley, T.M.L. Coal to gas: The influence of methane leakage. Clim. Chang. 2011, 108, 601–608. [Google Scholar] [CrossRef]
- McKechnie, J.; Colombo, S.; Chen, J.; Mabee, W.; MacLean, H.L. Forest Bioenergy or Forest Carbon? Assessing Trade-Offs in Greenhouse Gas Mitigation with Wood-Based Fuels. Environ. Sci. Technol. 2011, 45, 789–795. [Google Scholar] [CrossRef]
- Li, X.; Qian, J.; Yang, C.; Chen, B.; Wang, X.; Jiang, Z. New Power System Planning and Evolution Path with Multi-Flexibility Resource Coordination. Energies 2024, 17, 273. [Google Scholar] [CrossRef]
- The White House. Fact Sheet: President Biden Sets 2030 Greenhouse Gas Pollution Reduction Target Aimed at Creating Good-Paying Union Jobs and Securing U.S. Leadership on Clean Energy Technologies; The White House: Washington, DC, USA, 2021.
- van Kooten, G.C. Wind power: The economic impact of intermittency. Lett. Spat. Resour. Sci. 2010, 3, 1–17. [Google Scholar] [CrossRef]
- Chen, H.; Pilong, C.; Rocha-Garrido, P.; Frogg, D.; Jayachandran, M.; Manno, D.; Sexauer, J.; Callagha, C.; Dropkin, R.; Mulhern, J.; et al. Grid Resilience With High Renewable Penetration: A PJM Approach. IEEE Trans. Sustain. Energy 2023, 14, 1169–1177. [Google Scholar] [CrossRef]
- Reulein, D.; Tiwari, S.; Hestvik, B.; Kvannli, A.; Pinel, D.; Andresen, C.A.; Farahmand, H. Large-scale Offshore Wind Development and Decarbonization Pathways of the Norwegian Energy System. In Proceedings of the 2023 19th International Conference on the European Energy Market (EEM), Lappeenranta, Finland, 6–8 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Akish, E.; Capotondi, A.; Compo, G.P. Evaluation and Bias Correction of the ERA5 Reanalysis over the United States for Wind and Solar Energy Applications. Energies 2024, 17, 1667. [Google Scholar] [CrossRef]
- Callaway, D.S. Tapping the energy storage potential in electric loads to deliver load following and regulation, with application to wind energy. Energy Convers. Manag. 2009, 50, 1389–1400. [Google Scholar] [CrossRef]
- Callaway, D.S.; Hiskens, I.A. Achieving Controllability of Electric Loads. Proc. IEEE 2011, 99, 184–199. [Google Scholar] [CrossRef]
- Lal, D.C.; Vineeth, V.; Devesh, S.; Chakrabarti, S.; Singh, S.N.; Ankush, S.; Alamgir, H.M. An improved decentralized scheme for incentive-based demand response from residential customers. Energy 2023, 284, 128568. [Google Scholar] [CrossRef]
- Gupta, S.K.; Ghose, T.; Chatterjee, K. Coordinated control of Incentive-Based Demand Response Program and BESS for frequency regulation in low inertia isolated grid. Electr. Power Syst. Res. 2022, 209, 108037. [Google Scholar] [CrossRef]
- Sarker, E.; Seyedmahmoudian, M.; Jamei, E.; Horan, B.; Stojcevski, A. Optimal management of home loads with renewable energy integration and demand response strategy. Energy 2020, 210, 118602. [Google Scholar] [CrossRef]
- Zheng, S.; Sun, Y.; Li, B.; Qi, B.; Shi, K.; Li, Y.; Tu, X. Incentive-Based Integrated Demand Response for Multiple Energy Carriers Considering Behavioral Coupling Effect of Consumers. IEEE Trans. Smart Grid 2020, 11, 3231–3245. [Google Scholar] [CrossRef]
- Yaghmaee, M.H. Incentive-Based Demand Response Program for Blockchain Network. IEEE Syst. J. 2024, 18, 134–145. [Google Scholar] [CrossRef]
- International Energy Agency IEA. Net Zero by 2050, A Roadmap for the Global Energy Sector. October 2021. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 1 April 2024).
- Halder, A.; Geng, X.; Kumar, P.R.; Xie, L. Architecture and Algorithms for Privacy Preserving Thermal Inertial Load Management by a Load Serving Entity. IEEE Trans. Power Syst. 2017, 32, 3275–3286. [Google Scholar] [CrossRef]
- Yao, L.; Teo, J.C.; Wang, C.-H. Resident-Centric Distributed Community Energy Management System. IEEE Trans. Sustain. Energy 2023, 14, 849–863. [Google Scholar] [CrossRef]
- Pandey, V.C.; Gupta, N.; Niazi, K.R.; Swarnkar, A.; Rawat, T.; Konstantinou, C. A Bi-Level Decision Framework for Incentive-Based Demand Response in Distribution Systems. IEEE Trans. Energy Mark. Policy Regul. 2023, 1, 211–225. [Google Scholar] [CrossRef]
- Ruiz, P.A.; Philbrick, C.R.; Sauer, P.W. Wind power day-ahead uncertainty management through stochastic unit commitment policies. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–9. [Google Scholar] [CrossRef]
- Sioshansi, R.; Short, W. Evaluating the Impacts of Real-Time Pricing on the Usage of Wind Generation. IEEE Trans. Power Syst. 2009, 24, 516–524. [Google Scholar] [CrossRef]
- Constantinescu, E.M.; Zavala, V.M.; Rocklin, M.; Lee, S.; Anitescu, M. A Computational Framework for Uncertainty Quantification and Stochastic Optimization in Unit Commitment With Wind Power Generation. IEEE Trans. Power Syst. 2011, 26, 431–441. [Google Scholar] [CrossRef]
- Mena, R.; Catalán, C.; Viveros, P.; Zio, E. A Two-Stage Stochastic Unit Commitment Model for Wind-integrated Power Systems Flexibility Assessment. In Proceedings of the 2022 17th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Manchester, UK, 12–15 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, T.; Zhang, H.; Zeng, Z.; Siano, P.; Shahidehpour, M. A Two-Stage Stochastic Unit Commitment With Mixed-Integer Recourses for Nuclear Power Plants to Accommodate Renewable Energy. IEEE Trans. Sustain. Energy 2024, 15, 859–870. [Google Scholar] [CrossRef]
- Danish, M.; Ashraf, I.; Kirmani, S. Demand Side Management in Smart Home using Grey Wolf Optimization. In Proceedings of the 2023 International Conference in Advances in Power, Signal, and Information Technology (APSIT), Bhubaneswar, India, 9–11 June 2023; pp. 560–565. [Google Scholar] [CrossRef]
- Borenstein, S.; Holland, S. On the Efficiency of Competitive Electricity Markets with Time-Invariant Retail Prices. RAND J. Econ. 2005, 36, 469–493. [Google Scholar]
- Joskow, P.; Tirole, J. Retail electricity competition. RAND J. Econ. 2006, 37, 799–815. [Google Scholar] [CrossRef]
- Joskow, P.; Tirole, J. Reliability and Competitive Electricity Markets. Natl. Bur. Econ. Res. 2004, 38, 60–84. [Google Scholar]
- Sioshansi, R. OR Forum—Modeling the Impacts of Electricity Tariffs on Plug-In Hybrid Electric Vehicle Charging, Costs, and Emissions. Oper. Res. 2012, 60, 506–516. [Google Scholar] [CrossRef]
- Alfaverh, F.; Denai, M.; Sun, Y. A Dynamic Peer-to-Peer Electricity Market Model for a Community Microgrid With Price-Based Demand Response. IEEE Trans. Smart Grid 2023, 14, 3976–3991. [Google Scholar] [CrossRef]
- Schweppe, F.C. (Ed.) Spot pricing of electricity. In The Kluwer International Series in Engineering and Computer Science; Power Electronics & Power Systems, No. SECS 46; Kluwer Academic: Boston, MA, USA, 1988. [Google Scholar]
- Borenstein, S.; Jaske, M.; Rosenfeld, A. Dynamic Pricing, Advanced Metering, and Demand Response in Electricity Markets; UC Berkeley, Center for the Study of Energy Markets: Berkeley, CA, USA, 2002. [Google Scholar]
- Hirst, E.; Kirby, B. Ancillary Service Details: Dynamic Scheduling; ORN/CON-438; Oak Ridge National Laboratory: Knoxville, TN, USA, 1997; Available online: https://digital.library.unt.edu/ark:/67531/metadc699085/m2/1/high_res_d/631228.pdf (accessed on 1 April 2024).
- Chen, S.; Cheng, R.S. Operating Reserves Provision From Residential Users Through Load Aggregators in Smart Grid: A Game Theoretic Approach. IEEE Trans. Smart Grid 2019, 10, 1588–1598. [Google Scholar] [CrossRef]
- Wang, H.; Jia, Y.; Shi, M.; Xie, P.; Lai, C.S.; Li, K. A Hybrid Incentive Program for Managing Electric Vehicle Charging Flexibility. IEEE Trans. Smart Grid 2023, 14, 476–488. [Google Scholar] [CrossRef]
- Mohajeryami, S.; Doostan, M.; Asadinejad, A.; Schwarz, P. Error Analysis of Customer Baseline Load (CBL) Calculation Methods for Residential Customers. IEEE Trans. Ind. Appl. 2017, 53, 5–14. [Google Scholar] [CrossRef]
- Asadinejad, A.; Tomsovic, K. Optimal use of incentive and price based demand response to reduce costs and price volatility. Electr. Power Syst. Res. 2017, 144, 215–223. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust solutions of Linear Programming problems contaminated with uncertain data. Math. Program. 2000, 88, 411–424. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Zhang, B.; Wang, B. Robust Look-Ahead Power Dispatch With Adjustable Conservativeness Accommodating Significant Wind Power Integration. IEEE Trans. Sustain. Energy 2015, 6, 781–790. [Google Scholar] [CrossRef]
- Asadinejad, A.; Tomsovic, K.; Varzaneh, M.G. Examination of incentive based demand response in western connection reduced model. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Price, J.E.; Goodin, J. Reduced network modeling of WECC as a market design prototype. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- 20% Wind Energy by 2030 Increasing Wind Energy’s Contribution to U.S. Electricity Supply. U.S. Department of Energy; DOE/GO-102008-2578; December 2008. Available online: https://www.nrel.gov/docs/fy09osti/42864.pdf (accessed on 1 April 2024).
- Asadinejad, A. Electricity Market Designs for Demand Response from Residential Customers; University of Tennessee: Knoxville, TN, USA, 2017; Available online: https://trace.tennessee.edu/utk_graddiss/4378/ (accessed on 1 April 2024).
- Hamidi, R.J.; Bhadra, A.B. Protection and Monitoring of Digital Energy Systems Operation. In Energy Systems Transition: Digitalization, Decarbonization, Decentralization and Democratization; Vahidinasab, V., Mohammadi-Ivatloo, B., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 131–162. [Google Scholar] [CrossRef]
- You, X.; Wu, H.; Zhang, J.; Jin, S.; Ding, Y.; Siano, P. Optimal day-ahead and intra-day scheduling of energy and operating reserve considering fluctuating wind power. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Shandong Electric Power Research Institute; Li, N.; Han, Y.; Lin, J.; Pan, Z.; Hu, B. Day-ahead to intraday optimization model for power systems with reliability constraints. In Proceedings of the 2023 IEEE Sustainable Power and Energy Conference (iSPEC), Chongqing, China, 28–30 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Shi, Q.; Chen, C.-F.; Mammoli, A.; Li, F. Estimating the Profile of Incentive-Based Demand Response (IBDR) by Integrating Technical Models and Social-Behavioral Factors. IEEE Trans. Smart Grid 2020, 11, 171–183. [Google Scholar] [CrossRef]
- Mohammadi, J.; Mosadeghi, M.; Rahimi-Kian, A.; Ghazizadeh, M.S. Impacts of load reduction offers on load profile. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Panapakidis, I.P.; Bouhouras, A.S.; Christoforidis, G.C. Utilizing Short-Term Load Forecasts in the Assessment of Demand Response Programs. In Proceedings of the 2019 8th International Conference on Modern Power Systems (MPS), Cluj Napoca, Romania, 21–23 May 2019; pp. 1–6. [Google Scholar] [CrossRef]



| Generation Type | Number of Units | Generation Type | Number of Units |
|---|---|---|---|
| Solar | 4 | Nuclear | 4 |
| wind | 16 | Hydropower | 27 |
| Gas-fired | 50 | Geothermal | 6 |
| Coal-fired | 17 | Biomass | 3 |
| Area | Average Case ($) | Worst Case ($) | Missed Case ($) | Area | Average Case ($) | Worst Case ($) | Missed Case ($) |
|---|---|---|---|---|---|---|---|
| July | February | ||||||
| Fresno | −9283 | 3480 | 2511 | Fresno | −67,225 | 7434 | 5246 |
| Nevada | −9387 | 5753 | 6038 | Nevada | −58,673 | 11,492 | 10,754 |
| San Diego | −10,022 | 16,902 | 6362 | San Diego | −18,327 | 4410 | 2519 |
| Idaho | −13,147 | 5130 | 4559 | Idaho | −209,917 | 15,818 | 14,758 |
| Bay area | −20,152 | 6684 | 2939 | Bay area | −193,073 | 23,863 | 20,679 |
| SMUD | −27,720 | 8722 | 11,583 | SMUD | −196,412 | 19,161 | 12,026 |
| Rocky Mt. | −43,850 | 8677 | 16,102 | Rockey Mt. | −269,841 | 57,312 | 82,120 |
| Southwest | −109,953 | 55,277 | 32,276 | Southwest | −160,336 | 51,141 | 47,221 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jalilzadeh Hamidi, R.; Asadinejad, A. Improvement of Economic Integration of Renewable Energy Resources through Incentive-Based Demand Response Programs. Energies 2024, 17, 2545. https://doi.org/10.3390/en17112545
Jalilzadeh Hamidi R, Asadinejad A. Improvement of Economic Integration of Renewable Energy Resources through Incentive-Based Demand Response Programs. Energies. 2024; 17(11):2545. https://doi.org/10.3390/en17112545
Chicago/Turabian StyleJalilzadeh Hamidi, Reza, and Ailin Asadinejad. 2024. "Improvement of Economic Integration of Renewable Energy Resources through Incentive-Based Demand Response Programs" Energies 17, no. 11: 2545. https://doi.org/10.3390/en17112545
APA StyleJalilzadeh Hamidi, R., & Asadinejad, A. (2024). Improvement of Economic Integration of Renewable Energy Resources through Incentive-Based Demand Response Programs. Energies, 17(11), 2545. https://doi.org/10.3390/en17112545





