Economic Optimal Scheduling of Integrated Energy System Considering Wind–Solar Uncertainty and Power to Gas and Carbon Capture and Storage
Abstract
:1. Introduction
- The low-carbon economy and wind-scenery consumption effect of integrated energy systems have not been adequately explored, despite the necessity of effectively quantifying wind-scenery uncertainty.
- The sensitivity analysis of the construction scale parameters of P2G-CCS equipment has yet to be studied.
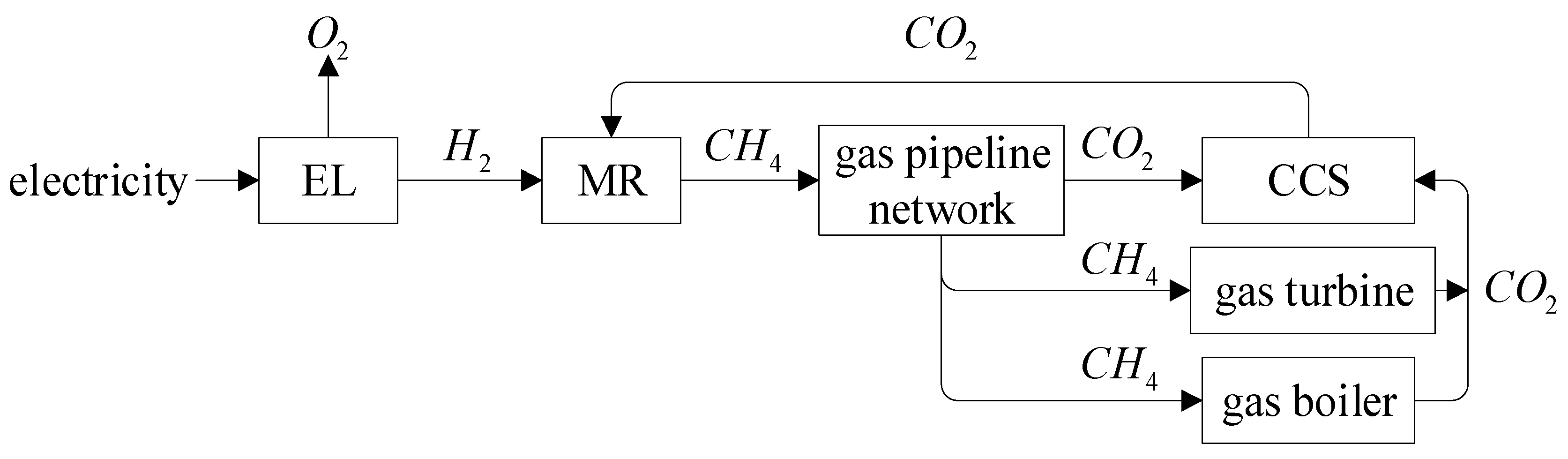
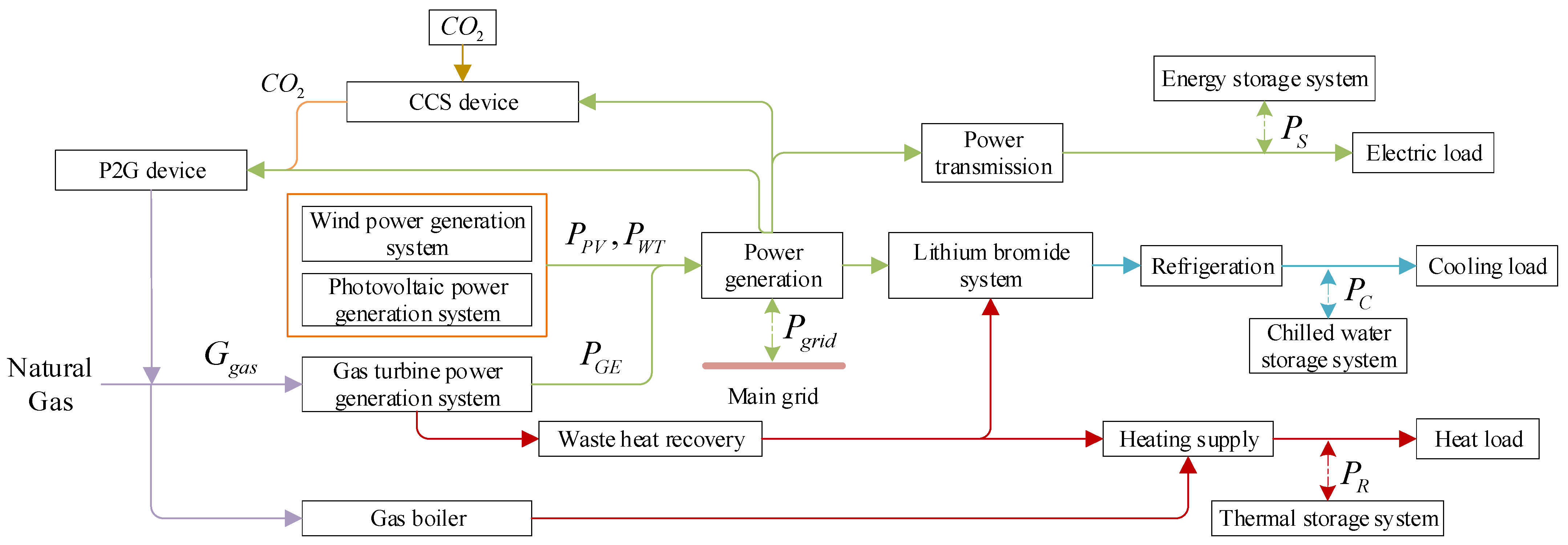
2. PIES System Architecture
3. PIES Modelling
3.1. Wind Turbine Systems
- : Actual power of the WTG.
- : Rated power of the WTG.
- : Real-time wind velocity.
- : Cut-in wind velocity of the turbine during normal operation.
- : Rated wind velocity of the turbine.
- : Maximum wind velocity of the turbine during normal operation.
- : Current moment.
3.2. Photovoltaic System
- : Actual power generated by the solar photovoltaic panel.
- : Rated power of the solar photovoltaic panel.
- : Current ambient light intensity.
- : Light intensity in the ideal environment.
- : Power temperature coefficient.
- : Surface temperature of the solar photovoltaic panel at work.
- : Surface temperature of the solar photovoltaic panel in the ideal environment.
3.3. Wind and Solar Scene Production and Weakening
- : The actual operating power of the turbine.
- : The shape factor of the turbine output.
- : The scale factor.
- : The actual operating power of the PV.
- : The tracking rate at the maximum power point.
- : The radiation area of the PV.
- : The conversion efficiency.
- : The solar incidence angle.
3.3.1. Latin Hypercube Sampling Based on Probability Distributions
3.3.2. Scene Weakening
- : The Euclidean distance.
- /: Two scenes in space.
3.4. Energy Storage Equipment
- (1)
- Accumulators’ energy storage
- /: The storage power of the battery storage equipment at t, t − 1, kW.
- /: The charging and discharging efficiency of the battery.
- /: The charging and discharging power of the storage battery at t, kW.
- /: The starting and stopping working state of the energy storage equipment.
- (2)
- Heat and cold storage equipment
- /: The stored thermal power of heat storage equipment at t, t − 1, kW.
- /: The charging and discharging efficiency of heat storage equipment.
- /: The charging and discharging power of thermal energy storage at t, kW.
- /: The starting and stopping working state of energy storage equipment.where:
- /: The stored thermal power of cold storage equipment at t, t − 1, kW.
- /: The charging and discharging efficiency of cold storage equipment.
- /: The charging and discharging power of thermal energy storage at t, kW.
- /: The starting and stopping working state of energy storage equipment.
3.5. Gas Internal Combustion Engine Systems
- : The electrical energy generated by the combustion engine, kW.
- : The flow rate of natural gas, .
- : The electrical energy conversion efficiency of the combustion engine.
- : The available waste heat generated in the process of generating electricity by the combustion engine.
- : The waste heat recovery efficiency of the combustion engine.
3.6. Lithium Bromide Absorption Refrigeration System
- : The refrigeration capacity of the lithium bromide unit.
- : The heat absorbed and consumed by the lithium bromide unit for refrigeration.
- : The conversion efficiency of the lithium bromide refrigeration unit.
3.7. The Waste Heat Recovery Device
- : The heat generated by the waste heat recovery device.
- : The heat absorbed by the waste heat recovery device from the internal combustion engine.
- : The energy recovery efficiency of the waste heat recovery device.
3.8. P2G Device
- : The natural gas flow rate produced by P2G equipment.
- : The electrical power consumed by the P2G equipment.
- : The electric-to-gas efficiency of the P2G equipment.
- : The lower heating value.
3.9. Objective Function
- : The minimum operating cost of the integrated energy system for one day.
- : The number of generated scenarios.
- : The probability of the scenario occurring.
- : The carbon emission cost under scenario .where
- : The maintenance cost of the system’s basic equipment under scenario .
- ////////: The maintenance cost factors for , , , , , , , , and energy storage units (), respectively.
- //////: The output power of each device at time .
- : The energy storage charging power at time .
- : The energy storage discharging power at time (energy storage cannot be charged and discharged simultaneously at the same time).where
- : The system construction cost of scenario .
- : The number of equipment types in the system.
- : The construction cost factor for equipment .
- : The installed capacity of equipment .where
- : The system power purchase costs of scenario .
- : The main grid tariff, which is sold to the system at time-of-day tariffs.
- : The main grid power purchase price from the system.
- : The electricity purchased by the system from the main grid.
- : The electricity sold by the system to the main grid.where
- : The cost of gas purchased by the system from the natural gas side of scenario .
- : The price of natural gas.
- : The exchange power of gas boiler at time .
- : The electrical power generated by the combustion engine at time .
- : The exchange power of P2G at time .
- /: The efficiency values of natural gas consumption in gas boilers and combustion engines, respectively.
- : The efficiency value of MR’s consumption of hydrogen to make natural gas.where
- : The wind and light abandonment costs of the system under scenario .
- : The abandonment penalty cost factor.
- : The WT and PV power generation at moment .
- : The local consumption of WT and PV energy at time .
3.10. Constraints
- (1)
- Electric power balance constraint
- : The system electrical load demand.
- : At time t, the exchange power between the integrated energy system and the main grid, where a positive value indicates the system purchasing electricity from the main grid, and a negative value indicates the system selling electricity to the main grid.
- : At time t, the sum of the output power from photovoltaic panels and wind turbines.
- (2)
- Cooling power balance constraint
- : The cooling energy produced by lithium bromide.
- : The cooling energy exchange of the energy storage system.
- : The system cooling energy demand.
- (3)
- Thermal power balance constraint
- : The thermal load demand of the system.
- (4)
- The safety constraint on power exchange of the main grid transmission lines
- : The maximum allowable power exchange of the transmission lines.
- (5)
- The constraints of the electricity storage equipment
- : The maximum charging and discharging power of the electricity storage equipment at time t.
- : The minimum charging and discharging power of the electricity storage equipment at time t.
- : The maximum number of charge and discharge cycles allowed for the energy storage equipment within one day.
- : The installed capacity of the electricity storage system equipment, kWh.
- : The minimum state of charge threshold for the energy storage system.
- : The maximum state of charge threshold for the energy storage system.
- (6)
- The constraints of the thermal storage equipment
- : At time t, the maximum charging and discharging cooling power of the thermal energy storage equipment.
- : At time t, the minimum charging and discharging cooling power of the thermal energy storage equipment.
- : The maximum charging and discharging cycles allowed for thermal energy storage equipment within one day.
- : The installed capacity of the cold energy storage system equipment, kWh.
- : The minimum capacity state threshold of the energy storage system.
- : The maximum capacity state threshold of the energy storage system.
- (7)
- Thermal energy storage device operating power constraint
- : At time t, the maximum charging and discharging heat power of the thermal energy storage equipment.
- : At time t, the minimum charging and discharging heat power of the thermal energy storage equipment.
- : The maximum number of heat charge and discharge cycles allowed for the thermal storage equipment within one day.
- : The installed capacity of the thermal energy storage system equipment, kWh.
- : The minimum capacity state threshold of the energy storage system.
- : The maximum capacity state threshold of the energy storage system.
- (8)
- The operational power constraints of the internal combustion engine equipment
- : The maximum operating power of the gas engine.
- : The minimum operating power of the gas engine.
- : The maximum ramping-up power of the gas engine unit.
- : The maximum ramping-down power of the gas engine unit [34].
- (9)
- Lithium bromide equipment operating power constraint
- : The maximum operating power of the lithium bromide system.
- : The minimum operating power of the lithium bromide system.
- (10)
- Power to gas (P2G) equipment operating power constraint
- : The maximum operating power allowed for P2G equipment.
3.11. Stepped Carbon Trading Mechanism
- (1)
- Carbon emission calculation
- : The actual carbon emission of the equipment.
- ////: The carbon emission coefficients of power grid purchase, wind and solar power generation, gas turbine, gas boiler and energy storage, respectively.
- (2)
- Carbon quota calculation
- : The carbon emission quota of equipment.
- ////: Initial carbon emission coefficient of power grid purchase, wind and solar power generation, gas turbine, gas boiler and energy storage, respectively.
- : One operating cycle, taking the value of 24 h a day.
- (3)
- Carbon trading mechanism
- : Stepped carbon transaction costs.
- : Carbon trading base price.
- : Actual carbon emissions minus carbon quotas.
- : The length of carbon emissions interval.
- : Trading price growth rate.
- : The growth rate of transaction base price.
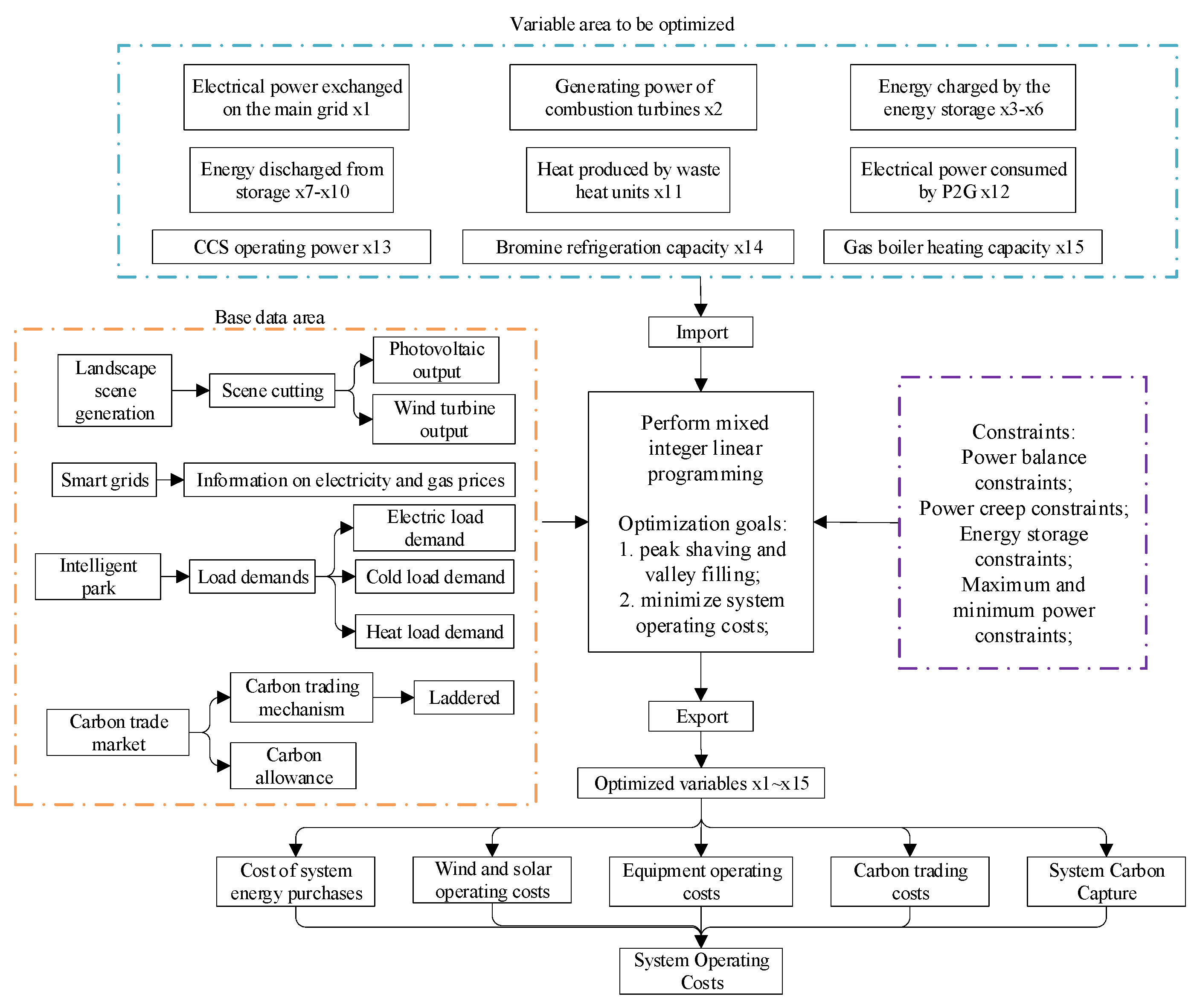
4. Multi-Objective Optimization Solution
5. Example Analysis and Simulation
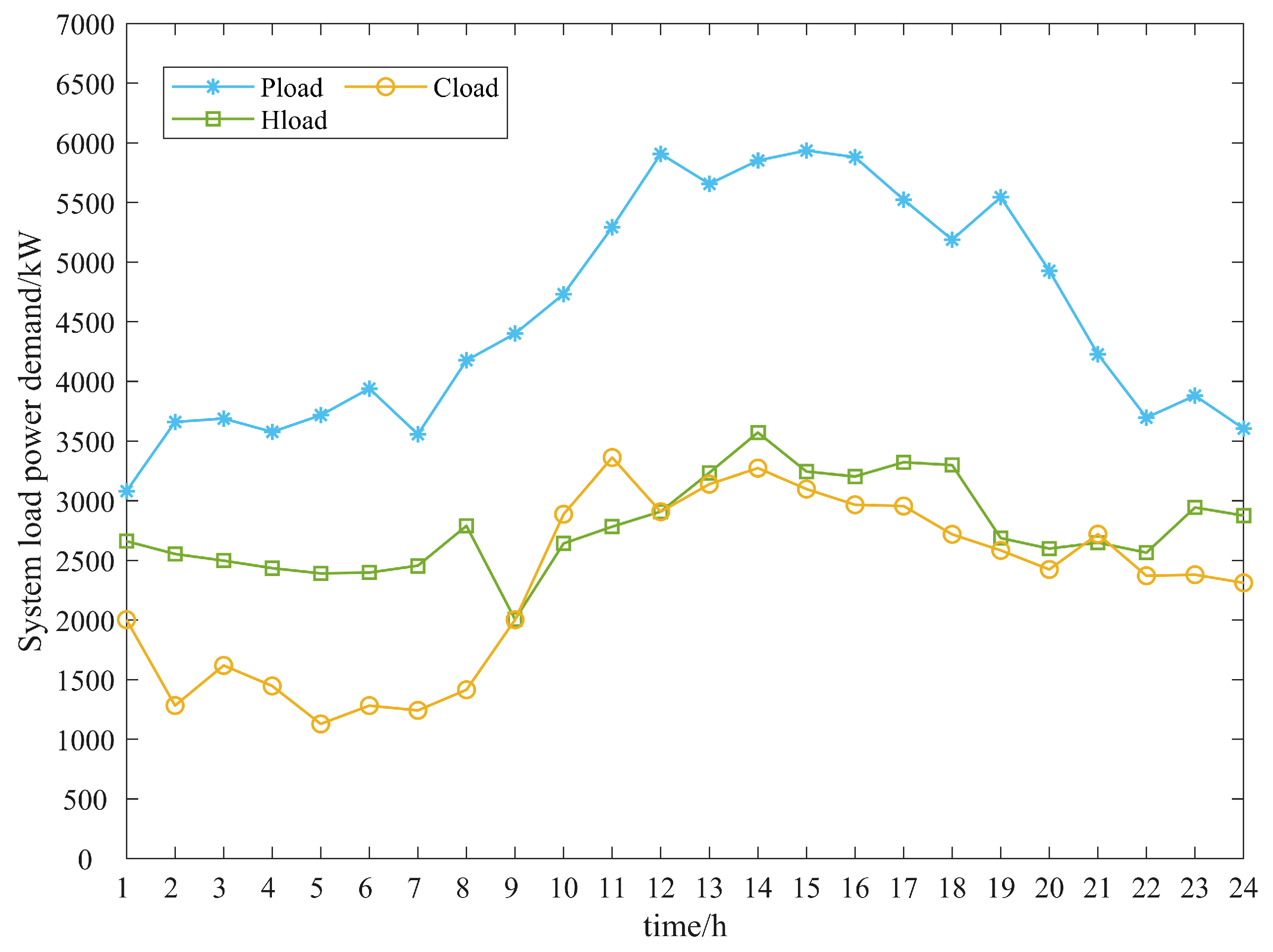
5.1. Basic Data
5.2. Generation and Reduction of Landscape Scenes
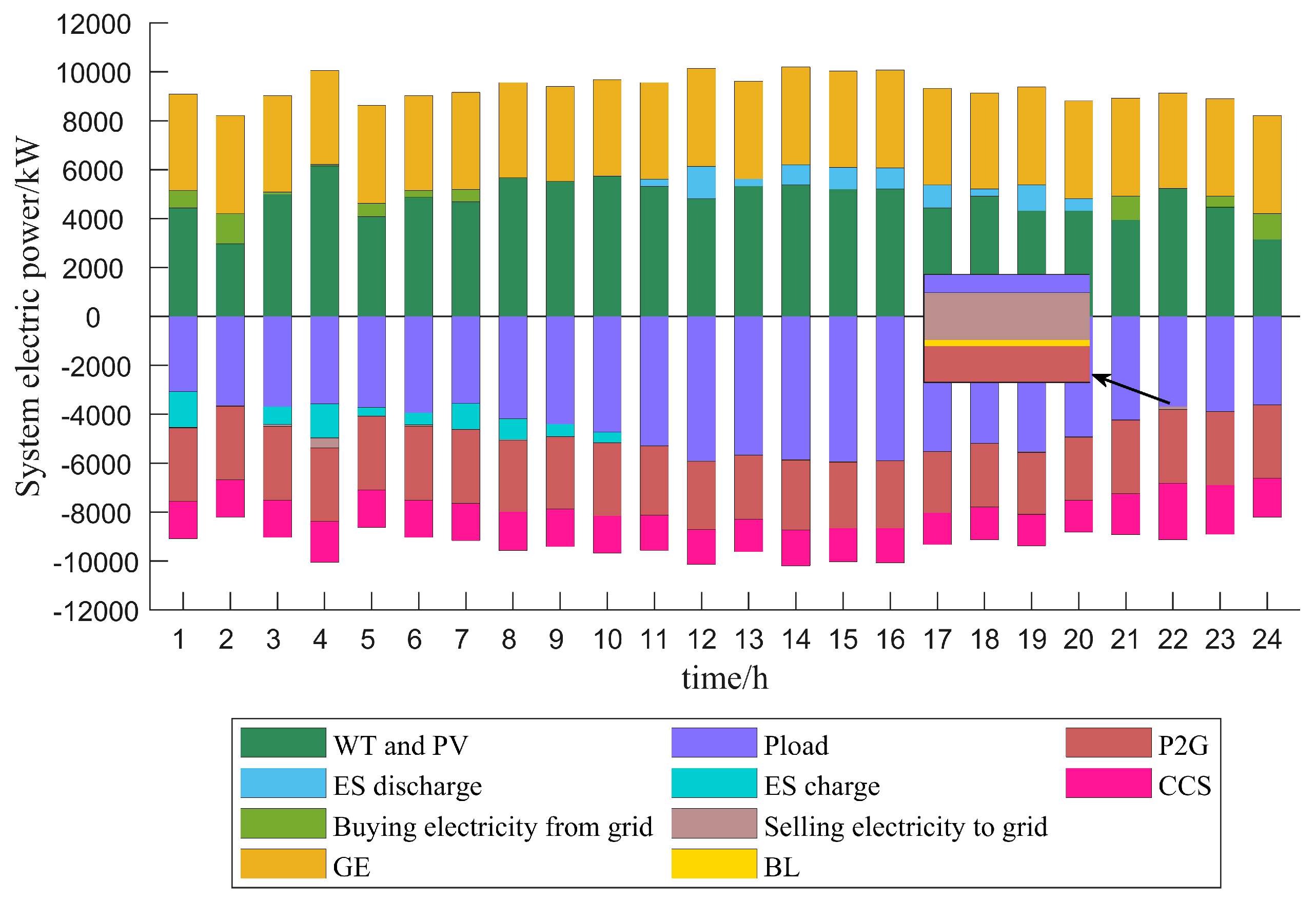
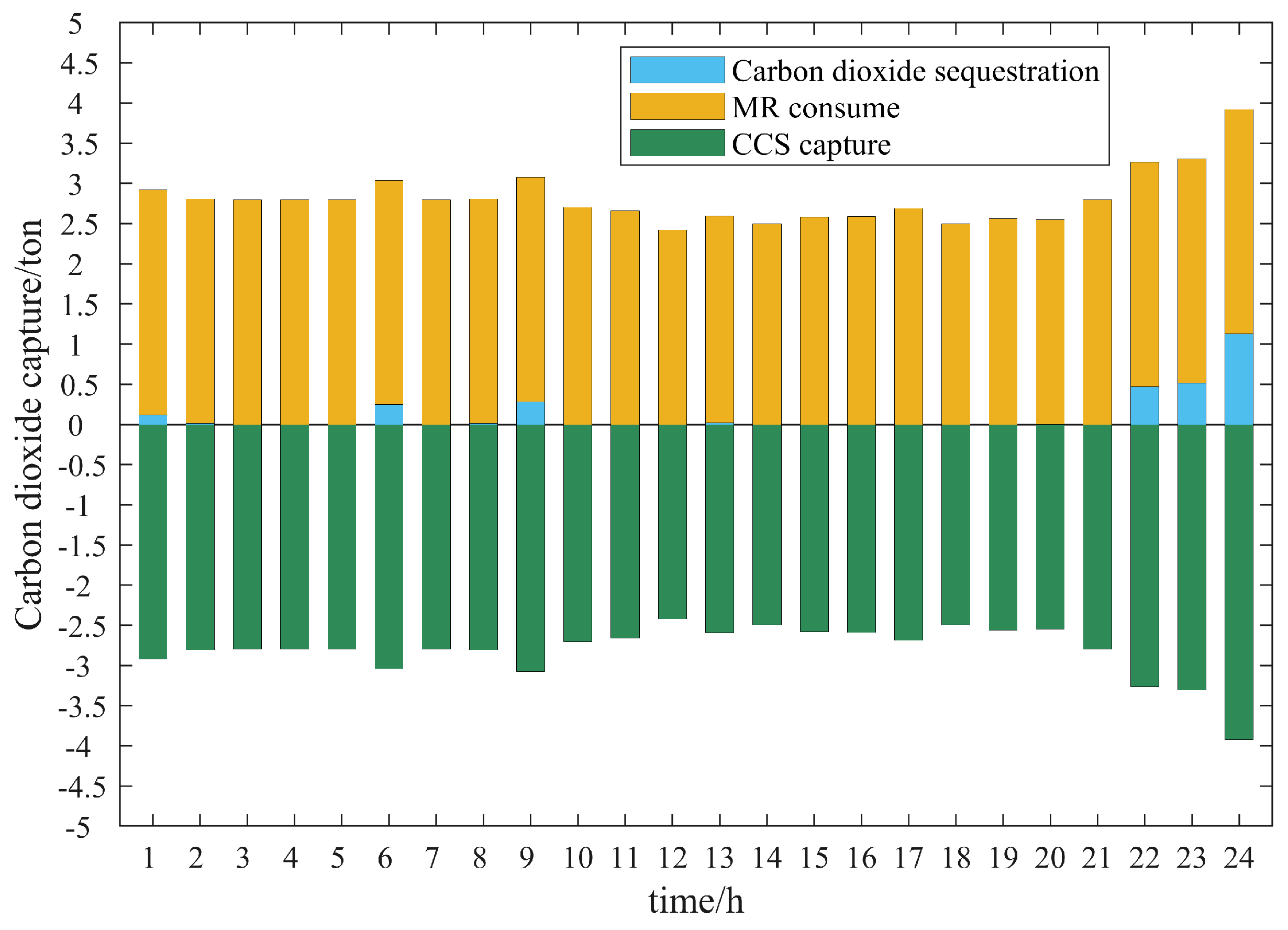
5.3. Example Validation Analysis
6. Conclusions
- Considering the uncertainty of wind and solar output, the proposed model can more effectively improve the reliability, stability and economy of the IES, and reduce the operating costs of the system.
- The introduction of P2G-CCS can more effectively help the system to solve the problem of wind and solar consumption, achieve the balance of energy supply, reduce the carbon emissions of the system and achieve the goal of the low-carbon economic operation of the system.
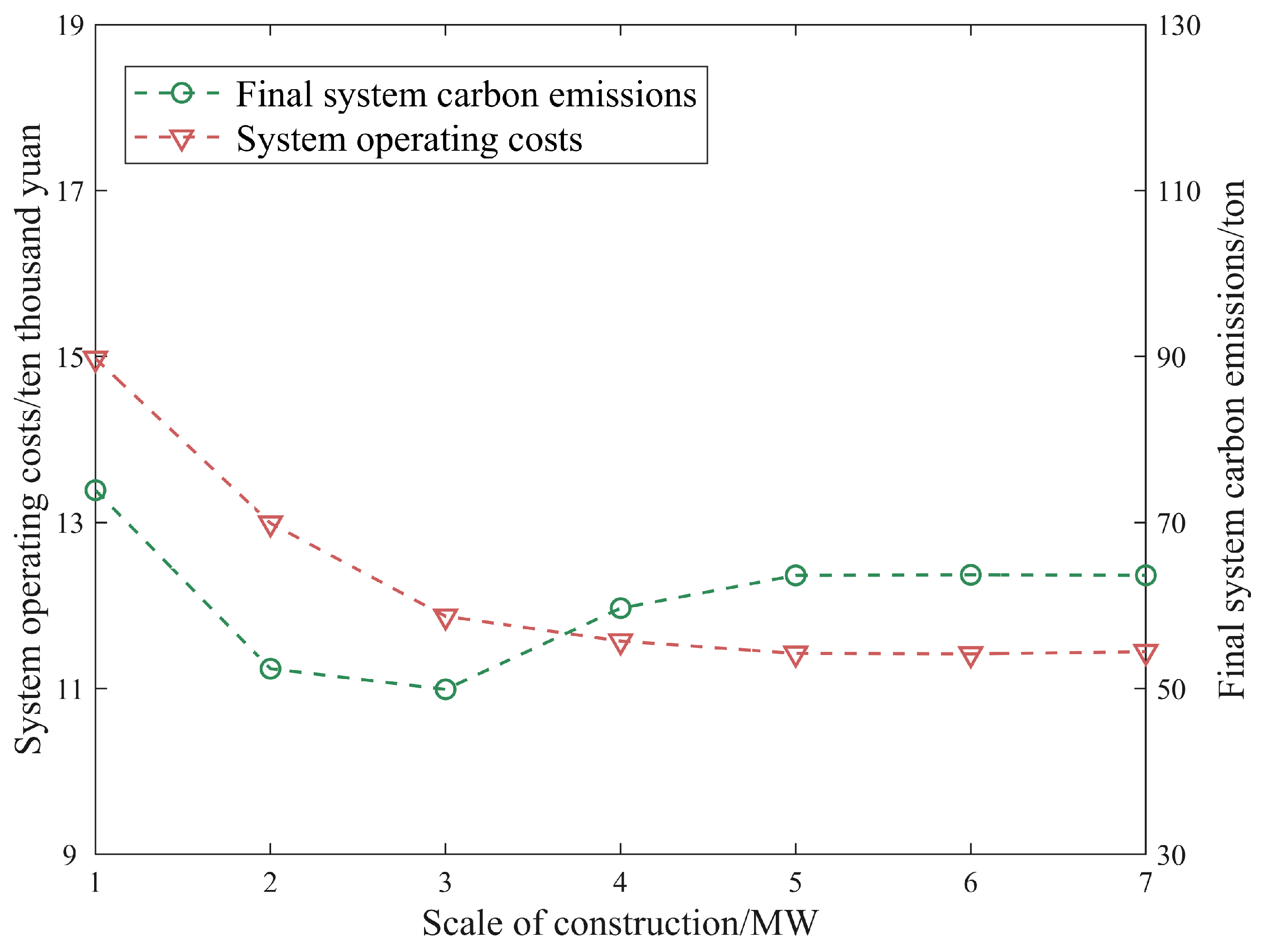
- With the increase in P2G-CCS construction scale parameters, the system’s operating costs gradually decrease. However, due to the influence of the scale of other equipment architecture of the system, the carbon emissions of the system show a trend of decreasing first and then increasing. Therefore, in the system architecture of this paper, it is suggested that the value of the P2G-CCS construction scale parameters should be between 3 MWh and 4 MWh.
- The integrated energy system optimization model proposed in this paper, which takes into account the wind and light uncertainty and introduces P2G-CCS, can greatly improve the wind and light consumption rate, reduce the system’s operating costs and carbon emissions, and achieve stable, efficient and environmentally friendly operation of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CS | cold energy storage |
| CCS | carbon capture and storage |
| CCU | carbon capture and utilization |
| CSP-CHP | concentrated solar power and combined heat and power |
| CvaR | conditional value-at-risk |
| EL | electrolysis system |
| ES | electrical energy storage |
| GB | gas boiler |
| GE | gas engine |
| GPC | generalized polynomial chaos |
| HGT | hydrogen-doped gas units |
| HS | thermal energy storage |
| IEGS | Integrated Electricity–Gas System |
| IES | integrated energy systems |
| LB | lithium bromide |
| LHS | Latin hypercube sampling |
| MR | methane reactor |
| PIES | park integrated energy system |
| P2G | power to gas |
| probability density functions | |
| PV | photovoltaic power generation |
| S-CO2 | supercritical carbon dioxide |
| WT | wind turbine power generation |
References
- Fan, M.; Li, Z.; Ding, T.; Huang, L.; Dong, F.; Ren, Z.; Liu, C. Uncertainty Evaluation Algorithm in Power System Dynamic Analysis with Correlated Renewable Energy Sources. IEEE Trans. Power Syst. 2021, 36, 5602–5611. [Google Scholar] [CrossRef]
- Tan, Z.; De, G.; Li, M.; Lin, H.; Yang, S.; Huang, L.; Tan, Q. Combined Electricity-Heat-Cooling-Gas Load Forecasting Model for Integrated Energy System Based on Multi-Task Learning and Least Square Support Vector Machine. J. Clean. Prod. 2020, 248, 119252. [Google Scholar] [CrossRef]
- Gilani, M.A.; Kazemi, A.; Ghasemi, M. Distribution System Resilience Enhancement by Microgrid Formation Considering Distributed Energy Resources. Energy 2020, 191, 116442. [Google Scholar] [CrossRef]
- Li, F.; Chen, S.; Ju, C.; Zhang, X.; Ma, G.; Huang, W. Research on Short-Term Joint Optimization Scheduling Strategy for Hydro-Wind-Solar Hybrid Systems Considering Uncertainty in Renewable Energy Generation. Energy Strategy Rev. 2023, 50, 101242. [Google Scholar] [CrossRef]
- Nayak, A.; Maulik, A.; Das, D. An Integrated Optimal Operating Strategy for a Grid-Connected AC Microgrid under Load and Renewable Generation Uncertainty Considering Demand Response. Sustain. Energy Technol. Assess. 2021, 45, 101169. [Google Scholar] [CrossRef]
- Abdelmalak, M.; Benidris, M. A Polynomial Chaos-Based Approach to Quantify Uncertainties of Correlated Renewable Energy Sources in Voltage Regulation. IEEE Trans. Ind. Appl. 2021, 57, 2089–2097. [Google Scholar] [CrossRef]
- Cao, W.; Yu, J.; Xu, M. Optimization Scheduling of Virtual Power Plants Considering Source-Load Coordinated Operation and Wind–Solar Uncertainty. Processes 2023, 12, 11. [Google Scholar] [CrossRef]
- Dupačová, J.; Gröwe-Kuska, N.; Römisch, W. Scenario Reduction in Stochastic Programming. Math. Program. 2003, 95, 493–511. [Google Scholar] [CrossRef]
- Duan, J.; Xia, Y.; Cheng, R.; Gao, Q.; Liu, F. Low Carbon and Economic Optimal Operation of Electricity-Gas Integrated Energy System Considering Demand Response. Sustain. Energy Grids Netw. 2024, 38, 101290. [Google Scholar]
- Wang, R.; Wen, X.; Wang, X.; Fu, Y.; Zhang, Y. Low Carbon Optimal Operation of Integrated Energy System Based on Carbon Capture Technology, LCA Carbon Emissions and Ladder-Type Carbon Trading. Appl. Energy 2022, 311, 118664. [Google Scholar] [CrossRef]
- Yan, N.; Ma, G.; Li, X.; Guerrero, J.M. Low-Carbon Economic Dispatch Method for Integrated Energy System Considering Seasonal Carbon Flow Dynamic Balance. IEEE Trans. Sustain. Energy 2023, 14, 576–586. [Google Scholar] [CrossRef]
- Chen, H.; Wu, H.; Kan, T.; Zhang, J.; Li, H. Low-Carbon Economic Dispatch of Integrated Energy System Containing Electric Hydrogen Production Based on VMD-GRU Short-Term Wind Power Prediction. Int. J. Electr. Power Energy Syst. 2023, 154, 109420. [Google Scholar] [CrossRef]
- Li, M.; Qin, J.; Han, Z.; Niu, Q. Low-carbon Economic Optimization Method for Integrated Energy Systems Based on Life Cycle Assessment and Carbon Capture Utilization Technologies. Energy Sci. Eng. 2023, 11, 4238–4255. [Google Scholar] [CrossRef]
- Li, W.; He, M.; Cai, T. Low-Carbon Economic Dispatch of Hydrogen-Containing Integrated Energy System Considering Stepped Demand Response. Energy Rep. 2024, 11, 4222–4232. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Z.; Shi, Z. Low Carbon Economic Dispatch of Integrated Energy Systems Considering Utilization of Hydrogen and Oxygen Energy. Int. J. Electr. Power Energy Syst. 2024, 158, 109923. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, J.; Li, M.; Guo, J.; Xu, Z.; Li, W. Bi-Level Optimization Dispatch of Integrated-Energy Systems with P2G and Carbon Capture. Front. Energy Res. 2022, 9, 784703. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Liu, L.; Wang, Z.; Li, X.; Huang, J.; Huang, J.; Guo, P.; Xiong, W. Operation Optimization for Integrated Energy System Based on Hybrid CSP-CHP Considering Power-to-Gas Technology and Carbon Capture System. J. Clean. Prod. 2023, 391, 136119. [Google Scholar] [CrossRef]
- Liang, Y.-L.; Zhang, H.; Yang, C.-T.; Li, K.-J. Research on Optimization Scheduling of Integrated Electricity-Gas System Considering Carbon Trading and P2G Operation Characteristics. Electr. Power Syst. Res. 2023, 225, 109797. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, W.; Chen, Z.; Li, R.; Niu, Y. Modeling and Optimal Dispatch of a Carbon-Cycle Integrated Energy System for Low-Carbon and Economic Operation. Energy 2022, 240, 122795. [Google Scholar] [CrossRef]
- Zhu, X.; Xue, J.; Hu, M.; Liu, Z.; Gao, X.; Huang, W. Low-Carbon Economy Dispatching of Integrated Energy System with P2G-HGT Coupling Wind Power Absorption Based on Stepped Carbon Emission Trading. Energy Rep. 2023, 10, 1753–1764. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Ji, X.; Ye, P.; Li, J. Unit Commitment of Integrated Energy System Considering Conditional Value-at-Risk and P2G. Electr. Power Syst. Res. 2023, 221, 109398. [Google Scholar] [CrossRef]
- Sun, H.; Sun, X.; Kou, L.; Ke, W. Low-Carbon Economic Operation Optimization of Park-Level Integrated Energy Systems with Flexible Loads and P2G under the Carbon Trading Mechanism. Sustainability 2023, 15, 15203. [Google Scholar] [CrossRef]
- Pan, C.; Jin, T.; Li, N.; Wang, G.; Hou, X.; Gu, Y. Multi-Objective and Two-Stage Optimization Study of Integrated Energy Systems Considering P2G and Integrated Demand Responses. Energy 2023, 270, 126846. [Google Scholar] [CrossRef]
- Yang, B. Multi-objective Optimization of Integrated Gas–Electricity Energy System Based on Improved Multi-object Cuckoo Algorithm. Energy Sci. Eng. 2021, 9, 1839–1857. [Google Scholar] [CrossRef]
- Wu, D.; Han, S.; Wang, L.; Li, G.; Guo, J. Multi-Parameter Optimization Design Method for Energy System in Low-Carbon Park with Integrated Hybrid Energy Storage. Energy Convers. Manag. 2023, 291, 117265. [Google Scholar] [CrossRef]
- Qiao, Y.; Hu, F.; Xiong, W.; Li, Y. Energy Hub-based Configuration Optimization Method of Integrated Energy System. Int. J. Energy Res. 2022, 46, 23287–23309. [Google Scholar] [CrossRef]
- Sun, H.; Zou, H.; Wen, J.; Ke, W.; Kou, L. Optimal Scheduling Considering Carbon Capture and Demand Response under Uncertain Output Scenarios for Wind Energy. Sustainability 2024, 16, 970. [Google Scholar] [CrossRef]
- Haghighat Mamaghani, A.; Avella Escandon, S.A.; Najafi, B.; Shirazi, A.; Rinaldi, F. Techno-Economic Feasibility of Photovoltaic, Wind, Diesel and Hybrid Electrification Systems for off-Grid Rural Electrification in Colombia. Renew. Energy 2016, 97, 293–305. [Google Scholar] [CrossRef]
- Ju, L.; Tan, Z.; Yuan, J.; Tan, Q.; Li, H.; Dong, F. A Bi-Level Stochastic Scheduling Optimization Model for a Virtual Power Plant Connected to a Wind–Photovoltaic–Energy Storage System Considering the Uncertainty and Demand Response. Appl. Energy 2016, 171, 184–199. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Zhao, D.; Tian, W. Optimal Scheduling of an Isolated Microgrid With Battery Storage Considering Load and Renewable Generation Uncertainties. IEEE Trans. Ind. Electron. 2019, 66, 1565–1575. [Google Scholar] [CrossRef]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Lei, K.; Chang, J.; Wang, X.; Guo, A.; Wang, Y.; Ren, C. Peak Shaving and Short-Term Economic Operation of Hydro-Wind-PV Hybrid System Considering the Uncertainty of Wind and PV Power. Renew. Energy 2023, 215, 118903. [Google Scholar] [CrossRef]
- Cho, J.; Jeong, S.; Kim, Y. Commercial and Research Battery Technologies for Electrical Energy Storage Applications. Prog. Energy Combust. Sci. 2015, 48, 84–101. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, W.; Fan, X.; He, S.; Wang, H.; Wu, J.; Shi, R. Low-Carbon Optimal Operation Strategy of Multi-Park Integrated Energy System Considering Multi-Energy Sharing Trading Mechanism and Asymmetric Nash Bargaining. Energy Rep. 2023, 10, 255–284. [Google Scholar] [CrossRef]
- Chen, J.; Tang, Z.; Huang, Y.; Qiao, A.; Liu, J. Asymmetric Nash Bargaining-Based Cooperative Energy Trading of Multi-Park Integrated Energy System under Carbon Trading Mechanism. Electr. Power Syst. Res. 2024, 228, 110033. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M.T. Techno-Economic Optimization of Hybrid Photovoltaic/Wind Generation Together with Energy Storage System in a Stand-Alone Micro-Grid Subjected to Demand Response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]


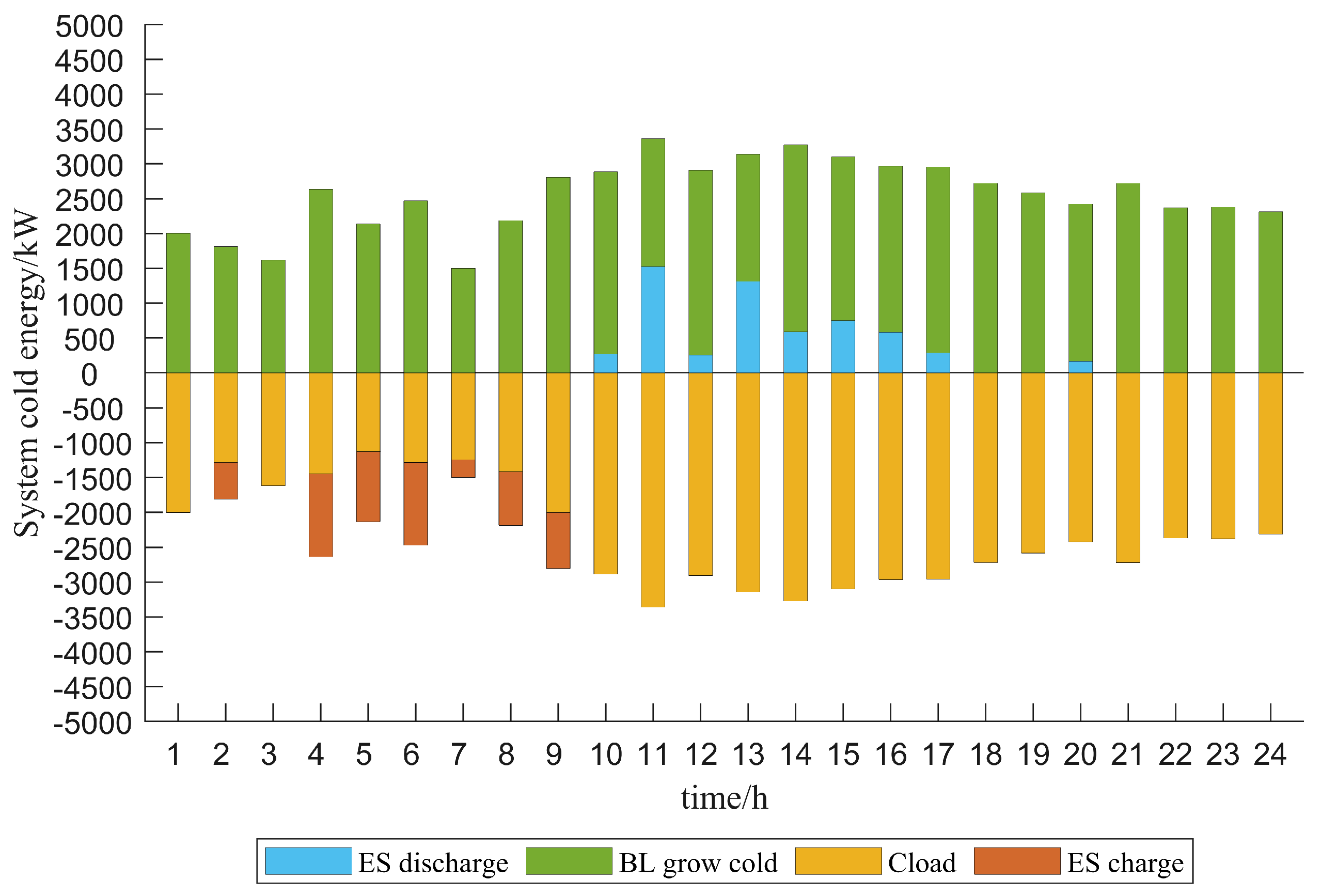
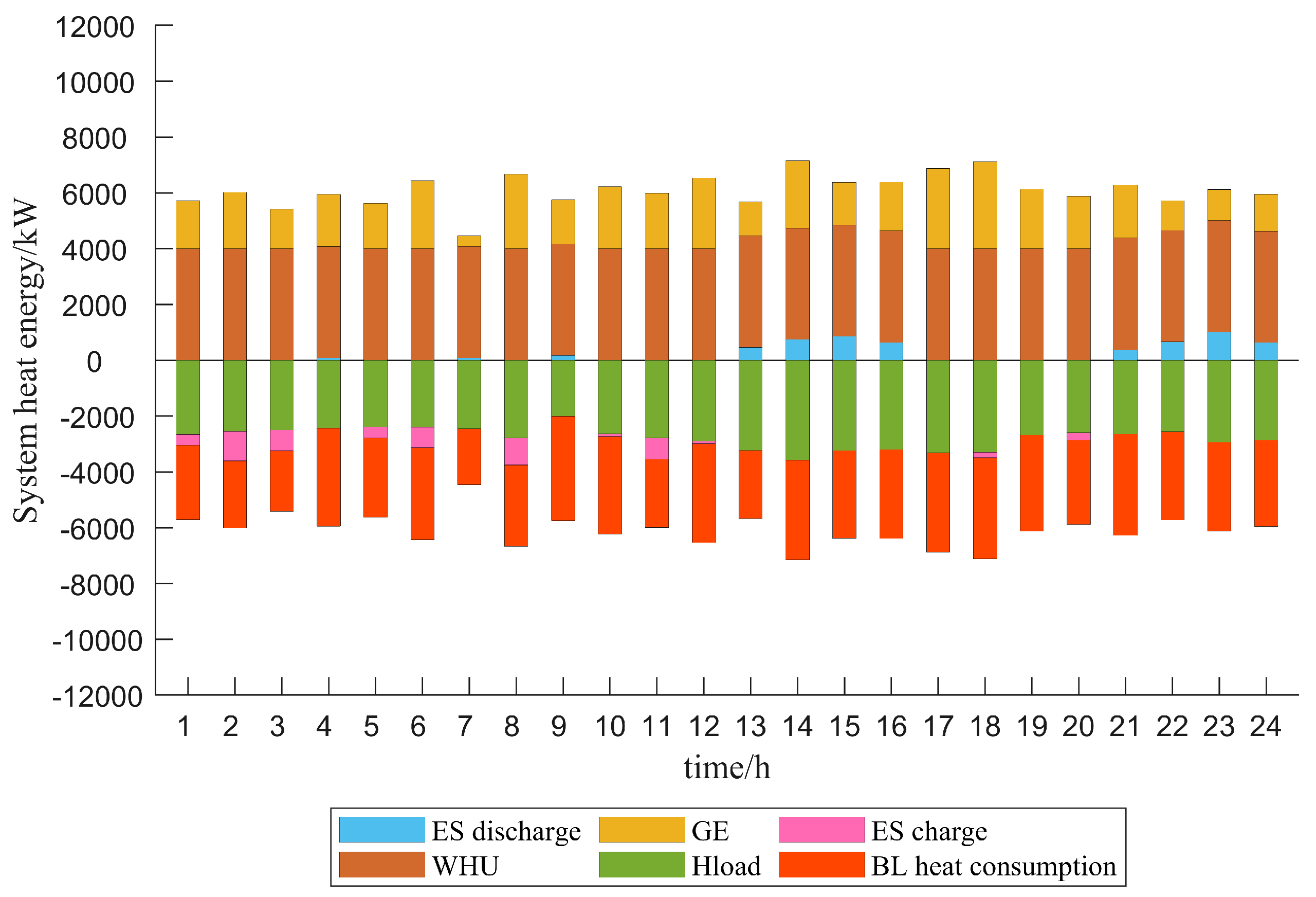

| Source of Carbon Emissions | Carbon Allowance/(kg/kWh) |
|---|---|
| Wind turbine | 0.078 |
| Photovoltaic generator | 0.078 |
| Gas boiler | 0.152 |
| Energy storage | 0 |
| Grids | 0.798 |
| Time | Electricity Price/yuan |
|---|---|
| 00:00–07:00 | 0.62 |
| 08:00–11:00 | 1.14 |
| 12:00–16:00 | 0.83 |
| 17:00–20:00 | 1.14 |
| 21:00–23:00 | 0.62 |
| Main grid electricity tariff | 0.36 |
| Source of Carbon Emissions | Carbon Emission Factor (kg/kWh) |
|---|---|
| Wind turbine | 0.105 |
| Photovoltaic generator | 0.111 |
| Natural gas (gas boiler) | 0.236 |
| Energy storage | 0.112 |
| Grids | 1.303 |
| Parameter Name | Value | Unit |
|---|---|---|
| 3000 | kW | |
| 4000 | kW | |
| 2830 | kW | |
| 4000 | kW | |
| 3000 | kW | |
| 3000 | kW | |
| 5000 | kW | |
| 2000 | kW | |
| 10,000 | kWh | |
| 2000 | kW | |
| 10,000 | kWh | |
| 2000 | kW | |
| 10,000 | kWh | |
| 10 | times | |
| 10 | times | |
| 10 | times | |
| 1.07 | ||
| 0.25 | ||
| 0.55 |
| Scenario | Probability Value |
|---|---|
| 1 | 0.158 |
| 2 | 0.258 |
| 3 | 0.133 |
| 4 | 0.195 |
| 5 | 0.256 |
| Scenario | Total System Operating Cost/million | Carbon Trading Costs/USD million | Carbon Emissions/ton | Cost of Wind and Light Abandonment/yuan | Wind and Light Rejection Rate |
|---|---|---|---|---|---|
| 1 | 20.31 | 1.04 | 118.68 | 8339 | 12.07 |
| 2 | 13.12 | −1.83 | 61.37 | 2096 | 3.24 |
| 3 | 18.74 | 0.93 | 106.07 | 6231 | 10.64 |
| 4 | 11.61 | −2.25 | 57.42 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, P.; Du, S.; Dong, H. Economic Optimal Scheduling of Integrated Energy System Considering Wind–Solar Uncertainty and Power to Gas and Carbon Capture and Storage. Energies 2024, 17, 2770. https://doi.org/10.3390/en17112770
Zhang Y, Zhang P, Du S, Dong H. Economic Optimal Scheduling of Integrated Energy System Considering Wind–Solar Uncertainty and Power to Gas and Carbon Capture and Storage. Energies. 2024; 17(11):2770. https://doi.org/10.3390/en17112770
Chicago/Turabian StyleZhang, Yunlong, Panhong Zhang, Sheng Du, and Hanlin Dong. 2024. "Economic Optimal Scheduling of Integrated Energy System Considering Wind–Solar Uncertainty and Power to Gas and Carbon Capture and Storage" Energies 17, no. 11: 2770. https://doi.org/10.3390/en17112770
APA StyleZhang, Y., Zhang, P., Du, S., & Dong, H. (2024). Economic Optimal Scheduling of Integrated Energy System Considering Wind–Solar Uncertainty and Power to Gas and Carbon Capture and Storage. Energies, 17(11), 2770. https://doi.org/10.3390/en17112770







