Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro–Thermo–Fluidic Simulations
Abstract
1. Introduction
2. HVLH Design and Materials
3. Theory of Electro–Thermo–Fluidic Simulation
4. Simulation Setup and Results
4.1. Simulation Setup
4.2. Simulation Results
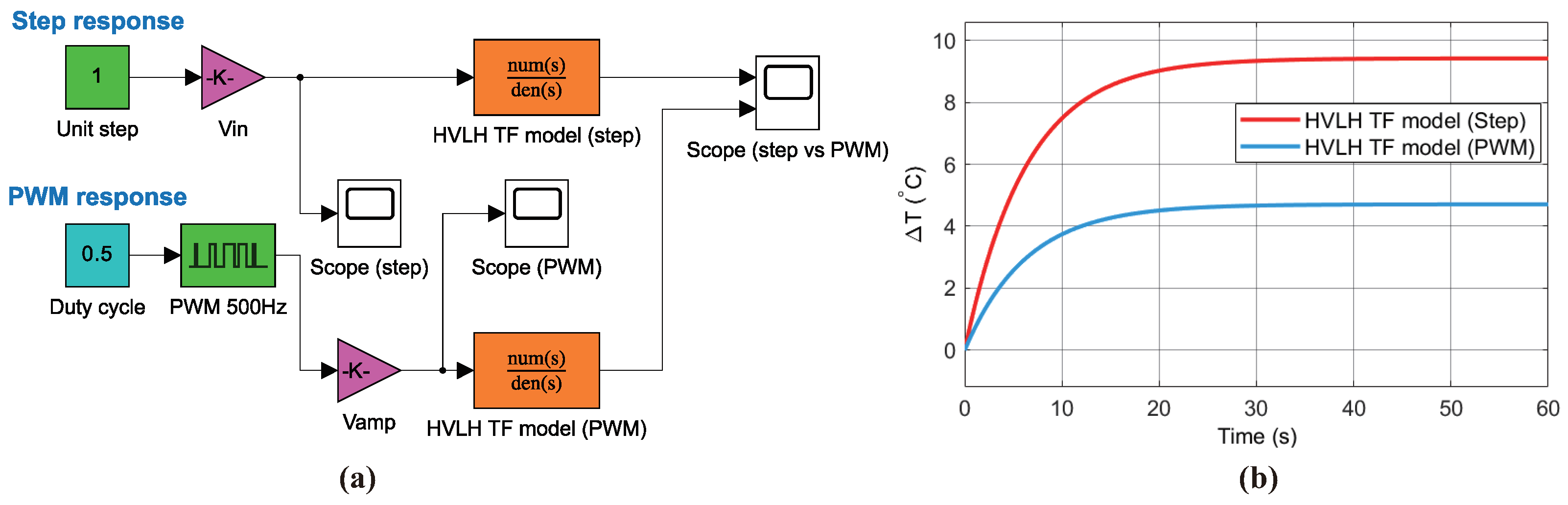
5. Transfer Function Modeling and Discussion
6. Conclusions
- This study represents the first attempt to model and simulate the HVLH by separately modeling the conductive heating layer in the electric domain, thereby calculating Joule heating and analyzing transient conjugate heat transfer. This approach improves the accuracy of predicting the thermal performance and power consumption of HVLHs.
- In addition, this research is pioneering in the modeling of the transfer function of the HVLH component, enabling its integration into system-level HVAC modeling. The derived transfer function is essential for the development and implementation of control strategies for electric vehicle heating systems.
- The results of the regression analysis for the transfer function and its parameters demonstrate a high degree of precision in reproducing the simulation data. This accurate correlation underscores the reliability of the transfer function model and its prospective usefulness in forecasting the performance of HVAC at the system level.
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | diffusion coefficient, |
| electric field intensity vector, | |
| model parameter weighting factor | |
| current density vector, | |
| k | specific turbulent kinetic energy, |
| thermal conductivity, W/m·K | |
| DC gain, ° | |
| specific heat capacity at constant pressure, J/kg·K | |
| Kays–Crawford turbulent Prandtl number | |
| far-field Prandtl number | |
| Q | fluid volume flow rate, LPM |
| Joule heating rate, | |
| s | Laplace variable, rad/s |
| t | time variable, s |
| rise time, s | |
| settling time, s | |
| T | absolute temperature, K |
| temperature increase from inlet to outlet, ° | |
| steady-state value of , ° | |
| u | velocity field component, |
| V | electric potential field, V |
| voltage amplitude for step input, V | |
| Creek symbols | |
| turbulent model parameter | |
| turbulent model parameter | |
| turbulent model parameter | |
| specific rate of turbulent kinetic energy dissipation in model, J/kg·s | |
| dynamic viscosity, Pa·s | |
| turbulent viscosity, Pa·s | |
| eddy viscosity, | |
| density, | |
| electric conductivity, S/m | |
| turbulent model parameter | |
| turbulent model parameter | |
| turbulent model parameter | |
| Reynolds stress tensor, Pa | |
| specific rate of turbulent kinetic energy dissipation, J/kg·s | |
| Abbreviations | |
| 3D | three-dimensional |
| CFD | computational fluid dynamics |
| CHT | conjugate heat transfer |
| DC | direct current |
| EV | electric vehicle |
| HVAC | heating, ventilation, and air conditioning |
| HVH | high-voltage heater |
| HVLH | high-voltage layer heater |
| IGBT | insulated gate bipolar transistor |
| LPM | liters per minute |
| PHEV | plug-in hybrid electric vehicle |
| PCB | printed circuit board |
| PTC | positive temperature coeffieicnt |
| PWM | pulse width modulation |
| SST | shear stress transport |
| TFE | thick-film heating element |
References
- Li, B.; Kuo, H.; Wang, X.; Chen, Y.; Wang, Y.; Gerada, D.; Worall, S.; Stone, I.; Yan, Y. Thermal Management of Electrified Propulsion System for Low-Carbon Vehicles. Automot. Innov. 2020, 3, 299–316. [Google Scholar] [CrossRef]
- Lei, S.; Xin, S.; Liu, S. Separate and Integrated Thermal Management Solutions for Electric Vehicles: A Review. J. Power Sources 2022, 550, 232133. [Google Scholar] [CrossRef]
- Park, M.H.; Kim, S.C. Heating Performance Characteristics of High-Voltage PTC Heater for an Electric Vehicle. Energies 2017, 10, 1494. [Google Scholar] [CrossRef]
- Park, M.H.; Kim, S.C. Effects of Geometric Parameters and Operating Conditions on the Performance of a High-Voltage PTC Heater for an Electric Vehicle. Appl. Therm. Eng. 2018, 143, 1023–1033. [Google Scholar] [CrossRef]
- Shin, Y.H.; Ahn, S.K.; Kim, S.C. Performance Characteristics of PTC Elements for an Electric Vehicle Heating System. Energies 2016, 9, 813. [Google Scholar] [CrossRef]
- Paunović, V.; Mitić, V.; Đorđević, M.; Prijić, Z. Electrical Properties of Rare Earth Doped BaTiO3 Ceramics. In Proceedings of the 2017 IEEE 30th International Conference on Microelectronics (MIEL), Nis, Serbia, 9–11 October 2017; pp. 183–186. [Google Scholar] [CrossRef]
- Cap, C.; Hainzlmaier, C. Layer Heater for Electric Vehicles. ATZ Worldw. 2013, 115, 16–19. [Google Scholar] [CrossRef]
- Stifel, T. Optimization and Protection of Traction Batteries with an HV Coolant Heater. ATZ Worldw. 2021, 123, 44–47. [Google Scholar] [CrossRef]
- Dong, F.; Feng, Y.; Wang, Z.; Ni, J. Effects on Thermal Performance Enhancement of Pin-Fin Structures for Insulated Gate Bipolar Transistor (IGBT) Cooling in High Voltage Heater System. Int. J. Therm. Sci. 2019, 146, 106106. [Google Scholar] [CrossRef]
- Dong, F.; Wang, Z.; Feng, Y.; Ni, J. Numerical Study on Flow and Heat Transfer Performance of Serpentine Parallel Flow Channels in a High Voltage Heater System. Therm. Sci. 2022, 26, 735–752. [Google Scholar] [CrossRef]
- Son, K.J. Thermo-Fluid Simulation for Flow Channel Design of 7 kW High-Voltage Heater for Electric Vehicles. J. Korea Converg. Soc. 2022, 13, 191–196. [Google Scholar] [CrossRef]
- Son, K.J. Optimal Power Distribution of High-Voltage Coolant Heater for Electric Vehicles through Electro-Thermofluidic Simulations. Int. J. Automot. Technol. 2023, 24, 995–1003. [Google Scholar] [CrossRef]
- Bellocchi, S.; Leo Guizzi, G.; Manno, M.; Salvatori, M.; Zaccagnini, A. Reversible Heat Pump HVAC System with Regenerative Heat Exchanger for Electric Vehicles: Analysis of Its Impact on Driving Range. Appl. Therm. Eng. 2018, 129, 290–305. [Google Scholar] [CrossRef]
- Basciotti, D.; Dvorak, D.; Gellai, I. A Novel Methodology for Evaluating the Impact of Energy Efficiency Measures on the Cabin Thermal Comfort of Electric Vehicles. Energies 2020, 13, 3872. [Google Scholar] [CrossRef]
- Dvorak, D.; Basciotti, D.; Gellai, I. Demand-Based Control Design for Efficient Heat Pump Operation of Electric Vehicles. Energies 2020, 13, 5440. [Google Scholar] [CrossRef]
- Kulkarni, A.; Brandes, G.; Rahman, A.; Paul, S. A Numerical Model to Evaluate the HVAC Power Demand of Electric Vehicles. IEEE Access 2022, 10, 96239–96248. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Speziale, C.G.; Abid, R.; Anderson, E.C. Critical Evaluation of Two-Equation Models for near-Wall Turbulence. AIAA J. 1992, 30, 324–331. [Google Scholar] [CrossRef]
- Rivero, E.P.; Granados, P.; Rivera, F.F.; Cruz, M.; González, I. Mass Transfer Modeling and Simulation at a Rotating Cylinder Electrode (RCE) Reactor under Turbulent Flow for Copper Recovery. Chem. Eng. Sci. 2010, 65, 3042–3049. [Google Scholar] [CrossRef]
- Weigand, B.; Ferguson, J.R.; Crawford, M.E. An Extended Kays and Crawford Turbulent Prandtl Number Model. Int. J. Heat Mass Transf. 1997, 40, 4191–4196. [Google Scholar] [CrossRef]
- Luo, D.; Wang, R.; Yan, Y.; Sun, Z.; Zhou, W.; Ding, R. Comparison of Different Fluid-Thermal-Electric Multiphysics Modeling Approaches for Thermoelectric Generator Systems. Renew. Energy 2021, 180, 1266–1277. [Google Scholar] [CrossRef]
- Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Doraghi, Q.; Ahmad, L.; Norman, L.; Axcell, B.; Wrobel, L.; Dai, S. Thermoelectric Generator (TEG) Technologies and Applications. Int. J. Thermofluids 2021, 9, 100063. [Google Scholar] [CrossRef]
- Son, K.J. Thermo-Electro-Fluidic Simulation Study of Impact of Blower Motor Heat on Performance of Peltier Cooler for Protective Clothing. Energies 2023, 16, 4052. [Google Scholar] [CrossRef]
- Drumheller, D.S. Hypervelocity Impact of Mixtures. Int. J. Impact Eng. 1987, 5, 261–268. [Google Scholar] [CrossRef]
- Son, K.J.; Fahrenthold, E.P. Impact Dynamics Simulation for Magnetorheological Fluid Saturated Fabric Barriers. J. Comput. Nonlinear Dyn. 2024, 19, 061002. [Google Scholar] [CrossRef]
- Zhang, X.; Jane Wang, Q.; He, T.; Liu, Y.; Li, Z.; Kim, H.J.; Pack, S. Fully Coupled Thermo-Viscoelastic (TVE) Contact Modeling of Layered Materials Considering Frictional and Viscoelastic Heating. Tribol. Int. 2022, 170, 107506. [Google Scholar] [CrossRef]
- Kwon, B.W. Development of 7 kW-Class Thick Film Resistance Heating Electric Heater (10% Weight Reduction) for Lighter Green Vehicle Cooling, Heating and HVAC System; Final Project Report (Written in Korean) No. P0017526; Korean Ministry of Trade, Industry and Energy (MOTIE): Sejong, Republic of Korea, 2023.
- Franlkin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 8th ed.; Higher Education, Inc.: Upper Saddle River, NJ, USA, 2018; pp. 137–142. [Google Scholar]
- Shin, Y.H.; Sim, S.; Kim, S.C. Performance Characteristics of a Modularized and Integrated PTC Heating System for an Electric Vehicle. Energies 2016, 9, 18. [Google Scholar] [CrossRef]

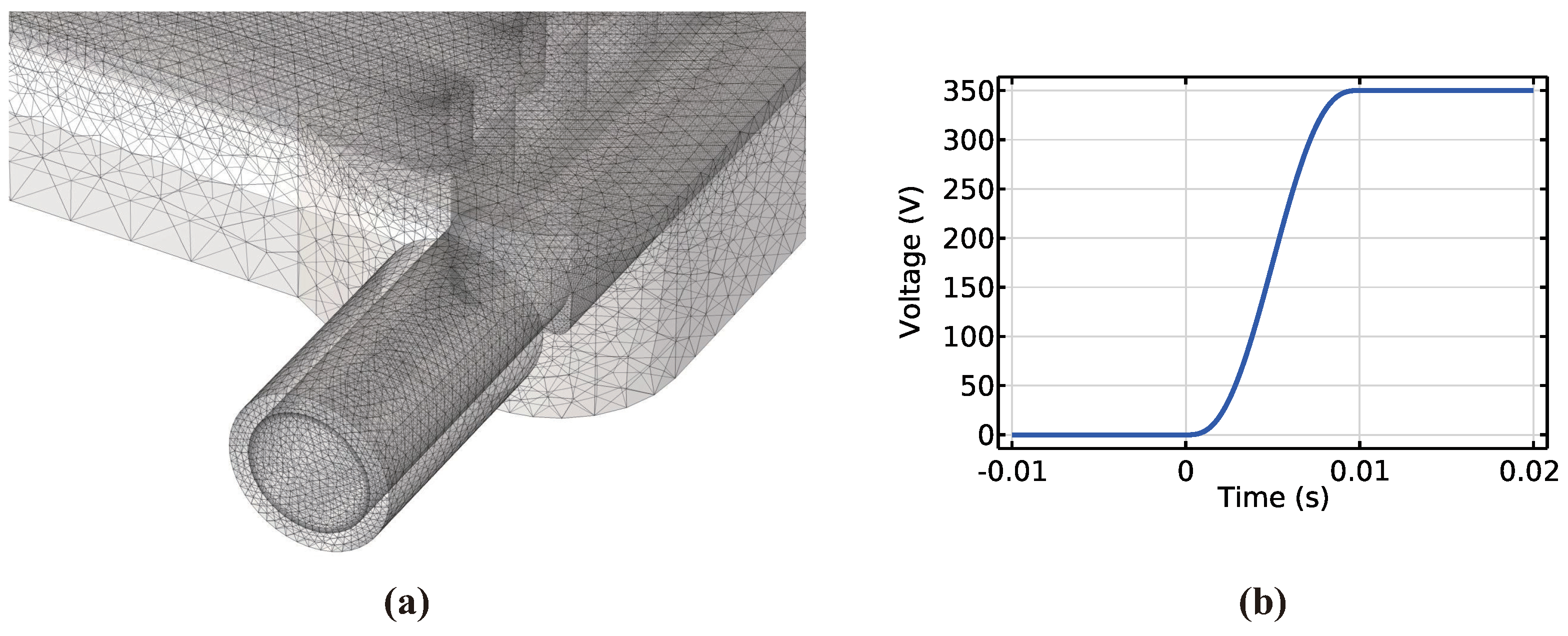
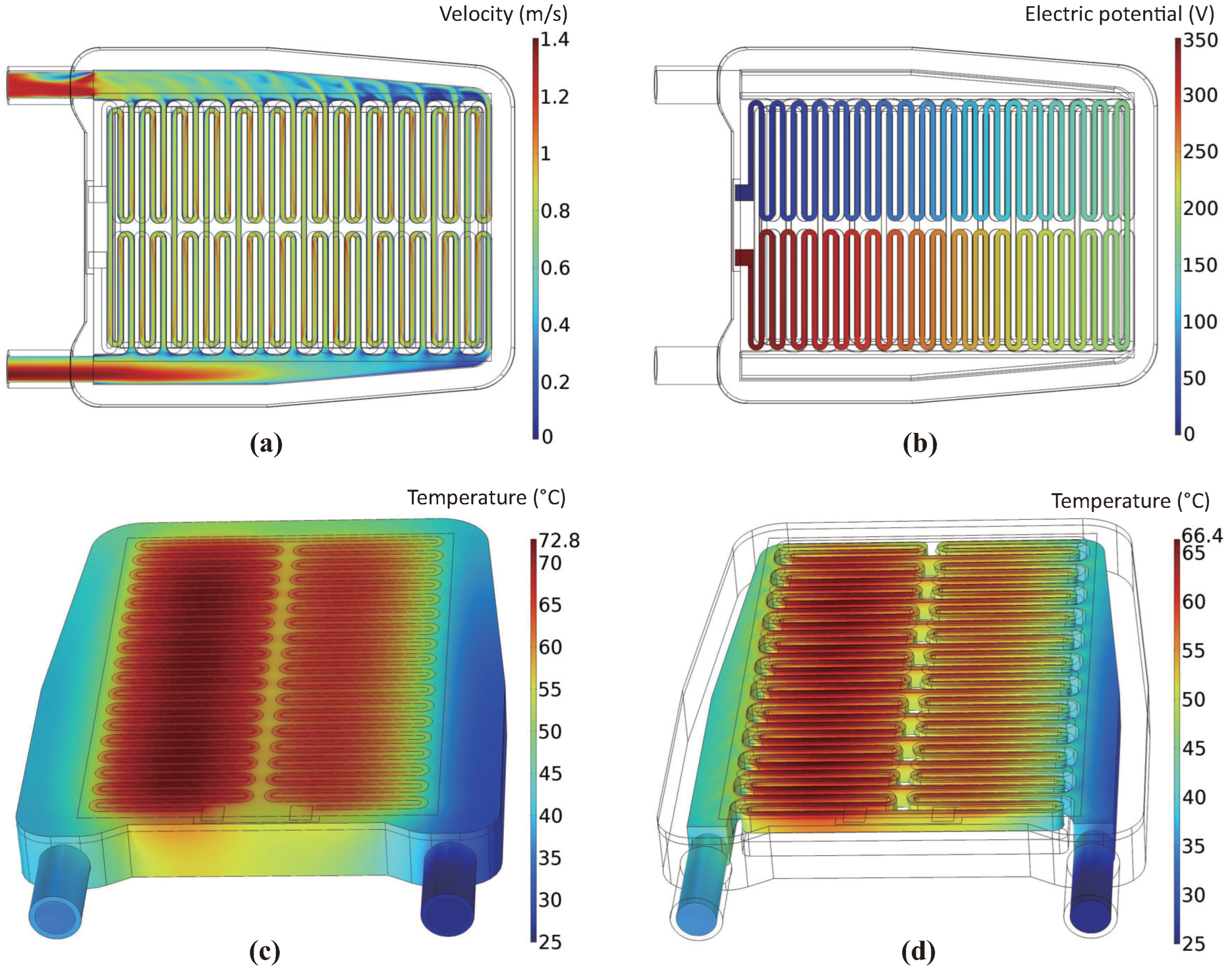
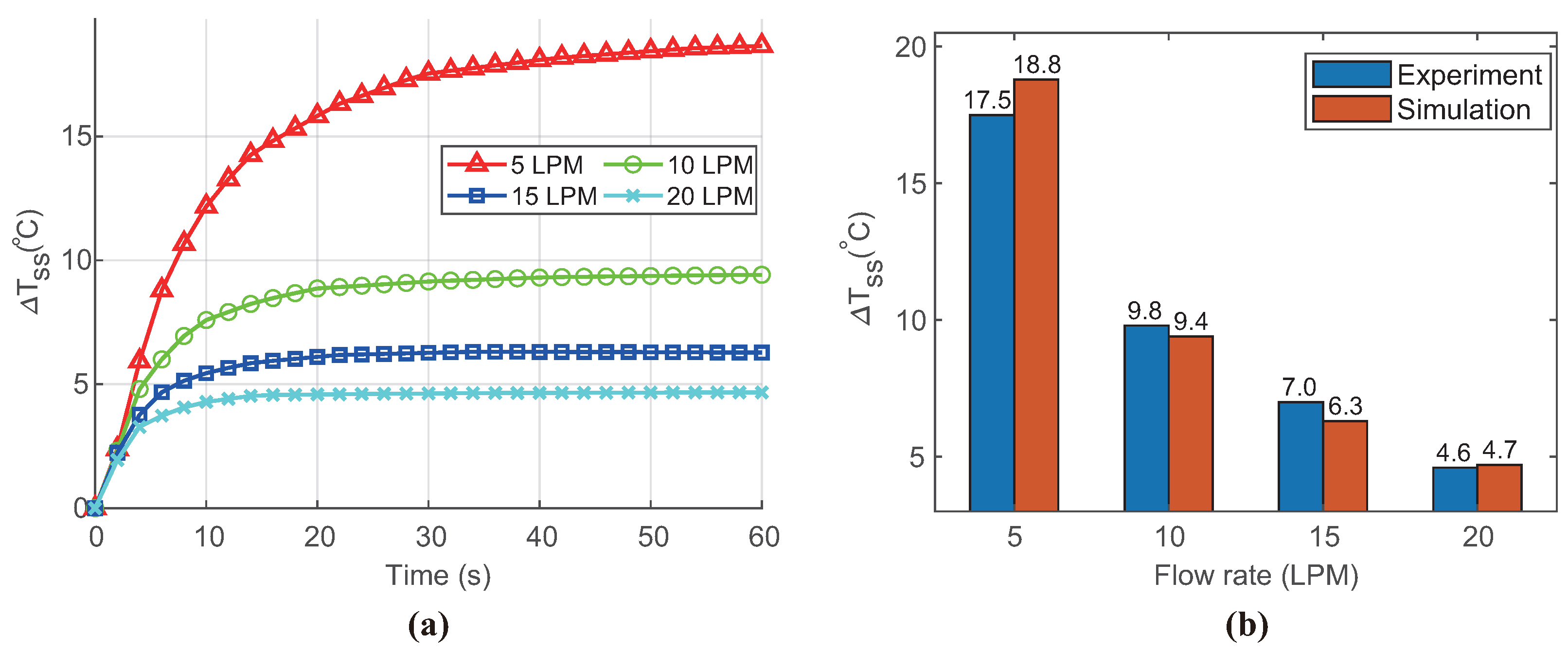
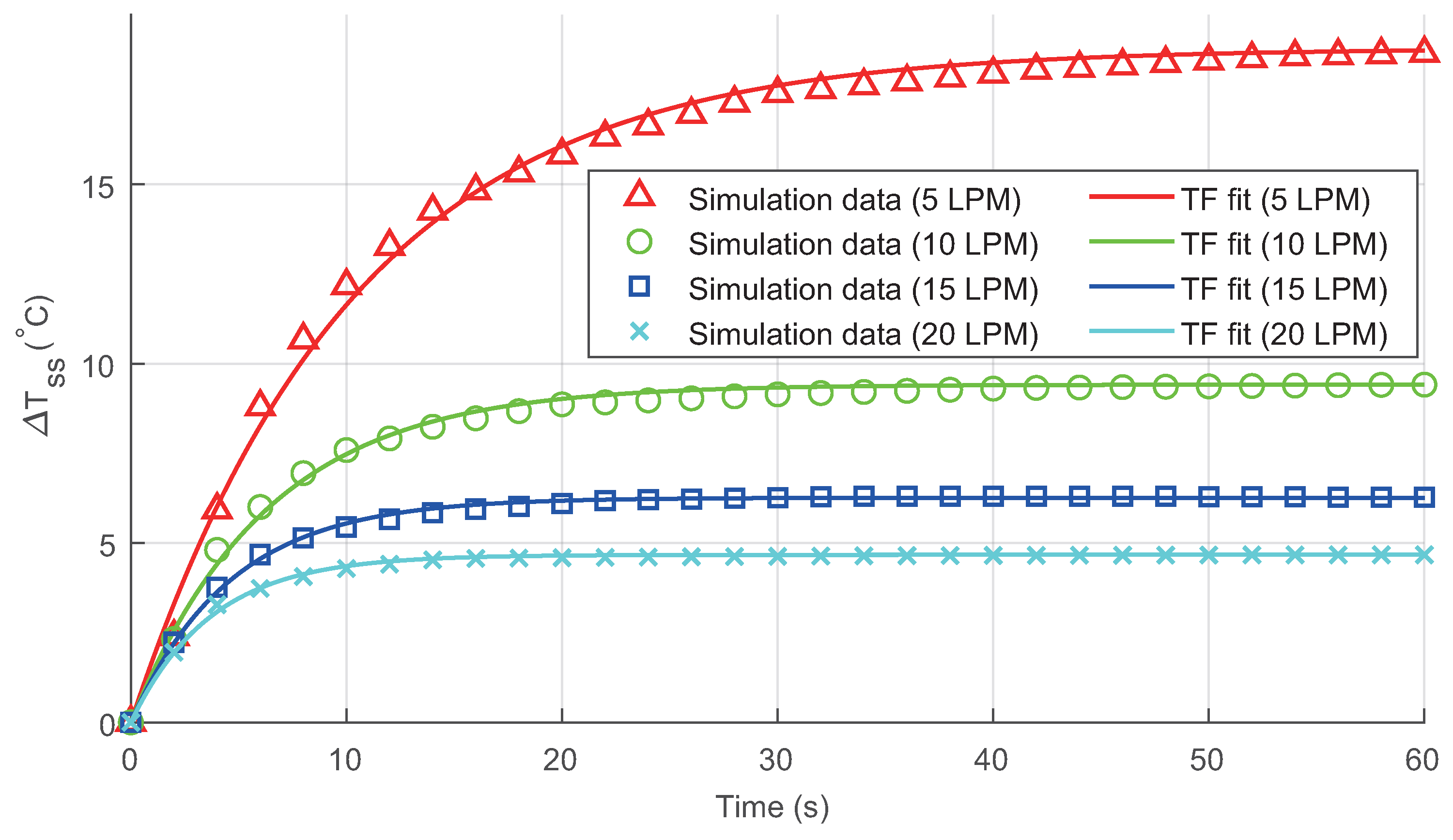
| Material | Density (kg/m3) | Heat Capacity (J/kg·K) | Thermal Conductivity (W/m·K) | Electrical Conductivity (S/m) | Dynamic Viscosity (Pa·s) |
|---|---|---|---|---|---|
| ALDC2 | – | 896 | 167 | – | – |
| – | 730 | 35 | – | – | |
| Ag-Pd | 11,743 | 341 | 127 | – | |
| Coolant | 1070.1 | 3354 | 0.37 | – |
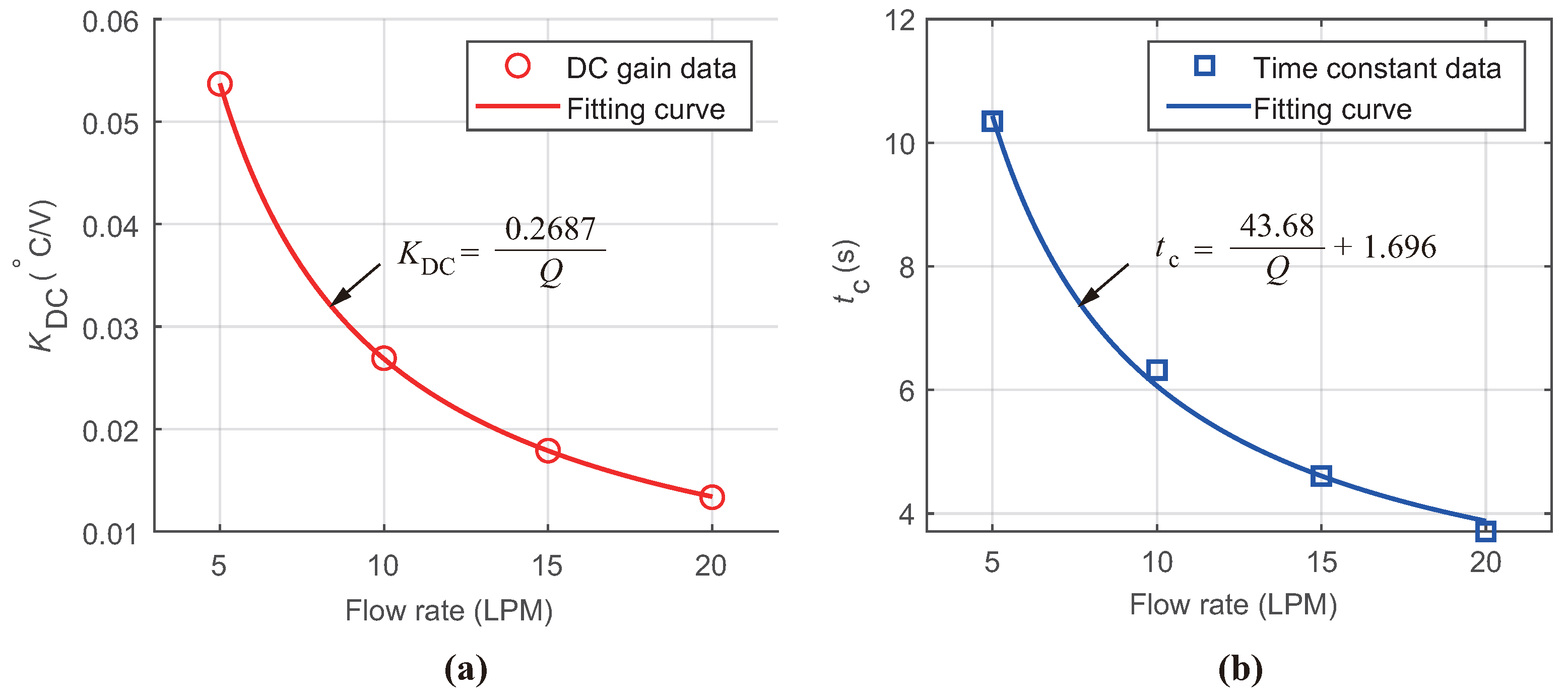
| Flow Rate (LPM) | (°) | (s) | (s) | (s) |
|---|---|---|---|---|
| 5 | 0.0537 | 10.3 | 22.8 | 47.6 |
| 10 | 0.0269 | 6.32 | 13.9 | 29.1 |
| 15 | 0.0179 | 4.61 | 10.1 | 21.2 |
| 20 | 0.0133 | 3.71 | 8.16 | 17.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, K.J. Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro–Thermo–Fluidic Simulations. Energies 2024, 17, 2935. https://doi.org/10.3390/en17122935
Son KJ. Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro–Thermo–Fluidic Simulations. Energies. 2024; 17(12):2935. https://doi.org/10.3390/en17122935
Chicago/Turabian StyleSon, Kwon Joong. 2024. "Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro–Thermo–Fluidic Simulations" Energies 17, no. 12: 2935. https://doi.org/10.3390/en17122935
APA StyleSon, K. J. (2024). Model Characterization of High-Voltage Layer Heater for Electric Vehicles through Electro–Thermo–Fluidic Simulations. Energies, 17(12), 2935. https://doi.org/10.3390/en17122935






