An Experimental Performance Assessment of a Passively Controlled Wind Turbine Blade Concept: Part A—Isotropic Materials
Abstract
:1. Introduction
1.1. Context and Importance of Renewable Energy
1.2. Small Wind Energy Converter Systems
1.3. Literature Review
1.3.1. Passive Control Concepts
1.3.2. Passive Twist Coupled Control Concepts
1.3.3. Passive Control Numerical Codes and Algorithms Studies
1.4. Scope
2. Methodology
2.1. Overview
- A brief overview of the key points of the Blade Geometry Algorithm, which will not be detailed extensively in this paper as it is the subject of another study. This will include an introduction to the concept and the fundamental steps involved.
- A detailed presentation of the test campaign conducted for all three blades, highlighting experimental setups and findings.
- An explanation of the measurement apparatus and the configuration of the wind tunnel used during the tests.
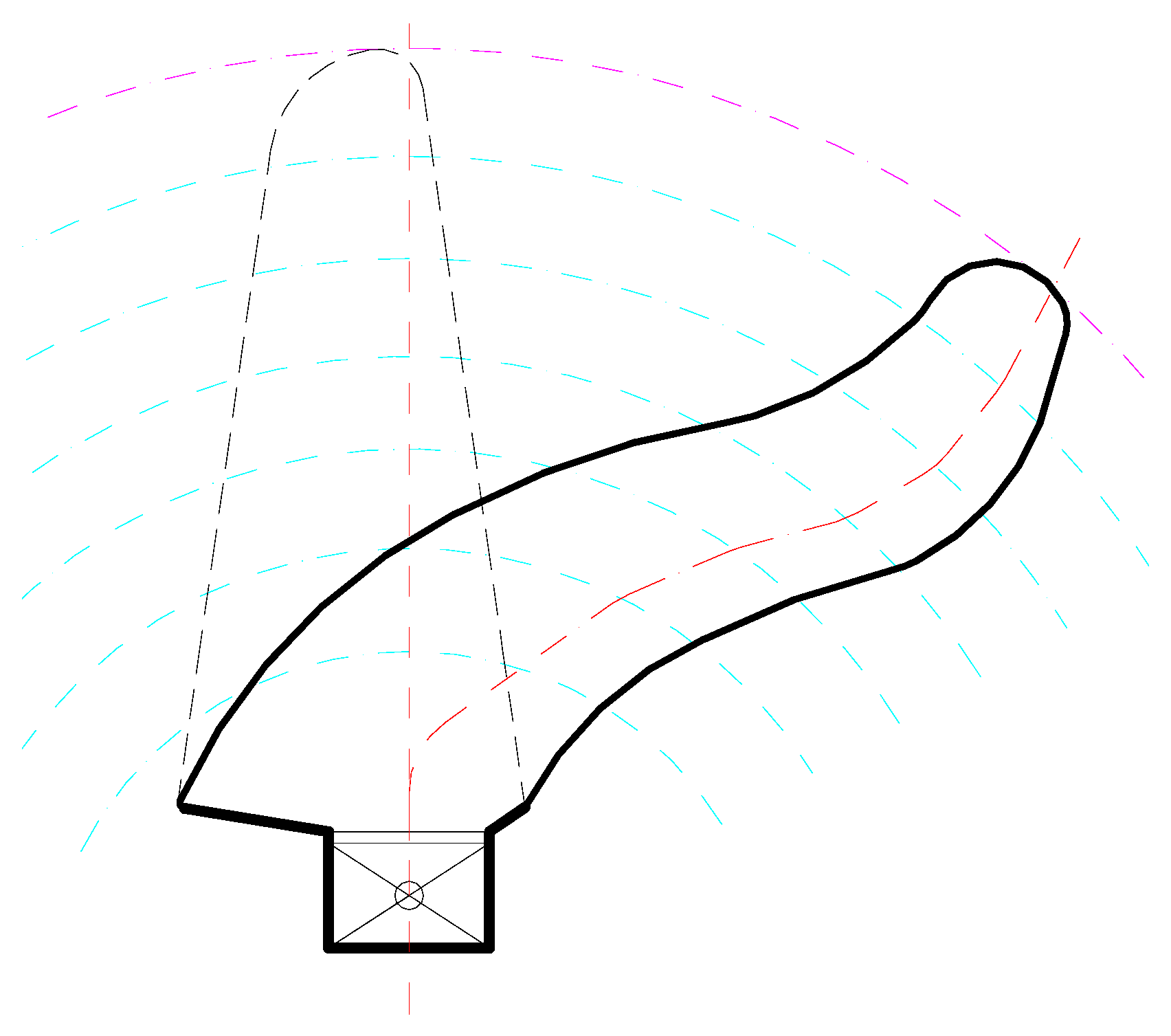
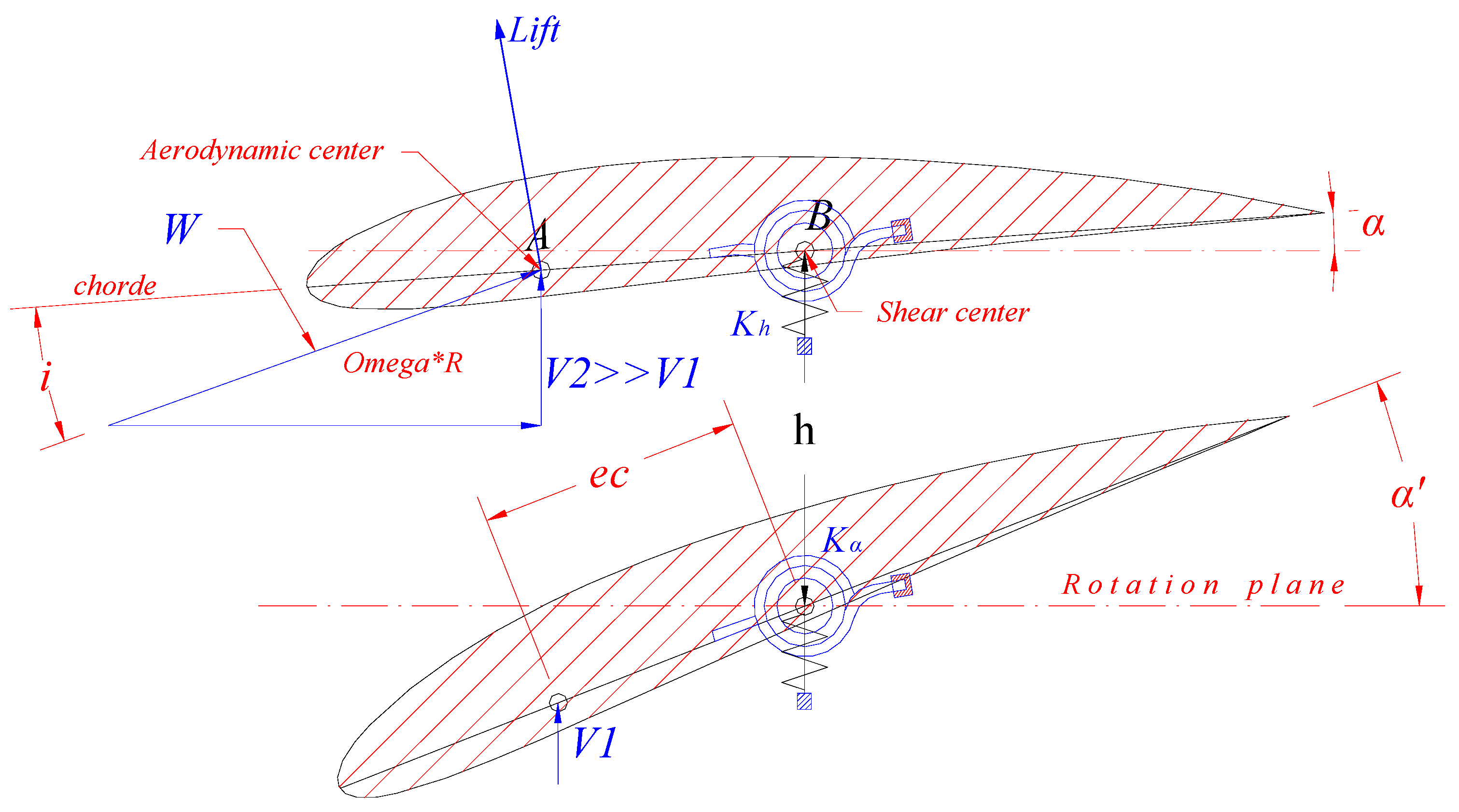
2.2. Blade Geometry Algorithm
- -
- Quick start-up of the blade to ensure rapid response to wind conditions.
- -
- Achievement of nominal velocity at nominal wind speeds (8–10 m/s).
- -
- Maintenance of a stable power yield plateau from nominal speed up to the cutoff speed.
- -
- Initiation of stalling in the wind blade when wind speeds exceed the cutoff threshold.
2.3. Blade Materials and Construction
2.3.1. Blade Material
2.3.2. Post-Construction Procedure
2.4. Measurement Campaign
2.4.1. Types of Measurements
2.4.2. Measurement Sets and Designation
2.5. Experimental Apparatus
- -
- An externally calibrated hotwire anemometer for wind speeds (already mentioned before).
- -
- Known weights for calibrating the load cell used for measuring drag.
- -
- Standard weights for torque calibration.
- -
- A tachometer to verify the rpm measurements.
3. Results for Isotropic Blades
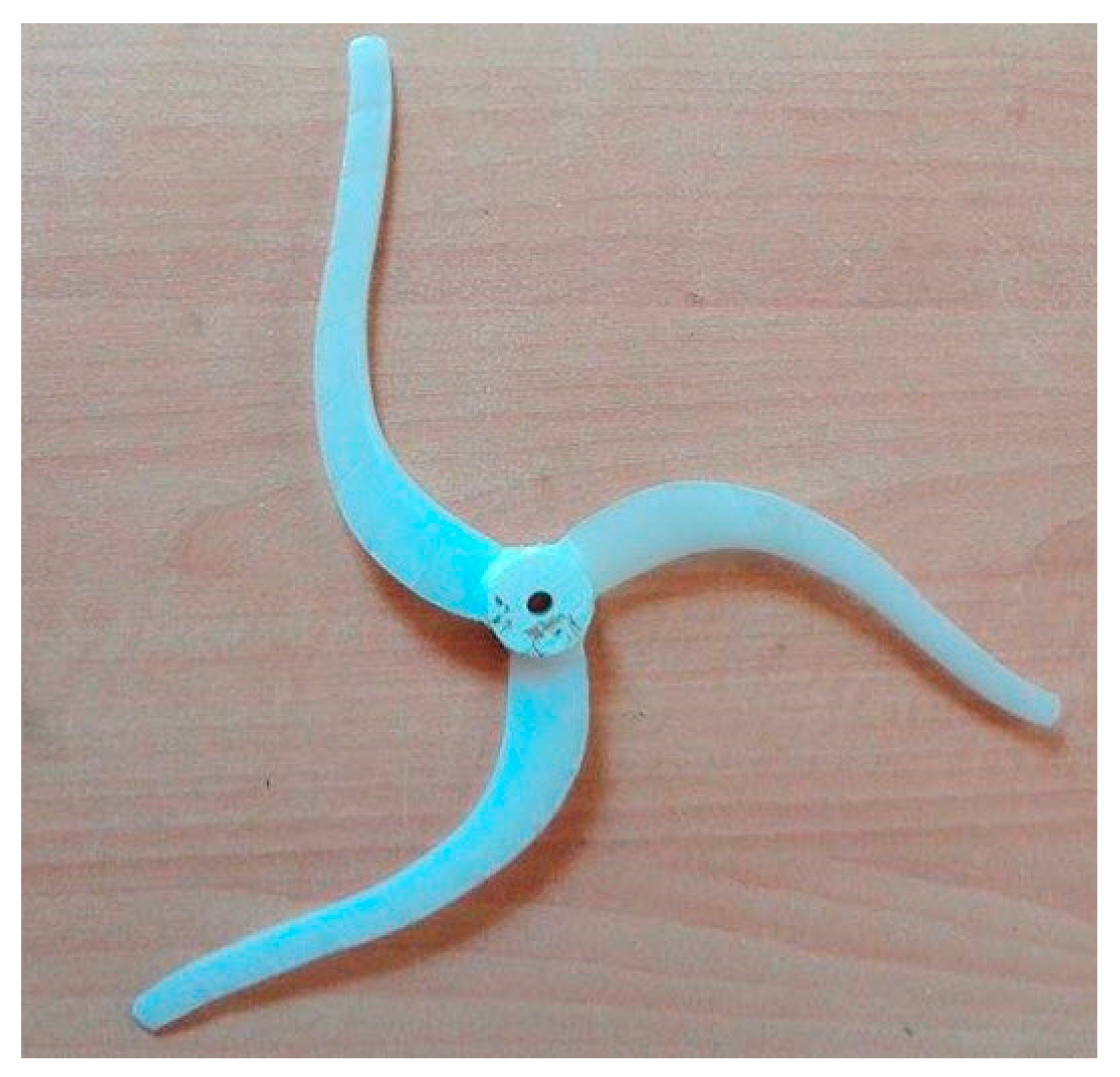
3.1. Geometry for Isotropic Blades
3.2. Straight Blade Isotropic Material
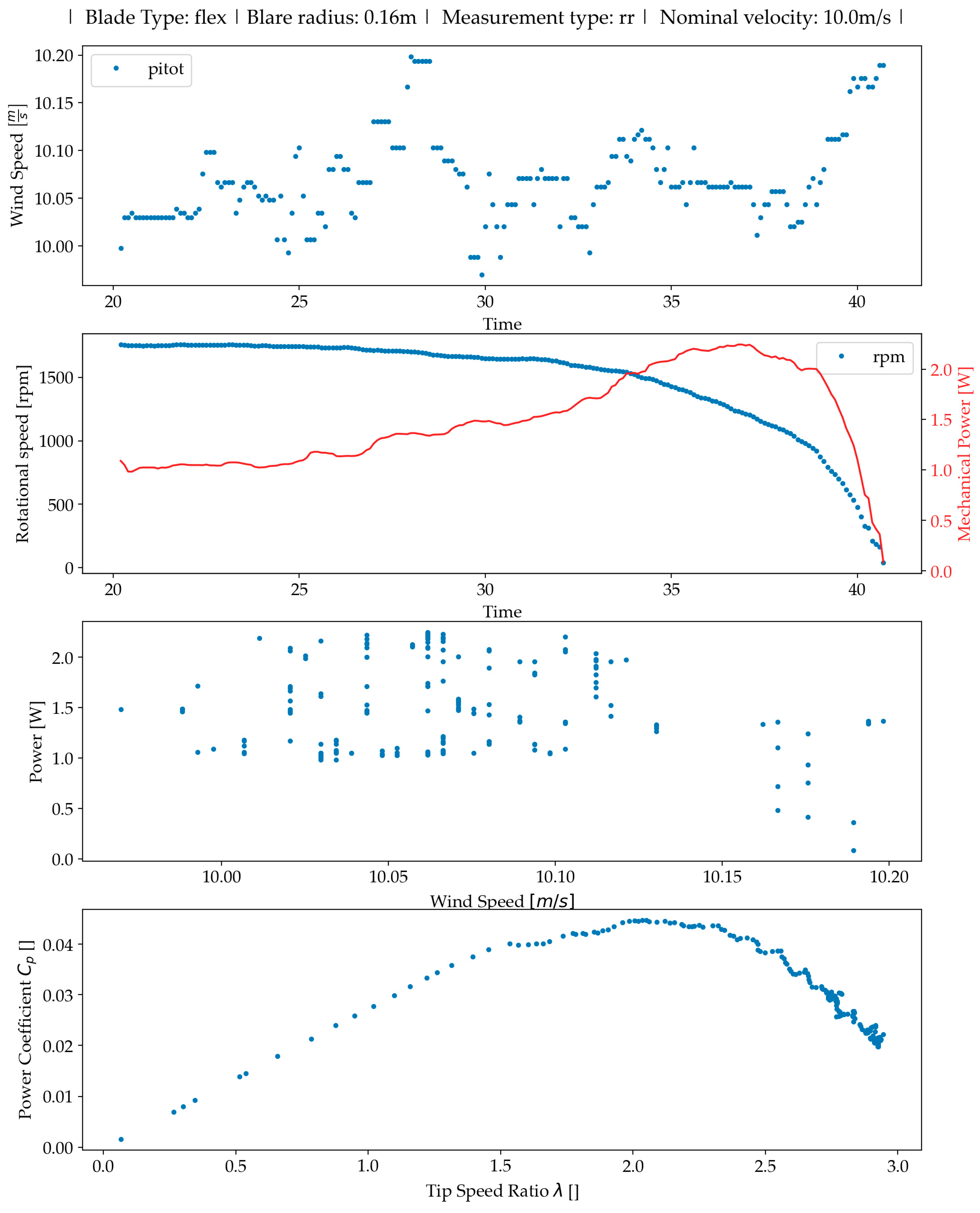
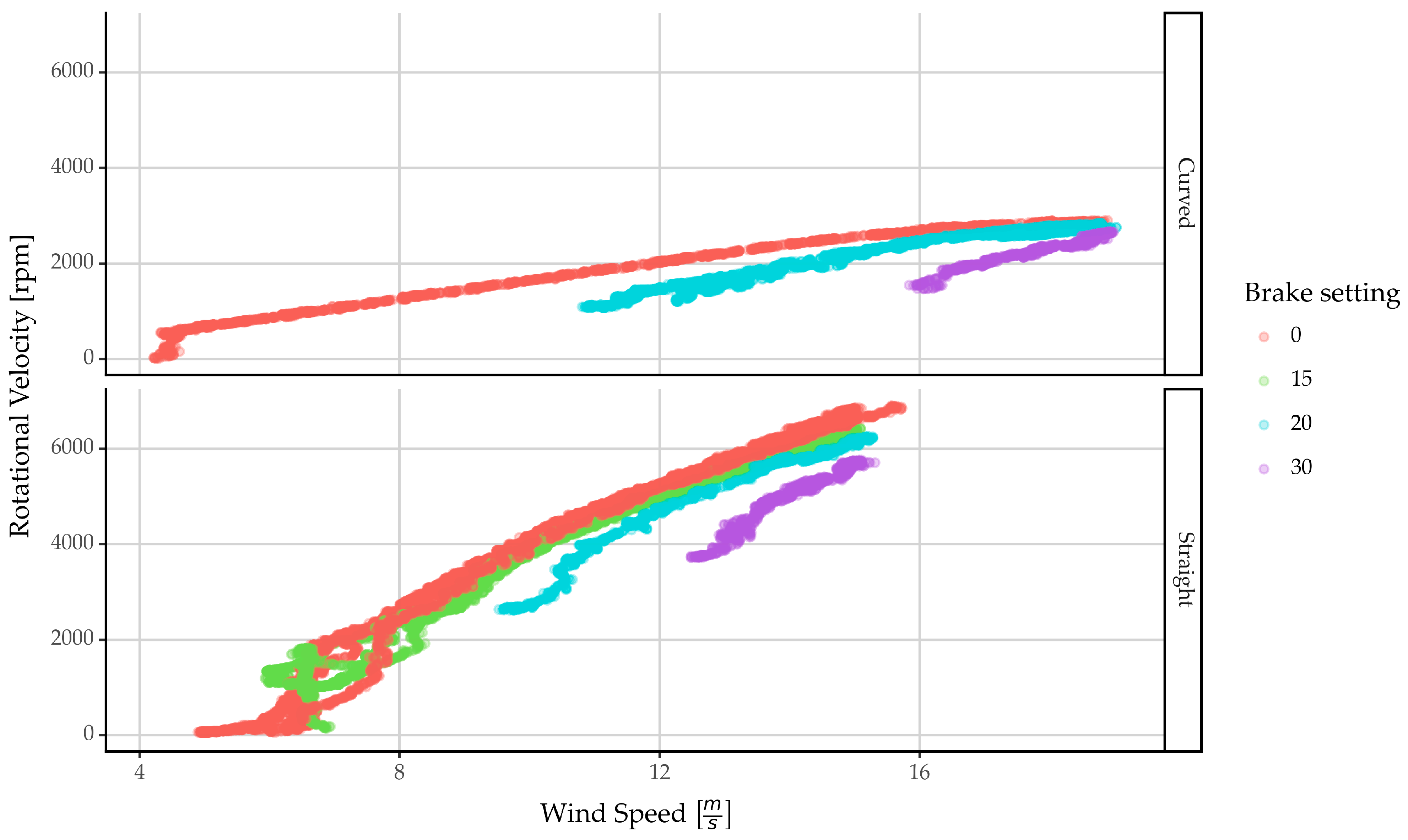
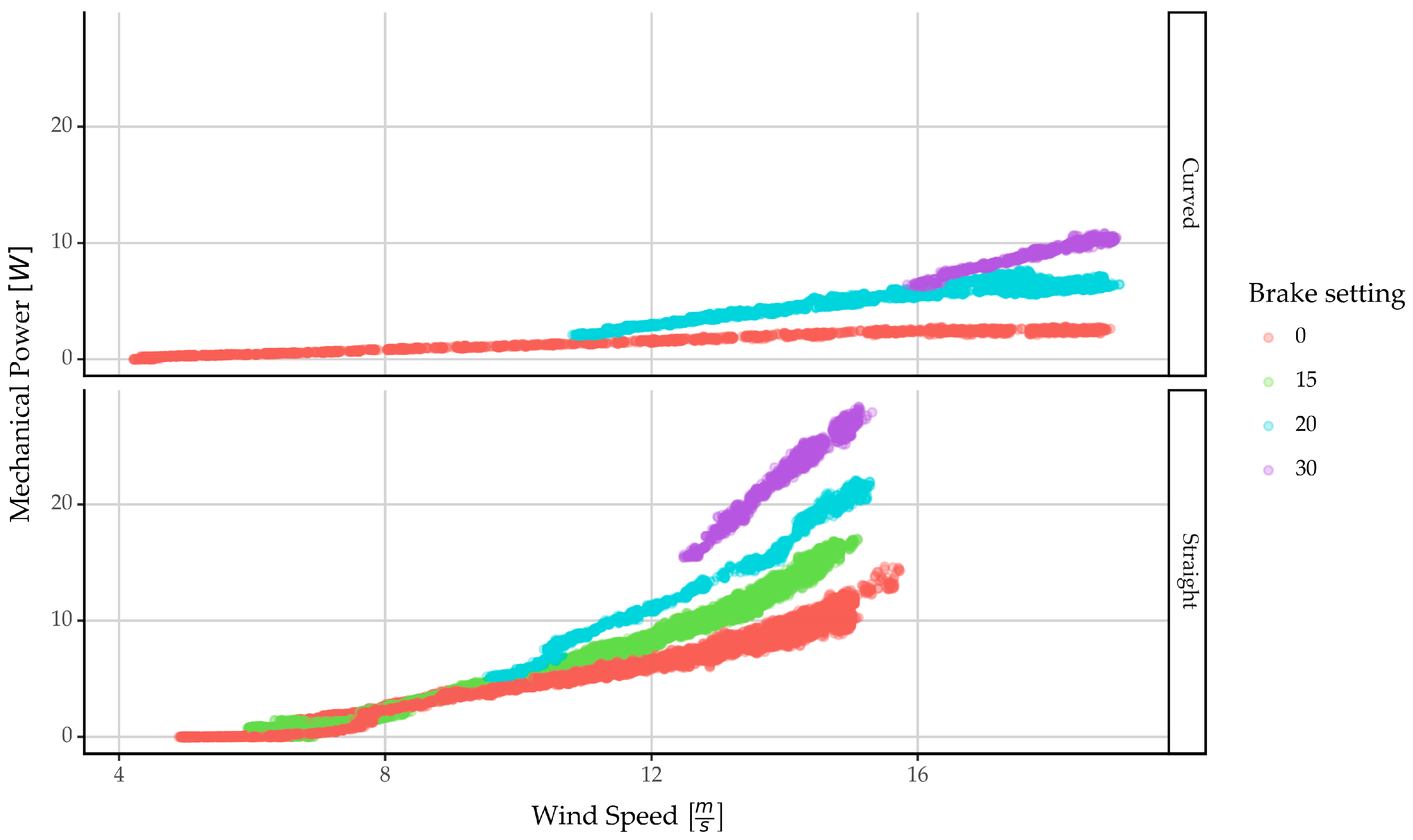
3.2.1. Straight Blade Measurements with Increasing Velocity
3.2.2. Straight Blade Measurements with Constant Velocity
3.3. Flexible Curved Blade: Isotropic Material
3.3.1. Flexible Curved Blade Measurements with Increasing Velocity
3.3.2. Flexible Curved Blade Measurements with Constant Velocity
4. Discussion
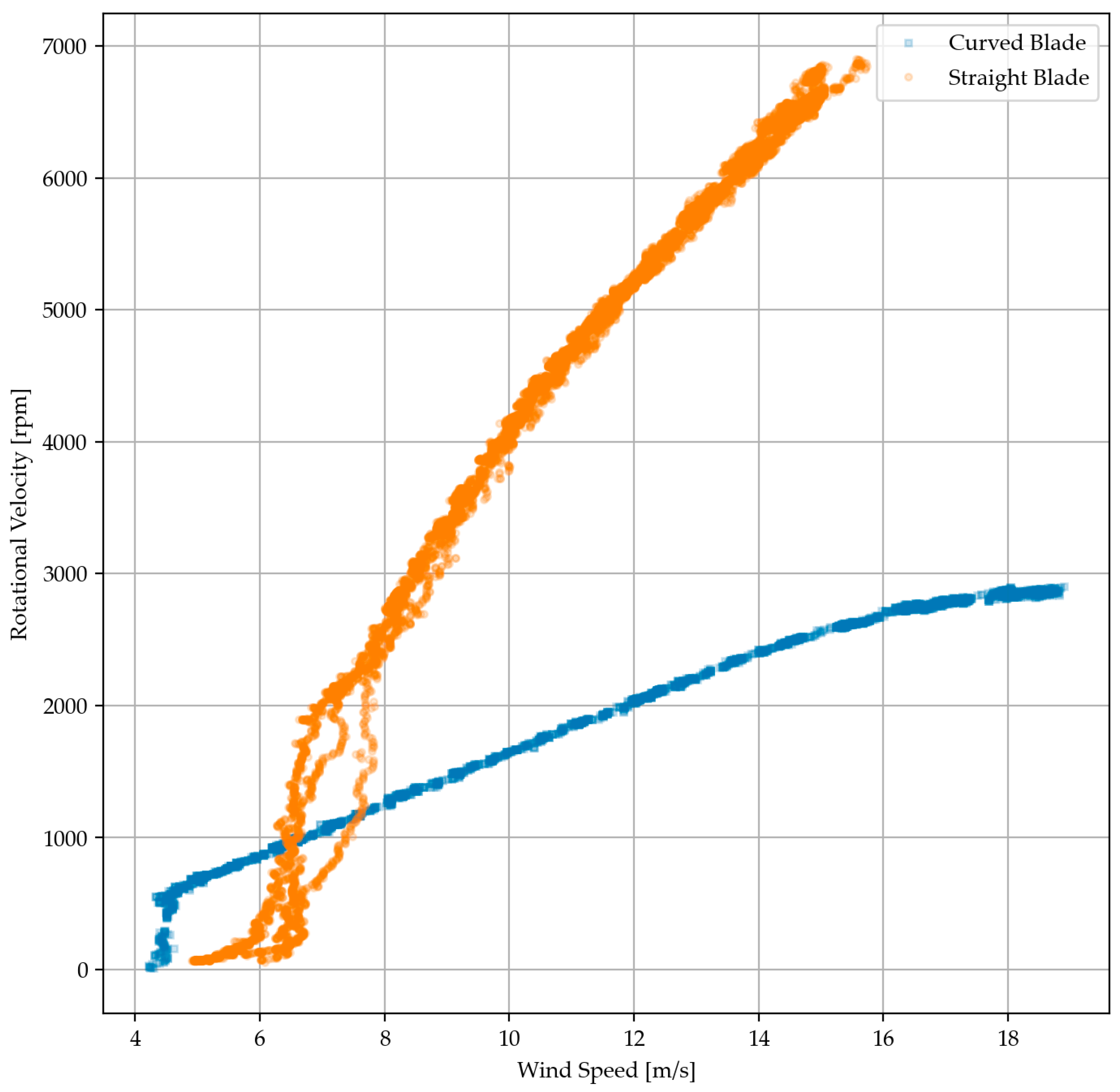
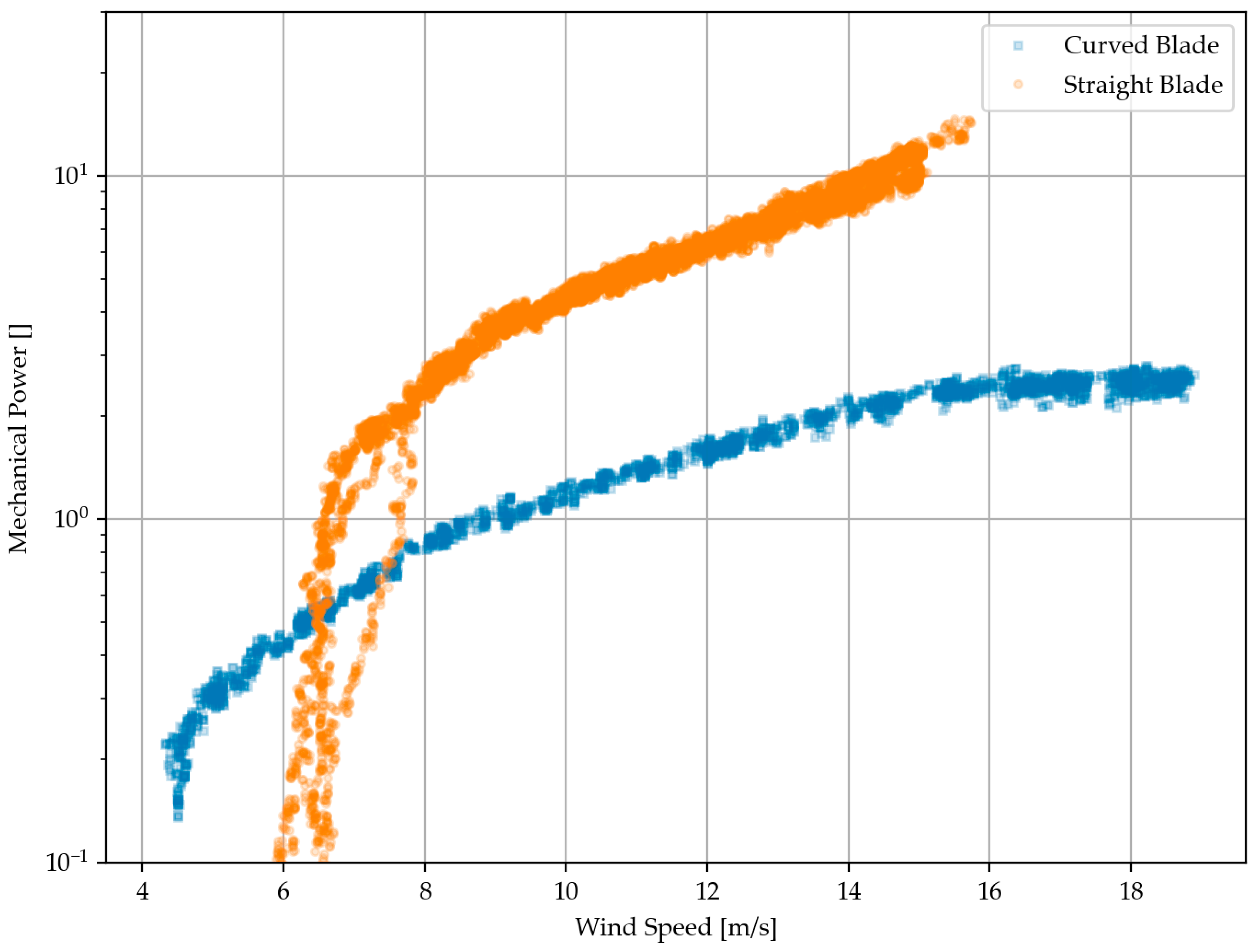
4.1. Self-Regulation of Wind Turbine Blade
4.1.1. Rotational Velocity
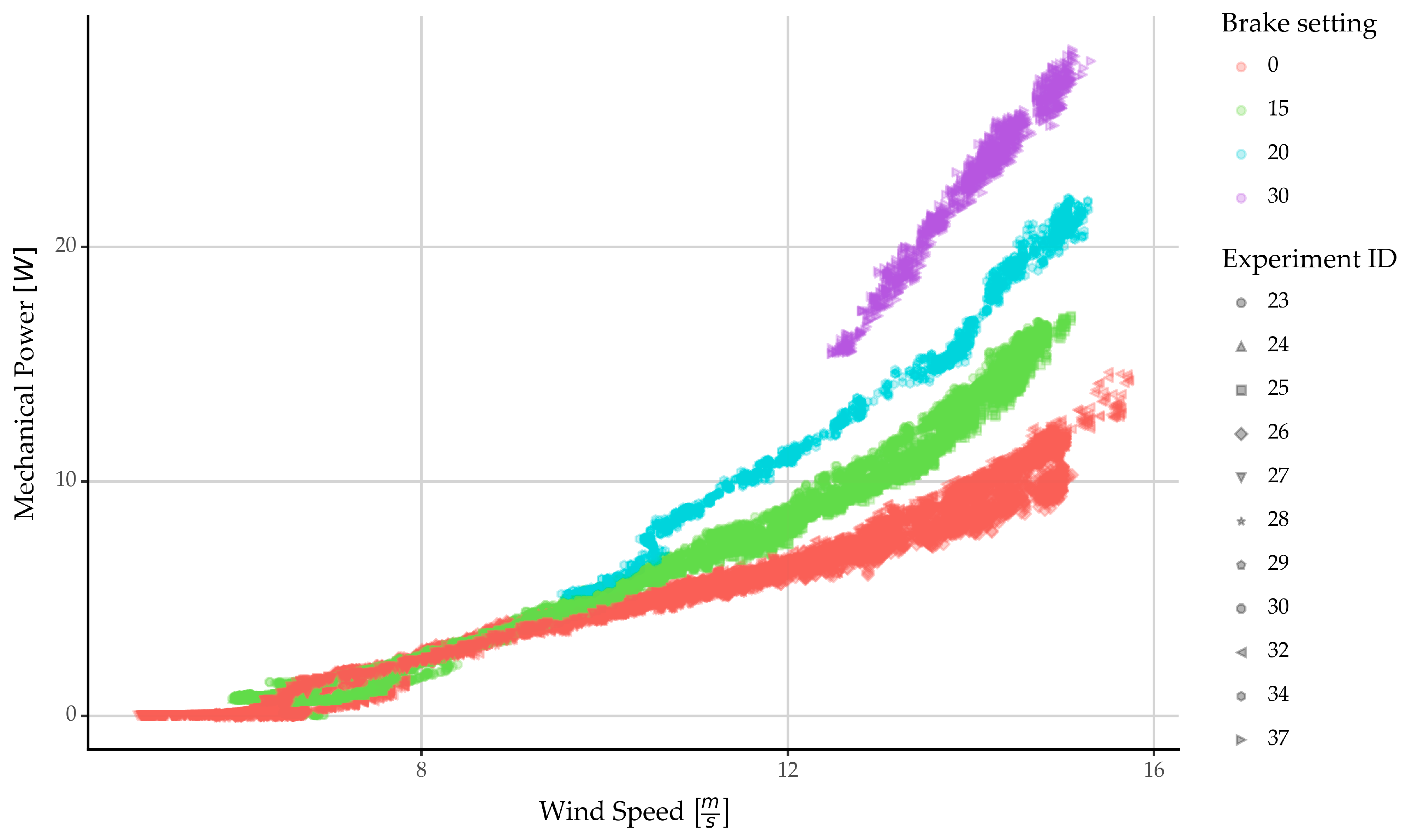
4.1.2. Power vs. Wind Speed
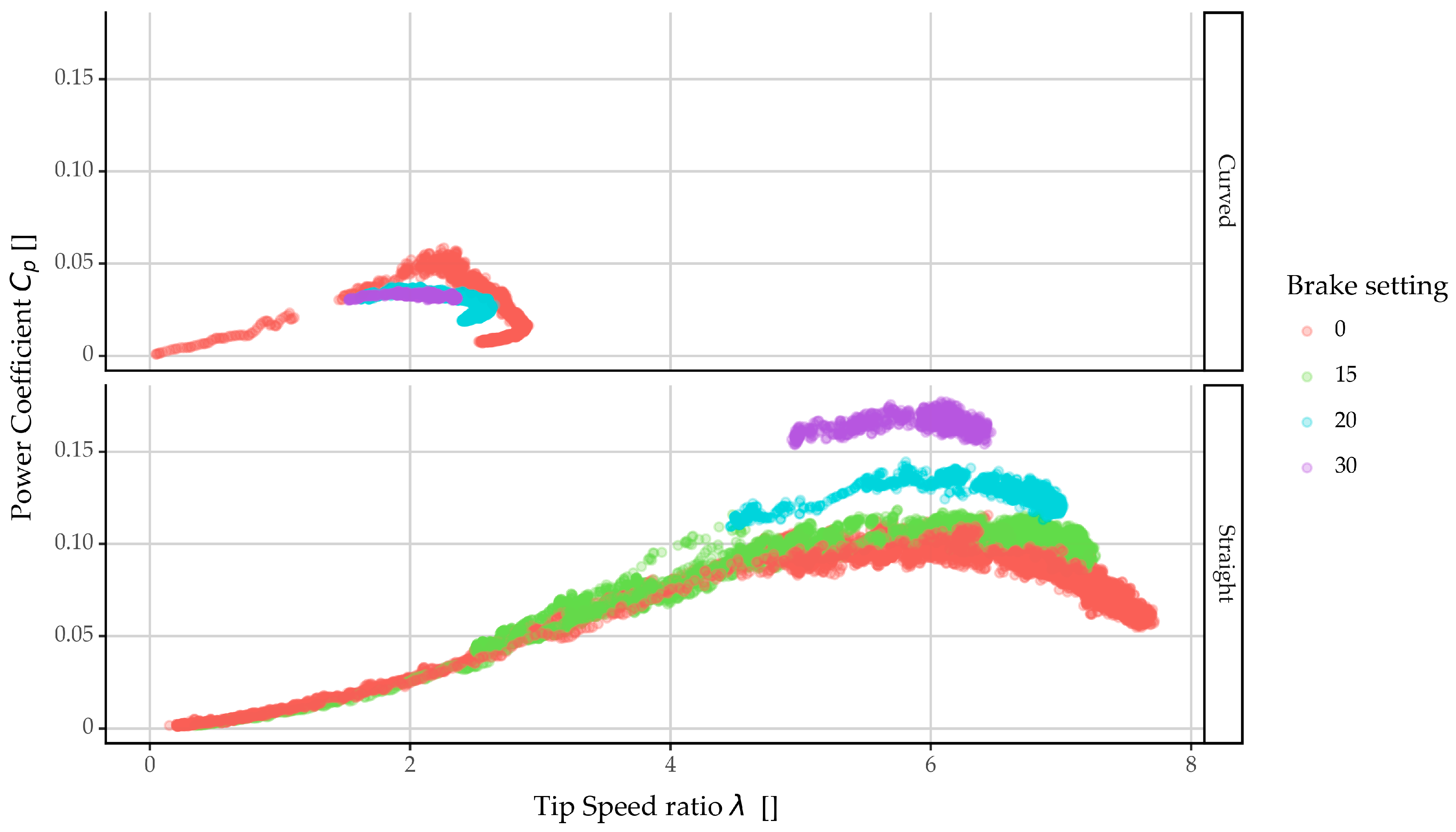
4.2. Power Coefficient vs. Tip Speed Ratio
5. Conclusions
Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations:
| Cp | Power Coefficient |
| MPPT | Maximum Power Point Tracking |
| TSR | Tip Speed Ratio |
| WECS | Wind Energy Converter Systems |
References
- Doukas, H. Energy Citizenship—A New Dimension in Energy Policy Making. Available online: https://www.e-mc2.gr/news/energy-citizenship-new-dimension-energy-policy-making (accessed on 6 February 2024).
- Roesch, R.; Taylor, M.; Al-Zoghoul, S.; Ralon, P.; Sorokina, O. IRENA Report—Renewable Power Generation Costs in 2022; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2022; ISBN 978-92-9260-544-5. [Google Scholar]
- IEA. World Energy Outlook 2013; IEA: Paris, France, 2013. [Google Scholar]
- International Energy Agency (IEA). Global Electricity Generation by Technology, 2015, 2021 and 2027; IEA: Paris, France, 2022. [Google Scholar]
- European Union Electricity and Heat Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_and_heat_statistics (accessed on 3 May 2023).
- Frequently Asked Questions (FAQs)—U.S. Energy Information Administration (EIA). Available online: https://www.eia.gov/tools/faqs/faq.php (accessed on 9 February 2024).
- Hutchinson, M.; Zhao, F. Global Wind Report 2022; Global Wind Energy Council: Brussels, Belgium, 2022. [Google Scholar]
- Ponta, F.L.; Otero, A.D.; Rajan, A.; Lago, L.I. The Adaptive-Blade Concept in Wind-Power Applications. Energy Sustain. Dev. 2014, 22, 3–12. [Google Scholar] [CrossRef]
- Liebst, B.S. Wind Turbine Gust Load Alleviation Utilizing Curved Blades. J. Propuls. Power 1986, 2, 371–377. [Google Scholar] [CrossRef]
- Christakis, D. The Development of Wind Energy Systems in Crete. In Proceedings of the Seminar for the New Trends on Wind Energy, Chanea, Greece; 1991. [Google Scholar]
- Serra, M.F.G.; van Schoor, M.C. Aeroelastic Tailoring of a Horizontal Axis Wind Turbine. Wind Eng. 1995, 19, 193–207. [Google Scholar]
- Eggers, A.J., Jr.; Ashley, H.; Rock, S.M.; Chaney, K.; Digumarthi, R. Effects of Blade Bending on Aerodynamic Control of Fluctuating Loads on Teetered HAWT Rotors. J. Sol. Energy Eng. 1996, 118, 239–245. [Google Scholar] [CrossRef]
- Tran, D.-H.; Sareni, B.; Roboam, X.; Espanet, C. Integrated Optimal Design of a Passive Wind Turbine System: An Experimental Validation. IEEE Trans. Sustain. Energy 2010, 1, 48–56. [Google Scholar] [CrossRef]
- Infield, D.G.; Feuchtwang, J.B. Design Criteria for Passive Pitch Control of Wind Turbines Using Self-Twisting Blades. Int. J. Ambient. Energy 1995, 16, 139–146. [Google Scholar] [CrossRef]
- Infield, D.G.; Feuchtwang, J.B.; Fitches, P. Development and Testing of a Novel Self-Twisting Wind Turbine Rotor. In 1999 European Wind Energy Conference; Routledge: London, UK, 1999; ISBN 978-1-315-07433-7. [Google Scholar]
- Lobitz, D.W.; Veers, P.S.; Migliore, P.G. Enhanced Performance of HAWTs Using Adaptive Blades. In Proceedings of the Wind 1996 ASME Wind Energy Symposium, Houston, TX, USA, January 29–2 February 1996; Report Number: CONF-960154. American Society of Mechanical Engineers: New York, NY, USA; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 1996. [Google Scholar]
- Lobitz, D.; Veers, P. Aeroelastic Behavior of Twist-Coupled HAWT Blades. In 1998 ASME Wind Energy Symposium; Aerospace Sciences Meetings; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1998. [Google Scholar]
- Eisler, G.R.; Veers, P.S. Parameter Optimization Applied to Use of Adaptive Blades on a Variable Speed Wind Turbine; Sandia National Laboratories: Albuquerque, NM, USA, 1998. [Google Scholar]
- Lobitz, D.; Laino, D. Load Mitigation with Twist-Coupled HAWT Blades. In 37th Aerospace Sciences Meeting and Exhibit; Aerospace Sciences Meetings; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1999. [Google Scholar]
- Lobitz, D.; Veers, P.; Laino, D. Performance of Twist-Coupled Blades on Variable Speed Rotors. In 2000 ASME Wind Energy Symposium; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar]
- Condaxakis, C.G.; Christakis, D.G.; Frandsen, S.T.; Eboueya, M. Passive Controlled Wind Turbine Blades. In Proceedings of the 1999 European Wind Energy Conference, Nice, France, 1 March 1999; James & James Ltd.: Nice, France, 1999. [Google Scholar]
- Christakis, D.G.; Condaxakis, C.G.; Eboueya, M.; Granier, P. A Contribution to the Passive Controlled Optimised Wind Motor Design. In Proceedings of the Computational Engineering in Systems Applications CESA, Nabeul-Hamamet, Tunisia, 1 April 1998; IEEE: Nabeul-Hamamet, Tunisia, 1998. [Google Scholar]
- Zuteck, M. Adaptive Blade Concept Assessment: Curved Platform Induced Twist Investigation; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA; Livermore, CA, USA, 2002. [Google Scholar]
- Larwood, S.; Zutek, M. Swept Wind Turbine Blade Aeroelastic Modeling for Loads and Dynamic Behavior. In Proceedings of the WINDPOWER 2006, Pittsburgh, PA, USA, 4–7 June 2006. [Google Scholar]
- Ashwill, T.D. Sweep-Twist Adaptive Rotor Blade: Final Project Report; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2010. [Google Scholar]
- Masoudi, M.; Pope, K. Numerical Predictions on Fluid-Structure Bend-Twist Coupling of Wind Turbine Blades. Int. J. Mech. Eng. Robot. Res. 2019, 8, 506–510. [Google Scholar] [CrossRef]
- Wiens, M.; Meyer, T.; Wenske, J. Exploiting Bend-Twist Coupling in Wind Turbine Control for Load Reduction⁎. IFAC-Pap. 2020, 53, 12139–12144. [Google Scholar] [CrossRef]
- Tamayo-Avendaño, J.M.; Patiño-Arcila, I.D.; Nieto-Londoño, C.; Sierra-Pérez, J. Fluid–Structure Interaction Analysis of a Wind Turbine Blade with Passive Control by Bend–Twist Coupling. Energies 2023, 16, 6619. [Google Scholar] [CrossRef]
- Riva, R.; Spinelli, M.; Sartori, L.; Cacciola, S.; Croce, A. Stability Analysis of Wind Turbines with Bend-Twist Coupled Blades. J. Phys. Conf. Ser. 2018, 1037, 062014. [Google Scholar] [CrossRef]
- Voutsinas, S.G.; Belessis, M.A.; Rados, K.G. Investigation of the Yawed Operation of Wind Turbines by Means of a Vortex Particle Method. In Proceedings of the AGARD Conference Proceedings AGARD CP; Advisory Group for Aerospace Research and Development (AGARD): Neuilly sur Seine, France, 1995. [Google Scholar]
- Capuzzi, M.; Pirrera, A.; Weaver, P.M. Structural Design of a Novel Aeroelastically Tailored Wind Turbine Blade. Thin-Walled Struct. 2015, 95, 7–15. [Google Scholar] [CrossRef]
- MacPhee, D.; Beyene, A. A Flexible Turbine Blade for Passive Blade Pitch Control in Wind Turbines. In Proceedings of the 2011 IEEE Power Engineering and Automation Conference, Wuhan, China, 8–9 September 2011; Volume 1, pp. 196–199. [Google Scholar]
- Larwood, S.; van Dam, C.P.; Schow, D. Design Studies of Swept Wind Turbine Blades. Renew. Energy 2014, 71, 563–571. [Google Scholar] [CrossRef]
- Shen, X.; Chen, J.-G.; Zhu, X.-C.; Liu, P.-Y.; Du, Z.-H. Multi-Objective Optimization of Wind Turbine Blades Using Lifting Surface Method. Energy 2015, 90, 1111–1121. [Google Scholar] [CrossRef]
- Khalafallah, M.G.; Ahmed, A.M.; Emam, M.K. CFD Study of Some Factors Affecting Performance of HAWT with Swept Blades. Int. J. Sustain. Energy 2017, 36, 489–501. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Tsai, Y.-F.; Huang, C.-C.; Li, M.-H.; Hsiao, F.-B. The Design and Analysis of Passive Pitch Control for Horizontal Axis Wind Turbine. Energy Procedia 2014, 61, 683–686. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Shiah, Y.C. Experiments on the Performance of Small Horizontal Axis Wind Turbine with Passive Pitch Control by Disk Pulley. Energies 2016, 9, 353. [Google Scholar] [CrossRef]
- Chu, Y.-J.; Chong, W.-T. A Biomimetic Wind Turbine Inspired by Dryobalanops Aromatica Seed: Numerical Prediction of Rigid Rotor Blade Performance with OpenFOAM®. Comput. Fluids 2017, 159, 295–315. [Google Scholar] [CrossRef]
- Krogstad, P.-Å.; Lund, J.A. An Experimental and Numerical Study of the Performance of a Model Turbine. Wind Energy 2012, 15, 443–457. [Google Scholar] [CrossRef]
- Larsen, G.C.; Frandsen, S.T.; Sørensen, P.E.; Courtney, M. Design Basis for Horizontal-Axis Wind Turbines. Theoretical Background; Risoe National Lab.: Roskilde, Denmark, 1990. [Google Scholar]
- Le Gouriérès Désiré; Le Gouriérès, D. Energie Éolienne: Théorie, Conception et Calcul Pratique Des Installations/Par Désiré Le Gourières, …; Eyrolles: Paris, France, 1980. [Google Scholar]
- Hansen, M. The Classical Blade Element Momentum Method. In Aerodynamics of Wind Turbines, 2nd ed.; Routledge: London, UK, 2007; ISBN 978-1-84977-040-8. [Google Scholar]
- Zhang, X.; Jia, J.; Zheng, L.; Yi, W.; Zhang, Z. Maximum Power Point Tracking Algorithms for Wind Power Generation System: Review, Comparison and Analysis. Energy Sci. Eng. 2023, 11, 430–444. [Google Scholar] [CrossRef]
- Kesraoui, M.; Korichi, N.; Belkadi, A. Maximum Power Point Tracker of Wind Energy Conversion System. Renew. Energy 2011, 36, 2655–2662. [Google Scholar] [CrossRef]




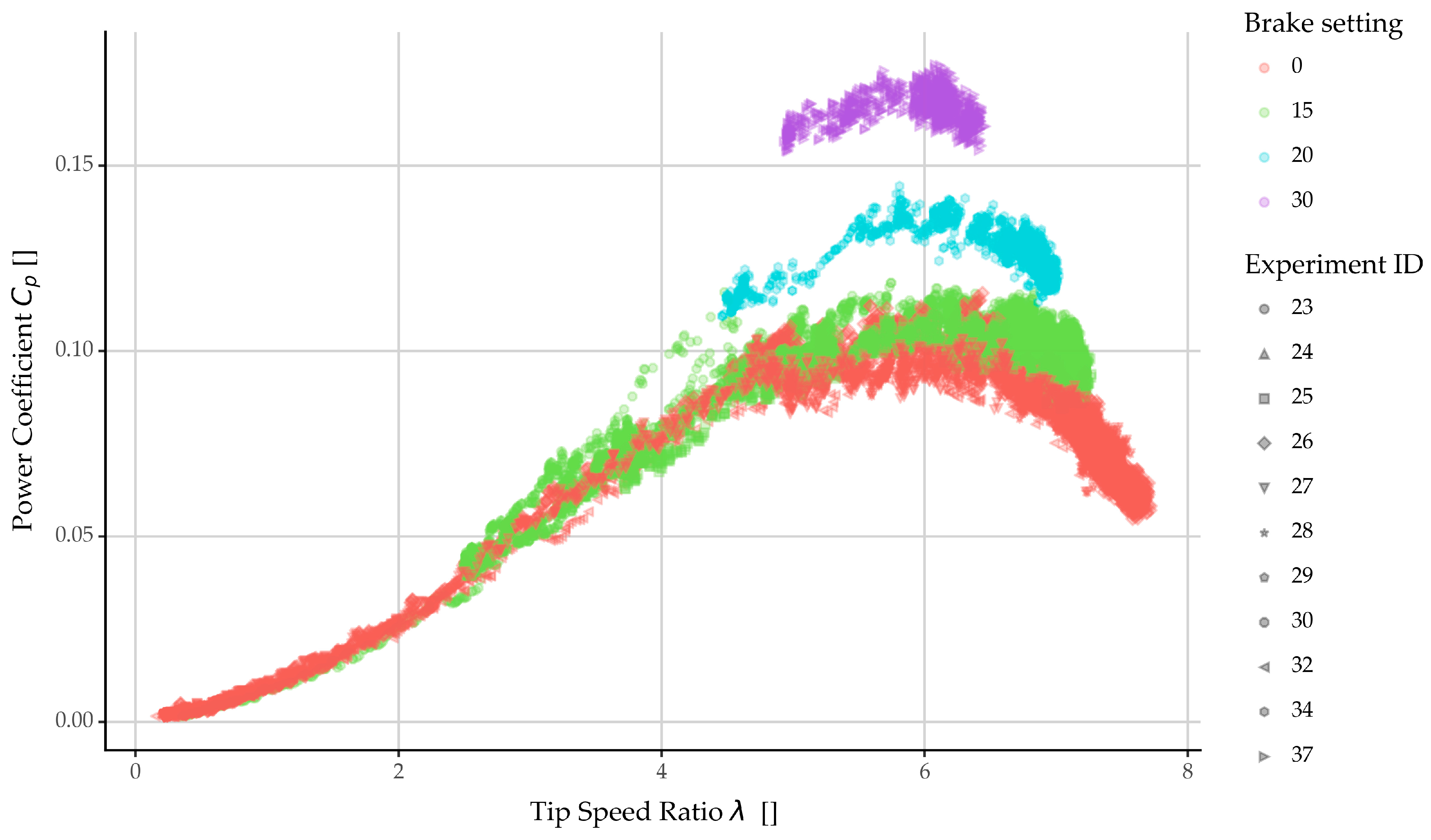
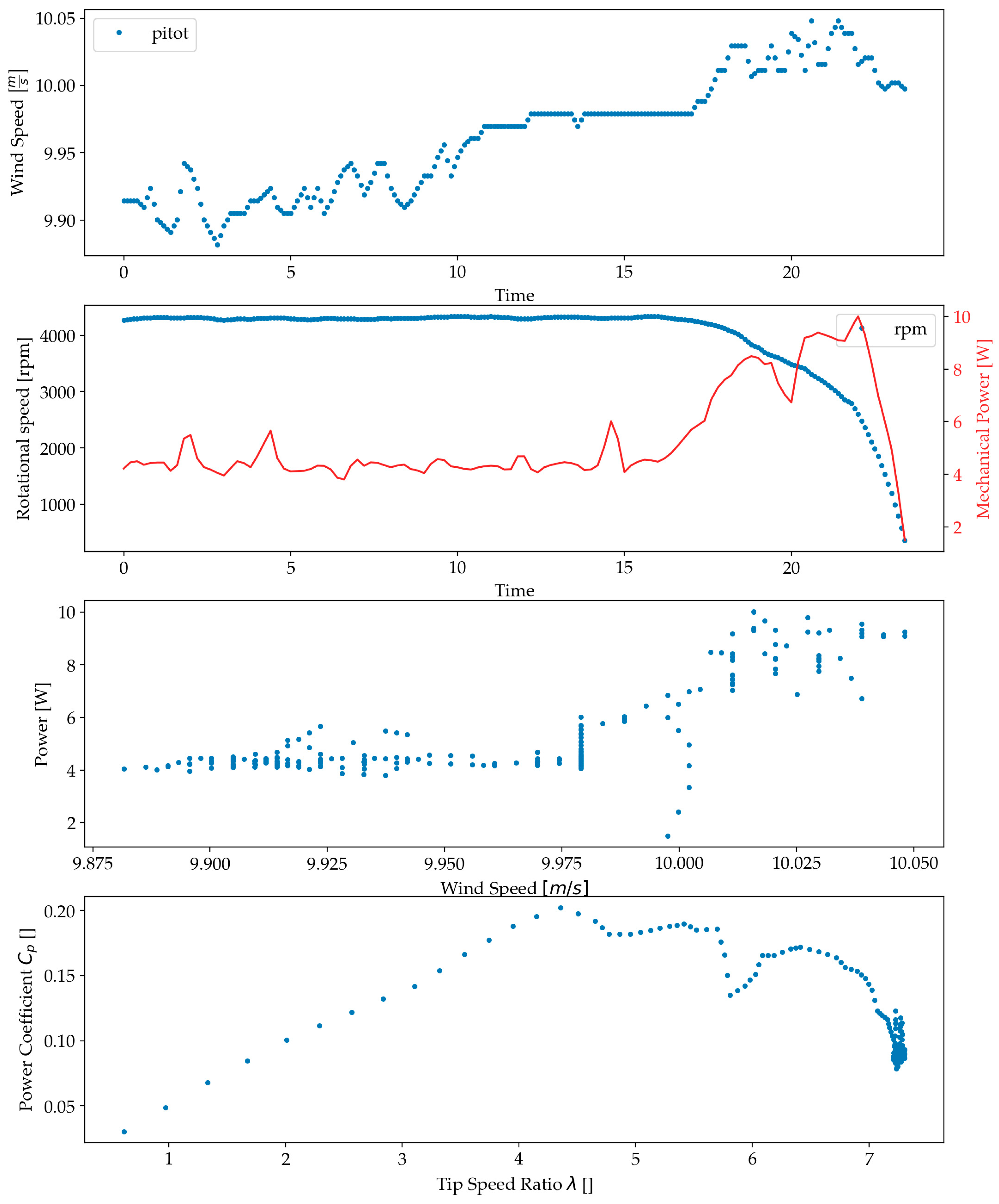

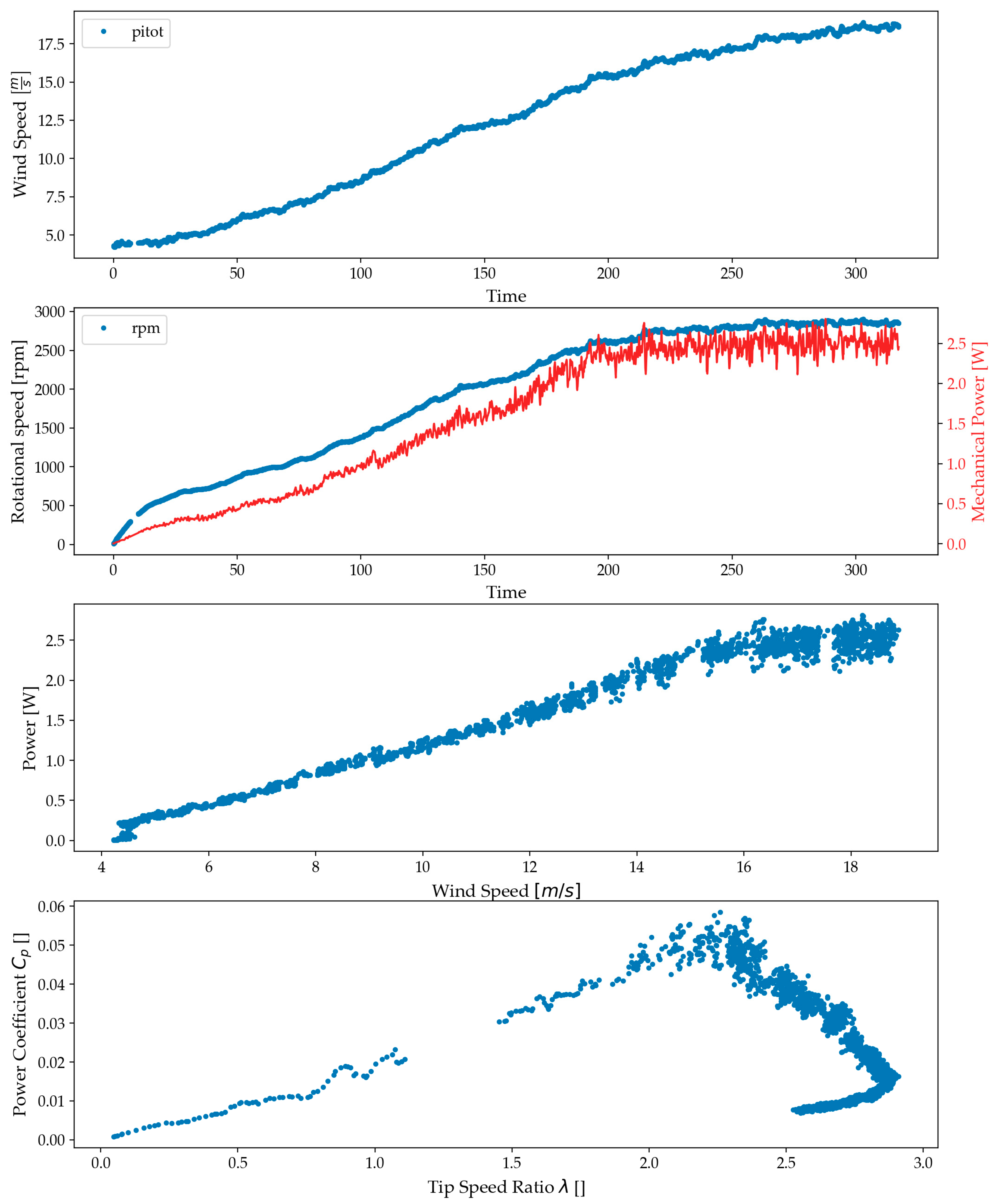

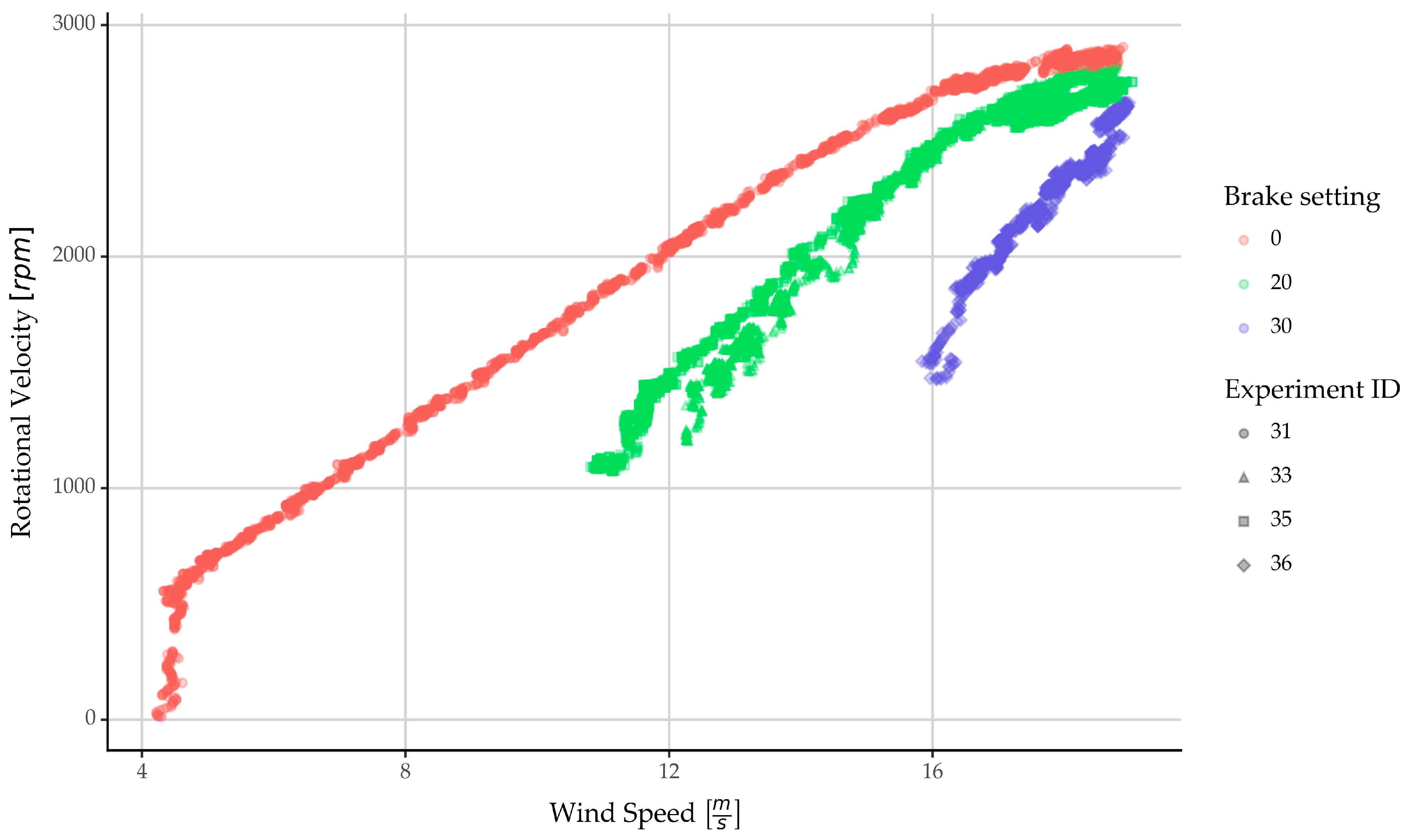


| Dataset Name | Blade Type | Radius [m] | Wind Speed Velocity | Load |
|---|---|---|---|---|
| ISO.Curved.RR.<xx>.<y> | Isotropic curved | 0.160 | 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 | Ramp |
| ISO.Straight.RR.<xx>.<y> | Isotropic straight | 0.160 | 6, 8, 10, 12, 14 | Ramp |
| Dataset Name | Exp. UID | Blade Type | Radius [m] | Type of Meas. | Load | Wind Speed Velocity Range | Max rpm during Test |
|---|---|---|---|---|---|---|---|
| VV. 0907.23 | 23 | straight | 0.16 | VV | 15 | 6–15 | 6300 |
| VV. 0907.24 | 24 | straight | 0.16 | VV | 15 | 6–15 | 6300 |
| VV. 0908.25 | 25 | straight | 0.16 | VV | 15 | 6–15 | 6400 |
| VV. 0908.26 | 26 | straight | 0.16 | VV | 0 | 6–15 | 6900 |
| VV. 0908.27 | 27 | straight | 0.16 | VV | 0 | 5–15 | 6700 |
| VV. 0908.28 | 28 | straight | 0.16 | VV | 0 | 7–15 | 6700 |
| VV. 0908.29 | 29 | straight | 0.16 | VV | 15 | 6–15 | 6300 |
| VV. 0908.30 | 30 | straight | 0.16 | VV | 15 | 6–15 | 6200 |
| VV. 0908.31 | 31 | curved | 0.16 | VV | 0 | 4–19 | 2900 |
| VV. 0908.32 | 32 | straight | 0.16 | VV | 0 | 6–15 | 6900 |
| VV. 0908.33 | 33 | curved | 0.16 | VV | 20 | 12–19 | 2800 |
| VV. 0908.34 | 34 | straight | 0.16 | VV | 20 | 9–15 | 6300 |
| VV. 0908.35 | 35 | curved | 0.16 | VV | 20 | 10–19 | 2800 |
| VV. 0908.36 | 36 | curved | 0.16 | VV | 30 | 15–19 | 2700 |
| VV. 0908.37 | 37 | straight | 0.16 | VV | 30 | 12–15 | 5800 |
| Measurement | Device | Model Name | Company, Country |
|---|---|---|---|
| Wind speed Pitot | differential pressure transducer | HD408T | Delta Ohm (now Senseca), Italy |
| Torque | Rotating Torquemeter | No DR2112L | SCAIME, France |
| Rotational Velocity | Rotating Torquemeter | No DR2112L | SCAIME, France |
| Drag | Load Cell | model No SP4MC6MR | HBM (now HBK), Germany |
| DAQ | Multifunction Data Acquisition card | NI-USB-6353 | National Instruments, USA |
| Seg. No | Radius [m] | Chord [m] | Pitch Angle [deg] | Eccentricity [deg] |
|---|---|---|---|---|
| 1 | 0.016 | 0.0238 | 27.095 | 0.00 |
| 2 | 0.032 | 0.0242 | 19.599 | 0.00 |
| 3 | 0.048 | 0.0227 | 14.057 | 2.51 |
| 4 | 0.064 | 0.0202 | 10.436 | 8.71 |
| 5 | 0.080 | 0.0177 | 8.009 | 17.22 |
| 6 | 0.096 | 0.0156 | 6.310 | 25.11 |
| 7 | 0.112 | 0.0138 | 5.073 | 32.37 |
| 8 | 0.128 | 0.0123 | 4.141 | 37.44 |
| 9 | 0.144 | 0.0111 | 3.418 | 40.73 |
| 10 | 0.160 | 0.0101 | 2.846 | 42.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadakis, N.; Condaxakis, C. An Experimental Performance Assessment of a Passively Controlled Wind Turbine Blade Concept: Part A—Isotropic Materials. Energies 2024, 17, 3049. https://doi.org/10.3390/en17123049
Papadakis N, Condaxakis C. An Experimental Performance Assessment of a Passively Controlled Wind Turbine Blade Concept: Part A—Isotropic Materials. Energies. 2024; 17(12):3049. https://doi.org/10.3390/en17123049
Chicago/Turabian StylePapadakis, Nikolaos, and Constantinos Condaxakis. 2024. "An Experimental Performance Assessment of a Passively Controlled Wind Turbine Blade Concept: Part A—Isotropic Materials" Energies 17, no. 12: 3049. https://doi.org/10.3390/en17123049
APA StylePapadakis, N., & Condaxakis, C. (2024). An Experimental Performance Assessment of a Passively Controlled Wind Turbine Blade Concept: Part A—Isotropic Materials. Energies, 17(12), 3049. https://doi.org/10.3390/en17123049








