Analysis of Stray Current Leakage in Subway Traction Power Supply System Based on Field-Circuit Coupling
Abstract
1. Introduction
- (1)
- In this paper, a field-circuit coupling method is proposed.
- (2)
- In this paper, two scenarios are modeled, analyzed, and discussed for the mainline and depot of the subway line, respectively.
- (3)
- This paper analyzes the current leakage and distribution law at the mainline and depot of the subway.
- (4)
- The methodology presented in this paper will facilitate the design of stray current mitigation measures for high-risk areas in both the mainline and the subway depot.
2. Modeling Fundamental
2.1. The Finite Element Field
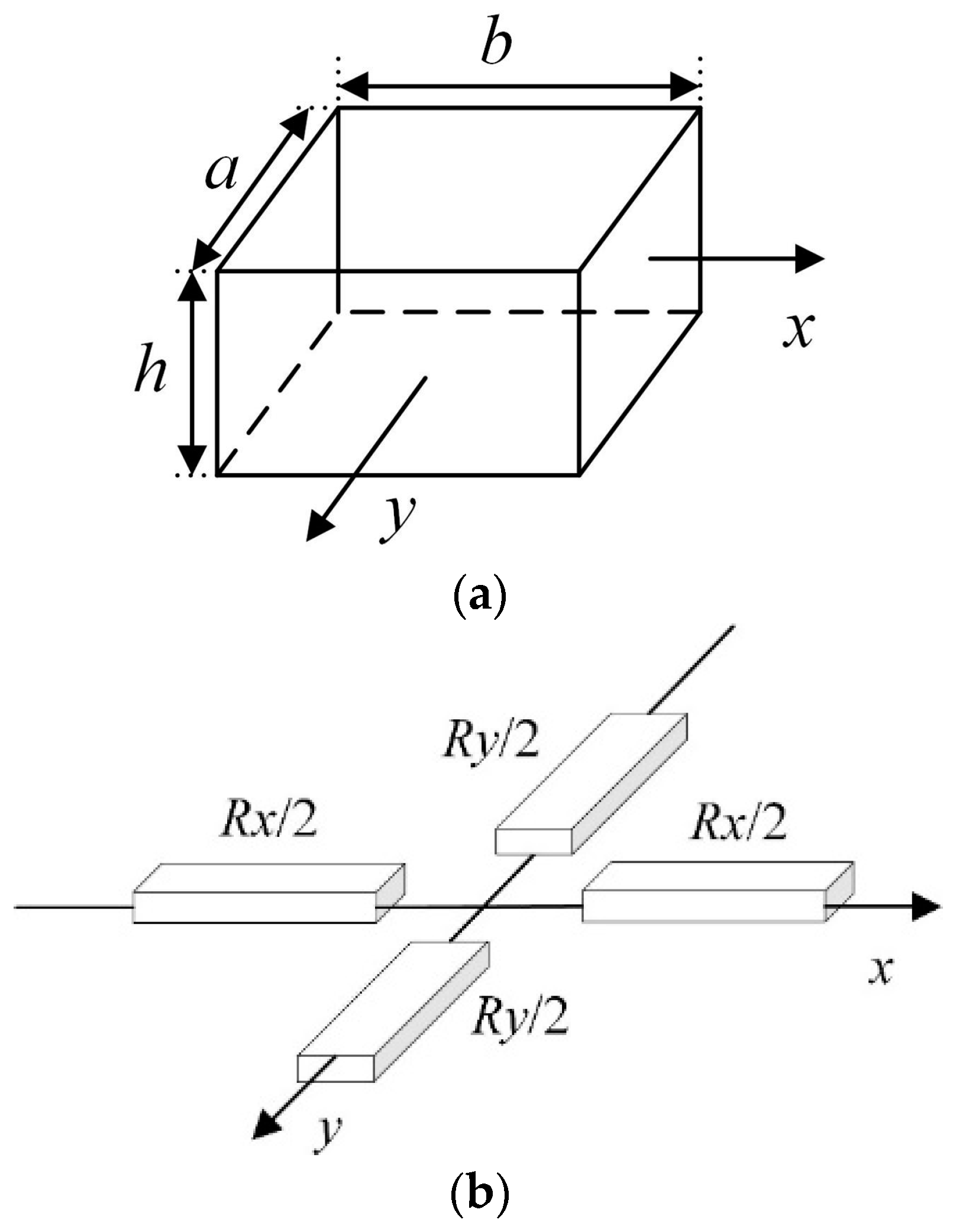
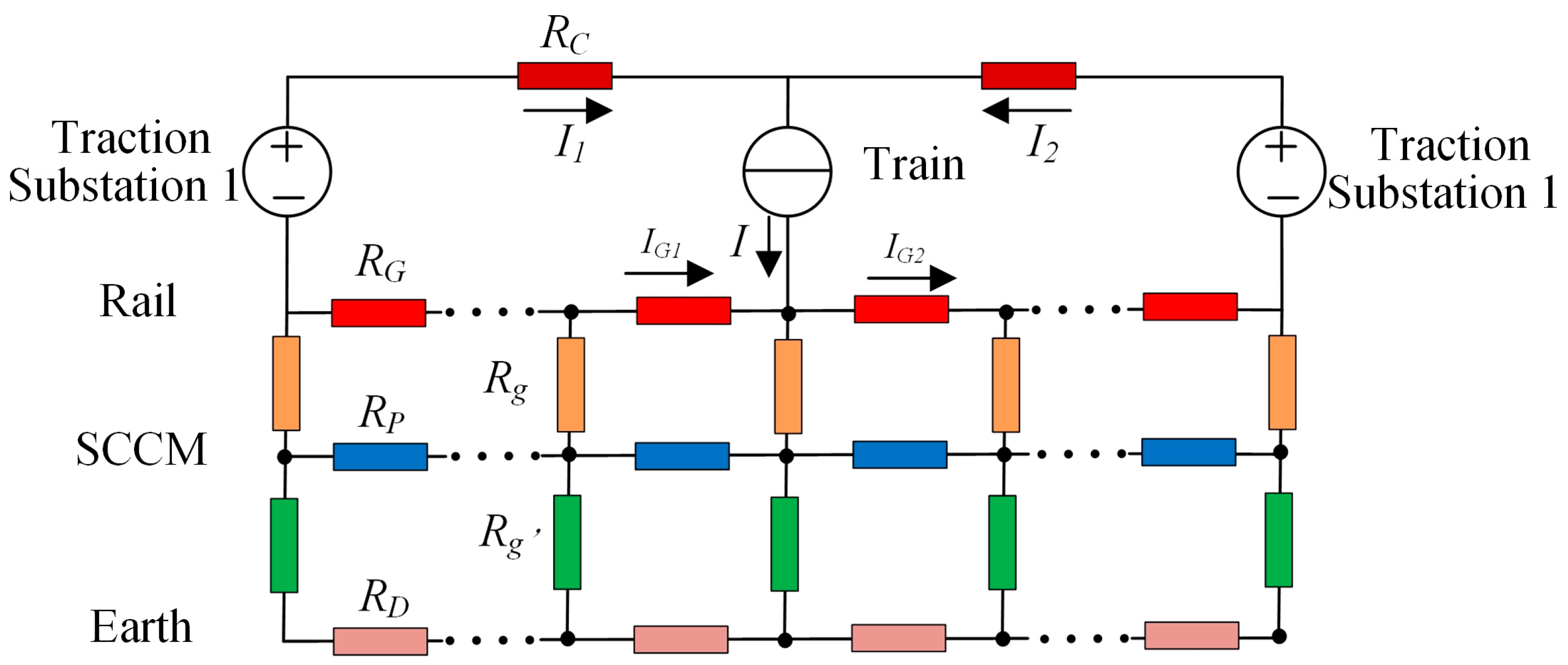
2.2. The Resistor Network
- (1)
- Overhead contact line equivalent
- (2)
- Rail equivalent
- (3)
- SCCM equivalent
- (4)
- Earth equivalent
- (5)
- Track-bed equivalent
- (6)
- Rail-to-SCCM transition resistance equivalent
- (7)
- SCCM-to-earth transition resistance equivalent
- (8)
- OWCD equivalent
2.3. Field-Circuit Coupling
3. Modeling of Field-Circuit Coupling
3.1. Modeling of Current Leakage at the Mainline
3.1.1. Modeling of Field-Circuit Coupling
3.1.2. Modeling of Finite Element Field
3.1.3. Modeling of Resistive Networks
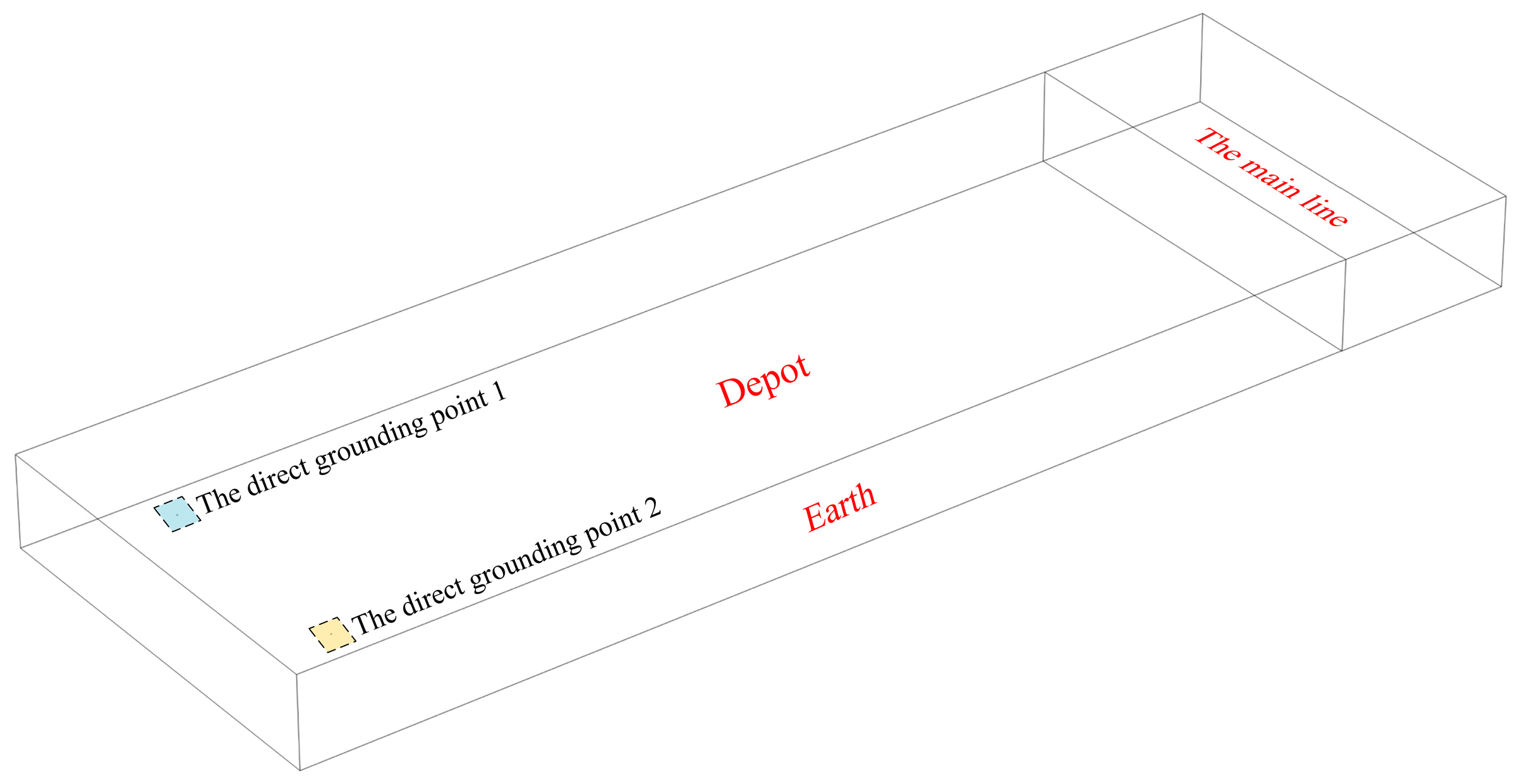
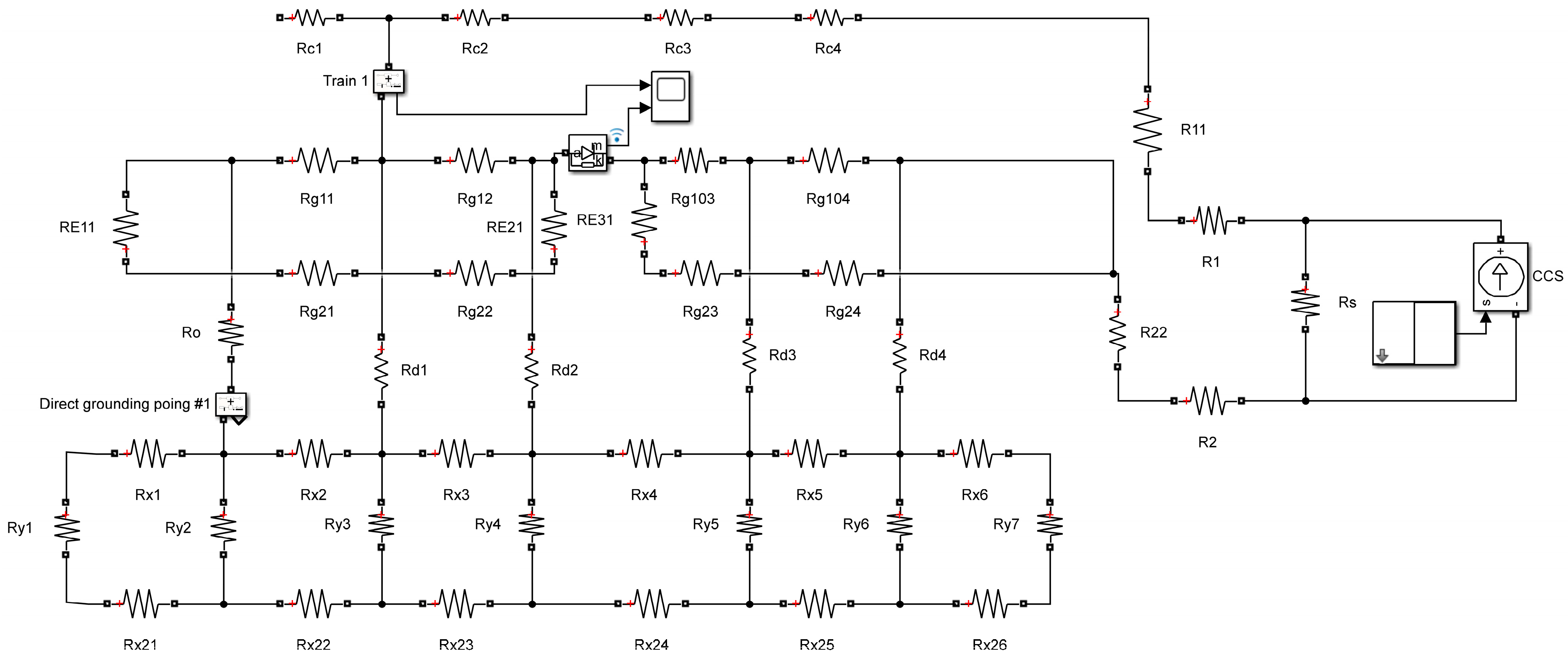
3.2. Modeling of Current Leakage at the Depot
3.2.1. Modeling of Field-Circuit Coupling
3.2.2. Modeling of Finite Element Field
3.2.3. Modeling of Resistive Networks
4. Analysis of Results
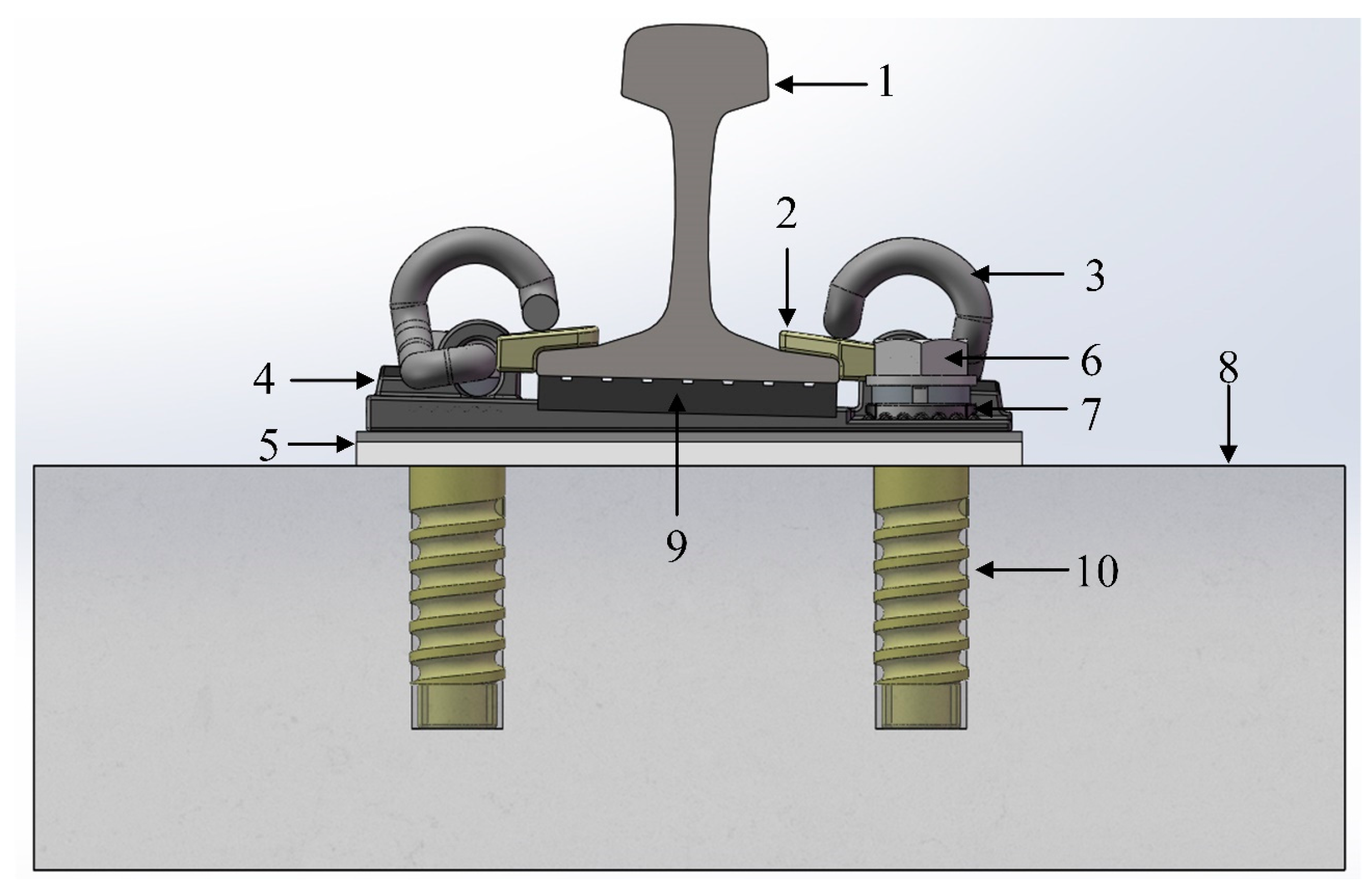
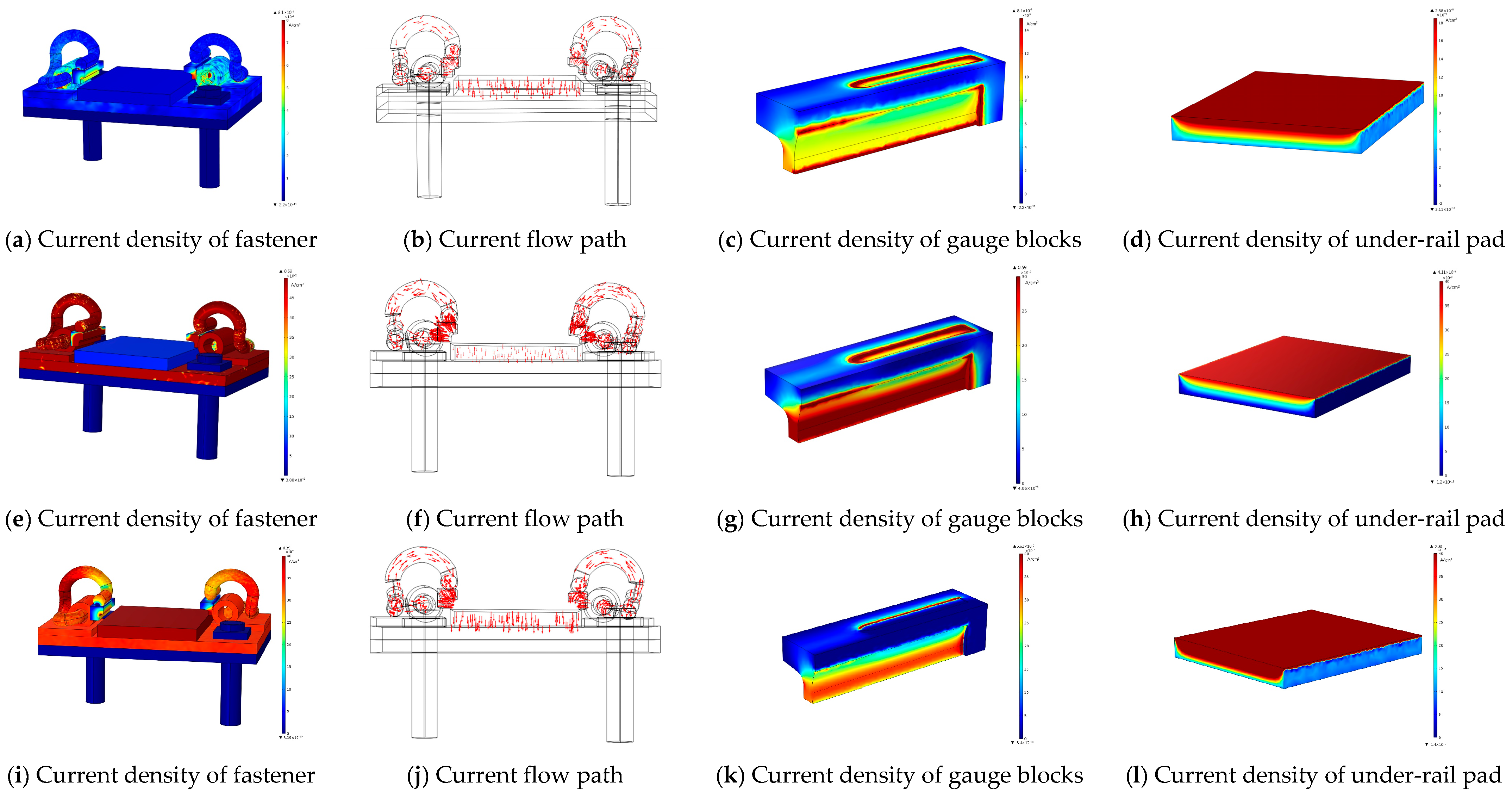
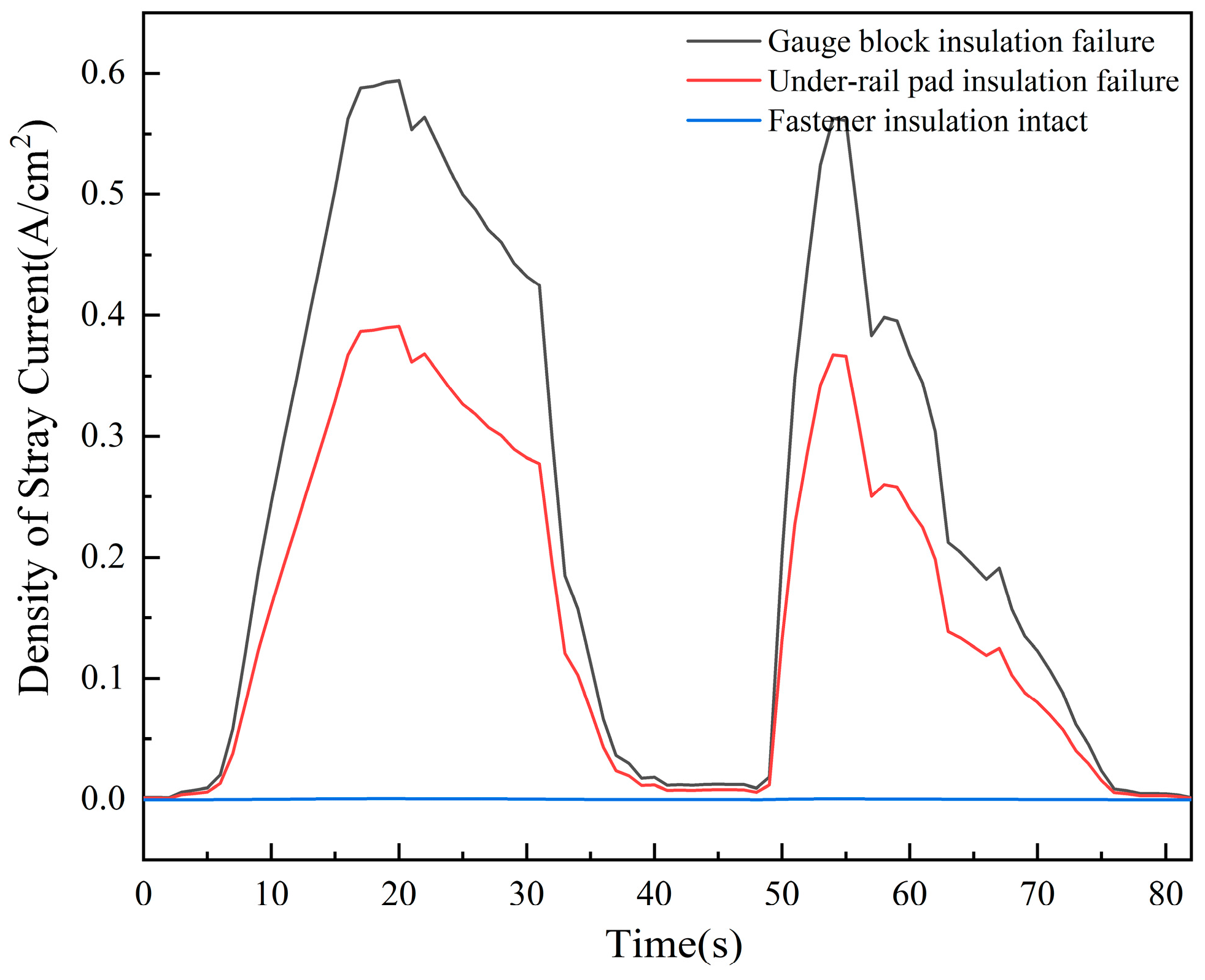
4.1. Analysis of Current Leakage under Different Insulation Properties of Fasteners at the Mainline
4.1.1. Fastener Insulation Intact
4.1.2. Gauge Block Insulation Failure
4.1.3. Under-Rail Pad Insulation Failure
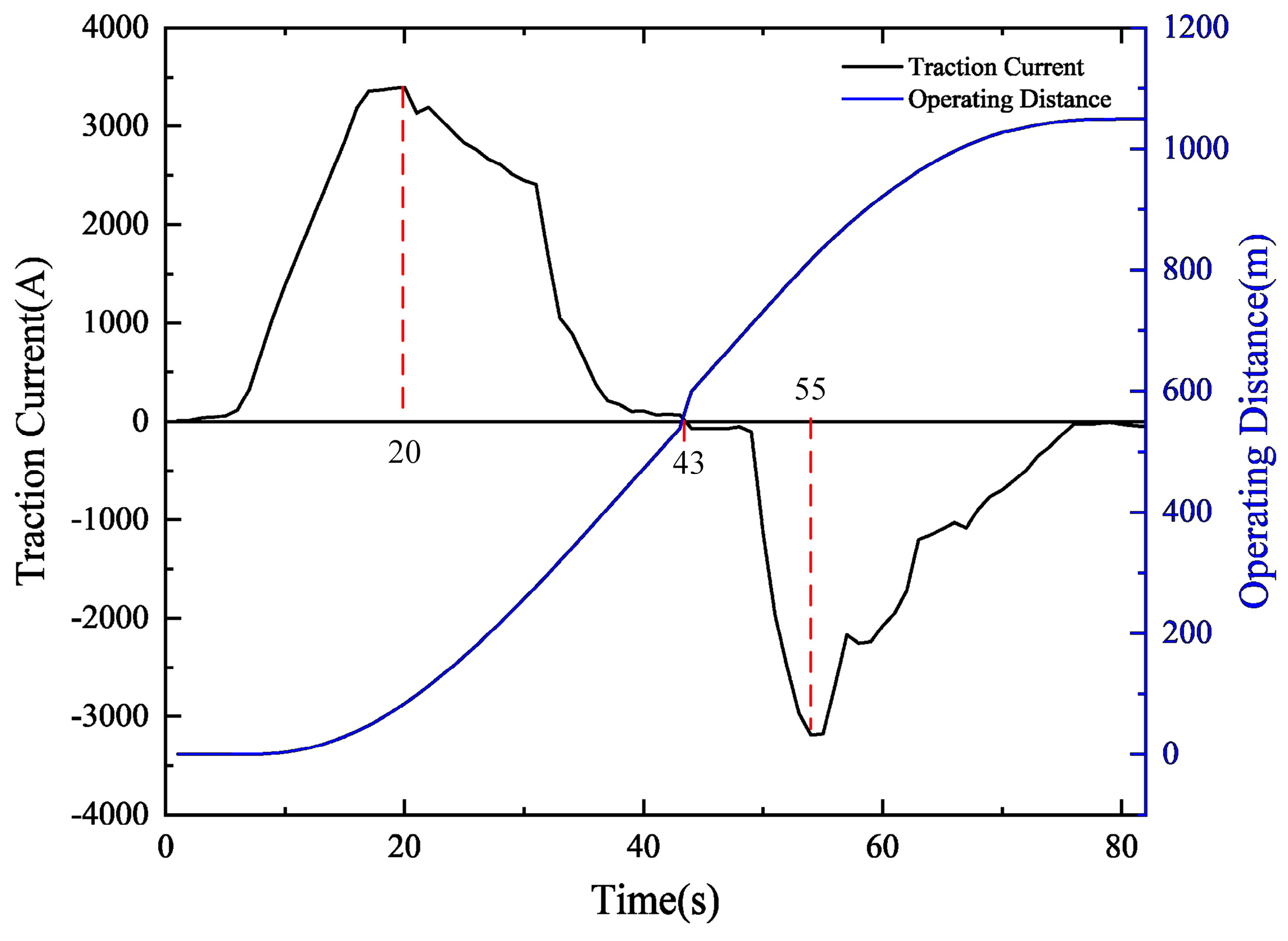
4.2. Analysis of Current Leakage under Different Positions of Trains at the Depot
4.2.1. The Train in the Inner Zone of the Depot
4.2.2. The Train in the Outer Zone of the Depot
4.2.3. The Train on the Mainline
4.2.4. Two Trains in the Depot
5. Discussion
5.1. Discussion of the Situation at the Mainline
5.2. Discussion of the Situation at the Depot
6. Results
- (1)
- This paper proposes a field-circuit coupling method and analyzes the leakage current and its distribution law in two scenarios: subway mainline and the depot. The applicability and effectiveness of the proposed field-circuit coupling method are verified through these analyses.
- (2)
- This paper builds a model of current leakage from fasteners on the subway mainline. By modeling the structure of type III fasteners, it studies and analyzes the influence of fasteners on rail current leakage under three different insulating conditions. It is found that the failure of the gauge block results in the greatest degree of current leakage from the rails.
- (3)
- This paper builds a current leakage model of the grounding point at the subway depot and investigates four different actual subway depot line layouts and grounding situations. Simulation results indicate that the characteristics of stray current distribution in the depot are primarily influenced by the operational status of the OWCD, which is in turn affected by changes in rail potential. Additionally, when multiple trains are running in the depot, the complex operational status of the OWCD leads to a more varied and intricate distribution of stray current.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Liu, C. Discrete modeling and calculation of traction return-current network for 400 km/h high-speed railway. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2023, 237, 445–457. [Google Scholar] [CrossRef]
- Chen, L.; Huang, K.; Wei, K.; Gao, D.; Peng, Q.; Lin, S. Study on the Potential Distribution Characteristics of Substation Grounding Grid Considering Stray Current. In Proceedings of the 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, 11–13 November 2022; pp. 1284–1289. [Google Scholar]
- Li, C.; Du, Q.; Guo, Y.; Liu, Y.; Yang, F.; Chen, L.; Zhang, X.; Huang, G.; Gao, G.; Wu, G. Modeling of Stray Currents from Metro Intruding into Power System Considering the Complex Geological Conditions in Modern Megacities. IEEE Trans. Transp. Electrif. 2023, 9, 1653–1663. [Google Scholar] [CrossRef]
- Zhou, Q.; Lin, S.; Lin, X.; Wang, A. A Uniform Model for Stray Current of Long-Line DC Metro Systems. IEEE Trans. Transp. Electrif. 2022, 8, 2915–2927. [Google Scholar] [CrossRef]
- Zheng, Z.; Du, G.; Huang, W.; Wang, J.; Fan, M.; Zhu, Z. Coupling Effect of Reflux Safety Parameters in Main line and Depot of Multitrain DC Traction Power Systems. IEEE Trans. Transp. Electrif. 2022, 8, 527–541. [Google Scholar] [CrossRef]
- Song, C.; Li, Z.; Wang, H.; Liu, X. Analysis of influence law of rail transition resistance on subway stray current. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15–17 April 2022; pp. 1631–1635. [Google Scholar]
- Gao, H.; Wei, R.; Liu, J.; Wang, Z.; Zhong, H.; Cao, Y.; Tang, M.; Zhang, J. Analysis of Stray Current Intrusion into Grid Substation under Multiple Factors. In Proceedings of the 2022 4th International Conference on Control and Robotics (ICCR), Guangzhou, China, 2–4 December 2022; pp. 188–192. [Google Scholar]
- Liu, W.; Pan, Z.; Tang, Y.; Zhou, L.; Bhatti, A.A.; Niu, J. A Field-Circuit Coupling Diffusion Model for Stray Current of DC Metro System. IEEE Trans. Transp. Electrif. 2023; early access. [Google Scholar]
- Mariscotti, A.; Fichera, F.; Ogunsola, A. Evaluating stray current from DC electrified transit systems with lumped parameter and multi-layer soil models. In Proceedings of the IEEE Eurocon 2013, Zagreb, Croatia, 1–4 July 2013; pp. 1187–1192. [Google Scholar]
- Wang, C.; Li, W.; Wang, Y.; Xu, S.; Fan, M. Stray Current Distributing Model in the Subway System: A review and outlook. Int. J. Electrochem. Sci. 2018, 13, 1700–1727. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, L.; Pan, Z.; Bhatti, A.A.; Huang, X.; Zhang, J. Dynamic diffusion model of stray current in DC traction power supply system. IEEE Trans. Power Deliv. 2023, 38, 2170–2182. [Google Scholar] [CrossRef]
- Vranesic, K.; Serdar, M.; Lakusic, S.; Kolar, V.; Mariscotti, A. Dynamic Stray Current Measuring Methods in Urban Areas. Balt. J. Road Bridge Eng. 2022, 17, 146–170. [Google Scholar] [CrossRef]
- Zhu, J.; Mao, C.; Wang, Z.; Chen, J.; Wang, D.; Luan, L.; Qiao, Y.; Wang, H. A novel suppression method for grounding transformer against earth current from urban rail transit. IEEE Trans. Ind. Electron. 2020, 68, 11651–11662. [Google Scholar] [CrossRef]
- Du, G.; Wang, J.; Jiang, X.; Zhang, D.; Yang, L.; Hu, Y. Evaluation of Rail Potential and Stray Current with Dynamic Traction Networks in Multitrain Subway Systems. IEEE Trans. Transp. Electrif. 2020, 6, 784–796. [Google Scholar] [CrossRef]
- Vranesic, K.; Lakusic, S.; Serdar, M.; Alar, V. Detrimental effect of stray current on rails and fastening systems in urban railway tracks. Constr. Build. Mater. 2023, 400, 132645. [Google Scholar] [CrossRef]
- Chang, W.C.; Kuo, C.C.; Lin, W.C.; Hsieh, M.N. Simulation of Stray and Core Shielding Loss for Power Transformer Based on 2D/3D FEM. IEEE Access 2023, 11, 16943–16950. [Google Scholar] [CrossRef]
- Jabbehdari, S.; Mariscotti, A. Distribution of stray current based on 3-Dimensional earth model. In Proceedings of the 2015 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles (ESARS), Aachen, Germany, 3–5 March 2015; pp. 1–6. [Google Scholar]
- Lin, S.; Liu, X.; Zhang, X.; Cai, Z. Research on Stray Current Distribution in a Multitrain Subway System using Finite Element Modeling. Int. J. Electrochem. Sci. 2021, 16, 211250. [Google Scholar] [CrossRef]
- Kunpeng, L.; Xiaobin, C.; Hao, S.; Chao, X.; Yunyun, Z.; Wei, L.; Haiou, S.; Zhixin, H. The Equivalent Circuit and Influencing Factors of Subway Rail Fastener Track-to-earth Resistance. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Bangkok, Thailand, 6–9 June 2018; pp. 1–5. [Google Scholar]
- Lin, S.; Huangfu, Y.; Zhou, Q.; Wang, A. Evaluation and Analysis Model of Stray Current in the Metro Depot. IEEE Trans. Transp. Electrif. 2021, 7, 1780–1794. [Google Scholar] [CrossRef]
- Cai, Z.; Zhang, X.; Cheng, H. Evaluation of DC-Subway Stray Current Corrosion with Integrated Multi-Physical Modeling and Electrochemical Analysis. IEEE Access 2019, 7, 168404–168411. [Google Scholar] [CrossRef]
- Ni, Y.; Yu, K.; Zhuo, C.; Zeng, X.; He, F.; Leng, Y.; Han, W. Study on distribution characteristics of metro stray current. In Proceedings of the 2021 IEEE International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Qingdao, China, 2–4 July 2021; pp. 19–25. [Google Scholar]
- Vranešić, K.; Lakušić, S.; Serdar, M. Influence of Stray Current on Fastening System Components in Urban Railway Tracks. Appl. Sci. 2023, 13, 5757. [Google Scholar] [CrossRef]
- Mariscotti, A. Stray Current Protection and Monitoring Systems: Characteristic Quantities, Assessment of Performance and Verification. Sensors 2020, 20, 6610. [Google Scholar] [CrossRef] [PubMed]

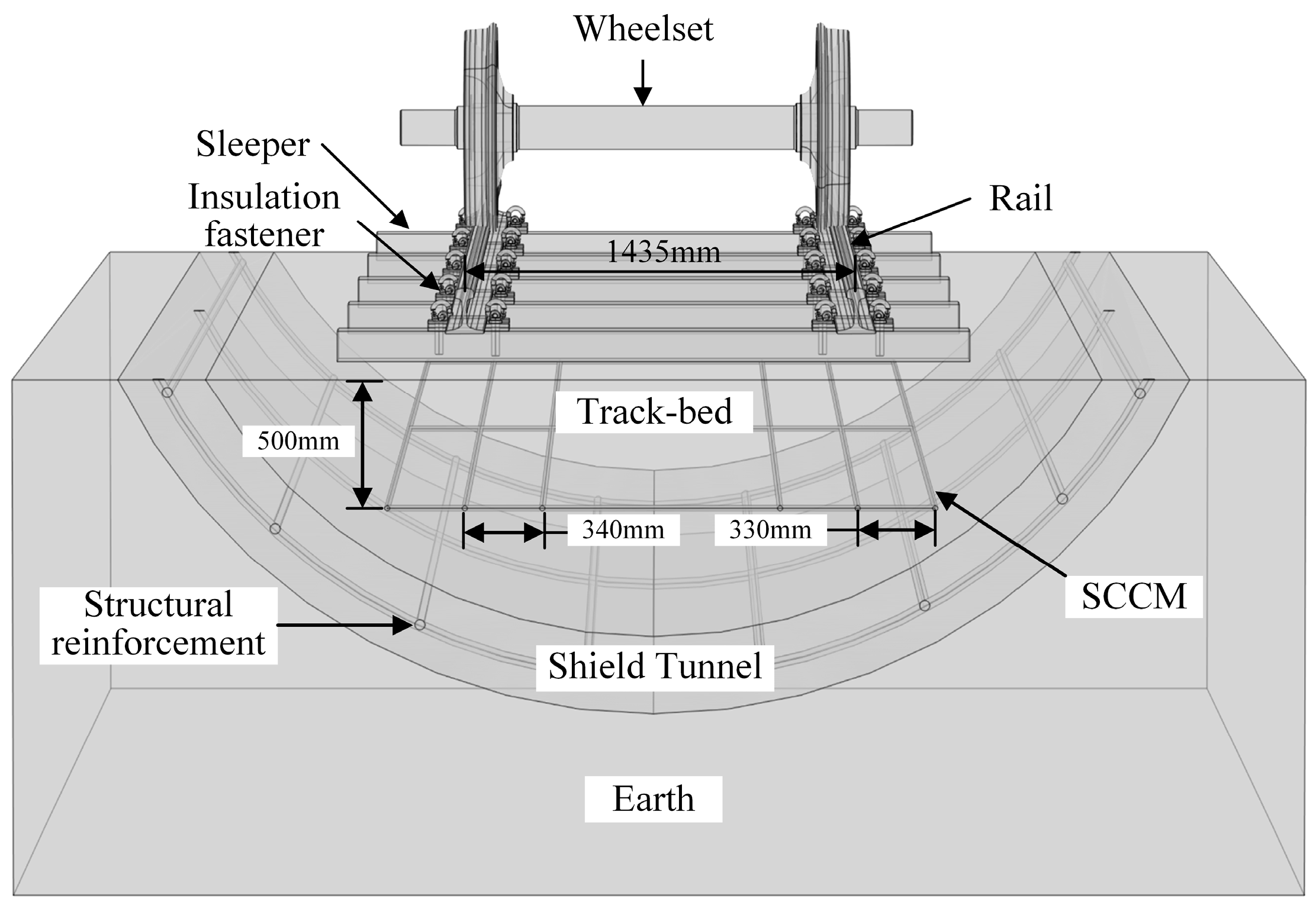


| Project | Relative Permittivity | Conductivity (S/m) |
|---|---|---|
| Rail | 1 | 3 × 106 |
| SCCM | 1 | 2.8 × 106 |
| Reinforcing bar | 1 | 2.9 × 106 |
| Tunnel concrete | 1 | 2 × 10−3 |
| Track-bed concrete | 1 | 2 × 10−3 |
| Earth | 1 | 2 × 10−2 |
| Structure | Material | Relative Permittivity | Conductivity (S/m) |
|---|---|---|---|
| Elastic strip | 60Si2Mn | 1 | 2.38 × 106 |
| Gauge block | Glass fiber-reinforced polyamide | 1.63 | 1 × 10−10 |
| Iron tie-plate | QT450-10 | 1 | 2 × 106 |
| Under-rail pad | Thermoplastic polyester elastomer | 5 | 1.587 × 10−12 |
| Elastic pad | Thermoplastic polyester elastomer | 5 | 1.587 × 10−12 |
| Gasket | Q235-A steel | 1 | 3 × 106 |
| Bolt | S45C steel | 1 | 4.59 × 107 |
| Insulated bushing | Glass fiber-reinforced polyamide | 1.63 | 1 × 10−10 |
| Mode | Train Position | Traction Current | State | Direct Grounding Points #1 and #2 Current |
|---|---|---|---|---|
| 1 | inner zone of the depot (x = 200, y = 180) | 280 A | acceleration | 65 A; −64 A |
| 2 | outer zone of the depot (x = 600, y = 180) | 420 A | acceleration | 0 A; −0.02 A |
| 3 | Mainline (x = 1300, y = 250) | 1500 A | acceleration | 0.012 A; −0.012 A |
| 4 | inner zone of the depot (x = 600, y = 180) | 420 A | acceleration | Current at Train 1: 0.54 A |
| outer zone of the depot (x = 1200, y = 250) | −420 A | deceleration | Current at Train 2: −0.54 A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Tang, Z.; Chen, X.; Liu, X.; Liu, Y. Analysis of Stray Current Leakage in Subway Traction Power Supply System Based on Field-Circuit Coupling. Energies 2024, 17, 3121. https://doi.org/10.3390/en17133121
Lin S, Tang Z, Chen X, Liu X, Liu Y. Analysis of Stray Current Leakage in Subway Traction Power Supply System Based on Field-Circuit Coupling. Energies. 2024; 17(13):3121. https://doi.org/10.3390/en17133121
Chicago/Turabian StyleLin, Shan, Zhixi Tang, Xia Chen, Xuehua Liu, and Yunsheng Liu. 2024. "Analysis of Stray Current Leakage in Subway Traction Power Supply System Based on Field-Circuit Coupling" Energies 17, no. 13: 3121. https://doi.org/10.3390/en17133121
APA StyleLin, S., Tang, Z., Chen, X., Liu, X., & Liu, Y. (2024). Analysis of Stray Current Leakage in Subway Traction Power Supply System Based on Field-Circuit Coupling. Energies, 17(13), 3121. https://doi.org/10.3390/en17133121








