Multi-Functional Device Based on Superconducting Magnetic Energy Storage
Abstract
1. Introduction
- (1)
- Enhancing power system stability: This application domain seeks to fortify the stability and reliability of power systems utilizing SMES. By storing and dispensing electrical energy, SMES systems aid in balancing energy flow in power systems, thereby mitigating voltage and frequency fluctuations, consequently bolstering power system stability [14,15,16,17].
- (2)
- Improving power quality: This category predominantly utilizes SMES systems to ameliorate power quality. As a fast-response energy storage device, SMES injects active and reactive power into the grid swiftly, within a single cycle [18]. Through energy storage and release, SMES mitigates current and voltage fluctuations, diminishes harmonics, and ameliorates sags, thereby enhancing power quality [19,20,21,22,23,24].
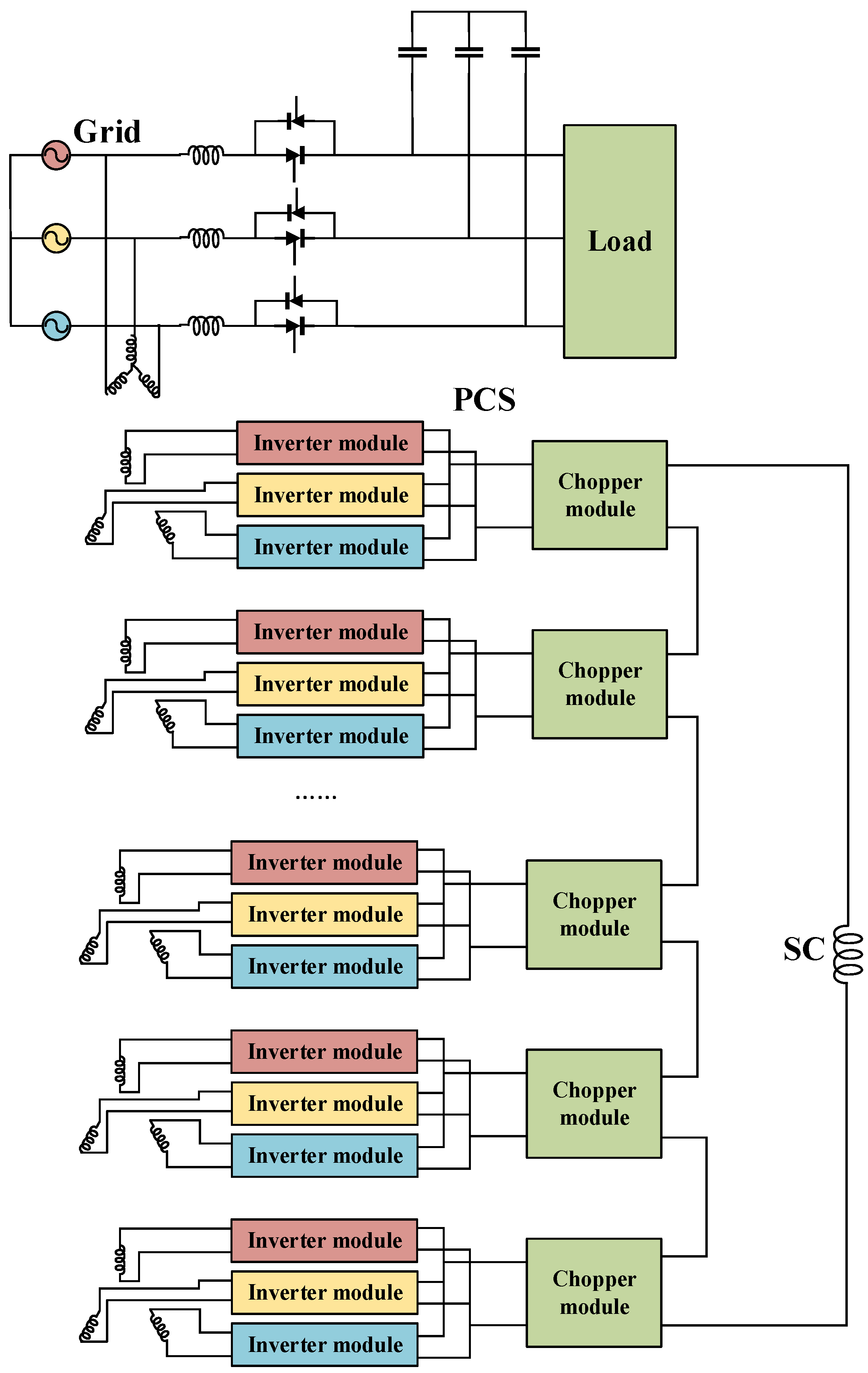
2. Operational Principle and Topology Design Methodology
2.1. Select the PCS Rated Voltage
2.2. Design of the L Filter Inductance
2.3. Design of the Capacitance of the DC Link Capacitor
2.4. Design of the Inductance of the Grid-Side Inductor
2.5. Design of the Capacitance of the Grid-Side Capacitor
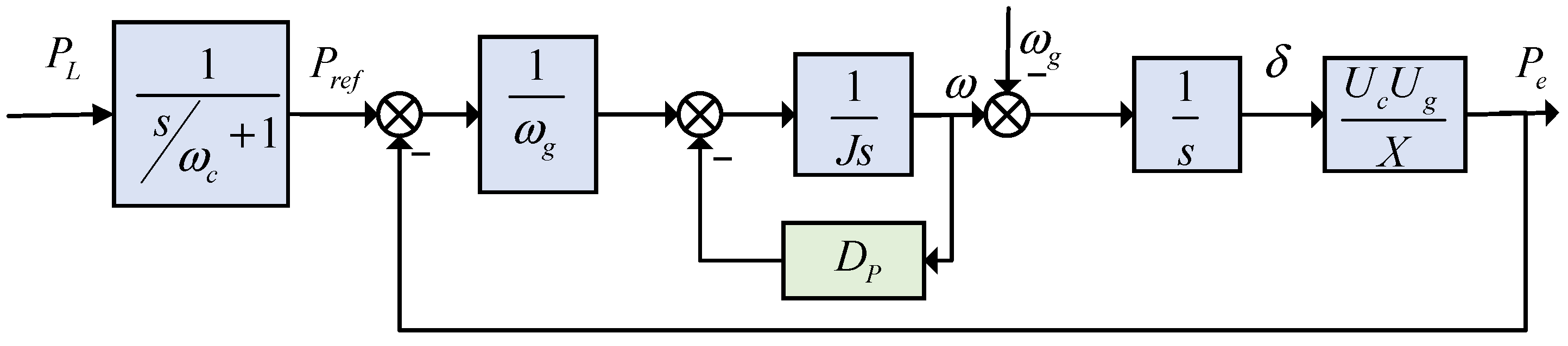
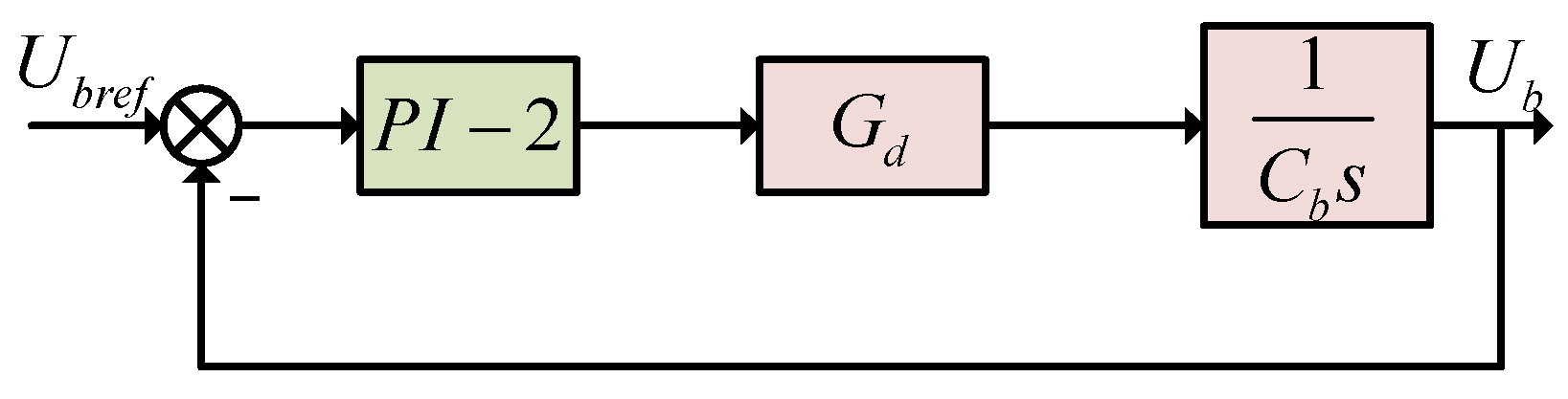
3. Inverter Outer Power Control Loop
3.1. Active Power Loop
3.2. Reactive Power Loop
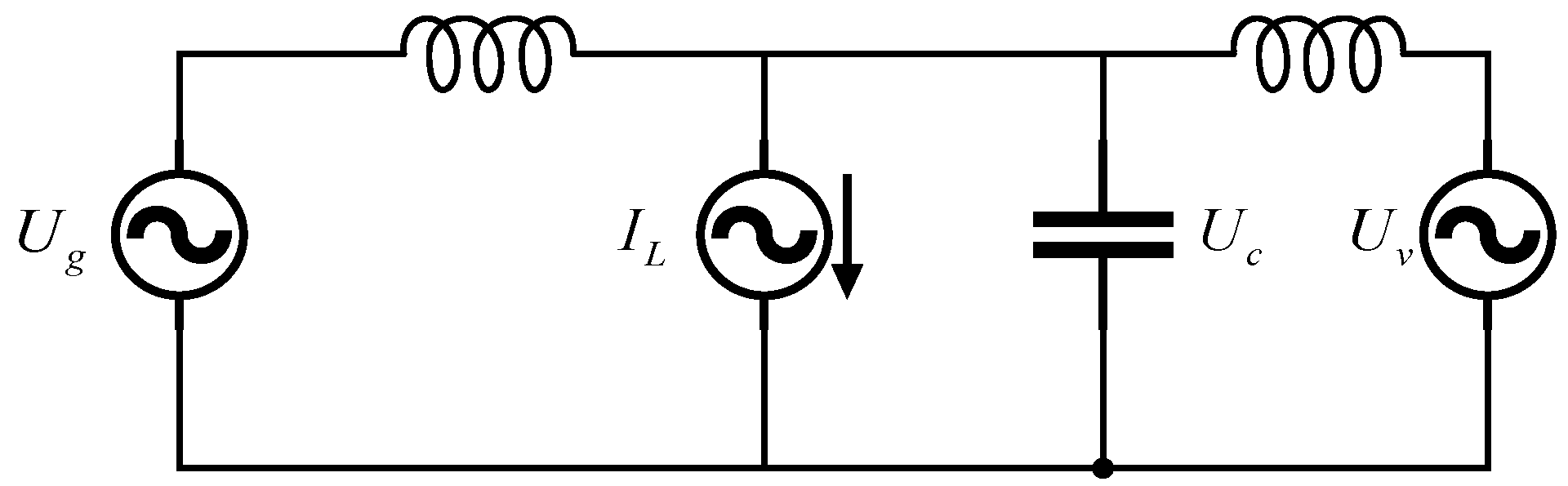
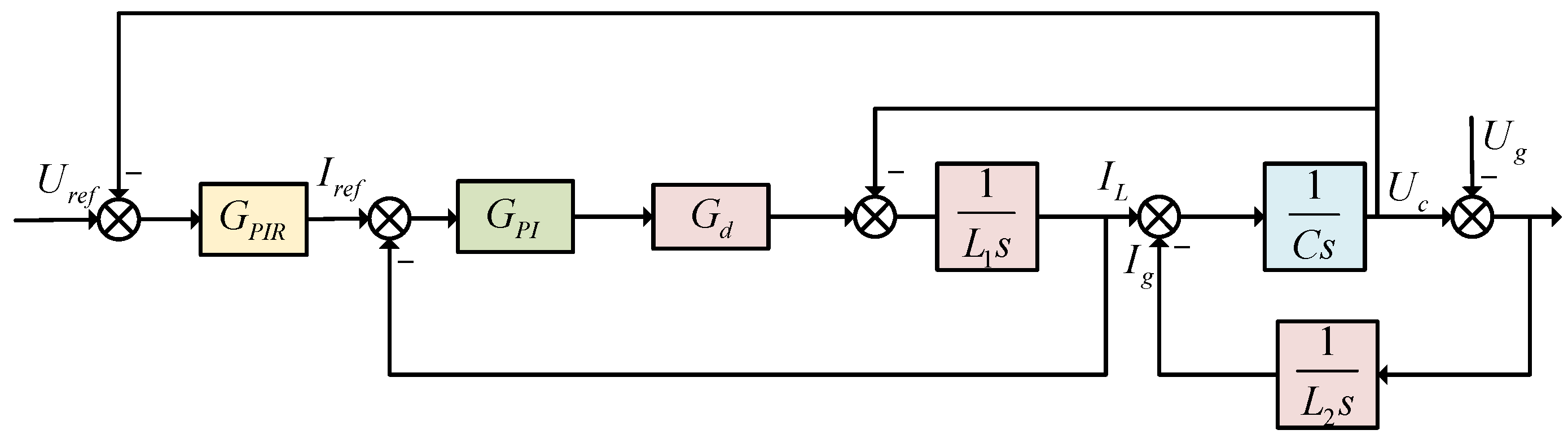
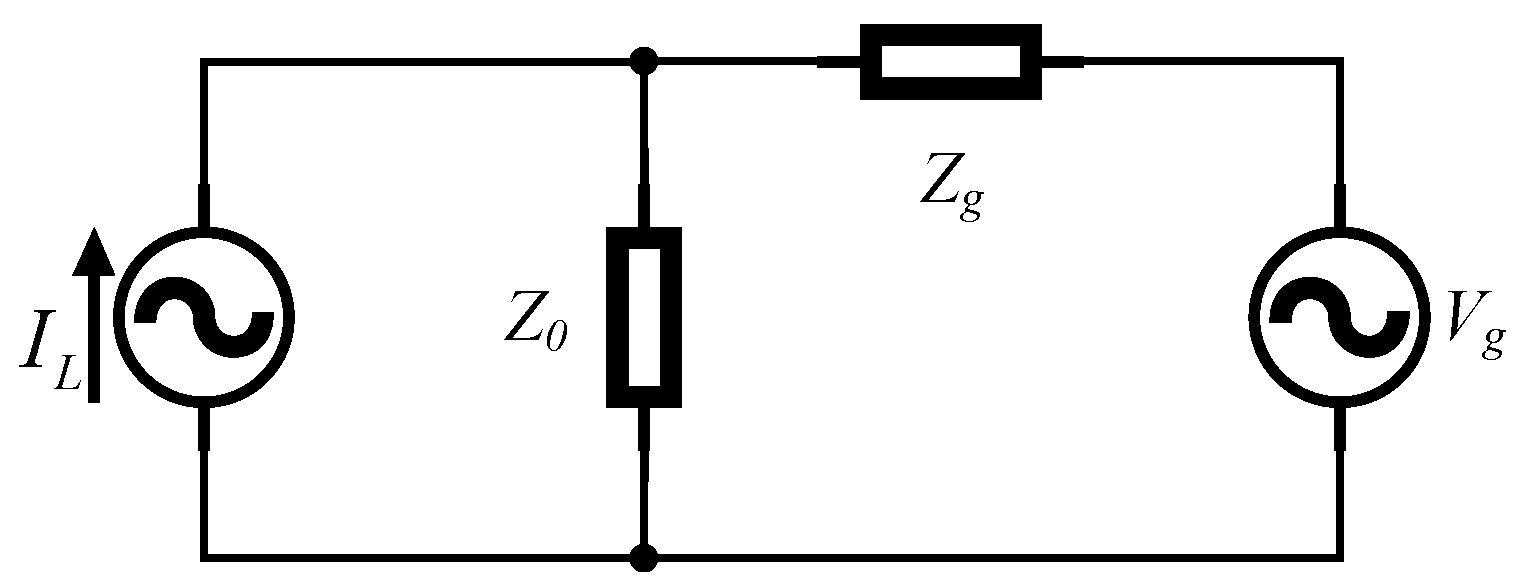
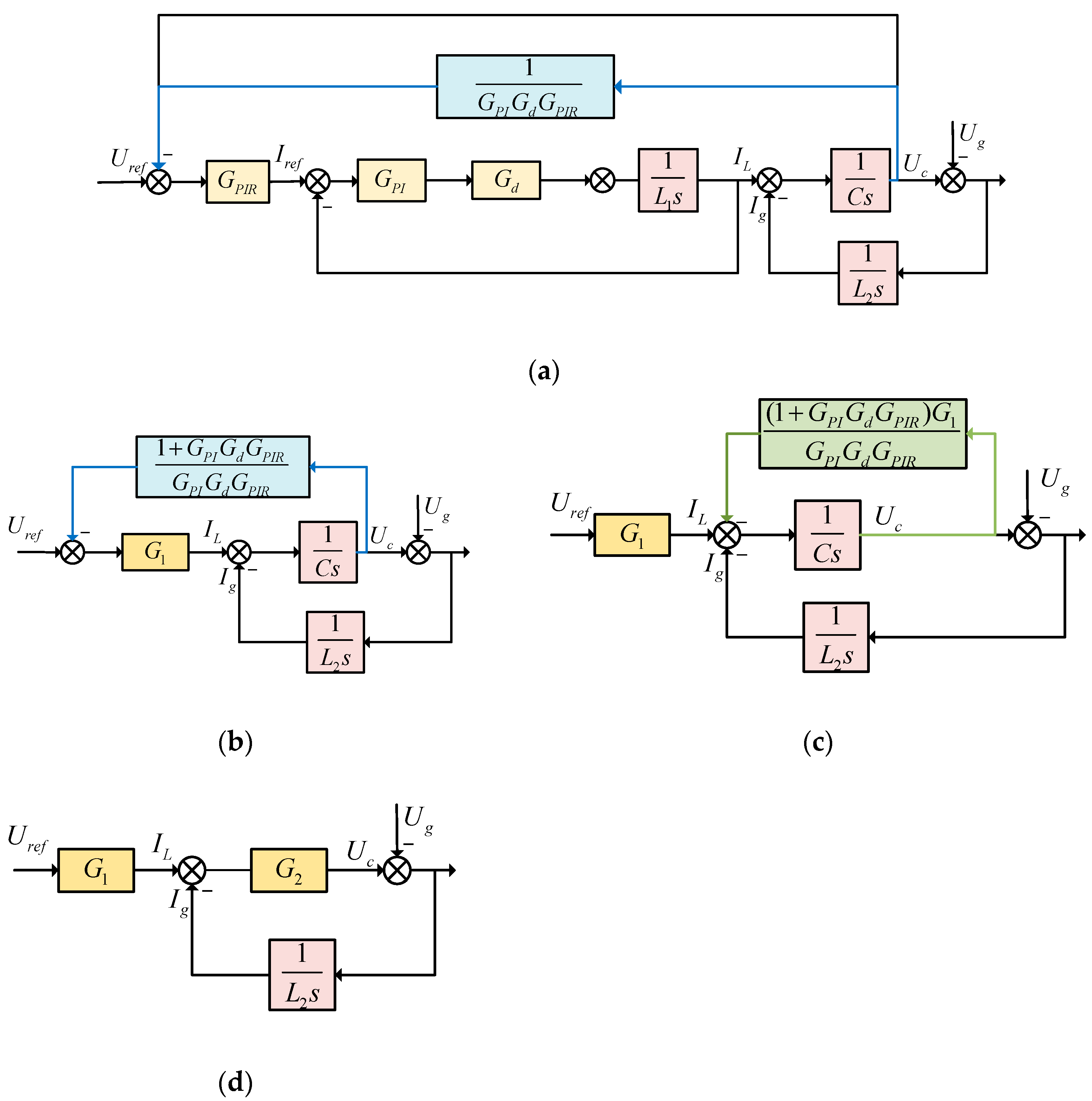
4. Inverter Inner Voltage and Current Control Loop
4.1. Realization of Voltage Sag Compensation
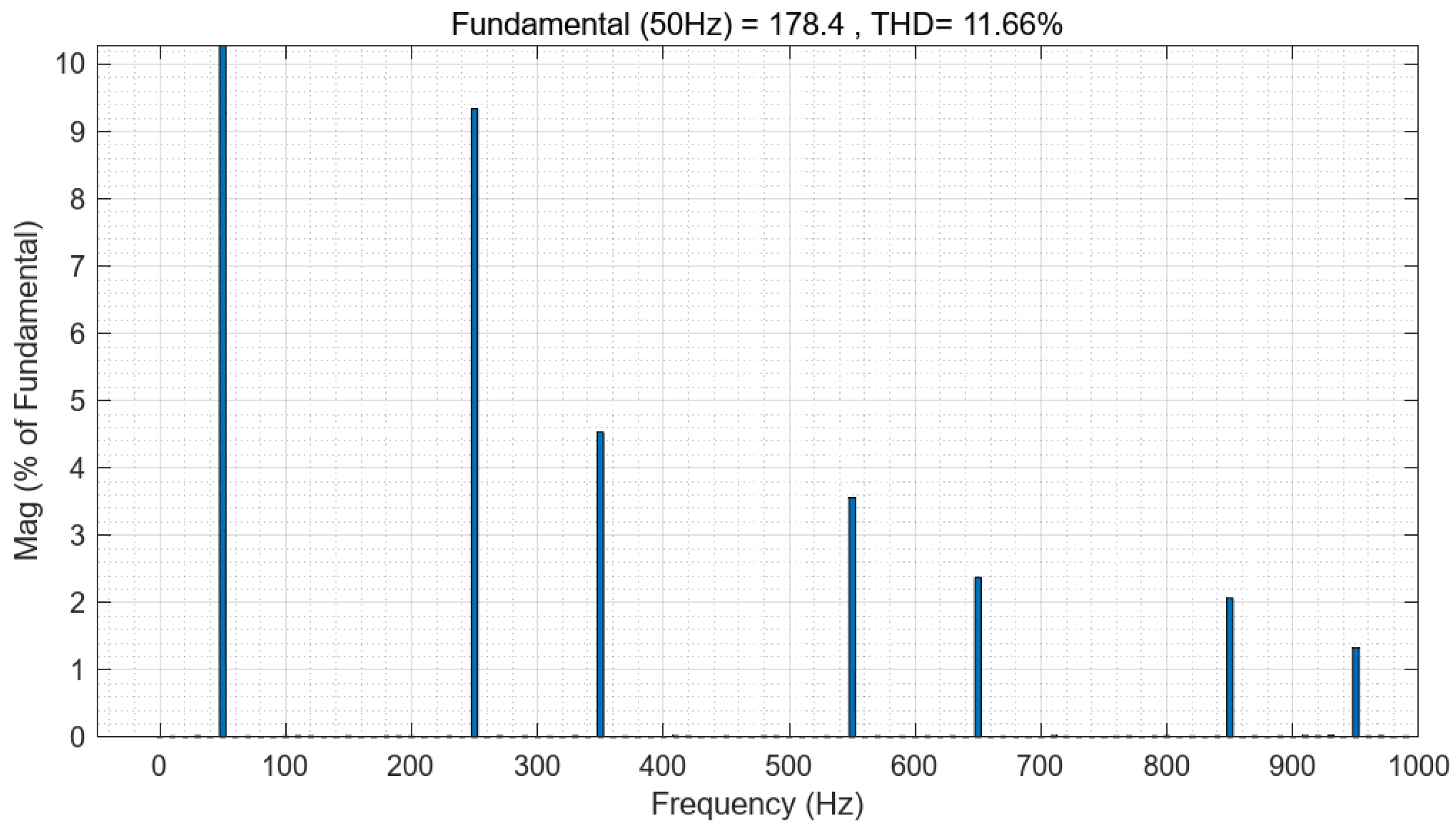
4.2. Realization of Current Harmonic Compensation
5. Chopper Module Control
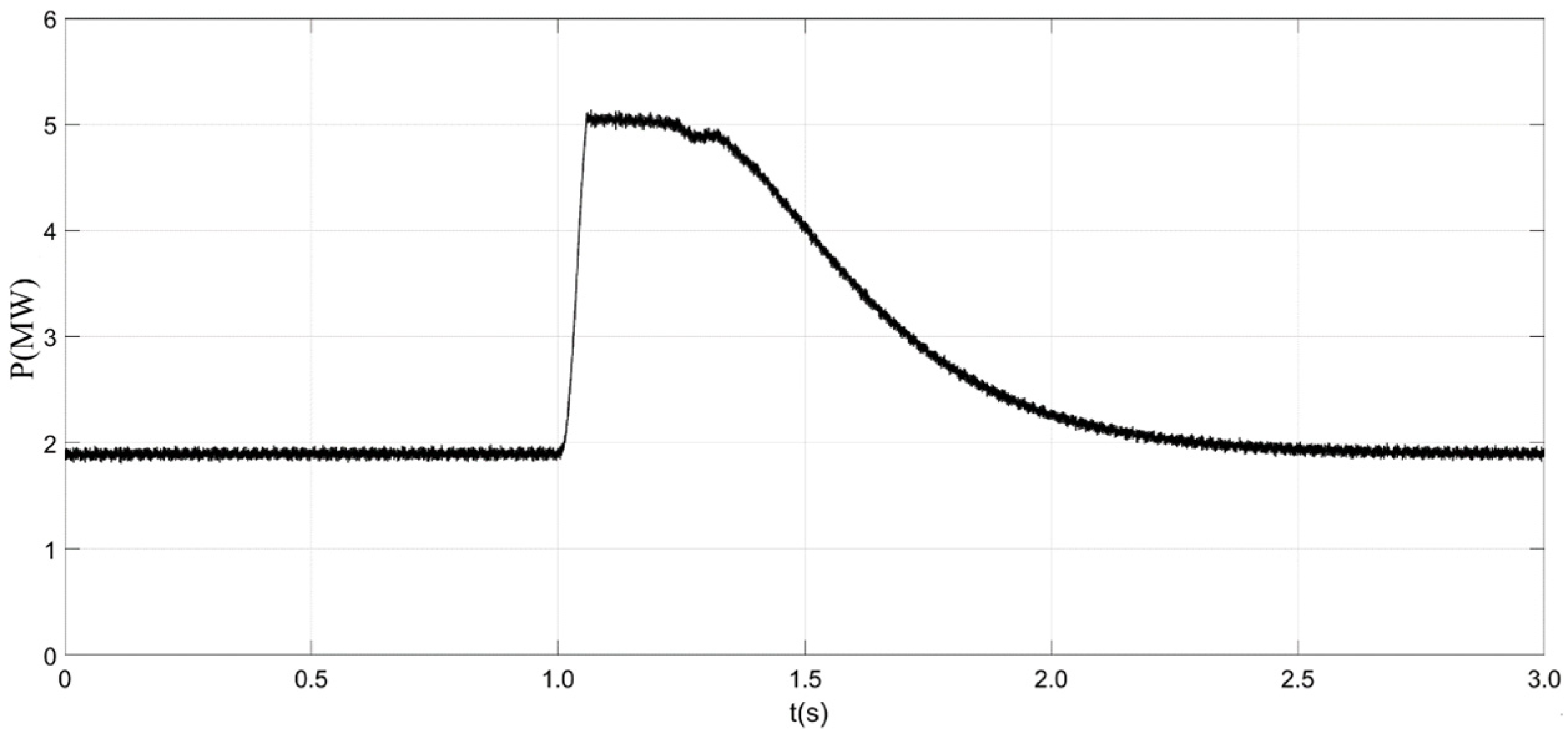
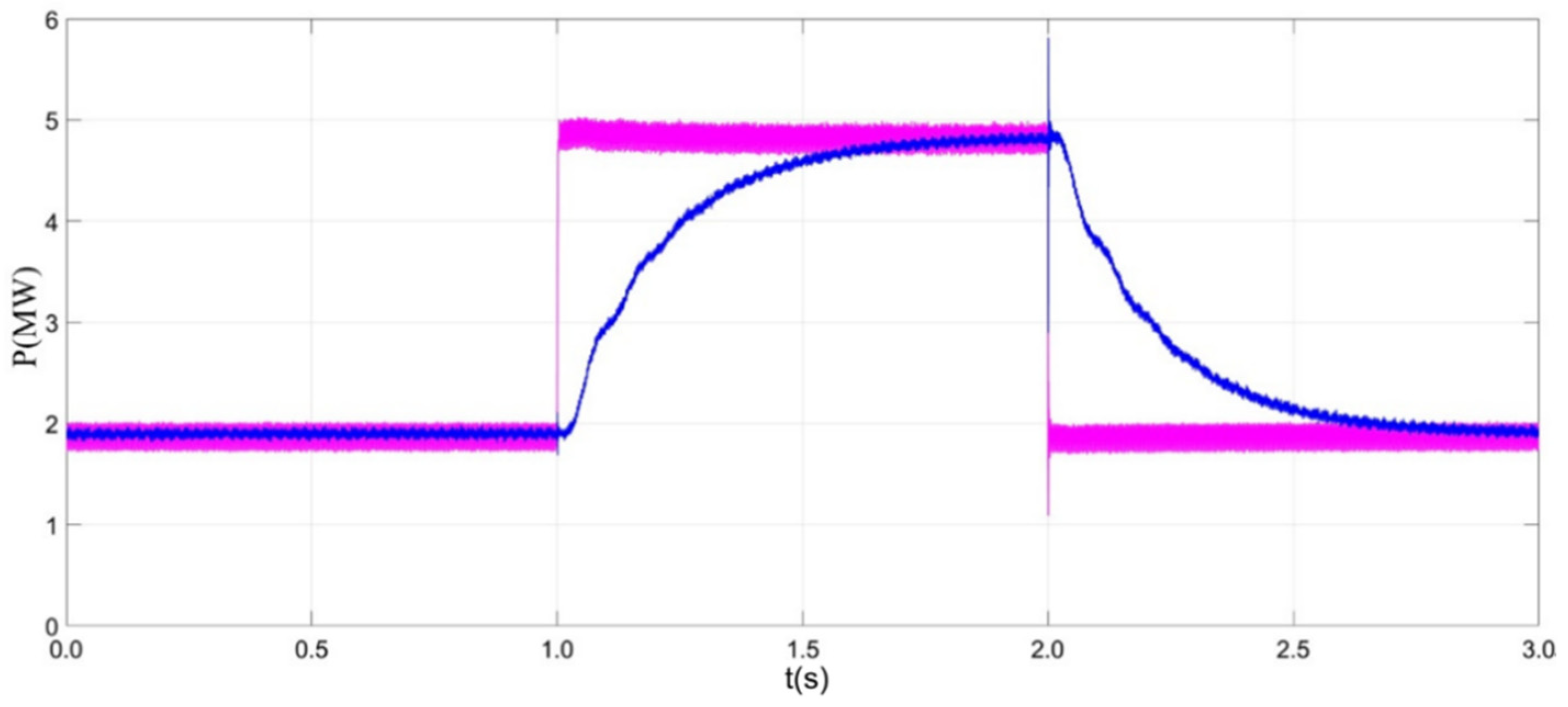
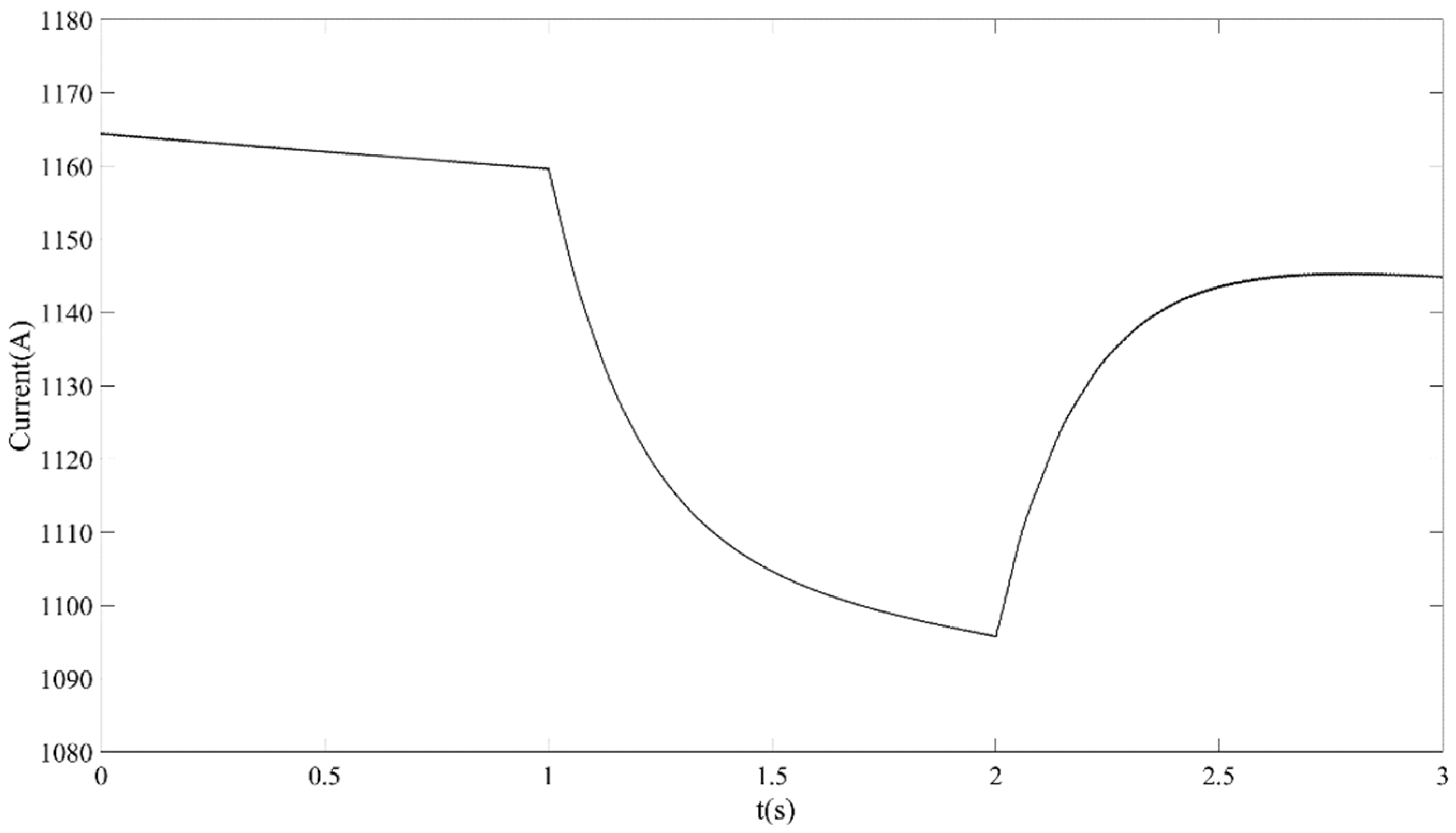
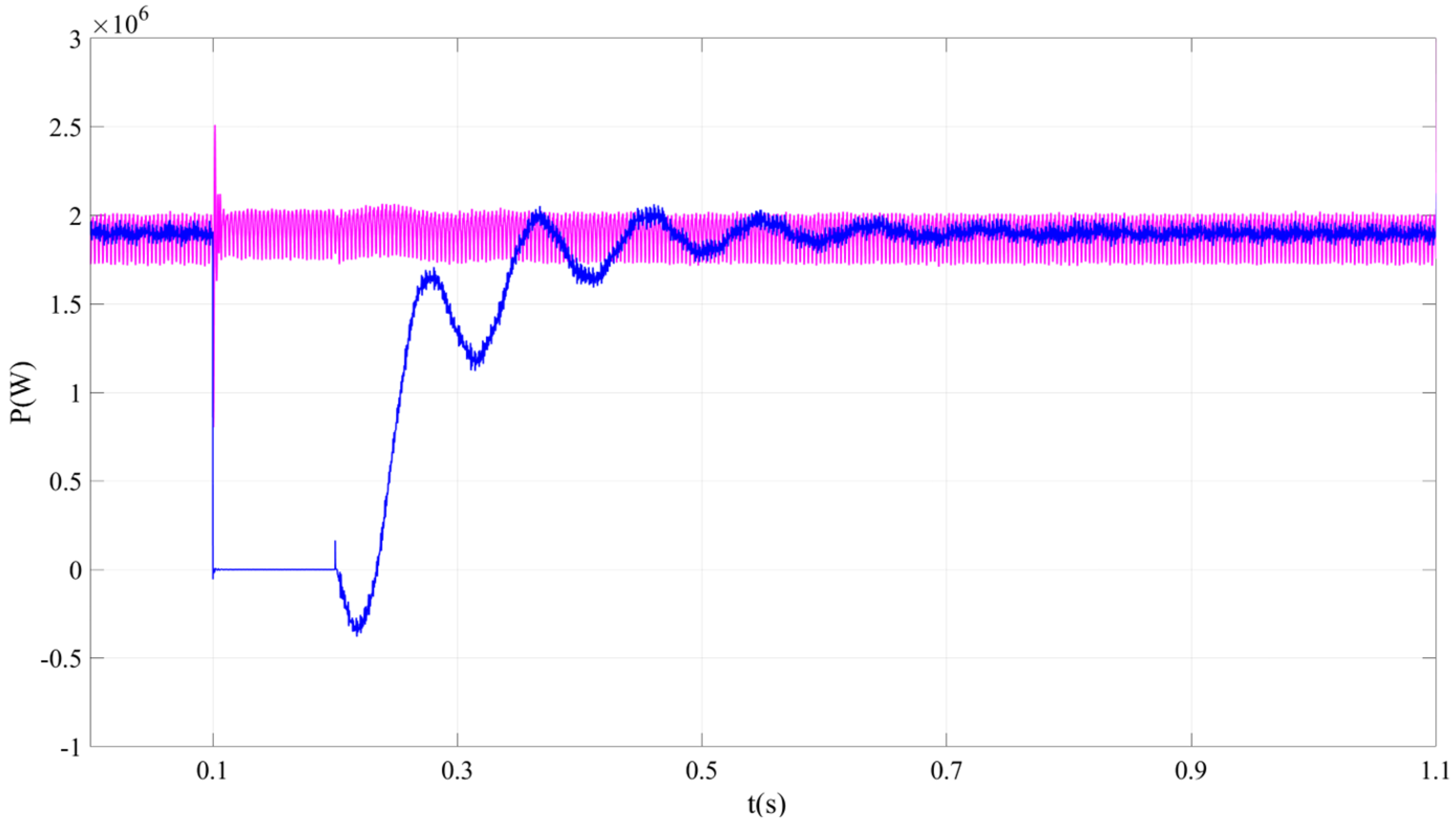
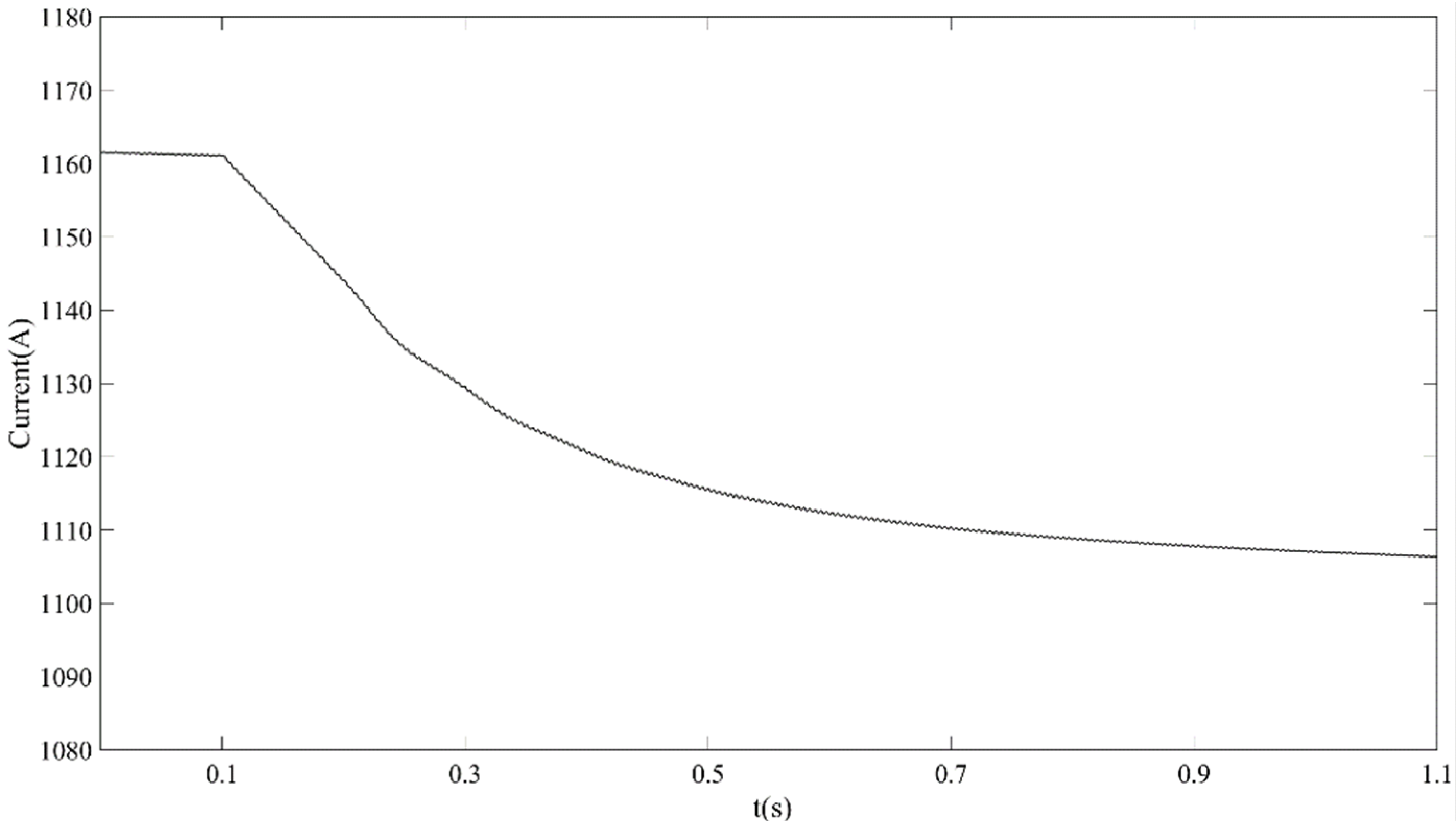
6. Simulation Results
7. Performance Comparison with the Existing Methods
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AL Shaqsi, A.Z.; Sopian, K.; Al-Hinai, A. Review of energy storage services, applications, limitations, and benefits. Energy Rep. 2020, 6, 288–306. [Google Scholar] [CrossRef]
- Sonia; Dahiya, A.K. Superconducting magnetic energy storage coupled static compensator for stability enhancement of the doubly fed induction generator integrated system. J. Energy Storage 2021, 44, 103232. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, M.; Jiang, S.; Gou, H.; Zhou, P.; Yang, R.; Shen, B. Energy reliability enhancement of a data center/wind hybrid DC network using superconducting magnetic energy storage. Energy 2023, 263, 125622. [Google Scholar] [CrossRef]
- Nam, G.D.; Sung, H.J.; Go, B.S.; Park, M.; Yu, I.K. Design and Comparative Analysis of MgB2 and YBCO Wire-Based-Superconducting Wind Power Generators. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, D.; Wang, D.; Shi, J.; Zhu, B.; Ma, S.; Zhang, M.; Pan, Y. Design and control of a new power conditioning system based on superconducting magnetic energy storage. J. Energy Storage 2022, 51, 104359. [Google Scholar] [CrossRef]
- Ren, J.; Xiao, X.; Zheng, Z. In Application of CSC-based SMES to Improve the LVRT Capability of DFIG-based WECS. In Proceedings of the 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 16–18 October 2020; pp. 1–2. [Google Scholar]
- Adetokun, B.B.; Oghorada, O.; Abubakar, S.J. Superconducting magnetic energy storage systems: Prospects and challenges for renewable energy applications. J. Energy Storage 2022, 55, 105663. [Google Scholar] [CrossRef]
- Zhou, A.; Shi, J.; Dai, Q.; Zhang, Z.; Xia, Z.; Zhou, X.; Zhang, C.; Tang, Y. The Supplementary Design Method of HTS SMES System Considering Voltage Distribution Characteristic. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Shi, J.; Lin, D.; Liao, M.; Yang, W.; Zhang, Z.; Zou, X.; Xu, Y.; Ren, L. The Influence of SMES Magnet Operation Parameters on Voltage Distribution Characteristic. IEEE Trans. Appl. Supercond. 2022, 32, 1–5. [Google Scholar] [CrossRef]
- Xiao, L.; Dai, S.; Lin, L.; Zhang, J.; Guo, W.; Zhang, D.; Gao, Z.; Song, N.; Teng, Y.; Zhu, Z.; et al. Development of the World’s First HTS Power Substation. IEEE Trans. Appl. Supercond. 2012, 22, 5000104. [Google Scholar] [CrossRef]
- Dai, S.; Xiao, L.; Wang, Z.; Guo, W.; Zhang, J.; Zhang, D.; Gao, Z.; Song, N.; Zhang, Z.; Zhu, Z.; et al. Development and Demonstration of a 1 MJ High-Tc SMES. IEEE Trans. Appl. Supercond. 2012, 22, 5700304. [Google Scholar]
- Ren, L.; Xu, Y.; Zuo, W.; Shi, X.; Jiao, F.; Liu, Y.; Deng, J.; Li, J.; Shi, J.; Wang, S.; et al. Development of a Movable HTS SMES System. IEEE Trans. Appl. Supercond. 2015, 25, 1–9. [Google Scholar] [CrossRef]
- Liu, W.; Dai, S.; Ma, T.; Shi, Y. Voltage Distribution Characteristic of the D-Shaped Coil of HTS-SMES under High-Frequency Impulse. IEEE Trans. Appl. Supercond. 2022, 32, 1–10. [Google Scholar] [CrossRef]
- Jose, P.A.; Deepak, M. In Fast Frequency Support from Doubly Fed Induction Generators in Coordination with Super-conducting Magnetic Energy Storage Systems. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar]
- Shi, J.; Tang, Y.; Xia, Y.; Ren, L.; Li, J.; Jiao, F. Energy Function Based SMES Controller for Transient Stability Enhancement. IEEE Trans. Appl. Supercond. 2012, 22, 5701304. [Google Scholar]
- Shi, J.; Zhou, A.; Liu, Y.; Ren, L.; Tang, Y.; Li, J. Voltage Distribution Characteristic of HTS SMES Magnet. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Alsharif, A.; Khalid, M. In PV/Fuel Cell/ Superconducting Magnetic Energy Storage Coupled with VSG to Improve Frequency and Voltage Regulation of Power Grid. In Proceedings of the 2023 IEEE PES GTD International Conference and Exposition (GTD), Istanbul, Turkiye, 22–25 May 2023; pp. 350–355. [Google Scholar]
- Salama, H.S.; Said, S.M.; Vokony, I.; Hartmann, B. Adaptive Coordination Strategy Based on Fuzzy Control for Electric Vehicles and Superconducting Magnetic Energy Storage—Towards Reliably Operating Utility Grids. IEEE Access 2021, 9, 61662–61670. [Google Scholar] [CrossRef]
- Malla, S.G.; Al Jaafari, K.; Al Hosani, K.; Muduli, U.R. In Improvement of Power Quality through SMES Control in a Standalone Hybrid Microgrid System. In Proceedings of the 2023 IEEE IAS Global Conference on Emerging Technologies (GlobConET), London, UK, 19–21 May 2023; pp. 1–6. [Google Scholar]
- Song, M.; Shi, J.; Liu, Y.; Xu, Y.; Hu, N.; Tang, Y.; Ren, L.; Li, J. 100 kJ/50 kW HTS SMES for Micro-Grid. IEEE Trans. Appl. Supercond. 2015, 25, 1–6. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yoo, H.J.; Kim, H.M. Applying Model Predictive Control to SMES System in Microgrids for Eddy Current Losses Reduction. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Guo, W.; Xiao, L.; Dai, S. Enhancing Low-Voltage Ride-Through Capability and Smoothing Output Power of DFIG with a Superconducting Fault-Current Limiter–Magnetic Energy Storage System. IEEE Trans. Energy Convers. 2012, 27, 277–295. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, J.; Song, N.; Gao, Z.; Ma, T.; Zhu, Z.; Xu, X.; Li, L.; Wang, Y.; Dai, S.; et al. Overview and Development Progress of a 1-MVA/1-MJ Superconducting Fault Current Limiter-Magnetic Energy Storage System. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar]
- Xie, Q.; Zheng, Z.; Xiao, X.; Huang, C.; Zheng, J.; Ren, J. Enhancing HVRT capability of DFIG-based wind farms using cooperative rotor-side SMES considering the blocking fault of LCC-HVDC system. CSEE J. Power Energy 2021, 7, 698–707. [Google Scholar]
- Jin, J.X.; Xu, W.; Chen, X.Y.; Zhou, X.; Zhang, J.Y.; Gong, W.Z.; Ren, A.L.; Xin, Y. In Developments of SMES devices and potential applications in smart grids. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012. [Google Scholar]
- Amaro, N.; Pina, J.M.; Martins, J.; Ceballos, J.M. In Integration of SMES devices in power systems—Opportunities and challenges. In Proceedings of the 2015 9th International Conference on Compatibility and Power Electronics (CPE), Costa da Caparica, Portugal, 24–26 June 2015. [Google Scholar]
- Chen, X.Y.; Jin, J.X.; Xin, Y.; Shu, B.; Tang, C.L.; Zhu, Y.P.; Sun, R.M. Integrated SMES Technology for Modern Power System and Future Smart Grid. IEEE Trans. Appl. Supercond. 2014, 24, 1–5. [Google Scholar] [CrossRef]
- Liu, W.; Dai, S.; Ma, T.; Shi, Y.; Song, M.; Xia, Y. Longitudinal Insulation Design of Hybrid Toroidal Magnet for 10 MJ High-Temperature Superconducting Magnetic Energy Storage. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 366–375. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive Virtual Inertia Control Strategy of VSG for Micro-Grid Based on Improved Bang-Bang Control Strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, D.; Yin, S.; Lei, Y.; He, T. In Improved Adaptive Inertia and Damping Coefficient Control Strategy of VSG Based on Optimal Damping Ratio. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 102–107. [Google Scholar]
- Xu, J.; Wang, J.; Li, K.; Gui, X.; Liu, Q.; Jiang, G.; Xue, J. In A New Adaptive Frequency Control Strategy for VSG Based on Grid Forming Converter of Renewable Energy. In Proceedings of the 2023 Power Electronics and Power System Conference (PEPSC), Hangzhou, China, 24–26 November 2023; pp. 53–60. [Google Scholar]
- Quan, X.; Yu, R.; Zhao, X.; Lei, Y.; Chen, T.; Li, C.; Huang, A.Q. Photovoltaic Synchronous Generator: Architecture and Control Strategy for a Grid-Forming PV Energy System. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 936–948. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C. PWM Rectifier and Its Control; China Machine Press: Beijing, China, 2012. [Google Scholar]
- Jiao, J.; Nelms, R.M. In Regulating output impedance using a PI controller to improve the stability of a single phase inverter under weak grid. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; p. 1. [Google Scholar]
- Guo, W.; Xiao, L.; Dai, S.; Lin, L. Control Strategy of a 0.5 MVA/1 MJ SMES Based Dynamic Voltage Restorer. IEEE Trans. Appl. Supercond. 2010, 20, 1329–1333. [Google Scholar]
- Guo, W.; Zhang, G.; Zhang, J.; Song, N.; Gao, Z.; Xu, X.; Jing, L.; Teng, Y.; Zhu, Z.; Xiao, L. Development of a 1-MVA/1-MJ Superconducting Fault Current Limiter–Magnetic Energy Storage System for LVRT Capability Enhancement and Wind Power Smoothing. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
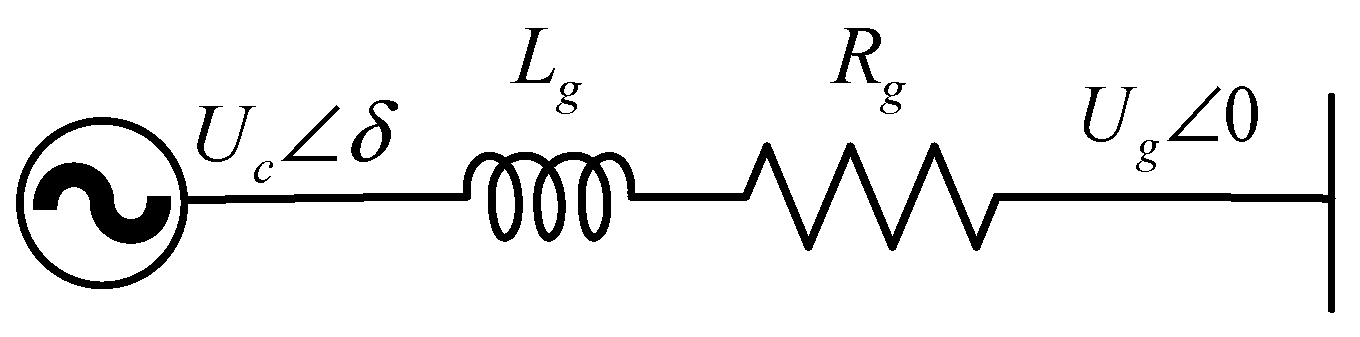
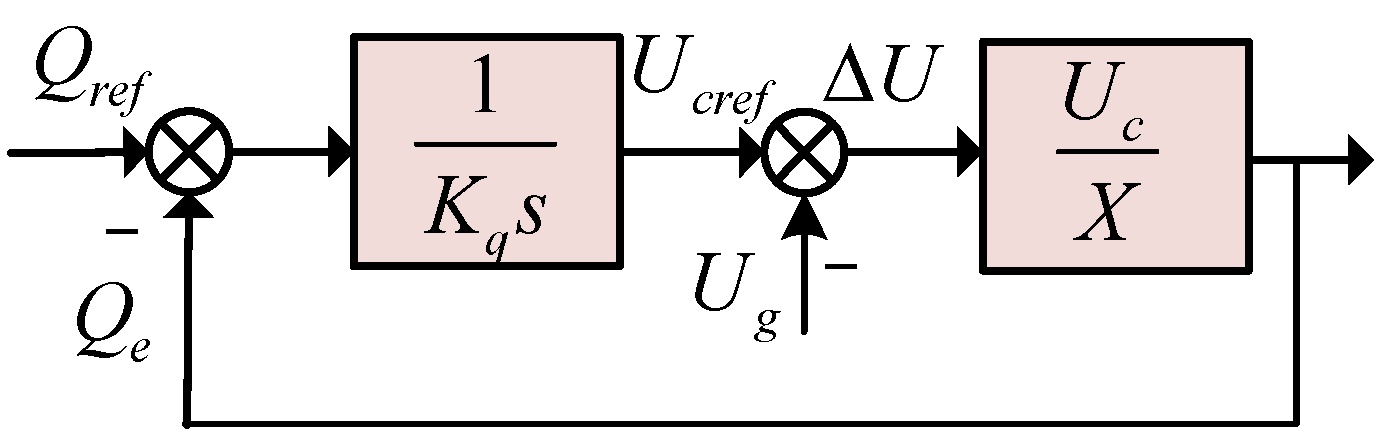








| Name | Unit | Value |
|---|---|---|
| Maximum operating current | A | 1600 |
| Maximum operating voltage | kV | 10 |
| Number of magnet modules | \ | 16 |
| Maximum magnetic field on coil surface | T | 5.91 |
| Maximum vertical magnetic field on coil surface | T | 3.55 |
| Coil self-induction | H | 6.366 |
| Maximum energy storage | MJ | 11.9 |
| Maximum effective output energy | MJ | 10 |
| Cooling mode | \ | Liquid hydrogen immersion cooling |
| Name | Unit | Value |
|---|---|---|
| Three-phase DC voltage source (line voltage RMS) | kV | 10 |
| Grid-side inductance | mH | 3.2 |
| Grid-side resistance | R | 0.2 |
| Grid-side capacitance | μF | 10 |
| DC capacitance | mF | 50 |
| Inductance of SC | H | 6.366 |
| Filter inductance | mH | 0.5 |
| Filter resistance | R | 0.0314 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Hong, Y.; Lan, J.; Yang, Y. Multi-Functional Device Based on Superconducting Magnetic Energy Storage. Energies 2024, 17, 3175. https://doi.org/10.3390/en17133175
Guo W, Hong Y, Lan J, Yang Y. Multi-Functional Device Based on Superconducting Magnetic Energy Storage. Energies. 2024; 17(13):3175. https://doi.org/10.3390/en17133175
Chicago/Turabian StyleGuo, Wenyong, Yun Hong, Jianyu Lan, and Yahong Yang. 2024. "Multi-Functional Device Based on Superconducting Magnetic Energy Storage" Energies 17, no. 13: 3175. https://doi.org/10.3390/en17133175
APA StyleGuo, W., Hong, Y., Lan, J., & Yang, Y. (2024). Multi-Functional Device Based on Superconducting Magnetic Energy Storage. Energies, 17(13), 3175. https://doi.org/10.3390/en17133175







