Design of a Wave Generation System Using an Oscillating Paddle-Type Device Anchored to Fixed Structures on the Coast
Abstract
1. Introduction
2. Materials and Methods
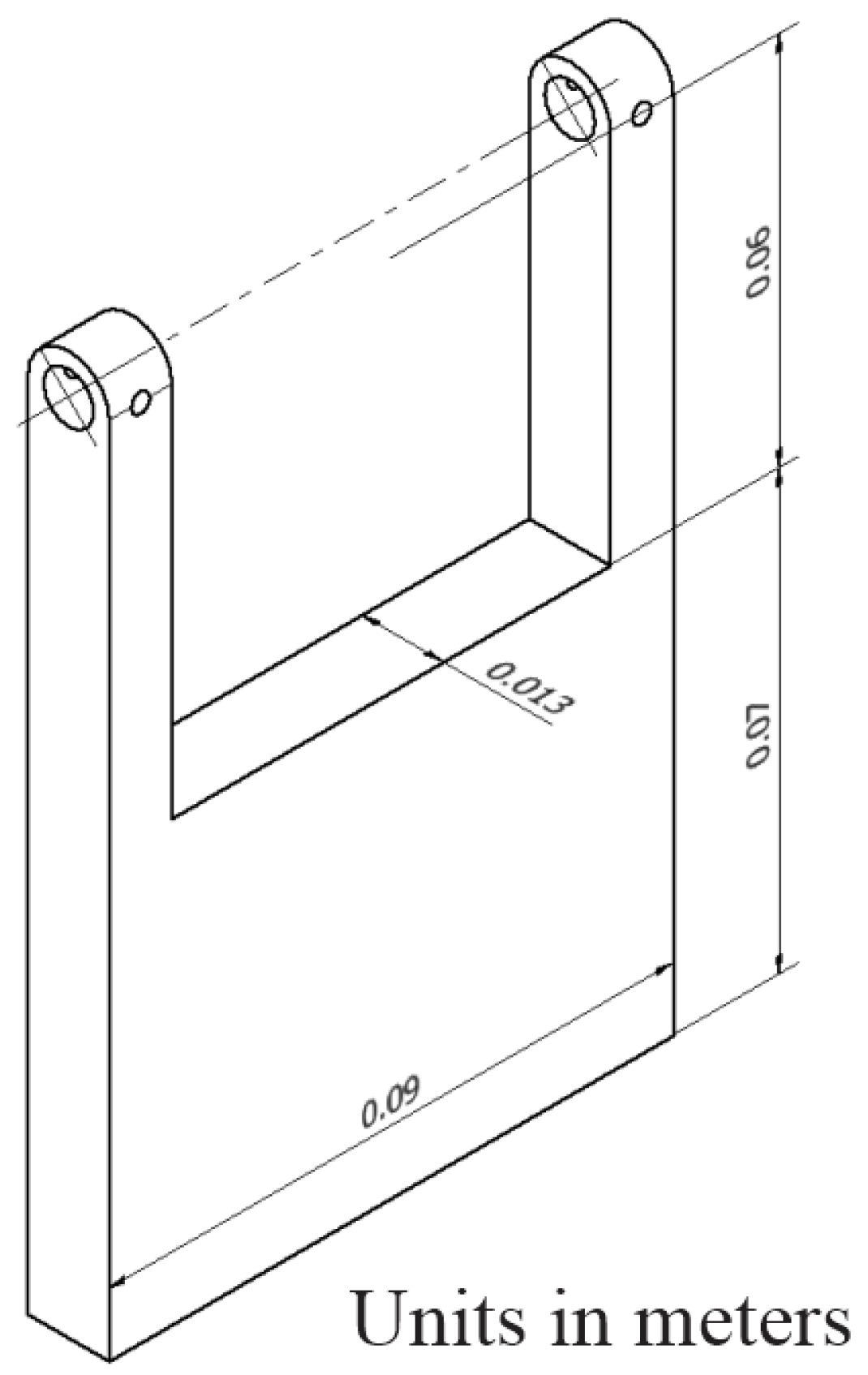
2.1. Geometry of the Wave Energy Converter Device
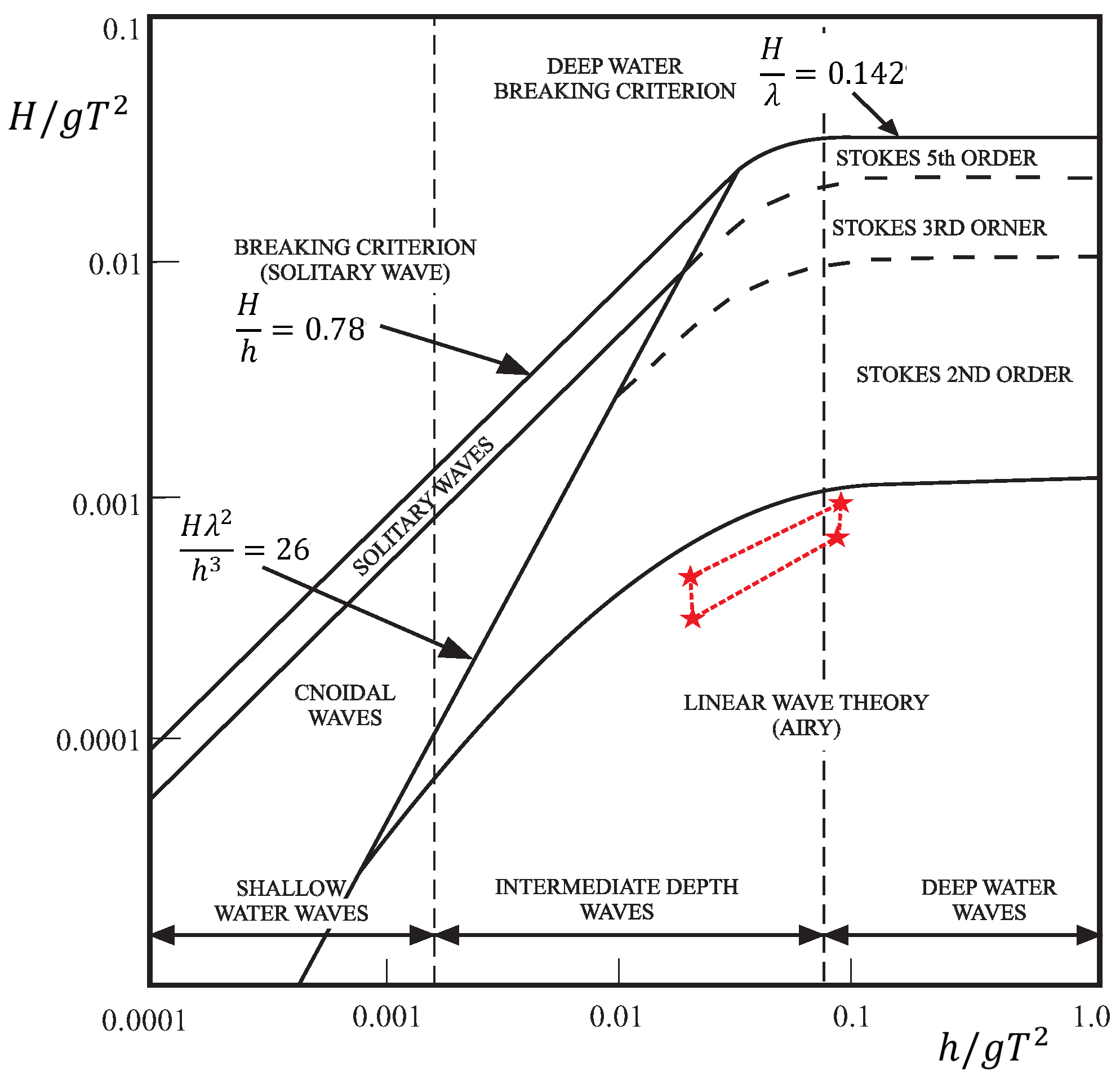
2.2. Wave Resource
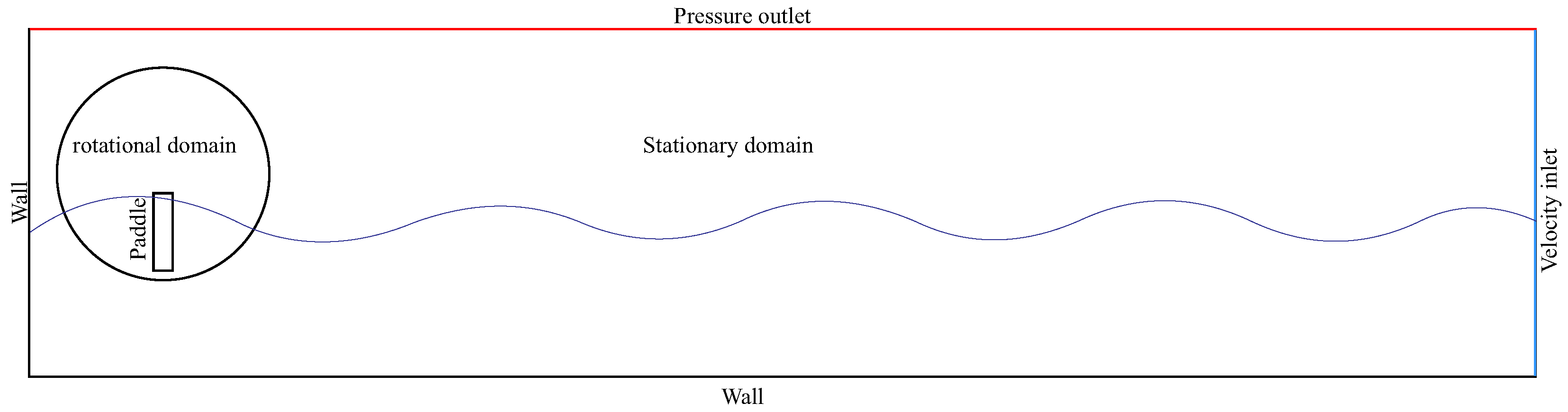
2.3. Computational Simulation
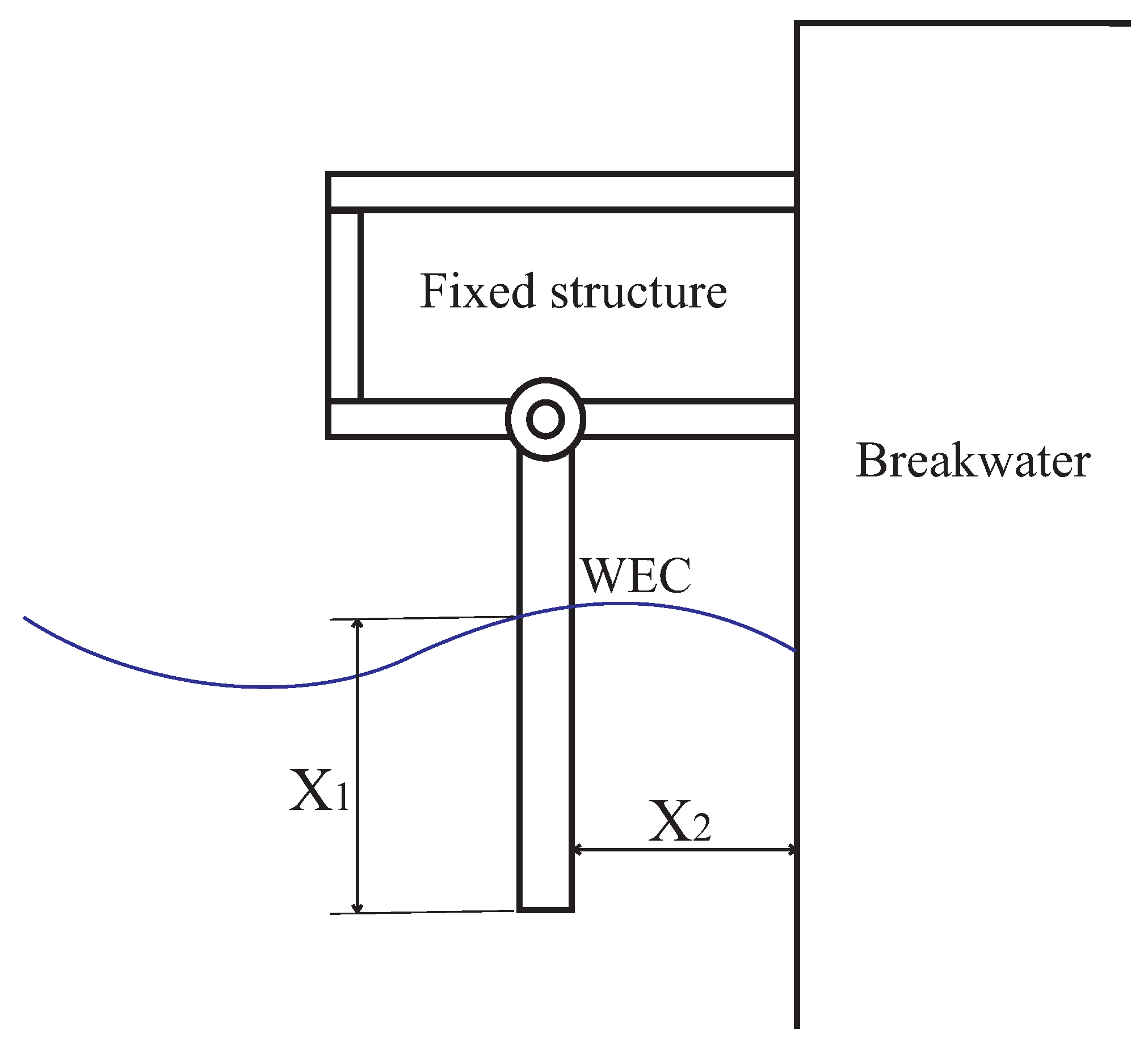
2.4. Optimization of the Wave Energy Generation System
2.5. Experimental Validation
3. Results
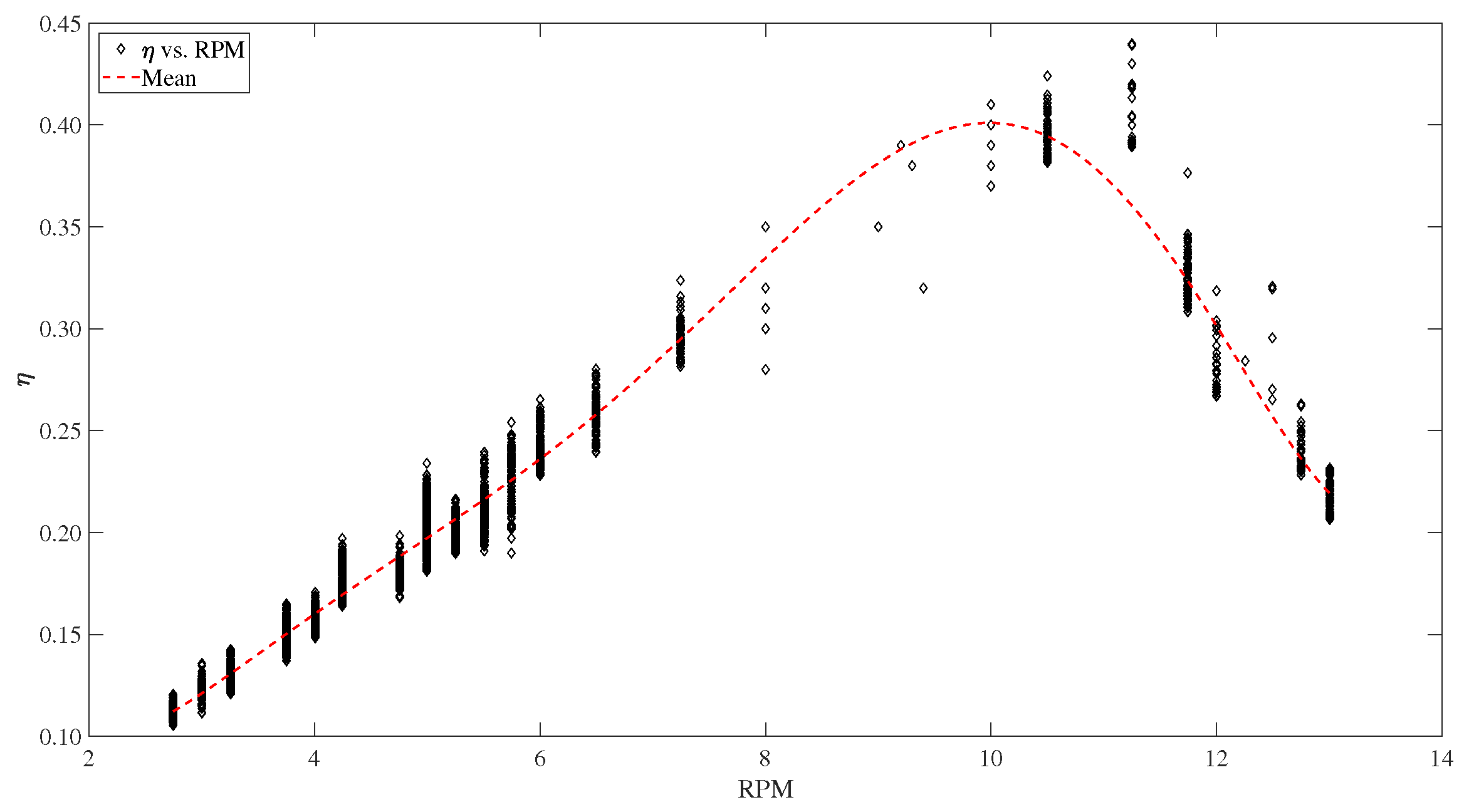
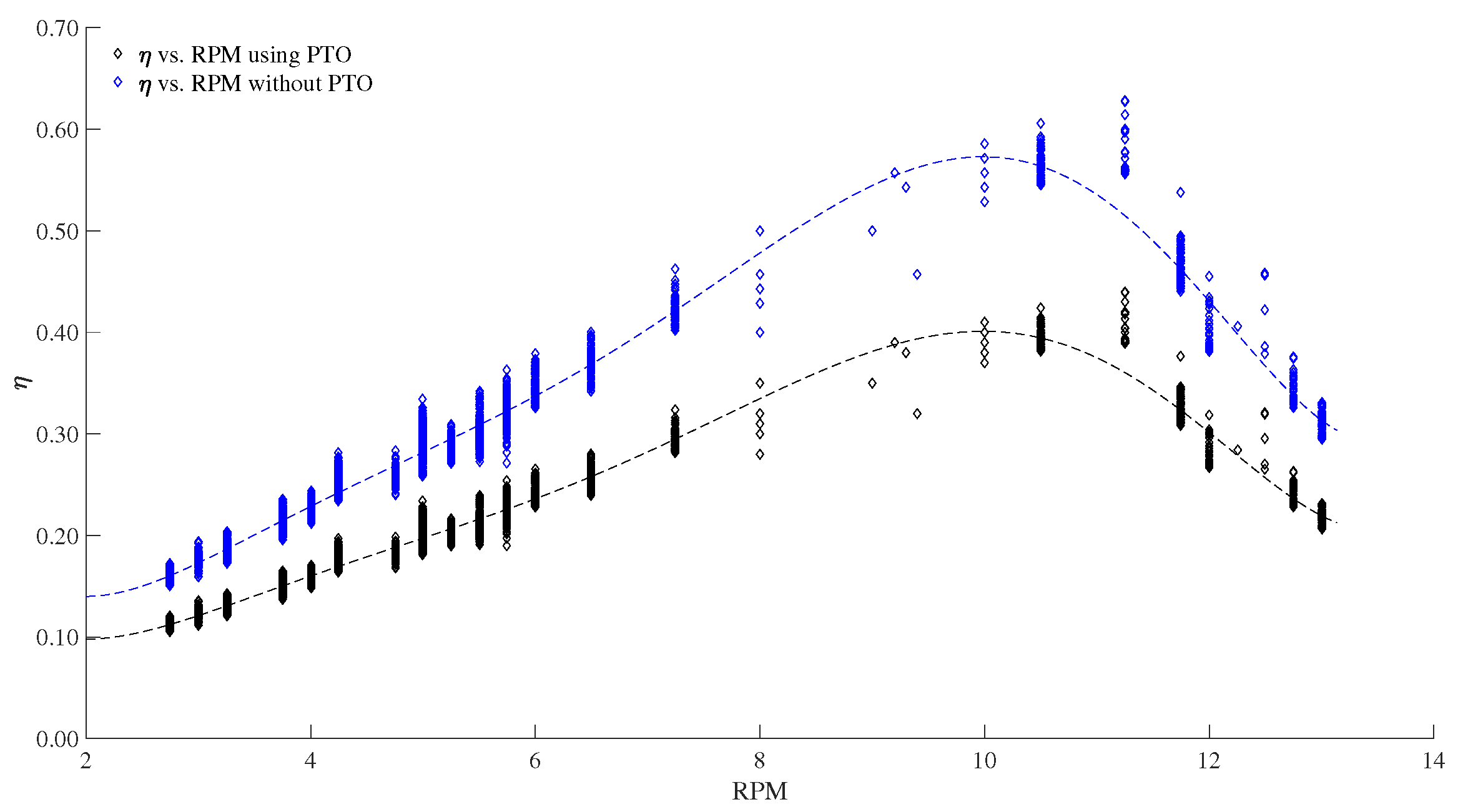
3.1. Results of the Numerical Simulations
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murdock, H.E.; Gibb, D.; André, T.; Sawin, J.L.; Brown, A.; Ranalder, L.; Collier, U.; Dent, C.; Epp, B.; Hareesh Kumar, C.; et al. Renewables 2021-Global Status Report 2021. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2021_Full_Report.pdf (accessed on 17 April 2022).
- Wilches, C.R.T. Planeamiento Estratégico del Sector de las Fuentes No Convencionales de Energía Renovable en Colombia. Ph.D. Thesis, Pontificia Universidad Catolica del Peru, San Miguel, Peru, 2017. [Google Scholar]
- AK-BHD. WMO Greenhouse Gas Bulletin; World Meteorological Organization: Geneva, Switzerland, 2021.
- Tu, Q.; Mo, J.; Betz, R.; Cui, L.; Fan, Y.; Liu, Y. Achieving grid parity of solar PV power in China-The role of Tradable Green Certificate. Energy Policy 2020, 144, 111681. [Google Scholar] [CrossRef]
- Dato, P. Investment in energy efficiency, adoption of renewable energy and household behavior: Evidence from OECD countries. Energy J. 2018, 39, 213–244. [Google Scholar] [CrossRef]
- Sun, P.; Xu, B.; Wang, J. Long-term trend analysis and wave energy assessment based on ERA5 wave reanalysis along the Chinese coastline. Appl. Energy 2022, 324, 119709. [Google Scholar] [CrossRef]
- Gunn, K.; Stock-Williams, C. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; De Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Tao, T. A novel oscillating wave surge converter by hollowing out the flap bottom: Numerical studies using smoothed particle hydrodynamics. Ocean Eng. 2024, 303, 117694. [Google Scholar] [CrossRef]
- Henry, A.; Folley, M.; Whittaker, T. A conceptual model of the hydrodynamics of an oscillating wave surge converter. Renew. Energy 2018, 118, 965–972. [Google Scholar] [CrossRef]
- Mottahedi, H.R.; Anbarsooz, M.; Passandideh-Fard, M. Application of a fictitious domain method in numerical simulation of an oscillating wave surge converter. Renew. Energy 2018, 121, 133–145. [Google Scholar] [CrossRef]
- Liu, Y.; Cho, Y.H.; Mizutani, N.; Nakamura, T. Simplified BEM-based mathematical model for bottom-hinged oscillating wave surge converters under large-amplitude regular waves. Ocean Eng. 2023, 272, 113893. [Google Scholar] [CrossRef]
- Dias, F.; Renzi, E.; Gallagher, S.; Sarkar, D.; Wei, Y.; Abadie, T.; Cummins, C.; Rafiee, A. Analytical and computational modelling for wave energy systems: The example of oscillating wave surge converters. Acta Mech. Sin. 2017, 33, 647–662. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, Y.; Dias, F.; Hu, X. An efficient fully Lagrangian solver for modeling wave interaction with oscillating wave surge converter. Ocean Eng. 2021, 236, 109540. [Google Scholar] [CrossRef]
- Pathak, A.; Freniere, C.; Raessi, M. Advanced computational simulations of water waves interacting with wave energy converters. Eur. J. Comput. Mech. 2017, 26, 172–204. [Google Scholar] [CrossRef]
- Brito, M.; Ferreira, R.M.; Teixeira, L.; Neves, M.G.; Gil, L. Experimental investigation of the flow field in the vicinity of an oscillating wave surge converter. J. Mar. Sci. Eng. 2020, 8, 976. [Google Scholar] [CrossRef]
- Saeidtehrani, S. Flap-type wave energy converter arrays: Nonlinear dynamic analysis. Ocean Eng. 2021, 236, 109463. [Google Scholar] [CrossRef]
- Ning, D.; Liu, C.; Zhang, C.; Göteman, M.; Zhao, H.; Teng, B. Hydrodynamic performance of an oscillating wave surge converter in regular and irregular waves: An experimental study. J. Mar. Sci. Technol. 2017, 25, 4. [Google Scholar]
- Jiang, X.; Day, S.; Clelland, D. Hydrodynamic responses and power efficiency analyses of an oscillating wave surge converter under different simulated PTO strategies. Ocean Eng. 2018, 170, 286–297. [Google Scholar] [CrossRef]
- Wei, Y.; Rafiee, A.; Elsaesser, B.; Dias, F. Numerical simulation of an oscillating wave surge converter. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, Nantes, France, 9–14 June 2013; Volume 55317, p. V001T01A012. [Google Scholar]
- Cheng, Y.; Li, G.; Ji, C.; Fan, T.; Zhai, G. Fully nonlinear investigations on performance of an OWSC (oscillating wave surge converter) in 3D (three-dimensional) open water. Energy 2020, 210, 118526. [Google Scholar] [CrossRef]
- Whittaker, T.; Folley, M. Nearshore oscillating wave surge converters and the development of Oyster. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 345–364. [Google Scholar] [CrossRef]
- Liu, Y.; Cho, Y.H.; Mizutani, N.; Nakamura, T. Study on the resonant behaviors of a bottom-hinged oscillating wave surge converter. J. Mar. Sci. Eng. 2021, 10, 2. [Google Scholar] [CrossRef]
- Schmitt, P.; Elsäßer, B. The application of Froude scaling to model tests of Oscillating Wave Surge Converters. Ocean Eng. 2017, 141, 108–115. [Google Scholar] [CrossRef]
- Cheng, Y.; Xi, C.; Dai, S.; Ji, C.; Cocard, M. Wave energy extraction for an array of dual-oscillating wave surge converter with different layouts. Appl. Energy 2021, 292, 116899. [Google Scholar] [CrossRef]
- Wei, Y.; Rafiee, A.; Henry, A.; Dias, F. Wave interaction with an oscillating wave surge converter, Part I: Viscous effects. Ocean Eng. 2015, 104, 185–203. [Google Scholar] [CrossRef]
- Wei, Y.; Abadie, T.; Henry, A.; Dias, F. Wave interaction with an oscillating wave surge converter. Part II: Slamming. Ocean Eng. 2016, 113, 319–334. [Google Scholar] [CrossRef]
- Ferrer, P.; Causon, D.; Qian, L.; Mingham, C.; Ma, Z. Numerical simulation of wave slamming on a flap type oscillating wave energy device. In Proceedings of the Twenty-Sixth (2016) International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- Kumawat, A.; Karmakar, D.; Guedes Soares, C. Wave energy conversion by multiple bottom-hinged surging WEC. In Proceedings of the Fourth International Conference in Ocean Engineering (ICOE2018); Springer: Berlin, Germany, 2019; Volume 2, pp. 913–929. [Google Scholar]
- Spyrou, K.; Themelis, N.; Tigkas, I. International Towing Tank Conference. 2004. Available online: https://www.ittc.info/media/10938/volume-i.pdf (accessed on 20 January 2023).
- Bozzi, S.; Besio, G.; Passoni, G. Wave power technologies for the Mediterranean offshore: Scaling and performance analysis. Coast. Eng. 2018, 136, 130–146. [Google Scholar] [CrossRef]
- Bozzi, S.; Archetti, R.; Passoni, G. Wave electricity production in Italian offshore: A preliminary investigation. Renew. Energy 2014, 62, 407–416. [Google Scholar] [CrossRef]
- Hadadpour, S.; Etemad-Shahidi, A.; Jabbari, E.; Kamranzad, B. Wave energy and hot spots in Anzali port. Energy 2014, 74, 529–536. [Google Scholar] [CrossRef]
- Gunawardane, S.; Bandara, G.; Lee, Y.H. Hydrodynamic analysis of a novel wave energy converter: Hull Reservoir Wave Energy Converter (HRWEC). Renew. Energy 2021, 170, 1020–1039. [Google Scholar] [CrossRef]
- De Alwis, V.; De Silva, A.; Gunawardane, S.; Lee, Y.H. Computational fluid dynamic simulation of hull reservoir wave energy device. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2217, p. 012041. [Google Scholar]
- Gioia, D.G.; Pasta, E.; Brandimarte, P.; Mattiazzo, G. Data-driven control of a pendulum wave energy converter: A gaussian process regression approach. Ocean Eng. 2022, 253, 111191. [Google Scholar] [CrossRef]
- Portilla, J.; Caicedo, A.L.; Padilla-Hernández, R.; Cavaleri, L. Spectral wave conditions in the Colombian Pacific Ocean. Ocean Model. 2015, 92, 149–168. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991; Volume 2. [Google Scholar]
- Beneduce, M. Design of a Wavemaker for the Water Tank at the Politecnico di Torino. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2019. [Google Scholar]
- Izquierdo, U.; Esteban, G.A.; Blanco, J.M.; Albaina, I.; Peña, A. Experimental validation of a CFD model using a narrow wave flume. Appl. Ocean Res. 2019, 86, 1–12. [Google Scholar] [CrossRef]
- Le Méhauté, B. An Introduction to Hydrodynamics and Water Waves; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Bouali, B.; Larbi, S. Sequential optimization and performance prediction of an oscillating water column wave energy converter. Ocean Eng. 2017, 131, 162–173. [Google Scholar] [CrossRef]
- Rubio-Clemente, A.; Velásquez, L.; Chica, E. Design of a water channel to model the wave conditions in the Colombian Pacific Ocean. Renew. Energy Power Qual. J. 2022, 20, 405–412. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J.V. Geometric optimisation of wave energy conversion devices: A survey. Appl. Energy 2021, 297, 117100. [Google Scholar] [CrossRef]
- Hayati, M.; Nikseresht, A.H.; Haghighi, A.T. Sequential optimization of the geometrical parameters of an OWC device based on the specific wave characteristics. Renew. Energy 2020, 161, 386–394. [Google Scholar] [CrossRef]
- Ning, D.z.; Zhou, Y.; Mayon, R.; Johanning, L. Experimental investigation on the hydrodynamic performance of a cylindrical dual-chamber Oscillating Water Column device. Appl. Energy 2020, 260, 114252. [Google Scholar] [CrossRef]
- Sorensen, R.M. Basic Wave Mechanics: For Coastal and Ocean Engineers; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Liu, Y.; Cavalier, G.; Pastor, J.; Viera, R.J.; Guillory, C.; Judice, K.; Guiberteau, K.; Kozman, T.A. Design and construction of a wave generation system to model ocean conditions in the Gulf of Mexico. Int. J. Energy Technol. 2012, 4, 1–7. [Google Scholar]
- Saincher, S.; Banerjeea, J. Design of a numerical wave tank and wave flume for low steepness waves in deep and intermediate water. Procedia Eng. 2015, 116, 221–228. [Google Scholar] [CrossRef]
- Qin, S.; Fan, J.; Zhang, H.; Su, J.; Wang, Y. Flume experiments on energy conversion behavior for oscillating buoy devices interacting with different wave types. J. Mar. Sci. Eng. 2021, 9, 852. [Google Scholar] [CrossRef]
- Castedo, R.; Reifarth, C.; Santos, A.P.; Losada, J.; López, L.M.; Chiquito, M.; Mancilla, J.M. Application of grid convergence index to shock wave validated with LS-DYNA and ProsAir. Ing. Investig. 2019, 39, 20–26. [Google Scholar] [CrossRef]
- Schleicher, W.; Riglin, J.; Oztekin, A. Numerical characterization of a preliminary portable micro-hydrokinetic turbine rotor design. Renew. Energy 2015, 76, 234–241. [Google Scholar] [CrossRef]
- Riglin, J.D.; Schleicher, W.C.; Oztekin, A. Cavitation Phenomena and Performance Implications in Archimedes Flow Turbines. J. Fluids Eng. 2016, 138, 031303. [Google Scholar] [CrossRef]
- Mansour, A.; Laurien, E. Numerical error analysis for three-dimensional CFD simulations in the two-room model containment THAI+: Grid convergence index, wall treatment error and scalability tests. Nucl. Eng. Des. 2018, 326, 220–233. [Google Scholar] [CrossRef]
- Roy, C.J. Grid convergence error analysis for mixed-order numerical schemes. AIAA J. 2003, 41, 595–604. [Google Scholar] [CrossRef]
- Phillips, T.S.; Roy, C.J. Richardson extrapolation-based discretization uncertainty estimation for computational fluid dynamics. J. Fluids Eng. 2014, 136, 121401. [Google Scholar] [CrossRef]
- Gutiérrez Marcantoni, L.F. Simulación de Flujos Compresibles con openFoam™. Master’s Thesis, Universidad Nacional de Córdoba, Córdoba, Argentina, 2013. [Google Scholar]
- Yang, I.; Tezdogan, T.; Incecik, A. Numerical investigations of a pivoted point absorber wave energy converter integrated with breakwater using CFD. Ocean Eng. 2023, 274, 114025. [Google Scholar] [CrossRef]
- Humberto, G.P.; De La Vara, R. Análisis y Diseño de Experimentos; Mc Graw Hill: New York, NY, USA, 2008. [Google Scholar]
- Yaguas, O.J. Metodología de superficie de respuesta para la optimización de una producción agrícola. Rev. Ing. Ind. 2017, 16, 205–222. [Google Scholar] [CrossRef]
- Sun, B.; Li, C.; Yang, S.; Zhang, H. A simplified method and numerical simulation for wedge-shaped plunger wavemaker. Ocean Eng. 2021, 241, 110023. [Google Scholar] [CrossRef]
- Rezaei, S.; Rahimi, A.; Parvizian, J.; Mansourzadeh, S.; Düster, A. Dimensional optimization of a two-body Wave energy converter using response surface methodology. Ocean Eng. 2022, 261, 112186. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Kamizuru, Y. Development of Hydrostatic Drive Trains for Wave Energy Converters; Shaker: Herzogenrath, Germany, 2014; Volume 352. [Google Scholar]
- Babarit, A. A database of capture width ratio of wave energy converters. Renew. Energy 2015, 80, 610–628. [Google Scholar] [CrossRef]
- Flocard, F.; Finnigan, T. Experimental investigation of power capture from pitching point absorbers. In Proceedings of the Eight European Wave and Tidal Energy Conference, Upsalla, Sweden, 7–10 September 2009. [Google Scholar]
- Islam, M.; Jahra, F.; Hiscock, S. Data analysis methodologies for hydrodynamic experiments in waves. J. Nav. Archit. Mar. Eng. 2016, 13, 1. [Google Scholar] [CrossRef][Green Version]
- Windt, C.; Davidson, J.; Ringwood, J.V. Numerical analysis of the hydrodynamic scaling effects for the Wavestar wave energy converter. J. Fluids Struct. 2021, 105, 103328. [Google Scholar] [CrossRef]






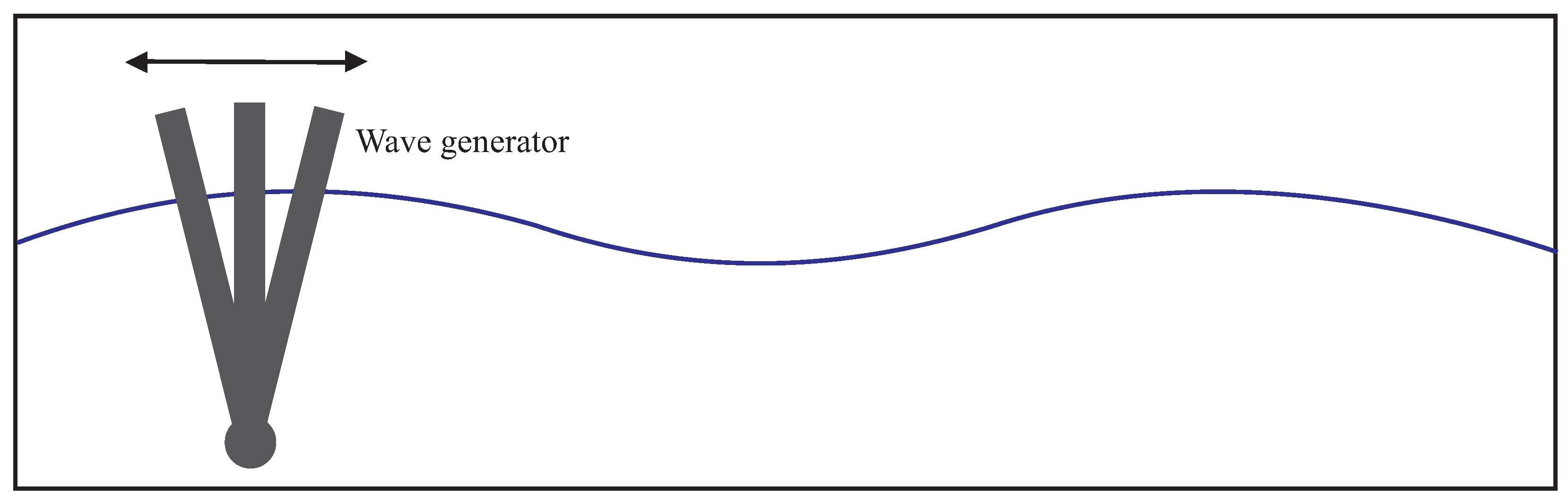
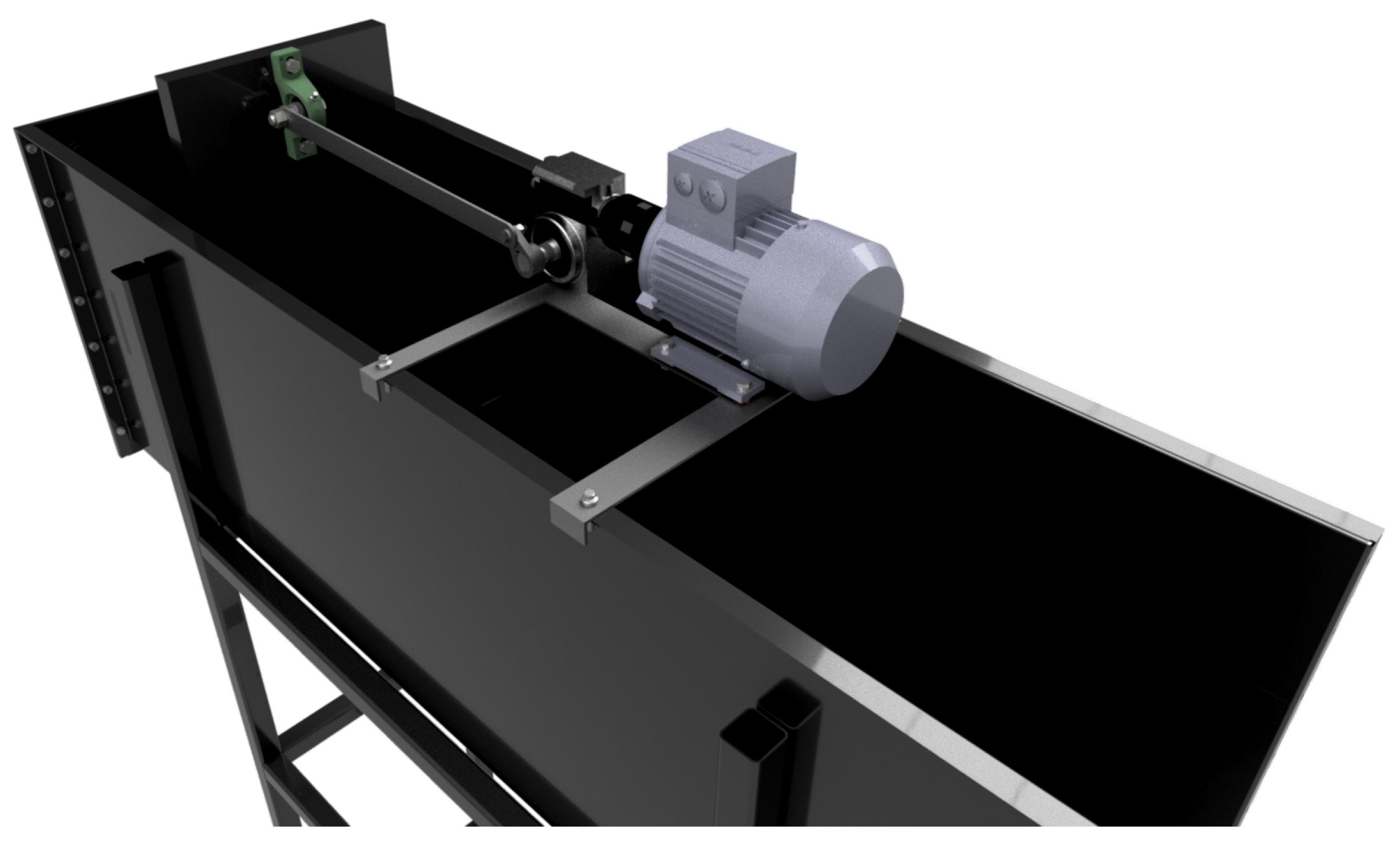
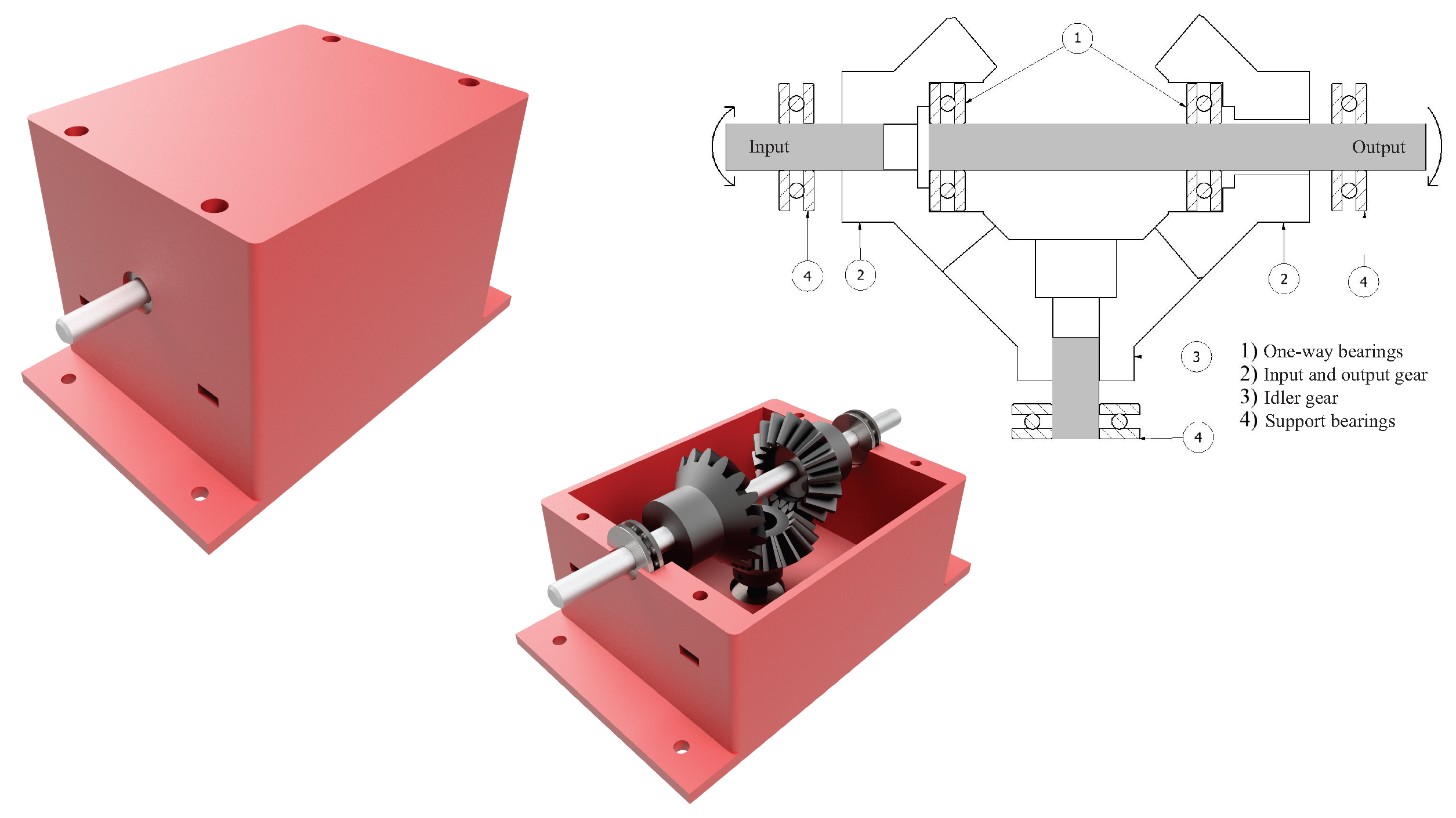

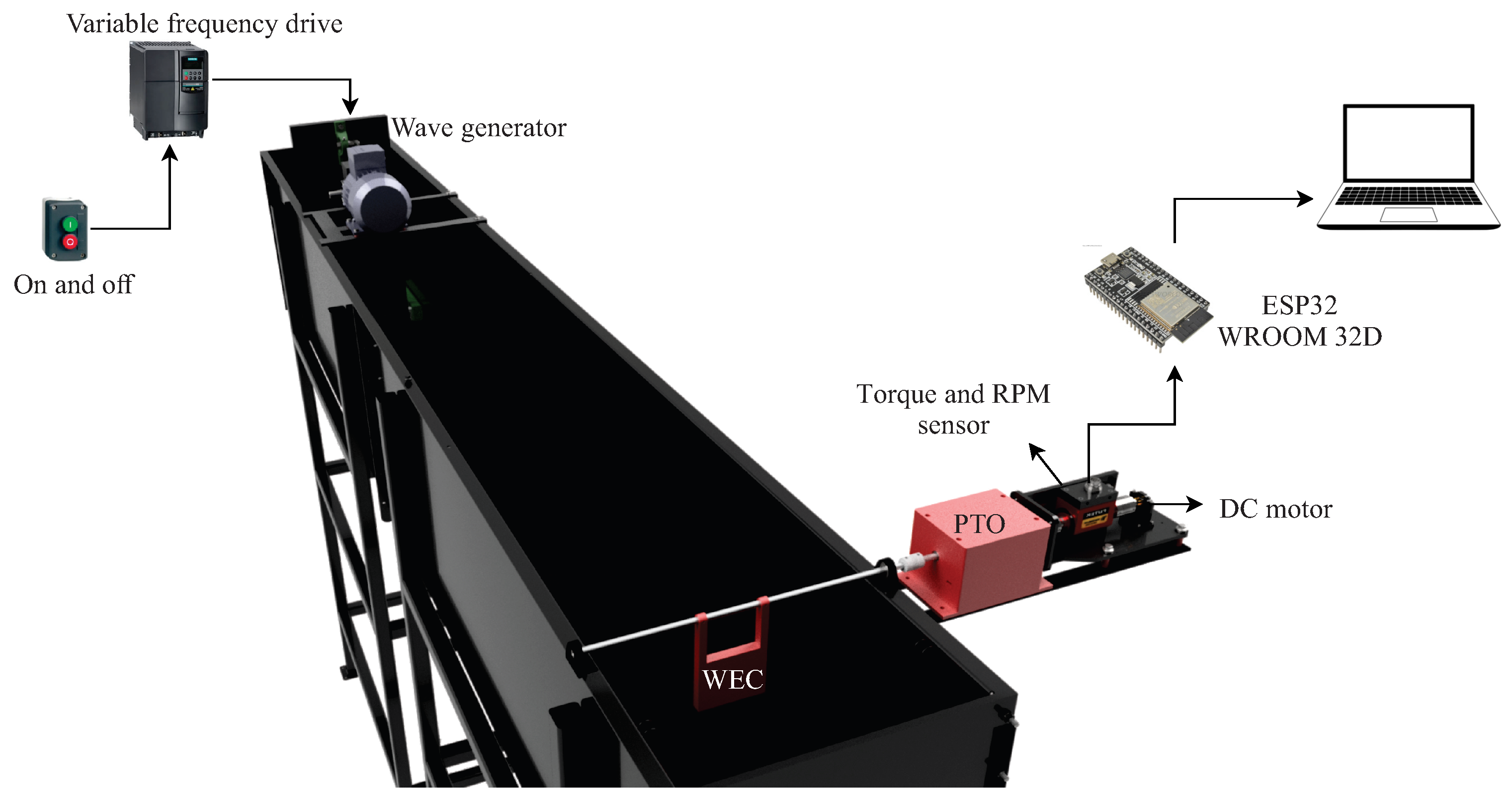

| Author | H × W × T (m) | Scale | Remarks |
|---|---|---|---|
| Dias et al. [13] | Oyster WEC | 1:25 y 1:40 | A numerical simulation was performed through the smoothed particle hydrodynamics (SPH) method. Efficiency up to 80% was found. |
| Zhang et al. [14] | 1.08 × 0.48 × 0.12 | 1:25 | A numerical simulation was performed through the SPH method. The numerical wave tank (NWT) was 18.4 m long, 4.58 m wide and 1 m high. A maximum efficiency of 40% was achieved. |
| Ashish et al. [15] | 1.08 × 0.48 × 0.12 | 1:33 | A numerical simulation was performed. The computational domain was 28.8 m × 4.608 m × 1.152 m. |
| Brito et al. [16] | 0.84 × 1.13 × 0.17 | 1:25 | An experimental investigation was conducted. The wave tank (WT) was 60 m long, 1.5 m wide and 1.8 m high. A power capture up to 40% was found. |
| Saeidtehrani et al. [17] | 0.072 × 0.05 × 0.043 | 1:40 | Experimental and numerical investigations were carried out. The WT was 9 m long, 0.27 m wide, and 0.5 m deep. |
| Ning et al. [18] | 1.05 × 0.8 × 0.15 | 1:05 | An experimental study was conducted. The WT was 60 m long, 4 m wide, and 2.5 m deep. A power capture up to 60% was found. |
| Jiang et al. [19] | 0.305 (RA: Oyster WEC) | 1:40 | Experimental research was conducted. The WT was 21.6 m long, 1.6 m wide, and 0.45 m deep. the output power found was around 10 W. |
| Wei et al. [20] | 1.04 × 0.48 × 0.12 | 1:30 | A numerical simulation was performed. The VOF method was used. The NWT was 39.13 m long, 4.58 wide and an operating depth up to 0.8 m. Power capture factor up to 80% was found. |
| Cheng et al. [21] | - | - | A numerical investigation was carried out, and a maximum efficiency of 57% was achieved. |
| Whittaker et al. [22] | 11 × 18 × 1.8 (Oyster) | - | The study reported the state-of-the-art about oyster devices. |
| Ferrer et al. [23] | 10 × 26 × 4 | - | A numerical model was performed. The VOF method and the standard k-epsilon turbulence model were used. Capture width ratio up to 0.6 was found. |
| Liu et al. [24] | - | 1:40 | Experimental and numerical investigations were conducted. The WT was 20 m long, 4.58 m wide, and 0.8 m deep. The standard k-omega SST turbulence model was used. |
| Schmitt et al. [25] | 0.31 × 0.646 × 0.0875 | 1:40 | A numerical investigation was performed. Efficiencies of up to 67% were achieved within an array of wave energy converters. |
| Cheng et al. [26] | 1.04 × 0.48 × 0.12 | 1:25 | Experimental and numerical studies were used. The WT was 18 m long, 4.58 m wide, and 0.4–0.8 m deep. The standard k-epsilon turbulence model and the VOF method were implemented. |
| Wei et al. [27] | 0.31 × 0.646 × 0.0875 | 1:40 | Experimental and numerical studies; WT is 16.7 m long, 0.65 m wide, and 0.305 deep. |
| Ferrer et al. [28] | 0.31 × 0.646 × 0.0875 | 1:40 | A numerical investigation was implemented. The NWT was 16.77 m long, 1.5 m wide, and 0.646 m deep. The VOF method was used. |
| Location | Wave Height Mean (H, m) | Wave Period Mean (T, s) |
|---|---|---|
| Tumaco | 1.01 m | 6.86 s |
| Gorgona Island | 1.13 m | 7.76 s |
| Buenaventura Harbour | 0.96 m | 8.21 s |
| Solano Bay | 1.17 m | 10.61 s |
| = 30 | Wave Height (H) | Wave Period (T) | Wave Length (L) | Depth (d) |
|---|---|---|---|---|
| Real | 0.99 m | 7.31 s | 80.9 m | 13 m |
| Scaled model | 0.033 m | 1.33 s | 2.3 m | 0.43 m |
| Mesh Quality | Minimum | Maximum | Average |
|---|---|---|---|
| Element Quality | 0.7384 | 1 | 0.9999 |
| Aspect Ratio | 1 | 2.0202 | 1.0024 |
| Orthogonal Quality | 0.7505 | 1 | 0.9999 |
| Skewness | 1.30 × | 0.485 | 3.78 × |
| = Torque [Nm] | ||
|---|---|---|
| 0.91301 | ||
| 0.89569 | ||
| 0.85959 | ||
| 0.91878 | ||
| 2.18% | ||
| 4.64% | ||
| R | 1.019 | |
| = Torque [Nm] | ||
|---|---|---|
0.00025 | 0.0005 | 0.001 |
| 0.242465 | ||
| 0.246874 | ||
| 0.262861 | ||
| 0.240995 | ||
| 0.86% | ||
| 3.08% | ||
| R | 0.982 | |
| Parameters | Value |
|---|---|
| Wave height | 0.33 m |
| Wave length | 2.3 m |
| Turbulence model | standard k- |
| Method | PISO-VOF |
| Material of oscillating paddle | PLA |
| Mass of oscillating paddle | 0.109 kg |
| Inertia | 0.0019 kg m2 |
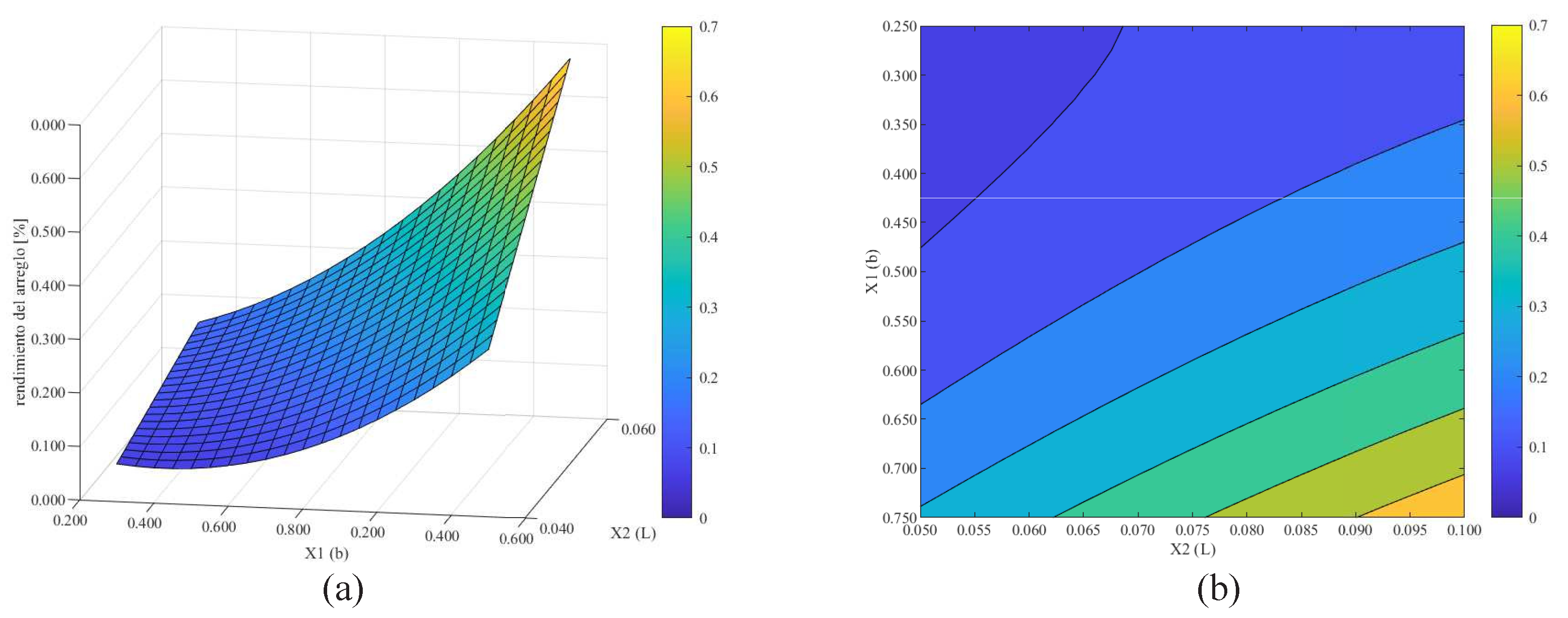
| Independent Factor | Values | ||
|---|---|---|---|
| Factor level | −1 | 0 | 1 |
| X1 (%b) | 0.25 | 0.50 | 0.75 |
| X2 (%L) | 0.05 | 0.075 | 0.10 |
| 0.25 | 0.05 | 0.058 |
| 0.50 | 0.05 | 0.142 |
| 0.75 | 0.05 | 0.269 |
| 0.25 | 0.075 | 0.113 |
| 0.50 | 0.075 | 0.212 |
| 0.75 | 0.075 | 0.557 |
| 0.25 | 0.10 | 0.158 |
| 0.5 | 0.10 | 0.321 |
| 0.75 | 0.10 | 0.648 |
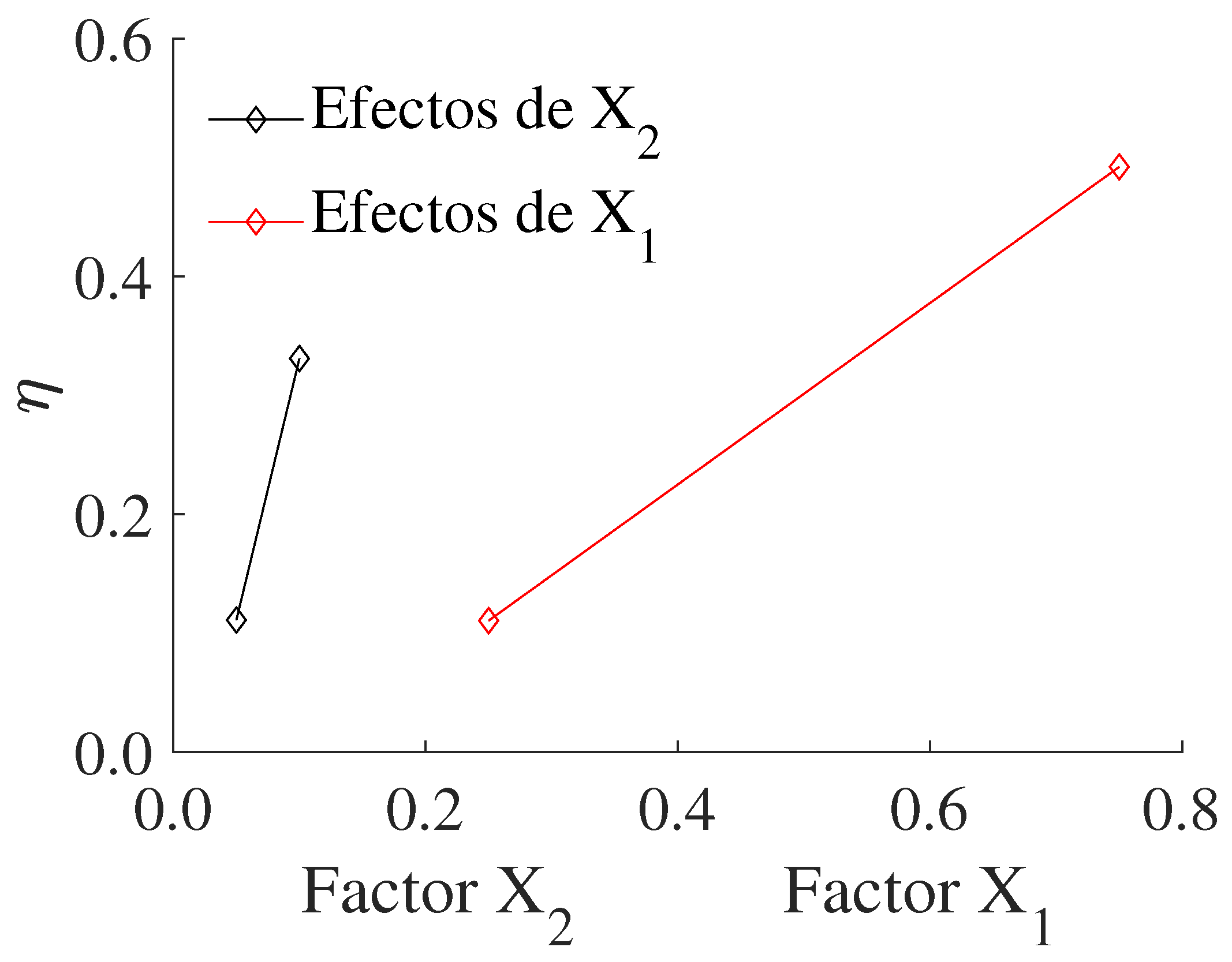
| Term | Effect | Sum of Squares (SS) | Degrees of Freedom (df) | Mean Square (MS) | F-Ratio | p-Value |
|---|---|---|---|---|---|---|
| Model | 0.32513 | 4 | 0.32513 | 54.96 | 7.70 × | |
| X1 | −13.612 | 0.21862 | 1 | 0.21862 | 147.71 | 1.89 × |
| X2 | −11.933 | 0.07020 | 1 | 0.07020 | 47.43 | 0.000463 |
| X12 | 12.872 | 0.01682 | 1 | 0.01682 | 11.36 | 0.015024 |
| X1X2 | 111.680 | 0.01949 | 1 | 0.01949 | 13.17 | 0.010983 |
| Error | 0.03847 | 6 |
| Parameters | Scaling |
|---|---|
| Wave height and length | |
| Wave period | |
| Wave frequency | |
| Power density | |
| Linear displacement | |
| Angular displacement | 1 |
| Linear velocity | |
| Angular velocity | |
| Linear acceleration | 1 |
| Angular acceleration | |
| Mass | |
| Force | |
| Torque | |
| Power | |
| Linear stiffness | |
| Angular stiffness | |
| Linear damping | |
| Angular damping |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castaño Serna, J.P.; Rubio-Clemente, A.; Chica, E. Design of a Wave Generation System Using an Oscillating Paddle-Type Device Anchored to Fixed Structures on the Coast. Energies 2024, 17, 3209. https://doi.org/10.3390/en17133209
Castaño Serna JP, Rubio-Clemente A, Chica E. Design of a Wave Generation System Using an Oscillating Paddle-Type Device Anchored to Fixed Structures on the Coast. Energies. 2024; 17(13):3209. https://doi.org/10.3390/en17133209
Chicago/Turabian StyleCastaño Serna, Juan Pablo, Ainhoa Rubio-Clemente, and Edwin Chica. 2024. "Design of a Wave Generation System Using an Oscillating Paddle-Type Device Anchored to Fixed Structures on the Coast" Energies 17, no. 13: 3209. https://doi.org/10.3390/en17133209
APA StyleCastaño Serna, J. P., Rubio-Clemente, A., & Chica, E. (2024). Design of a Wave Generation System Using an Oscillating Paddle-Type Device Anchored to Fixed Structures on the Coast. Energies, 17(13), 3209. https://doi.org/10.3390/en17133209








