Real-Time Simulation System for Small Scale Regional Integrated Energy Systems
Abstract
1. Introduction
- Modeling and control of device-level units and energy networks: Averaged switch models of device-level units in DMG are developed and verified in PSIM; the unified energy path method is utilized in both DHNs and NGNs. These models and methods provide new perspectives for understanding and calculating complex energy systems.
- Development of energy control algorithms: Hierarchical control strategies for DMG island operation mode and multi-energy dispatch strategies are designed for RIES. These strategies and algorithms can effectively calculate the energy flow and ensure stable operation of the RIES.
- DSP-based real-time simulation platform design: A novel simulation platform is built, using DSP as the core processing unit to support highly complex system model iteration and data communication. Through this platform, real-time simulation results of the mathematical models and proposed control algorithms can be achieved.
2. Device-Level Unit Modeling
2.1. Photovoltaic Generation Unit
2.2. Micro Turbine Generation Unit
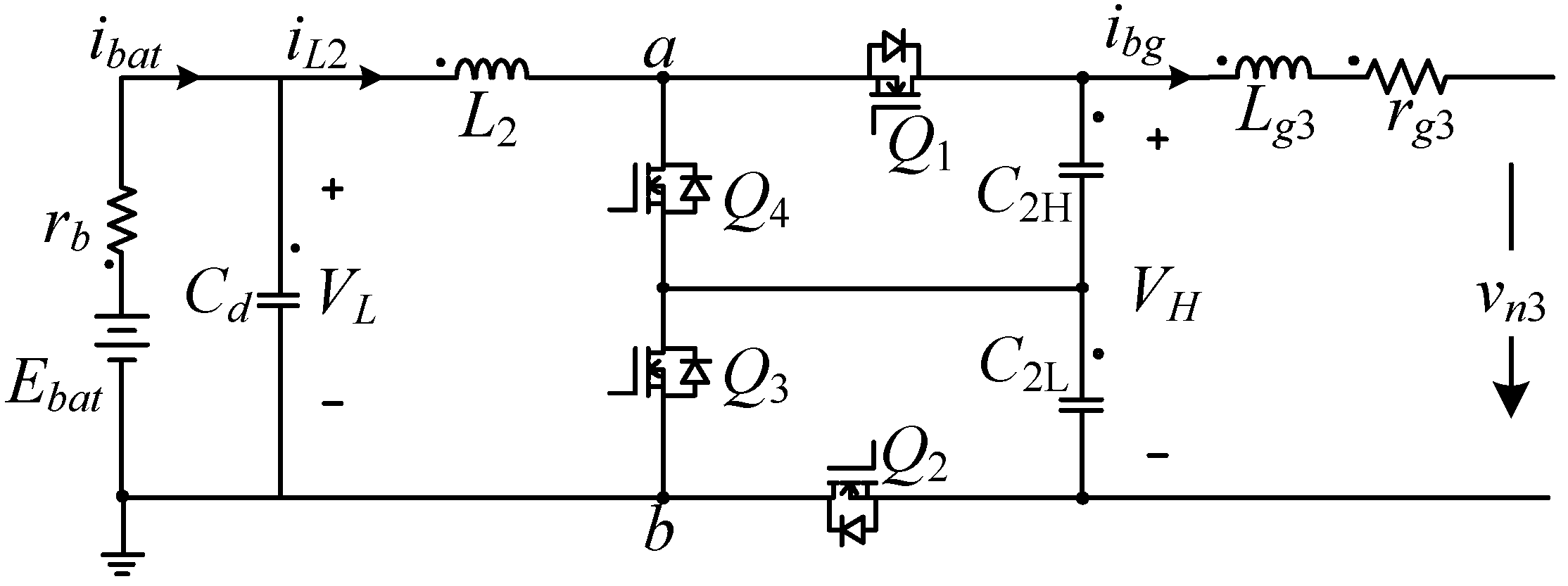
2.3. Energy Storage Unit
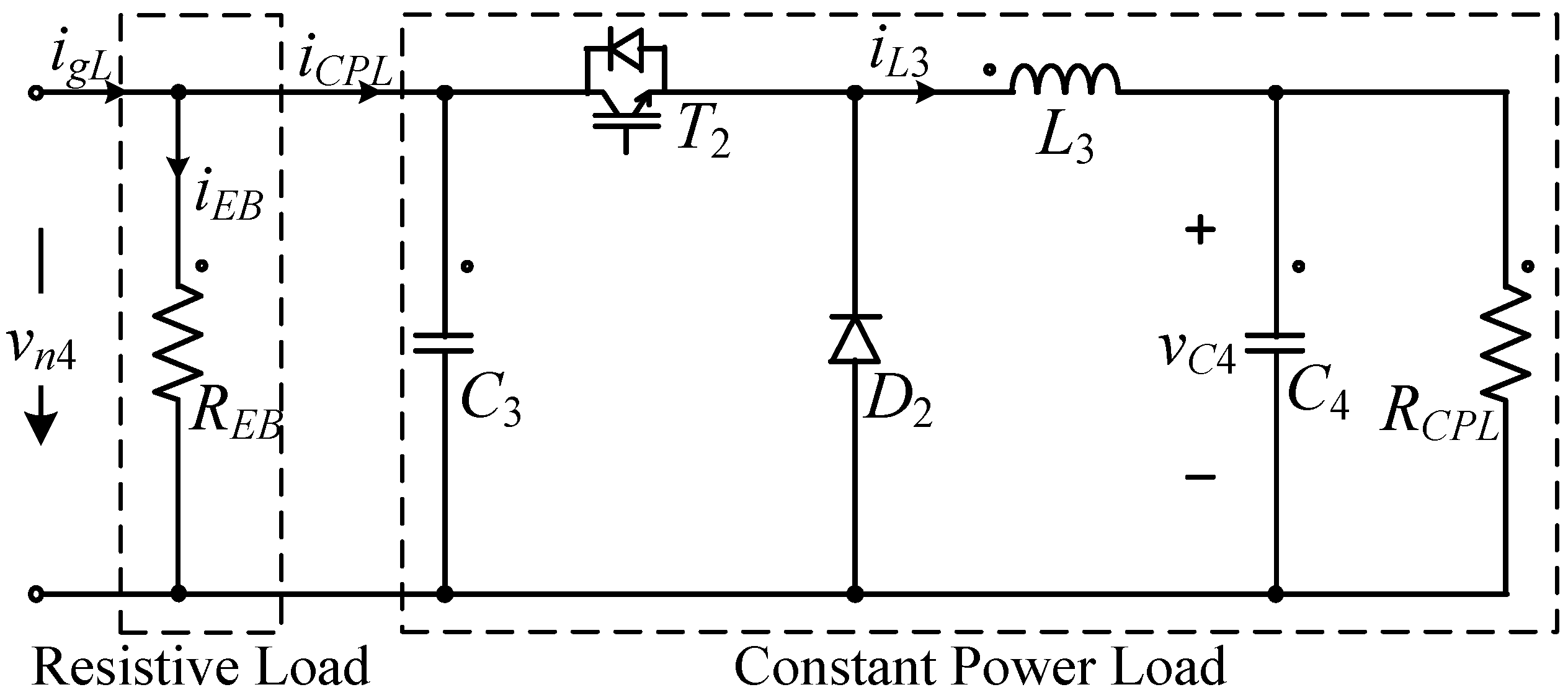
2.4. Load Unit
3. Energy Networks Modeling
3.1. District Heat Network
3.1.1. Model Establishment
3.1.2. Node-Loop Equations
3.2. Natural Gas Network
3.2.1. Model Establishment
3.2.2. Node-Loop Equations
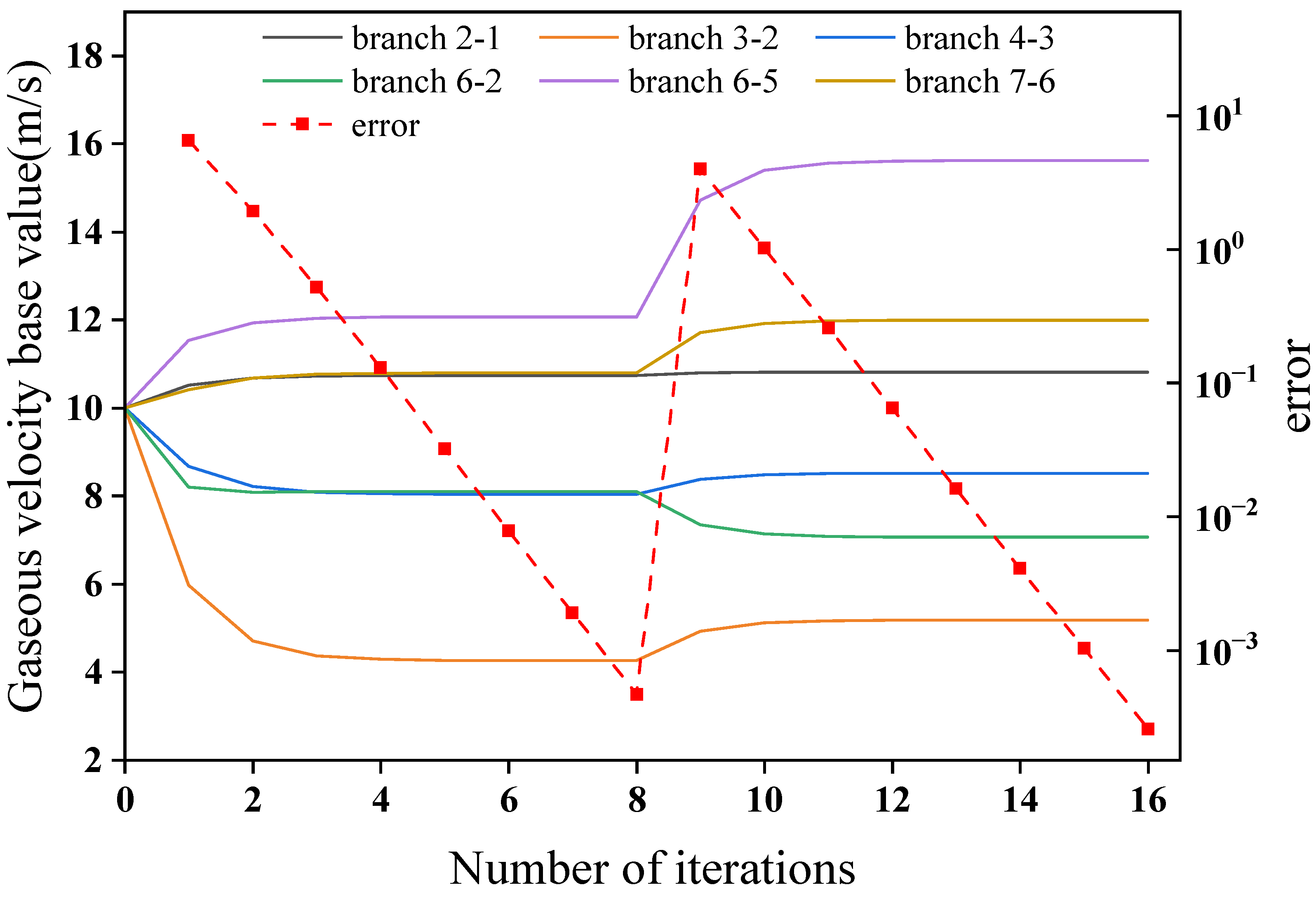
3.3. Steady-State Energy Flow Correction
- (1)
- Initially specify the branch mass flow or velocity base value .
- (2)
- Update the hydraulic or gas matrix equation, then conduct the hydraulic and gaseous steady-state flow calculation, obtaining the actual branch mass flow value .
- (3)
- Calculate the distance between the branch mass flow base value and the actual value : If (where is a predefined convergence threshold), the accuracy requirements are met, and the iteration ends. Otherwise, update the branch mass flow or velocity base value according to Equation (29) and return to step (2).
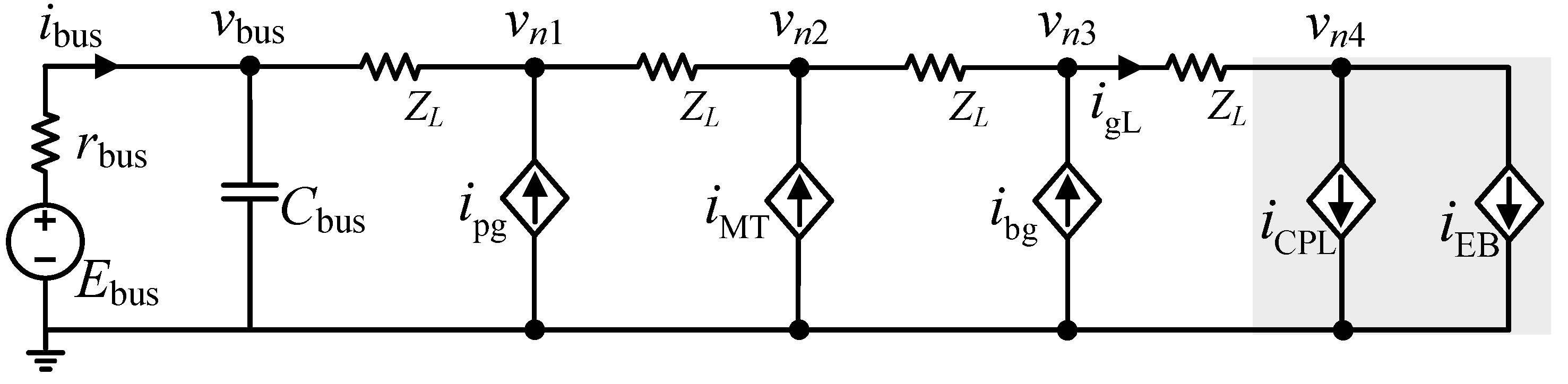
4. RIES Operation Control Strategies
4.1. Hierarchical Island Strategy
4.1.1. Device Control Layer
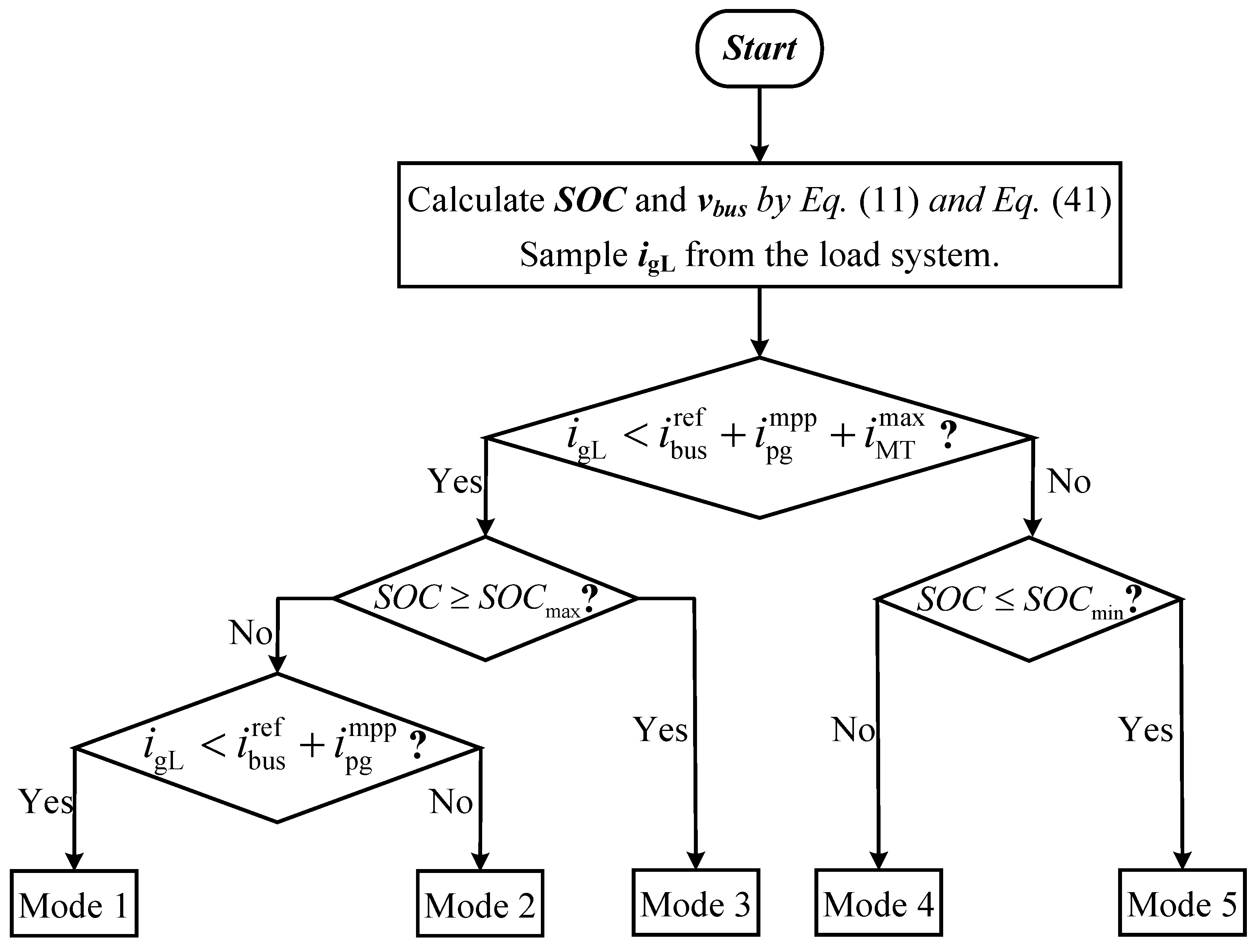
4.1.2. Bus Control Layer
- Mode 1: The PV generation unit operates in MPPT mode, and the BAT storage unit charges rapidly at maximum charging current. The bus control layer adjusts the output of the MT generation unit according to Equation (32) to stabilize the bus voltage, where is a proportional coefficient.
- Mode 2: The PV generation unit operates in MPPT mode, and the MT generation unit reaches its rated power. The bus control layer adjusts the charging power of the BAT storage unit according to Equation (33) to stabilize the bus voltage, where is a proportional coefficient.
- Mode 3: If the BAT storage unit is fully charged and disabled in Mode 1, the PV generation unit operates in CV mode; if the BAT storage unit is fully charged and disabled in Mode 2, the PV generation unit operates in MPPT mode. The bus control layer adjusts the output of the MT generation unit according to Equation (32) to stabilize the bus voltage.
- Mode 4: The PV generation unit operates in MPPT mode, and the MT generation unit reaches its rated power. The bus control layer adjusts the discharge power of the BAT storage unit according to Equation (34) to stabilize the bus voltage, where is a proportional coefficient.
- Mode 5: The PV generation unit operates in MPPT mode, and the MT generation unit reaches its rated power. If the BAT storage unit is disabled due to insufficient capacity, the bus control layer needs to dump non-critical loads to maintain bus voltage stability.
4.2. Multi-Energy Dispatch Strategy
4.2.1. Thermal-Led
4.2.2. Electricity-Led
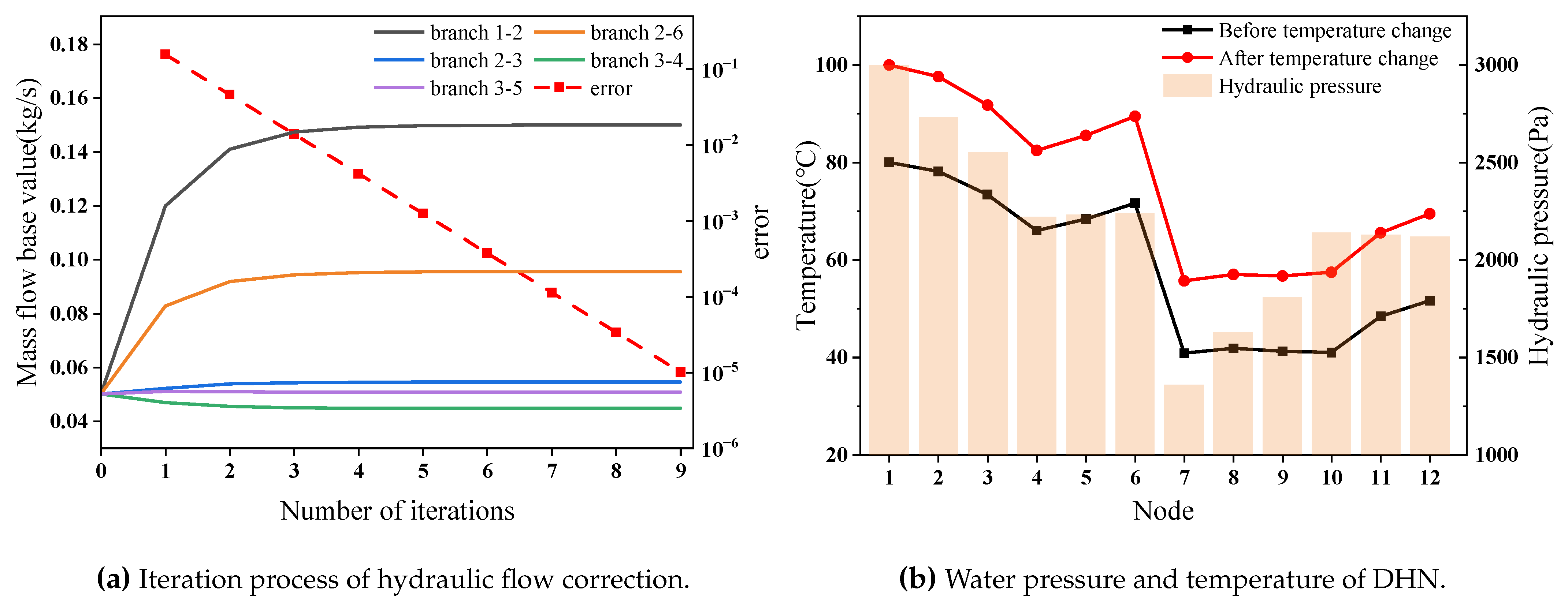
- To conduct hydraulic flow calculation, after correcting the flow error, perform thermal flow calculation and calculate the total thermal power at the DHN source, i.e., the thermal load demand, based on Equation (18).
- Based on the thermal load demand and dispatch mode, calculate the electrical power output of MT, the electrical power consumed by EB, and the fuel consumption of MT. The HIS is used to control the DMG until the DC bus voltage converges.
- Convert the fuel quantity to natural gas mass flow rate using Equation (41), and input it into MT coupling node for gaseous flow calculation until flow error is corrected.Here, is the lower heating value of natural gas, taken as 13.52 kWh/kg.
- Determine if the DHN, NGN, and DMG all meet convergence criteria. If they do, the process ends; otherwise, continue with flow calculation.
5. Real-Time Platform Implementation and Experimental Verification
5.1. Iteration Technique
5.2. Case Configuration
5.3. Experimental Results
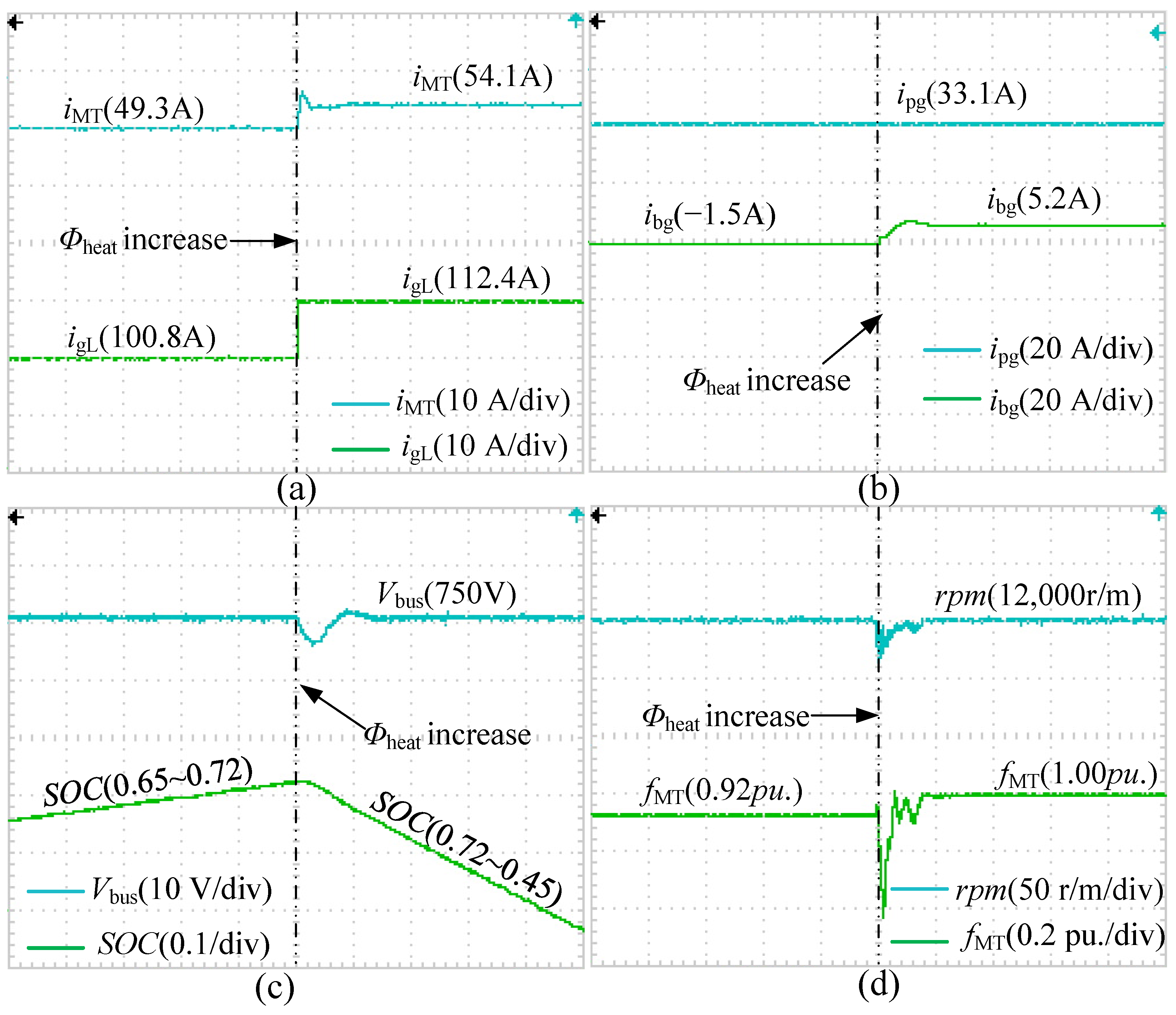
5.3.1. Thermal-Led Experiment
5.3.2. Electricity-Led Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| System | Parameters | Value |
|---|---|---|
| DC Grid Backbone | , | 760 V, 0.5 |
| 2.2 mF | ||
| PV Generation Unit | , | 470 F, 1 mF |
| , | 2.5 mH, 0.1 mH | |
| 1 | ||
| , | 0.25, 0.105 | |
| , | 0.00025, 2.5 | |
| MT Generation Unit | , | 5 , 2.2mF |
| , D | 0.2475 , 0.0005 | |
| J, | 0.001 , 1 | |
| , | 5.95 mH, 0.1 mH | |
| 0.5 | ||
| , | 298.3, 0.0012 | |
| , | 3 , 1.75 | |
| BAT Storage Unit | , | 400 V, 1 mF |
| , | 0.5 , 0.5 | |
| , | 1 mF, 1 mF | |
| , | 0.4, 0.9 | |
| , | 0.001, 1.1948 | |
| , | 0.00025, 0.5 | |
| Load Unit | , | 470 F, 1 mF |
| 1.5 mH | ||
| , | 0, −0.13529 |
| Pipe | Length | Diameter | Fraction | Heat Dissipation | |
|---|---|---|---|---|---|
| 1–2 | 30 m | 0.04 m | 0.05 | 0.5 | 0 |
| 2–3 | 50 m | 0.04 m | 0.05 | 0.5 | 0 |
| 3–5 | 30 m | 0.025 m | 0.05 | 0.5 | 0 |
| 2–6 | 40 m | 0.025 m | 0.05 | 0.5 | 0 |
| 3–4 | 40 m | 0.025 m | 0.05 | 0.5 | 0 |
| 8–7 | 10 m | 0.04 m | 0.05 | 0.5 | 0 |
| 9–8 | 50 m | 0.04 m | 0.05 | 0.5 | 0 |
| 11–9 | 30 m | 0.025 m | 0.05 | 0.5 | 0 |
| 12–8 | 40 m | 0.025 m | 0.05 | 0.5 | 0 |
| 10–9 | 40 m | 0.025 m | 0.05 | 0.5 | 0 |
| 6–12 | 2 m | 0.02 m | 0.08 | 0 | 20 ℃ |
| 4–10 | 2 m | 0.02 m | 0.08 | 0 | 25 ℃ |
| 5–11 | 2 m | 0.02 m | 0.08 | 0 | 20 ℃ |
| Device | Parameters |
|---|---|
| Valve | |
| Pump |
| Pipe | Length | Diameter | Fraction |
|---|---|---|---|
| 2–1 | 20 m | 0.06 m | 0.25 |
| 3–2 | 10 m | 0.06 m | 0.25 |
| 4–3 | 50 m | 0.08 m | 0.25 |
| 6–2 | 10 m | 0.06 m | 0.25 |
| 6–5 | 20 m | 0.06 m | 0.25 |
| 7–6 | 30 m | 0.08 m | 0.25 |
References
- Stennikov, V.; Barakhtenko, E.; Sokolov, D.; Zhou, B. Current State of Research on the Energy Management and Expansion Planning of Integrated Energy Systems. Energy Rep. 2022, 8, 10025–10036. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, W.; Zhu, L.; Sun, Z.; Ma, D.; Chen, W. Prospect of Typical Application of Integrated Energy System. IOP Conf. Ser. Earth Environ. Sci. 2021, 651, 022030. [Google Scholar] [CrossRef]
- Chicco, G.; Riaz, S.; Mazza, A.; Mancarella, P. Flexibility From Distributed Multienergy Systems. Proc. IEEE 2020, 108, 1496–1517. [Google Scholar] [CrossRef]
- Cheng, H.; Hu, X.; Wang, L.; Liu, Y.; Yu, Q. Review on research of regional integrated energy system planning. Autom. Electr. Power Syst. 2019, 43, 2–13. [Google Scholar]
- Fan, H.; Wang, C.; Liu, L.; Li, X. Review of Uncertainty Modeling for Optimal Operation of Integrated Energy System. Front. Energy Res. 2022, 9, 641337. [Google Scholar] [CrossRef]
- Ilyushin, P.; Gerasimov, D.; Suslov, K. Method for Simulation Modeling of Integrated Multi-Energy Systems Based on the Concept of an Energy Hub. Appl. Sci. 2023, 13, 7656. [Google Scholar] [CrossRef]
- Qiao, Y.; Hu, F.; Xiong, W.; Li, Y. Energy hub-based configuration optimization method of integrated energy system. Int. J. Energy Res. 2022, 46, 23287–23309. [Google Scholar] [CrossRef]
- Chen, B.; Guo, Q.; Yin, G.; Wang, B.; Pan, Z.; Chen, Y.; Wu, W.; Sun, H. Energy-Circuit-Based Integrated Energy Management System: Theory, Implementation, and Application. Proc. IEEE 2022, 110, 1897–1926. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, N.; Botterud, A.; Kang, C. On An Equivalent Representation of the Dynamics in District Heating Networks for Combined Electricity-Heat Operation. IEEE Trans. Power Syst. 2020, 35, 560–570. [Google Scholar] [CrossRef]
- Li, M.; Ye, J. Fractional Order Modeling of Thermal Circuits for an Integrated Energy System Based on Natural Transformation. Electronics 2022, 11, 914. [Google Scholar] [CrossRef]
- Qu, L.; Ouyang, B.; Yuan, Z.; Zeng, R. Steady-State Power Flow Analysis of Cold-Thermal-Electric Integrated Energy System Based on Unified Power Flow Model. Energies 2019, 12, 4455. [Google Scholar] [CrossRef]
- Massrur, H.R.; Niknam, T.; Aghaei, J.; Shafie-khah, M.; Catalao, J.P.S. Fast Decomposed Energy Flow in Large-Scale Integrated Electricity-Gas-Heat Energy Systems. IEEE Trans. Sustain. Energy 2018, 9, 1565–1577. [Google Scholar] [CrossRef]
- Zhu, M.; Xu, C.; Dong, S.; Tang, K.; Gu, C. An Integrated Multi-Energy Flow Calculation Method for Electricity-Gas-Thermal Integrated Energy Systems. Prot. Control Mod. Power Syst. 2021, 6, 5. [Google Scholar] [CrossRef]
- Liang, Z.; Mu, L. Unified calculation of multi-energy flow for integrated energy system based on difference grid. J. Renew. Sustain. Energy 2022, 14, 066301. [Google Scholar] [CrossRef]
- Xue, Y.; Li, Z.; Lin, C.; Guo, Q.; Sun, H. Coordinated Dispatch of Integrated Electric and District Heating Systems Using Heterogeneous Decomposition. IEEE Trans. Sustain. Energy 2020, 11, 1495–1507. [Google Scholar] [CrossRef]
- Yao, S.; Gu, W.; Wu, J.; Lu, H.; Zhang, S.; Zhou, Y.; Lu, S. Dynamic energy flow analysis of the heat-electricity integrated energy systems with a novel decomposition-iteration algorithm. Appl. Energy 2022, 322, 119492. [Google Scholar] [CrossRef]
- Yao, S.; Gu, W.; Wu, J.; Qadrdan, M.; Lu, H.; Lu, S.; Zhou, Y. Fast and generic energy flow analysis of the integrated electric power and heating networks. IEEE Trans. Smart Grid 2023, 15, 355–367. [Google Scholar] [CrossRef]
- Sergi, B.; Pambour, K. An evaluation of co-simulation for modeling coupled natural gas and electricity networks. Energies 2022, 15, 5277. [Google Scholar] [CrossRef]
- Gusain, D.; Cvetković, M.; Palensky, P. Simplifying multi-energy system co-simulations using energysim. SoftwareX 2022, 18, 101021. [Google Scholar] [CrossRef]
- El Zerk, A.; Ouassaid, M. Real-time fuzzy logic based energy management system for microgrid using hardware in the loop. Energies 2023, 16, 2244. [Google Scholar] [CrossRef]
- Guan, A.; Zhou, S.; Gu, W.; Lu, S.; Wu, Z.; Gao, M. An Experimental Platform of Heating Network Similarity Model for Test of Integrated Energy Systems. IEEE Trans. Ind. Inform. 2023, 20, 5517–5528. [Google Scholar] [CrossRef]
- Meng, Q.; Jin, X.; Luo, F.; Wang, Z.; Hussain, S. Distributionally Robust Scheduling for Benefit Allocation in Regional Integrated Energy System with Multiple Stakeholders. J. Mod. Power Syst. Clean Energy 2024, 321, 119202. [Google Scholar]
- Tan, J.; Wu, Q.; Zhang, X. Optimal Planning of Integrated Electricity and Heat System Considering Seasonal and Short-Term Thermal Energy Storage. IEEE Trans. Smart Grid 2023, 14, 2697–2708. [Google Scholar] [CrossRef]
- Ma, Y.; Han, X.; Zhang, T.; Li, A.; Song, Z.; Li, T.; Wang, Y. Research on station-network planning of electricity-thermal-cooling regional integrated energy system considering multiple-load clusters and network costs. Energy 2024, 297, 131281. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Kyriakou, D.G.; Kanellos, F.D. Energy and power management system for microgrids of large-scale building prosumers. IET Energy Syst. Integr. 2023, 5, 228–244. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.; Deng, S.; Yue, D. Real-time distributed economic dispatch scheme of grid-connected microgrid considering cyberattacks. IET Renew. Power Gener. 2020, 14, 2750–2758. [Google Scholar] [CrossRef]
- Pradhan, C.; Senapati, M.K.; Ntiakoh, N.K.; Calay, R.K. Roach Infestation Optimization MPPT Algorithm for Solar Photovoltaic System. Electronics 2022, 11, 927. [Google Scholar] [CrossRef]
- Rowen, W.I. Simplified Mathematical Representations of Heavy-Duty Gas Turbines. J. Eng. Power 1983, 105, 865–869. [Google Scholar] [CrossRef]
- Hackl, C.M.; Pecha, U.; Schechner, K. Modeling and Control of Permanent-Magnet Synchronous Generators Under Open-Switch Converter Faults. IEEE Trans. Power Electron. 2019, 34, 2966–2979. [Google Scholar] [CrossRef]
- Chen, B.; Wu, W.; Guo, Q.; Sun, H. An efficient optimal energy flow model for integrated energy systems based on energy circuit modeling in the frequency domain. Appl. Energy 2022, 326, 119923. [Google Scholar] [CrossRef]
- Khan, R.; Nasir, M.; Schulz, N.N. An Optimal Neighborhood Energy Sharing Scheme Applied to Islanded DC Microgrids for Cooperative Rural Electrification. IEEE Access 2023, 11, 116956–116966. [Google Scholar] [CrossRef]
- Shafiee, Q.; Dragičević, T.; Vasquez, J.C.; Guerrero, J.M. Hierarchical Control for Multiple DC-Microgrids Clusters. IEEE Trans. Energy Convers. 2014, 29, 922–933. [Google Scholar] [CrossRef]
- Barati, F.; Ahmadi, B.; Keysan, O. A Hierarchical Control of Supercapacitor and Microsources in Islanded DC Microgrids. IEEE Access 2023, 11, 7056–7066. [Google Scholar] [CrossRef]
- Krishan, R.; Rohith, Y. Load and Generation Converters Control Strategy to Enhance the Constant Power Load Stability Margin in a DC Microgrid. IEEE Access 2024, 12, 35972–35983. [Google Scholar] [CrossRef]


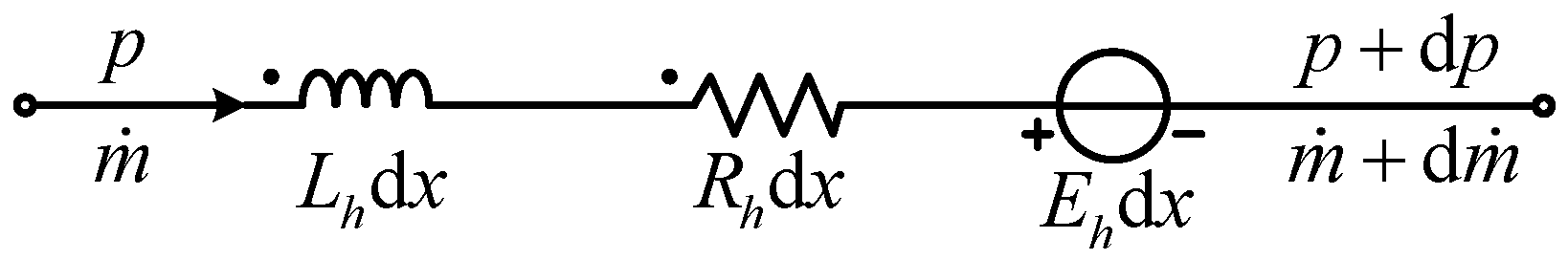










| Node Gas Pressure (Pa) | Branch Mass Flow Rates (kg/s) | ||||
|---|---|---|---|---|---|
| Node | Before | After | Branch | Before | After |
| 1 | 9640.55 | 9629.93 | 2–1 | 0.0025 | 0.0025 |
| 2 | 9795.54 | 9785.08 | 3–2 | 0.00113 | 0.0012 |
| 3 | 9810.94 | 9802.70 | 4–3 | 0.00363 | 0.0037 |
| 4 | 10,000 | 10,000 | 6–2 | 0.00137 | 0.0013 |
| 5 | 7607.72 | 7553.61 | 6–5 | 0.00265 | 0.00287 |
| 6 | 7824.96 | 7811.33 | 6–7 | 0.00402 | 0.00417 |
| 7 | 8000 | 8000 | |||
| Node Gas Pressure (Pa) | Branch Mass Flow Rates (kg/s) | ||||
|---|---|---|---|---|---|
| Node | Before | After | Branch | Before | After |
| 1 | 9657.92 | 9628.56 | 2–1 | 0.0025 | 0.0025 |
| 2 | 9812.64 | 9783.73 | 3–2 | 0.00099 | 0.00121 |
| 3 | 9824.60 | 9801.64 | 4–3 | 0.00349 | 0.00371 |
| 4 | 10,000 | 10,000 | 6–2 | 0.00151 | 0.00129 |
| 5 | 7692.76 | 7546.53 | 6–5 | 0.00225 | 0.0029 |
| 6 | 7847.85 | 7809.59 | 7–6 | 0.00375 | 0.00419 |
| 7 | 8000 | 8000 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Qi, R.; Xu, S.; Hashimoto, S. Real-Time Simulation System for Small Scale Regional Integrated Energy Systems. Energies 2024, 17, 3211. https://doi.org/10.3390/en17133211
Jiang W, Qi R, Xu S, Hashimoto S. Real-Time Simulation System for Small Scale Regional Integrated Energy Systems. Energies. 2024; 17(13):3211. https://doi.org/10.3390/en17133211
Chicago/Turabian StyleJiang, Wei, Renjie Qi, Song Xu, and Seiji Hashimoto. 2024. "Real-Time Simulation System for Small Scale Regional Integrated Energy Systems" Energies 17, no. 13: 3211. https://doi.org/10.3390/en17133211
APA StyleJiang, W., Qi, R., Xu, S., & Hashimoto, S. (2024). Real-Time Simulation System for Small Scale Regional Integrated Energy Systems. Energies, 17(13), 3211. https://doi.org/10.3390/en17133211






