Addressing Data Scarcity in Solar Energy Prediction with Machine Learning and Augmentation Techniques
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Random Forest Regressor
- Bootstrapped dataset: Before constructing each DT in RF, a bootstrapped dataset is formed by randomly selecting data points from the original training dataset, with replacement. This ensures that each data point from the original training dataset has an equal chance of being chosen. As a result, some data points may be selected multiple times, while others may not be selected at all. Each DT in RF is trained on its own bootstrapped dataset, enabling them to learn from slightly different perspectives of the original training dataset. This diversity among the trees enhances the overall robustness and effectiveness of the RF model.
- The root node: The root node symbolizes the starting point of the decision tree. It encompasses the entire bootstrapped dataset, serving as the foundation for the subsequent partitioning process. At this initial stage, the algorithm evaluates various predictors to determine the optimal split that divides the dataset into more homogeneous subsets. This decision sets the course for further branching, shaping the structure of the tree as it progresses. Ultimately, the root node plays a crucial role in guiding the recursive partitioning process, leading to the formation of internal nodes and leaf nodes that collectively constitute the DT model.
- The internal node: Each internal node represents a pivotal point in the decision tree’s path. At these nodes, the bootstrapped dataset undergoes division into subsets based on true/false conditions, determined by predictors like zenith angle, dew point temperature, cloud opacity, etc. Utilizing the mean squared error (MSE), the algorithm selects the optimal split at each node. This process aims to minimize the variance within each subset, thus facilitating the creation of groups with closely aligned GHI values. The recursive splitting continues from the root node down the tree until reaching the leaf nodes, guiding the tree’s evolution toward more refined predictions. The mean squared error (MSE) is calculated using the following formula:Here, n represents the number of samples, denotes the actual GHI values, and signifies the predicted GHI values for each sample.
- Stopping criteria: Stopping criteria prevent the algorithm from excessively splitting the data, ensuring the model does not become overly complex or specific to the training data. The algorithm typically stops when each group of data at a node becomes quite small, either containing just one sample or having samples with identical GHI values. This ensures better generalization to new data.
- The leaf node: A leaf node represents the endpoint of a branch in the tree. It signifies a terminal point where no further splits occur. Each leaf node contains the predicted GHI value for the subset of data that has traversed through the tree and arrived at that specific node. This prediction is based on a particular combination of inputs (e.g., air temperature, cloud opacity) and is calculated as the average GHI value derived from the actual GHI values of the samples in that subset. Leaf nodes serve as the final predictions made by the decision tree model.
- Ensemble aggregation: Each decision tree within the RF makes a prediction at its leaf nodes based on the data it was trained on. The RF model then collects these predictions from all its trees and typically calculates the average to determine the final prediction. This means the RF’s prediction is essentially an average of the predictions from each decision tree, each contributing based on the subset of the data from which it has learned. This ensemble method enhances the prediction’s accuracy and stability, as it combines the strengths of multiple trees, rather than depending on just one.
- Prediction on unseen data: When new predictors are introduced, the tree uses the splits it learned during training to navigate the new data point down the tree. The new data follow splits introduced during model training, and any deviation in predictor values leads to a corresponding adjustment in the predicted target value. Since the model has been trained on a variety of data samples, it can handle different scales and distributions in the predictors space. The final prediction for the unseen target is derived by averaging the predictions from all the trees, which compensates for any individual tree’s errors and leads to a more accurate and stable prediction.
2.3. Extreme Gradient Boosting Regressor
- Initialization: Given a training dataset , where () represents the predictors and () represents the target variable, we initialize the regression model with a constant prediction, i.e., the mean of the target variable:
- Sequential Fitting of Weak Learners: For where M is the predefined number of iterations, we fit a weak learner typically a shallow decision tree (a decision tree with minimal levels of splits), to the residuals of the training data by minimizing a loss function, mean squared error (MSE):
- Residual Calculation: We calculate the residuals, which are the differences between the observed target values () and the current model predictions ().
- Focusing on Residuals: We train the next weak learner to predict these residuals. This directs the learning towards the most challenging cases.
- Combining Weak Learners: We update the model by adding the weighted (scaled) prediction of the new weak learner to the previous model is the learning rate that scales the contribution of .
- Termination: We continue the process until reaching the maximum number of iterations , or until the model no longer shows improvement. The final regression model is represented as:where
- is the final ensemble model after M iterations;
- is the prediction of the m-th weak learner;
- ) is the learning rate for the m-th weak learner.
2.4. Data Sampling and Representation Optimization Based on Cloud Opacity Levels
- Transparent: These are thin clouds through which light passes easily, and through which people can even see the blue sky. We could consider these as clouds with opacity from 0% to about 33%.
- Translucent: These are medium-thickness clouds that let some sunlight through, but through which people cannot see the blue sky. These could be clouds with opacity from about 34% to about 66%.
- Opaque: These are thick clouds that do not allow light to pass directly, although light can diffuse through them. Such thick clouds often look gray. When the sky is overcast, or when these clouds are in front of the sun, it is impossible to tell where the sun is. These would be clouds with opacity from about 67% to 100%.
2.5. Synthetic Data Generation
- Flipping: mirroring existing data points to introduce variations that capture inverted scenarios, such as changes in solar angles.
- Rotating: applying rotations to data points to simulate different solar angles and azimuths, thereby expanding the dataset’s coverage of potential conditions.
- Scaling: introducing scaling factors to data points to represent varying magnitudes of meteorological and atmospheric quantities, effectively diversifying the dataset.
- Introducing Random Noise: injecting controlled random noise into the synthetic data to mimic the inherent variability in real-world atmospheric conditions.
2.6. Model Testing
3. Results and Discussion
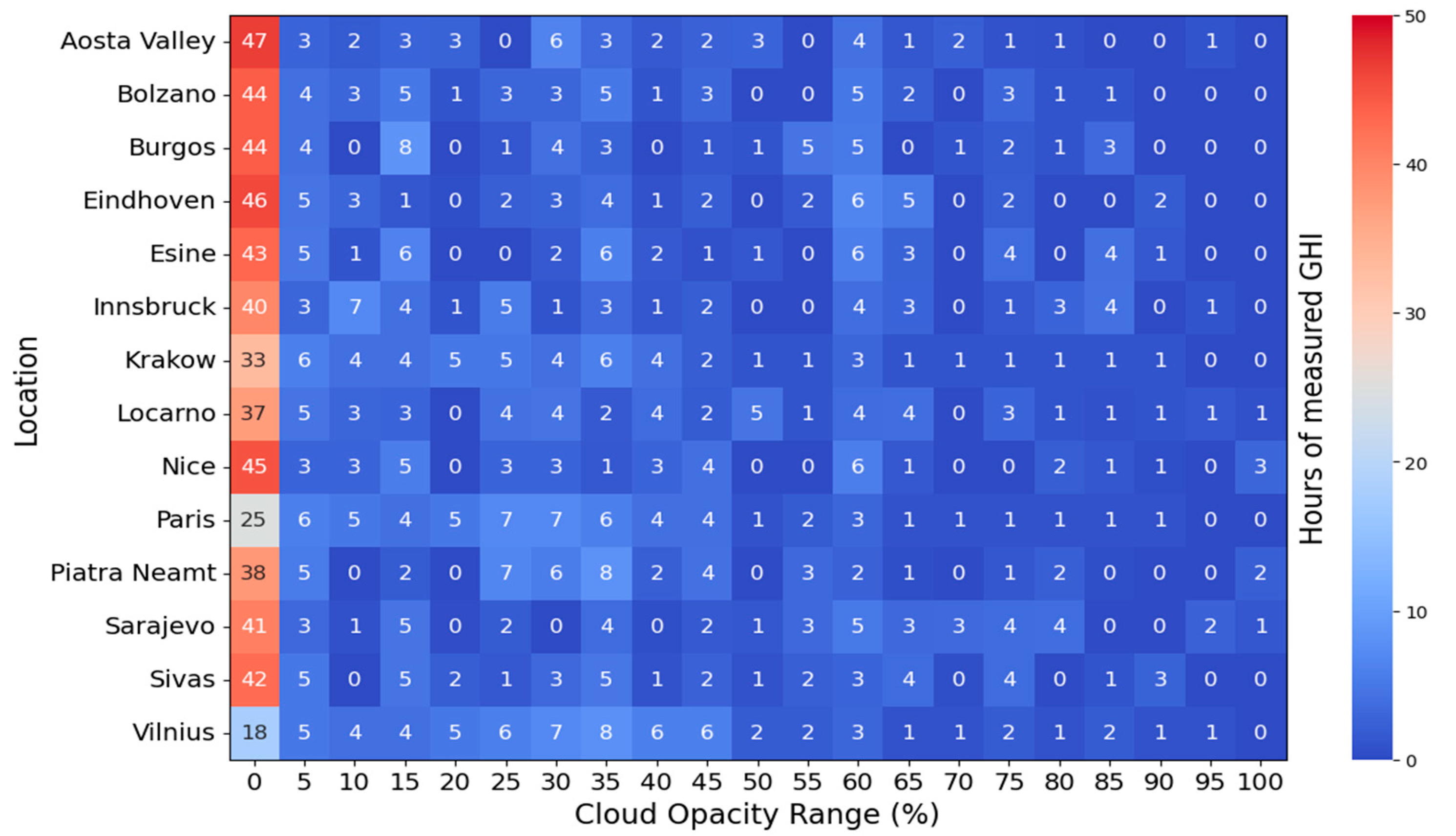
3.1. Preference for Clear Sky Days and Training Impact
3.2. Practical Implications and Data Collection
3.3. Model Accuracy and Reliability
- Random Distribution: with no guided distribution of the training data.
- Best Distribution: with guided best distribution of the training data to improve model accuracy.
- Synthetic Data: incorporating synthetic data to further enhance the model accuracy.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Solar PV. In Renewables 2020 Analysis and Forecast to 2025; IEA Publications: Paris, France, 2020; pp. 36–38. [Google Scholar]
- Allal, Z.; Noura, H.N.; Chahine, K. Machine Learning Algorithms for Solar Irradiance Prediction: A Recent Comparative Study. e-Prime-Adv. Electr. Eng. Electron. Energy 2024, 7, 100453. [Google Scholar] [CrossRef]
- Kamil, R.; Garniwa, P.M.P.; Lee, H. Performance Assessment of Global Horizontal Irradiance Models in All-Sky Conditions. Energies 2021, 14, 7939. [Google Scholar] [CrossRef]
- de Sá Campos, M.H.; Tiba, C. Global Horizontal Irradiance Modeling for All Sky Conditions Using an Image-Pixel Approach. Energies 2020, 13, 6719. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems, 2nd ed.; Academic Press: San Diego, CA, USA, 2013; pp. 45–67. [Google Scholar]
- Maisanam, A.; Podder, B.; Sharma, K.K.; Biswas, A. Solar Resource Assessment Using GHI Measurements at a Site in Northeast India. In Advances in Mechanical Engineering, Lecture Notes in Mechanical Engineering; Springer: Singapore, 2020; pp. 1253–1265. [Google Scholar]
- El Alani, O.; Ghennioui, H.; Abraim, M.; Ghennioui, A.; Blanc, P.; Saint-Drenan, Y.-M.; Naimi, Z. Solar Energy Resource Assessment Using GHI and DNI Satellite Data for Moroccan Climate. In Proceedings of the International Conference on Advanced Technologies for Humanity, Lecture Notes on Data Engineering and Communications Technologies, Rabat, Morocco, 26–27 November 2021; Springer: Cham, Switzerland, 2022; pp. 275–285. [Google Scholar]
- Ashenfelter, O.; Storchmann, K. Using Hedonic Models of Solar Radiation and Weather to Assess the Economic Effect of Climate Change: The Case of Mosel Valley Vineyards. Rev. Econ. Stat. 2010, 92, 333–349. [Google Scholar] [CrossRef]
- Srećković, V.A. New Challenges in Exploring Solar Radiation: Influence, Consequences, Diagnostics, Prediction. Appl. Sci. 2023, 13, 4126. [Google Scholar] [CrossRef]
- Zhu, T.; Guo, Y.; Li, Z.; Wang, C. Solar Radiation Prediction Based on Convolution Neural Network and Long Short-Term Memory. Energies 2021, 14, 8498. [Google Scholar] [CrossRef]
- Radhoush, S.; Whitaker, B.M.; Nehrir, H. An Overview of Supervised Machine Learning Approaches for Applications in Active Distribution Networks. Energies 2023, 16, 5972. [Google Scholar] [CrossRef]
- Hissou, H.; Benkirane, S.; Guezzaz, A.; Azrour, M.; Beni-Hssane, A. A Novel Machine Learning Approach for Solar Radiation Estimation. Sustainability 2023, 15, 10609. [Google Scholar] [CrossRef]
- Peng, T.; Li, Y.; Song, Z.; Fu, Y.; Nazir, M.S.; Zhang, C. Hybrid Intelligent Deep Learning Model for Solar Radiation Forecasting Using Optimal Variational Mode Decomposition and Evolutionary Deep Belief Network—Online Sequential Extreme Learning Machine. J. Build. Eng. 2023, 76, 107227. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Solar Radiation Prediction Using Artificial Neural Network Techniques: A Review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.K.; Sharma, J.D. Comparison of Regression and Artificial Neural Network Models for Estimation of Global Solar Radiations. Renew. Sustain. Energy Rev. 2015, 52, 1294–1299. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Coimbra, C.F.M. Assessment of Forecasting Techniques for Solar Power Production with No Exogenous Inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. A Novel Hybrid Approach Based on Self-Organizing Maps, Support Vector Regression and Particle Swarm Optimization to Forecast Solar Irradiance. Energy 2015, 82, 570–577. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine Learning Methods for Solar Radiation Forecasting: A Review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Elizabeth Michael, N.; Mishra, M.; Hasan, S.; Al-Durra, A. Short-Term Solar Power Predicting Model Based on Multi-Step CNN Stacked LSTM Technique. Energies 2022, 15, 2150. [Google Scholar] [CrossRef]
- Alharkan, H.; Habib, S.; Islam, M. Solar Power Prediction Using Dual Stream CNN-LSTM Architecture. Sensors 2023, 23, 945. [Google Scholar] [CrossRef] [PubMed]
- Whang, S.E.; Roh, Y.; Song, H.; Lee, J.G. Data Collection and Quality Challenges in Deep Learning: A Data-Centric AI Perspective. VLDB J. 2023, 32, 791–813. [Google Scholar] [CrossRef]
- Sai Srinivas, T.A.; Thanmai, B.T.; Donald, A.D.; Thippanna, G.; Srihith, I.V.D.; Sai, I.V. Training Data Alchemy: Balancing Quality and Quantity in Machine Learning Training. J. Netw. Secur. Data Min. 2023, 6, 7–10. [Google Scholar] [CrossRef]
- Budach, L.; Feuerpfeil, M.; Ihde, N.; Nathansen, A.; Noack, N.; Patzlaff, H.; Naumann, F.; Harmouch, H. The Effects of Data Quality on Machine Learning Performance. arXiv 2022, arXiv:2207.14529. [Google Scholar] [CrossRef]
- Quach, S.; Thaichon, P.; Martin, K.D.; Weaven, S.; Palmatier, R.W. Digital Technologies: Tensions in Privacy and Data. J. Acad. Mark. Sci. 2022, 50, 1299–1323. [Google Scholar] [CrossRef]
- Ju, W.; Yi, S.; Wang, Y.; Xiao, Z.; Mao, Z.; Li, H.; Gu, Y.; Qin, Y.; Yin, N.; Wang, S.; et al. A Survey of Graph Neural Networks in Real World: Imbalance, Noise, Privacy and OOD Challenges. arXiv 2024, arXiv:2403.04468. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Li, P.; Lin, Z.; Sindakis, S.; Aggarwal, S. Overview of Data Quality: Examining the Dimensions, Antecedents, and Impacts of Data Quality. J. Knowl. Econ. 2024, 15, 1159–1178. [Google Scholar] [CrossRef]
- Subramanian, E.; Karthik, M.M.; Krishna, G.P.; Prasath, D.V.; Kumar, V.S. Solar Power Prediction Using Machine Learning. arXiv 2023, arXiv:2303.07875. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Bright, J.M. Solcast: Validation of a Satellite-Derived Solar Irradiance Dataset. Sol. Energy 2019, 189, 435–449. [Google Scholar] [CrossRef]
- Solcast. Irradiance and Weather Data: How Solcast Generates Irradiance and Weather Data. Available online: https://solcast.com/irradiance-data-methodology (accessed on 13 May 2024).
- Maharana, K.; Mondal, S.; Nemade, B. A Review: Data Pre-processing and Data Augmentation Techniques. Glob. Transit. Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Topographic-Map. Topographic Maps and Satellite Images. Topographic-Map.com 2024. Available online: https://en-us.topographic-map.com/ (accessed on 19 May 2024).
- Visual Crossing. Weather Data Services. Visual Crossing 2024. Available online: https://www.visualcrossing.com/weather/weather-data-services (accessed on 13 May 2024).
- Solcast. Global Solar Irradiance Data and PV System Power Output Data. Solcast 2024. Available online: https://solcast.com/data-for-researchers (accessed on 13 May 2024).
- El-Amarty, N.; Marzouq, M.; El Fadili, H.; Dosse Bennani, S.; Ruano, A. A Comprehensive Review of Solar Irradiation Estimation and Forecasting Using Artificial Neural Networks: Data, Models and Trends. Environ. Sci. Pollut. Res. 2023, 30, 5407–5439. [Google Scholar] [CrossRef] [PubMed]
- Pedro, H.T.C.; Larson, D.P.; Coimbra, C.F.M. A Comprehensive Dataset for the Accelerated Development and Benchmarking of Solar Forecasting Methods. J. Renew. Sustain. Energy 2019, 11, 036102. [Google Scholar] [CrossRef]
- Guzman, R.; Chepfer, H.; Noel, V.; Vaillant de Guélis, T.; Kay, J.E.; Raberanto, P.; Cesana, G.; Vaughan, M.A.; Winker, D.M. Direct Atmosphere Opacity Observations from CALIPSO Provide New Constraints on Cloud-Radiation Interactions. J. Geophys. Res. Atmos. 2017, 122, 1066–1085. [Google Scholar] [CrossRef]
- S’COOL. Cloud Visual Opacity. NASA Globe 2024. Available online: https://www.globe.gov/web/s-cool/home/observation-and-reporting/cloud-visual-opacity (accessed on 19 May 2024).
- Settles, B.; Active Learning Literature Survey. Computer Sciences Technical Report 1648. 2010. Available online: https://burrsettles.com/pub/settles.activelearning.pdf (accessed on 20 May 2024).
- Mendyl, A.; Mabasa, B.; Bouzghiba, H.; Weidinger, T. Calibration and Validation of Global Horizontal Irradiance Clear Sky Models against McClear Clear Sky Model in Morocco. Appl. Sci. 2023, 13, 320. [Google Scholar] [CrossRef]
- Poulinakis, K.; Drikakis, D.; Kokkinakis, I.W.; Spottswood, S.M. Machine-Learning Methods on Noisy and Sparse Data. Mathematics 2023, 11, 236. [Google Scholar] [CrossRef]
- Reis, I.; Baron, D.; Shahaf, S. Probabilistic Random Forest: A Machine Learning Algorithm for Noisy Data Sets. Astron. J. 2019, 157, 16. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Alessandrini, S.; Haupt, S.E.; Deng, A.; Kosovic, B.; Lee, J.A.; Delle Monache, L. The Role of Unresolved Clouds on Short-Range Global Horizontal Irradiance Predictability. Mon. Weather Rev. 2016, 144, 3099–3107. [Google Scholar] [CrossRef]
- Al-lahham, A.; Theeb, O.; Elalem, K.; Alshawi, T.A.; Alshebeili, S.A. Sky Imager-Based Forecast of Solar Irradiance Using Machine Learning. arXiv 2020, arXiv:2310.17356. Available online: https://arxiv.org/pdf/2310.17356 (accessed on 25 May 2024).
- Nie, Y.; Paletta, Q.; Scott, A.; Pomares, L.M.; Arbod, G.; Sgouridis, S.; Lasenby, J.; Brandt, A. Sky Image-Based Solar Forecasting Using Deep Learning with Multi-Location Data: Training Models Locally, Globally or via Transfer Learning? arXiv 2022, arXiv:2211.02108. Available online: https://arxiv.org/pdf/2211.02108 (accessed on 25 May 2024).
- Vasanthakumari, P.; Zhu, Y.; Brettin, T.; Partin, A.; Shukla, M.; Xia, F.; Narykov, O.; Weil, M.R.; Stevens, R.L. A Comprehensive Investigation of Active Learning Strategies for Conducting Anti-Cancer Drug Screening. Cancers 2024, 16, 530. [Google Scholar] [CrossRef] [PubMed]
- Hino, H. Active Learning: Problem Settings and Recent Developments. arXiv 2020, arXiv:2012.04225. [Google Scholar] [CrossRef]
- Zellweger, F.; Sulmoni, E.; Malle, J.T.; Baltensweiler, A.; Jonas, T.; Zimmermann, N.E.; Ginzler, C.; Karger, D.N.; De Frenne, P.; Frey, D.; et al. Microclimate Mapping Using Novel Radiative Transfer Modeling. Biogeosciences 2024, 21, 605–623. [Google Scholar] [CrossRef]
- Ohler, L.M.; Lechleitner, M.; Junker, R.R. Microclimatic Effects on Alpine Plant Communities and Flower-Visitor Interactions. Sci. Rep. 2020, 10, 1366. [Google Scholar] [CrossRef]
- Krishnan, N.; Kumar, K.R.; Inda, C.S. How Solar Radiation Forecasting Impacts the Utilization of Solar Energy: A Critical Review. J. Clean. Prod. 2023, 388, 135860. [Google Scholar] [CrossRef]
- Solargis. Combining Model Uncertainty and Interannual Variability. Available online: https://solargis.com/docs/accuracy-and-comparisons/combining-model-uncertainty-and-interannual-variability (accessed on 19 May 2024).
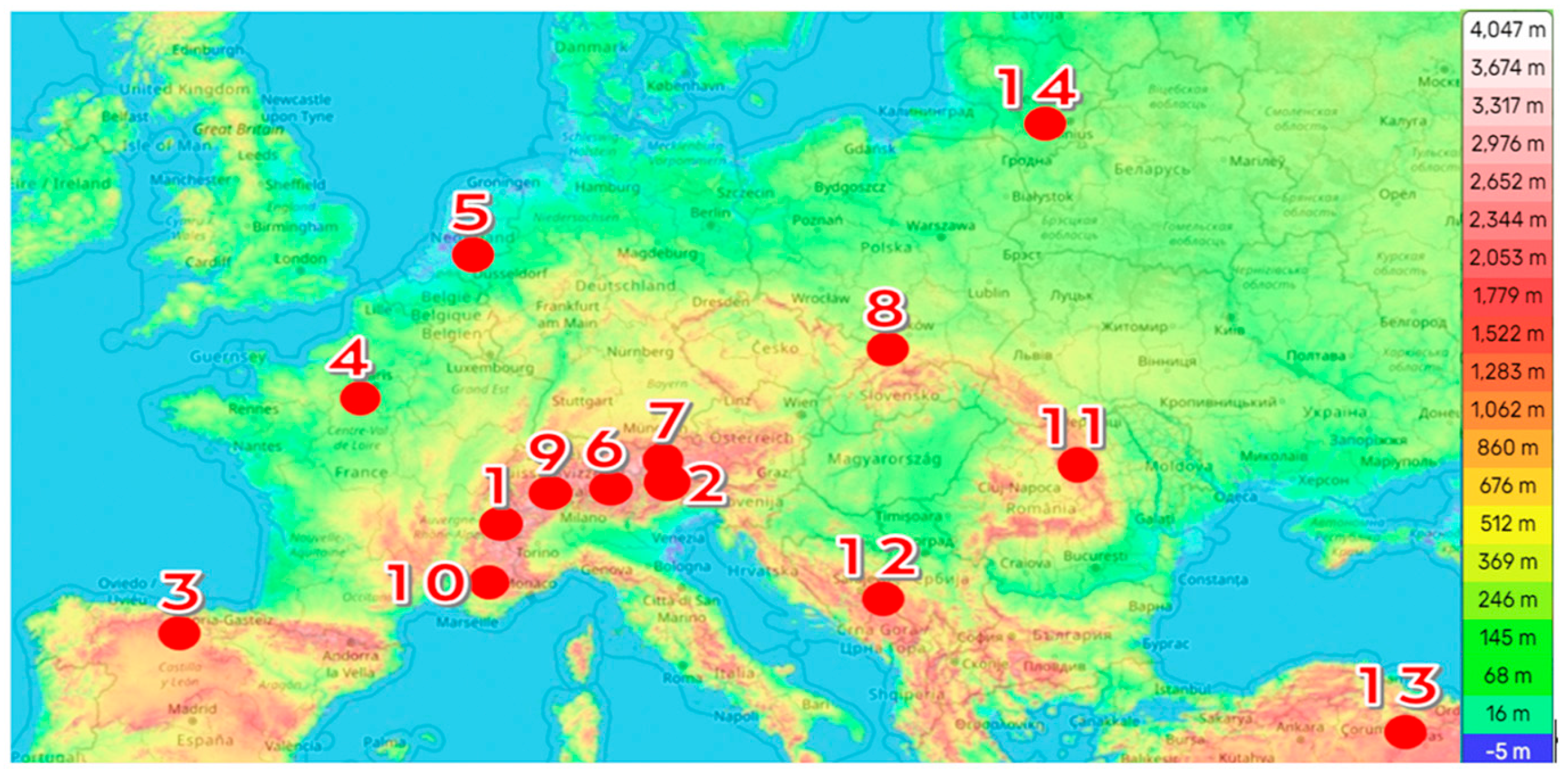


| № | Station Code Name | Site | County | Latitude (°) | Longitude (°) | Altitude (m) |
|---|---|---|---|---|---|---|
| 1 | EW5468 Saint-Christophe | Aosta Valley | Italy | 45.75 | 7.343 | 951 |
| 2 | UniBZ | Bolzano | Italy | 46.50 | 11.35 | 262 |
| 3 | LEBG | Burgos | Spain | 42.37 | −3.63 | 859 |
| 4 | CW1292 Coignieres FR | Paris | France | 48.812 | 2.276 | 28 |
| 5 | EHEH | Eindhoven | Netherlands | 51.45 | 5.42 | 17 |
| 6 | IW2LAO-13 Esine IT | Esine | Italy | 45.92 | 10.25 | 286 |
| 7 | LOWI | Innsbruck | Austria | 47.27 | 11.35 | 574 |
| 8 | EPKK | Krakow | Poland | 50.08 | 19.8 | 219 |
| 9 | LSZL | Locarno | Switzerland | 46.16 | 8.88 | 200 |
| 10 | LFMN | Nice | France | 43.65 | 7.2 | 4 |
| 11 | YO8RBY-13 Piatra Neamt | Piatra Neamt | Romania | 46.96 | 26.387 | 345 |
| 12 | LQSA | Sarajevo | Bosnia–Herzegovina | 43.82 | 18.32 | 518 |
| 13 | LTAR | Sivas | Turkey | 39.79 | 36.9 | 1285 |
| 14 | EYVI | Vilnius | Lithuania | 54.63 | 25.28 | 112 |
| Variable | Description | Units |
|---|---|---|
| GHI | The total amount of shortwave radiation received from above by a surface horizontal to the ground | W·m−2 |
| Air temperature | The temperature of the air | °C |
| Azimuth | The angle between the projected vector of the sun on the ground and a reference vector on that ground | degrees |
| Cloud opacity | The thickness or density of clouds affecting sunlight | % |
| Dew point temperature | The temperature at which air must be cooled to become saturated with water vapor | °C |
| Precipitable water | The total atmospheric water vapor contained in a vertical column of unit cross-sectional area | kg·m−2 |
| Relative humidity | The amount of water vapor present in air expressed as a percentage of the amount needed for saturation at the same temperature | % |
| Surface pressure | The pressure exerted by the atmosphere at the earth’s surface | hPa |
| Wind direction 10 m | The direction from which the wind is blowing at 10 m above the surface | degrees |
| Wind speed 10 m | The speed of the wind measured at 10 m above the surface | m·s−1 |
| Zenith | The angle away from the vertical direction to the sun at its highest point | degrees |
| Month | The month of the year | - |
| Day | The day of the month | - |
| Hours | The hour of the day in 24 h format | - |
| City | Scenario | R2 | RMSE [W m−2] | MAE [W m−2] | MBE [W m−2] |
|---|---|---|---|---|---|
| Aosta Valley | Random Distribution | 0.84 | 99.75 | 71.36 | 39.03 |
| Best Distribution | 0.93 | 68.16 | 48.25 | 20.10 | |
| Synthetic Data | 0.97 | 42.64 | 20.33 | 3.13 | |
| Bolzano | Random Distribution | 0.79 | 114.93 | 78.61 | 38.58 |
| Best Distribution | 0.88 | 87.90 | 57.77 | 20.57 | |
| Synthetic Data | 0.91 | 74.61 | 41.82 | 3.06 | |
| Burgos | Random Distribution | 0.83 | 103.47 | 72.97 | 39.14 |
| Best Distribution | 0.91 | 73.74 | 50.69 | 20.74 | |
| Synthetic Data | 0.96 | 52.93 | 29.07 | 3.32 | |
| Eindhoven | Random Distribution | 0.81 | 107.88 | 77.83 | 38.80 |
| Best Distribution | 0.91 | 76.26 | 53.88 | 19.71 | |
| Synthetic Data | 0.95 | 53.52 | 28.90 | 3.16 | |
| Esine | Random Distribution | 0.80 | 110.58 | 73.93 | 38.80 |
| Best Distribution | 0.88 | 86.25 | 58.87 | 19.93 | |
| Synthetic Data | 0.93 | 66.40 | 38.62 | 3.12 | |
| Innsbruck | Random Distribution | 0.81 | 108.11 | 73.96 | 38.71 |
| Best Distribution | 0.89 | 82.96 | 55.76 | 20.78 | |
| Synthetic Data | 0.93 | 67.84 | 39.53 | 3.00 | |
| Krakow | Random Distribution | 0.86 | 94.88 | 65.29 | 39.11 |
| Best Distribution | 0.92 | 68.87 | 47.57 | 19.52 | |
| Synthetic Data | 0.97 | 45.93 | 19.03 | 3.06 | |
| Locarno | Random Distribution | 0.80 | 111.75 | 77.77 | 38.73 |
| Best Distribution | 0.88 | 88.42 | 61.68 | 20.25 | |
| Synthetic Data | 0.92 | 69.97 | 38.42 | 3.06 | |
| Nice | Random Distribution | 0.78 | 118.18 | 80.65 | 29.05 |
| Best Distribution | 0.84 | 98.56 | 67.60 | 9.63 | |
| Synthetic Data | 0.88 | 87.31 | 53.51 | −9.07 | |
| Paris | Random Distribution | 0.78 | 118.09 | 83.24 | 43.98 |
| Best Distribution | 0.90 | 80.52 | 51.28 | 24.72 | |
| Synthetic Data | 0.94 | 62.62 | 31.73 | 7.56 | |
| Piatra Neamt | Random Distribution | 0.86 | 94.75 | 68.18 | 27.66 |
| Best Distribution | 0.94 | 58.95 | 44.31 | 6.49 | |
| Synthetic Data | 0.97 | 40.03 | 32.57 | −11.89 | |
| Sarajevo | Random Distribution | 0.84 | 101.49 | 69.58 | 36.15 |
| Best Distribution | 0.92 | 71.01 | 45.89 | 16.49 | |
| Synthetic Data | 0.94 | 59.46 | 33.62 | −1.01 | |
| Sivas | Random Distribution | 0.75 | 124.18 | 87.09 | 41.58 |
| Best Distribution | 0.85 | 97.64 | 64.37 | 23.78 | |
| Synthetic Data | 0.89 | 84.30 | 46.38 | 6.93 | |
| Vilnius | Random Distribution | 0.78 | 117.47 | 83.78 | 39.59 |
| Best Distribution | 0.88 | 86.98 | 58.93 | 20.38 | |
| Synthetic Data | 0.92 | 71.53 | 39.86 | 3.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gevorgian, A.; Pernigotto, G.; Gasparella, A. Addressing Data Scarcity in Solar Energy Prediction with Machine Learning and Augmentation Techniques. Energies 2024, 17, 3365. https://doi.org/10.3390/en17143365
Gevorgian A, Pernigotto G, Gasparella A. Addressing Data Scarcity in Solar Energy Prediction with Machine Learning and Augmentation Techniques. Energies. 2024; 17(14):3365. https://doi.org/10.3390/en17143365
Chicago/Turabian StyleGevorgian, Aleksandr, Giovanni Pernigotto, and Andrea Gasparella. 2024. "Addressing Data Scarcity in Solar Energy Prediction with Machine Learning and Augmentation Techniques" Energies 17, no. 14: 3365. https://doi.org/10.3390/en17143365
APA StyleGevorgian, A., Pernigotto, G., & Gasparella, A. (2024). Addressing Data Scarcity in Solar Energy Prediction with Machine Learning and Augmentation Techniques. Energies, 17(14), 3365. https://doi.org/10.3390/en17143365







