A Data-Driven Method for Calculating Neutron Flux Distribution Based on Deep Learning and the Discrete Ordinates Method
Abstract
1. Introduction
2. Methodology
2.1. Deep Learning Neural Network
2.2. Discrete Ordinates Method Transport Solution
2.3. Dataset Acquisition and Construction
2.4. Deep Learning Neural Network Topology Construction and Model Training
2.5. Model Evaluation
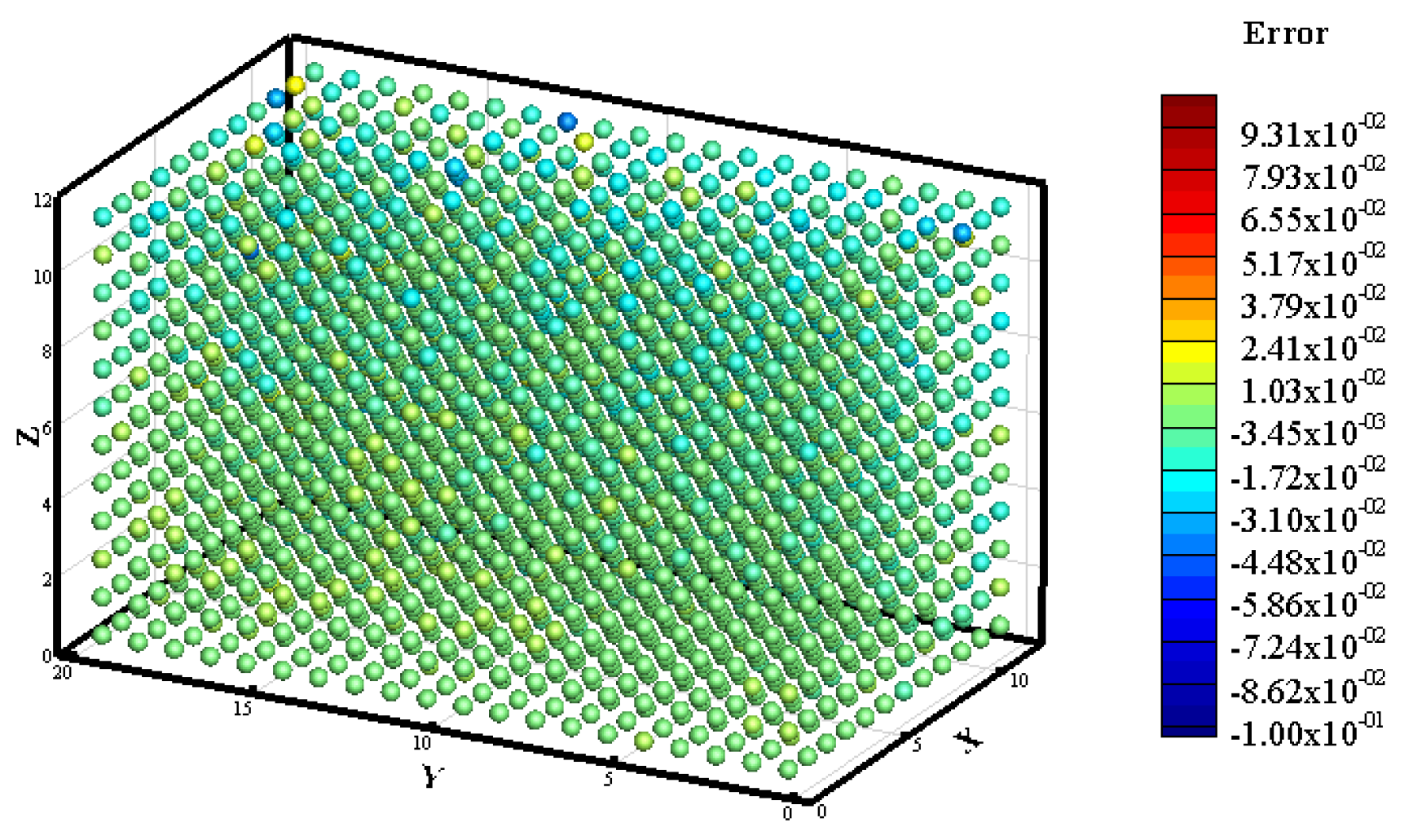
3. Numerical Result Analysis
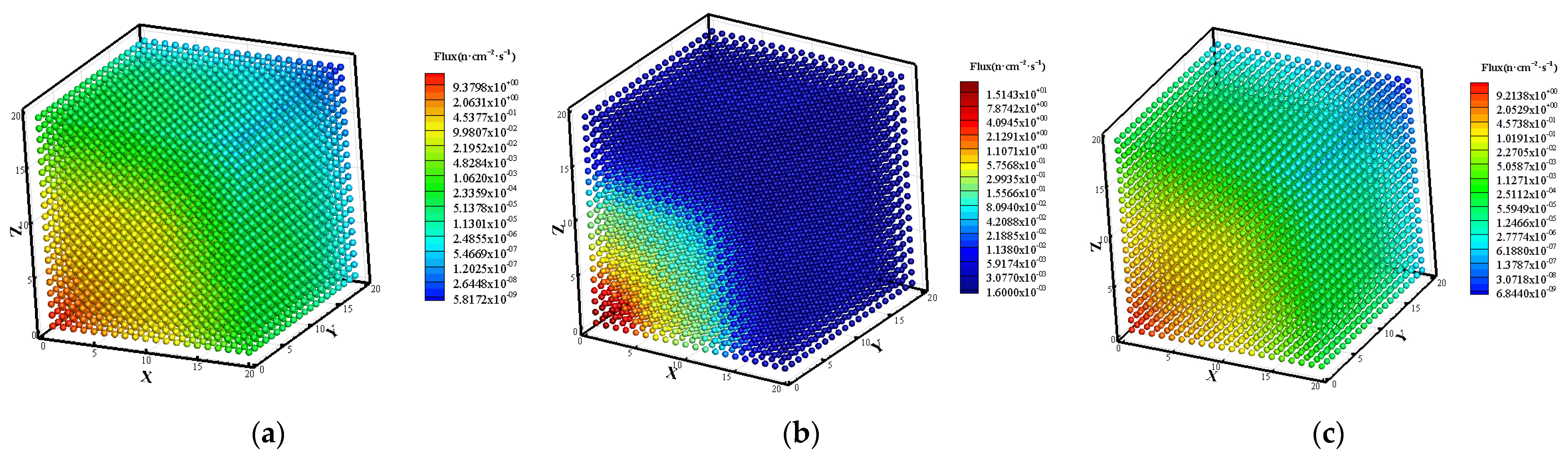
3.1. Prediction of Neutron Flux Distribution in Kobayashi-1 Geometric Shield Region 1
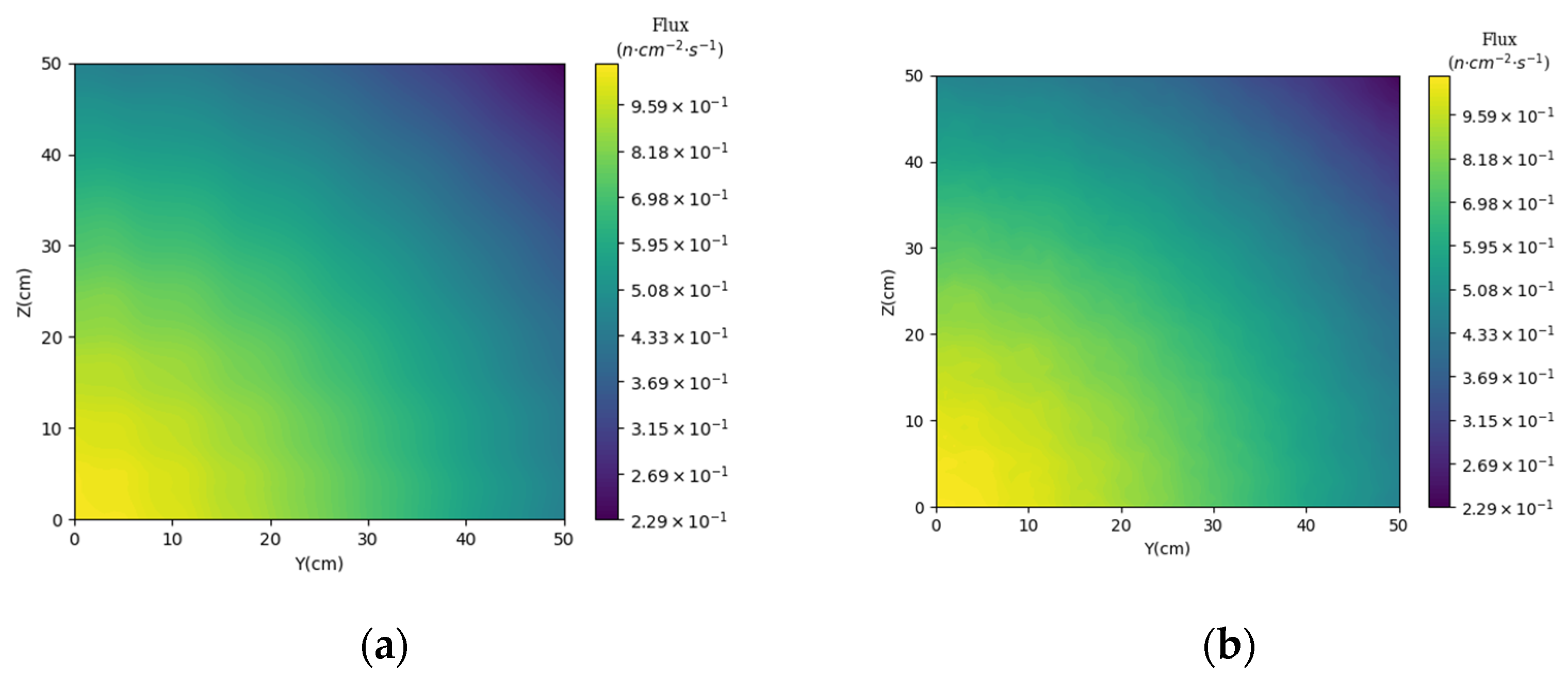
3.2. Prediction of Neutron Flux Distribution in Kobayashi-1 Geometric Shield Region 2
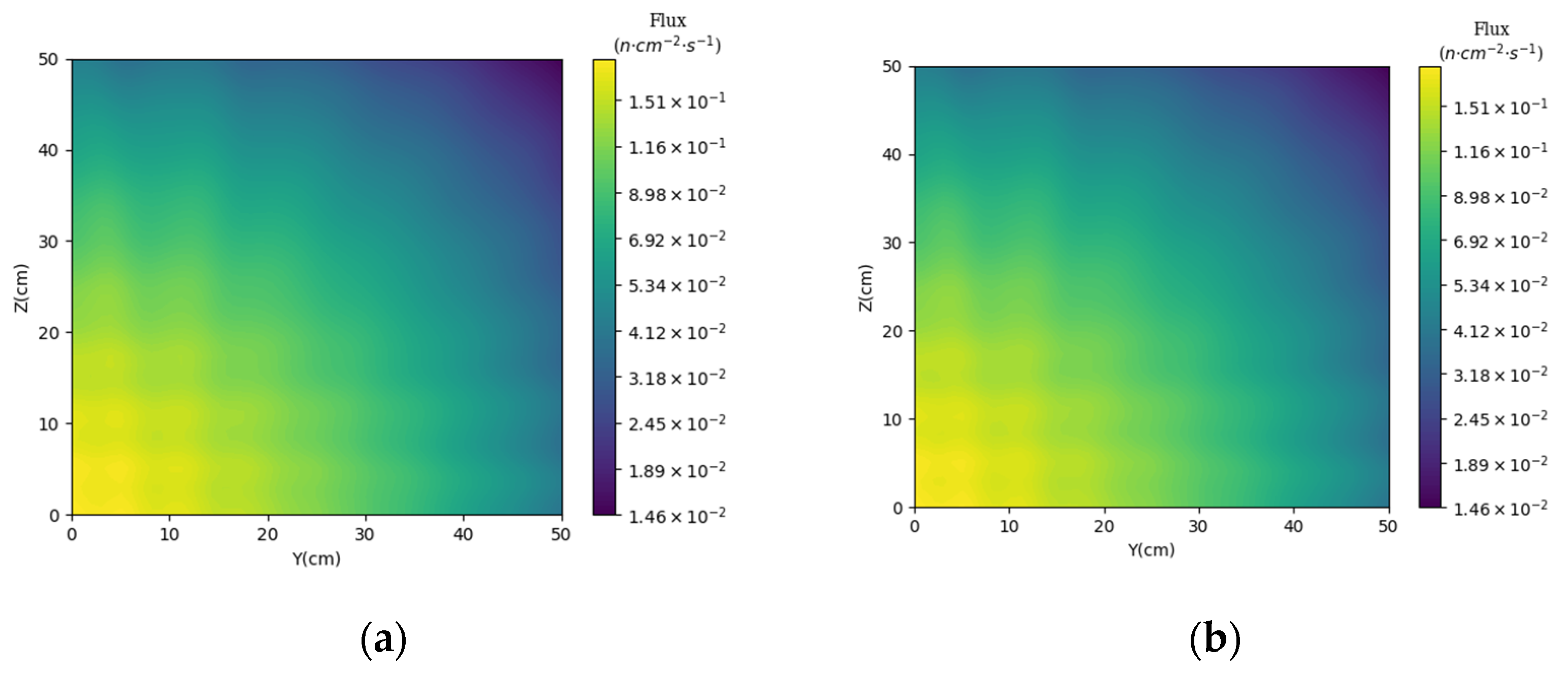
3.3. Prediction of Neutron Flux Distribution in Kobayashi-2 Geometry
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bell, G.I.; Glasstone, S. Nuclear Reactor Theory; US Atomic Energy Commission: Washington, DC, USA, 1970. [Google Scholar]
- Larsen, E.W. An Overview of Neutron Transport Problems and Simulation Techniques. Comput. Methods Transp. 2004, 48, 513–533. [Google Scholar] [CrossRef]
- Lewis, E.E.; Miller, W.F. Computational Methods of Neutron Transport; John Wiley and Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Adams, M.L.; Larsen, E.W. Fast Iterative Methods for Discrete Ordinates Particle Transport Calculations. Prog. Nucl. Energy 2012, 40, 3–159. [Google Scholar] [CrossRef]
- Gong, C.Y.; Liu, J.; Chi, L.H.; Huang, H.W.; Fang, J.Y.; Gong, Z.H. GPU Accelerated Simulations of 3D Deterministic Particle Transport Using Discrete Ordinates Method. J. Comput. Phys. 2011, 230, 6010–6022. [Google Scholar] [CrossRef]
- Baker, R.S.; Koch, K.R. An SN Algorithm for the Massively Parallel CM-200 Computer. Nucl. Sci. Eng. 1998, 128, 312–320. [Google Scholar] [CrossRef]
- Plimpton, S.; Hendrickson, B.; Burns, S.; McLendon, W. Parallel Algorithms for Radiation Transport on Unstructured Grids. In Proceedings of the SC ’00: Proceedings of the 2000 ACM/IEEE Conference on Supercomputing, Dallas, TX, USA, 4–10 November 2000; p. 25. [Google Scholar] [CrossRef]
- Mo, Z.Y.; Zhang, A.Y.; Zhang, Y. A New Parallel Algorithm for Vertex Priorities of Data Flow Acyclic Digraphs. J. Supercomput. 2014, 68, 49–64. [Google Scholar] [CrossRef]
- Baker, R.S. A Block Adaptive Mesh Refinement Algorithm for the Neutral Particle Transport Equation. Nucl. Sci. Eng. 2002, 141, 1–12. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, E.E. Spatial Adaptivity Applied to the Variational Nodal PN Equations. Nucl. Sci. Eng. 2002, 142, 57–63. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ragusa, J.C. Application of hp Adaptivity to the Multigroup Diffusion Equations. Nucl. Sci. Eng. 2009, 161, 22–48. [Google Scholar] [CrossRef]
- Lathouwers, D. Goal-Oriented Spatial Adaptivity for the SN Equations on Unstructured Triangular Meshes. Ann. Nucl. Energy 2011, 38, 1373–1381. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, L.; Liu, C.; Chen, Y.X. Goal-Oriented Regional Angular Adaptive Algorithm for the SN Equations. Nucl. Sci. Eng. 2018, 189, 120–134. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, B.; Chen, Y.X. Spatial Adaptive Algorithm for Discrete Ordinates Shielding Calculation. At. Energy Sci. Technol. 2018, 52, 2233–2242. (In Chinese) [Google Scholar] [CrossRef]
- Liu, C.; Zhang, B.; Zhang, L.; Chen, Y.X. Nonmatching Discontinuous Cartesian Grid Algorithm Based on the Multilevel Octree Architecture for Discrete Ordinates Transport Calculation. Nucl. Sci. Eng. 2020, 194, 1175–1201. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, B.; Wang, X.Y.; Zhang, L.; Chen, Y.X. Reformulation and Evaluation of Robust Characteristic-based Discretization for the Discrete Ordinates Equation on Structured Hexahedron Grids. Prog. Nucl. Energy 2020, 126, 103403. [Google Scholar] [CrossRef]
- Allen, E.J. Stochastic Difference Equations and A Stochastic Partial Differential Equation for Neutron Transport. J. Differ. Equ. Appl. 2012, 18, 1267–1285. [Google Scholar] [CrossRef]
- Hajas, T.Z.; Tolnai, G.; Margoczi, M.; Legrady, D. Noise Term Modeling of Dynamic Monte Carlo Using Stochastic Differential Equations. Ann. Nucl. Energy 2024, 195, 110061. [Google Scholar] [CrossRef]
- Berry, J.J.; Gil-Delgado, G.G.; Osborne, A.G.S. Classification of Group Structures for a Multigroup Collision Probability Model Using Machine Learning. Ann. Nucl. Energy 2021, 160, 108367. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Sun, G.M.; Yang, Z.H.; Wang, H.; Fang, L.; Wang, J.Y. BP Neural Network Based Reconstruction Method for Radiation Field Applications. Nucl. Eng. Des. 2021, 380, 111228. [Google Scholar] [CrossRef]
- Li, Z.G.; Sun, J.; Wei, C.L.; Sui, Z.; Qian, X.Y. A New Cross-sections Calculation Method in HTGR Engineering Simulator System Based on Machine Learning Methods. Ann. Nucl. Energy 2020, 145, 107553. [Google Scholar] [CrossRef]
- Zhu, Q.J.; Tian, L.C.; Yang, X.H.; Gan, L.F.; Zhao, N.; Ma, Y.Y. Advantages of artificial neural network in neutron spectra unfolding. Chin. Phys. Lett. 2014, 31, 69–72. [Google Scholar] [CrossRef]
- Cao, C.L.; Gan, Q.; Song, J.; Long, P.C.; Wu, B.; Wu, Y.C. A Two-Step Neutron Spectrum Unfolding Method for Fission Reactors Based on Artificial Neural Network. Ann. Nucl. Energy 2019, 139, 107219. [Google Scholar] [CrossRef]
- dos Santos, M.C.; Pinheiro VH, C.; do Desterro FS, M.; de Avellar, R.K.; Schirru, R.; dos Santos Nicolau, A.; de Lima, A.M.M. Deep Rectifier Neural Network Applied to the Accident Identification Problem in A PWR Nuclear Power Plant. Ann. Nucl. Energy 2019, 133, 400–408. [Google Scholar] [CrossRef]
- Cao, C.L.; Gan, Q.; Song, J.; Long, P.C.; Wu, B.; Wu, Y.C. An Artificial Neural Network-based Neutron Field Reconstruction Method for Reactor. Ann. Nucl. Energy 2020, 138, 107195. [Google Scholar] [CrossRef]
- Song, Y.M.; Zhao, Y.B.; Li, X.X.; Wang, K.; Zhang, Z.H.; Luo, W.; Zhu, Z.C. A Method for Optimizing the Shielding Structure of Marine Reactors. Nucl. Sci. Eng. 2017, 37, 355–361. (In Chinese) [Google Scholar]
- Song, Y.M.; Zhang, Z.H.; Mao, J.; Lu, C.; Tang, S.Q.; Xiao, F.; Lyu, H.W. Research on Fast Intelligence Multi-objective Optimization Method of Nuclear Reactor Radiation Shielding. Ann. Nucl. Energy 2020, 149, 107771. [Google Scholar] [CrossRef]
- Vasseur, A.; Makovicka, L.; Martin, É.; Sauget, M.; Contassot-Vivier, S.; Bahi, J. Dose Calculations Using Artificial Neural Networks: A Feasibility Study for Photon Beams. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2018, 266, 1085–1093. [Google Scholar] [CrossRef]
- Wang, J.; Peng, X.; Chen, Z. Surrogate Modeling for Neutron Diffusion Problems Based on Conservative Physics-informed Neural Networks with Boundary Conditions Enforcement. Ann. Nucl. Energy 2022, 176, 109234. [Google Scholar] [CrossRef]
- Yann, L.C.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Fowler, T.B.; Vondy, D.R. Nuclear Reactor Core Analysis Code; ORNL-TM-2496; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 1969. [Google Scholar]
- Semenza, L.A.; Lewis, E.E.; Rossow, E.C. The Application of the Finite Element Method to the Multigroup Neutron Diffusion Equation. Nucl. Sci. Eng. 1972, 47, 302–310. [Google Scholar] [CrossRef]
- Chen, Y.X.; Zhang, B.; Zhang, L.; Zheng, J.X.; Zheng, Y.; Liu, C. ARES: A Parallel Discrete Ordinates Transport Code for Radiation Shielding Applications and Reactor Physics Analysis. Sci. Technol. Nucl. Ins. 2017, 2017, 2596727. [Google Scholar] [CrossRef]
- Kobayashi, K.; Sugimura, N.; Nagaya, Y. 3D Radiation Transport Benchmark Problems and Results for Simple Geometries with Void Region. Prog. Nucl. Energy 2001, 39, 119–144. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Zheng, X. TensorFlow: Large Scale Machine Learning on Heterogeneous Distributed Systems. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Smith, L.N. A Disciplined Approach to Neural Network Hyperparameters: Part 1–Learning Rate, Batch Size, Momentum, and Weight Decay. arXiv 2018, arXiv:1803.09820. [Google Scholar]


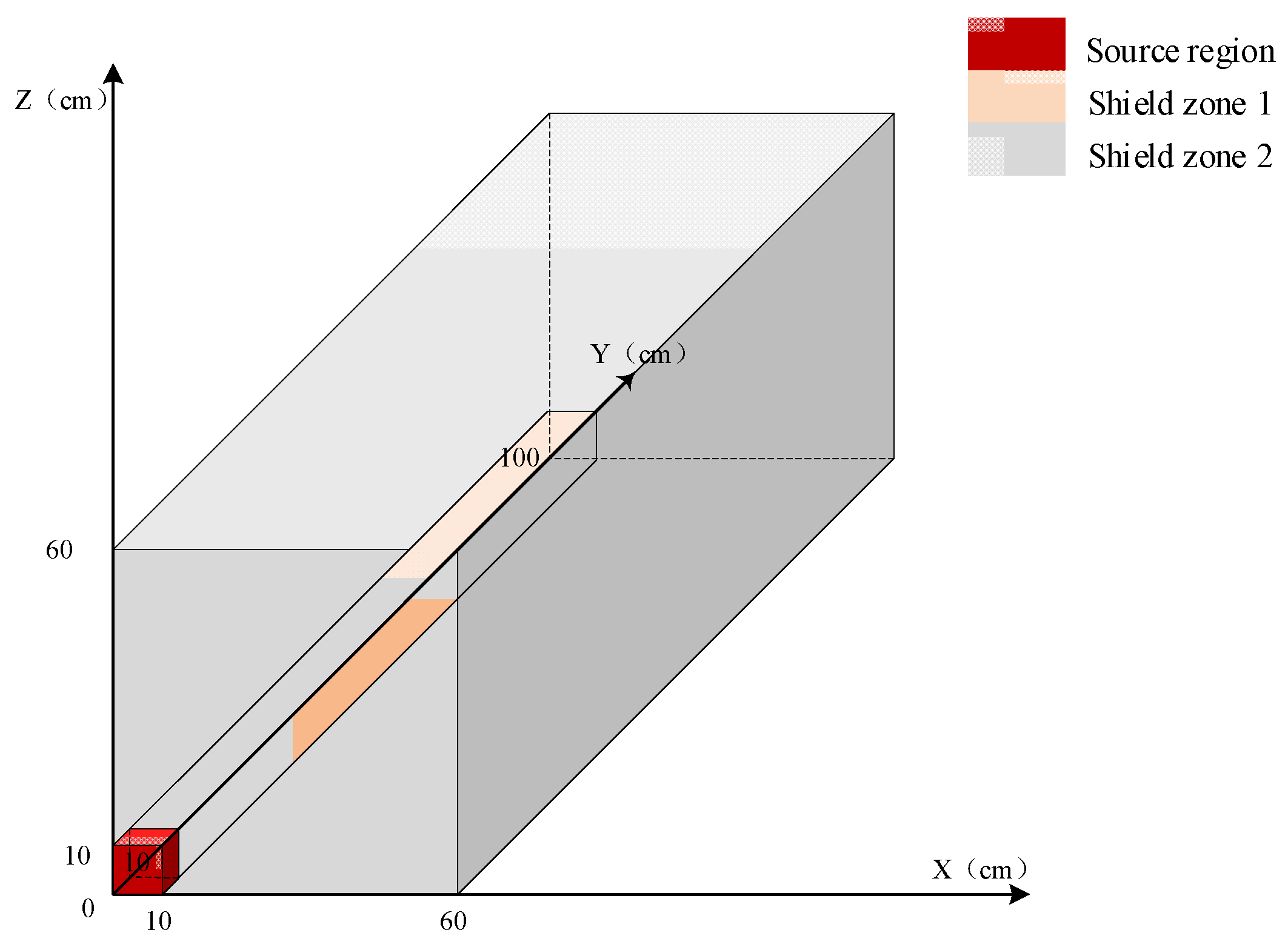


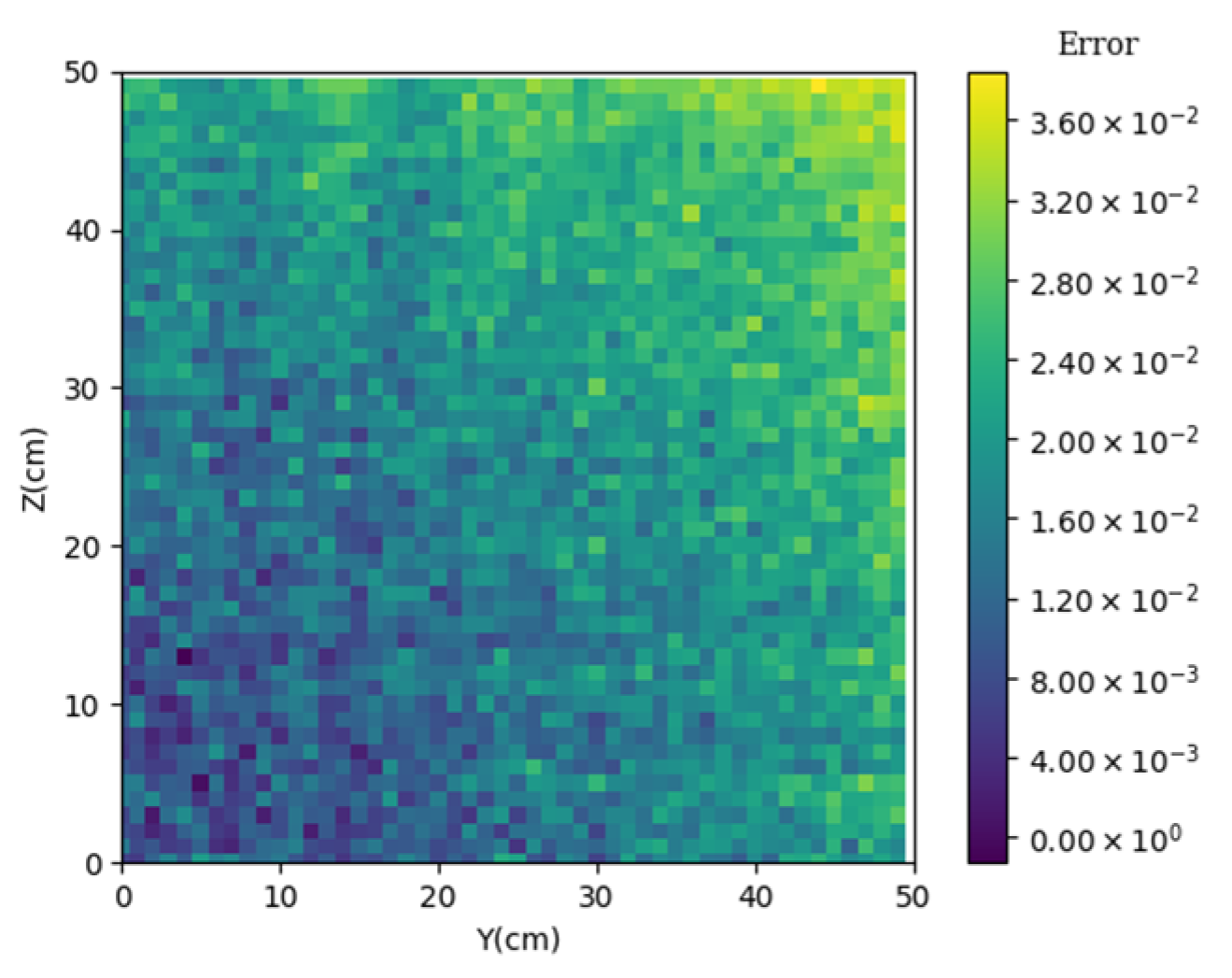


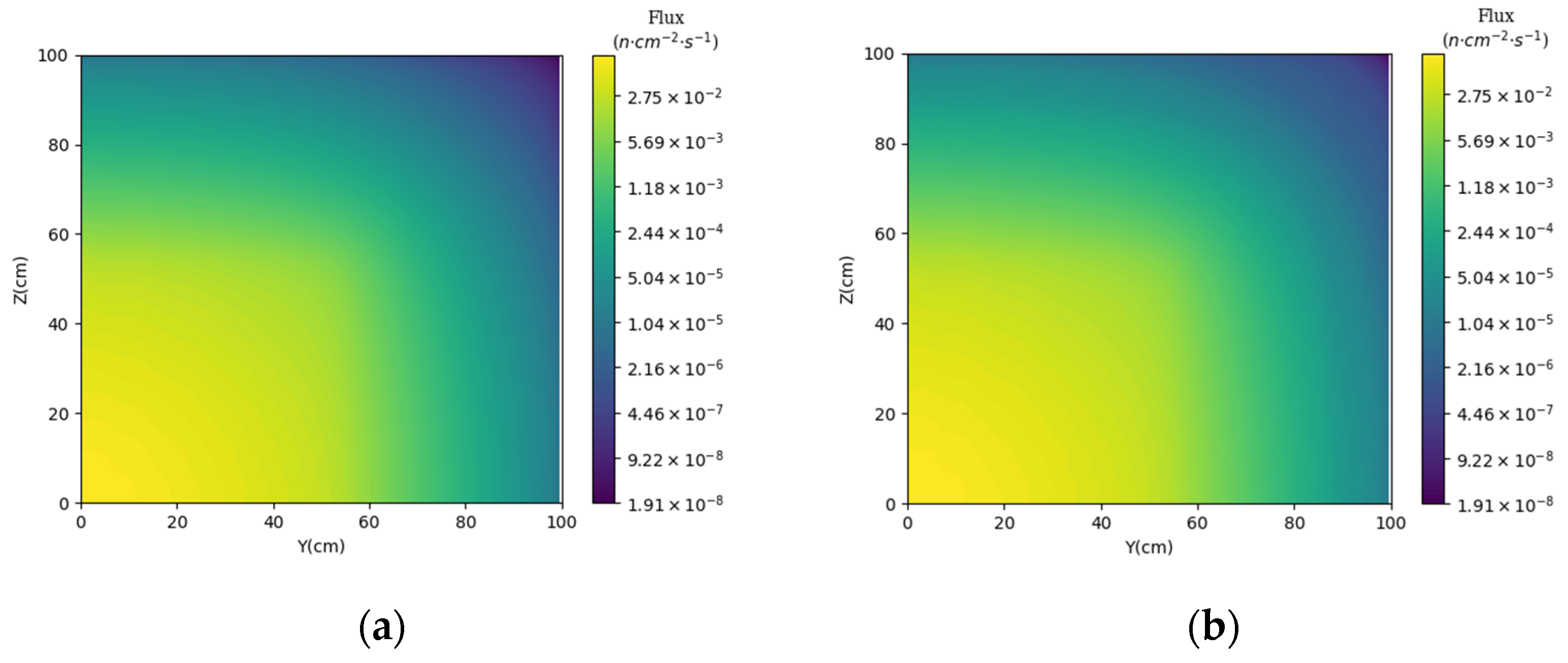
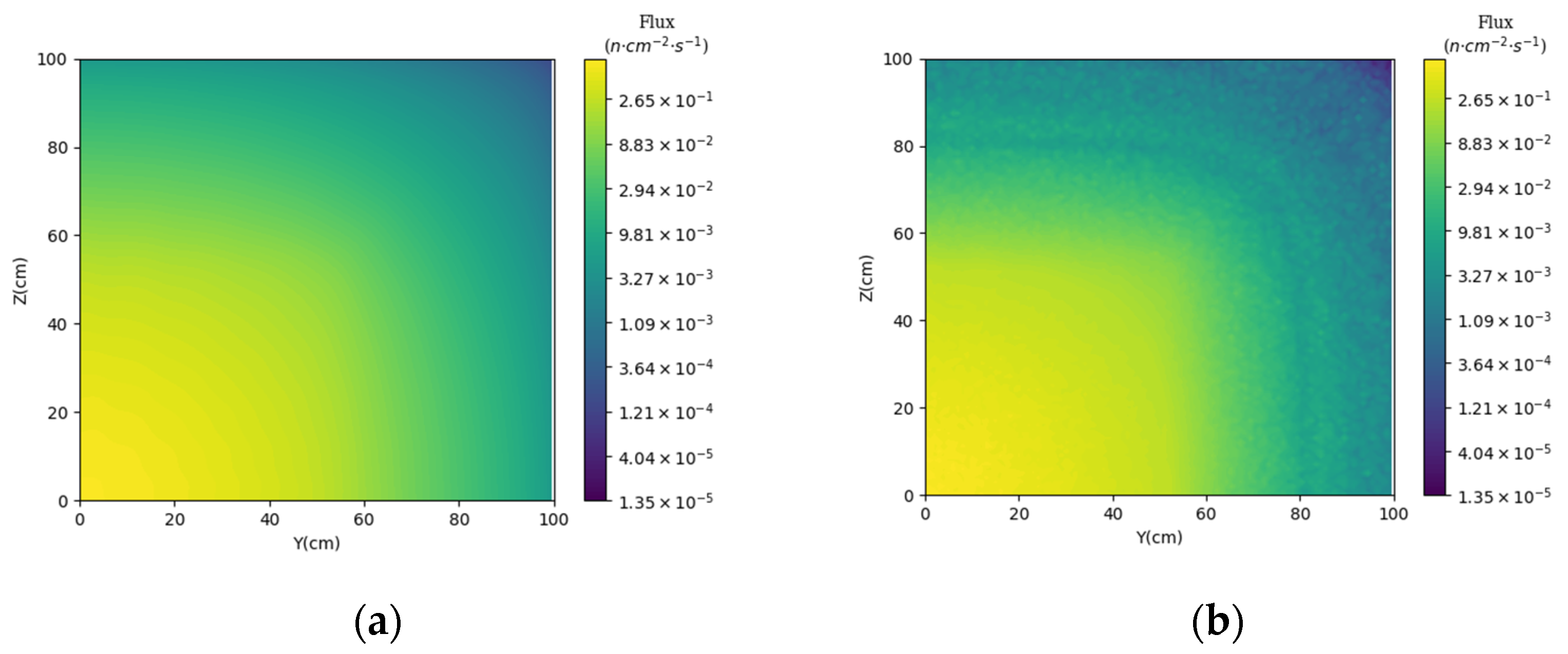


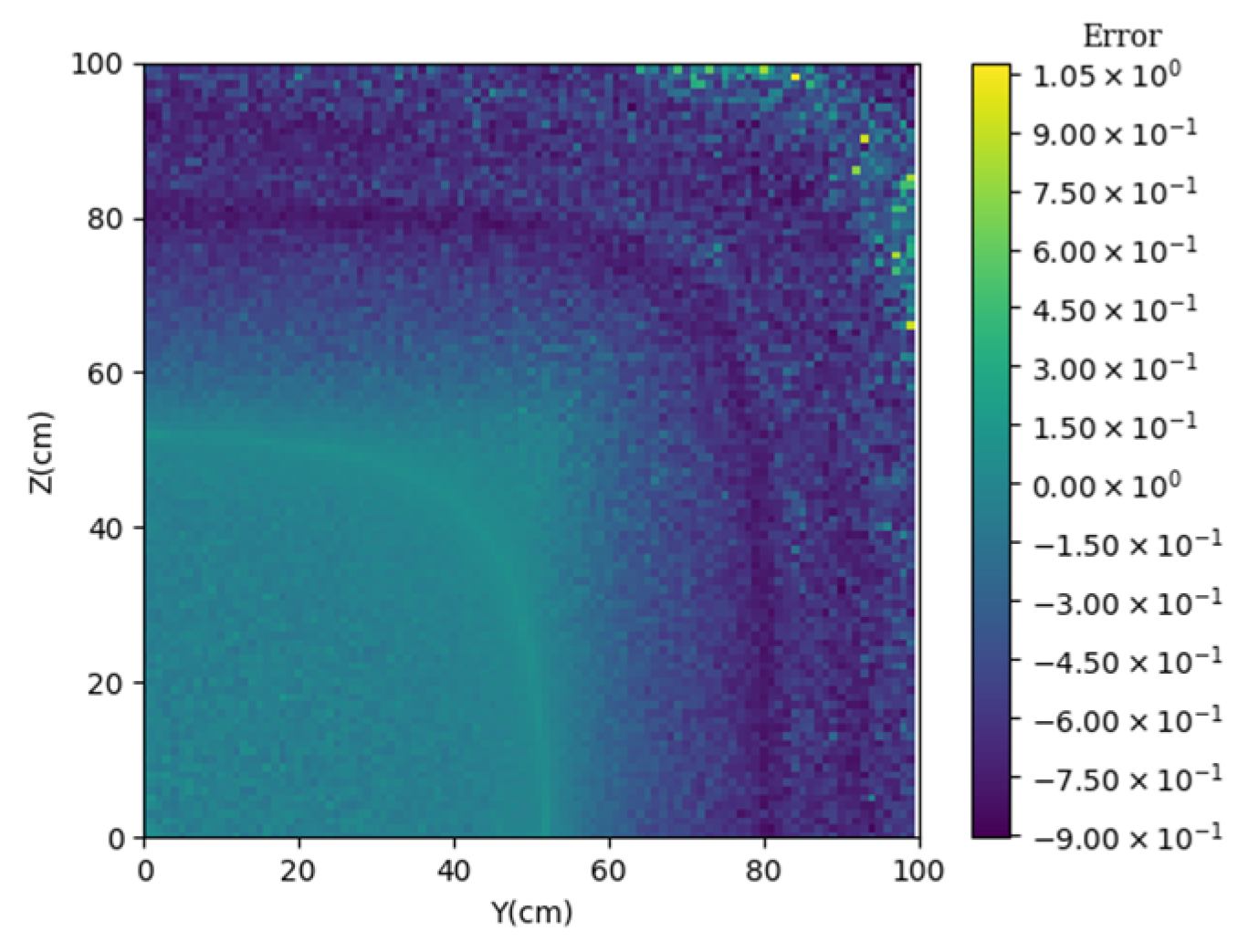

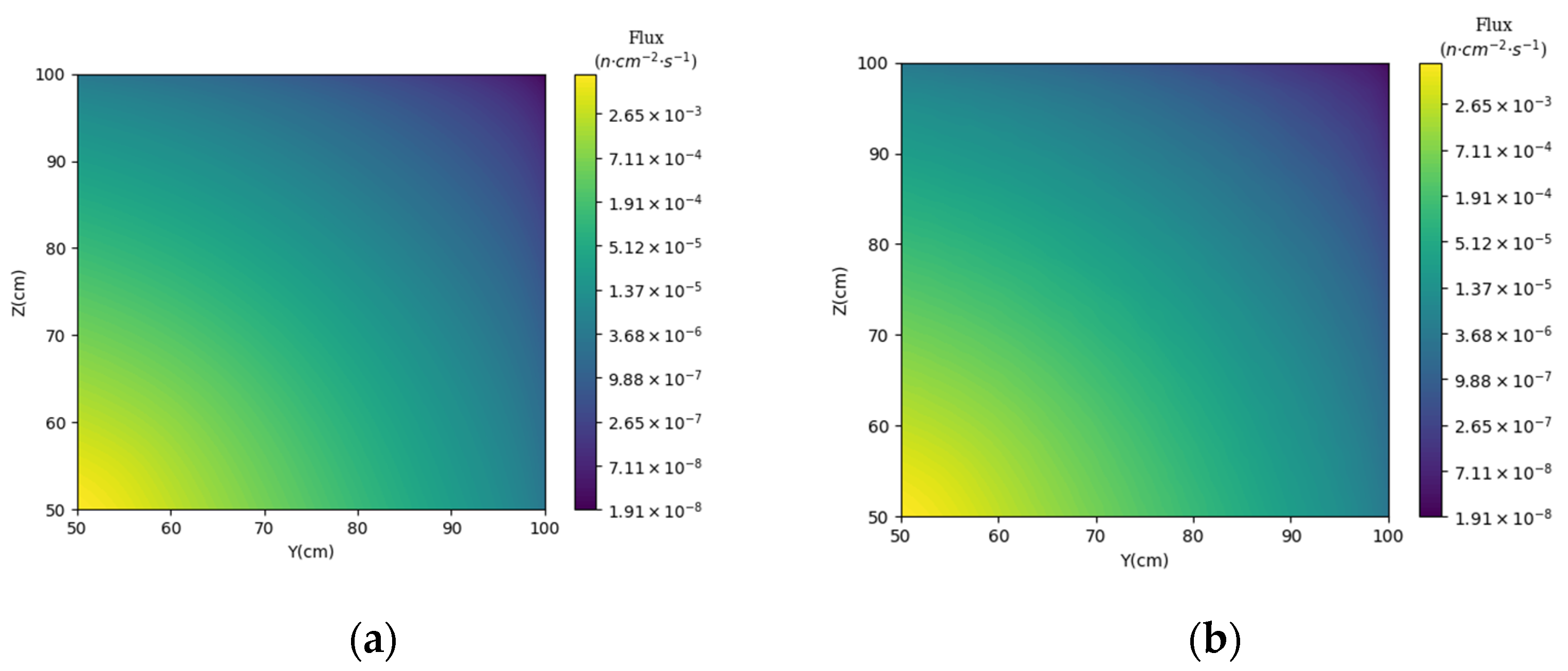
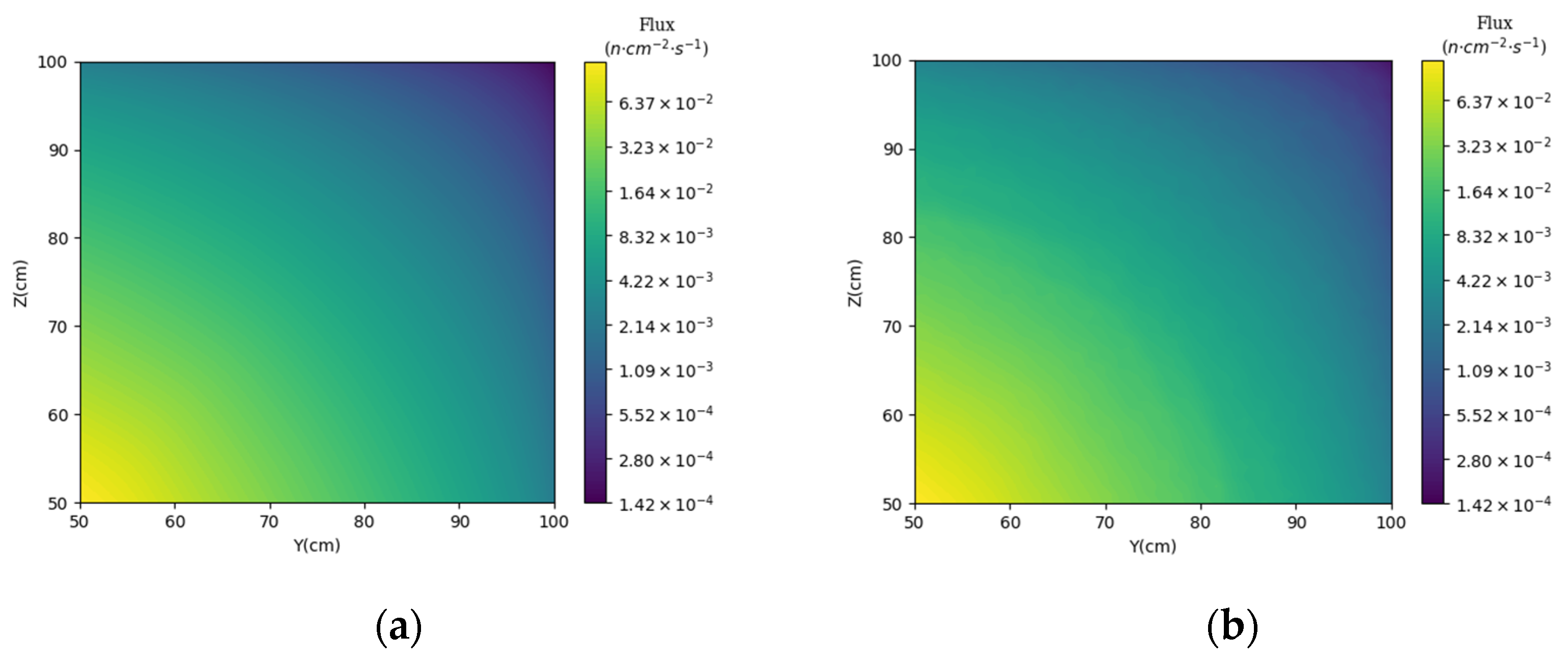

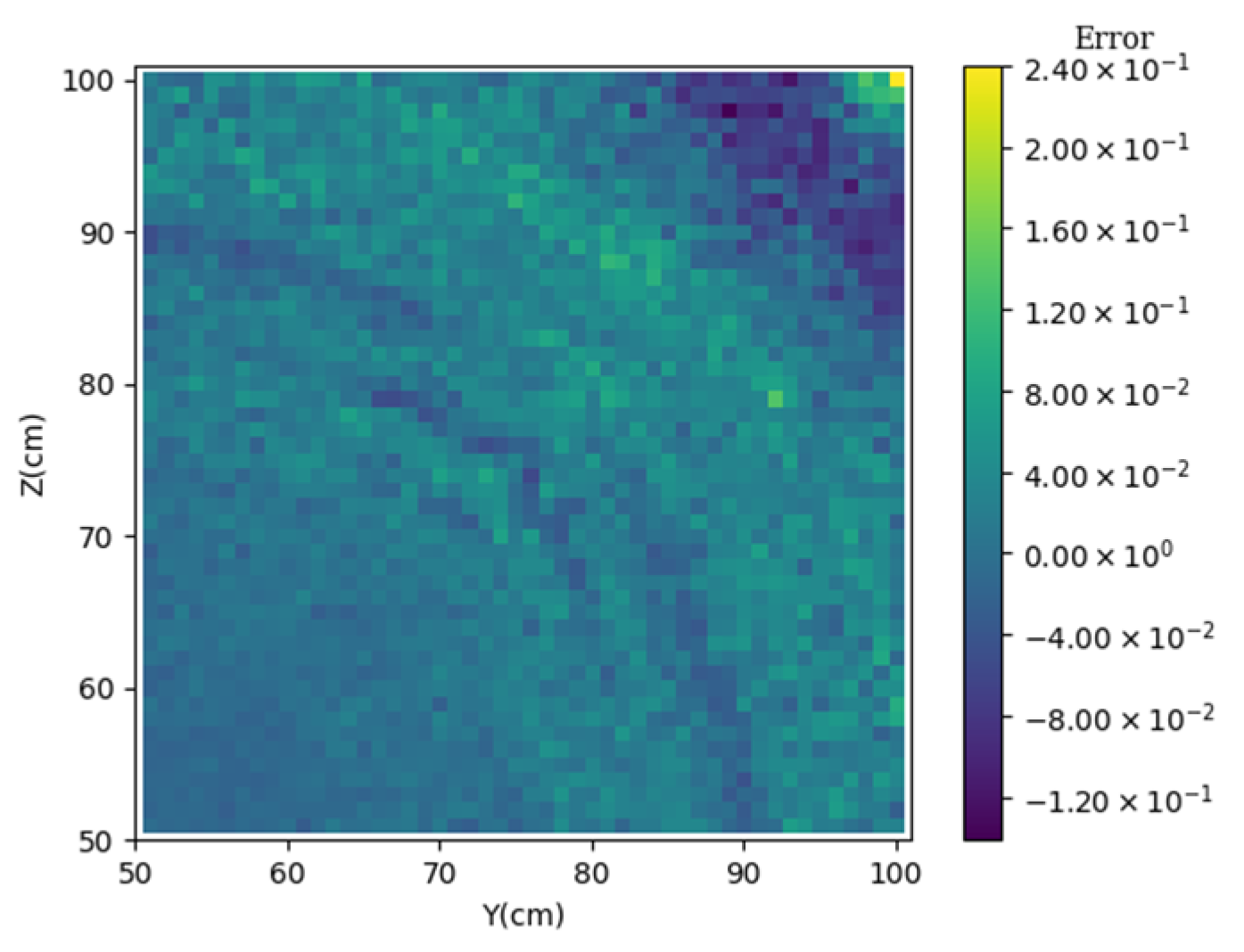


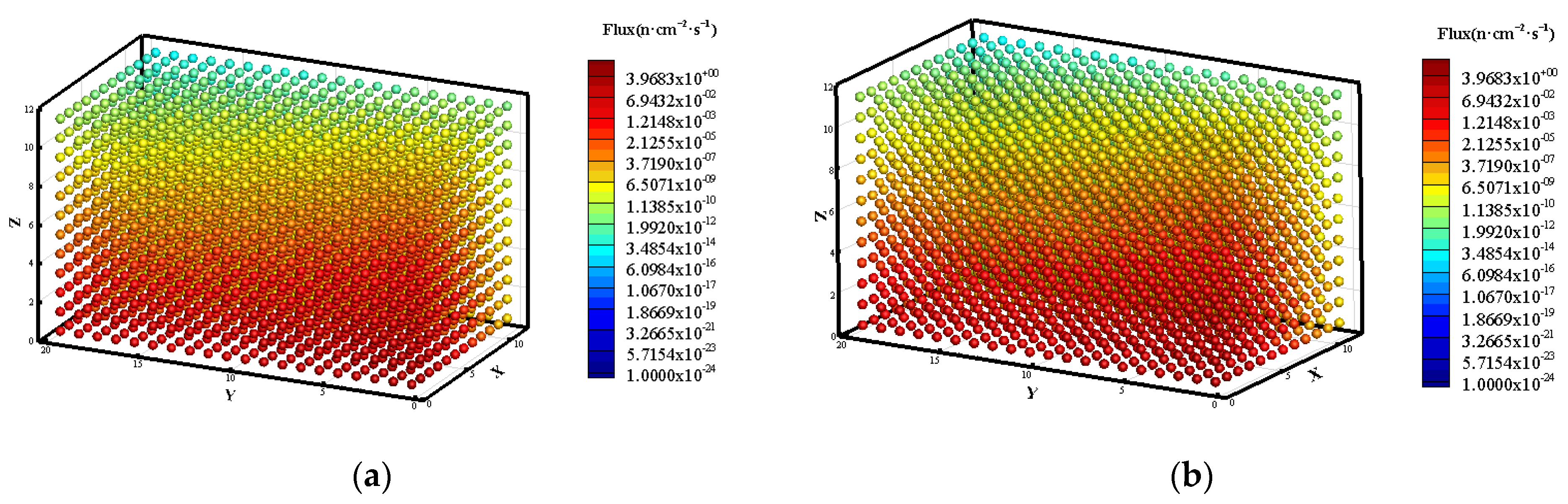
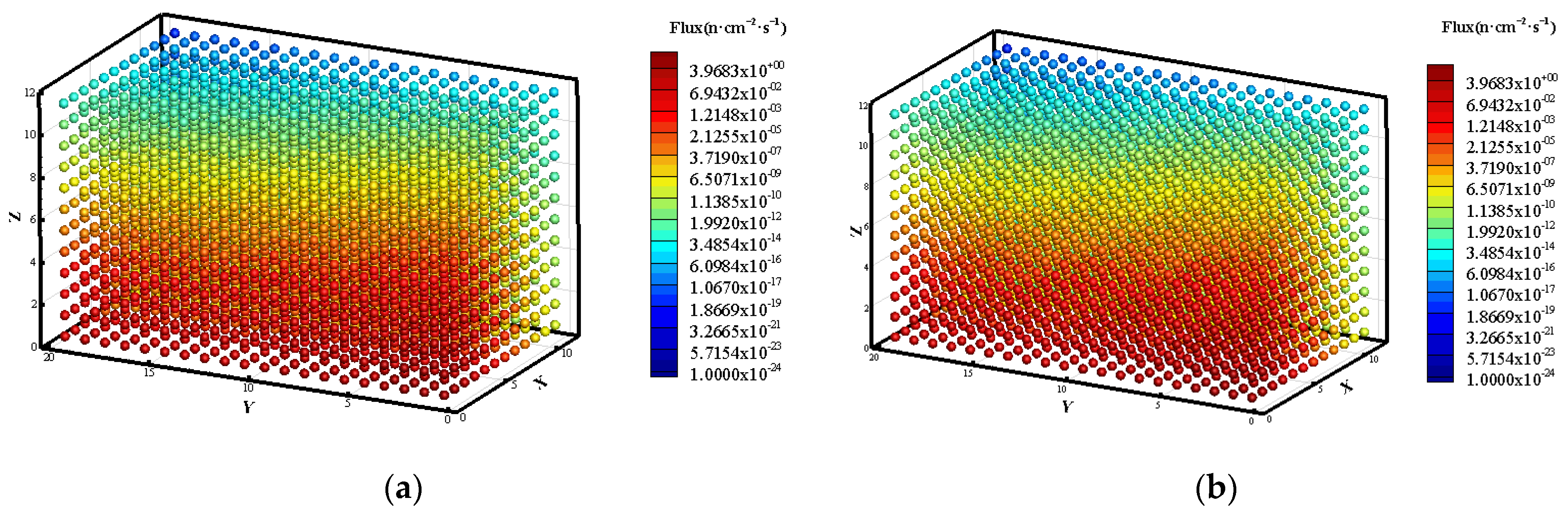
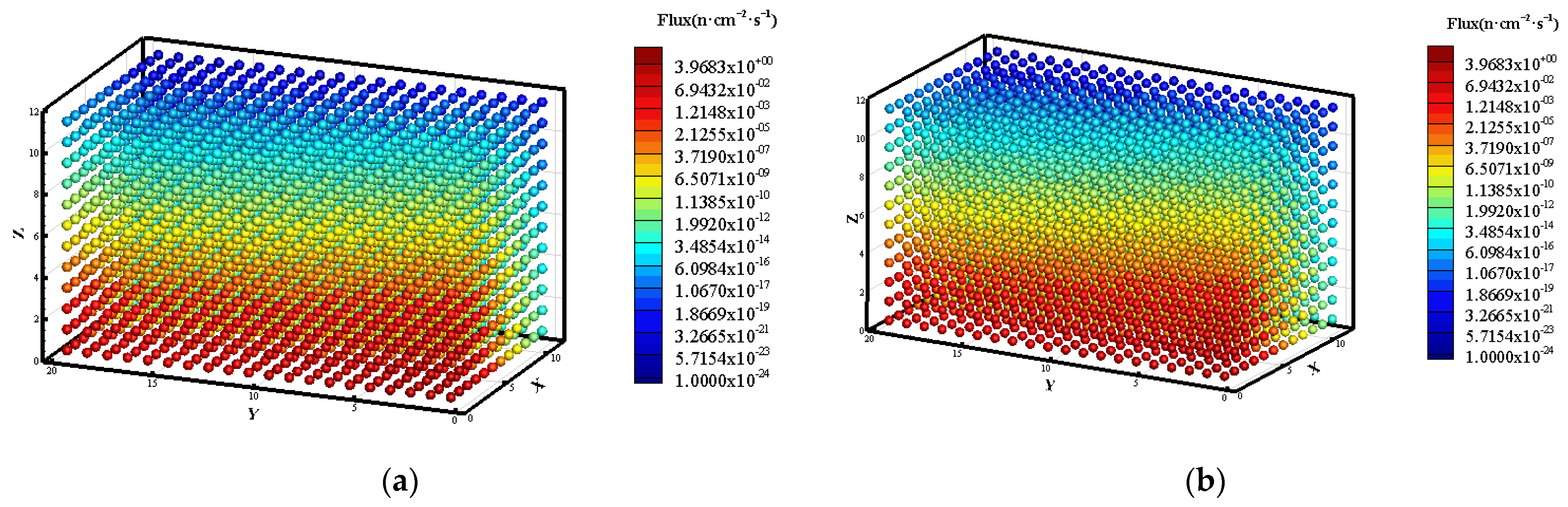
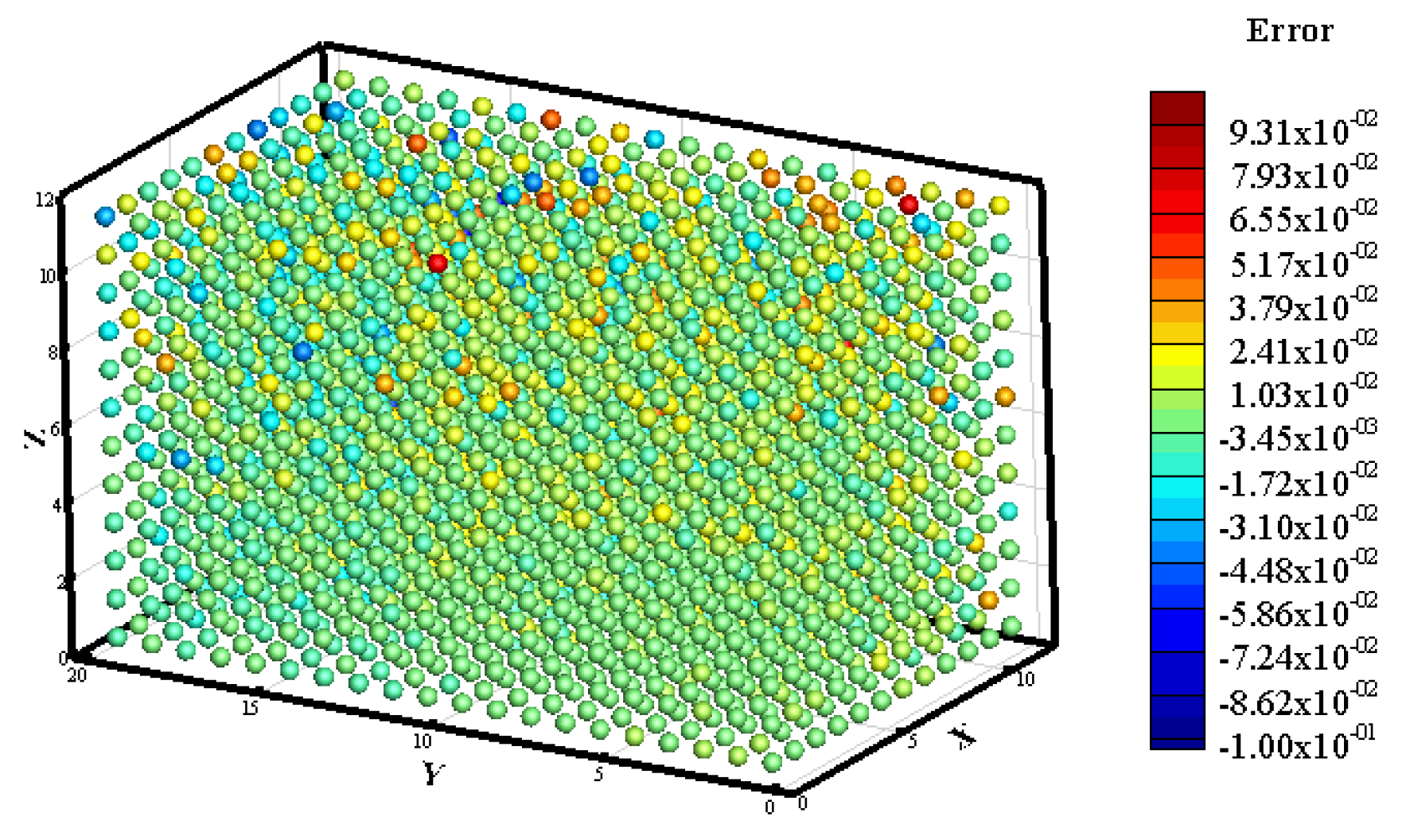
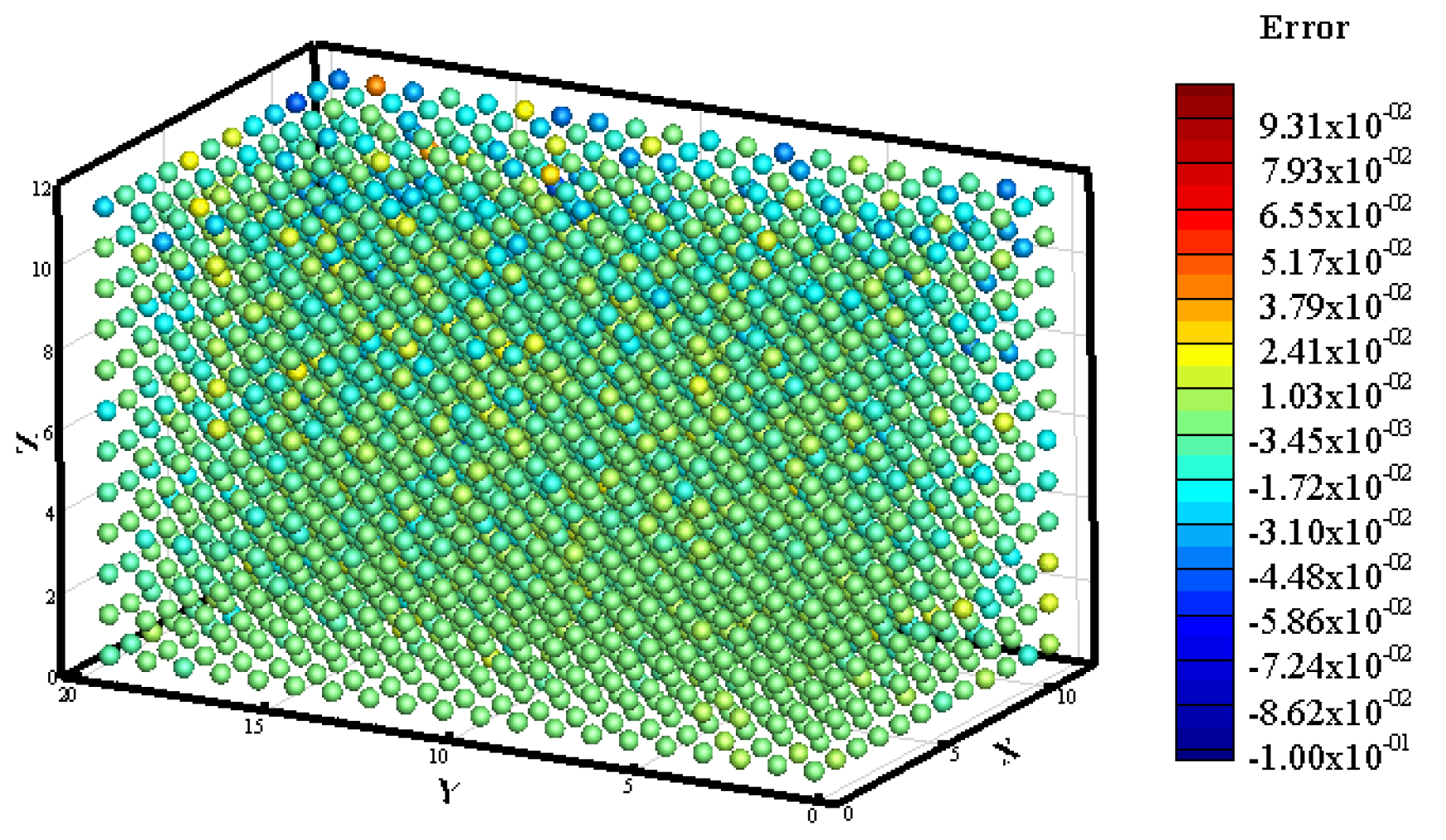
| Zone | S (n·cm−3·s−1) | Σt (cm−1) | Σs (cm−1) |
|---|---|---|---|
| Source region | 1–1 × 101 | 5 × 10−2–1 | 5 × 10−2–1 |
| Shield zone 1 | 0 | 1 × 10−4–5 × 10−2 | 1 × 10−4–5 × 10−2 |
| Shield zone 2 | 0 | 5 × 10−2–1 | 5 × 10−2–1 |
| Zone | Nuclide | The Range of Atom Density (barn−1·cm−1) |
|---|---|---|
| Source region | 2H | 1 × 10−4–1 × 10−1 |
| 16O | 1 × 10−4–1 × 10−1 | |
| 235U | 1 × 10−6–1 × 10−2 | |
| 238U | 1 × 10−4–1 × 10−4 | |
| 56Fe | 1 × 10−7–1 × 10−4 | |
| 10B | 1 × 10−8–1 × 10−5 | |
| 91Zr | 1 × 10−5–1 × 10−2 | |
| 14C | 1 × 10−8–1 × 10−5 | |
| Shield zone 1 | 2H | 5 × 10−8–1 × 10−5 |
| 14N | 1 × 10−7–1 × 10−4 | |
| 16O | 1 × 10−7–1 × 10−4 | |
| Shield zone 2 | 2H | 1 × 10−4–1 × 10−1 |
| 16O | 1 × 10−4–1 × 10−1 | |
| 14C | 1 × 10−6–1 × 10−3 | |
| 27Al | 1 × 10−5–1 × 10−2 | |
| 28Si | 1 × 10−4–1 × 10−1 | |
| 32S | 1 × 10−6–1 × 10−3 | |
| 40Ca | 1 × 10−5–1 × 10−2 | |
| 56Fe | 1 × 10−5–1 × 10−2 |
| Zone | S (n·cm−3·s−1) | Σt (cm−1) |
|---|---|---|
| Source region | 1–1 × 101 | (1 × 10−1–1) + Σs0 |
| Shield zone 1 | 0 | (1 × 10−4–1 × 10−2) + Σs0 |
| Shield zone 2 | 0 | (1 × 10−1–1) + Σs0 |
| Standardized Method | No Standardization | Log Standardization |
|---|---|---|
| Train loss | 2.90 × 10−3 | 6.90 × 10−3 |
| Initial Learning Rates | 1 × 10−3 | 1 × 10−4 | 1 × 10−5 |
|---|---|---|---|
| Train loss | 9.80 × 10−3 | 2.74 × 10−2 | 1.44 × 10−1 |
| Test loss | 7.76 × 10−2 | 4.35 × 10−2 | 1.60 × 10−1 |
| Batch Size | 1 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|
| Train loss | 1.31 × 10−2 | 1.89 × 10−2 | 2.74 × 10−2 | 5.11 × 10−2 | 5.01 × 10−2 |
| Test loss | 5.63 × 10−2 | 3.56 × 10−2 | 4.35 × 10−2 | 7.70 × 10−2 | 7.01 × 10−2 |
| Time Spent (s) | 2.41 | 6.90 × 10−1 | 5.00 × 10−1 | 4.70 × 10−1 | 4.30 × 10−1 |
| Activation Function | Relu | ELU | Sigmoid | Tanh |
|---|---|---|---|---|
| Train loss | 4.01 × 10−2 | 2.74 × 10−2 | 4.75 | 9.13 × 10−2 |
| Test loss | 9.36 × 10−2 | 4.35 × 10−2 | 4.51 | 2.90 × 10−1 |
| Learning Rate Decline | 100 | 200 | 300 | 400 |
|---|---|---|---|---|
| Train loss | 1.12 × 10−1 | 2.73 × 10−2 | 2.74 × 10−2 | 2.68 × 10−2 |
| Test loss | 1.41 × 10−1 | 4.46 × 10−2 | 4.35 × 10−2 | 4.82 × 10−2 |
| Hidden Layers | 2 | 3 | 4 | 6 | 8 |
|---|---|---|---|---|---|
| Train loss | 5.30 × 10−3 | 2.70 × 10−3 | 2.50 × 10−3 | 3.70 × 10−3 | 1.20 × 10−3 |
| Test loss | 7.40 × 10−3 | 4.90 × 10−3 | 5.20 × 10−3 | 6.10 × 10−3 | 1.85 × 10−2 |
| Number of Neurons | 200 | 500 | 800 | 1000 | 1500 |
|---|---|---|---|---|---|
| Train loss | 7.60 × 10−3 | 3.20 × 10−3 | 2.50 × 10−3 | 2.40 × 10−3 | 3.30 × 10−3 |
| Test loss | 1.35 × 10−2 | 5.50 × 10−3 | 5.20 × 10−3 | 4.80 × 10−3 | 5.30 × 10−3 |
| Hidden Layers | 3 | 4 | 6 | 8 |
|---|---|---|---|---|
| Train loss | 3.77 × 10−2 | 3.26 × 10−2 | 1.26 × 10−2 | 9.60 × 10−3 |
| Test Loss | 7.26 × 10−2 | 6.14 × 10−2 | 6.90 × 10−2 | 1.19 × 10−1 |
| Number of Neurons | 200 | 500 | 800 | 1000 | 1500 |
|---|---|---|---|---|---|
| Train loss | 3.47 × 10−2 | 3.91 × 10−2 | 3.26 × 10−2 | 1.36 × 10−2 | 1.89 × 10−2 |
| Test Loss | 7.64 × 10−2 | 7.75 × 10−2 | 6.14 × 10−2 | 6.47 × 10−2 | 6.26 × 10−2 |
| Hidden Layers | 3 | 4 | 6 | 7 |
|---|---|---|---|---|
| Train loss | 1.28 × 10−2 | 9.80 × 10−3 | 6.60 × 10−3 | 6.60 × 10−3 |
| Test loss | 1.90 × 10−2 | 1.43 × 10−2 | 1.65 × 10−2 | 2.01 × 10−2 |
| Number of Neurons | 200 | 500 | 800 | 1000 | 1500 |
|---|---|---|---|---|---|
| Train loss | 1.42 × 10−2 | 9.70 × 10−3 | 9.80 × 10−3 | 7.20 × 10−3 | 6.70 × 10−3 |
| Test loss | 1.93 × 10−2 | 1.55 × 10−2 | 1.43 × 10−2 | 1.46E × 10−2 | 1.53 × 10−2 |
| Hidden Layers | 3 | 4 | 6 | 8 |
|---|---|---|---|---|
| Train loss | 1.50 × 10−3 | 1.30 × 10−3 | 7.57 × 10−4 | 7.70 × 10−4 |
| Test loss | 2.20 × 10−3 | 1.91 × 10−3 | 2.30 × 10−3 | 2.70 × 10−3 |
| Number of Neurons | 800 | 1000 | 1500 | 2000 | 2500 |
|---|---|---|---|---|---|
| Train loss | 1.40 × 10−3 | 1.30 × 10−3 | 8.52 × 10−3 | 6.86 × 10−4 | 6.23 × 10−4 |
| Test loss | 2.00 × 10−3 | 1.91 × 10−3 | 1.70 × 10−3 | 1.50 × 10−3 | 1.50 × 10−3 |
| Validation Use Case | S (n·cm−3·s−1) | Σt (cm−1) | Σs (cm−1) |
|---|---|---|---|
| 1 | 9.26 | 9.24 × 10−1 | 4.55 × 10−1 |
| 2 | 8.29 | 6.84 × 10−1 | 5.35 × 10−1 |
| 3 | 5.32 | 3.23 × 10−1 | 8.06 × 10−1 |
| Validation Use Case | Shielding Zone 1 Σt (cm−1) | Shielding Zone 1 Σs (cm−1) | Shielding Zone 2 Σt (cm−1) | Shielding Zone 2 Σs (cm−1) |
|---|---|---|---|---|
| 1 | 3.47 × 10−2 | 8.20 × 10−3 | 3.55 × 10−1 | 3.29 × 10−1 |
| 2 | 3.02 × 10−2 | 2.33 × 10−2 | 1.21 × 10−1 | 1.04 × 10−1 |
| 3 | 3.61 × 10−2 | 1.35 × 10−2 | 5.59 × 10−1 | 5.16 × 10−2 |
| Validation Use Case | Source Region S (n·cm−3·s−1) | Source Region Σt (cm−1) | Shielding Zone 1 Σt (cm−1) | Shielding Zone 2 Σt (cm−1) |
|---|---|---|---|---|
| 4 | 2.00 | 1.80 | 5.70 × 10−3 | 7.26 × 10−1 |
| 5 | 7.60 | 1.58 | 8.44 × 10−3 | 1.49 |
| 6 | 3.19 | 2.81 | 5.92 × 10−3 | 1.74 |
| Zone | P0 Scattering Coefficients (cm−1) | P1 Scattering Coefficients (cm−1) | P2 Scattering Coefficients (cm−1) | P3 Scattering Coefficients (cm−1) |
|---|---|---|---|---|
| Source region | 1.02 | 1.05 × 10−1 | 3.87 × 10−2 | 8.23 × 10−3 |
| Shield zone 1 | 5.41 × 10−4 | 1.36 × 10−4 | 5.24 × 10−5 | 7.50 × 10−6 |
| Shield zone 2 | 6.02 × 10−1 | 2.84 × 10−1 | 1.16 × 10−1 | 1.66 × 10−2 |
| Zone | P0 Scattering Coefficients (cm−1) | P1 Scattering Coefficients (cm−1) | P2 Scattering Coefficients (cm−1) | P3 Scattering Coefficients (cm−1) |
|---|---|---|---|---|
| Source region | 1.32 | 3.20 × 10−1 | 1.27 × 10−1 | 2.09 × 10−2 |
| Shield zone 1 | 6.35 × 10−4 | 1.38 × 10−4 | 5.30 × 10−5 | 7.59 × 10−6 |
| Shield zone 2 | 1.34 | 6.57 × 10−1 | 2.69 × 10−1 | 3.85 × 10−2 |
| Zone | P0 Scattering Coefficients (cm−1) | P1 Scattering Coefficients (cm−1) | P2 Scattering Coefficients (cm−1) | P3 Scattering Coefficients (cm−1) |
|---|---|---|---|---|
| Source region | 1.76 | 6.64 × 10−1 | 2.69 × 10−1 | 4.02 × 10−2 |
| Shield zone 1 | 6.72 × 10−4 | 7.56 × 10−5 | 2.17 × 10−5 | 3.08 × 10−6 |
| Shield zone 2 | 1.52 | 7.93 × 10−1 | 3.25 × 10−1 | 4.65 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, B.; Yang, S.; Chen, Y. A Data-Driven Method for Calculating Neutron Flux Distribution Based on Deep Learning and the Discrete Ordinates Method. Energies 2024, 17, 3440. https://doi.org/10.3390/en17143440
Li Y, Zhang B, Yang S, Chen Y. A Data-Driven Method for Calculating Neutron Flux Distribution Based on Deep Learning and the Discrete Ordinates Method. Energies. 2024; 17(14):3440. https://doi.org/10.3390/en17143440
Chicago/Turabian StyleLi, Yanchao, Bin Zhang, Shouhai Yang, and Yixue Chen. 2024. "A Data-Driven Method for Calculating Neutron Flux Distribution Based on Deep Learning and the Discrete Ordinates Method" Energies 17, no. 14: 3440. https://doi.org/10.3390/en17143440
APA StyleLi, Y., Zhang, B., Yang, S., & Chen, Y. (2024). A Data-Driven Method for Calculating Neutron Flux Distribution Based on Deep Learning and the Discrete Ordinates Method. Energies, 17(14), 3440. https://doi.org/10.3390/en17143440





