Predictive Modeling of Conveyor Belt Deterioration in Coal Mines Using AI Techniques
Abstract
:1. Introduction
2. Materials and Methods
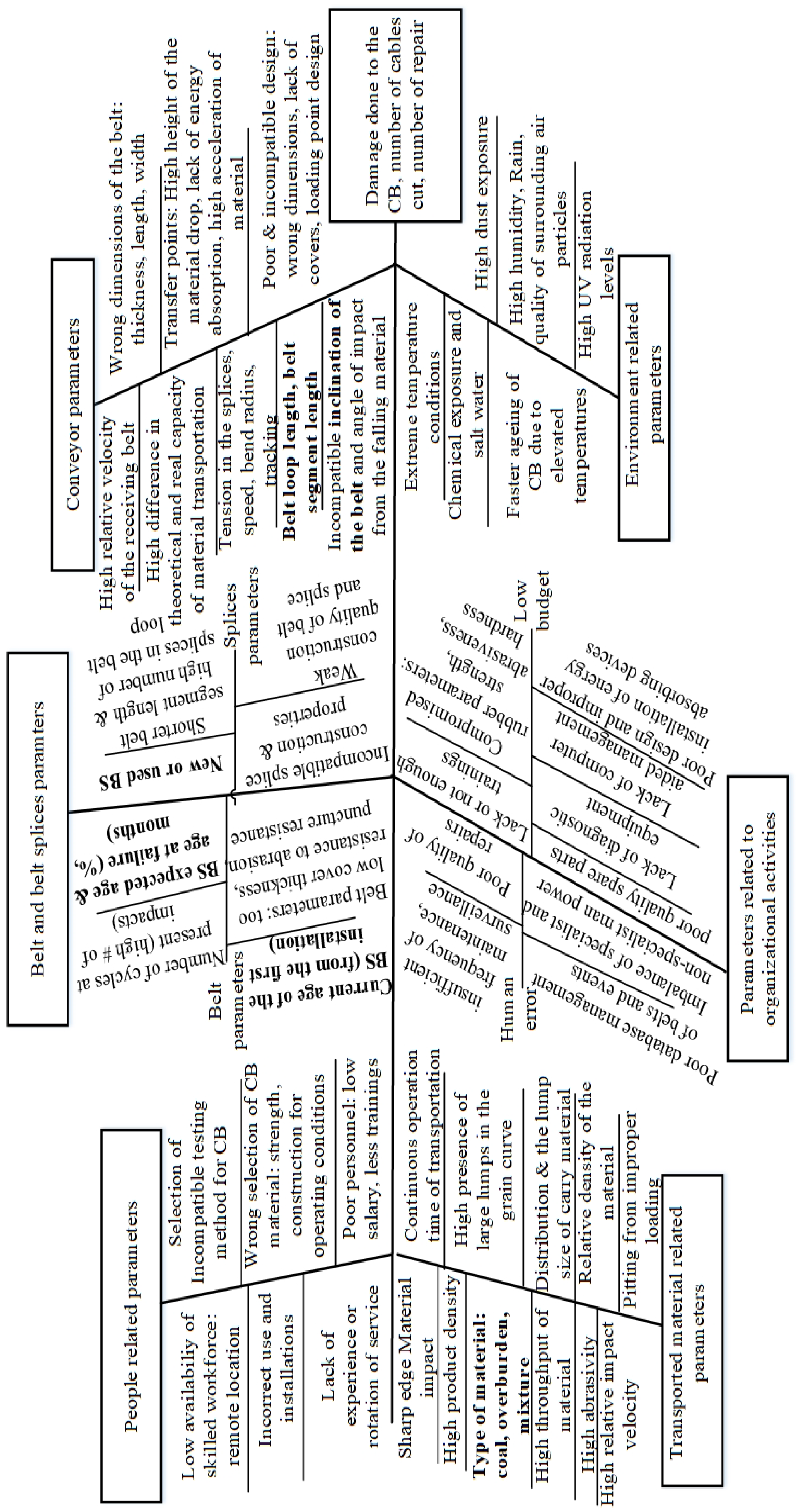
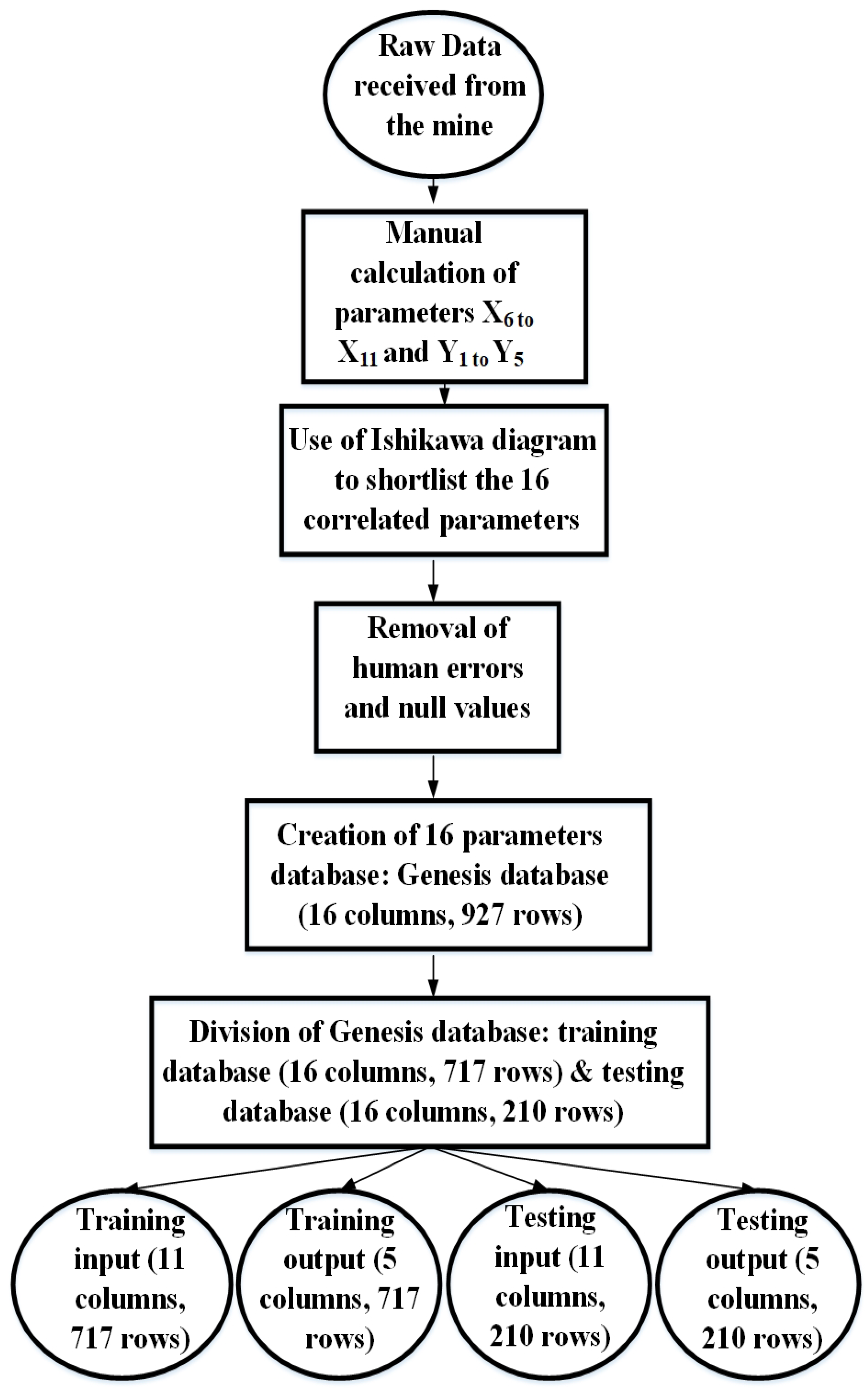
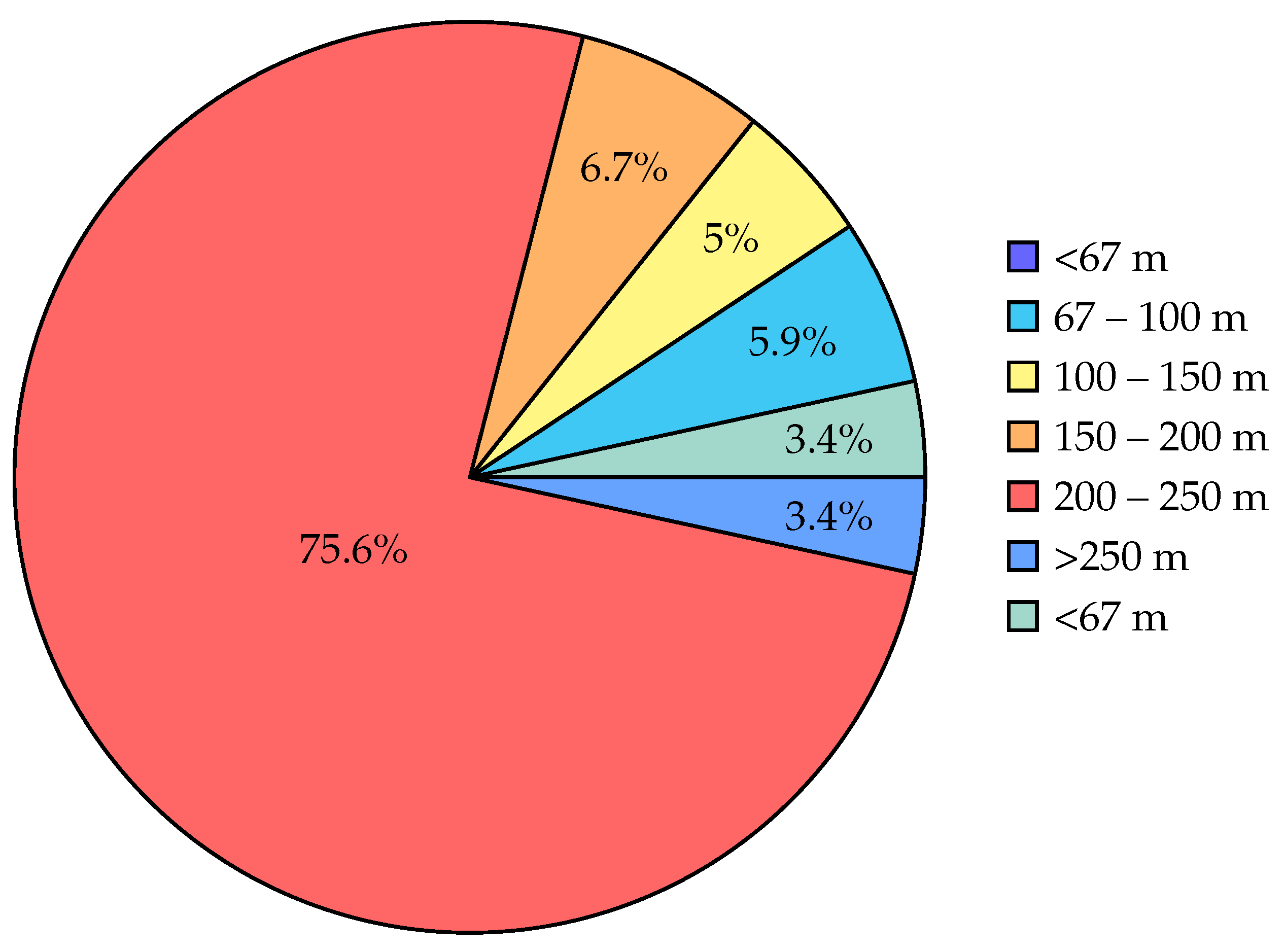
2.1. Datasets with Factors Influencing CB Damage and Operational Flowchart of the Study
- Whether the BS is new or moved.
- Belt position: whether it is flat or inclined.
- Material being carried: coal, overburden, or a mixture of coal and overburden.
- Age of the BS compared to its initial expectancy.
- Total length of the BL and the total number of BSs within it.
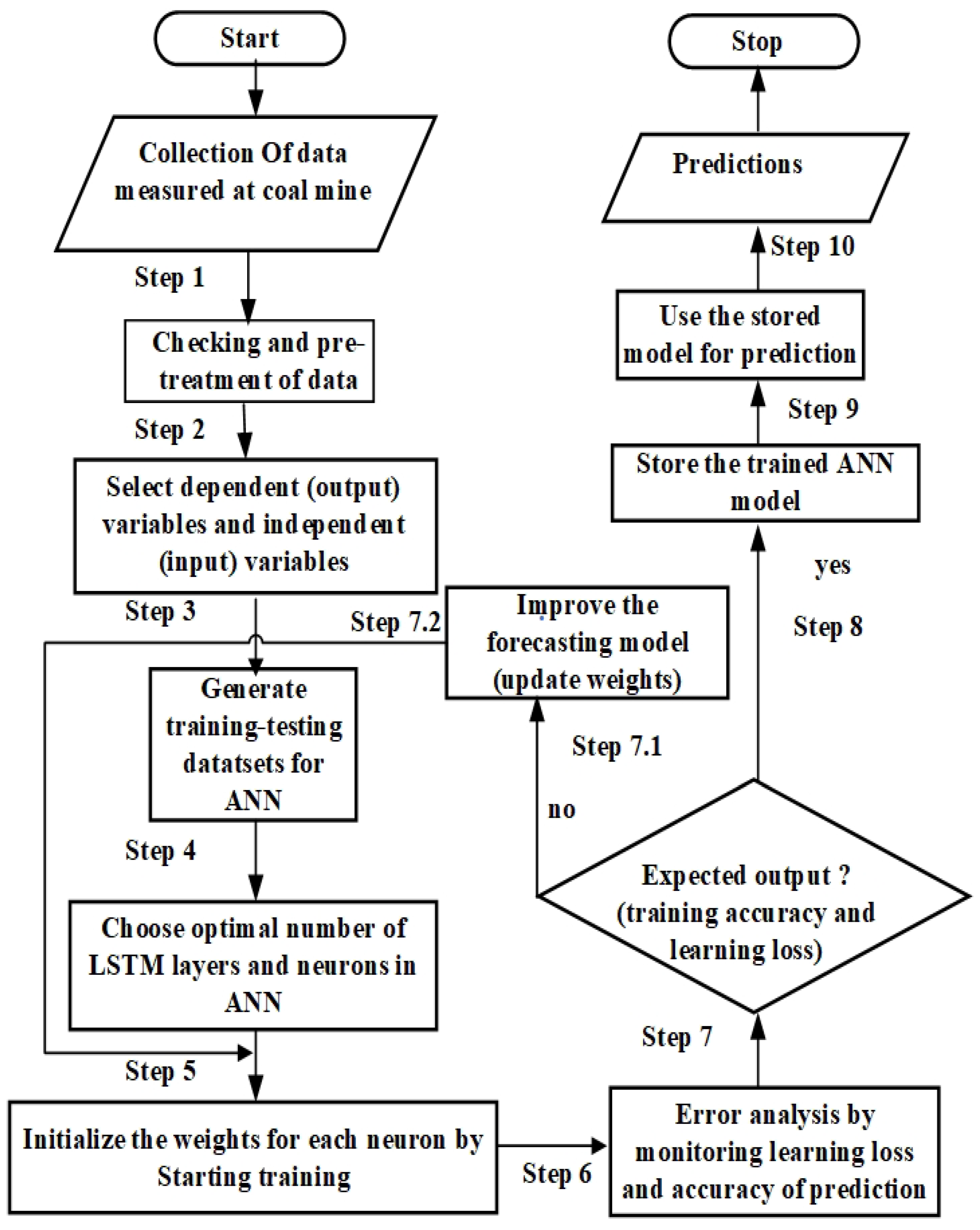
2.2. Artificial Neural Network
- Structure of Artificial Neural Networks
- (a)
- Neurons (Nodes):
- Neurons are the fundamental processing units of an ANN. Each neuron receives inputs, processes them, and generates an output.
- A neuron combines the input data with a set of weights, adds a bias, and passes the result through an activation function to produce the final output.
- (b)
- Layers:
- Input Layer: This is the first layer of the network, where the input data are fed into the system. Each node in this layer represents a distinct feature of the input data.
- Hidden Layers: Situated between the input and output layers, these layers perform the main computations. Each hidden layer contains multiple neurons, and the network’s depth is determined by the number of hidden layers.
- Output Layer: This is the layer that generates the final output of the network. The number of nodes in this layer corresponds to the number of desired output classes or values.
- (c)
- Weights and Biases:
- Weights: Parameters within the network that transform input data within neurons. Each connection between neurons has an associated weight, determining the strength and direction of the input signal.
- Biases: Values added to the weighted sum of inputs before passing through the activation function. Biases enable the activation function to shift left or right, which is crucial for learning complex patterns.
- (d)
- Activation Functions:
- Activation functions determine whether a neuron should be activated, introducing non-linearity into the network and enabling it to learn more complex patterns.
- Common activation functions include:
- −
- Sigmoid: Produces outputs between 0 and 1, useful for probability-based outputs.
- −
- Tanh (Hyperbolic Tangent): Outputs range from —1 to 1, centered around zero, making it beneficial for zero-centered data.
- −
- ReLU (Rectified Linear Unit): Outputs the input directly if it is positive; otherwise, it outputs zero. It helps mitigate the vanishing gradient problem.
- How ANNs Work
- (a)
- Forward Propagation:
- This involves passing the input data through the network to obtain the output.
- In each layer, a neuron computes a weighted sum of its inputs, adds a bias, and applies an activation function to generate an output.
- This process continues from the input layer, through the hidden layers, to the output layer, where the final prediction or classification is generated.
- (b)
- Learning (Training):
- Training an ANN involves adjusting its weights and biases to minimize the error between its predictions and the actual target values.
- A common approach to training involves supervised learning, where the network is trained on a labeled dataset. Each example in the dataset consists of an input and its corresponding correct output.
- (c)
- Back-propagation:
- Back-propagation is a fundamental algorithm for training ANNs. It functions by propagating the error backward from the output layer to the input layer, adjusting the weights and biases to minimize the error.
- The process involves:
- −
- Calculating the error at the output layer.
- −
- Using the derivative of the activation function to determine the gradient of the error with respect to each weight.
- −
- Adjusting the weights and biases in the direction that reduces the error, typically using an optimization algorithm like gradient descent.
- Types of Neural Networks
- (a)
- Feedforward Neural Networks:
- The simplest type of ANN where connections between nodes do not form cycles.
- Information moves in one direction—from input nodes, through hidden nodes (if any), to output nodes.
- (b)
- Convolutional Neural Networks (CNNs):
- Primarily used for image and video recognition.
- They use convolutional layers to automatically and adaptively learn spatial hierarchies of features from input images.
- (c)
- Recurrent Neural Networks (RNNs):
- Designed to recognize sequences and patterns in sequential data.
- They have connections that form directed cycles, allowing information to persist across steps.
- (d)
- Generative Adversarial Networks (GANs):
- Consist of two neural networks, a generator and a discriminator, that compete against each other.
- Used for generating new, synthetic instances of data that can pass for real data.
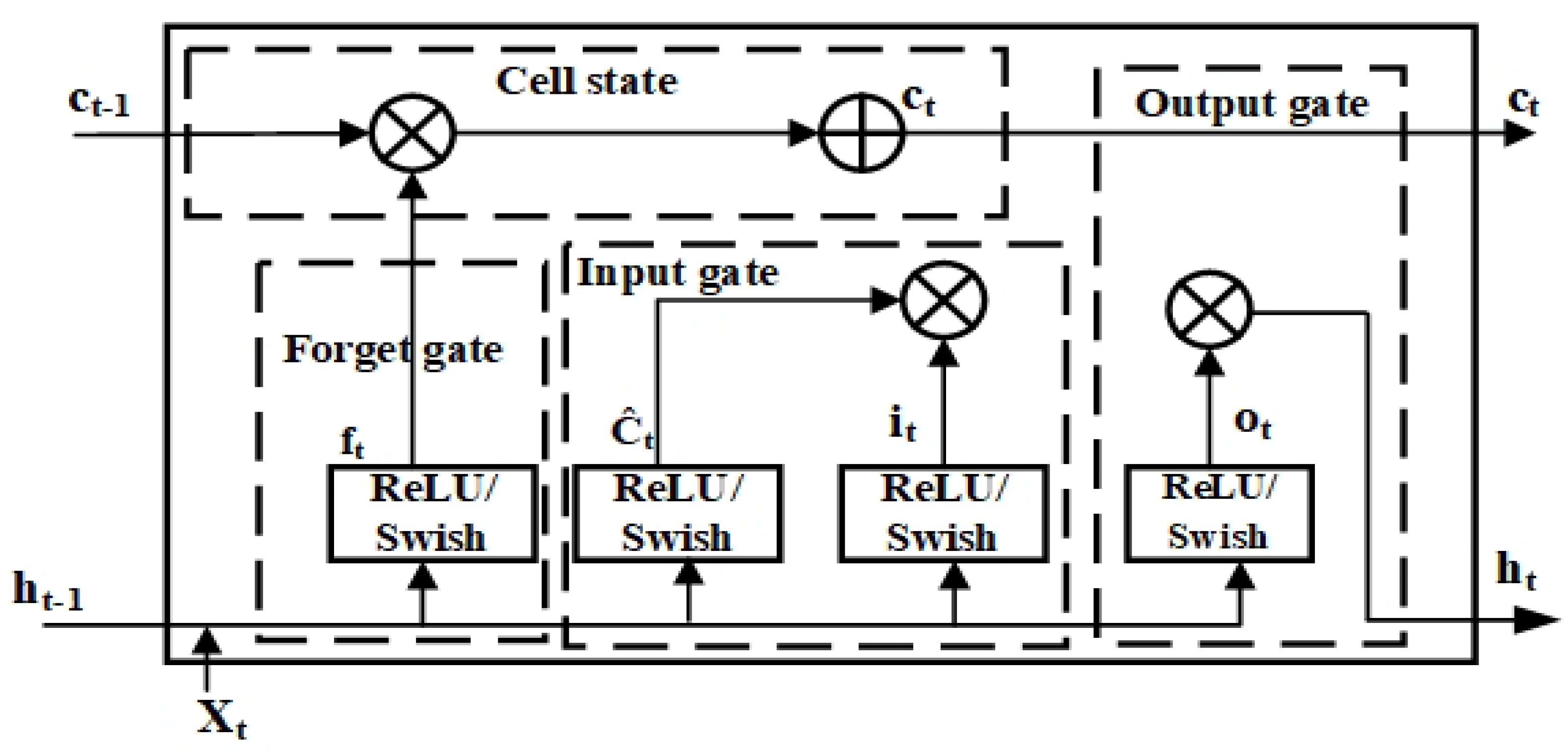
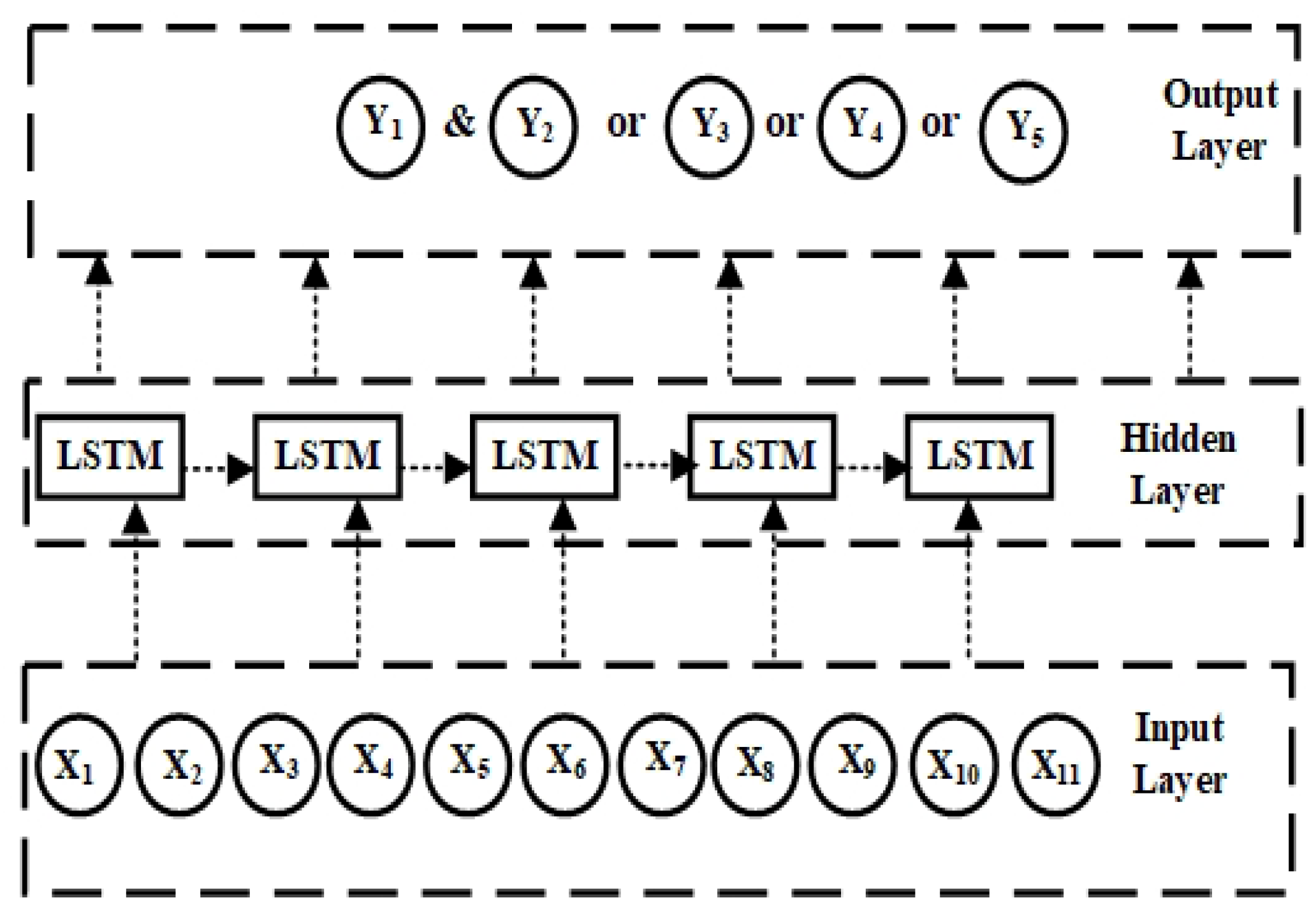
2.3. Long Short-Term Memory (LSTM) Model
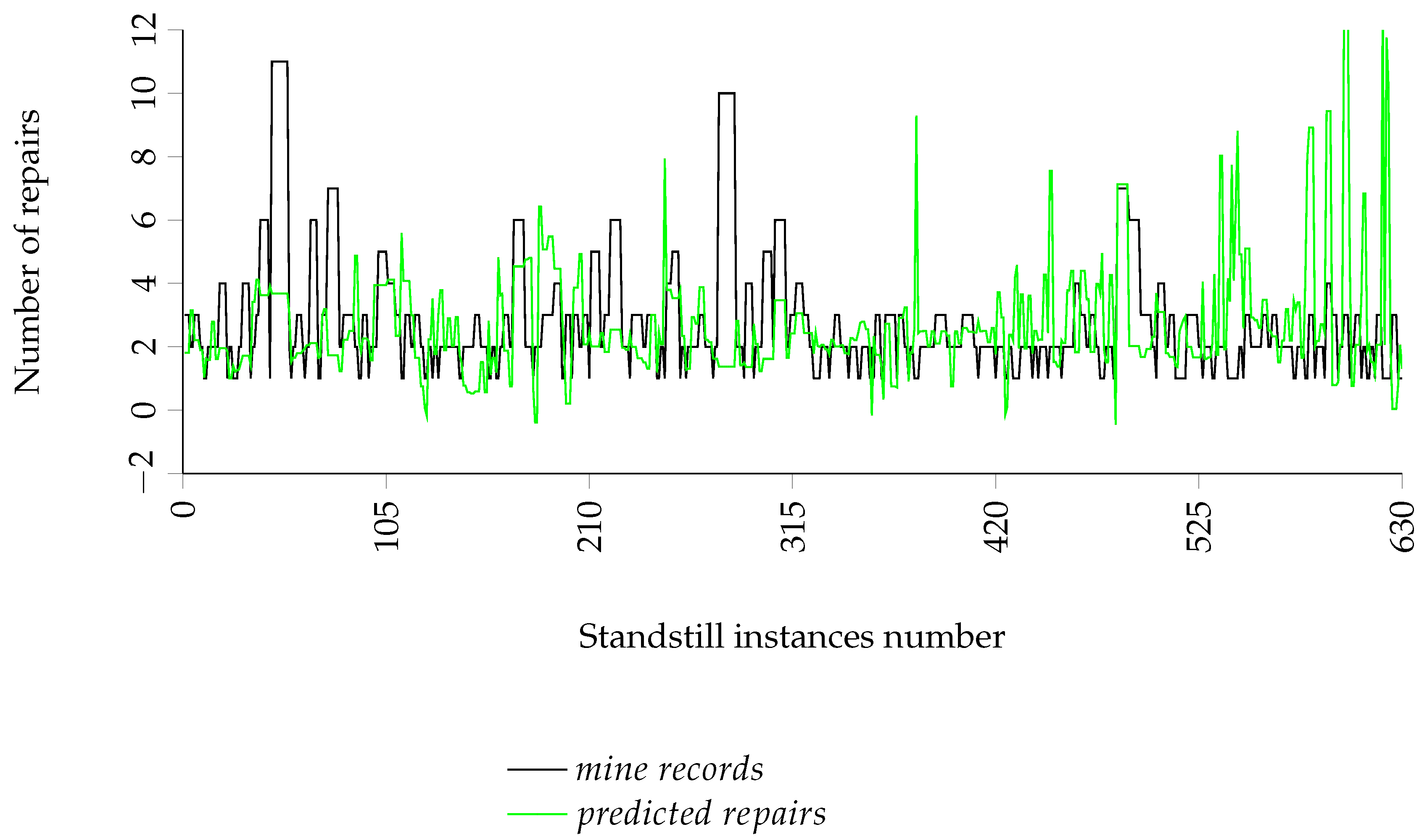
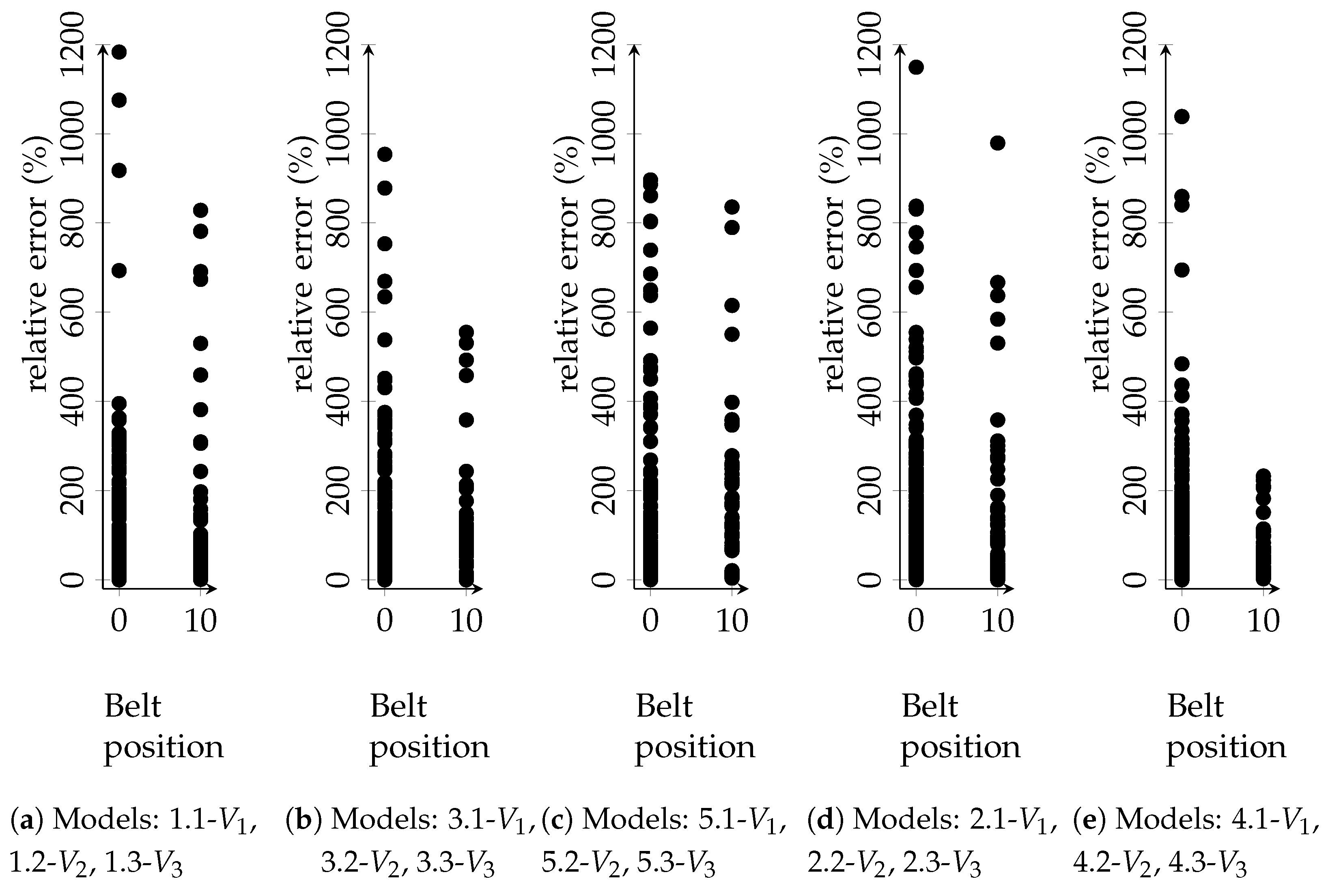
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| BL | Belt loop |
| BS | Belt segment |
| CB | Conveyor belt |
| CBS | Conveyor belt system |
| Previous time step | |
| Value generated by the tanh function | |
| Cell state information | |
| Forget gate at t | |
| Hidden state | |
| Previous hidden state | |
| HL | Hidden layer |
| Input gate at t | |
| IL | Input layer |
| Km | Kilometer |
| LSTM | Long short-term memory |
| m | meters |
| MSE | Mean squared error |
| OL | Output layer |
| Output gate state | |
| ReLU | Rectified linear unit |
| RNN | Recurrent neural network |
| SGD | Stochastic gradient descent |
| t | Time step |
| Variation 1 | |
| Variation 2 | |
| Variation 3 | |
| Input at the particular time |
References
- Koivisto, K. Conveyor Engineering; BoD-Books on Demand: Helsinki, Finland, 2018. [Google Scholar]
- Skocir, T. Mechanical Conveyors: Selection and Operation; Routledge: London, UK, 2018. [Google Scholar]
- Song, X.; Yu, X.; Zhou, C.; Xu, B.; Chen, L.; Yagoub, A.E.A.; Emeka, O.C.; Wahia, H. Conveyor belt catalytic infrared as a novel apparatus for blanching processing applied to sweet potatoes in the industrial scale. LWT 2021, 149, 111827. [Google Scholar] [CrossRef]
- Thapa, K.N.K.; Kalaivani, S.; Vanaja, S.; Sheela, J.J.J.; Deepika, Y. Differential Amplifier Based Speed Monitoring Circuit for Airport and Production Industry. In Proceedings of the 2021 Fifth International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud)(I-SMAC), Palladam, India, 11–13 November 2021; pp. 1–4. [Google Scholar]
- Wijaya, E.O.; Setyadi, A.; Rimawan, E. Minimize Conveyor Belt Damage in Coal-Fired Power Plants Using SEM-PLS and FMEA Methods. Nveo-Nat. Volatiles Essent. Oils J. NVEO 2021, 8, 1283–1289. [Google Scholar]
- Rosita, N.D. Coal Transport Through The Conveyor Belt: Literature Study Of Process And Supporting Factors. J. Sains Teknol. Transp. Marit. 2023, 5, 44–49. [Google Scholar] [CrossRef]
- Kold, J.; Silverman, C. Conveyors used in the food industry. In Handbook of Hygiene Control in the Food Industry; Elsevier: Amsterdam, The Netherlands, 2016; pp. 367–382. [Google Scholar]
- Chen, J.; Lau, S.K.; Chen, L.; Wang, S.; Subbiah, J. Modeling radio frequency heating of food moving on a conveyor belt. Food Bioprod. Process. 2017, 102, 307–319. [Google Scholar] [CrossRef]
- Rashid, S.; Bashir, O.; Majid, I. Different mechanical conveyors in food processing. In Transporting Operations of Food Materials within Food Factories; Elsevier: Amsterdam, The Netherlands, 2023; pp. 253–263. [Google Scholar]
- Kumar, N. Fundamentals of conveyors. In Transporting Operations of Food Materials within Food Factories; Elsevier: Amsterdam, The Netherlands, 2023; pp. 221–251. [Google Scholar]
- Żur, T.; Hardygóra, M. Belt Conveyors in Mining; Śląsk Publishers: Katowice, Poland, 1979. [Google Scholar]
- Jurdziak, L.; Blazej, R.; Bajda, M. Conveyor Belt 4.0. In Intelligent Systems in Production Engineering and Maintenance; Springer: Cham, Switzerland, 2019; pp. 645–654. [Google Scholar]
- Rao, D.S. The Belt Conveyor: A Concise Basic Course; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Zrnić, N.; Đorđević, M.; Gašić, V. Historical background and evolution of belt conveyors. Found. Sci. 2022, 29, 225–255. [Google Scholar] [CrossRef]
- Zrnić, N.; Đorđević, M.; Gašić, V. History of belt conveyors until the end of the 19th century. In International Symposium on History of Machines and Mechanisms; Springer: Cham, Switzerland, 2022; pp. 210–223. [Google Scholar]
- Solomon, M.D.; Heineken, W.; Scheffler, M.; Birth, T. Energy Conveyor Belt—A Detailed Analysis of a New Type of Hydrokinetic Device. Energies 2023, 16, 2188. [Google Scholar] [CrossRef]
- Chen, X.; Kong, Y.; Wang, M.; Huang, X.; Huang, Y.; Lv, Y.; Li, G. Wear and aging behavior of vulcanized natural rubber nanocomposites under high-speed and high-load sliding wear conditions. Wear 2022, 498–499, 204341. [Google Scholar] [CrossRef]
- Andrejiova, M.; Grincova, A.; Marasova, D. Measurement and simulation of impact wear damage to industrial conveyor belts. Wear 2016, 368–369, 400–407. [Google Scholar] [CrossRef]
- Nins, B.; Penagos, J.J.; Moreira, L.; Münch, D.; Falqueto, P.; Viáfara, C.C.; da Costa, A.R. Abrasiveness of iron ores: Analysis of service-worn conveyor belts and laboratory Dry Sand/Rubber Wheel tests. Wear 2022, 506, 204439. [Google Scholar] [CrossRef]
- Andrejiova, M.; Grincova, A. Classification of impact damage on a rubber-textile conveyor belt using Naïve-Bayes methodology. Wear 2018, 414, 59–67. [Google Scholar] [CrossRef]
- Marasova, D.; Andrejiova, M.; Grincova, A. Dynamic Model of Impact Energy Absorption by a Conveyor Belt in Interaction with the Support System. Energies 2022, 15, 64. [Google Scholar] [CrossRef]
- Hrabovsky, L.; Fries, J. Transport Performance of a Steeply Situated Belt Conveyor. Energies 2021, 14, 7984. [Google Scholar] [CrossRef]
- Doroszuk, B.; Krol, R.; Wajs, J. Simple Design Solution for Harsh Operating Conditions: Redesign of Conveyor Transfer Station with Reverse Engineering and DEM Simulations. Energies 2021, 14, 4008. [Google Scholar] [CrossRef]
- Bindzár, P. Impact cradle–the most critical place regarding to failure of conveyors belt. In Proceedings of the Development of New Technologies and Equipment for Mine Haulage and Hoisting, 5th International Symposium on Mine Haulage and Hoisting, Beograd–Vrdnik, Belgrade, Serbia, 25–27 September 2002; Volume 25, p. 27. [Google Scholar]
- Marasová, D. Mathematical and Experimental Support for Belt Conveyors. In Ostrava: Vysoká Škola Báňská—Technická Univerzita Ostrava, Czech Republic 76 s. : il.; 2013. Available online: https://katalog.vsb.cz/records/4f0ad9dc-312e-487c-b3c6-ec743f33d980 (accessed on 19 January 2023).
- Gharahasanlou, A.N.; Mokhtarei, A.; Khodayarei, A.; Ataei, M. Fault tree analysis of failure cause of crushing plant and mixing bed hall at Khoy cement factory in Iran. Case Stud. Eng. Fail. Anal. 2014, 2, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Huang, H.; Jiao, R.; Pei, J.; Xu, Y.; Wang, Y. The study of wear particle emissions of soft rubber on rolling contact under braking conditions. Wear 2022, 506, 204431. [Google Scholar] [CrossRef]
- Kirjanów-Błażej, A.; Jurdziak, L.; Błażej, R.; Rzeszowska, A. Calibration procedure for ultrasonic sensors for precise thickness measurement. Measurement 2023, 214, 112744. [Google Scholar] [CrossRef]
- Fedorko, G.; Molnar, V.; Marasova, D.; Grincova, A.; Dovica, M.; Zivcak, J.; Toth, T.; Husakova, N. Failure analysis of belt conveyor damage caused by the falling material. Part I: Experimental measurements and regression models. Eng. Fail. Anal. 2014, 36, 30–38. [Google Scholar] [CrossRef]
- Cerny, J.; Kyas, K.; Krumal, M.; Manas, D.; Manas, M.; Stanek, M. WEAR PROCESS OF TIRES. In Annals of DAAAM & Proceedings; DAAAM International: Vienna, Austria, 2010; pp. 1189–1190. [Google Scholar]
- Szrek, J.; Jakubiak, J.; Zimroz, R. A Mobile Robot-Based System for Automatic Inspection of Belt Conveyors in Mining Industry. Energies 2022, 15, 327. [Google Scholar] [CrossRef]
- Bajda, M.; Błażej, R.; Jurdziak, L. Analysis of changes in the length of belt sections and the number of splices in the belt loops on conveyors in an underground mine. Eng. Fail. Anal. 2019, 101, 436–446. [Google Scholar] [CrossRef]
- Bajda, M.; Błażej, R.; Jurdziak, L.; Hardygóra, M. Impact of differences in durability of vulcanized and adhesive joints on the operating costs of conveyor belts in underground mines. In Zeszyty Naukowe Instytutu Gospodarki Surowcami Mineralnymi Polskiej Akademii Nauk; Instytut Gospodarki Surowcami Mineralnymi i Energią PAN: Krakow, Poland, 2017; pp. 71–88. [Google Scholar]
- Wozniak, D.; Hardygóra, M. Aspects of Selecting Appropriate Conveyor Belt Strength. Energies 2021, 14, 6018. [Google Scholar] [CrossRef]
- Jurdziak, L.; Bajda, M.; Blazej, R. Estimation of Purchase and Replacement Costs of Conveyor Belts and their Splices in an Underground Mine Based on their Durability. Iop Conf. Ser. Earth Environ. Sci. 2019, 221, 012099. [Google Scholar] [CrossRef]
- Bugaric, U.; Tanasijevic, M.; Polovina, D.; Ignjatovic, D.; Jovancic, P. Lost production costs of the overburden excavation system caused by rubber belt failure; [Koszty utraconej produkcji wywołane uszkodzeniem gumowej taśmy transportowej w układzie maszynowym do zdejmowania nadkładu]. Eksploat. Niezawodn. 2012, 14, 333–341. [Google Scholar]
- Ilic, D. Development of design criteria for reducing wear in iron ore transfer chutes. Wear 2019, 434-435, 202986. [Google Scholar] [CrossRef]
- Maintenance of Belt Conveyor Systems in Poland—An Overview. Available online: https://www.wipro.com/natural-resources/predictive-failure-model-for-conveyor-belt-systems/ (accessed on 19 January 2023).
- Bajda, M.; Hardygóra, M.; Marasová, D. Energy Efficiency of Conveyor Belts in Raw Materials Industry. Energies 2022, 15, 3080. [Google Scholar] [CrossRef]
- Kawalec, W.; Król, R. Generating of electric energy by a declined overburden conveyor in a continuous surface mine. Energies 2021, 14, 4030. [Google Scholar] [CrossRef]
- Blazej, R.; Jurdziak, L. Condition-based conveyor belt replacement strategy in lignite mines with random belt deterioration. IOP Conf. Ser. Earth Environ. Sci. 2017, 95, 042051. [Google Scholar] [CrossRef]
- van der Laan, B.Z. System reliability analysis of belt conveyor. In Transportation Engineering; Delft University of Technology: Delft, The Netherlands, 2016. [Google Scholar]
- Fedorko, G.; Molnár, V.; Michalik, P.; Dovica, M.; Kelemenová, T.; Tóth, T. Failure analysis of conveyor belt samples under tensile load. J. Ind. Text. 2019, 48, 1364–1383. [Google Scholar] [CrossRef]
- Zimroz, R.; Król, R. Failure analysis of belt conveyor systems for condition monitoring purposes. Min. Sci. 2009, 128, 255. [Google Scholar]
- Bajda, M.; Hardygóra, M. Laboratory tests of operational durability and energy-efficiency of conveyor belts. IOP Conf. Ser. Earth Environ. Sci. 2019, 261, 012002. [Google Scholar] [CrossRef]
- Zimroz, R.; Hardygóra, M.; Blazej, R. Maintenance of Belt Conveyor Systems in Poland—An Overview. In Proceedings of the 12th International Symposium Continuous Surface Mining-Aachen 2014; Springer International Publishing: Cham, Switzerland, 2015; pp. 21–30. [Google Scholar]
- Belchatów Mine, Poland. Available online: https://euracoal.eu/info/country-profiles/poland (accessed on 19 January 2023).
- Jurdziak, L.; Błażej, R.; Burduk, A.; Bajda, M.; Kirjanów-Błażej, A.; Kozłowski, T.; Olchówka, D. Optimization of the operating costs of conveyor belts in a mine in various strategies of their replacement and diagnostics. Transp. Przem. Masz. Rob. 2020, 4, 50. [Google Scholar]
- Parmar, P.; Burduk, A.; Jurdziak, L. Ishikawa Diagram Indicating Potential Causes for Damage Occurring to the Rubber Conveyor Belt Operating at Coal Mining Site. In Proceedings of the International Conference on Intelligent Systems in Production Engineering and Maintenance, Wrocław, Poland, 13–15 September 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 704–713. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Medsker, L.; Jain, L.C. Recurrent Neural Networks: Design and Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness-Knowl.-Based Syst. 1998, 06, 107–116. [Google Scholar] [CrossRef]
- Olchówka, D.; Blażej, R.; Jurdziak, L. Selection of measurement parameters using the DiagBelt magnetic system on the test conveyor. J. Phys. Conf. Ser. 2022, 2198, 012042. [Google Scholar] [CrossRef]
- Kirjanów-Błażej, A.; Jurdziak, L.; Burduk, R.; Błażej, R. Forecast of the remaining lifetime of steel cord conveyor belts based on regression methods in damage analysis identified by subsequent DiagBelt scans. Eng. Fail. Anal. 2019, 100, 119–126. [Google Scholar] [CrossRef]
- Błażej, R.; Jurdziak, L.; Kozłowski, T.; Kirjanów, A. The use of magnetic sensors in monitoring the condition of the core in steel cord conveyor belts–Tests of the measuring probe and the design of the DiagBelt system. Measurement 2018, 123, 48–53. [Google Scholar] [CrossRef]
- Rzeszowska, A.; Jurdziak, L.; Błażej, R.; Kirjanów-Błażej, A. Application of Clustering and SOM Analysis for Identification of Conveyor Belt Damage Based on Data from the Diagbelt + Magnetic System. In Advances in Production; Springer: Cham, Switzerland, 2023; pp. 461–475. [Google Scholar]



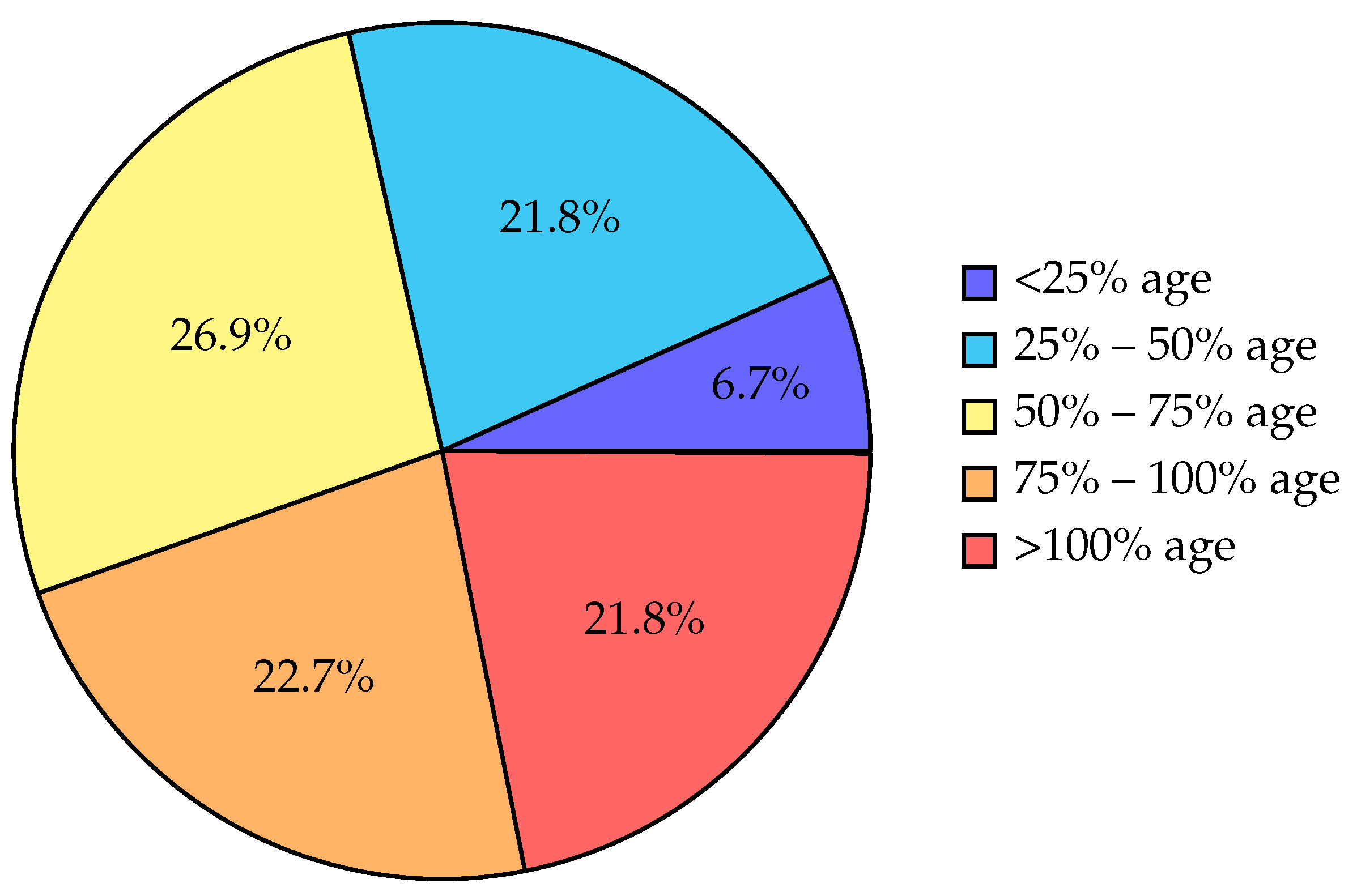

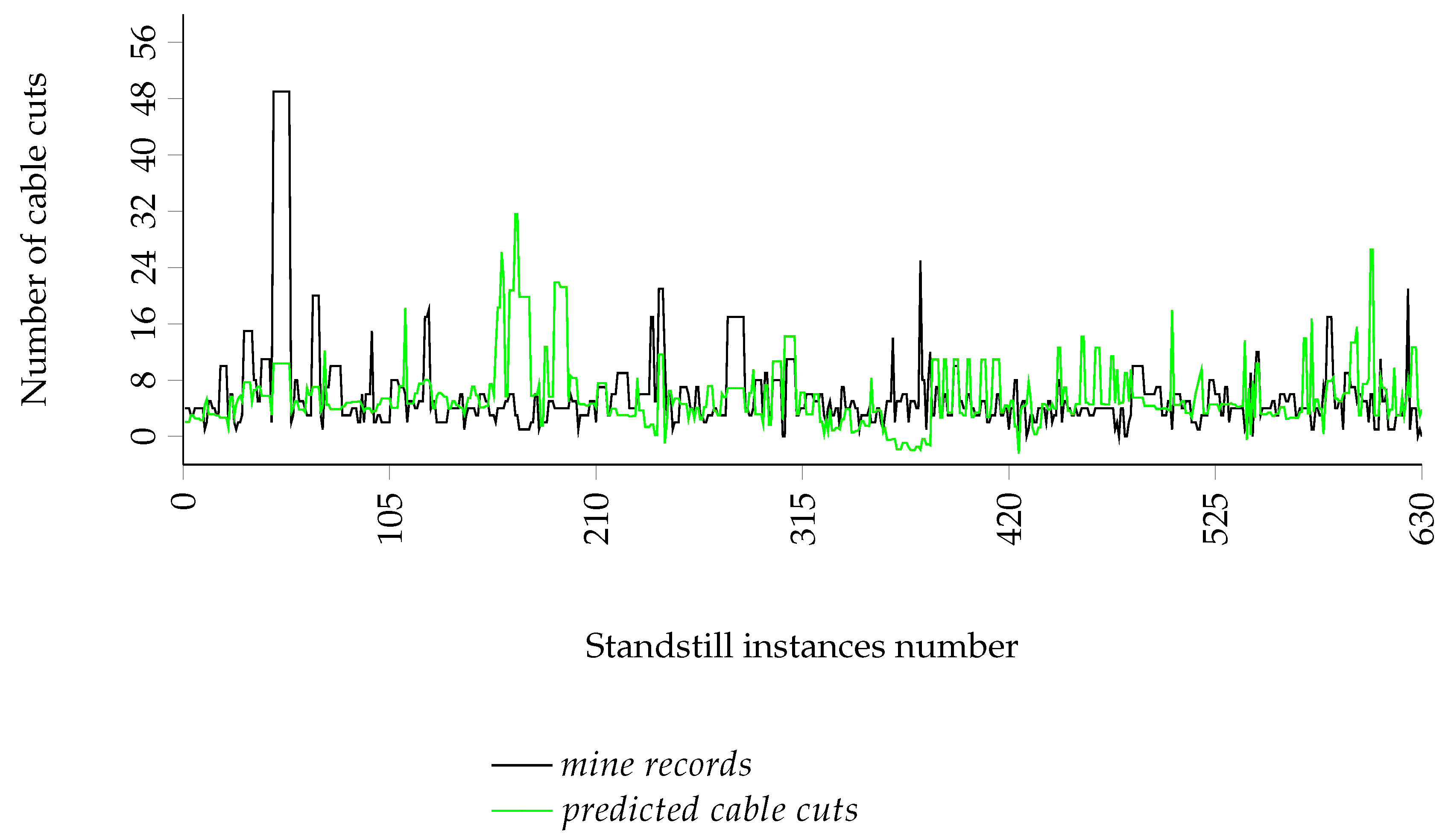
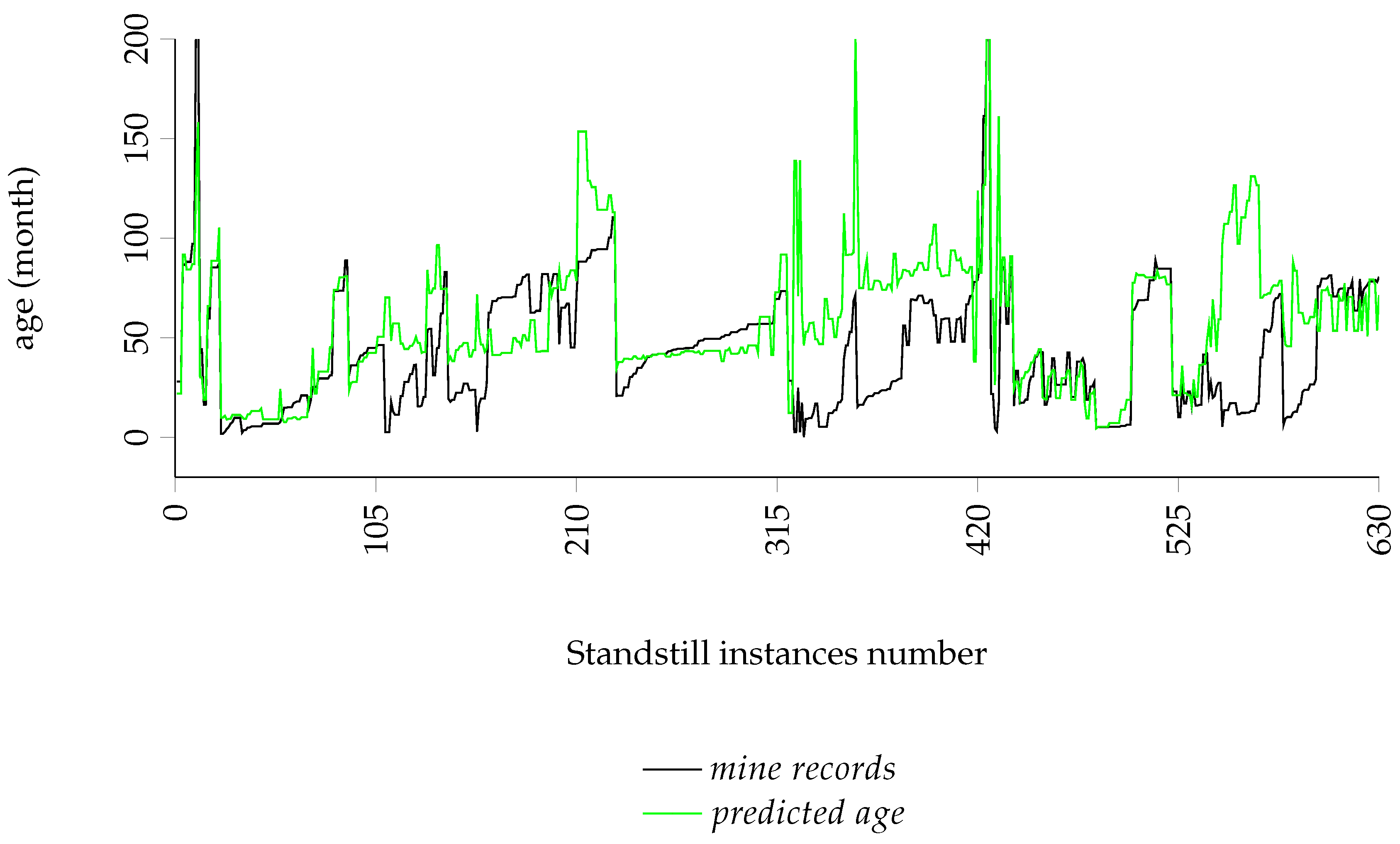

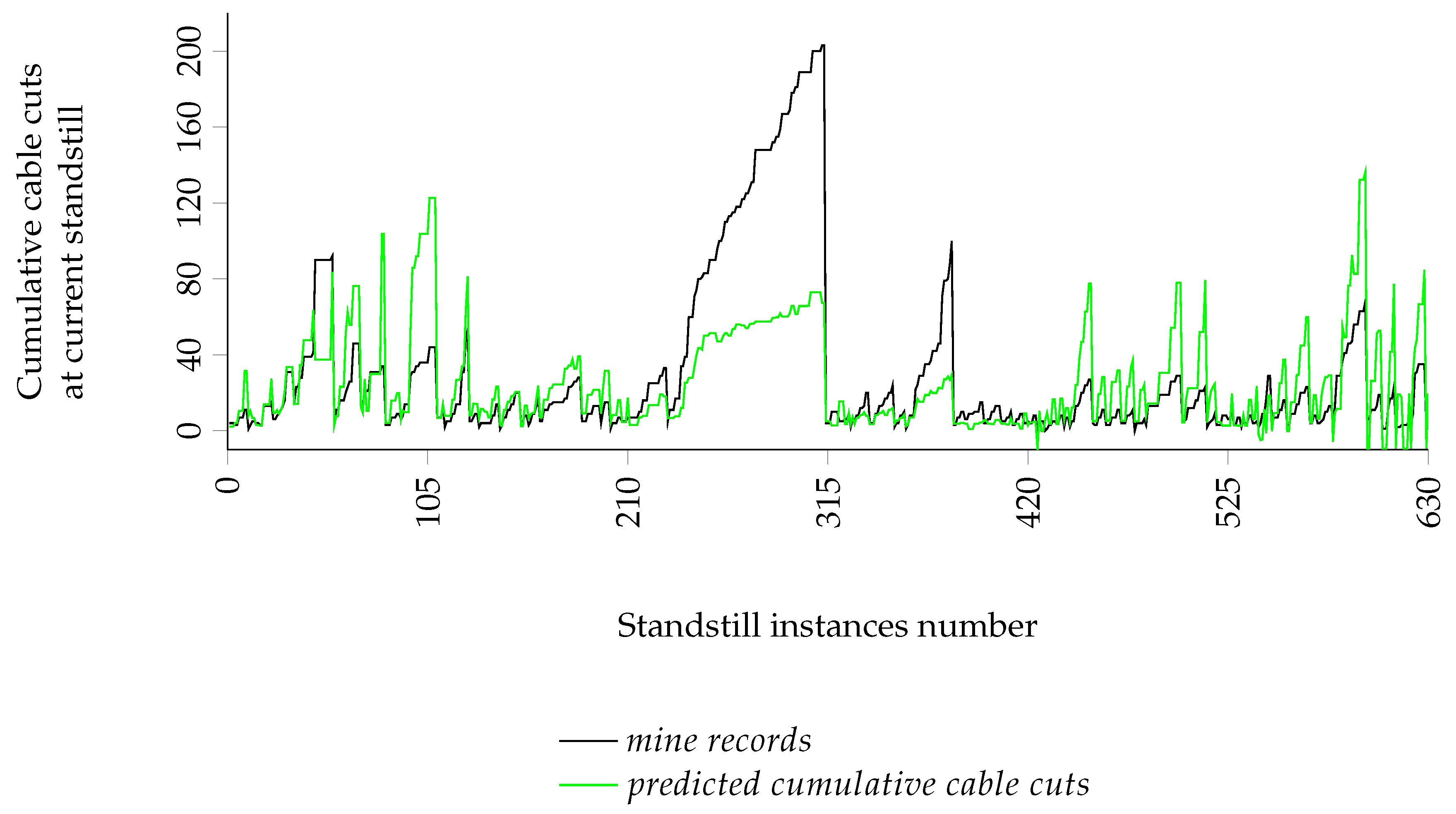
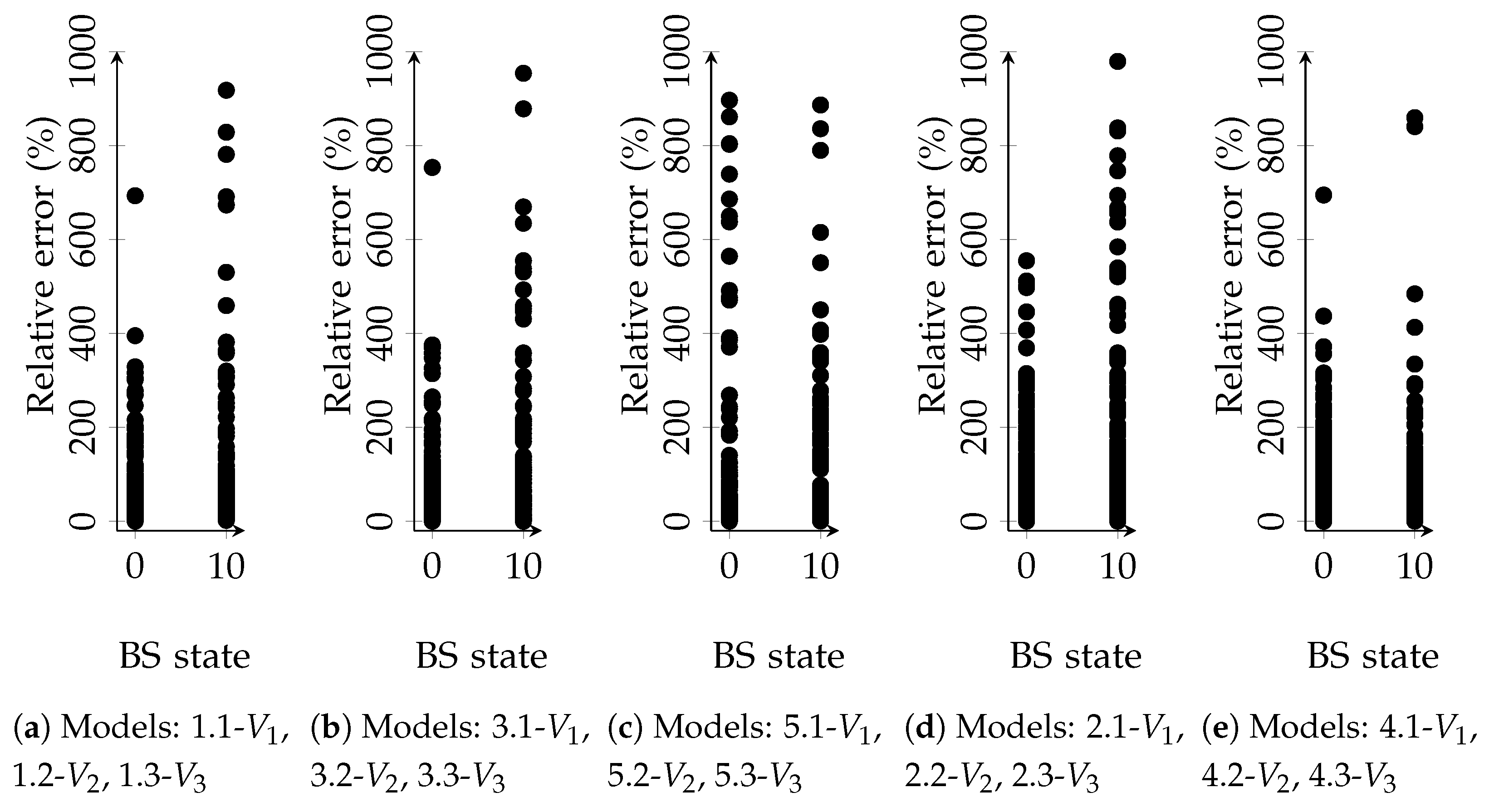



| Age at current srepair: standstill | |
| Number of small repairs at current standstill | |
| Cumulative number of small repairs at current standstill | |
| ine | Number of cable/s cut at current standstill |
| Cumulative number of cuts at current standstill |
| Belt loop length | |
| Belt segment length | |
| Transported material | |
| Inclination of the conveyor belt | |
| New or moved belt segment | |
| Completed percentage life compared to human estimation | |
| ine | Age at previous repair: standstill |
| Number of small repairs during previous standstill | |
| ine | Previous cumulative number of small repairs |
| ine | Previous number of cables cut |
| Previous cumulative number of cuts |
| Model | Input Parameters | Output Parameters |
|---|---|---|
| Model 1 | to | and |
| Model 2 | to | and |
| Model 3 | to | and |
| Model 4 | to | and |
| Model 5 | to |
| Database | Database | Database | |
|---|---|---|---|
| BL & BS used for training | 11 & 92 | 11 & 98 | 11 & 79 |
| BL & BS used for testing | 11 & 27 | 9 & 21 | 11 & 40 |
| Genesis Database | Database for Testing | Database for Testing | Database for Testing |
|---|---|---|---|
| BL1: BS1 to BS8 | BL1: BS1, BS8 | BL1: BS2 | BL1: BS3 to BS7 |
| BL2: BS9 to BS13 | BL2: BS9 to BS11 | BL2: BS12, BS13 | |
| BL3: BS14 to BS16 | BL3: BS16 | BL3: BS14, BS15 | |
| BL4: BS17 to BS33 | BL4: BS27 to BS29, BS32, BS33 | BL4: BS17 | BL4: BS19 to BS26, BS28 |
| BL5: BS35 to BS47 | BL5: BS47 | BL5: BS46 | BL5: BS34 to BS42, BS43 |
| BL6: BS48 to BS59 | BL6: BS57 | BL6: BS48 | BL6: BS50 to BS56 |
| BL7: BS60 to BS64 | BL7: BS62 | BL7: BS63, BS64 | BL7: BS60, BS61 |
| BL8: BS65 to BS74 | BL8: BS71 to BS73 | BL8: BS65, BS66 | BL8: BS67, BS68 |
| BL9: BS75 to BS83 | BL9: BS81to BS83 | BL9: BS75, BS80 | BL9: BS77 to BS78 |
| BL10: BS84 to BS92 | BL10: BS84 to BS86 BS92 | BL10: BS87 | BL10: BS88 |
| BL11: BS93 to BS119 | BL11: BS102, BS103, BS112, BS115, BS116 | BL11: BS93 to BS101, BS119 | BL11: BS107, BS109, BS111, BS113, BS114, BS117, |
| Model | Input Parameters | Output Parameters |
|---|---|---|
| Model 1.1- | to | and |
| Model 1.2- | to | and |
| Model 1.3- | to | and |
| Model 2.1- | to | and |
| Model 2.2- | to | and |
| Model 2.3- | to | and |
| Model 3.1- | to | and |
| Model 3.2- | to | and |
| Model 3.3- | to | and |
| Model 4.1- | to | and |
| Model 4.2- | to | and |
| Model 4.3- | to | and |
| Model 5.1- | to | |
| Model 5.2- | to | |
| Model 5.3- | to |
| Combi-nation | Input Layer (IL) Neurons | Neurons × Hidden Layer (HL) | Output Layer (OL) Neurons | Batch Size | Epochs | Accuracy % for Training/ Validation |
|---|---|---|---|---|---|---|
| 1 | 11 | 2 | 16 | 60 | 97/75 | |
| 2 | 11 | 2 | 16 | 60 | 97/83 | |
| 3 | 11 | 2 | 16 | 60 | 98/71 | |
| 4 | 11 | 2 | 16 | 90 | 98/77 |
| Parameters’ Status Condition | |Maximum — Minimum| | |||
|---|---|---|---|---|
| ≤200 m BS length | 24.8% | 15.2% | 10.9% | 13.9% |
| >200 m BS length | 75.2% | 84.8% | 89.1% | 13.9% |
| Transported material: coal | 10.9% | 9.6% | 8.5% | 2.4% |
| Transported material: mixture of coal and sand, rock | 51.9% | 49.5% | 52.8% | 3.3% |
| Transported material: overburden | 37.2% | 40.9% | 38.7% | 3.7% |
| Belt position: flat | 84.2% | 86.2% | 84.8% | 2% |
| Belt position: inclined | 15.8% | 13.8% | 15.2% | 2% |
| Belt condition: new | 47.2% | 84.8% | 62.4% | 37.6% |
| Belt condition: moved from another BL | 52.8% | 15.2% | 37.6% | 37.6% |
| Age at current repair months | 77.6% | 87.1% | 79% | 9.5% |
| Age at previous repair > 60 months | 22.4% | 12.9% | 21% | 9.5% |
| Parameters’ Status Condition | |Maximum — Minimum| | |||
|---|---|---|---|---|
| ≤200 m BS length | 10.3% | 13.2% | 14.4% | 4.1% |
| >200 m BS length | 89.7% | 86.8% | 85.6% | 4.1% |
| Transported material: coal | 6.8% | 7.3% | 7.5% | 0.7% |
| Transported material: mixture of coal and sand, rock | 52.8% | 53.6% | 52.6% | 1% |
| Transported material: overburden | 40.4% | 39.1% | 39.9% | 1.3% |
| Belt position: flat | 85.6% | 85.0% | 85.6% | 0.6% |
| Belt position: inclined | 14.4% | 15% | 14.4% | 0.6% |
| Belt condition: new | 52.8% | 41.9% | 48.4% | 10.9% |
| Belt condition: moved from another BL | 47.2% | 58.1% | 51.6% | 10.9% |
| Age at current repair months | 82.5% | 79.6% | 82% | 2.9% |
| Age at previous repair > 60 months | 17.5% | 20.4% | 18% | 2.9% |
| Parameters | Activation Function | Testing Dataset Version | Optimizer | Median Value of Relative Error | A | B | C |
|---|---|---|---|---|---|---|---|
| Age | ReLU | Nadam | 60 | 47 | 11 | 40 | |
| Repairs | 45 | 53 | 34 | 11 | |||
| Age | ReLU | Nadam | 27 | 65 | 9 | 25 | |
| Repairs | 29 | 71 | 21 | 7 | |||
| Age | ReLU | Nadam | 47 | 51 | 18 | 30 | |
| Repairs | 46 | 50 | 19 | 31 |
| Parameters | Activation Function | Testing Dataset Version | Optimizer | Median Value of Relative Error | A | B | C |
|---|---|---|---|---|---|---|---|
| Age | Swish | Adam | 40 | 53 | 15 | 31 | |
| Cumulative repairs | 111 | 24 | 23 | 51 | |||
| Age | Swish | Adam | 33 | 62 | 15 | 21 | |
| Cumulative repairs | 31 | 80 | 15 | 3 | |||
| Age | Swish | Adam | 55 | 48 | 17 | 34 | |
| Cumulative repairs | 131 | 22 | 19 | 57 |
| Parameters | Activation Function | Testing Dataset Version | Optimizer | Median Value of Relative Error | A | B | C |
|---|---|---|---|---|---|---|---|
| Age | Swish | Adam | 49 | 50 | 29 | 19 | |
| Cable cuts | 52 | 46 | 26 | 26 | |||
| Age | Swish | Adam | 28 | 59 | 11 | 29 | |
| Cable cuts | 56 | 49 | 28 | 22 | |||
| Age | Swish | Adam | 36 | 62 | 14 | 22 | |
| Cable cuts | 34 | 62 | 16 | 21 |
| Parameters | Activation Function | Testing Dataset Version | Optimizer | Median Value of Relative Error | A | B | C |
|---|---|---|---|---|---|---|---|
| Age | ReLU | RMSprop | 26 | 70 | 9.5 | 20 | |
| Cumulative number of cable cuts | 55 | 43 | 31 | 25 | |||
| Age | ReLU | RMSprop | 33 | 58 | 12 | 28 | |
| Cumulative number of cable cuts | 52 | 43 | 54 | 2.8 | |||
| Age | ReLU | RMSprop | 42 | 54 | 18 | 27 | |
| Cumulative number of cable cuts | 107 | 23 | 22 | 55 |
| Activation Function | Testing Dataset Version | Optimizer | Median Value of Relative Error | A | B | C |
|---|---|---|---|---|---|---|
| ReLU | Nadam | 36 | 65 | 12 | 21 | |
| ReLU | Nadam | 27 | 58 | 16 | 24 | |
| ReLU | Nadam | 22 | 66 | 6.2 | 28.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parmar, P.; Jurdziak, L.; Rzeszowska, A.; Burduk, A. Predictive Modeling of Conveyor Belt Deterioration in Coal Mines Using AI Techniques. Energies 2024, 17, 3497. https://doi.org/10.3390/en17143497
Parmar P, Jurdziak L, Rzeszowska A, Burduk A. Predictive Modeling of Conveyor Belt Deterioration in Coal Mines Using AI Techniques. Energies. 2024; 17(14):3497. https://doi.org/10.3390/en17143497
Chicago/Turabian StyleParmar, Parthkumar, Leszek Jurdziak, Aleksandra Rzeszowska, and Anna Burduk. 2024. "Predictive Modeling of Conveyor Belt Deterioration in Coal Mines Using AI Techniques" Energies 17, no. 14: 3497. https://doi.org/10.3390/en17143497
APA StyleParmar, P., Jurdziak, L., Rzeszowska, A., & Burduk, A. (2024). Predictive Modeling of Conveyor Belt Deterioration in Coal Mines Using AI Techniques. Energies, 17(14), 3497. https://doi.org/10.3390/en17143497








