A Hybrid Beat Frequency Oscillation Suppression Strategy for DC Microgrids †
Abstract
:1. Introduction
- (1)
- (2)
- It proposes a hybrid method to reduce beat frequency oscillations. A detailed investigation was conducted to study the impacts of the switching frequency channel setting and line inductor selection. The effectiveness of the method was experimentally validated.
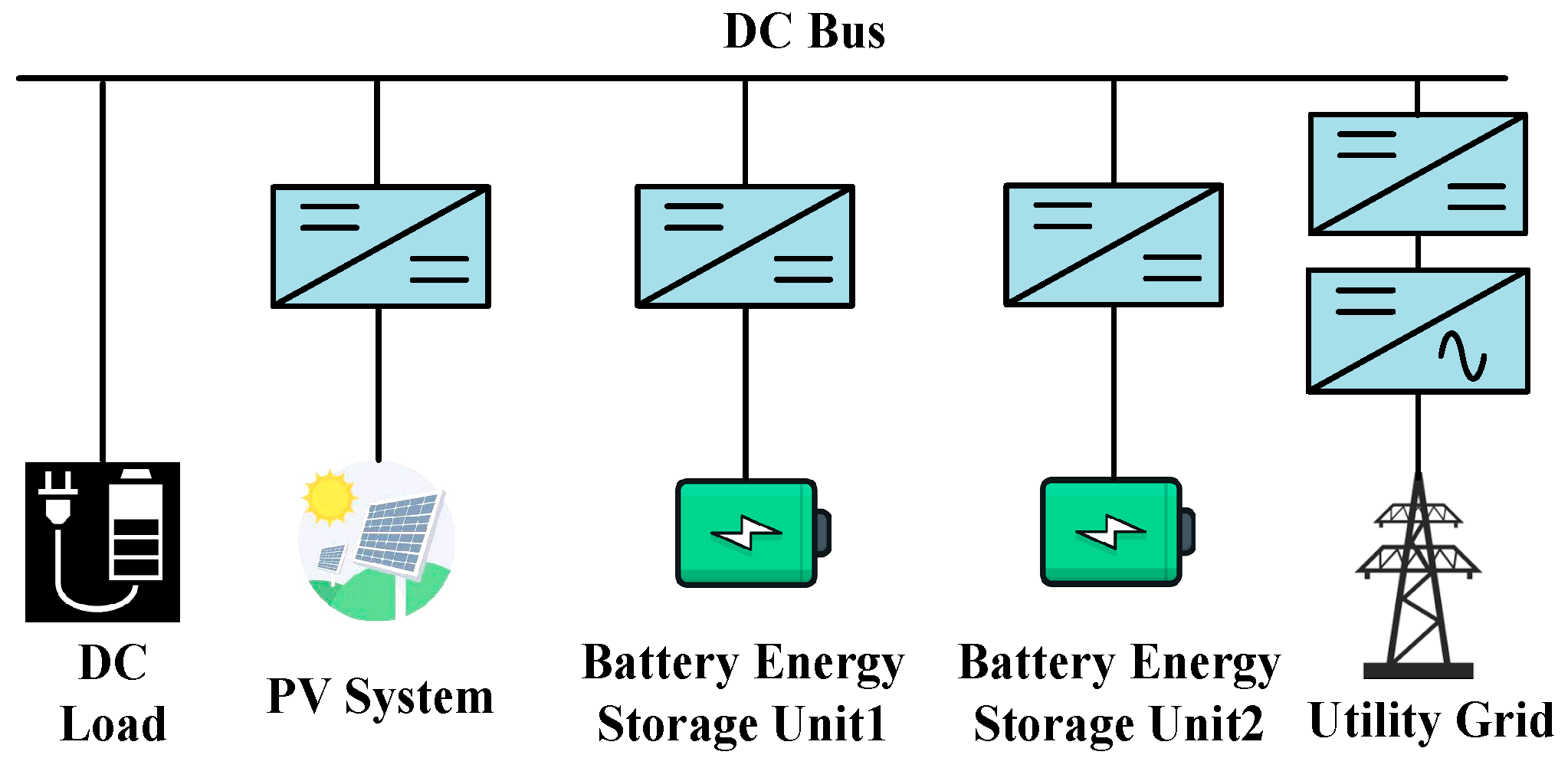
2. Beat Frequency Oscillation Analysis for Parallel Connected Boost Converters
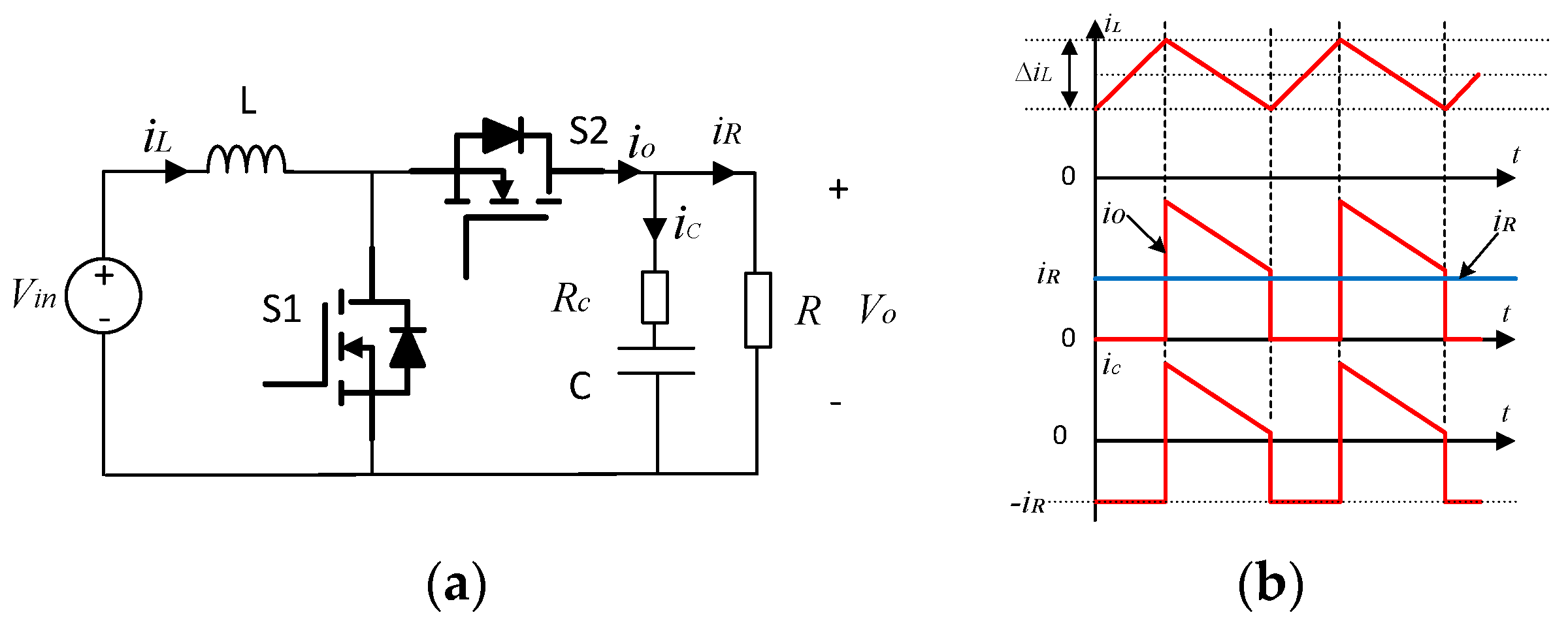
2.1. Reviewo of Buck Converters and Boost Converters Output Voltage Ripples
2.2. Closed Loop Output Impedance of Boost Converters
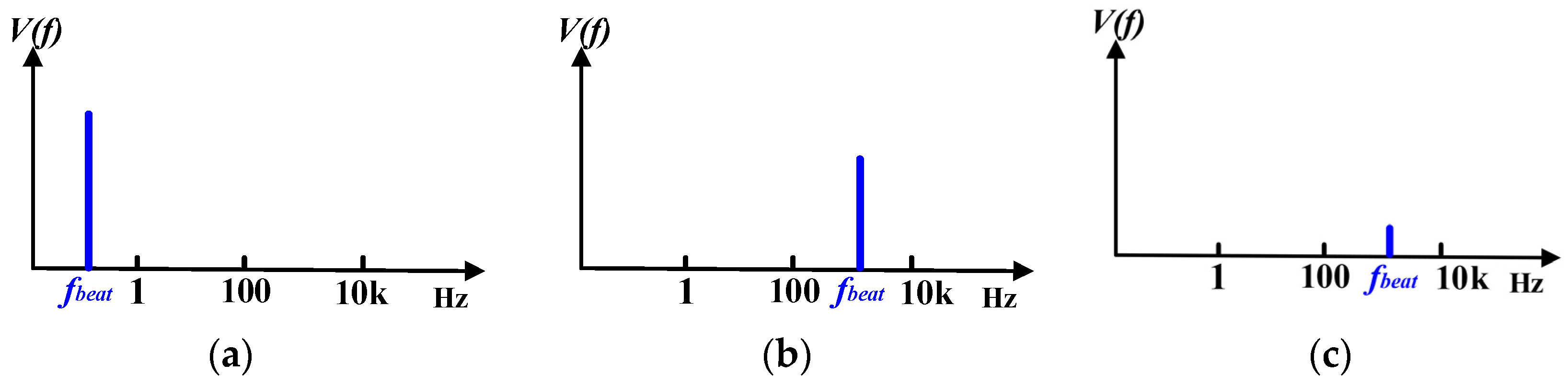
2.3. Beat Frequency Oscillation Analysis for Two Parallel-Connected Boost Converters
3. The Proposed Hybrid Method to Mitigate the Beat Frequency Oscillation
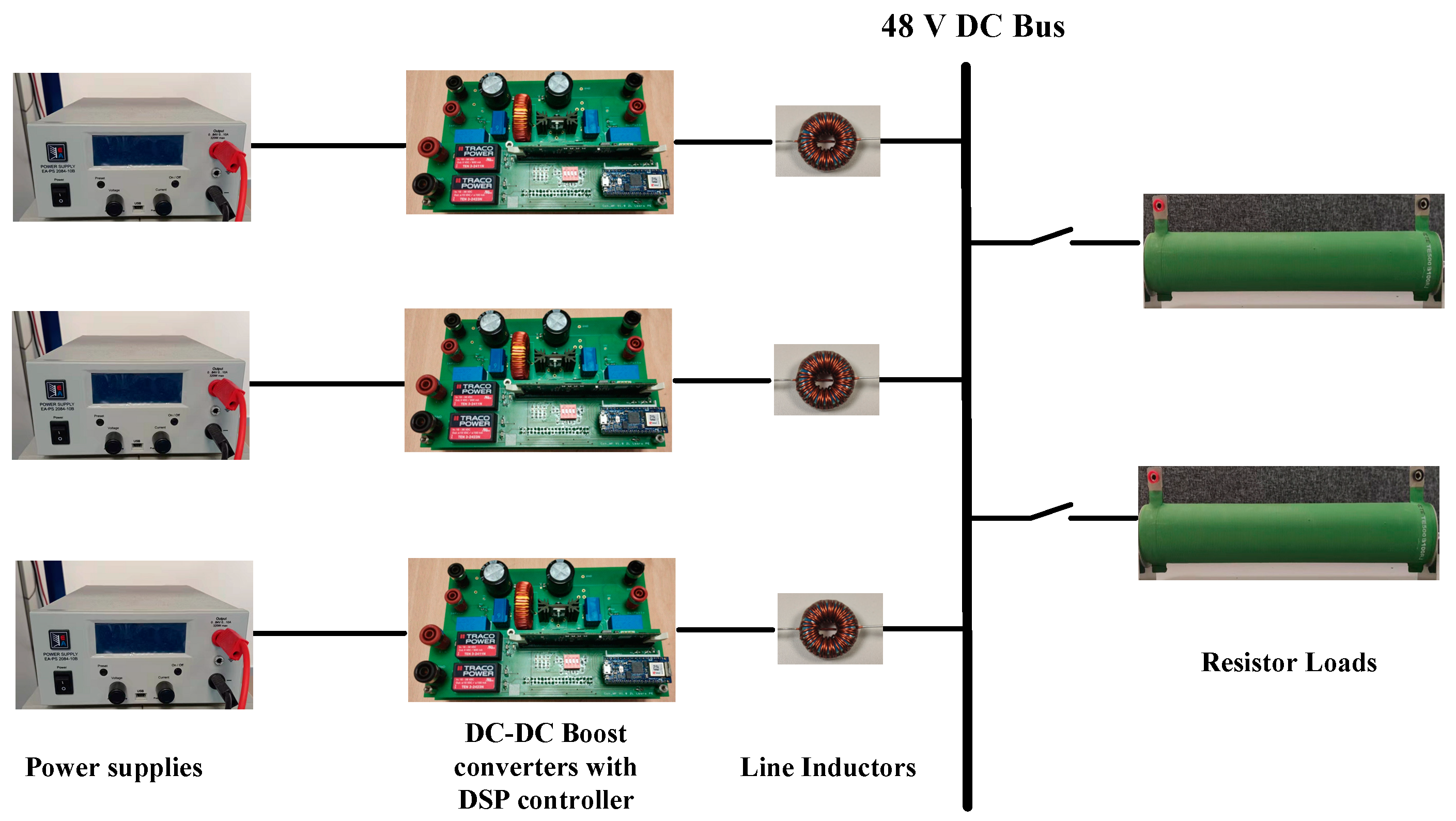
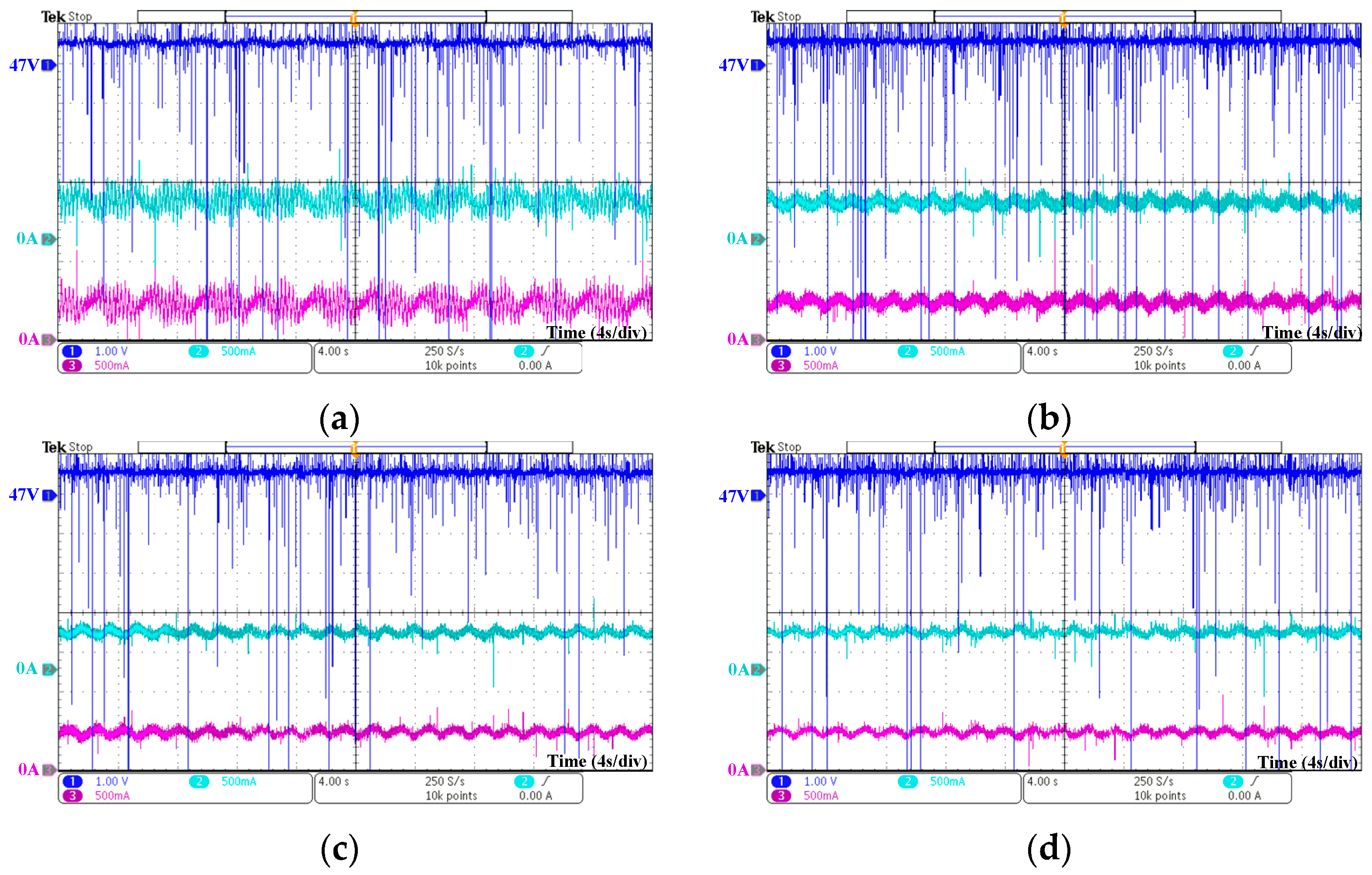
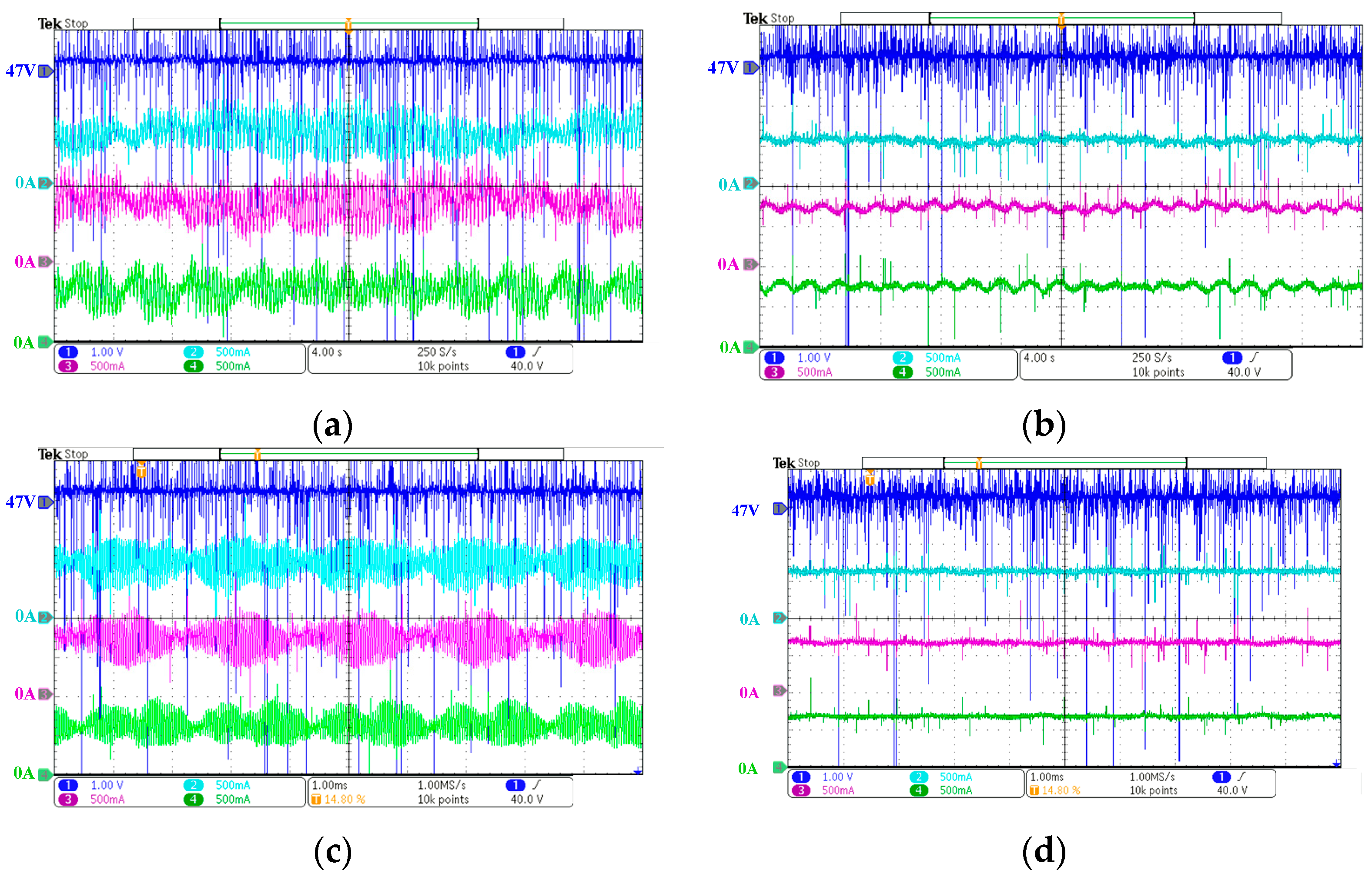
4. Experimental Verification
4.1. Experimental Results of a DC Microgrid with Two Parallel-Connected Boost Converters
4.2. Experimental Result of a DC Microgrid with Three Parallel-Connected Boost Converters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Q.; Vafamand, N.; Chen, L.; Dragičević, T.; Xie, L.; Blaabjerg, F. Review on Advanced Control Technologies for Bidirectional DC/DC Converters in DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1205–1221. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172. [Google Scholar] [CrossRef]
- Shafiee, Q.; Dragičević, T.; Vasquez, J.C.; Guerrero, J.M. Hierarchical control for multiple DC-microgrids clusters. IEEE Trans. Energy Convers. 2014, 29, 922–933. [Google Scholar] [CrossRef]
- Mohammadi, F.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B.; Ali, M.H.; Wei, W.; Erdinç, O.; Shirkhani, M. Robust control strategies for microgrids: A review. IEEE Syst. J. 2021, 16, 2401–2412. [Google Scholar] [CrossRef]
- Hosseinipour, A.; Hojabri, H. Small-Signal Stability Analysis and Active Damping Control of DC Microgrids Integrated With Distributed Electric Springs. IEEE Trans. Smart Grid 2020, 11, 3737–3747. [Google Scholar] [CrossRef]
- Santos Neto, P.J.; dos Santos Barros, T.A.; Silveira, J.P.; Ruppert Filho, E.; Vasquez, J.C.; Guerrero, J.M. Power management strategy based on virtual inertia for DC microgrids. IEEE Trans. Power Electron. 2020, 35, 12472–12485. [Google Scholar] [CrossRef]
- Zhu, X.; Meng, F.; Xie, Z.; Yue, Y. An Inertia and Damping Control Method of DC–DC Converter in DC Microgrids. IEEE Trans. Energy Convers. 2020, 35, 799–807. [Google Scholar] [CrossRef]
- Qiu, Y.; Xu, M.; Sun, J.; Lee, F.C. A generic high-frequency model for the nonlinearities in buck converters. IEEE Trans. Power Electron. 2007, 22, 1970–1977. [Google Scholar] [CrossRef]
- Sun, J.; Bing, Z.; Karimi, K.J. Input impedance modeling of multipulse rectifiers by harmonic linearization. IEEE Trans. Power Electron. 2009, 24, 2812–2820. [Google Scholar] [CrossRef]
- Yue, X.; Wang, X.; Blaabjerg, F. Review of Small-Signal Modeling Methods Including Frequency-Coupling Dynamics of Power Converters. IEEE Trans. Power Electron. 2019, 34, 3313–3328. [Google Scholar] [CrossRef]
- Qiu, Y.; Xu, M.; Yao, K.; Sun, J.; Lee, F.C. Multifrequency small signal model for buck and multiphase buck converters. IEEE Trans. Power Electron. 2006, 21, 1185–1192. [Google Scholar] [CrossRef]
- Yue, X.; Boroyevich, D.; Lee, F.C.; Chen, F.; Burgos, R.; Zhuo, F. Beat Frequency Oscillation Analysis for Power Electronic Converters in DC Nanogrid Based on Crossed Frequency Output Impedance Matrix Model. IEEE Trans. Power Electron. 2018, 33, 3052–3064. [Google Scholar] [CrossRef]
- Ambatipudi, R. Simple techniques minimize cross-coupling in distributed power systems. Powerconversion Intell. Motion-Engl. Ed. 1998, 24, 8–15. [Google Scholar]
- Mandal, K.; Banerjee, S. Synchronization Phenomena in Microgrids With Capacitive Coupling. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 364–371. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Y.; Lin, Z. Beat Frequency Oscillation Analysis for a DC Microgrid with Multiple Boost Converters. In Proceedings of the 2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 9–12 June 2023; pp. 866–870. [Google Scholar]
- Yue, X.; Boroyevich, D.; Burgos, R.; Zhuo, F. A frequency domain model for beat frequency oscillation analysis in microgrid. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar]
- Yue, X.; Zhuo, F.; Yang, S.; Pei, Y.; Yi, H. A Matrix-Based Multifrequency Output Impedance Model for Beat Frequency Oscillation Analysis in Distributed Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 80–92. [Google Scholar] [CrossRef]
- Chakraborty, S.S.; Hatua, K. Modeling with Beat Frequency Dynamics and Phase-Frequency Control Design for a Dual-Bridge Series Resonant Converter. IEEE Trans. Ind. Electron. 2022, 69, 7952–7962. [Google Scholar] [CrossRef]
- Yue, X.; Högrud, M. Beat Frequency Oscillation Analysis for Voltage Regulators in Telecom Power System. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 2135–2140. [Google Scholar]
- Ding, D.; Zhao, N.; Wang, G.; Zhang, G.; Zhang, X.; Mijatovic, N.; Xu, D. Suppression of Beat Phenomenon for Electrolytic Capacitorless Motor Drives Accounting for Sampling Delay of DC-Link Voltage. IEEE Trans. Ind. Electron. 2022, 69, 1167–1176. [Google Scholar] [CrossRef]
- Li, K.; Tan, S.-C.; Hui, R.S.Y. On Beat Frequency Oscillation of Two-Stage Wireless Power Receivers. IEEE Trans. Power Electron. 2020, 35, 12741–12751. [Google Scholar] [CrossRef]
- Alshareef, M.; Lin, Z.; Li, F.; Wang, F. A grid interface current control strategy for DC microgrids. CES Trans. Electr. Mach. Syst. 2021, 5, 249–256. [Google Scholar] [CrossRef]







| Parameters | Value |
|---|---|
| Switching frequency fs | 25 kHz |
| Input voltage Vin | 25 V |
| Output voltage Vo | 50 V |
| Inductor L | 500 µH |
| Capacitor C | 470 µF |
| ESR of inductor RL | 37 mΩ |
| ESR of capacitor Rc | 8 mΩ |
| Load resistor R | 47 Ω |
| Voltage loop PI compensator Kvp,Kvi | 0.90, 175.9 |
| Current loop PI compensator Kip,Kii | 0.02, 30.3 |
| Droop coefficient Rd | 1 Ω |
| Filter Inductance | 0 µH | 47 µH | 220 µH | 500 µH | ||
|---|---|---|---|---|---|---|
| Oscillation Amplitude (A) | ||||||
| Switching Frequency Channels | ||||||
| fs1 = 25.0 kHz, fs2 = 25.0 kHz | 0.554 | 0.241 | 0.220 | 0.204 | ||
| fs1 = 24.95 kHz, fs2 = 25.0 kHz | 0.548 | 0.194 | 0.128 | 0.104 | ||
| fs1 = 24.5 kHz, fs2 = 25.0 kHz | 0.492 | 0.163 | 0.085 | 0.063 | ||
| fs1 = 24.0 kHz, fs2 = 25.0 kHz | 0.480 | 0.162 | 0.076 | 0.052 | ||
| fs1 = 25.0 kHz, fs2 = 30.0 kHz | 0.456 | 0.162 | 0.055 | 0.051 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Lin, Z. A Hybrid Beat Frequency Oscillation Suppression Strategy for DC Microgrids. Energies 2024, 17, 3513. https://doi.org/10.3390/en17143513
Xu H, Lin Z. A Hybrid Beat Frequency Oscillation Suppression Strategy for DC Microgrids. Energies. 2024; 17(14):3513. https://doi.org/10.3390/en17143513
Chicago/Turabian StyleXu, Haoge, and Zhengyu Lin. 2024. "A Hybrid Beat Frequency Oscillation Suppression Strategy for DC Microgrids" Energies 17, no. 14: 3513. https://doi.org/10.3390/en17143513
APA StyleXu, H., & Lin, Z. (2024). A Hybrid Beat Frequency Oscillation Suppression Strategy for DC Microgrids. Energies, 17(14), 3513. https://doi.org/10.3390/en17143513







