A Gap Nonlinearity Compensation Strategy for Non-Direct-Drive Servo Systems
Abstract
1. Introduction
2. Identification of Nonlinear Gap Models and Their Influence
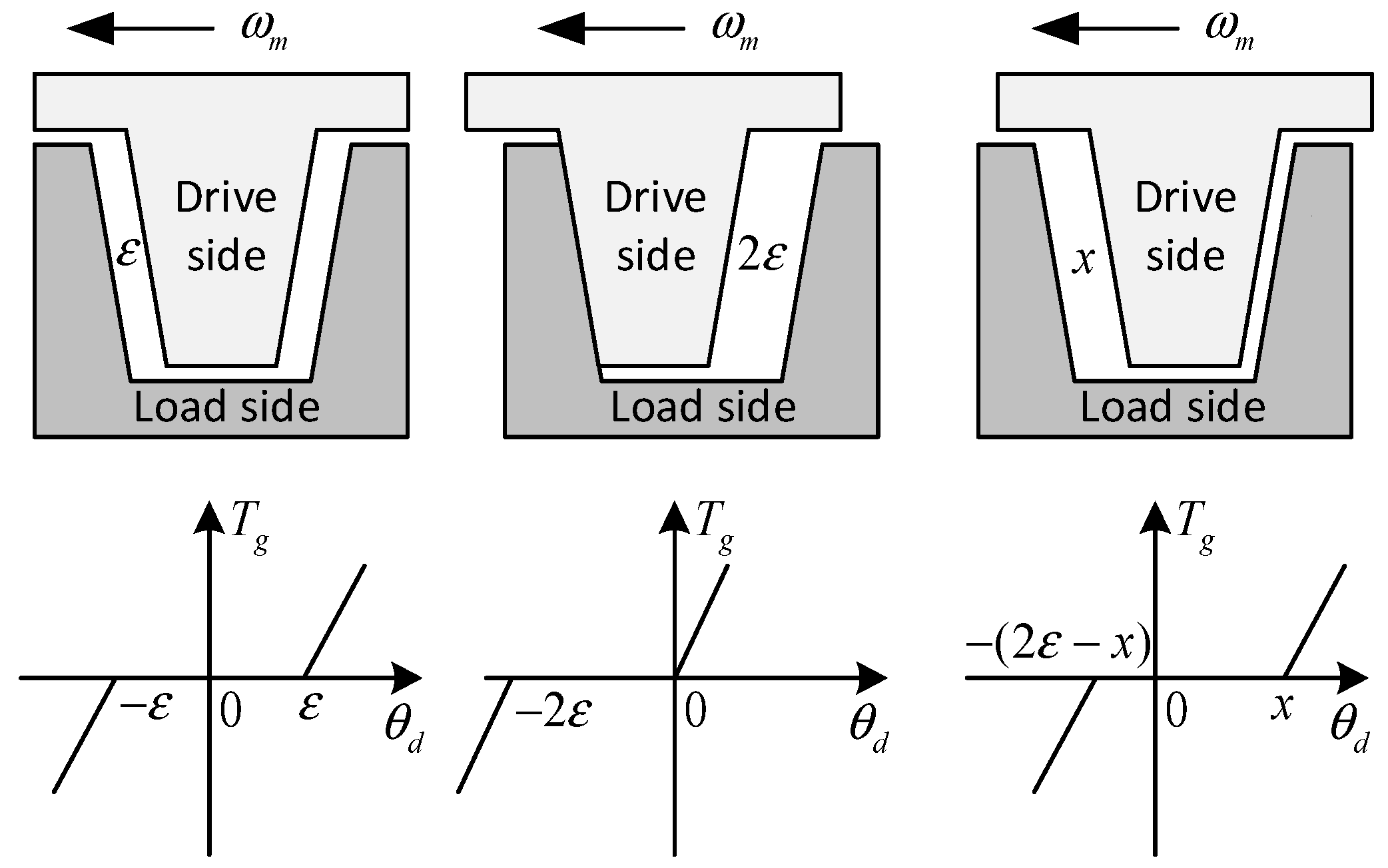
2.1. Gap Dead-zone Model
2.2. Gap Amplitude Identification
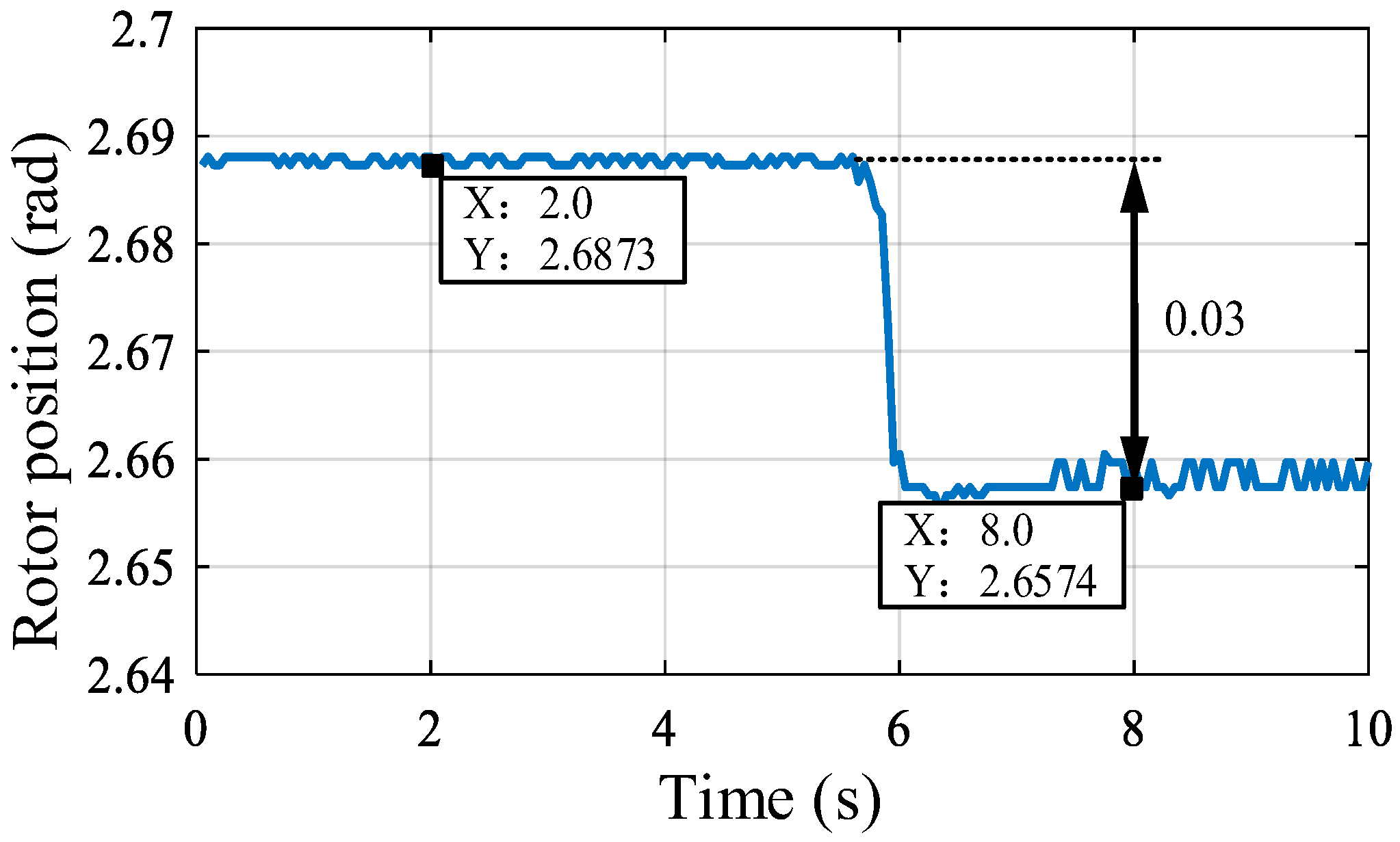
2.2.1. Identification of Gap Amplitude Based on Incremental Torque Pulses
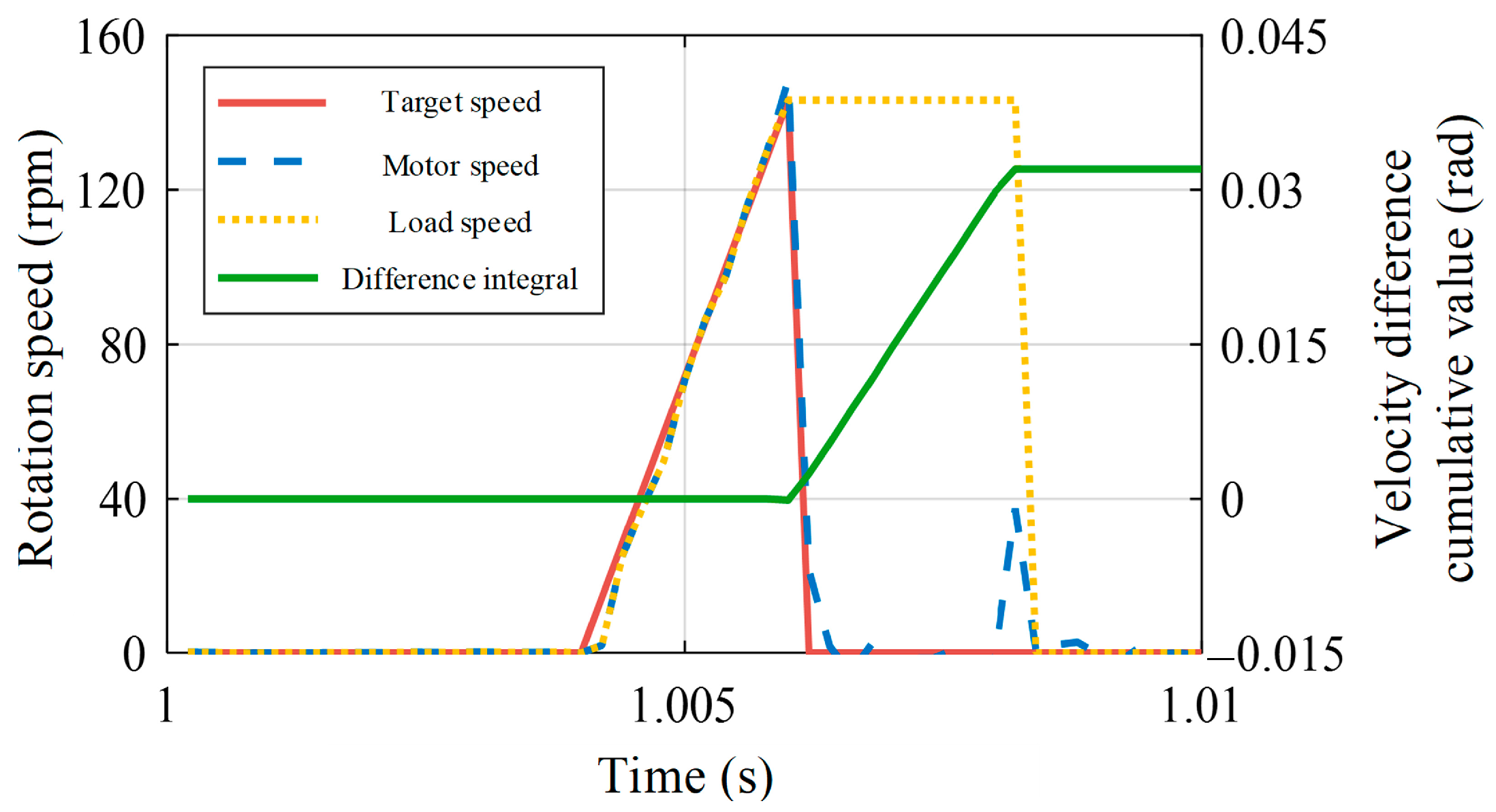
2.2.2. Gap Amplitude Identification Based on Velocity Difference Integration
2.3. Impact of Two-Position Feedback Structures
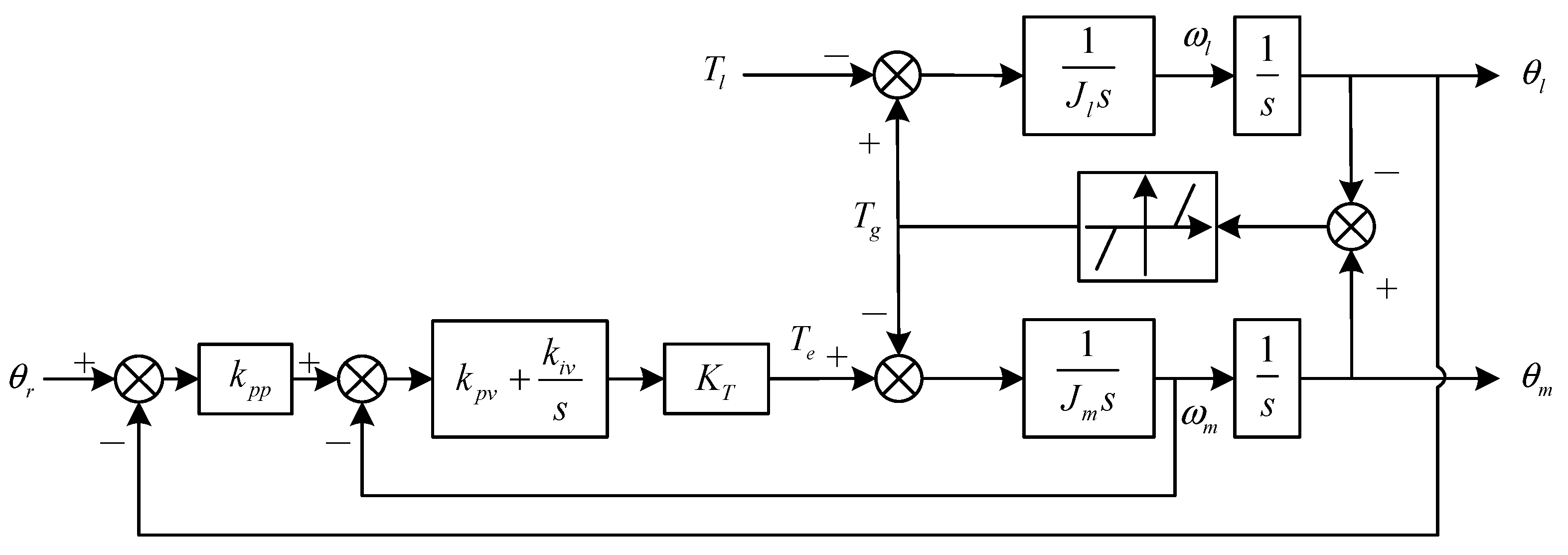
3. Under the Fully Closed-Loop Control Structure, Gap Nonlinearity Compensation Based on State Feedback
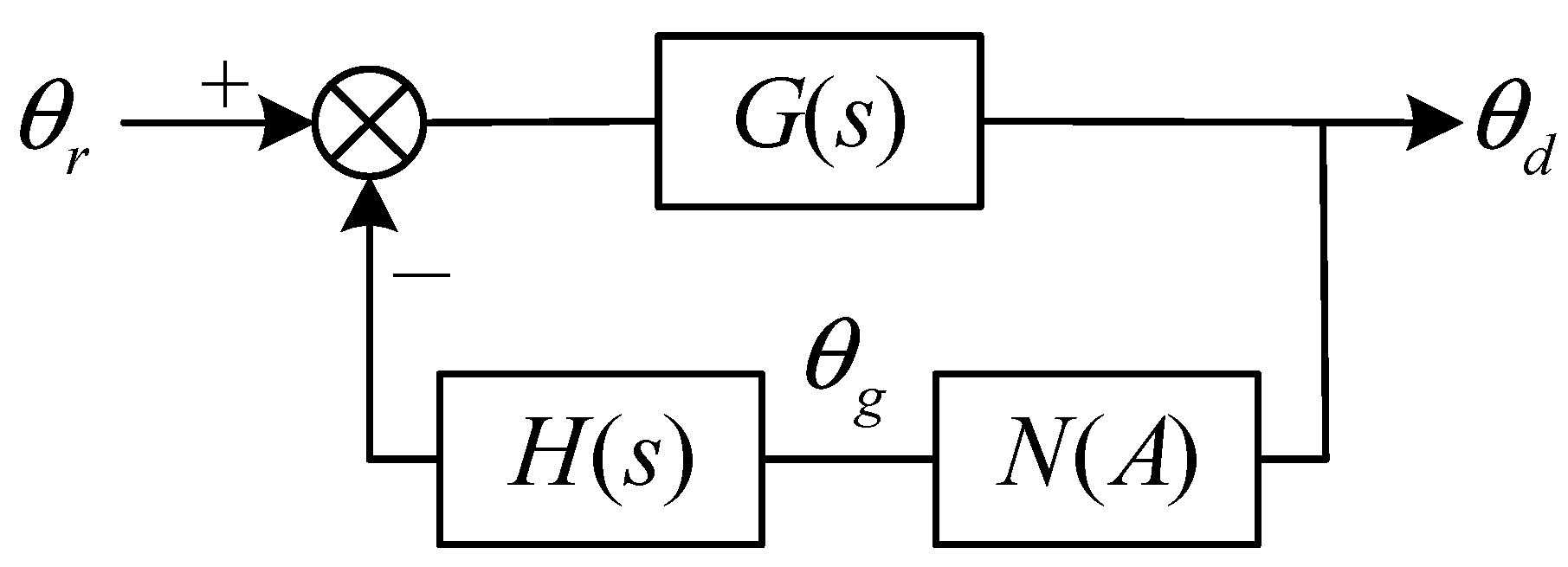
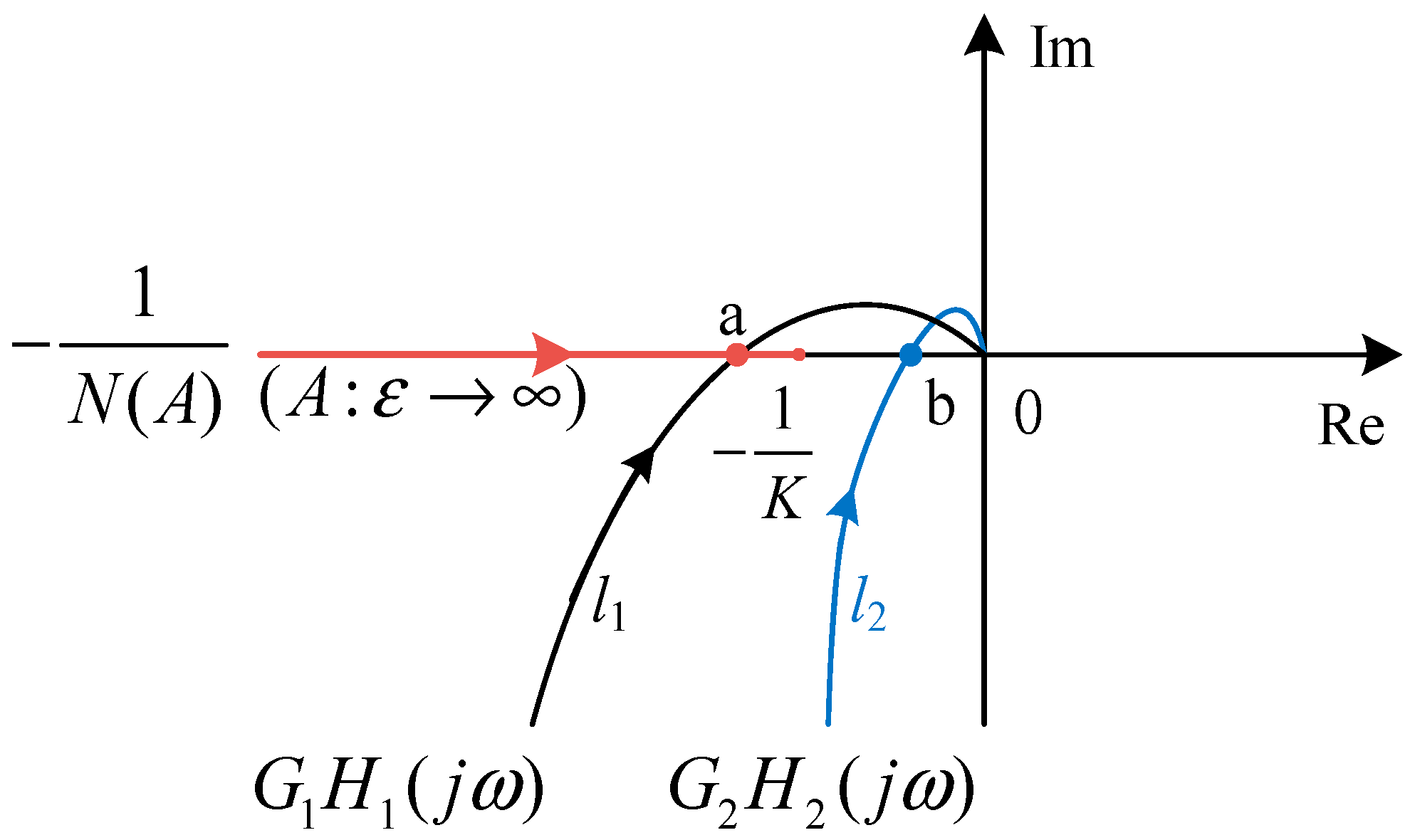
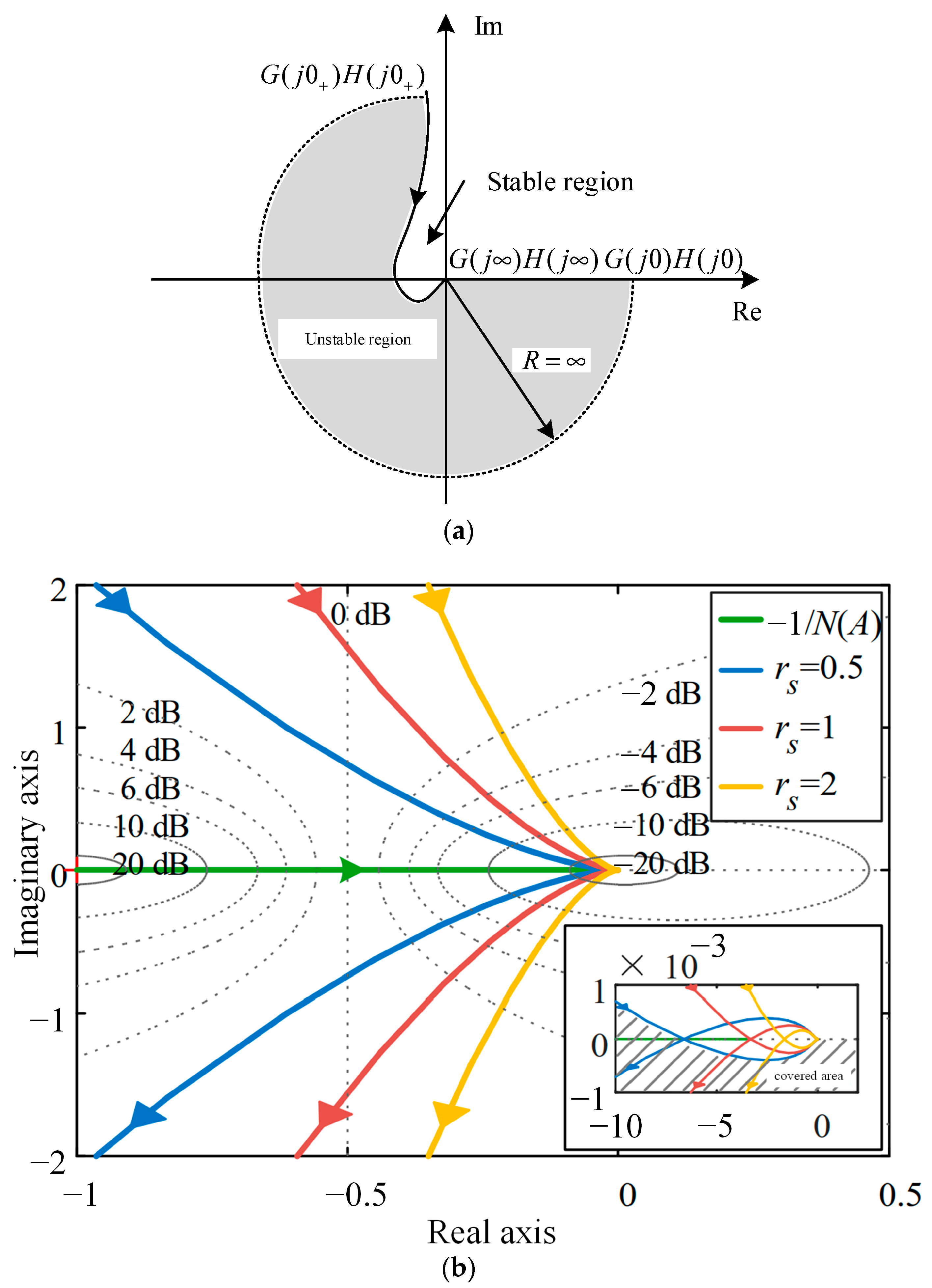
3.1. Analysis of Limit-Cycle Oscillation Mechanism
3.2. Suppression of Limit-Cycle Oscillations Using Notch Filters
3.3. Suppression of Limit-Cycle Oscillations Based on State Feedback
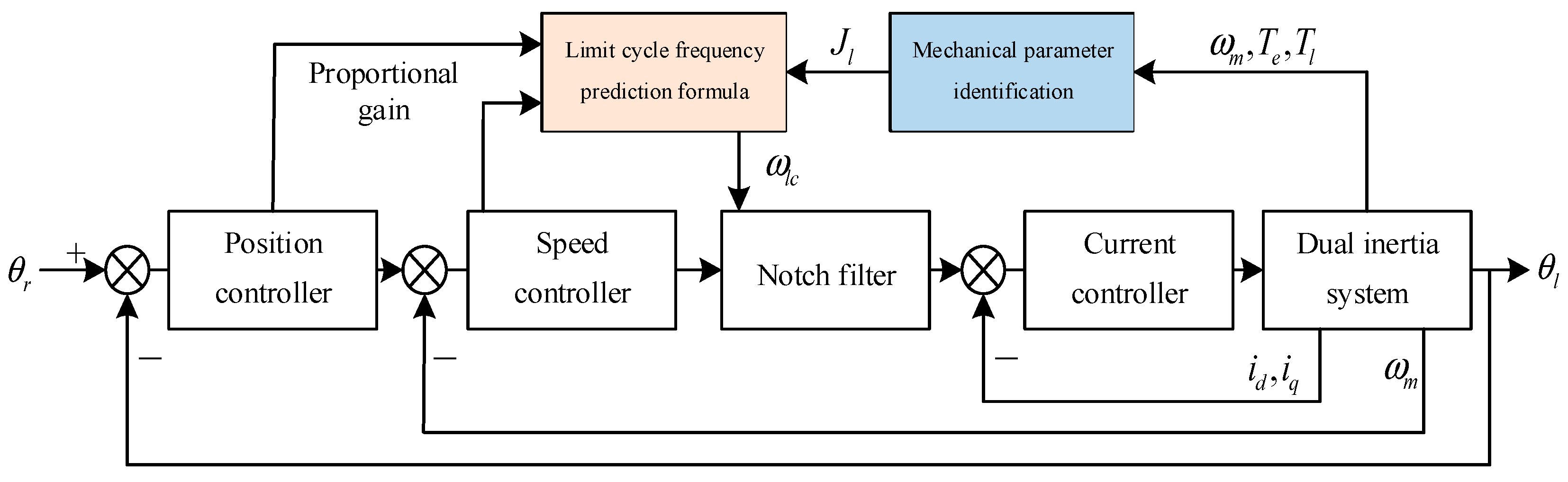
3.3.1. Structural Design
3.3.2. Design of Feedback Parameters
3.3.3. Steady-State Error
4. Simulation Validation
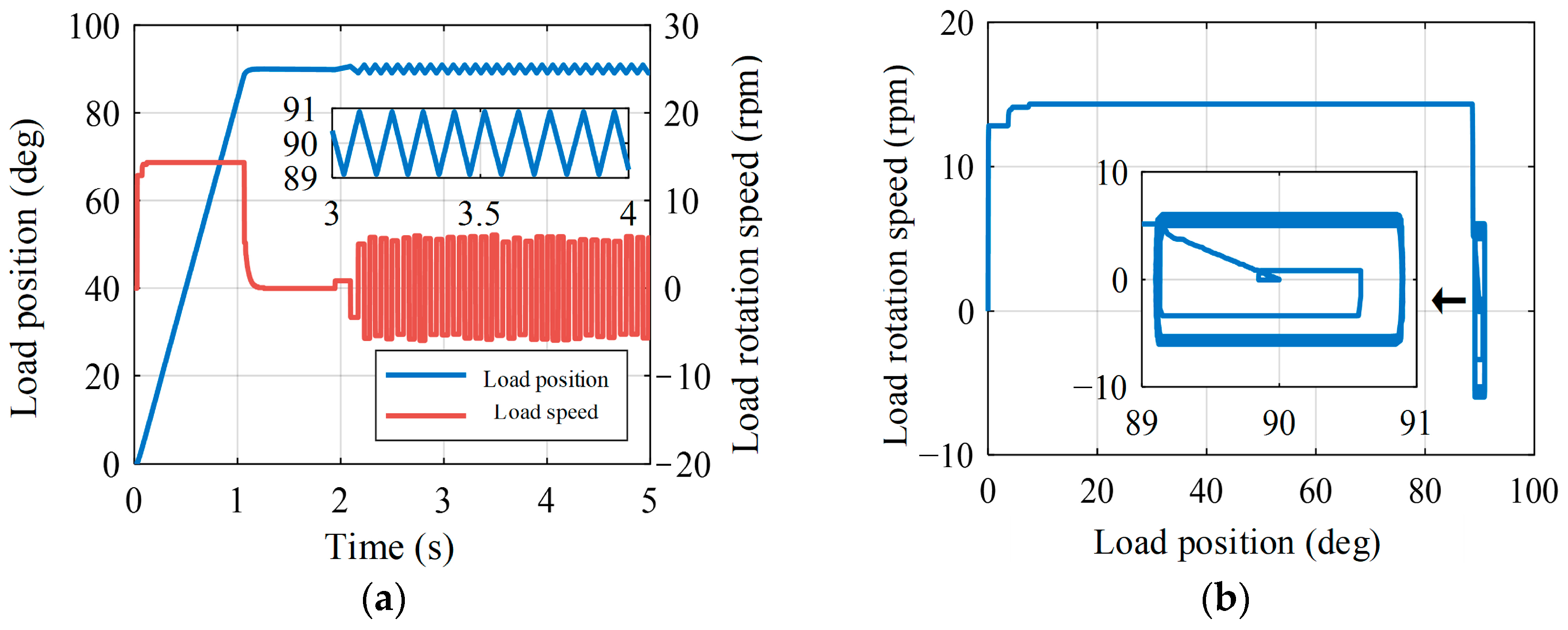
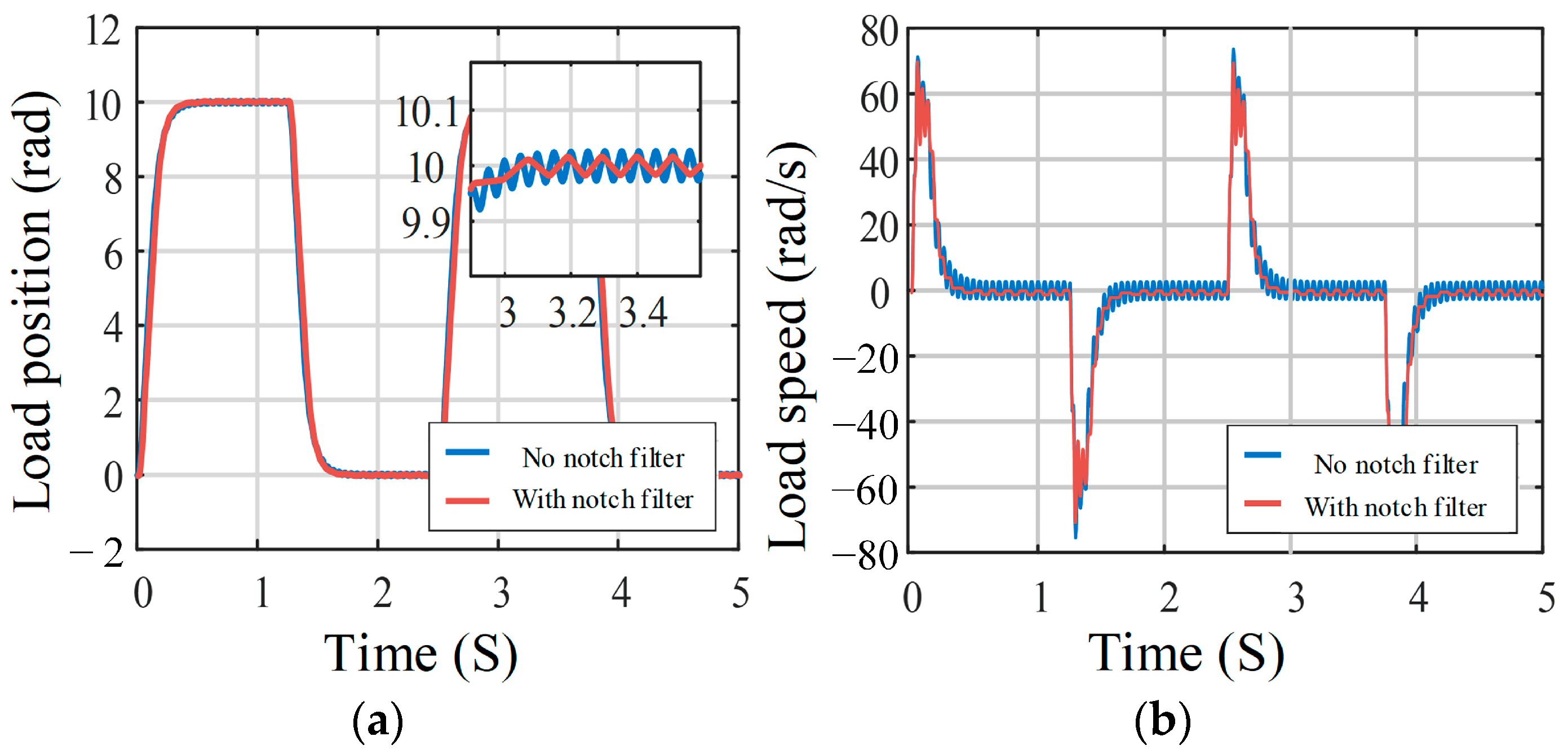
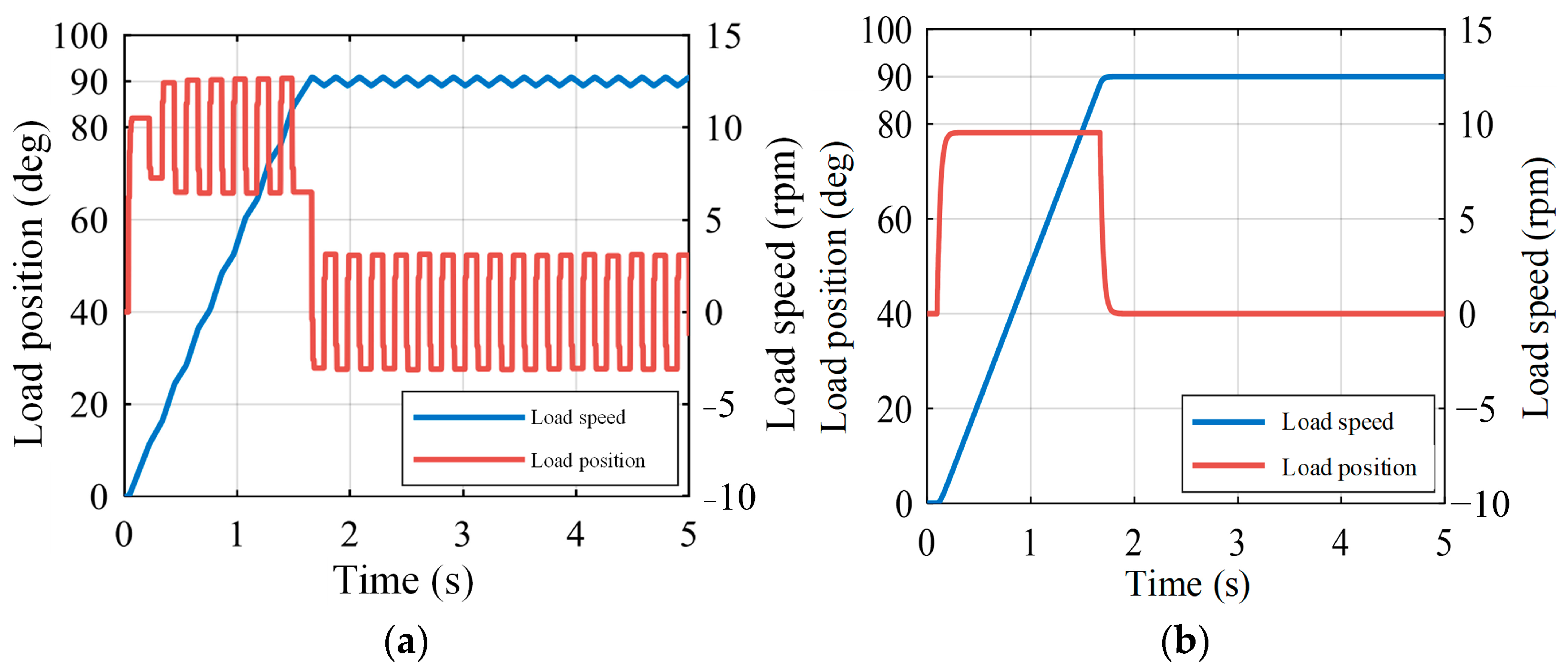
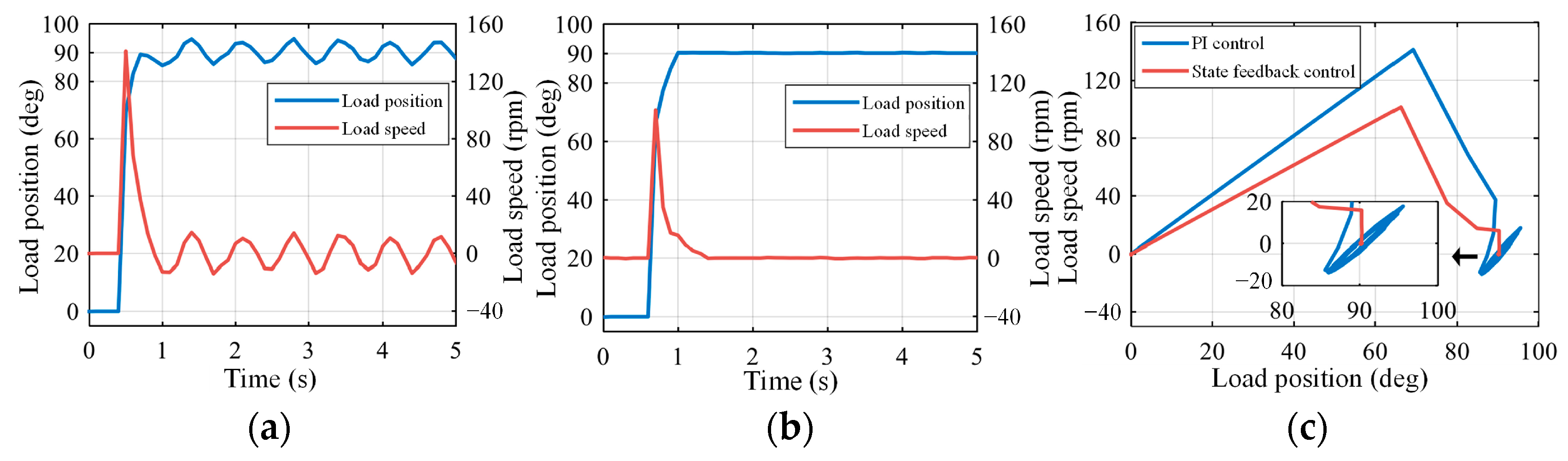
4.1. Comparison between PI Control and State-Feedback Control
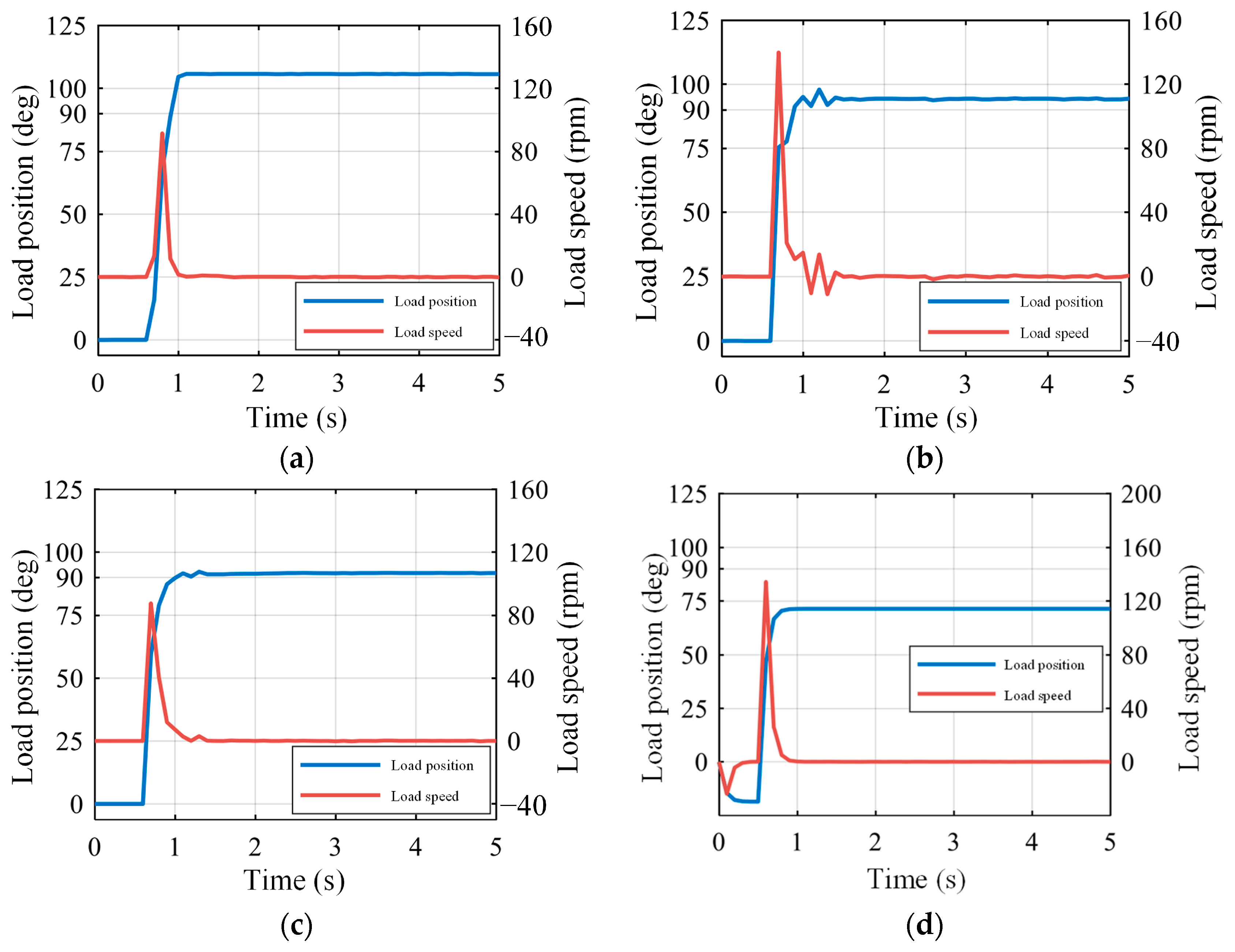
4.2. Robustness under Varying System Parameters
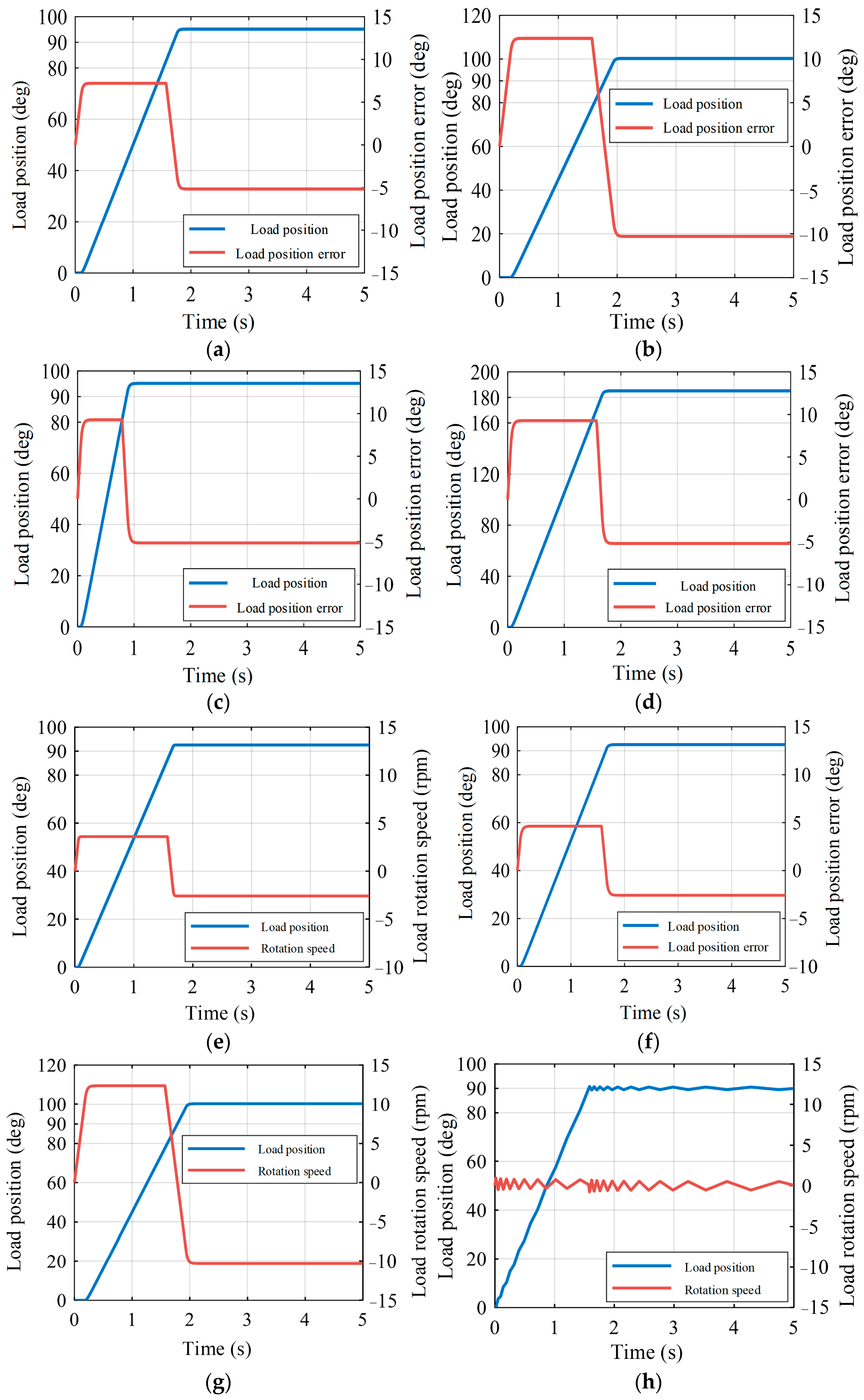
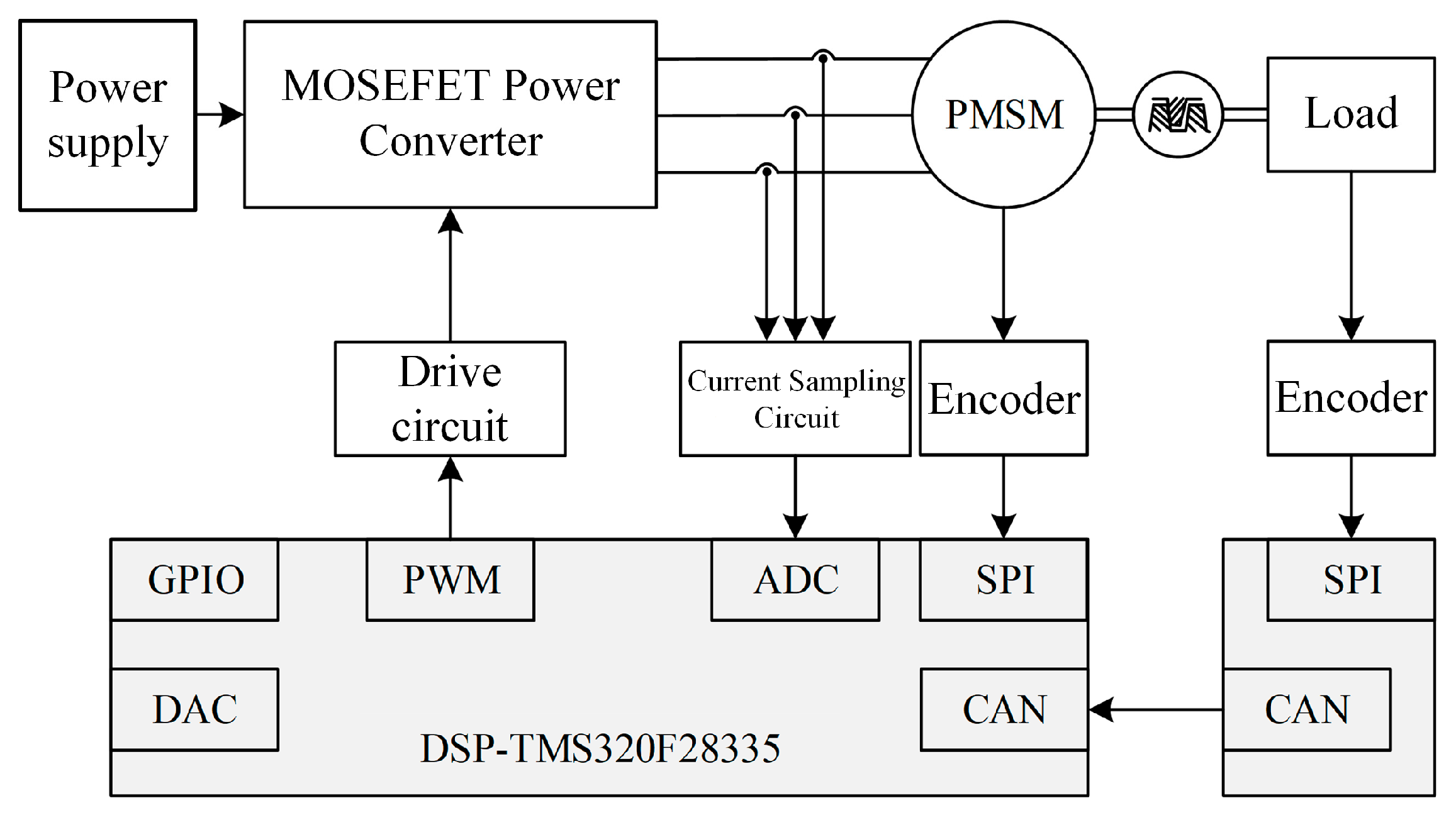
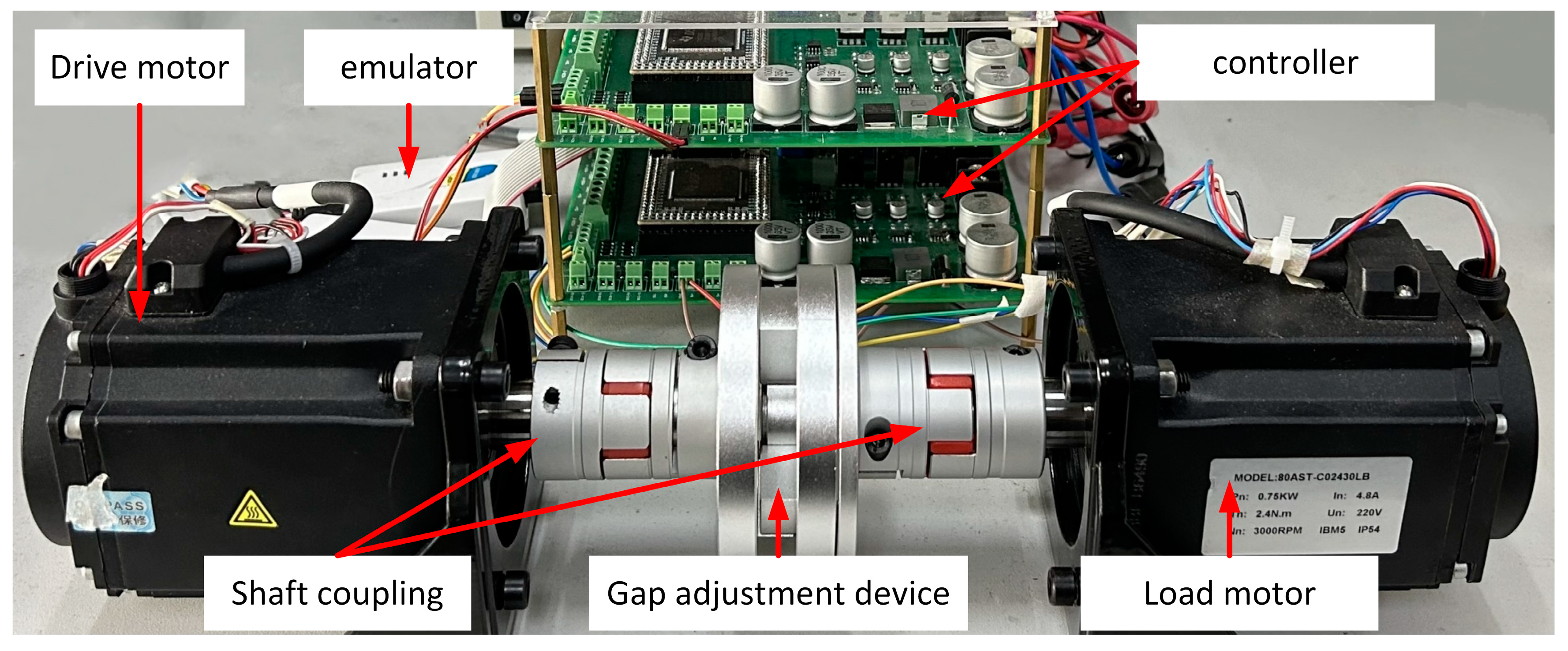
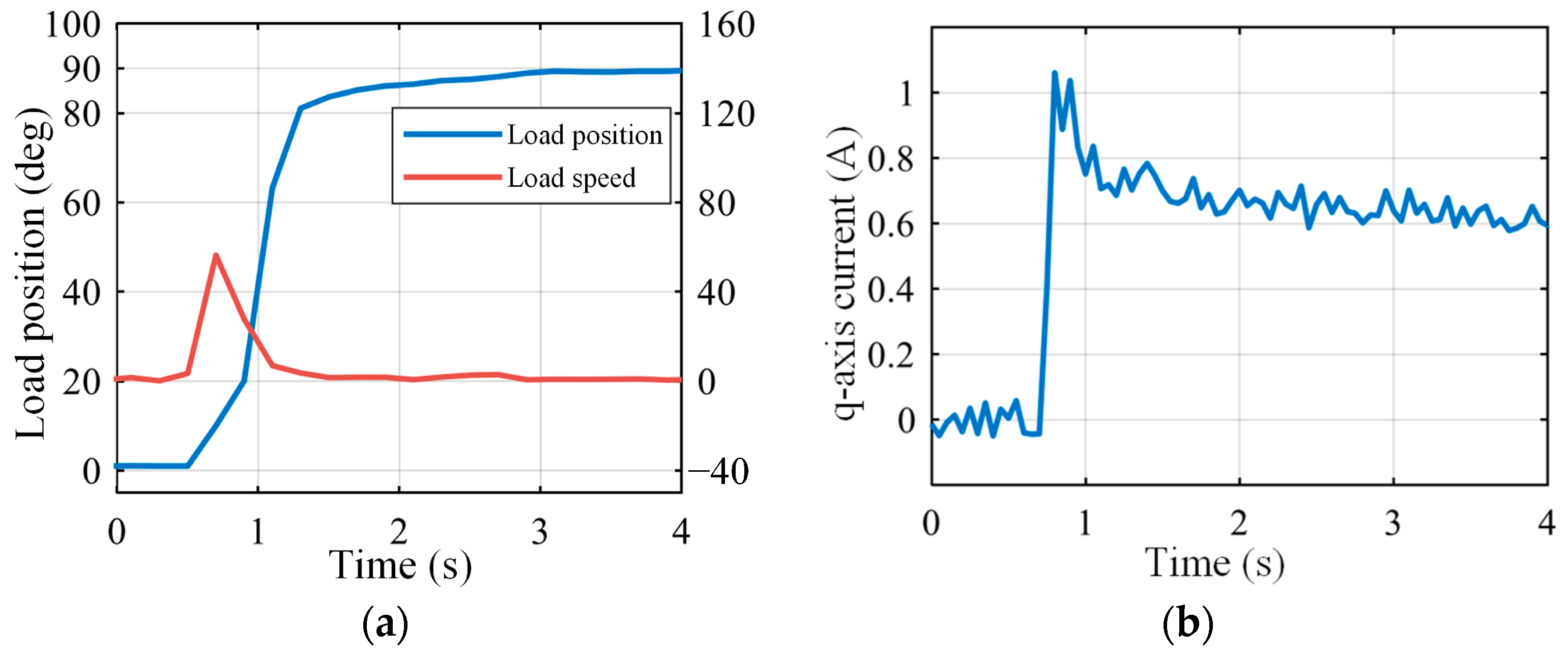
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Z.; Lin, S.; Zhu, D.; Wen, G. Vibration Control of a Riser-Vessel System Subject to Input Backlash and Extraneous Disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 516–520. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, R. A Disturbance-Observer-Based Feedforward-Feedback Control Strategy for Driveline Launch Oscillation of Hybrid Electric Vehicles Considering Nonlinear Backlash. IEEE Trans. Veh. Technol. 2022, 71, 3727–3736. [Google Scholar] [CrossRef]
- Wang, C. Research on Mechanical Parameter Identification and Oscillation Suppression Techniques in Servo Drive Systems; Harbin Institute of Technology: Harbin, China, 2018. [Google Scholar]
- Hao, Q.; Li, G.; Ooi, B.T. Approximate model and low-order harmonic reduction for high-voltage direct current tap based on series single-phase modular multilevel converter. IET Gener. Transm. Distrib. 2013, 7, 1046–1054. [Google Scholar] [CrossRef]
- Reddy, P.; Shahbakhti, M.; Ravichandran, M.; Doering, J. Real-Time Estimation of Backlash Size in Automotive Drivetrains. IEEE/ASME Trans. Mechatron. 2022, 27, 3362–3372. [Google Scholar] [CrossRef]
- Yang, M.; Tang, S.; Tan, J.; Xu, D. Study of On-line Backlash Identification for PMSM Servo System. In Proceedings of the Annual Conference of the IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 2036–2042. [Google Scholar]
- Ahmad, N.J.; Ebraheem, H.K.; Alnaser, M.J.; Alostath, J.M. Adaptive Control of a DC Motor with Uncertain Deadzone Nonlinearity at the Input. In Proceedings of the Chinese Control and Decision Conference (CCDC), Mianyang, China, 23–25 May 2011; pp. 4295–4299. [Google Scholar]
- Shi, Z.; Zuo, Z. Backstepping Control for Gear Transmission Servo Systems with Backlash Nonlinearity. IEEE Trans. Autom. Sci. Eng. 2015, 12, 752–757. [Google Scholar] [CrossRef]
- Omisore, O.M.; Han, S.P.; Ren, L.X.; Wang, G.S.; Ou, F.L.; Li, H.; Wang, L. Towards Characterization and Adaptive Compensation of Backlash in a Novel Robotic Catheter System for Cardiovascular Interventions. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 824–838. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Z.; Chen, C.L.; Zhang, Y. Fuzzy Control of Switched Systems with Unknown Backlash and Nonconstant Control Gain: A Parameterized Smooth Inverse. IEEE Trans. Fuzzy Syst. 2022, 30, 4876–4890. [Google Scholar] [CrossRef]
- Yang, M.; Wang, C.; Xu, D.; Zheng, W.; Lang, X. Shaft Torque Limiting Control Using Shaft Torque Compensator for Two-Inertia Elastic System with Backlash. IEEE/ASME Trans. Mechatron. 2016, 21, 2902–2911. [Google Scholar] [CrossRef]
- Bai, C.; Yin, Z.; Li, T.; Zhang, Y.; Yuan, D.; Zhang, P. Backstepping Control Collaborative Shaft Torque Observer for Limit Cycle Oscillation Suppression of Fully Closed-Loop Gear Transmission Servo System. IEEE Trans Power Electron. 2024, 39, 4513–4526. [Google Scholar] [CrossRef]
- Ghaffari, A.; Mohammadiasl, E. Calculating the Frequency of Oscillation for Servo Axes Distressed by Clearance or Preloading. IEEE/ASME Trans. Mechatron. 2013, 18, 922–931. [Google Scholar] [CrossRef]


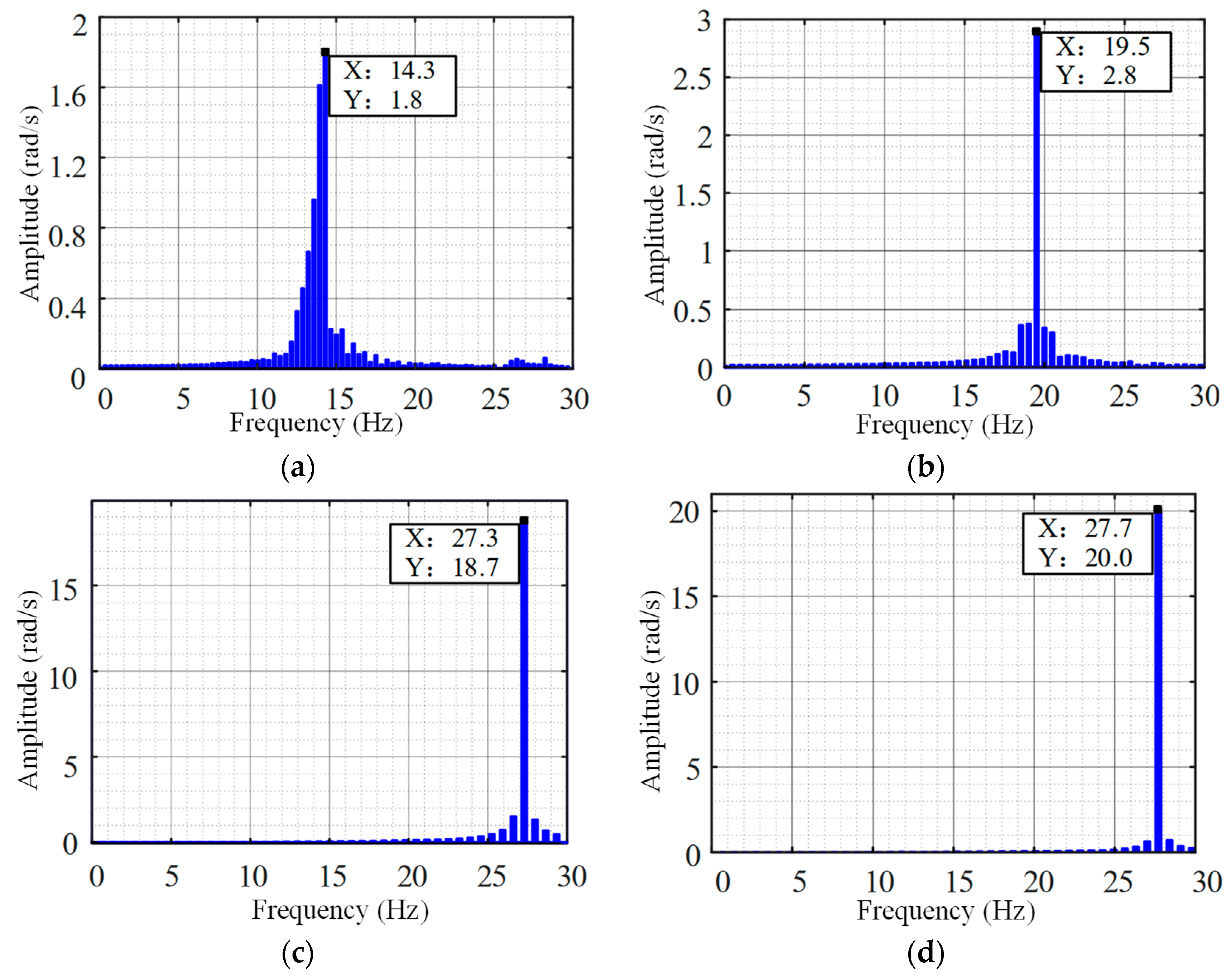
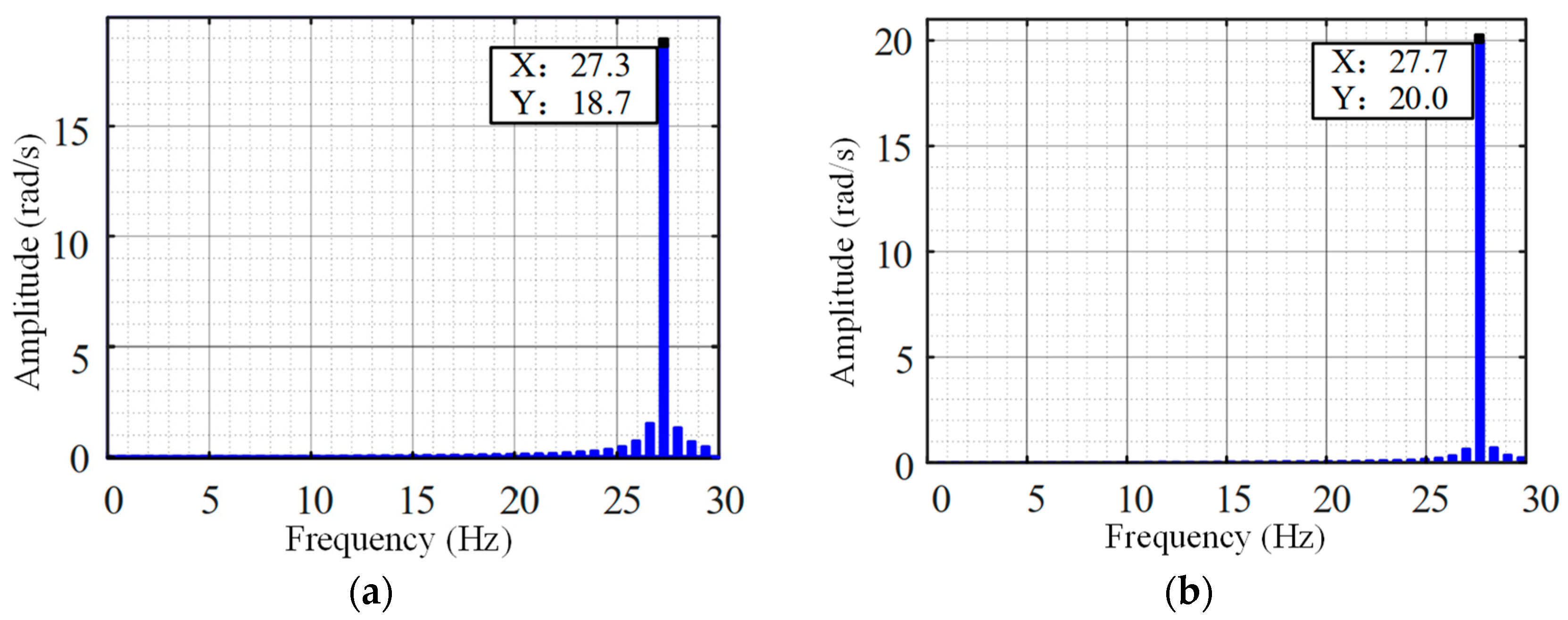




| Parameters | Value |
|---|---|
| Rotation inertia of motor (kg·m2) | 6.3 × 104 |
| Shaft stiffness (N·m/rad) | 22 |
| Anti-resonance frequency ωARF (rad/s) | 186 |
| Velocity ring scaling factor kpv | 0.3 |
| Position ring scale factor kpp | 26, 35, 88, 130 |
| Gap value 2ε (rad) | 0.01, 0.02, 0.05 |
| Parameters | Value |
|---|---|
| Damping coefficient ζ1 of the conjugate dominant poles | 0.7 |
| Conjugate dominant pole natural frequency ω1 (rad/s) | 50 |
| Non-conjugate dominant pole damping coefficient ζ2 | 1 |
| The natural frequency, ω2 (rad/s), of the non-conjugate dominant pole | 250 |
| Feedback coefficient k1 | −17.0625 |
| Feedback coefficient k2 | −0.0273 |
| Velocity loop proportional coefficient kpv | 0.1024 |
| Position loop proportional coefficient kpp | 27.78 |
| Gap value of 2ε (rad) | 0.3 |
| Parameters | Values |
|---|---|
| Rated power (W) | 750 |
| Rated current (A) | 3 |
| Rated torque (N·m) | 2.39 |
| Motor pole pairs | 5 |
| Moment of inertia | 1.82 × 10−4 |
| kpp | kpv | k1 | Theoretical Static Differential (Deg) | Experimental Static Differential (Deg) | |
|---|---|---|---|---|---|
| Parameter 1 | 9 | 0.1024 | −17.0625 | 15.91 | 15.67 |
| Parameter 2 | 27.7 | 0.1024 | −17.0625 | 5.17 | 4.38 |
| Parameter 3 | 27.7 | 0.1024 | −6.1425 | 1.86 | 1.75 |
| Parameter 4 20% rated load | 27.7 | 0.1024 | −17.0625 | −18.31 | −17.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Ji, R.; Zhou, C.; Sohel, R.M.; Liu, K.; Hua, W.; Ye, H. A Gap Nonlinearity Compensation Strategy for Non-Direct-Drive Servo Systems. Energies 2024, 17, 3582. https://doi.org/10.3390/en17143582
Wang B, Ji R, Zhou C, Sohel RM, Liu K, Hua W, Ye H. A Gap Nonlinearity Compensation Strategy for Non-Direct-Drive Servo Systems. Energies. 2024; 17(14):3582. https://doi.org/10.3390/en17143582
Chicago/Turabian StyleWang, Bo, Runze Ji, Chengpeng Zhou, Rana M. Sohel, Kai Liu, Wei Hua, and Hairong Ye. 2024. "A Gap Nonlinearity Compensation Strategy for Non-Direct-Drive Servo Systems" Energies 17, no. 14: 3582. https://doi.org/10.3390/en17143582
APA StyleWang, B., Ji, R., Zhou, C., Sohel, R. M., Liu, K., Hua, W., & Ye, H. (2024). A Gap Nonlinearity Compensation Strategy for Non-Direct-Drive Servo Systems. Energies, 17(14), 3582. https://doi.org/10.3390/en17143582









