Research on Parameter Correction of Distribution Network Model Based on CIM Model and Measurement Data
Abstract
1. Introduction
2. CIM-Based Distribution Network Topology Construction
2.1. Introduction to CIM and XML Files
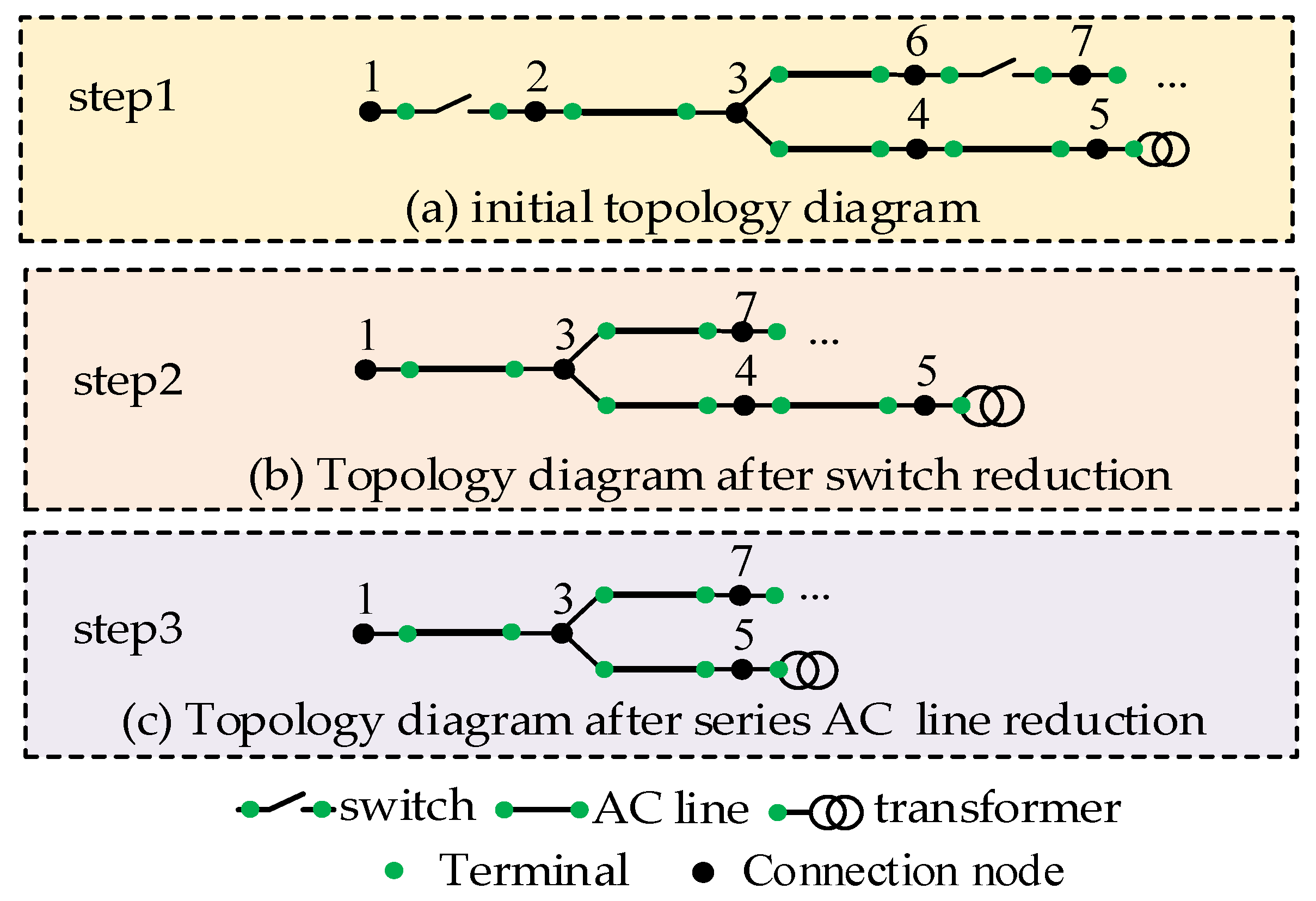
2.2. Topology Construction and Topology Reduction
2.3. Missing Parameters and Abnormal Data Replacement
3. Distribution Network Line Parameter Correction
3.1. Distribution Network Parameter Basis Correction
3.2. Distribution Network Parameter Fine Correction
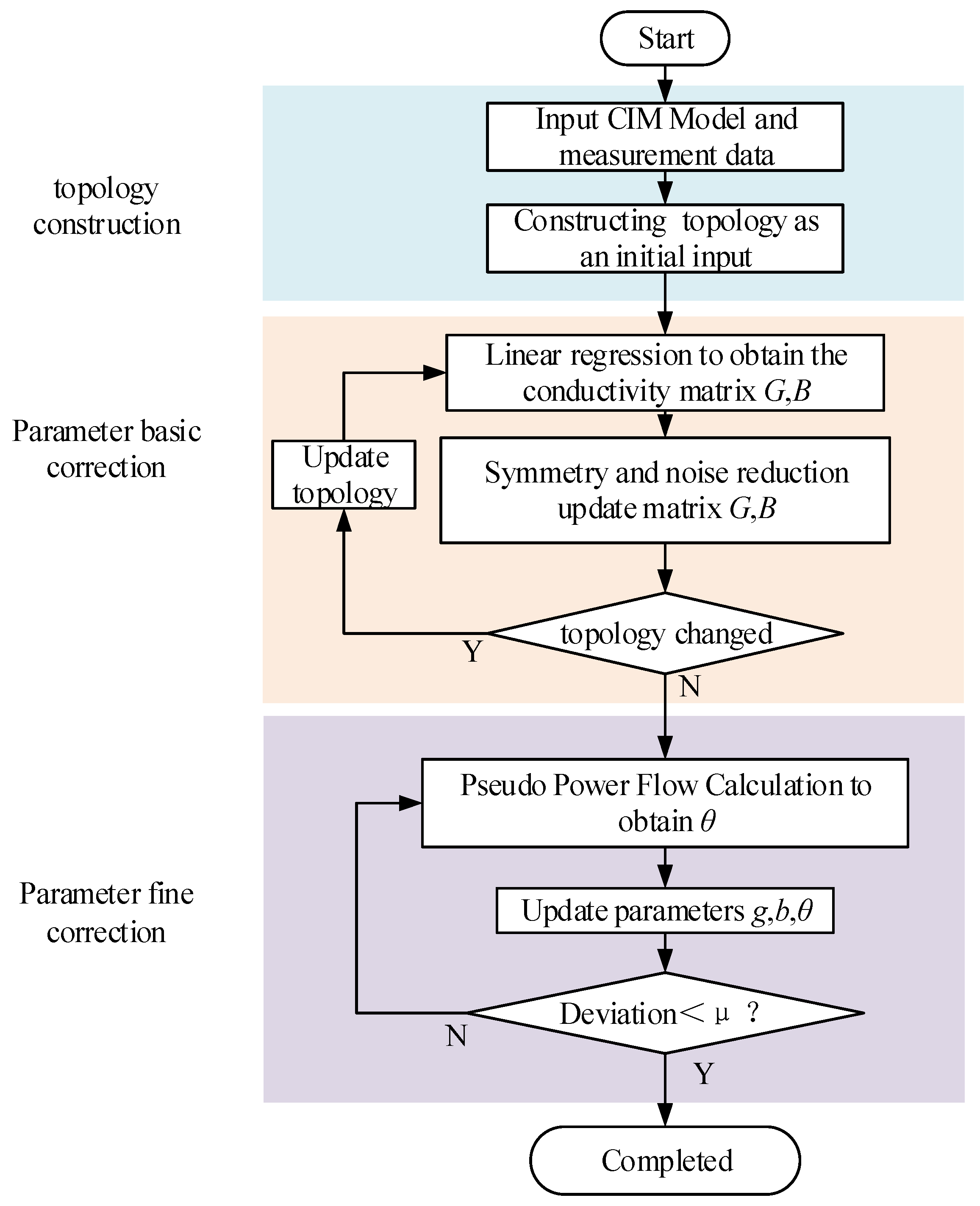
3.3. Overall Flowchart of the Algorithm
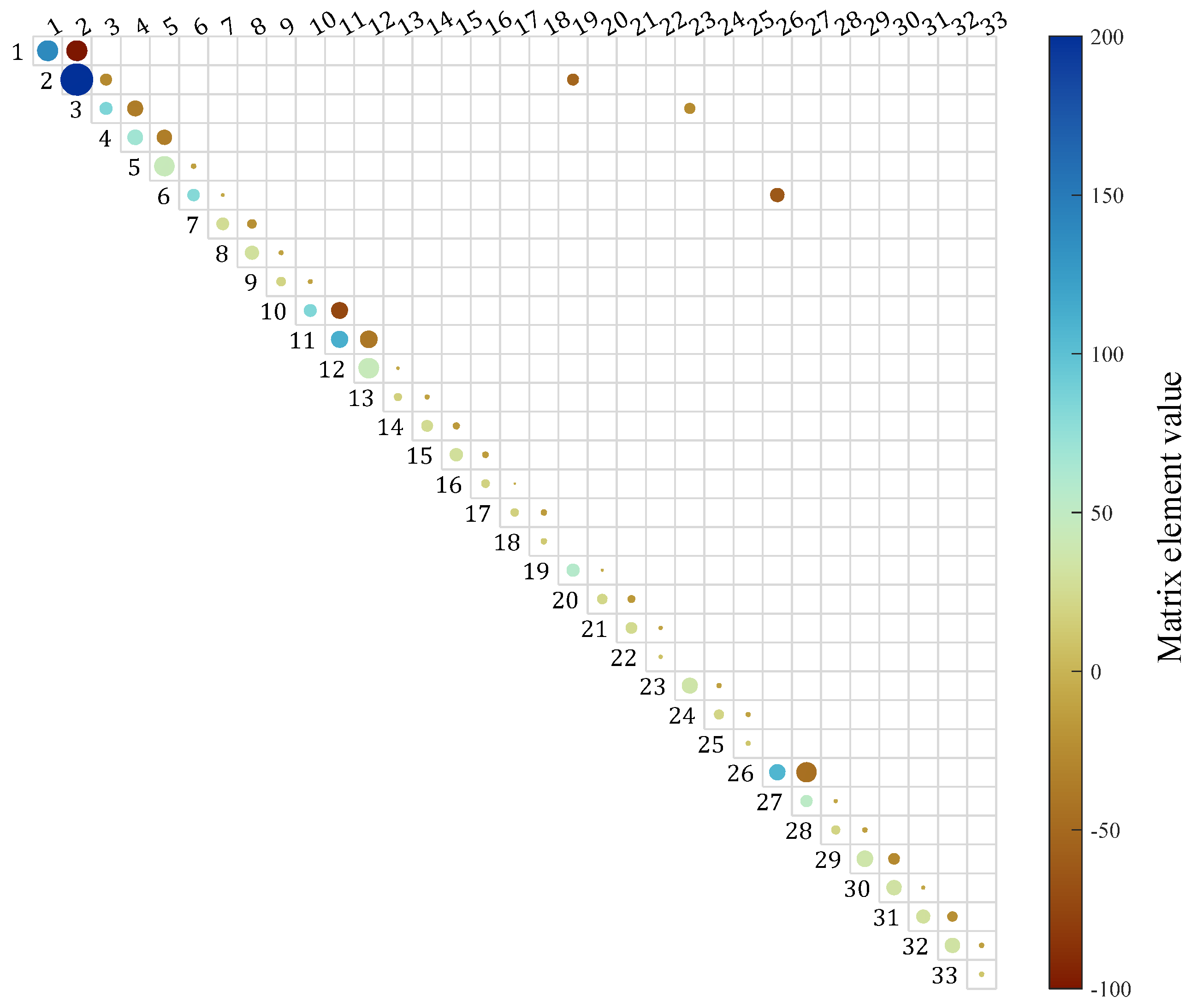
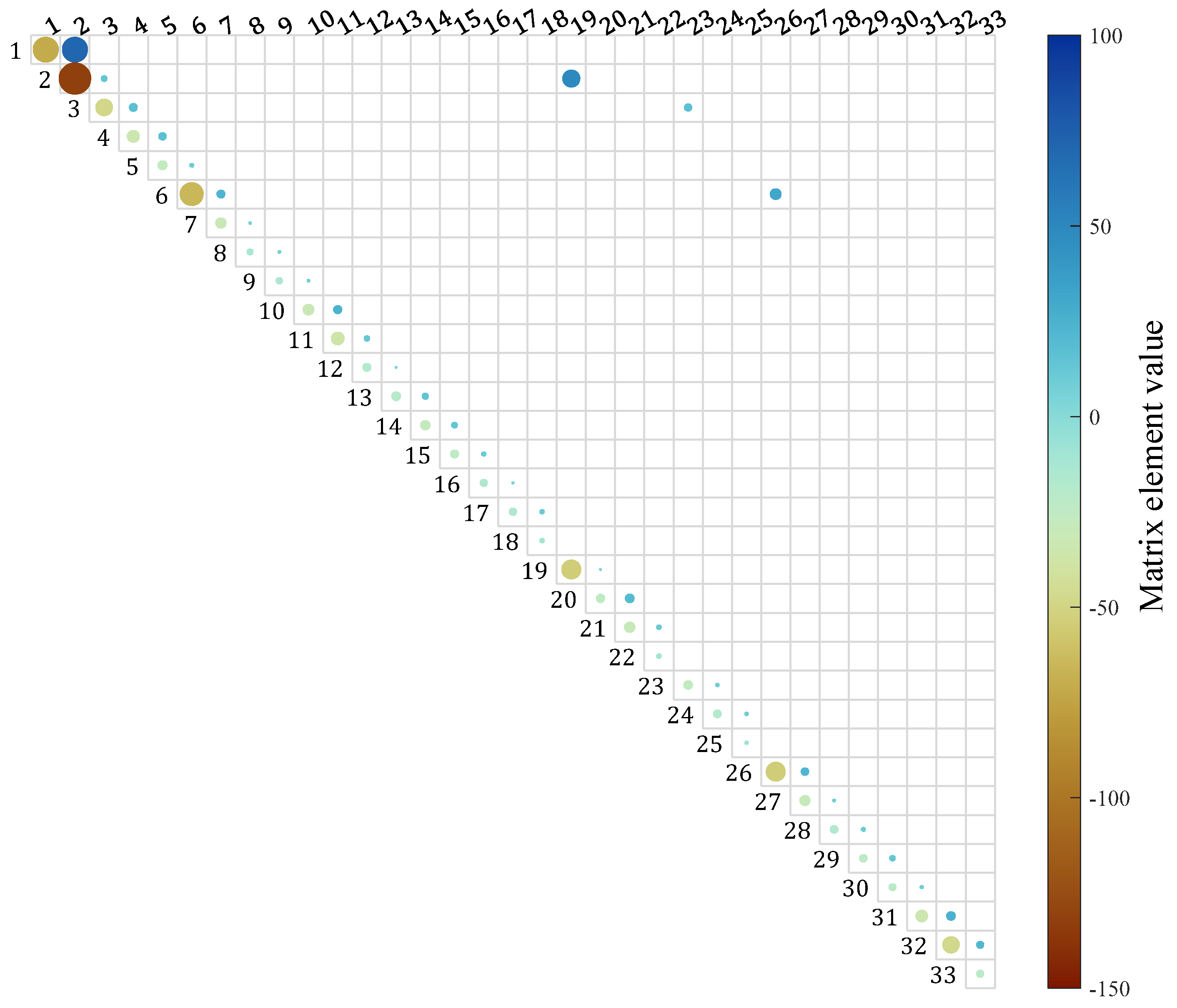
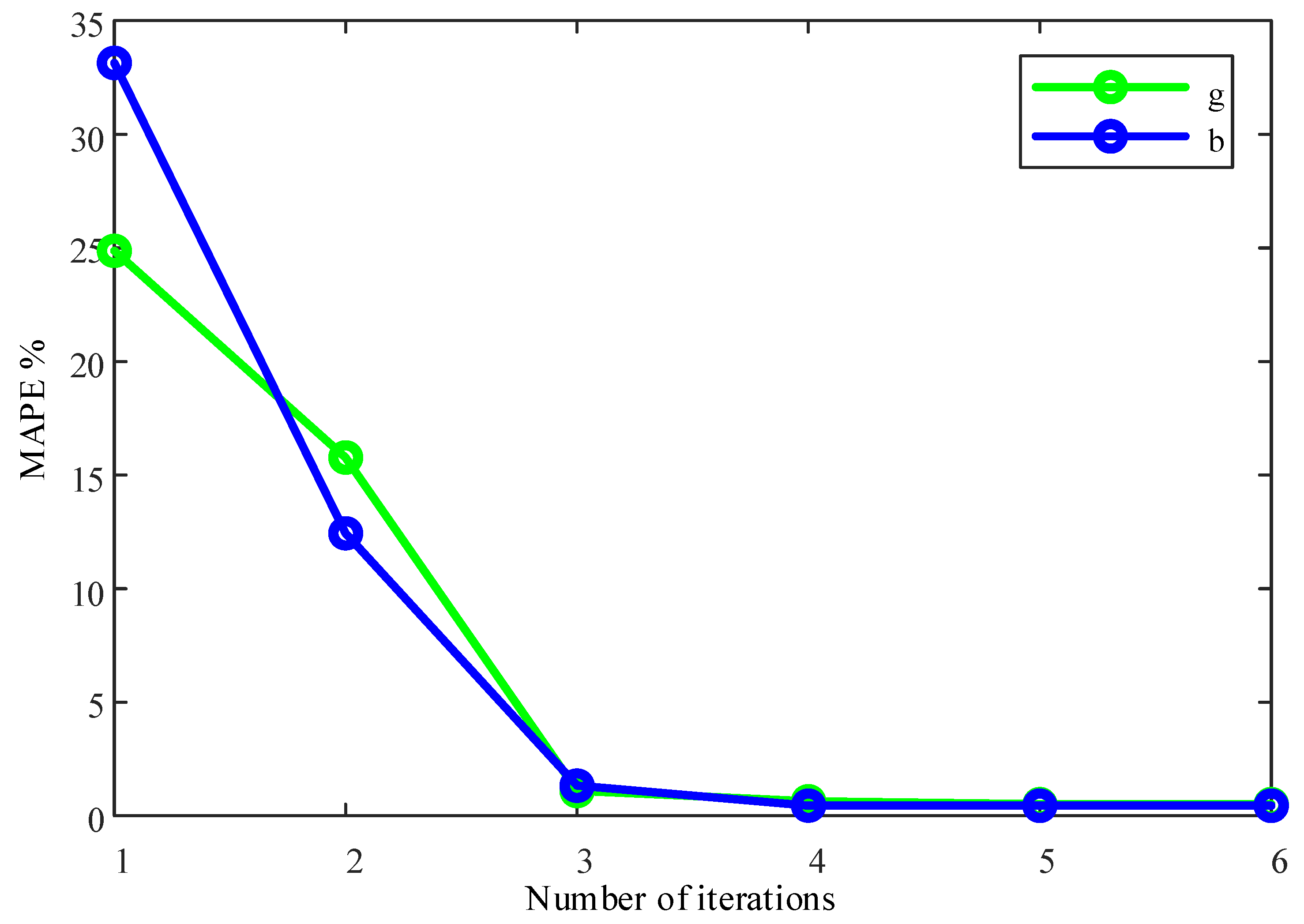
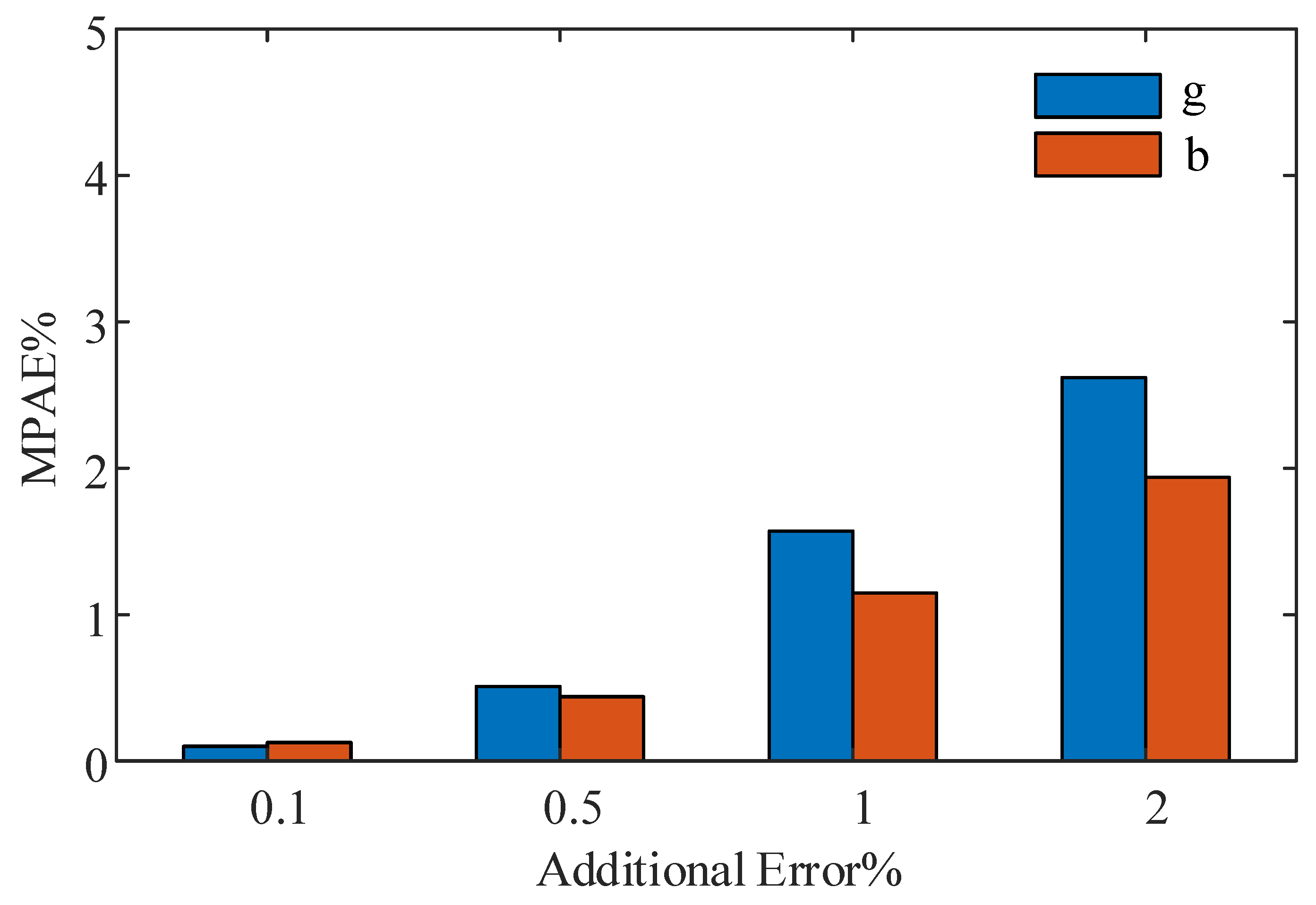
4. Case Study
4.1. A 10 kV Distribution Network of the Southern Power Grid
4.1.1. Interpretation of CIM Models
4.1.2. Topology Construction and Reduction
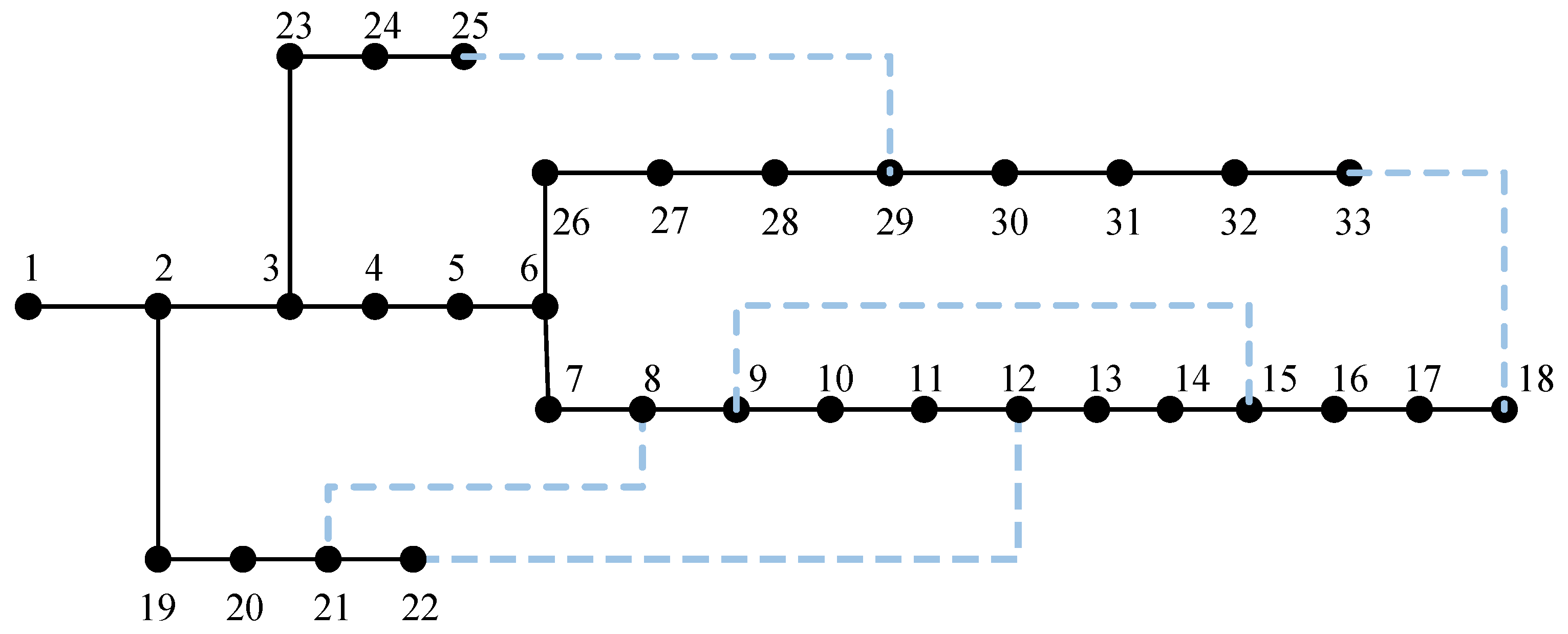
4.2. IEEE 33-Bus Arithmetic Example
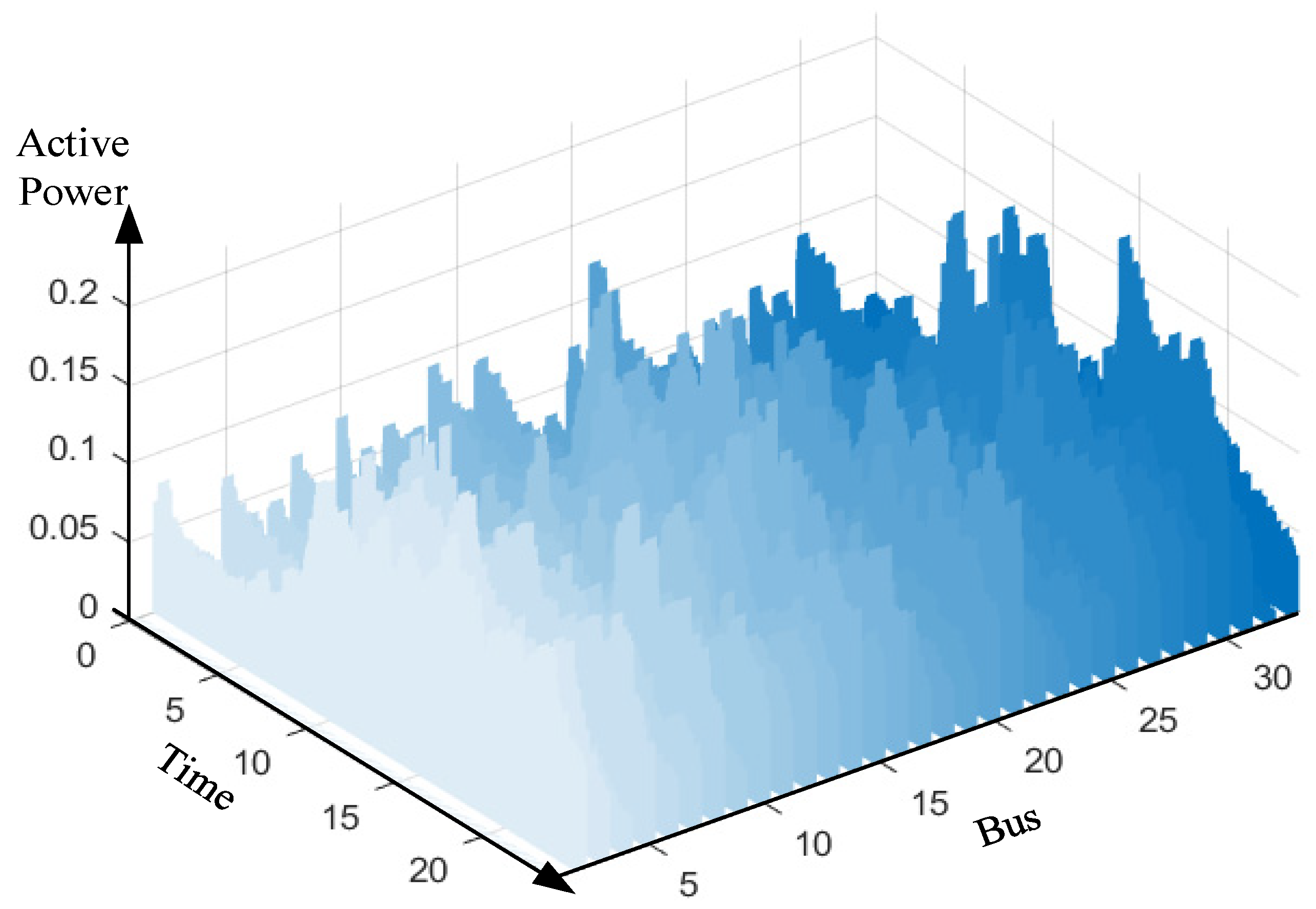
4.2.1. Data Sources
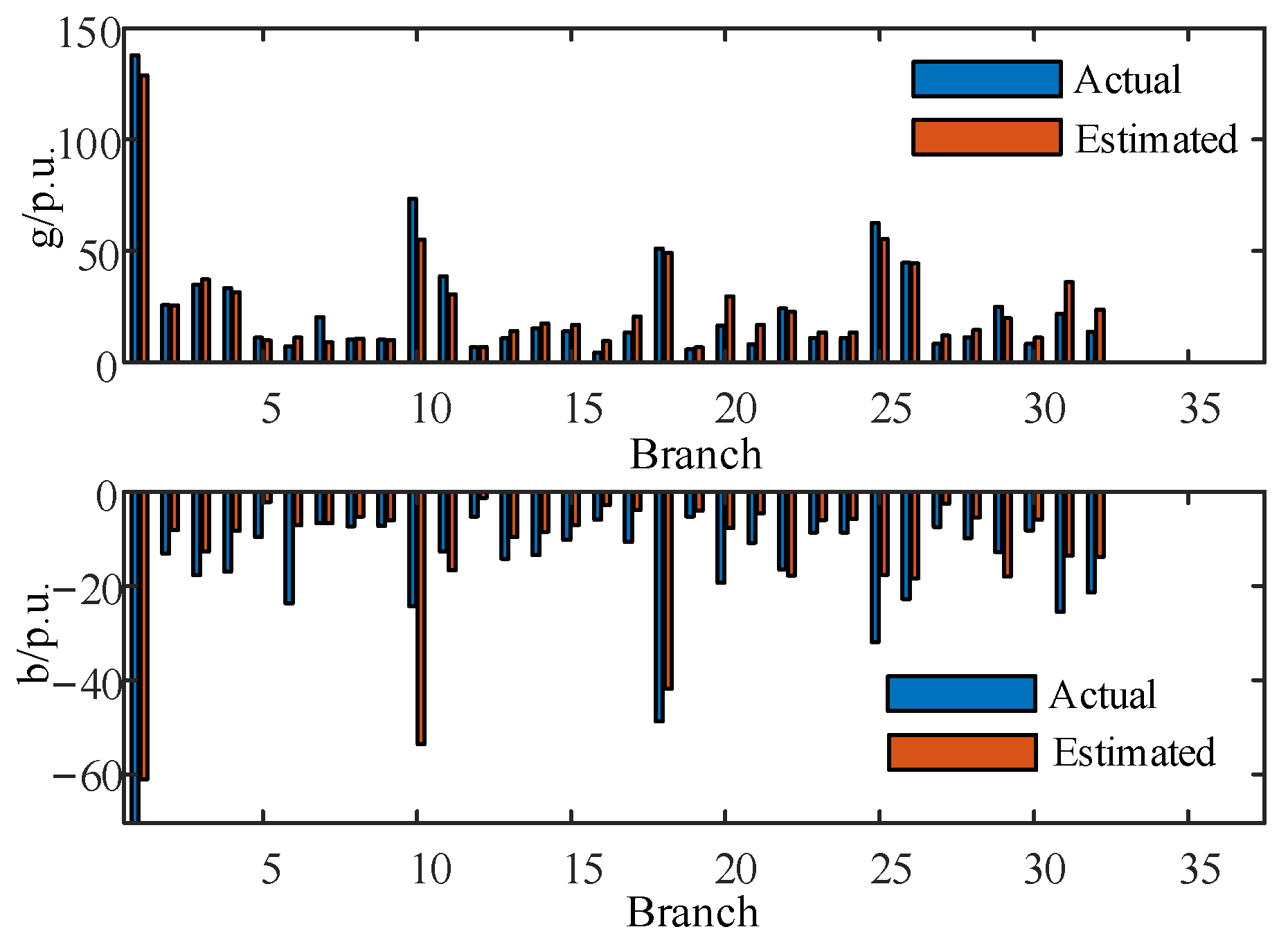
4.2.2. Parameter Identification and Correction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| From-Bus | To-Bus | R/p.u. | x/p.u. | g/p.u. | b/p.u. |
|---|---|---|---|---|---|
| 1 | 2 | 0.005752591 | 0.002932449 | 137.9797487 | 70.33674826 |
| 2 | 3 | 0.030759517 | 0.015666764 | 25.81372643 | 13.14772151 |
| 3 | 4 | 0.022835666 | 0.011629967 | 34.77210183 | 17.70907044 |
| 4 | 5 | 0.023777793 | 0.01211039 | 33.39366716 | 17.00790028 |
| 5 | 6 | 0.051099481 | 0.044111518 | 11.21344567 | 9.679983017 |
| 6 | 7 | 0.011679881 | 0.038608497 | 7.178626562 | 23.72934891 |
| 7 | 8 | 0.044386045 | 0.014668484 | 20.31132637 | 6.712388009 |
| 8 | 9 | 0.064264305 | 0.046170471 | 10.2632184 | 7.373574386 |
| 9 | 10 | 0.0651378 | 0.046170471 | 10.21826246 | 7.242829715 |
| 10 | 11 | 0.012266371 | 0.004055514 | 73.49046416 | 24.29745763 |
| 11 | 12 | 0.023359763 | 0.007724195 | 38.58938266 | 12.76005762 |
| 12 | 13 | 0.091592232 | 0.072063371 | 6.743516093 | 5.305695563 |
| 13 | 14 | 0.033791794 | 0.044479634 | 10.82958145 | 14.2548165 |
| 14 | 15 | 0.036873985 | 0.03281847 | 15.13248987 | 13.46817203 |
| 15 | 16 | 0.046563544 | 0.034003928 | 14.00647124 | 10.22849635 |
| 16 | 17 | 0.08042397 | 0.107377542 | 4.468506866 | 5.966097995 |
| 17 | 18 | 0.045671331 | 0.035813312 | 13.55850447 | 10.63194203 |
| 2 | 19 | 0.010232375 | 0.009764431 | 51.15021119 | 48.8110247 |
| 19 | 20 | 0.093850842 | 0.084566834 | 5.880551785 | 5.298829869 |
| 20 | 21 | 0.025549741 | 0.029848586 | 16.55068241 | 19.3354004 |
| 21 | 22 | 0.044230064 | 0.058480517 | 8.226906073 | 10.87752724 |
| 3 | 23 | 0.028151509 | 0.019235617 | 24.21601005 | 16.54653346 |
| 23 | 24 | 0.056028491 | 0.044242542 | 10.9933197 | 8.68080512 |
| 24 | 25 | 0.055903706 | 0.043743402 | 11.09484588 | 8.681469249 |
| 6 | 26 | 0.012665683 | 0.006451387 | 62.68900914 | 31.93124899 |
| 26 | 27 | 0.017731957 | 0.009028199 | 44.78550993 | 22.80247462 |
| 27 | 28 | 0.066073688 | 0.058255904 | 8.515218246 | 7.507704699 |
| 28 | 29 | 0.050176072 | 0.043712206 | 11.33053184 | 9.870891083 |
| 29 | 30 | 0.031664208 | 0.016128469 | 25.07560365 | 12.7724996 |
| 30 | 31 | 0.06079528 | 0.060084005 | 8.321106011 | 8.22375317 |
| 31 | 32 | 0.01937288 | 0.022579856 | 21.886343 | 25.50939624 |
| 32 | 33 | 0.021275852 | 0.033080519 | 13.75312955 | 21.3838982 |
| 21 | 8 | 0.124785058 | 0.124785058 | 4.00689 | 4.00689 |
| 9 | 15 | 0.124785058 | 0.124785058 | 4.00689 | 4.00689 |
| 12 | 22 | 0.124785058 | 0.124785058 | 4.00689 | 4.00689 |
| 18 | 33 | 0.031196264 | 0.031196264 | 16.02756 | 16.02756 |
| 25 | 29 | 0.031196264 | 0.031196264 | 16.02756 | 16.02756 |
Appendix B
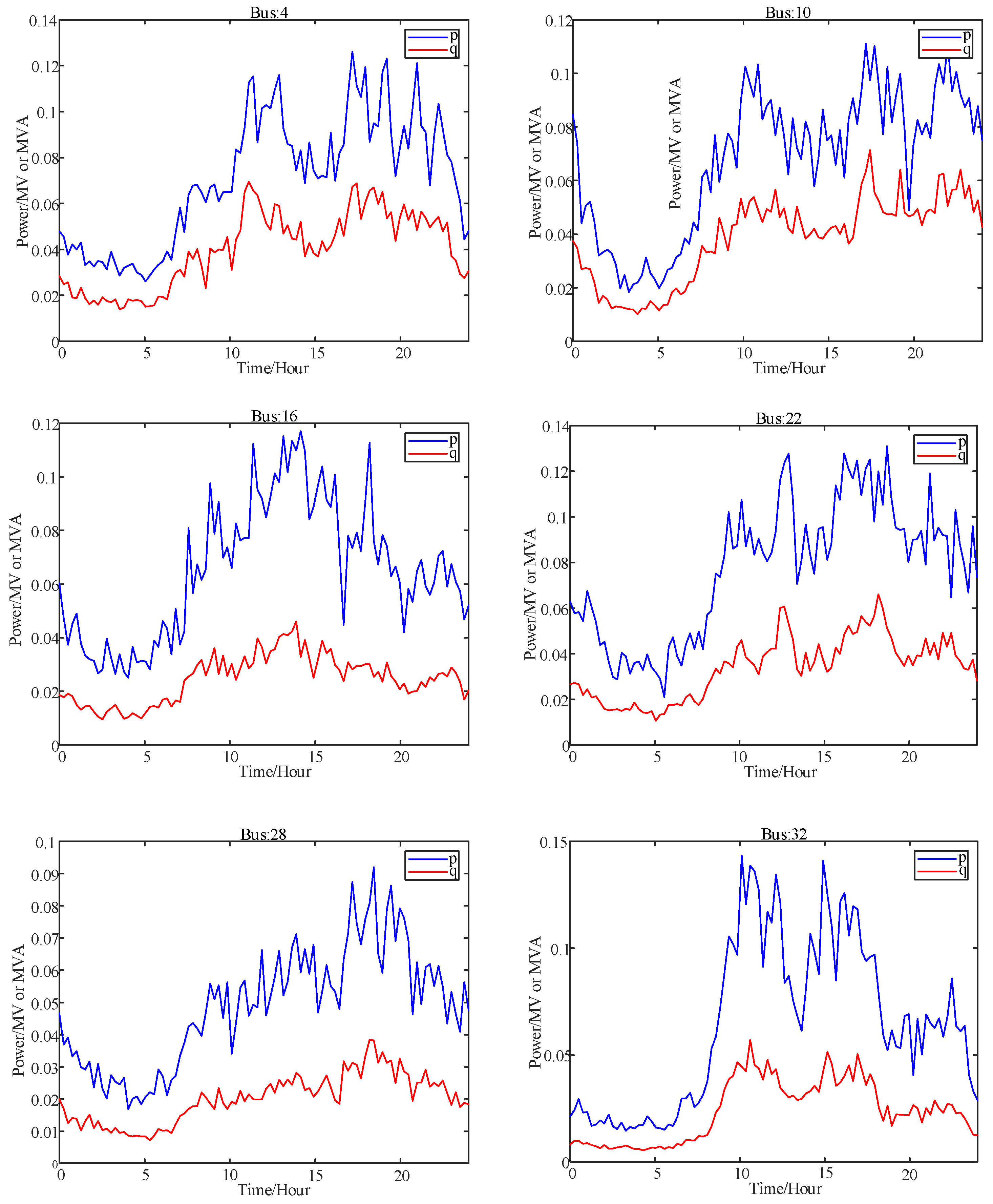
Appendix C

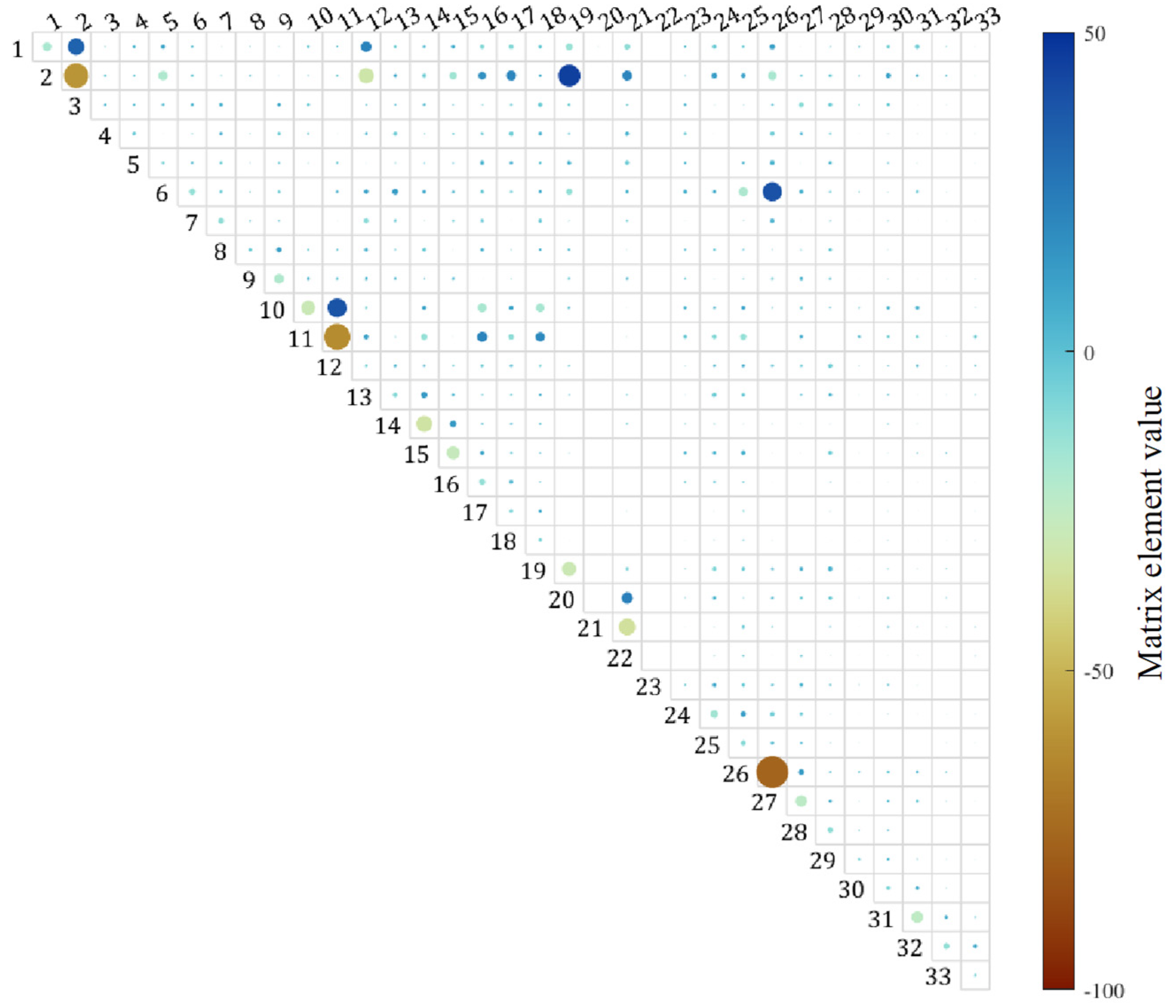
References
- Liu, D. Planning Strategy of New Energy System for Power Distribution Network Considering Uncertainty of Source and Load. Guangdong Power 2023, 36, 77–83. [Google Scholar]
- Zhu, Y.; Yao, R.; Wang, L.; Bai, H.; Li, W.; Du, W.; Xu, M. Sensitivity Analysis Method for Resonant Frequency of Power Grids Based on Singular Value Decomposition. South. Power Syst. Technol. 2024, 1–8. [Google Scholar]
- Zhang, Y.; Hu, Y.; Wang, D. Automatic Modeling Method of Distribution Network Topology Based on Power Line Communication. Electr. Autom. 2022, 44, 61–62, 66. [Google Scholar]
- Zhou, L. Research on Self-Healing Technology of Active Distribution Network; Southeast University: Nanjing, China, 2017. [Google Scholar]
- Li, B.; Sun, M.; Chen, X.; Li, B.; Ji, X.; Xiao, F. Line Parameter Identification Method for Multi-ring Medium-voltage Distribution Network Based on Phaseless Measurement. Autom. Electr. Power Syst. 2023, 47, 22–30. [Google Scholar]
- Sun, K.; Wang, D.; Ge, X.; Wang, W.; Sun, W. Topoloqical Evolution Model of Power System Based on Positioning Probability and Attenuation Mechanism. Proc. CSU-EPSA 2021, 33, 22–28. [Google Scholar]
- Ma, D.; Shen, C.; Chen, Y.; Li, D. Feasibility Study on the Convergence Criterion of Power Flow Calculation Based on Deep Learning. South. Power Syst. Technol. 2020, 14, 46–54. [Google Scholar]
- Kusic, G.L.; Garrison, D.L. Measurement of transmission line parameters from SCADA data. In Proceedings of the IEEE PES Power Systems Conference & Exposition, New York, NY, USA, 10–13 October 2004; Volume 1, pp. 440–445. [Google Scholar]
- Li, H.; Weng, Y.; Vittal, V.; Blasch, E. Distribution Grid Topology and Parameter Estimation Using Deep-Shallow Neural Network with Physical Consistency. IEEE Trans. Smart Grid 2024, 15, 655–666. [Google Scholar] [CrossRef]
- Dutta, R.; Patel, V.S.; Chakrabarti, S.; Sharma, A.; Das, R.K.; Mondal, S. Parameter Estimation of Distribution Lines Using SCADA Measurements. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Shah, P.; Zhao, X. Network Identification Using μ-PMU and Smart Meter Measurements. IEEE Trans. Ind. Inform. 2022, 18, 7572–7586. [Google Scholar] [CrossRef]
- Guo, Y.; Yuan, Y.; Wang, Z. Distribution Grid Modeling Using Smart Meter Data. IEEE Trans. Power Syst. 2022, 37, 1995–2004. [Google Scholar] [CrossRef]
- Yu, J.; Weng, Y.; Rajagopal, R. PaToPaEM: A Data-Driven Parameter and Topology Joint Estimation Framework for Time-Varying System in Distribution Grids. IEEE Trans. Power Syst. 2019, 34, 1682–1692. [Google Scholar] [CrossRef]
- Park, S.; Deka, D.; Backhaus, S.; Chertkov, M. Learning With End-Users in Distribution Grids: Topology and Parameter Estimation. IEEE Trans. Control Netw. Syst. 2020, 7, 1428–1440. [Google Scholar] [CrossRef]
- Luan, W.; Peng, J.; Maras, M.; Lo, J.; Harapnuk, B. Smart Meter Data Analytics for Distribution Network Connectivity Verification. IEEE Trans. Smart Grid 2015, 6, 1964–1971. [Google Scholar] [CrossRef]
- Pappu, S.J.; Bhatt, N.; Pasumarthy, R.; Rajeswaran, A. Identifying Topology of Low Voltage Distribution Networks Based on Smart Meter Data. IEEE Trans. Smart Grid 2018, 9, 5113–5122. [Google Scholar] [CrossRef]
- Zhao, J.; Li, L.; Xu, Z.; Wang, X.; Wang, H.; Shao, X. Full-Scale Distribution System Topology Identification Using Markov Random Field. IEEE Trans. Smart Grid 2020, 11, 4714–4726. [Google Scholar] [CrossRef]
- Tian, Z.; Wu, W.; Zhang, B. A Mixed Integer Quadratic Programming Model for Topology Identification in Distribution Network. IEEE Trans. Power Syst. 2016, 31, 823–824. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, G. Introduction to IEC61970 standard series. Autom. Electr. Power Syst. 2002, 14, 1–6. [Google Scholar]
- Chen, G.; Zhang, Z.; Hong, X.; Li, C. Modeling Method for Digital Twin of Distribution Automation Terminal Based on lEC 61968. Power System Technol. 2024, 1–9. [Google Scholar] [CrossRef]
- Cai, W.; Fang, W.; Zhu, W.; Liu, P.; Xia, W. Power system graph model data fusion technology based on CIM/SVG. J. Shenyang Univ. Technol. 2023, 45, 656–660. [Google Scholar]
- Xu, Y.; Ma, W.; Zhao, L.; Weng, Y.; Zhen, H.; Shi, J.; Zhai, H.; He, X. Multi-Granularity Power Flow Calculation Data Construction Method Based on ClM. South. Power Grid Technol. 2022, 16, 40–47. [Google Scholar]
- Wang, X.; Zhang, J.; Du, X.; He, X.; Zhang, W.; Zhao, B.; Liu, Q. Optimal Allocation of Energy Storage in Distribution Networks Based on Electric Common Information Model. South. Power Syst. Technol. 2024, 18, 112–123. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, T. Research on CIM model based on IEC61970. Sci. Technol. Inf. 2013, 89+93. [Google Scholar]
- Ao, X.; Wang, C.; Zhu, W.; Xiao, Y. Derivation and Comparison of Two Versions of Linear Power Flow Method for Distribution Networks. Power Syst. Technol. 2017, 41, 4004–4013. [Google Scholar]
- Zhang, J.; Wang, Y.; Weng, Y.; Zhang, N. Topology identification and line parameter estimation for non-PMU distribution network: A numerical method. IEEE Trans. Smart Grid 2020, 11, 4440–4453. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, X. Decompositions and Generalized Inverses of Matrices. Univ. Math. 2019, 36, 57–66. [Google Scholar]

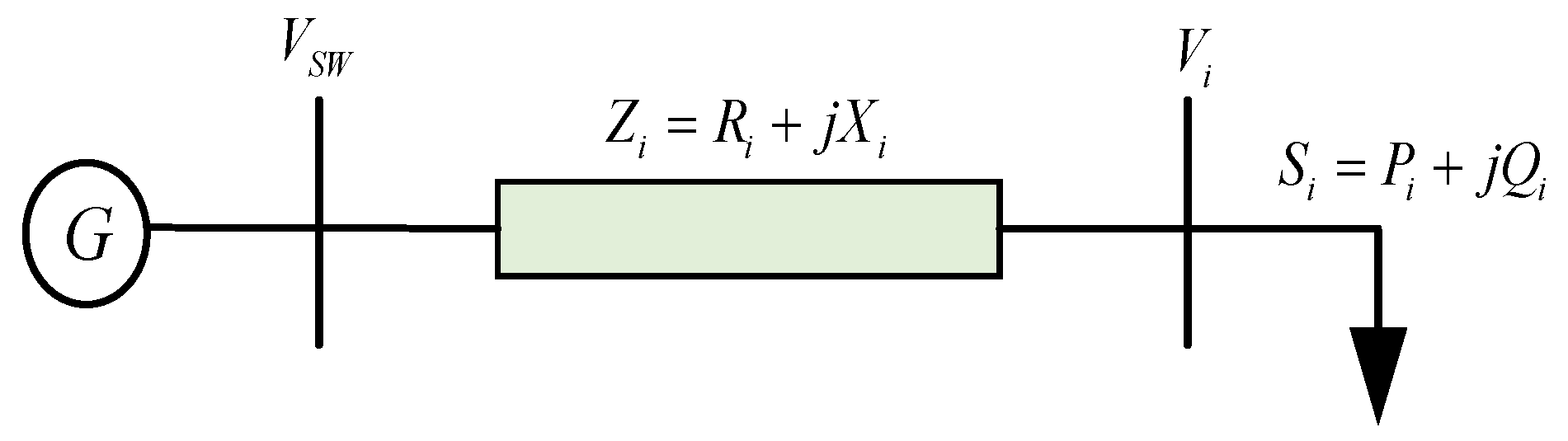



| No. | Type | CIM Model Class Name |
|---|---|---|
| 1 | AC LINE | Circuit |
| 2 | ACLineSegment | |
| 3 | Junction | |
| 4 | SWITCH | Breaker |
| 5 | LoadBreakSwitch | |
| 6 | Disconnector | |
| 7 | GroundDisconnector | |
| 8 | Fuse | |
| 9 | TRANSFORMER | PowerTransformer |
| 10 | TERMINAL | Terminal |
| 11 | NODE | ConnectivityNode |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, K.; Wu, L.; Zhang, B.; Yao, R.; Bai, H.; Yang, W.; Xu, M. Research on Parameter Correction of Distribution Network Model Based on CIM Model and Measurement Data. Energies 2024, 17, 3611. https://doi.org/10.3390/en17153611
Zhou K, Wu L, Zhang B, Yao R, Bai H, Yang W, Xu M. Research on Parameter Correction of Distribution Network Model Based on CIM Model and Measurement Data. Energies. 2024; 17(15):3611. https://doi.org/10.3390/en17153611
Chicago/Turabian StyleZhou, Ke, Lifang Wu, Biyun Zhang, Ruotian Yao, Hao Bai, Weichen Yang, and Min Xu. 2024. "Research on Parameter Correction of Distribution Network Model Based on CIM Model and Measurement Data" Energies 17, no. 15: 3611. https://doi.org/10.3390/en17153611
APA StyleZhou, K., Wu, L., Zhang, B., Yao, R., Bai, H., Yang, W., & Xu, M. (2024). Research on Parameter Correction of Distribution Network Model Based on CIM Model and Measurement Data. Energies, 17(15), 3611. https://doi.org/10.3390/en17153611






