Collaborative Planning of Distribution Network, Data Centres and Renewable Energy in the Power Distribution IoT via Interval Optimization
Abstract
:1. Introduction
- ▪
- How can a collaborative optimization of DCs, RESs, and DNs be developed from a long-term planning perspective to promote carbon reduction?
- ▪
- How can multidimensional uncertain factors be modeled in a collaborative planning setting?
- ▪
- How can the mathematical model with interval variables be solved efficiently?
2. Literature Review
Contributions and Paper Organization
3. Model Framework
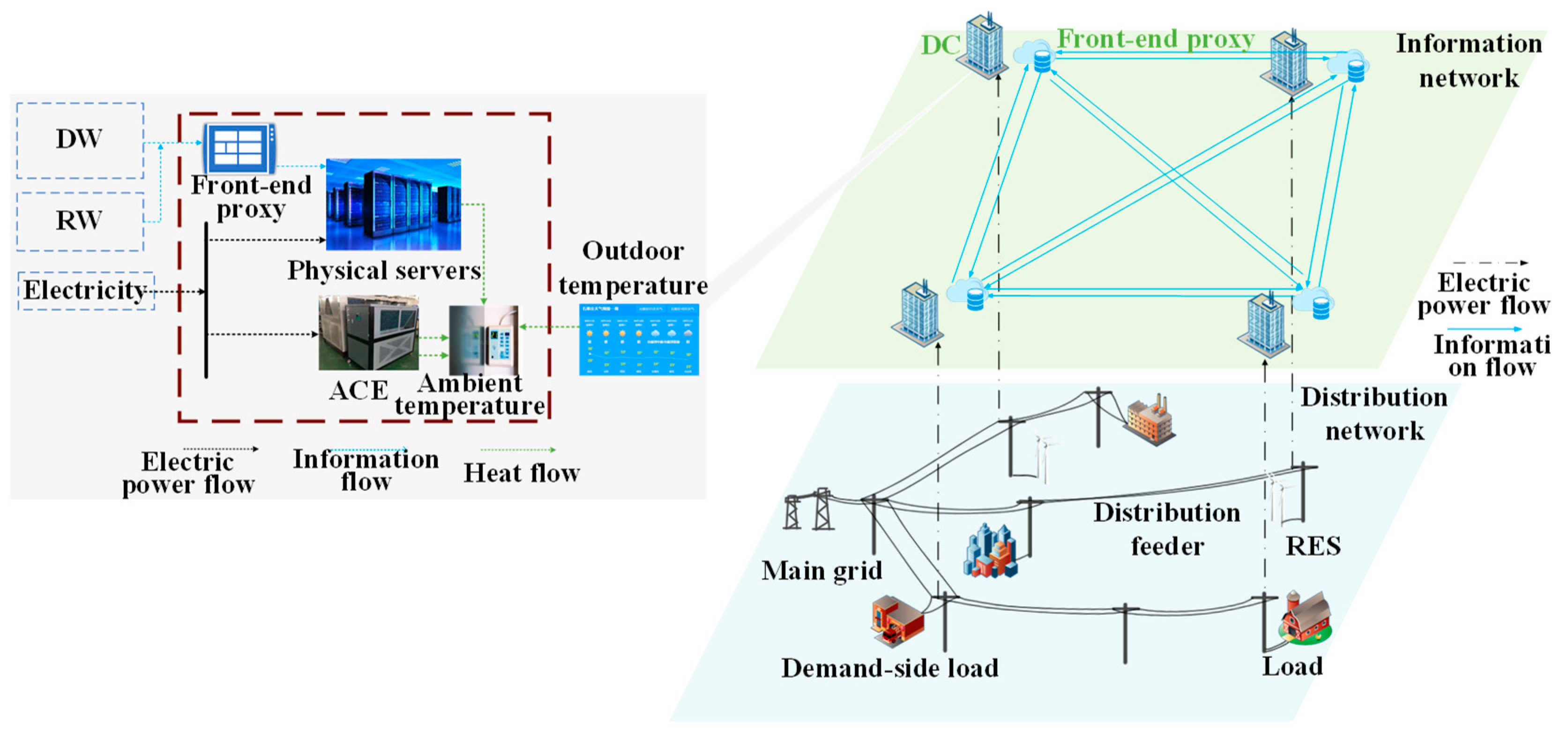
3.1. System Structure
3.2. Model Framework
4. DC Modeling
4.1. Information Domain
4.1.1. Delay-Tolerant Workloads (DW)
4.1.2. Real-Time Workloads (RWs)
4.1.3. Quality of Service Requirement
4.2. Physical Domain
4.2.1. Thermodynamic Process
4.2.2. Power Consumption Characteristics
5. A Collaborative Planning Model for the DN and DC Based on Interval Optimization
5.1. Objective Function
5.2. Constraints Conditions
5.2.1. Planning Stage
5.2.2. Operation Stage
- (1)
- RES
- (2)
- DN
5.2.3. Uncertain Variables
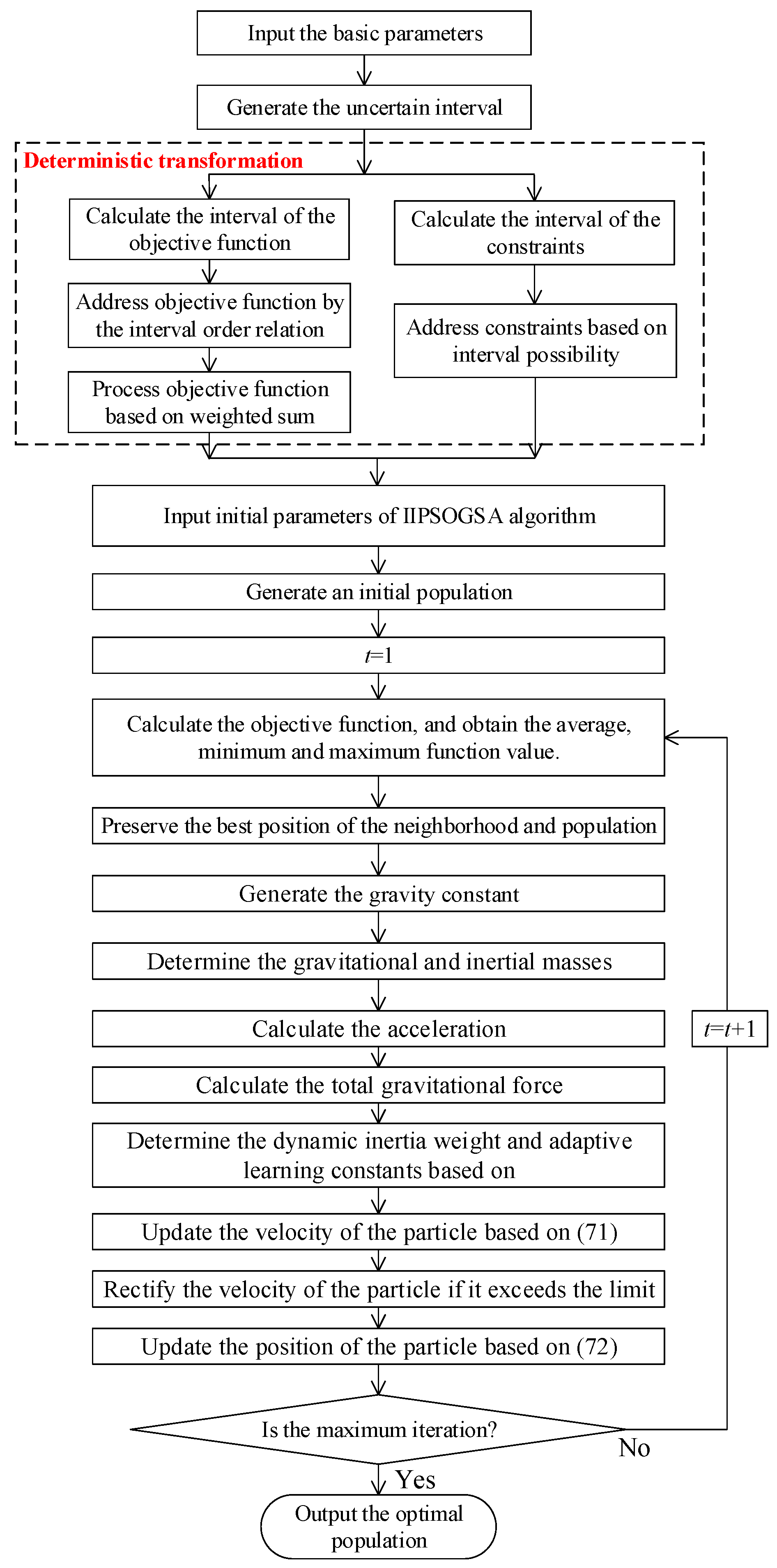
6. Solution Algorithm
6.1. Deterministic Transformation
6.2. Improved Integrated PSOGSA Algorithms
6.2.1. Traditional PSO and GSA
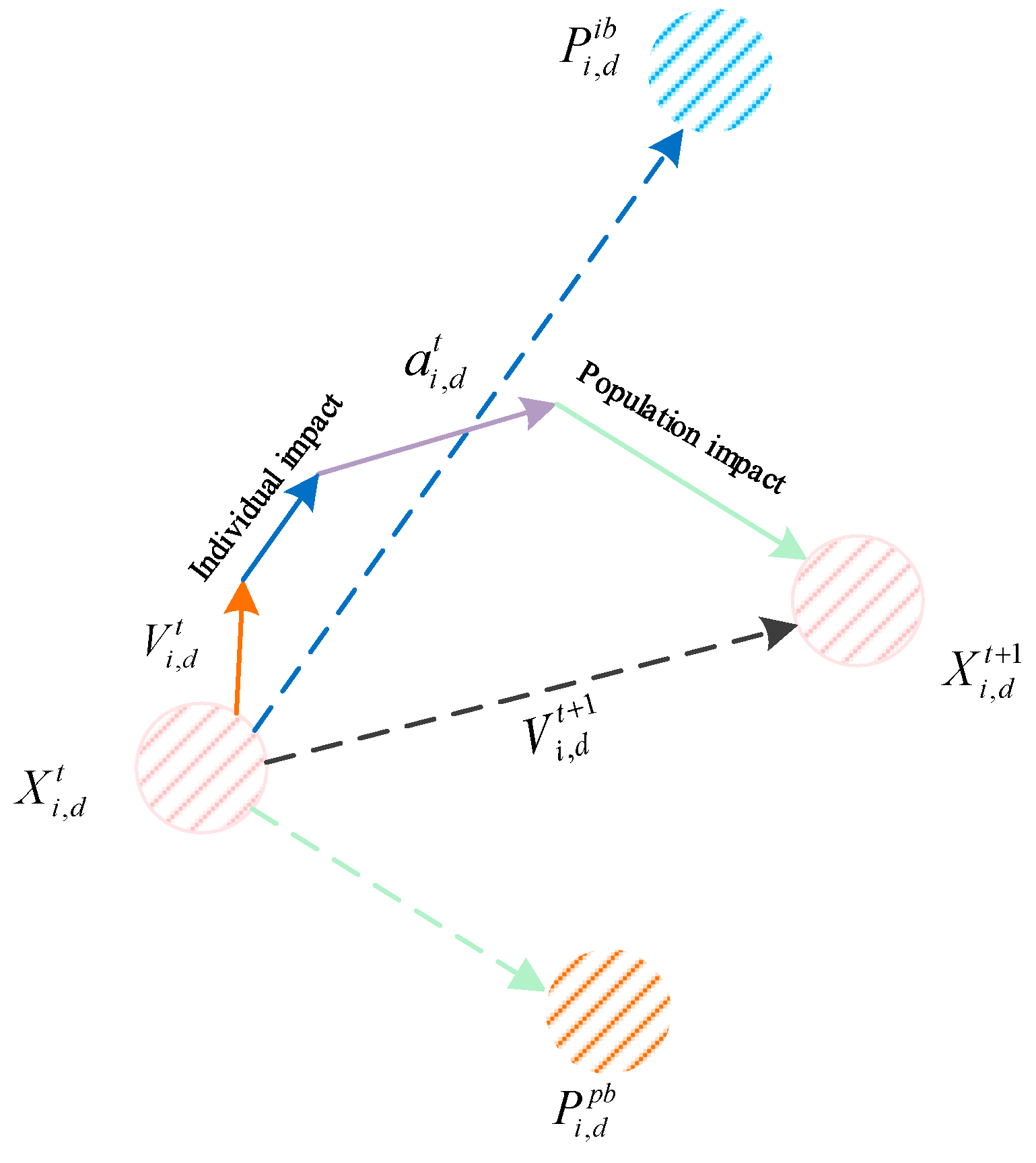
6.2.2. IIPSOA-GSA
- (1)
- Improved particle-updating scheme
- (2)
- Adaptive parameter strategy
6.3. Steps of the Algorithm
7. Case Study
7.1. Test System and Parameters
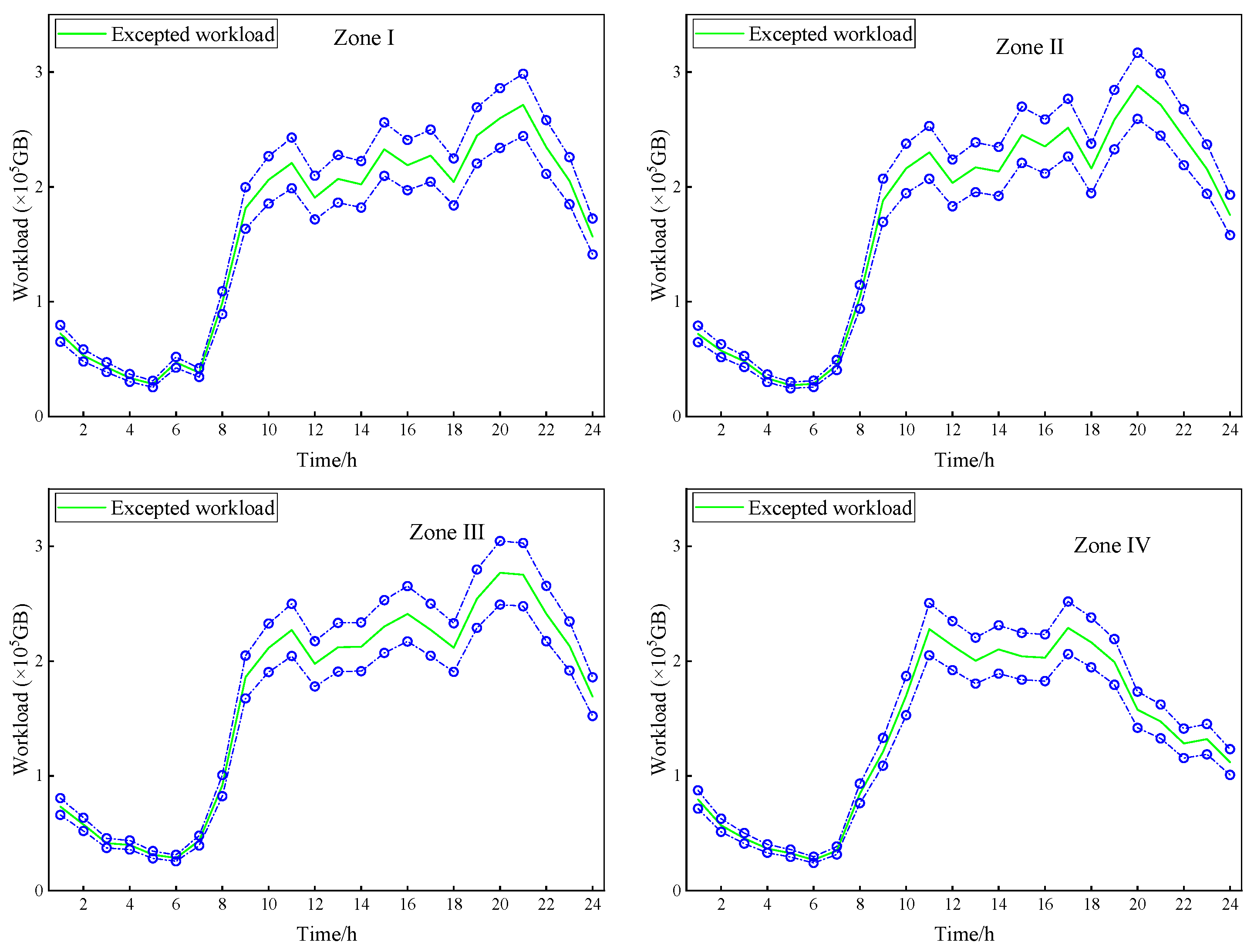
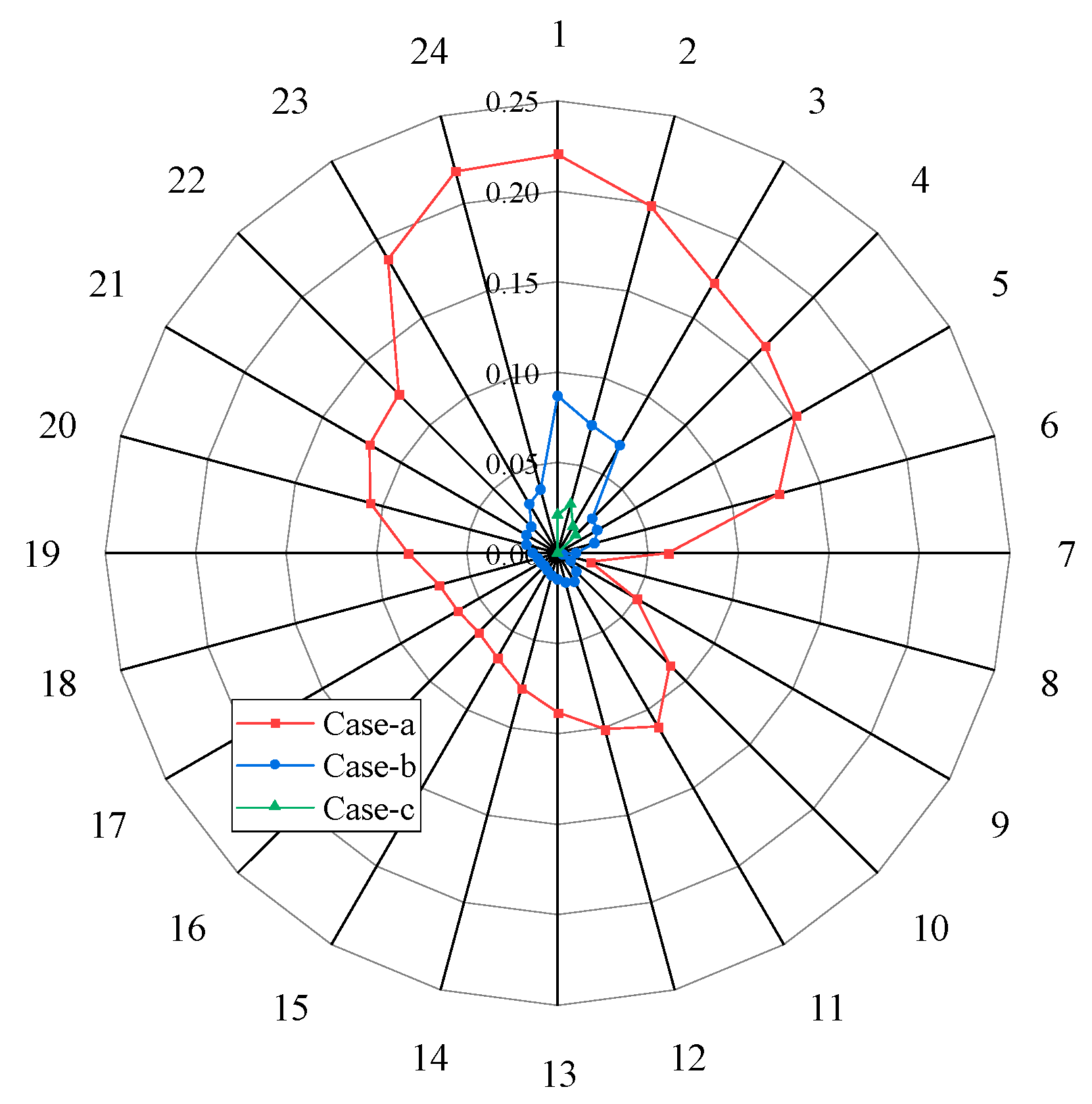
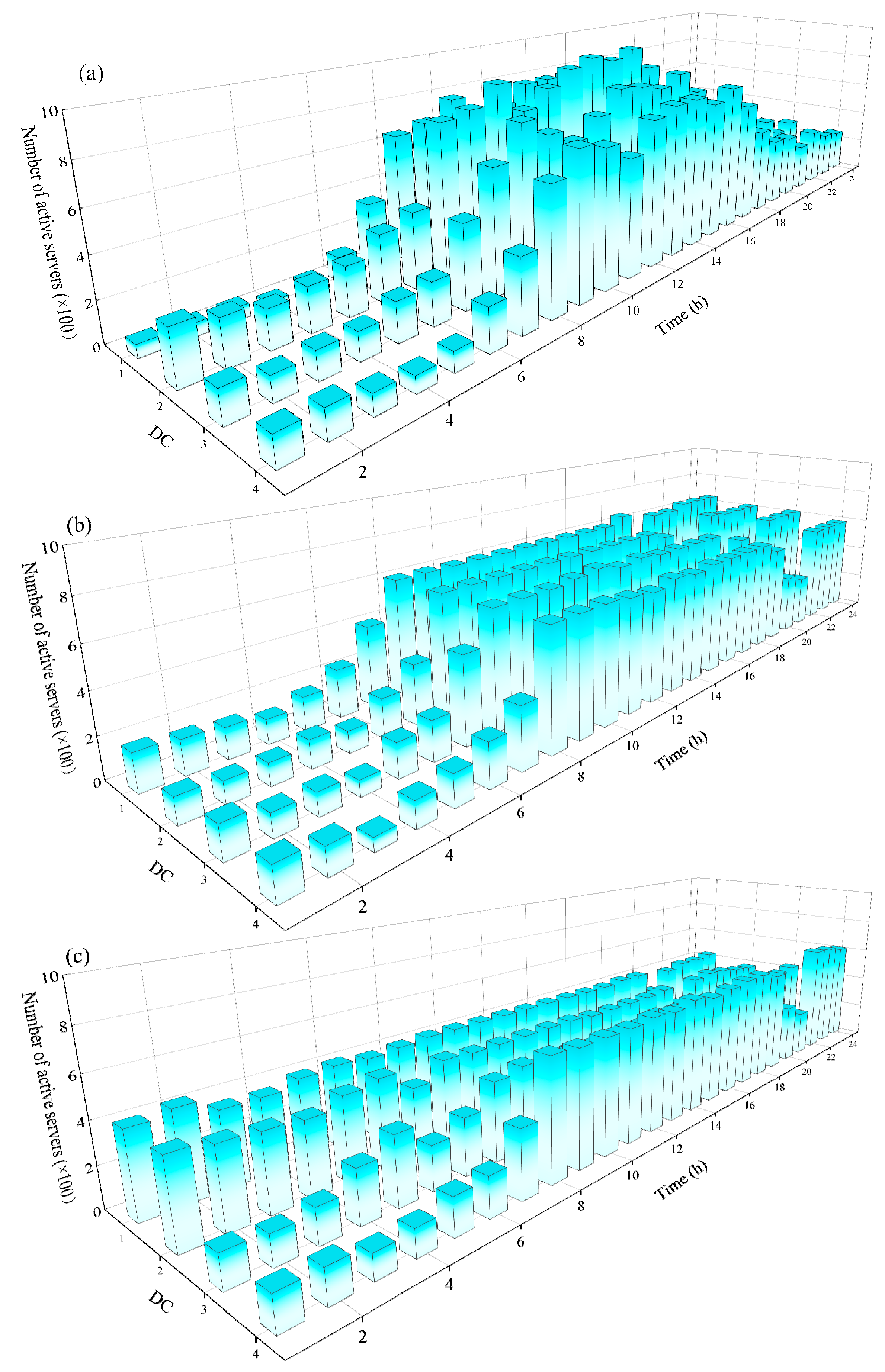
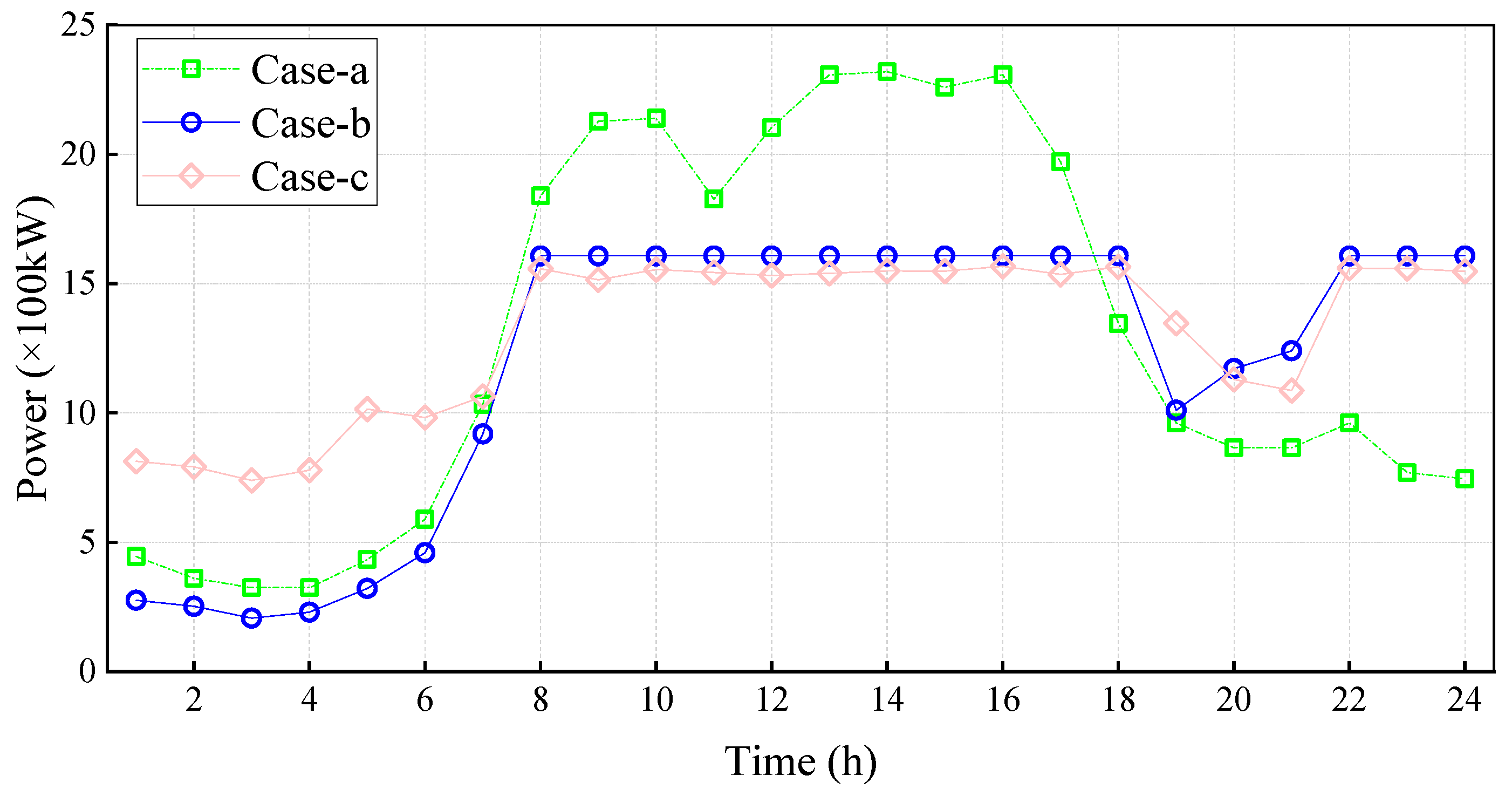
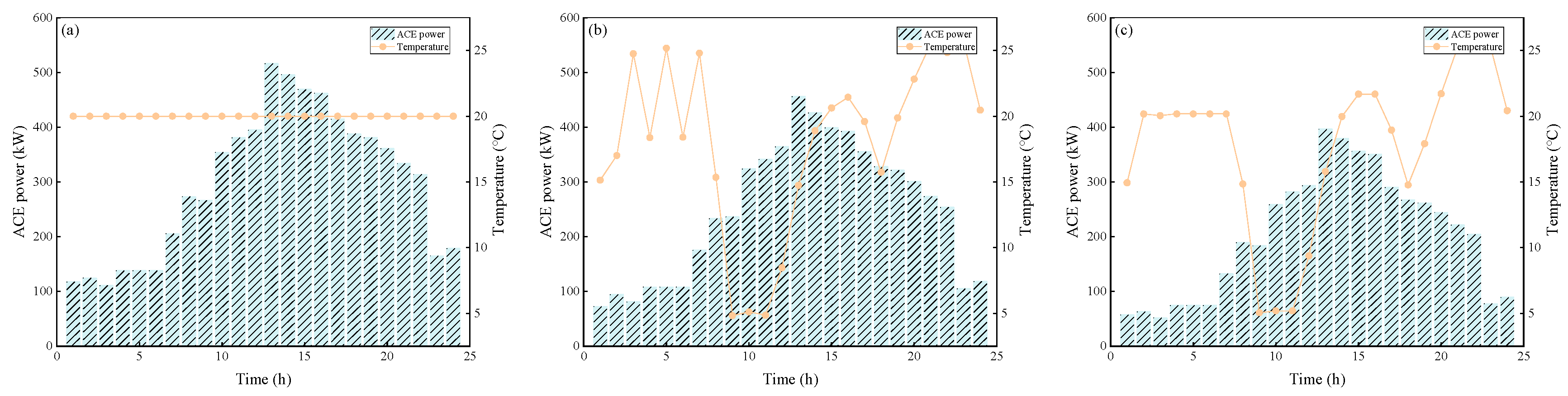
7.2. Results of the Experiments
7.3. Discussion
7.3.1. Performance of DC Demand Response
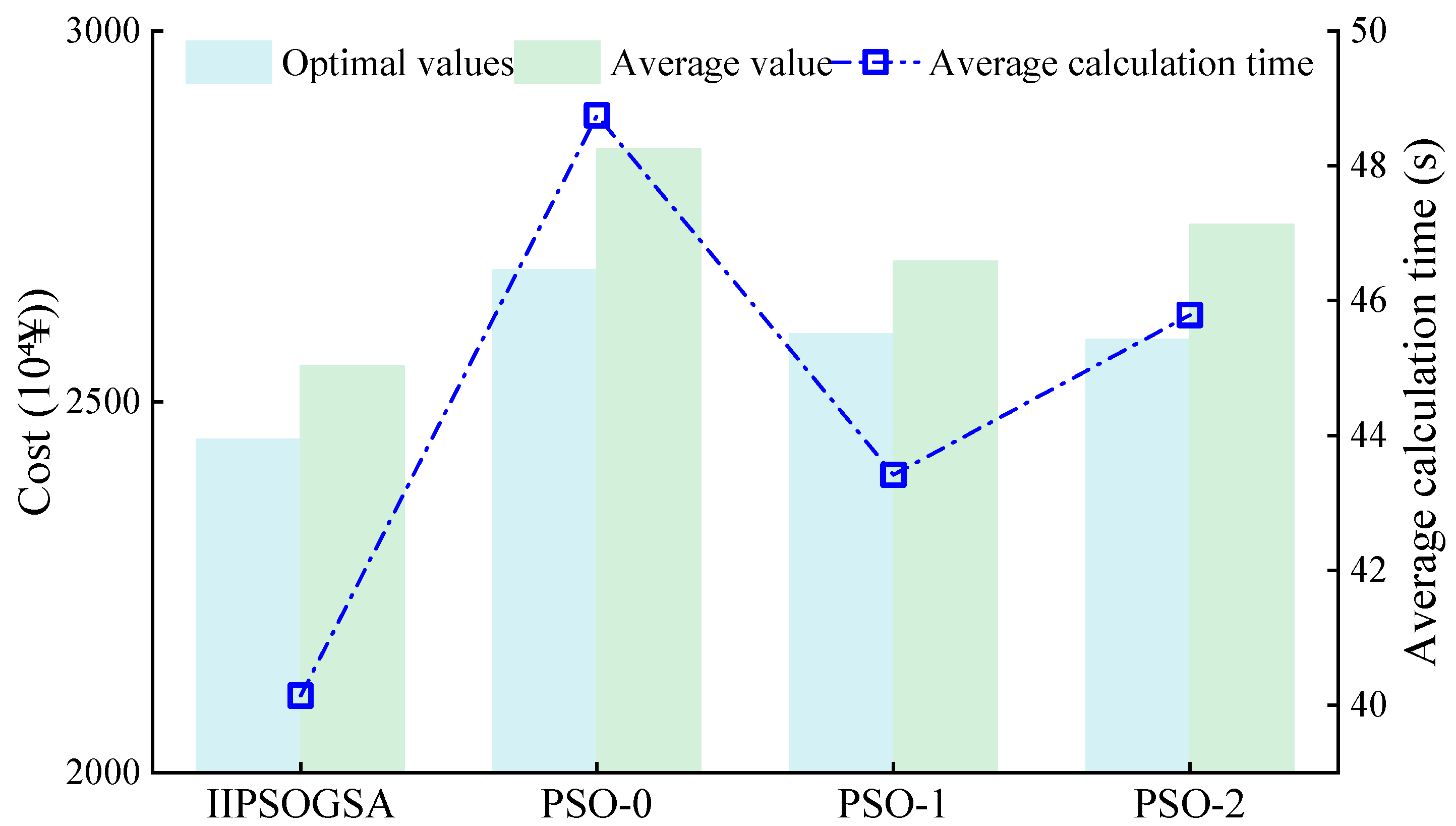
7.3.2. Performance of the Proposed Algorithm
8. Imitations of the Proposed Framework
9. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indicates (Sets) | |
| i | Load node |
| d | DC node |
| t | Time periods |
| j | RES node |
| Variables | |
| Data workload capacity transferred from time t to time t’ | |
| Number of data transferred between the two DCs | |
| Quantity of DW/RW data at the end of scheduling | |
| Waiting time for data workloads in the queue | |
| Data-processing time | |
| Indoor/outdoor temperature of the DC | |
| Upper and lower bounds of the indoor temperature of the DC | |
| Indoor-temperature variation rates of the data center | |
| Total active power consumption of the DC at time t for node d | |
| Active power of servers / ACE | |
| Number of servers in the powered-on state at time t | |
| Number of installed servers | |
| Maximum CPU utilization | |
| Cooling power of the DC | |
| ACE installation capacity | |
| Capacity expansion of the distribution transformer | |
| Investment cost for equipment X | |
| Investment cost for the distribution line | |
| Binary variable representing the linear selection | |
| Length of the line | |
| Purchased power from the main grid | |
| Purchase price of electricity | |
| Cost coefficient for DW participating in demand response | |
| Intensity of carbon emissions for electricity production on the grid side | |
| Maximum expansion capacity of the substation | |
| Maximum installation number of equipment X | |
| / | Active/reactive power flowing through line ij at time t |
| Active/reactive power of the load at time t | |
| Reactive power of RES/DC at time t | |
| Maximum/minimum allowable voltage values at node i | |
| / | Resistance/reactance of line ij |
| Capacities of line ij before and after the transformation | |
| Uncertain variables | |
| Interval of RES load factor | |
| Interval of electricity price | |
| Interval of carbon emission coefficient | |
| Interval of electric load demand | |
| Interval of workloads | |
| Parameters | |
| Ratio of DW/RW in the total data workloads | |
| Initial amount of DW/RW | |
| The maximum allowable delay time for users | |
| Air density | |
| Specific heat capacity of air | |
| Wall area of the DC room | |
| The unit wall heat exchange coefficient | |
| Operating heat dissipation coefficient of the equipment | |
| Energy efficiency coefficient of the DC/ACE | |
| Average utilization of the server | |
| Server processing rate | |
| Server spare coefficient | |
| Standby/peak power consumption of a single server |
References
- Koot, M.; Wijnhoven, F. Usage impact on data center electricity needs: A system dynamic forecasting model. Appl. Energy 2021, 291, 116798. [Google Scholar] [CrossRef]
- Ting, Y.; Han, J.; Yucheng, H. Study on carbon neutrality regulation method of interconnected multi-datacenter based on spatio-temporal dual-dimensional computing load migration. Proc. CSEE 2022, 42, 164–177. [Google Scholar]
- Li, C.; Yan, Z.; Yao, Y.; Deng, Y.; Shao, C.; Zhang, Q. Coordinated low-carbon dispatching on source-demand side for integrated electricity-gas system based on integrated demand response exchange. IEEE Trans. Power Syst. 2024, 39, 1287–1303. [Google Scholar] [CrossRef]
- Zhu, X.; Zhan, X.; Sun, Y.; Zhang, Y. Cloud-edge collaborative distributed optimal dispatching strategy for an electric-gas integrated energy system considering carbon emission reductions. Int. J. Electr. Power Energy Syst. 2022, 143, 108458. [Google Scholar] [CrossRef]
- Chen, M.; Gao, C.; Shahidehpour, M.; Li, Z.; Chen, S.; Li, D. Internet data center load modeling for demand response considering the coupling of multiple regulation methods. IEEE Trans. Smart Grid 2021, 12, 2060–2076. [Google Scholar] [CrossRef]
- Sakanova, A.; Alimohammadi, S.; McEvoy, J.; Battaglioli, S.; Persoons, T. Multi-objective layout optimization of a generic hybrid-cooled data centre blade server. Appl. Therm. Eng. 2019, 156, 514–523. [Google Scholar] [CrossRef]
- Ajmal, M.S.; Iqbal, Z.; Khan, F.Z.; Bilal, M.; Mehmood, R.M. Cost-based energy efficient scheduling technique for dynamic voltage and frequency scaling system in cloud computing. Sustain. Energy. Technol. 2021, 45, 101210. [Google Scholar]
- Arshad, U.; Aleem, M.; Srivastava, G.; Lin, J. Utilizing power consumption and SLA violations using dynamic VM consolidation in cloud data centers. Renew. Sustain. Energy Rev. 2022, 167, 112782. [Google Scholar] [CrossRef]
- Qu, S.; Duan, K.; Guo, Y.; Feng, Y.; Wang, C.; Xing, Z. Real-time optimization of the liquid-cooled data center based on cold plates under different ambient temperatures and thermal loads. Appl. Energy 2024, 363, 123101. [Google Scholar] [CrossRef]
- Zou, Z.; Yang, C.; Hu, L.; Zhang, Q. A novel data center free radiating system driven by waste heat and wind energy system (DCFRWWs) and its operation performance analysis. Energy Build. 2024, 310, 114061. [Google Scholar]
- Chen, T.; Wang, X.; Giannakis, G.B. Cooling-aware energy and workload management in data centers via stochastic optimization. IEEE J. Sel. Top. Signal Process 2015, 10, 402–415. [Google Scholar] [CrossRef]
- Chen, S.; Li, P.; Ji, H.; Hao, Y.; Ji, H.; Wu, J.; Wang, C. Operational flexibility of active distribution networks with the potential from data centers. Appl. Energy 2021, 293, 116935. [Google Scholar] [CrossRef]
- Liu, X. Research on collaborative scheduling of internet data center and regional integrated energy system based on electricity-heat-water coupling. Energy 2024, 292, 130462. [Google Scholar] [CrossRef]
- Han, O.; Ding, T.; Mu, C.; Jia, W.; Ma, Z. Coordinative optimization between multiple data center operators and a system operator based on two-level distributed scheduling algorithm. IEEE Internet Things J 2023, 10, 7517–7527. [Google Scholar] [CrossRef]
- Lian, T.; Li, Y.; Zhao, Y.; Yu, C.; Zhao, T.; Wu, L. Robust multi-objective optimization for islanded data center microgrid operations. Appl. Energy 2023, 330, 120344. [Google Scholar] [CrossRef]
- Huang, S.; Yan, D.; Chen, Y. An online algorithm for combined computing workload and energy coordination within a regional data center cluster. Int. J. Electr. Power Energy Syst. 2024, 158, 109971. [Google Scholar] [CrossRef]
- Xiao, J.; Yang, Y.; Cui, S.; Wang, Y. Cooperative online schedule of interconnected data center microgrids with shared energy storage. Energy 2023, 285, 129522. [Google Scholar] [CrossRef]
- Liu, W.; Yan, Y.; Sun, Y.; Mao, H.; Cheng, M.; Wang, P.; Ding, Z. Online job scheduling scheme for low-carbon data center operation, An information and energy nexus perspective. Appl. Energy 2023, 338, 120918. [Google Scholar] [CrossRef]
- Wu, Z.; Lin, C.; Wang, J.; Zhou, M.; Li, G.; Xia, Q. Incentivizing the spatiotemporal flexibility of data centers toward power system coordination. IEEE Trans. Netw. Sci. Eng. 2023, 10, 1766–1778. [Google Scholar] [CrossRef]
- Wang, J.; Deng, H.; Liu, Y.; Guo, Z.; Wang, Y. Coordinated optimal scheduling of integrated energy system for data center based on computing load shifting. Energy 2023, 267, 126585. [Google Scholar] [CrossRef]
- Wan, T.; Tao, Y.; Qiu, J.; Lai, S. Internet data centers participating in electricity network transition considering carbon-oriented demand response. Appl. Energy 2023, 329, 120305. [Google Scholar] [CrossRef]
- Qi, W.; Li, J.; Liu, Y.; Liu, C. Planning of distributed internet data center microgrids. IEEE Trans. Smart Grid 2017, 10, 762–771. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.; Wu, J.; Liu, K.; Sun, X.; Guan, X. Optimal planning of internet data centers decarbonized by hydrogen-water-based energy systems. IEEE Trans. Autom. Sci. Eng. 2022, 20, 1577–1590. [Google Scholar] [CrossRef]
- Li, W.; Qian, T.; Zhang, Y.; Shen, Y.; Wu, C.; Tang, W. Distributionally robust chance-constrained planning for regional integrated electricity–heat systems with data centers considering wind power uncertainty. Appl. Energy 2023, 336, 120787. [Google Scholar] [CrossRef]
- Vafamehr, A.; Khodayar, M.E.; Manshadi, S.D.; Ahmad, I.; Lin, J. A framework for expansion planning of data centers in electricity and data networks under uncertainty. IEEE Trans. Smart Grid 2017, 10, 305–316. [Google Scholar] [CrossRef]
- Zeng, B.; Xu, F.; Liu, Y.; Gong, D.; Zhu, X. Multi-objective interval optimization approach for energy hub planning with consideration of renewable energy and demand response synergies. Proc. CSEE 2021, 41, 7212–7224. [Google Scholar]
- Li, Y.; Wang, P.; Gooi, H.; Ye, J.; Wu, L. Multi-objective optimal dispatch of microgrid under uncertainties via interval optimization. IEEE Trans. Smart Grid 2019, 10, 2046–2058. [Google Scholar] [CrossRef]
- Jiang, T.; Li, X.; Kou, X.; Zhang, R.; Tian, G.; Li, F. Available transfer capability evaluation in electricity-dominated integrated hybrid energy systems with uncertain wind power: An interval optimization solution. Appl. Energy 2022, 314, 119001. [Google Scholar] [CrossRef]
- Su, Y.; Zhou, Y.; Tan, M. An interval optimization strategy of household multi-energy system considering tolerance degree and integrated demand response. Appl. Energy 2020, 260, 114144. [Google Scholar] [CrossRef]
- Wang, W.; Dong, H.; Luo, Y.; Zhang, C.; Zeng, B.; Xu, F.; Zeng, M. An Interval Optimization-Based Approach for Electric–Heat–Gas Coupled Energy System Planning Considering the Correlation between Uncertainties. Energies 2021, 14, 2457. [Google Scholar] [CrossRef]
- Song, J.; Zhang, Z.; Mu, Y.; Wang, X.; Chen, H.; Pan, Q.; Li, Y. Enhancing environmental sustainability via interval optimization for low-carbon economic dispatch in renewable energy power systems: Leveraging the flexible cooperation of wind energy and carbon capture power plants. J. Clean. Prod. 2024, 442, 140937. [Google Scholar] [CrossRef]
- Wang, P.; Cao, Y.; Ding, Z.; Tang, H.; Wang, X.; Cheng, M. Stochastic programming for cost optimization in geographically distributed internet data centers. CSEE JPES 2022, 8, 1215–1232. [Google Scholar]
- Chinese Grids’ Transformation to Benefit Digital&Tech Companies Globally. Available online: https://energyiceberg.com (accessed on 13 April 2024).
- Dong, H.; Wang, L.; Zhang, X.; Zeng, M. A two-stage stochastic collaborative planning approach for data centers and distribution network incorporating demand response and multivariate uncertainties. J. Clean. Prod. 2024, 451, 141482. [Google Scholar] [CrossRef]
- Zeng, B.; Wang, W.; Zhang, W.; Wang, Y.; Tang, C.; Wang, J. Optimal configuration planning of vehicle sharing station-based electro-hydrogen micro-energy systems for transportation decarbonization. J. Clean. Prod. 2023, 387, 135906. [Google Scholar] [CrossRef]
- Lei, G.; Xu, C. Optimal intelligent reconfiguration of distribution network in the presence of distributed generation and storage system. Energy Eng. 2024, 119, 2005–2029. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, L.; Han, Z. Optimal data center energy management with hybrid quantum-classical multi-cuts benders’ decomposition method. IEEE Trans. Sustain. Energy 2024, 15, 847–858. [Google Scholar] [CrossRef]
- Zeng, B.; Zhang, W.; Hu, P.; Sun, J.; Gong, D. Synergetic renewable generation allocation and 5G base station placement for decarbonizing development of power distribution system: A multi-objective interval evolutionary optimization approach. Appl. Energy 2023, 351, 121831. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, K.; Yang, S.; Liu, H. Multi-objective optimal load dispatch of micro-grid with stochastic access of electric vehicles. J. Clean. Prod. 2018, 195, 187–199. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, K.; Yang, S. Multi-objective optimal dispatch of micro-grid containing electric vehicles. J. Clean. Prod. 2017, 165, 1572–1581. [Google Scholar] [CrossRef]



| Reference | Interacts with DN | Research Field | Uncertainty Handling | |||
|---|---|---|---|---|---|---|
| Ignores Uncertainty | SO | RO | IO | |||
| [6] | × | Operation | √ | × | × | × |
| [7] | × | Operation | √ | × | × | × |
| [8] | × | Operation | √ | × | × | × |
| [9] | × | Operation | √ | × | × | × |
| [10] | × | Operation | √ | × | × | × |
| [11] | √ | Operation | √ | × | × | × |
| [12] | √ | Operation | √ | × | × | × |
| [13] | √ | Operation | √ | × | × | × |
| [14] | √ | Operation | √ | × | × | × |
| [15] | √ | Operation | × | × | √ | × |
| [16] | √ | Operation | √ | × | × | × |
| [17] | √ | Operation | √ | × | × | × |
| [18] | √ | Operation | √ | × | × | × |
| [19] | √ | Operation | √ | × | × | × |
| [20] | √ | Operation | √ | × | × | × |
| [21] | √ | DC self-planning | √ | √ | × | × |
| [22] | √ | DC self-planning | √ | × | × | × |
| [23] | √ | DC self-planning | √ | × | × | × |
| [24] | √ | DC self-planning | × | × | √ | × |
| [25] | √ | DC self-planning | × | √ | × | × |
| This paper | √ | Collaborative planning | × | × | × | √ |
| Equipment | Parameters | |
|---|---|---|
| Technical | Economic | |
| Wind Turbine | = 100 kW | = 7000 RMB/kW |
| = 10 | ||
| = 6% | ||
| = 20 | ||
| Server | = 600 W | = 15,200 RMB/unit |
| = 300 W | ||
| = 500 | ||
| = 1500 | ||
| = 8% | ||
| = 20 | ||
| ACE | = 50 kW | = 835 RMB/kW |
| = 4 | ||
| = 10 | ||
| = 8% | ||
| = 20 | ||
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 1.2 kg/m3 | 1.09 W/(m2·k) | ||
| 1000 J/(kg·°C) | 1000 m2 | ||
| 0.9 | RMB 0.1/Gbps |
| Distribution Line Model | Resistivity (Ω/km) | Reactance (Ω/km) | Current Rating (A) | Construction Cost (RMB 10⁴/km) |
|---|---|---|---|---|
| 1 | 0.076 | 0.069 | 410 | 60 |
| 2 | 0.046 | 0.066 | 713 | 80 |
| 3 | 0.035 | 0.06 | 1025 | 100 |
| Investment Cost (10⁴ RMB) | System Operation (RMB 10⁴) | Carbon Emissions (RMB 10⁴) | Total Cost (RMB 10⁴) | |||||
|---|---|---|---|---|---|---|---|---|
| Case | Distribution Line | Transformer | Server | ACE | Wind Turbine | |||
| I | 85.43 | 37.94 | 512.57 | 11.25 | 253.12 | 2746.46 | 1640.12 | 5261.12 |
| II | 62.46 | 31.92 | 512.57 | 11.25 | 234.78 | 2476.68 | 1357.49 | 4681.86 |
| III | 39.34 | 10.65 | 267.31 | 6.12 | 216.72 | 1963.22 | 894.78 | 3404.91 |
| Distribution Line (From-To Nodes) | WT/Unit (Node) | Server/Unit (Node) | ACE/Unit (Node) | |||
|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | ||||
| I | 6–7/7–8/8–9/3–23/23–24/ 6–26/26–27/27–28/28–29 | 3–4/4–5/5–6 | 1–2/2–3 | 6 (8), 10 (13), 10 (19), 10 (25), 10 (26), 10 (30) | 995 (18), 984 (22), 985 (25), 963 (33) | 3 (18), 4 (22), 4 (25), 4 (33) |
| II | 6–7/7–8/8–9/ 3–23/6–26/ | 3–4/4–5/5–6 | 1–2/2–3 | 7 (9), 10 (13), 9 (19), 10 (23), 10 (26) | 995 (13), 984 (19), 985 (23), 963 (26) | 3 (13), 4 (19), 4 (23), 4(26) |
| III | 4–5/5–6/6–7 | 2–3/3–4 | 1–2 | 9 (18), 8 (22), 10 (25), 9 (33) | 476 (13), 472 (19), 463 (25), 652 (26) | 2 (13), 2 (19), 2 (25), 3 (26) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Wu, W.; Feng, W.; Qin, J.; Ao, Y. Collaborative Planning of Distribution Network, Data Centres and Renewable Energy in the Power Distribution IoT via Interval Optimization. Energies 2024, 17, 3623. https://doi.org/10.3390/en17153623
Su L, Wu W, Feng W, Qin J, Ao Y. Collaborative Planning of Distribution Network, Data Centres and Renewable Energy in the Power Distribution IoT via Interval Optimization. Energies. 2024; 17(15):3623. https://doi.org/10.3390/en17153623
Chicago/Turabian StyleSu, Lei, Wenxiang Wu, Wanli Feng, Junda Qin, and Yuqi Ao. 2024. "Collaborative Planning of Distribution Network, Data Centres and Renewable Energy in the Power Distribution IoT via Interval Optimization" Energies 17, no. 15: 3623. https://doi.org/10.3390/en17153623
APA StyleSu, L., Wu, W., Feng, W., Qin, J., & Ao, Y. (2024). Collaborative Planning of Distribution Network, Data Centres and Renewable Energy in the Power Distribution IoT via Interval Optimization. Energies, 17(15), 3623. https://doi.org/10.3390/en17153623





