Planning a Hybrid Battery Energy Storage System for Supplying Electric Vehicle Charging Station Microgrids
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Research Gap and Contribution
- A new formulation is presented for planning off-grid microgrids, including hybrid battery energy storage systems (HBESS). The formulation is able to specify the capacity of each system component and take advantage of the benefits of different battery technologies in terms of cost and degradation characteristics. The formulation is based on a mixed integer linear programming (MILP) approach to guarantee reaching a global or near-optimal global solution to the problem.
- The formulation includes an energy management scheme that can set the reliability level of the system and the capacity fading of different types of batteries in order to manage the planning cost and defer battery replacement.
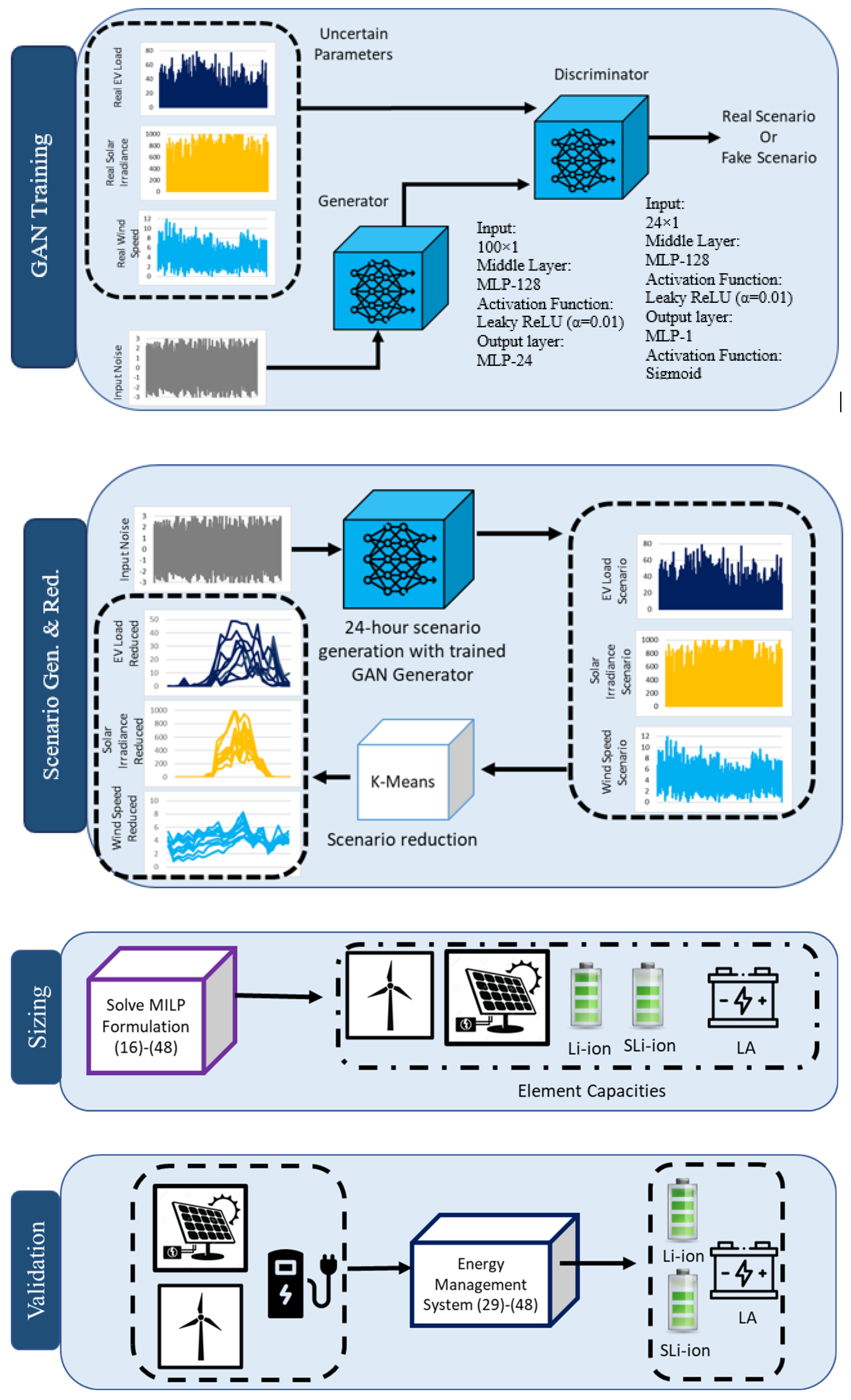
- A scenario generation approach based on GAN is developed to capture the uncertainties caused by wind speed, solar irradiation, EV load and the temporal correlation of these uncertain parameters. The method is designed to generate scenarios for each season to emulate stochastic generation and consumption.
2. System Model and Methodology
2.1. PV Generation Modelling
2.2. Wind Generation Modelling
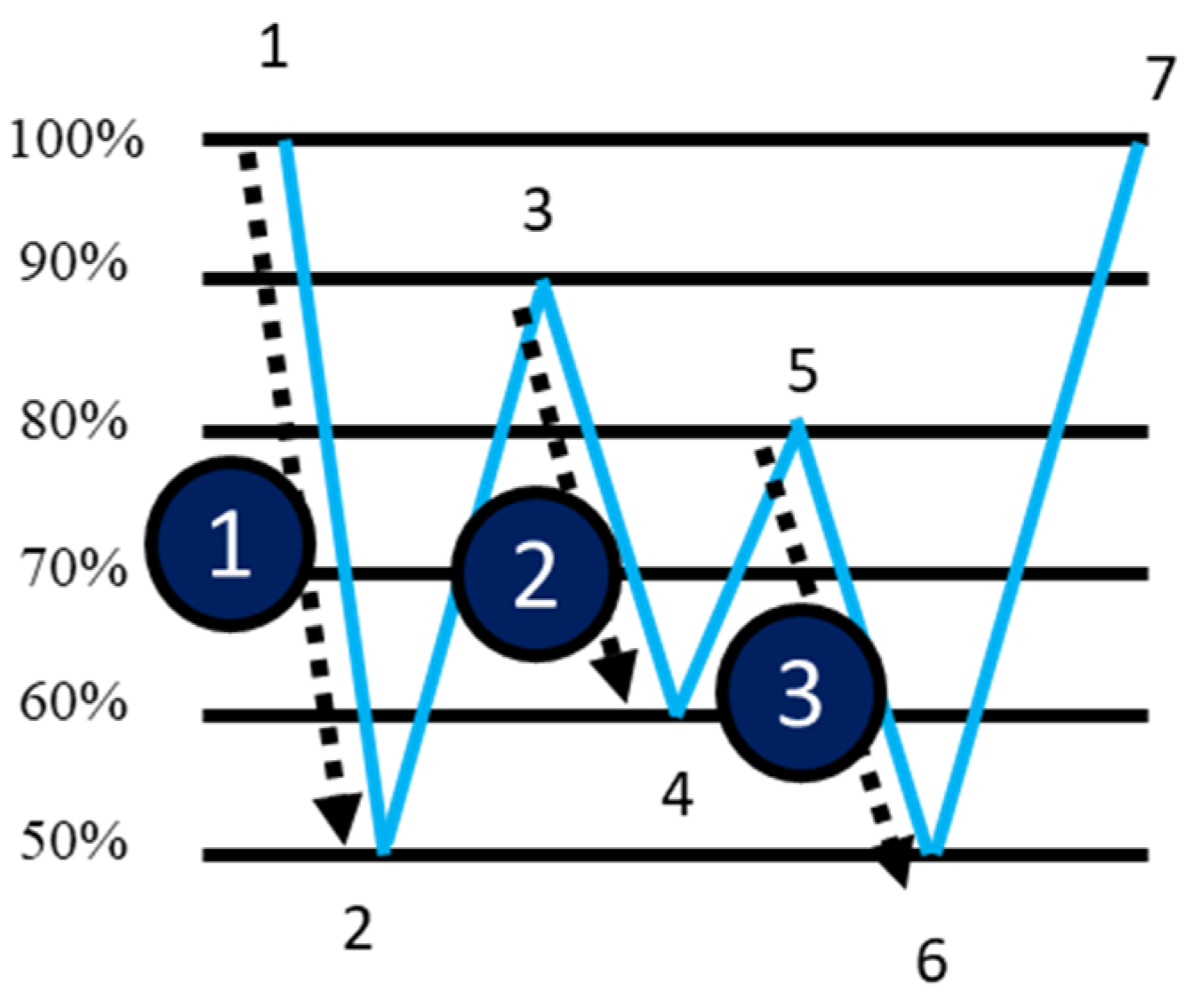
2.3. Battery Capacity Fading Model
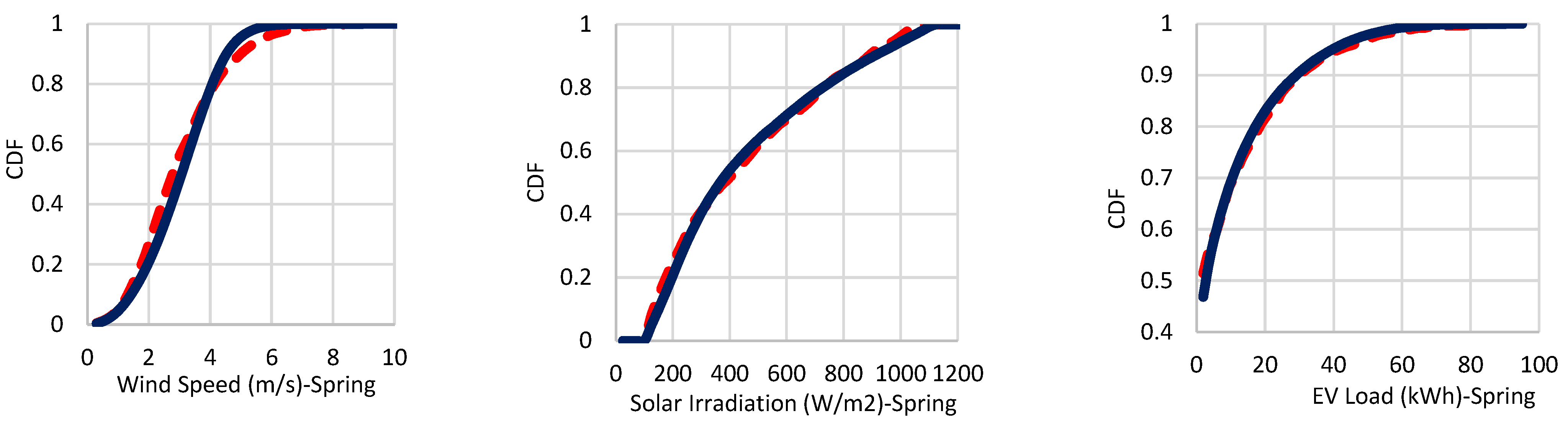
2.4. Uncertainty Modelling
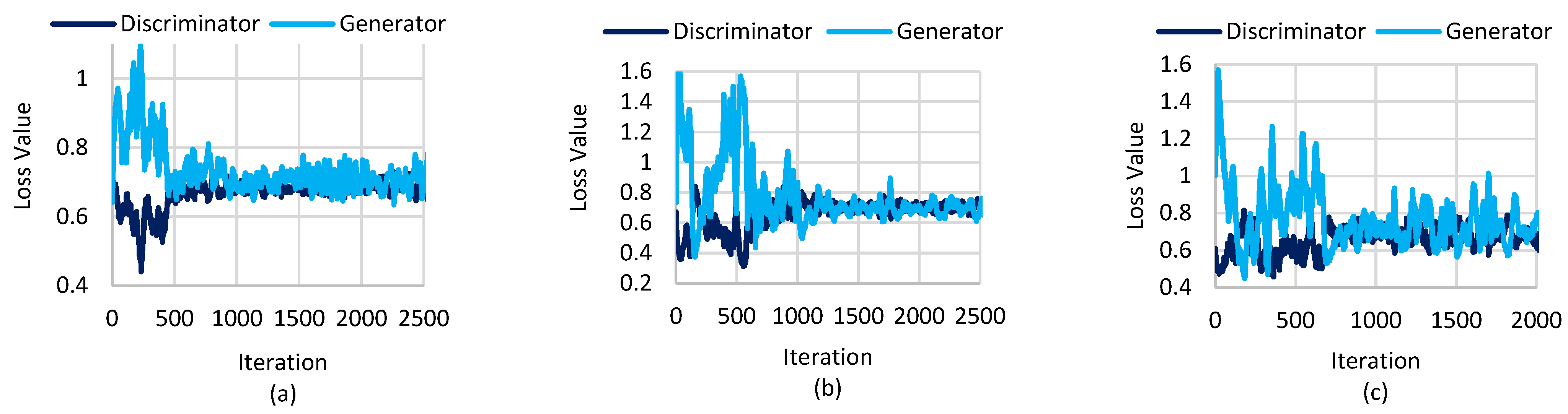
2.4.1. Scenario Generation
| Algorithm 1: Training of GAN for scenario generation |
| Default Values: Mini-Batch (, number of iterations () Initialise hyperparameters and for generator and discriminator |
 |
2.4.2. Scenario Reduction
| Algorithm 2: k-means algorithm |
| Input: Input data set: Output: Output: Cluster Centroids: C Data set of each cluster: D |
| Initialisation: Select k random points from the dataset as the centroids |
| While : For i = 1 to j: For i=1 to k: Return: C and D |
2.4.3. Methodology
3. Microgrid Planning Formulation
3.1. Microgrid Capacity Sizing
3.2. Capacity Sizing Assessment with the Energy Management System
4. Simulations and Results
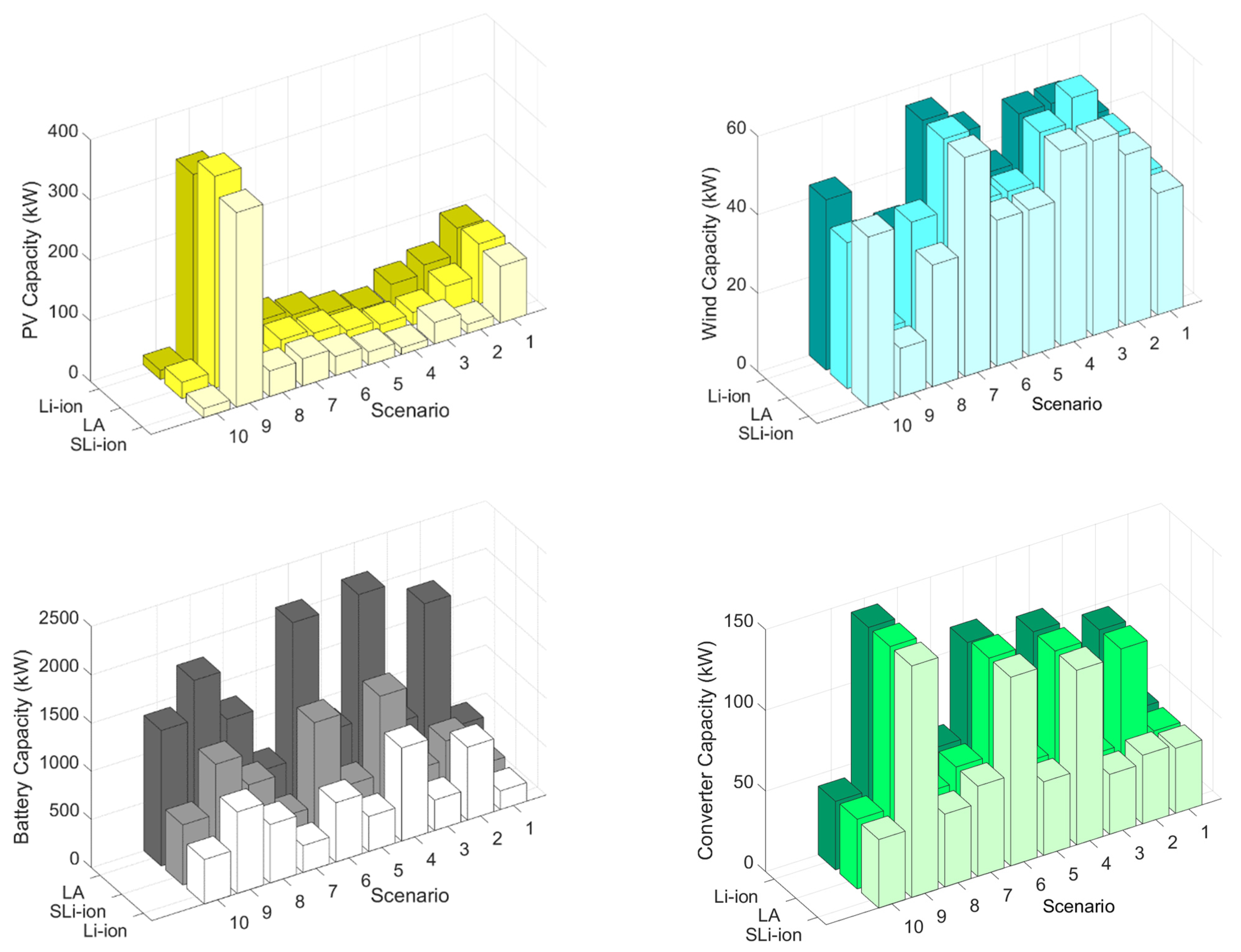
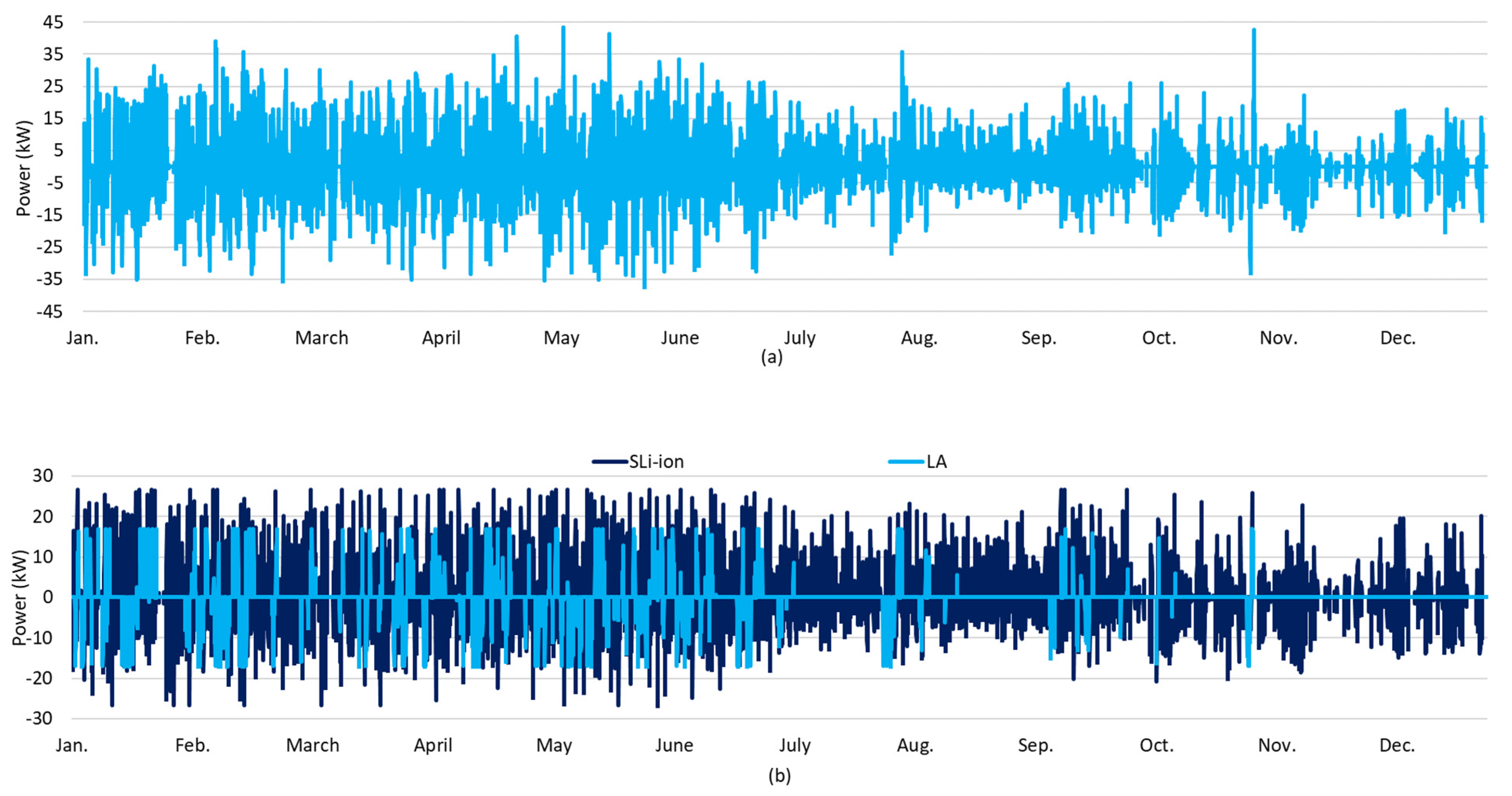
4.1. Single BESS Technology Use
4.2. Hybrid BESS
4.3. Capacity Evaluation
5. Conclusive Remarks, Discussions, and Future Work
5.1. Conclusive Remarks
5.2. Discussions
5.3. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets and indices | Parameters | Variables | |||
| Index for set of time | Capital cost of system (£/kW) or (£/kWh) | Power or capacity of component in (kW) or (kWh) | |||
| Index for set of year | Fixed Operation and maintenance cost (£/y) | Power of component (kW) | |||
| Index for set of scenario | Variable Operation and maintenance cost (£/kWh/y) | Unmet load (kWh) | |||
| Index for set of battery technologies | Time interval (h) | Renewable spillage (kWh) | |||
| Total number of time intervals | Wind generation (kW) | Binary variable indicating operation mode of battery | |||
| Total number of years | PV generation (kW) | Battery stored energy (kWh) | |||
| Total number of time intervals | Maximum capacity of each element (kW) or (kWh) | Expected energy not supplied (kWh) | |||
| Total number of battery technologies | Large value | Number of each component | |||
| Index for PV generation | Unit capacity of each component (kW) or (kWh) | Total battery capacity fade (kWh) | |||
| Index for wind generation | PV generation for 1 kW of installed PV panel (kW) | Objective Function for scenario s | |||
| BESS | Indices for battery | Wind generation for 1 wind turbine installed (kW) | |||
| Battery charge | End of life battery capacity (%) | ||||
| Battery Discharge | Efficiency | ||||
| Residual value of each type of battery at the end of planning horizon | EV | Electric vehicle charger load (kW) | |||
| Conv | Index for converter | Discount rate |
References
- Dong, F.; Zhu, J.; Li, Y.; Chen, Y.; Gao, Y.; Hu, M.; Qin, C.; Sun, J. How green technology innovation affects carbon emission efficiency: Evidence from developed countries proposing carbon neutrality targets. Environ. Sci. Pollut. Res. 2022, 29, 35780–35799. [Google Scholar] [CrossRef]
- Safi, A.; Chen, Y.; Wahab, S.; Zheng, L.; Rjoub, H. Does environmental taxes achieve the carbon neutrality target of G7 economies? Evaluating the importance of environmental R&D. J. Environ. Manag. 2021, 293, 112908. [Google Scholar]
- Li, C.; Chen, D.; Li, Y.; Li, F.; Li, R.; Wu, Q.; Liu, X.; Wei, J.; He, S.; Zhou, B.; et al. Exploring the interaction between renewables and energy storage for zero-carbon electricity systems. Energy 2022, 261, 125247. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Z.; Su, H.; Zhang, L. Bi-level framework for microgrid capacity planning under dynamic wireless charging of electric vehicles. Int. J. Electr. Power Energy Syst. 2022, 141, 108204. [Google Scholar] [CrossRef]
- Rezaei, N.; Khazali, A.; Mazidi, M.; Ahmadi, A. Economic energy and reserve management of renewable-based microgrids in the presence of electric vehicle aggregators: A robust optimization approach. Energy 2020, 201, 117629. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Mohamed, S.; Ismail, M.; Qaraqe, K.A.; Serpedin, E. Joint Planning of Smart EV Charging Stations and DGs in Eco-Friendly Remote Hybrid Microgrids. IEEE Trans. Smart Grid 2019, 10, 5819–5830. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, L.; Hou, R.; Wang, C.; Wang, X. A hybrid stochastic/robust-based multi-period investment planning model for island microgrid. Int. J. Electr. Power Energy Syst. 2021, 130, 106998. [Google Scholar] [CrossRef]
- Cao, X.; Wang, J.; Zeng, B. A Chance Constrained Information-Gap Decision Model for Multi-Period Microgrid Planning. IEEE Trans. Power Syst. 2017, 33, 2684–2695. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P.; Williams, A. Techno-economic analysis of the lithium-ion and lead-acid battery in microgrid systems. Energy Convers. Manag. 2018, 177, 122–142. [Google Scholar] [CrossRef]
- Koh, S.; Smith, L.; Miah, J.; Astudillo, D.; Eufrasio, R.; Gladwin, D.; Brown, S.; Stone, D. Higher 2nd life Lithium Titanate battery content in hybrid energy storage systems lowers environmental-economic impact and balances eco-efficiency. Renew. Sustain. Energy Rev. 2021, 152, 111704. [Google Scholar] [CrossRef]
- Rey, J.M.; Jiménez-Vargas, I.; Vergara, P.P.; Osma-Pinto, G.; Solano, J. Sizing of an autonomous microgrid considering droop control. Int. J. Electr. Power Energy Syst. 2021, 136, 107634. [Google Scholar] [CrossRef]
- Tahir, H.; Park, D.-H.; Park, S.-S.; Kim, R.-Y. Optimal ESS size calculation for ramp rate control of grid-connected microgrid based on the selection of accurate representative days. Int. J. Electr. Power Energy Syst. 2022, 139, 108000. [Google Scholar] [CrossRef]
- Chen, X.; Dong, W.; Yang, Q. Robust optimal capacity planning of grid-connected microgrid considering energy management under multi-dimensional uncertainties. Appl. Energy 2022, 323, 119642. [Google Scholar] [CrossRef]
- Garmabdari, R.; Moghimi, M.; Yang, F.; Gray, E.; Lu, J. Multi-objective energy storage capacity optimisation considering Microgrid generation uncertainties. Int. J. Electr. Power Energy Syst. 2020, 119, 105908. [Google Scholar] [CrossRef]
- Guo, L.; Hou, R.; Liu, Y.; Wang, C.; Lu, H. A novel typical day selection method for the robust planning of stand-alone wind-photovoltaic-diesel-battery microgrid. Appl. Energy 2020, 263, 114606. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, W.; Wang, X.; Li, H. An MILP-Based Planning Model of a Photovoltaic/Diesel/Battery Stand-Alone Microgrid Considering the Reliability. IEEE Trans. Smart Grid 2021, 12, 3809–3818. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Mouli, G.R.C.; Qin, Z.; Elizondo, L.R.; Bauer, P. Techno-Economical Model Based Optimal Sizing of PV-Battery Systems for Microgrids. IEEE Trans. Sustain. Energy 2019, 11, 1657–1668. [Google Scholar] [CrossRef]
- Soykan, G.; Er, G.; Canakoglu, E. Optimal sizing of an isolated microgrid with electric vehicles using stochastic programming. Sustain. Energy Grids Netw. 2022, 32, 100850. [Google Scholar] [CrossRef]
- Xie, R.; Wei, W.; Shahidehpour, M.; Wu, Q.; Mei, S. Sizing Renewable Generation and Energy Storage in Stand-Alone Microgrids Considering Distributionally Robust Shortfall Risk. IEEE Trans. Power Syst. 2022, 37, 4054–4066. [Google Scholar] [CrossRef]
- Bagheri, F.; Dagdougui, H.; Gendreau, M. Stochastic optimization and scenario generation for peak load shaving in Smart District microgrid: Sizing and operation. Energy Build. 2022, 275, 112426. [Google Scholar] [CrossRef]
- Alharbi, T.; Bhattacharya, K.; Kazerani, M. Planning and Operation of Isolated Microgrids Based on Repurposed Electric Vehicle Batteries. IEEE Trans. Ind. Inform. 2019, 15, 4319–4331. [Google Scholar] [CrossRef]
- Gong, K.; Wang, X.; Jiang, C.; Shahidehpour, M.; Liu, X.; Zhu, Z. Security-constrained optimal sizing and siting of BESS in hybrid AC/DC. IEEE Trans. Sustain. Energy 2021, 12, 2110–2122. [Google Scholar] [CrossRef]
- Han, H.; Liu, H.; Zuo, X.; Shi, G.; Sun, Y.; Liu, Z.; Su, M. Optimal Sizing Considering Power Uncertainty and Power Supply Reliability Based on LSTM and MOPSO for SWPBMs. IEEE Syst. J. 2022, 16, 4013–4023. [Google Scholar] [CrossRef]
- Masoud, T.M.; El-Saadany, E.F. Correlating optimal size, cycle life estimation, and technology selection of batteries: A two-stage approach for microgrid applications. IEEE Trans. Sustain. Energy 2020, 11, 1257–1267. [Google Scholar] [CrossRef]
- Kebede, A.A.; Coosemans, T.; Messagie, M.; Jemal, T.; Behabtu, H.A.; Van Mierlo, J.; Berecibar, M. Techno-economic analysis of lithium-ion and lead-acid batteries in stationary energy storage application. J. Energy Storage 2021, 40, 102748. [Google Scholar] [CrossRef]
- Dascalu, A.; Sharkh, S.; Cruden, A.; Stevenson, P. Performance of a hybrid battery energy storage system. Energy Rep. 2022, 8, 1–7. [Google Scholar] [CrossRef]
- Yang, Y.; Qiu, J.; Zhang, C.; Zhao, J.; Wang, G. Flexible Integrated Network Planning Considering Echelon Utilization of Second Life of Used Electric Vehicle Batteries. IEEE Trans. Transp. Electrif. 2021, 8, 263–276. [Google Scholar] [CrossRef]
- Dascalu, A.; Fraser, E.J.; Al-Wreikat, Y.; Sharkh, S.M.; Wills, R.G.A.; Cruden, A.J. A techno-economic analysis of a hybrid energy storage system for EV off-grid charging. In Proceedings of the 2023 International Conference on Clean Electrical Power (ICCEP), Terassini, Italy, 27–29 June 2023. [Google Scholar]
- Hafez, A.Z.; Soliman, A.; El-Metwally, K.A.; Ismail, I.M. Tilt and azimuth angles in solar energy applications-A review. Renew. Sustain. Energy Rev. 2017, 77, 147–168. [Google Scholar] [CrossRef]
- Johnson, G.L. Wind Energy Systems; Citeseer: Manhattan, KS, USA, 1985. [Google Scholar]
- Wind-Turbine-Models, Aventa AV-7. 2023. Available online: https://en.wind-turbine-models.com/turbines/1529-aventa-av7 (accessed on 15 January 2024).
- Fallahifar, R.; Kalantar, M. Optimal planning of lithium ion battery energy storage for microgrid applications: Considering capacity degradation. J. Energy Storage 2023, 57, 106103. [Google Scholar] [CrossRef]
- Ke, X.; Lu, N.; Jin, C. Control and Size Energy Storage Systems for Managing Energy Imbalance of Variable Generation Resources. IEEE Trans. Sustain. Energy 2014, 6, 70–78. [Google Scholar] [CrossRef]
- Naderi, M.; Palmer, D.; Smith, M.J.; Ballantyne, E.E.F.; Stone, D.A.; Foster, M.P.; Gladwin, D.T.; Khazali, A.; Al-Wreikat, Y.; Cruden, A.; et al. Techno-Economic Planning of a Fully Renewable Energy-Based Autonomous Microgrid with Both Single and Hybrid Energy Storage Systems. Energies 2024, 17, 788. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Kirschen, D.S.; Zhang, B. Model-Free Renewable Scenario Generation Using Generative Adversarial Networks. IEEE Trans. Power Syst. 2018, 33, 3265–3275. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Miraftabzadeh, S.M.; Colombo, C.G.; Longo, M.; Foiadelli, F. K-Means and Alternative Clustering Methods in Modern Power Systems. IEEE Access 2023, 11, 119596–119633. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 15 January 2024).
- Photovoltaic Geographical Information System (PVGIS). Available online: https://joint-research-centre.ec.europa.eu/photovoltaic-geographical-information-system-pvgis_en (accessed on 15 January 2024).
- Open Data Scotland, Perth & Kinross Council, Electric Vehicle Charging Points. Available online: https://opendata.scot/datasets/perth+%2526+kinross+council-electric+vehicle+charging+points/ (accessed on 15 January 2024).
- Raybaut, P. Spyder-Documentation. 2009. Available online: https://pythonhosted.org (accessed on 15 January 2024).
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2023. Available online: http://www.gurobi.com/ (accessed on 15 January 2024).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Marutho, D.; Handaka, S.H.; Wijaya, E. The Determination of Cluster Number at k-Mean Using Elbow Method and Purity Evaluation on Headline News. In Proceedings of the 2018 International Seminar on Application for Technology of Information and Communication, Semarang, Indonesia, 21–22 September 2018. [Google Scholar]
- Greenwood, D.; Walker, S.; Wade, N.; Munoz-Vaca, S.; Crossland, A.; Patsios, C. 30—Integration of High Penetrations of Intermittent Renewable Generation in Future Electricity Networks Using Storage. In Future Energy, 3rd ed.; Letcher, T.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 649–668. ISBN 9780081028865. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]



| Ref. | Uncertainty Modeling | Battery Degradation | Microgrid Reliability | Scenario Generation | Hybrid BESS Management | 2nd Life Li-Ion BESS |
|---|---|---|---|---|---|---|
| [4] | No | No | No | No | No | No |
| [6] | Stochastic | No | Yes | Not Specified | No | No |
| [7] | Stochastic/Robust | No | No | Not Specified | No | No |
| [8] | Chance constrained | No | Yes | Monte Carlo simulation | No | No |
| [9] | No | No | No | No | No | No |
| [11] | No | Yes | Yes | No | No | No |
| [13] | Scenario based | No | No | GAN | No | No |
| [14] | Stochastic | Yes | Yes | Monte Carlo simulation | No | No |
| [15] | Robust | No | Yes | No | No | No |
| [16] | No | No | Yes | No | No | No |
| [18] | Stochastic | No | Yes | Monte Carlo simulation | No | No |
| [19] | Robust | No | Yes | No | No | No |
| [20] | Stochastic | No | No | GAN | No | No |
| [21] | Stochastic | Yes | No | Not Specified | No | Yes |
| [23] | No | No | Yes | No | No | No |
| [27] | Stochastic | No | No | GAN | No | Yes |
| Current Research | Stochastic | Yes | Yes | GAN | Yes | Yes |
| Component | CAPEX (£/kW) | Fixed OPEX (£/kW/Year) | Variable OPEX (£/kWh) |
|---|---|---|---|
| Wind | 5000 | 83 | 0.016 |
| PV | 730 | 50 | 0.008 |
| Li-ion Battery | 335 | 8 | 0.00024 |
| LA Battery | 80 | 8 | 0.00024 |
| SLi-ion Battery | 150 | 8 | 0.00024 |
| Converter | 90 | - | - |
| Parameter | Li-Ion | LA | SLi-Ion |
|---|---|---|---|
| (%) | 97–97% | 90–90% | 97–97% |
| (%) | 20% | 50% | 20% |
| (%) | 100% | 100% | 80% |
| (per 1000 cycle) (%) | 4.5% | 61.5% | 4.5% |
| (per month) (%) | 0.125 | 0.125 | 0.125 |
| EOL (%) | 60 | 70 | 60 |
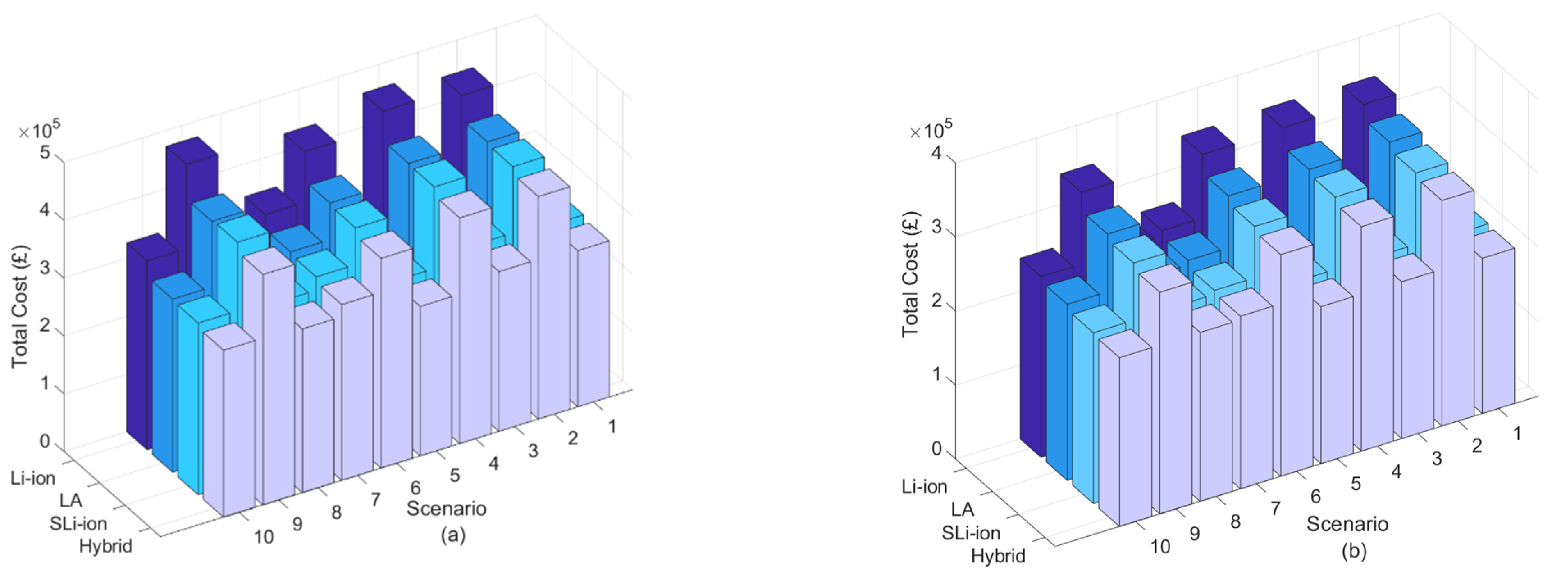
| BESS Type | Scenario#1 Cost (£) | Scenario#2 Cost (£) | Scenario#3 Cost (£) | Scenario#4 Cost (£) | Scenario#5 Cost (£) | Scenario#6 Cost (£) | Scenario#7 Cost (£) | Scenario#8 Cost (£) | Scenario#9 Cost (£) | Scenario#10 Cost (£) |
|---|---|---|---|---|---|---|---|---|---|---|
| Li-ion | 371,433 | 559,212 | 438,444 | 606,928 | 362,084 | 540,559 | 480,344 | 423,876 | 774,297 | 417,563 |
| LA | 358,098 | 473,140 | 416,131 | 496,903 | 325,166 | 447,650 | 448,255 | 361,067 | 702,401 | 367,656 |
| SLi-ion | 352,144 | 478,819 | 406,921 | 510,220 | 325,681 | 457,867 | 452,566 | 363,209 | 689,997 | 371,382 |
| Hybrid | 347,909 | 452,658 | 397,476 | 479,286 | 314,873 | 430,677 | 444,727 | 344,331 | 674,013 | 354,413 |
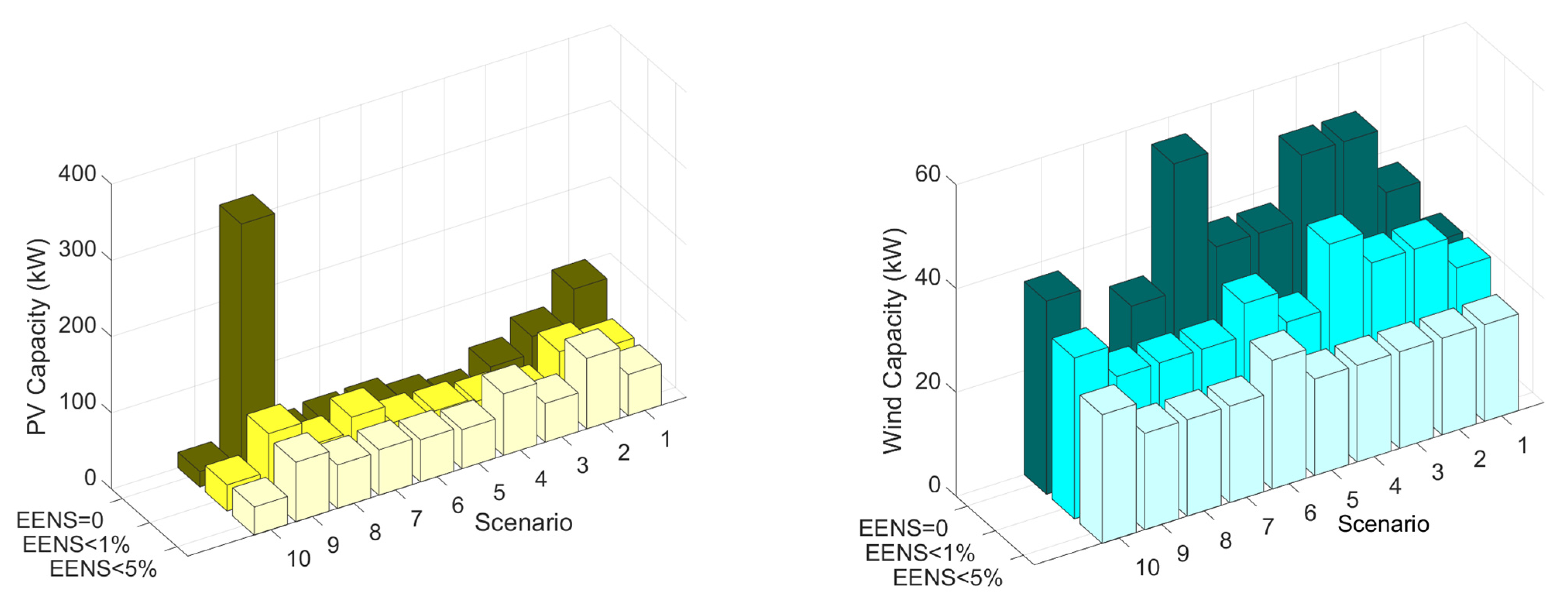
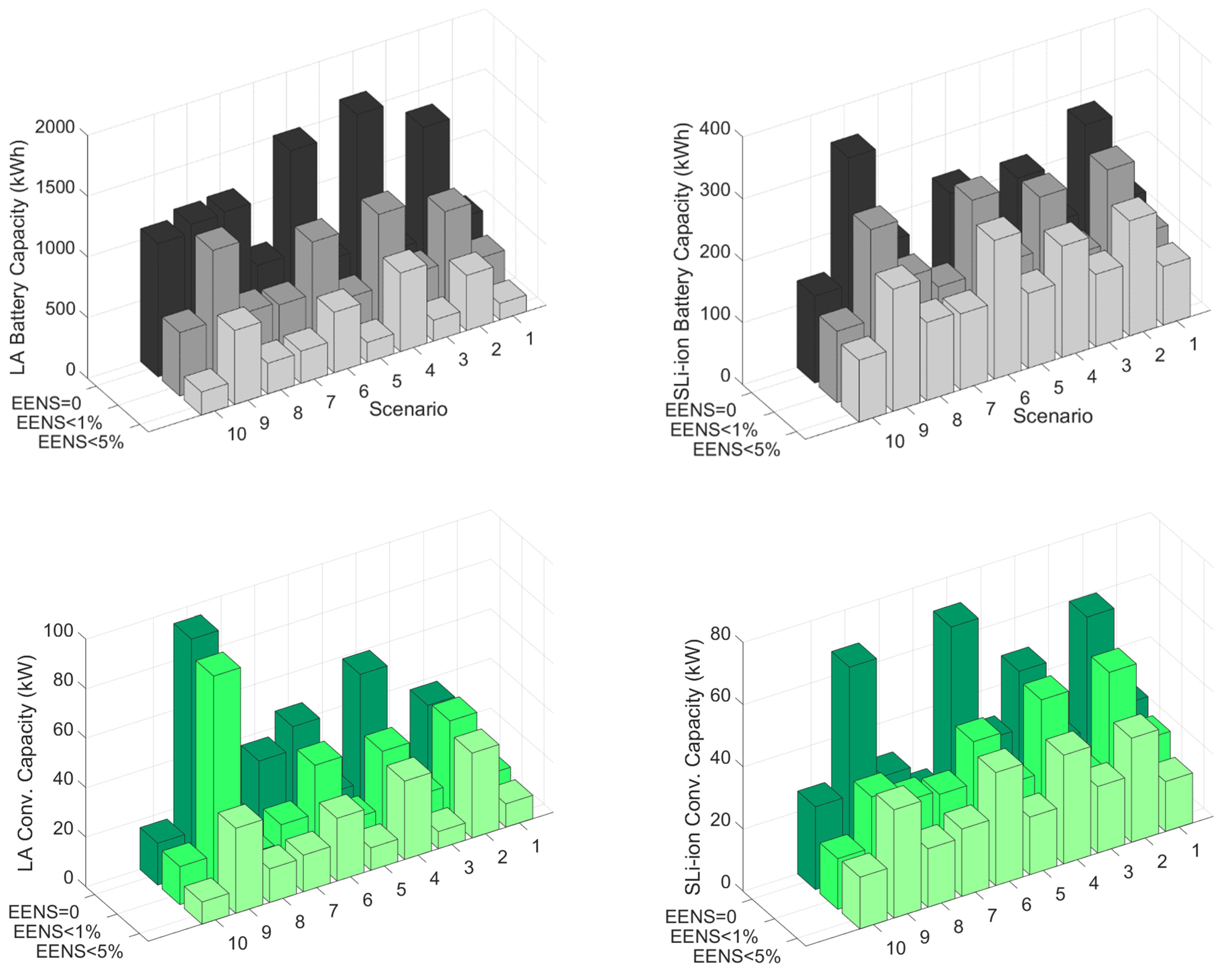
| Reliability Level | PV (kW) | Wind (kW) | Battery (kWh) | Converter (kW) |
|---|---|---|---|---|
| = 0 | 65 | 6.3 × 6.2 | 887 | 73 |
| = 1% | 60.3 | 4.7 × 6.2 | 620 | 56 |
| = 5% | 64.4 | 3.3 × 6.2 | 393 | 42 |
| = 0 | = 1% | = 5% | ||||
|---|---|---|---|---|---|---|
| Single | Hybrid | Single | Hybrid | Single | Hybrid | |
| LA Degradation | 170 kWh—12.7% | 88 kWh—8.5% | 152 kWh—15.2% | 60 kWh—9.1% | 123.2 kWh—19.3% | 33 kWh—9.6% |
| SLi-ion Degradation | 29 kWh—4% | 11.72 kWh—6.08% | 22.8 kWh—4.4% | 12 kWh—6.8% | 16 kWh—5.3% | 11 kWh—7.5% |
| Scenario | Total Cost (£) | PV (kW) | Wind (kW) | Li-ion (kWh) | LA (kWh) |
|---|---|---|---|---|---|
| #1 | 346,155 | 102 | 4 × 6.2 | 109 | 500 |
| #2 | 448,986 | 55 | 6 × 6.2 | 272 | 1230 |
| #3 | 395,758 | 35 | 8 × 6.2 | 101 | 424 |
| #4 | 476,281 | 11 | 8 × 6.2 | 209 | 1534 |
| #5 | 313,068 | 21 | 6 × 6.2 | 109 | 506 |
| #6 | 427,170 | 33 | 6 × 6.2 | 269 | 1306 |
| #7 | 443,391 | 33 | 9 × 6.2 | 89 | 588 |
| #8 | 341,802 | 29 | 5 × 6.2 | 197 | 1043 |
| #9 | 669,309 | 327 | 2 × 6.2 | 365 | 949 |
| #10 | 352,700 | 20 | 6 × 6.2 | 105 | 1089 |
| Battery Type | PV (kW) | Wind (kW) | BESS (kWh) | Conv. (kW) | Total Plan Cost (£) | EENS (%) |
|---|---|---|---|---|---|---|
| Li-ion | 67.4 | 7 × 6.2 | 540 | 73 | 446,672 | 0.64 |
| LA | 69.7 | 7 × 6.2 | 1330 | 73 | 373,851 | 0.5 |
| SLi-ion | 67 | 7 × 6.2 | 792 | 73 | 371,962 | 0.54 |
| Hybrid | 67 | 6 × 6.2 | 1033LA- 261SLi-ion | 31 LA- 42 SLi-ion | 357,270 | 0.49 |
| Study Cases | EENS (%) | LA Degradation (%) | Li-Ion Degradation (%) |
|---|---|---|---|
| Base Case | 0.36% | 9.5% | 5.5% |
| 10% Wind Generation decrease | 0.43% | 9.7% | 5.7% |
| 10% PV Generation decrease | 0.41% | 9.7% | 5.7% |
| 10% EV charging increase | 0.71% | 10.3% | 6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khazali, A.; Al-Wreikat, Y.; Fraser, E.J.; Sharkh, S.M.; Cruden, A.J.; Naderi, M.; Smith, M.J.; Palmer, D.; Gladwin, D.T.; Foster, M.P.; et al. Planning a Hybrid Battery Energy Storage System for Supplying Electric Vehicle Charging Station Microgrids. Energies 2024, 17, 3631. https://doi.org/10.3390/en17153631
Khazali A, Al-Wreikat Y, Fraser EJ, Sharkh SM, Cruden AJ, Naderi M, Smith MJ, Palmer D, Gladwin DT, Foster MP, et al. Planning a Hybrid Battery Energy Storage System for Supplying Electric Vehicle Charging Station Microgrids. Energies. 2024; 17(15):3631. https://doi.org/10.3390/en17153631
Chicago/Turabian StyleKhazali, Amirhossein, Yazan Al-Wreikat, Ewan J. Fraser, Suleiman M. Sharkh, Andrew J. Cruden, Mobin Naderi, Matthew J. Smith, Diane Palmer, Dan T. Gladwin, Martin P. Foster, and et al. 2024. "Planning a Hybrid Battery Energy Storage System for Supplying Electric Vehicle Charging Station Microgrids" Energies 17, no. 15: 3631. https://doi.org/10.3390/en17153631
APA StyleKhazali, A., Al-Wreikat, Y., Fraser, E. J., Sharkh, S. M., Cruden, A. J., Naderi, M., Smith, M. J., Palmer, D., Gladwin, D. T., Foster, M. P., Ballantyne, E. E. F., Stone, D. A., & Wills, R. G. (2024). Planning a Hybrid Battery Energy Storage System for Supplying Electric Vehicle Charging Station Microgrids. Energies, 17(15), 3631. https://doi.org/10.3390/en17153631









