Distributed and Multi-Agent Reinforcement Learning Framework for Optimal Electric Vehicle Charging Scheduling
Abstract
1. Introduction
1.1. Related Work
1.2. Main Contributions
2. Materials and Methods
2.1. Markov Decision Process Framework
2.2. State
2.3. Action
2.4. Transition Function
2.5. Reward
3. Proposed DR-MARL Method
3.1. Problem Transformation
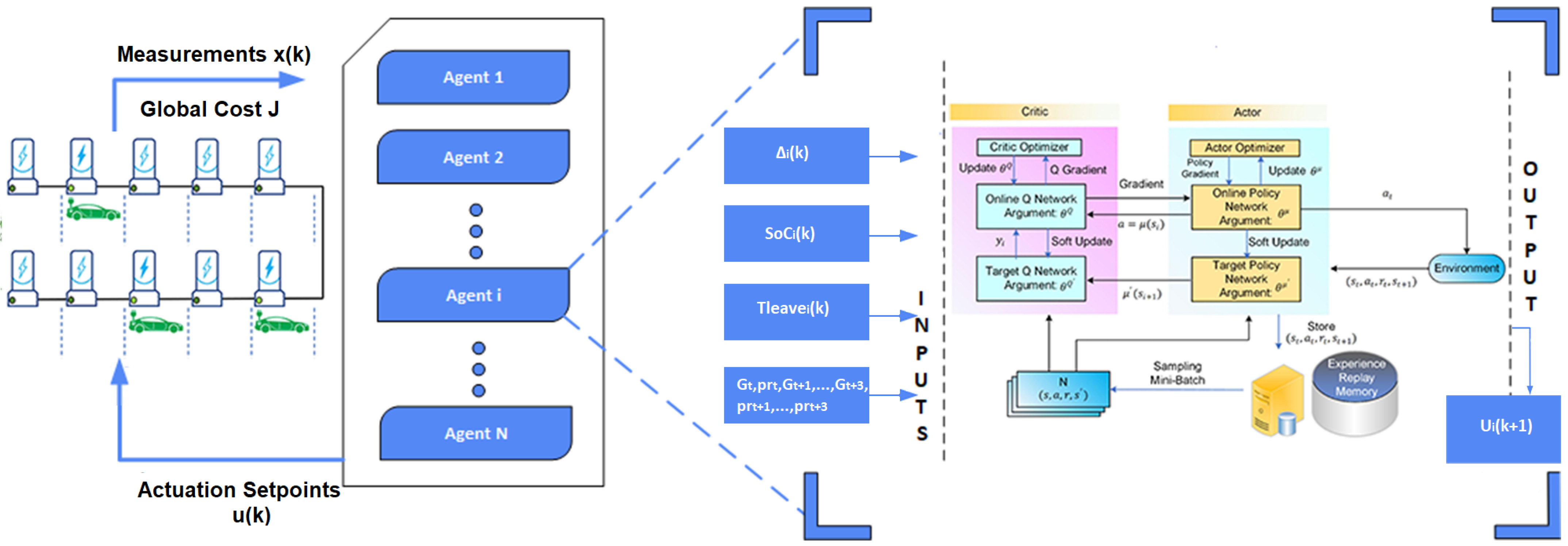
3.2. DR-MARL—Global Coordination
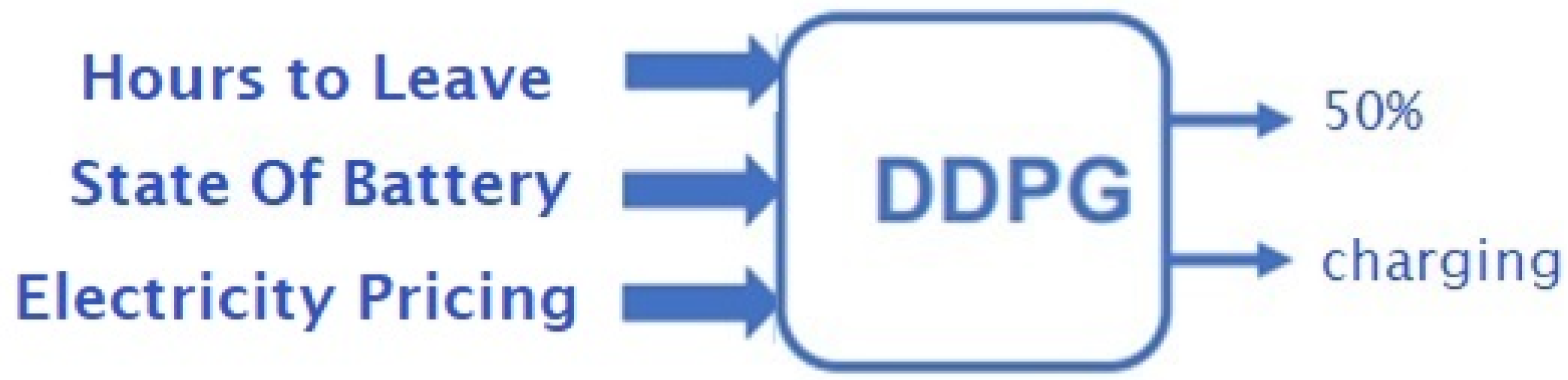
3.3. Local Agent—DDPG
4. Results
4.1. Setup of Numerical Study
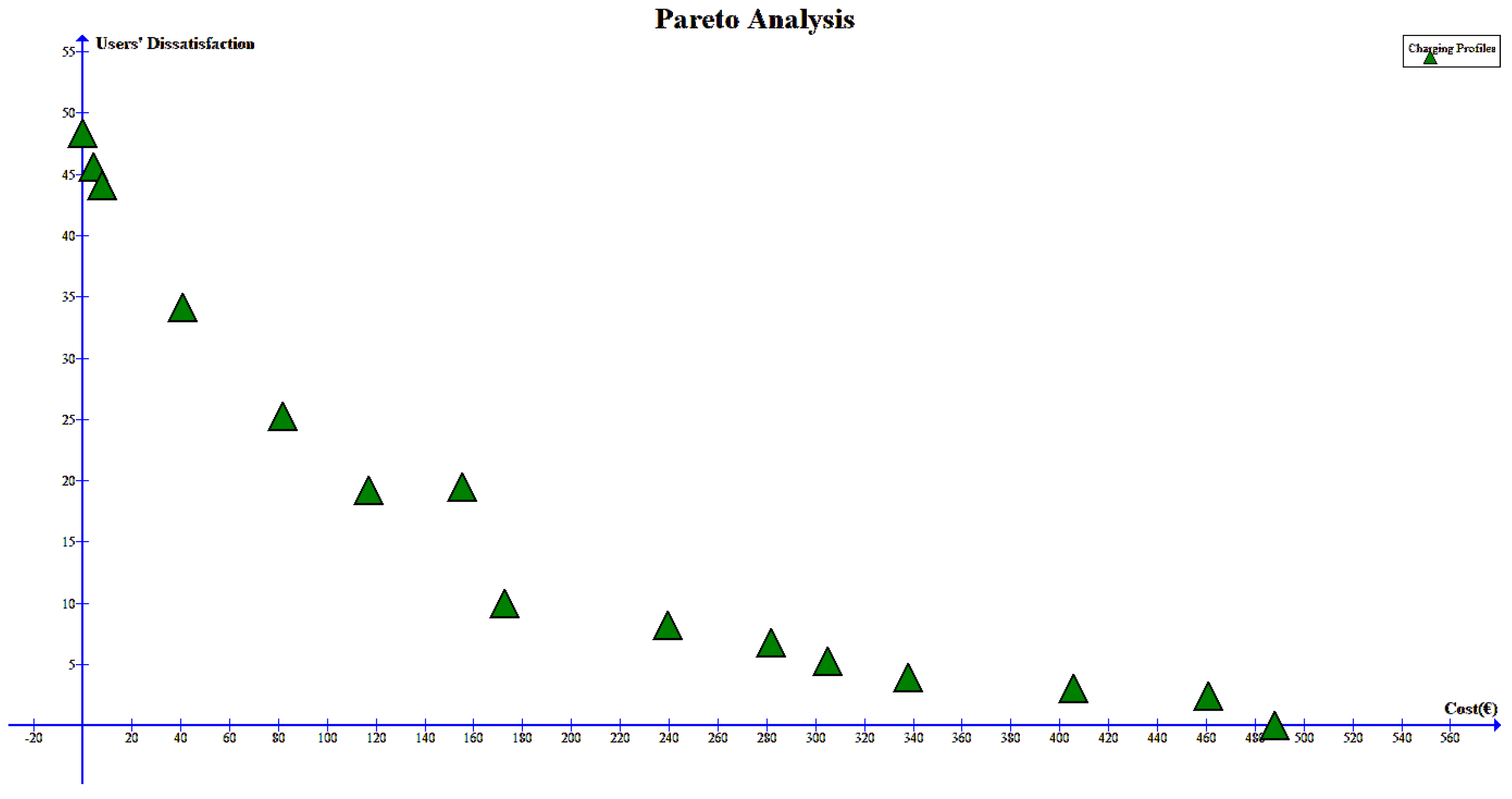
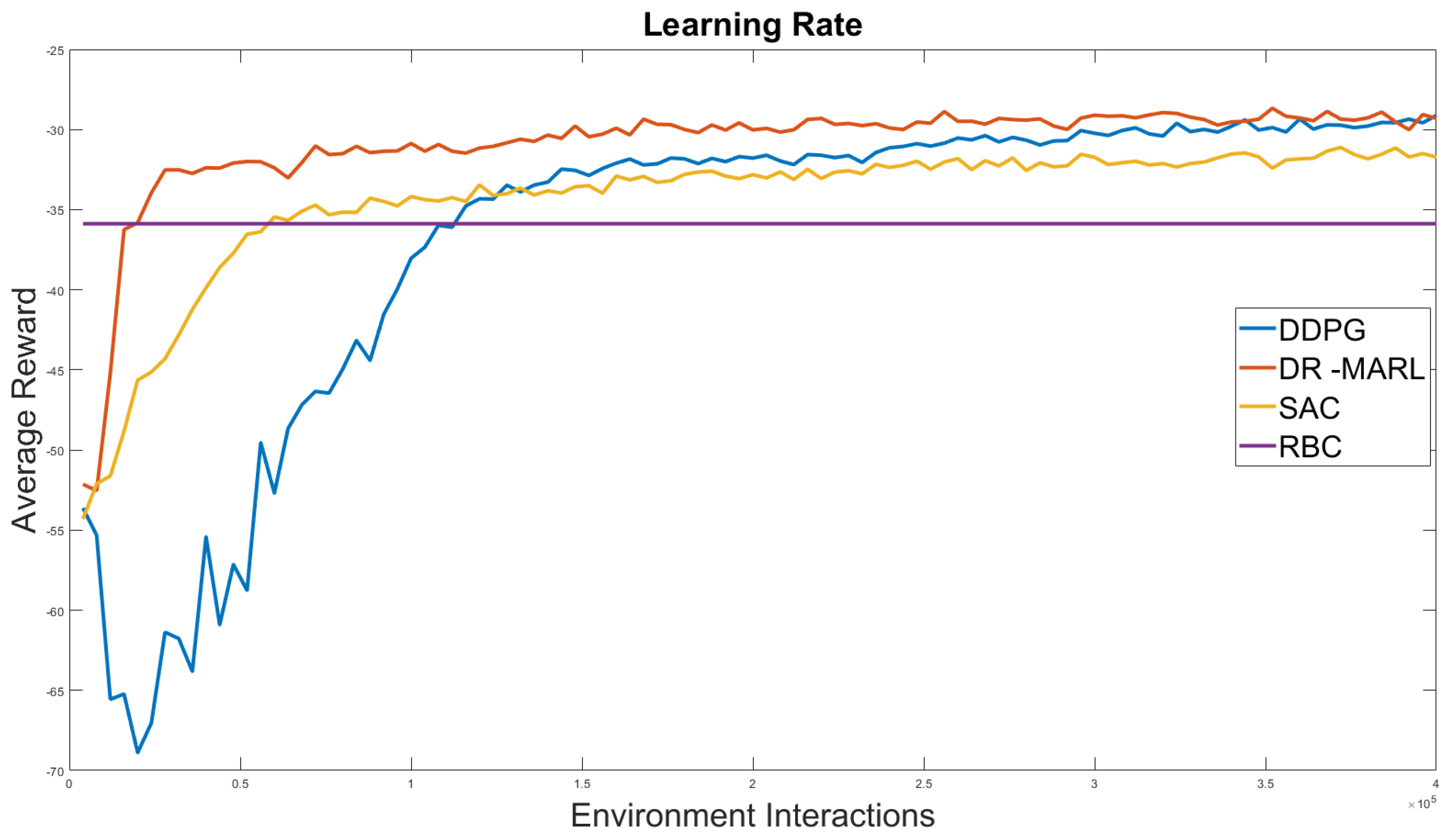
4.2. Cost Comparison with Baseline Methods
4.3. Scalability Analysis
5. Discussion
5.1. Limitations
5.2. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations and Symbols
| DDPG | Deep Deterministic Policy Gradient |
| DQN | Deep Q-Network |
| DR | Demand–Response |
| DR-MARL | Difference Reward-Multi-Agent Reinforcement Learning |
| EV | Electric vehicle |
| EVCS | electric vehicle charging station |
| HATRPO | Heterogeneous-Agent Trust Region Policy Optimisation |
| MADDPG | Multi-Agent DDPG |
| MARL | Multi-Agent Reinforcement Learning |
| MAPPO | Multi-Agent Proximal Policy Optimization |
| MDP | Markov Decision Process |
| ML | Machine Learning |
| PEVs | plug-in electric vehicles |
| PV | photovoltaic |
| R | reward function |
| RES | energy storage |
| RBC | Rule-Based Controller |
| RL | Reinforcement Learning |
| S | state space |
| SAC | Soft Actor–Critic |
| SARSA | State–Action–Reward–State–Action |
| SoC | state of charge |
| TD3 | Twin Delayed Deep Deterministic Policy Gradient |
| V2G | Vehicle to Grid |
| discrepancy for each vehicle i at timestep t | |
| weights of the actor network | |
| weights of the critic network | |
| actor network | |
| target actor network | |
| policy of DDPG algorithm | |
| A | space of actions |
| EV maximum battery capacity | |
| solar radiation value at time step t | |
| unknown, nonlinear function | |
| non-negative, nonlinear, scalar function | |
| global cost function | |
| L | mean square error of estimated and expected reward |
| charging/discharging power for each vehicle i at timestep t | |
| charging/discharging efficiency | |
| Ornstein–Uhlenberk (O-U) noise | |
| P | state transition probability |
| maximum charging power output of each charging spot | |
| power demand for each vehicle i at timestep t | |
| total power demand of the EVCS for energy company | |
| overall requested power from the grid at timestep t | |
| mean production of solar power at timestep t | |
| electricity price at time step t | |
| critic network | |
| target critic network | |
| remaining hours until departure for an EV | |
| decision set-point of the i charging spot at the k timestep | |
| measurement vector of the vehicle i at timestep t | |
| immediate reward |
References
- Yilmaz, M.; Krein, P.T. Review of the impact of vehicle-to-grid technologies on distribution systems and utility interfaces. IEEE Trans. Power Electron. 2012, 28, 5673–5689. [Google Scholar] [CrossRef]
- Dallinger, D.; Link, J.; Büttner, M. Smart grid agent: Plug-in electric vehicle. IEEE Trans. Sustain. Energy 2014, 5, 710–717. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Ouyang, M. Energy consumption of electric vehicles based on real-world driving patterns: A case study of Beijing. Appl. Energy 2015, 157, 710–719. [Google Scholar] [CrossRef]
- Rodrigues, Y.R.; de Souza, A.Z.; Ribeiro, P.F. An inclusive methodology for Plug-in electrical vehicle operation with G2V and V2G in smart microgrid environments. Int. J. Electr. Power Energy Syst. 2018, 102, 312–323. [Google Scholar] [CrossRef]
- Wang, K.; Gu, L.; He, X.; Guo, S.; Sun, Y.; Vinel, A.; Shen, J. Distributed energy management for vehicle-to-grid networks. IEEE Netw. 2017, 31, 22–28. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2023; Technical Report; IEA: Paris, France, 2023. [Google Scholar]
- Lu, C.; Wang, Z.; Wu, C. Storage-Aided Service Surcharge Design for EV Charging Stations. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 13–17 December 2021; pp. 5653–5658. [Google Scholar]
- Wang, E.; Ding, R.; Yang, Z.; Jin, H.; Miao, C.; Su, L.; Zhang, F.; Qiao, C.; Wang, X. Joint Charging and Relocation Recommendation for E-Taxi Drivers via Multi-Agent Mean Field Hierarchical Reinforcement Learning. IEEE Trans. Mob. Comput. 2022, 21, 1274–1290. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.S.; Masoum, M.A. Real-time coordination of plug-in electric vehicle charging in smart grids to minimize power losses and improve voltage profile. IEEE Trans. Smart Grid 2011, 2, 456–467. [Google Scholar] [CrossRef]
- Tursini, M.; Parasiliti, F.; Fabri, G.; Della Loggia, E. A fault tolerant e-motor drive system for auxiliary services in hybrid electric light commercial vehicle. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 16–19 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Tang, W.; Bi, S.; Zhang, Y.J. Online charging scheduling algorithms of electric vehicles in smart grid: An overview. IEEE Commun. Mag. 2016, 54, 76–83. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, B.; Chiang, Y.Y.; Zhang, X.; Chen, Y.; Li, M.; Li, F. BiS4EV: A fast routing algorithm considering charging stations and preferences for electric vehicles. Eng. Appl. Artif. Intell. 2021, 104, 104378. [Google Scholar] [CrossRef]
- Zou, N.; Qian, L.; Li, H. Auxiliary frequency and voltage regulation in microgrid via intelligent electric vehicle charging. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 662–667. [Google Scholar]
- Liu, N.; Chen, Q.; Liu, J.; Lu, X.; Li, P.; Lei, J.; Zhang, J. A heuristic operation strategy for commercial building microgrids containing EVs and PV system. IEEE Trans. Ind. Electron. 2014, 62, 2560–2570. [Google Scholar] [CrossRef]
- Shareef, H.; Islam, M.M.; Mohamed, A. A review of the stage-of-the-art charging technologies, placement methodologies, and impacts of electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 403–420. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, Y.J. A model predictive control approach for low-complexity electric vehicle charging scheduling: Optimality and scalability. IEEE Trans. Power Syst. 2016, 32, 1050–1063. [Google Scholar] [CrossRef]
- Franco, J.F.; Rider, M.J.; Romero, R. A mixed-integer linear programming model for the electric vehicle charging coordination problem in unbalanced electrical distribution systems. IEEE Trans. Smart Grid 2015, 6, 2200–2210. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M.A. Optimal scheduling of electric vehicle charging and vehicle-to-grid services at household level including battery degradation and price uncertainty. Iet Gener. Transm. Distrib. 2014, 8, 1007. [Google Scholar] [CrossRef]
- Zhao, J.; Wan, C.; Xu, Z.; Wang, J. Risk-based day-ahead scheduling of electric vehicle aggregator using information gap decision theory. IEEE Trans. Smart Grid 2015, 8, 1609–1618. [Google Scholar] [CrossRef]
- Balasubramaniam, S.; Syed, M.H.; More, N.S.; Polepally, V. Deep learning-based power prediction aware charge scheduling approach in cloud based electric vehicular network. Eng. Appl. Artif. Intell. 2023, 121, 105869. [Google Scholar]
- Zhang, M.; Chen, J. The energy management and optimized operation of electric vehicles based on microgrid. IEEE Trans. Power Deliv. 2014, 29, 1427–1435. [Google Scholar] [CrossRef]
- Yao, L.; Lim, W.H.; Tsai, T.S. A real-time charging scheme for demand response in electric vehicle parking station. IEEE Trans. Smart Grid 2016, 8, 52–62. [Google Scholar] [CrossRef]
- Momber, I.; Siddiqui, A.; San Roman, T.G.; Söder, L. Risk averse scheduling by a PEV aggregator under uncertainty. IEEE Trans. Power Syst. 2014, 30, 882–891. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Yuan, S.; Kosmatopoulos, E.B. An adaptive learning-based approach for nearly optimal dynamic charging of electric vehicle fleets. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2066–2075. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Michailidis, P.; Kosmatopoulos, E.B. A cognitive stochastic approximation approach to optimal charging schedule in electric vehicle stations. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 484–489. [Google Scholar]
- Korkas, C.D.; Terzopoulos, M.; Tsaknakis, C.; Kosmatopoulos, E.B. Nearly optimal demand side management for energy, thermal, EV and storage loads: An Approximate Dynamic Programming approach for smarter buildings. Energy Build. 2022, 255, 111676. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Dimitrov, S.; Lguensat, R. Reinforcement learning based algorithm for the maximization of EV charging station revenue. In Proceedings of the 2014 International Conference on Mathematics and Computers in Sciences and in Industry, Varna, Bulgaria, 13–15 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 235–239. [Google Scholar]
- Wen, Z.; O’Neill, D.; Maei, H. Optimal demand response using device-based reinforcement learning. IEEE Trans. Smart Grid 2015, 6, 2312–2324. [Google Scholar] [CrossRef]
- Zhang, Y.; Rao, X.; Liu, C.; Zhang, X.; Zhou, Y. A cooperative EV charging scheduling strategy based on double deep Q-network and Prioritized experience replay. Eng. Appl. Artif. Intell. 2023, 118, 105642. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Yang, Y.; Liu, F. More intelligent and robust estimation of battery state-of-charge with an improved regularized extreme learning machine. Eng. Appl. Artif. Intell. 2021, 104, 104407. [Google Scholar] [CrossRef]
- Liu, J.; Guo, H.; Xiong, J.; Kato, N.; Zhang, J.; Zhang, Y. Smart and resilient EV charging in SDN-enhanced vehicular edge computing networks. IEEE J. Sel. Areas Commun. 2019, 38, 217–228. [Google Scholar] [CrossRef]
- Lee, J.; Lee, E.; Kim, J. Electric vehicle charging and discharging algorithm based on reinforcement learning with data-driven approach in dynamic pricing scheme. Energies 2020, 13, 1950. [Google Scholar] [CrossRef]
- Ding, T.; Zeng, Z.; Bai, J.; Qin, B.; Yang, Y.; Shahidehpour, M. Optimal electric vehicle charging strategy with Markov decision process and reinforcement learning technique. IEEE Trans. Ind. Appl. 2020, 56, 5811–5823. [Google Scholar] [CrossRef]
- Haydari, A.; Yılmaz, Y. Deep reinforcement learning for intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2020, 23, 11–32. [Google Scholar] [CrossRef]
- Wan, Z.; Li, H.; He, H.; Prokhorov, D. Model-free real-time EV charging scheduling based on deep reinforcement learning. IEEE Trans. Smart Grid 2018, 10, 5246–5257. [Google Scholar]
- Wang, S.; Bi, S.; Zhang, Y.A. Reinforcement learning for real-time pricing and scheduling control in EV charging stations. IEEE Trans. Ind. Inform. 2019, 17, 849–859. [Google Scholar] [CrossRef]
- Abdalrahman, A.; Zhuang, W. Dynamic pricing for differentiated PEV charging services using deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1415–1427. [Google Scholar] [CrossRef]
- Yan, L.; Chen, X.; Zhou, J.; Chen, Y.; Wen, J. Deep reinforcement learning for continuous electric vehicles charging control with dynamic user behaviors. IEEE Trans. Smart Grid 2021, 12, 5124–5134. [Google Scholar] [CrossRef]
- Ye, Z.; Gao, Y.; Yu, N. Learning to Operate an Electric Vehicle Charging Station Considering Vehicle-grid Integration. IEEE Trans. Smart Grid 2022, 13, 3038–3048. [Google Scholar] [CrossRef]
- Fang, X.; Wang, J.; Song, G.; Han, Y.; Zhao, Q.; Cao, Z. Multi-agent reinforcement learning approach for residential microgrid energy scheduling. Energies 2019, 13, 123. [Google Scholar] [CrossRef]
- Abdullah, H.M.; Gastli, A.; Ben-Brahim, L. Reinforcement learning based EV charging management systems—A review. IEEE Access 2021, 9, 41506–41531. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Karatzinis, G.; Korkas, C.; Terzopoulos, M.; Tsaknakis, C.; Stefanopoulou, A.; Michailidis, I.; Kosmatopoulos, E. Chargym: An EV Charging Station Model for Controller Benchmarking. In Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations, Crete, Greece, 17–20 June 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 241–252. [Google Scholar]
- Škugor, B.; Deur, J. Dynamic programming-based optimisation of charging an electric vehicle fleet system represented by an aggregate battery model. Energy 2015, 92, 456–465. [Google Scholar] [CrossRef]
- Lund, H.; Kempton, W. Integration of renewable energy into the transport and electricity sectors through V2G. Energy Policy 2008, 36, 3578–3587. [Google Scholar] [CrossRef]
- NordPool. 2016. Available online: http://www.nordpoolspot.com/Market-data1/ (accessed on 16 July 2024).
- Korkas, C.D.; Baldi, S.; Michailidis, I.; Kosmatopoulos, E.B. Intelligent energy and thermal comfort management in grid-connected microgrids with heterogeneous occupancy schedule. Appl. Energy 2015, 149, 194–203. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective optimisation using evolutionary algorithms: An introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–34. [Google Scholar]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. A distributed, plug-n-play algorithm for multi-robot applications with a priori non-computable objective functions. Int. J. Robot. Res. 2019, 38, 813–832. [Google Scholar] [CrossRef]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of ppo in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]
- Kuba, J.G.; Chen, R.; Wen, M.; Wen, Y.; Sun, F.; Wang, J.; Yang, Y. Trust region policy optimisation in multi-agent reinforcement learning. arXiv 2021, arXiv:2109.11251. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6382–6393. [Google Scholar]



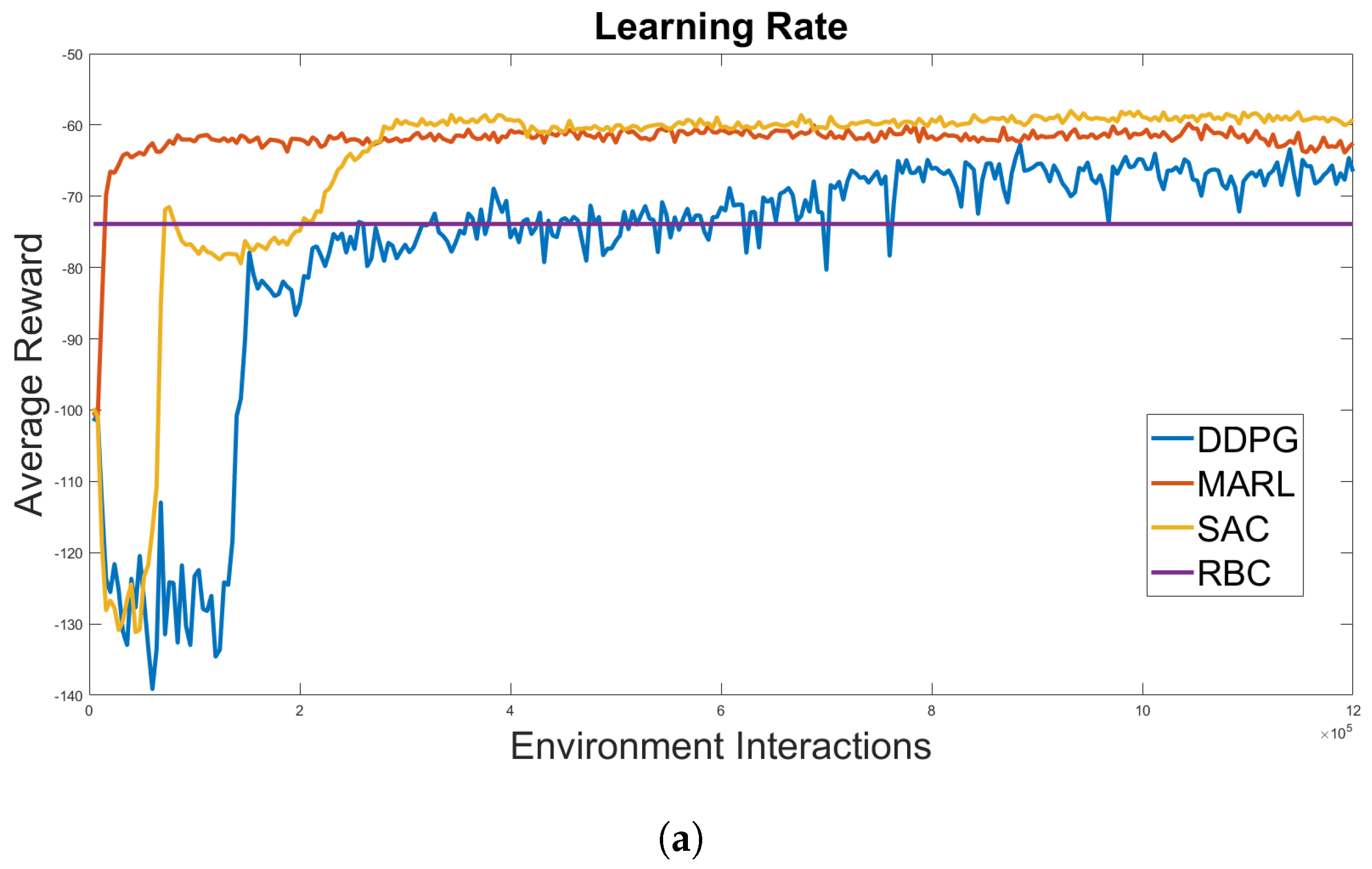
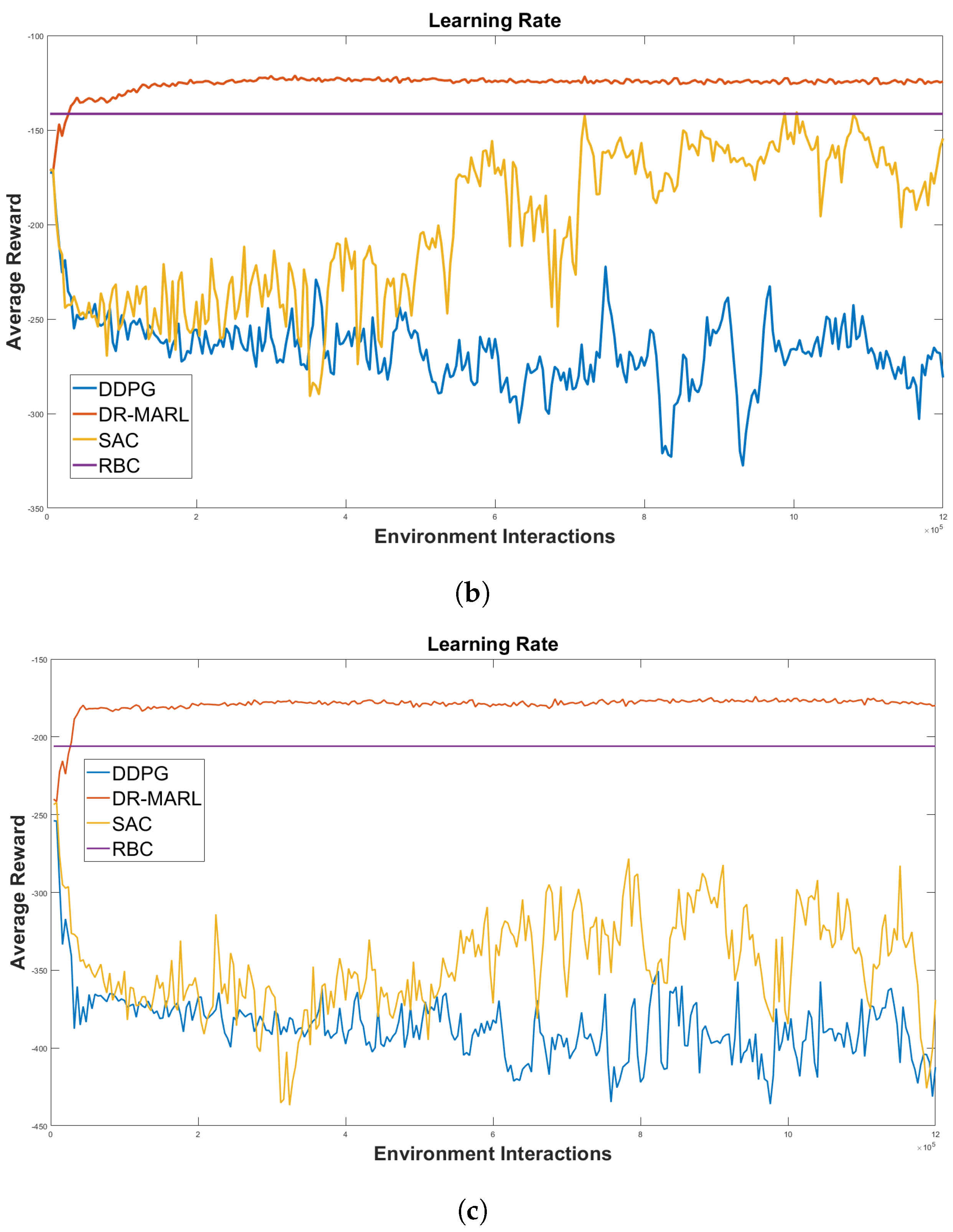
| RBC | DDPG | SAC | DR-MARL | |
|---|---|---|---|---|
| Price 1 | −35.29 | −29.45 | −31.41 | −30.79 |
| Price 2 | −36.96 | −25.91 | −27.11 | −26.09 |
| Price 3 | −36.06 | −29.53 | −31.43 | −30.34 |
| Price 4 | −34.50 | −29.58 | −30.59 | −30.86 |
| Price Random | −35.88 | −30.21 | −30.84 | −30.94 |
| RBC | DDPG | SAC | DR-MARL | |
|---|---|---|---|---|
| Std | - | 2.84 | 2.33 | 3.32 |
| RBC | DDPG | SAC | DR-MARL | |
|---|---|---|---|---|
| −71.83 | −66.76 | −61.24 | −61.69 | |
| −141.45 | −250.89 | −152.33 | −123.45 | |
| −207.34 | −380.76 | −344.69 | −175.12 |
| DDPG | SAC | DR-MARL | |
|---|---|---|---|
| 110k | 60k | 20k | |
| 400k | 200k | 20k | |
| - | - | 25k | |
| - | - | 27k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korkas, C.D.; Tsaknakis, C.D.; Kapoutsis, A.C.; Kosmatopoulos, E. Distributed and Multi-Agent Reinforcement Learning Framework for Optimal Electric Vehicle Charging Scheduling. Energies 2024, 17, 3694. https://doi.org/10.3390/en17153694
Korkas CD, Tsaknakis CD, Kapoutsis AC, Kosmatopoulos E. Distributed and Multi-Agent Reinforcement Learning Framework for Optimal Electric Vehicle Charging Scheduling. Energies. 2024; 17(15):3694. https://doi.org/10.3390/en17153694
Chicago/Turabian StyleKorkas, Christos D., Christos D. Tsaknakis, Athanasios Ch. Kapoutsis, and Elias Kosmatopoulos. 2024. "Distributed and Multi-Agent Reinforcement Learning Framework for Optimal Electric Vehicle Charging Scheduling" Energies 17, no. 15: 3694. https://doi.org/10.3390/en17153694
APA StyleKorkas, C. D., Tsaknakis, C. D., Kapoutsis, A. C., & Kosmatopoulos, E. (2024). Distributed and Multi-Agent Reinforcement Learning Framework for Optimal Electric Vehicle Charging Scheduling. Energies, 17(15), 3694. https://doi.org/10.3390/en17153694







