A Coupled Model of Multiscaled Creep Deformation and Gas Flow for Predicting Gas Depletion Characteristics of Shale Reservoir at the Field Scale
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equation for Reservoir Deformation
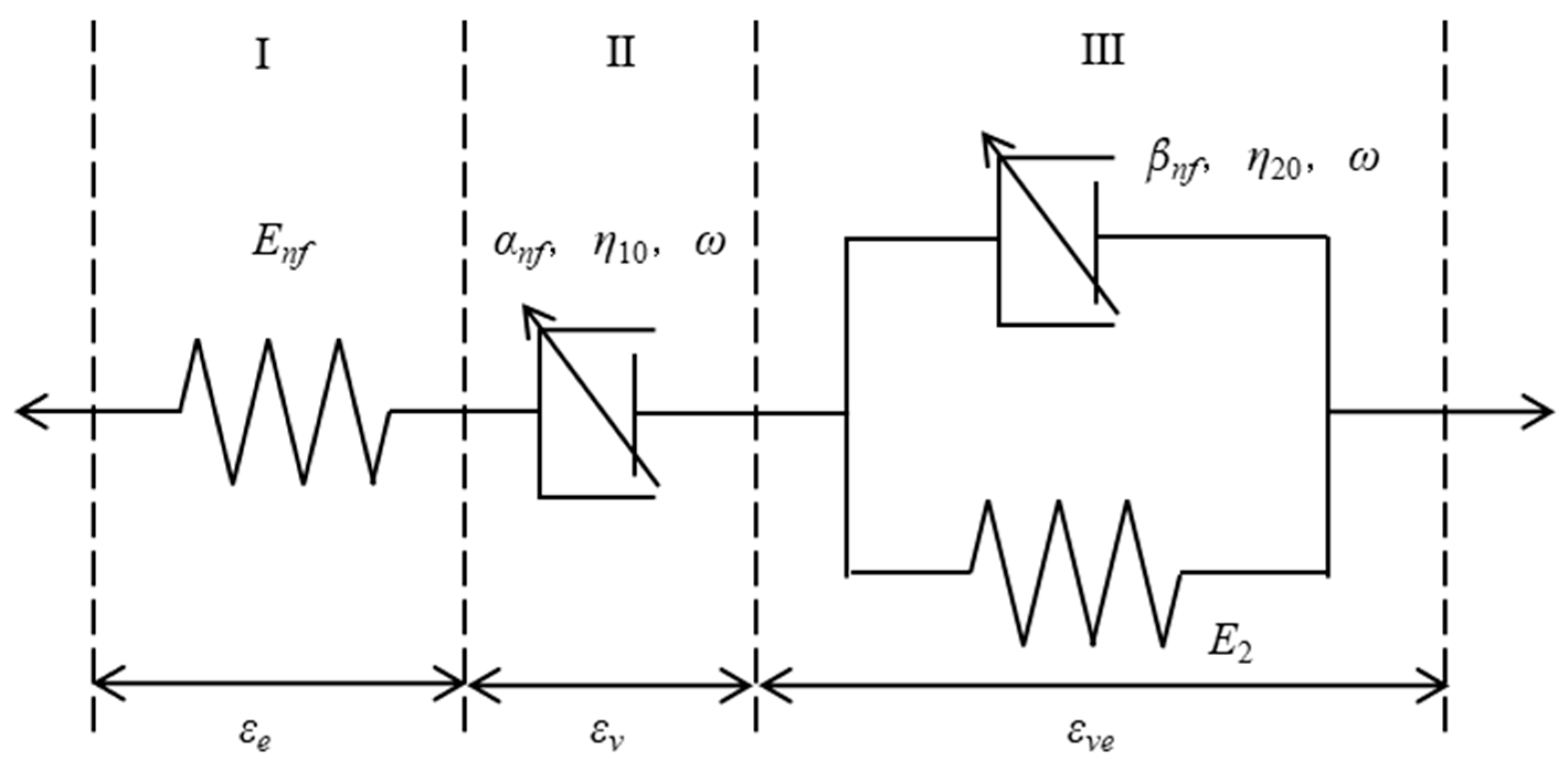
2.1.1. Modified Nonlinear Fractional-Order Shale Creep Model
2.1.2. Navier-Type Governing Equation for Shale Reservoir
2.2. Governing Equation for Gas Flow
2.2.1. Gas Flow in the Hydraulic Fracture System
2.2.2. Slip Flow in the Natural Fracture
2.2.3. Gas Diffusion in Organic Matter
2.3. Permeability Models
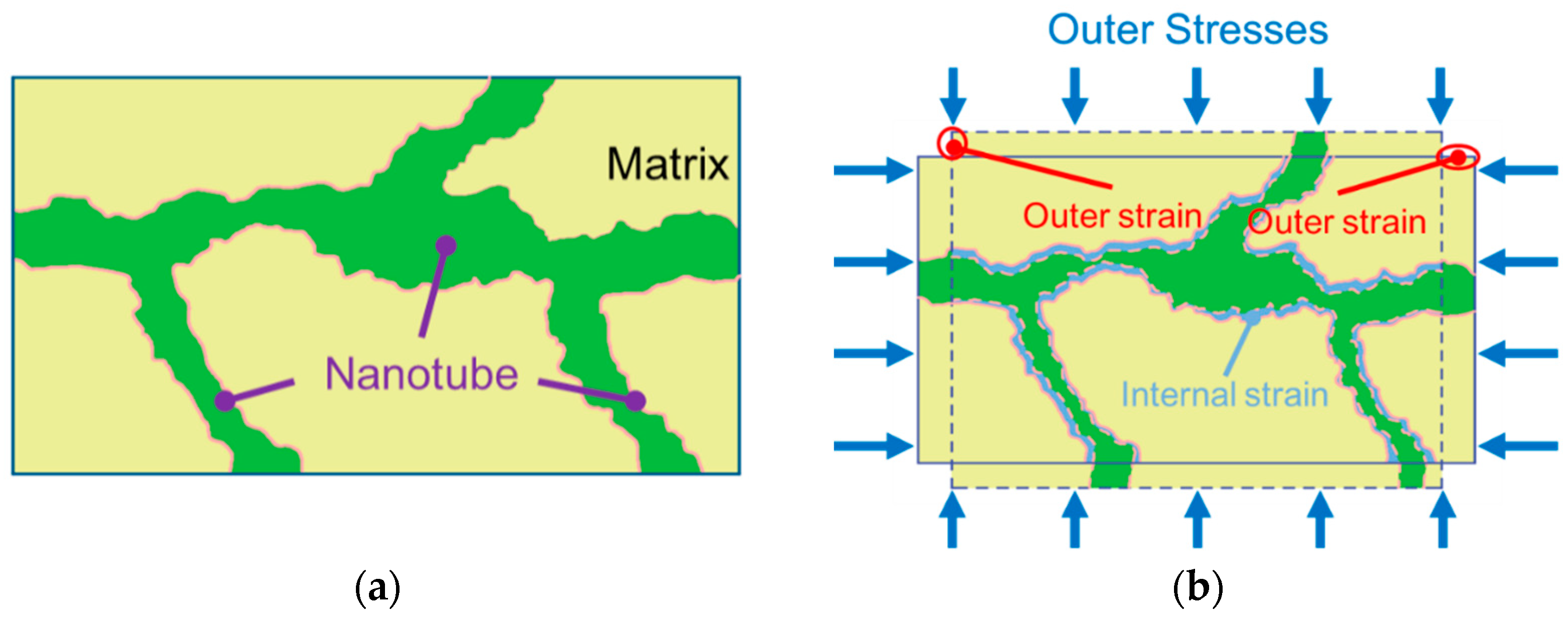
2.3.1. Definition of Internal Strain
2.3.2. Intrinsic Permeability of the Natural Fracture
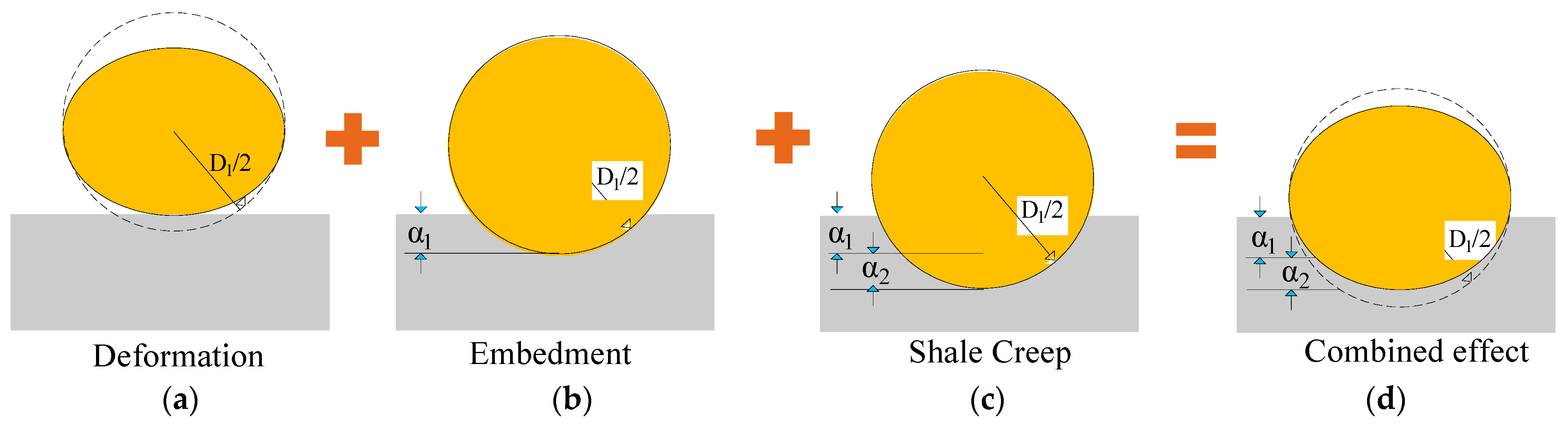
2.3.3. The Permeability Model of Hydraulic Fractures
2.4. Coupling Process
- (i)
- The gas flow in the hydraulic fracture system impacts the creep deformation of the shale reservoir (Equation (12)) and enlarges the closure pressure—pc. As a result, the aperture and permeability of hydraulic fractures decrease following Equations (34) and (37). As a return, the variation in permeability impacts the gas flow characteristics in hydraulic fractures as defined in Equation (13).
- (ii)
- The gas depletion in natural fractures lowers the gas pressure in shale reservoirs and impacts the stress–strain state of shale reservoirs, as determined by Equation (12). On the other hand, the strain in shale reservoirs impacts the permeability of natural fractures (Equation (32)), and the creep strain is considered. As a result, the redefined permeability determines the gas pressure distribution following Equation (17);
- (iii)
- The gas flow in hydraulic fractures, natural fractures, and shale matrices all impact the stress state of shale reservoirs and, thus, creep deformation. In addition, mass transfer occurs between different systems. The mass transfer term between hydraulic fractures and natural fractures is co-dominated by the pore pressure difference between them and the permeability in natural fracture systems (Equation (21)). The mass transfer between natural fractures and matrix systems is determined by the effective diffusion coefficient (Equation (22)) in the matrix system.
3. Model Verification
3.1. Field Data Selection and Geometric Model
3.2. Module Selection and Parameter Determination
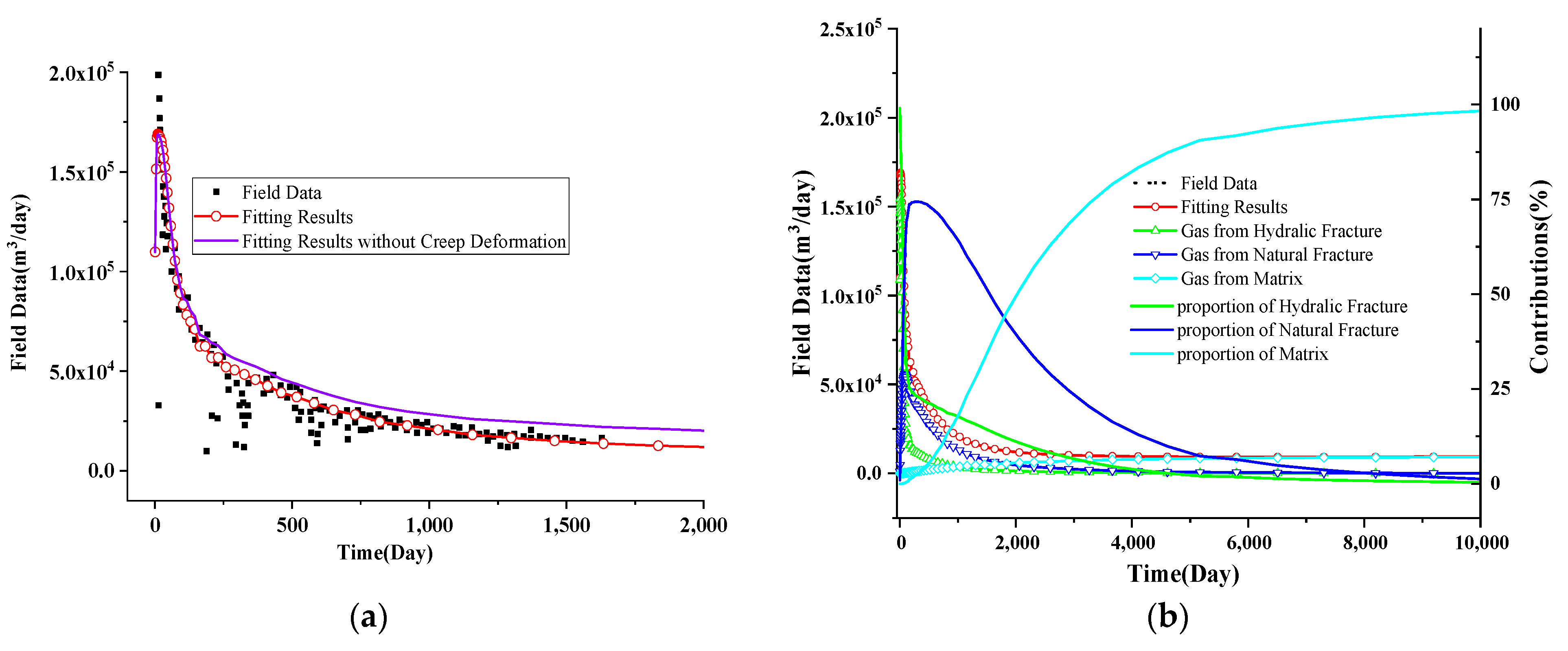
3.3. Verification Results
3.4. Permeability Evolutions
4. Results and Discussion
4.1. Impacts of the Creep Behavior of the Hydraulic Fracture System
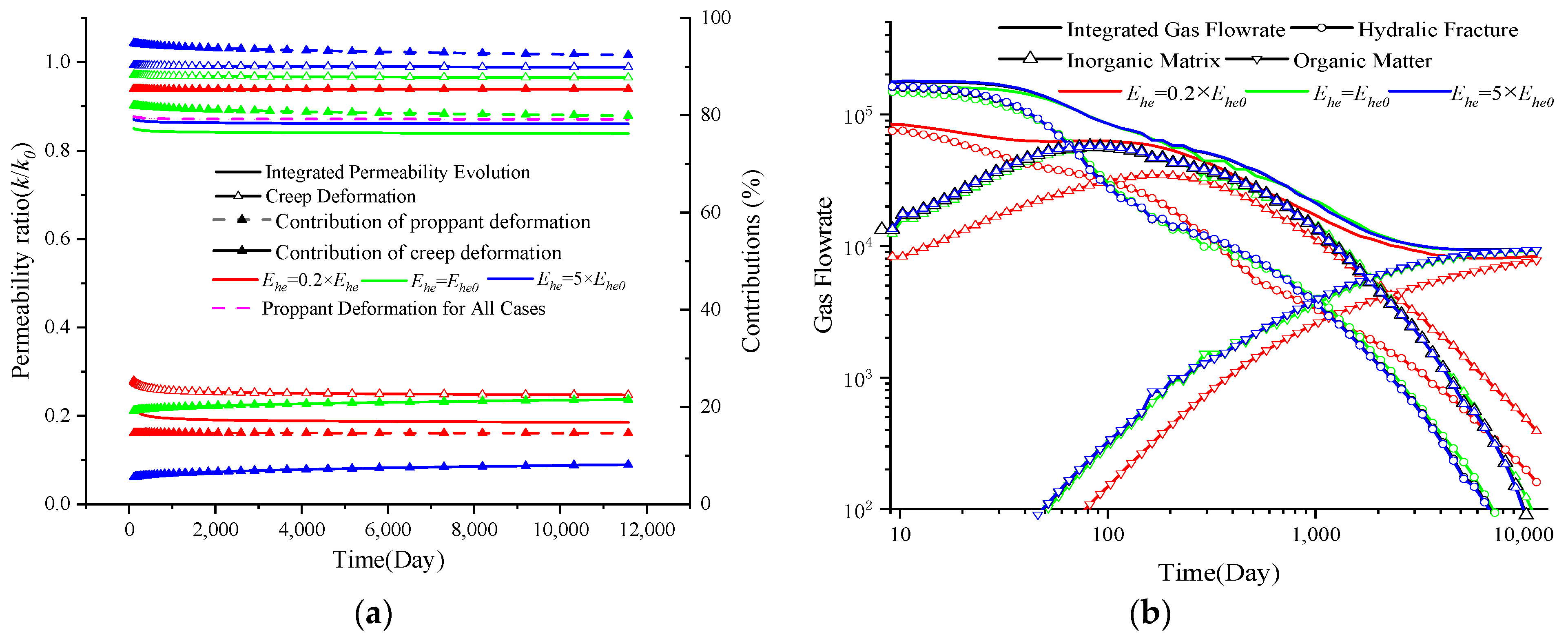
4.1.1. The Impact of Ehe
4.1.2. The Impact of ηhf
4.1.3. The Impact of ahf
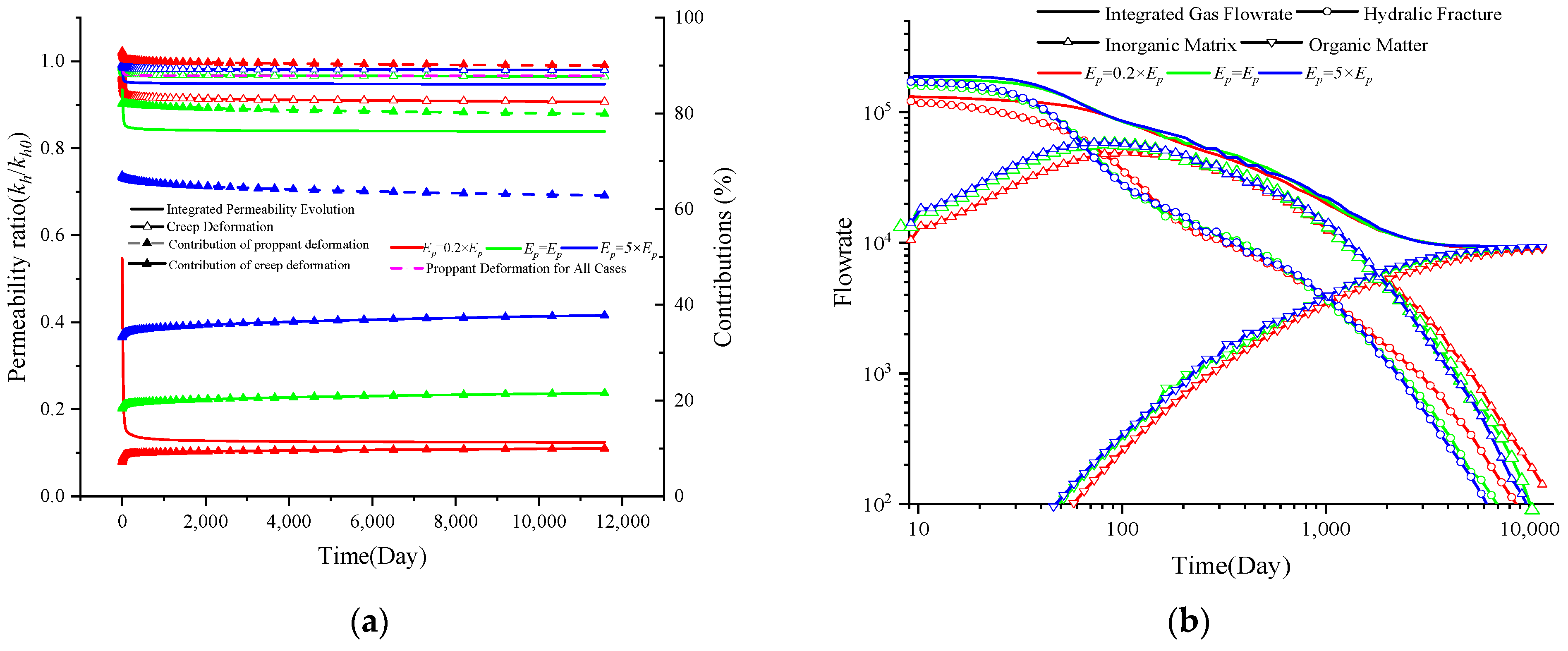
4.2. Impacts of the Proppant Type
4.3. Impacts of the Creep Behavior of the Natural Fracture System
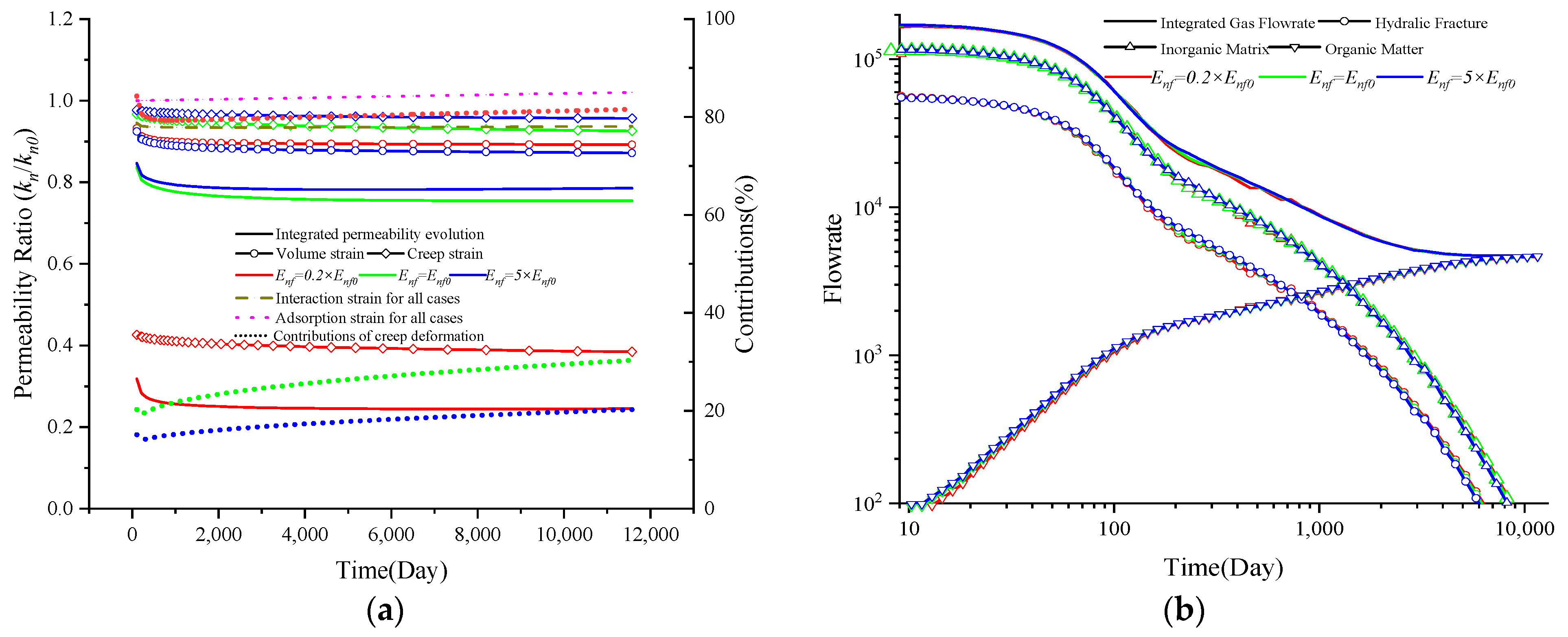
4.3.1. The Impact of anf
4.3.2. The Impact of βnf
4.3.3. The Impact of Enf
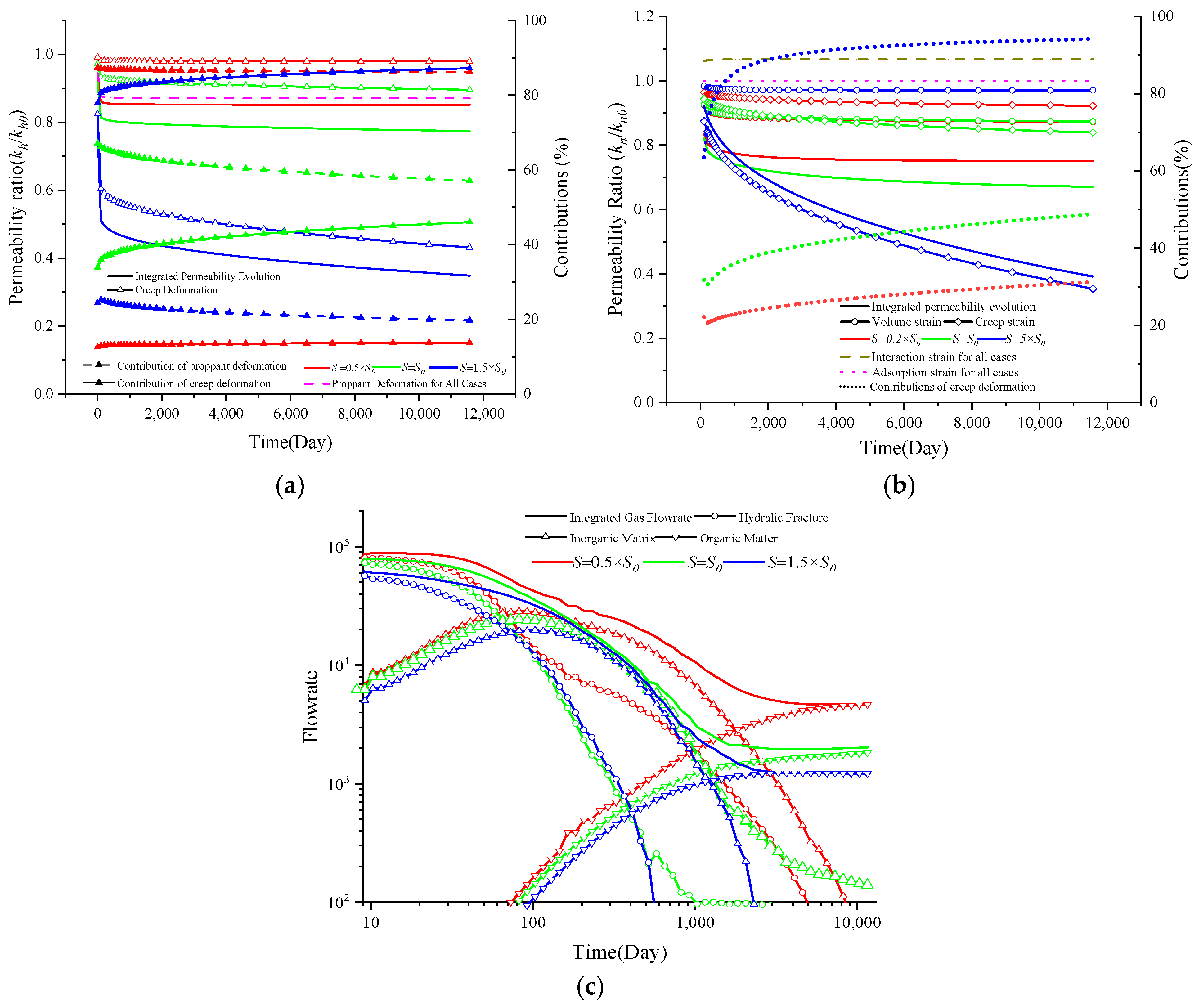
4.4. The Impacts of Formation Stress
4.5. Discussion
4.5.1. Comparisons with Previous Work
4.5.2. Limitations and Future Work
4.5.3. Guidance to the Field Application
- (a)
- History matching and extension to future analyses. In this work, a fully coupled model, including a multiscaled viscoelasticity constitutive model and a classical triple-porosity model, is proposed to investigate the impact of creep deformation on shale gas depletion characteristics. The real parameter should be determined to characterize the time-dependent deformation of the hydraulic fracture system and natural fracture system. In this work, some empirical value has been employed, which may not always be true. A creep deformation–gas seepage experiment should be conducted to measure the real value. Then the fully coupled model may be applied to history match existing gas production data and then predict subsequent production.
- (b)
- Implications for in situ shale gas exploitation. (i) The viscoelasticity properties of shale reservoir have a significant impact on shale gas depletion; therefore, it is essential to conduct creep deformation-gas seepage analysis of shale; (ii) the first stage of creep deformation significantly affects the initial permeability, while the second stage dominates the long-term permeability evolution. The impact of gas depletion is concentrated in the long term. (iii) Also, the properties of proppant directly affect the flow properties of the hydraulic fracture, and rates of shale gas depletion.
5. Conclusions
- (a)
- A multiscaled creep constitutive model is established to govern the viscoelastic behavior of hydraulic and natural fractures of shale reservoirs. Specially, the impact of effective stress on the characteristic parameter is considered. Correspondingly, a triple porosity model replicates the multi-gas flow in shale reservoirs. The permeabilities of hydraulic and natural fractures serve as the coupling parameters between them. In this approach, the creep deformation and corresponding gas flow in each subsystem are linked.
- (b)
- Both the properties of the proppant and shale reservoir impact the conductivity of the hydraulic fracture. A smaller Young’s modulus of the proppant leads to a greater reduction in conductivity at the initial time. The significant transient creep stage exhibits a much lower initial permeability. However, the dominant role of the second creep stage increases with depletion time. The impacts are concentrated at early times for the gas flow rate, and a smaller difference in the long-term stage can be observed for different values.
- (c)
- The permeability evolution of natural fractures (nanotubes) is mainly dominated by the creep characteristics and effective stress of shale reservoirs and is less controlled by the adsorption strain. Similarly, the first stage of creep deformation significantly affects the initial permeability, while the second stage dominates the long-term permeability evolution.
- (d)
- The in situ stress significantly impacts creep deformation, contributing to permeability evolution and further gas depletion characteristics. Obviously, greater stress results in a greater reduction in permeability for both NFs and HFs. Moreover, the deep buried formation has a lower gas flow rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Bažant, Z.P.; Xie, H.; Rahimi-Aghdam, S. Anisotropic microplane constitutive model for coupling creep and damage in layered geomaterials such as gas or oil shale. Int. J. Rock Mech. Min. Sci. 2019, 124, 104074. [Google Scholar] [CrossRef]
- Hughes, J.D. Energy: A reality check on the shale revolution. Nature 2013, 494, 307–308. [Google Scholar] [CrossRef] [PubMed]
- Wasaki, A.; Akkutlu, I.Y. Permeability of Organic-rich Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 29 October 2014; Society of Petroleum Engineers: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Cheng, W.; Cui, G.; Tan, Y.; Elsworth, D.; Wang, C.; Yang, C.; Chen, T.; Jiang, C. A multi-layer nanocased model to explain the U-shaped evolution of shale gas permeability at constant confining pressure. Fuel 2024, 359, 130478. [Google Scholar] [CrossRef]
- Cui, G.; Tan, Y.; Chen, T.; Feng, X.-T.; Elsworth, D.; Pan, Z.; Wang, C. Multidomain Two-Phase Flow Model to Study the Impacts of Hydraulic Fracturing on Shale Gas Production. Energy Fuels 2020, 34, 4273–4288. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, S.; Tang, S.; Cui, G.; Ma, Y.; Sun, M.; Pan, Z. Impact of water saturation on gas permeability in shale: Experimental and modelling. J. Nat. Gas Sci. Eng. 2021, 95, 104062. [Google Scholar] [CrossRef]
- Li, Y.; Ghassemi, A. Creep Behavior of Barnett, Haynesville, And Marcellus Shale. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 1 January 2012; American Rock Mechanics Association: Chicago, IL, USA, 2012; p. 7. [Google Scholar]
- Peng, Y.; Zhao, J.; Sepehrnoori, K.; Li, Z. Fractional model for simulating the viscoelastic behavior of artificial fracture in shale gas. Eng. Fract. Mech. 2020, 228, 106892. [Google Scholar] [CrossRef]
- Wilczynski, P.M.; Domonik, A.; Lukaszewski, P. Brittle Creep and Viscoelastic Creep in Lower Palaeozoic Shales from the Baltic Basin, Poland. Energies 2021, 14, 4633. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Qu, Z.; Yin, Y.; Kang, Q.; Yu, B.; Tao, W.-Q. Modeling of multi-scale transport phenomena in shale gas production—A critical review. Appl. Energy 2020, 262, 114575. [Google Scholar] [CrossRef]
- Iferobia, C.C.; Ahmad, M. A review on the experimental techniques and applications in the geomechanical evaluation of shale gas reservoirs. J. Nat. Gas Sci. Eng. 2020, 74, 103090. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Feng, X.-T.; Zhang, D.; Connell, L.D.; Li, S. Laboratory characterisation of fracture compressibility for coal and shale gas reservoir rocks: A review. Int. J. Coal Geol. 2019, 204, 1–17. [Google Scholar] [CrossRef]
- Scholz, C.H. Mechanism of creep in brittle rock. J. Geophys. Res. 1968, 73, 3295–3302. [Google Scholar] [CrossRef]
- Mighani, S.; Bernabé, Y.; Boulenouar, A.; Mok, U.; Evans, B. Creep Deformation in Vaca Muerta Shale From Nanoindentation to Triaxial Experiments. J. Geophys. Res. Solid Earth 2019, 124, 7842–7868. [Google Scholar] [CrossRef]
- Geng, Z.; Bonnelye, A.; Chen, M.; Jin, Y.; Dick, P.; David, C.; Fang, X.; Schubnel, A. Elastic Anisotropy Reversal During Brittle Creep in Shale. Geophys. Res. Lett. 2017, 44, 10887–10895. [Google Scholar] [CrossRef]
- Chester, F.; Chester, J.; Kronenberg, A.; Hajash, A. Subcritical creep compaction of quartz sand at diagenetic conditions: Effects of water and grain size. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, Z.; Rahman, S.S. Experimental investigation of the primary and secondary creep behaviour of shale gas reservoir rocks from deep sections of the Cooper Basin. J. Nat. Gas Sci. Eng. 2020, 73, 103044. [Google Scholar] [CrossRef]
- Brantut, N.; Heap, M.; Meredith, P.; Baud, P. Time-dependent cracking and brittle creep in crustal rocks: A review. J. Struct. Geol. 2013, 52, 17–43. [Google Scholar] [CrossRef]
- Geng, Z.; Bonnelye, A.; Chen, M.; Jin, Y.; Dick, P.; David, C.; Fang, X.; Schubnel, A. Time and temperature dependent creep in tournemire shale. J. Geophys. Res. Solid Earth 2018, 123, 9658–9675. [Google Scholar] [CrossRef]
- Rassouli, F.S.; Zoback, M.D. Comparison of Short-Term and Long-Term Creep Experiments in Shales and Carbonates from Unconventional Gas Reservoirs. Rock Mech. Rock Eng. 2018, 51, 1995–2014. [Google Scholar] [CrossRef]
- Cao, W.; Chen, K.; Tan, X.; Chen, H. A novel damage-based creep model considering the complete creep process and multiple stress levels. Comput. Geotech. 2020, 124, 103599. [Google Scholar] [CrossRef]
- Welch, S.w.J.; Rorrer, R.A.L.; Duren, R.G. Application of Time-Based Fractional Calculus Methods to Viscoelastic Creep and Stress Relaxation of Materials. Mech. Time-Depend. Mater. 1999, 3, 279–303. [Google Scholar] [CrossRef]
- Sheahan, T.C. Interpretation of undrained creep tests in terms of effective stresses. Can. Geotech. J. 1995, 32, 373–379. [Google Scholar] [CrossRef]
- Wang, R.; Li, L.; Simon, R. A model for describing and predicting the creep strain of rocks from the primary to the tertiary stage. Int. J. Rock Mech. Min. Sci. 2019, 123, 104087. [Google Scholar] [CrossRef]
- Yahya, O.; Aubertin, M.; Julien, M. A unified representation of the plasticity, creep and relaxation behavior of rocksalt. Int. J. Rock Mech. Min. Sci. 2000, 37, 787–800. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 84. [Google Scholar]
- Zhou, J.; Zhang, J.; Wang, J.; Li, F.; Zhou, Y. Research on nonlinear damage hardening creep model of soft surrounding rock under the stress of deep coal resources mining. Energy Rep. 2022, 8, 1493–1507. [Google Scholar] [CrossRef]
- Blair, G.S. The role of psychophysics in rheology. J. Colloid Sci. 1947, 2, 21–32. [Google Scholar] [CrossRef]
- Chang, C.; Zoback, M. Creep in unconsolidated shale and its implication on rock physical properties. In Proceedings of the 42nd US Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Du, J.; Hu, L.; Meegoda, J.N.; Zhang, G. Shale softening: Observations, phenomenological behavior, and mechanisms. Appl. Clay Sci. 2018, 161, 290–300. [Google Scholar] [CrossRef]
- Rafieepour, S.; Zheng, D.; Miska, S.; Ozbayoglu, E.; Takach, N.; Yu, M.; Zhang, J. Combined experimental and well log evaluation of anisotropic mechanical properties of shales: An application to wellbore stability in bakken formation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 26–29 October 2020. [Google Scholar]
- Pyrak-Nolte, L.; Morris, J. Single fractures under normal stress: The relation between fracture specific stiffness and fluid flow. Int. J. Rock Mech. Min. Sci. 2000, 37, 245–262. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 2: Ductile creep, brittle strength, and their relation to the elastic modulus. Geophysics 2013, 78, D393–D402. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 2013, 78, D381–D392. [Google Scholar] [CrossRef]
- Zheng, D.; Miska, S.; Ozbayoglu, E.; Zhang, J. Combined experimental and well log study of anisotropic strength of shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 16–18 October 2023. [Google Scholar]
- Hasbani, J.; Hryb, D. On the characterization of the viscoelastic response of the Vaca Muerta Formation. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Rybacki, E.; Herrmann, J.; Wirth, R.; Dresen, G. Creep of Posidonia shale at elevated pressure and temperature. Rock Mech. Rock Eng. 2017, 50, 3121–3140. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Wu, Y.; Haque, A.; Connell, L.D. Experimental study of permeability and its anisotropy for shale fracture supported with proppant. J. Nat. Gas Sci. Eng. 2017, 44, 250–264. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Kang, J.; Zhou, F.; Connell, L.D.; Yang, Y. Experimental study of impact of anisotropy and heterogeneity on gas flow in coal. Part I: Diffusion and adsorption. Fuel 2018, 232, 444–453. [Google Scholar] [CrossRef]
- Cui, G.; Liu, J.; Wei, M.; Feng, X.; Elsworth, D. Evolution of permeability during the process of shale gas extraction. J. Nat. Gas Sci. Eng. 2018, 49, 94–109. [Google Scholar] [CrossRef]
- Shi, F. XFEM-based numerical modeling of well performance considering proppant transport, embedment, crushing and rock creep in shale gas reservoirs. J. Pet. Sci. Eng. 2021, 201, 108523. [Google Scholar] [CrossRef]
- Peng, Y.; Luo, A.; Li, Y.; Wu, Y.; Xu, W.; Sepehrnoori, K. Fractional model for simulating Long-Term fracture conductivity decay of shale gas and its influences on the well production. Fuel 2023, 351, 129052. [Google Scholar] [CrossRef]
- Cui, G.; Xia-Ting, F.; Pan, Z.; Chen, T.; Liu, J.; Elsworth, D.; Tan, Y.; Wang, C. Impact of shale matrix mechanical interactions on gas transport during production. J. Pet. Sci. Eng. 2020, 184, 106524. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Y.; Sun, Q.; Wang, Y. Multiscale mass transfer coupling of triple-continuum and discrete fractures for flow simulation in fractured vuggy porous media. Int. J. Heat Mass Transf. 2018, 116, 484–495. [Google Scholar] [CrossRef]
- Sheng, M.; Li, G.; Sutula, D.; Tian, S.; Bordas, S.P.A. XFEM modeling of multistage hydraulic fracturing in anisotropic shale formations. J. Pet. Sci. Eng. 2018, 162, 801–812. [Google Scholar] [CrossRef]
- Ambrose, R.J.; Hartman, R.C.; Campos, M.D.; Akkutlu, I.Y.; Sondergeld, C. New Pore-Scale Considerations for Shale Gas in Place Calculations. In Proceedings of the SPE Unconventional Gas Conference, Pittsburgh, PA, USA, 23–25 February 2010. [Google Scholar]
- Akkutlu, I.Y.; Fathi, E. Multiscale Gas Transport in Shales With Local Kerogen Heterogeneities. SPE J. 2012, 17, 1002–1011. [Google Scholar] [CrossRef]
- Huang, J.; Ghassemi, A. Poro-viscoelastic modeling of production from shale gas reservoir: An adaptive dual permeability model. J. Pet. Sci. Eng. 2017, 158, 336–350. [Google Scholar] [CrossRef]
- An, C.; Killough, J.; Xia, X. Investigating the effects of stress creep and effective stress coefficient on stress-dependent permeability measurements of shale rock. J. Pet. Sci. Eng. 2021, 198, 108155. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Wang, J.; Xiong, Y.; Peng, P.a. New insights into hydration-induced creep behavior of shale: A comparison study of brittle black shale and clayey oil shale at micro-scale. Mar. Pet. Geol. 2022, 138, 105554. [Google Scholar] [CrossRef]
- Zheng, D.; Ozbayoglu, E.; Miska, S.; Zhang, J. Experimental study of anisotropic strength properties of shale. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023. [Google Scholar]
- Cui, G.; Cheng, W.; Xiong, W.; Chen, T.; Li, Y.; Feng, X.-T.; Liu, J.; Elsworth, D.; Pan, Z. Influence of Well Types on Optimizing the Co-production of Gas from Coal and Tight Formations. Energy Fuels 2022, 36, 6736–6754. [Google Scholar] [CrossRef]
- Cui, G.; Zhao, Y.; Liu, J.; Wei, M.; Elsworth, D. A Gaussian Decomposition Method and its applications to the prediction of shale gas production. Fuel 2018, 224, 331–347. [Google Scholar] [CrossRef]
- Wang, J.G.; Kabir, A.; Liu, J.; Chen, Z. Effects of non-Darcy flow on the performance of coal seam gas wells. Int. J. Coal Geol. 2012, 93, 62–74. [Google Scholar] [CrossRef]
- Sun, Z.; Elsworth, D.; Cui, G.; Li, Y.; Zhu, A.; Chen, T. Impacts of rate of change in effective stress and inertial effects on fault slip behavior: New insights into injection-induced earthquakes. J. Geophys. Res. Solid Earth 2024, 129, e2023JB027126. [Google Scholar] [CrossRef]
- Ma, T.; Rutqvist, J.; Oldenburg, C.M.; Liu, W.; Chen, J. Fully coupled two-phase flow and poromechanics modeling of coalbed methane recovery: Impact of geomechanics on production rate. J. Nat. Gas Sci. Eng. 2017, 45, 474–486. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, J.; Kabir, A. Combined effects of directional compaction, non-Darcy flow and anisotropic swelling on coal seam gas extraction. Int. J. Coal Geol. 2013, 109–110, 1–14. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, D.; Wang, J.G. Evaluation of the non-Darcy effect in coalbed methane production. Fuel 2014, 121, 1–10. [Google Scholar] [CrossRef]
- Cooke, C.E., Jr. Conductivity of Fracture Proppants in Multiple Layers. J. Pet. Technol. 1973, 25, 1101–1107. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.S.; Wei, M.Y.; Pan, Z.J.; Connell, L.D. Why coal permeability changes under free swellings: New insights. Int. J. Coal Geol. 2014, 133, 35–46. [Google Scholar] [CrossRef]
- Cui, G.; Liu, J.; Wei, M.; Shi, R.; Elsworth, D. Why shale permeability changes under variable effective stresses: New insights. Fuel 2018, 213, 55–71. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, Z.; Zhang, X.; Liu, J.; Elsworth, D.; Cui, G. Controlling effects of differential swelling index on evolution of coal permeability. J. Rock Mech. Geotech. Eng. 2020, 12, 461–472. [Google Scholar] [CrossRef]
- Danesh, N.N.; Chen, Z.; Aminossadati, S.M.; Kizil, M.S.; Pan, Z.; Connell, L.D. Impact of creep on the evolution of coal permeability and gas drainage performance. J. Nat. Gas Sci. Eng. 2016, 33, 469–482. [Google Scholar] [CrossRef]
- Shi, F.; Wang, X.; Liu, C.; Liu, H.; Wu, H. A coupled extended finite element approach for modeling hydraulic fracturing in consideration of proppant. J. Nat. Gas Sci. Eng. 2016, 33, 885–897. [Google Scholar] [CrossRef]
- Li, K.; Gao, Y.; Lyu, Y.; Wang, M. New mathematical models for calculating proppant embedment and fracture conductivity. SPE J. 2015, 20, 496–507. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Elsworth, D. How sorption-induced matrix deformation affects gas flow in coal seams: A new FE model. Int. J. Rock Mech. Min. Sci. 2008, 45, 1226–1236. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Viscous relaxation model for predicting least principal stress magnitudes in sedimentary rocks. J. Pet. Sci. Eng. 2014, 124, 416–431. [Google Scholar] [CrossRef]
- Shao, Y.; Huang, X.; Xing, Y. An integrated study on the sensitivity and uncertainty associated with the evaluation of stimulated reservoir volume (SRV). J. Pet. Sci. Eng. 2017, 159, 903–914. [Google Scholar] [CrossRef]
- Khanna, A.; Kotousov, A.; Sobey, J.; Weller, P. Conductivity of narrow fractures filled with a proppant monolayer. J. Pet. Sci. Eng. 2012, 100, 9–13. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Feng, X.-T.; Connell, L.D. Laboratory study of proppant on shale fracture permeability and compressibility. Fuel 2018, 222, 83–97. [Google Scholar] [CrossRef]
- Rassouli, F.S.; Zoback, M.D. A Comparison of Short-Term and Long-Term Creep Experiments in Unconventional Reservoir Formations. In Proceedings of the 50th U.S. Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26 June 2016; American Rock Mechanics Association: Houston, TX, USA, 2016; p. 7. [Google Scholar]
- Zhou, H.W.; Wang, L.J.; Rong, T.L.; Zhang, L.; Ren, W.G.; Su, T. Creep-based permeability evolution in deep coal under unloading confining pressure. J. Nat. Gas Sci. Eng. 2019, 65, 185–196. [Google Scholar] [CrossRef]
- Danesh, N.N.; Chen, Z.; Connell, L.D.; Kizil, M.S.; Pan, Z.; Aminossadati, S.M. Characterisation of creep in coal and its impact on permeability: An experimental study. Int. J. Coal Geol. 2017, 173, 200–211. [Google Scholar] [CrossRef]








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Gas density (kg/m3) | 0.714 | Bottom hole pressure (MPa) | 3.45 |
| Reservoir temperature (°C) | 65.6 | Gas viscosity (Pa·s) | 2.01 × 10–5 |
| Fracture space (m) | 30.5 | Initial Gas Pressure (MPa) | 20.3 |
| HF permeability (m2) | 5 × 10–17 | NF permeability (m2) | 1 × 10–18 |
| Young’s modulus of NF (m2) | 2 × 10–18 | Viscosity coefficient of NF (GPa·h) | 60 |
| Frictional order of NF-αf | 0.2 | Frictional order of NF-βf | 0.14 |
| Young’s modulus of HF (m2) | 0.06 | Viscosity coefficient of HF (GPa·h) | 30 |
| Frictional order of HF | 0.34 | Young’s modulus of Proppant (GPa) | 35 |
| Young’s modulus of formation (GP) | 20 | Surface diffusion coefficient (s) | 4.5 × 109 |
| Diameter of proppant (m) | 7 × 10−4 | Possion ratio of formation | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Cui, G.; Tan, Y.; Zhu, A.; Liu, C.; Li, Y. A Coupled Model of Multiscaled Creep Deformation and Gas Flow for Predicting Gas Depletion Characteristics of Shale Reservoir at the Field Scale. Energies 2024, 17, 3752. https://doi.org/10.3390/en17153752
Yang D, Cui G, Tan Y, Zhu A, Liu C, Li Y. A Coupled Model of Multiscaled Creep Deformation and Gas Flow for Predicting Gas Depletion Characteristics of Shale Reservoir at the Field Scale. Energies. 2024; 17(15):3752. https://doi.org/10.3390/en17153752
Chicago/Turabian StyleYang, Daosong, Guanglei Cui, Yuling Tan, Aiyu Zhu, Chun Liu, and Yansen Li. 2024. "A Coupled Model of Multiscaled Creep Deformation and Gas Flow for Predicting Gas Depletion Characteristics of Shale Reservoir at the Field Scale" Energies 17, no. 15: 3752. https://doi.org/10.3390/en17153752
APA StyleYang, D., Cui, G., Tan, Y., Zhu, A., Liu, C., & Li, Y. (2024). A Coupled Model of Multiscaled Creep Deformation and Gas Flow for Predicting Gas Depletion Characteristics of Shale Reservoir at the Field Scale. Energies, 17(15), 3752. https://doi.org/10.3390/en17153752






