Controller Hardware in the Loop Platform for Evaluating Current-Sharing and Hot-Swap in Microgrids
Abstract
:1. Introduction
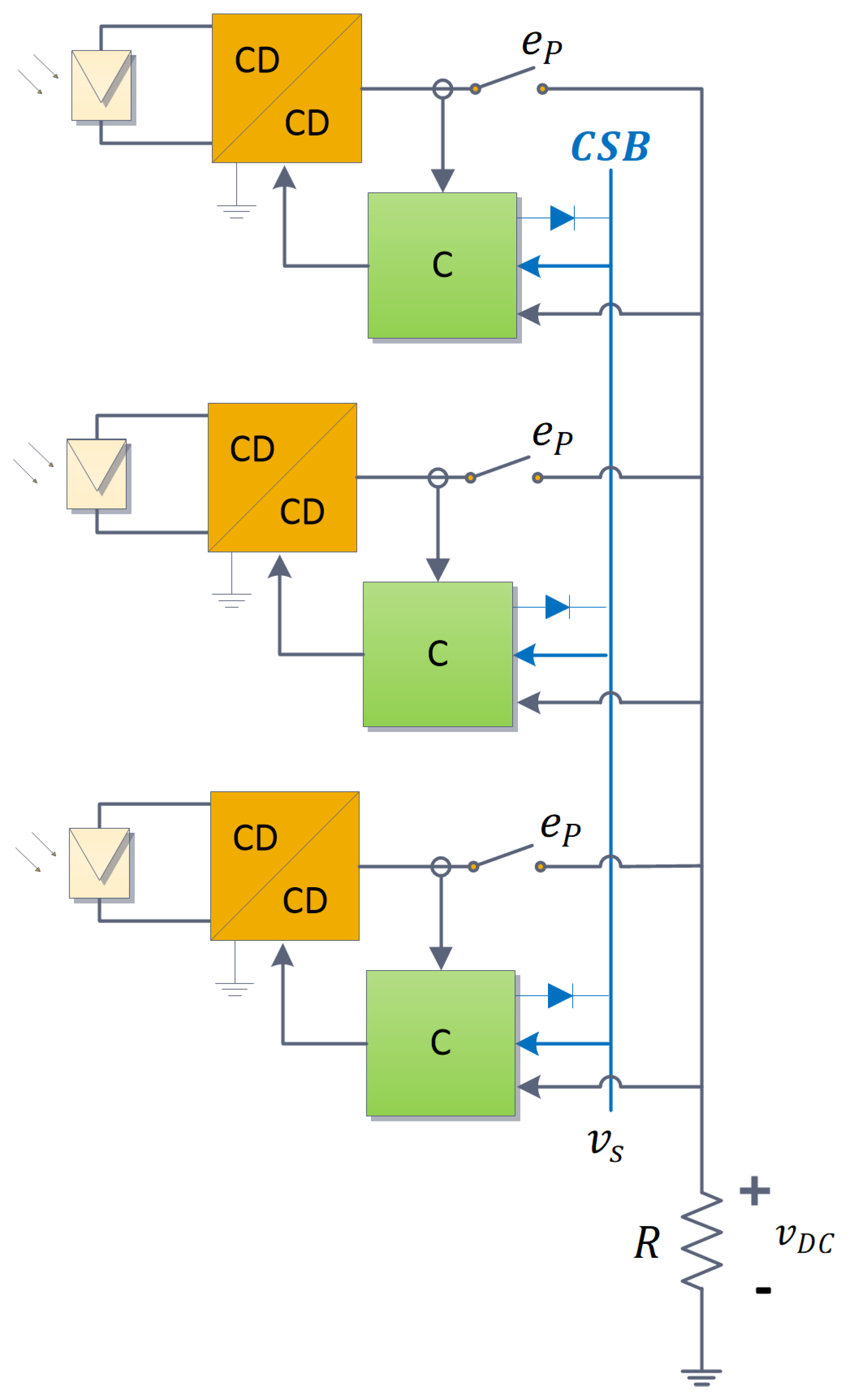
2. System Description
3. HIL Platform Description
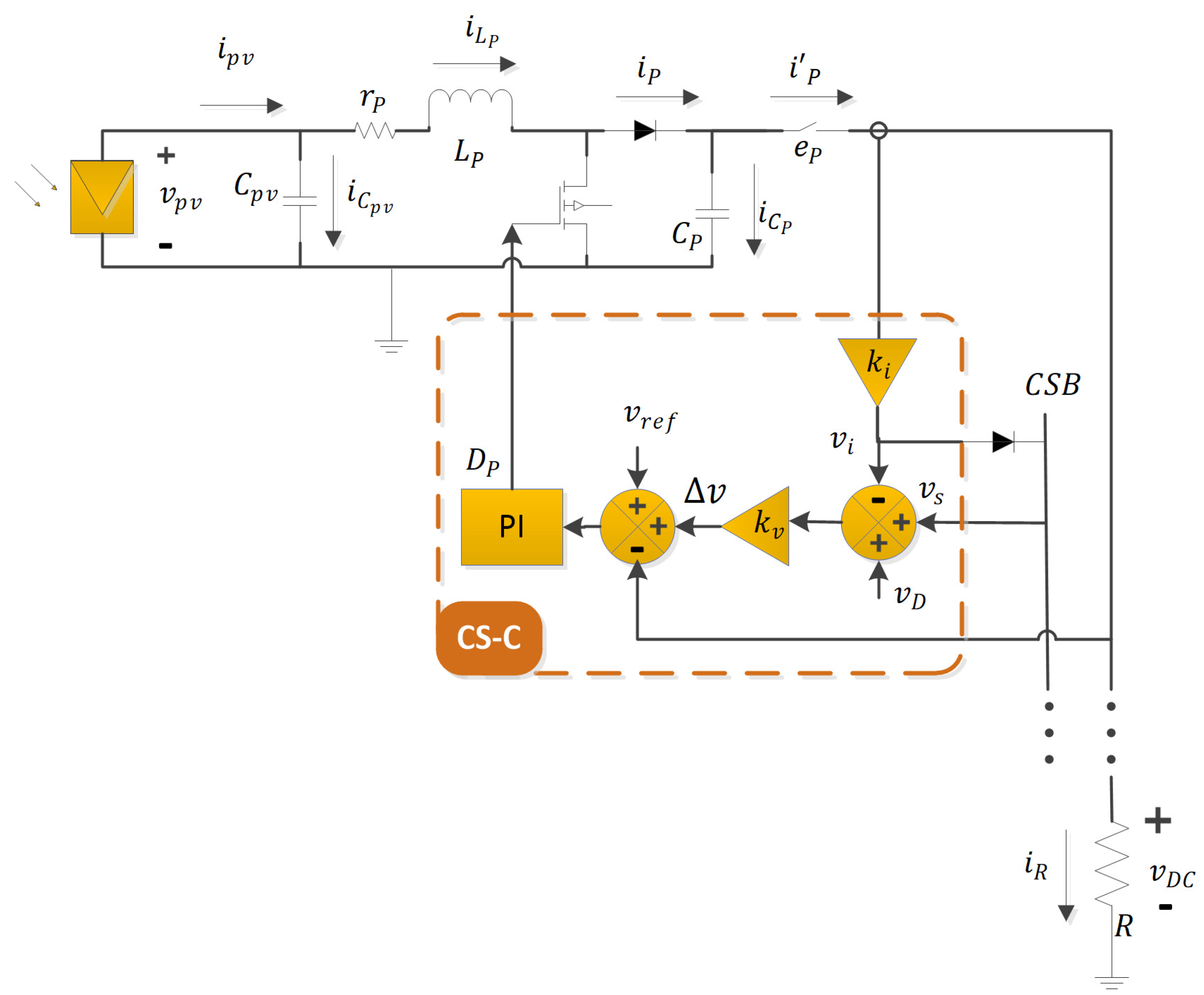
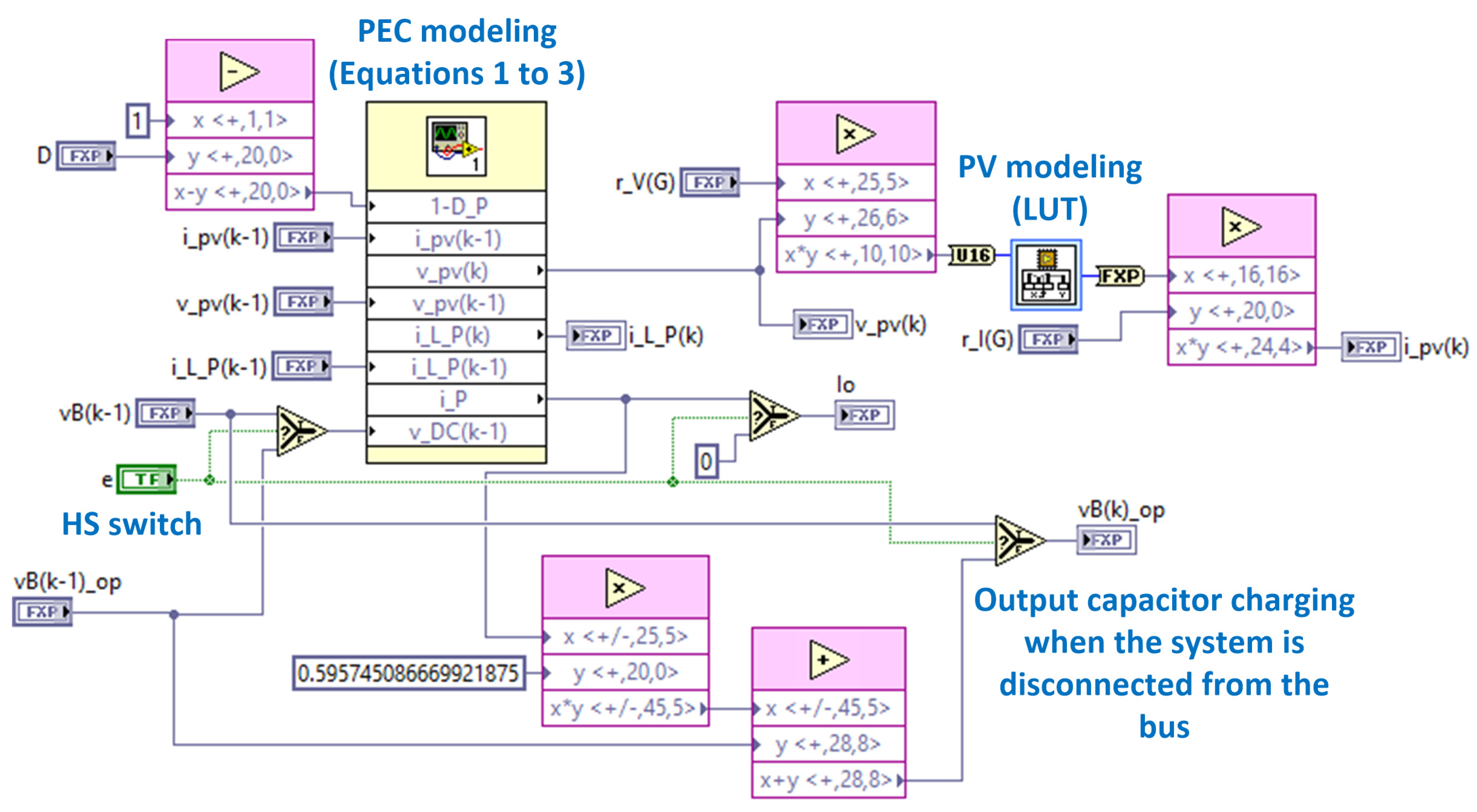
3.1. System Modeling
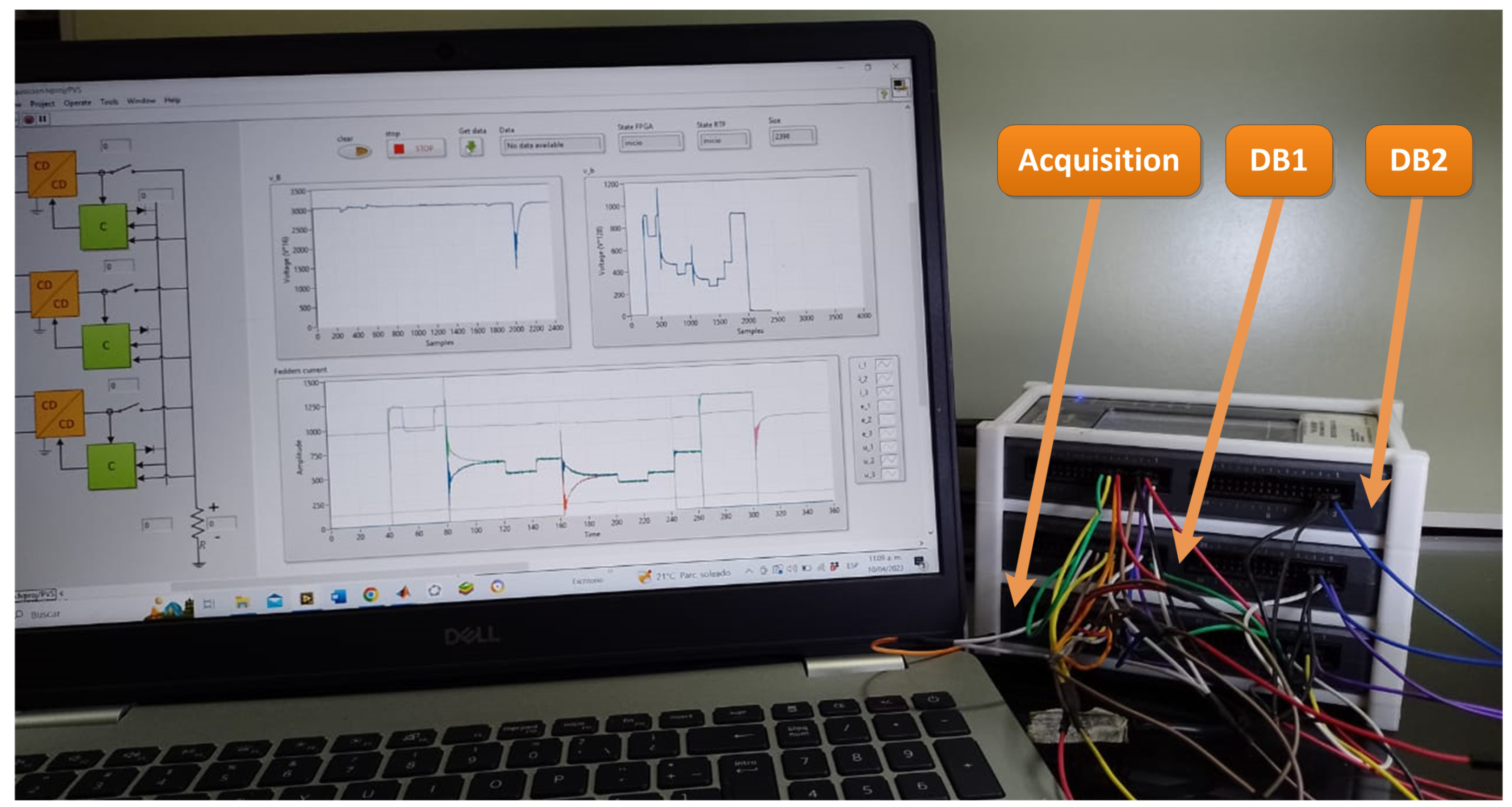
3.2. Platform Implementation
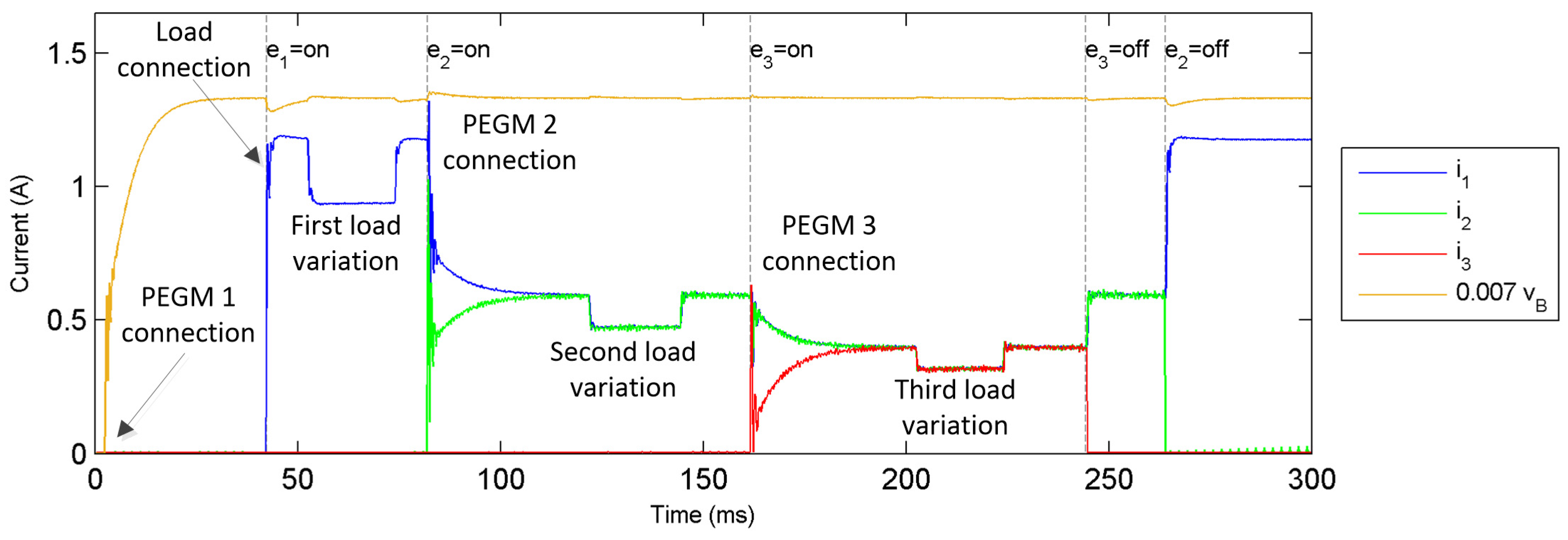
4. Results
5. Conclusions
- First is to integrate the HIL platform in a DC-µG that includes more elements of a distinct nature, e.g., a battery energy storage system, a wind turbine, a main grid interconnection, etc. An aspect contributing to this goal includes the validation of the HIL platform not only with a variable load, but also with a single equation describing both the DC bus dynamics and all the connected elements to it.
- Next is to validate the HIL platform in the face of variations of some other parameters such as the power supplied by the PV, shading of one or various panels, the sudden disconnection of loads from the grid, and the connection of R-L, R-C, and R-L-C loads. In a similar way to the previous goal, a single equation describing the DC bus dynamics and one that is independent from the PEC models will avoid an adjustment in the PEGM after modifying the characteristics and behavior of the connected loads to the bus.
- Lastly, with the inclusion of additional functions for the PEGM local controllers, e.g., an MPPT, it will be possible to evaluate more operative modes of a DC-µG. As the weather variables have a slower time response, the MPPT demand a lower latency during an emulation than other elements such as the PECs contained in the PEGM. Therefore, this particularity allows the use of the RTP in the SoC to implement MPPT controllers without affecting the performance of other embedded systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ullah, S.; Haidar, A.M.A.; Zen, H. Assessment of technical and financial benefits of AC and DC microgrids based on solar photovoltaic. Electr. Eng. 2020, 102, 1297–1310. [Google Scholar] [CrossRef]
- Datta, U.; Kalam, A.; Shi, J. Hybrid PV–wind renewable energy sources for microgrid application: An overview. In Hybrid-Renewable Energy Systems in Microgrids; Woodhead Publishing: Sawston, UK, 2018; pp. 1–22. [Google Scholar] [CrossRef]
- Sood, V.K.; Abdelgawad, H. Microgrids architectures. In Distributed Energy Resources in Microgrids; Academic Press: Cambridge, MA, USA, 2019; pp. 1–31. [Google Scholar] [CrossRef]
- Kolluri, R.R.; Mareels, I.; de Hoog, J. Controlling DC microgrids in communities, buildings and data centers. IET Smart Grid 2020, 3, 376–384. [Google Scholar] [CrossRef]
- Al-Tameemi, Z.H.A.; Lie, T.T.; Foo, G.; Blaabjerg, F. Optimal Coordinated Control of DC Microgrid Based on Hybrid PSO–GWO Algorithm. Electricity 2022, 3, 346–364. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, Y.; Tan, S.-C.; Hui, S.Y.R. Efficient Improvement of Photovoltaic-Battery Systems in Standalone DC Microgrids Using a Local Hierarchical Control for the Battery System. IEEE Trans. Power Electron. 2019, 34, 10796–10807. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef]
- Li, Z.; Ren, Z.; Li, H.; Wang, C.; Wang, C.; Hao, L. An Optimal Operation Method of Hybrid AC/DC Distribution Network Under the Goal of Peaking Carbon Dioxide Emissions and Carbon Neutrality. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 997–1004. [Google Scholar] [CrossRef]
- Tao, P.; Zhang, Y.; Zhao, J. Distributed Energy Storage Cluster Control Method for DC Microgrid Considering Flexibility. Math. Probl. Eng. 2022, 2022, 6761595. [Google Scholar] [CrossRef]
- Nojavan, S.; Pashaei-Didani, H.; Mohammadi, A.; Ahmadi-Nezamabad, H. Energy management concept of AC, DC, and hybrid AC/DC microgrids. In Risk-Based Energy Management; Academic Press: Cambridge, MA, USA, 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Mostafa, M.H.; Abdel Aleem, S.H.E.; Ali, S.G.; Abdelaziz, A.Y. Energy-management solutions for microgrids. In Distributed Energy Resources in Microgrids; Academic Press: Cambridge, MA, USA, 2019; pp. 483–515. [Google Scholar] [CrossRef]
- Merai, M.; Naouar, M.W.; Slama-Belkhodja, I. Coordinated control of multiple Multi-Function Grid connected Converters for power quality improvement in micro-grid applications. In Proceedings of the 2016 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22–24 March 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zahraoui, Y.; Alhamrouni, I.; Mekhilef, S.; Basir Khan, M.R.; Seyedmahmoudian, M.; Stojcevski, A.; Horan, B. Energy management system in microgrids: A comprehensive review. Sustainability 2021, 13, 10492. [Google Scholar] [CrossRef]
- Shahgholian, G. A brief review on microgrids: Operation, applications, modeling, and control. Int. Trans. Electr. Energy Syst. 2021, 31, e12885. [Google Scholar] [CrossRef]
- Ishraque, M.F.; Shezan, S.A.; Ali, M.M.; Rashid, M.M. Optimization of load dispatch strategies for an islanded microgrid connected with renewable energy sources. Appl. Energy 2021, 292, 116879. [Google Scholar] [CrossRef]
- Raya-Armenta, J.M.; Bazmohammadi, N.; Avina-Cervantes, J.G.; Sáez, D.; Vasquez, J.C.; Guerrero, J.M. Energy management system optimization in islanded microgrids: An overview and future trends. Renew. Sustain. Energy Rev. 2021, 149, 111327. [Google Scholar] [CrossRef]
- Salcedo, R.; Corbet, E.; Smith, C.; Limpaecher, E.; Rekha, R.; Nowocin, J.; Lauss, G.; Fonkwe, E.; Almeida, M.; Gartner, P.; et al. Banshee distribution network benchmark and prototyping platform for hardware-in-the-loop integration of microgrid and device controllers. J. Eng. 2019, 2019, 5365–5373. [Google Scholar] [CrossRef]
- AhmadiAhangar, R.; Rosin, A.; Niaki, A.N.; Palu, I.; Korõtko, T. A review on real-time simulation and analysis methods of microgrids. Int. Trans. Electr. Energy Syst. 2019, 29, e12106. [Google Scholar] [CrossRef]
- Lauss, G.; Strunz, K. Accurate and stable hardware-in-the-loop (HIL) real-time simulation of integrated power electronics and power systems. IEEE Trans. Power Electron. 2020, 36, 10920–10932. [Google Scholar] [CrossRef]
- Kumar, G.B.; Palanisamy, K. Energy management of renewable energy-based microgrid system with HESS for various operation modes. Front. Energy Res. 2022, 10, 995034. [Google Scholar] [CrossRef]
- Kikusato, H.; Ustun, T.S.; Suzuki, M.; Sugahara, S.; Hashimoto, J.; Otani, K.; Shirakawa, K.; Yabuki, R.; Watanabe, K.; Shimizu, T. Microgrid Controller Testing Using Power Hardware-in-the-Loop. Energies 2020, 13, 2044. [Google Scholar] [CrossRef]
- Ghanbari, N.; Bhattacharya, S. Adaptive Droop Control Method for Suppressing Circulating Currents in DC Microgrids. IEEE Open Access J. Power Energy 2020, 7, 100–110. [Google Scholar] [CrossRef]
- Nigam, S.; Ajala, O.; Domínguez-García, A.D.; Sauer, P.W. Controller hardware in the loop testing of microgrid secondary frequency control schemes. Electr. Power Syst. Res. 2021, 190, 106757. [Google Scholar] [CrossRef]
- Muñoz-Jadán, Y.; Espinoza-Bolaños, M.; Donoso Merlet, F.; Hidalgo-León, R.; Soriano Idrovo, G.; Jácome-Ruíz, P. Hardware-in-the-Loop for Wind Energy Conversion with Resonant Current Control and Active Damping. IEEE Lat. Am. Trans. 2019, 17, 1146–1154. [Google Scholar] [CrossRef]
- Zamiri, E.; Sanchez, A.; Yushkova, M.; Martínez-García, M.S.; de Castro, A. Comparison of different design alternatives for hardware-in-the-loop of power converters. Electronics 2021, 10, 926. [Google Scholar] [CrossRef]
- Jiang, W.; Sun, L.; Chen, Y.; Ma, H.; Hashimoto, S. A hardware-in-the-loop-on-chip development system for teaching and development of dynamic systems. Electronics 2021, 10, 801. [Google Scholar] [CrossRef]
- Martinez-Armero, Y.; Lopez-Blandon, S.; Giraldo, E. Low-cost Arduino-based Hardware-In-the-Loop Platform for Simulation and Control of Dynamic Systems. IAENG Int. J. Comput. Sci 2023, 50, 4. [Google Scholar]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A review of microgrid energy management and control strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Sharma, S.; Iyer, V.M.; Bhattacharya, S.; Kikuchi, J.; Zou, K.; Gupta, M. A Methodology for Seamless Hot-Swap of Converters in DC Microgrids. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3143–3150. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Trip, S.; De Persis, C.; Cheng, X.; Ferrara, A.; van der Schaft, A. A Robust Consensus Algorithm for Current Sharing and Voltage Regulation in DC Microgrids. IEEE Trans. Control Syst. Technol. 2019, 27, 1583–1595. [Google Scholar] [CrossRef]
- Shebani, M.M.; Iqbal, M.T.; Quaicoe, J.E. Control Algorithm for Equal Current Sharing between Parallel-Connected Boost Converters in a DC Microgrid. J. Electr. Comput. Eng. 2020, 1, 1–11. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhuang, X.; Liu, Y.; Wang, C.; Guo, H. A Novel Autonomous Current-Sharing Control Strategy for Multiple Paralleled DC–DC Converters in Islanded DC Microgrid. Energies 2019, 12, 3951. [Google Scholar] [CrossRef]
- Tucci, M.; Meng, L.; Guerrero, J.M.; Ferrari-Trecate, G. Plug-and-play control and consensus algorithms for current sharing in DC microgrids. IFAC-PapersOnLine 2017, 50, 12440–12445. [Google Scholar] [CrossRef]
- Mesbah, M.A.; Sayed, K.; Ahmed, A.; Aref, M.; Elbarbary, Z.M.S.; Almuflih, A.S.; Mossa, M.A. Adaptive Control Approach for Accurate Current Sharing and Voltage Regulation in DC Microgrid Applications. Energies 2024, 17, 284. [Google Scholar] [CrossRef]
- Noroozi, N.; Trip, S.; Geiselhart, R. Model predictive control of DC microgrids: Current sharing and voltage regulation. IFAC-PapersOnLine 2018, 51, 124–129. [Google Scholar] [CrossRef]
- Bai, H.; Zhang, H.; Li, C. Voltage regulation and current sharing for multi-bus DC microgrids. IFAC-PapersOnLine 2020, 53, 13018–13023. [Google Scholar] [CrossRef]
- Duan, M.; Duan, J.; Sun, L. Sensorless Current-Sharing Scheme for Multiphase DC-DC Boost Converters. IEEE Trans. Power Electron. 2023, 38, 1398–1405. [Google Scholar] [CrossRef]
- Chen, Z.; Xiang, T.; Wu, Y.; Zhao, L.; Tang, X. Current Sharing Strategy of Three-Phase Series Capacitor Buck Converter for Wide Output Voltage Range Application. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 836–849. [Google Scholar] [CrossRef]
- Estrada, L.; Vázquez, N.; Vaquero, J.; de Castro, Á.; Arau, J. Real-Time Hardware in the Loop Simulation Methodology for Power Converters Using LabVIEW FPGA. Energies 2020, 13, 373. [Google Scholar] [CrossRef]
- Ma, D.; Chen, W.; Ruan, X. A Review of Voltage/Current Sharing Techniques for Series–Parallel-Connected Modular Power Conversion Systems. IEEE Trans. Power Electron. 2020, 35, 12383–12400. [Google Scholar] [CrossRef]
- Samano-Ortega, V.; Rodriguez-Estrada, H.; Rodríguez-Segura, E.; Padilla-Medina, J.; Aguilera-Alvarez, J.; Martinez-Nolasco, J. Power Sharing Control in a Grid-Tied DC Microgrid: Controller Hardware in the Loop Validation. Appl. Sci. 2021, 11, 9295. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, Y.; Blaabjerg, F. Distributed Control of Islanded Series PV-Battery-Hybrid Systems with Low Communication Burden. In Proceedings of the 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Dubrovnik, Croatia, 28 September–1 October 2020; pp. 315–321. [Google Scholar] [CrossRef]
- Kanathipan, K.; Emamalipour, R.; Lam, J. A Single-Switch High-Gain PV Microconverter with Low-Switch-Voltage-to-High-Voltage-Bus Ratio. IEEE Trans. Power Electron. 2020, 35, 9530–9540. [Google Scholar] [CrossRef]
- Pan, Y.; Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. A Series Interharmonic Filter for Cascaded H-bridge PV Inverters. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 341–346. [Google Scholar] [CrossRef]
- Lin, Z.; Xie, W.; Dong, M.; Lan, J. Research of S3MPR Engineering Application on Space Power Sources. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 817–823. [Google Scholar]
- Keysight Technologies, Inc. Keysight Technologies Series E4360 Modular Solar Array Simulator. Available online: http://literature.cdn.keysight.com/litweb/pdf/E4360-90001.pdf (accessed on 16 May 2024).
- Shen, Y.; Qin, Z.; Wang, H. Modeling and Control of DC-DC Converters. In En Control of Power Electronic Converters and Systems; Academic Press: Cambridge, MA, USA, 2018; pp. 69–92. [Google Scholar] [CrossRef]
- VictorSamano. HiL_Current-Sharing, GitHub Repository. 2024. Available online: https://github.com/VictorSamano/HiL_Current-Sharing (accessed on 2 July 2024).
- Photovoltaics, D.G.; Storage, E. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE Std 1547-2018 (Revision of IEEE Std 1547-2003); IEEE: Piscataway, NJ, USA, 2018; pp. 1–138. [Google Scholar] [CrossRef]





| Constant | Value | Units |
|---|---|---|
| 330 | µF | |
| 0.4 | Ω | |
| 110 | µH | |
| 28 | µs | |
| 47 | µF | |
| 0.004 | -- | |
| 1 | -- | |
| 6 | V/A | |
| 2 | -- |
| Category | Parameter | Value |
|---|---|---|
| Processor | Type | Xilinx Z-7010 (SoC) |
| Speed | 667 MHz | |
| Cores | 2 | |
| FPGA | Type | Xilinx Z-7010 (SoC) |
| Clock frequency | 40 MHz | |
| Logic cells | 28 k | |
| DSP slices | 80 | |
| Block RAM | 2.1 Mb | |
| Analog Inputs | Sample rate | 500 kS/s |
| Resolution | 12 bits | |
| Configuration | 8 single-ended + 2 differentials | |
| Analog Outputs | Update rate | 345 kS/s |
| Resolution | 12 bits | |
| Digital I/O | Configuration | Two 16 DIO lines ports + 8 DIO lines port |
| Logic Level | 5 V compatible LVTTL input; 3.3 V LVTTL output |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Nolasco, J.; Sámano-Ortega, V.; Rodriguez-Estrada, H.; Santoyo-Mora, M.; Rodriguez-Segura, E.; Zavala-Villalpando, J. Controller Hardware in the Loop Platform for Evaluating Current-Sharing and Hot-Swap in Microgrids. Energies 2024, 17, 3803. https://doi.org/10.3390/en17153803
Martínez-Nolasco J, Sámano-Ortega V, Rodriguez-Estrada H, Santoyo-Mora M, Rodriguez-Segura E, Zavala-Villalpando J. Controller Hardware in the Loop Platform for Evaluating Current-Sharing and Hot-Swap in Microgrids. Energies. 2024; 17(15):3803. https://doi.org/10.3390/en17153803
Chicago/Turabian StyleMartínez-Nolasco, Juan, Víctor Sámano-Ortega, Heriberto Rodriguez-Estrada, Mauro Santoyo-Mora, Elias Rodriguez-Segura, and José Zavala-Villalpando. 2024. "Controller Hardware in the Loop Platform for Evaluating Current-Sharing and Hot-Swap in Microgrids" Energies 17, no. 15: 3803. https://doi.org/10.3390/en17153803
APA StyleMartínez-Nolasco, J., Sámano-Ortega, V., Rodriguez-Estrada, H., Santoyo-Mora, M., Rodriguez-Segura, E., & Zavala-Villalpando, J. (2024). Controller Hardware in the Loop Platform for Evaluating Current-Sharing and Hot-Swap in Microgrids. Energies, 17(15), 3803. https://doi.org/10.3390/en17153803







