Effect of Bore Parameters and Effective Mass Ratio on Launcher Effective Efficiency
Abstract
1. Introduction
2. The Calculation of the Launcher Effective Efficiency
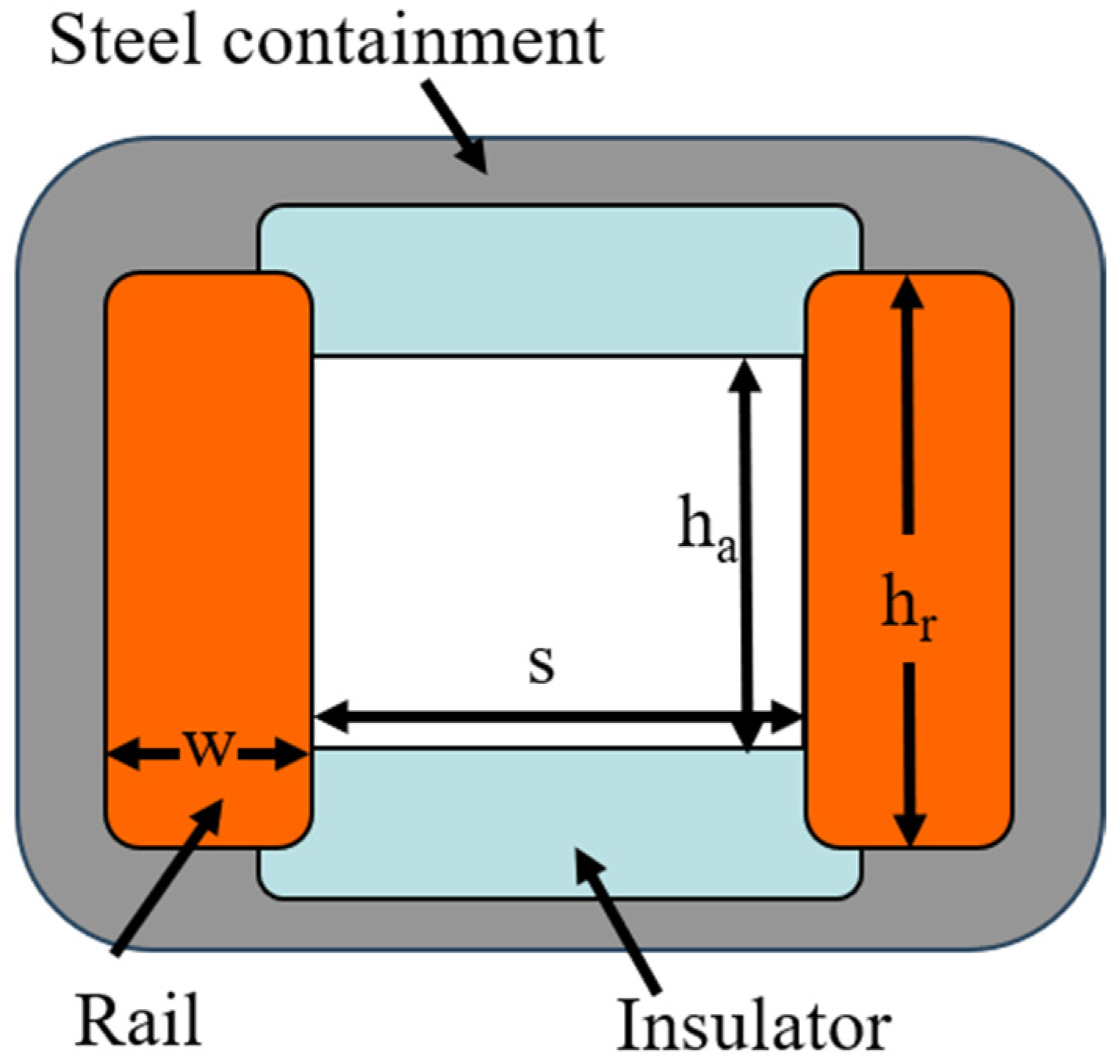
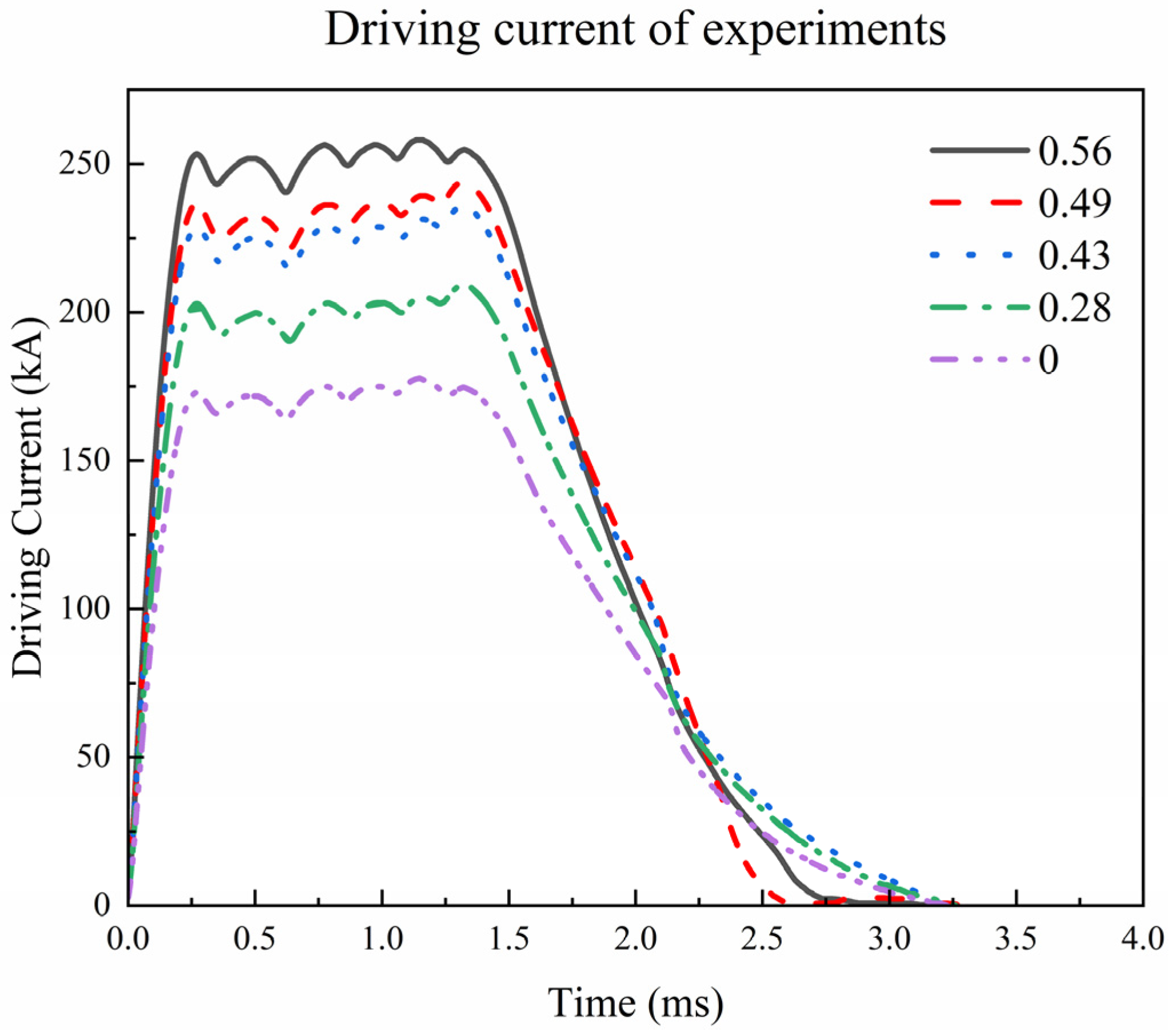
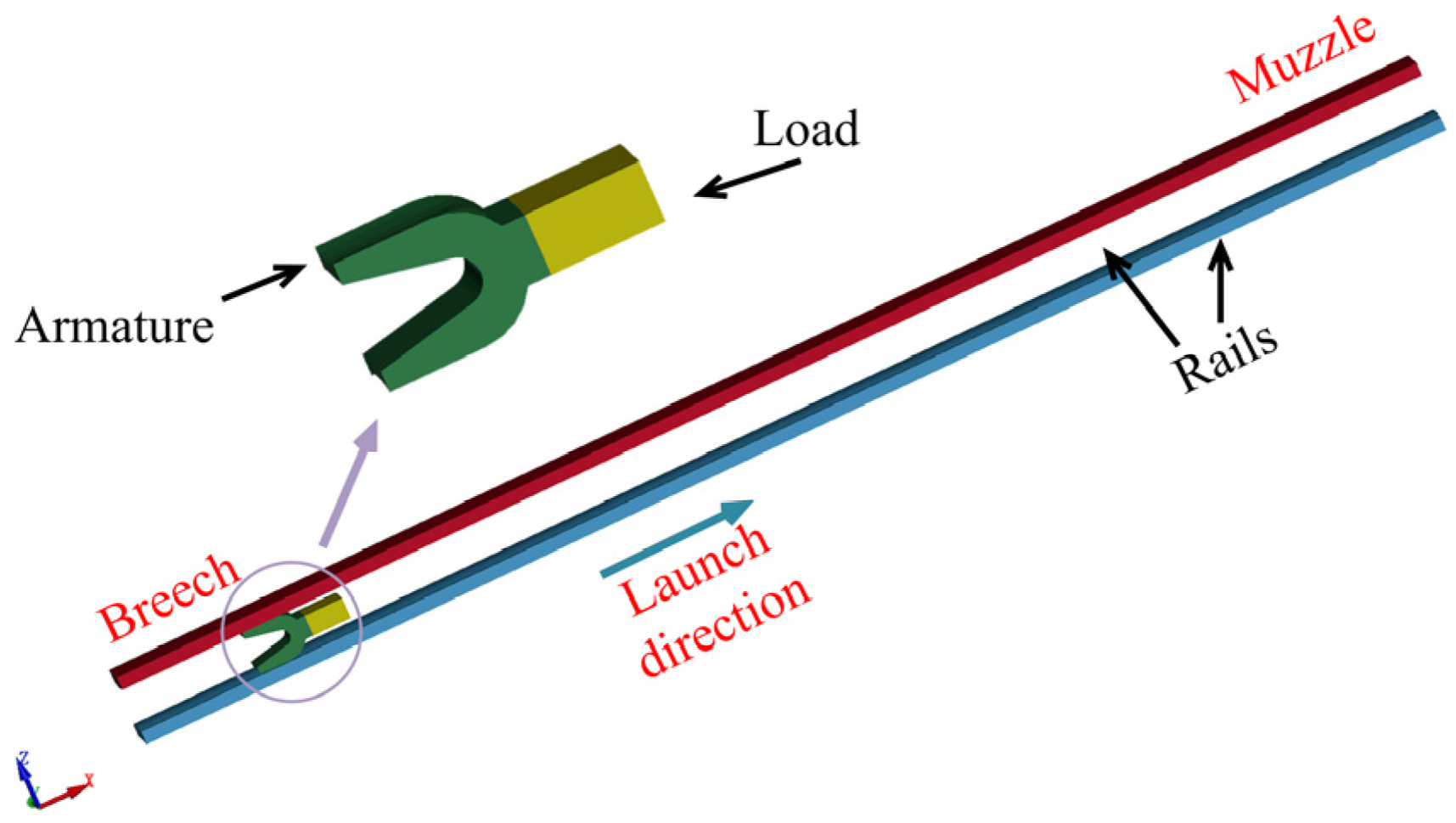
3. Experiment Setup
4. Results and Discussion of Experiments
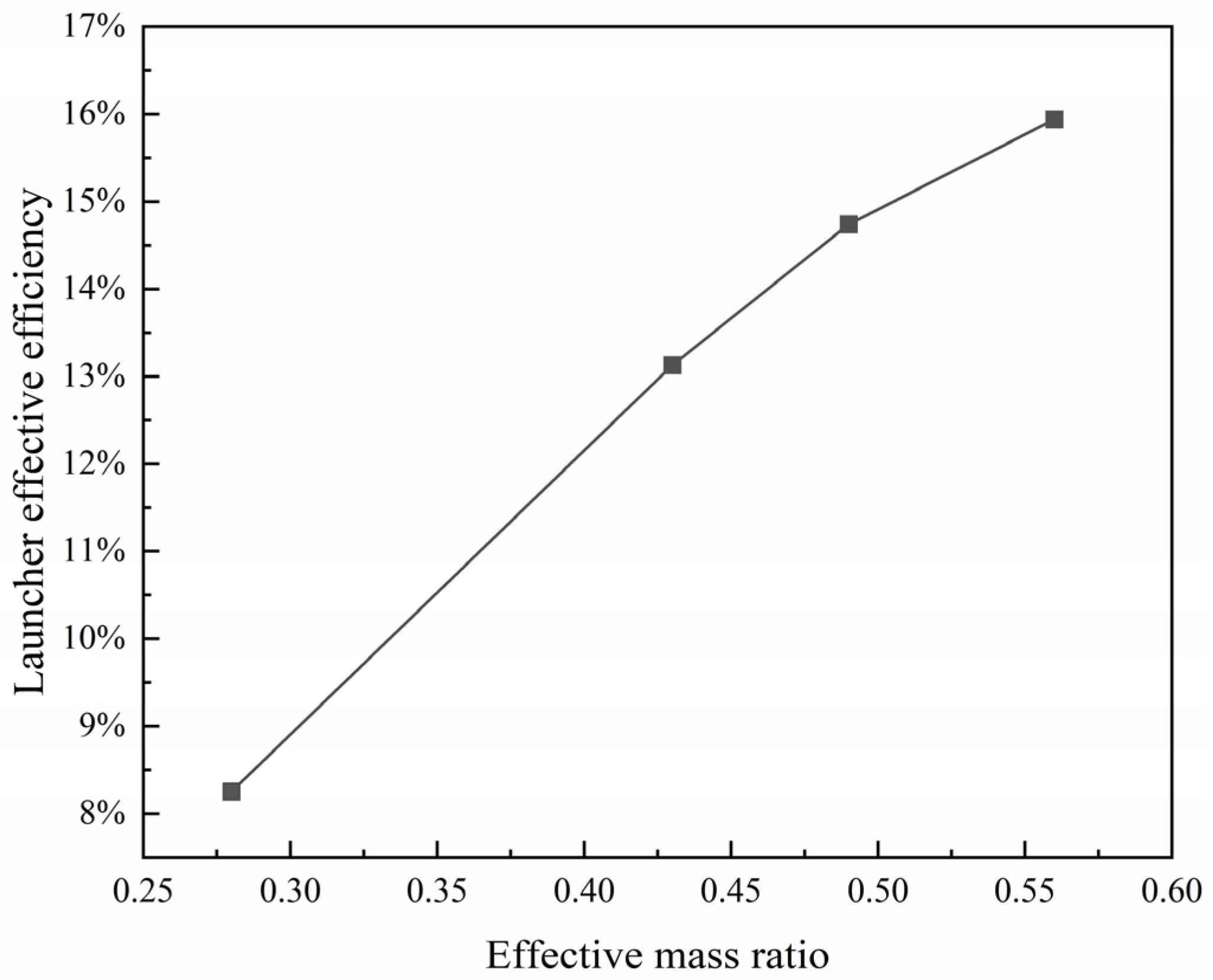
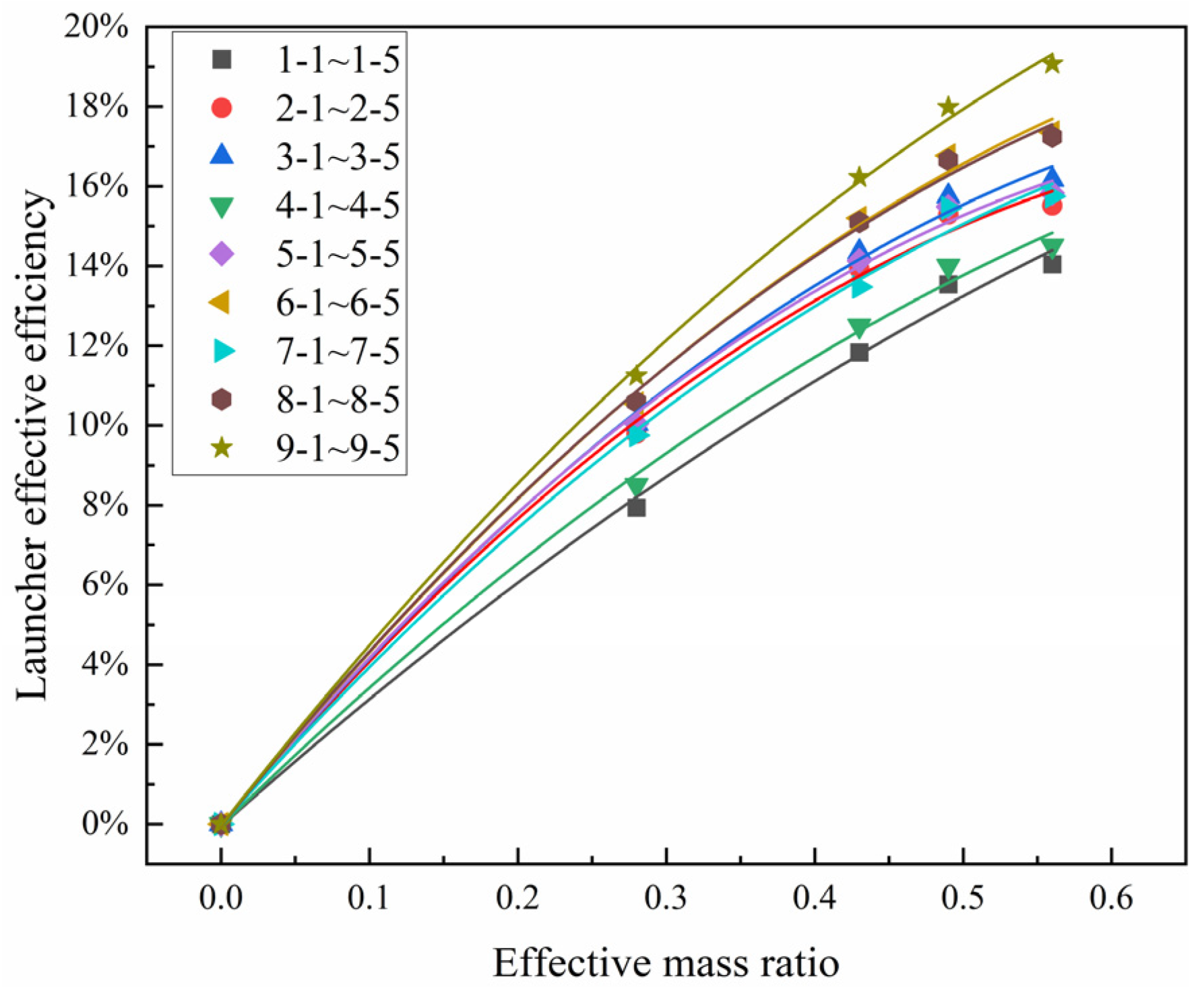
4.1. Effect of Effective Mass Ratio on Launcher Effective Efficiency
4.2. Effect of Rail Separation on Launcher Effective Efficiency
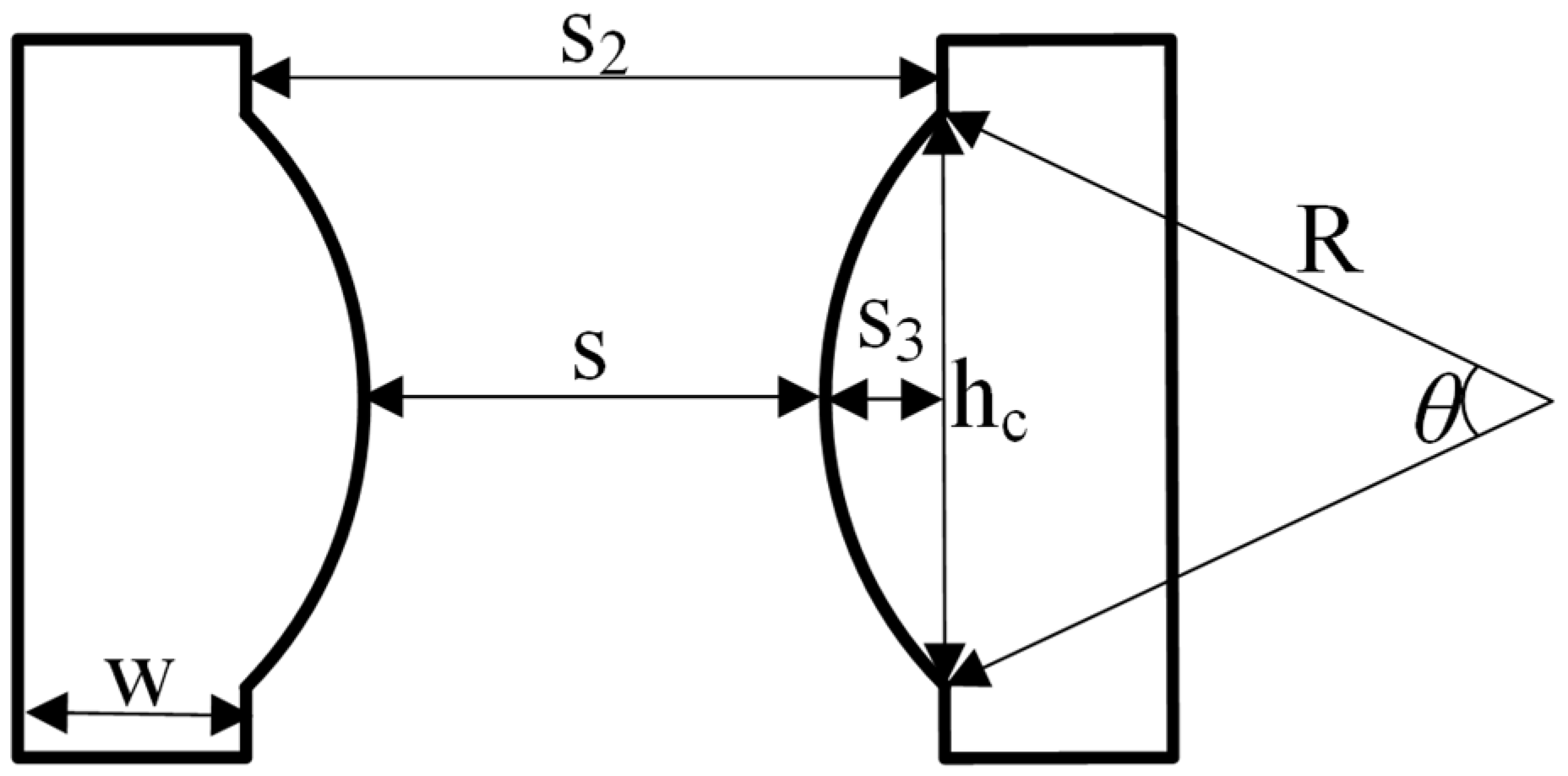
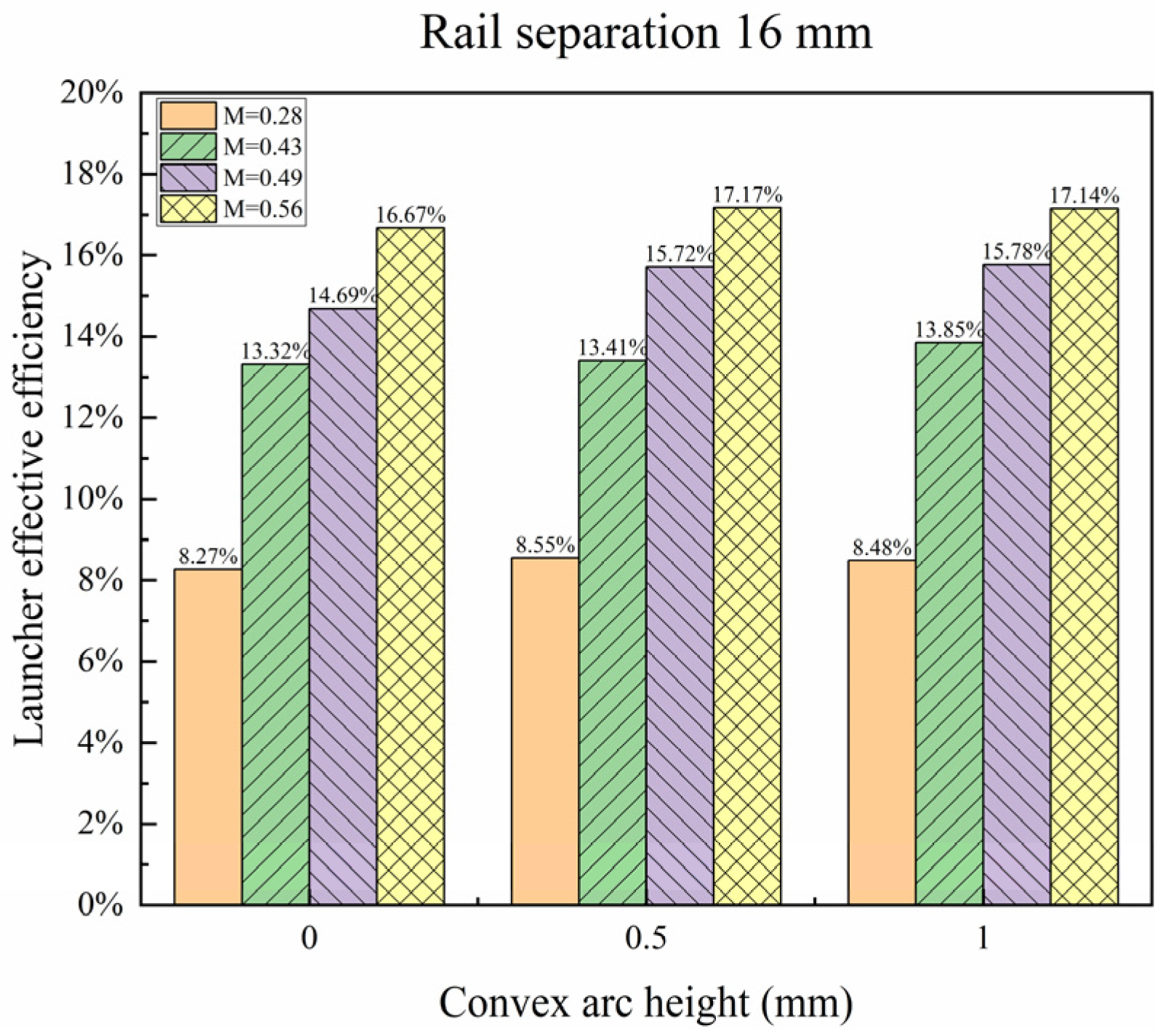
4.3. Effect of Convex Arc Height on Launcher Effective Efficiency
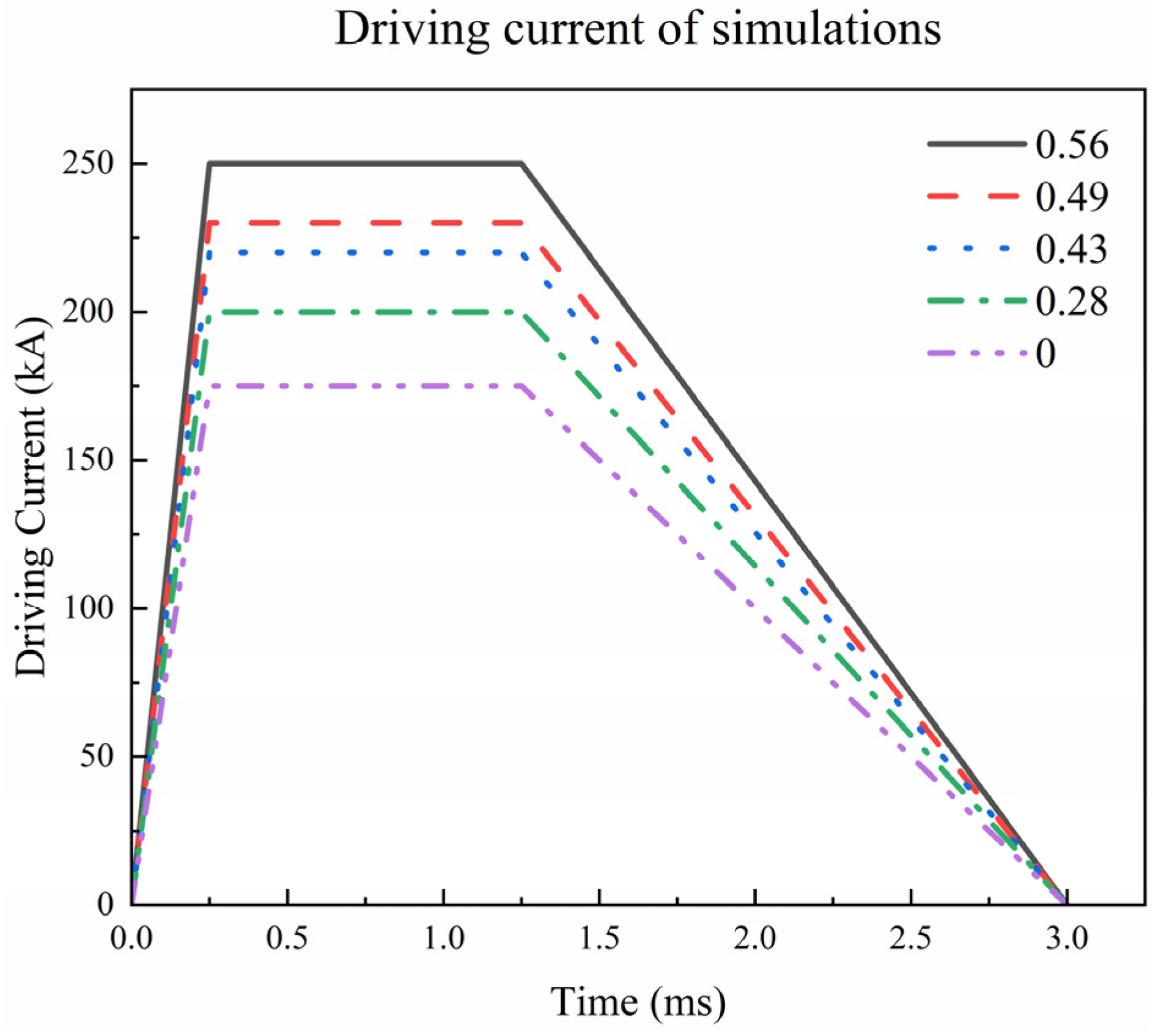
5. Simulation Theory and Modeling
6. Results and Discussion of Simulation
7. Conclusions
- The launcher effective efficiency increases with the growth of the effective mass ratio, and the launcher effective efficiency improves from 7.91% to 17.17% when the effective mass ratio rises from 0.28 to 0.56. The average increment of the launcher effective efficiency is 8.24% under different cross-section geometrical parameters.
- The launcher efficiency increases with the increment in the rail separation; the launcher effective efficiency rises by 0.70% on average when the rail separation increases from 14 mm to 16 mm, and the increase in the launcher effective efficiency decreases with the increment in rail separation;
- The launcher effective efficiency increases with the increment in the convex arc height; when the convex arc height increases from 0 mm to 1 mm, the launcher effective efficiency rises by 0.77% on average.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Yan, P.; Yuan, W. Electromagnetic Gun Technology and Its Development. High Volt. Eng. 2014, 40, 1052–1064. [Google Scholar]
- Marshall, R.A.; Wang, Y. Railguns: Their Science and Technology; China Machine Press: Beijing, China, 2004. [Google Scholar]
- Fair, H.D. Guest Editorial The Past, Present, and Future of Electromagnetic Launch Technology and the IEEE International EML Symposia. IEEE Trans. Plasma Sci. 2013, 41, 1024–1027. [Google Scholar] [CrossRef]
- Wang, Y.; Marshall, R.A.; Cheng, S. Physics of Electric Launch; Science Press: Beijing, China, 2004; pp. 1–47. [Google Scholar]
- Ellis, R.L.; Poynor, J.C.; McGlasson, B.T.; Smith, A.N. Influence of bore and rail geometry on an electromagnetic naval railgun system. IEEE Trans. Magn. 2005, 41, 182–187. [Google Scholar] [CrossRef]
- Marshall, R.A. Railgun bore geometry, round or square? IEEE Trans. Magn. 1999, 35, 427–431. [Google Scholar] [CrossRef]
- McFarland, J.; McNab, I.R. A long-range naval railgun. IEEE Trans. Magn. 2003, 39, 289–294. [Google Scholar] [CrossRef]
- Zhu, R.; Zhang, Q.; Li, Z.; Jin, L.; Wang, R. Impact physics model and influencing factors of gouging for electromagnetic rail launcher. In Proceedings of the 2014 17th International Symposium on Electromagnetic Launch Technology, La Jolla, CA, USA, 7–11 July 2014; pp. 1–6. [Google Scholar]
- Hsieh, K.T.; Kim, B.K. International railgun modelling effort. IEEE Trans. Magn. 1997, 33, 245–248. [Google Scholar] [CrossRef]
- Meger, R.A.; Cooper, K.; Jones, H.; Neri, J.; Qadri, S.; Singer, I.L.; Sprague, J.; Wahl, K.J. Analysis of rail surfaces from a multishot railgun. IEEE Trans. Magn. 2005, 41, 211–213. [Google Scholar] [CrossRef]
- Bauer, D.P. Achieving high efficiency with conventional railgun launchers. IEEE Trans. Magn. 1995, 31, 263–266. [Google Scholar] [CrossRef]
- Khatibzadeh, A.; Besmi, M.R. Improve dimension of projectile for increasing efficiency of electromagnetic launcher. In Proceedings of the 4th Annual International Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 13–14 February 2013; pp. 55–59. [Google Scholar]
- Fat, O.V.; Usuba, S.; Yoshida, M.; Kakudate, Y.; Yokoi, H.; Fujiwara, S. Electromagnetic processes and launch efficiency of railgun systems. IEEE Trans. Magn. 1997, 33, 532–537. [Google Scholar]
- Li, Z.X.; Hao, S.P.; Ma, F.Q.; Li, B.M. Current Situation and Development of Pulsed Power Supply Module Technology for Electric Gun. Acta Armamentarii 2020, 41, 1–7. [Google Scholar]
- Liu, X.; Yu, X.; Li, Z. Inductance calculation and energy density optimization of the tightly coupled inductors used in inductive pulsed power supplies. IEEE Trans. Plasma Sci. 2017, 45, 1026–1031. [Google Scholar] [CrossRef]
- Sung, V.; Odendaal, W.G. The Effect of Changing Launch Package Mass on the Electromechanical Conversion Efficiency of Railguns. IEEE Trans. Plasma Sci. 2019, 47, 2521–2531. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, W.; Niu, Q.; Dong, S. Numerical Analysis of Aerodynamic Thermal Properties of Hypersonic Blunt-Nosed Body with Angles of Fire. Energies 2023, 16, 1740. [Google Scholar] [CrossRef]
- Ceylan, D.; Keysan, O. Effect of conducting containment on electromagnetic launcher efficiency. In Proceedings of the 2017 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF) Book of Abstracts, Lodz, Poland, 14–16 September 2017; pp. 1–2. [Google Scholar]
- Liu, S.; Miao, H.; Liu, M. Investigation of the Armature Contact Efficiency in a Railgun. IEEE Trans. Plasma Sci. 2019, 47, 3315–3319. [Google Scholar] [CrossRef]
- Cao, G.; Xiang, H.; Qiao, Z.; Liang, C.; Yuan, X.; Wang, J.; Lei, B. Utilization Optimization of Capacitive Pulsed Power Supply in Railgun. Energies 2022, 15, 5051. [Google Scholar] [CrossRef]
- Liu, X.; Yu, X.; Liu, X. Influences of electric parameters of pulsed power supply on electromagnetic railgun system. IEEE Trans. Plasma Sci. 2016, 43, 3260–3267. [Google Scholar]
- Chang, X.; Yu, X.; Liu, X.; Li, Z. Armature Velocity Control Strategy and System Efficiency Optimization of Railguns. IEEE Trans. Plasma Sci. 2018, 46, 3634–3639. [Google Scholar] [CrossRef]
- Gong, C.; Yu, X.; Liu, X. Study on the system efficiency of the synchronously-triggered capacitive pulsed-power supply in the electromagnetic railgun system. In Proceedings of the 2014 17th International Symposium on Electromagnetic Launch Technology, La Jolla, CA, USA, 7–11 July 2014; pp. 1–6. [Google Scholar]
- Geng, Y.; Xu, L. Analysis of Projectile Motion in Bore and Transfer Efficiency for Electromagnetic Railgun. In Proceedings of the 2010 WASE International Conference on Information Engineering, Beidai, China, 14–15 August 2010; Volume 3, pp. 156–160. [Google Scholar]
- Ge, X.; Cao, B.; Li, J.; Sun, X.; Yang, Y.L. Research on evaluation of electromagnetic railgun efficiency. In Proceedings of the 2014 17th International Symposium on Electromagnetic Launch Technology, La Jolla, CA, USA, 7–11 July 2014; pp. 1–5. [Google Scholar]
- Wen, Y.; Dai, L.; Lin, F. Effect of Geometric Parameters on Equivalent Load and Efficiency in Rectangular Bore Railgun. IEEE Trans. Plasma Sci. 2021, 49, 1428–1433. [Google Scholar] [CrossRef]
- Meyer, R.T.; DeCarlo, R.A.; Dickerson, J. Energy Transfer Efficiency Optimization in an Electromagnetic Railgun. IEEE Trans. Plasma Sci. 2017, 45, 702–710. [Google Scholar] [CrossRef]
- Yuan, J.; Geng, Y.; Shen, Z.; Li, J. Approach for Simulating Air Gap Between Armature and Rails Based on the Finite-Element Method. IEEE Trans. Plasma Sci. 2017, 45, 1591–1595. [Google Scholar] [CrossRef]
- Bayati, M.S.; Keshtkar, A. Study of the Current Distribution, Magnetic Field, and Inductance Gradient of Rectangular and Circular Railguns. IEEE Trans. Plasma Sci. 2013, 41, 1376–1381. [Google Scholar] [CrossRef]
- Powell, J.D.; Zielinski, A.E. Current and heat transport in the solid-armature railgun. IEEE Trans. Magn. 1995, 31, 645–650. [Google Scholar] [CrossRef]
- Powell, J.D.; Zielinski, A.E. Observation and simulation of solid-armature railgun performance. IEEE Trans. Magn. 1999, 35, 84–89. [Google Scholar] [CrossRef]
- Lin, Q.-H.; Li, B.-M. Numerical simulation of interior ballistic process of railgun based on the multi-field coupled model. Def. Technol. 2016, 12, 101–105. [Google Scholar] [CrossRef]
- Hsieh, K. A Lagrangian formulation for mechanically, thermally coupled electromagnetic diffusive processes with moving conductors. IEEE Trans. Magn. 1995, 31, 604–609. [Google Scholar] [CrossRef]



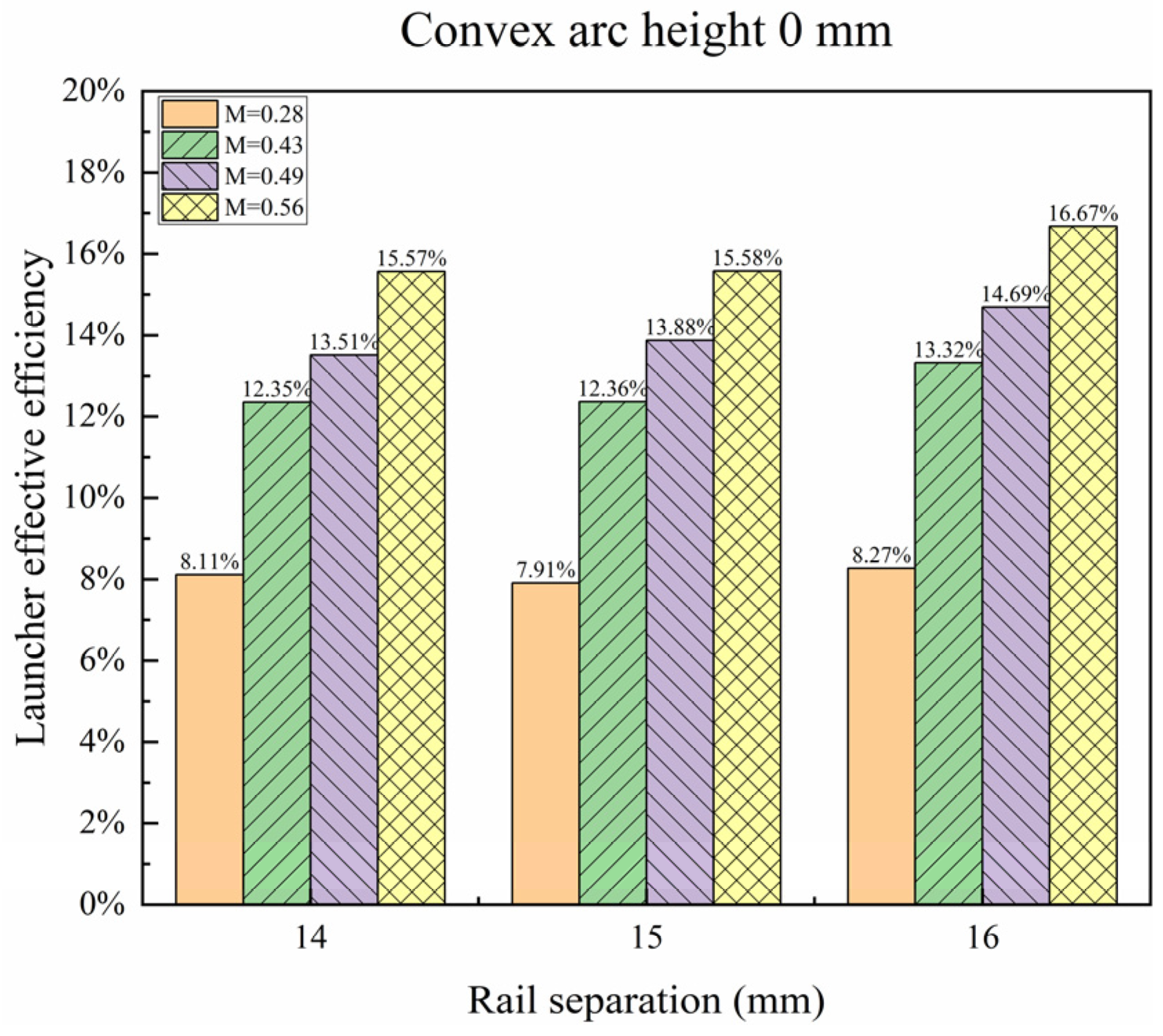
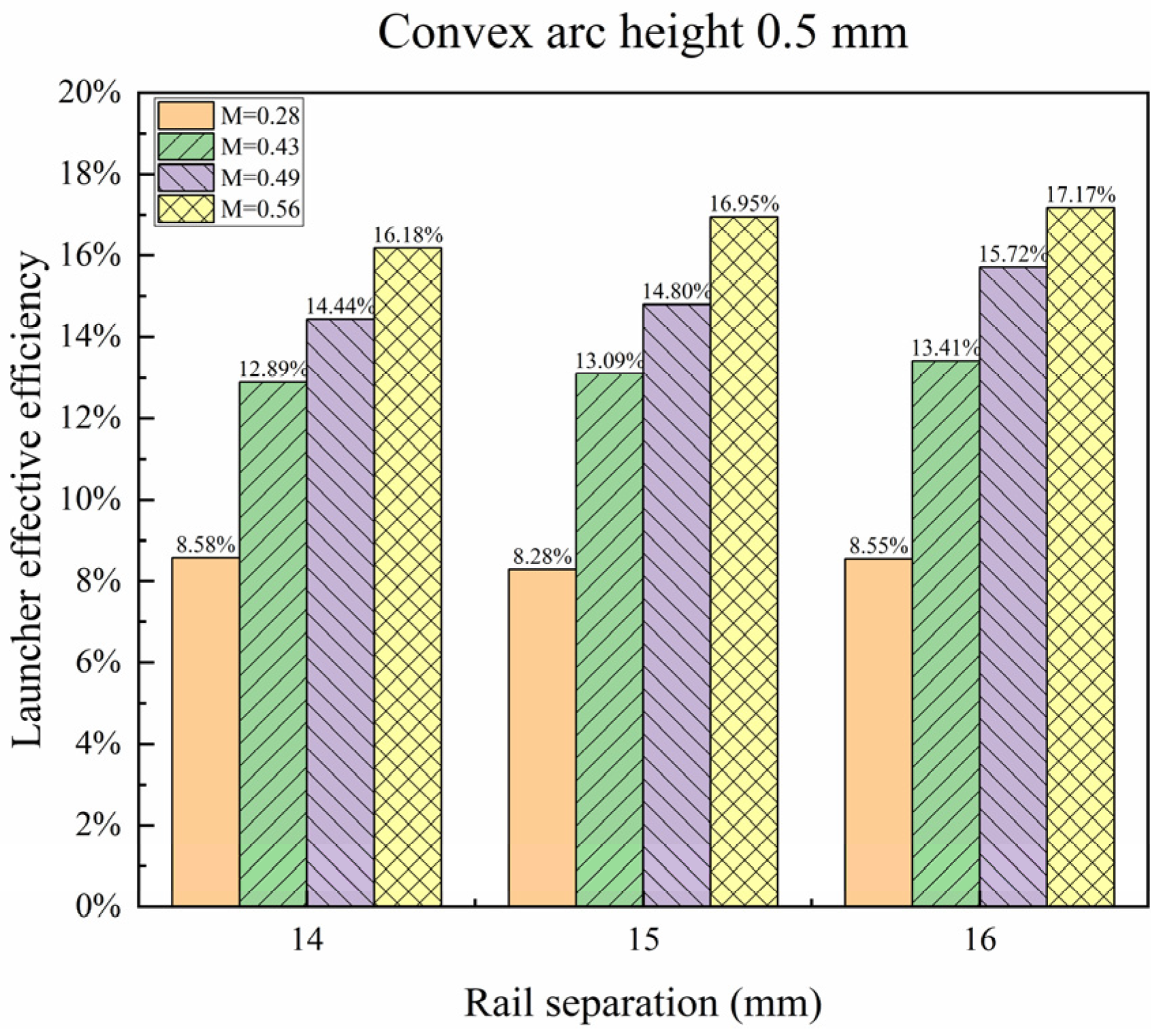
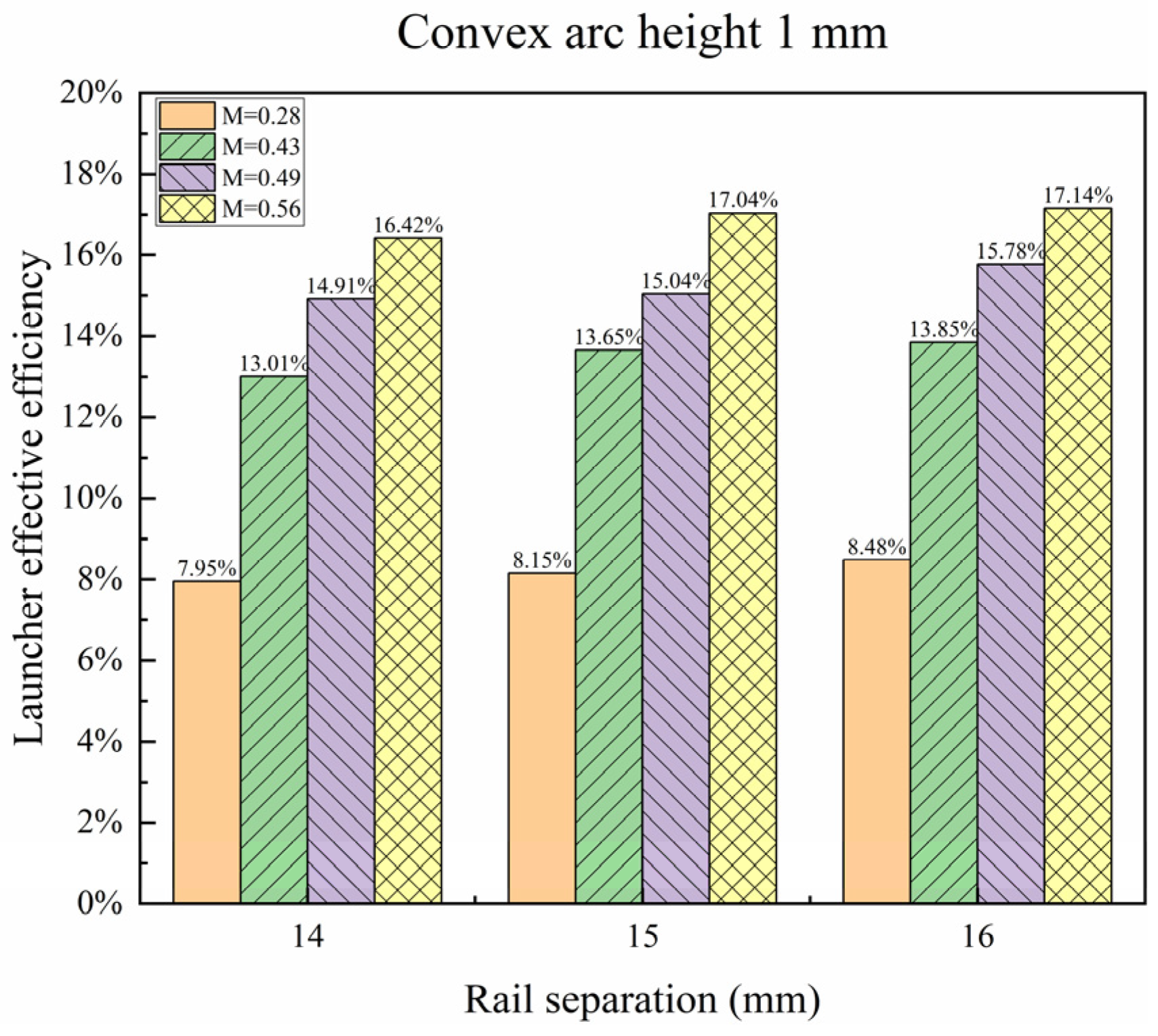

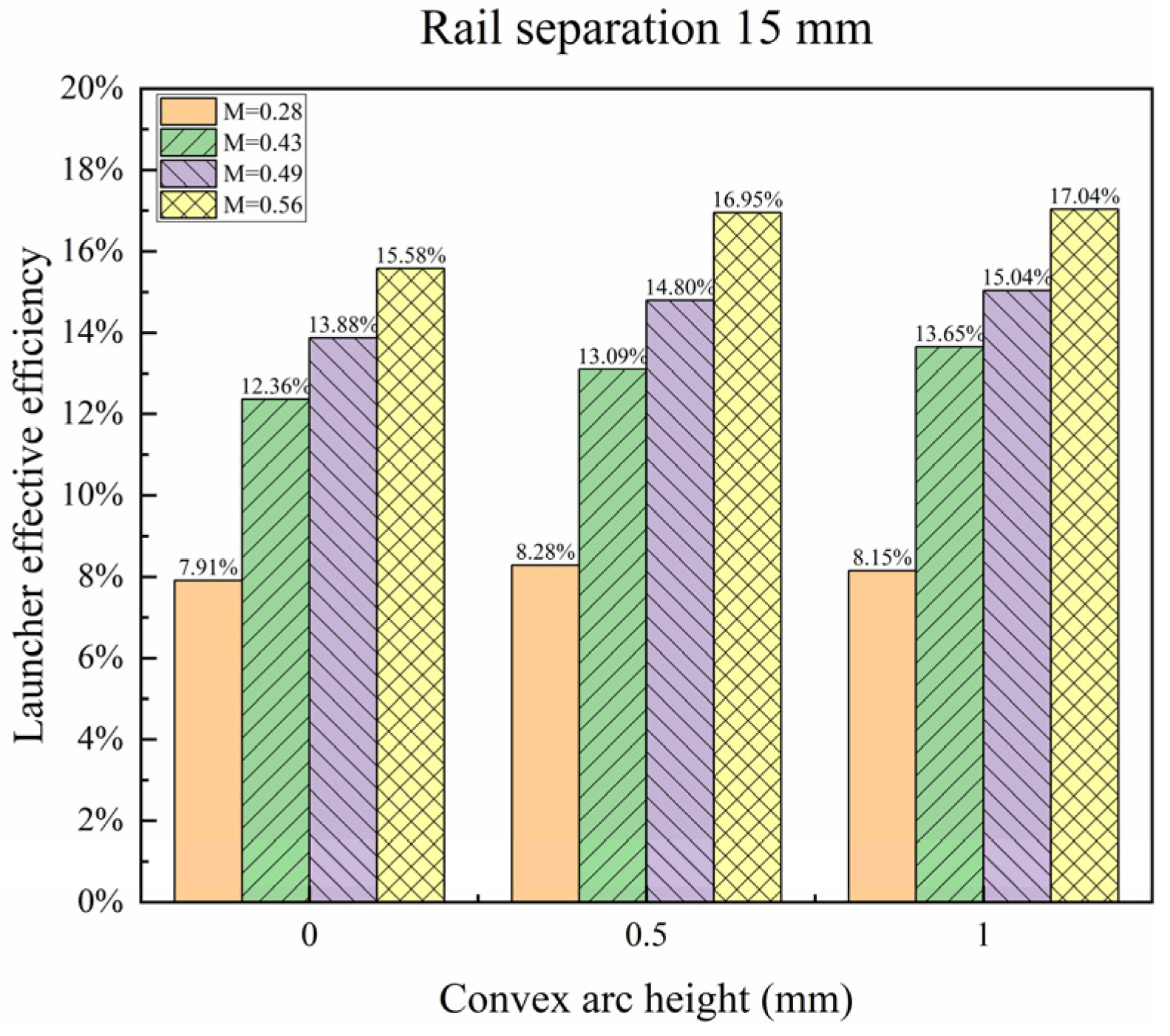

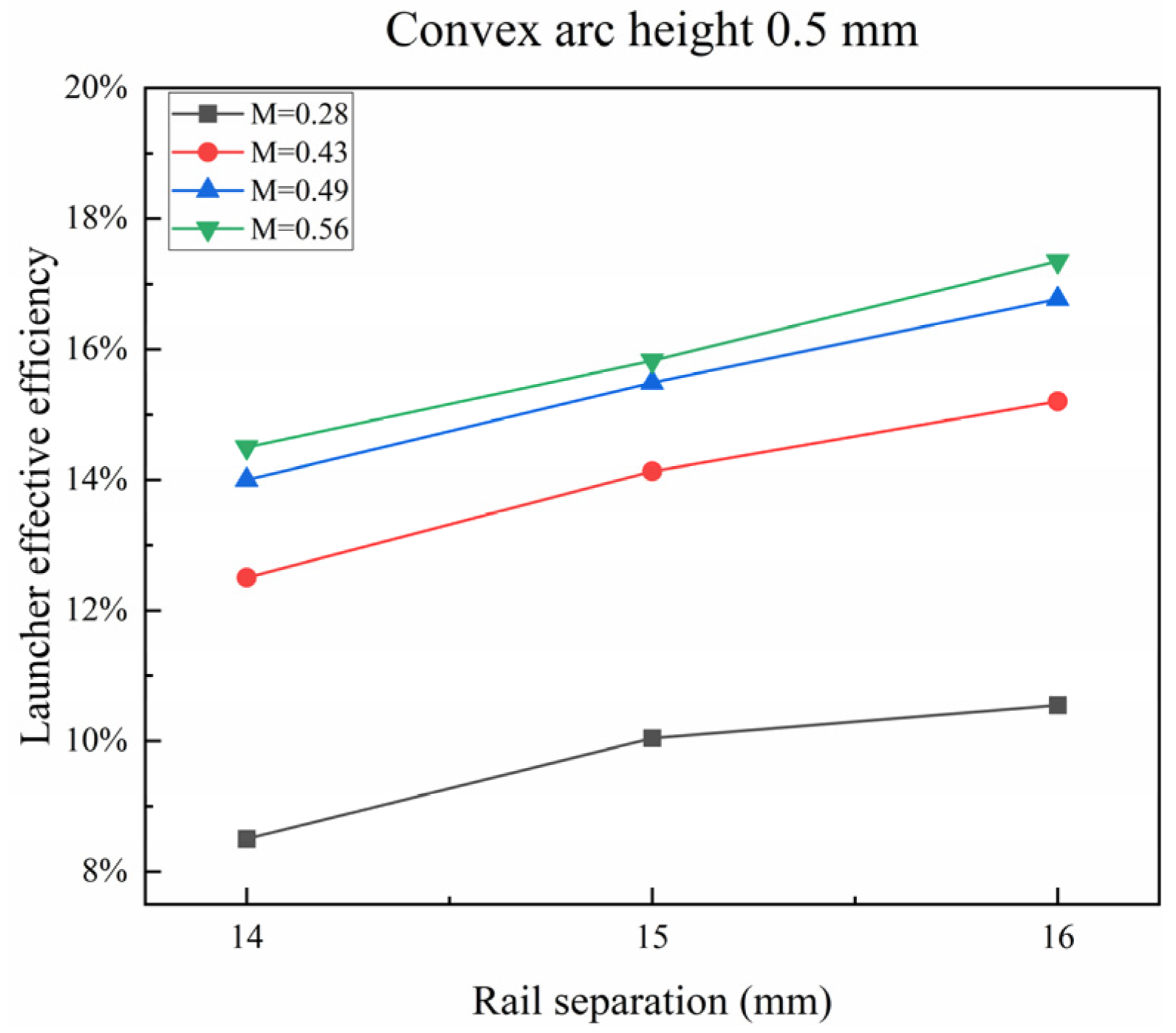


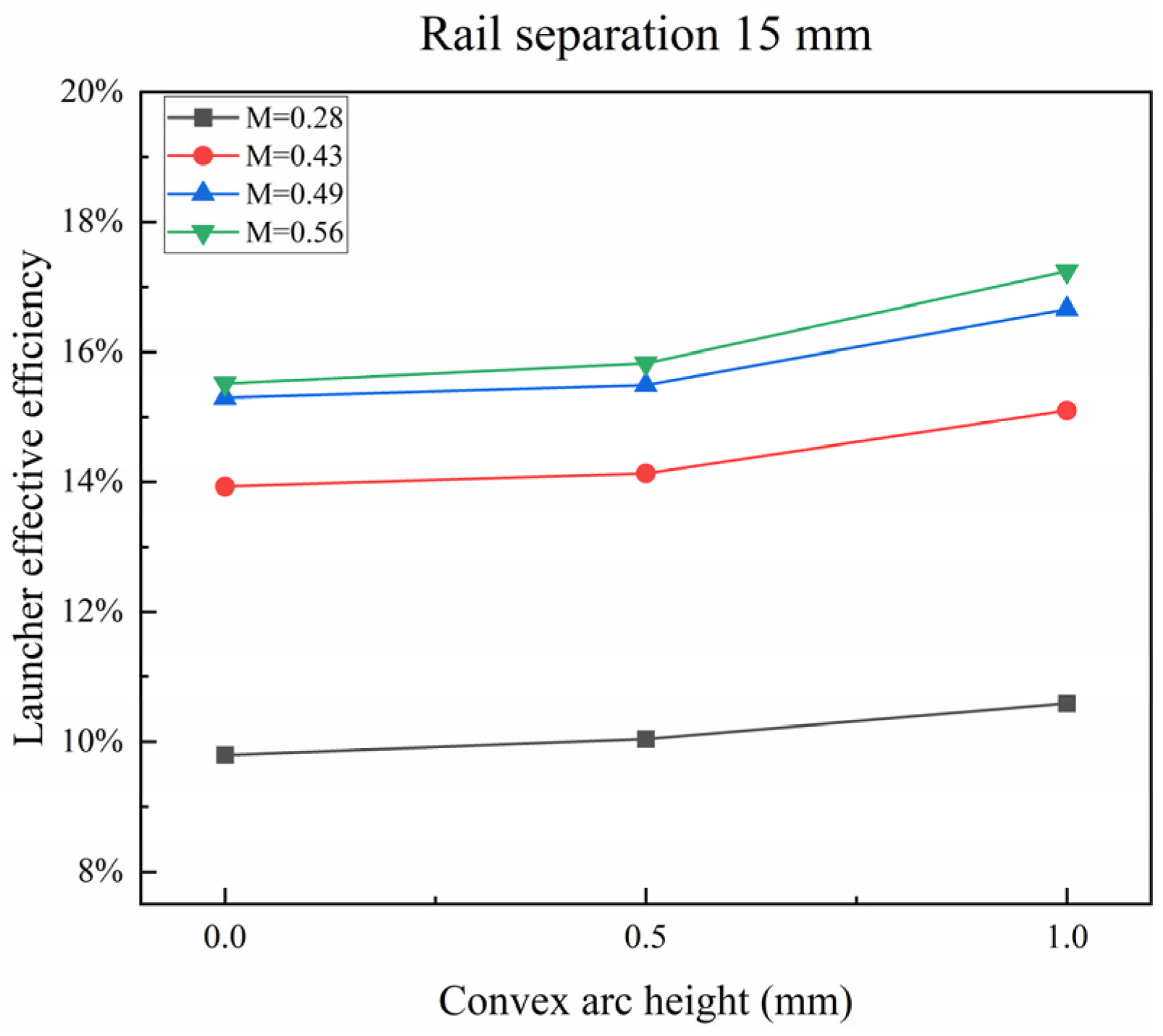
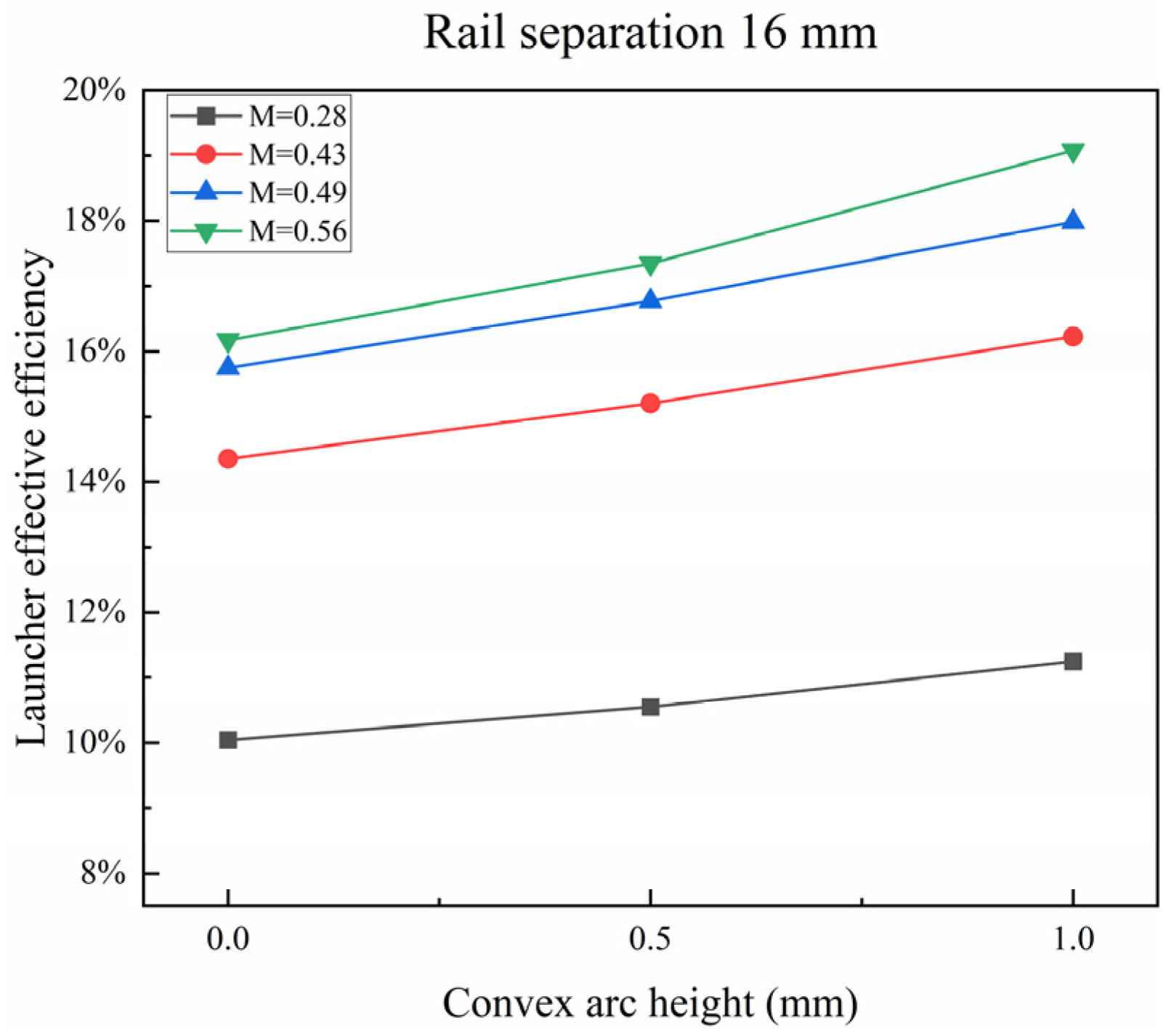
| Rail Separation (mm) | Convex Arc Height (mm) | Effective Mass Ratio | Launcher Effective Efficiency |
|---|---|---|---|
| 14 | 0 | 0.28 | 8.11% |
| 0.43 | 12.35% | ||
| 0.49 | 13.51% | ||
| 0.56 | 15.57% | ||
| 15 | 0 | 0.28 | 7.91% |
| 0.43 | 12.36% | ||
| 0.49 | 13.88% | ||
| 0.56 | 15.58% | ||
| 16 | 0 | 0.28 | 8.27% |
| 0.43 | 13.32% | ||
| 0.49 | 14.69% | ||
| 0.56 | 16.67% | ||
| 14 | 0.5 | 0.28 | 8.58% |
| 0.43 | 12.89% | ||
| 0.49 | 14.44% | ||
| 0.56 | 16.18% | ||
| 15 | 0.5 | 0.28 | 8.28% |
| 0.43 | 13.32% | ||
| 0.49 | 14.69% | ||
| 0.56 | 16.67% | ||
| 16 | 0.5 | 0.28 | 8.55% |
| 0.43 | 13.41% | ||
| 0.49 | 15.72% | ||
| 0.56 | 17.17% | ||
| 14 | 1 | 0.28 | 7.95% |
| 0.43 | 13.01% | ||
| 0.49 | 14.91% | ||
| 0.56 | 16.42% | ||
| 15 | 1 | 0.28 | 8.15% |
| 0.43 | 13.65% | ||
| 0.49 | 15.04% | ||
| 0.56 | 17.04% | ||
| 16 | 1 | 0.28 | 8.48% |
| 0.43 | 13.85% | ||
| 0.49 | 15.78% | ||
| 0.56 | 17.14% |
| Armature | Rail | |
|---|---|---|
| Electrical conductivity (S/m) | 2.5 × 107 | 5 × 108 |
| Thermal conductivity (W/m·K) | 167 | 401 |
| Specific Heat (J/kg·K) | 896 | 385 |
| Mass density (kg/m3) | 2700 | 8930 |
| Young’s modulus (Pa) | 6.89 × 1010 | 1.1 × 1011 |
| Poisson’s ratio | 0.33 | 0.343 |
| Model Number | Rail Separation (mm) | Convex Arc Height (mm) | Effective Mass Ratio |
|---|---|---|---|
| 1-1~1-5 | 14 | 0 | 0, 0.28, 0.43, 0.49, 0.56 |
| 2-1~2-5 | 15 | 0 | 0, 0.28, 0.43, 0.49, 0.56 |
| 3-1~3-5 | 16 | 0 | 0, 0.28, 0.43, 0.49, 0.56 |
| 4-1~4-5 | 14 | 0.5 | 0, 0.28, 0.43, 0.49, 0.56 |
| 5-1~5-5 | 15 | 0.5 | 0, 0.28, 0.43, 0.49, 0.56 |
| 6-1~6-5 | 16 | 0.5 | 0, 0.28, 0.43, 0.49, 0.56 |
| 7-1~7-5 | 14 | 1 | 0, 0.28, 0.43, 0.49, 0.56 |
| 8-1~8-5 | 15 | 1 | 0, 0.28, 0.43, 0.49, 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, N.; Li, J.; Yan, P.; Tian, W. Effect of Bore Parameters and Effective Mass Ratio on Launcher Effective Efficiency. Energies 2024, 17, 3817. https://doi.org/10.3390/en17153817
Xiao N, Li J, Yan P, Tian W. Effect of Bore Parameters and Effective Mass Ratio on Launcher Effective Efficiency. Energies. 2024; 17(15):3817. https://doi.org/10.3390/en17153817
Chicago/Turabian StyleXiao, Nan, Jun Li, Ping Yan, and Wen Tian. 2024. "Effect of Bore Parameters and Effective Mass Ratio on Launcher Effective Efficiency" Energies 17, no. 15: 3817. https://doi.org/10.3390/en17153817
APA StyleXiao, N., Li, J., Yan, P., & Tian, W. (2024). Effect of Bore Parameters and Effective Mass Ratio on Launcher Effective Efficiency. Energies, 17(15), 3817. https://doi.org/10.3390/en17153817






