Justifying and Implementing Concept of Object-Oriented Observers of Thermal State of Rolling Mill Motors
Abstract
1. Introduction
- When mastering new rolling profiles;
- To optimize speed and load regimes of electric drives, including for increasing productivity and rolling rhythm regularity [7];
- To improve the load alignment system for the upper and lower rolls of the stand.
2. Literature Review
2.1. Motor Thermal Regime Monitoring
2.2. Average Loss Analysis
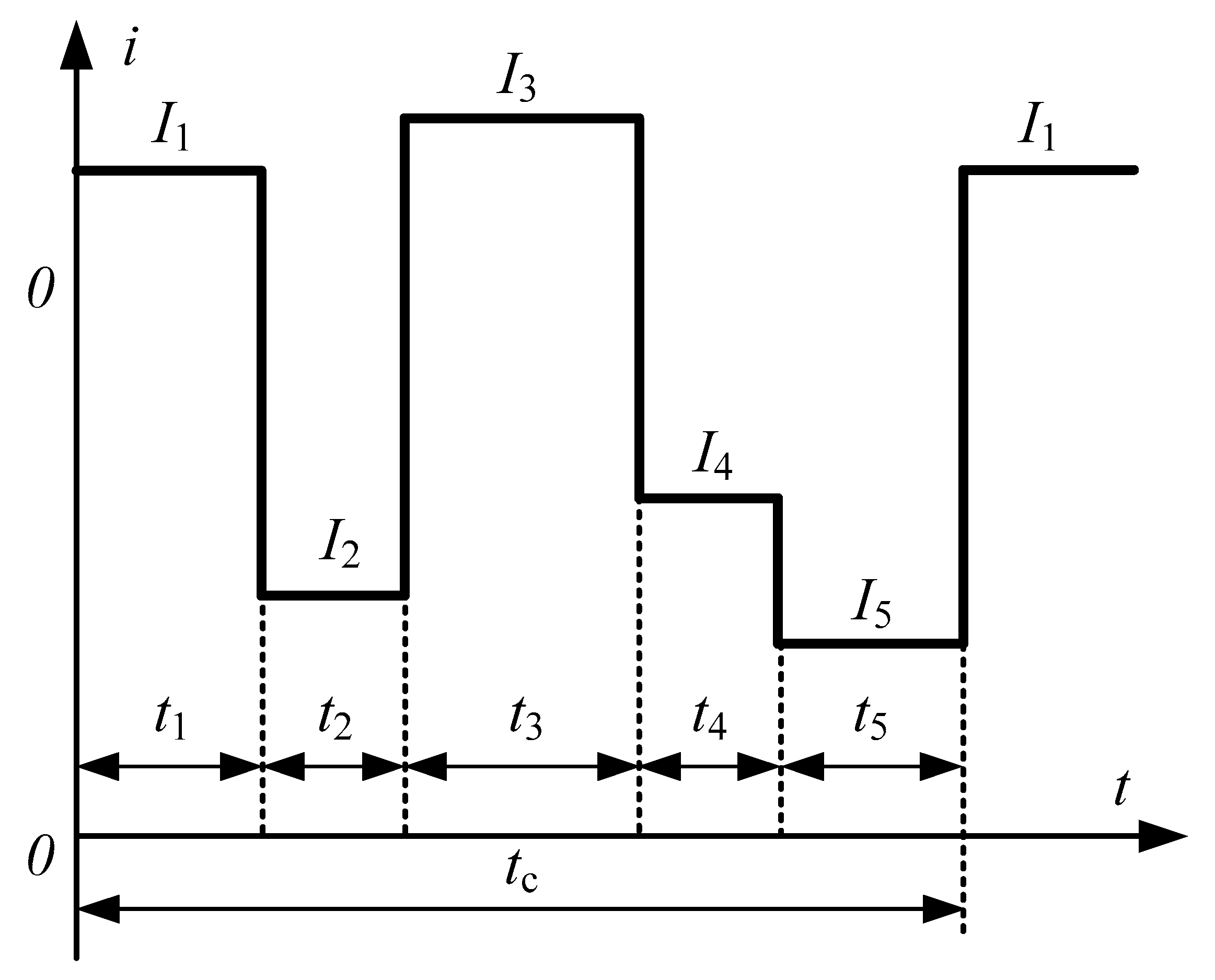
- A single-mass heating model is used, which allows for obtaining the simplest analytical dependencies between the power losses and the motor temperature since, in this case, the temperature change on each section of the load diagram is described by an exponential dependence with a single-time constant;
- The linear temperature dependence of the insulation thermal aging rate (its thermal resource consumption rate) is assumed since only in this case will the average temperature value determine the average insulation aging rate.
3. Problem Statement
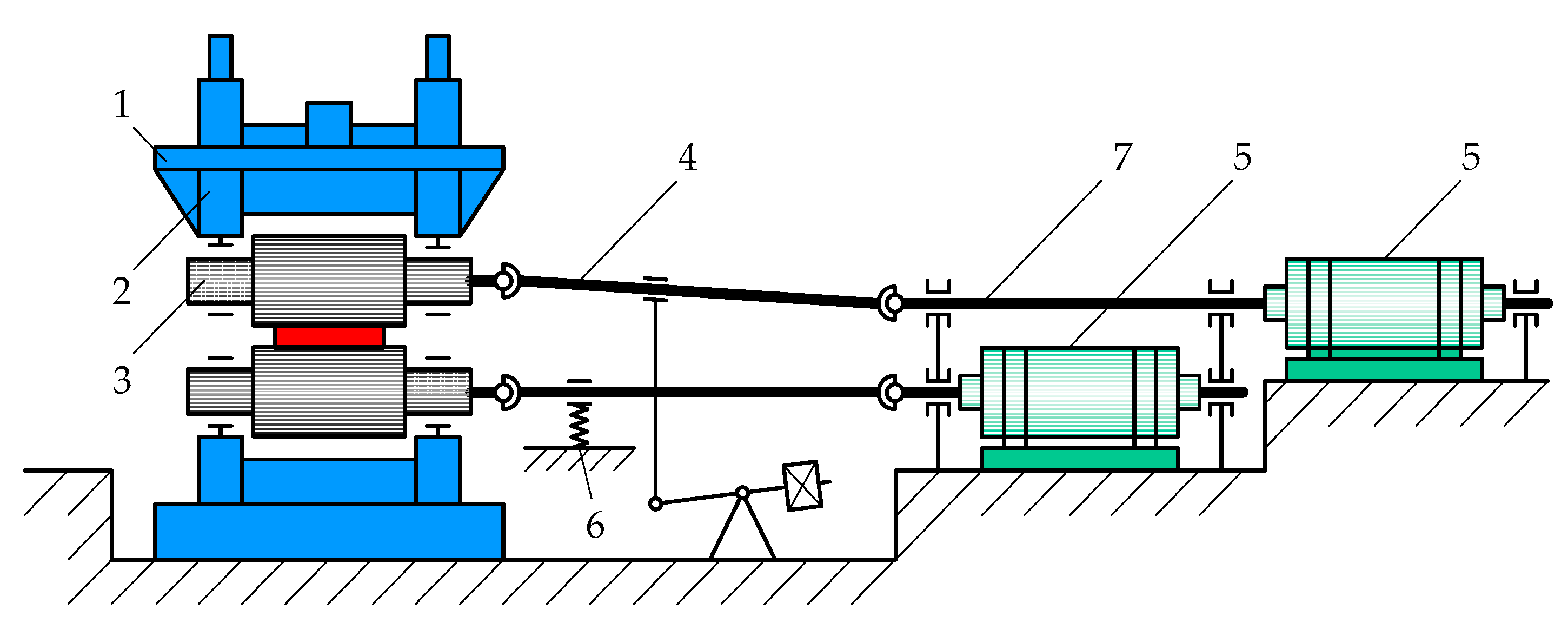
3.1. Specifics of the Research Object
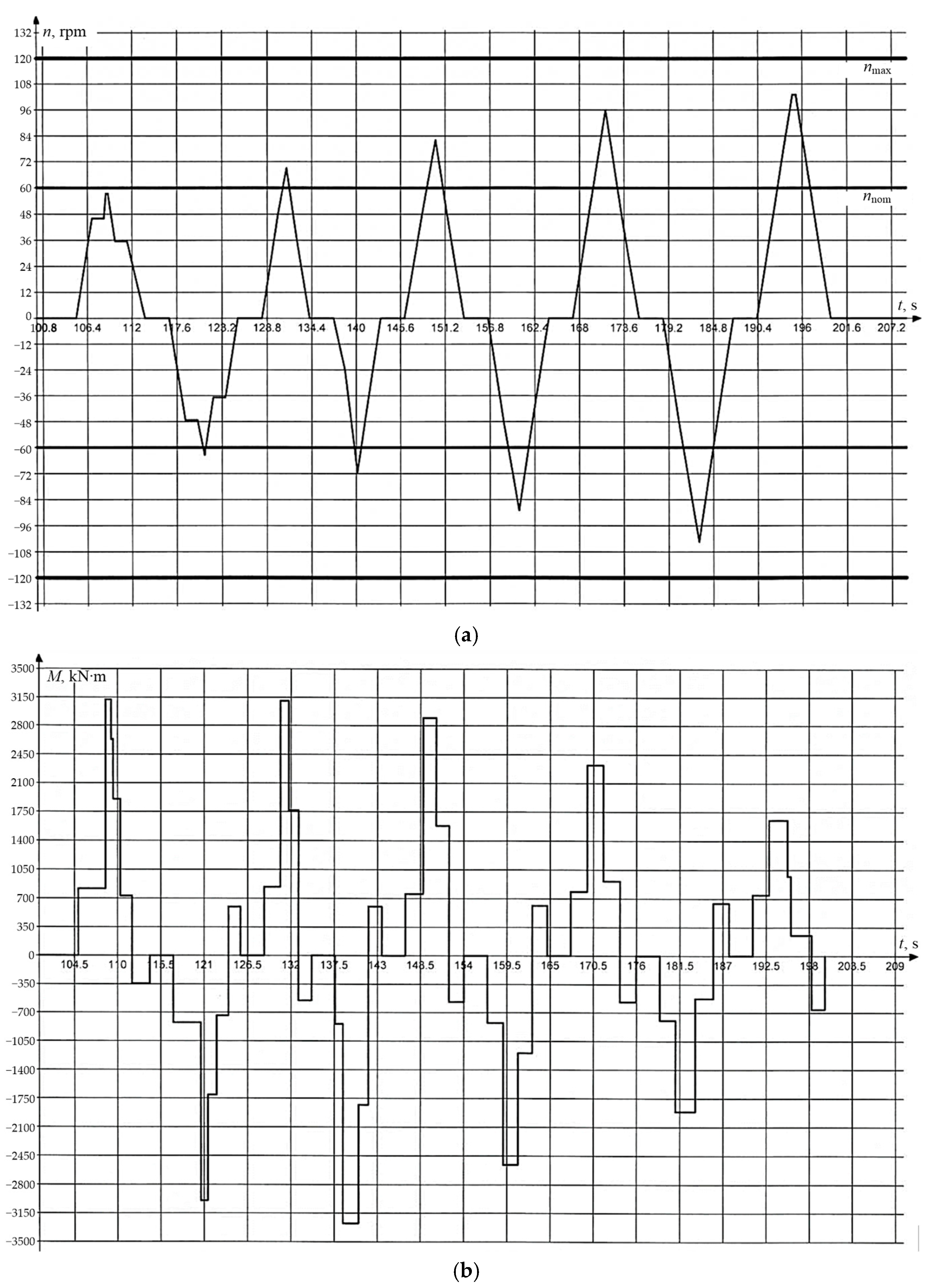
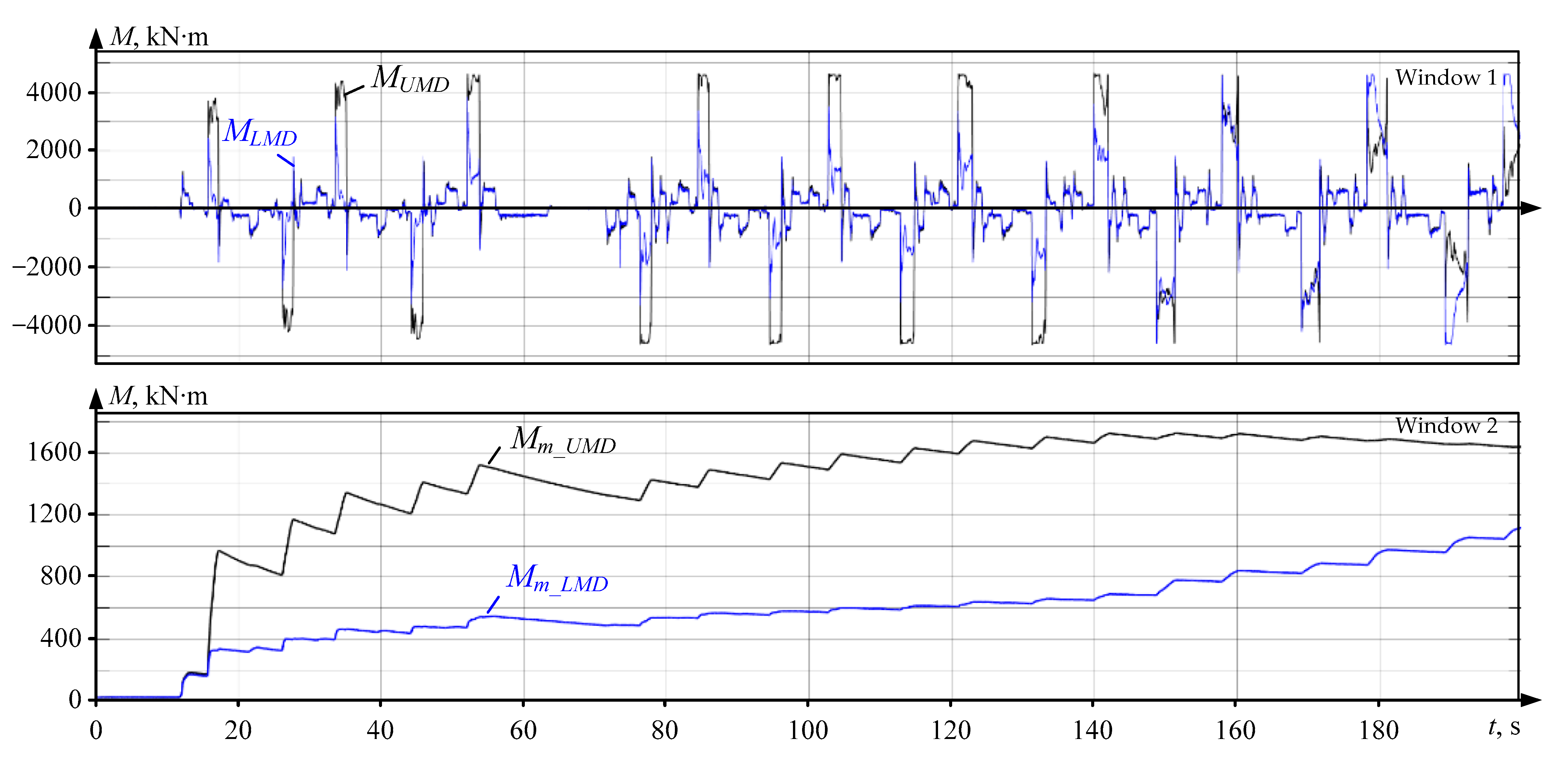
3.2. Analyzing Load Diagrams
4. Materials and Methods
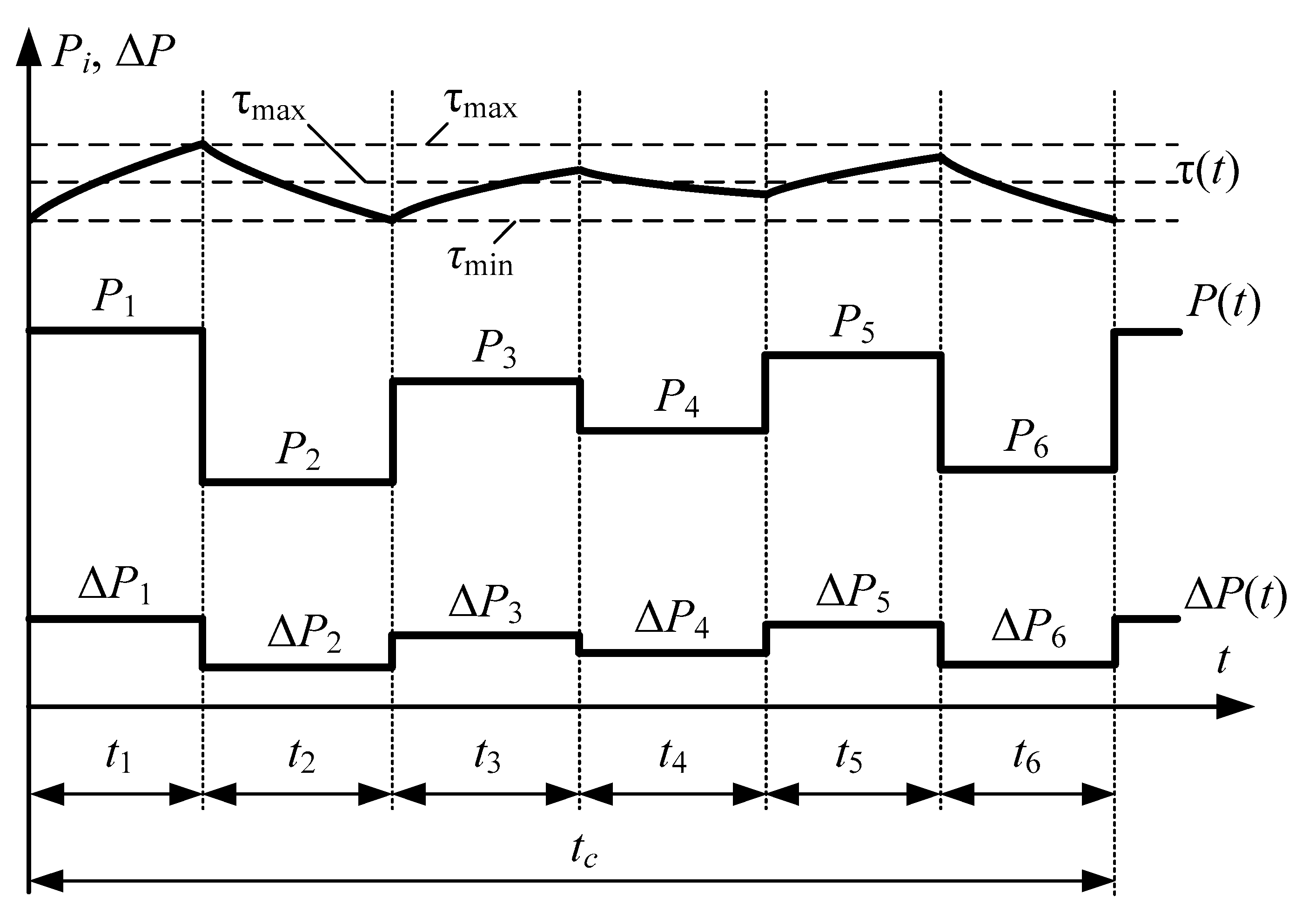
4.1. Methods for Calculating Equivalent Loads
4.2. Example Calculation Using Conventional Technique
- When calculating equivalent parameters in the rough rolling mode using the method with identical load diagrams for UMD and LMD, a two-fold error is obtained;
- It is advisable to check the motors for heating by calculating effective torques or currents built based on real digitized time diagrams recorded for UMD and LMD during the rolling of a specific batch;
- The thermal states of UMD and LMD motors should be compared based on determining the ratios of effective torques or currents over the same period of operation.
5. Implementation
- Reading data arrays obtained from direct measurements with the IbaPDA system. If necessary, smoothing and averaging of data is performed using statistical processing algorithms;
- Exporting data from the system to a Matlab file;
- Calculating equivalent load parameters for a given time interval. The following intervals can be taken: one pass, all passes of rough or finish rolling a full cycle, or several cycles;
- Averaging and comparing the results with the rated motor parameters.
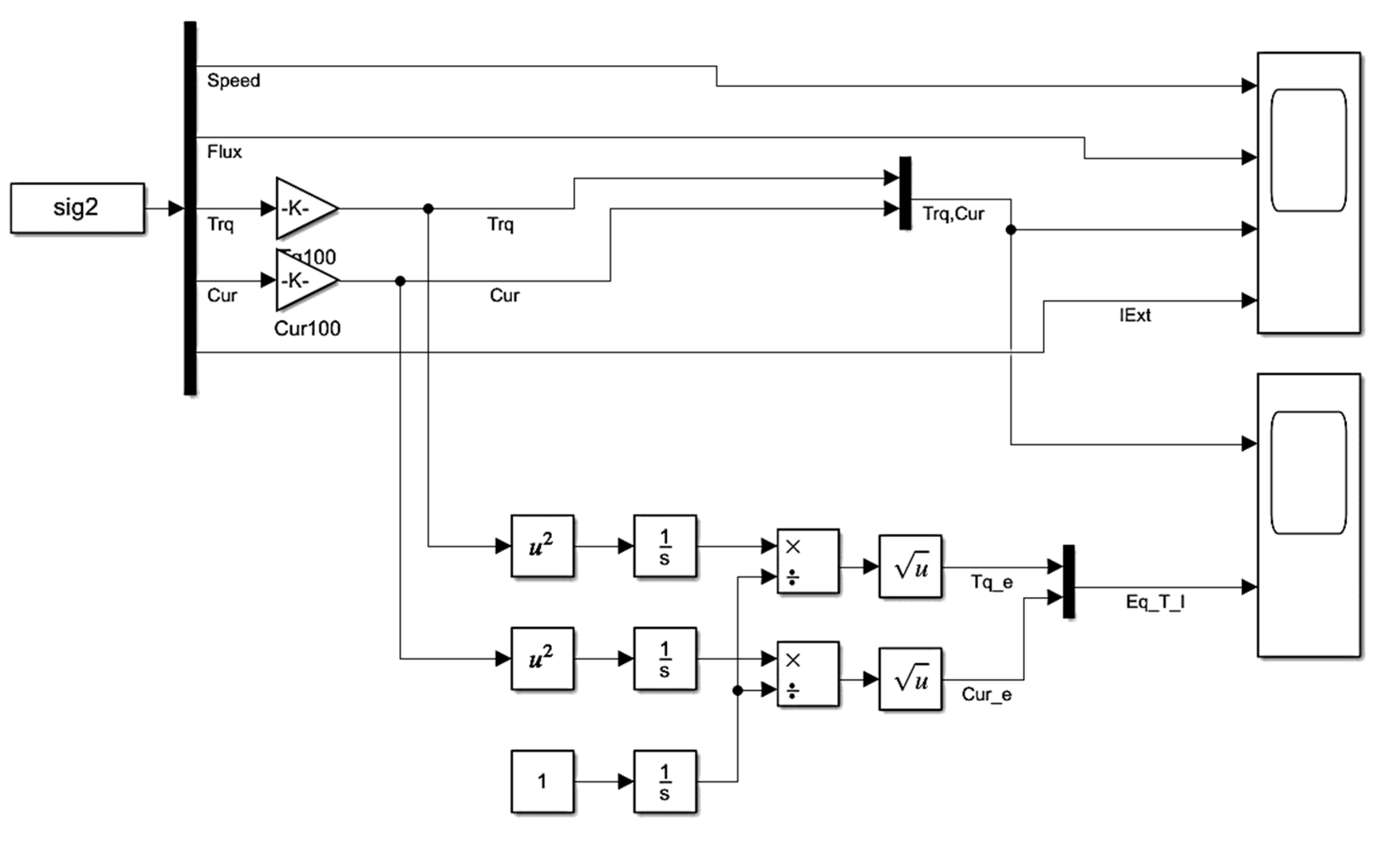
5.1. Automatic Calculation of Equivalent Currents for the Rolling Cycle
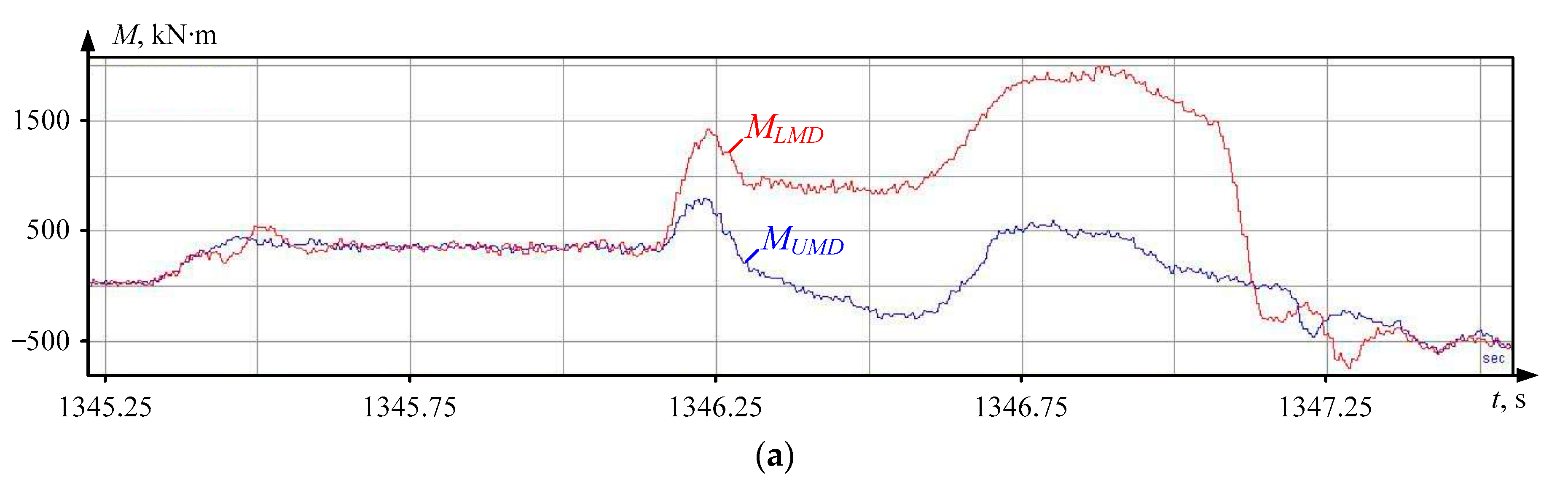
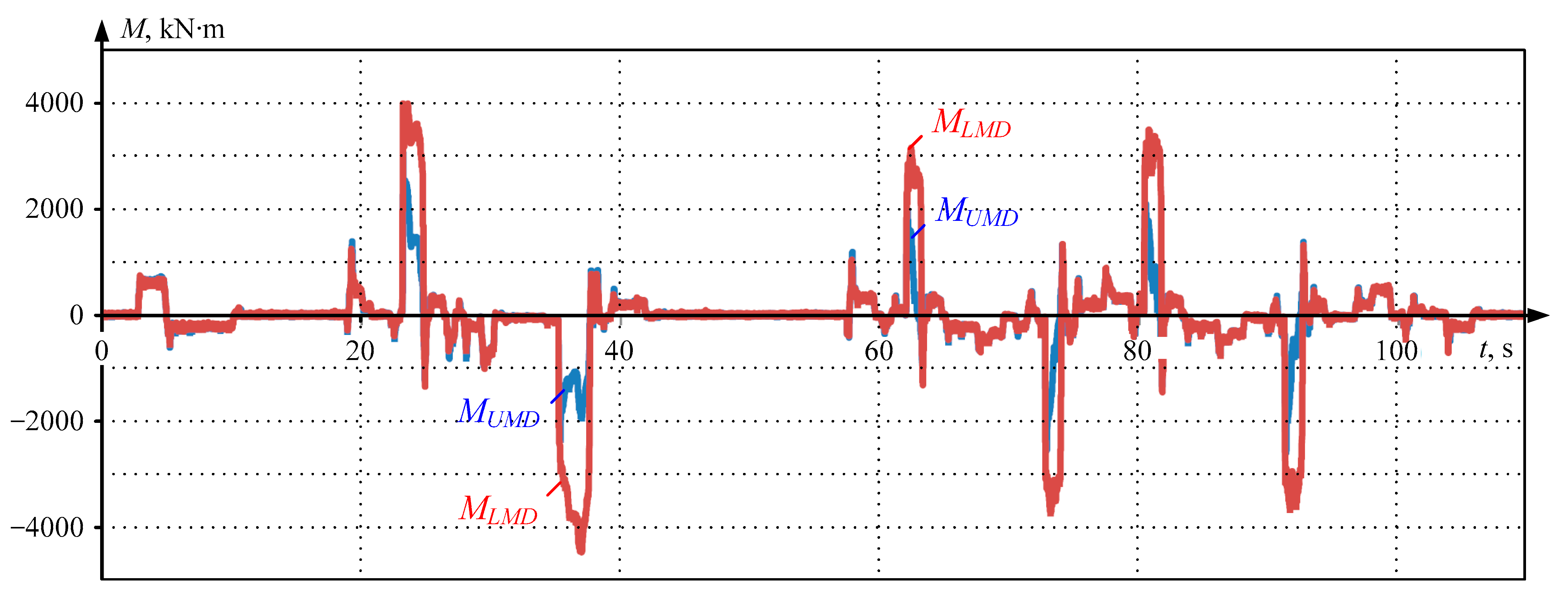
- During the rolling of a heavy stock batch, the upper roll motor is more loaded (and, obviously, heats up more) than the lower one. However, this conclusion is valid only for the considered case where the motor temperatures before rolling match the ambient temperature, corresponding to complete motor cooling. Section 6 will discuss motor heating during the rolling of several batches of the same stock;
- The ratio of equivalent currents is similar: during rolling, increases by 1.5 times (from 650 to 980 A).
5.2. Structure of Object-Oriented Thermal State Observer
6. Results
6.1. Restoring Equivalent Currents and Motor Temperatures
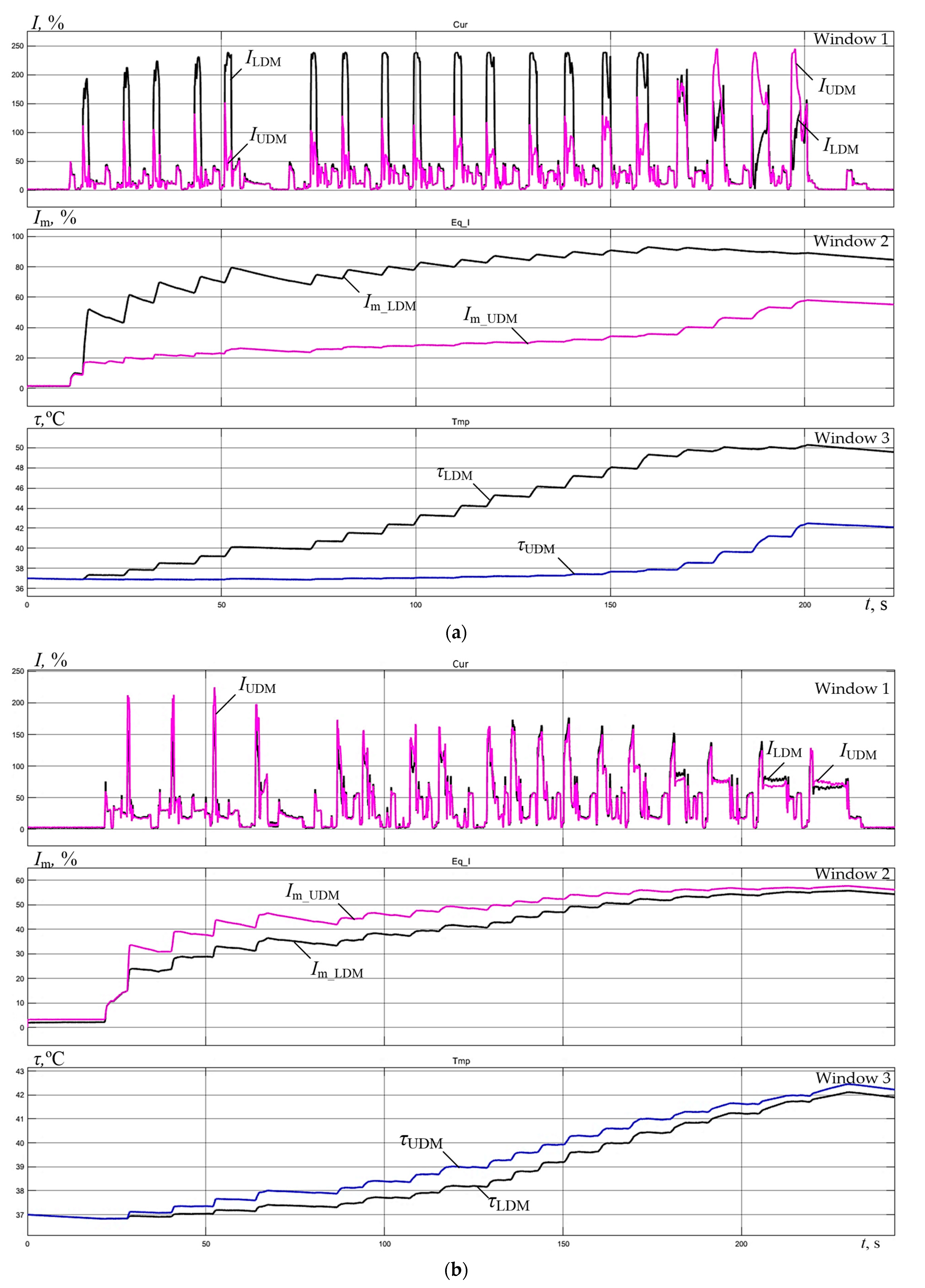
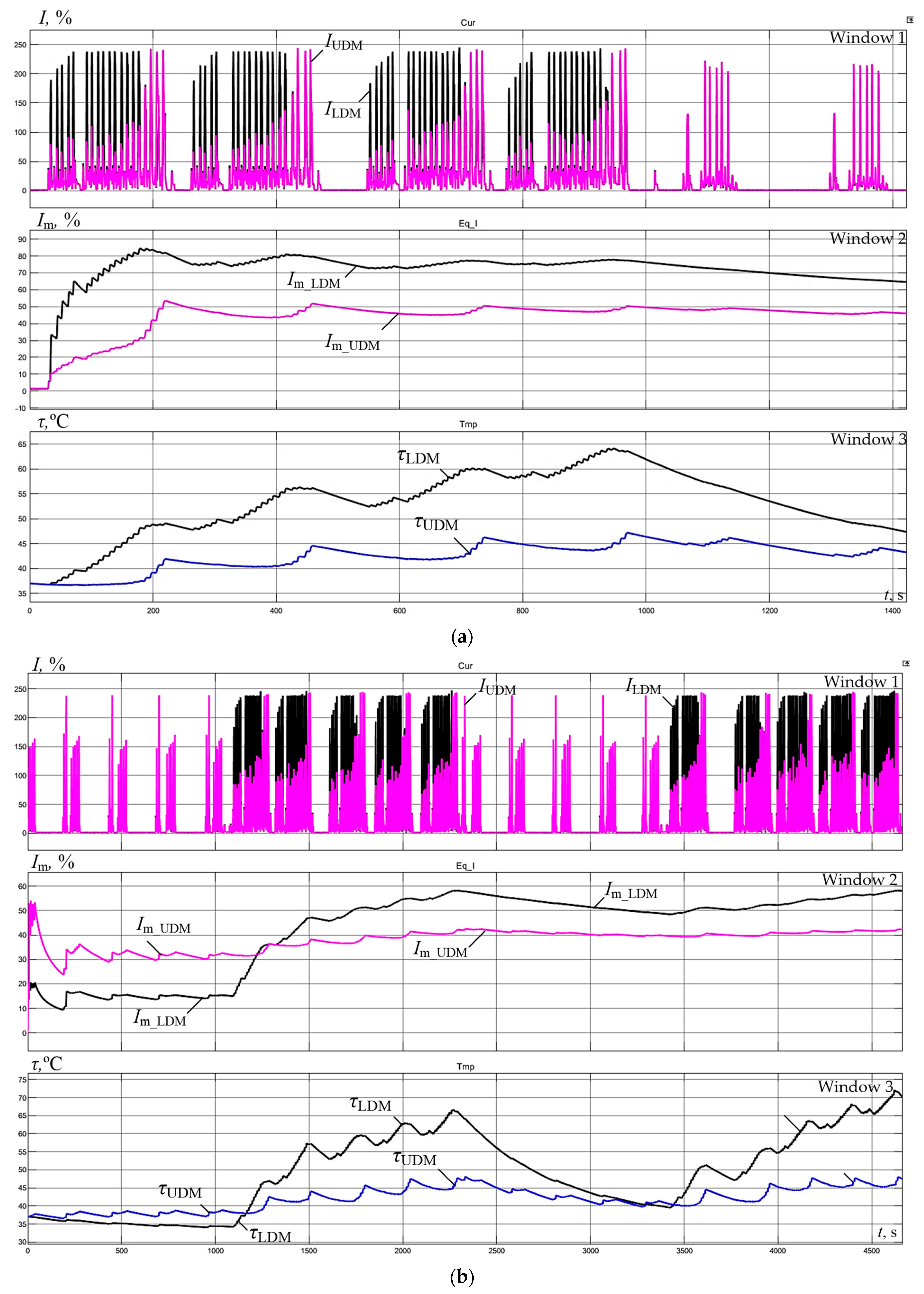
- With a large “ski” setting (Figure 15a), in all passes except the last four, the LMD current (window 1) exceeds the UMD current. Therefore, at the end of rolling, the equivalent current is higher and equal to 85% of the rated value, while the current is 55% of the rated value. Similar currents with a “ski” of 1.5% in Figure 15b at the end of rolling are virtually identical and equal to 55%. The alignment of equivalent currents in the second case indirectly confirms that the thermal regime of the LMD motor improves. Since the equivalent currents of the motors are significantly below the rated value (below 100%), we can assert that overheating does not occur in either case. This is confirmed by the temperature plots in window 3;
- The dependencies in window 3 show that during the finish rolling, the temperature plots reach steady-state values. Thereat, the difference in steady-state values in Figure 15a is 16% (50 °C for LMD and 42 °C for UMD). The steady-state temperature in Figure 15b is the same for both motors and is approximately 42 °C;
- 3.
- Speed mismatch during rolling significantly affects motor heating. With a large “ski” (Figure 15a), the LMD and UMD motor temperatures at the end of the rolling cycle differ by 16% or 1.2 times. This confirms the advisability of load leveling across passes to improve thermal modes. Along with improving the thermal balance of the motors, this will improve their efficiency [63,64] (this is explained below in Section 6.2).
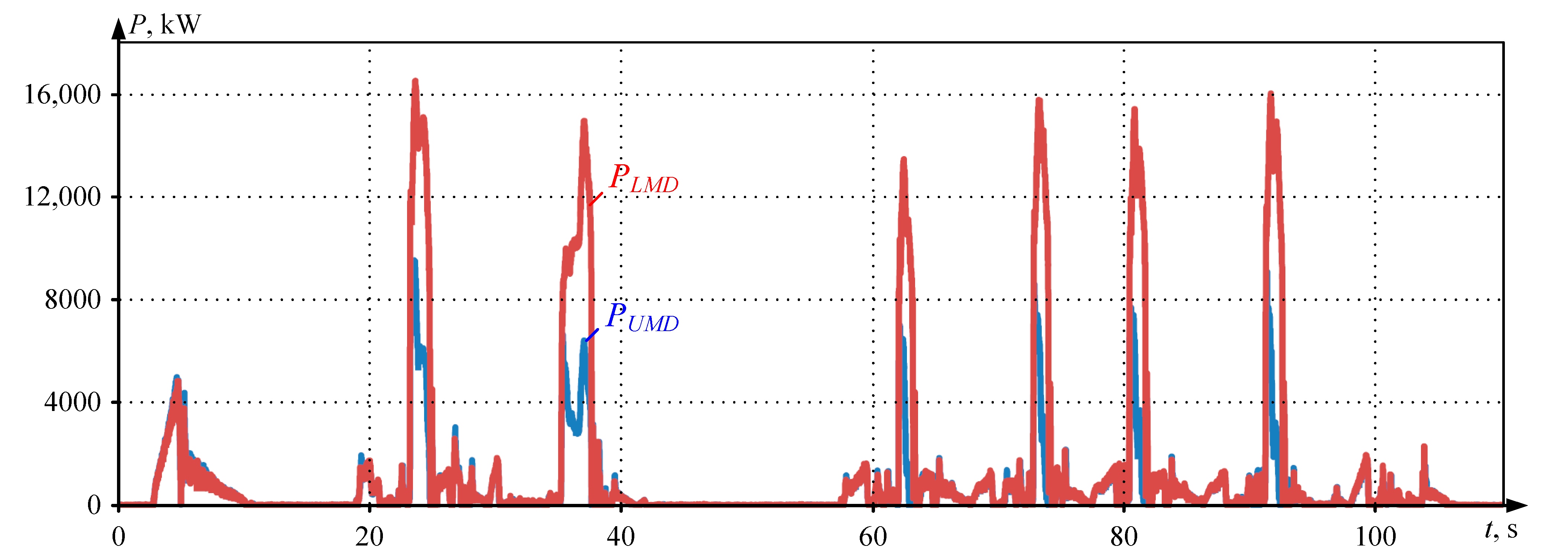
6.2. Experimental Assessment of Electricity Losses
- -
- Rolling with equalizing speeds and loads due to the adoption of adaptive LDC;
- -
- Rolling with a “ski” set, equal to 7% of a rolling speed established.
- -
- With loads balancing—0.633 MW;
- -
- With a “ski” of 7%—0.752 MW.
7. Discussion of Results
8. Conclusions
- The implementation of the IIoT concept in industrial enterprises should be carried out through the introduction of modern online monitoring technologies based on observers (digital shadows) of the coordinates of electromechanical and mechatronic systems. The concept of an object-oriented observer (object-oriented digital shadow) has been introduced. This is a hardware and software device that continuously monitors the state of a specific industrial facility by tracking the coordinates that determine its state;
- Experimental studies of the operating modes of the mill 5000 horizontal stand drives showed a significant difference in the UMD and LMD motor loads. At the roughing stage, the average LMD torque and current are greater than those of the UMD; in the finishing stage, their ratio is reversed. With the existing speed control system settings, load leveling occurs only in the last passes. This leads to disproportionate load distribution, different motor heating, and the need to control their temperature during rolling;
- It was shown that known methods for analyzing motor load and thermal modes are based on calculations using smoothed load diagrams identical to UMD and LMD, leading to inaccurate thermal state assessments. The relevance of developing a technique for online motor temperature monitoring by processing arrays of currents or torques recorded during rolling has been justified;
- A technique for calculating equivalent loads was developed, allowing automated motor heating checks based on data obtained during rolling. It comprises the following steps:
- Reading data arrays created as a result of direct measurements by the IbaPDA system;
- Exporting data to a Matlab-Simulink file;
- Calculating equivalent load parameters over a given time interval (one pass, all roughing or finishing passes, full cycle, etc.);
- Comparing the results with the motor’s rated parameters.
- 5.
- Based on the proposed technique’s algorithm, an object-oriented root mean square torque and current observer and the thermal state observer for rolling stand motors were developed. The thermal state observer uses the motor thermal model scheme and models to calculate heat exchange in Matlab-Simulink based on parameters from IbaPDA;
- 6.
- The thermal modes of motors in the finishing passes during rolling with different “skies” were studied. It is confirmed that leveling the equivalent currents ensures temperature equality. It is found that regardless of speed mismatches, the equivalent currents of UMD and LMD motors are significantly below the rated values, so no motor overheating occurs when rolling the analyzed product range;
- 7.
- The developed technique is a tool for determining the constraints the drive imposes on the rolling program in an automated mode. This allows for optimizing speed and load modes, which is relevant when mastering new rolling products.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Yang, Y.; Jiang, P. Remote Monitoring and Maintenance for Equipment and Production Lines on Industrial Internet: A Literature Review. Machines 2023, 11, 12. [Google Scholar] [CrossRef]
- Errandonea, I.; Beltrán, S.; Arrizabalaga, S. Digital Twin for maintenance: A literature review. Comput. Ind. 2020, 123, 103316. [Google Scholar] [CrossRef]
- Attaran, M.; Attaran, S.; Celik, B.G. The impact of digital twins on the evolution of intelligent manufacturing and Industry 4.0. Adv. Comput. Intell. 2023, 3, 11. [Google Scholar] [CrossRef]
- Brecher, C.; Dalibor, M.; Rumpe, B.; Schilling, K.; Wortmann, A. An Ecosystem for Digital Shadows in Manufacturing. Procedia CIRP 2021, 104, 833–838. [Google Scholar] [CrossRef]
- Radionov, A.A.; Bovshik, P.A.; Loginov, B.M.; Karandaev, A.S.; Khramshin, V.R. Construction Principle for Object-Oriented Digital Twins of Mechatronic Complexes of Rolling Mills. In Proceedings of the 2023 International Russian Smart Industry Conference (SmartIndustryCon), Sochi, Russia, 27–31 March 2023; pp. 516–522. [Google Scholar] [CrossRef]
- Eleftheriou, O.T.; Christos-Nikolaos, E. Anagnostopoulos. Digital twins: A brief overview of applications, challenges and enabling technologies in the last decade. Digit. Twin 2022, 2, 2. [Google Scholar] [CrossRef]
- Hu, X.L.; Zhang, Q.S.; Zhong, Z.H.; Yong, T.I.; Liu, X.H.; Wang, G.D. Application of Approximation Full-Load Distribution Method to Pass Scheduling on Plate Mill With Hydro-Bending System. J. Iron Steel Res. Int. 2006, 13, 22–26. [Google Scholar] [CrossRef]
- Kun, E.; Szemmelveisz, T. Energy efficiency enhancement in the Hot Rolling Mill. Mater. Sci. Eng. 2014, 3, 43–50. [Google Scholar]
- Orcajo, G.A.; Rodríguez, J.; Ardura, P.; Cano, J.M.; Norniella, J.G.; Llera, R.; Cifrián, D. Dynamic estimation of electrical demand in hot rolling mills. In Proceedings of the 2015 IEEE Industry Applications Society Annual Meeting, Addison, TX, USA, 18–22 October 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Lagerev, A.V. Loading of Lifting and Transport Equipment; BSTU: Bryansk, Russia, 2010; p. 180. [Google Scholar] [CrossRef]
- Ali, A.H.; Kazmi, S.M.H.; Poonja, H.A.; Khan, H.; Shirazi, M.A.; Uddin, R. Motor Parametric Calculations for Robot Locomotion. Eng. Proc. 2022, 20, 8. [Google Scholar] [CrossRef]
- Philipp, M.; Schwenzfeier, W.; Fischer, F.D.; Wödlinger, R.; Fischer, C. Front end bending in plate rolling influenced by circumferential speed mismatch and geometry. J. Mater. Process. Technol. 2007, 184, 224–232. [Google Scholar] [CrossRef]
- Lee, K.; Han, J.; Park, J.; Kim, B.; Ko, D. Prediction and control of front-end curvature in hot finish rolling process. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, L.; Cui, X.; Zhu, X. Research on numerical simulation and process parameters of three-roll bending based on thickness characteristics of extra-thick plate. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
- Karandaev, A.S.; Zinchenko, M.A.; Semitko, A.Y.; Evdokimov, S.A.; Petukhova, O.I. Technological Causes of Vertical Workpiece Asymmetry in Plate Rolling Mills. In Lecture Notes in Mechanical Engineering, Proceedings of the 8th International Conference on Industrial Engineering, ICIE 2022, Sochi, Russia, 16–20 May 2022; Radionov, A.A., Gasiyarov, V.R., Eds.; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Tang, J. Motor Sizing Basics Part 3: How to Calculate Speed, Acceleration Torque, and RMS Torque. Available online: https://blog.orientalmotor.com/motor-sizing-basics-part-3-acceleration-torque-and-rms-torque (accessed on 22 May 2024).
- Semenova, M.N.; Yakushev, I.A.; Zagolilo, S.A.; Kharitonov, Y.; Shevchuk, V.A.; Ivshin, I.V. Calculation and Construction of Load Diagrams and Static Characteristics of Multi-Motor Electric Drive System Using Methods of Equivalent Forces and Reduced Moments. E3S Web Conf. 2020, 220, 01033. [Google Scholar] [CrossRef]
- Saheba, R.; Rotea, M.; Wasynczuk, O.; Pekarek, S.; Jordan, B. Virtual Thermal Sensing for Electric Machines. IEEE Control Syst. Mag. 2010, 30, 42–56. [Google Scholar]
- Stephen Ejiofor, O.; Justin, U.; Damian Benneth, N.; Uche, O. Development and thermal modeling of an induction machine. Int. J. Eng. Technol. 2019, 8, 500–508. [Google Scholar] [CrossRef]
- Beguenane, R.; Benbouzid, M.E.H. Induction motors thermal monitoring by means of rotor resistance identification. IEEE Trans. Energy Convers. 1999, 14, 566–570. [Google Scholar] [CrossRef]
- Wallscheid, O. Thermal Monitoring of Electric Motors: State-of-the-Art Review and Future Challenges. IEEE Open J. Ind. Appl. 2021, 2, 204–223. [Google Scholar] [CrossRef]
- Ma, T.; Komatsu, T.; Wang, B.; Wang, Y.; Lin, C. Observer Designs for Simultaneous Temperature and Loss Estimation for Electric Motors: A Comparative Study. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 1234–1241. [Google Scholar] [CrossRef]
- Nestler, H.; Sattler, P.K. On-line-estimation of temperatures in electrical machines by an observer. Electr. Mach. Power Syst. 1993, 21, 39–50. [Google Scholar] [CrossRef]
- Bagheripoor, M.; Bisadi, H. An investigation on the roll force and torque fluctuations during hot strip rolling process. Prod. Manuf. Res. 2014, 2, 128–141. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, D.; Zhang, X.; Huang, W.; Zheng, G. Optimization of Rolling Schedule for Single-Stand Reversible Cold Rolling Mill Based on Multiobjective Artificial Fish Swarm Algorithm. Wirel. Commun. Mob. Comput. 2022, 2022, 9167017. [Google Scholar] [CrossRef]
- Jia, C.; Shan, X.; Niu, Z. High Precision Prediction of Rolling Force Based on Fuzzy and Nerve Method for Cold Tandem Mill. J. Iron Steel Res. Int. 2008, 15, 23–27. [Google Scholar] [CrossRef]
- Zhou, F.-Q.; Cao, J.; Zhang, J.; Yin, X.; Jia, S.-H.; Zeng, W. Prediction model of rolling force for tandem cold rolling mill based on neural networks and mathematical models. J. Cent. South Univ. (Sci. Technol.) 2006, 37, 1155–1160. [Google Scholar]
- Lian, W.; Du, F. Reliability Prediction of Near-Isothermal Rolling of TiAl Alloy Based on Five Neural Network Models. Materials 2023, 16, 6709. [Google Scholar] [CrossRef] [PubMed]
- Specht, A.; Bocker, J. Observer for the rotor temperature of IPMSM. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010. [Google Scholar] [CrossRef]
- Specht, A.; Wallscheid, O.; Bocker, J. Determination of rotor temperature for an interior permanent magnet synchronous machine using a precise flux observer. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; pp. 1501–1507. [Google Scholar] [CrossRef]
- Milanfar, P.; Lang, J.H. Monitoring the thermal condition of permanent-magnet synchronous motors. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1421–1429. [Google Scholar] [CrossRef]
- Gundabattini, E.; Mystkowski, A.; Idzkowski, A.; Singh R, R.; Solomon, D.G. Thermal Mapping of a High-Speed Electric Motor Used for Traction Applications and Analysis of Various Cooling Methods—A Review. Energies 2021, 14, 1472. [Google Scholar] [CrossRef]
- Meng, T.; Zhang, P. A Review of Thermal Monitoring Techniques for Radial Permanent Magnet Machines. Machines 2022, 10, 18. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiao, M.; Lu, K.; Wu, Z.; Tao, B. A Simplified Thermal Model and Online Temperature Estimation Method of Permanent Magnet Synchronous Motors. Appl. Sci. 2019, 9, 3158. [Google Scholar] [CrossRef]
- Sonnaillon, M.O.; Bisheimer, G.; De Angelo, C.; García, G.O. Online Sensorless Induction Motor Temperature Monitoring. IEEE Trans. Energy Convers. 2010, 25, 273–280. [Google Scholar] [CrossRef]
- Foti, S.; Testa, A.; De Caro, S.; Scelba, G.; Scarcella, G. Sensorless Rotor and Stator Temperature Estimation in Induction Motor Drives. In Proceedings of the 2020 ELEKTRO, Taormina, Italy, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Czerwinski, D.; Gęca, J.; Kolano, K. Machine Learning for Sensorless Temperature Estimation of a BLDC Motor. Sensors 2021, 21, 4655. [Google Scholar] [CrossRef]
- Gao, Z.; Habetler, T.G.; Harley, R.G.; Colby, R.S. A Sensorless Rotor Temperature Estimator for Induction Machines Based on Current Harmonic Spectral Estimation Scheme. In Proceedings of the 2006 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 431–437. [Google Scholar] [CrossRef]
- Sarapulov, F.N.; Goman, V.; Trekin, G.E. Temperature calculation for linear induction motor in transport application with multiphysics approach. IOP Conf. Ser. Mater. Sci. Eng. 2020, 966, 012105. [Google Scholar] [CrossRef]
- Zyuzev, A.M.; Metelkov, V.P. Allowance for the Influence of Temperature Fluctuations on the Induction Motor Stator Winding Thermal Resource. Russ. Internet J. Electr. Eng. 2015, 2, 62–71. [Google Scholar]
- Anders, D.; Münker, T.; Artel, J.; Weinberg, K. A dimensional analysis of front-end bending in plate rolling applications. J. Mater. Process. Technol. 2012, 212, 1387–1398. [Google Scholar] [CrossRef]
- Varshavsky, E.A.; Khrapov, M.A.; Basurov, V.M. System of Automated Control of the Workpiece’s Front End Bending in the Roughing Stand with Individual Roll Drive. In Proceedings of the XI Congress of Millers, Magnitogorsk, Russia, 9–11 October 2017; pp. 57–62. [Google Scholar]
- Kiefer, T.; Kugi, A. An analytical approach for modelling asymmetrical hot rolling of heavy plate. Math. Comput. Model. Dyn. Syst. 2008, 14, 249–267. [Google Scholar] [CrossRef]
- Chikishev, D.N.; Pozhidaeva, E.B. Analysis of the causes of vertical bending of the strip front end at hot rolling on the basis of mathematical modeling. Izvestia VUZov. Chernaya Metall. = Izv. Ferr. Metall. 2016, 59, 204–208. [Google Scholar] [CrossRef][Green Version]
- Gasiyarov, V.R.; Radionov, A.A.; Loginov, B.M.; Zinchenko, M.A.; Gasiyarova, O.A.; Karandaev, A.S.; Khramshin, V.R. Method for Defining Parameters of Electromechanical System Model as Part of Digital Twin of Rolling Mill. J. Manuf. Mater. Process. 2023, 7, 183. [Google Scholar] [CrossRef]
- Klyuchev, V.I. Electric Drive Theory: Textbook for Universities; Energoatomizdat: Moscow, Russia, 2001; p. 760. [Google Scholar]
- Shreiner, R.T. Electromechanical and Thermal Modes of Asynchronous Motors in Frequency Control Systems: Textbook; Academy of Vocational Education: Ekaterinburg, Russia, 2008; p. 360. [Google Scholar]
- Shishko, V.B.; Trusov, V.A.; Chichenev, N.A. Fundamentals of Technology of Rolling on Reversing Mills: Textbook; MISIS: Moscow, Russia, 2007; p. 92. [Google Scholar]
- Tomashevsky, N.I.; Tomashevsky, D.N.; Emelyanov, A.A.; Ippolitov, V.V. Development of Electric Drives of Production Mechanisms. Guidance Manual; RSVPU: Ekaterinburg, Russia, 2006; p. 229. [Google Scholar]
- ibaPDA Scalable Basic Software for Measured Data Collection. Available online: https://www.iba-ag.com/ru/ibapda (accessed on 7 October 2023). (In Russian).
- Kuvshinov, A.A.; Grekov, E.L. Electric Drive Theory: Lecture Notes: In 2 Part; IPK GOU OSU: Orenburg, Russia, 2009; p. 197. [Google Scholar]
- Temperature Rise and Life of an AC Motor. Available online: https://www.orientalmotor.com/ac-motors-gear-motors/technology/temperature-rise-and-life-of-an-ac-motor.html (accessed on 22 May 2024).
- Zyuzev, A.M.; Metelkov, V.P. Thermodynamic Models for Thermal Testing of Asynchronous Motors. Electr. Eng. 2012, 9, 48–52. [Google Scholar]
- Chilikin, M.G.; Sandler, A.S. General Course of Electric Drive; Energoizdat: Moscow, Russia, 1981; p. 576. [Google Scholar]
- Sivyakova, G.; Orlov, S.Y.; Wójcik, W.; Komada, P. Development of simulation model of electric drive of decoiler. Prz. Elektrotech. 2014, 90, 173–176. [Google Scholar] [CrossRef]
- Shreiner, R.T.; Polyakov, V.N.; Medvedev, A.V. Electromechanical Resource of an RMP-Controlled Synchronous Drive in Intermittent Operating Modes. ESC 2014, 3, 9–13. [Google Scholar]
- Gasiyarov, V.R.; Bovshik, P.A.; Loginov, B.M.; Karandaev, A.S.; Khramshin, V.R.; Radionov, A.A. Substantiating and Implementing Concept of Digital Twins for Virtual Commissioning of Industrial Mechatronic Complexes Exemplified by Rolling Mill Coilers. Machines 2023, 11, 276. [Google Scholar] [CrossRef]
- Gasiyarov, V.R.; Radionov, A.A.; Loginov, B.M.; Karandaev, A.S.; Gasiyarova, O.A.; Khramshin, V.R. Development and Practical Implementation of Digital Observer for Elastic Torque of Rolling Mill Electromechanical System. J. Manuf. Mater. Process. 2023, 7, 41. [Google Scholar] [CrossRef]
- Metelkov, V.P. About Calculation of Parameters of Two-Mass Thermodynamic Model of Induction Motor. Bulletin of the South Ural State University. Ser. Power Eng. 2016, 16, 58–65. [Google Scholar]
- Anuchin, A.S.; Fedorova, K.G. A two-mass thermal model of the induction motor. Russ. Electr. Eng. 2014, 85, 83–86. [Google Scholar] [CrossRef]
- Anuchin, A.S.; Fedorova, K.G. Using a Two-Mass Thermal Model to Choose an Asynchronous Motor. Vestn. ISPEU 2013, 3, 1–3. [Google Scholar]
- Chenchevoi, V.; Romashykhin, I.; Romashykhina, Z.; Al-Mashakbeh, A.S. Analysis of the special features of the thermal process in an induction generator at high saturation of the magnetic system. Electr. Eng. Electromech. 2017, 3, 16–18. [Google Scholar] [CrossRef][Green Version]
- Specification Guideelectric Motors. Available online: https://static.weg.net/medias/downloadcenter/ha0/h5f/WEG-motors-specification-of-electric-motors-50039409-brochure-english-web.pdf (accessed on 22 May 2024).
- Shabanov, V.A.; Khakimov, E.F.; Kalimgulov, A.R.; Sergeenkova, E.V. Studying the Fependence of the Motor and Frequency Converter Efficiency on the Load Factor and Rotation Speed. Electr. Data Process. Facil. Syst. 2019, 4, 83–90. [Google Scholar]
- Karandayev, A.S.; Loginov, B.M.; Zinchenko, M.A.; Mazitov, D.M.; Podolko, A.S. Speed Coordination System for Electric Drives of a Plate Mill Stand: Theory and Development. In Proceedings of the 2021 International Ural Conference on Electrical Power Engineering (UralCon), Magnitogorsk, Russia, 24–26 September 2021; pp. 566–571. [Google Scholar] [CrossRef]
- Gasiyarov, V.R.; Kornilov, G.P.; Loginov, B.M.; Zinchenko, M.A.; Khramshin, R.R.; Odintsov, K.E. Adaptive Load Division Controller for Electric Drives of Roll Stand. In Proceedings of the 2023 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 15–19 May 2023; pp. 1135–1140. [Google Scholar] [CrossRef]
- Magura, D.; Fedák, V.; Kyslan, K. Modeling and Analysis of Multi-motor Drive Properties in a Web Processing Continuous Line. Procedia Eng. 2014, 96, 281–288. [Google Scholar] [CrossRef][Green Version]
- Radionov, A.A.; Petukhova, O.I.; Erdakov, I.N.; Karandaev, A.S.; Loginov, B.M.; Khramshin, V.R. Developing an Automated System to Control the Rolled Product Section for aWire Rod Mill with Multi-Roll Passes. J. Manuf. Mater. Process. 2022, 6, 88. [Google Scholar] [CrossRef]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital Twin: Enabling Technologies, Challenges and Open Research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in manufacturing: A categorical literature review and classification. IFAC-PapersOnLine 2018, 11, 1016–1022. [Google Scholar] [CrossRef]
- Voronin, S.S.; Loginov, B.M.; Gasiyarova, O.A.; Evdokimov, S.A.; Karandaev, A.S.; Khramshin, V.R. Telemetry System to Monitor Elastic Torque on Rolling Stand Spindles. J. Manuf. Mater. Process. 2024, 8, 85. [Google Scholar] [CrossRef]






| Parameter | Averaging from 0 to 110 s | Averaging from 0 to 220 s |
|---|---|---|
| , kN·m | 448.7 | 317.6 |
| , kN·m | 965.6 | 683.0 |
| , kN·m | 1414.0 | 1000.6 |
| Parameter | Averaging from 0 to 220 s | Averaging from 0 to 110 s |
|---|---|---|
| UMD Motor Power , kW | 183.4 | 359.0 |
| LMD Rated Motor Power , kW | 346.9 | 684.9 |
| Sum , kW | 530.3 | 1044.0 |
| Parameter | Designation | Value | Unit of Measure |
|---|---|---|---|
| Stator iron mass | 70,000 | kg | |
| Stator winding mass | 5000 | kg | |
| Stator winding heat capacity | 385 | J/(kg·K) | |
| Stator iron heat capacity | 447 | J/(kg·K) | |
| Stator winding-to-iron contact area | 3 | ||
| Stator winding to iron heat transfer coefficient | 200 | W/(m·K) | |
| Insulation thickness between the winding and the stator iron | D | 0.0044 | m |
| Stator heat removal coefficient | 1500 | ||
| Electrical resistance of the stator winding | stator | 0.07 | Ohm |
| Temperature coefficient of winding resistance | 0.0043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voronin, S.S.; Radionov, A.A.; Karandaev, A.S.; Erdakov, I.N.; Loginov, B.M.; Khramshin, V.R. Justifying and Implementing Concept of Object-Oriented Observers of Thermal State of Rolling Mill Motors. Energies 2024, 17, 3878. https://doi.org/10.3390/en17163878
Voronin SS, Radionov AA, Karandaev AS, Erdakov IN, Loginov BM, Khramshin VR. Justifying and Implementing Concept of Object-Oriented Observers of Thermal State of Rolling Mill Motors. Energies. 2024; 17(16):3878. https://doi.org/10.3390/en17163878
Chicago/Turabian StyleVoronin, Stanislav S., Andrey A. Radionov, Alexander S. Karandaev, Ivan N. Erdakov, Boris M. Loginov, and Vadim R. Khramshin. 2024. "Justifying and Implementing Concept of Object-Oriented Observers of Thermal State of Rolling Mill Motors" Energies 17, no. 16: 3878. https://doi.org/10.3390/en17163878
APA StyleVoronin, S. S., Radionov, A. A., Karandaev, A. S., Erdakov, I. N., Loginov, B. M., & Khramshin, V. R. (2024). Justifying and Implementing Concept of Object-Oriented Observers of Thermal State of Rolling Mill Motors. Energies, 17(16), 3878. https://doi.org/10.3390/en17163878








