Review of Data-Driven Models in Wind Energy: Demonstration of Blade Twist Optimization Based on Aerodynamic Loads
Abstract
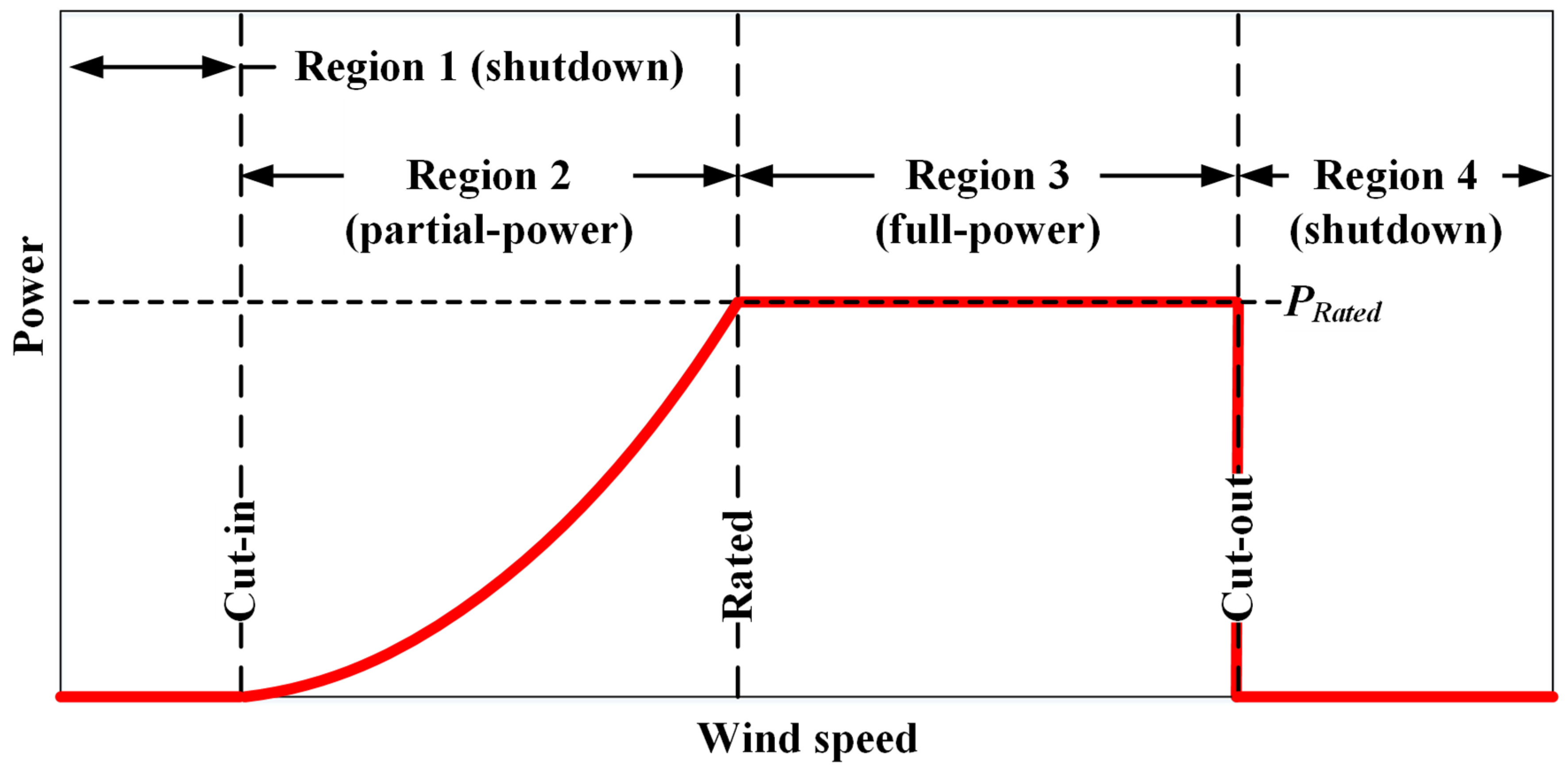
:1. Introduction
2. Data-Driven Methods in Wind Energy
2.1. Wake Modeling
2.2. Performance Monitoring
2.3. Condition Monitoring
2.4. Other Data-Driven Efforts
2.5. Future of Data-Driven Research
2.6. Implications to Adaptive Aerostructures
3. Methodology
4. Results
4.1. Optimization of Thrust Load
4.2. Future Work
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Global Wind Energy Council. Global Wind Energy Report 2023; Global Wind Energy Council: Brussels, Belgium, 2023. [Google Scholar]
- Ashuri, T.; Zaaijer, M.B.; Martins, J.R.R.A.; van Bussel, G.J.W.; van Kuik, G.A.M. Multidisciplinary design optimization of offshore wind turbines for minimum levelized cost of energy. Renew. Energy 2014, 68, 893–905. [Google Scholar] [CrossRef]
- Ebenhoch, R.; Matha, D.; Marathe, S.; Muñoz, P.C.; Molins, C. Comparative Levelized Cost of Energy Analysis. Energy Procedia 2015, 80, 108–122. [Google Scholar] [CrossRef]
- Ziyaei, P.; Khorasanchi, M.; Sayyaadi, H.; Sadollah, A. Minimizing the levelized cost of energy in an offshore wind farm with non-homogeneous turbines through layout optimization. Ocean Eng. 2022, 249, 110859. [Google Scholar] [CrossRef]
- Bertagnolio, F.; Herr, M.; Madsen, K.D. A roadmap for required technological advancements to further reduce onshore wind turbine noise impact on the environment. WIREs Energy Environ. 2023, 12, e469. [Google Scholar] [CrossRef]
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S.U. A Review of Recent Advancements in Offshore Wind Turbine Technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Chang, C.C.W.; Ding, T.J.; Ping, T.J.; Chao, K.C.; Bhuiyan, M.A.S. Getting more from the wind: Recent advancements and challenges in generators development for wind turbines. Sustain. Energy Technol. Assess. 2022, 53, 102731. [Google Scholar] [CrossRef]
- Darwish, A.S.; Al-Dabbagh, R. Wind energy state of the art: Present and future technology advancements. Renew. Energy Environ. Sustain. 2020, 5, 7. [Google Scholar] [CrossRef]
- Hall, J.F.; Palejiya, D.; Shaltout, M.L.; Chen, D. An Integrated Control and Design Framework for Optimizing Energy Capture and Component Life for a Wind Turbine Variable Ratio Gearbox. J. Sol. Energy Eng. 2015, 137, 021022. [Google Scholar] [CrossRef]
- Rajendran, S.; Jena, D.; Diaz, M.; Rodríguez, J. Terminal Integral Synergetic Control for Wind Turbine at Region II Using a Two-Mass Model. Processes 2023, 11, 616. [Google Scholar] [CrossRef]
- Mirzaei, M.J.; Hamida, M.A.; Plestan, F. Super-twisting control of offshore wind turbine in region III with self-tuning adaptive gains. In Proceedings of the 2022 16th International Workshop on Variable Structure Systems (VSS), Rio de Janeiro, Brazil, 11–14 September 2022; pp. 172–177. [Google Scholar] [CrossRef]
- Nejadkhaki, H.K.; Hall, J.F. Control framework and integrative design method for an adaptive wind turbine blade. J. Dyn. Syst. Meas. Control 2020, 142, 101001. [Google Scholar] [CrossRef]
- Giammichele, L.; D’Alessandro, V.; Falone, M.; Ricci, R. Experimental assessment of a morphing trailing edge device for wind turbine blade performance improvement. J. Renew. Sustain. Energy 2024, 16, 013306. [Google Scholar] [CrossRef]
- Roetzer, J.; Battaglia, F.; Hall, J.F. A Modeling Framework to Analyze Active Adaptive Aerostructures. In Design in the Era of Industry 4.0; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A.; Visingardi, A.; Federico, L.; Barbarino, M.; Vitagliano, P.L. Aeroacoustic and Structural Achievements for a Morphing Blade Twist System Developed for the European Project “Shape Adaptive Blades for Rotorcraft Efficiency”. In Proceedings of the ASME 2022 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Dearborn, MI, USA, 12–14 September 2022. [Google Scholar] [CrossRef]
- Nejadkhaki, H.K.; Sohrabi, A.; Purandare, T.P.; Battaglia, F.; Hall, J.F. A variable twist blade for horizontal axis wind turbines: Modeling and analysis. Energy Convers. Manag. 2021, 248, 114771. [Google Scholar] [CrossRef]
- Liew, J.; Heck, K.S.; Howland, M.F. Unified Momentum Model for Rotor Aerodynamics Across Operating Regimes. arXiv 2023, arXiv:2401.09623. [Google Scholar] [CrossRef]
- Qizi, Q.U.R.; Kombos, C.; Champlin, E.; Kranc, S.C.; Das, M. Field data based validation of an aero-servo-elastic solver for high-fidelity LES of industrial wind turbines. Wind Energy Sci. 2024, 9, 25–48. [Google Scholar] [CrossRef]
- Batay, S.; Kamalov, B.; Zhangaskanov, D.; Zhao, Y.; Wei, D.; Zhou, T.; Su, X. Adjoint-Based High-Fidelity Concurrent Aerodynamic Design Optimization of Wind Turbine. Fluids 2023, 8, 85. [Google Scholar] [CrossRef]
- Larsén, X.G.; Staneva, J.; Rutgersson, A.; Lundquist, J. Editorial: Offshore wind energy: Modeling and measurements. Front. Energy Res. 2023, 11, 1146071. [Google Scholar] [CrossRef]
- Veers, P.; Bottasso, C.; Manuel, L.; Naughton, J.; Pao, L.; Paquette, J.; Robertson, A.; Robinson, M.; Ananthan, S.; Barlas, A.; et al. Grand Challenges in the Design, Manufacture, and Operation of Future Wind Turbine Systems. Wind Energy Sci. 2023, 8, 1071–1131. [Google Scholar] [CrossRef]
- De Lellis, M.; Reginatto, R.; Saraiva, R.; Trofino, A. The Betz limit applied to Airborne Wind Energy. Renew. Energy 2018, 127, 32–40. [Google Scholar] [CrossRef]
- Johnson, K.E.; Fingersh, L.J.; Balas, M.J.; Pao, L.Y. Methods for Increasing Region 2 Power Capture on a Variable-Speed Wind Turbine. J. Sol. Energy Eng. 2004, 126, 1092–1100. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Wind Turbine Control for Load Reduction. Wind Energy 2003, 6, 229–244. [Google Scholar] [CrossRef]
- Ravikumar, K.; Subbiah, R.; Ranganathan, N.; Bensingh, J.; Kader, A.; Nayak, S.K. A review on fatigue damages in the wind turbines: Challenges in determining and reducing fatigue failures in wind turbine blades. Wind Eng. 2020, 44, 434–451. [Google Scholar] [CrossRef]
- Pacheco, J.; Pimenta, F.; Pereira, S.; Cunha, Á.; Magalhães, F. Fatigue Assessment of Wind Turbine Towers: Review of Processing Strategies with Illustrative Case Study. Energies 2022, 15, 4782. [Google Scholar] [CrossRef]
- Dong, X.; Lian, J.; Wang, H.; Yu, T.; Zhao, Y. Structural vibration monitoring and operational modal analysis of offshore wind turbine structure. Ocean Eng. 2018, 150, 280–297. [Google Scholar] [CrossRef]
- Costa, Á.M.; Orosa, J.A.; Vergara, D.; Fernández-Arias, P. New Tendencies in Wind Energy Operation and Maintenance. Appl. Sci. 2021, 11, 1386. [Google Scholar] [CrossRef]
- Cross, P.; Ma, X. Nonlinear system identification for model-based condition monitoring of wind turbines. Renew. Energy 2014, 71, 166–175. [Google Scholar] [CrossRef]
- van der Veen, G.; van Wingerden, J.; Fleming, P.; Scholbrock, A.; Verhaegen, M. Global data-driven modeling of wind turbines in the presence of turbulence. Control Eng. Pract. 2013, 21, 441–454. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, X.; Cheng, X.; Jiang, G.; Masisi, L.; Huang, W. A Physics-Based and Data-Driven Feature Extraction Model for Blades Icing Detection of Wind Turbines. IEEE Sens. J. 2023, 23, 3944–3954. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Data-driven modeling for unsteady aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2021, 125, 100725. [Google Scholar] [CrossRef]
- Pandit, R.; Astolfi, D.; Hong, J.; Infield, D.; Santos, M. SCADA data for wind turbine data-driven condition/performance monitoring: A review on state-of-art, challenges and future trends. Wind. Eng. 2022, 47, 422–441. [Google Scholar] [CrossRef]
- Schmid, P.J.; Sesterhenn, J. Dynamic mode decomposition of numerical and experimental data. In Bulletin of the American Physical Society, Proceedings of the Sixty-First Annual Meeting of the APS Division of Fluid Dynamics, San Antonio, TX, USA, 23–25 November 2008; American Physical Society: College Park, MD, USA, 2008. [Google Scholar]
- Schmid, P.J.; Li, L.; Juniper, M.P.; Pust, O. Applications of the dynamic mode decomposition. Theor. Comput. Fluid Dyn. 2011, 25, 249–259. [Google Scholar] [CrossRef]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016. [Google Scholar]
- Hardesty, L. Explained: Neural Networks; MIT News Office: Cambridge, MA, USA, 2017. [Google Scholar]
- Balas, V.E.; Kumar, R.; Srivastava, R. Recent Trends and Advances in Artificial Intelligence and Internet of Things; Springer Nature: Berlin, Germany, 2019. [Google Scholar]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated feedback recurrent neural networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2067–2075. [Google Scholar]
- Zhao, R.; Wang, D.Z.; Yan, R.Q.; Mao, K.Z.; Shen, F.; Wang, J.J. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Trans. Ind. Electron. 2018, 65, 1539–1548. [Google Scholar] [CrossRef]
- Dym, H.; McKean, H.P. Gaussian Processes, Function Theory, and the Inverse Spectral Problem; Courier Corporation: Chelmsford, MA, USA, 2008. [Google Scholar]
- Härdle, W.K.; Simar, L. Applied Multivariate Statistical Analysis; Springer Nature: Berlin, Germany, 2019. [Google Scholar]
- Tinsley, H.E.; Brown, S.D. (Eds.) Handbook of Applied Multivariate Statistics and Mathematical Modeling; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Ali, N.; Cal, R.B. Data-driven modeling of the wake behind a wind turbine array. J. Renew. Sustain. Energy 2020, 12, 033304. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, C.; Wei, S.; Deng, Z.; Jiao, Z. Sparsity Promoting Dynamic Mode Decomposition for Data-Driven Modeling of Wind Turbine Wake. J. Phys. Conf. Ser. 2023, 2474, 012028. [Google Scholar] [CrossRef]
- Nai-Zhi, G.; Ming-Ming, Z.; Bo, L. A data-driven analytical model for wind turbine wakes using machine learning method. Energy Convers. Manag. 2022, 252, 115130. [Google Scholar] [CrossRef]
- Renganathan, S.A.; Maulik, R.; Letizia, S.; Iungo, G.V. Data-driven wind turbine wake modeling via probabilistic machine learning. Neural Comput. Appl. 2022, 34, 6171–6186. [Google Scholar] [CrossRef]
- Steiner, J.; Dwight, R.; Viré, A. Data-driven turbulence modeling for wind turbine wakes under neutral conditions. J. Phys. Conf. Ser. 2020, 1618, 062051. [Google Scholar] [CrossRef]
- Geibel, M.; Bangga, G. Data Reduction and Reconstruction of Wind Turbine Wake Employing Data Driven Approaches. Energies 2022, 15, 3773. [Google Scholar] [CrossRef]
- Long, H.; Li, P.; Gu, W. A data-driven evolutionary algorithm for wind farm layout optimization. Energy 2020, 208, 118310. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, W.; Jiang, Z.; Pan, L. Data-driven multi-objective predictive control of offshore wind farm based on evolutionary optimization. Renew. Energy 2020, 160, 974–986. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D.; Foley, A.M. Lidar assisted wake redirection in wind farms: A data driven approach. Renew. Energy 2020, 152, 484–493. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X. Wind farm wake modeling based on deep convolutional conditional generative adversarial network. Energy 2022, 238, 121747. [Google Scholar] [CrossRef]
- Guo, N.-Z.; Shi, K.-Z.; Li, B.; Qi, L.-W.; Wu, H.-H.; Zhang, Z.-L.; Xu, J.-Z. A physics-inspired neural network model for short-term wind power prediction considering wake effects. Energy 2022, 261, 125208. [Google Scholar] [CrossRef]
- Gao, L.; Hong, J. Data-driven yaw misalignment correction for utility-scale wind turbines. J. Renew. Sustain. Energy 2021, 13, 063302. [Google Scholar] [CrossRef]
- Ti, Z.; Deng, X.W.; Yang, H. Wake modeling of wind turbines using machine learning. Appl. Energy 2020, 257, 114025. [Google Scholar] [CrossRef]
- Zehtabiyan-Rezaie, N.; Iosifidis, A.; Abkar, M. Data-driven fluid mechanics of wind farms: A review. J. Renew. Sustain. Energy 2022, 14, 032703. [Google Scholar] [CrossRef]
- Astolfi, D.; De Caro, F.; Vaccaro, A. Characterizing the Wake Effects on Wind Power Generator Operation by Data-Driven Techniques. Energies 2023, 16, 5818. [Google Scholar] [CrossRef]
- Wang, L.; Xie, J.; Luo, W.; Wang, Z.; Zhang, B.; Chen, M.; Tan, A.C. Effectiveness of data-driven wind turbine wake models developed by machine/deep learning with spatial-segmentation technique. Sustain. Energy Technol. Assess. 2022, 53, 102499. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X. A novel dynamic wind farm wake model based on deep learning. Appl. Energy 2020, 277, 115552. [Google Scholar] [CrossRef]
- Kusiak, A.; Zhang, Z. Control of wind turbine power and vibration with a data-driven approach. Renew. Energy 2012, 43, 73–82. [Google Scholar] [CrossRef]
- Pandit, R.; Infield, D.; Santos, M.; Peñas, M. Accounting for Environmental Conditions in Data-Driven Wind Turbine Power Models. IEEE Trans. Sustain. Energy 2023, 14, 168–177. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Zou, R.; Zhang, F.; Li, Y.; Hu, Q. A novel data-driven deep learning approach for wind turbine power curve modeling. Energy 2023, 270, 126908. [Google Scholar] [CrossRef]
- Dinkla, R.; Oomen, T.; van Wingerden, J.-W.; Mulders, S.P. Data-Driven LIDAR Feedforward Predictive Wind Turbine Control. In Proceedings of the 2023 IEEE Conference on Control Technology and Applications (CCTA), Bridgetown, Barbados, 16–18 August 2023; pp. 559–565. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Z.; Hao, L.; Xing, Z.; Chen, M.; Zhang, P. Data-driven robust value iteration control with application to wind turbine pitch control. Optim. Control Appl. Methods 2023, 44, 637–646. [Google Scholar] [CrossRef]
- Xie, J.; Dong, H.; Zhao, X. Data-driven torque and pitch control of wind turbines via reinforcement learning. Renew. Energy 2023, 215, 118893. [Google Scholar] [CrossRef]
- Manzar, M.N.; Khaki-Sedigh, A. Online data-driven control of variable speed wind turbines using the simultaneous perturbation stochastic approximation approach. Optim. Control Appl. Methods 2023, 44, 2082–2092. [Google Scholar] [CrossRef]
- Yang, J.; Zheng, S.; Song, D.; Su, M.; Yang, X.; Joo, Y.H. Data-driven modeling for fatigue loads of large-scale wind turbines under active power regulation. Wind Energy 2021, 24, 558–572. [Google Scholar] [CrossRef]
- Mulders, S.P.; Liu, Y.; Spagnolo, F.; Christensen, P.B.; van Wingerden, J.-W. An iterative data-driven learning algorithm for calibration of the internal model in advanced wind turbine controllers. IFAC-PapersOnLine 2023, 56, 8406–8413. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Abbasnejad, E.; Mirjalili, S.; Groppi, D.; Heydari, A.; Tjernberg, L.B.; Garcia, D.A.; Alexander, B.; Shi, Q.; et al. Wind turbine power output prediction using a new hybrid neuro-evolutionary method. Energy 2021, 229, 120617. [Google Scholar] [CrossRef]
- Karamichailidou, D.; Kaloutsa, V.; Alexandridis, A. Wind turbine power curve modeling using radial basis function neural networks and tabu search. Renew. Energy 2021, 163, 2137–2152. [Google Scholar] [CrossRef]
- Sun, H.; Qiu, C.; Lu, L.; Gao, X.; Chen, J.; Yang, H. Wind turbine power modelling and optimization using artificial neural network with wind field experimental data. Appl. Energy 2020, 280, 115880. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, X.; Collu, M. Wind power prediction based on high-frequency SCADA data along with isolation forest and deep learning neural networks. Int. J. Electr. Power Energy Syst. 2020, 118, 105835. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, X. Wind power forecasting of an offshore wind turbine based on high-frequency SCADA data and deep learning neural network. Energy 2020, 201, 117693. [Google Scholar] [CrossRef]
- Fahim, M.; Sharma, V.; Cao, T.-V.; Canberk, B.; Duong, T.Q. Machine Learning-Based Digital Twin for Predictive Modeling in Wind Turbines. IEEE Access 2022, 10, 14184–14194. [Google Scholar] [CrossRef]
- Trizoglou, P.; Liu, X.; Lin, Z. Fault detection by an ensemble framework of Extreme Gradient Boosting (XGBoost) in the operation of offshore wind turbines. Renew. Energy 2021, 179, 945–962. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Y.; Zheng, Y.; Gao, R.X.; Zhang, F. An integrated fault diagnosis and prognosis approach for predictive maintenance of wind turbine bearing with limited samples. Renew. Energy 2020, 145, 642–650. [Google Scholar] [CrossRef]
- Tuerxun, W.; Chang, X.; Hongyu, G.; Zhijie, J.; Huajian, Z. Fault Diagnosis of Wind Turbines Based on a Support Vector Machine Optimized by the Sparrow Search Algorithm. IEEE Access 2021, 9, 69307–69315. [Google Scholar] [CrossRef]
- He, Q.; Pang, Y.; Jiang, G.; Xie, P. A Spatio-Temporal Multiscale Neural Network Approach for Wind Turbine Fault Diagnosis with Imbalanced SCADA Data. IEEE Trans. Ind. Inform. 2021, 17, 6875–6884. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, Y.; Feng, Y.; Li, Y.; Kusiak, A. Diagnosis of wind turbine faults with transfer learning algorithms. Renew. Energy 2021, 163, 2053–2067. [Google Scholar] [CrossRef]
- Huang, N.; Chen, Q.; Cai, G.; Xu, D.; Zhang, L.; Zhao, W. Fault Diagnosis of Bearing in Wind Turbine Gearbox under Actual Operating Conditions Driven by Limited Data with Noise Labels. IEEE Trans. Instrum. Meas. 2021, 70, 3502510. [Google Scholar] [CrossRef]
- Hsu, J.-Y.; Wang, Y.-F.; Lin, K.-C.; Chen, M.-Y.; Hsu, J.H.-Y. Wind Turbine Fault Diagnosis and Predictive Maintenance through Statistical Process Control and Machine Learning. IEEE Access 2020, 8, 23427–23439. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, P.; Yang, X.; Hu, A.; Su, H. Fault detection of wind turbine based on SCADA data analysis using CNN and LSTM with attention mechanism. Measurement 2021, 175, 109094. [Google Scholar] [CrossRef]
- Xiang, L.; Yang, X.; Hu, A.; Su, H.; Wang, P. Condition monitoring and anomaly detection of wind turbine based on cascaded and bidirectional deep learning networks. Appl. Energy 2022, 305, 117925. [Google Scholar] [CrossRef]
- Cho, S.; Choi, M.; Gao, Z.; Moan, T. Fault detection and diagnosis of a blade pitch system in a floating wind turbine based on Kalman filters and artificial neural networks. Renew. Energy 2021, 169, 1–13. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, Z.; Sun, R.; Chen, X. Data-driven multiscale sparse representation for bearing fault diagnosis in wind turbine. Wind Energy 2019, 22, 587–604. [Google Scholar] [CrossRef]
- Li, M.; Yu, D.; Chen, Z.; Xiahou, K.; Ji, T.; Wu, Q.H. A Data-Driven Residual-Based Method for Fault Diagnosis and Isolation in Wind Turbines. IEEE Trans. Sustain. Energy 2019, 10, 895–904. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, P.; Zhao, Z.; Lai, C.S.; Lai, L.L.; Wang, X. Fault Diagnosis Approach of Main Drive Chain in Wind Turbine Based on Data Fusion. Appl. Sci. 2021, 11, 5804. [Google Scholar] [CrossRef]
- Bilal, B.; Adjallah, K.H.; Sava, A. Data-Driven Fault Detection and Identification in Wind Turbines Through Performance Assessment. In Proceedings of the 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 18–21 September 2019; pp. 123–129. [Google Scholar] [CrossRef]
- Man, J.; Zhang, Z.; Zhou, Q. Data-driven predictive analytics of unexpected wind turbine shut-downs. IET Renew. Power Gener. 2018, 12, 1833–1842. [Google Scholar] [CrossRef]
- Solimine, J.; Inalpolat, M. An unsupervised data-driven approach for wind turbine blade damage detection under passive acoustics-based excitation. Wind Eng. 2022, 46, 1311–1330. [Google Scholar] [CrossRef]
- Yu, D.; Chen, Z.; Xiahou, K.; Li, M.; Ji, T.; Wu, Q. A radically data-driven method for fault detection and diagnosis in wind turbines. Int. J. Electr. Power Energy Syst. 2018, 99, 577–584. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, Z.; Jiang, Y.; Zhu, J. Wind turbine health state monitoring based on a Bayesian data-driven approach. Renew. Energy 2018, 125, 172–181. [Google Scholar] [CrossRef]
- Maldonado-Correa, J.; Martín-Martínez, S.; Artigao, E.; Gómez-Lázaro, E. Using SCADA Data for Wind Turbine Condition Monitoring: A Systematic Literature Review. Energies 2020, 13, 3132. [Google Scholar] [CrossRef]
- Bakdi, A.; Kouadri, A.; Mekhilef, S. A data-driven algorithm for online detection of component and system faults in modern wind turbines at different operating zones. Renew. Sustain. Energy Rev. 2019, 103, 546–555. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Chu, X.; Liu, Q.; Xue, D. Anomaly detection and critical SCADA parameters identification for wind turbines based on LSTM-AE neural network. Renew. Energy 2021, 172, 829–840. [Google Scholar] [CrossRef]
- Kouadri, A.; Hajji, M.; Harkat, M.-F.; Abodayeh, K.; Mansouri, M.; Nounou, H.; Nounou, M. Hidden Markov model based principal component analysis for intelligent fault diagnosis of wind energy converter systems. Renew. Energy 2020, 150, 598–606. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault diagnosis of rolling bearing of wind turbines based on the Variational Mode Decomposition and Deep Convolutional Neural Networks. Appl. Soft Comput. 2020, 95, 106515. [Google Scholar] [CrossRef]
- Wu, Y.; Yuan, H.; Wen, T. A Combined Data-Driven and Simulation Approach for Wind Turbine Blade Icing Prediction in Cold Regions. In Proceedings of the 2023 13th International Conference on Power and Energy Systems (ICPES), Chengdu, China, 8–10 December 2023; pp. 496–502. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, F.; Liu, Y.; Liu, X.; Huang, L. Wind turbine blade icing detection: A federated learning approach. Energy 2022, 254, 124441. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, F.; Zhao, M.; Li, G.; Zhang, H.; Chen, S. Temporal Attention Convolutional Neural Network for Estimation of Icing Probability on Wind Turbine Blades. IEEE Trans. Ind. Electron. 2022, 69, 6371–6380. [Google Scholar] [CrossRef]
- Xiao, J.; Li, C.; Liu, B.; Huang, J.; Xie, L. Prediction of wind turbine blade icing fault based on selective deep ensemble model. Knowl.-Based Syst. 2022, 242, 108290. [Google Scholar] [CrossRef]
- Yi, H.; Jiang, Q.; Yan, X.; Wang, B. Imbalanced Classification Based on Minority Clustering Synthetic Minority Oversampling Technique with Wind Turbine Fault Detection Application. IEEE Trans. Ind. Inform. 2021, 17, 5867–5875. [Google Scholar] [CrossRef]
- Yan, J.; Nuertayi, A.; Yan, Y.; Liu, S.; Liu, Y. Hybrid physical and data driven modeling for dynamic operation characteristic simulation of wind turbine. Renew. Energy 2023, 215, 118958. [Google Scholar] [CrossRef]
- Dong, X.; Yang, Q.; Ma, W. Data-Driven Dynamic Modeling Methods for Offshore Wind Turbine Generators. In Frontier Academic Forum of Electrical Engineering; Springer Nature: Singapore, 2023; Volume 1054, pp. 947–956. [Google Scholar] [CrossRef]
- Tan, M.; Zhang, Z. Wind Turbine Modeling with Data-Driven Methods and Radially Uniform Designs. IEEE Trans. Ind. Inform. 2016, 12, 1261–1269. [Google Scholar] [CrossRef]
- Reiman, A.P.; Ramachandran, T.; Orrell, A.C. Data-Driven Generic Turbines for Distributed Wind Modeling, Optimization, and Economic Studies. In Proceedings of the 2022 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), New Orleans, LA, USA, 24–28 April 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Mou, F.; Nejadkhaki, H.K.; Estes, A.; Hall, J. A Weighted Least Squares Approach for the Design of Adaptive Aerodynamic Structures Subjected to an Out-Of-Plane Transformation. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Volume 2B: 44th Design Automation Conference, Quebec City, QC, Canada, 26–29 August 2018; ASME: New York, NY, USA, 2018. V02BT03A043. [Google Scholar] [CrossRef]
- Nejadkhaki, H.K.; Hall, J.F. Modeling and Design Method for an Adaptive Wind Turbine Blade with Out-of-Plane Twist. J. Sol. Energy Eng. 2018, 140, 051010. [Google Scholar] [CrossRef]
- Nejadkhaki, H.K.; Hall, J.F. A Design Methodology Region 2 Efficiency. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 2A: 43rd Design Automation Conference, Cleveland, OH, USA, 6–9 August 2017; ASME: New York, NY, USA, 2017. V02AT03A025. [Google Scholar] [CrossRef]
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine [Sound/Visual Production (Digital)]; Danish Wind Power Research 2013: Fredericia, Denmark, 2013. [Google Scholar]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. Definition of the IEA 15-Megawatt Offshore Reference Wind Turbine; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2020.

| Training Data | ||||
| Decision Tree | SVM | Neural Network | GPR | |
| Pitch (°) | 1.4327 | 0.12141 | 0.54099 | 0.019475 |
| Thrust Load (N) | 18,881 | 17,635 | 3105.6 | 483.04 |
| Test Data | ||||
| Decision Tree | SVM | Neural Network | GPR | |
| Pitch (°) | 1.0738 | 0.12149 | 0.67701 | 0.0092139 |
| Thrust Load (N) | 19,982 | 28,100 | 4186.3 | 473.74 |
| Training Data | ||||
| Decision Tree | SVM | Neural Network | GPR | |
| Pitch (°) | 1.4142 | 0.15206 | 0.016374 | 0.015752 |
| Thrust Load (N) | 30,819 | 3012.5 | 6193.7 | 905.24 |
| Test Data | ||||
| Decision Tree | SVM | Neural Network | GPR | |
| Pitch (°) | 1.2089 | 0.10908 | 0.016508 | 0.013788 |
| Thrust Load (N) | 27,067 | 2835 | 5860.7 | 649.35 |
| Wind Speed (m/s) | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|
| Thrust Force (kN) | Original | 1007 | 903.0 | 828.8 | 770.5 | 722.7 | 683.3 |
| Optimized | 996.0 | 893.1 | 815.5 | 753.7 | 703.0 | 661.8 | |
| Improvement (%) | 1.09 | 1.10 | 1.60 | 2.18 | 2.73 | 3.15 | |
| Wind Speed (m/s) | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|
| Thrust Force (kN) | Original | 1489 | 1349 | 1243 | 1156 | 1085 | 1024 |
| Optimized | 1480 | 1335 | 1225 | 1136 | 1061 | 996.8 | |
| Improvement (%) | 0.60 | 1.04 | 1.45 | 1.73 | 2.21 | 2.66 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roetzer, J.; Li, X.; Hall, J. Review of Data-Driven Models in Wind Energy: Demonstration of Blade Twist Optimization Based on Aerodynamic Loads. Energies 2024, 17, 3897. https://doi.org/10.3390/en17163897
Roetzer J, Li X, Hall J. Review of Data-Driven Models in Wind Energy: Demonstration of Blade Twist Optimization Based on Aerodynamic Loads. Energies. 2024; 17(16):3897. https://doi.org/10.3390/en17163897
Chicago/Turabian StyleRoetzer, James, Xingjie Li, and John Hall. 2024. "Review of Data-Driven Models in Wind Energy: Demonstration of Blade Twist Optimization Based on Aerodynamic Loads" Energies 17, no. 16: 3897. https://doi.org/10.3390/en17163897
APA StyleRoetzer, J., Li, X., & Hall, J. (2024). Review of Data-Driven Models in Wind Energy: Demonstration of Blade Twist Optimization Based on Aerodynamic Loads. Energies, 17(16), 3897. https://doi.org/10.3390/en17163897






