A Cost-Effective Energy Management Approach for On-Grid Charging of Plug-in Electric Vehicles Integrated with Hybrid Renewable Energy Sources
Abstract
:1. Introduction
1.1. Literature Survey
| Authors | Application Area | Connectivity Type | Objective Function | Main Findings |
|---|---|---|---|---|
| [3,27,28] | India | Various Connection | Optimizing charging station capacities and locations; RES integration | Crafted models and algorithms aimed at optimizing PEV Charging Systems and managing energy efficiently. |
| [29,30] | India Delhi, globally applicable | Off-grid; On-grid | Optimally sizing and siting PEV Charging and RESs; accurate SOC estimation | Investigated microgrids and formulated deep learning models tailored for energy management |
| [31,32] | Globally applicable | Various Connection | Managing PEV charging stations; assessing and implementing V2G technologies | Introduced smart charging systems and suggested V2G technologies. |
| [33,34] | India; Nigeria; UK | Off-grid; Various Connection | Reducing energy costs; minimizing power outages; retrofitting considerations | Examined the technical feasibility and financial sustainability of hybrid electrical systems and retrofitting initiatives |
| [35,36] | Globally applicable | V2G/V2V technologies | Minimizing operational costs; real-time management and strategic capacity allocation | Created control systems for intelligent PEV Charging and established frameworks for managing EV charging processes. |
| [37,38] | Globally applicable, Brazil | Grid-connected; On-grid | Quality power transfer with minimized harmonic currents; analyzing grid impact and reliability | Showcased models for PEV charging integrated with the grid; scrutinized the reliability of power systems. |
| [39,40] | Globally applicable | Grid-tied; Off-grid | Coordinating expansion of PEV infrastructure; maximal PV power utilization | Suggested models for aligning PEV infrastructure with RESs; fine-tuned charging schedules for optimization. |
| [41,42] | Remote areas with islanded microgrids | Islanded microgrids | Voltage and frequency control; Cost-effective energy storage alternatives | PEVs demonstrate efficacy as energy storage within isolated microgrid setups; Advanced innovative control structures and systems are proposed to achieve energy self-sufficiency. |
| [43,44] | Grid-challenged environments for PEV charging | Hybrid stations; Standalone stations | Low-carbon PEV charging; Alleviation of grid stress | Hybrid charging stations offer support for eco-friendly charging, alleviating strain on the grid; Advocated for grid-independent stations to decrease reliance on fossil fuels and emissions. |
1.2. Knowledge Gap
1.3. Contribution
- The study investigates the application of various algorithms to optimize a hybrid Renewable Energy-based PEV charging station in Surat, India. This involves a comprehensive comparative evaluation of these methods, emphasizing their capacity to enhance the design and effectiveness of PEV charging stations. Consequently, it contributes to the advancement of sustainable, environmentally friendly, and economically viable charging solutions;
- A practical energy management approach was devised by integrating dynamic weather data and PEV load demand. This method offers the versatility of utilizing the RES in grid-connected configurations;
- To showcase the practicability and effectiveness of the proposed methodologies, an extensive analysis of the techno-economic results of the suggested scenarios was carried out, offering a thorough assessment of their efficacy;
- A recently developed Pufferfish Optimization Algorithm (POA) is presented for optimizing the different possible configurations of the hybrid energy systems and implementing cost-effective power scheduling, considering fluctuations in PEV load demand;
- This research work equips stakeholders, including policymakers, utilities, and PEV charging infrastructure developers with valuable information to make informed decisions by providing a comprehensive analysis of both technical functionalities and economic implications. It offers a framework for designing and implementing hybrid renewable energy-integrated PEV charging systems that are both environmentally sustainable and economically viable.
2. System Configuration
2.1. Description of the Selected Site and PEV Load
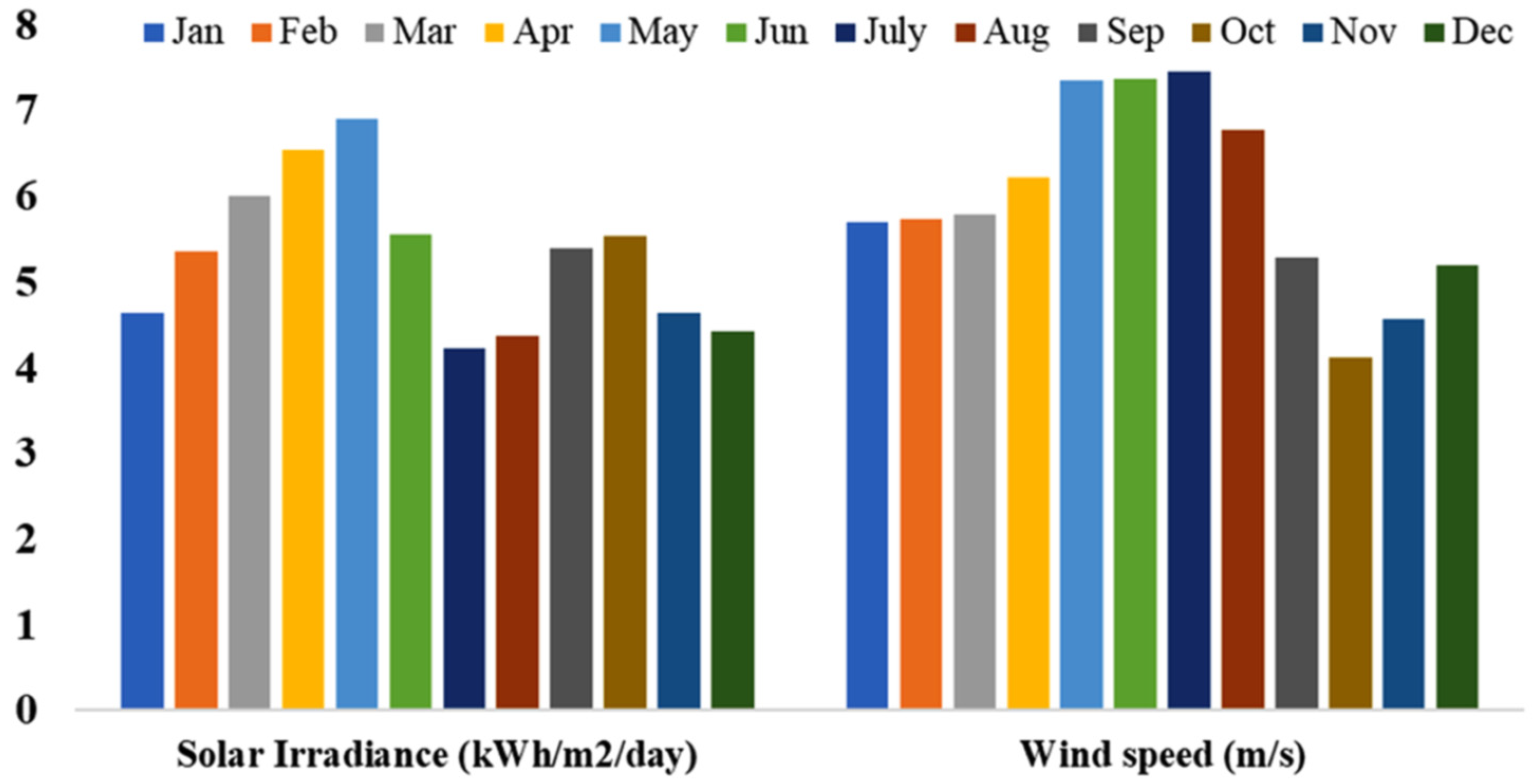
2.2. Description of Solar and Wind Potentials in the Surat Region
3. Mathematical Modeling of Hybrid Energy System
3.1. Solar Photovoltaic
3.2. Wind Energy
3.3. Battery Energy Storage
3.4. Bi-Directional Inverter
3.5. Utility Grid
4. Objective Functions, Constraints, and Energy Management Strategy
4.1. Objective Functions
4.1.1. Total Net Present Cost (TNPC)
4.1.2. Cost of Energy (COE)
4.1.3. Life Cycle Emission (LCE)
4.2. Operational Constraints
4.2.1. Reliability Constraint
4.2.2. BES Constraint
4.2.3. Balancing in Power
4.2.4. Restriction on Decision Variables
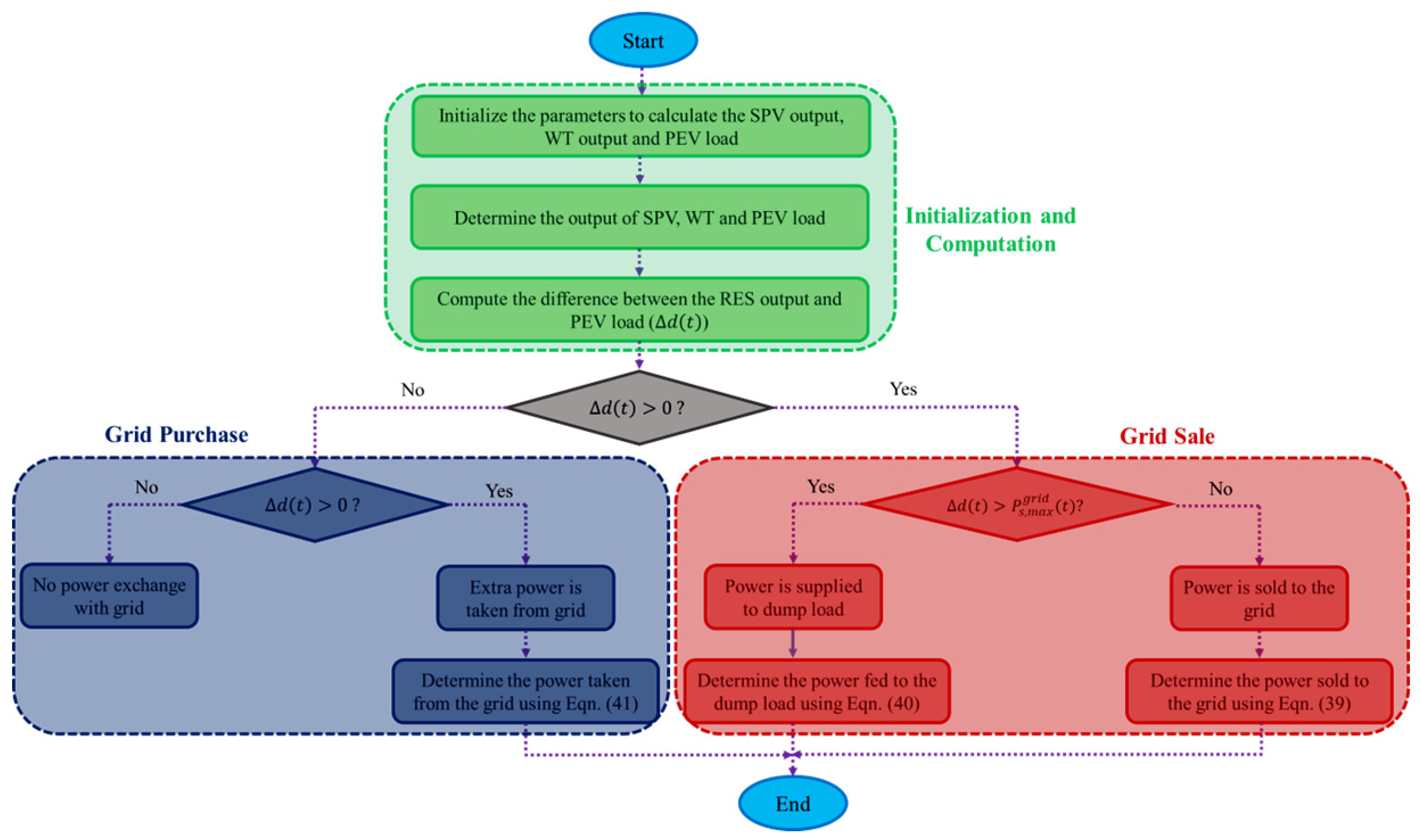
4.3. Energy Management Strategy
- When exceeds zero, it indicates that the total power generated by RES is sufficient for charging PEVs. Moreover, any surplus power is identified to be sold to the grid, which can be expressed in Equation (34):
- When the output from RES is ample to meet the energy requirements of PEV loads and exceeds the maximum selling capacity of the electric network, the surplus electric power is diverted to the dump load. The calculation for this surplus can be articulated as follows:
- If , it indicates that the power generated by the renewable components is insufficient to meet the load demand of PEVs. Therefore, the necessary electric power is obtained from the national grid, as detailed below:
- If , no power exchange occurs with the grid, and the energy demands of PEVs are met solely by the power generated from SPV and WT systems;
- If the collective output of RES and grid power is insufficient to fulfill the peak load demand, it results in a power deficit, which can be depicted as the combined output of RES and grid power falls short of meeting the peak load demand, a power deficiency emerges which can be represented as follows:
4.4. Current Energy Grid
5. Pufferfish Optimization Algorithm
5.1. Initialization of POA
5.2. Mathematical Modelling of POA
5.2.1. Phase 1: Predator Attack Towards Pufferfish (Exploration Phase)
5.2.2. Phase 2: Defense Mechanism of Pufferfish against Predators (Exploitation Phase)
5.3. Repetition Process and Flowchart of POA
5.4. Implementation of the Proposed POA for Designing SPV/WT/Grid-Based PEV Charging Stations
6. Simulation Outcomes and Discussions
6.1. Performance Analysis of the Various Designs of PEV Charging Station
6.2. Analysis of Simulation Results for Different Weather Conditions
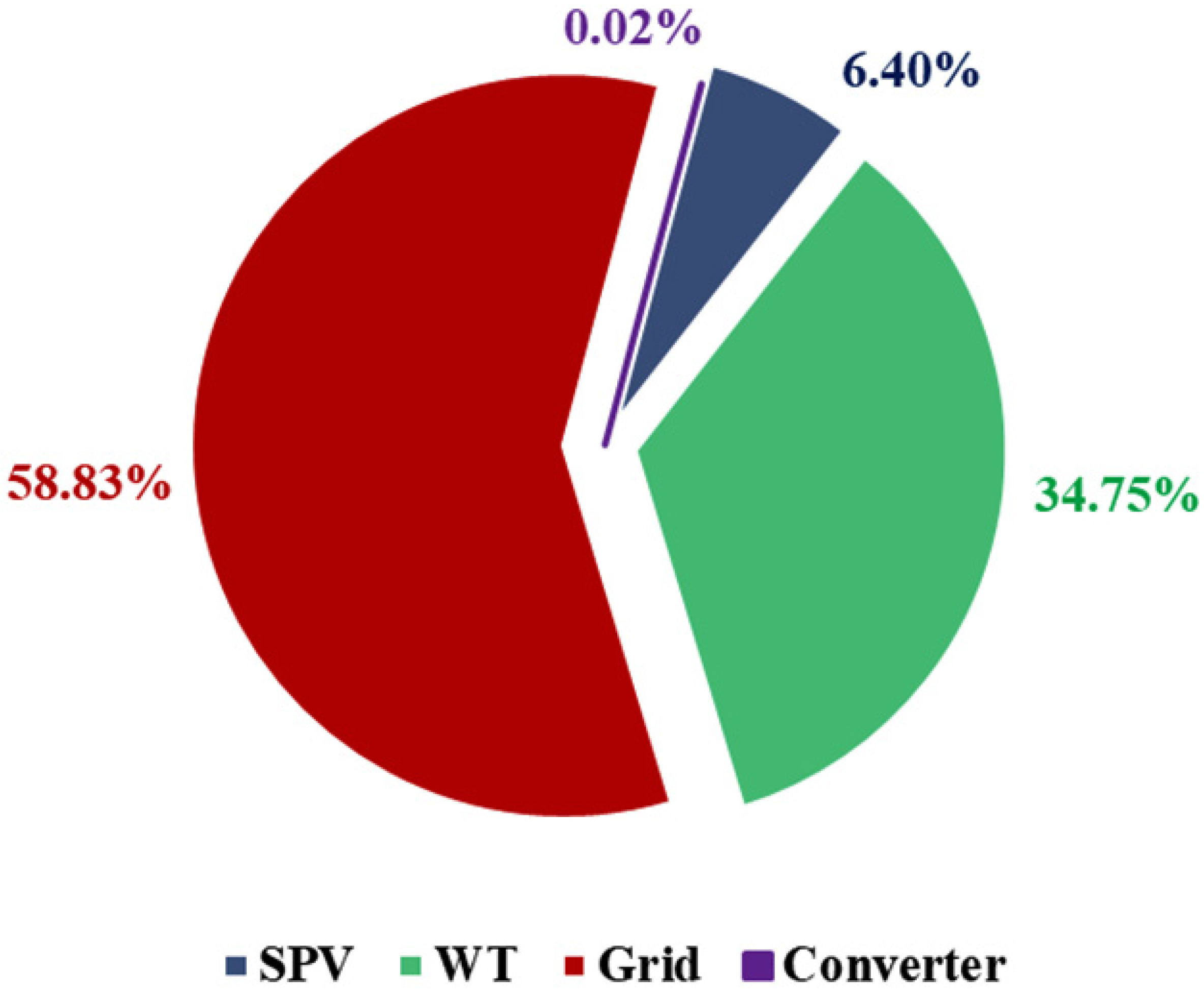
6.3. Energy Output by System Components
6.4. Cost-Wise Breakdown of System Component
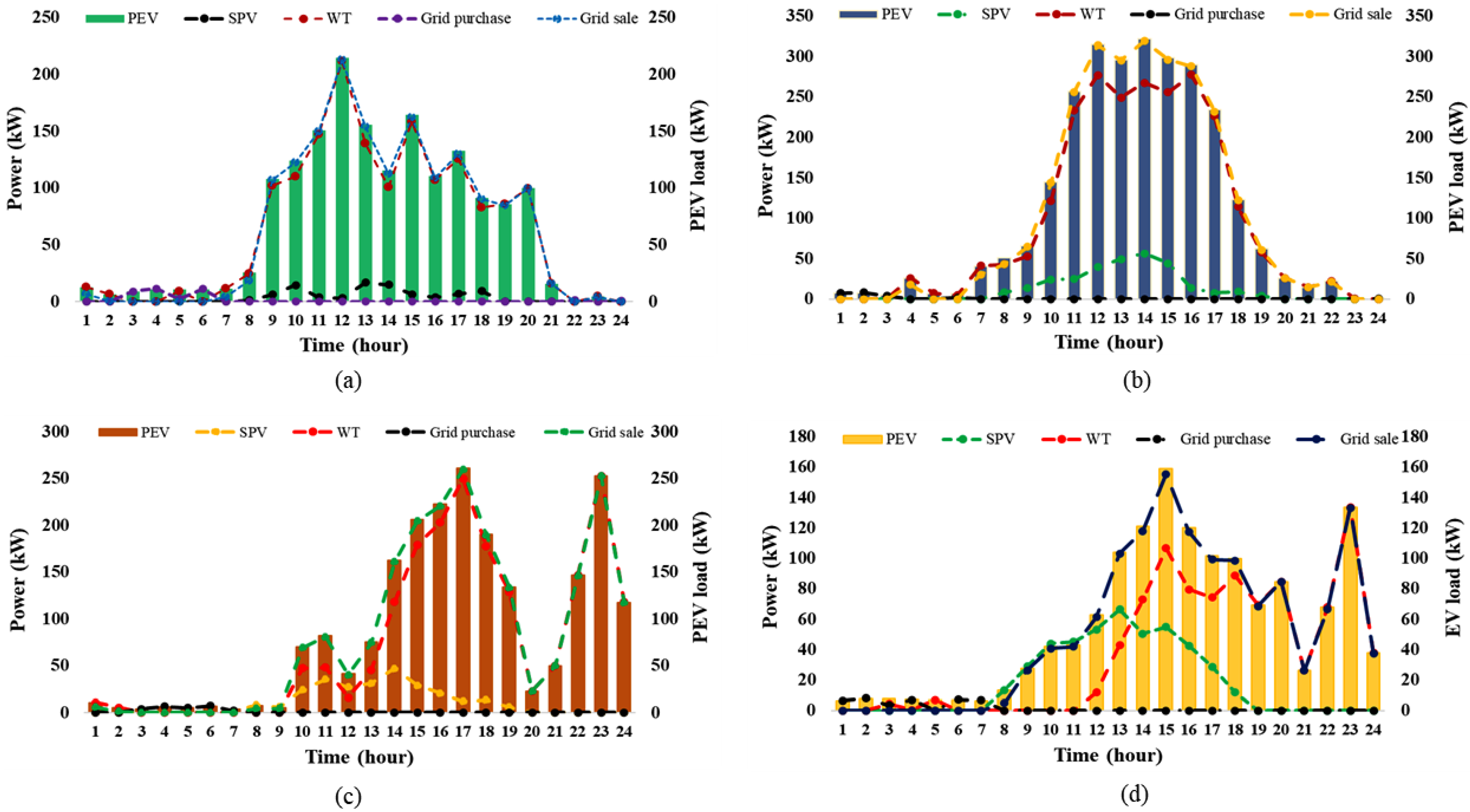
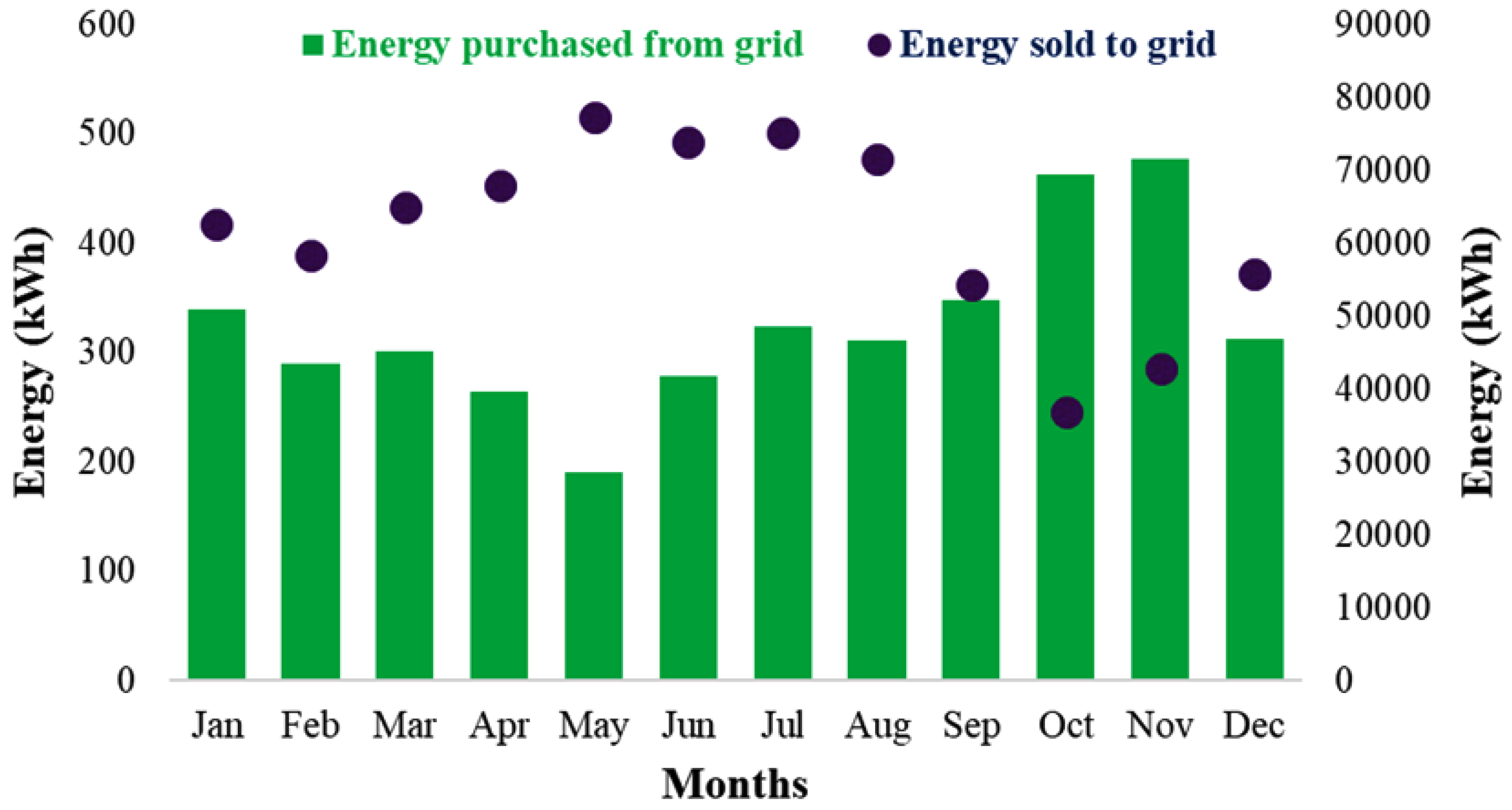
6.5. Monthly Grid Power Purchase and Sale
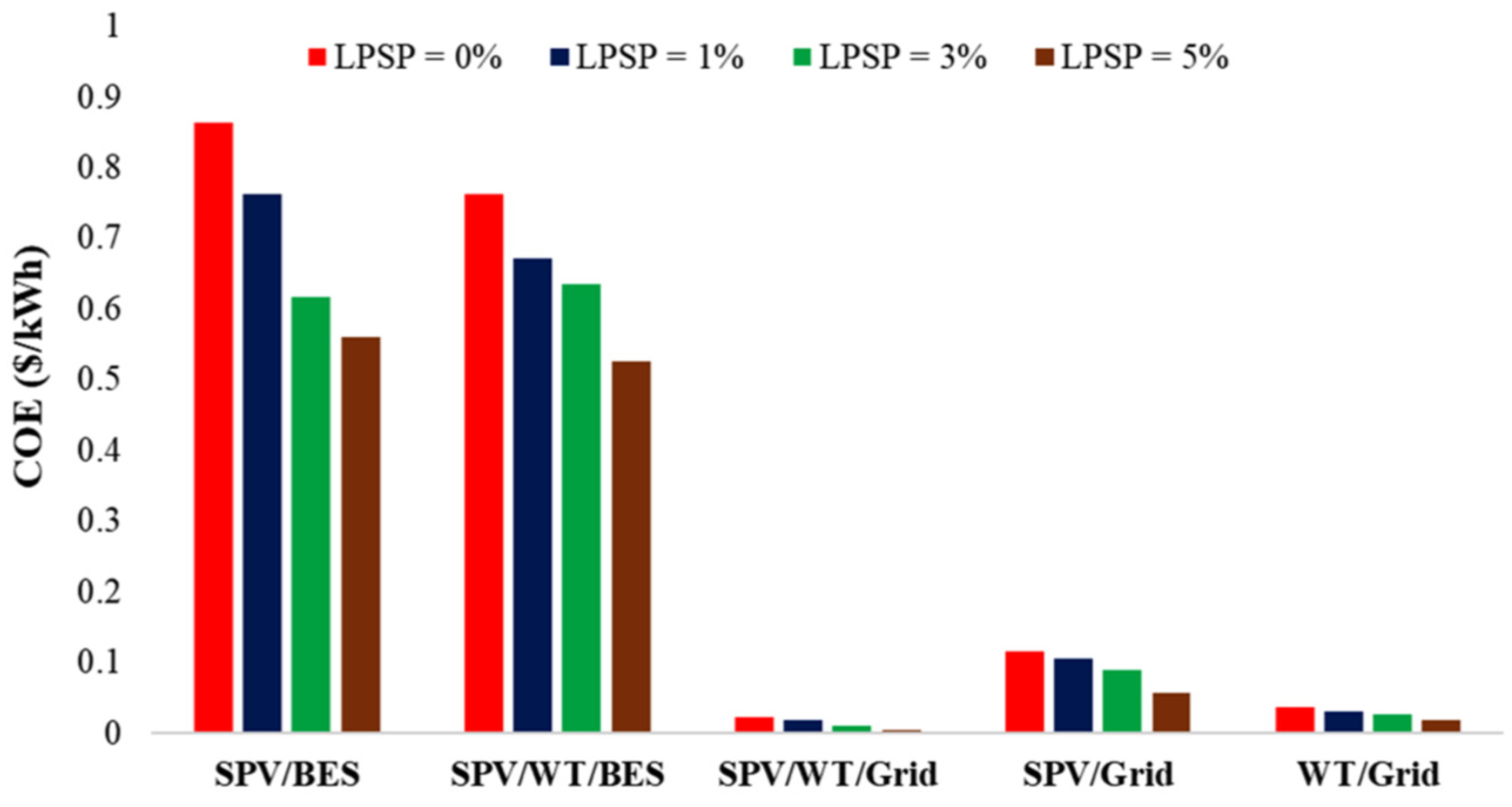
6.6. Impact of LPSP Levels on TNPC and COE for Various Configurations Using POA
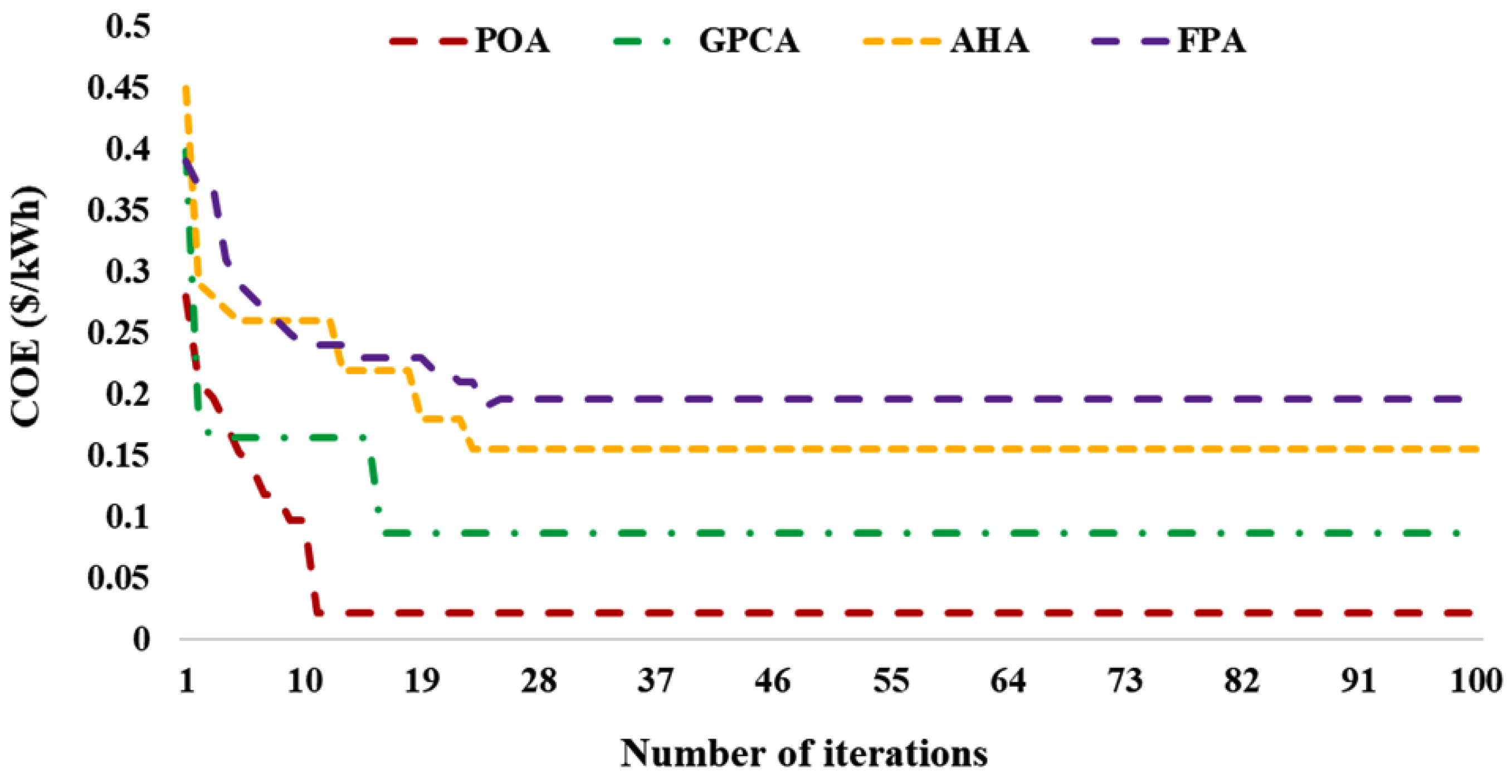
6.7. Impact of LPSP Levels on TNPC and COE for SPV/WT/Grid Combination Using Different Optimization Algorithms
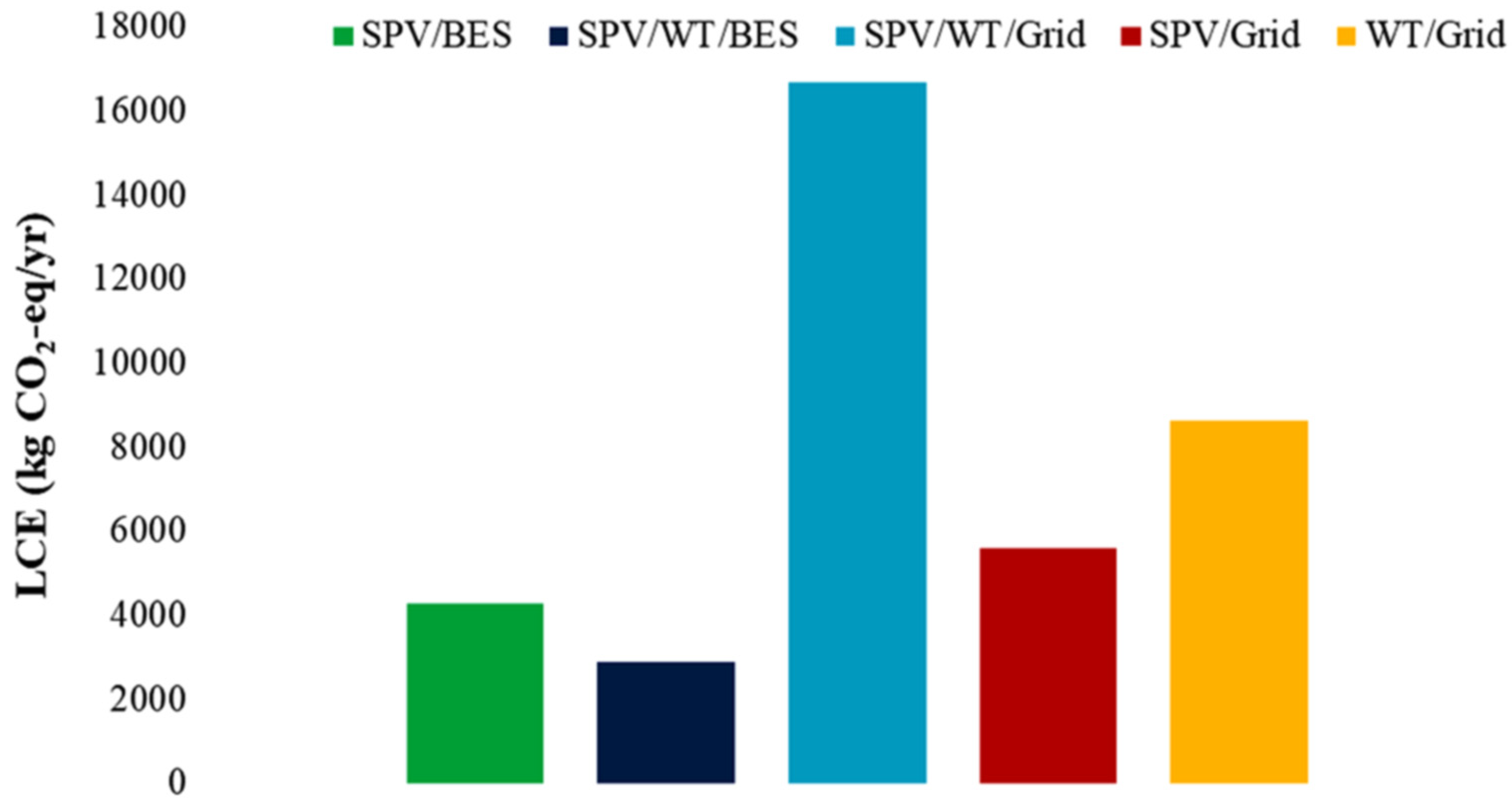
6.8. Environmental Feasibility of the Proposed PEV Charging Station Design
- (1)
- SPV and BES Combination:
- (2)
- SPV, WT, and BES Combination:
- (3)
- SPV, WT, and Grid Combination:
- (4)
- SPV and Grid Combination:
- (5)
- WT, and Grid Combination:
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviations
| Nomenclature | |||
| PEV | Plug-in Electric Vehicle | BBO | Branch Bound Optimizer |
| SDG | Sustainable Development Goals | GA | Genetic Algorithm |
| SPV | Solar Photovoltaic | WT | Wind Turbine |
| DG | Diesel Generator | BES | Battery Energy Storage |
| SOC | State of Charge | EMS | Energy Management Strategy |
| RF | Renewable Fraction | TNPC | Total Net Present Cost |
| RES | Renewable Energy Sources | COE | Cost of Energy |
| GWO | Grey Wolf Optimization | LPSP | lack of Power Supply Probability |
| GPCA | Giza Pyramids Construction Algorithm | POWER | Prediction of Worldwide Energy Resource |
| FPA | Flower Pollination Algorithm | AC | Alternating Current |
| MSME | Micro, Small, and Medium-sized Enterprises | DC | Direct Current |
| PSO | Particle Swarm Optimization | CRF | Capital Recovery Factor |
| NOCT | Nominal Operating Cell Temperature | Depth of discharge | |
| POA | Pufferfish Optimization Algorithm | V2G | Vehicle to Grid |
| G2V | Grid to Vehicle | LCE | Life Cycle Analysis |
| V2V | Vehicle to Vehicle | AHA | Artificial Hummingbird Algorithm |
| Abbreviations | |||
| Electrical output power of the SPV module | Escalation rate | ||
| Solar irradiance at time instant | Interest rate | ||
| Actual efficiency of the SPV panel | Lifespan of the project | ||
| Effective area of the SPV panel | Number of SPV panels | ||
| Maximum efficiency of SPV cell | cost of replacement of each SPV unit | ||
| Efficiency at the operating point of MPPT | Capital cost of WT panel | ||
| Temperature coefficient | Initial cost of WT | ||
| Actual operating temperature and | Area of WT | ||
| Maximum temperature of the SPV module | Annual cost of maintaining and operating a WT system | ||
| Ambient temperature | Cost of replacement of each WT unit | ||
| Nominal Operating Cell Temperature | Number of WT | ||
| Ambient temperature at NOCT | Capital cost of BES, | ||
| Solar irradiance at NOCT | Initial cost of BES device | ||
| Electrical power output of the wind farm | Power rating of BES device | ||
| Cut-in wind speed | Annual cost of maintaining and operating a WT system | ||
| Cut-off wind speed | Number of BES | ||
| Rated power of the wind turbine | Cost of replacement of each BES unit | ||
| Rated wind speed | Capital cost of BES | ||
| Wind speed at a specific height | Initial cost of the inverter | ||
| Mechanical output power of WT | Power rating of the inverter | ||
| Area of the wind farm | Unit cost for selling electricity to the utility grid | ||
| Efficiency of the WT | Unit cost of purchasing electricity from the utility grid | ||
| and | WT constants | Number of components of energy system | |
| Electrical energy stored in BES at time | Energy generated by each system component | ||
| Electrical power charged/discharged into/from the BES | Upper threshold of system reliability tolerance | ||
| ƛ | Self-discharge rate of BES | Maximum purchase from the grid | |
| Minimum battery energy | Maximum sell to the grid | ||
| Maximum depth-of-discharge | Deferrable load | ||
| Overall energy capacity of the battery bank | Maximum limit on SPV used | ||
| Efficiency of inverter | Minimum limit on SPV used | ||
| Input power to bidirectional inverter | Minimum limit on WT used | ||
| Output power of bidirectional inverter | Maximum limit on WT used | ||
| Efficiency at 10% of nominal power | Minimum limit on BES units used | ||
| Efficiency at 100% of nominal power | Maximum limit on BES units used | ||
| Amount of energy taken from the grid | Maximum iterations | ||
| Energy demand of PEVs | Total number of population members | ||
| Electrical power output of RES | Matrix of POA population | ||
| Lifetime equivalent CO2 emissions | POA member | ||
| Electrical power fed to the grid | dimension within the search space | ||
| Capital cost of the SPV panel | Lower bounds of the decision variable | ||
| Initial cost of the SPV system | Upper bounds of the decision variable | ||
| Area of SPV system | Annual cost of maintaining and operating an SPV system | ||
References
- Vayá, M.G.; Andersson, G. Self Scheduling of Plug-In Electric Vehicle Aggregator to Provide Balancing Services for Wind Power. IEEE Trans. Sustain. Energy 2015, 7, 886–899. [Google Scholar] [CrossRef]
- Reddy, M.S.K.; Selvajyothi, K. Optimal placement of electric vehicle charging station for unbalanced radial distribution systems. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 1–15. [Google Scholar] [CrossRef]
- Eid, A.; Mohammed, O.; El-Kishky, H. Efficient operation of battery energy storage systems, electric-vehicle charging stations and renewable energy sources linked to distribution systems. J. Energy Storage 2022, 55, 105644. [Google Scholar] [CrossRef]
- Mohammad, A.; Zuhaib, M.; Ashraf, I.; Alsultan, M.; Ahmad, S.; Sarwar, A.; Abdollahian, M. Integration of Electric Vehicles and Energy Storage System in Home Energy Management System with Home to Grid Capability. Energies 2021, 14, 8557. [Google Scholar] [CrossRef]
- Mahmoud, F.S.; Abdelhamid, A.M.; Al Sumaiti, A.; El-Sayed, A.-H.M.; Diab, A.A.Z. Sizing and Design of a PV-Wind-Fuel Cell Storage System Integrated into a Grid Considering the Uncertainty of Load Demand Using the Marine Predators Algorithm. Mathematics 2022, 10, 3708. [Google Scholar] [CrossRef]
- Fares, D.; Fathi, M.; Mekhilef, S. Performance evaluation of metaheuristic techniques for optimal sizing of a stand-alone hybrid PV/wind/battery system. Appl. Energy 2022, 305, 117823. [Google Scholar] [CrossRef]
- Kumar, P.; Pal, N.; Sharma, H. Techno-economic analysis of solar photo-voltaic/diesel generator hybrid system using different energy storage technologies for isolated islands of India. J. Energy Storage 2021, 41, 102965. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M. Integration of electric vehicle charging stations and capacitors in distribution systems with vehicle-to-grid facility. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 1–30. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M.; Alsaidan, I.; Almasoudi, F.M. AI-Based Approach for Optimal Placement of EVCS and DG With Reliability Analysis. IEEE Access 2021, 9, 154204–154224. [Google Scholar] [CrossRef]
- Ahmad, F.; Ashraf, I.; Iqbal, A.; Marzband, M.; Khan, I. A novel AI approach for optimal deployment of EV fast charging station and reliability analysis with solar based DGs in distribution network. Energy Rep. 2022, 8, 11646–11660. [Google Scholar] [CrossRef]
- Ud-Din Khan, S.; Wazeer, I.; Almutairi, Z.; Alanazi, M. Techno-economic analysis of solar photovoltaic powered electrical energy storage (EES) system. Alex. Eng. J. 2022, 61, 6739–6753. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Placement of electric vehicle fast charging stations in distribution network considering power loss, land cost, and electric vehicle population. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 1693–1709. [Google Scholar] [CrossRef]
- Bilal, M.; Ahmad, F.; Rizwan, M. Techno-economic assessment of grid and renewable powered electric vehicle charging stations in India using a modified metaheuristic technique. Energy Convers. Manag. 2023, 284, 116995. [Google Scholar] [CrossRef]
- Li, Z.; Su, S.; Jin, X.; Xia, M.; Chen, Q.; Yamashita, K. Stochastic and distributed optimal energy management of active distribution network with integrated office buildings. CSEE J. Power Energy Syst. 2022, 10, 504–517. [Google Scholar] [CrossRef]
- Sadati, S.M.B.; Moshtagh, J.; Shafie-Khah, M.; Rastgou, A.; Catalão, J.P.S. Optimal Charge Scheduling of Electric Vehicles in Solar Energy Integrated Power Systems Considering the Uncertainties. In Electric Vehicles in Energy Systems; Springer International Publishing: Cham, Switzerland, 2020; pp. 73–128. [Google Scholar]
- Ahmad, F.; Iqbal, A.; Asharf, I.; Marzband, M.; Khan, I. Placement and Capacity of EV Charging Stations by Considering Uncertainties with Energy Management Strategies. IEEE Trans. Ind. Appl. 2023, 59, 3865–3874. [Google Scholar] [CrossRef]
- Marinescu, C. Progress in the Development and Implementation of Residential EV Charging Stations Based on Renewable Energy Sources. Energies 2022, 16, 179. [Google Scholar] [CrossRef]
- Ding, B.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Sun, H. A CCP-based distributed cooperative operation strategy for multi-agent energy systems integrated with wind, solar, and buildings. Appl. Energy 2024, 365, 123275. [Google Scholar] [CrossRef]
- Leone, C.; Longo, M.; Fernandez-Ramirez, L.M.; Garcia-Trivino, P. Multi-Objective Optimization of PV and Energy Storage Systems for Ultra-Fast Charging Stations. IEEE Access 2022, 10, 14208–14224. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Darwish Ahmad, A.; Abubaker, A.M.; Alrbai, M.; Ayadi, O.; Al-Dahidi, S.; Akafuah, N.K. Techno-economic assessment of photovoltaic-based charging stations for electric vehicles in developing countries. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 523–541. [Google Scholar] [CrossRef]
- Zhang, H.; Zhai, X.; Zhang, J.; Bai, X.; Li, Z. Mechanism Analysis of the Effect of the Equivalent Proportional Coefficient of Inertia Control for a Doubly Fed Wind Generator on Frequency Stability in Extreme Environments. Sustainability 2024, 16, 4965. [Google Scholar] [CrossRef]
- Syed Mohammed, A.; Anuj; Lodhi, A.S.; Murtaza, Q. Techno-economic feasibility of hydrogen based electric vehicle charging station: A case study. Int. J. Energy Res. 2022, 46, 14145–14160. [Google Scholar] [CrossRef]
- Borroy Vicente, S.; Fernández, G.; Galan, N.; Llombart Estopiñán, A.; Salani, M.; Derboni, M.; Giuffrida, V.; Hernández-Callejo, L. Assessment of the Technical Impacts of Electric Vehicle Penetration in Distribution Networks: A Focus on System Management Strategies Integrating Sustainable Local Energy Communities. Sustainability 2024, 16, 6464. [Google Scholar] [CrossRef]
- Nishanthy, J.; Charles Raja, S.; Praveen, T.; Jeslin Drusila Nesamalar, J.; Venkatesh, P. Techno-economic analysis of a hybrid solar wind electric vehicle charging station in highway roads. Int. J. Energy Res. 2022, 46, 7883–7903. [Google Scholar] [CrossRef]
- Nandini, K.K.; Jayalakshmi, N.S.; Jadoun, V.K. Risk-based dynamic pricing by metaheuristic optimization approach for electric vehicle charging infrastructure powered by grid integrated microgrid system. Electr. Power Syst. Res. 2024, 230, 110250. [Google Scholar] [CrossRef]
- Oladigbolu, J.O.; Mujeeb, A.; Al-Turki, Y.A.; Rushdi, A.M. A Novel Doubly-Green Stand-Alone Electric Vehicle Charging Station in Saudi Arabia: An Overview and a Comprehensive Feasibility Study. IEEE Access 2023, 11, 37283–37312. [Google Scholar] [CrossRef]
- Verma, R.; Sharma, S.K.; Singh, P.; Bhutto, J.K.; Alharbi, A.R.A. Analysis and Sizing of Charging Stations in Kota City. Sustainability 2022, 14, 11759. [Google Scholar] [CrossRef]
- Karmaker, A.K.; Hossain, M.A.; Pota, H.R.; Onen, A.; Jung, J. Energy Management System for Hybrid Renewable Energy-Based Electric Vehicle Charging Station. IEEE Access 2023, 11, 27793–27805. [Google Scholar] [CrossRef]
- Krishnamurthy, N.K.; Sabhahit, J.N.; Jadoun, V.K.; Gaonkar, D.N.; Shrivastava, A.; Rao, V.S.; Kudva, G. Optimal Placement and Sizing of Electric Vehicle Charging Infrastructure in a Grid-Tied DC Microgrid Using Modified TLBO Method. Energies 2023, 16, 1781. [Google Scholar] [CrossRef]
- Vellingiri, M.T.; Mehedi, I.M.; Palaniswamy, T. A Novel Deep Learning-Based State-of-Charge Estimation for Renewable Energy Management System in Hybrid Electric Vehicles. Mathematics 2022, 10, 260. [Google Scholar] [CrossRef]
- Ahmadi, S.E.; Kazemi-Razi, S.M.; Marzband, M.; Ikpehai, A.; Abusorrah, A. Multi-objective stochastic techno-economic-environmental optimization of distribution networks with G2V and V2G systems. Electr. Power Syst. Res. 2023, 218, 109195. [Google Scholar] [CrossRef]
- Ekren, O.; Hakan Canbaz, C.; Güvel, Ç.B. Sizing of a solar-wind hybrid electric vehicle charging station by using HOMER software. J. Clean. Prod. 2021, 279, 123615. [Google Scholar] [CrossRef]
- Alsaidan, I.; Bilal, M.; Alaraj, M.; Rizwan, M.; Almasoudi, F.M. A Novel EA-Based Techno–Economic Analysis of Charging System for Electric Vehicles: A Case Study of Qassim Region, Saudi Arabia. Mathematics 2023, 11, 2052. [Google Scholar] [CrossRef]
- Oladigbolu, J.O.; Mujeeb, A.; Imam, A.A.; Rushdi, A.M. Design, Technical and Economic Optimization of Renewable Energy-Based Electric Vehicle Charging Stations in Africa: The Case of Nigeria. Energies 2022, 16, 397. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Choi, D.-H. Distributionally Robust Model Predictive Control for Smart Electric Vehicle Charging Station With V2G/V2V Capability. IEEE Trans. Smart Grid 2023, 14, 4621–4633. [Google Scholar] [CrossRef]
- Yang, D.; Sarma, N.J.S.; Hyland, M.F.; Jayakrishnan, R. Dynamic modeling and real-time management of a system of EV fast-charging stations. Transp. Res. Part C Emerg. Technol. 2021, 128, 103186. [Google Scholar] [CrossRef]
- Khan, W.; Ahmad, F.; Alam, M.S. Fast EV charging station integration with grid ensuring optimal and quality power exchange. Eng. Sci. Technol. Int. J. 2019, 22, 143–152. [Google Scholar] [CrossRef]
- Almutairi, A. Impact Assessment of Diverse EV Charging Infrastructures on Overall Service Reliability. Sustainability 2022, 14, 13295. [Google Scholar] [CrossRef]
- Wang, B.; Dehghanian, P.; Zhao, D. Coordinated Planning of Electric Vehicle Charging Infrastructure and Renewables in Power Grids. IEEE Open Access J. Power Energy 2023, 10, 233–244. [Google Scholar] [CrossRef]
- Ullah, Z.; Wang, S.; Wu, G.; Hasanien, H.M.; Rehman, A.U.; Turky, R.A.; Elkadeem, M.R. Optimal scheduling and techno-economic analysis of electric vehicles by implementing solar-based grid-tied charging station. Energy 2023, 267, 126560. [Google Scholar] [CrossRef]
- Omar, N.; Kumar Tiwari, A.; Seethalekshmi, K.; Anand Shrivastava, N. A Novel Controller Design for Small-Scale Islanded Microgrid Integrated with Electric Vehicle-Based Energy Storage Management. Int. Trans. Electr. Energy Syst. 2022, 2022, 5059215. [Google Scholar] [CrossRef]
- Al Wahedi, A.; Bicer, Y. Assessment of a stand-alone hybrid solar and wind energy-based electric vehicle charging station with battery, hydrogen, and ammonia energy storages. Energy Storage 2019, 1, e84. [Google Scholar] [CrossRef]
- Engelhardt, J.; Zepter, J.M.; Gabderakhmanova, T.; Marinelli, M. Energy management of a multi-battery system for renewable-based high power EV charging. eTransportation 2022, 14, 100198. [Google Scholar] [CrossRef]
- Al Wahedi, A.; Bicer, Y. Development of an off-grid electrical vehicle charging station hybridized with renewables including battery cooling system and multiple energy storage units. Energy Rep. 2020, 6, 2006–2021. [Google Scholar] [CrossRef]
- Bilal, M.; Alsaidan, I.; Alaraj, M.; Almasoudi, F.M.; Rizwan, M. Techno-Economic and Environmental Analysis of Grid-Connected Electric Vehicle Charging Station Using AI-Based Algorithm. Mathematics 2022, 10, 924. [Google Scholar] [CrossRef]
- Kamal, M.M.; Ashraf, I.; Fernandez, E. Sustainable electrification planning of rural microgrid using renewable resources and its environmental impact assessment. Environ. Sci. Pollut. Res. 2022, 29, 86376–86399. [Google Scholar] [CrossRef]
- Kamal, M.M.; Mohammad, A.; Ashraf, I.; Fernandez, E. Rural electrification using renewable energy resources and its environmental impact assessment. Environ. Sci. Pollut. Res. 2022, 29, 86562–86579. [Google Scholar] [CrossRef] [PubMed]
- Anand, P.; Rizwan, M.; Bath, S.K. Sizing of renewable energy based hybrid system for rural electrification using grey wolf optimisation approach. IET Energy Syst. Integr. 2019, 1, 158–172. [Google Scholar] [CrossRef]
- Jahangiri, M.; Nematollahi, O.; Haghani, A.; Raiesi, H.A.; Alidadi Shamsabadi, A. An optimization of energy cost of clean hybrid solar-wind power plants in Iran. Int. J. Green Energy 2019, 16, 1422–1435. [Google Scholar] [CrossRef]
- Mandal, S.; Das, B.K.; Hoque, N. Optimum sizing of a stand-alone hybrid energy system for rural electrification in Bangladesh. J. Clean. Prod. 2018, 200, 12–27. [Google Scholar] [CrossRef]
- Nirbheram, J.S.; Mahesh, A.; Bhimaraju, A. Techno-economic optimization of standalone photovoltaic-wind turbine-battery energy storage system hybrid energy system considering the degradation of the components. Renew. Energy 2024, 222, 119918. [Google Scholar] [CrossRef]










| Component | SPV | WT | BES | Inverter |
|---|---|---|---|---|
| Manufacturer | Generic flat plate | Generic | Generic lead acid | Generic |
| Capital cost (USD) | 1300 | 1098 | 235 | 127 |
| Replacement cost (USD) | 0 | 1098 | 190 | 127 |
| Operation and Maintenance cost (USD) | 20 | 2 | 2 | 1 |
| Rated capacity (kW) | 1 | 10 | 1 kWh | 1 |
| Lifetime (years) | 25 | 20 | 15 | 15 |
| Lifetime equivalent CO2 emissions (kg CO2-eq per year) | 0.045 | 0.011 | 0.028 | – |
| Configurations for PEV CS Model | SPV/BES | SPV/WT/BES | SPV/WT/Grid | SPV/Grid | WT/Grid |
|---|---|---|---|---|---|
| PEV charging station scenarios | C1 | C2 | C3 | C4 | C5 |
| COE (USD/kWh) | 0.8642 | 0.7632 | 0.022 | 0.1150 | 0.03 |
| TNPC (USD) | 296,975.10 | 262,254.80 | 222,762.80 | 283,615.1 | 247,177.40 |
| Number of SPV used | 57 | 38 | 75 | 15 | – |
| Number of WT used | – | 1 | 224 | – | 225 |
| Battery units | 276 | 342 | – | – | – |
| Converter capacity (kW) | – | 38.7 | 60 | 19.7 | 19.7 |
| Renewable fraction (%) | 100 | 100 | 99.5 | 50.2 | 98.8 |
| SPV production (kWh/year) | 94,643 | 63,327 | 12,6191 | 24,002 | – |
| Wind production (kWh/year) | – | 1872 | 645,722 | – | 636,062 |
| Grid purchase (kWh/year) | – | – | 3902 | 21,834 | 7849 |
| Grid sales (kWh/year) | – | – | 741,494 | 16,606 | 615,212 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, M.; Bokoro, P.N.; Sharma, G.; Pau, G. A Cost-Effective Energy Management Approach for On-Grid Charging of Plug-in Electric Vehicles Integrated with Hybrid Renewable Energy Sources. Energies 2024, 17, 4194. https://doi.org/10.3390/en17164194
Bilal M, Bokoro PN, Sharma G, Pau G. A Cost-Effective Energy Management Approach for On-Grid Charging of Plug-in Electric Vehicles Integrated with Hybrid Renewable Energy Sources. Energies. 2024; 17(16):4194. https://doi.org/10.3390/en17164194
Chicago/Turabian StyleBilal, Mohd, Pitshou N. Bokoro, Gulshan Sharma, and Giovanni Pau. 2024. "A Cost-Effective Energy Management Approach for On-Grid Charging of Plug-in Electric Vehicles Integrated with Hybrid Renewable Energy Sources" Energies 17, no. 16: 4194. https://doi.org/10.3390/en17164194
APA StyleBilal, M., Bokoro, P. N., Sharma, G., & Pau, G. (2024). A Cost-Effective Energy Management Approach for On-Grid Charging of Plug-in Electric Vehicles Integrated with Hybrid Renewable Energy Sources. Energies, 17(16), 4194. https://doi.org/10.3390/en17164194






