Analysis of Soot Deposition Effects on Exhaust Heat Exchanger for Waste Heat Recovery System
Abstract
1. Introduction
2. Modeling
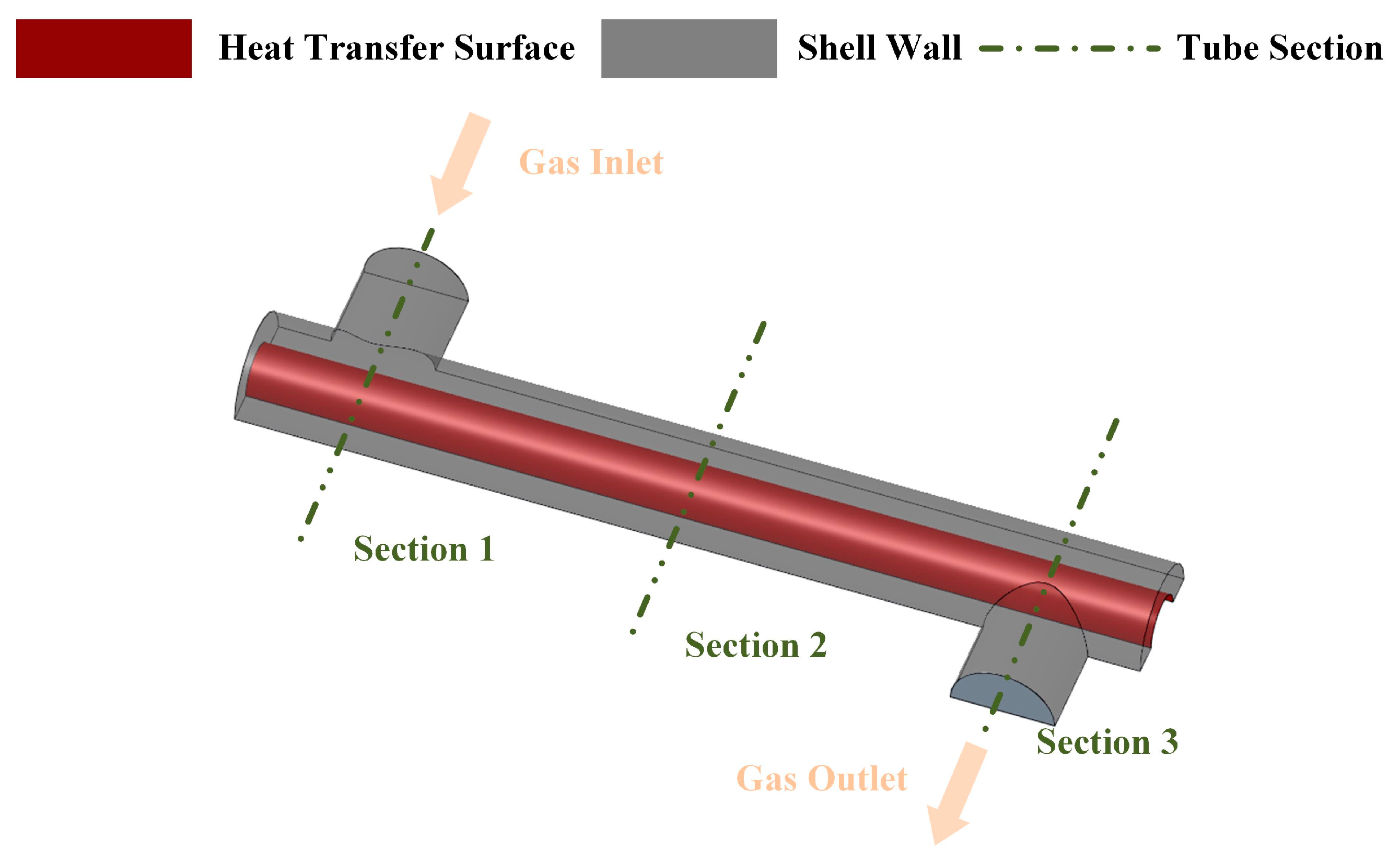
2.1. Computational Domain
2.2. Boundary Conditions and Numerical Method
2.3. Assumptions
- (a)
- Only soot particles are considered in deposition.
- (b)
- During the simulation process, the properties of the exhaust gas and soot particle are considered as a function of temperature and a constant value, respectively.
- (c)
- Interactions between soot particles are not considered.
- (d)
- The impact of the deposit layer thickness on the flow area is not considered.
2.4. Deposition Model
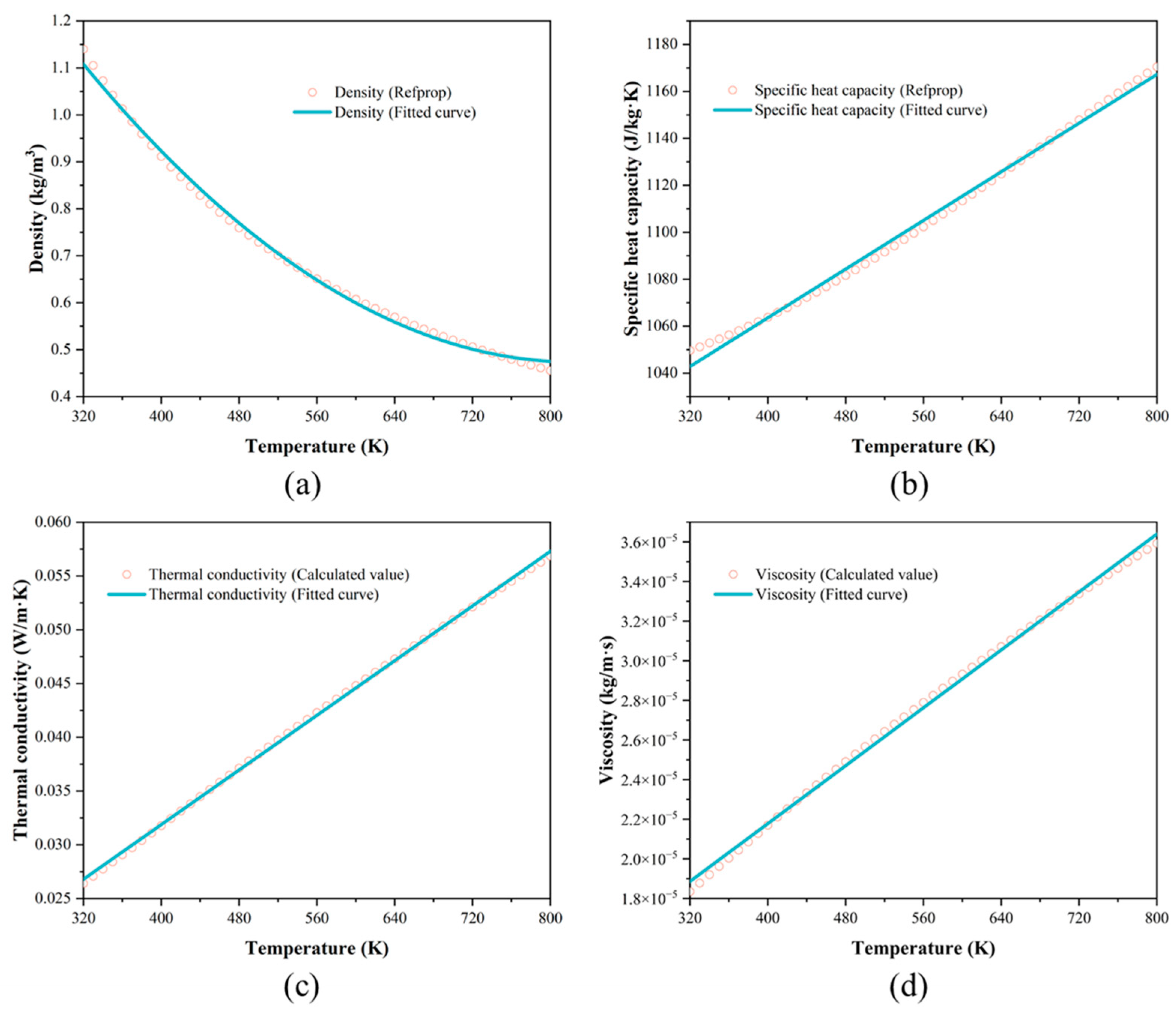
2.5. Exhaust Gas Properties and Soot Parameters
2.6. Data Processing
2.7. Model Verification
3. Long-Term Performance under Different Exhaust Conditions
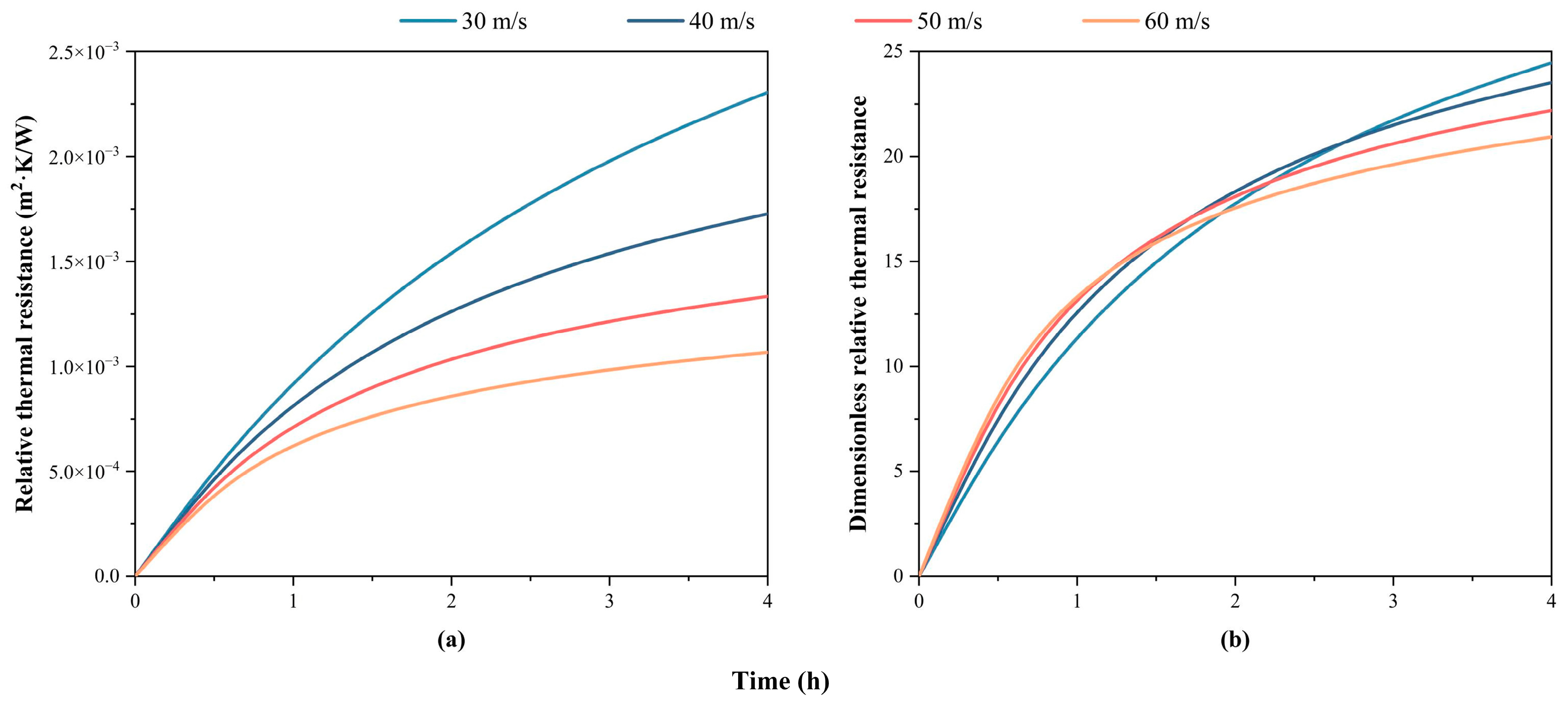
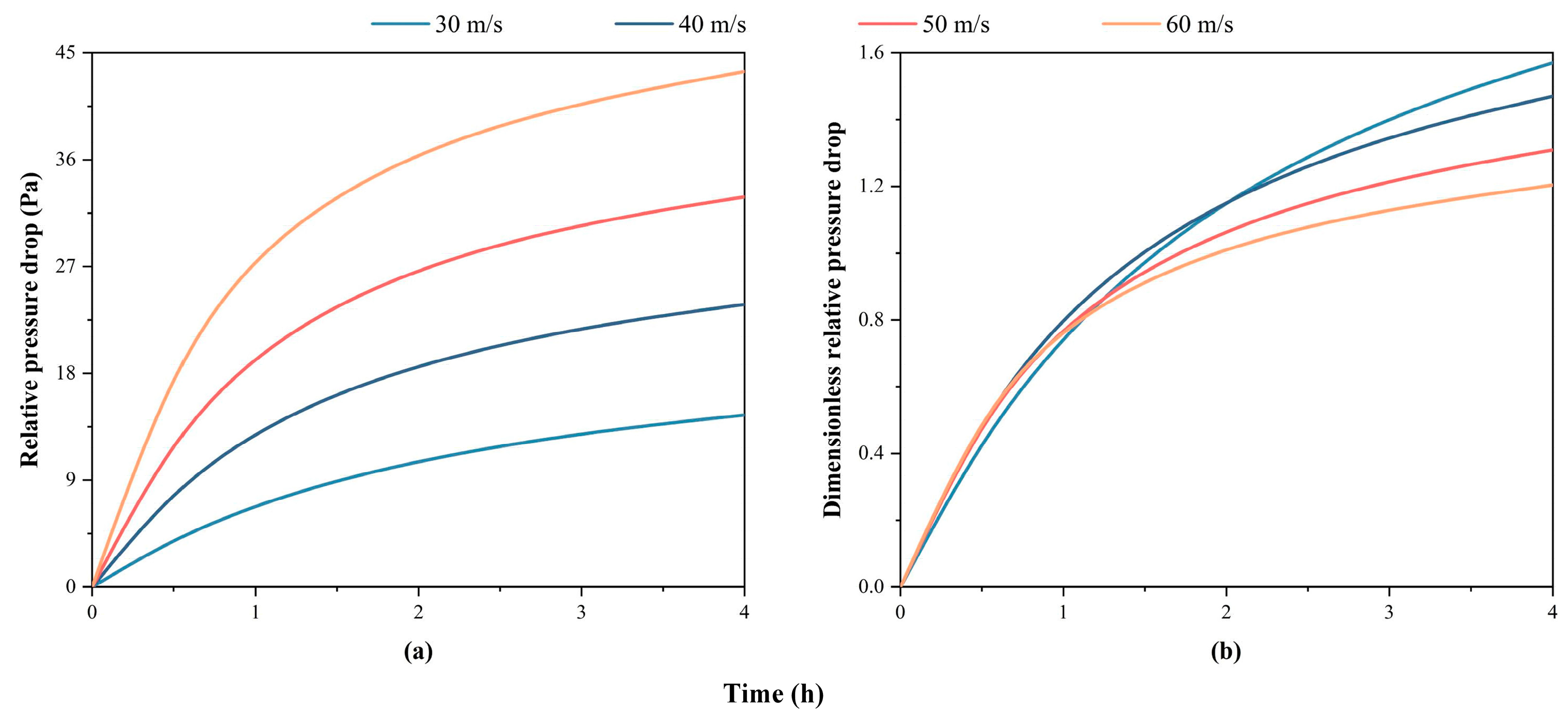
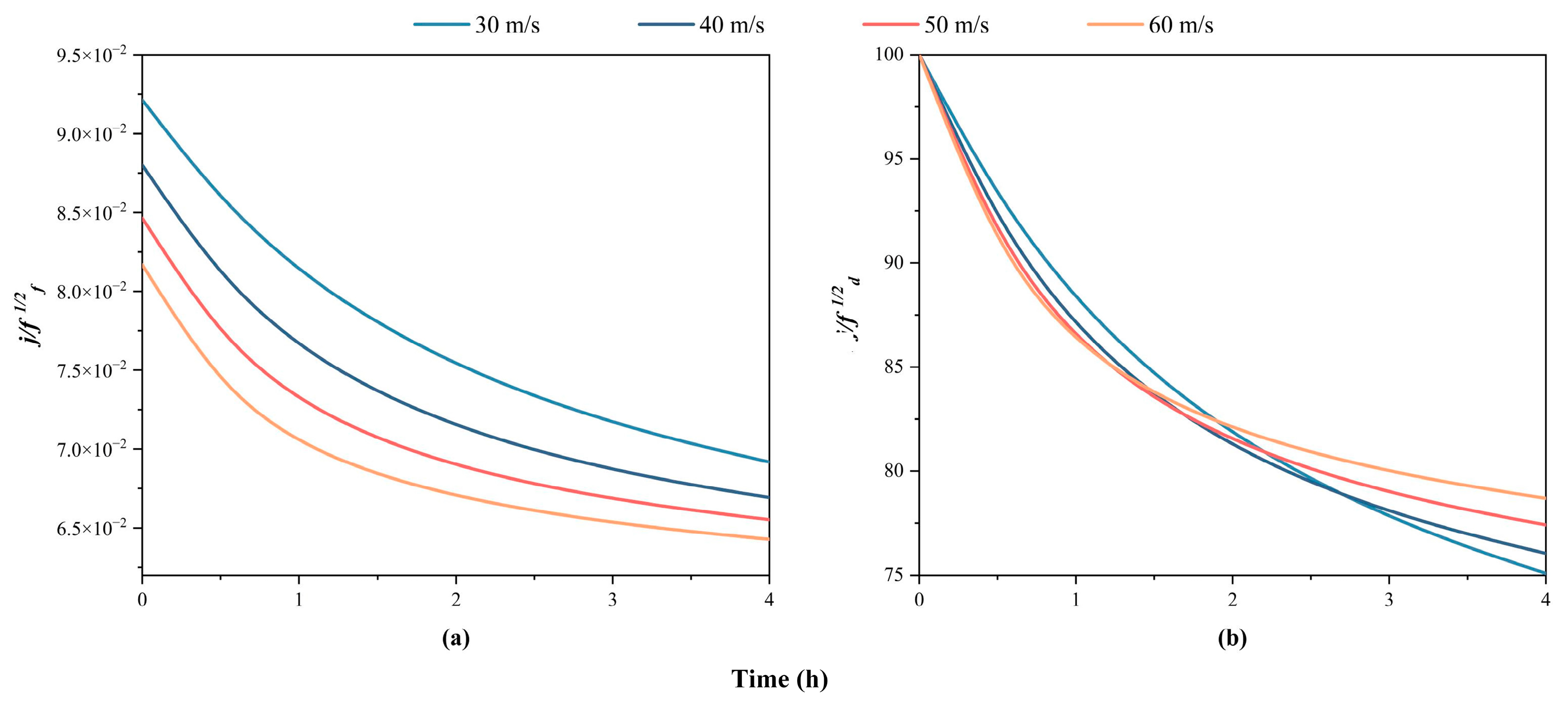
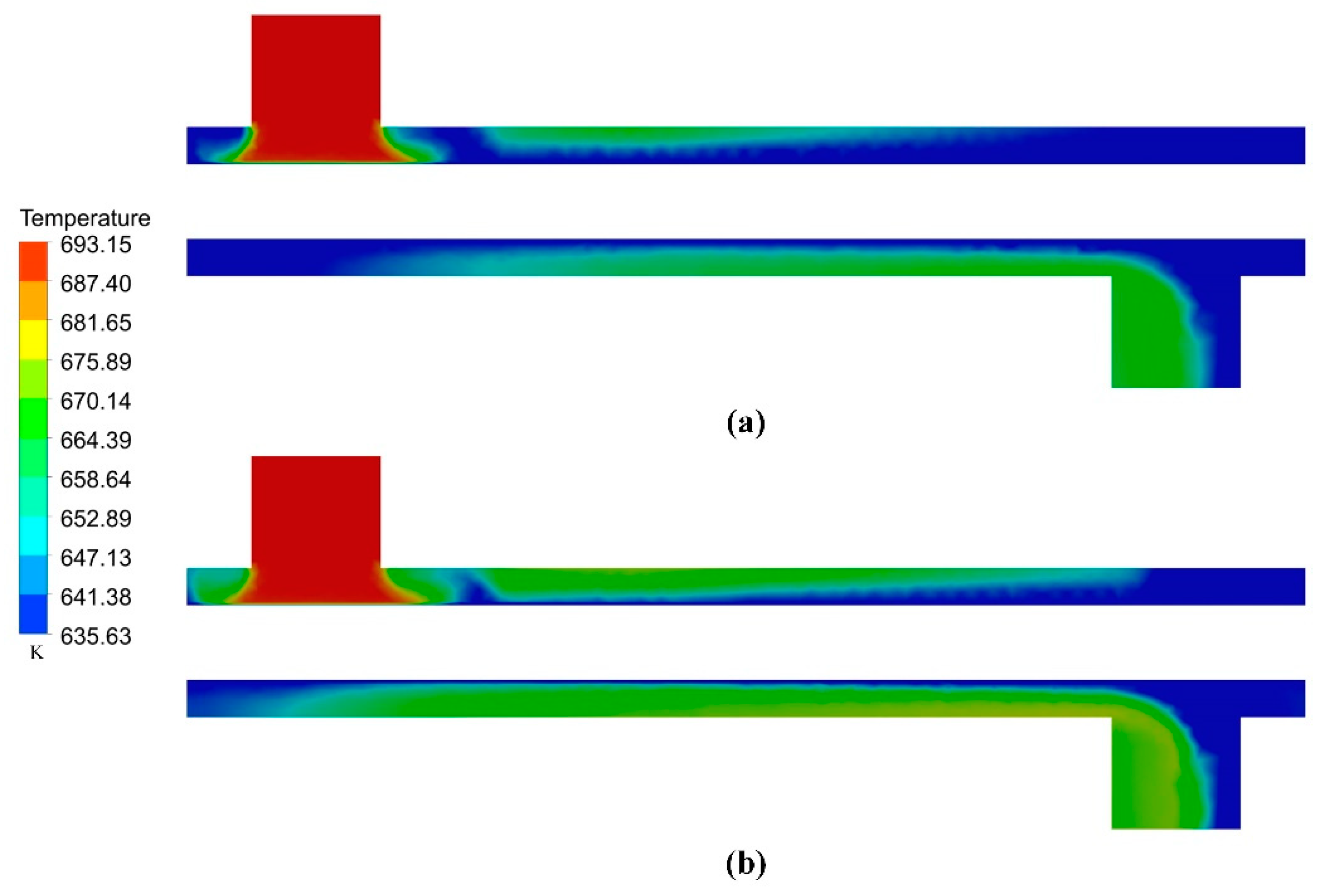
3.1. Thermal–Hydraulic Performance
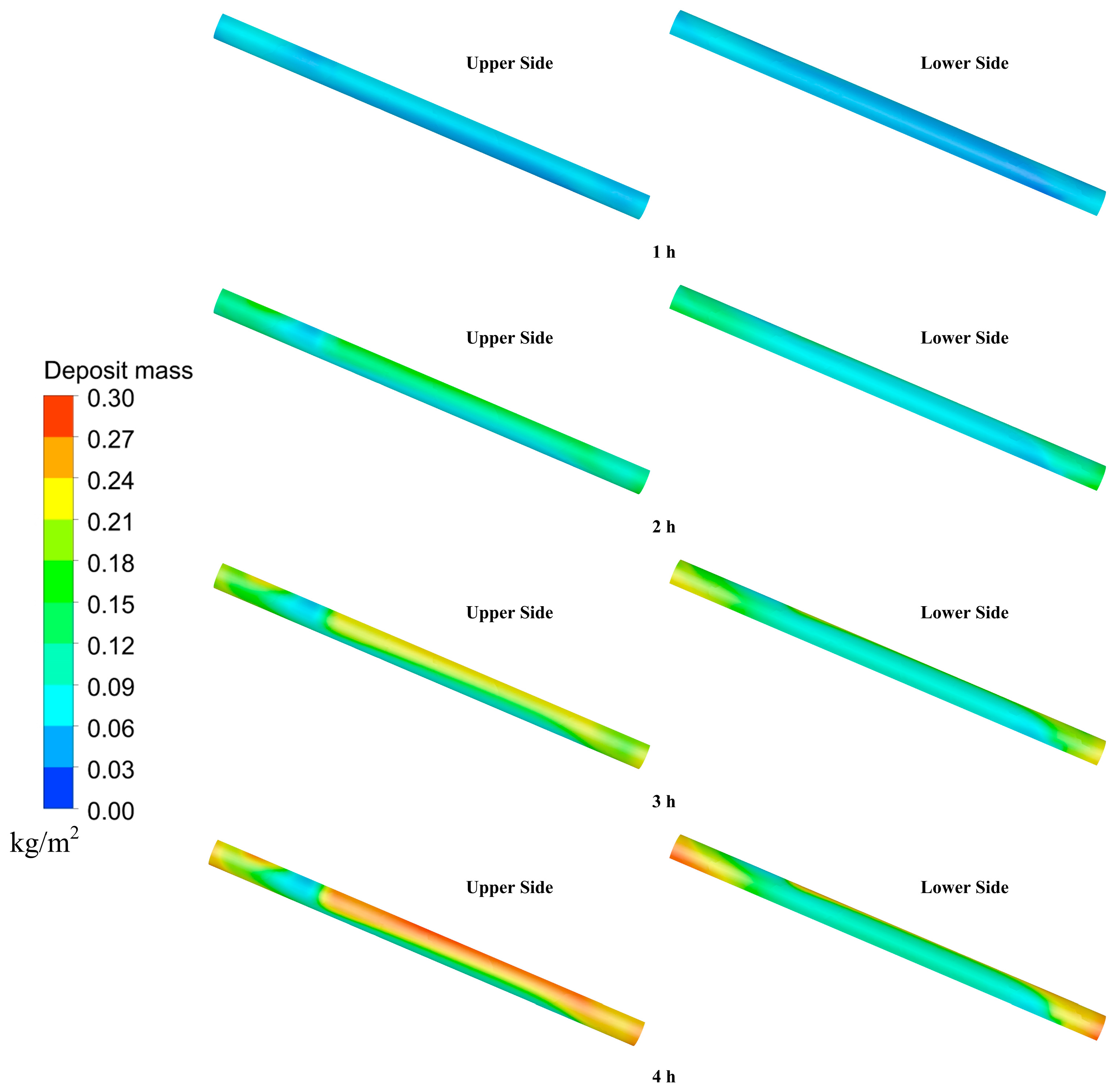
3.2. Deposition Distribution in Exhaust Heat Exchanger
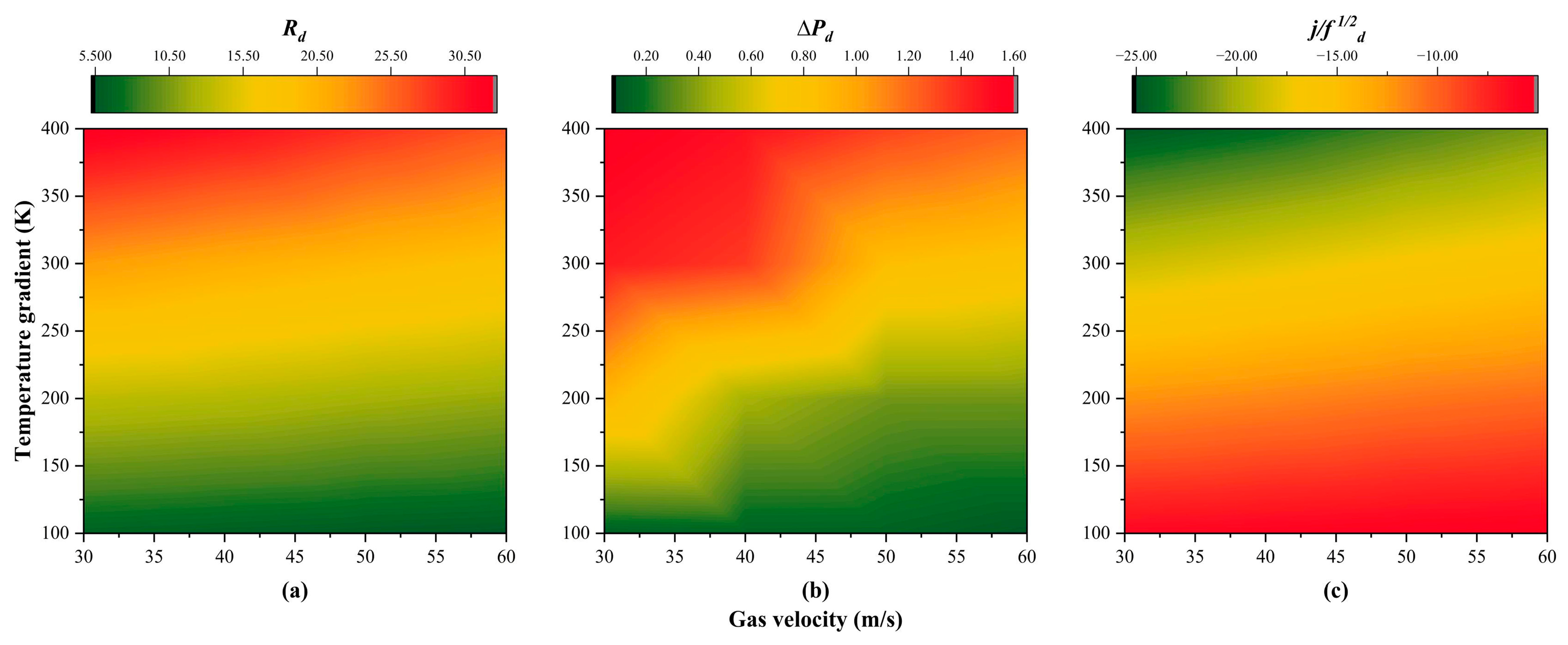
4. Performance Variation under All Engine Operating Conditions
5. Conclusions
- (1)
- Soot deposition is primarily influenced by thermophoresis, and both thermal resistance and pressure drop rise gradually during the 4 h deposition period.
- (2)
- The exhaust heat exchanger with high gas velocity and low temperature gradient exhibits optimal performance after the 4 h deposition period.
- (3)
- Under all engine-operating conditions, the deterioration in the normalized relative varies from 5.26% to 24.91%. Meanwhile, in the design of the exhaust heat exchangers, employing a high-design gas velocity is an effective method for mitigating soot deposition.
- (4)
- It is undeniable that the deposit layer thickness on the flow area will be non-negligible after prolonged deposition. In future works, this aspect will be integrated into the deposition model to better guide the design of exhaust heat exchangers with superior long-term performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- BP p.l.c. BP Statistical Review of World Energy 2019; BP Plc: London, UK, 2019. [Google Scholar]
- Doğan, B.; Driha, O.M.; Balsalobre Lorente, D.; Shahzad, U. The mitigating effects of economic complexity and renewable energy on carbon emissions in developed countries. Sustain. Dev. 2021, 29, 1–284. [Google Scholar] [CrossRef]
- Bagherian, M.A.; Mehranzamir, K.; Pour, A.B.; Rezania, S.; Taghavi, E.; Nabipour-Afrouzi, H.; Dalvi-Esfahani, M.; Alizadeh, S.M. Classification and analysis of optimization techniques for integrated energy systems utilizing renewable energy sources: A review for CHP and CCHP systems. Processes 2021, 9, 339. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- European Commission. Horizon 2020 Work Programme from 2018 to 2020. Available online: https://ec.europa.eu/commission/presscorner/detail/en/MEMO_17_4123 (accessed on 27 October 2017).
- Plotkin, S.; Stephens, T.; McManus, W. Vehicle Technology Deployment Pathways: An Examination of Timing and Investment Constraints; Argonne National Laboratory: Lemont, IL, USA, 2013. [Google Scholar]
- Pesyridis, A.; Asif, M.S.; Mehranfar, S.; Mahmoudzadeh Andwari, A.; Gharehghani, A.; Megaritis, T. Design of the organic Rankine cycle for high-efficiency diesel engines in marine applications. Energies 2023, 16, 4374. [Google Scholar] [CrossRef]
- Pandiyarajan, V.; Pandian, M.C.; Malan, E.; Velraj, R.; Seeniraj, R. Experimental investigation on heat recovery from diesel engine exhaust using finned shell and tube heat exchanger and thermal storage system. Appl. Energy 2011, 88, 77–87. [Google Scholar] [CrossRef]
- Cho, K.-C.; Shin, K.-Y.; Shim, J.; Bae, S.-S.; Kwon, O.-D. Performance Analysis of a Waste Heat Recovery System for a Biogas Engine Using Waste Resources in an Industrial Complex. Energies 2024, 17, 727. [Google Scholar] [CrossRef]
- Steinhagen, R.; Müller-Steinhagen, H.; Maani, K. Problems and costs due to heat exchanger fouling in New Zealand industries. Heat Transf. Eng. 1993, 14, 19–30. [Google Scholar] [CrossRef]
- Bott, T.R. Fouling of Heat Exchangers; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Müller-Steinhagen, H.; Malayeri, M.; Watkinson, A. Heat Exchanger Fouling: Mitigation and Cleaning Strategies. Heat Transf. Eng. 2011, 32, 189–196. [Google Scholar] [CrossRef]
- Hurt, R.H.; Crawford, G.P.; Shim, H.-S. Equilibrium nanostructure of primary soot particles. Proc. Combust. Inst. 2000, 28, 2539–2546. [Google Scholar] [CrossRef]
- Lee, B.U.; Byun, D.S.; Bae, G.-N.; Lee, J.-H. Thermophoretic deposition of ultrafine particles in a turbulent pipe flow: Simulation of ultrafine particle behaviour in an automobile exhaust pipe. J. Aerosol Sci. 2006, 37, 1788–1796. [Google Scholar] [CrossRef]
- Park, S.; Lee, K.S.; Park, J. Parametric study on EGR cooler fouling mechanism using model gas and Light-Duty diesel engine exhaust gas. Energies 2018, 11, 3161. [Google Scholar] [CrossRef]
- Grillot, J.; Icart, G. Fouling of a cylindrical probe and a finned tube bundle in a diesel exhaust environment. Exp. Therm. Fluid Sci. 1997, 14, 442–454. [Google Scholar] [CrossRef]
- Abd-Elhady, M.; Rindt, C.; Wijers, J.; Van Steenhoven, A.; Bramer, E.A.; Van der Meer, T.H. Minimum gas speed in heat exchangers to avoid particulate fouling. Int. J. Heat Mass Transf. 2004, 47, 3943–3955. [Google Scholar] [CrossRef]
- Abd-Elhady, M.S.; Zornek, T.; Malayeri, M.R.; Balestrino, S.; Szymkowicz, P.G.; Müller-Steinhagen, H. Influence of gas velocity on particulate fouling of exhaust gas recirculation coolers. Int. J. Heat Mass Transf. 2011, 54, 838–846. [Google Scholar] [CrossRef]
- Aiello, V.C.; Kini, G.; Staedter, M.A.; Garimella, S. Investigation of fouling mechanisms for diesel engine exhaust heat recovery. Appl. Therm. Eng. 2020, 181, 115973. [Google Scholar] [CrossRef]
- Lee, B.-H.; Hwang, M.-Y.; Seon, C.-Y.; Jeon, C.-H. Numerical prediction of characteristics of ash deposition in heavy fuel oil heat recovery steam generator. J. Mech. Sci. Technol. 2014, 28, 2889–2900. [Google Scholar] [CrossRef]
- Kasper, R.; Turnow, J.; Kornev, N. Numerical modeling and simulation of particulate fouling of structured heat transfer surfaces using a multiphase Euler-Lagrange approach. Int. J. Heat Mass Transf. 2017, 115, 932–945. [Google Scholar] [CrossRef]
- Han, Z.; Xu, Z.; Sun, A.; Yu, X. The deposition characteristics of micron particles in heat exchange pipelines. Appl. Therm. Eng. 2019, 158, 113732. [Google Scholar] [CrossRef]
- Silaipillayarputhur, K.; Khurshid, H. The design of shell and tube heat exchangers–A review. Int. J. Mech. Prod. Eng. Res. Dev. 2019, 9, 87–102. [Google Scholar]
- Patel, D.S.; Parmar, R.R.; Prajapati, V.M. CFD Analysis of Shell and tube heat exchangers-A review. Int. Res. J. Eng. Technol. 2015, 17, 2231–2235. [Google Scholar]
- Hu, S.; Liang, Y.; Ding, R.; Xing, L.; Su, W.; Lin, X.; Zhou, N. Research on Off-Design Characteristics and Control of an Innovative S-CO2 Power Cycle Driven by the Flue Gas Waste Heat. Energies 2024, 17, 1871. [Google Scholar] [CrossRef]
- ANSYS Fluent. ANSYS FLUENT Theory Guide: Version 2020R1. Available online: https://ansyshelp.ansys.com/ (accessed on 30 July 2024).
- Wang, Q.-W.; Lin, M.; Zeng, M.; Tian, L. Investigation of turbulent flow and heat transfer in periodic wavy channel of internally finned tube with blocked core tube. J. Heat Transf. 2008, 130, 061801. [Google Scholar] [CrossRef]
- Jiaqiang, E.; Han, D.; Deng, Y.; Zuo, W.; Qian, C.; Wu, G.; Peng, Q.; Zhang, Z. Performance enhancement of a baffle-cut heat exchanger of exhaust gas recirculation. Appl. Therm. Eng. 2018, 134, 86–94. [Google Scholar]
- Epstein, N. Thinking about heat transfer fouling: A 5 × 5 matrix. Heat Transf. Eng. 1983, 4, 43–56. [Google Scholar] [CrossRef]
- Abarham, M.; Hoard, J.; Assanis, D.N.; Styles, D.; Curtis, E.W.; Ramesh, N. Review of soot deposition and removal mechanisms in EGR coolers. SAE Int. J. Fuels Lubr. 2010, 3, 690–704. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, T.; Tian, H.; Shu, G.; Zhang, H. Experimental and numerical investigation of soot deposition on exhaust heat exchanger tube banks. Therm. Sci. Eng. Prog. 2023, 39, 101699. [Google Scholar] [CrossRef]
- Pulkrabek, W.W. Engineering fundamentals of the internal combustion engine. J. Eng. Gas Turbines Power 2004, 126, 106. [Google Scholar] [CrossRef]
- Li, X. Research on Design and Performance Optimization of Diesel Engine Waste Heat Recovery Bottoming System and Exhaust Heat Exchanger; Tianjin University: Tianjin, China, 2014. [Google Scholar]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST reference fluid thermodynamic and transport properties–REFPROP. NIST Stand. Ref. Database 2002, 23, v7. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. The Properties of Gases and Liquids; Mcgraw-Hill: New York, NY, USA, 2001; Volume 5. [Google Scholar]
- Warey, A.; Balestrino, S.; Szymkowicz, P.; Malayeri, M.R. A one-dimensional model for particulate deposition and hydrocarbon condensation in exhaust gas recirculation coolers. Aerosol Sci. Technol. 2012, 46, 198–213. [Google Scholar] [CrossRef]
- Tian, J. Study on Effect of PODE on PM Properties of Diesel Engine Exhaust and DPF Regeneration; Jiangsu University: Zhenjiang, China, 2020. [Google Scholar]
- Malayeri, M.R.; Zornek, T.; Balestrino, S.; Warey, A.; Szymkowicz, P.G. Deposition of nanosized soot particles in various EGR coolers under thermophoretic and isothermal conditions. Heat Transf. Eng. 2013, 34, 665–673. [Google Scholar] [CrossRef]
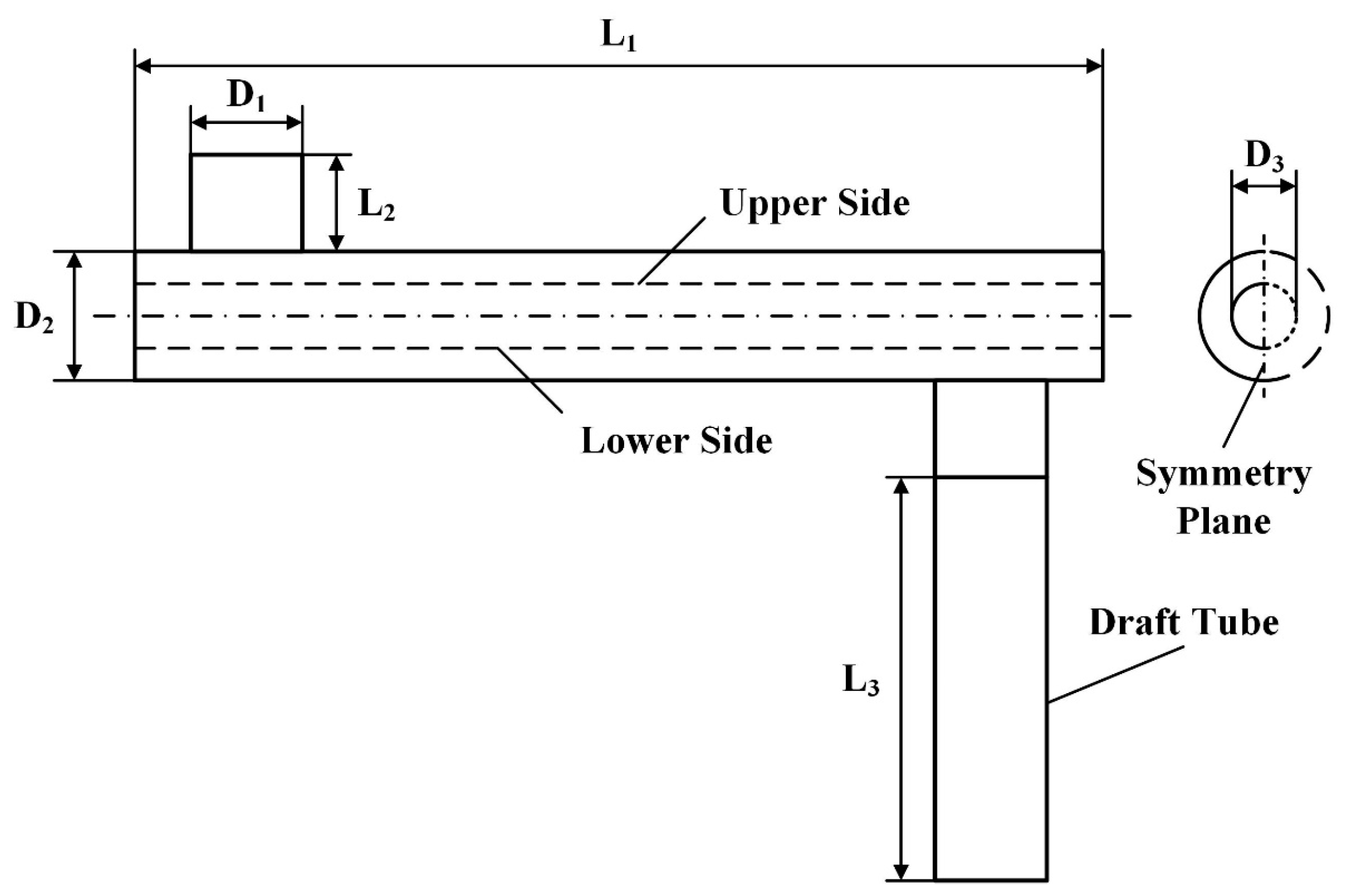




| Parameter | Unit | Values |
|---|---|---|
| Inlet temperature of exhaust gas | K | 393.15–693.15 |
| Inlet velocity of exhaust gas | m/s | 30–60 |
| Outlet pressure of exhaust gas | Pa | 0 |
| Temperature of tube wall | K | 293.15 |
| Parameter | Formulas | / |
|---|---|---|
| Deposit Process | ||
| Diffusion deposition velocity | , where , | = 1.380649 × 10−23 J/K |
| Inertial impaction deposition velocity | / | |
| Thermophoretic deposition velocity | , where , | = 1.17, = 1.2 = 1.1 |
| Particle-sticking probability | , where | = 10–20 J |
| Removal Process | ||
| Removal mass | = 1 | |
| Parameter | Unit | Temperature (K) | Formula |
|---|---|---|---|
| Density | kg/m3 | 320–800 | |
| Specific heat capacity | J/(kg∙K) | ||
| Thermal conductivity | W/(m∙K) | ||
| Viscosity | kg/(m∙s) |
| Parameter | Unit | Value |
|---|---|---|
| Soot particles | ||
| Diameter | nm | 130 |
| Mass concentration | kg/m3 | 1.7 × 10−5 |
| Density | kg/m3 | 1800 |
| Thermal conductivity | W/m∙K | 0.5 |
| Deposit layer | ||
| Density | kg/m3 | 35 |
| Thermal conductivity | W/m∙K | 0.05 |
| Inlet Gas Velocity (m/s) | Inlet Gas Temperature (K) | Tube Wall Temperature (K) | Number | Number of Grids | Heat Exchange Capacity (W) |
|---|---|---|---|---|---|
| 30 | 673.15 | 353.15 | Grid 1 | 57,954 | 121.57 |
| Grid 2 | 76,588 | 126.85 | |||
| Grid 3 | 98,918 | 125.62 | |||
| Grid 4 | 117,994 | 127.21 | |||
| Grid 5 | 136,568 | 125.73 | |||
| Grid 6 | 161,024 | 126.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Li, H.; Wu, Y.; Che, J.; Fang, M.; Li, X. Analysis of Soot Deposition Effects on Exhaust Heat Exchanger for Waste Heat Recovery System. Energies 2024, 17, 4259. https://doi.org/10.3390/en17174259
Chen T, Li H, Wu Y, Che J, Fang M, Li X. Analysis of Soot Deposition Effects on Exhaust Heat Exchanger for Waste Heat Recovery System. Energies. 2024; 17(17):4259. https://doi.org/10.3390/en17174259
Chicago/Turabian StyleChen, Tianyu, Hanqing Li, Yuzeng Wu, Jiaqi Che, Mingming Fang, and Xupeng Li. 2024. "Analysis of Soot Deposition Effects on Exhaust Heat Exchanger for Waste Heat Recovery System" Energies 17, no. 17: 4259. https://doi.org/10.3390/en17174259
APA StyleChen, T., Li, H., Wu, Y., Che, J., Fang, M., & Li, X. (2024). Analysis of Soot Deposition Effects on Exhaust Heat Exchanger for Waste Heat Recovery System. Energies, 17(17), 4259. https://doi.org/10.3390/en17174259






