Contemporary and Conventional Passive Methods of Intensifying Convective Heat Transfer—A Review
Abstract
:1. Introduction
2. The Variety of Heat Transfer Intensification Methods
- Co-current—the flow of media takes place in parallel and consistent directions;
- Counter-current (counterflow)—the flow of media takes place in parallel and opposite directions;
- Cross—the flow of factors takes place in directions perpendicular to one another;
- Mixed—the design of the exchanger combines the features of two or more systems.
- Diaphragmless heat exchangers—heat exchange occurs during direct contact of factors and is inseparably related to mass exchange;
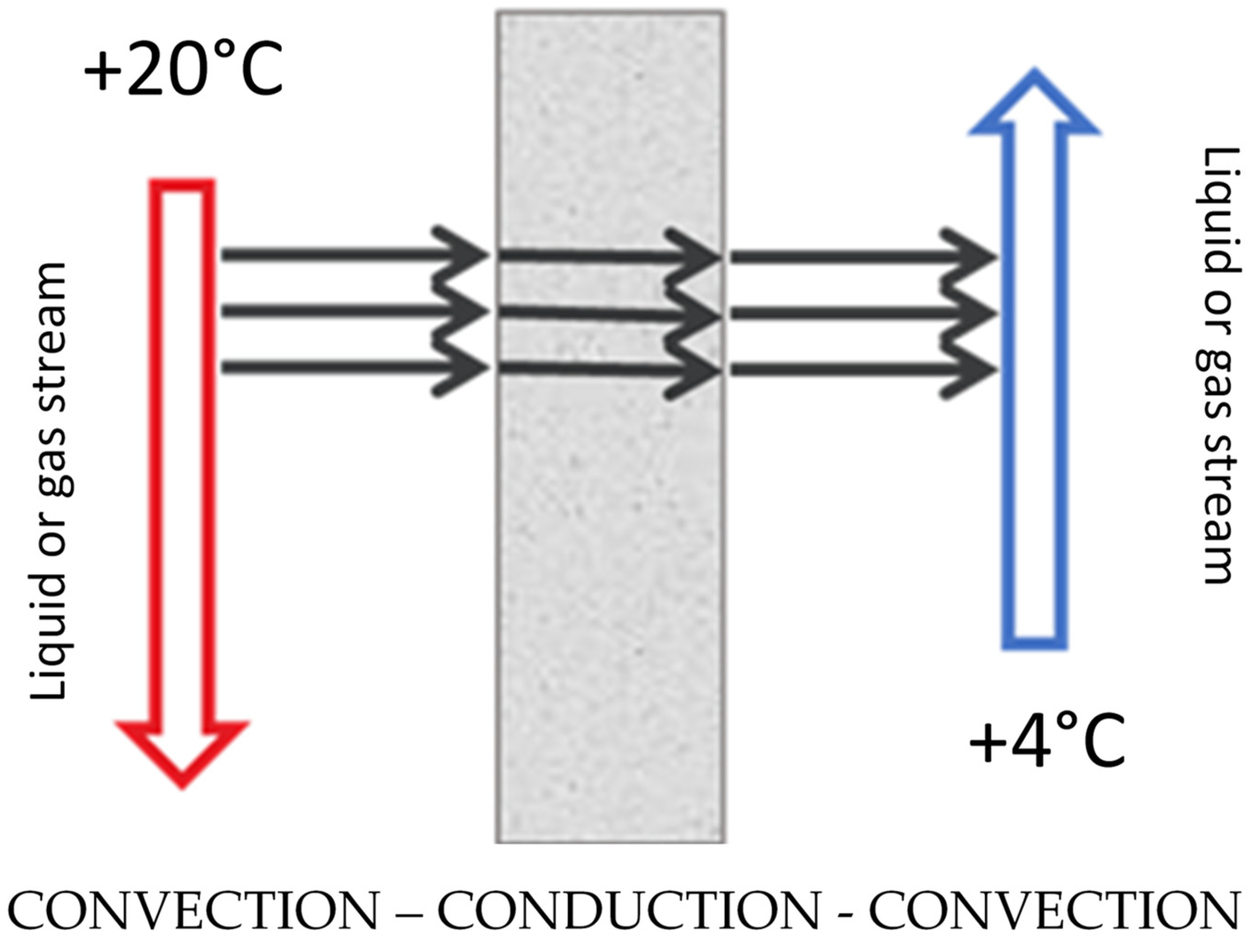
- Recuperators—heat exchange agents are separated from one another by a partition through which heat penetrates (usually the partition is made up of pipe walls, sometimes plates); heat from the medium with a higher temperature is taken over by the wall, then heat conduction through the partition takes place, and in the next step heat is transferred from the other side of the partition by a medium with a lower temperature;
- Regenerators—heat transfer takes place through a solid material filling, which can move or remain stationary; fluids flow in them alternately through channels in the filling mass.
3. New Approaches to Heat Exchangers’ Construction
Helically Coiled Tubes
4. Passive Methods
4.1. Ribs, Perforations, Partitions
4.2. Metal Foams
4.3. Twisted Tapes
4.4. Surface Layers Modifications
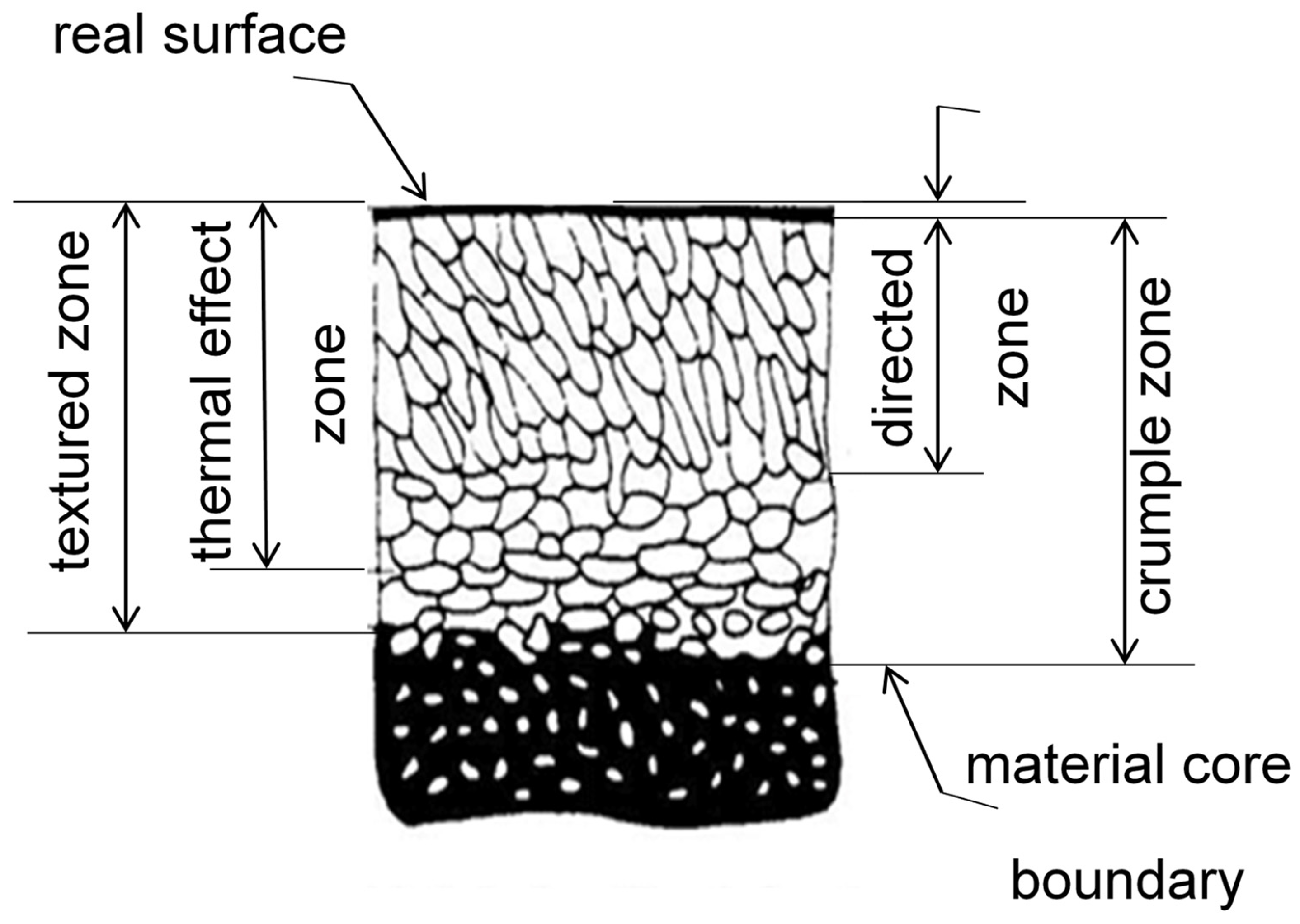
- Near-surface zone—directly adjacent to the real surface, does not have a proper structure;
- Directed zone—there are directed grains in it,
- Thermal effect zone—there is a change in grain size, phase transitions, or chemical reactions caused by thermal processes;
- Textured zone—there is a crystalline texture in it;
- Crumple zone—the zone in which plastic deformation has occurred.
- The conventional division of zones in the surface layer is presented in Figure 3.
- Reduction in the volume or weight of the heat transfer surface material for the same pumping power and heat load, which can result in lower production costs.
- Increasing the total heat transfer coefficient for equal pumping power and constant total length of the exchanger tubes, which can be achieved in two ways:
- by obtaining an increased heat load for a constant temperature of the influent liquid;
- by providing a reduced mean logarithmic temperature difference for a constant heat load.
- Reduction of pumping power for equal heat load and total length of exchanger tubes.
4.4.1. Microchannels
4.4.2. Dimples
4.5. Nanofluids
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pudlik, W. Wymiana i Wymienniki Ciepła: Podręcznik dla Studentów Wydziałów Mechanicznych Specjalizujących się w Technikach Cieplnych i Chłodniczych; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2012. [Google Scholar]
- Ullrich, H.-J. Technika Chłodnicza—Poradnik. Tom 1; IPPU MASTA Sp.z o.o.: Gdańsk, Poland, 1999. [Google Scholar]
- Reif-Acherman, S. Early and current experimental methods for determining thermal conductivities of metals. Int. J. Heat Mass Transf. 2014, 77, 542–563. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Fundamentals of Materials Science and Engineering: An Integrated Approach; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Zhao, J.; Dong, H.; Wang, X.; Fu, X. Research on heat transfer characteristic of crude oil during the tubular heating process in the floating roof tank. Case Stud. Therm. Eng. 2017, 10, 142–153. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Madejski, J.; Nowak, A.J. Teoria Wymiany Ciepła; Wydawnictwa Uczelniane PS: Szczecin, Poland, 1998. [Google Scholar]
- Romanowski, R. Wiktor Schauberger; genialny leśniczy. In Projektowanie i Konstrukcje Inżynierskie; ITER: Warszawa, Poland, 2014; Volume 12. [Google Scholar]
- Mikielewicz, D.; Stąsiek, A.; Jewartowski, M.; Stąsiek, J. Measurements of heat transfer enhanced by the use of transverse vortex generators. Appl. Therm. Eng. 2012, 49, 61–72. [Google Scholar]
- Bergles, A.E.; Webb, R.L.; American Society of Mechanical Engineers. Augmentation of Convective Heat and Mass Transfer; American Society of Mechanical Engineers (ASME): New York, NY, USA, 1970; 162p. [Google Scholar]
- Ibrahim, T.K.; Mohammed, M.N.; Kamil Mohammed, M.; Najafi, G.; Azwadi Che Sidik, N.; Basrawi, F.; Abdalla, A.N.; Hoseini, S.S. Experimental study on the effect of perforations shapes on vertical heated fins performance under forced convection heat transfer. Int. J. Heat Mass Transf. 2018, 118, 832–846. [Google Scholar] [CrossRef]
- Mareš, J.; Hubík, P.; Šesták, J.; Špička, V.; Krištofik, J.; Stávek, J. Phenomenological approach to the caloric theory of heat. Thermochim. Acta 2008, 474, 16–24. [Google Scholar] [CrossRef]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 1. [Google Scholar]
- Szolc, T. Maszynoznawstwo dla Zasadniczych Szkół Zawodowych Chłodniczych, 5th ed.; Izabela, H., Ed.; Wydawnictwa Szkolne i Pedagogiczne: Warszawa, Poland, 1988. [Google Scholar]
- Leszczyński, H. Aparatura i Urządzenia Chłodnicze; Wydawnictwa Szkolne i Pedagogiczne: Warszawa, Poland, 1990; p. 430. [Google Scholar]
- Alam, T.; Kim, M.-H. A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew. Sustain. Energy Rev. 2018, 81, 813–839. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Abou Al-Sood, M.M.; El-Said, E.M.S.; Younes, M.M.; El-Fakharany, M.K. A comprehensive review of methods of heat transfer enhancement in shell and tube heat exchangers. J. Therm. Anal. Calorim. 2023, 148, 7539–7578. [Google Scholar] [CrossRef]
- Sadeghianjahromi, A.; Wang, C.-C. Heat transfer enhancement in fin-and-tube heat exchangers—A review on different mechanisms. Renew. Sustain. Energy Rev. 2021, 137, 110470. [Google Scholar] [CrossRef]
- Azeez mohammed Hussein, H.; Zulkifli, R.; Faizal Bin Wan Mahmood, W.M.; Ajeel, R.K. Structure parameters and designs and their impact on performance of different heat exchangers: A review. Renew. Sustain. Energy Rev. 2022, 154, 111842. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Al-Sood, M.M.A.; El-Fakharany, M.K.; El-Said, E.M.S. A comparative numerical study of shell and multi-tube heat exchanger performance with different baffles configurations. Int. J. Therm. Sci. 2022, 179, 107655. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Abou Al-Sood, M.M.; El-Said, E.M.S.; El-Fakharany, M.K.; Younes, M.M. Study of heat transfer and pressure drop for novel configurations of helical tube heat exchanger: A numerical and experimental approach. J. Therm. Anal. Calorim. 2023, 148, 6267–6282. [Google Scholar] [CrossRef]
- Venkata Rao, R.; Majethia, M. Design optimization of shell-and-tube heat exchanger using Rao algorithms and their variants. Therm. Sci. Eng. Prog. 2022, 36, 101520. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mahariq, I.; Alhuyi Nazari, M.; Accouche, O.; Bhatti, M.M. Comprehensive review on exergy analysis of shell and tube heat exchangers. J. Therm. Anal. Calorim. 2022, 147, 12301–12311. [Google Scholar] [CrossRef]
- Indumathy, M.; Sobana, S.; Panda, B.; Panda, R.C. Modelling and control of plate heat exchanger with continuous high-temperature short time milk pasteurization process—A review. Chem. Eng. J. Adv. 2022, 11, 100305. [Google Scholar] [CrossRef]
- Mastani Joybari, M.; Selvnes, H.; Sevault, A.; Hafner, A. Potentials and challenges for pillow-plate heat exchangers: State-of-the-art review. Appl. Therm. Eng. 2022, 214, 118739. [Google Scholar] [CrossRef]
- Aboul Khail, A.; Erişen, A. Heat transfer and performance enhancement investigation of novel plate heat exchanger. Therm. Sci. Eng. Prog. 2022, 34, 101368. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Abou Al-Sood, M.M.; El-Said, E.M.; Younes, M.M.; El-Fakharany, M.K. Evaluating the effects of bifurcation angle on the performance of a novel heat exchanger based on contractual theory. Renew. Energy 2023, 219, 119463. [Google Scholar] [CrossRef]
- Xu, P.; Zhou, T.; Xing, J.; Fu, Z. Numerical investigation of heat transfer enhancement in helically coiled specifically-shaped tube heat exchangers. Nucl. Eng. Des. 2022, 396, 111896. [Google Scholar] [CrossRef]
- Miansari, M.; Darvishi, M.R.; Toghraie, D.; Barnoon, P.; Shirzad, M.; Alizadeh, A.a. Numerical investigation of grooves effects on the thermal performance of helically grooved shell and coil tube heat exchanger. Chin. J. Chem. Eng. 2022, 44, 424–434. [Google Scholar] [CrossRef]
- Tuncer, A.D.; Sözen, A.; Khanlari, A.; Gürbüz, E.Y.; Variyenli, H.İ. Analysis of thermal performance of an improved shell and helically coiled heat exchanger. Appl. Therm. Eng. 2021, 184, 116272. [Google Scholar] [CrossRef]
- Wang, G.; Liu, A.; Dbouk, T.; Wang, D.; Peng, X.; Ali, A. Optimal shape design and performance investigation of helically coiled tube heat exchanger applying MO-SHERPA. Int. J. Heat Mass Transf. 2022, 184, 122256. [Google Scholar] [CrossRef]
- Ali, S.K.; Azzawi, I.D.J.; Khadom, A.A. Experimental validation and numerical investigation for optimization and evaluation of heat transfer enhancement in double coil heat exchanger. Therm. Sci. Eng. Prog. 2021, 22, 100862. [Google Scholar] [CrossRef]
- Fan, M.; Bao, Z.; Liu, S.; Huang, W. Flow and heat transfer in the eccentric annulus of the helically coiled tube-in-tube heat exchanger used in an aero-engine. Int. J. Therm. Sci. 2022, 179, 107636. [Google Scholar] [CrossRef]
- Lebbihiat, N.; Atia, A.; Arıcı, M.; Meneceur, N.; Hadjadj, A.; Chetioui, Y. Thermal performance analysis of helical ground-air heat exchanger under hot climate: In situ measurement and numerical simulation. Energy 2022, 254, 124429. [Google Scholar] [CrossRef]
- Liu, P.; Wang, R.; Liu, S.; Bao, Z. Experimental study on the thermal-hydraulic performance of a tube-in-tube helical coil air–fuel heat exchanger for an aero-engine. Energy 2023, 267, 126626. [Google Scholar] [CrossRef]
- Pathak, S.; Shukla, S.K.; Sagade, A.A. Novel multi-helical coil heat exchanger-based small-scale organic Rankine cycle: A detailed heat transfer analysis. Energy 2023, 277, 127684. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Abou Al-Sood, M.M.; El-Said, E.M.S.; Younes, M.M.; El-Fakharany, M.K. Experimental and numerical investigation of a novel fractal tube configuration in helically tube heat exchanger. Int. J. Therm. Sci. 2023, 187, 108175. [Google Scholar] [CrossRef]
- Vivekanandan, M.; Venkatesh, R.; Periyasamy, R.; Mohankumar, S.; Devakumar, L. Experimental and CFD investigation of helical coil heat exchanger with flower baffle. Mater. Today Proc. 2021, 37, 2174–2182. [Google Scholar] [CrossRef]
- Heydari, O.; Miansari, M.; Arasteh, H.; Toghraie, D. Optimizing the hydrothermal performance of helically corrugated coiled tube heat exchangers using Taguchi’s empirical method: Energy and exergy analysis. J. Therm. Anal. Calorim. 2021, 145, 2741–2752. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, C.-c.; Zhu, Y.-j.; Wu, X.-h.; Jin, T.-x.; Li, J.-n. Investigation of heat transfer Exergy loss number and its application in optimization for the shell and helically coiled tube heat exchanger. Appl. Therm. Eng. 2022, 211, 118424. [Google Scholar] [CrossRef]
- Awasarmol, U.V.; Pise, A.T. An experimental investigation of natural convection heat transfer enhancement from perforated rectangular fins array at different inclinations. Exp. Therm. Fluid Sci. 2015, 68, 145–154. [Google Scholar] [CrossRef]
- Mikuž, B.; Tiselj, I. URANS prediction of flow fluctuations in rod bundle with split-type spacer grid. Int. J. Heat Fluid Flow 2017, 64, 10–22. [Google Scholar] [CrossRef]
- Kurian, R.; Balaji, C.; Venkateshan, S.P. Experimental investigation of near compact wire mesh heat exchangers. Appl. Therm. Eng. 2016, 108, 1158–1167. [Google Scholar] [CrossRef]
- Pham, K.-Q.; Nguyen, Q.-H.; Duy, V.; Dinh, C.T. Effects of Boot-Shaped Rib On Heat Transfer Characteristics of Internal Cooling Turbine Blades. J. Heat Transf. 2020, 142, 102106. [Google Scholar] [CrossRef]
- Dinh, C.-T.; Do, K.-D.C.; Chung, D.-H.; Truong, H.-S. Effects of pin-fins with trapezoidal endwall on heat transfer characteristics in gas turbine blade internal cooling channels. J. Mech. Sci. Technol. 2023, 37, 2199–2210. [Google Scholar] [CrossRef]
- Do, K.-D.C.; Chung, D.-H.; Tran, D.-Q.; Dinh, C.-T.; Nguyen, Q.-H.; Kim, K.-Y. Numerical Investigation of Heat Transfer Characteristics of Pin-Fins with Roughed Endwalls in Gas Turbine Blade Internal Cooling Channels. Int. J. Heat Mass Transf. 2022, 195, 123125. [Google Scholar] [CrossRef]
- Paknezhad, M.; Rashidi, A.M.; Yousefi, T.; Saghir, Z. Effect of aluminum-foam heat sink on inclined hot surface temperature in the case of free convection heat transfer. Case Stud. Therm. Eng. 2017, 10, 199–206. [Google Scholar] [CrossRef]
- Changdar, A.; Chakraborty, S.S. Laser processing of metal foam—A review. J. Manuf. Process. 2021, 61, 208–225. [Google Scholar] [CrossRef]
- Bucher, T.; Bolger, C.; Zhang, M.; Chen, C.J.; Yao, Y.L. Effect of Geometrical Modeling on Prediction of Laser-Induced Heat Transfer in Metal Foam. Procedia Manuf. 2016, 5, 1265–1282. [Google Scholar] [CrossRef]
- Plocek, M.; Zawadzki, A. Złożone (kombinowane) metody intensyfikacji konwekcyjnej wymiany ciepła przy przepływie jednofazowym płynów w rurach. Chłodnictwo Organ Nacz. Organ. Tech. 2007, 42, 14–22. [Google Scholar]
- Zawadzki, A.; Plocek, M.; Kapusta, T.; Kasieczka, W. Charakterystyki wymiany ciepła i oporów przepływu dla jednofazowego przepływu w rurze poziomej z mikroożebrowaniem wewnętrznym i wkładkami ze skręconej taśmy—Badania eksperymentalne—XI dni chłodnictwa. In Proceedings of the Międzynarodowa Konferencja Chłodnicza XL Dni Chłodnictwa Poznań, Poznań, Poland, 15–17 October 2008. [Google Scholar]
- Marner, W.; Bergles, A.E. Augmentation of tubeside laminar flow heat transfer by means of twisted-tape inserts, static-mixer inserts, and internally finned tubes. In Proceedings of the International Heat Transfer Conference Digital Library, Toronto, ON, Canada, 7–11 August 1978. [Google Scholar]
- Usui, H.; Sano, Y.; Iwashita, K. Heat transfer enhancement effects by combined use of internally grooved rough surfaces and twisted tapes. Heat Transf. Jpn. Res 1984, 13, 19–32. [Google Scholar] [CrossRef]
- Singh Suri, A.R.; Kumar, A.; Maithani, R. Effect of square wings in multiple square perforated twisted tapes on fluid flow and heat transfer of heat exchanger tube. Case Stud. Therm. Eng. 2017, 10, 28–43. [Google Scholar] [CrossRef]
- Mashoofi, N.; Pourahmad, S.; Pesteei, S.M. Study the effect of axially perforated twisted tapes on the thermal performance enhancement factor of a double tube heat exchanger. Case Stud. Therm. Eng. 2017, 10, 161–168. [Google Scholar] [CrossRef]
- Hameed, V.M.; Hussein, M.A. Effect of new type of enhancement on inside and outside surface of the tube side in single pass heat exchanger. Appl. Therm. Eng. 2017, 122, 484–491. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Chaedir, B.A.; Sasmito, A.P. Laminar convective heat transfer in helical tube with twisted tape insert. Int. J. Heat Mass Transf. 2020, 150, 119309. [Google Scholar] [CrossRef]
- Liaw, K.L.; Kurnia, J.C.; Sasmito, A.P. Turbulent convective heat transfer in helical tube with twisted tape insert. Int. J. Heat Mass Transf. 2021, 169, 120918. [Google Scholar] [CrossRef]
- Implements, T. Charakterystyka Warstwy Wierzchniej. 2021. Available online: https://www.tizimplements.pl/charakterystyka-warstwy-wierzchniej/ (accessed on 2 May 2023).
- Sinha, G.K.; Dharmaraj, R.H.; Haridas, D.; Srivastava, A. Performance evaluation of compact channels with surface modifications for heat transfer enhancement: An interferometric study in developing flow regime. Int. J. Heat Fluid Flow 2017, 64, 55–65. [Google Scholar] [CrossRef]
- Webb, R.L. Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design. Int. J. Heat Mass Transf. 1981, 24, 715–726. [Google Scholar] [CrossRef]
- Zimparov, V.D.; Vulchanov, N.L. Performance evaluation criteria for enhanced heat transfer surfaces. Int. J. Heat Mass Transf. 1994, 37, 1807–1816. [Google Scholar] [CrossRef]
- Bergles, A.; Bunn, R.; Junkhan, G. Extended performance evaluation criteria for enhanced heat transfer surfaces. Lett. Heat Mass Transf. 1974, 1, 113–120. [Google Scholar] [CrossRef]
- Bergles, A.; Blumenkrantz, A.; Taborek, J. Performance evaluation criteria for enhanced heat transfer surfaces. In Proceedings of the International Heat Transfer Conference Digital Library, Tokyo, Japan, 3–7 September 1974. [Google Scholar]
- Webb, R.; Eckert, E. Application of rough surfaces to heat exchanger design. Int. J. Heat Mass Transf. 1972, 15, 1647–1658. [Google Scholar] [CrossRef]
- Webb, R.; Scott, M. A parametric analysis of the performance of internally finned tubes for heat exchanger application. J. Heat Transf. 1980, 102, 38–43. [Google Scholar] [CrossRef]
- Leong, K.C.; Ho, J.Y.; Wong, K.K. A critical review of pool and flow boiling heat transfer of dielectric fluids on enhanced surfaces. Appl. Therm. Eng. 2017, 112, 999–1019. [Google Scholar] [CrossRef]
- Mori, S.; Utaka, Y. Critical heat flux enhancement by surface modification in a saturated pool boiling: A review. Int. J. Heat Mass Transf. 2017, 108, 2534–2557. [Google Scholar] [CrossRef]
- Jacobi, A.M.; Shah, R.K. Heat transfer surface enhancement through the use of longitudinal vortices: A review of recent progress. Exp. Therm. Fluid Sci. 1995, 11, 295–309. [Google Scholar] [CrossRef]
- Canpolat, C. Characteristics of flow past a circular cylinder with a rectangular groove. Flow Meas. Instrum. 2015, 45, 233–246. [Google Scholar] [CrossRef]
- Canpolat, C.; Sahin, B. Influence of single rectangular groove on the flow past a circular cylinder. Int. J. Heat Fluid Flow 2017, 64, 79–88. [Google Scholar] [CrossRef]
- Forooghi, P.; Flory, M.; Bertsche, D.; Wetzel, T.; Frohnapfel, B. Heat transfer enhancement on the liquid side of an industrially designed flat-tube heat exchanger with passive inserts—Numerical investigation. Appl. Therm. Eng. 2017, 123, 573–583. [Google Scholar] [CrossRef]
- Wen, R.; Li, Q.; Wang, W.; Latour, B.; Li, C.H.; Li, C.; Lee, Y.-C.; Yang, R. Enhanced bubble nucleation and liquid rewetting for highly efficient boiling heat transfer on two-level hierarchical surfaces with patterned copper nanowire arrays. Nano Energy 2017, 38, 59–65. [Google Scholar] [CrossRef]
- Hu, H.; Xu, C.; Zhao, Y.; Shaeffer, R.; Ziegler, K.J.; Chung, J.N. Modification and enhancement of cryogenic quenching heat transfer by a nanoporous surface. Int. J. Heat Mass Transf. 2015, 80, 636–643. [Google Scholar] [CrossRef]
- Taha, T.J.; Mojet, B.L.; Lefferts, L.; van der Meer, T.H. Effect of carbon nanofiber surface morphology on convective heat transfer from cylindrical surface: Synthesis, characterization and heat transfer measurement. Int. J. Therm. Sci. 2016, 105, 13–21. [Google Scholar] [CrossRef]
- Li, Y.-Y.; Liu, Z.-H.; Zheng, B.-C. Experimental study on the saturated pool boiling heat transfer on nano-scale modification surface. Int. J. Heat Mass Transf. 2015, 84, 550–561. [Google Scholar] [CrossRef]
- Das, S.; Saha, B.; Bhaumik, S. Experimental study of nucleate pool boiling heat transfer of water by surface functionalization with SiO2 nanostructure. Exp. Therm. Fluid Sci. 2017, 81, 454–465. [Google Scholar] [CrossRef]
- Das, S.; Saha, B.; Bhaumik, S. Experimental study of nucleate pool boiling heat transfer of water by surface functionalization with crystalline TiO2 nanostructure. Appl. Therm. Eng. 2017, 113, 1345–1357. [Google Scholar] [CrossRef]
- Asadi, M.; Xie, G.; Sunden, B. A review of heat transfer and pressure drop characteristics of single and two-phase microchannels. Int. J. Heat Mass Transf. 2014, 79, 34–53. [Google Scholar] [CrossRef]
- Harris, M.; Wu, H.; Zhang, W.; Angelopoulou, A. Overview of recent trends in microchannels for heat transfer and thermal management applications. Chem. Eng. Process. Process Intensif. 2022, 181, 109155. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Steinke, M.E.; Kandlikar, S.G. Single-phase liquid friction factors in microchannels. Int. J. Therm. Sci. 2006, 45, 1073–1083. [Google Scholar] [CrossRef]
- Rosa, P.; Karayiannis, T.G.; Collins, M.W. Single-phase heat transfer in microchannels: The importance of scaling effects. Appl. Therm. Eng. 2009, 29, 3447–3468. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.D.; Wang, H.S. Numerical study of laminar flow and heat transfer in microchannel heat sink with offset ribs on sidewalls. Appl. Therm. Eng. 2016, 92, 32–41. [Google Scholar] [CrossRef]
- Tang, W.; Sun, L.; Liu, H.; Xie, G.; Mo, Z.; Tang, J. Improvement of flow distribution and heat transfer performance of a self-similarity heat sink with a modification to its structure. Appl. Therm. Eng. 2017, 121, 163–171. [Google Scholar] [CrossRef]
- Soleimanikutanaei, S.; Ghasemisahebi, E.; Lin, C.-X. Numerical study of heat transfer enhancement using transverse microchannels in a heat sink. Int. J. Therm. Sci. 2018, 125, 89–100. [Google Scholar] [CrossRef]
- Yadav, V.; Baghel, K.; Kumar, R.; Kadam, S.T. Numerical investigation of heat transfer in extended surface microchannels. Int. J. Heat Mass Transf. 2016, 93, 612–622. [Google Scholar] [CrossRef]
- Li, Y.F.; Xia, G.D.; Ma, D.D.; Jia, Y.T.; Wang, J. Characteristics of laminar flow and heat transfer in microchannel heat sink with triangular cavities and rectangular ribs. Int. J. Heat Mass Transf. 2016, 98, 17–28. [Google Scholar] [CrossRef]
- Isaev, S.; Leontiev, A.; Gritskevich, M.; Nikushchenko, D.; Guvernyuk, S.; Sudakov, A.; Chung, K.-M.; Tryaskin, N.; Zubin, M.; Sinyavin, A. Development of energy efficient structured plates with zigzag arrangement of multirow inclined oval trench dimples. Int. J. Therm. Sci. 2023, 184, 107988. [Google Scholar] [CrossRef]
- Leontiev, A.I.; Kiselev, N.A.; Vinogradov, Y.A.; Strongin, M.M.; Zditovets, A.G.; Burtsev, S.A. Experimental investigation of heat transfer and drag on surfaces coated with dimples of different shape. Int. J. Therm. Sci. 2017, 118, 152–167. [Google Scholar] [CrossRef]
- Leontiev, A.I.; Kiselev, N.A.; Burtsev, S.A.; Strongin, M.M.; Vinogradov, Y.A. Experimental investigation of heat transfer and drag on surfaces with spherical dimples. Exp. Therm. Fluid Sci. 2016, 79, 74–84. [Google Scholar] [CrossRef]
- Isaev, S.A.; Kornev, N.V.; Leontiev, A.I.; Hassel, E. Influence of the Reynolds number and the spherical dimple depth on turbulent heat transfer and hydraulic loss in a narrow channel. Int. J. Heat Mass Transf. 2010, 53, 178–197. [Google Scholar] [CrossRef]
- Rao, Y.; Li, B.; Feng, Y. Heat transfer of turbulent flow over surfaces with spherical dimples and teardrop dimples. Exp. Therm. Fluid Sci. 2015, 61, 201–209. [Google Scholar] [CrossRef]
- Rafid, M.; Azad, A.K.; Prottoy, S.M.; Alam, S.; Rahman, M.; Miah, M.J.; Hossain, M.S.; Rahman, M.M. Augmentation of heat exchanger performance with hybrid nanofluids: Identifying research gaps and future indications—A review. Int. Commun. Heat Mass Transf. 2024, 155, 107537. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transfer. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Taylor, R.; Coulombe, S.; Otanicar, T.; Phelan, P.; Gunawan, A.; Lv, W.; Rosengarten, G.; Prasher, R.; Tyagi, H. Small particles, big impacts: A review of the diverse applications of nanofluids. J. Appl. Phys. 2013, 113, 011301. [Google Scholar] [CrossRef]
- Shah, T.R.; Koten, H.; Ali, H.M. Performance effecting parameters of hybrid nanofluids. In Hybrid Nanofluids for Convection Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2020; pp. 179–213. [Google Scholar]
- Maleki, Y.; Mehrpooya, M.; Pourfayaz, F. Cold thermal energy storage by encapsulated phase change materials system using hybrid nanofluids as the heat transfer fluid. Int. J. Energy Res. 2021, 45, 15265–15283. [Google Scholar] [CrossRef]
- Jamshed, W.; Nasir, N.A.A.M.; Isa, S.S.P.M.; Safdar, R.; Shahzad, F.; Nisar, K.S.; Eid, M.R.; Abdel-Aty, A.-H.; Yahia, I. Thermal growth in solar water pump using Prandtl–Eyring hybrid nanofluid: A solar energy application. Sci. Rep. 2021, 11, 18704. [Google Scholar] [CrossRef]
- Zhou, Z.; Lv, Y.; Qu, J.; Sun, Q.; Grachev, D. Performance evaluation of hybrid oscillating heat pipe with carbon nanotube nanofluids for electric vehicle battery cooling. Appl. Therm. Eng. 2021, 196, 117300. [Google Scholar] [CrossRef]
- Javadi, H.; Urchueguia, J.F.; Mousavi Ajarostaghi, S.S.; Badenes, B. Impact of employing hybrid nanofluids as heat carrier fluid on the thermal performance of a borehole heat exchanger. Energies 2021, 14, 2892. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, L.; Liu, C.; Abdollahi, S.A. Thermal performance augmentation in a pipe employing hybrid nanofluid and a plate as turbulator with V-shaped double-winglet ribs. Sci. Rep. 2024, 14, 7363. [Google Scholar] [CrossRef] [PubMed]
- Ho, M.L.G.; Oon, C.S.; Tan, L.L.; Wang, Y.; Hung, Y.M. A review on nanofluids coupled with extended surfaces for heat transfer enhancement. Results Eng. 2023, 17, 100957. [Google Scholar] [CrossRef]
- Pandya, N.S.; Shah, H.; Molana, M.; Tiwari, A.K. Heat transfer enhancement with nanofluids in plate heat exchangers: A comprehensive review. Eur. J. Mech.-B/Fluids 2020, 81, 173–190. [Google Scholar] [CrossRef]
- Gabir, M.M.; Albayati, I.M.; Hatami, M.; Alkhafaji, D. An experimental investigation of the convective heat transfer augmentation in U-bend double pipe heat exchanger using water-MgO-Cmc fluid. Sci. Rep. 2024, 14, 12442. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhu, J.; Zhang, X.; Chen, Y. Heat transfer and pressure drop of nanofluids containing carbon nanotubes in laminar flows. Exp. Therm. Fluid Sci. 2013, 44, 716–721. [Google Scholar] [CrossRef]
- Borode, A.O.; Ahmed, N.A.; Olubambi, P.A. Electrochemical corrosion behavior of copper in graphene-based thermal fluid with different surfactants. Heliyon 2021, 7, e05949. [Google Scholar] [CrossRef]
- Smallman, R.E.; Ngan, A.H.W. Chapter 16—Oxidation, Corrosion and Surface Engineering. In Modern Physical Metallurgy, 8th ed.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 617–657. [Google Scholar] [CrossRef]
- Ali, A.R.I.; Salam, B. A review on nanofluid: Preparation, stability, thermophysical properties, heat transfer characteristics and application. SN Appl. Sci. 2020, 2, 1636. [Google Scholar] [CrossRef]
- Marzouk, S.A.; Aljabr, A.; Almehmadi, F.A.; Alqaed, S.; Sharaf, M.A. Numerical study of heat transfer, exergy efficiency, and friction factor with nanofluids in a plate heat exchanger. J. Therm. Anal. Calorim. 2023, 148, 11269–11281. [Google Scholar] [CrossRef]
- Cunegatto, E.H.T.; Gotardo, M.; Zinani, F.S.F. Numerical analysis of tube arrangements with one, two, and four degrees of freedom for heat transfer with pseudoplastic fluids. Int. J. Heat Mass Transf. 2023, 208, 124080. [Google Scholar] [CrossRef]
- Ghalambaz, S.; Abbaszadeh, M.; Sadrehaghighi, I.; Younis, O.; Ghalambaz, M.; Ghalambaz, M. A forty years scientometric investigation of artificial intelligence for fluid-flow and heat-transfer (AIFH) during 1982 and 2022. Eng. Appl. Artif. Intell. 2024, 127, 107334. [Google Scholar] [CrossRef]
- Omara, Z. Effects of surface injection or ejection at various angles on the heat transfer and flowfield in a rectangular channel. J. Contemp. Technol. Appl. Eng. 2023, 2, 1–11. [Google Scholar] [CrossRef]
- Sircar, A.; Kimber, M.; Rokkam, S.; Botha, G. Turbulent flow and heat flux analysis from validated large eddy simulations of flow past a heated cylinder in the near wake region. Phys. Fluids 2020, 32, 125119. [Google Scholar] [CrossRef]
- Al-Askaree, E.H.; Al-Muhsen, N.F.O. Experimental investigation on thermal performance of solar water heater equipped with Serpentine fin core heat exchanger. Clean. Eng. Technol. 2023, 12, 100593. [Google Scholar] [CrossRef]
- Rasslan, W.B.; Abdel-Kawi, M.A.; Nosier, S.A.; El-Maghlany, W.M.; Abdel-Aziz, M.H.; Sedahmed, G.H.; Fathalla, A.S. Experimental mass and heat transfer at a serpentine tube heat exchanger located at the wall of a square stirred tank reactor. Appl. Therm. Eng. 2023, 219, 119438. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozłowska, E.; Szkodo, M. Contemporary and Conventional Passive Methods of Intensifying Convective Heat Transfer—A Review. Energies 2024, 17, 4268. https://doi.org/10.3390/en17174268
Kozłowska E, Szkodo M. Contemporary and Conventional Passive Methods of Intensifying Convective Heat Transfer—A Review. Energies. 2024; 17(17):4268. https://doi.org/10.3390/en17174268
Chicago/Turabian StyleKozłowska, Ewa, and Marek Szkodo. 2024. "Contemporary and Conventional Passive Methods of Intensifying Convective Heat Transfer—A Review" Energies 17, no. 17: 4268. https://doi.org/10.3390/en17174268
APA StyleKozłowska, E., & Szkodo, M. (2024). Contemporary and Conventional Passive Methods of Intensifying Convective Heat Transfer—A Review. Energies, 17(17), 4268. https://doi.org/10.3390/en17174268