A Novel Single-Stage Boost Single-Phase Inverter and Its Composite Control Strategy to Suppress Low-Frequency Input Ripples
Abstract
1. Introduction
2. Circuit Topology and Circuit Mode
2.1. Circuit Topology
2.2. Circuit Mode
3. Control Strategy
3.1. Output Voltage Feedback SPWM Control Strategy and Its Working Mode Design
3.2. Ideas for Suppressing Low-Frequency Ripple of Input Current
3.3. Two-Objective Three-Closed-Loop Composite Control Strategy and Its Working Mode Design
4. Design Key Circuit Parameters
4.1. Buffer Capacitor
4.1.1. Buffer Capacitor Voltage Average Limit Value Ucavg*
4.1.2. Buffer Capacitor Value Cb
4.2. Energy Storage Inductor
4.2.1. Energy Storage Inductor Current Limit Value IL*
4.2.2. Energy Storage Inductor Value L
4.3. Filter Capacitor
4.3.1. Input Filter Capacitance Value Ci
4.3.2. Output Filter Capacitance Value Cf
5. System Modeling and Controller Parameter Design
6. Simulation and Experiment
6.1. Simulation Analysis
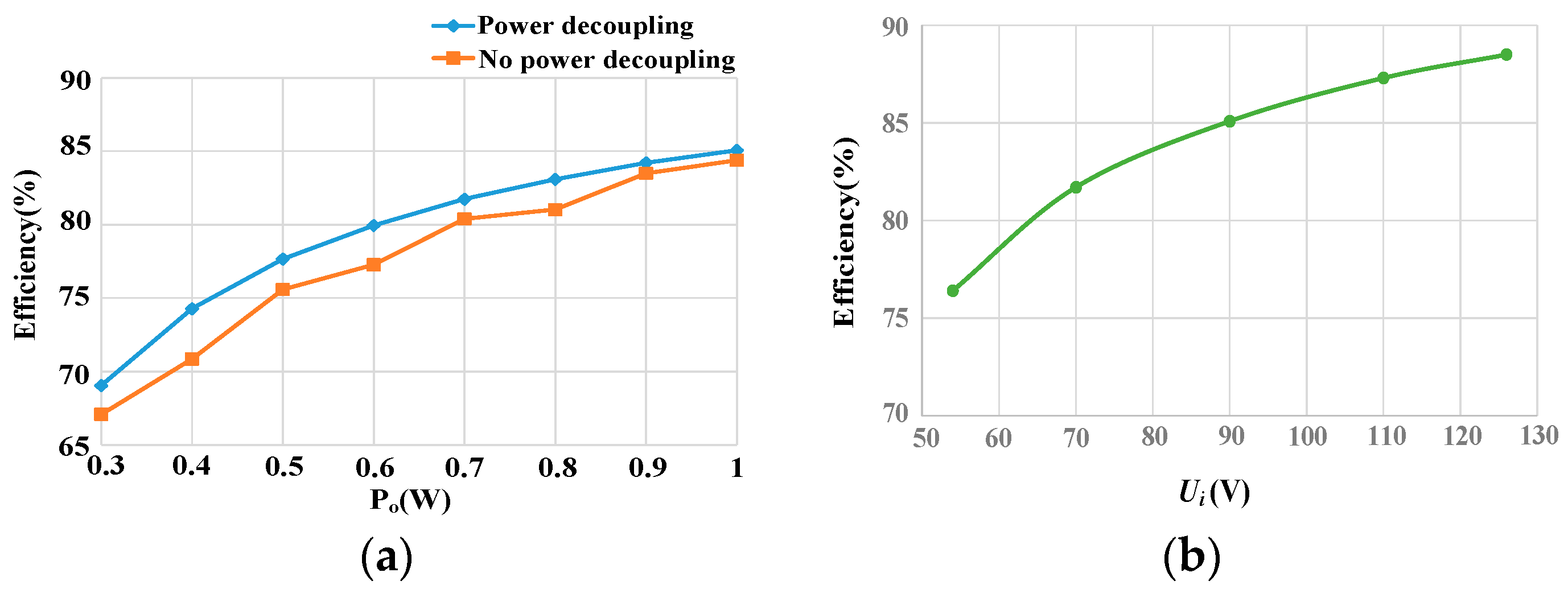
6.2. Experimental Results
7. Conclusions
- The circuit topology of the single-stage boost source single-phase inverter is proposed, which is mainly composed of the energy storage inductor, active buffer circuit, and single-phase current source inverter bridge and filter. The active buffer circuit provides the hardware conditions for the inverter energy feedback and input and output power decoupling, so the circuit has the ability of a single-stage boost inverter and can undertake the low-frequency ripple suppression of the input current.
- A three-closed-loop composite control strategy is proposed under the limitation of the inductor current and buffer capacitor voltage, and the limit values of the inductor current and buffer capacitor voltage are derived, respectively, according to the circuit boost transformation mechanism and working mode characteristics.
- The proposed inverter has four circuit modes in the boost stage, where the energy storage inductor can be demagnetized through the energy feed mode, and the circuit mainly works in the magnetizing mode and the energy feed mode. In the buck stage of the inverter, the energy storage inductor can only be demagnetized by the buffer capacitor, and the circuit mainly works in the buffer capacitor charging and discharging modes.
- The circuit parameters of the proposed inverter are analyzed and designed. The mathematical model of the inverter is established from the perspective of energy conservation, combined with the state space average method, and the controller parameters of the system are designed. The simulation and experiments show that the proposed inverter is equipped with good input current low-frequency ripple suppression and single-stage boost conversion capability. It has a simple circuit and control, the output voltage THD is low, and can adapt to various types of loads, such as resistive, resistive-inductive, and resistive-capacitive load, and has a good steady state and dynamic performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prasad, K.R.; Madhavi, S.V.; Satyanarayana, A.V.; Mallam, M.; Prasad, J.S.; Suman, J.V. Design and Management of an Integrated Solar-Wind Conversion System Using DFIG. In Proceedings of the 2024 International Conference on Advances in Modern Age Technologies for Health and Engineering Science (AMATHE), Shivamogga, Karnataka, India, 9–10 May 2024; pp. 1–6. [Google Scholar]
- Tang, M.; Li, J.; Qiu, J.; Guo, X.; An, B.; Zhang, Y.; Wang, W. MPPT Strategy of Waterborne Bifacial Photovoltaic Power Generation System Based on Economic Model Predictive Control. Energies 2023, 17, 152. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Yang, Y.; Kim, K.A.; Rodriguez, J. Power Electronics Technology for Large-Scale Renewable Energy Generation. Proc. IEEE 2023, 111, 335–355. [Google Scholar] [CrossRef]
- Rakib, K.; Salimullah, S.M.; Hossain, M.S.; Chowdhury, M.A.; Ahmed, J.S. Stability Analysis of Grid Integrated BESS Based Hybrid Photovoltaic (PV) and Wind Power Generation. In Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5–7 June 2020; pp. 1717–1720. [Google Scholar]
- Chen, Y.; Jiang, Z.; Wei, L.; Zhang, Y.; Jiang, J. An Asymmetric Full-Bridge Bidirectional DC–AC Converter With Power Decoupling and Common-Mode Current Suppression for V2G Application. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2870–2881. [Google Scholar] [CrossRef]
- Nie, L.; Zhu, G.; Luo, B.; Qi, E.; Zeng, D.; Huang, S. A Novel Control Method for the Active Power Decoupling Module with Plug-and-Play in Single Phase Inverter. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Xu, S.; Chang, L.; Shao, R. Single-Phase Voltage Source Inverter With Voltage Boosting and Power Decoupling Capabilities. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2977–2988. [Google Scholar] [CrossRef]
- Rekha, Y.; Christopher, I.W.; Jamuna, V. Fuel Cell Based Sl Quasi Z-Source Inverter for Motor Drive. In Proceedings of the 2019 Fifth International Conference on Electrical Energy Systems (ICEES), Chennai, India, 21–22 February 2019; pp. 1–6. [Google Scholar]
- Hwang, D.-H.; Lee, J.-Y.; Cho, Y. PCC Voltage Compensation of PV Inverter with Active Power Decoupling Circuit. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1403–1408. [Google Scholar]
- Seta, Y.; Shimizu, T. Low Power Factor Operation of PV Inverter with Power Decoupling Function. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Emar, W.; Issa, H.; Kanaker, H.; Fares, O.; Attar, H. A New Double-Switch SEPIC-Buck Topology for Renewable Energy Applications. Energies 2024, 17, 238. [Google Scholar] [CrossRef]
- Jain, S.; Shadmand, M.B.; Balog, R.S. Decoupled Active and Reactive Power Predictive Control for PV Applications Using a Grid-Tied Quasi-Z-Source Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1769–1782. [Google Scholar] [CrossRef]
- Sabeeh Al-Obaidi, S.A.; Hodge, K.C.; Enjeti, P. A Dual-Phase Output 4-Leg Inverter with Active Decoupling and Integrated Power Optimizer for Off-Grid Applications. In Proceedings of the 2018 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Charlotte, NC, USA, 25–28 June 2018; pp. 1–6. [Google Scholar]
- SeyyedHosseini, M.; Yazdian-Varjani, A.; Mohamadian, M. Power Decoupling Method for Single Stage Current Fed Flyback Micro Inverter. In Proceedings of the 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–6. [Google Scholar]
- Wickramasinghe Abeywardana, D.B.; Acuna, P.; Hredzak, B.; Aguilera, R.P.; Agelidis, V.G. Single-Phase Boost Inverter-Based Electric Vehicle Charger With Integrated Vehicle to Grid Reactive Power Compensation. IEEE Trans. Power Electron. 2018, 33, 3462–3471. [Google Scholar] [CrossRef]
- Chen, J.; Hu, H.; Wang, M.; Ge, Y.; Wang, K.; Huang, Y.; Yang, K.; He, Z.; Xu, Z.; Li, Y.R. Power Flow Control-Based Regenerative Braking Energy Utilization in AC Electrified Railways: Review and Future Trends. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6345–6365. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Y.; Wang, M.; Wang, K.; Huang, Y.; Xu, Z. Power Sharing and Storage-Based Regenerative Braking Energy Utilization for Sectioning Post in Electrified Railways. IEEE Trans. Transp. Electrif. 2024, 10, 2677–2688. [Google Scholar] [CrossRef]
- Li, T.; Shi, Y. Application of MMC-RPC in High-Speed Railway Traction Power Supply System Based on Energy Storage. Appl. Sci. 2022, 12, 10009. [Google Scholar] [CrossRef]
- Kan, S.; Ruan, X.; Dang, H.; Zhang, L.; Huang, X. Second Harmonic Current Reduction in Front-End DC−DC Converter for Two-Stage Single-Phase Photovoltaic Grid-Connected Inverter. IEEE Trans. Power Electron. 2019, 34, 6399–6410. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, X.; Ren, X. Second-Harmonic Current Reduction and Dynamic Performance Improvement in the Two-Stage Inverters: An Output Impedance Perspective. IEEE Trans. Ind. Electron. 2015, 62, 394–404. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, W.; He, P. A Novel Power Decoupling Circuit in Paralleled with AC Side in Photovoltaic Micro-Inverter. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 821–826. [Google Scholar]
- Watanabe, H.; Itoh, J.; Iwabuchi, A. Experimental Verification of DC to Single-Phase AC Converter with Power Decoupling Capability Using 1.2 kV SiC-MOSFET Module. In Proceedings of the 2019 IEEE Workshop on Wide Bandgap Power Devices and Applications in Asia (WiPDA Asia), Taipei, Taiwan, 23–25 May 2019; pp. 1–4. [Google Scholar]
- Xu, S.; Chang, L.; Shao, R.; Mohomad, A.H. Single-Phase Bridge Inverter with Active Power Decoupling Based on Buck-Boost Converter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 6725–6732. [Google Scholar]
- Bodele, N.; Kulkarni, P.S. A Zero-Leakage-Current Single-Stage PV-Battery Integrated Inverter with Active Power Decoupling. IEEE Trans. Circuits Syst. II Express Briefs 2024. [Google Scholar] [CrossRef]
- Kim, J.; Cha, H. Switching Cell Current Source Inverter With Active Power Decoupling Circuit. IEEE Trans. Ind. Electron. 2024, 71, 12183–12191. [Google Scholar] [CrossRef]
- Shi, S.; Sun, Y.; Dan, H.; Song, D.; Su, M.; Guo, B.; Tang, H. A General Closed-Loop Power-Decoupling Control for Reduced-Switch Converter-Fed IM Drives. Electr. Eng. 2020, 102, 2423–2433. [Google Scholar] [CrossRef]
- Jiang, J.; Sun, H.; Wang, H. A Comprehensive Review of Single-Phase Converter Topologies with 2ω-Ripple Suppress. Electr. Eng. 2024, 106, 225–262. [Google Scholar] [CrossRef]
- Tian, H.; Chen, M.; Liang, G.; Xiao, X. A Single-Phase Transformerless Common-Ground Type PV Inverter With Active Power Decoupling. IEEE Trans. Ind. Electron. 2023, 70, 3762–3772. [Google Scholar] [CrossRef]
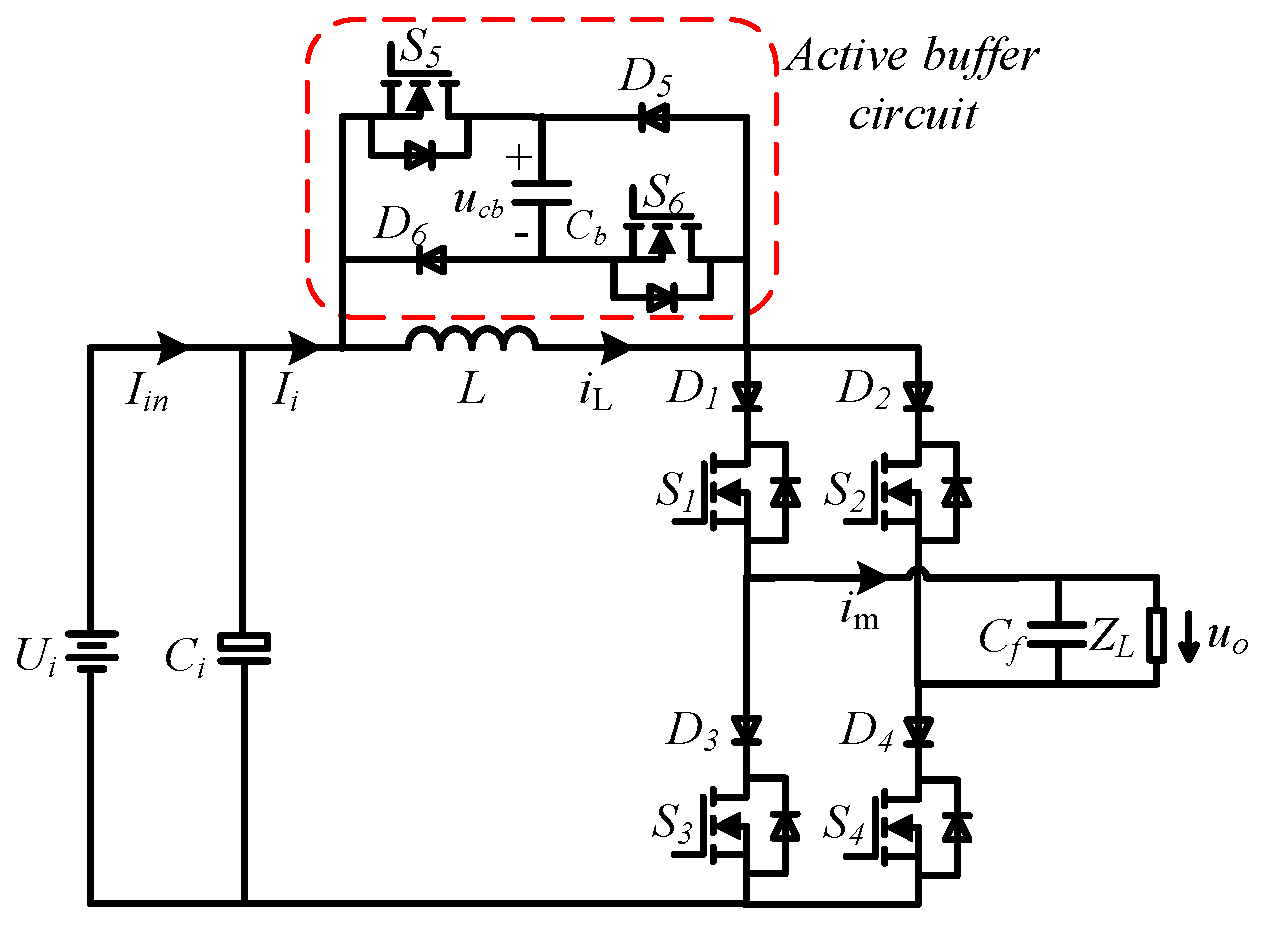

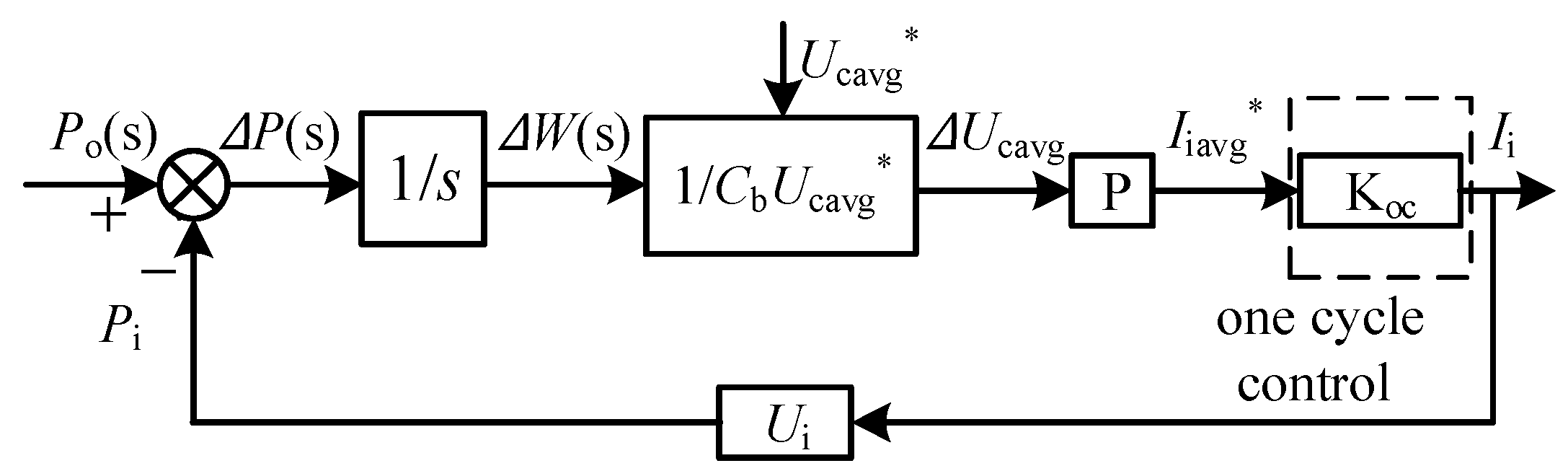
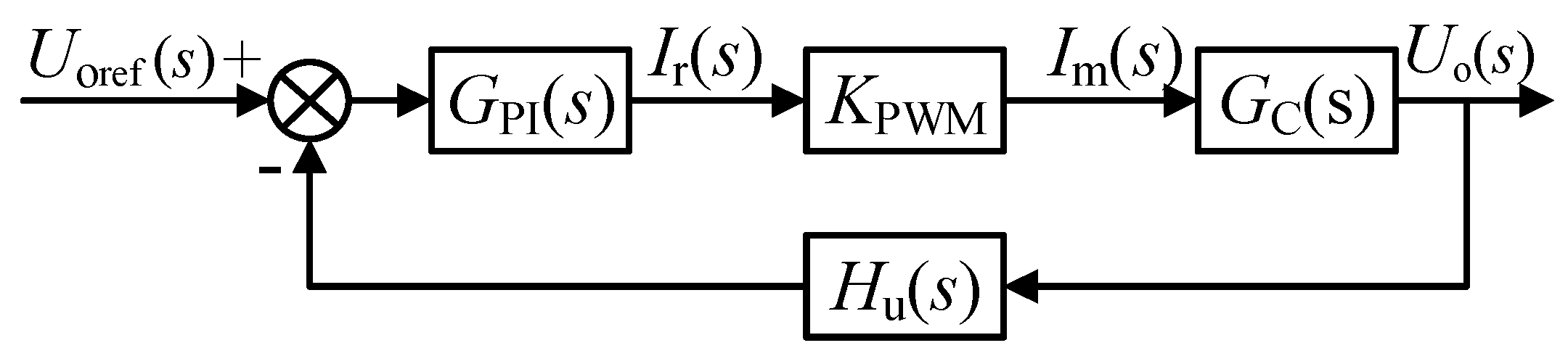




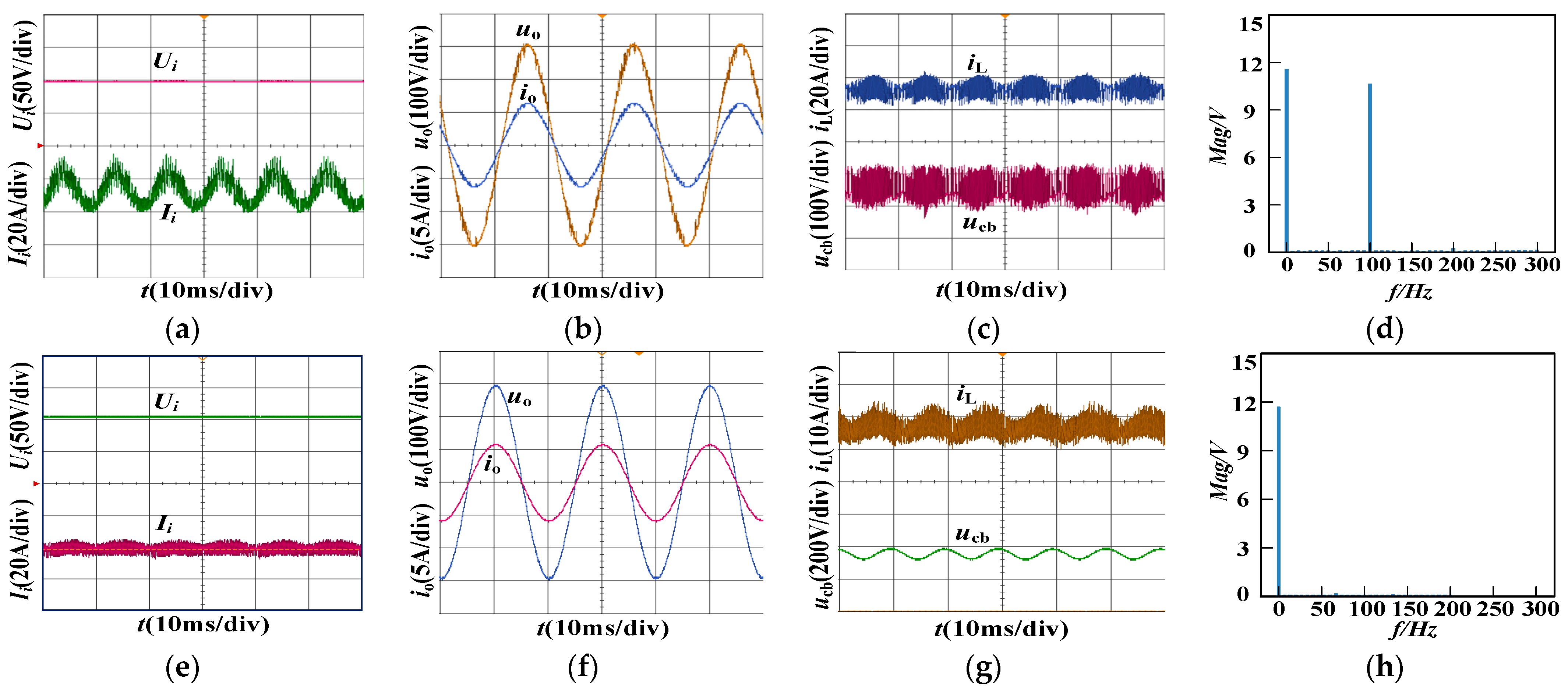


| Circuit Status | High-Frequency-Switching Interval | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|---|
| uo > 0, iL < IL*, ucb < Ucb* | (1 – d)TS | 1 | 0 | 1 | 0 | 0 | 0 |
| dTS | 1 | 0 | 0 | 1 | 0 | 0 | |
| uo > 0, iL < IL*, ucb > Ucb* | (1 – d)TS | 0 | 0 | 0 | 0 | 1 | 1 |
| dTS | 1 | 0 | 0 | 1 | 0 | 0 | |
| uo > 0, iL > IL* | (1 – d)TS | 0 | 0 | 0 | 0 | 0 | 0 |
| dTS | 1 | 0 | 0 | 1 | 0 | 0 | |
| uo < 0, iL < IL*, ucb < Ucb* | (1 – d)TS | 1 | 0 | 1 | 0 | 0 | 0 |
| dTS | 0 | 1 | 1 | 0 | 0 | 0 | |
| uo < 0, iL < IL*, ucb > Ucb* | (1 – d)TS | 0 | 0 | 0 | 0 | 1 | 1 |
| dTS | 0 | 1 | 1 | 0 | 0 | 0 | |
| uo < 0, iL > IL* | (1 – d)TS | 0 | 0 | 0 | 0 | 0 | 0 |
| dTS | 0 | 1 | 1 | 0 | 0 | 0 |
| isy0 | isy1 | isy2 | isy3 | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | x | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | x | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | x | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | x | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | x | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | x | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | x | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | x | 0 | 0 | 0 | 0 | 1 | 1 |
| Circuit Parameters | Numerical Values |
|---|---|
| Rated capacity S/VA | 1000 |
| Rated output voltage RMS Uo/V | 220 |
| Input voltage Ui/V | 90 |
| Energy storage inductor L/mH | 1.5 |
| Buffer capacitor Cb/uF | 120 |
| Input filter capacitor Ci/uF | 200 |
| Output filter capacitor Cf/uF | 16.8 |
| Switching frequency f/kHz | 50 |
| Parameters | [21] | [23] | [24] | [28] | Proposed |
|---|---|---|---|---|---|
| No. of levels | 2 | 1 | 1 | 1 | 1 |
| No. of switches | 12 | 6 | 7 | 5 | 6 |
| No. of diodes | 1 | 0 | 0 | 1 | 6 |
| Capacitance | 20 µF/10 µF | 100 µF/10 µF | 170 µF/220 µF/220 µF | 22 µF | 120 µF/200 µF/16.8 µF |
| Inductance | 70 µH/10 mH | 300 µH/0.8 mH | 2.5 mH/1.8 mH | 30 µH/1.5 mH | 1.5 mH |
| Control complexity | Complex | Complex | Medium | Medium | Simple |
| Boost level | Small | Medium | Larger | Larger | Larger |
| Rated power | 500 W | 400 W | 1000 W | 320 W | 1000 W |
| Secondary ripple content | 1.73% | - | - | 3.67% | 1.2% |
| Efficiency | - | - | 96.3% | 95.8% | 85% |
| Output voltage THD | - | - | 5.62% | 1.5% | |
| Output dynamic response time | - | - | 40 ms | 25 ms | 3 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Jiang, Z.; Lv, T.; Tong, X.; Jiang, B.; Qian, K. A Novel Single-Stage Boost Single-Phase Inverter and Its Composite Control Strategy to Suppress Low-Frequency Input Ripples. Energies 2024, 17, 4522. https://doi.org/10.3390/en17174522
Wei Y, Jiang Z, Lv T, Tong X, Jiang B, Qian K. A Novel Single-Stage Boost Single-Phase Inverter and Its Composite Control Strategy to Suppress Low-Frequency Input Ripples. Energies. 2024; 17(17):4522. https://doi.org/10.3390/en17174522
Chicago/Turabian StyleWei, Yong, Zhenying Jiang, Tao Lv, Xiaohan Tong, Benxu Jiang, and Kun Qian. 2024. "A Novel Single-Stage Boost Single-Phase Inverter and Its Composite Control Strategy to Suppress Low-Frequency Input Ripples" Energies 17, no. 17: 4522. https://doi.org/10.3390/en17174522
APA StyleWei, Y., Jiang, Z., Lv, T., Tong, X., Jiang, B., & Qian, K. (2024). A Novel Single-Stage Boost Single-Phase Inverter and Its Composite Control Strategy to Suppress Low-Frequency Input Ripples. Energies, 17(17), 4522. https://doi.org/10.3390/en17174522






