A Power-RPM Reduced-Order Model and Power Control Strategy of the Dual Three-Phase Permanent Magnet Synchronous Motor in a V/f Framework for Oscillation Suppression
Abstract
:1. Introduction
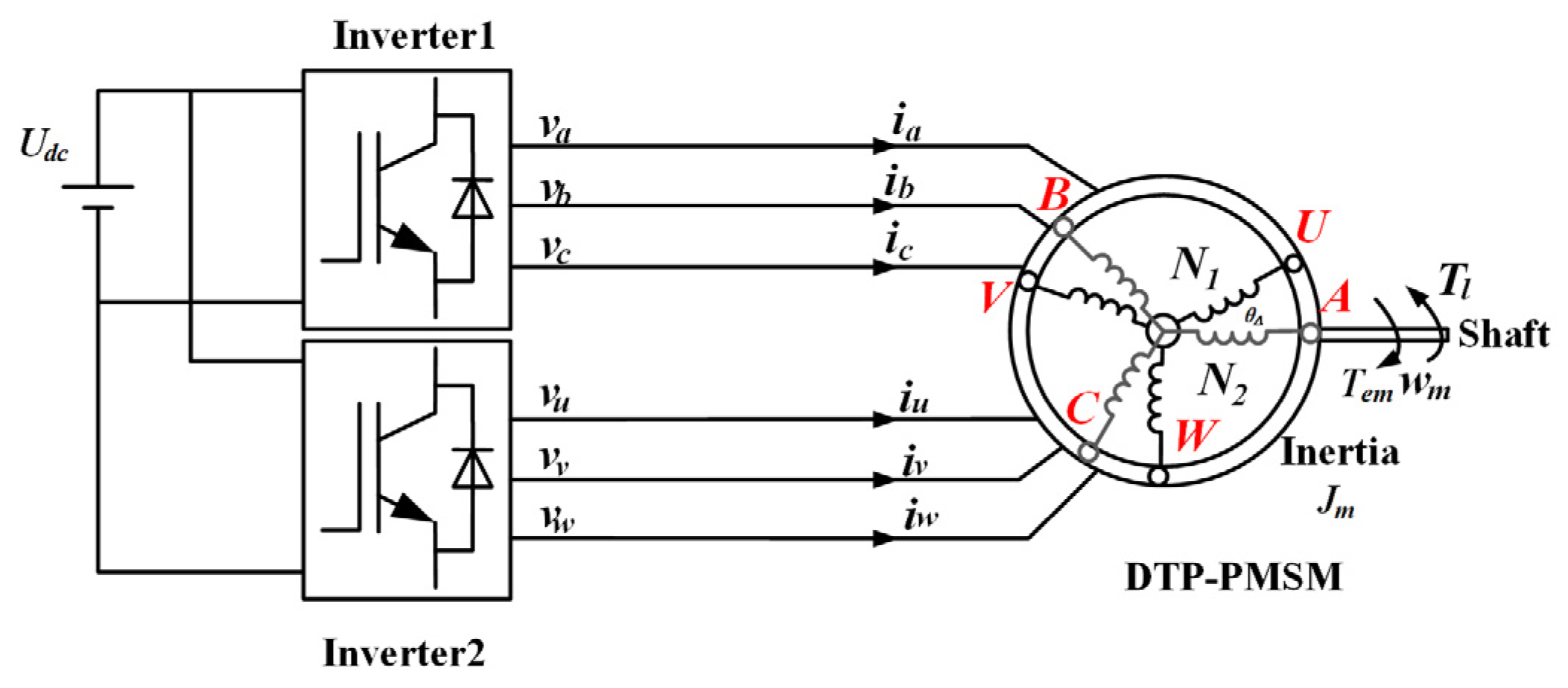
2. Power-RPM Reduced-Order Model and Oscillation Analysis
2.1. Power-RPM Reduced-Order Model
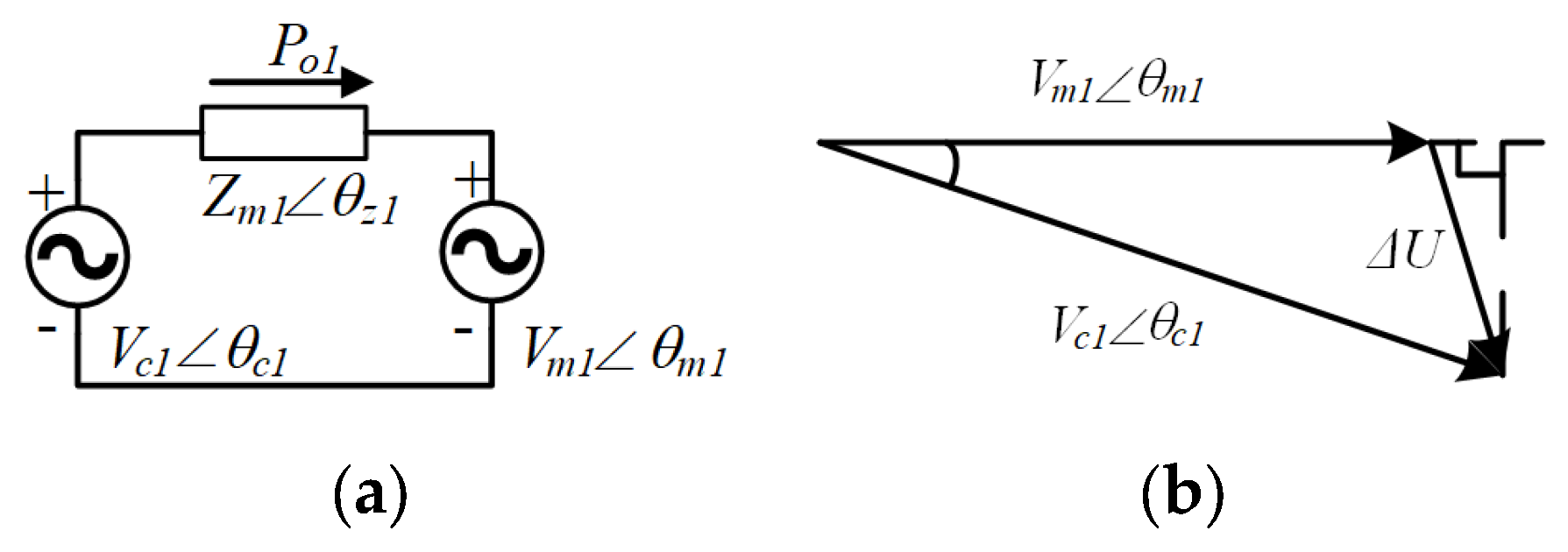
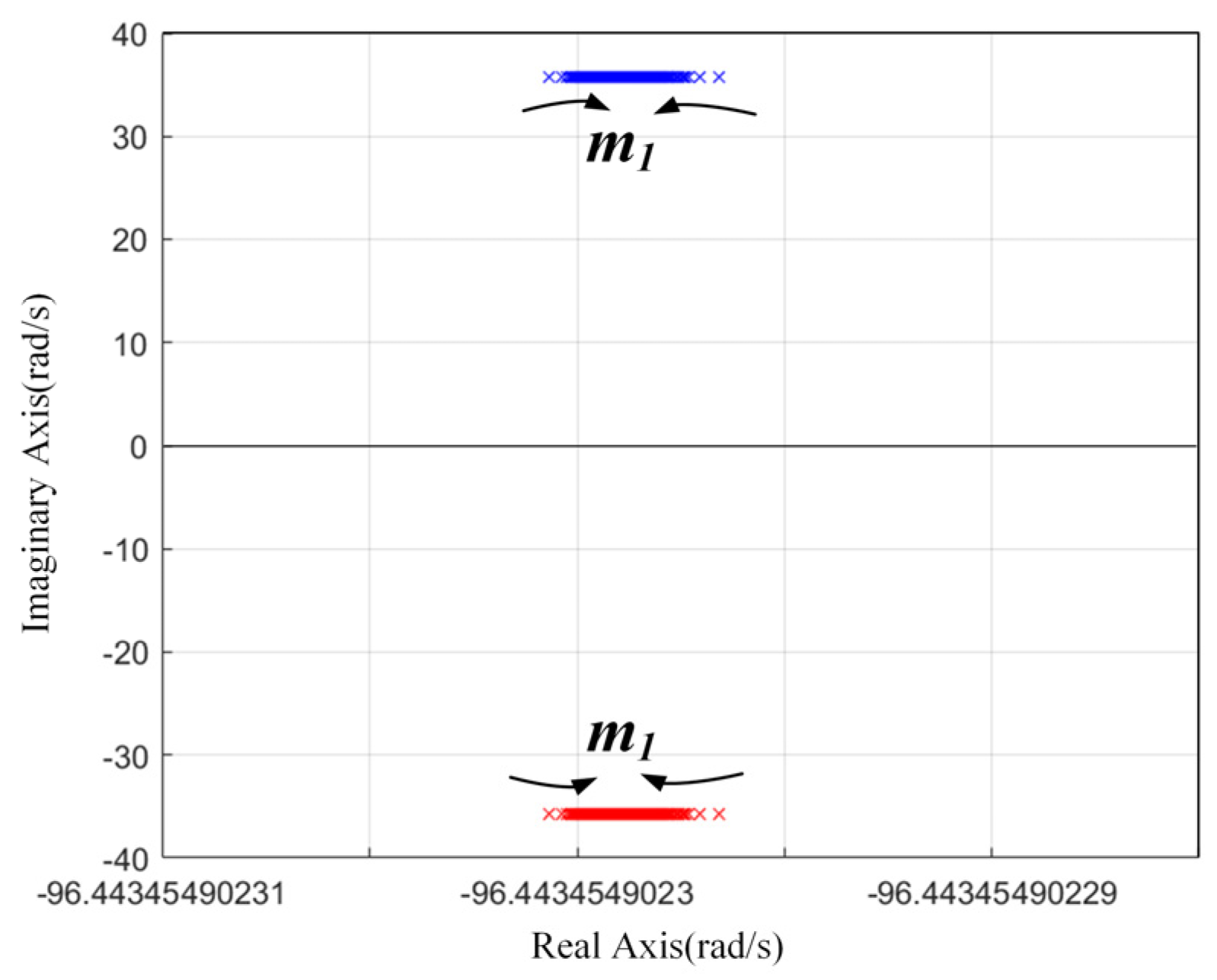
2.2. Oscillation Analysis
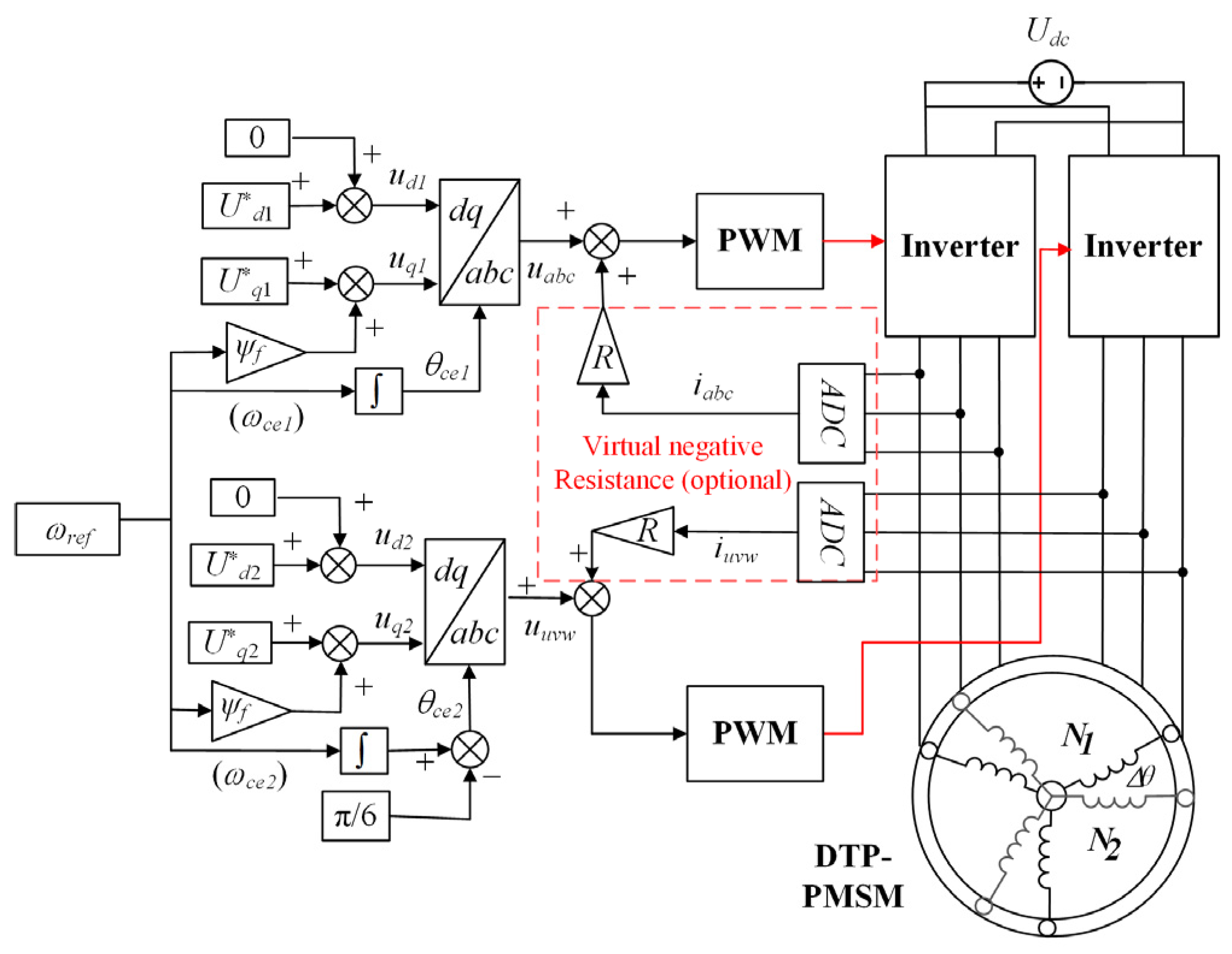
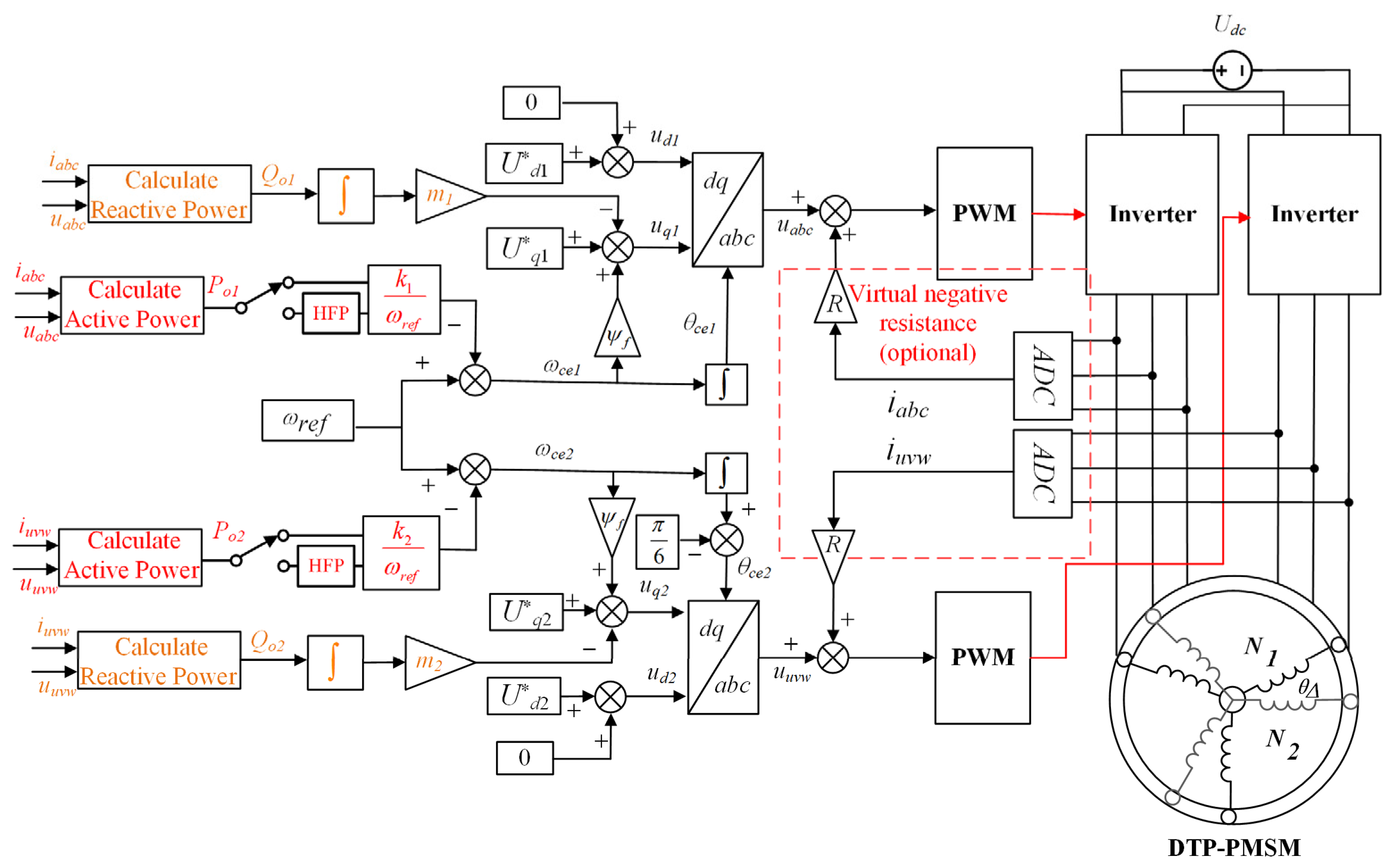
3. Power Control Strategy
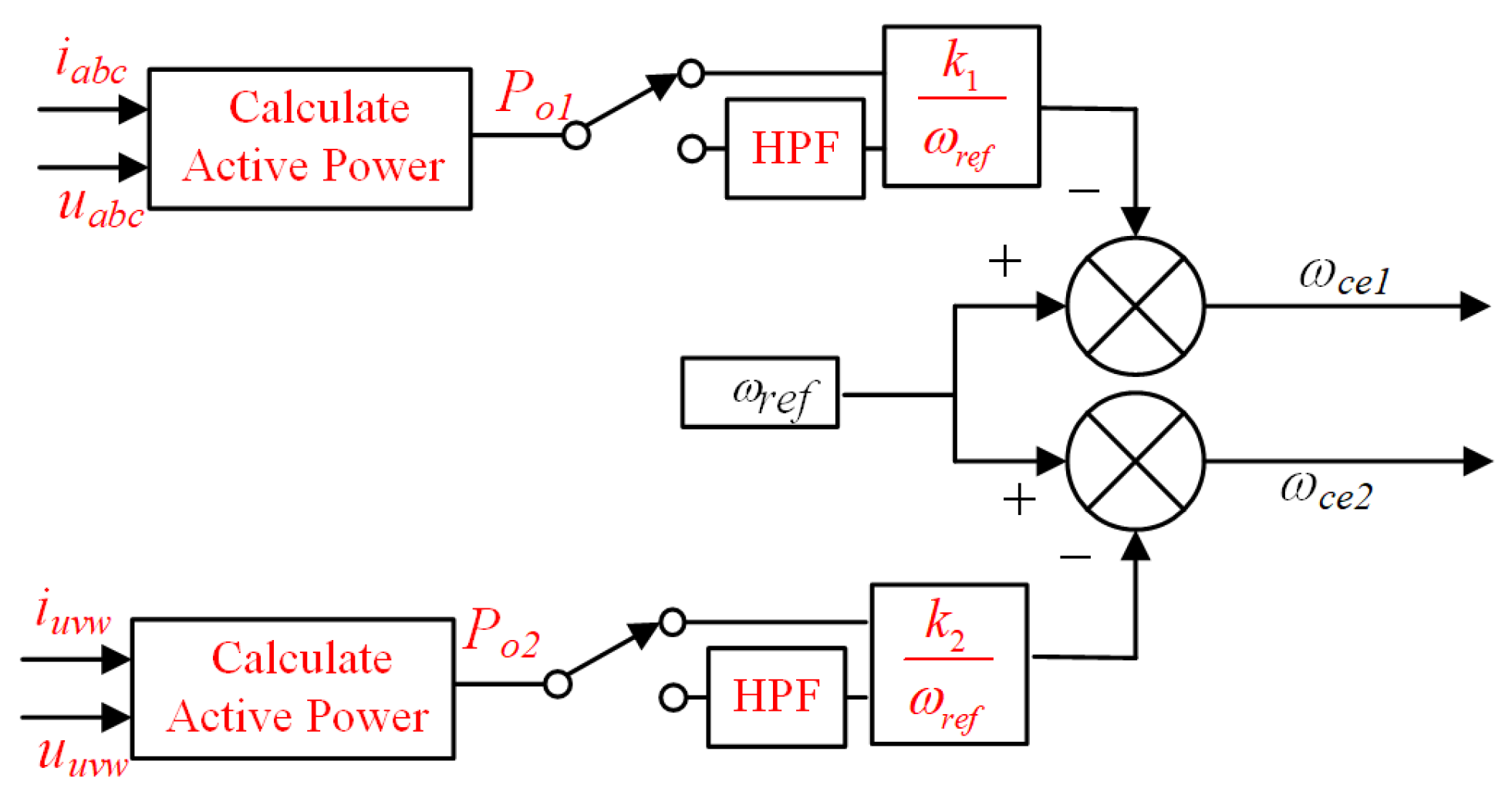
3.1. Active Power Feedback for Active Damping
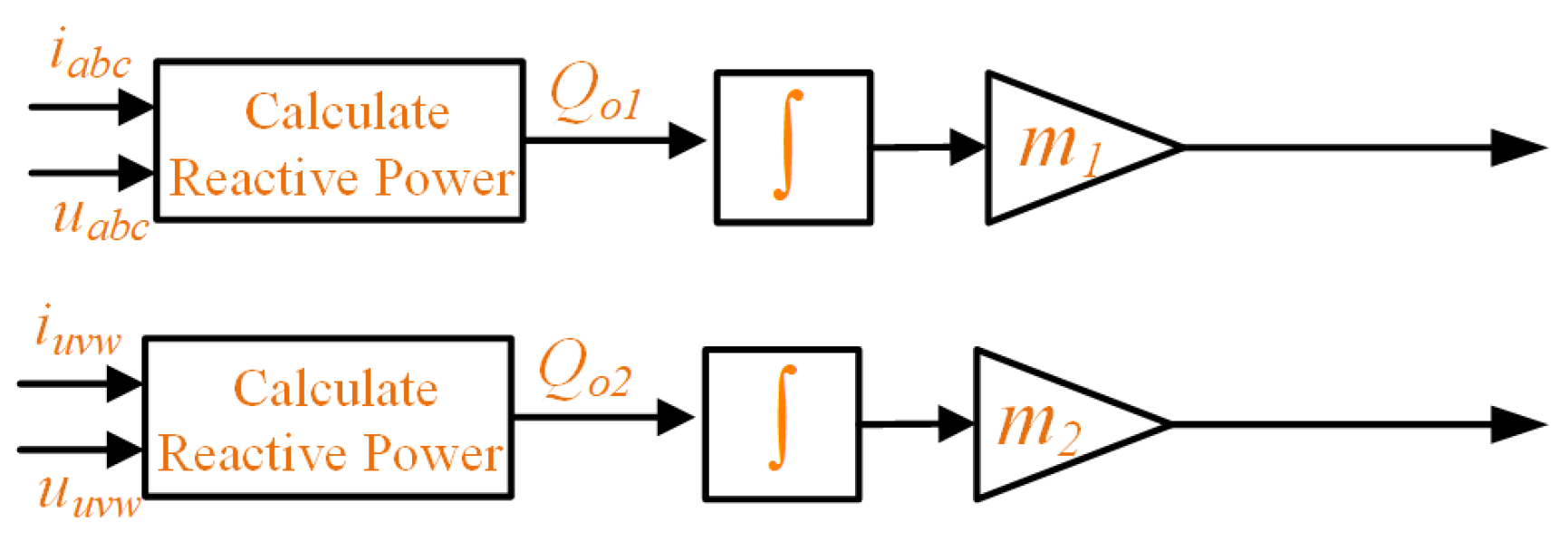
3.2. Reactive Power Droop Control for High Power Quality and Approaching of the Optimal TPA
- (1)
- Power-RPM Reduced-order Model is proposed to quantify oscillations and damping ratio.
- (2)
- The power feedback coefficient can be designed and optimized according to the formula based on Power-RPM Reduced-order Model. The effect of suppressing oscillation is excellent.
- (3)
- Based on Power-RPM Reduced-order Model, the proposed reactive power control can reduce stator current and reactive power, thereby improving power factor.
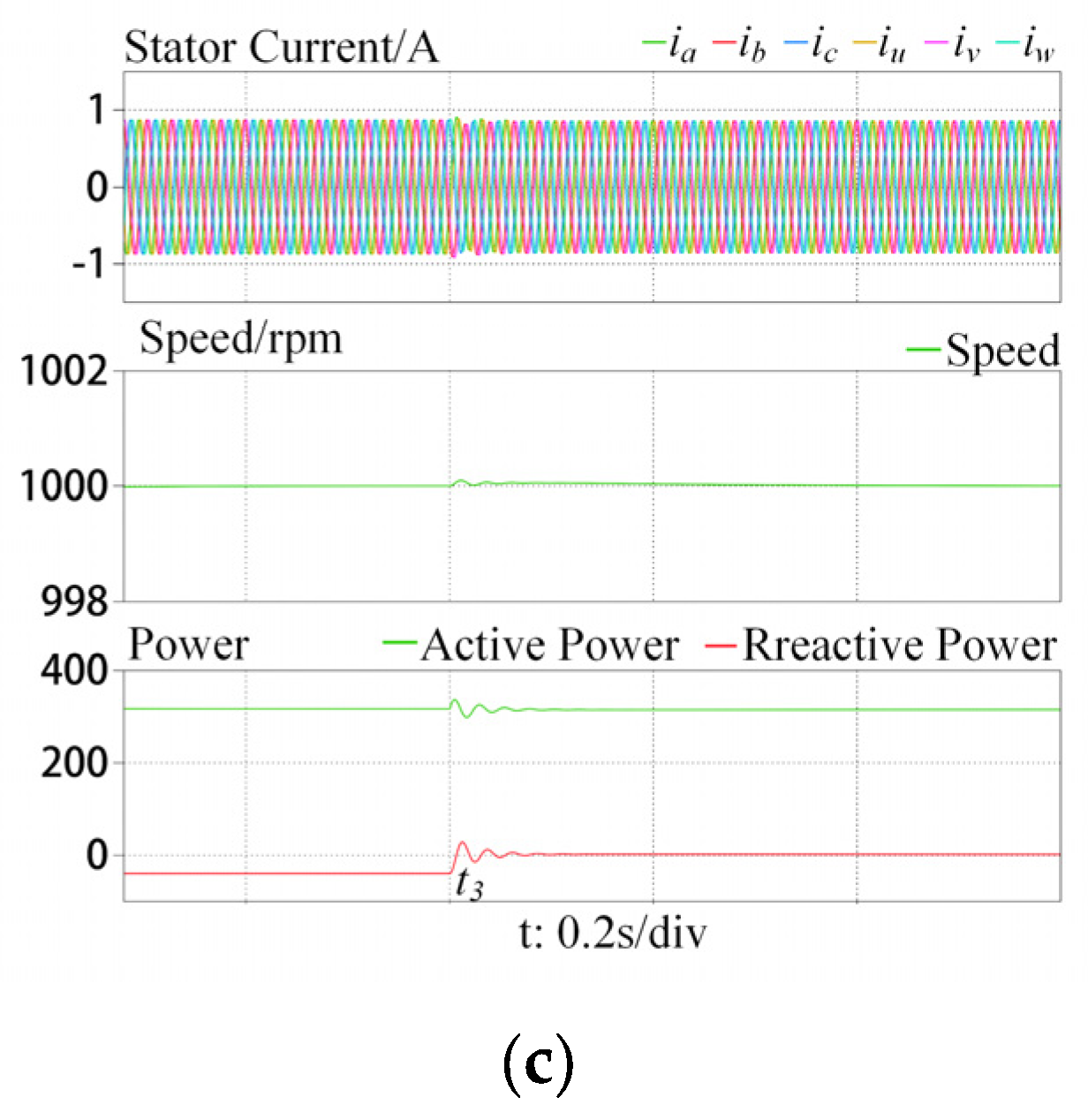
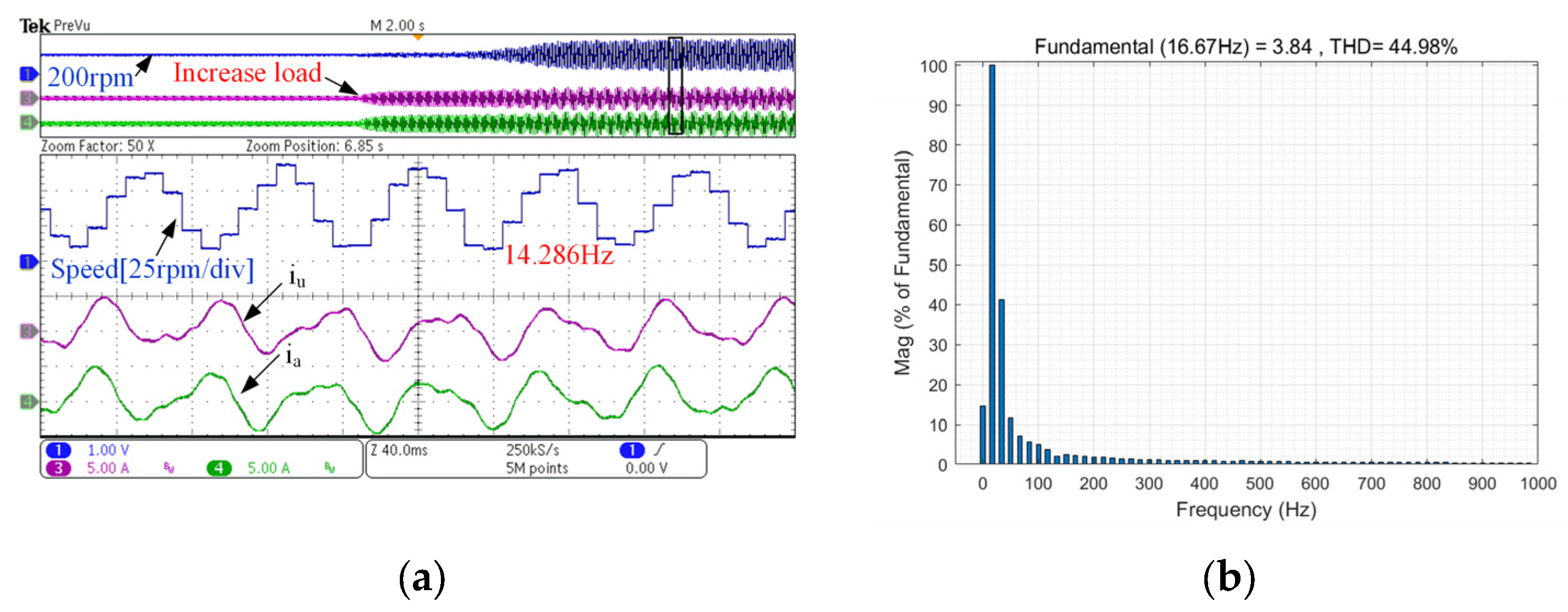
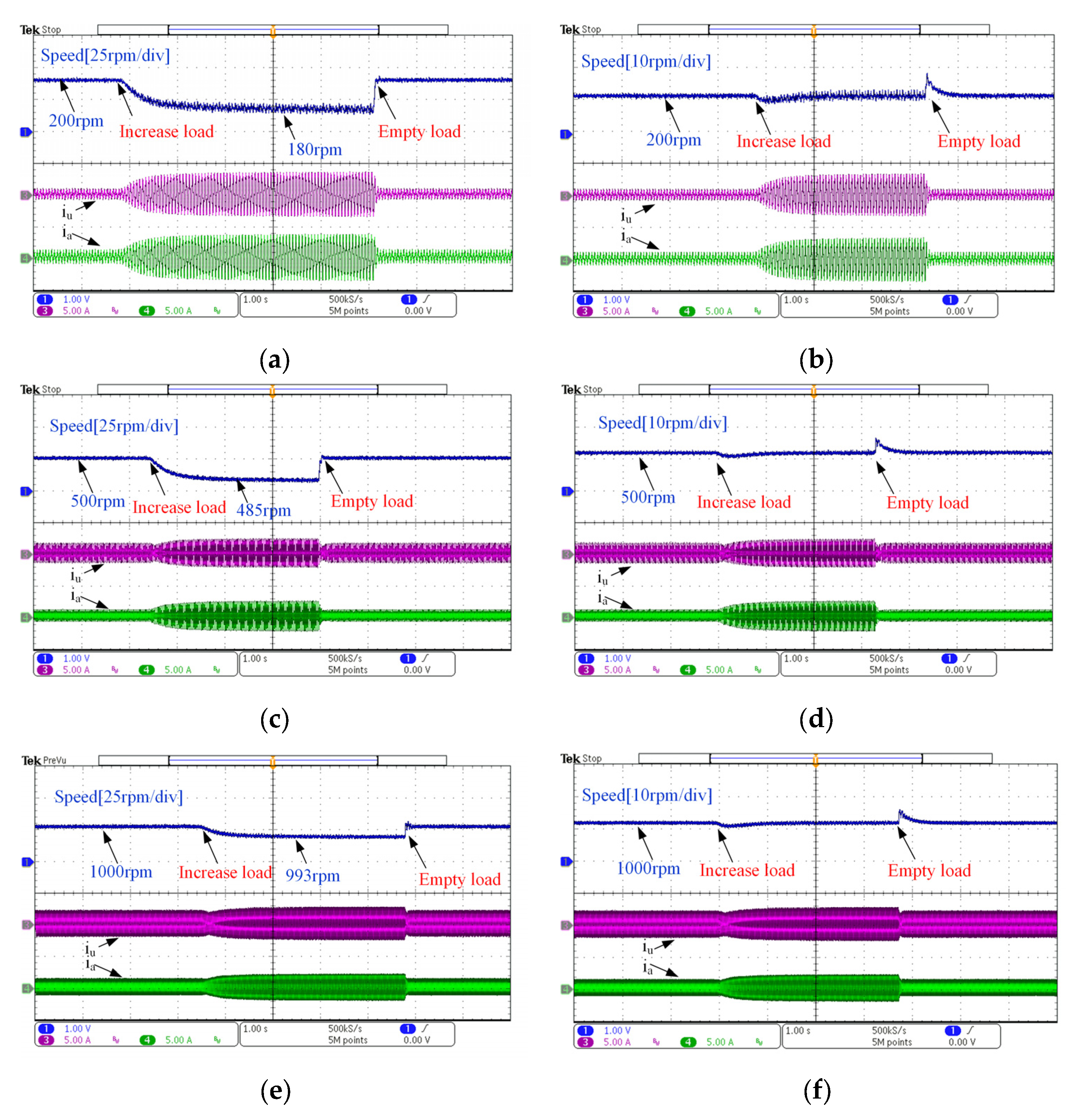
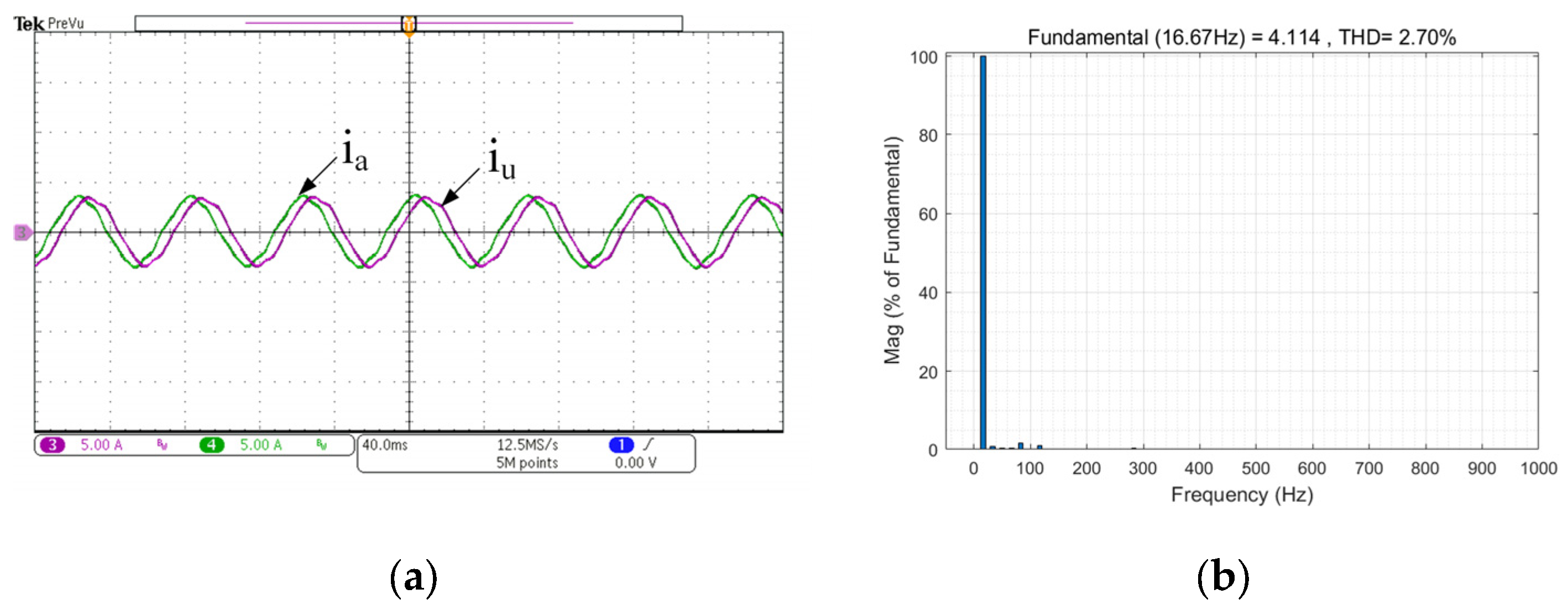
4. Simulation and Experimental Results
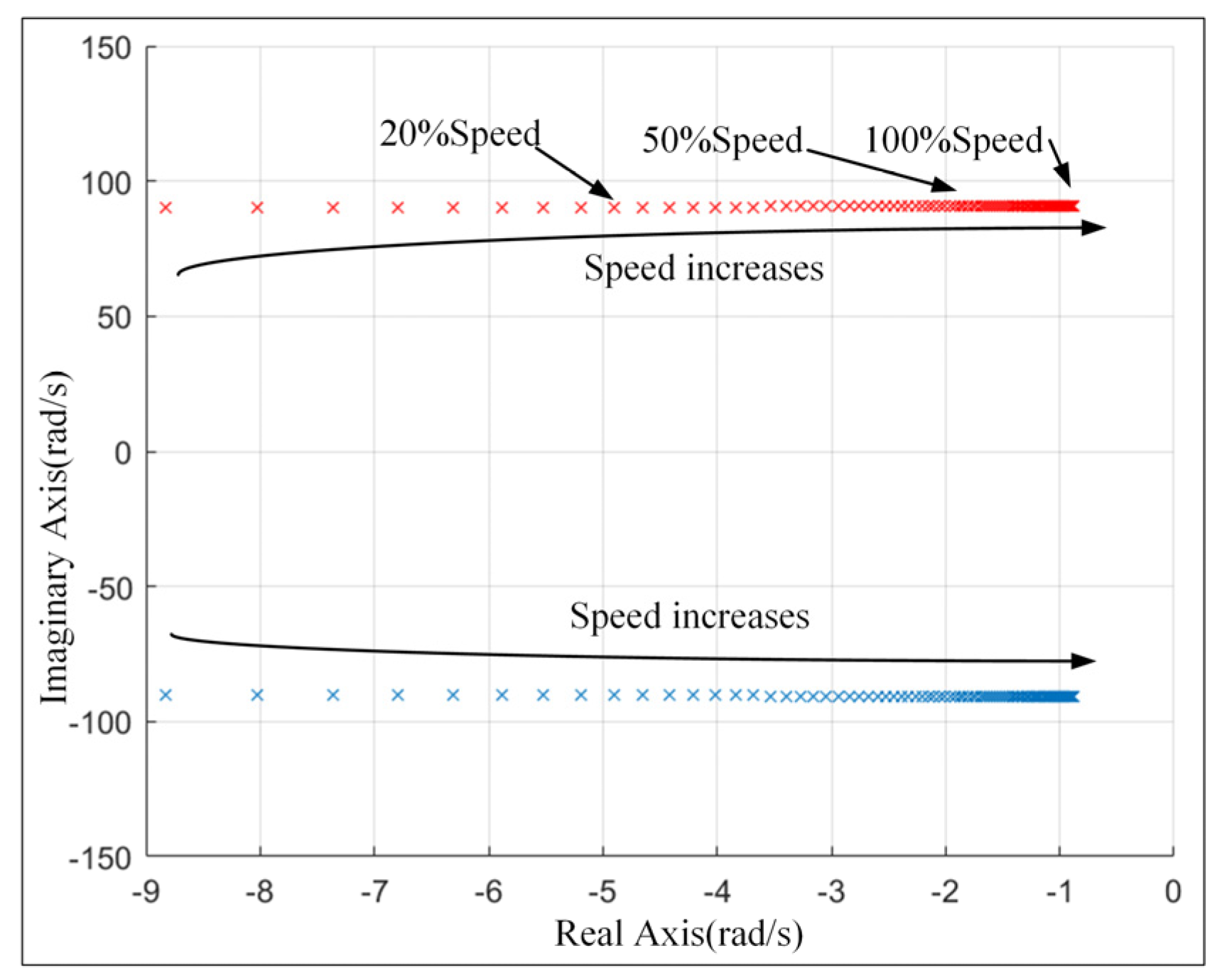
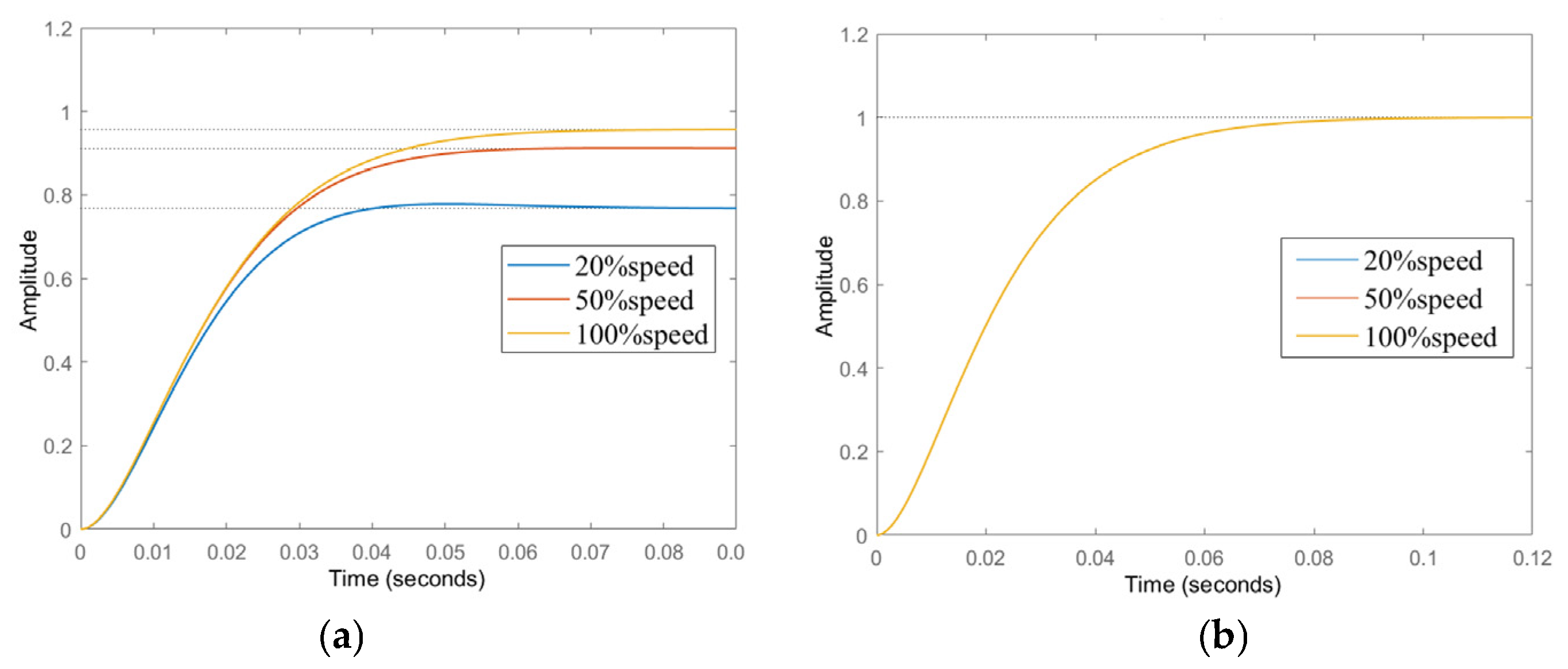
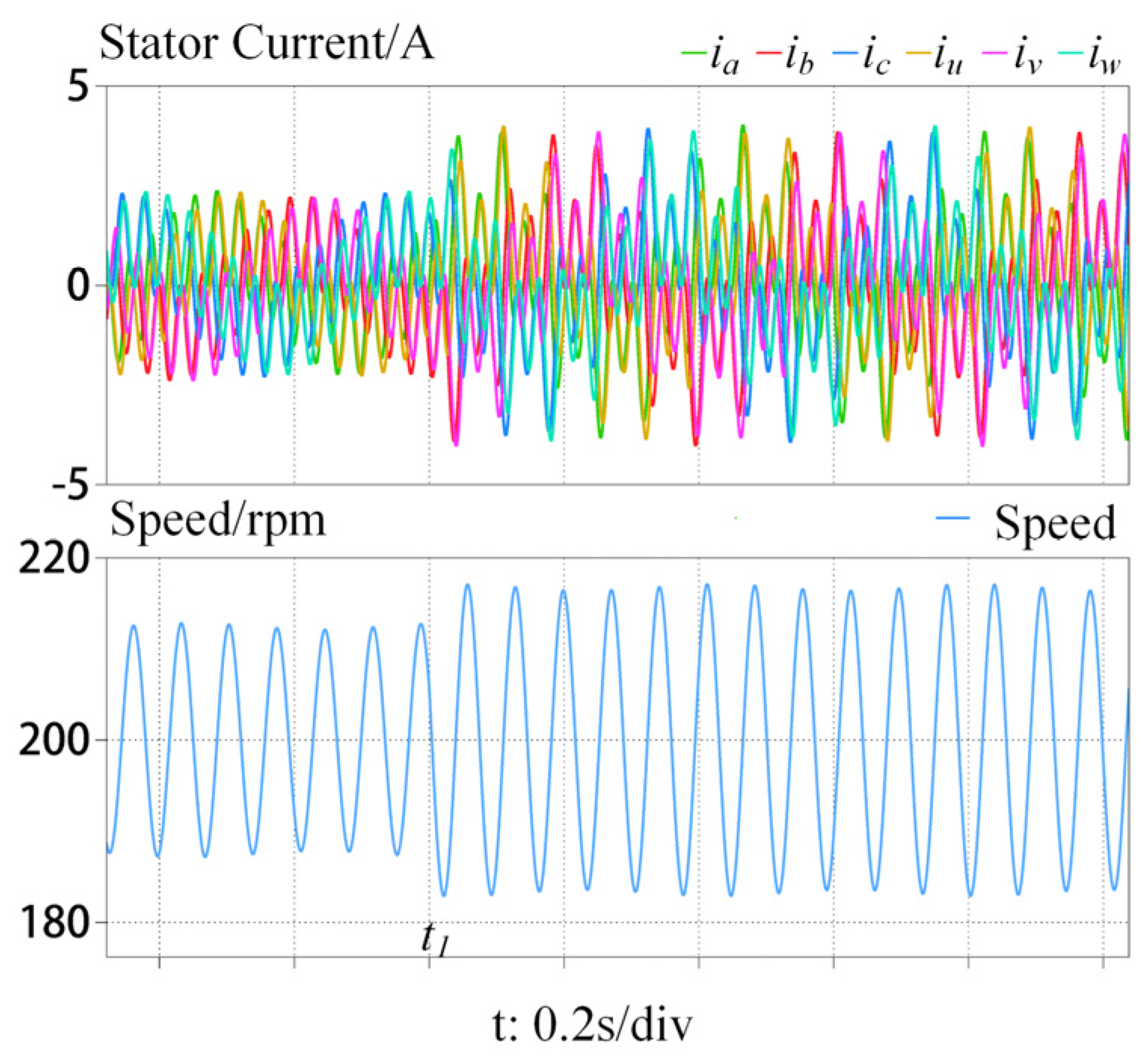
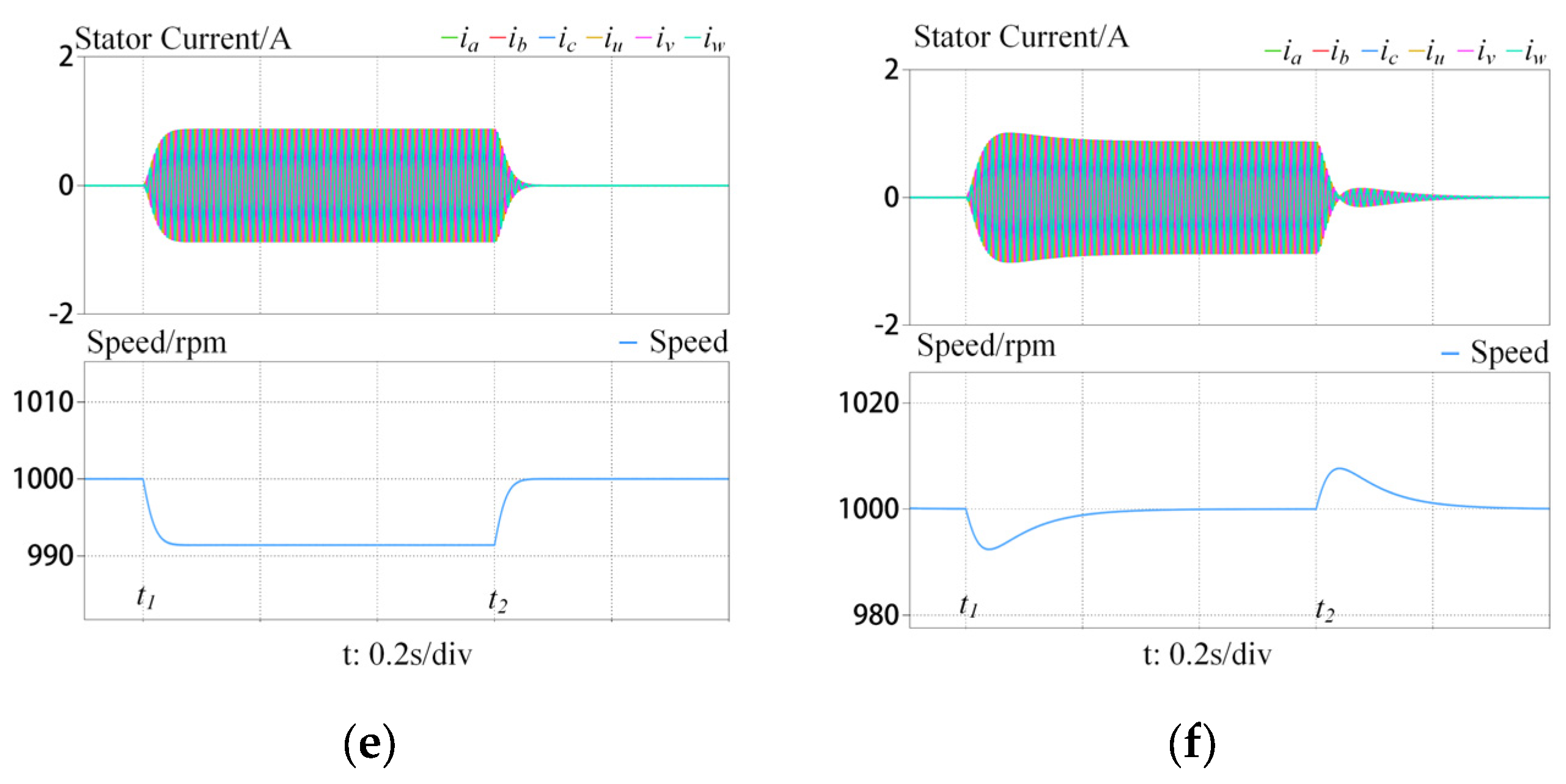
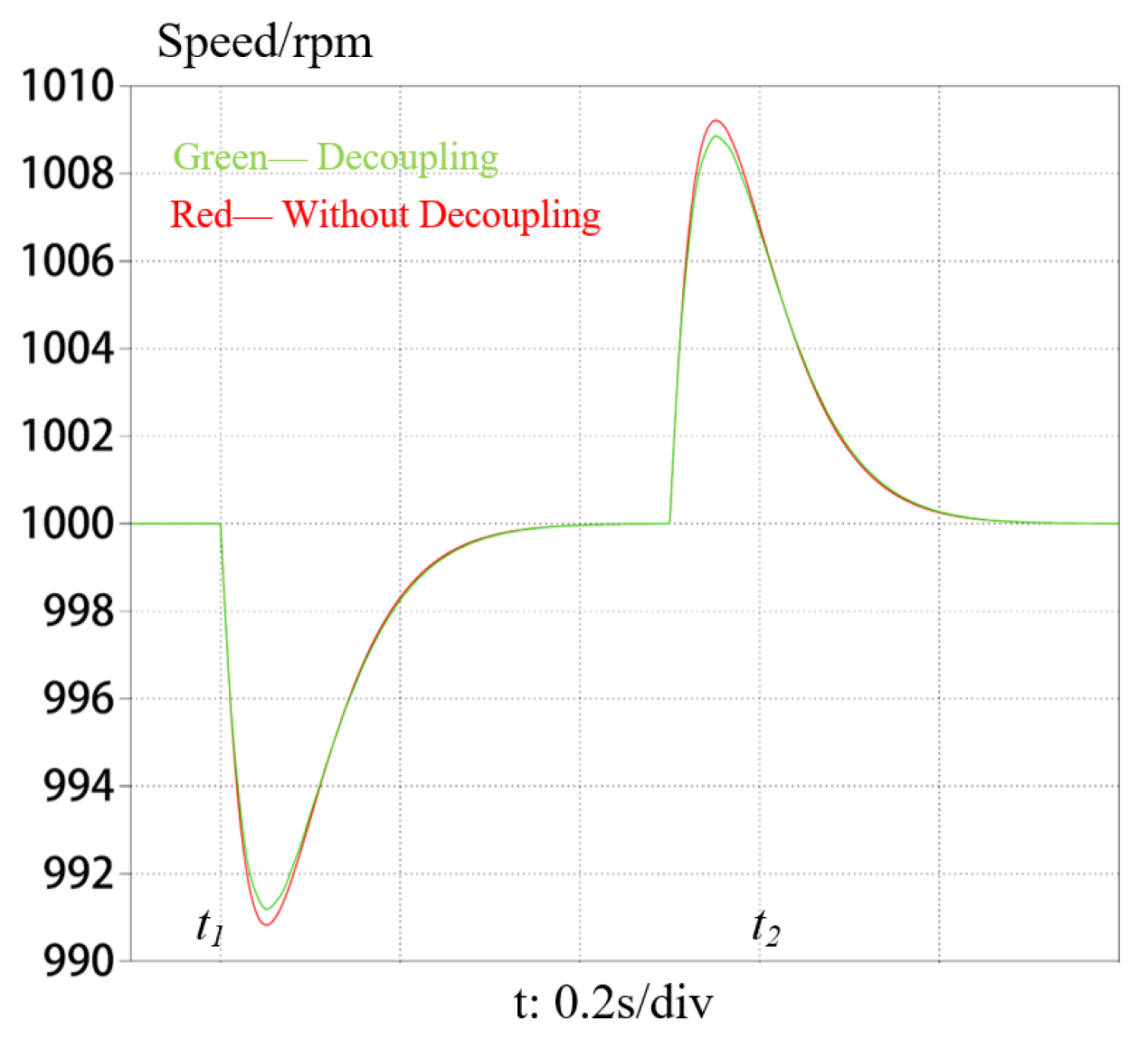
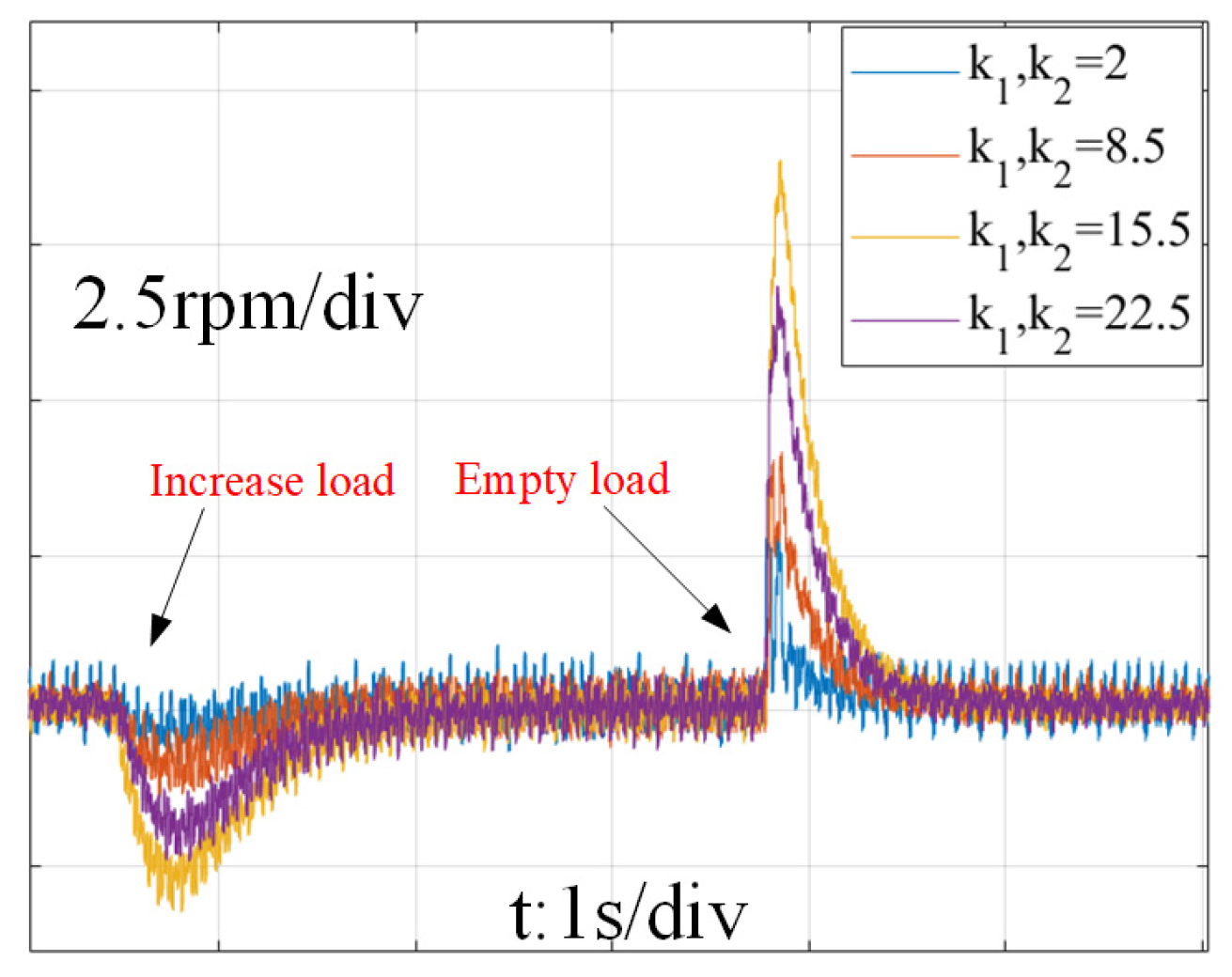
4.1. Simulation Results
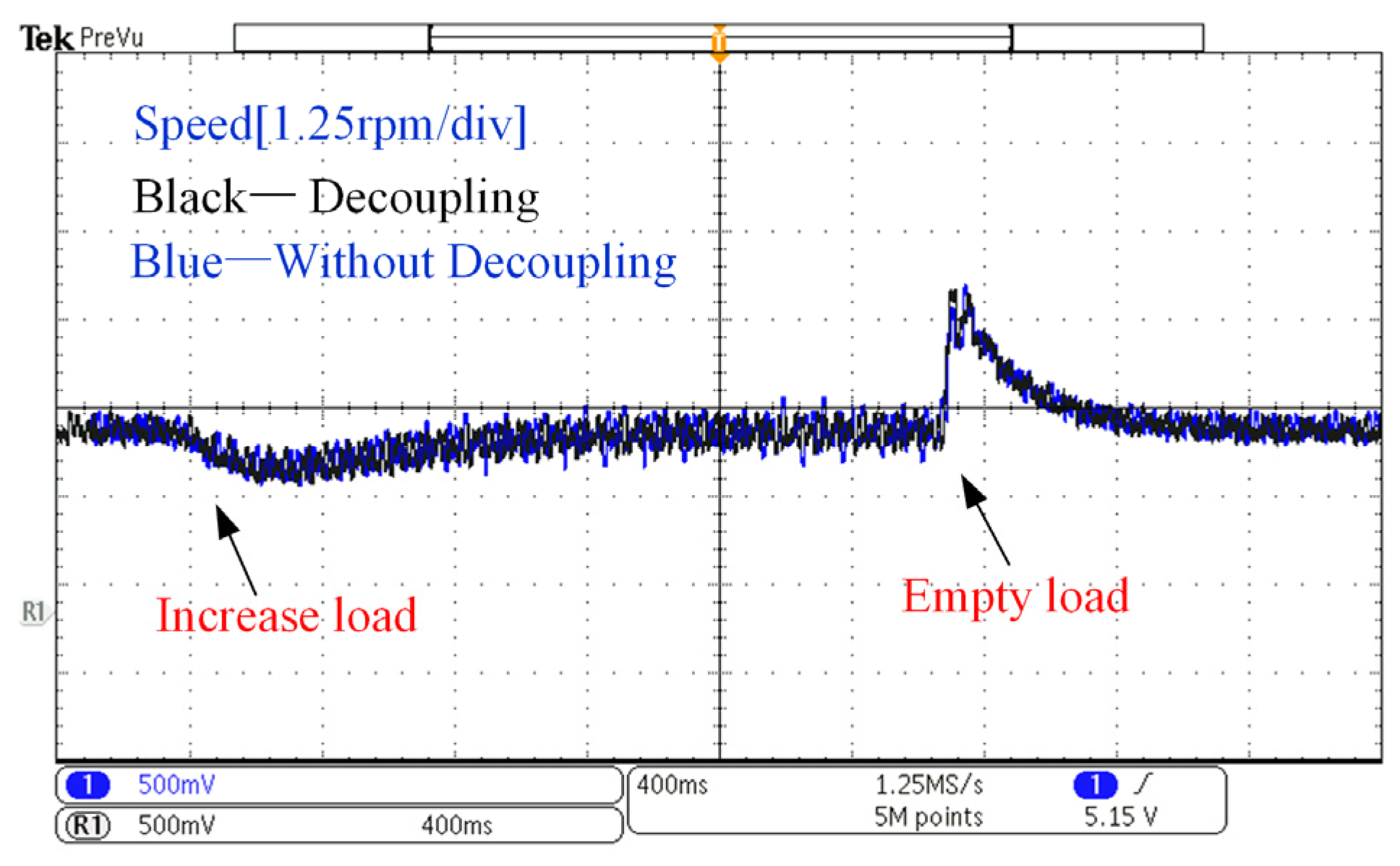
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, W.; Feng, J.; Tao, T.; Wang, C.; Liu, S. High-Frequency Harmonics and Vibration Reduction for Dual Three-Phase PMSM Using Multiple Randomized SVPWM Strategy. IEEE Trans. Power Electron. 2024, 39, 11455–11467. [Google Scholar] [CrossRef]
- Zheng, H.; Pei, X.; Liagas, C.; Brace, C.; Zeng, X. Extended Minimum Copper Loss Range Fault-Tolerant Control for Dual Three-Phase PMSM. IEEE Trans. Ind. Appl. 2024, 60, 6263–6276. [Google Scholar] [CrossRef]
- Levi, E.; Barrero, F.; Duran, M.J. Multiphase machines and drives-Revisited. IEEE Trans. Ind. Electron. 2015, 63, 429–432. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, K.; Li, Y.; Gu, M. Position sensorless control of dual three-phase IPMSM drives with high-frequency square-wave voltage injection. IEEE Trans. Ind. Electron. 2022, 70, 9925–9934. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z. A hybrid direct torque control scheme for dual three-phase PMSM drives with improved operation performance. IEEE Trans. Power Electron. 2018, 34, 1622–1634. [Google Scholar] [CrossRef]
- Li, H.S.; Zhou, Y.; Cao, Q.; Zhou, S. Mathematical derivation and analysis of the stability of open-loop control systems for permanent magnet synchronous motors. Chin. J. Electr. Eng. 2014, 1, 36–43. [Google Scholar]
- Cheng, A.; Jin, X. A stable V/F control method for permanent magnet synchronous motor drives. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; pp. 1–5. [Google Scholar]
- Perera, P.C.; Blaabjerg, F.; Pedersen, J.K.; Thogersen, P. A sensorless, stable V/f control method for permanent-magnet synchronous motor drives. IEEE Trans. Ind. Appl. 2003, 39, 783–791. [Google Scholar] [CrossRef]
- Tang, Z.; Akin, B. A new LMS based algorithm to suppress dead-time effects in PMSM V/f drives. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3156–3162. [Google Scholar]
- Wang, S.; Su, J.; Lu, G.; Yang, G. Decoupling Control for Aviation Dual-Redundancy Permanent Magnet Synchronous Motor with 0° Phase Shift. IEEE Trans. Energy Convers. 2023, 38, 2929–2937. [Google Scholar] [CrossRef]
- Tu, W.; Xiao, G.; Suo, C.; Yang, K. A design of sensorless permanent magnet synchronous motor drive based on V/f control. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar]
- Lee, K.; Han, Y. MTPA control strategy based on signal injection for V/f scalar-controlled surface permanent magnet synchronous machine drives. IEEE Access 2020, 8, 96036–96044. [Google Scholar] [CrossRef]
- Consoli, A.; Scelba, G.; Scarcella, G.; Cacciato, M. An effective energy-saving scalar control for industrial IPMSM drives. IEEE Trans. Ind. Electron. 2012, 60, 3658–3669. [Google Scholar] [CrossRef]
- Matsuki, Y.; Doki, S. High stability V/f control of PMSM using state feedback control based on nt coordinate system. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 2224–2228. [Google Scholar]
- Kim, W.J.; Kim, S.H. A simple MTPA operation scheme for V/f control of PMSMs. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 1297–1302. [Google Scholar]
- Saleh, S.A. Testing a $ V/f $ Control for Permanent Magnet Synchronous Motor Drives with Wavelet Modulated Power Electronic Converters. In Proceedings of the 2023 IEEE Industry Applications Society Annual Meeting (IAS), Nashville, TN, USA, 29 October–2 November 2023; pp. 1–8. [Google Scholar]
- Zhang, S.; Kang, J.; Yuan, J. Analysis and suppression of oscillation in V/F controlled induction motor drive systems. IEEE Trans. Transp. Electrif. 2021, 8, 1566–1574. [Google Scholar] [CrossRef]
- Tao, L.; Sun, J.; Tian, Z.; Huang, M.; Zha, X.; Gong, J. Speed-sensorless and motor parameters-free starting method for large-capacity synchronous machines based on virtual synchronous generator technology. IEEE Trans. Ind. Electron. 2020, 68, 6607–6618. [Google Scholar] [CrossRef]
- Zhong, Q.C. AC Ward Leonard drive systems: Revisiting the four-quadrant operation of AC machines. Eur. J. Control 2013, 19, 426–435. [Google Scholar] [CrossRef]
- Vidlak, M.; Gorel, L.; Makys, P. Performance evaluation, analysis, and comparison of the back-EMF-based sensorless FOC and stable V/f control for PMSM. In Proceedings of the 2022 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 22–24 June 2022; pp. 318–323. [Google Scholar]
- Tang, Z.; Li, X.; Dusmez, S.; Akin, B. A new V/f-based sensorless MTPA control for IPMSM drives. IEEE Trans. Power Electron. 2015, 31, 4400–4415. [Google Scholar] [CrossRef]
- Kim, W.J.; Kim, S.H. MTPA operation scheme with current feedback in V/f control for PMSM drives. J. Power Electron. 2020, 20, 524–537. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, Z.Q.; Wu, Z.Y.; Stone, D.; Foster, M. A simple sensorless position error correction method for dual three-phase permanent magnet synchronous machines. IEEE Trans. Energy Convers. 2020, 36, 895–906. [Google Scholar] [CrossRef]
- Choo, K.M.; Won, C.Y. Flying start of permanent-magnet-synchronous-machine drives based on a variable virtual resistance. IEEE Trans. Ind. Electron. 2020, 68, 9218–9228. [Google Scholar] [CrossRef]






| Control Method | Works | Model | Oscillation Analysis and Suppression | The Difficulty Level of Feedback Parameter Design | Power |
|---|---|---|---|---|---|
| V/f control without active damping | [6] | Fourth-order model in sub-PMSM | Root locus analysis. Unable to quantify oscillations and damping ratio. Unable to suppress oscillation. | None. | Poor power factor. |
| V/f control with current feedback | [17] | Fourth-order model in sub-PMSM | Bode diagram analysis. Unable to quantify oscillations. The design of current feedback parameters cannot be quantified and is complex. Poor suppression of oscillation effects. | Design based on bode diagram and unable to quantify. Complex. | Poor power factor. |
| V/f control with power feedback. | [8,11,12] | Fourth-order model in sub-PMSM | Root locus analysis. Unable to quantify oscillations and damping ratio. Excellent oscillation suppression effects. | Design based on root locus diagram and unable to quantify. Complex. | Poor power factor. |
| V/f control with Power-RPM Reduced-order Model | Proposed | Second-order model in sub-PMSM | Pole loci analysis, quantify oscillations and damping ratio in Power-RPM Reduced-order Model. Excellent oscillation suppression effects. | Design based on Power-RPM Reduced-order Model and quantify. Simple. | High power factor. |
| Parameters | Descriptions | Values |
|---|---|---|
| ψf | Rotor flux | 0.23396 Wb |
| Lq | q-axis inductance | 4.13 mH |
| Ld | d-axis inductance | 3.13 mH |
| Lqq | q-axis coupling inductances between two windings | 2.22 mH |
| Ldd | d-axis coupling inductances between two windings | 1.47 mH |
| Rs | Stator resistance | 0.5 Ω |
| n | Motor pole pairs | 5 |
| Jm | The total equivalent inertia of the machine and load | 0.070 kg·m2 |
| nrare | Rated speed | 1000 rpm |
| fre | System oscillation frequency | 14.286 Hz |
| k1 | Power feedback coefficient | 8.5 |
| k2 | Power feedback coefficient | 8.5 |
| m1/m2 | reactive power droop coefficient | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, R.; Wang, Y.; Deng, H.; Liu, X.; Guan, Y. A Power-RPM Reduced-Order Model and Power Control Strategy of the Dual Three-Phase Permanent Magnet Synchronous Motor in a V/f Framework for Oscillation Suppression. Energies 2024, 17, 4563. https://doi.org/10.3390/en17184563
Su R, Wang Y, Deng H, Liu X, Guan Y. A Power-RPM Reduced-Order Model and Power Control Strategy of the Dual Three-Phase Permanent Magnet Synchronous Motor in a V/f Framework for Oscillation Suppression. Energies. 2024; 17(18):4563. https://doi.org/10.3390/en17184563
Chicago/Turabian StyleSu, Riqing, Yuanze Wang, Hui Deng, Xiong Liu, and Yuanpeng Guan. 2024. "A Power-RPM Reduced-Order Model and Power Control Strategy of the Dual Three-Phase Permanent Magnet Synchronous Motor in a V/f Framework for Oscillation Suppression" Energies 17, no. 18: 4563. https://doi.org/10.3390/en17184563
APA StyleSu, R., Wang, Y., Deng, H., Liu, X., & Guan, Y. (2024). A Power-RPM Reduced-Order Model and Power Control Strategy of the Dual Three-Phase Permanent Magnet Synchronous Motor in a V/f Framework for Oscillation Suppression. Energies, 17(18), 4563. https://doi.org/10.3390/en17184563






