A Single-Phase Ground Fault Line Selection Method in Active Distribution Networks Based on Transformer Grounding Mode Modification
Abstract
1. Introduction
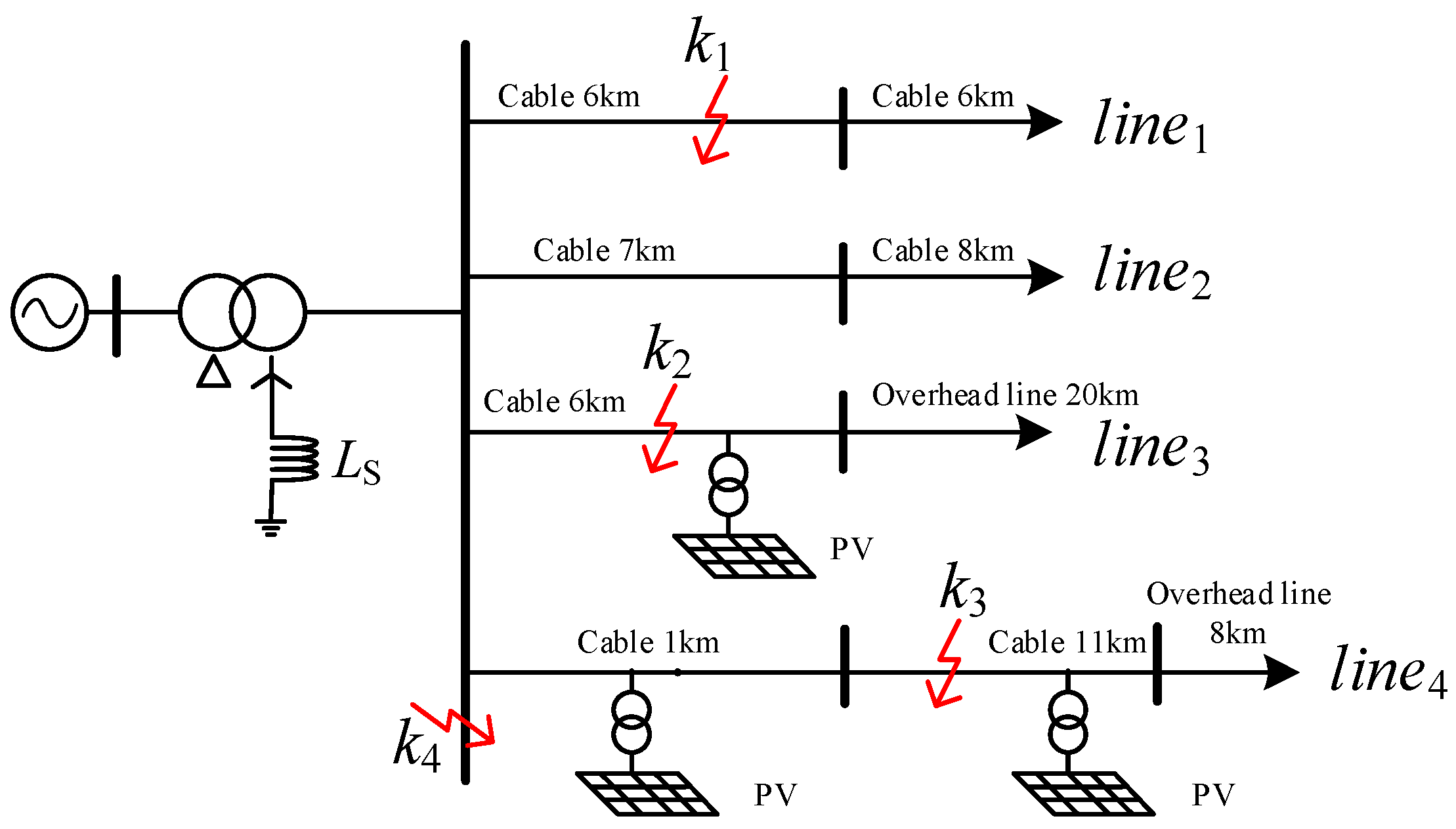
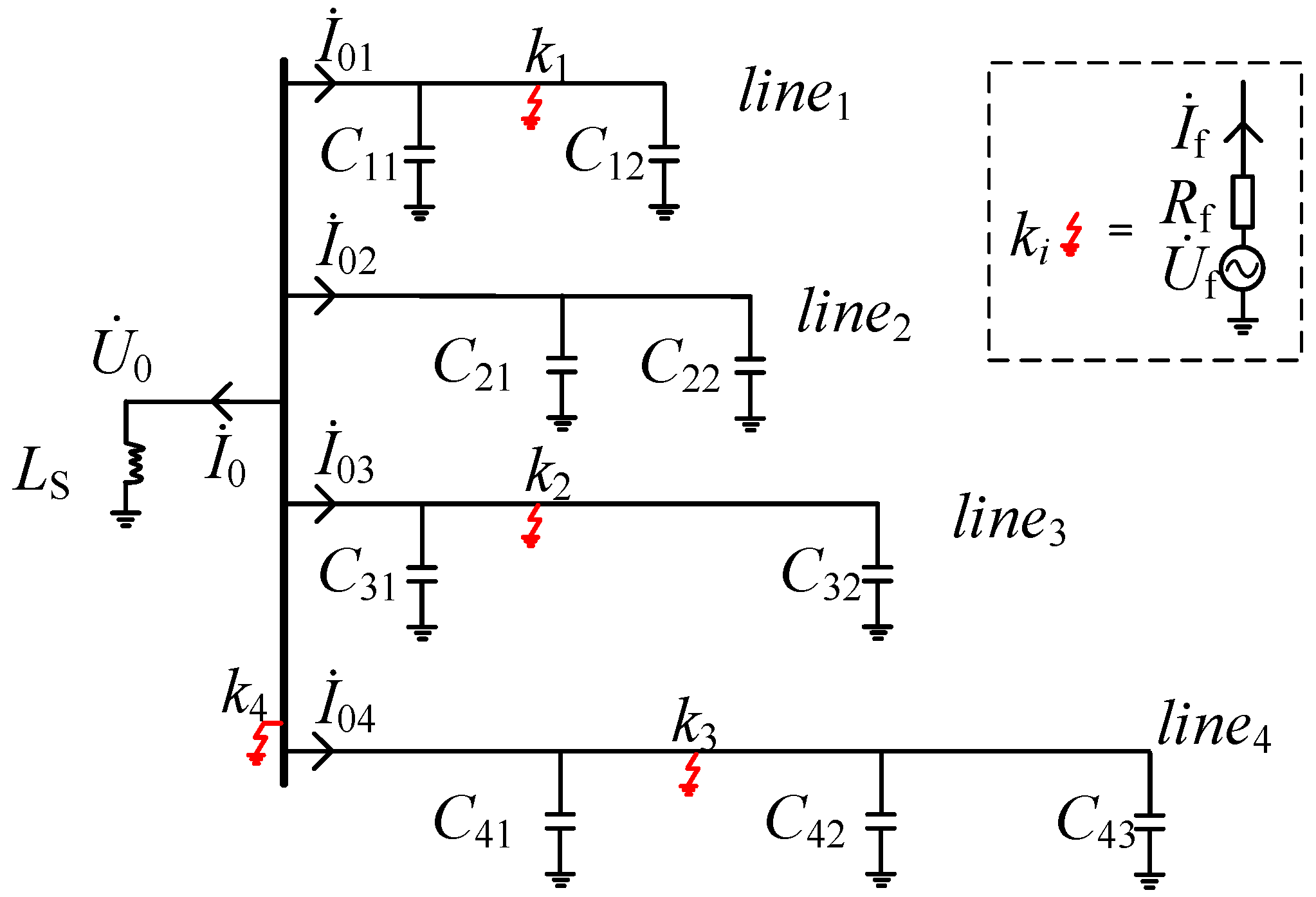
2. Analysis of SPGF Characteristics in ADNs with NEVAEC
2.1. Fault in Feeder Line3 (Fault Point k2)
2.2. Fault in Feeder Line4 (Fault Point k3)
2.3. Fault in Bus (Fault Point k4)
3. Construction of FLS Criteria for SPGF
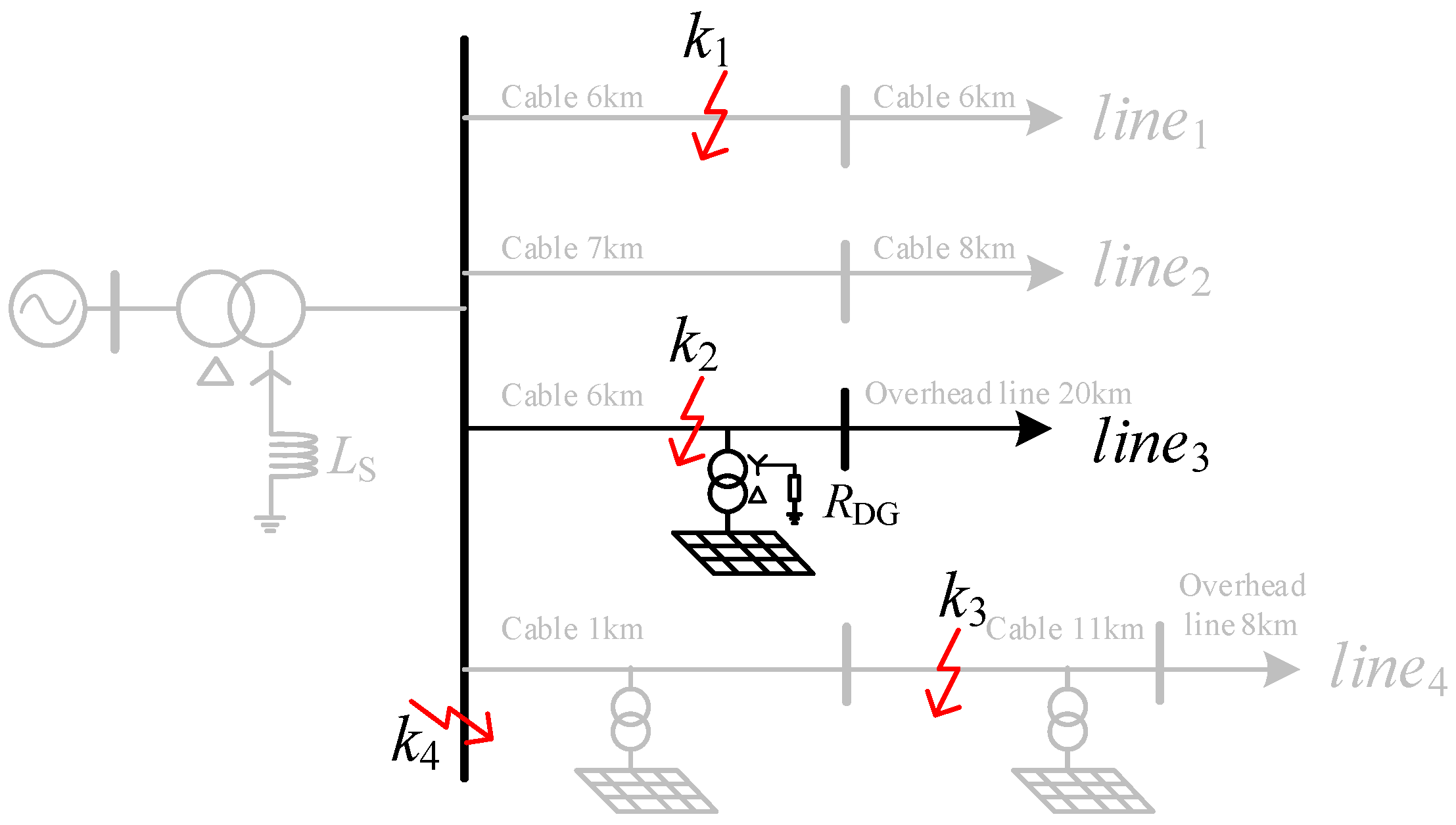
3.1. Fault in the Modified Feeder Line3 (Fault Point k2)
3.2. Fault in the Non-Modified Feeder Line4 (Fault Point k3)
3.3. Fault in the Bus (Fault Point k4)
3.4. FLS Method and Criteria
4. Simulation Verification
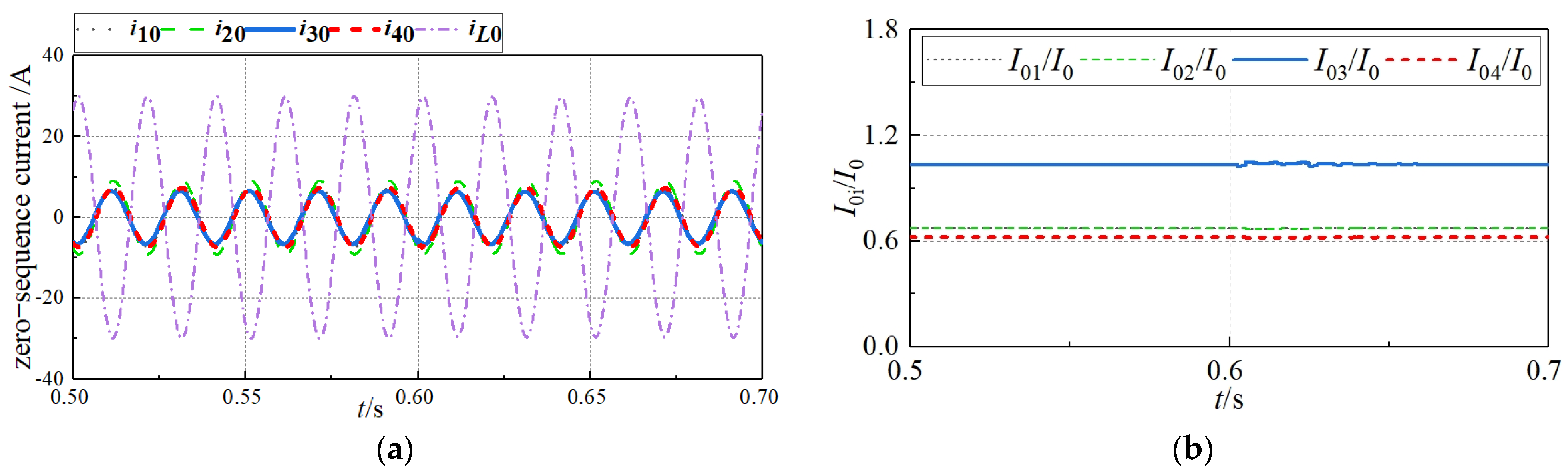
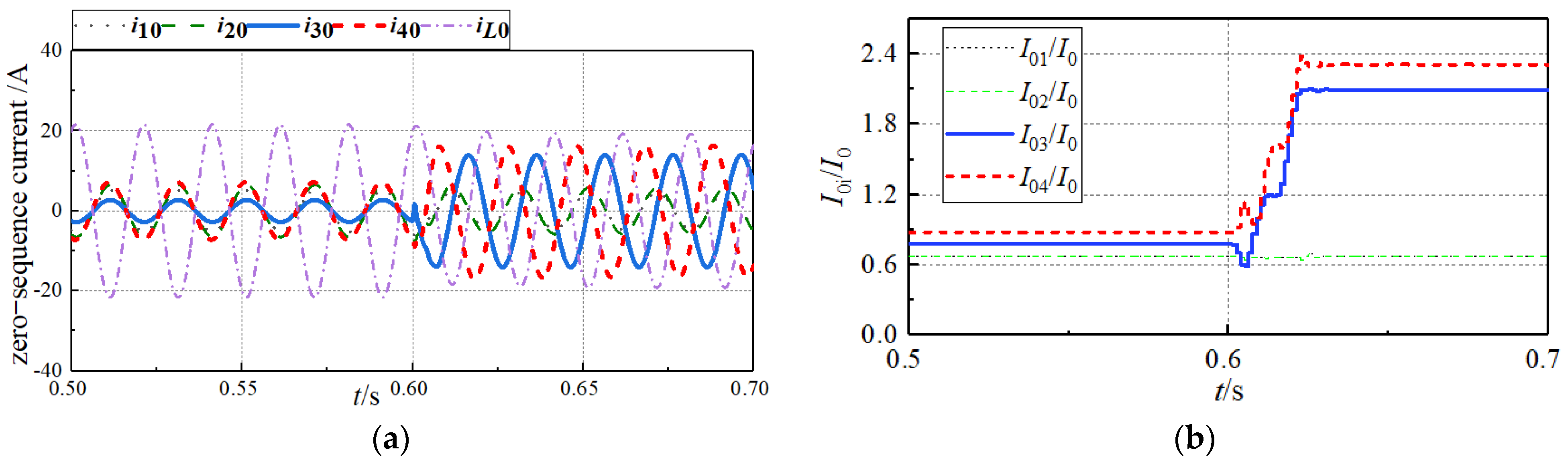
4.1. Different Fault Locations Simulation
4.2. Transient Impedance Tolerance Simulation
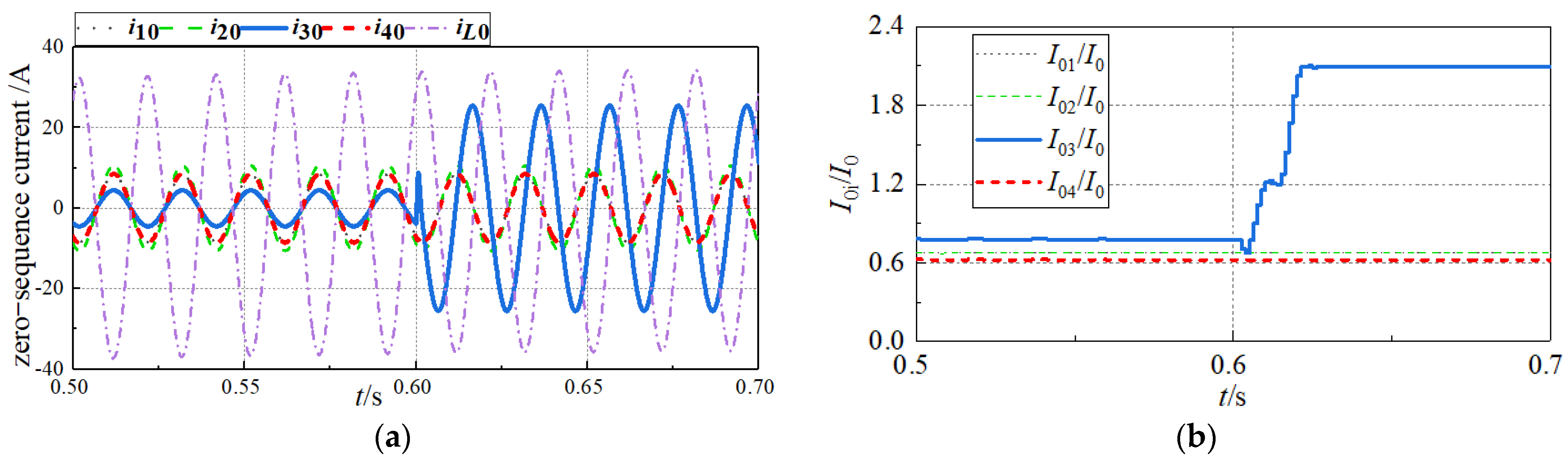
4.3. Impact of RDG Size on FLS Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PSCAD | Power Systems Computer Aided Design |
| DNs | distribution networks |
| NPU | neutral point ungrounded |
| LRNG | low resistance neutral grounding |
| FG | flexible grounding |
| NEVAEC | neutral earthing via arc extinguishing coil |
| SPGF | single-phase ground faults |
| FLS | fault line selection |
| DGs | distributed generations |
| ADNs | active distribution networks |
| RMS | Root Mean Square |
References
- Su, X.; Wei, H. A Fault-Line Selection Method for Small-Current Grounded System Based on Deep Transfer Learning. Energies 2022, 15, 3467. [Google Scholar] [CrossRef]
- Zhang, M.; Luan, W.; Ai, X.; Xu, B. Single-phase Grounding Fault Detection in Non-solidly Earthed Network Based on Negative Sequence Characteristics of Low-voltage Side. Power Syst. Technol. 2024, 48, 1654–1662. [Google Scholar]
- Zou, C.; Liu, D.; Lin, B.; Lu, Y.; Liu, J. Single-phase Ground Fault Location of Distribution Network with Distributed Generator Based on Characteristic Energy and BFAGA. High Volt. Eng. 2024, 50, 2706–2715. [Google Scholar]
- Qian, H.; Huang, Z.; Ruan, D. Single phase-to-earth fault location of small current grounding system with distributed generation. Electr. Mach. Control 2014, 18, 17–23. [Google Scholar]
- Xue, Y.; Guo, L.; Zhang, L.; Xu, B.; Li, T. Selection Problems of Neutral Grounding Mode in Active Distribution Networks. Autom. Electr. Power Syst. 2015, 39, 129–136. [Google Scholar]
- Ren, X.; Bai, Y.; Dai, Y.; Liang, R.; Gao, H.; Su, L.; Zhang, X.; Kong, L.; Zhang, P. Research on The Countermeasures of The Single-Phase-to-Earth Faults in Flexibly Grounded Distribution Networks. Alex. Eng. J. 2024, 98, 68–79. [Google Scholar] [CrossRef]
- Tian, J.; Li, H.; Jiang, L.; Shen, Z.; Ren, H.; Guo, L. Analysis of Single-phase Grounding Fault Characteristics of Low Resistance Grounding System with Multi-Distributed Power Supply. Power Syst. Prot. Control 2024, 52, 103–110. [Google Scholar]
- Shao, W.; Bai, J.; Cheng, Y.; Zhang, Z.; Li, N. Research on a Faulty Line Selection Method Based on the Zero-Sequence Disturbance Power of Resonant Grounded Distribution Networks. Energies 2019, 12, 846. [Google Scholar] [CrossRef]
- Norshahrani, M.; Mokhlis, H.; Abu Bakar, A.H.; Jamian, J.J.; Sukumar, S. Progress on Protection Strategies to Mitigate the Impact of Renewable Distributed Generation on Distribution Systems. Energies 2017, 10, 1864. [Google Scholar] [CrossRef]
- Cui, Q.; El-Arroudi, K.; Weng, Y. A Feature Selection Method for High Impedance Fault Detection. IEEE Trans. Power Deliv. 2019, 34, 1203–1215. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Wu, W.; Zhang, J.; Bai, W.; Guo, A.; Chen, Y. Faulty Line Selection Method Based on Comprehensive Dynamic Time Warping Distance in a Flexible Grounding System. Energies 2022, 15, 471. [Google Scholar] [CrossRef]
- Wang, W.; Gao, X.; Fan, B.; Zeng, X.; Yao, G. Faulty Phase Detection Method Under Single-Line-to-Ground Fault Considering Distributed Parameters Asymmetry and Line Impedance in Distribution Networks. IEEE Trans. Power Deliv. 2022, 37, 1513–1522. [Google Scholar] [CrossRef]
- Zhang, P.; Jin, M.; Liang, R.; Tang, Z.; Hou, M.; Peng, N.; Li, J. Faulty Cable Segment Identification of Low-Resistance Grounded Active Distributions via Grounding Wire Current-Based Approach. IEEE Trans. Ind. Inform. 2024, 20, 7708–7718. [Google Scholar] [CrossRef]
- Li, J.; Bi, H.; Li, C.; Li, J.; Zeng, D.; Wang, G. Analysis and calculation method for multiple faults in low-resistance grounded systems with inverter-interfaced distributed generators based on a PQ control strategy. Int. J. Electr. Power Energy Syst. 2022, 138, 0142–0615. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, S.; Li, Y.; Li, Z.; Wang, Q.; Geng, S. Analysis of single-phase grounding fault characteristics in petal-shaped distribution network with inverter-interfaced distributed generator. Electr. Power Autom. Equip. 2022, 42, 129–137. [Google Scholar]
- Kim, C.H.; Aggarwal, R.K. Closure on “a novel fault detection technique of high impedance arcing faults in transmission lines using the wavelet transform”. IEEE Trans. Power Deliv. 2003, 18, 1596–1597. [Google Scholar] [CrossRef]
- Park, S.; Sung, E.-T.; Wang, S.; Hong, S. Mixer-Free Phase and Amplitude Comparison Method for Built-in Self- Test of Multiple Channel Beamforming IC. In Proceedings of the 2023 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), San Diego, CA, USA, 11–13 June 2023; pp. 265–268. [Google Scholar]
- Cong, Z.; Liu, Y.; Fang, J.; Wang, P.; Guo, L.; Jiang, X. Root-Cause Identification of Single Line-to-Ground Fault in Urban Small Current Grounding Systems Based on Correlation Dimension and Average Resistance. IEEE Trans. Power Deliv. 2020, 35, 1834–1843. [Google Scholar] [CrossRef]
- He, R.; Hu, Z.; Wang, T. A Fault Line Selection Method for Resonant Grounding System Considering Injected Harmonics of Distributed Generation. Power Syst. Technol. 2019, 43, 670–680. [Google Scholar]
- Yuan, J.; Li, X.; Zhang, Z. Research on single-phase grounding fault selection technology for active distribution network based on injected signal. Electr. Meas. Instrum. 2020, 57, 44–49. [Google Scholar]
- Wang, P.; Xu, B.; Chen, H.; Wang, W.; Liang, D.; Sun, Z. Influence of Error of Zero-sequence Current Transformer on Small-current High-resistance Grounding Protection and Type Selection. Autom. Electr. Power Syst. 2023, 47, 154–162. [Google Scholar]
- Pirmani, S.; Fernando, W.; Mahmud, M. Single line-to-ground fault current analysis for resonant grounded power distribution networks in bushfire prone areas. Electr. Power Syst. Res. 2024, 237, 110883. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Zeng, X.; Huang, X.; Song, Q. Faulty Feeder Detection Based on Space Relative Distance for Compensated Distribution Network with IIDG Injections. IEEE Trans. Power Deliv. 2021, 36, 2459–2466. [Google Scholar] [CrossRef]

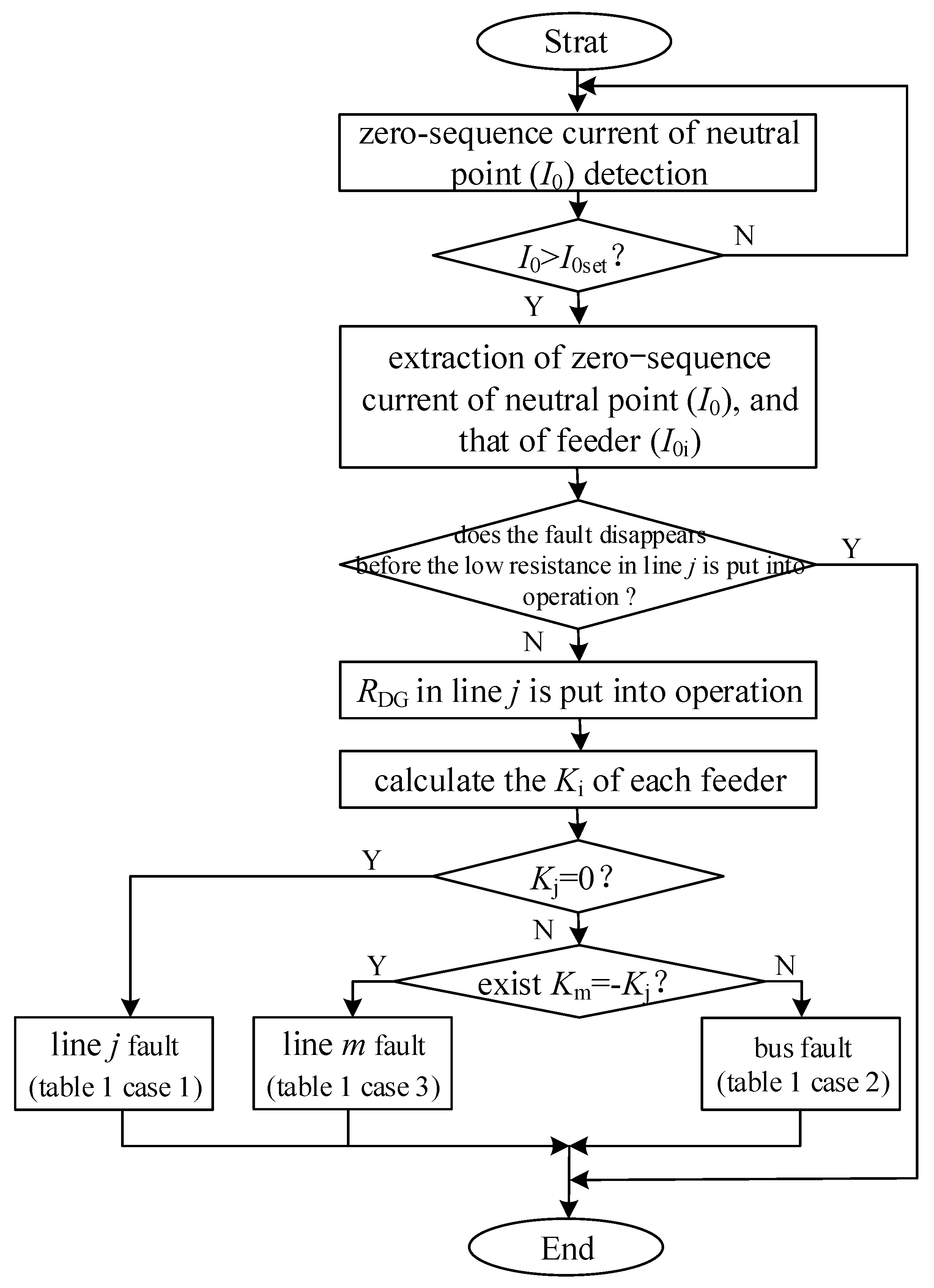
| Situation | Criterion Characteristics | SPGF Location |
|---|---|---|
| 1 | All Ki are zero | The modified line |
| 2 | One Ki is non-zero | The bus |
| 3 | Two Ki is non-zero | The non-modified line among the two non-zero lines |
| Line Type | Resistance (Ω/km) | Inductance (mH/km) | Capacitance (μF/km) | |||
|---|---|---|---|---|---|---|
| Positive Sequence | Zero Sequence | Positive Sequence | Zero Sequence | Positive Sequence | Zero Sequence | |
| Cable | 0.27 | 2.7 | 0.255 | 1.109 | 0.376 | 0.276 |
| Overhead line | 0.17 | 0.32 | 1.017 | 3.56 | 0.115 | 0.0062 |
| Fault Location | Transition Resistance/Ω | K1 | K2 | K3 | K4 | Selection Result |
|---|---|---|---|---|---|---|
| k1 | 0 | ¬ 0 | 0 | ¬ 0 | 0 | Line1 |
| 200 | ¬ 0 | 0 | ¬ 0 | 0 | Line1 | |
| 1000 | ¬ 0 | 0 | ¬ 0 | 0 | Line1 | |
| 2000 | ¬ 0 | 0 | ¬ 0 | 0 | Line1 | |
| k2 | 0 | 0 | 0 | 0 | 0 | Line3 |
| 200 | 0 | 0 | 0 | 0 | Line3 | |
| 1000 | 0 | 0 | 0 | 0 | Line3 | |
| 2000 | 0 | 0 | 0 | 0 | Line3 | |
| k3 | 0 | 0 | 0 | ¬ 0 | ¬ 0 | Line4 |
| 200 | 0 | 0 | ¬ 0 | ¬ 0 | Line4 | |
| 1000 | 0 | 0 | ¬ 0 | ¬ 0 | Line4 | |
| 2000 | 0 | 0 | ¬ 0 | ¬ 0 | Line4 | |
| k4 | 0 | 0 | 0 | ¬ 0 | 0 | Bus |
| 200 | 0 | 0 | ¬ 0 | 0 | Bus | |
| 1000 | 0 | 0 | ¬ 0 | 0 | Bus | |
| 2000 | 0 | 0 | ¬ 0 | 0 | Bus |
| RDG/Ω | K1 | K2 | K3 | K4 | Selection Result | |
|---|---|---|---|---|---|---|
| 10 | 0 | 0 | 0 | 0 | Line3 | correct result |
| 100 | 0 | 0 | 0 | 0 | Line3 | correct result |
| 300 | 0 | 0 | 0 | 0 | Line3 | correct result |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, S.; Xie, Q.; Ma, P.; Li, Y.; Chen, F.; Zhang, J.; Li, B.; Wang, C. A Single-Phase Ground Fault Line Selection Method in Active Distribution Networks Based on Transformer Grounding Mode Modification. Energies 2024, 17, 4743. https://doi.org/10.3390/en17184743
Su S, Xie Q, Ma P, Li Y, Chen F, Zhang J, Li B, Wang C. A Single-Phase Ground Fault Line Selection Method in Active Distribution Networks Based on Transformer Grounding Mode Modification. Energies. 2024; 17(18):4743. https://doi.org/10.3390/en17184743
Chicago/Turabian StyleSu, Shi, Qingyang Xie, Pengfei Ma, Yuan Li, Fahui Chen, Jing Zhang, Botong Li, and Changqi Wang. 2024. "A Single-Phase Ground Fault Line Selection Method in Active Distribution Networks Based on Transformer Grounding Mode Modification" Energies 17, no. 18: 4743. https://doi.org/10.3390/en17184743
APA StyleSu, S., Xie, Q., Ma, P., Li, Y., Chen, F., Zhang, J., Li, B., & Wang, C. (2024). A Single-Phase Ground Fault Line Selection Method in Active Distribution Networks Based on Transformer Grounding Mode Modification. Energies, 17(18), 4743. https://doi.org/10.3390/en17184743






