Analytical Method for Determining the Viscosity Index of Engine Lubricating Oils
Abstract
:1. Introduction
- 1.
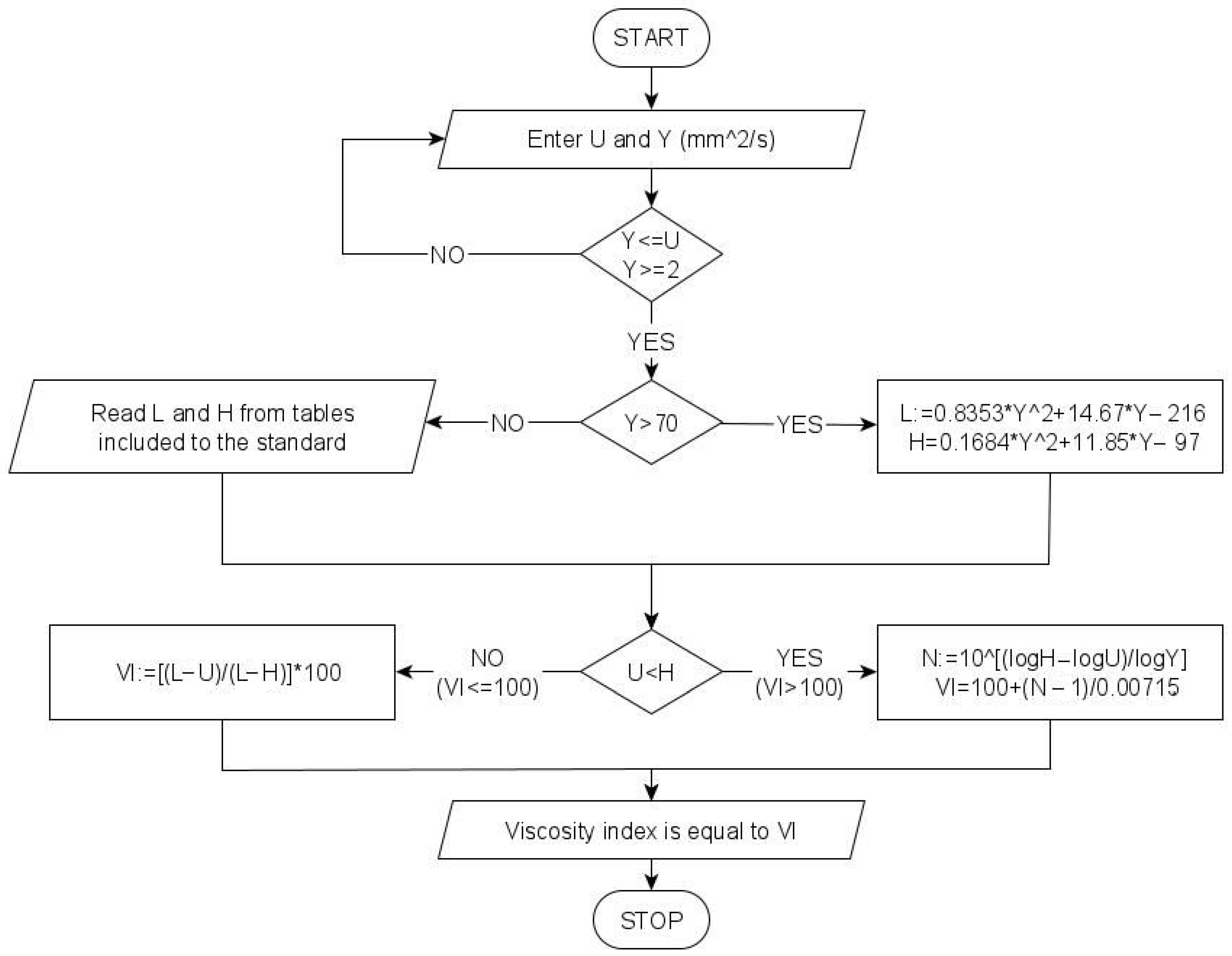
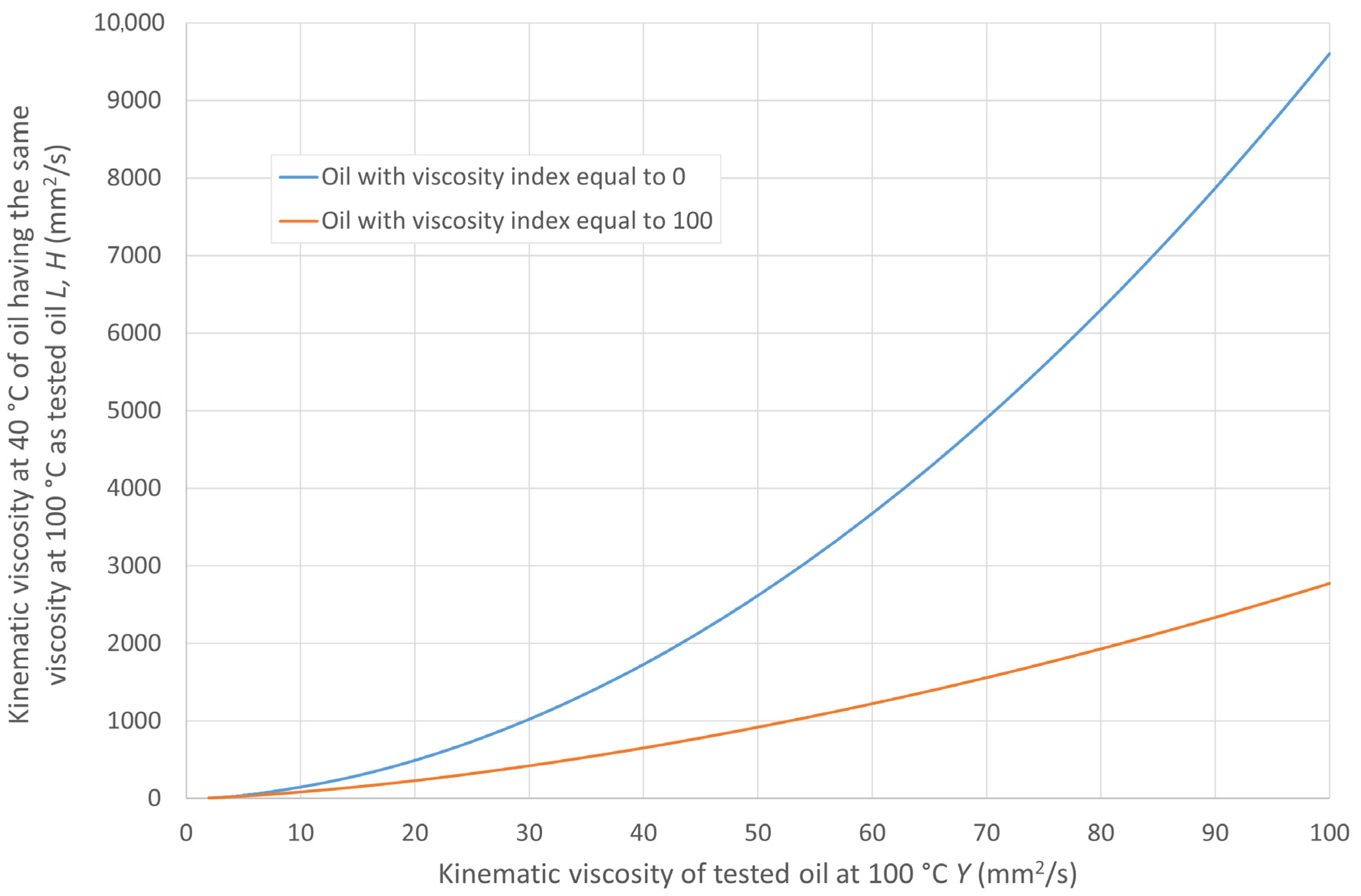
- Determination of the kinematic viscosity values at 40 °C of two hypothetical oils that have a kinematic viscosity at 100 °C equal to the kinematic viscosity of the oil under testing at 100 °C. The kinematic viscosity at 40 °C is determined for oil with a conventionally assigned viscosity index of 0 (VI = 0), labeled L, and for oil with a viscosity index of 100 (VI = 100), labeled H. According to the aforementioned viscosity standards, for a test oil with a kinematic viscosity at 100 °C labeled Y, which is greater than 2 mm2/s and smaller than 70 mm2/s, the values of L and H are read from a table that is an integral part of the standard. If the oil under testing has Y greater than 70 mm2/s, the values of L and H are calculated based on the following relationships:
- 2.
- Determination of viscosity index values based on functions of the viscosity of the tested oil U at 40 °C for oil with a viscosity index less than or equal to 100, or functions of the viscosity of the tested oil U and Y at 40 °C and 100 °C, respectively, for oil with a viscosity index greater than 100. The viscosity index can be calculated using the following formula:
2. Materials and Methods
- 1.
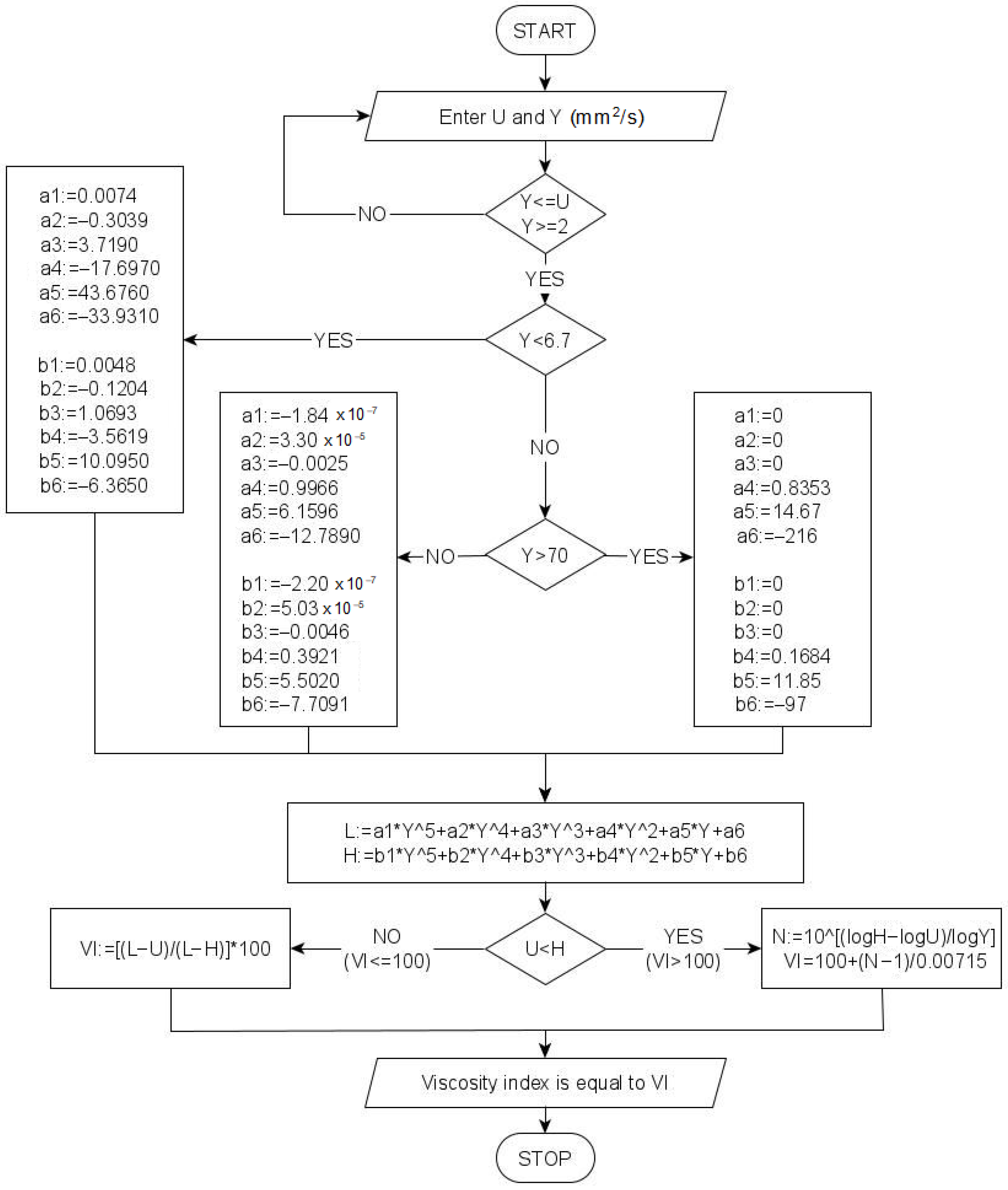
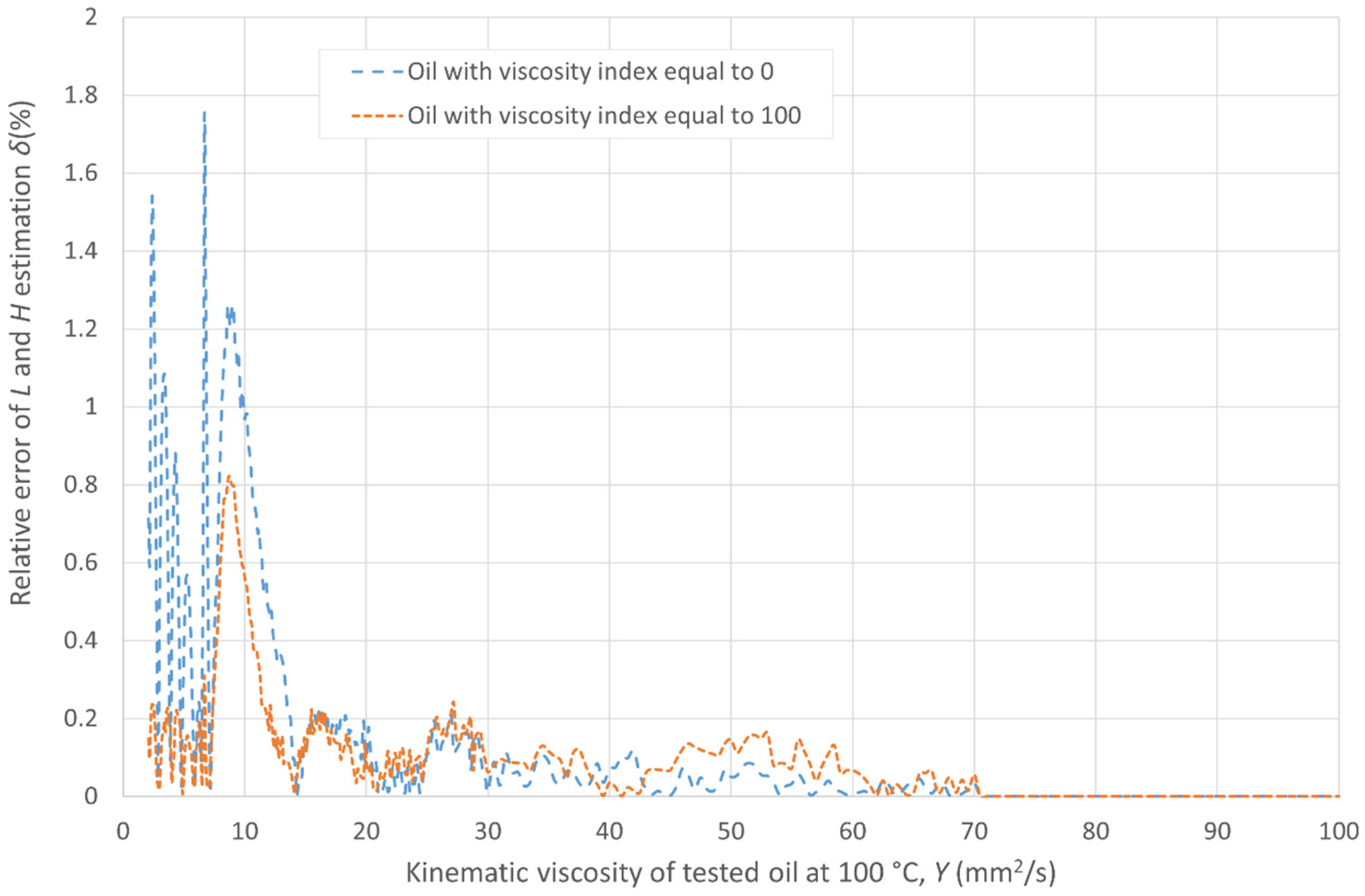
- The range of the lowest values of kinematic viscosity of the tested oil falling within 2.1 mm2/s ≤ Y < 6.7 mm2/s. The limit value of 6.7 is adopted for the accuracy of the model approximating the median range of kinematic viscosities indicated in the tables of the ASTM D2270 and ISO 2909 standards, below which the value of the relative percentage error of the proposed models is greater than 3%, which the authors adopted as the limit value.
- 2.
- The range of medians of kinematic viscosity of the tested oil is 6.7 mm2/s ≥ Y ≤ 70.0 mm2/s.
- 3.
- The range of highest kinematic viscosity values of the tested oil Y > 70.0 mm2/s is modeled by relations (3) and (4) (the range is derived from models indicated explicitly in ASTM D2270 and ISO 2909).
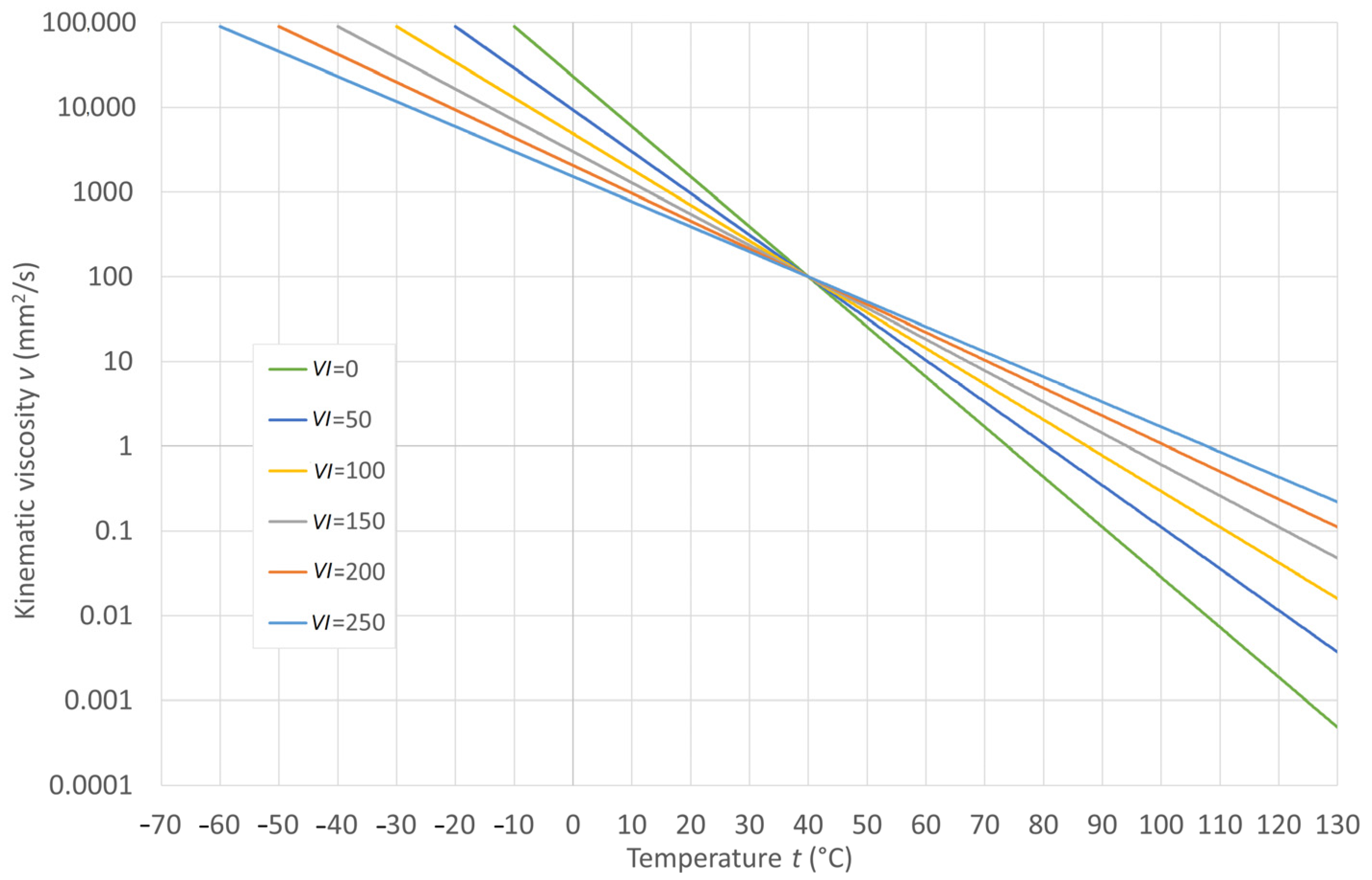
3. Results and Discussion
4. Example Application of the Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations and Symbols
| A | empirical parameters for determining dynamic viscosity |
| a1, a2, a3, a4, a5, a6 | coefficients of equations approximating the viscosity L |
| ASTM | standard of ASTM International, formerly known as the American Society for Testing and Materials |
| b1, b2, b3, b4, b5, b6 | coefficients of equations approximating the viscosity H |
| ΔE | activation energy of viscous flow |
| e | Euler number |
| f(Y) | empirical function to determine the viscosity L |
| f(Y) | empirical function to determine the viscosity H |
| H | kinematic viscosity at 40 °C of a hypothetical oil with VI = 100, which has (at 100 °C) a kinematic viscosity equal to that of the oil under test at 100 °C |
| ISO | International Organization for Standardization |
| L | kinematic viscosity at 40 °C of a hypothetical oil with VI = 0, which has (at 100 °C) a kinematic viscosity equal to that of the oil under test at 100 °C |
| RC | Clapeyron’s gas constant |
| R2 | coefficient of determination |
| SAE | SAE International, formerly the Society of Automotive Engineers |
| SAE 30, SAE 40 | viscosity grades of lubricating oil according to SAE J300 standard |
| T | absolute temperature in K |
| t | relative temperature in °C |
| TC23 | Technical Committee 23 of ISO |
| U | kinematic viscosity of the tested oil at 40 °C |
| VG | ISO viscosity grade |
| VI | viscosity index |
| VTC | viscosity–temperature coefficient |
| x | analyzed parameter (viscosity or viscosity index) |
| arithmetic mean of x determined from the model | |
| xi | the i-th value of the analyzed parameter x |
| the i-th value of x determined from the model | |
| Y | kinematic viscosity of the tested oil at 100 °C |
| shear rate | |
| δi | relative percentage error |
| ηt | dynamic viscosity at t |
| ρ15 | density at 15 °C. |
| ρt | density at t |
| τ | shear stresses |
Appendix A
References
- Wolak, A.; Zając, G.; Fijorek, K.; Janocha, P.; Matwijczuk, A. Experimental Investigation of the Viscosity Parameters Ranges—Case Study of Engine Oils in the Selected Viscosity Grade. Energies 2020, 13, 3152. [Google Scholar] [CrossRef]
- Mang, T. (Ed.) Encyclopedia of Lubricants and Lubrication; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-22646-5. [Google Scholar]
- Chybowski, L.; Szczepanek, M.; Gawdzińska, K. Arrhenius Equation for Calculating Viscosity in Assessing the Dilution Level of Lubricating Oil with Diesel Oil—A Case Study of SAE 30 and SAE 40 Grade Marine Lubricating Oils. Energies 2024, 17, 444. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die innere Reibung verdünnter wässeriger Lösungen. Z. Für Phys. Chem. 1887, 1U, 285–298. [Google Scholar] [CrossRef]
- Guzman, J. De Relation between fluidity and heat of fusion. An. Soc. Espan. Fis. Y. Quim. 1913, 11, 353–362. [Google Scholar]
- Seeton, C.J. Viscosity–temperature correlation for liquids. Tribol. Lett. 2006, 22, 67–78. [Google Scholar] [CrossRef]
- PN-ISO 3448:2009; Przemysłowe Ciekłe Środki Smarowe—Klasyfikacja Lepkościowa ISO. PKN: Warszawa, Poland, 2009.
- Society of Automotive Engineers. SAE J300-2021; Engine Oil Viscosity Classification. SAE International: Warrendale, PA, USA, 2021.
- Fitch, J. Don’t Ignore Viscosity Index When Selecting a Lubricant. Available online: https://www.machinerylubrication.com/Read/28956/lubricant-viscosity-index (accessed on 17 June 2024).
- Stanciu, I. Viscosity Index Improvers dor Multi-Grade Oil of Copolymers Polyethylene-Propylene and Hydrogenated Poly (Isoprene-Co-Styrene). J. Sci. Arts 2017, 4, 771–778. [Google Scholar]
- Hillman, D.E.; Lindley, H.M.; Paul, J.I.; Pickles, D. Application of gel permeation chromatography to the study of shear degradation of polymeric viscosity index improvers used in automotive engine oils. Br. Polym. J. 1975, 7, 397–407. [Google Scholar] [CrossRef]
- ASTM D 2270-10(2016); Standard Practice for Calculating Viscosity Index from Kinematic Viscosity at 40 °C and 100 °C. ASTM: West Conshohocken, PA, USA, 2016.
- ISO 2909:2002; Petroleum Products—Calculation of Viscosity Index from Kinematic Viscosity. ISO: Geneva, Switzerland, 2002.
- Paar, A. ASTM D 2270; Viscosity Index (VI) from 40 °C and 100 °C. Available online: https://wiki.anton-paar.com/pl-pl/wskaznik-lepkosci-vi-od-40c-i-100c-astm-d2270/ (accessed on 7 September 2022).
- Olezol. Viscosity Index (VI) Calculator. Available online: https://olezol.com/ (accessed on 7 September 2022).
- Evonik. Viscosity Index Calculator. Available online: https://oil-additives.evonik.com/media/public/misc/oil-additives-calculator/viscosity-index-en.html (accessed on 2 June 2024).
- Kluber. Lubrication Viscosity Index Calculator. Available online: https://www.klueber.com/us/en/products-service/tools-apps/viscosity-index-calculator/ (accessed on 2 June 2024).
- TriboNet. Viscosity Index Calculator (ISO 2909/ASTM D2270). Available online: https://www.tribonet.org/calculators/viscosity-index-calculator/ (accessed on 2 June 2024).
- Tandelta. Oil Cindition Monitoring. Available online: https://www.tandeltasystems.com/downloads/ (accessed on 3 September 2024).
- Machinery Lubrication. Continuous Oil Condition Monitoring for Machine Tool and Industrial Processing Equipment. Available online: https://www.machinerylubrication.com/Read/523/machine-tool-oil-analysis (accessed on 3 September 2024).
- Chybowski, L.; Szczepanek, M.; Sztangierski, R.; Brożek, P. A Quantitative and Qualitative Analysis of the Lubricity of Used Lubricating Oil Diluted with Diesel Oil. Appl. Sci. 2024, 14, 4567. [Google Scholar] [CrossRef]
- Chybowski, L. Study of the Relationship between the Level of Lubricating Oil Contamination with Distillation Fuel and the Risk of Explosion in the Crankcase of a Marine Trunk Type Engine. Energies 2023, 16, 683. [Google Scholar] [CrossRef]
- Taylor, R.I. Fuel-Lubricant Interactions: Critical Review of Recent Work. Lubricants 2021, 9, 92. [Google Scholar] [CrossRef]
- Castrol. Oil Contamination Identification. A List of the Top Offenders. Available online: https://web.archive.org/web/20230714034230/https://www.castrol.com/content/dam/castrol/country-sites/en_us/united-states/home/hd-focus-newsletter/labcheck-oil-contamination-infographic.pdf (accessed on 7 June 2023).
- I-Petrol. Klasyfikacja Lepkości ISO, wg PN-ISO 3448:2009. Available online: http://www.lubrina.pl/pl,wiedza,oleje-smarowe-klasyfikacja.html (accessed on 8 July 2024).
- Oleje-Smary. AGIP Cladium 120 SAE 30 CD. Available online: https://oleje-smary.pl/pl/p/AGIP-Cladium-120-SAE-30-CD-20-litrow/186 (accessed on 12 July 2022).
- Oleje-Smary. AGIP Cladium 120 SAE 40 CD. Available online: https://oleje-smary.pl/pl/p/AGIP-Cladium-120-SAE-40-CD-20-litrow/188 (accessed on 12 July 2022).
- PKN Orlen, S.A. Olej Napędowy. Ecodiesel Ultra B,D,F, Olej Napędowy Arktyczny Klasy 2, Efecta Diesel B,D,F, Verva ON B,D,F; PKN Orlen S.A.: Płock, Poland, 2021. [Google Scholar]
- PKN Orlen S.A. ZN-ORLEN-5—Przetwory Naftowe. Olej Napędowy EFECTA DIESEL; PKN Orlen S.A.: Płock, Poland, 2019. [Google Scholar]
| Y | a1 | a2 | a3 | a4 | a5 | a6 |
| (–) | ||||||
| 6.7 > ≥ 2.1 | 0.0074 | −0.3039 | 3.7190 | −17.6970 | 43.6760 | −33.9310 |
| 70.0 ≥ ≥ 6.7 | −1.84 × 10−7 | 3.20 × 10−5 | −0.0025 | 0.9966 | 6.1596 | −12.7890 |
| > 70 | 0 | 0 | 0 | 0.8353 | 14.6700 | −216.0000 |
| Y | b1 | b2 | b3 | b4 | b5 | b6 |
| (–) | ||||||
| 2.1 ≤ Y < 6.7 | 0.0048 | −0.1204 | 1.0693 | −3.5619 | 10.0950 | −6.3650 |
| 6.7 ≤ Y ≤ 70 | −2.20 × 10−7 | 5.03 × 10−5 | −0.0046 | 0.3921 | 5.5020 | −7.7091 |
| > 70 | 0 | 0 | 0 | 0.1684 | 11.8500 | −97.0000 |
| Range of Values | Model L | Model H | |||
|---|---|---|---|---|---|
| R2 | δmax | R2 | δmax | ||
| (mm2/s) | (–) | (%) | (–) | (%) | (mm2/s) |
| 2.1 ≤ Y < 6.7 | 0.9999 | <1.54 | 1.0000 | <0.24 | 2.1 ≤ Y < 6.7 |
| 6.7 ≤ Y ≤ 70 | 1.0000 | <1.74 | 1.0000 | <0.83 | 6.7 ≤ Y ≤ 70 |
| > 70 | 1.0000 | 0.00 | 1.0000 | 0.00 | > 70 |
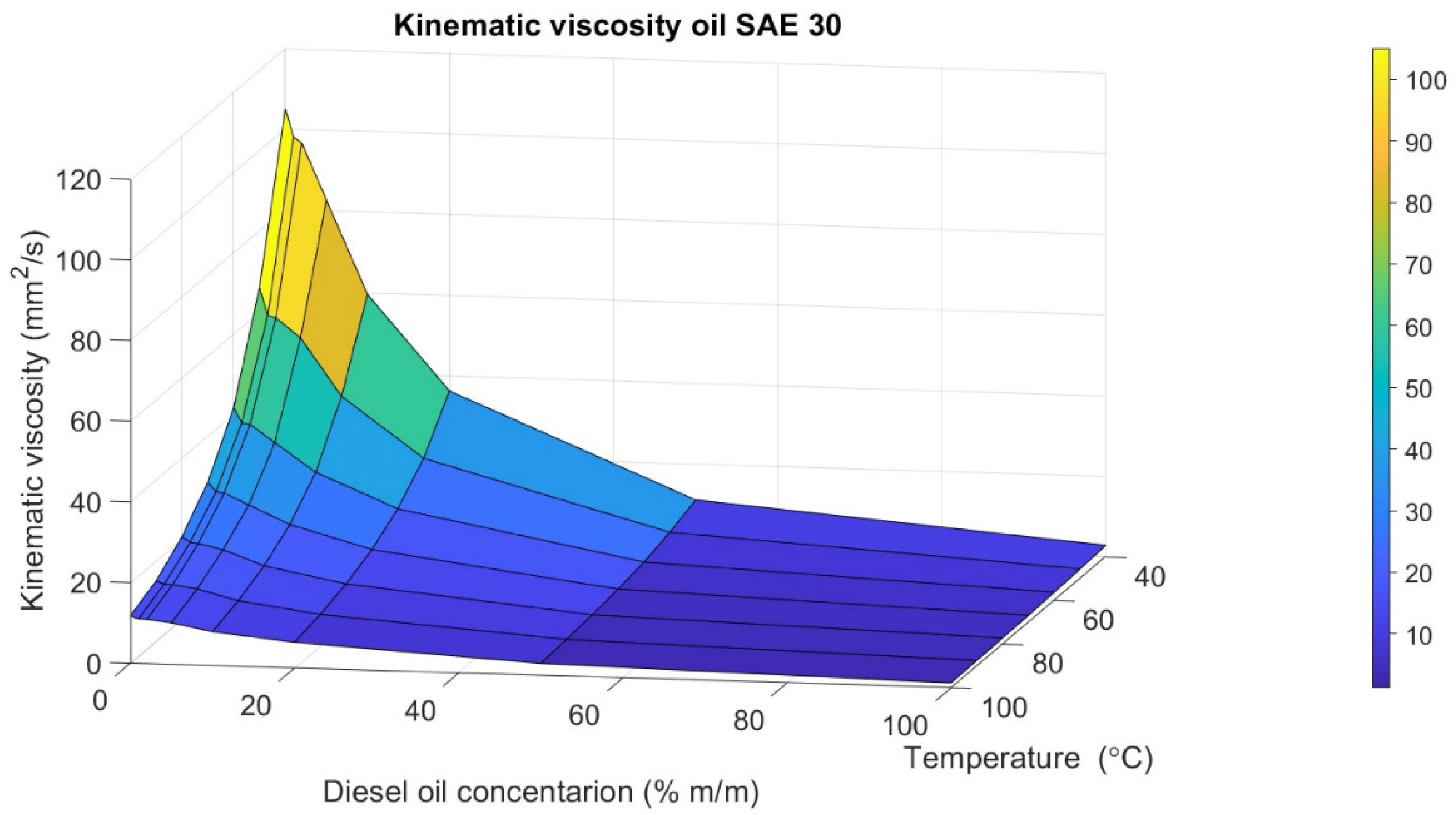
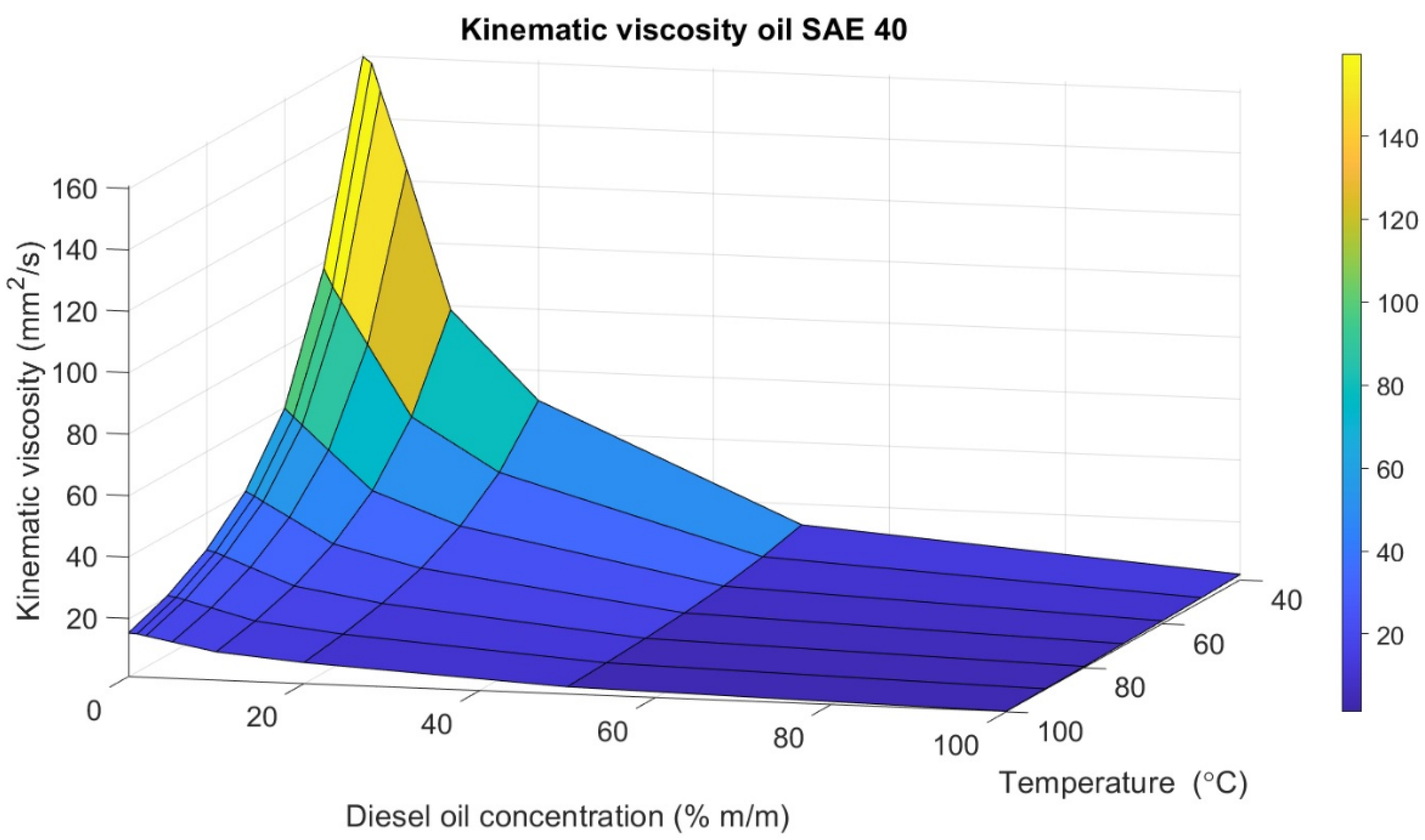
| SAE Viscosity Grade of Lubricating Oil Used to Prepare the Mixture [8] | Diesel Oil Content in the Lubricating Oil Mixture | Viscosity of the Mixture at 40 °C | ISO Viscosity Grade of the Mixture or the Limit Grades between Which the Mixture Is Rated [7] |
|---|---|---|---|
| SAE Grade | C | U | ISO VG |
| (–) | (% w/w) | (mm2/s) | (–) |
| SAE 30 | 0 | 105.01 | ISO VG 100 |
| 1 | 98.06 | ISO VG 100 | |
| 2 | 96.64 | ISO VG 100 | |
| 5 | 82.70 | [ISO VG 68, ISO VG 100] | |
| 10 | 59.61 | [ISO VG 46, ISO VG 68] | |
| 20 | 36.25 | [ISO VG 32, ISO VG 46]. | |
| 50 | 11.07 | [ISO VG 10, ISO VG 15]. | |
| 100 | 2.897 | ISO VG 3 | |
| SAE 40 | 0 | 159.90 | ISO VG 150 |
| 1 | 157.95 | ISO VG 150 | |
| 2 | 149.10 | [ISO VG 100, ISO VG 150] | |
| 5 | 123.95 | [ISO VG 100, ISO VG 150] | |
| 10 | 78.71 | [ISO VG 68, ISO VG 100] | |
| 20 | 50.29 | ISO VG 46 | |
| 50 | 13.25 | [ISO VG 10, ISO VG 15]. | |
| 100 | 2.897 | ISO VG 3 |
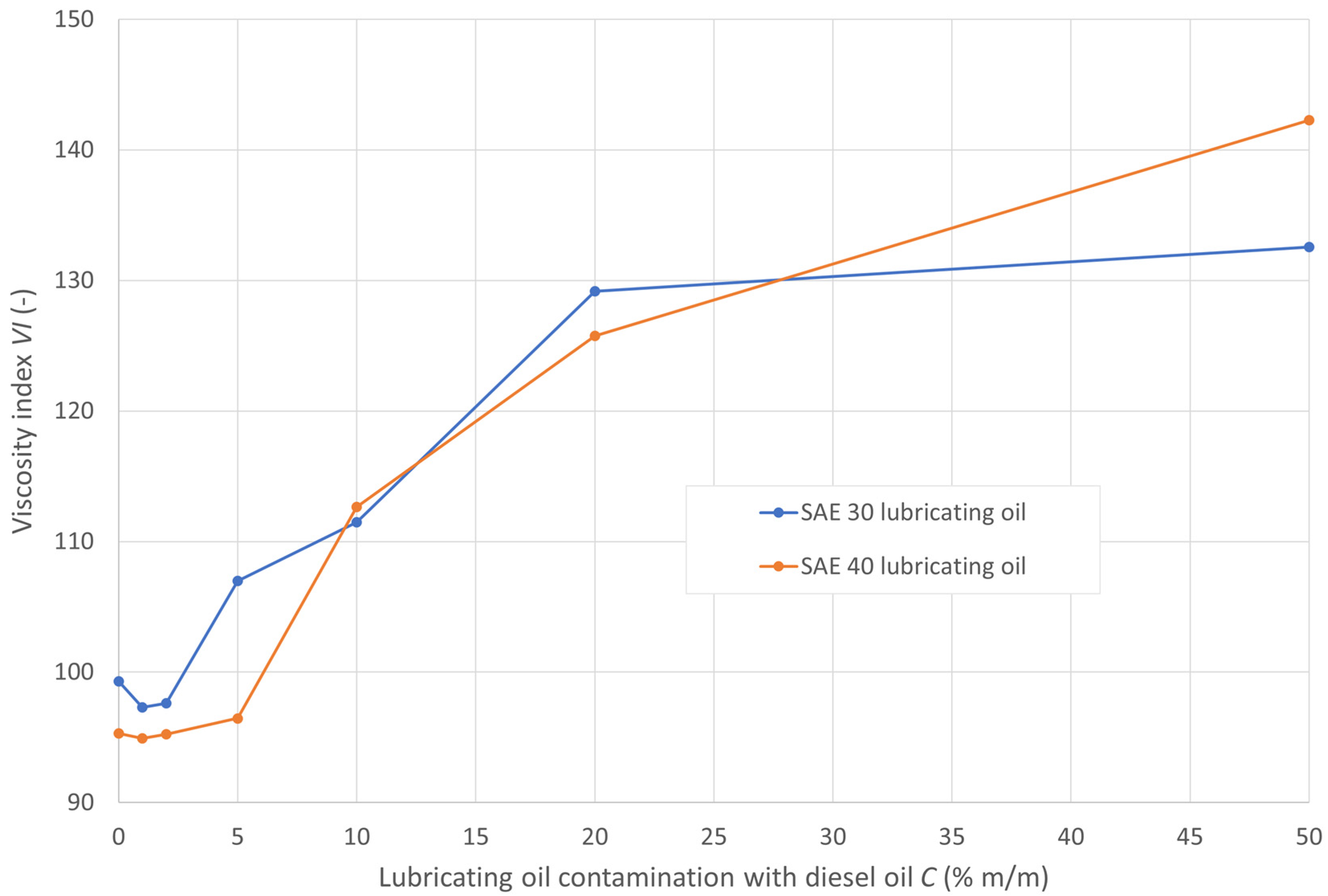
| SAE 30 Grade Oil Based Mixtures | Viscosity Index VI Determined by a Method | Percentage Relative Error between Methods | |||
|---|---|---|---|---|---|
| With diesel oil concentration of C | Manual calculation according to ASTM D2270/ISO 2909 | Calculation with Anton Paar calculator | Calculation using an analytical model | Analytical model vs. Anton Paar calculator | Analytical model vs. manual calculation according to ASTM D2270/ISO 2909 |
| (% w/w) | (–) | (–) | (–) | (%) | (%) |
| 0 | 99.27 | 99.28 | 98.90 | 0.38 | 0.38 |
| 1 | 97.18 | 97.29 | 96.46 | 0.85 | 0.74 |
| 2 | 97.49 | 97.62 | 96.78 | 0.86 | 0.73 |
| 5 | 106.76 | 106.97 | 106.04 | 0.88 | 0.67 |
| 10 | 111.58 | 111.46 | 110.33 | 1.02 | 1.12 |
| 20 | 128.91 | 129.17 | 129.20 | 0.03 | 0.22 |
| 50 | 132.37 | 132.57 | 132.25 | 0.24 | 0.09 |
| SAE 40 Grade Oil Based Mixtures | Viscosity Index VI Determined by a Method | Percentage Relative Error between Methods | |||
|---|---|---|---|---|---|
| With diesel oil concentration of C | Manual calculation according to ASTM D2270/ISO 2909 | Calculation with Anton Paar calculator | Calculation using an analytical model | Analytical model vs. Anton Paar calculator | Analytical model vs. manual calculation according to ASTM D2270/ISO 2909 |
| (% w/w) | (–) | (–) | (–) | (%) | (%) |
| 0 | 95.25 | 95.44 | 94.89 | 0.58 | 0.38 |
| 1 | 94.83 | 95.05 | 94.48 | 0.60 | 0.37 |
| 2 | 95.21 | 95.35 | 94.83 | 0.54 | 0.41 |
| 5 | 96.46 | 96.30 | 95.94 | 0.38 | 0.54 |
| 10 | 112.44 | 112.65 | 111.65 | 0.89 | 0.70 |
| 20 | 125.78 | 125.78 | 124.82 | 0.77 | 0.77 |
| 50 | 142.33 | 142.33 | 141.67 | 0.46 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chybowski, L.; Szczepanek, M.; Ćwirko, K.; Marosek, K. Analytical Method for Determining the Viscosity Index of Engine Lubricating Oils. Energies 2024, 17, 4908. https://doi.org/10.3390/en17194908
Chybowski L, Szczepanek M, Ćwirko K, Marosek K. Analytical Method for Determining the Viscosity Index of Engine Lubricating Oils. Energies. 2024; 17(19):4908. https://doi.org/10.3390/en17194908
Chicago/Turabian StyleChybowski, Leszek, Marcin Szczepanek, Konrad Ćwirko, and Konrad Marosek. 2024. "Analytical Method for Determining the Viscosity Index of Engine Lubricating Oils" Energies 17, no. 19: 4908. https://doi.org/10.3390/en17194908
APA StyleChybowski, L., Szczepanek, M., Ćwirko, K., & Marosek, K. (2024). Analytical Method for Determining the Viscosity Index of Engine Lubricating Oils. Energies, 17(19), 4908. https://doi.org/10.3390/en17194908







