Fault-Line Selection Method in Active Distribution Networks Based on Improved Multivariate Variational Mode Decomposition and Lightweight YOLOv10 Network
Abstract
:1. Introduction
- (1)
- Optimize the MVMD method by using the NGO, and the IMVMD method decomposes the fault characteristic signals, which suppresses modal confusion and pseudo-components to a certain extent;
- (2)
- Considering the spatio-temporal correlation between the source and load sides of the line, the fault characteristics of the line itself are focused by aligning the source and load signals, which can exclude the influence of load factors on the fault characteristics. The idea of spatio-temporal feature maps is also proposed to visualize the tiny fault features, taking into account the temporal and spatial features of the distribution network;
- (3)
- Further lightweight improvements are made to YOLOv10 to ensure detection accuracy while reducing the computational overhead so that the model can be better applied to scenarios with limited resources or real-time detection.
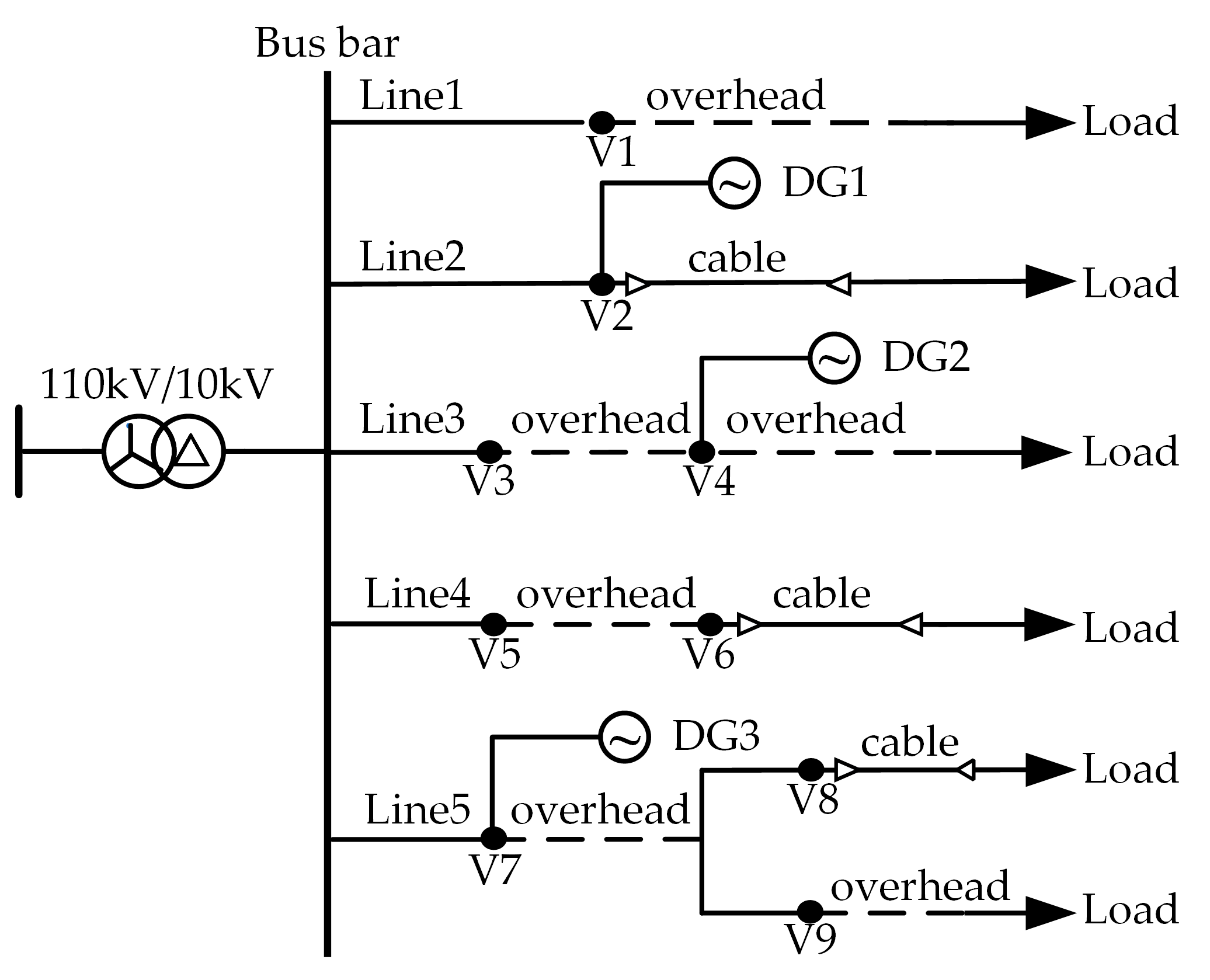
2. Analysis of Ground Fault Mechanism
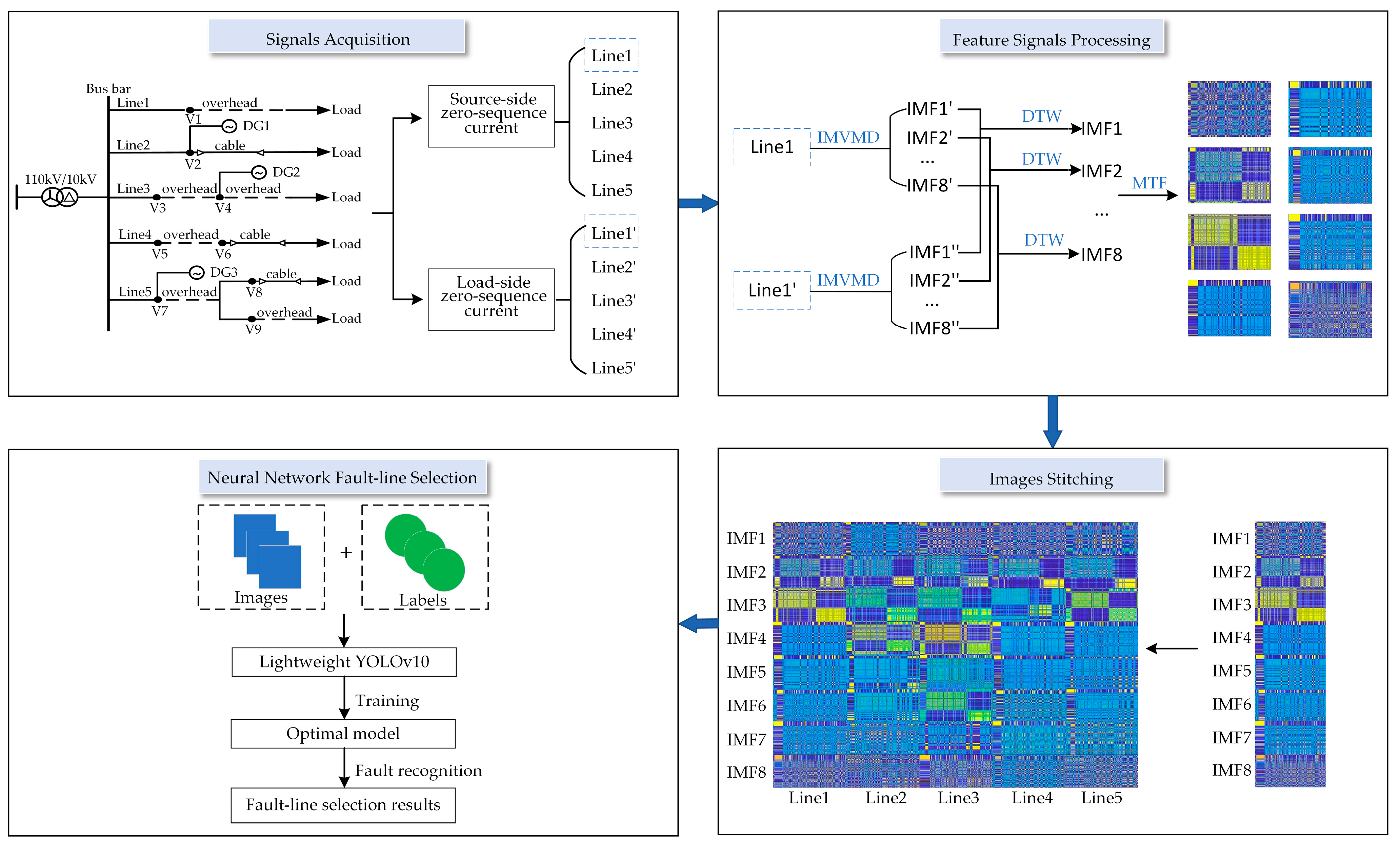
3. Method of IMVMD Signal Decomposition
3.1. MVMD Algorithm Based on NGO Optimization
3.2. Analysis of Decomposed Simulated Signals
4. Methods for Spatio-Temporal Feature Map Generation
4.1. Alignment Methodology of Source and Load Based on DTW
4.2. Generation Methodology of MTF Images
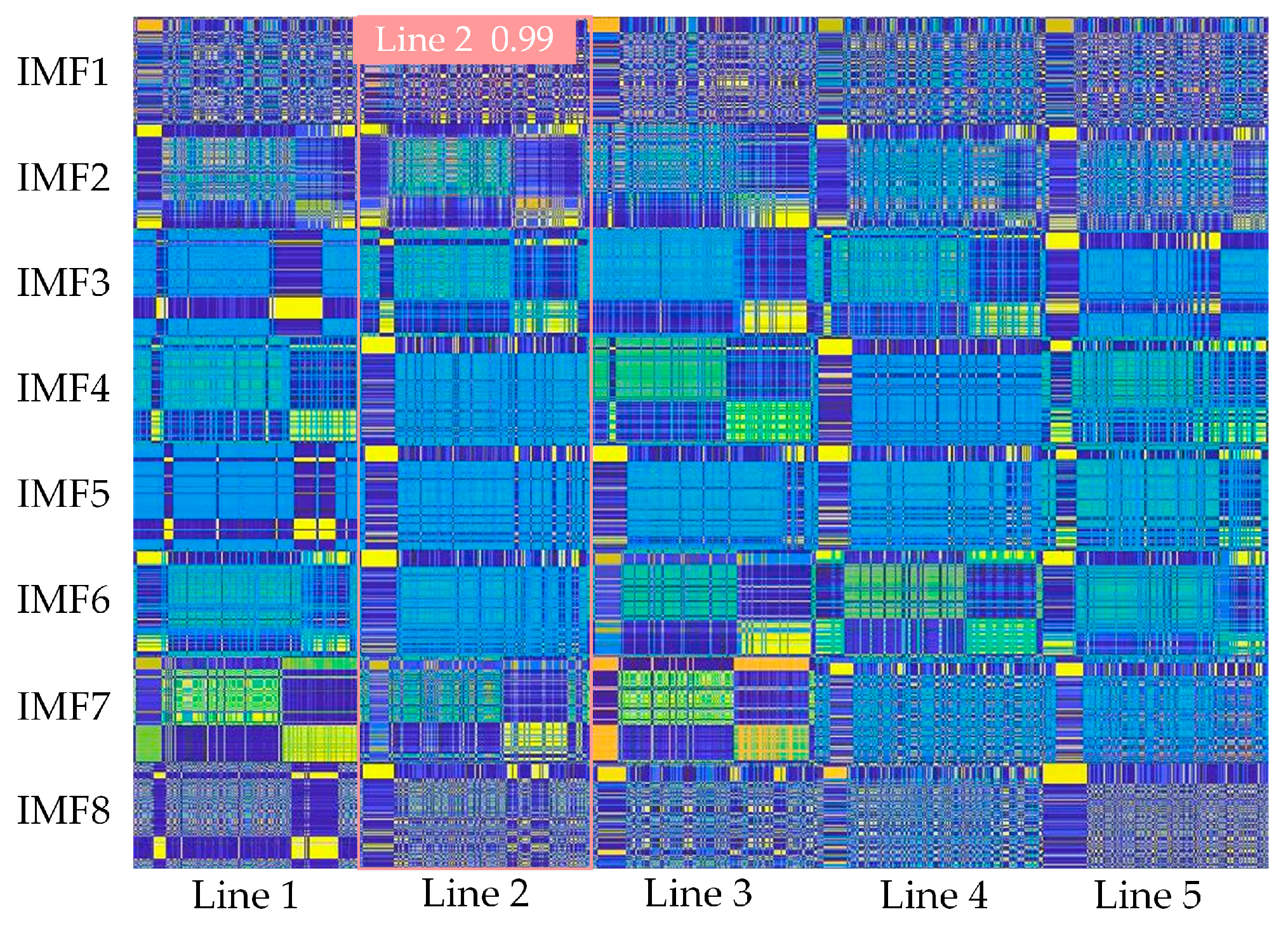
5. Method of Fault-Line Selection Based on Lightweight YOLOv10 Network
5.1. Lightweight YOLOv10 Neural Network Model
5.2. Flow of Fault-Line Selection Method
6. Experimental Results and Analysis
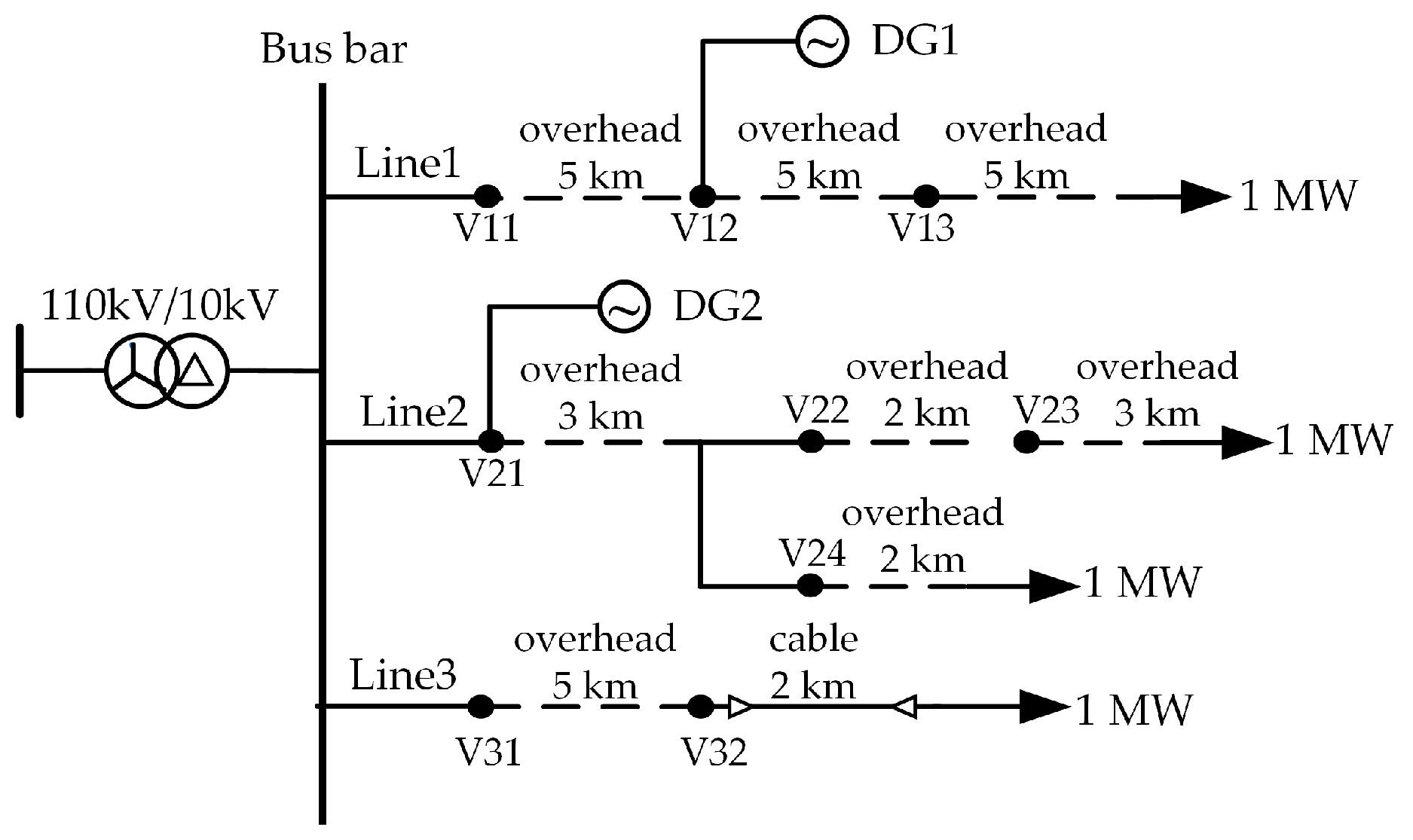
6.1. Active Distribution Network Model
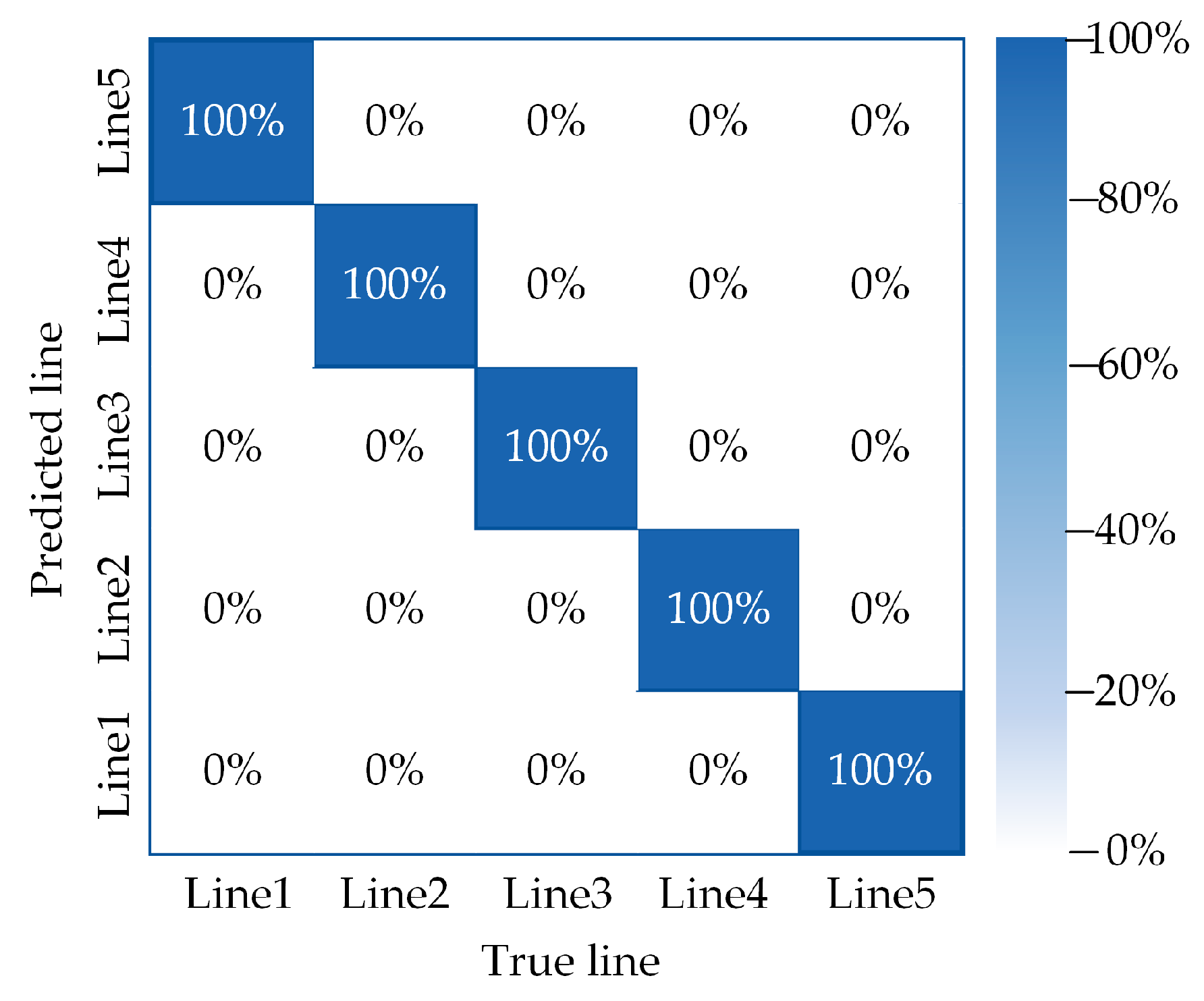
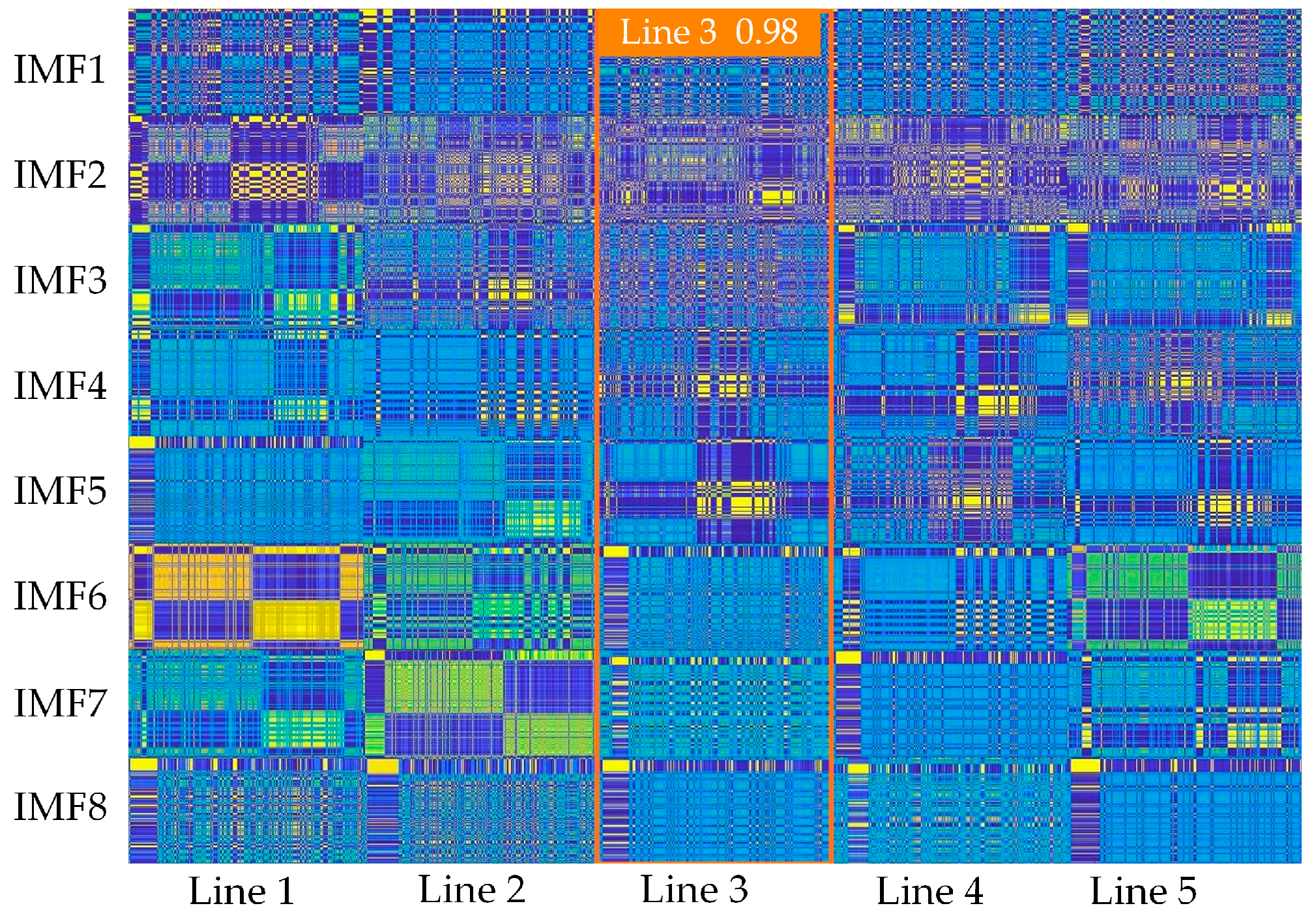
6.2. Analysis of Line Selection Results
6.3. Comparison and Verification
6.3.1. Comparison of Different Neural Networks
6.3.2. Verification of Noise Resistance
6.3.3. Comparative Verification of High-Impedance Faults
6.3.4. Comparative Verification of Two-Point Same-Phase Grounding Fault
6.3.5. Dynamic Mold Experiment
7. Conclusions
- (1)
- Optimization of MVMD using the NGO algorithm, simulation results show that the method of IMVMD can effectively inhibit modal aliasing and reduce the pseudo-component, the decomposition effect is significantly better than the traditional method, and at the same time, the noise in the signal can be effectively separated to reduce the noise interference on the extraction of effective information;
- (2)
- Calculation of optimal alignment paths corresponding to IMFs at both ends of the source and load by using DTW. Adopt the alignment method to reduce the influence of loads on fault information extraction and transform the one-dimensional sequence into a two-dimensional image through MTF to achieve the visualization of fault information, giving full play to the advantages of deep learning in image recognition;
- (3)
- The YOLOv10 network, the latest version of the YOLO series, has higher performance compared with existing neural networks. In this paper, YOLOv10 is further lightweight and improved to reduce the number of parameters and computational complexity under the condition of guaranteeing recognition accuracy, thus reducing the weight file and recognition time, which makes the model better applied to scenarios with limited resources or real-time detection;
- (4)
- The method in this paper has a good anti-interference ability, which can effectively reduce noise interference and the impact of load. For high-resistance grounding, two points of the same-phase ground fault case can ensure high accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kokor, A.; Smaka, S.; Grebovic, S.; Helac, V. Effects of Neutral Point Grounding Methods on Single-Phase Short Circuit Fault Characteristics. In Proceedings of the 21st International Symposium on INFOTEH-JAHORINA (INFOTEH), East Sarajevo, Bosnia and Herzegovina, 16–18 March 2022. [Google Scholar]
- Liang, J.F.; Jing, T.J.; Niu, H.N.; Wang, J.B. Two-Terminal Fault Location Method of Distribution Network Based on Adaptive Convolution Neural Network. IEEE Access 2020, 8, 54035–54043. [Google Scholar] [CrossRef]
- Al-Odienat, A.I.; Al-Maitah, K. A New Wide Area Protection Scheme Based on the Phase Angles of the Sequence Components. Electr. Power Components Syst. 2021, 49, 504–516. [Google Scholar] [CrossRef]
- Zhou, W.; Li, F.; Xie, C.; Wang, B.; Gong, L.; Yang, S. Adaptive Autoreclosing Scheme for Line-to-Line Nongrounded Faults on Double-Circuit Transmission Lines Based on Phase-to-Phase Reactive Power. IEEE Access 2020, 8, 144092–144104. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Shi, F.; Wu, Q.; Terzija, V.; Xie, W.; Fang, C. Location of Single Phase to Ground Faults in Distribution Networks Based on Synchronous Transients Energy Analysis. IEEE Trans. Smart Grid 2020, 11, 774–785. [Google Scholar] [CrossRef]
- Chen, B.; Yu, N.; Chen, B.; Tian, C.; Chen, Y.; Chen, G. Fault Location for Underground Cables in Ungrounded MV Distribution Networks Based on ZSC Signal Injection. IEEE Trans. Power Deliv. 2021, 36, 2965–2977. [Google Scholar] [CrossRef]
- Hou, S.; Xu, Y.; Guo, W. Distribution Network Fault-Line Selection Method Based on MICEEMDAN-Recurrence Plot-Yolov5. Processes 2022, 10, 2127. [Google Scholar] [CrossRef]
- Aker, E.; Othman, M.L.; Veerasamy, V.; Aris, I.; Wahab, N.I.A.; Hizam, H. Fault Detection and Classification of Shunt Compensated Transmission Line Using Discrete Wavelet Transform and Naive Bayes Classifier. Energies 2020, 13, 243. [Google Scholar] [CrossRef]
- Koley, S.; Chattopadhyay, S.; Hamim, S.A.; Debnath, S. High Impedance Single Line to Ground Fault Detection and Wavelet-alienation Based Faulty Phase Identification. In Proceedings of the IEEE 6th International Conference on Condition Assessment Techniques in Electrical Systems (IEEE CATCON), Durgapur, India, 17–19 December 2022; pp. 182–186. [Google Scholar]
- Larik, N.A.; Li, M.S.; Wu, Q.H. Enhanced Fault Detection and Localization Strategy for High-Speed Protection in Medium-Voltage DC Distribution Networks Using Extended Kalman Filtering Algorithm. IEEE Access 2024, 12, 30329–30344. [Google Scholar] [CrossRef]
- Atsever, M.B.; Hocaoglu, M.H. A faulty feeder selection method for distribution network with unintentional resonance in zero sequence circuit. Electr. Power Syst. Res. 2023, 223, 109587. [Google Scholar] [CrossRef]
- Hou, S.Z.; Guo, W. Optimal Denoising and Feature Extraction Methods Using Modified CEEMD Combined with Duffing System and Their Applications in Fault Line Selection of Non-Solid-Earthed Network. Symmetry 2020, 12, 536. [Google Scholar] [CrossRef]
- Niu, L.; Wu, G.; Xu, Z. Single Phase to Ground Fault Line Selection in DistributionNetwork Based on Signal Injection and Variational Mode Decomposition. In Proceedings of the 12th IEEE Energy Conversion Congress and Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 827–832. [Google Scholar]
- Yuan, J.; Jiao, Z.; Feng, G.; Chen, M.; Xu, M. Study on fault line detection methods based on multi-feature fusion in distribution systems. IET Gener. Transm. Distrib. 2021, 15, 860–869. [Google Scholar] [CrossRef]
- Cao, W.; Li, C.; Li, Z.; Wang, S.; Pang, H. Research on Low-Resistance Grounding Fault Line Selection Based on VMD with PE and K-Means Clustering Algorithm. Math. Probl. Eng. 2022, 2022, 5360302. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Keshavarz, A.; Shaker, H.R. Machine Learning-Based Fault Location for Smart Distribution Networks Equipped with Micro-PMU. Sensors 2022, 22, 945. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.; Rout, P.K. Detection and classification of micro-grid faults based on HHT and machine learning techniques. IET Gener. Transm. Distrib. 2018, 12, 388–397. [Google Scholar] [CrossRef]
- Veerasamy, V.; Wahab, N.I.A.; Othman, M.L.; Padmanaban, S.; Sekar, K.; Ramachandran, R.; Hizam, H.; Vinayagam, A.; Islam, M.Z. LSTM Recurrent Neural Network Classifier for High Impedance Fault Detection in Solar PV Integrated Power System. IEEE Access 2021, 9, 32672–32687. [Google Scholar] [CrossRef]
- Gao, J.; Guo, M.; Chen, D.-Y. Fault line detection using waveform fusion and one-dimensional convolutional neural network in resonant grounding distribution systems. CSEE J. Power Energy Syst. 2021, 7, 250–260. [Google Scholar] [CrossRef]
- Lu, T.; Hou, S.Z.; Xu, Y. Fault line selection algorithm for distribution networks based on AdapGL-GIN network. IET Gener. Transm. Distrib. 2023, 17, 4858–4874. [Google Scholar] [CrossRef]
- Rahul, S.; Sunitha, R.; Akhil, V.M. Oscillation Mode Assessment in Power System Using Multivariate Variational Mode Decomposition. In Proceedings of the 47th Annual Conference of the IEEE-Industrial-Electronics-Society (IECON), Electrical Network, Toronto, ON, Canada, 13–16 October 2021. [Google Scholar]
- Dehghani, M.; Hubalovsky, S.; Trojovsky, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Li, J.M.; Zhang, J.F. Adaptive Multiscale Noise Control Enhanced Stochastic Resonance Method Based on Modified EEMD with Its Application in Bearing Fault Diagnosis. Shock Vib. 2016, 2016, 1485412. [Google Scholar] [CrossRef]
- Wang, K.; Shao, Y.; Wang, L.; Zhou, H. Single-phase grounding fault line selection method based on dynamic time warping algorithm. Energy Rep. 2022, 8, 280–289. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, C.; Zhang, Q.; Wang, J.; Wang, Y.; Shi, Y.; Lin, C.; Jin, Y. A Method for Aero-Engine Gas Path Anomaly Detection Based on Markov Transition Field and Multi-LSTM. Aerospace 2021, 8, 374. [Google Scholar] [CrossRef]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G.J.A. YOLOv10: Real-Time End-to-End Object Detection. arXiv 2024, arXiv:2405.14458. [Google Scholar]
- Zhong, X.; Liu, X.; Gong, T.; Sun, Y.; Hu, H.; Liu, Q. FAGD-Net: Feature-Augmented Grasp Detection Network Based on Efficient Multi-Scale Attention and Fusion Mechanisms. Appl. Sci. 2024, 14, 5097. [Google Scholar] [CrossRef]
- Li, J.; Xu, R.; Liu, Y. An Improved Forest Fire and Smoke Detection Model Based on YOLOv5. Forests 2023, 14, 833. [Google Scholar] [CrossRef]
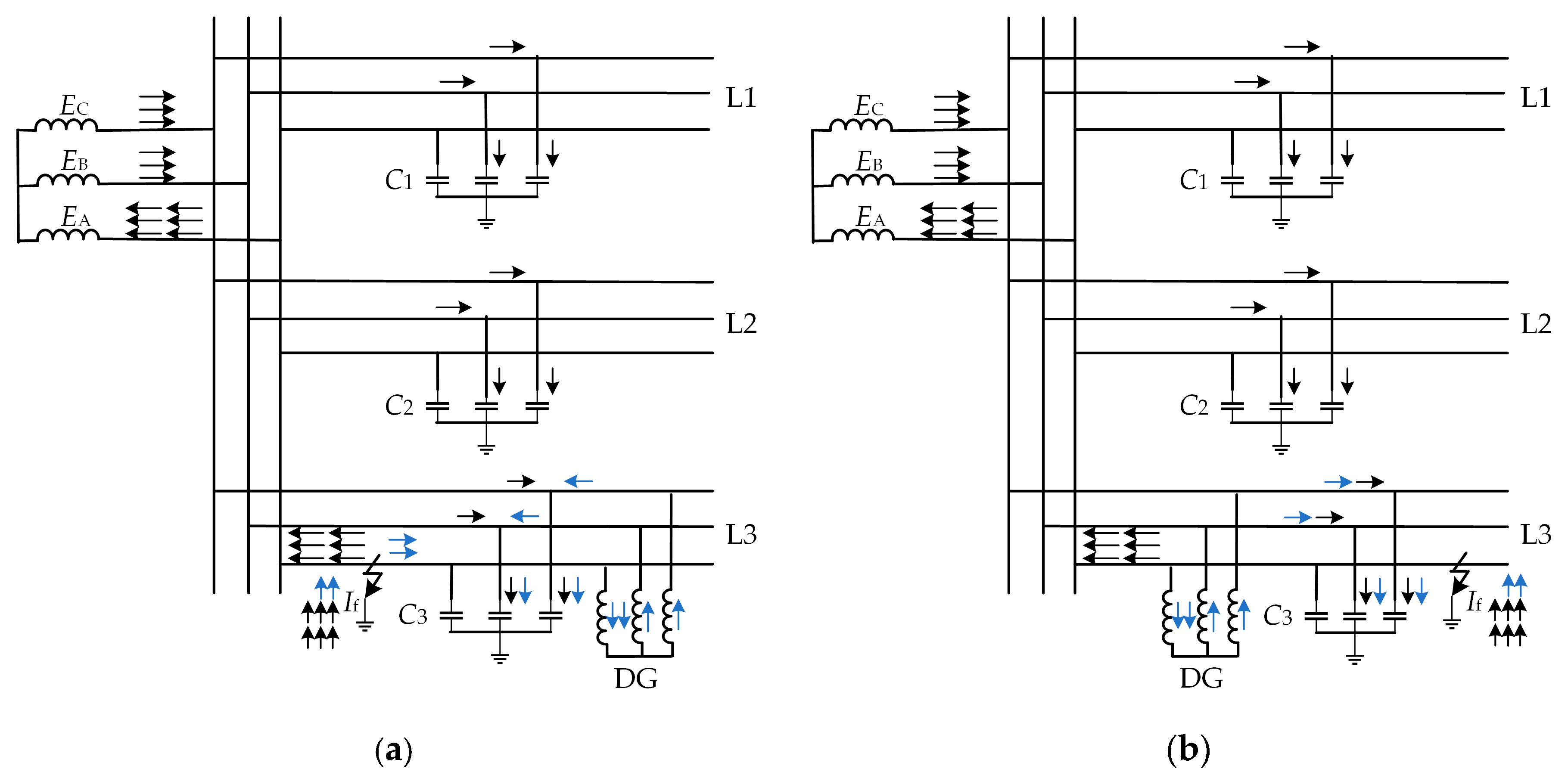

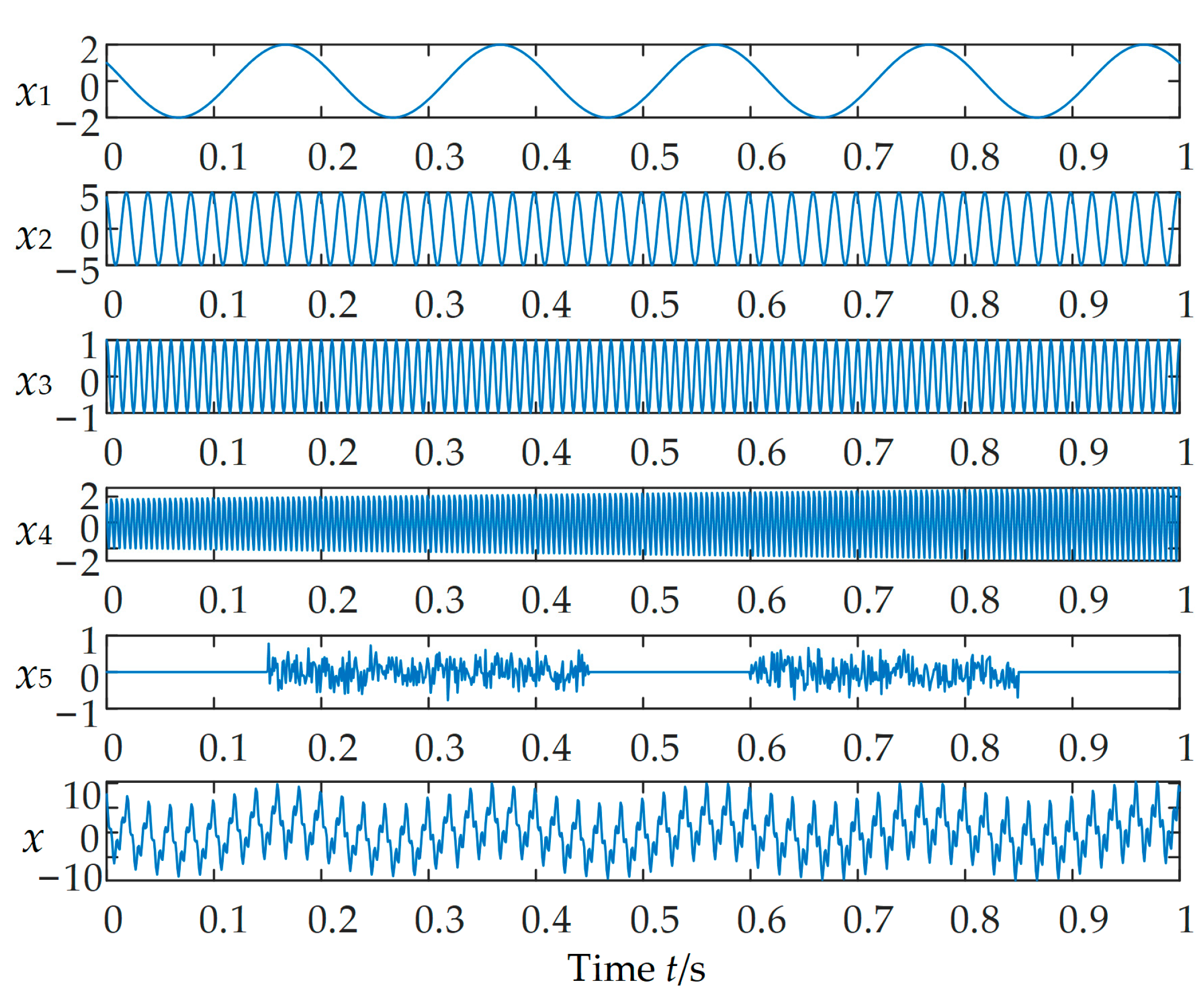
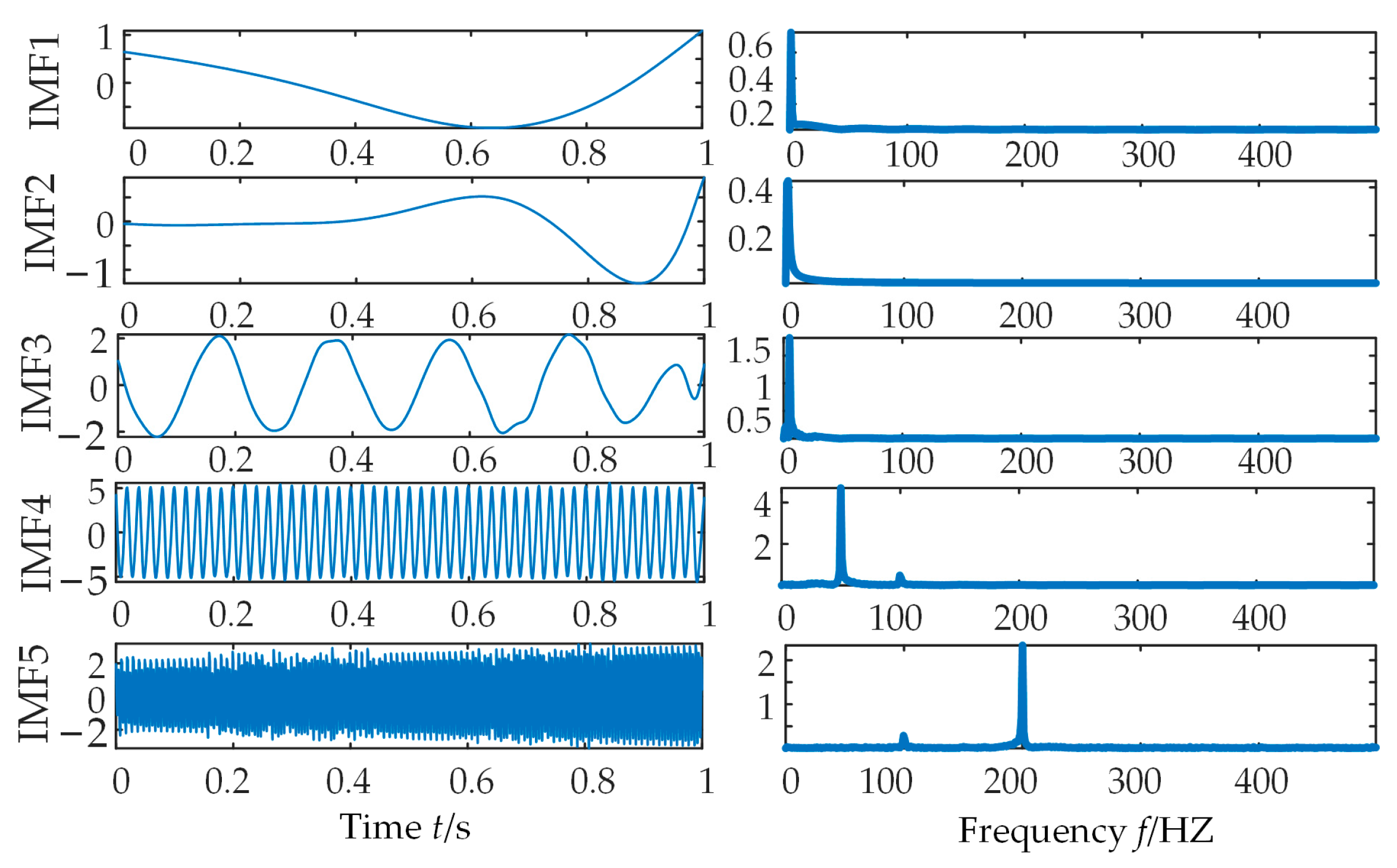


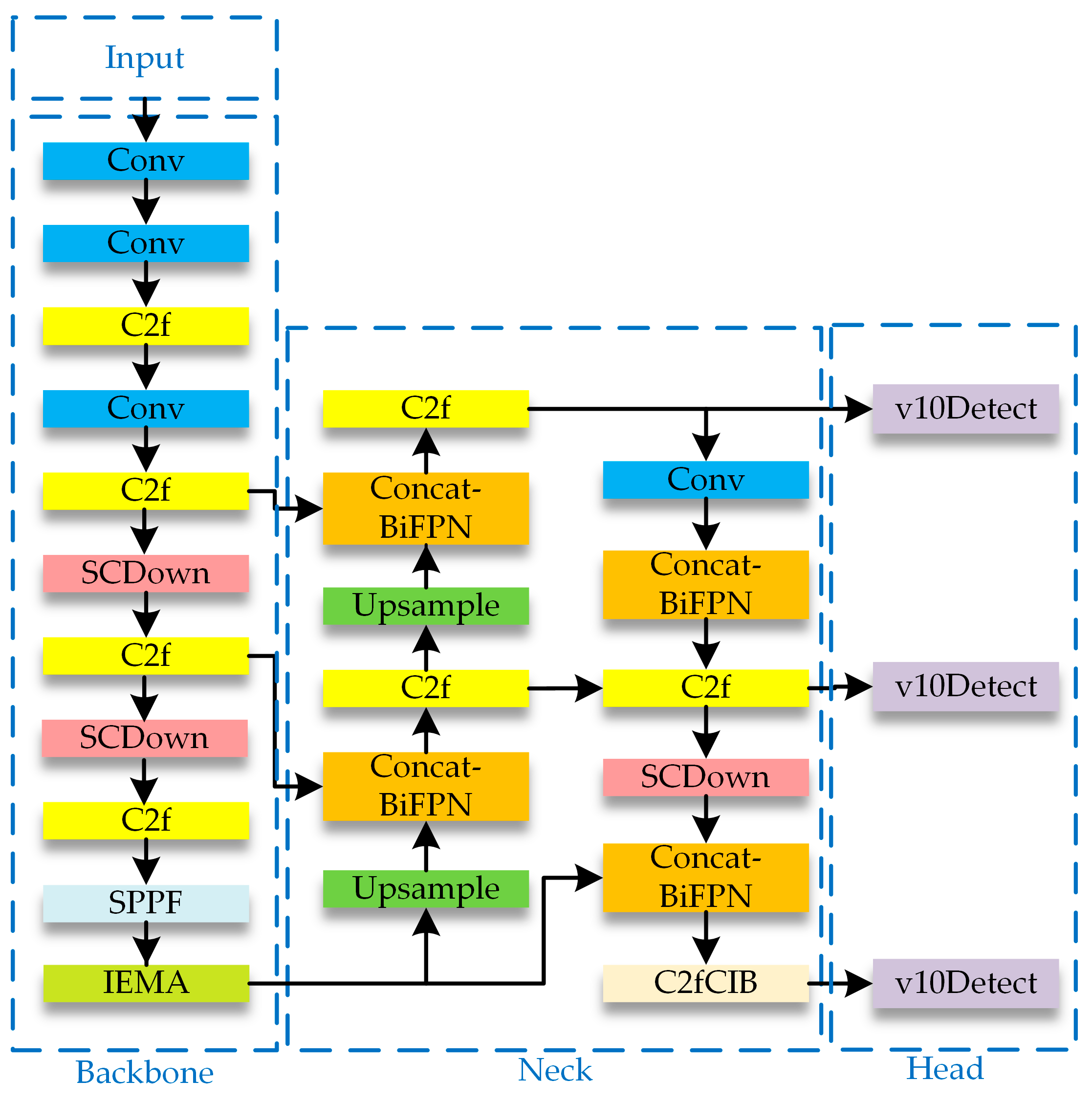


| Category | Methods | References | Schemes of Fault-Line Selection | Advantage | Limitations |
|---|---|---|---|---|---|
| Classified by fault characteristics | Zero-sequence current method | Refs. [8,9] | Wavelet transform | Suitable for many types of faults, high accuracy for high-resistance grounding | Selection of wavelet basis functions is empirically dependent and computationally and time-costly |
| Ref. [10] | Extended Kalman filters | Suitable for multiple topologies and different types of faults with short operating times | Weak anti-interference capability | ||
| Ref. [12] | MCEEMD and Duffing system | Independent of fault type, transition resistance | Susceptible to noise interference | ||
| Negative sequence current method | Ref. [11] | Moving average method | Unaffected by capacitor imbalance and transition resistance | Vulnerable to load imbalance and not applicable to distribution networks containing DGs | |
| Injection method | Ref. [13] | VMD and energy relative entropy | Unaffected by transition resistance, strong anti-interference ability | The selection of the number of decomposition layers of the VMD preset affects the line selection results | |
| Integrated methods | Ref. [14] | Multi-feature fusion based on fuzzy theory | Strong generalization capabilities | High computational complexity and time cost | |
| Classified by fault feature extraction methods | LSTM | Ref. [18] | LSTM mines the energy value characteristics of the current signal | High accuracy for high-resistance faults | Difficulty in effectively capturing long-distance dependencies |
| 1D-CNN | Ref. [19] | 1D-CNN extracts the significant fault features of the fused | Strong anti-interference ability | Neglecting the spatio-temporal correlation of the original signal | |
| 2D-CNN | Ref. [20] | The 1D signal is converted into a 2D image, and the fault features are extracted by 2D-CNN | Give full play to the advantages of deep learning in the field of image recognition | Lack of global characterization and high computational cost |
| Circuit Type | Resistance/(Ω·km−1) | Inductance/(mH·km−1) | Grounding Capacitance/(μF·km−1) | |||
|---|---|---|---|---|---|---|
| Positive Phase | Zero Phase | Positive Phase | Zero Phase | Positive Phase | Zero Phase | |
| Overhead Line | 0.178 | 0.25 | 1.21 | 5.54 | 0.015 | 0.012 |
| Cable Line | 0.27 | 2.7 | 0.255 | 1.02 | 0.339 | 0.28 |
| Model | Parameters/M | FLOPs/G | Weights File/MB | Training Rounds | Accuracy/% |
|---|---|---|---|---|---|
| YOLOv8 | 3.0 | 8.1 | 6.2 | 150 | 99.85 |
| YOLOv10 | 2.7 | 8.2 | 5.8 | 100 | 99.86 |
| Lightweight YOLOv10 | 2.6 | 8.2 | 5.4 | 100 | 99.88 |
| Faulty Line | Samples Size | Accuracy/% | ||
|---|---|---|---|---|
| Method 1 | Method 2 | This Paper | ||
| Line 1 | 200 | 91.21 | 95.67 | 99.99 |
| Line 2 | 300 | 93.18 | 95.26 | 99.97 |
| Line 3 | 500 | 92.23 | 94.28 | 99.98 |
| Line 4 | 600 | 90.33 | 94.42 | 99.98 |
| Line 5 | 800 | 90.15 | 94.39 | 99.99 |
| SNR/dB | Number of Samples | Accuracy/% | ||||
|---|---|---|---|---|---|---|
| Polarity Comparison | Amplitude Comparison | SVM | CNN | Lightweight YOLOv10 | ||
| 50 | 435 | 93.21 | 81.56 | 88.33 | 96.82 | 100 |
| 40 | 435 | 90.66 | 75.88 | 87.50 | 93.56 | 99.98 |
| 30 | 435 | 87.20 | 69.31 | 86.67 | 89.50 | 99.86 |
| 20 | 435 | 84.51 | 57.62 | 75.00 | 81.29 | 99.64 |
| Resistance/Ω | Faulty Line | Results | ||
|---|---|---|---|---|
| Ref. [12] | Ref. [15] | This Article | ||
| 2000 | Line 1 | Line 1 | Line 1 | Line 1 |
| Line 2 | Line 2 | Line 2 | Line 2 | |
| 2500 | Line 3 | Line 3 | Line 3 | Line 3 |
| Line 4 | Line 4 | Line 4 | Line 4 | |
| 3000 | Line 5 | Line 5 | Line 3 | Line 5 |
| Line 1 | Line 1 | Line 1 | Line 1 | |
| 4000 | Line 2 | Line 2 | Line 2 | Line 2 |
| Line 3 | Line 4 | Line 4 | Line 3 | |
| 5000 | Line 4 | Line 4 | Line 3 | Line 4 |
| Line 5 | Line 3 | Line 4 | Line 5 | |
| Fault Line | Type of Fault | Fault-Line Selection Results | ||
|---|---|---|---|---|
| Ref. [12] | Ref. [15] | This Paper | ||
| Line 1 | AG | Line 1 | Line 1 | Line 1 |
| Line 2 | Line 2 | Line 2 | ||
| Line 2 | BG | Unselected | Line 5 | Line 2 |
| Line 3 | Line 3 | |||
| Line 4 | CG | Line 5 | Unselected | Line 4 |
| Line 5 | Line 5 | |||
| Fault Type | Fault Line | Fault Point | Transition Resistance/Ω | Fault Close Angle | Fault Location Result |
|---|---|---|---|---|---|
| AG | Line 1 | V11 | 0 | 0° | Line 1 |
| BG | Line 1 | V12 | 100 | 30° | Line 1 |
| CG | Line 1 | V13 | 800 | 60° | Line 1 |
| AG | Line 2 | V21 | 400 | 60° | Line 2 |
| BG | Line 2 | V22 | 100 | 120° | Line 2 |
| CG | Line 2 | V23 | 1000 | 30° | Line 2 |
| BG | Line 2 | V24 | 0 | 90° | Line 2 |
| AG | Line 3 | V31 | 200 | 0° | Line 3 |
| CG | Line 3 | V32 | 400 | 60° | Line 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, S.; Wang, W. Fault-Line Selection Method in Active Distribution Networks Based on Improved Multivariate Variational Mode Decomposition and Lightweight YOLOv10 Network. Energies 2024, 17, 4958. https://doi.org/10.3390/en17194958
Hou S, Wang W. Fault-Line Selection Method in Active Distribution Networks Based on Improved Multivariate Variational Mode Decomposition and Lightweight YOLOv10 Network. Energies. 2024; 17(19):4958. https://doi.org/10.3390/en17194958
Chicago/Turabian StyleHou, Sizu, and Wenyao Wang. 2024. "Fault-Line Selection Method in Active Distribution Networks Based on Improved Multivariate Variational Mode Decomposition and Lightweight YOLOv10 Network" Energies 17, no. 19: 4958. https://doi.org/10.3390/en17194958
APA StyleHou, S., & Wang, W. (2024). Fault-Line Selection Method in Active Distribution Networks Based on Improved Multivariate Variational Mode Decomposition and Lightweight YOLOv10 Network. Energies, 17(19), 4958. https://doi.org/10.3390/en17194958





