Study on Reliability of PACSs with Integrated Consideration of Both Basic and Mission Reliability
Abstract
:1. Introduction
- a.
- Based on the analysis of architectures of IEDs, a multi-level model analogous to that of devices widely used in digital substations is proposed to provide the groundwork for fault severity judgment of protective relay devices and the mission reliability of PACSs.
- b.
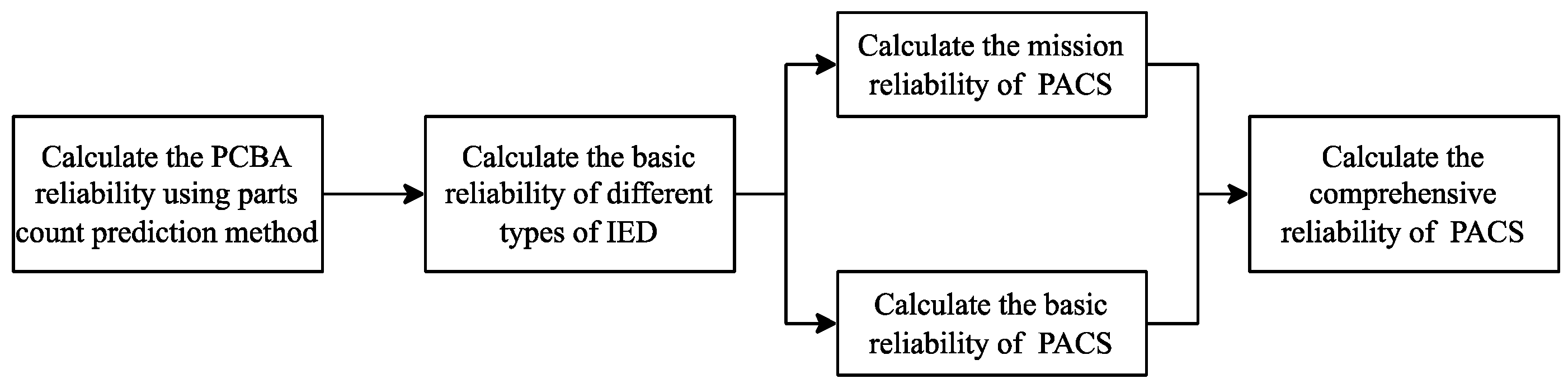
- The basic reliability of different types of IEDs is analyzed by the parts count prediction method.
- c.
- Taking four out of five PACS architectures proposed in CIGRE B5.60 TB as the objects under investigation, a quantitative analysis of mission reliability is performed. Consequently, a comprehensive reliability evaluation method is proposed, which takes both basic and mission reliability into consideration. The PACS architecture reliability is compared by the comprehensive reliability evaluation method.
2. Reliability of PACSs
2.1. Definition of Reliability
2.2. Basic Reliability and Mission Reliability of PACSs
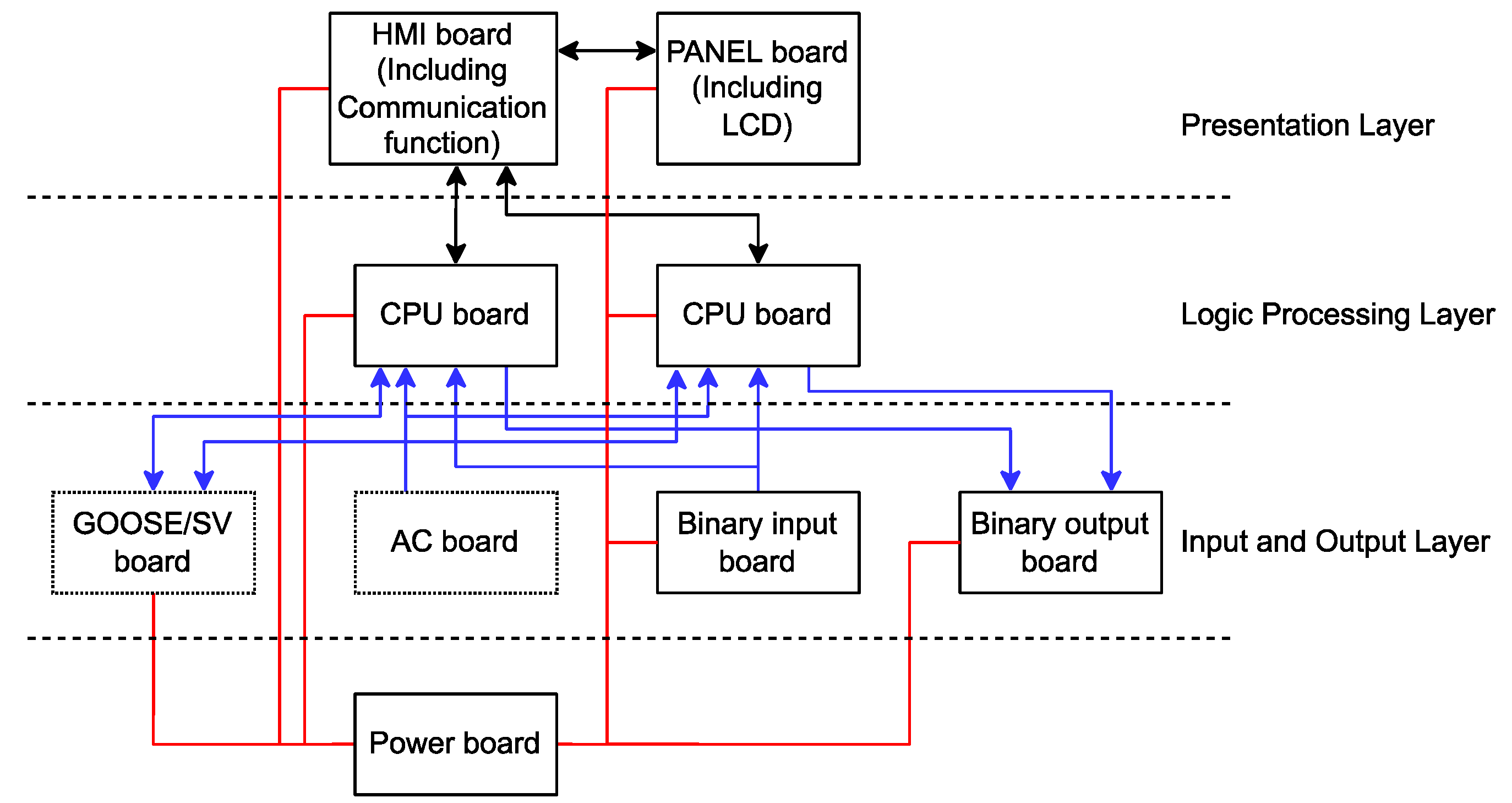
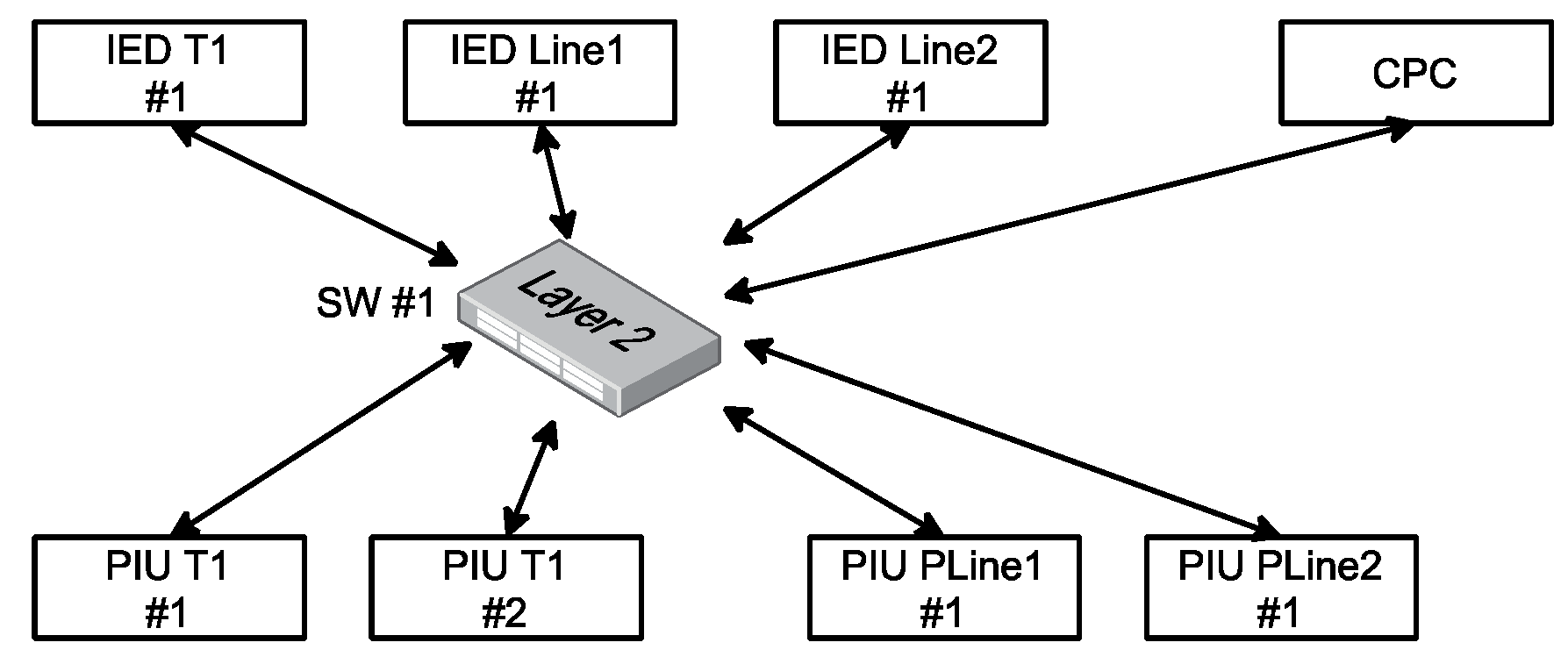
2.3. The Architecture of Protective Relay IED
3. Basic Reliability of PAC IEDs
3.1. Reliability Estimation Methods and Standards
3.2. Predication Method for Basic Reliability
3.3. Basic Reliability Line Protection Relay IED
3.4. Basic Reliability of PAC IEDs
4. Mission Reliability of PAC IEDs
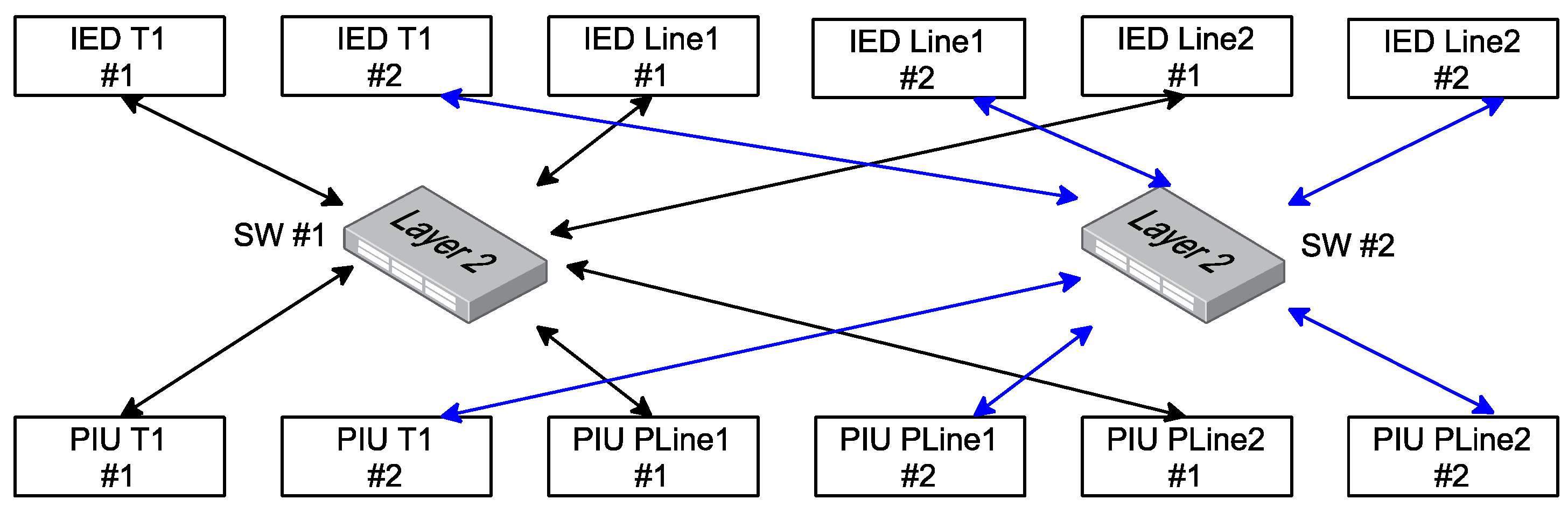
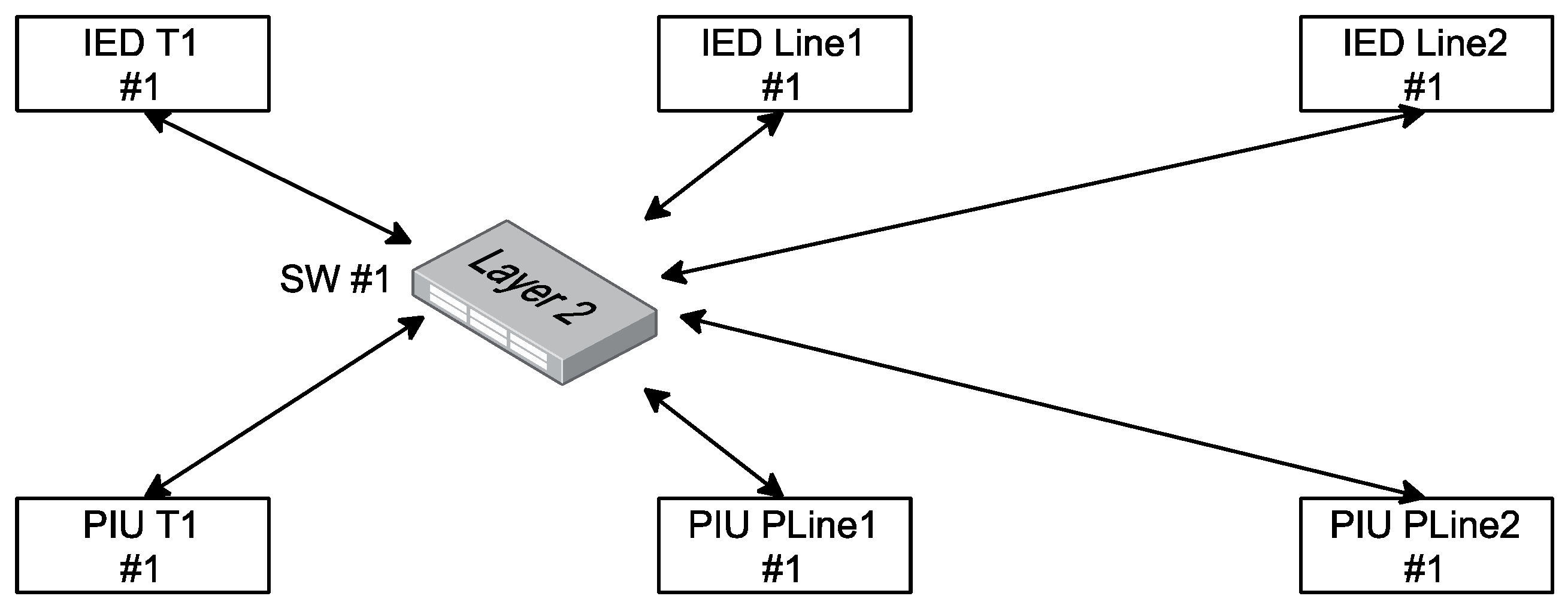
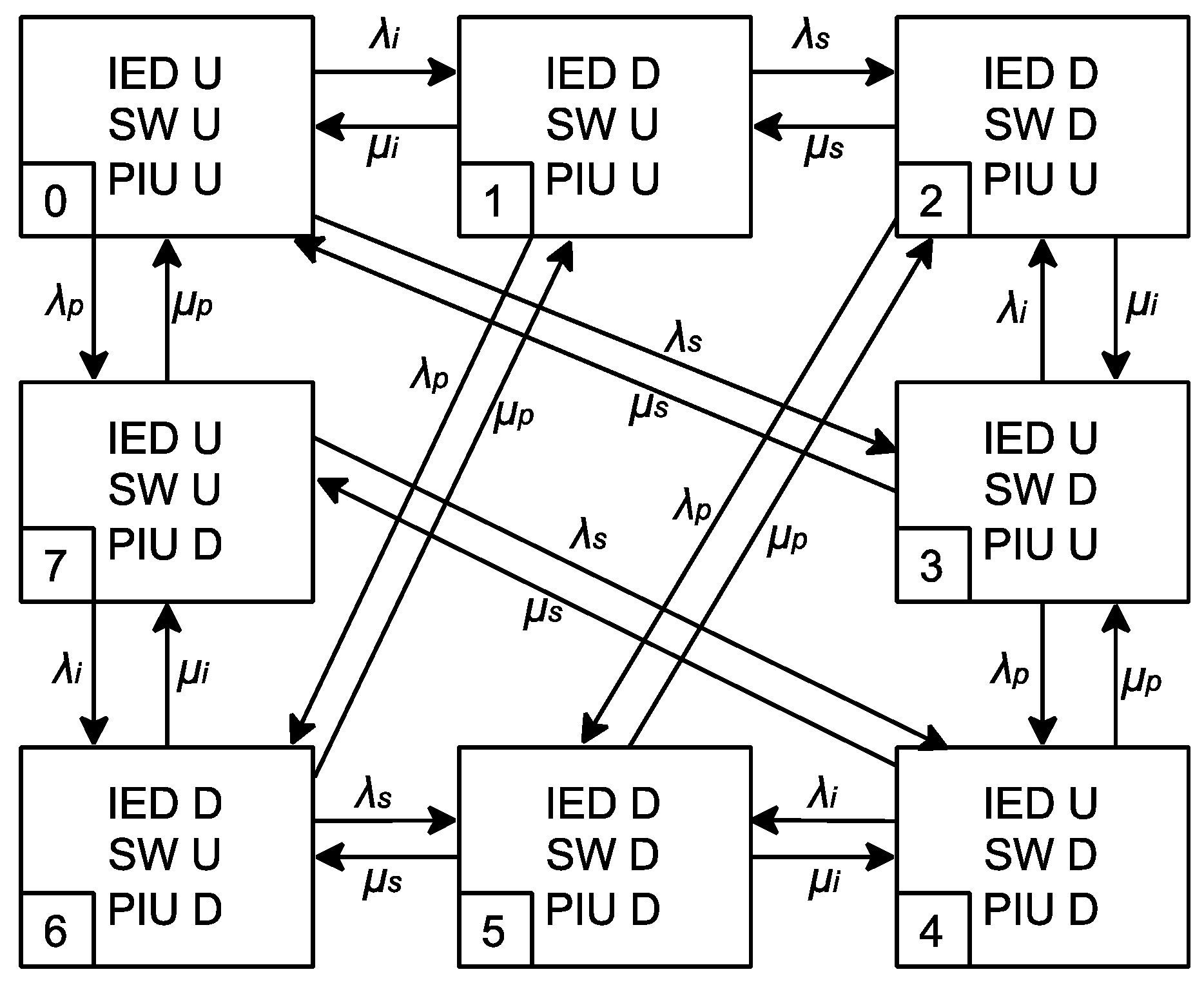
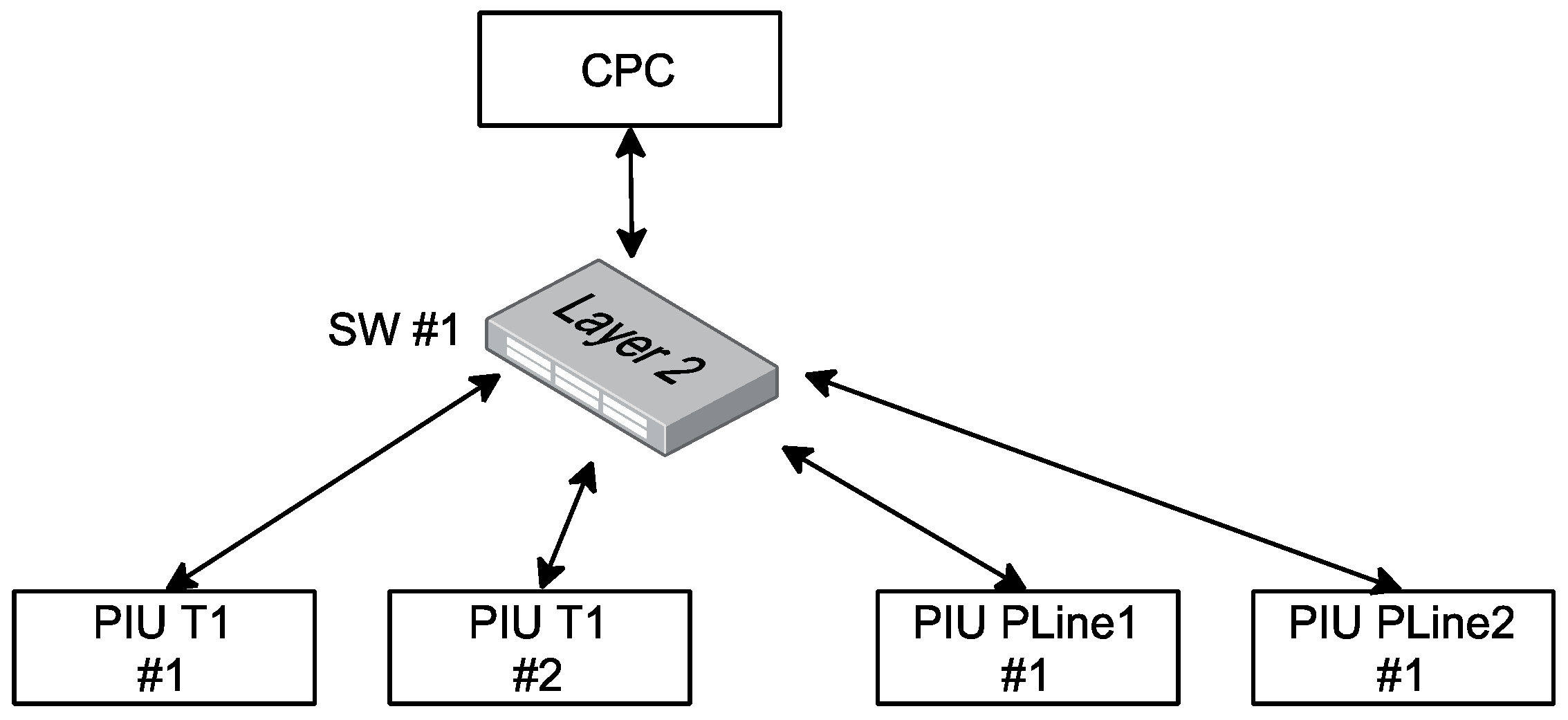
4.1. Reliability Analysis of Architecture 1
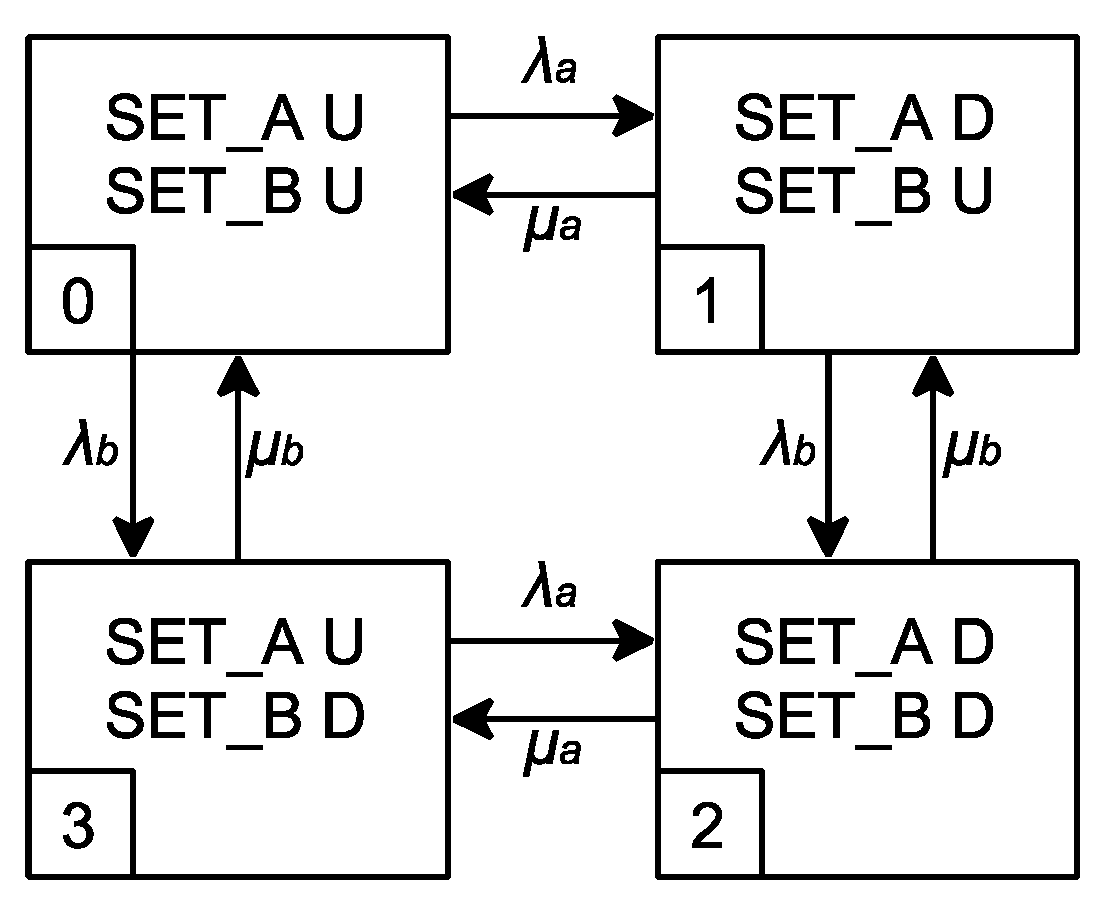
4.2. Reliability Analysis of Architecture 2
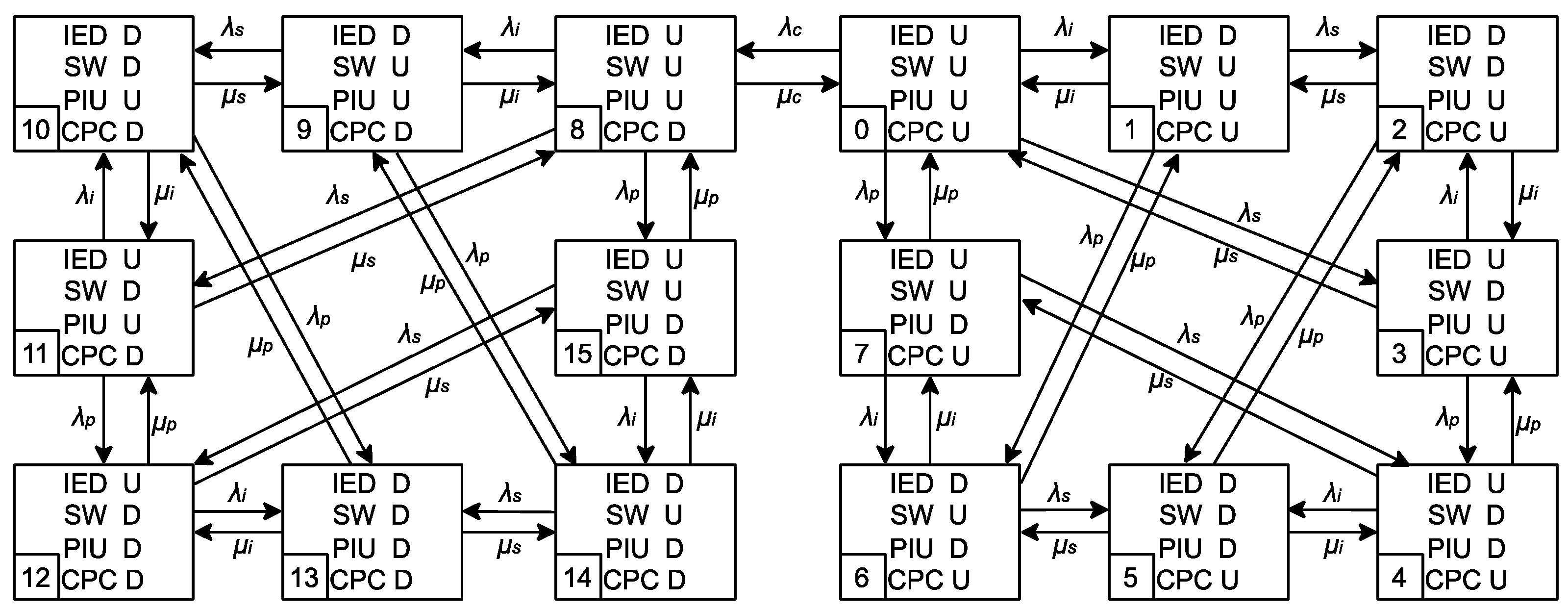
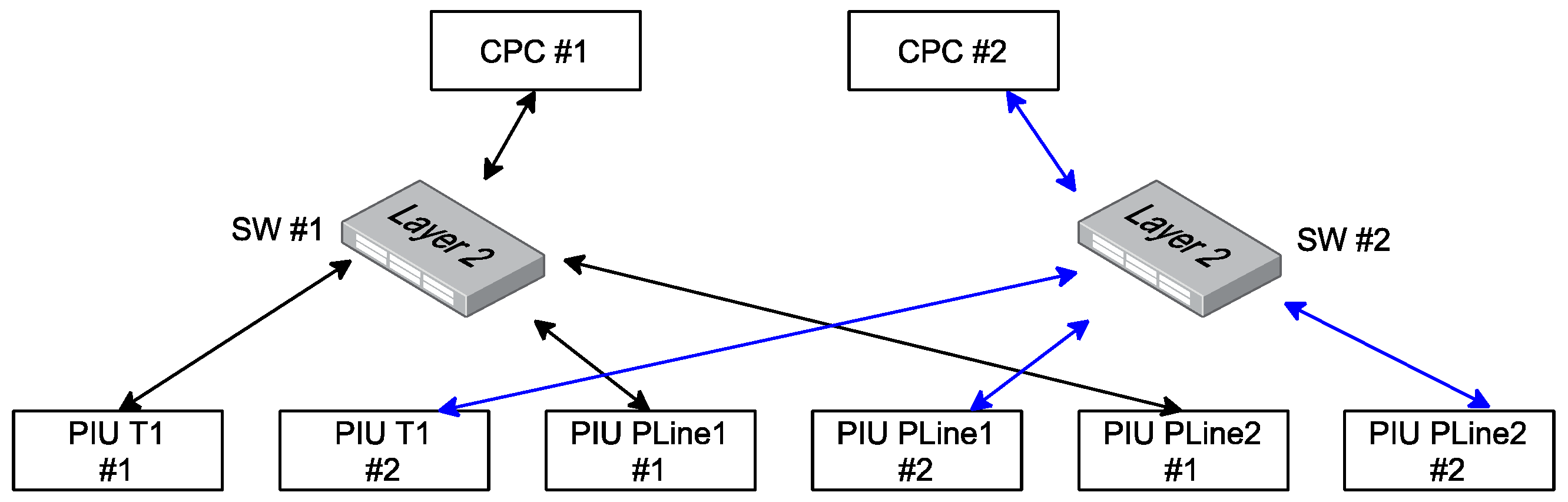
4.3. Reliability Analysis of Architecture 3 and Architecture 4
4.4. Comparison of the 4 Architectures
| Scheme A | : The failure rate is based on Table 4 |
| Scheme B | : The IED and PIU using IED’s failure rate |
| Scheme C | : The IED and PIU using PIU’s failure rate |
5. Comprehensive Reliability Selection Method of PACSs
5.1. Principles and Calculation Steps of Comprehensive Reliability Comparison Method
- (1)
- If you have a certain preference for either parameter, you can choose one with a smaller angle from the corresponding axis.
- (2)
- If the two parameters are expected to have different weights, all points are preprocessed in a way that the values on the less-weighted axis is uniformly multiplied by a known coefficient between (0, 1), normalized by using the larger weight as a base value, after which the same procedures still apply.
- (3)
- Detailed steps:
- i.
- Take the two parameters (basic and mission reliability) of multiple schemes as two individual number sequences and normalize them into the range of [−1, 1] with the help of Equation (12).
In Equation (12):Normalized value The value to be normalized The minimal value in the sequence The maximal value in the sequence - ii.
- Pair the two normalized values into a point suitable for the placement in the orthogonal coordinate system.
- iii.
- Select points in the first quadrant as candidates for comparison. If no candidates are available, all points are moved an equal amount of displacement in both directions towards the 1st quadrant until at least one point does appear in it.
- iv.
- Use Equation (13) to calculate Euclidean distance for each point and select the point of the largest value as the optimal solution.
| The distance from the coordinate point to the origin (also known as Euclidean distance) | |
| Normalized mission reliability value | |
| Normalized basic reliability value |
5.2. Basic Reliability of the 4 PACS Architectures
| Failure rate of architecture 1 | |
| Failure rate of digital sampling protective relay IED | |
| Failure rate of the switch | |
| Failure rate of PIUs |
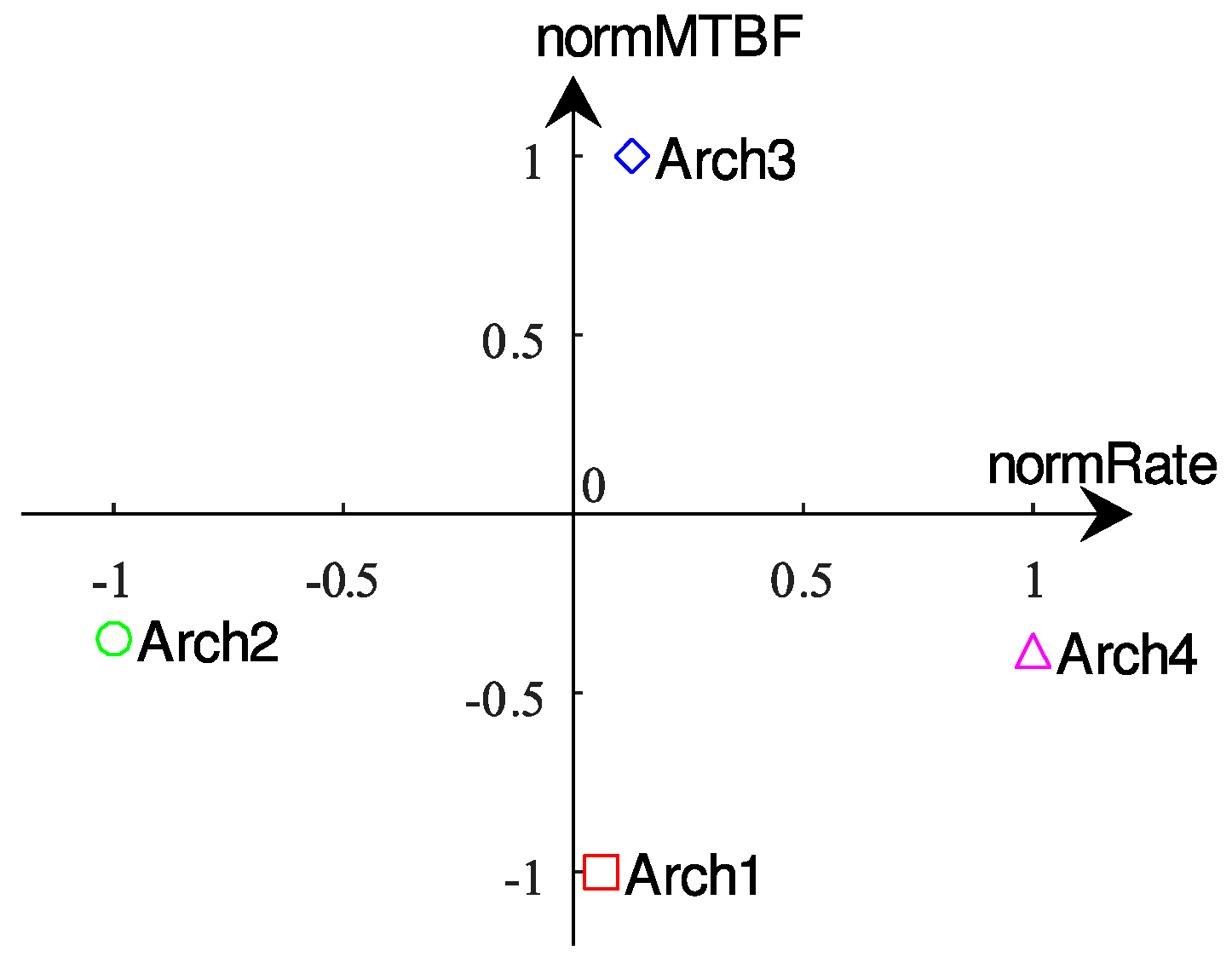
5.3. Architecture Selection Using Existing Method
5.4. Comprehensive Reliability Analysis of 4 PACS Architectures
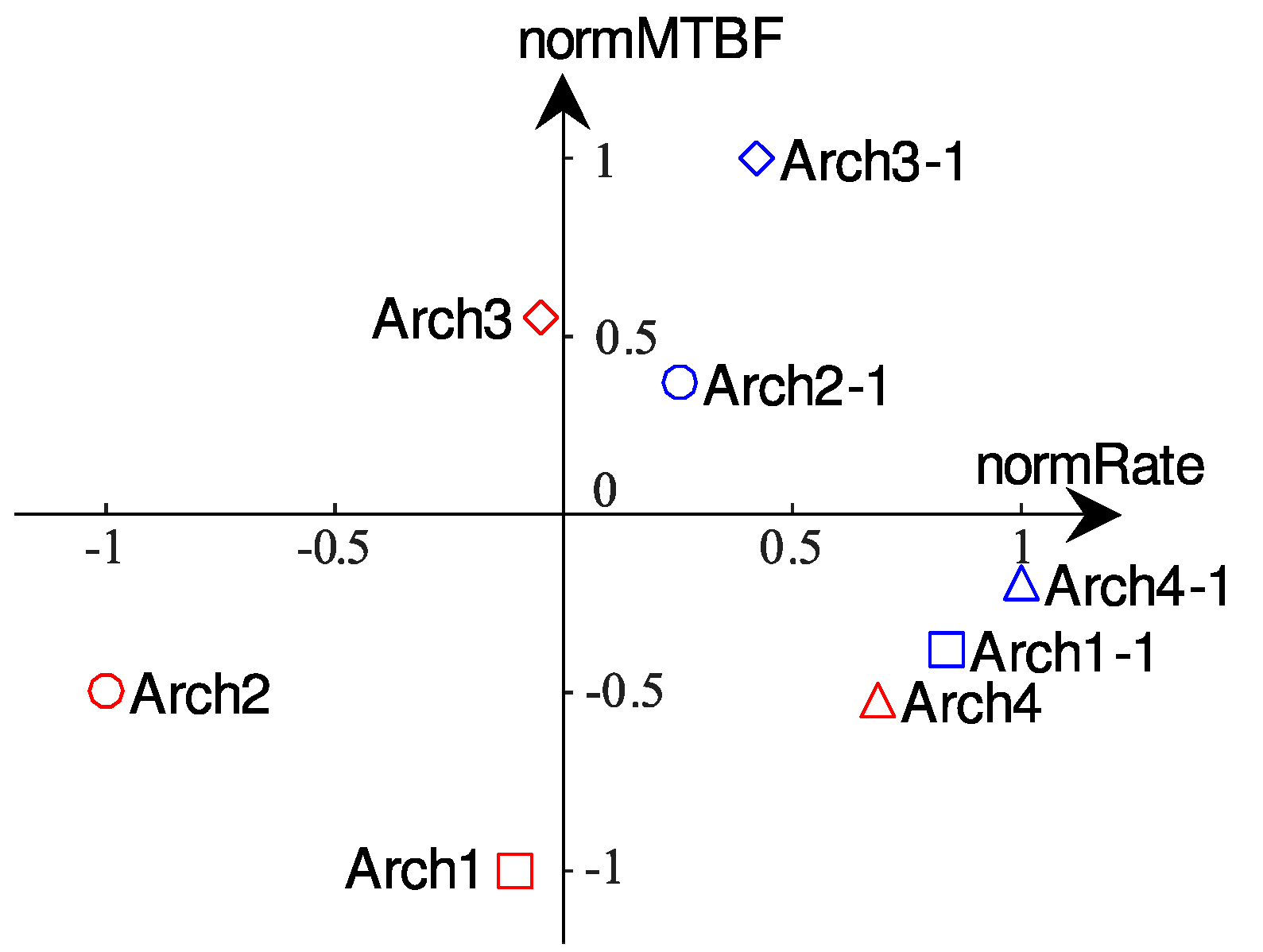
5.5. Comprehensive Reliability Analysis of 4 PACS Architectures (IED without LCD)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grimes, J.D. On Determining the Reliability of Protective Relay Systems. IEEE Trans. Reliab. 1970, R-19, 82–85. [Google Scholar] [CrossRef]
- He, J.; Guo, Z.; Yang, X.; Li, Y. Reliability and dynamic performance simulation of protective relayings. Power Syst. Technol. 2004, 28, 18–22. [Google Scholar]
- Wang, Q.; Wang, X. Reliability analysis of protective relays in low voltage distribution network. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, SUPERGEN’09, Nanjing, China, 6–7 April 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Xiong, X.; Chen, F.; Zhou, J.; Shen, Z. Reliability of Protection Relay Systems with Different Configurations. Autom. Electr. Power Syst. 2008, 32, 21–24. [Google Scholar] [CrossRef]
- Xiao, F.; Zhang, Z.; Yin, X. Reliability evaluation of protection system in smart substation based on process layer network. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 1–4 September 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Tavares, H.; Leite, H.; Pinto, A.; Vidal, P.; Santos, J. Applying Reliability Centered Maintenance to a digital protective relay. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Ye, Y.; Huang, T.; Xie, M.; Liu, H.; Zhao, Z. Research on the reliability analysis method of condition-based maintenance of relay protection equipment in substation. Power Syst. Prot. Control 2021, 49, 170–177. [Google Scholar] [CrossRef]
- Zhang, P.; Portillo, L.; Kezunovic, M. Reliability and Component Importance Analysis of All-Digital Protection Systems. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1380–1387. [Google Scholar] [CrossRef]
- Zhang, P.; Huo, C.; Kezunovic, M. A Novel Measure of omponent Importance Considering Cost for All-Digital Protection Systems. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Kanabar, M.G.; Sidhu, T.S. Reliability and availability analysis of IEC 61850 based substation communication architectures. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Kolesnikov, A.; Kulikov, A.; Lukicheva, I. Increasing the Reliability of the Centralized Protection of the Digital Substation. In Proceedings of the 2021 International Ural Conference on Electrical Power Engineering (UralCon), Magnitogorsk, Russian, 24–26 September 2021; pp. 42–48. [Google Scholar] [CrossRef]
- Das, N.; Islam, S. Analysis of power system communication architectures between substations using IEC 61850. In Proceedings of the 5th Brunei International Conference on Engineering and Technology (BICET 2014), Bandar Seri Begawan, Brunei, 1–3 November 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Falahati, B.; Chua, E. Failure modes in IEC 61850-enabled substation automation systems. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Loenders, R.; Van Hertem, D.; Beerten, J.; Chaffey, G.; Yang, L. Testing reliability performance of IEC61850-based digital substations. In Proceedings of the 15th International Conference on Developments in Power System Protection (DPSP 2020), Liverpool, UK, 9–12 March 2020; pp. 1–7. [Google Scholar] [CrossRef]
- CIGRE B5.60 WG; Protection, Automation and Control Architectures with Functionality Independent of Hardware; CIGRE: Paris, France, 2023.
- Ali, S.; Ali, S.; Shah, I.; Siddiqui, G.F.; Saba, T.; Rehman, A. Reliability Analysis for Electronic Devices Using Generalized Exponential Distribution. IEEE Access 2020, 8, 108629–108644. [Google Scholar] [CrossRef]
- Chen, L.; Qiu, Y.; Chen, J.; Huang, X. Reliability analysis of autonomous controllable protection device in power system. In Proceedings of the 2020 8th International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 7–10 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Xiao, J.; Song, K.; Wang, F.; Xu, H.; Xiong, F. The Risk Assessment Optimization for the Relay Protection System Based on Proportional Intensity Model. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; pp. 2519–2523. [Google Scholar] [CrossRef]
- Liao, Q.; Wang, X.; Ling, D.; Xiao, Z.; Huang, H.-Z. Equipment reliability analysis based on the Mean-rank method of two-parameter Weibull distribution. In Proceedings of the 2011 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Xi’an, China, 17–19 June 2011; pp. 361–364. [Google Scholar] [CrossRef]
- Lu, Z.; Li, J.; Yang, S.; Han, S.; Lu, Z. Research on Decision-making of Secondary Equipment Maintenance Based on Online Monitoring. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi’an, China, 21–24 October 2019; pp. 1578–1582. [Google Scholar] [CrossRef]
- MIL-HDBK-217F Notice 2; Military Handbook Reliability Prediction of Electronic Equipment. U.S. Department of Defense: Arlington County, VA, USA, 1995.
- GJB/Z 299C; Reliability Prediction Handbook for Electronic Equipment. 2006.
- SR-332 Issue 4; Reliability Prediction Procedure for Electronic Equipment. Telcordia: Piscataway Township, NJ, USA, 2016.
- Butnicu, D. POL DC-DC Converter Output Capacitor Bank’s Reliability Comparison using Prediction Standard MIL-HDBK-217F and SN 29500. In Proceedings of the 2021 IEEE 27th International Symposium for Design and Technology in Electronic Packaging (SIITME), Timisoara, Romania, 27–30 October 2021; pp. 169–172. [Google Scholar] [CrossRef]
- Hussain, B.; Beck, C.E.; Wiedman, T.E.; Sufana, C.R. Transmission system protection: A reliability study. IEEE Trans. Power Deliv. 1997, 12, 675–680. [Google Scholar] [CrossRef]
- Choudhary, K.; Sidharthan, P. Reliability prediction of Electronic Power Conditioner (EPC) using MIL-HDBK-217 based parts count method. In Proceedings of the 2015 International Conference on Computer, Communication and Control (IC4), Indore, India, 10–12 September 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, F.; Liu, P. Reliability Prediction of an Unmanned Ground Vehicular Computer Based Parts Count Method. In Proceedings of the 2019 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 17–19 October 2019; pp. 536–541. [Google Scholar] [CrossRef]
- Kong, L.; Ren, L. Evaluation of LCD Life. Chin. J. Liq. Cryst. Disp. 2011, 26, 154–157. [Google Scholar] [CrossRef]
- Zhu, J.; Ge, X.; Xie, R.; Sun, Z.; Zheng, X.; Tian, H. Study on the Constraints on Integration of Digital Distribution Substation Equipment and Necessary Maintenace Adjustment. In Proceedings of the 2020 International Symposium on Autonomous Systems (ISAS), Guangzhou, China, 6–8 December 2020; pp. 153–157. [Google Scholar] [CrossRef]
- Benabid, R.; Merrouche, D.; Bourenane, A.; Alzbutas, R. Reliability Assessment of Redundant Electrical Power Supply Systems using Fault Tree Analysis, Reliability Block Diagram, and Monte Carlo Simulation Methods. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Xu, L.; Liu, Y.; Chen, J.; Xu, S.; Chen, X.; Li, L. A Goal Oriented Reliability Assessment of System Protection Devices. In Proceedings of the 2022 4th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 25–28 March 2022; pp. 757–761. [Google Scholar] [CrossRef]
- Anderson, P.M.; Agarwal, S.K. An improved model for protective-system reliability. IEEE Trans. Reliab. 1992, 41, 422–426. [Google Scholar] [CrossRef]
- Anderson, P.M.; Chintaluri, G.M.; Magbuhat, S.M.; Ghajar, R.F. An improved reliability model for redundant protective systems-Markov models. IEEE Trans. Power Syst. 1997, 12, 573–578. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Z.; Zheng, S. Reliability analysis of protective relays in fault information processing system in China. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 5. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Wen, M.; Yin, X. A Novel Markov Model for Protective Relay Reliability. IEEE Trans. Power Deliv. 2023, 38, 2110–2118. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.; Wang, G.; Wang, T. Research on reliability evolutionary optimization of relays device based on Multi-Markov model. SN Appl. Sci. 2023, 5, 86. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Xing, F.; Wang, S.; Liu, Z.; Song, Z.; Jia, T.; Zhang, X.; Wang, L.; Xu, Y. Research on relay reliability evaluation based on information flow block diagram in smart substations. In Proceedings of the 2021 3rd International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 10–12 December 2021; pp. 1676–1680. [Google Scholar] [CrossRef]
- Xie, K.; Ma, H.; Hu, B.; Cao, K.; Li, C. Reliability Evaluation of Converter Transformer System in HVDC Transmission System Based on Markov State Space Graph Algorithm. Power Syst. Technol. 2011, 35, 71–78. [Google Scholar]
- Brito, M.P.; Griffiths, G. A Markov Chain State Transition Approach to Establishing Critical Phases for AUV Reliability. IEEE J. Ocean. Eng. 2011, 36, 139–149. [Google Scholar] [CrossRef]
- Etemadi, A.H.; Fotuhi-Firuzabad, M. Design and Routine Test Optimization of Modern Protection Systems with Reliability and Economic Constraints. IEEE Trans. Power Deliv. 2012, 27, 271–278. [Google Scholar] [CrossRef]
- Trofimov, A.; Khalyasmaa, A. Redundant Relay Protection Devices for Power Systems Reliability Model. In Proceedings of the 2020 5th International Conference on Green Technology and Sustainable Development (GTSD), Ho Chi Minh City, Vietnam, 27–28 November 2020; pp. 651–656. [Google Scholar] [CrossRef]



| Manual | Issue Date | Main Character |
|---|---|---|
| MIL-HDBK-217F Notice 2 [21] | 1995 | United States military standard, including parts count prediction method and part stress prediction method |
| GJB/Z 299C [22] | 2006 | Chinese national military standards, including the parts count prediction method and part stress prediction method; include reliability data for domestic and imported materials |
| Telcordia SR-332 Issue 4 [23] | 2016 | Applicable to the telecommunications industry, providing three prediction methods: parts count prediction method, integrating laboratory test data on units method, and integrating field data on units method |
| Board Categories | (10−6/h) | MTBF (h) |
|---|---|---|
| HMI board | 0.90796 | 1,101,370 |
| PANEL board | 7.64980 | 130,722 |
| CPU board | 0.75696 | 1,321,074 |
| Binary input board | 0.29726 | 3,364,058 |
| Binary output board | 0.51626 | 1,937,008 |
| AC board | 0.05410 | 18,484,288 |
| Mother board | 0.20945 | 4,774,409 |
| Board Categories | Number of Boards N | (10−6/h) | (10−6/h) |
|---|---|---|---|
| PANEL board | 1 | 7.65180 | 7.65180 |
| HMI board | 1 | 0.90666 | 0.90666 |
| CPU board | 2 | 0.75696 | 1.51392 |
| Binary input board | 5 | 0.51626 | 2.58130 |
| Binary output board | 2 | 0.29726 | 0.59452 |
| Mother board | 1 | 0.20945 | 0.20945 |
| AC board | 1 | 0.05410 | 0.05410 |
| Sum | 13.51175 |
| IED Categories | Failure Rate λ (10−6/h) | MTBF (h) | MTBF (Year) |
|---|---|---|---|
| 100 Mbit optical switch | 3.55796 | 281,060 | 32.08 |
| Merging unit | 3.55902 | 280,976 | 32.07 |
| PIU (Process Interface Unit) | 8.66631 | 115,389 | 13.17 |
| Digital sampling line protection relay IED | 11.59158 | 86,270 | 9.85 |
| Conventional sampling line protection relay IED | 13.51175 | 74,010 | 8.45 |
| Station domain protection relay IED | 15.33105 | 65,227 | 7.45 |
| IED Categories | Failure Rate λ (10−6/h) | MTBF (h) | MTBF (Year) |
|---|---|---|---|
| Digital sampling line protection relay IED | 3.88196 | 257,602 | 29.41 |
| Conventional sampling line protection relay IED | 5.85995 | 170,650 | 19.48 |
| Station domain protection relay IED | 7.62143 | 131,209 | 14.98 |
| This Article | B5.60 TB | Description |
|---|---|---|
| 1 | 1 | IEDs with process bus |
| 2 | 3 | Hybrid PACS with IEDs, process bus, and back-up CPC (centralized protection and control) system |
| 3 | 4 | CPC system with PIUs providing back-up-protection |
| 4 | 5 | Redundant CPC system |
| State | PIU | SW | IED |
|---|---|---|---|
| 0 | U | U | U |
| 1 | U | U | D |
| 2 | U | D | D |
| 3 | U | D | U |
| 4 | D | D | U |
| 5 | D | D | D |
| 6 | D | U | D |
| 7 | D | U | U |
| Failure Rate of Device Group | Failure Rate of Single Device (10−6/h) | Failure Rate of Device Group (10−6/h) |
|---|---|---|
| IED () | 11.59158 | 34.77474 |
| SW () | 3.55796 | 3.55796 |
| PIU () | 8.66631 | 25.99893 |
| State | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Steady-state probability | 99.8458% | 0.0833% | 0.0000% | 0.0085% | 0.0000% | 0.0000% | 0.0001% | 0.0623% |
| State | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Steady-state probability | 99.8971% | 0.0514% | 0.0000% | 0.0514% |
| Failure Rate of Device Group | Failure Rate of Single Device (10−6/h) | Failure Rate of Device Group (10−6/h) |
|---|---|---|
| IED () | 11.59158 | 30.91090 |
| SW () | 3.55796 | 3.55796 |
| PIU () | 8.66631 | 23.11016 |
| CPC () | 15.33105 | 15.33105 |
| State | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Steady-state probability | 99.8252% | 0.0741% | 0.0000% | 0.0085% | 0.0000% | 0.0000% | 0.0000% | 0.0554% |
| State | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Steady-state probability | 0.0367% | 0.0000% | 0.0000% | 0.0000% | 0.0000% | 0.0000% | 0.0000% | 0.0000% |
| Index | Architecture | Steady-State Probability | Reliability Rank |
|---|---|---|---|
| 1 | IEDs with process bus | 99.8971% | 3 |
| 2 | Hybrid PACS with IEDs, process bus and back-up CPC system | 99.8620% | 4 |
| 3 | CPC system with PIUs providing back-up-protection | 99.8993% | 2 |
| 4 | Redundant CPC system | 99.9282% | 1 |
| Index | Steady-State Probability | Unavailable Hours Per Year (1 − Steady-State Probability) |
|---|---|---|
| 1 | 99.8971% | 9.01 |
| 2 | 99.8620% | 12.09 |
| 3 | 99.8993% | 8.82 |
| 4 | 99.9282% | 6.29 |
| Index | Steady-State Probability | Steady-State Probability Variance | ||||
|---|---|---|---|---|---|---|
| Scheme | A | B | C | B − A | C − A | |
| 1 | 99.8971% | 99.8831% | 99.9112% | −0.0140% | 0.0141% | |
| 2 | 99.8620% | 99.7955% | 99.8806% | −0.0665% | 0.0186% | |
| 3 | 99.8993% | 99.8567% | 99.9153% | −0.0426% | 0.0160% | |
| 4 | 99.9282% | 99.8963% | 99.9389% | −0.0319% | 0.0107% | |
| Architecture | Failure Rate Equation of PACS Architecture | Failure Rate λ (10−6/h) | MTBF (h) |
|---|---|---|---|
| 1 | 6 + 2 + 6 | 128.66326 | 7772 |
| 2 | 3 + + + 4 | 88.32899 | 11,321 |
| 3 | + + 4 | 53.55425 | 18,673 |
| 4 | 2 + 2 + 6 | 89.77588 | 11,139 |
| Architecture | Steady-State Probability of Working Normally | MTBF (h) | Device Counts |
|---|---|---|---|
| 1 | 99.8971% | 7772 | 14 |
| 2 | 99.8620% | 11,321 | 9 |
| 3 | 99.8993% | 18,673 | 6 |
| 4 | 99.9282% | 11,139 | 10 |
| Architecture | Normalized Steady-State Probability of Working Normally | Normalized MTBF |
|---|---|---|
| 1 | 0.0604 | −1.0000 |
| 2 | −1.0000 | −0.3489 |
| 3 | 0.1269 | 1.0000 |
| 4 | 1.0000 | −0.3823 |
| Architecture | Normalized Steady-State Probability of Working Normally | Normalized MTBF |
|---|---|---|
| 1 | −0.1057 | −1.0000 |
| 2 | −1.0000 | −0.4945 |
| 3 | −0.0497 | 0.5527 |
| 4 | 0.6866 | −0.5204 |
| 1-1 | 0.8369 | −0.3785 |
| 2-1 | 0.2535 | 0.3706 |
| 3-1 | 0.4217 | 1.0000 |
| 4-1 | 1.0000 | −0.1914 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Jin, L. Study on Reliability of PACSs with Integrated Consideration of Both Basic and Mission Reliability. Energies 2024, 17, 365. https://doi.org/10.3390/en17020365
Chen X, Jin L. Study on Reliability of PACSs with Integrated Consideration of Both Basic and Mission Reliability. Energies. 2024; 17(2):365. https://doi.org/10.3390/en17020365
Chicago/Turabian StyleChen, Xinzhi, and Long Jin. 2024. "Study on Reliability of PACSs with Integrated Consideration of Both Basic and Mission Reliability" Energies 17, no. 2: 365. https://doi.org/10.3390/en17020365
APA StyleChen, X., & Jin, L. (2024). Study on Reliability of PACSs with Integrated Consideration of Both Basic and Mission Reliability. Energies, 17(2), 365. https://doi.org/10.3390/en17020365





