Emergency Prevention Control as a Means of Power Quality Improvement in a Shipboard Hybrid Electric Power System
Abstract
:1. Introduction
2. Materials and Methods
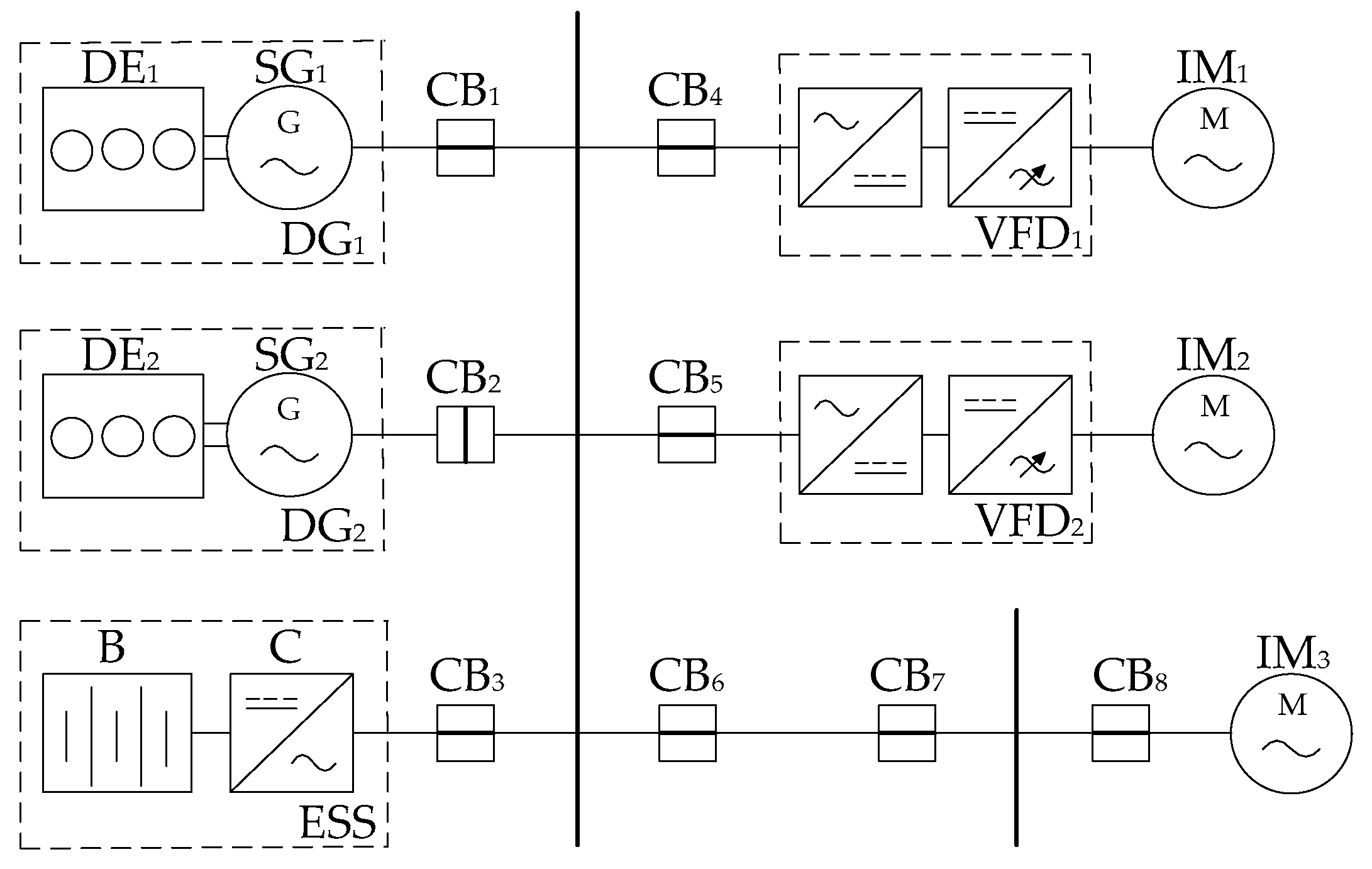
2.1. Problem Statement
- The vessel is considered as being operated offshore with calm seas where the thruster load does not exceed 5% and does not have a significant effect on the total consumption load and, thus, is not considered further.
- Synchronous diesel generator DG2 is assumed to be offline as a standby power source and is therefore also not considered.
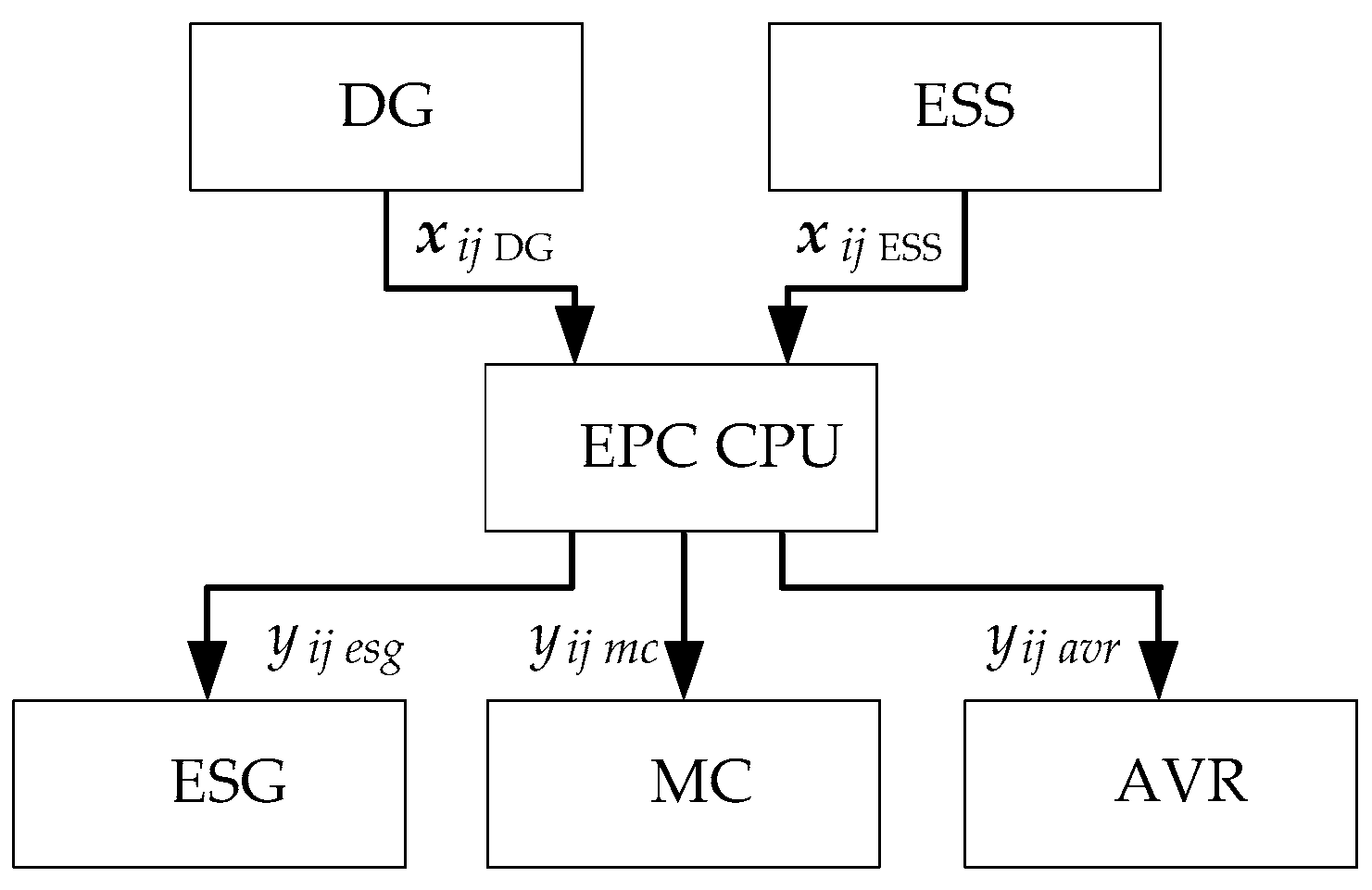
2.2. Development of SHEPS EPC System
- The ESG’s control signal, .
- The control signal for the ESS’s MC, .
- The AVR’s control signal, .
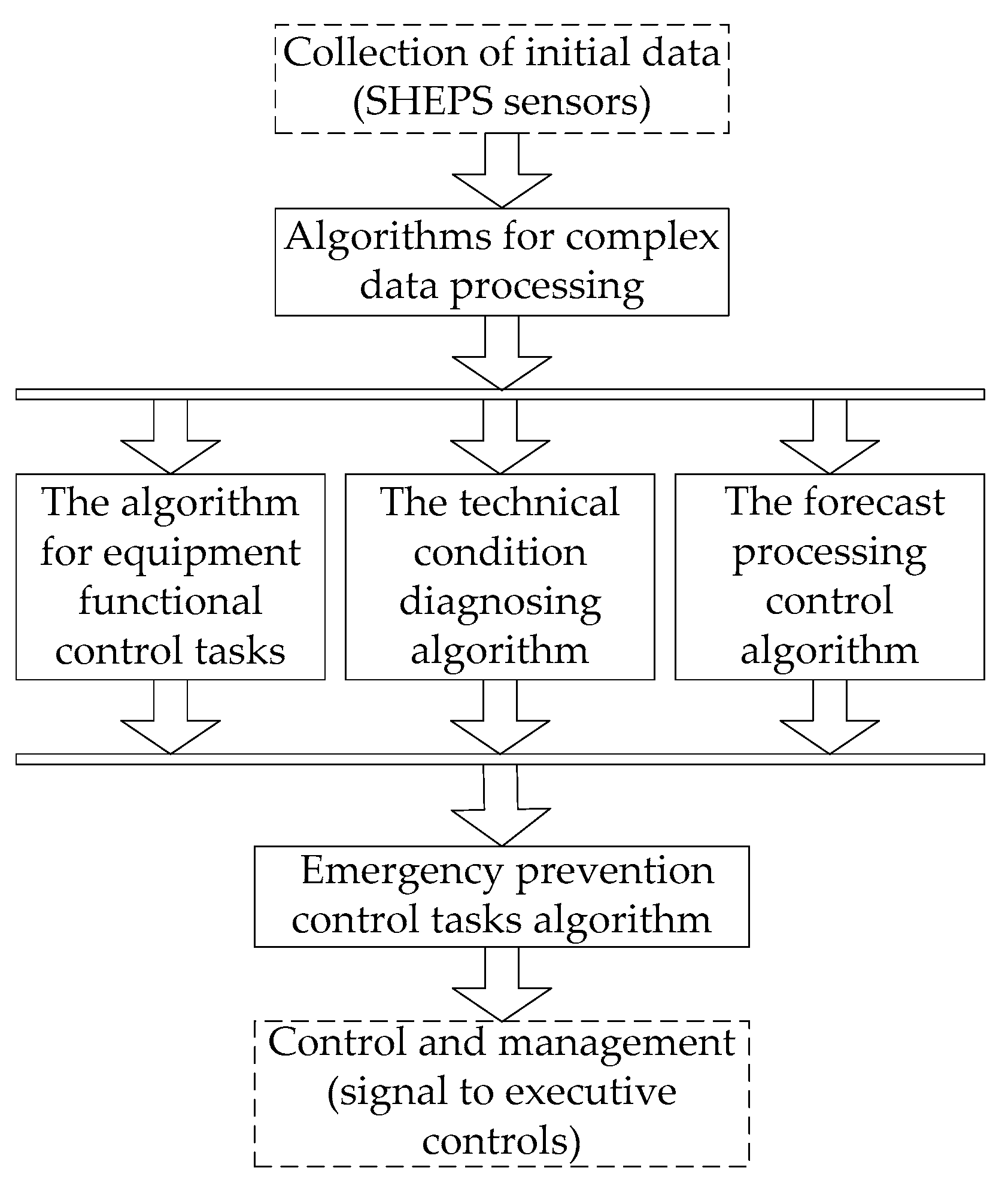
2.3. SHEPS EPC Algorithm
- Collection of SHEPS information;
- Processing of collected information according to specified and newly formed algorithms, determined by the state of the SHEPS and the EPC system;
- Forming of monitoring and control signals.
- Algorithms for complex processing of input data. The optimization of input data processing is based on eliminating their redundancy to increase the accuracy and reliability of the input parameter assessment. It is implemented as time- and function-dependent processing.
- Algorithms for control tasks of the SHEPS (functional algorithms). This set of algorithms is for control tasks determined by the power system tasks, which reflect the composition of input data, control, and monitoring interfaces. These algorithms determine the main characteristics of the entire power system.
- Algorithms for diagnosing the technical condition of the SHEPS, protecting the functional algorithms. These consist of test algorithms and performance monitoring and allow us to check the performance of equipment by testing under known conditions and to determine the location of faults.
- A forecast processing and management control algorithm based on the forecast results. This algorithm provides preparatory measures, for example, by turning off potentially faulty equipment in advance or turning on redundancy power sources. Based on the analysis of the possible fault scenarios or changes in the nature of the processes ongoing in the SHEPS operation, the algorithm prevents emergency modes and conditions. In addition, it provides the formation of control actions on changes in the state of SHEPS elements and modes to prevent the transition of the entire power system to the pre-fault area of operation.
- Algorithms for EPC tasks. These allow us to detect and correct errors in the control algorithms and forecast and prevent fault states and emergency conditions.
2.4. Mathematical Model of SHEPS under Study
2.4.1. Model of Diesel Engine and Engine Speed Governor
2.4.2. Model of the Synchronous Generator and Automatic Voltage Regulator
2.4.3. Model of Energy Storage System
2.4.4. Model of the Induction Motor
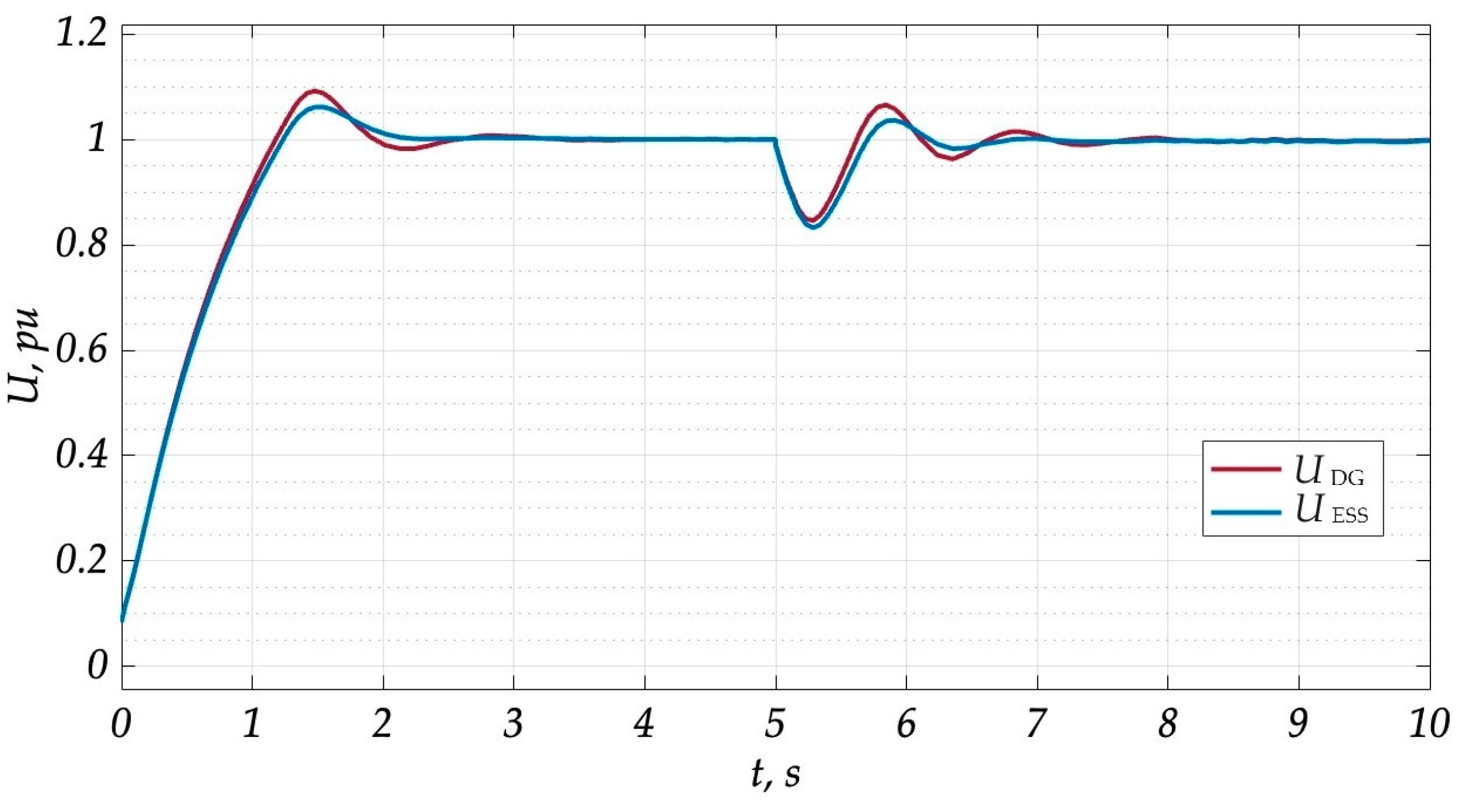
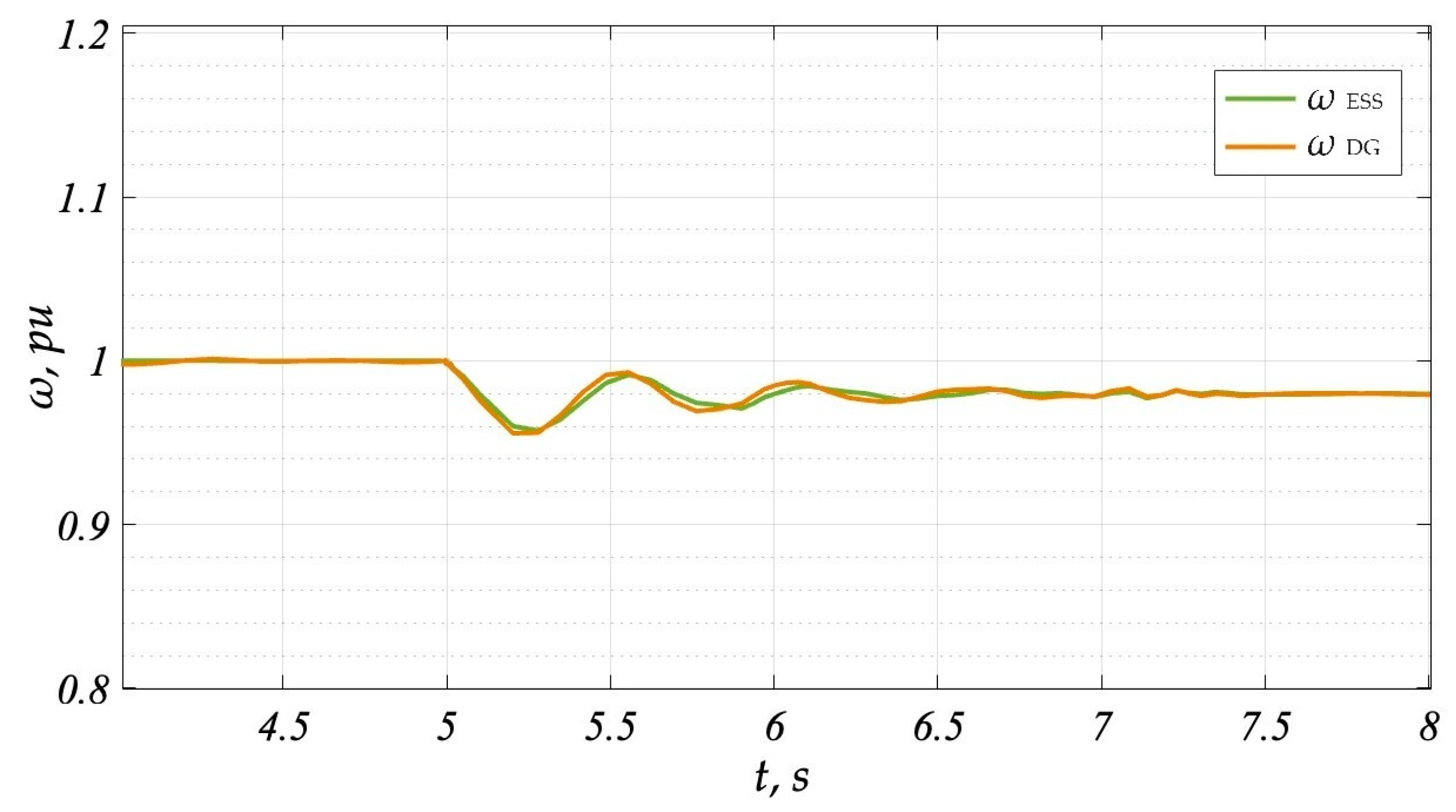
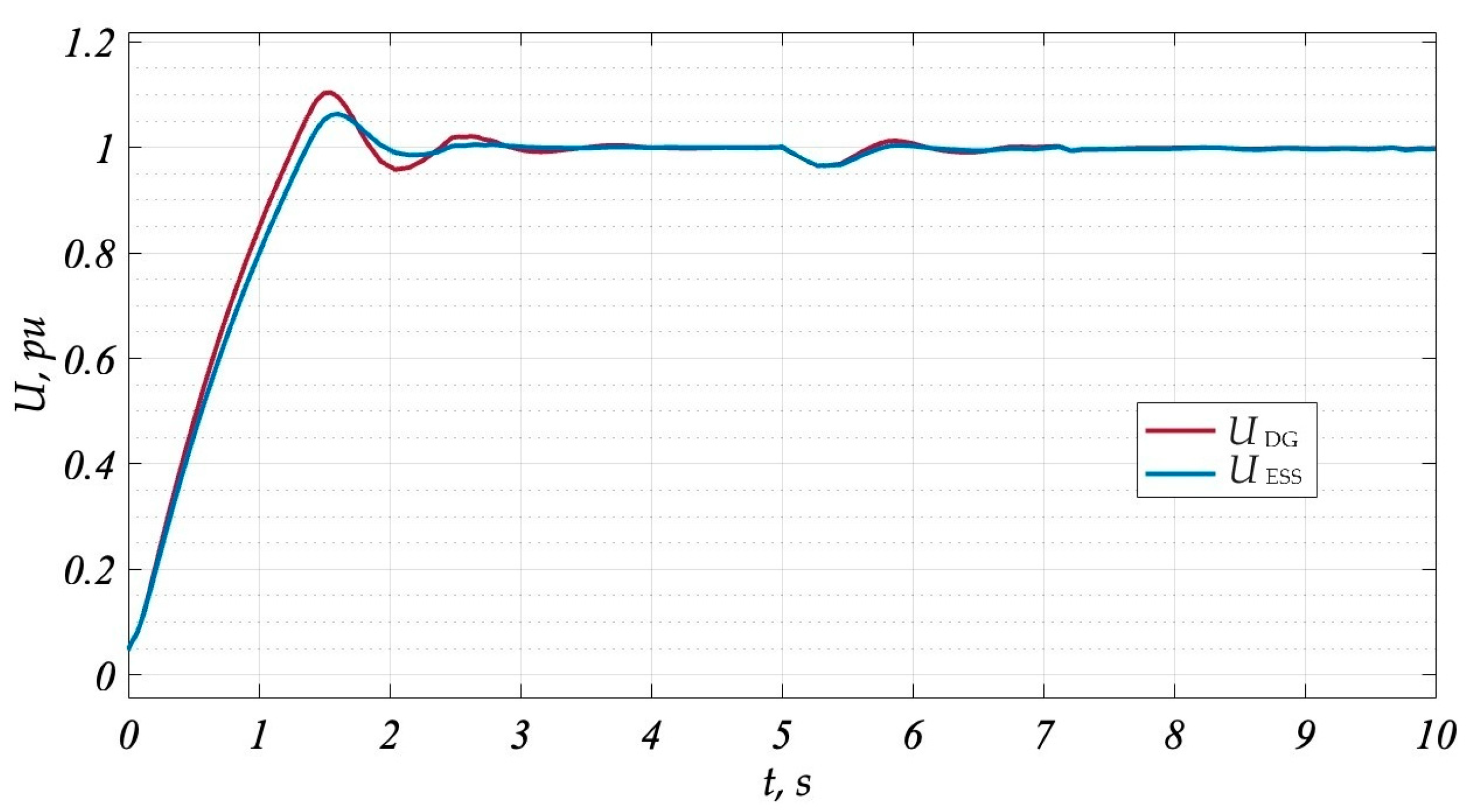
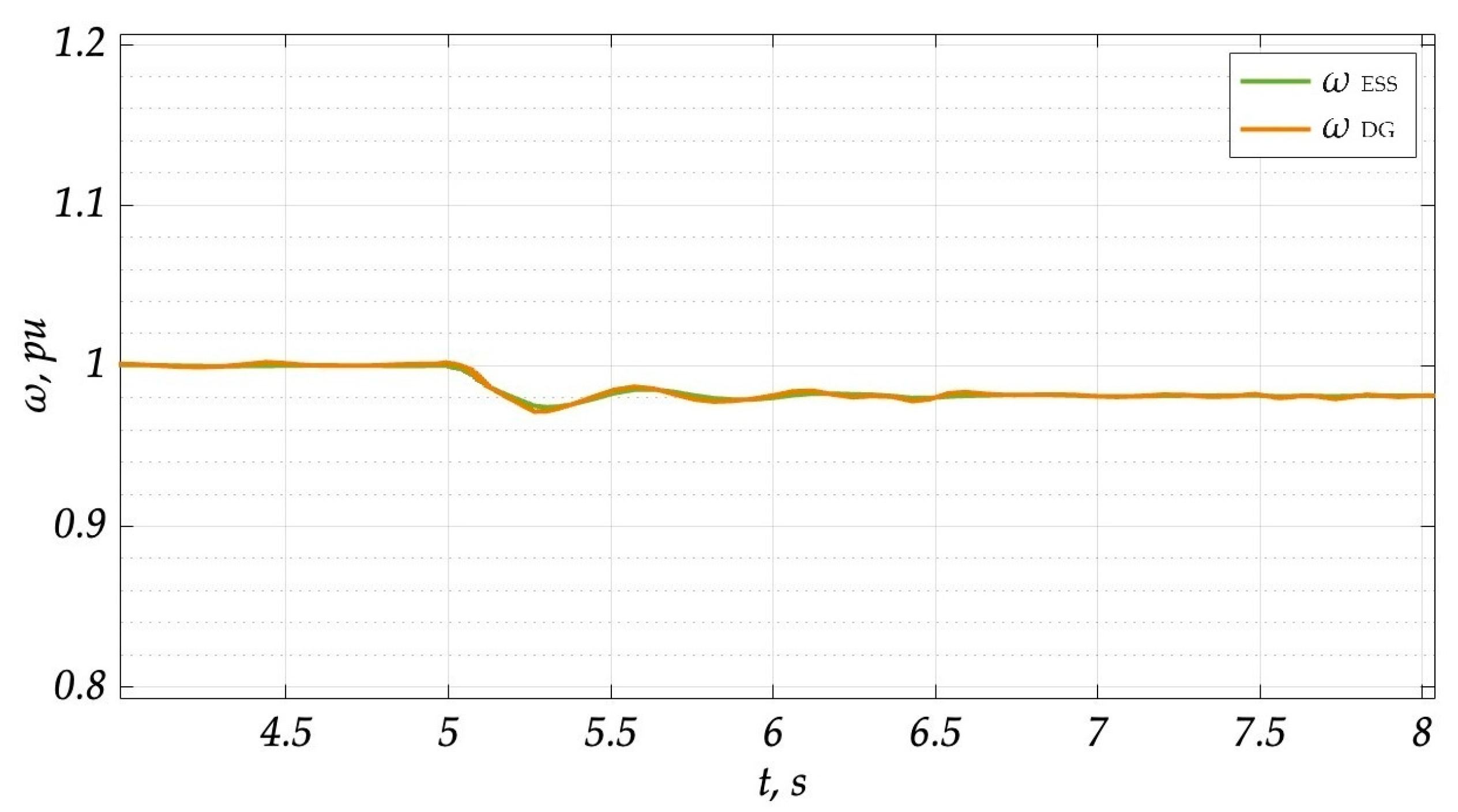
3. Computer Simulation Results
4. Discussion
4.1. Implementation of EPC System
4.2. Limitations
- The inverter model was adopted with the assumption that the battery discharge process is not considered but assumed to be constant, corresponding to the maximum charge level.
- The mathematical models of the monitoring circuits and instrumentation such as frequency and voltage sensors are not considered, assuming them to be ideal sensors without time constants.
- The generated harmonics of voltage and frequency are not considered while assessing the power quality.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sabin, D.; Norwalk, M.; Kittredge, K.; Johnston, S. IEEE Power Quality Standards. In Proceedings of the 2022 20th International Conference on Harmonics & Quality of Power (ICHQP), Naples, Italy, 29 May–1 June 2022; p. 21846300. [Google Scholar] [CrossRef]
- Amrouche, S.O.; Rekioua, D.; Rekioua, T.; Bacha, S. Overview of energy storage in renewable energy systems. Int. J. Hydrogen Energy 2016, 41, 20914–20927. [Google Scholar] [CrossRef]
- Ibrahim, H.; Ilinca, A.; Perron, J. Energy storage systems: Characteristics and comparisons. Renew. Sustain. Energy Rev. 2008, 12, 1221–1250. [Google Scholar] [CrossRef]
- Hadjipaschalis, I.; Poullikkas, A.; Efthimiou, V. Overview of current and future energy storage technologies for electric power applications. Renew. Sustain. Energy Rev. 2009, 13, 1513–1522. [Google Scholar] [CrossRef]
- Tan, X.; Li, Q.; Wang, H. Advances and trends of energy storage technology in microgrid. Int. J. Electr. Power Energy Syst. 2013, 44, 179–191. [Google Scholar] [CrossRef]
- Liu, J.; Yushi, M.; Ise, T.; Yoshizawa, J.; Watanabe, K. Parallel Operation of a Synchronous Generator and a Virtual Synchronous Generator under Unbalanced Loading Condition in Microgrids. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3741–3748. [Google Scholar] [CrossRef]
- Yuan, W.; He, Y.; Li, Z.; Ruan, Y.; Lu, L.; Li, B. A real-time aging monitoring method of parallel-connected IGBT modules. Mater. Sci. Semicond. Process. 2021, 124, 105555. [Google Scholar] [CrossRef]
- Sathik, M.M.; Prasanth, S.; Sasongko, F.; Pou, J. Online condition monitoring of IGBT modules using voltage change rate identification. Microelectron. Reliab. 2018, 88–90, 486–492. [Google Scholar] [CrossRef]
- Stamatakis, M.E.; Ioannides, M.G. State Transitions Logical Design for Hybrid Energy Generation with Renewable Energy Sources in LNG Ship. Energies 2021, 14, 7803. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, J.; Zhou, K.; Zhu, J.; Wang, Y. Research on Energy Management for Ship Hybrid Power System Based on Adaptive Equivalent Consumption Minimization Strategy. J. Mar. Sci. Eng. 2023, 11, 1271. [Google Scholar] [CrossRef]
- Kolodziejski, M.; Michalska-Pozoga, I. Battery Energy Storage Systems in Ships’ Hybrid/Electric Propulsion Systems. Energies 2023, 16, 1122. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; González-Rivera, E.; García-Triviño, P.; Vera, D. Performance Analysis of a Hybrid Electric Ship by Real-Time Verification. Energies 2022, 15, 2116. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Khajesalehi, J.; Afjei, S.E. Fault-tolerant virtual synchronous generator control of inverters in synchronous generator-based microgrids. Electr. Power Syst. Res. 2023, 218, 109173. [Google Scholar] [CrossRef]
- Liu, J.; Hossain, M.J.; Lu, J.; Rafi FH, M.; Li, H. A hybrid AC/DC microgrid control system based on a virtual synchronous generator for smooth transient performances. Electr. Power Syst. Res. 2018, 162, 169–182. [Google Scholar] [CrossRef]
- Ghodsi, M.R.; Tavakoli, A.; Samanfar, A. Microgrid Stability Improvement Using a Deep Neural Network Controller Based VSG. Int. Trans. Electr. Energy Syst. 2022, 2022, 7539173. [Google Scholar] [CrossRef]
- IEEE Guide for Identifying and Improving Voltage Quality in Power Systems. In IEEE Std 1250-2018 (Revision of IEEE Std 1250-2011); IEEE: Piscataway, NJ, USA, 2018; pp. 1–63. [CrossRef]
- Abs Rules for Building and Classing. Part 6: Rules For Equipment and Machinery Certification. Updated July 2018. [Electronic Resource]. Available online: https://ww2.eagle.org (accessed on 25 October 2023).
- Maity, A.; Bhattacharya, K.; Sanyal, A.N. Asynchronous operation of synchronous generators under field failure. In Proceedings of the 2014 First International Conference on Automation, Control, Energy and Systems (ACES), Adisaptagram, India, 1–2 February 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Tierielnyk, S.; Lukovtsev, V. Emergency Prevention Control System for Shipboard Electrical Power Plant. Int. J. Energy Environ. Econ. 2021, 29, 341–354. [Google Scholar]
- Fikari, S.G.; Sigarchian, S.G.; Chamorro, H.R. Modeling and Simulation of an Autonomous Hybrid Power System. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017; Volume 52, pp. 1–6. [Google Scholar] [CrossRef]
- Tamrakar, I.; Shilpakar, L.; Fernandes, B.; Nilsen, R. Voltage and frequency control of parallel operated synchronous generator and induction generator with STATCOM in micro hydro scheme. IET Gener. Transm. Distrib. 2007, 1, 743–750. [Google Scholar] [CrossRef]
- Tian, P.; Guerrero, J.M.; Mahtani, K.; Platero, C.A. Instantaneous Specific Protection Method Against Faulty Synchronizations of Synchronous Machines. IEEE Access 2021, 9, 88868–88878. [Google Scholar] [CrossRef]
- Gvozdeva, I.; Lukovtsev, V.; Tierielnyk, S. Forecasting of the performance of the shipboard electric power system on the basis of the artificialneural Network. Technol. Audit. Prod. Reserves 2017, 4, 43–49. [Google Scholar] [CrossRef]
- IEEE Committee Report. Dynamic Models for Steam and Hydro Turbines in Power System Studies. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1904–1915. [Google Scholar] [CrossRef]
- Stavrakakis, G.; Kariniotakis, G. A general simulation algorithm for the accurate assessment of isolated diesel-wind turbines systems interaction. I. A general multimachine power system model. IEEE Trans. Energy Convers. 1995, 10, 577–583. [Google Scholar] [CrossRef]
- Olive, D.W. Digital Simulation of Synchronous Machine Transients. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 1669–1675. [Google Scholar] [CrossRef]
- Krause, P.; Wasynczuk, O.; Sudhoff, S.; Pekarek, S. Analysis of Electric Machinery and Drive Systems, 3rd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2013; ISBN 9781118024294. [Google Scholar]
- IEEE Committee Report. Computer representation of excitation systems. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 1460–1464. [Google Scholar] [CrossRef]
- Rashid, M.H. Power Electronics Handbook, 3rd ed.; Butterworth-Heinemann Elsevier Ltd.: Oxford, UK, 2011; ISBN 978-0-12-581650-2. [Google Scholar]
- Torres, M.; Lopes, L.A.C. Inverter-Based Diesel Generator Emulator for the Study of Frequency Variations in a Laboratory-Scale Autonomous Power System. Energy Power Eng. 2013, 5, 274–283. [Google Scholar] [CrossRef]
- Stagg, G.; Ahmed, E.-A. Computer Methods in Power System Analysis; McGraw Hill: Singapore, 1968. [Google Scholar]
- Huang, C.; Huang, Y.; Chen, S.; Yang, S. A Hierarchical Optimization Method for Parameter Estimation of Diesel Generators. IEEE Access 2020, 8, 176467–176479. [Google Scholar] [CrossRef]
- Matlab Simulink—Simulation and Model-Based Design. Available online: https://www.mathworks.com/products/simulink.html (accessed on 26 March 2023).
- Seyedi, H.; Sanaye-Pasand, M. Design of New Load Shedding Special Protection Schemes for a Double Area Power System. Am. J. Appl. Sci. 2009, 6, 317–327. [Google Scholar] [CrossRef]
- Flower, J.; Parr, E. 13—Control Systems. In Electrical Engineer’s Reference Book, 6th ed.; Newnes: Oxford, UK, 2003; pp. 13–63. ISBN 9780750646376. [Google Scholar] [CrossRef]



| System Component | Parameters |
|---|---|
| Synchronous generator | = 1900 kW, = 690 V |
| Induction motor | = 735 kW, = 690 V |
| Energy storage system | = 1800 kW, = 690 V, = 1415 kWh |
| DE and ESG | |||||
| Parameter | Value | Parameter | Value | Parameter | Value |
| 0.99 pu | 1.1 pu | 1.23 s | |||
| 0.03 pu | −0.25 pu | 0.2 s | |||
| 0.012 pu | s | s | |||
| SG | |||||
| Parameter | Value | Parameter | Value | Parameter | Value |
| 2.183 s | 0.011 pu | 0.895 pu | |||
| 0.893 s | 0.929 pu | 0.947 pu | |||
| 0.592 s | 0.932 pu | 0.983 pu | |||
| 1.94 pu | 1.94 pu | ||||
| AVR | |||||
| Parameter | Value | Parameter | Value | Parameter | Value |
| 1 pu | 0.2 s | ||||
| 10 | 0 | ||||
| 0.03 pu | |||||
| ESS | |||||
| Parameter | Value | Parameter | Value | Parameter | Value |
| 1 pu | 0.0942 pu | 1 pu | |||
| 0.01 s | 0.015 pu | 0.087 pu | |||
| IM | |||||
| Parameter | Value | Parameter | Value | Parameter | Value |
| 0.204 pu | 0.944 pu | 0.12 pu | |||
| 0.046 pu | 0.23 s | 0.79 pu | |||
| 0.53 pu | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tierielnyk, S.; Lukovtsev, V. Emergency Prevention Control as a Means of Power Quality Improvement in a Shipboard Hybrid Electric Power System. Energies 2024, 17, 398. https://doi.org/10.3390/en17020398
Tierielnyk S, Lukovtsev V. Emergency Prevention Control as a Means of Power Quality Improvement in a Shipboard Hybrid Electric Power System. Energies. 2024; 17(2):398. https://doi.org/10.3390/en17020398
Chicago/Turabian StyleTierielnyk, Sergii, and Valery Lukovtsev. 2024. "Emergency Prevention Control as a Means of Power Quality Improvement in a Shipboard Hybrid Electric Power System" Energies 17, no. 2: 398. https://doi.org/10.3390/en17020398
APA StyleTierielnyk, S., & Lukovtsev, V. (2024). Emergency Prevention Control as a Means of Power Quality Improvement in a Shipboard Hybrid Electric Power System. Energies, 17(2), 398. https://doi.org/10.3390/en17020398








