A Deep Learning Approach to Optimize the Performance and Power Demand of Electric Scooters under the Effect of Operating and Structure Parameters
Abstract
:1. Introduction
2. Data Generation for Machine Learning
2.1. Experimental Setup
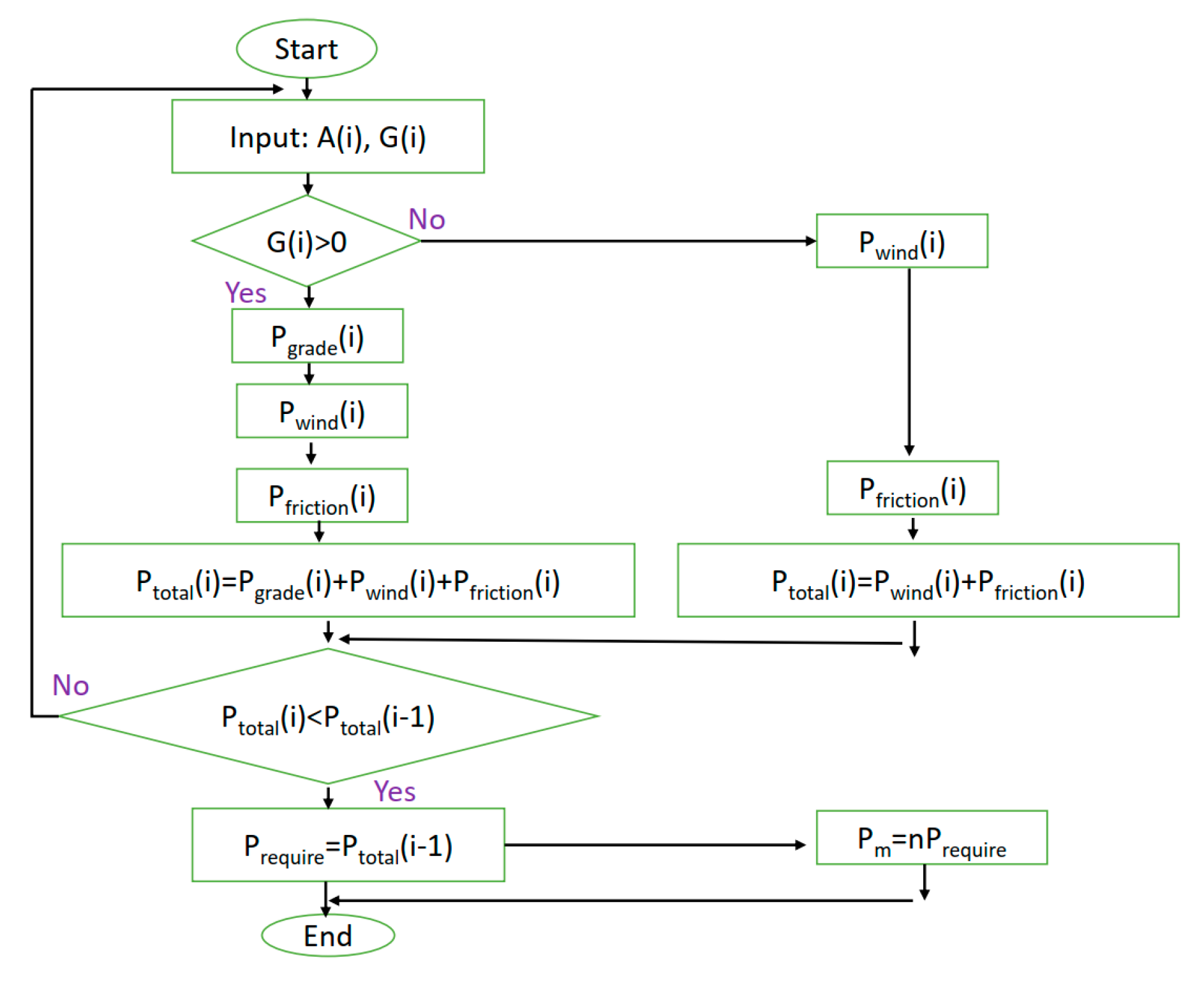
2.2. Simulation Study
3. Machine Learning
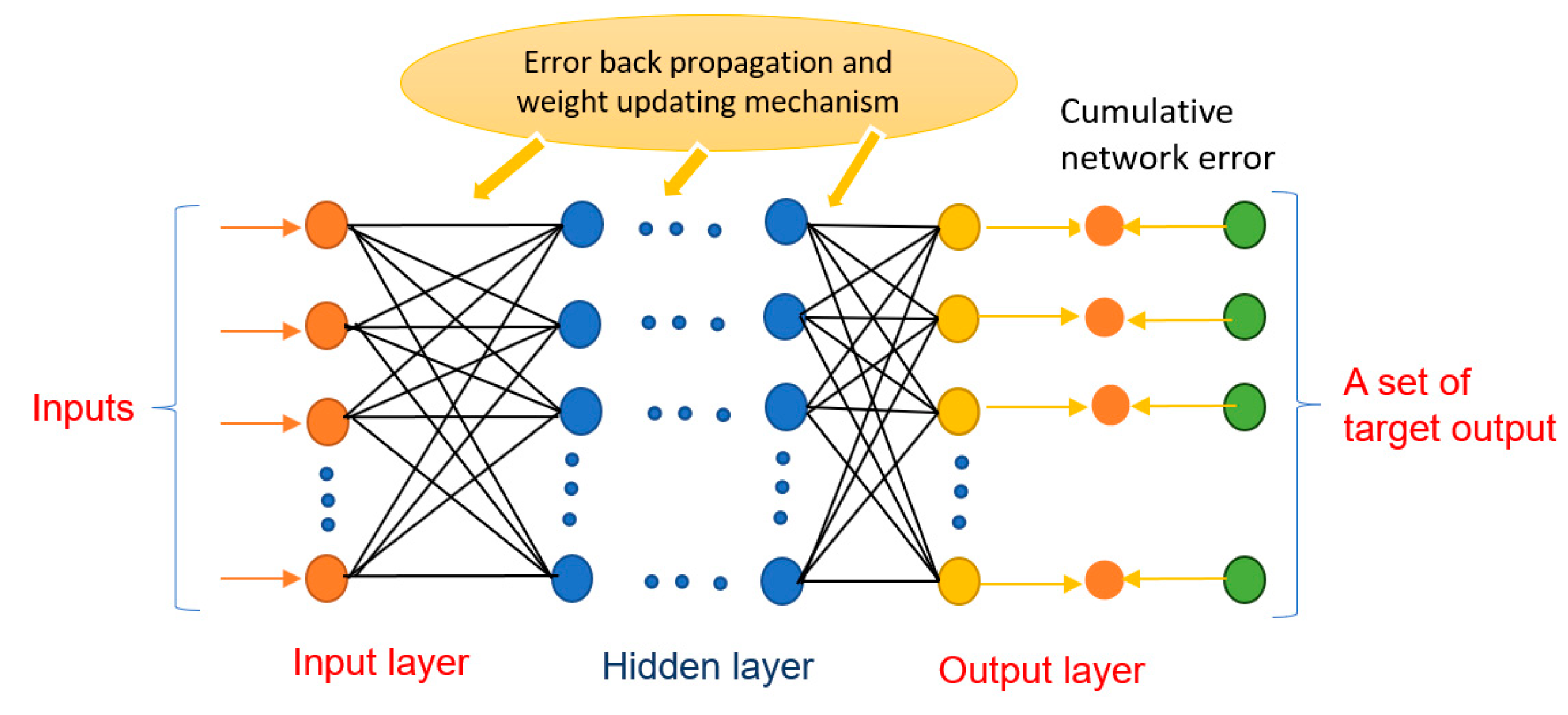
3.1. Artificial Neural Network Fundamental
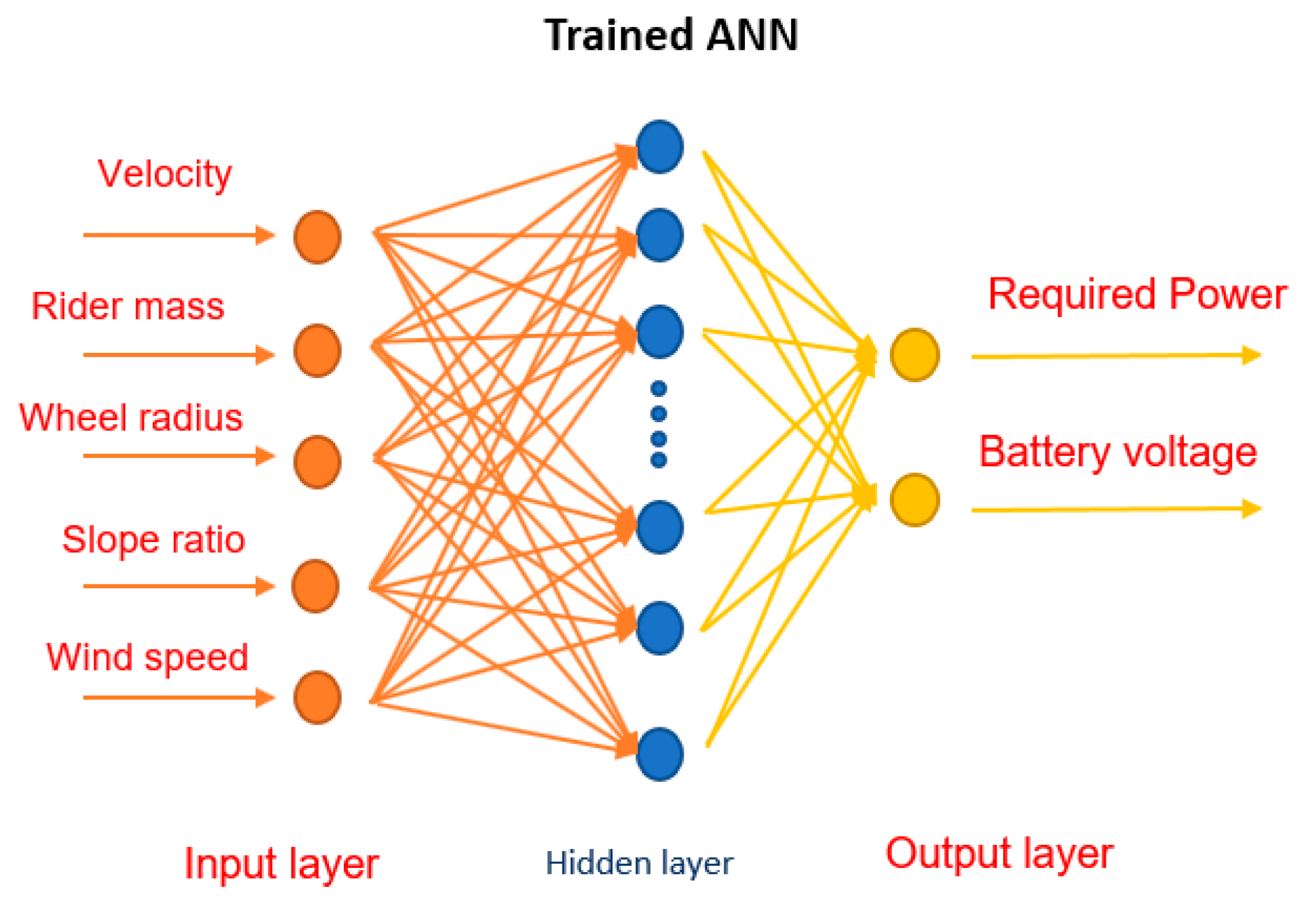
3.2. Development of ANN Model
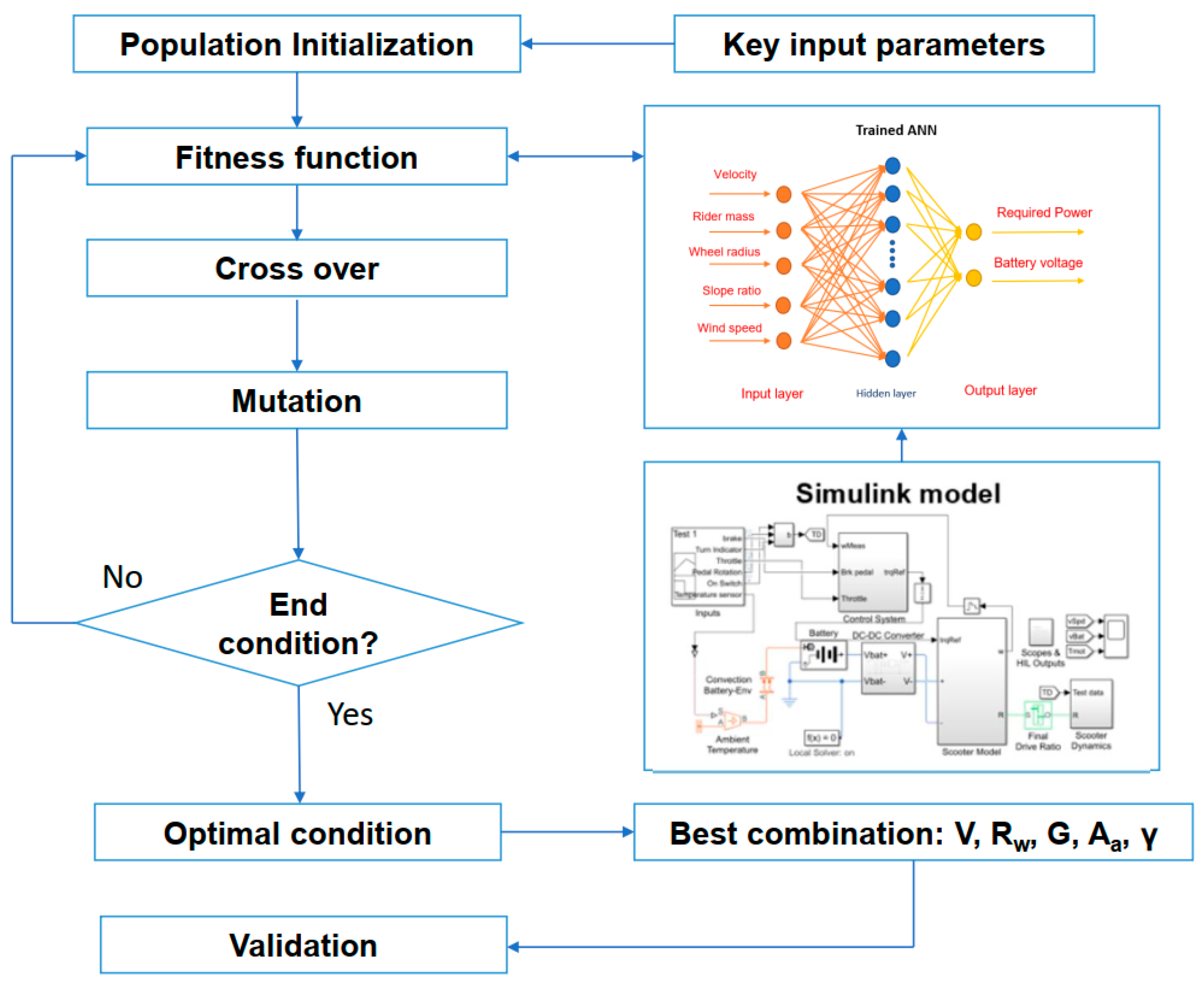
3.3. Genetic Optimization Algorithm
3.4. Model Creation
4. Results and Discussion
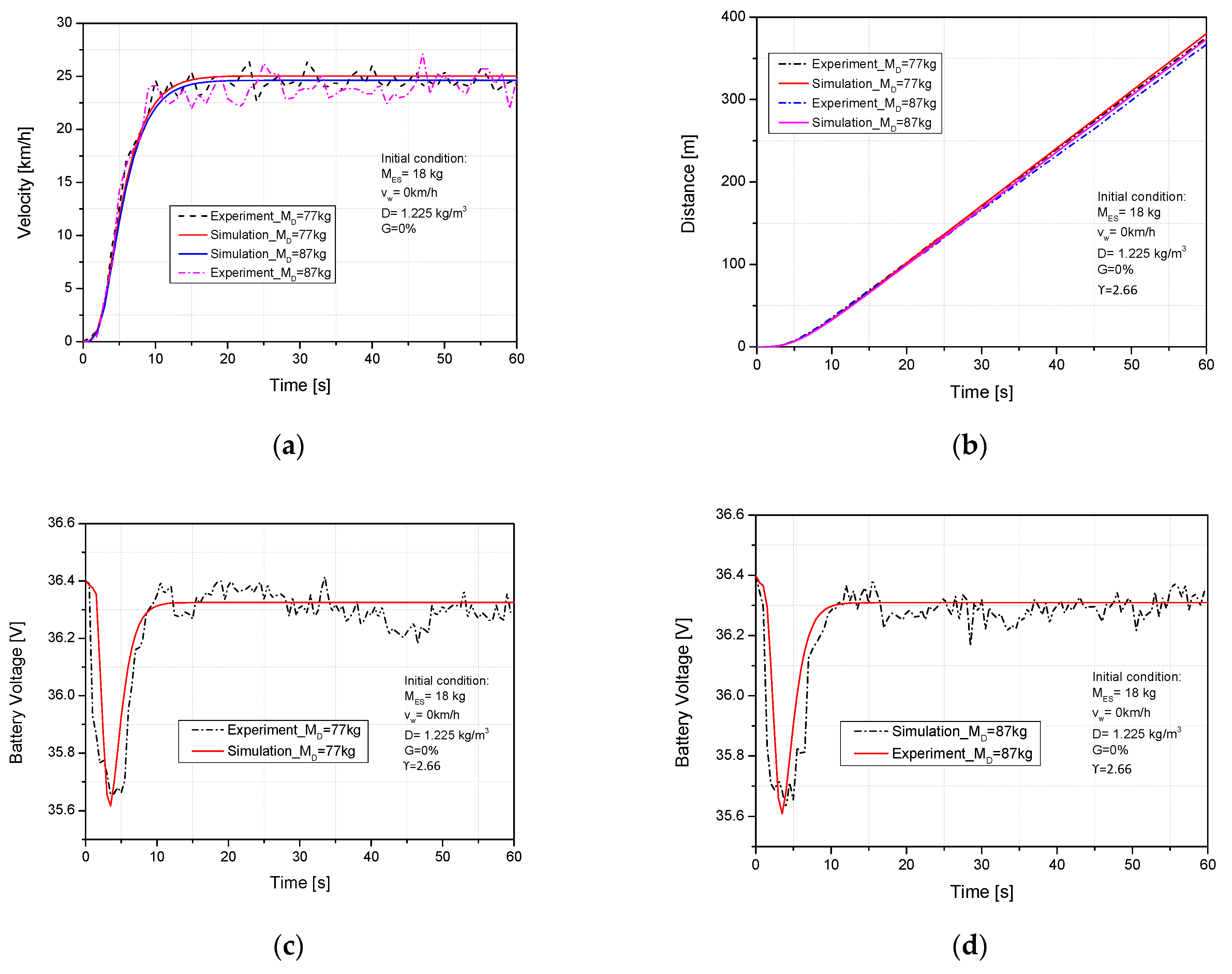
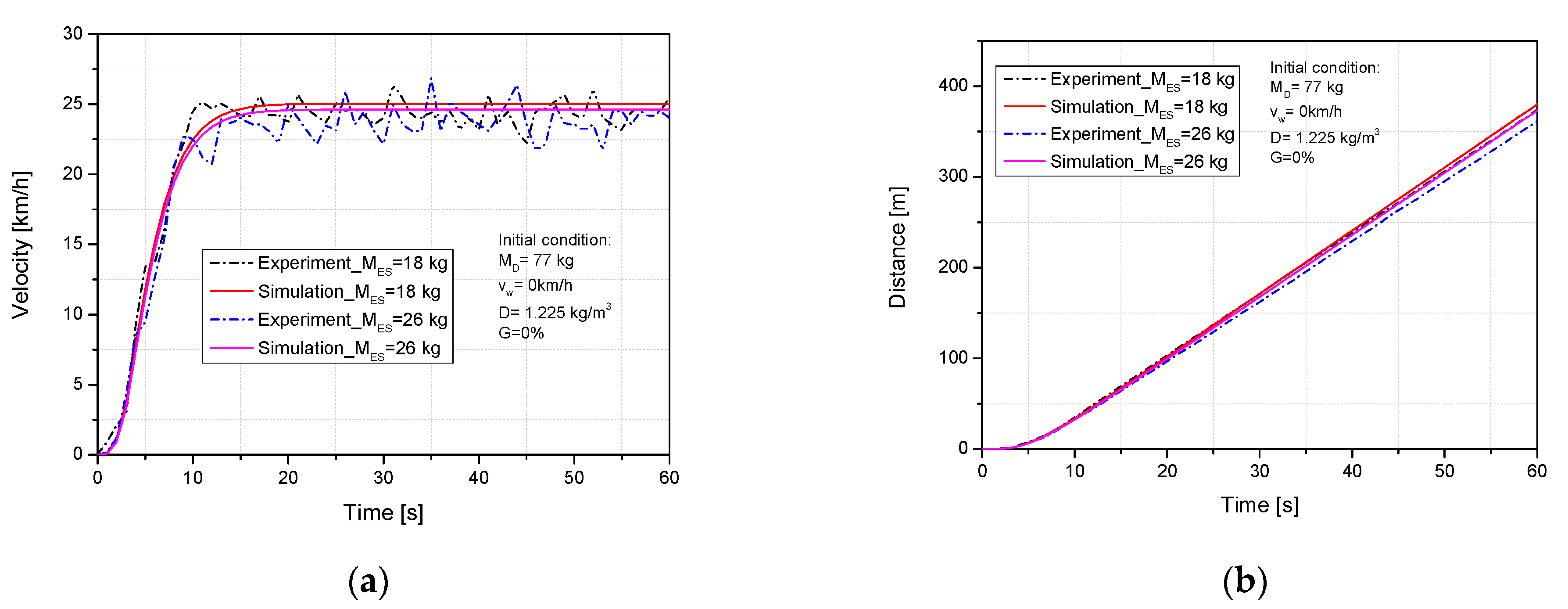
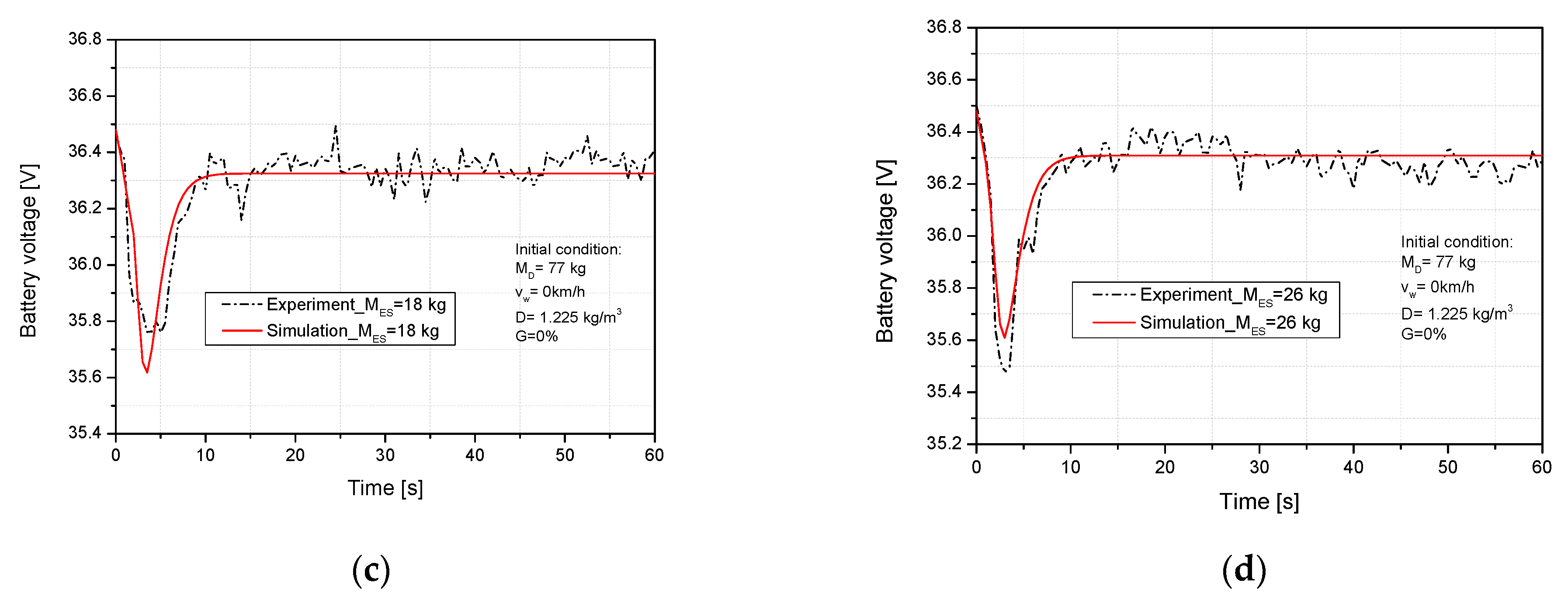
4.1. Validated Data
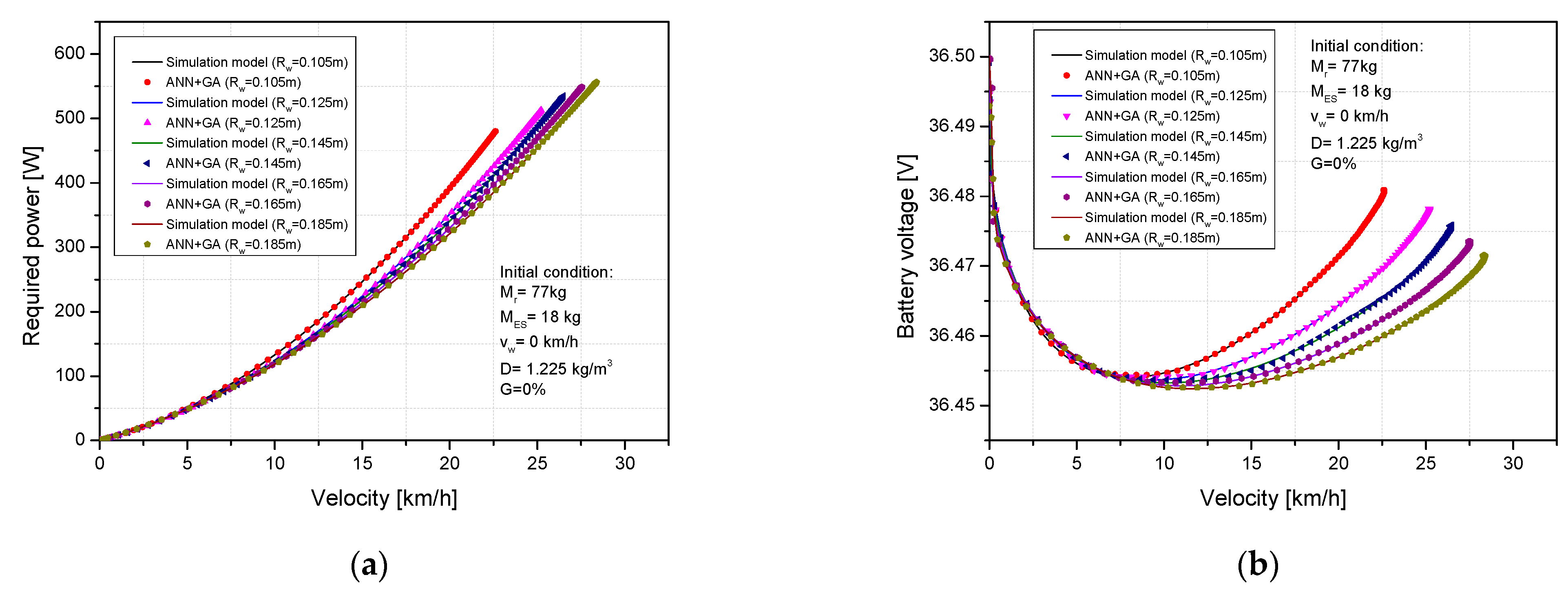
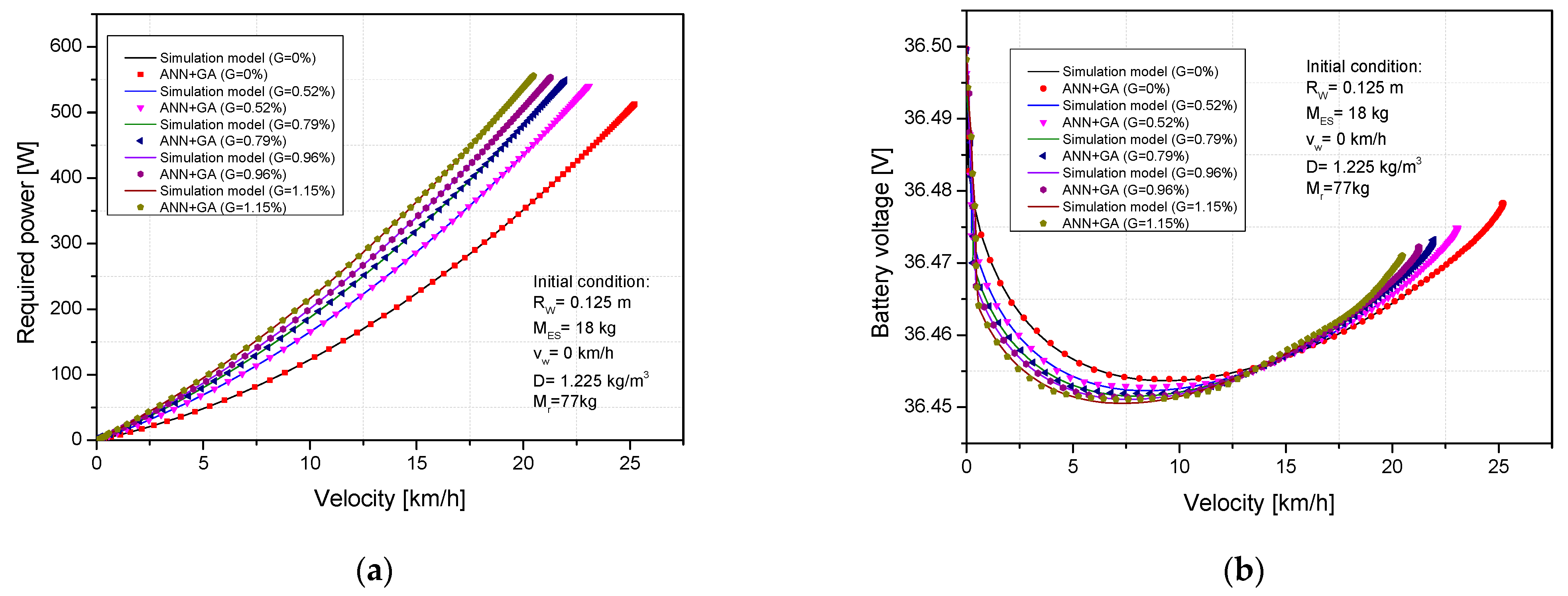
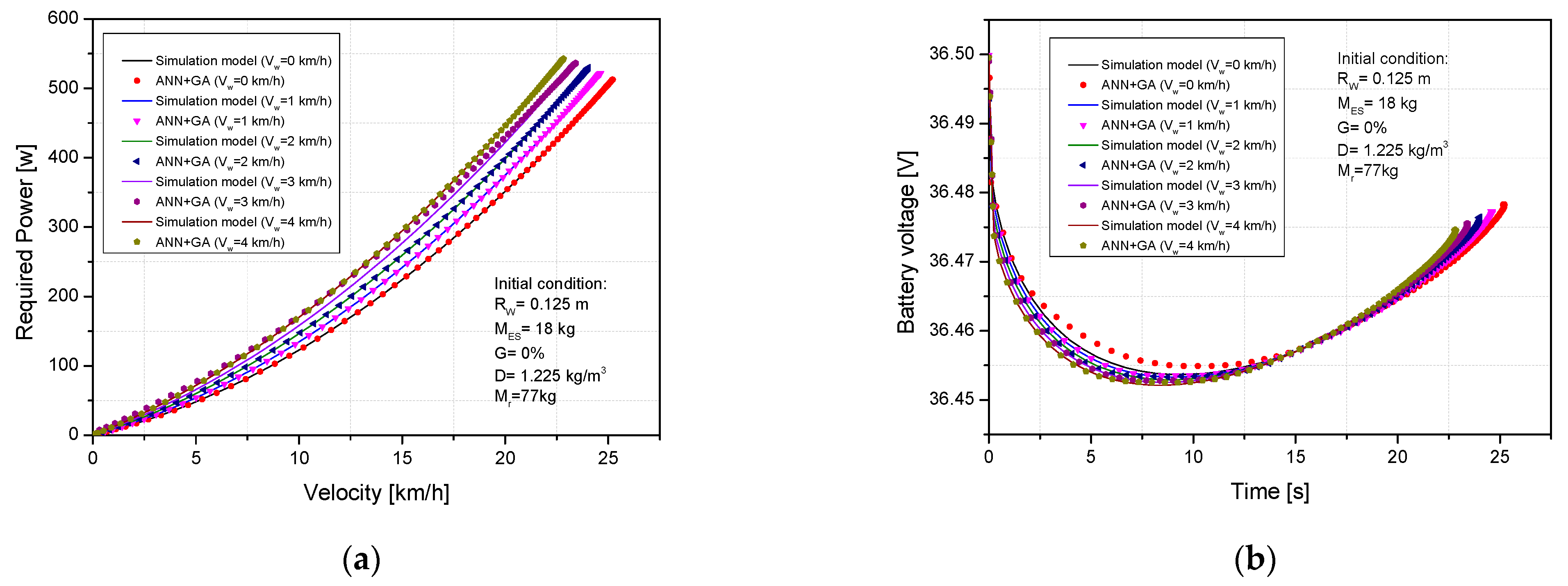
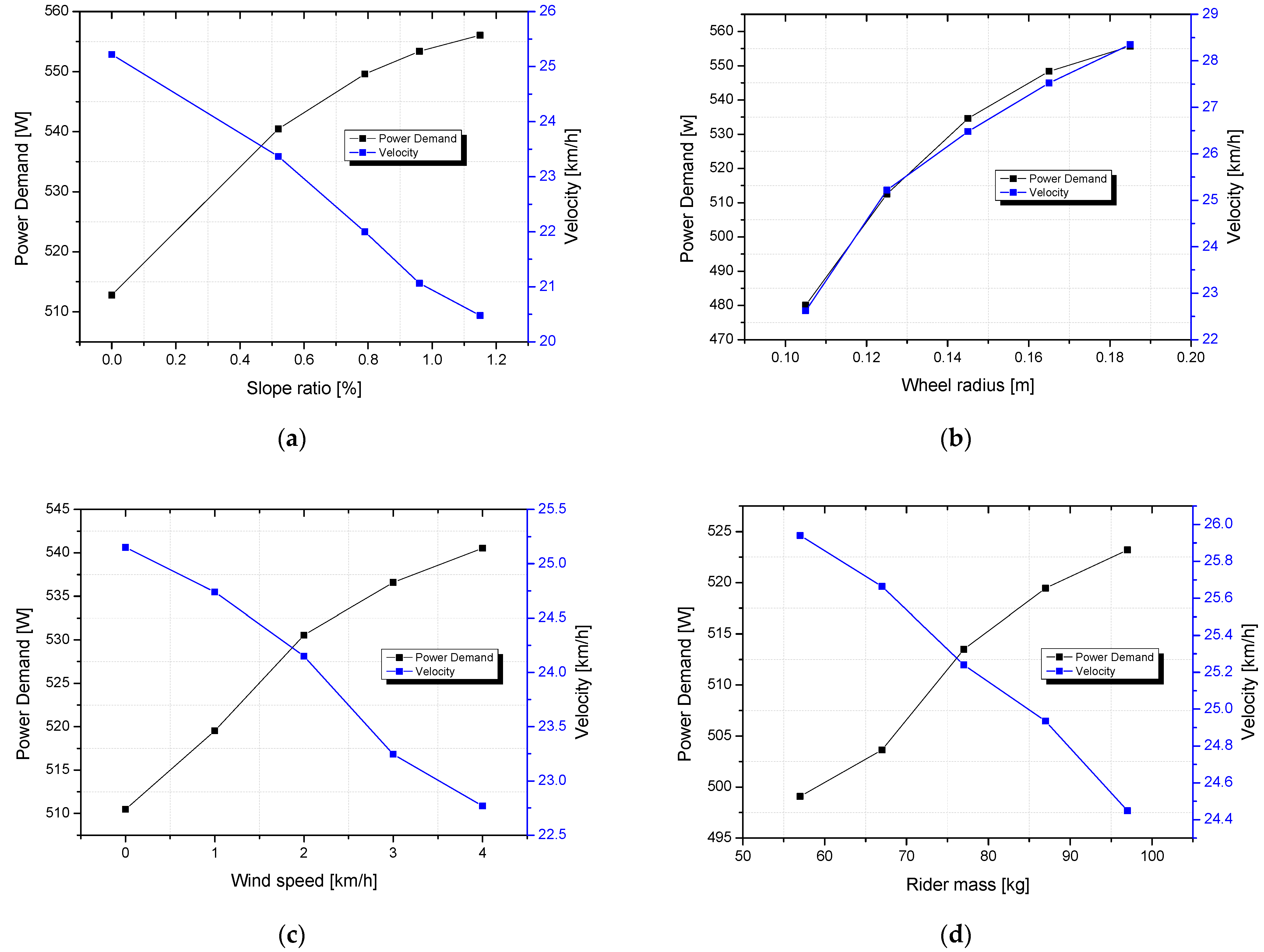
4.2. Prediction of Power Demand and Electricity Consumption under the Influence of Structure and Operating Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | |
| ANN | Artificial neural network |
| ES | Electric scooter |
| GA | Genetic algorithm |
| LIB | Lithium-ion battery |
| NOx | Nitrogen oxides |
| HC | hydrocarbons |
| CO2 | Carbon dioxide |
| CO | Carbon monoxide |
| PV | Photovoltaic |
| MSE | Mean square error |
| ECU | Electric control unit |
| LM | Levenberg-Marquardt |
| PC | Slope resistance force, N |
| Latin symbols | |
| Aa | Frontal area, m2 |
| Rw | Wheel radius, m |
| Ca | Coefficient of aerodynamic drag |
| Crr | Colling coefficient |
| Cs | Slope coefficient |
| Tpf | Propulsion torque, N |
| Tm | Moment motor, N.m |
| M | Scooter and rider mass, Kg |
| Fpf | Propulsion force, N |
| Frrf | Rolling resistance force, N |
| Fsrf | Slope resistance force, N |
| Fwrf | Wind resistance force, N |
| La | Armature inductance, H |
| Ec | The back emf |
| Ra | Armature resistance, ohm |
| ia | Armature current, A |
| Ua | Terminal voltage of motor, V |
| Tl | Load torque, N.m |
| Te | Electromechanical torque, N.m |
| Ta | Acceleration torque, N.m |
| J | Inertia torque, N.m |
| B1 | Viscous friction coefficient |
| wm | Motor speed, rpm |
| Kb | Torque constant, N.m |
| Total power of battery, W | |
| Total power to propel vehicle, W | |
| Power loss by internal resitance, W | |
| Total resistive power, W | |
| Loss in power transmission | |
| Current of battery, A | |
| Open circuit voltage, V | |
| Battery available energy | |
| Terminal voltage. V | |
| Pfriction | Friction power, W |
| Pgrade | Slope grade power, W |
| Pwind | Wind power |
| t | Time, s |
| b | Bias value of neuron |
| xi | Input value if neuron |
| wi | Linked weight of neuron |
| p | The number of inputs |
| Greek symbols | |
| α | Slope ratio |
| Air density, kg/m3 | |
References
- Röck, M.; Saade, M.R.M.; Balouktsi, M.; Rasmussen, F.N.; Birgisdottir, H.; Frischknecht, R.; Habert, G.; Lützkendorf, T.; Passer, A. Embodied GHG emissions of buildings—The hidden challenge for effective climate change mitigation. Appl. Energy 2020, 258, 114107. [Google Scholar] [CrossRef]
- Ylä-Anttila, T.; Gronow, A.; Stoddart, M.C.J.; Broadbent, J.; Schneider, V.; Tindall, D.B. Climate change policy networks: Why and how to compare them across countries. Energy Res. Soc. Sci. 2018, 45, 258–265. [Google Scholar] [CrossRef]
- Shafique, M.; Azam, A.; Rafiq, M.; Luo, X. Life cycle assessment of electric vehicles and internal combustion engine vehicles: A case study of Hong Kong. Res. Transp. Econ. 2022, 92, 101112. [Google Scholar] [CrossRef]
- Breuer, J.L.; Samsun, R.C.; Stolten, D.; Peters, R. How to reduce the greenhouse gas emissions and air pollution caused by light and heavy duty vehicles with battery-electric, fuel cell-electric and catenary trucks. Environ. Int. 2021, 152, 106474. [Google Scholar] [CrossRef] [PubMed]
- Tutak, M.; Brodny, J. Analysis of the level of energy security in the three seas initiative countries. Appl. Energy 2022, 311, 118649. [Google Scholar] [CrossRef]
- Kamyk, J.; Kot-Niewiadomska, A.; Galos, K. The criticality of crude oil for energy security: A case of Poland. Energy 2021, 220, 119707. [Google Scholar] [CrossRef]
- Foissaud, N.; Gioldasis, C.; Tamura, S.; Christoforou, Z.; Farhi, N. Free-floating e-scooter usage in urban areas: A spatiotemporal analysis. J. Transp. Geogr. 2022, 100, 103335. [Google Scholar] [CrossRef]
- Stefan, G. Integrating e-scooters in urban transportation: Problems, policies, and the prospect of system change. Transp. Res. Part D Transp. Environ. 2020, 79, 102230. [Google Scholar]
- Lee, M.; Chow, J.Y.J.; Yoon, G.; He, B.Y. Forecasting e-scooter substitution of direct and access trips by mode and distance. Transp. Res. Part D Transp. Environ. 2021, 96, 102892. [Google Scholar] [CrossRef]
- Rehborn, H.; Koller, M.; Kaufmann, S. Data-Driven Traffic Engineering: Understanding of Traffic and Applications Based on Three-Phase Traffic Theory; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Hichem, C.; Abdelfatah, N.; Kayisli, K. A Novel Method of Electric Scooter Torque Estimation Using the Space Vector Modulation Control. Int. J. Renew. Energy Dev. 2021, 10, 355–364. [Google Scholar] [CrossRef]
- Yuniarto, M.N.; Wiratno, S.E.; Nugraha, Y.U.; Sidharta, I.; Nasruddin, A. Modeling, Simulation, and Validation of An Electric Scooter Energy Consumption Model: A Case Study of Indonesian Electric Scooter. IEEE Access 2022, 10, 48510–48522. [Google Scholar] [CrossRef]
- Garman, C.M.; Como, S.G.; Campbell, I.C.; Wishart, J.; O’Brien, K.; McLean, S. Micro-Mobility Vehicle Dynamics and Rider Kinematics during Electric Scooter Riding; SAE Technical Paper 2020-01-0935; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Hu, J.-S.; Lu, F.; Zhu, C.; Cheng, C.-Y.; Chen, S.-L.; Ren, T.-J.; Mi, C.C. Hybrid Energy Storage System of an Electric Scooter Based on Wireless Power Transfer. IEEE Trans. Ind. Inform. 2018, 14, 4169–4178. [Google Scholar] [CrossRef]
- Di Giorgio, P.; Di Ilio, G.; Jannelli, E.; Conte, F.V. Numerical analysis of an energy storage system based on a metal hydride hydrogen tank and a lithium-ion battery pack for a plug-in fuel cell electric scooter. Int. J. Hydrogen Energy 2023, 48, 3552–3565. [Google Scholar] [CrossRef]
- Zhu, R.; Kondor, D.; Cheng, C.; Zhang, X.; Santi, P.; Wong, M.S.; Ratti, C. Solar photovoltaic generation for charging shared electric scooters. Appl. Energy 2022, 313, 118728. [Google Scholar] [CrossRef]
- Martínez-Navarro, A.; Cloquell-Ballester, V.-A.; Segui-Chilet, S. Photovoltaic Electric Scooter Charger Dock for the Development of Sustainable Mobility in Urban Environments. IEEE Access 2020, 8, 169486–169495. [Google Scholar] [CrossRef]
- Issi, F.; Kaplan, O. Simulation of a Wireless Charging Multiple E-Scooters using PV Array with Class-E Inverter Fed by PI Controlled Boost Converter for Constant Output Voltage. In Proceedings of the 10th International Conference on Smart Grid 2022, Istanbul, Turkey, 27–29 June 2022; pp. 61–65. [Google Scholar]
- Doubabi, H.; Oublaid, Y.; Salhi, I.; Chennani, M.; Essounbouli, N. A Reliable Power Management Strategy of a PV-Based Electric Scooters Charging Station. In Proceedings of the 7th International Conference on Optimization and Applications 2021, Wolfenbüttel, Germany, 19–20 May 2021; pp. 1–6. [Google Scholar]
- Hieu, L.T.; Khoa, N.X.; Lim, O.T. An investigation on the effective performance area of the electric bicycle with variable key input parameters. J. Clean. Prod. 2021, 321, 128862. [Google Scholar] [CrossRef]
- Hieu, L.T.; Lim, O.T. Effects of the Structure and Operating Parameters on the Performance of an Electric Scooter. Sustainability 2023, 15, 8976. [Google Scholar] [CrossRef]
- Hieu, L.T.; Khoa, N.X.; Lim, O.T. An Investigation on the Effects of Input Parameters on the Dynamic and Electric Consumption of Electric Motorcycles. Sustainability 2021, 13, 7285. [Google Scholar] [CrossRef]
- Channapattana, S.V.; Pawar, A.A.; Kamble, P.G. Optimisation of operating parameters of DI-CI engine fueled with second generation Bio-fuel and development of ANN based prediction model. Appl. Energy 2017, 187, 84–95. [Google Scholar] [CrossRef]
- Pai, P.S.; Rao, B.S. Artificial Neural Network based prediction of performance and emission characteristics of a variable compression ratio CI engine using WCO as a biodiesel at different injection timings. Appl. Energy 2011, 88, 2344–2354. [Google Scholar]
- Liu, X.; Fotouhi, A. Formula-E race strategy development using artificial neural networks and Monte Carlo tree search. Neural Comput. Appl. 2020, 32, 15191–15207. [Google Scholar] [CrossRef]
- Seo, J.; Park, S. Optimizing model parameters of artificial neural networks to predict vehicle emissions. Atmos. Environ. 2023, 294, 119508. [Google Scholar] [CrossRef]
- Yang, R.; Yan, Y.; Sun, X.; Wang, Q.; Zhang, Y.; Fu, J.; Liu, Z. An Artificial Neural Network Model to Predict Efficiency and Emissions of a Gasoline Engine. Processes 2022, 10, 204. [Google Scholar] [CrossRef]
- Carr, J. An introduction to genetic algorithms. Sr. Proj. 2014, 1, 7. [Google Scholar]
- Hieu, L.T.; Lim, O.T. A deep learning approach for optimize dynamic and required power in electric assisted bicycle under a structure and operating parameters. Appl. Energy 2023, 347, 121457. [Google Scholar] [CrossRef]





| Parameters | Value |
|---|---|
| ES mass | 18 kg |
| Radius of wheel | 0.125 m |
| Motor power | 250 W |
| Battery type | Rechargeable Li-ion |
| Battery voltage | 36 V |
| Battery capacity | 10 Ah |
| Type of network Function for training Function for learning Transfer function Performance function | Feedforward back propagation Levenberg–Marquardt LEARNDGM Mean squared error Tan sigmoid |
| Data selection | Training data set: 70% Training (randomly selected) Validation data set: 15% validation (randomly selected) Test data set: 15% test (randomly selected) |
| Input parameters | Wheel radius, scooter velocity, mass, slope ratio, wind speed |
| Output parameters | Required power, battery voltage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hieu, L.T.; Lim, O.T. A Deep Learning Approach to Optimize the Performance and Power Demand of Electric Scooters under the Effect of Operating and Structure Parameters. Energies 2024, 17, 427. https://doi.org/10.3390/en17020427
Hieu LT, Lim OT. A Deep Learning Approach to Optimize the Performance and Power Demand of Electric Scooters under the Effect of Operating and Structure Parameters. Energies. 2024; 17(2):427. https://doi.org/10.3390/en17020427
Chicago/Turabian StyleHieu, Le Trong, and Ock Taeck Lim. 2024. "A Deep Learning Approach to Optimize the Performance and Power Demand of Electric Scooters under the Effect of Operating and Structure Parameters" Energies 17, no. 2: 427. https://doi.org/10.3390/en17020427
APA StyleHieu, L. T., & Lim, O. T. (2024). A Deep Learning Approach to Optimize the Performance and Power Demand of Electric Scooters under the Effect of Operating and Structure Parameters. Energies, 17(2), 427. https://doi.org/10.3390/en17020427





