Innovative Transformer Life Assessment Considering Moisture and Oil Circulation
Abstract
:1. Introduction
2. Laboratory Experiments
2.1. Preparation and Pretreatment of Insulation Samples
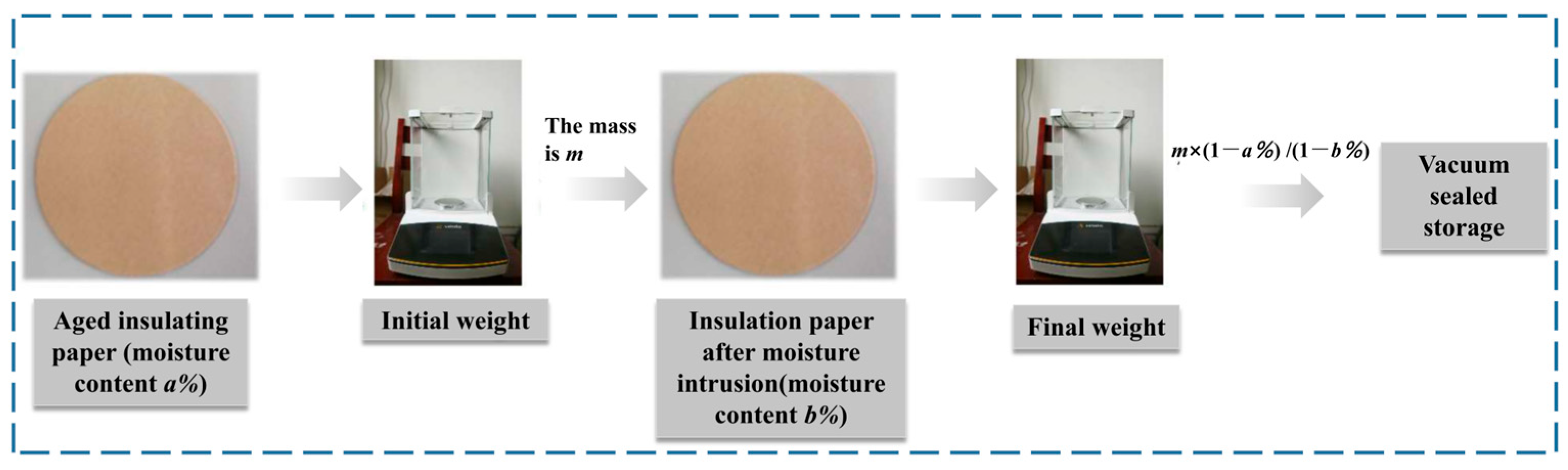
2.2. Moisture Intrusion Experiments
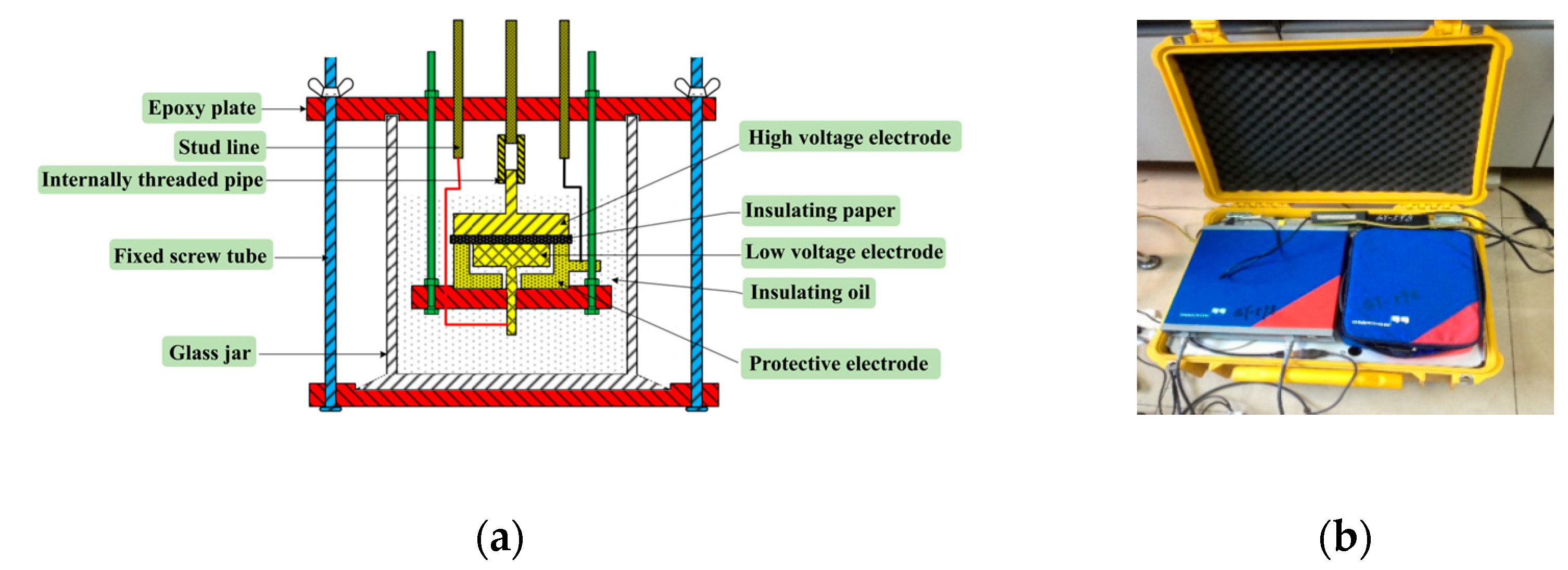
2.3. Frequency Domain Spectroscopy Measurements
2.4. Accelerated Thermal Aging Experiments
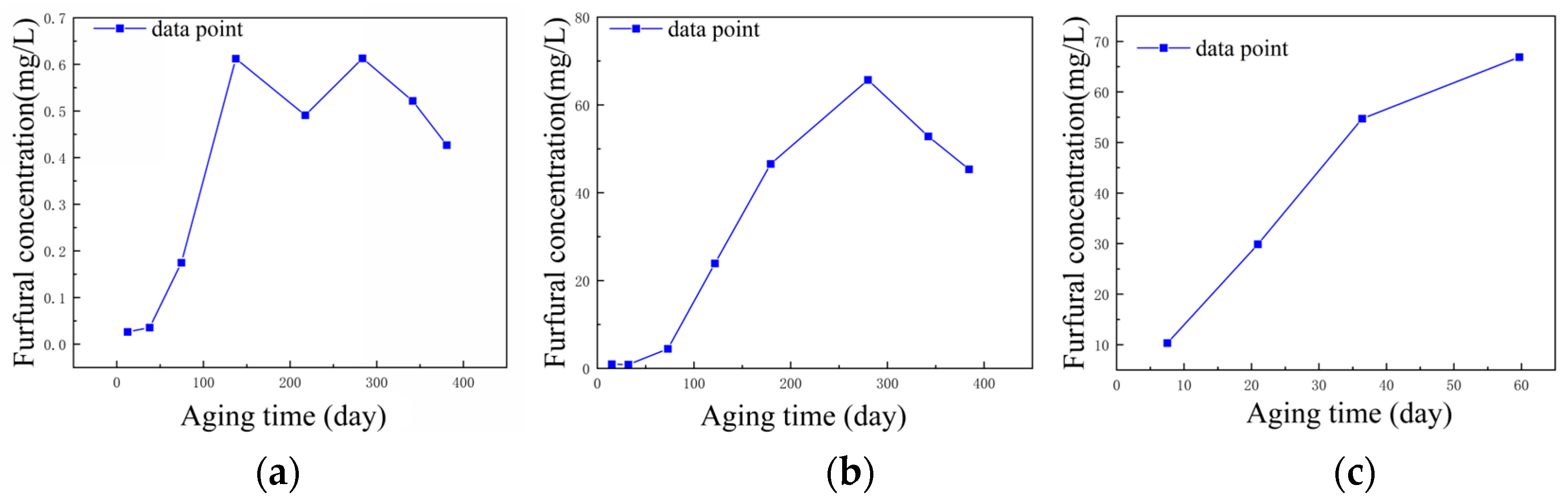
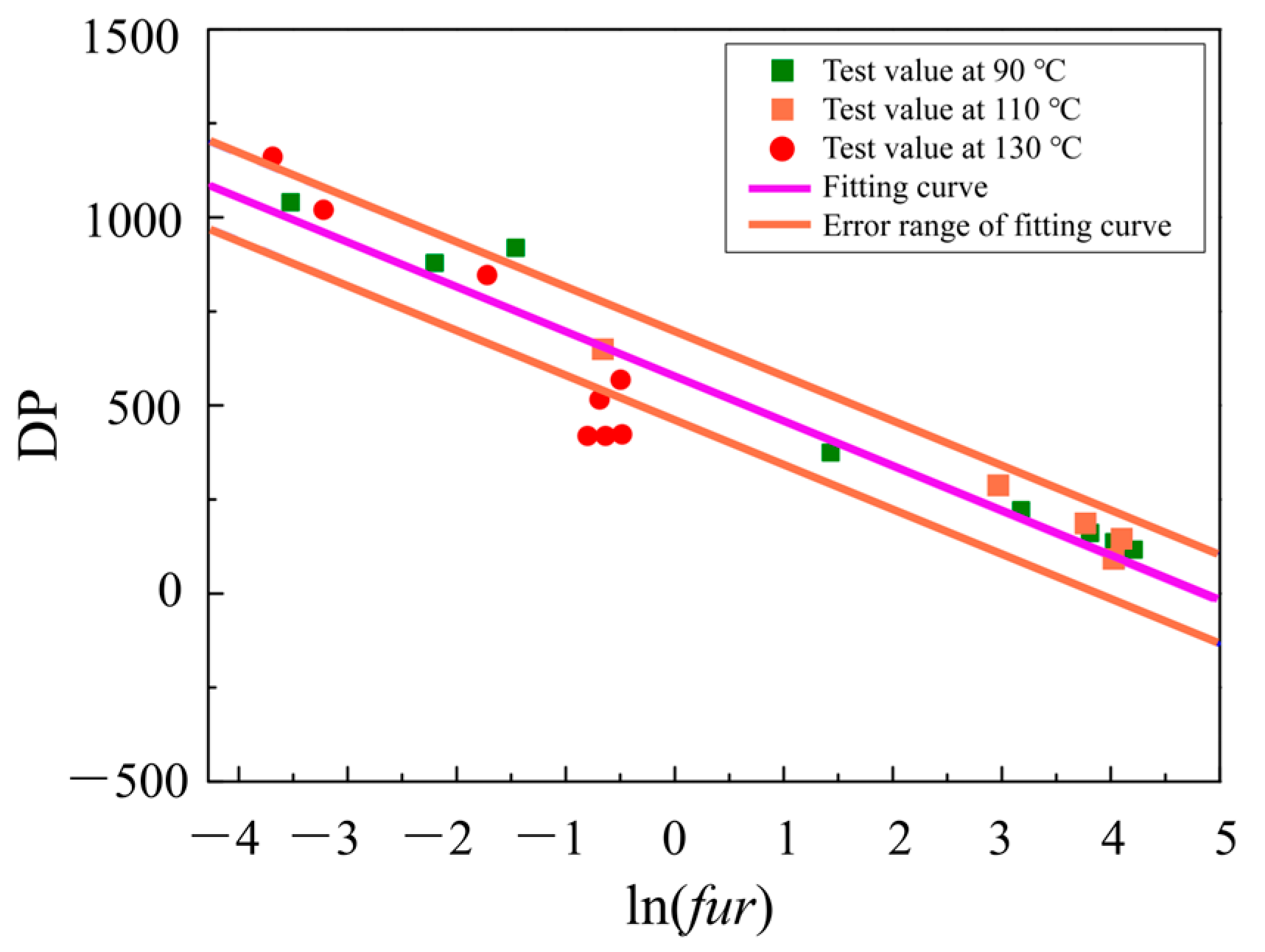
3. Average Polymerization Degree Evaluation of Insulating Pressboard Based on Furfural Content
4. Calculation of Hotspot Temperature under Different Oil Circulation Cooling Modes
4.1. Natural Oil Circulation Cooling Mode
4.2. Forced Oil Circulation Cooling Mode
4.3. Forced Oil Circulation Guided Cooling Mode
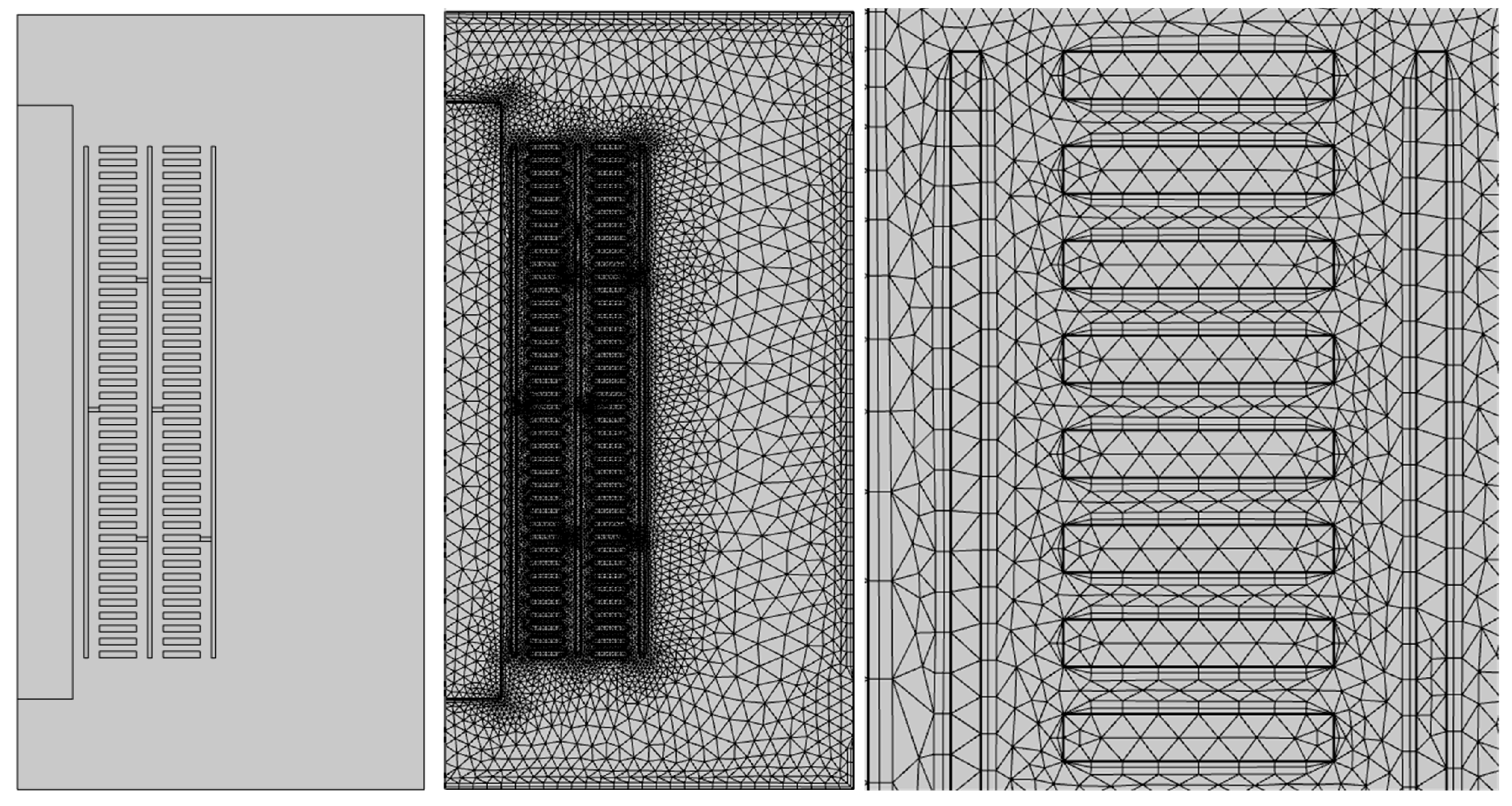
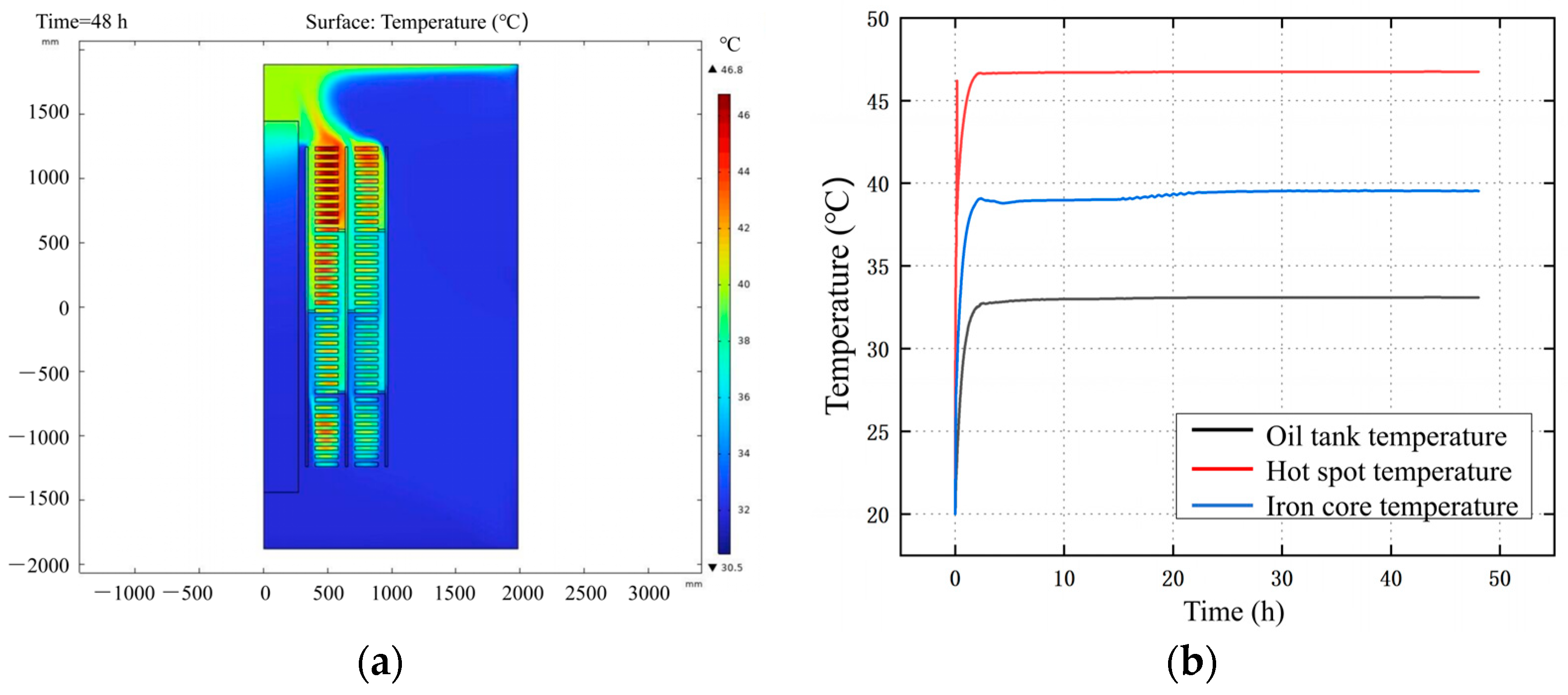
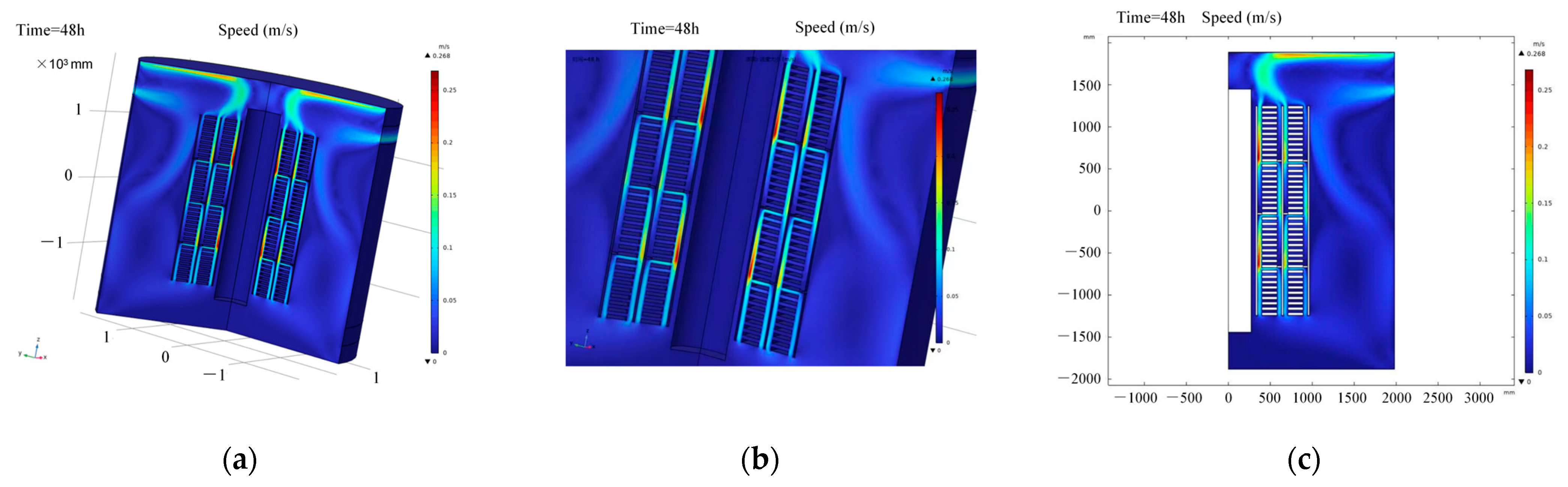
4.4. Simulation of Temperature Field in a Forced-Directed-Oil and Forced-Air Cooled (ODAF) Transformer
5. Moisture Evaluation of Insulating Papers Based on FDS Technology
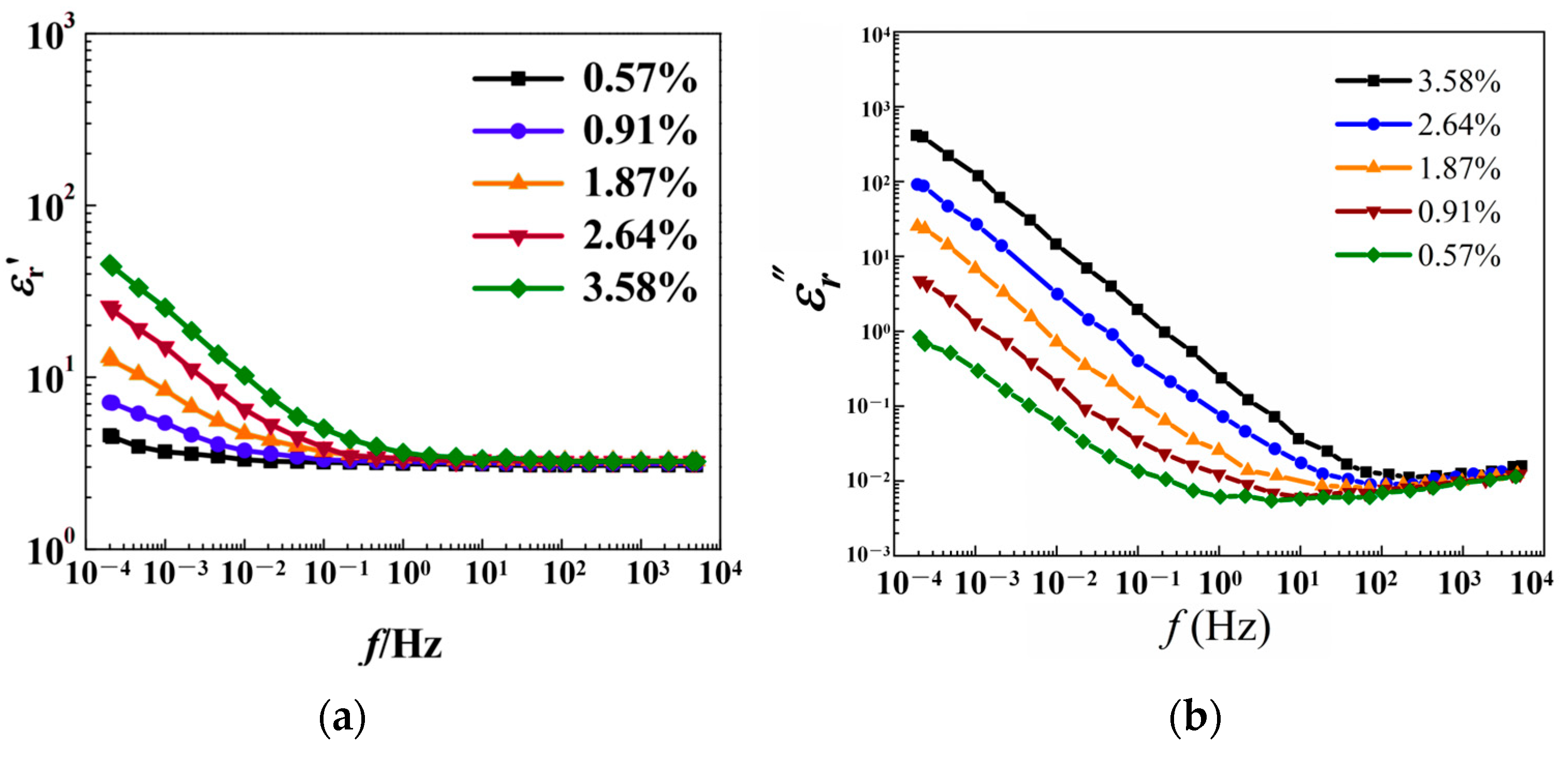
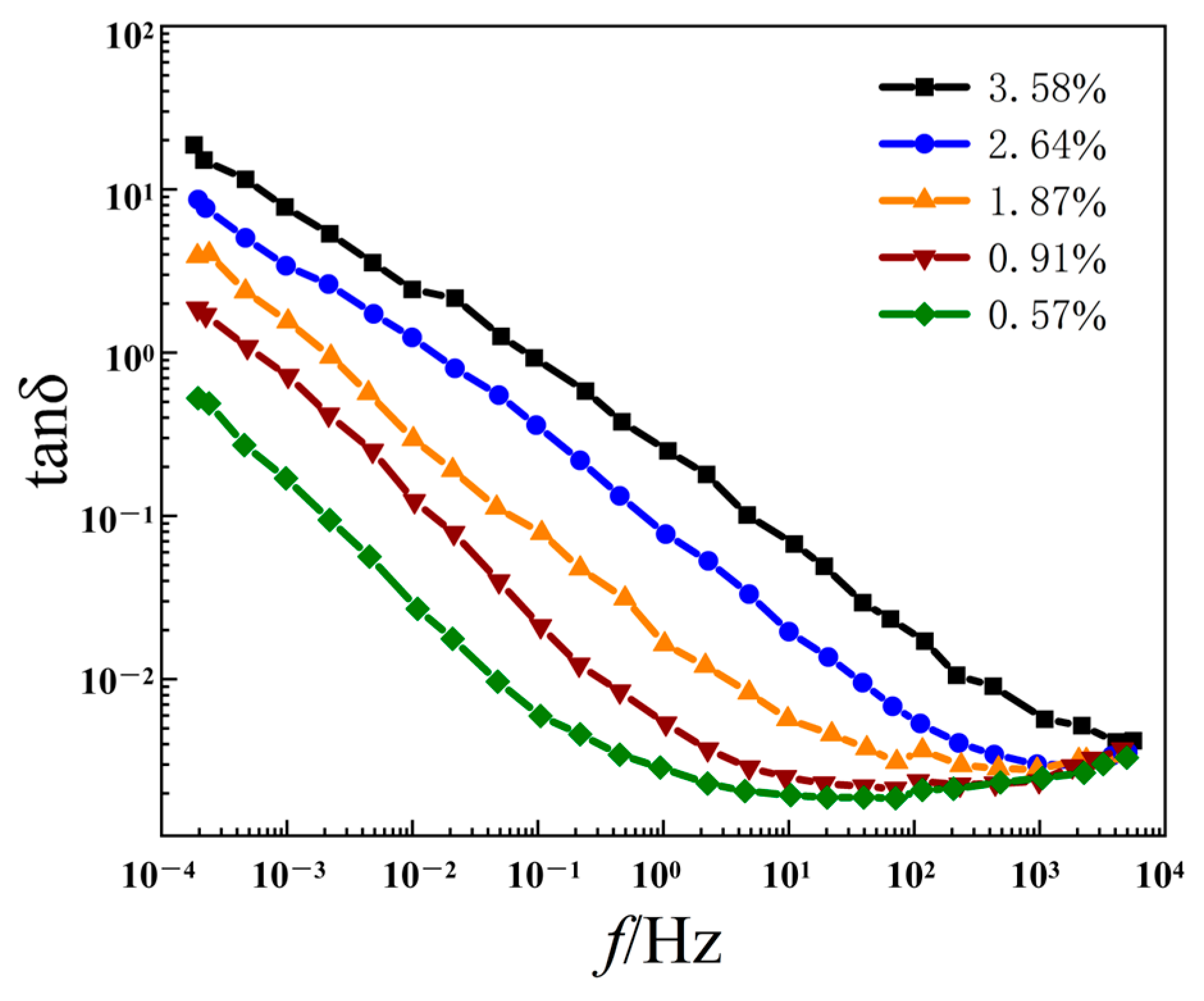
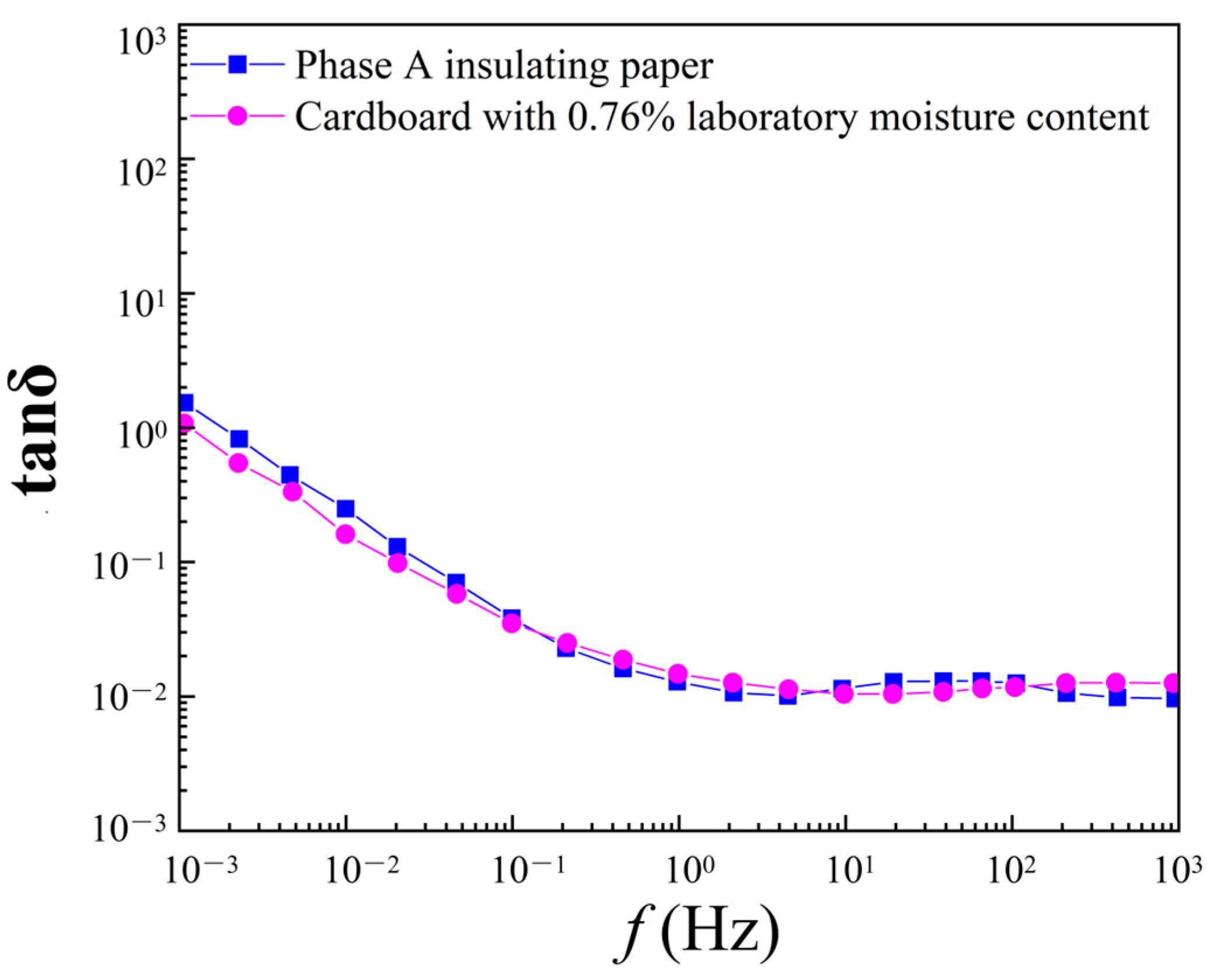
5.1. Effect of Moisture Content on the FDS Curve
5.2. Parameter Extraction Method of Frequency Domain Spectroscopy Characteristic
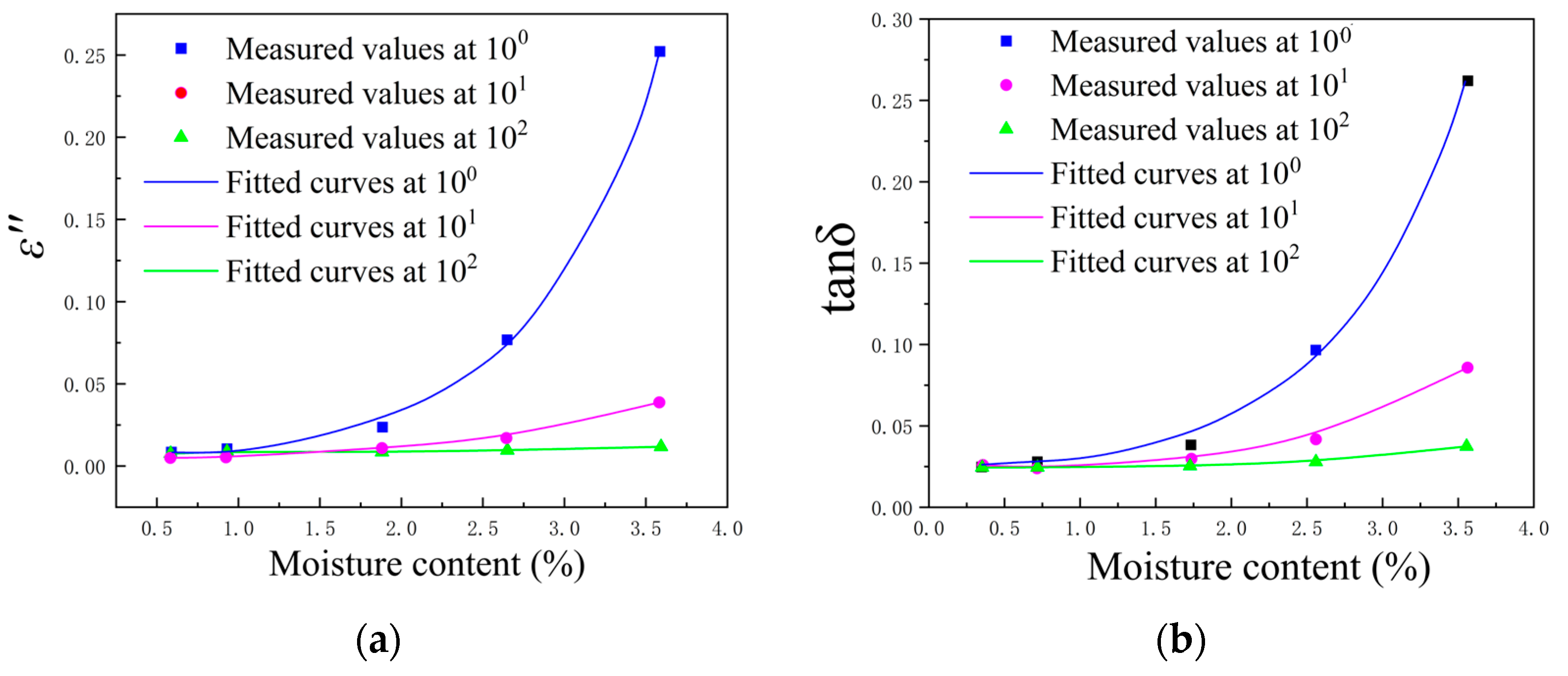
5.3. Assessment of Moisture Content
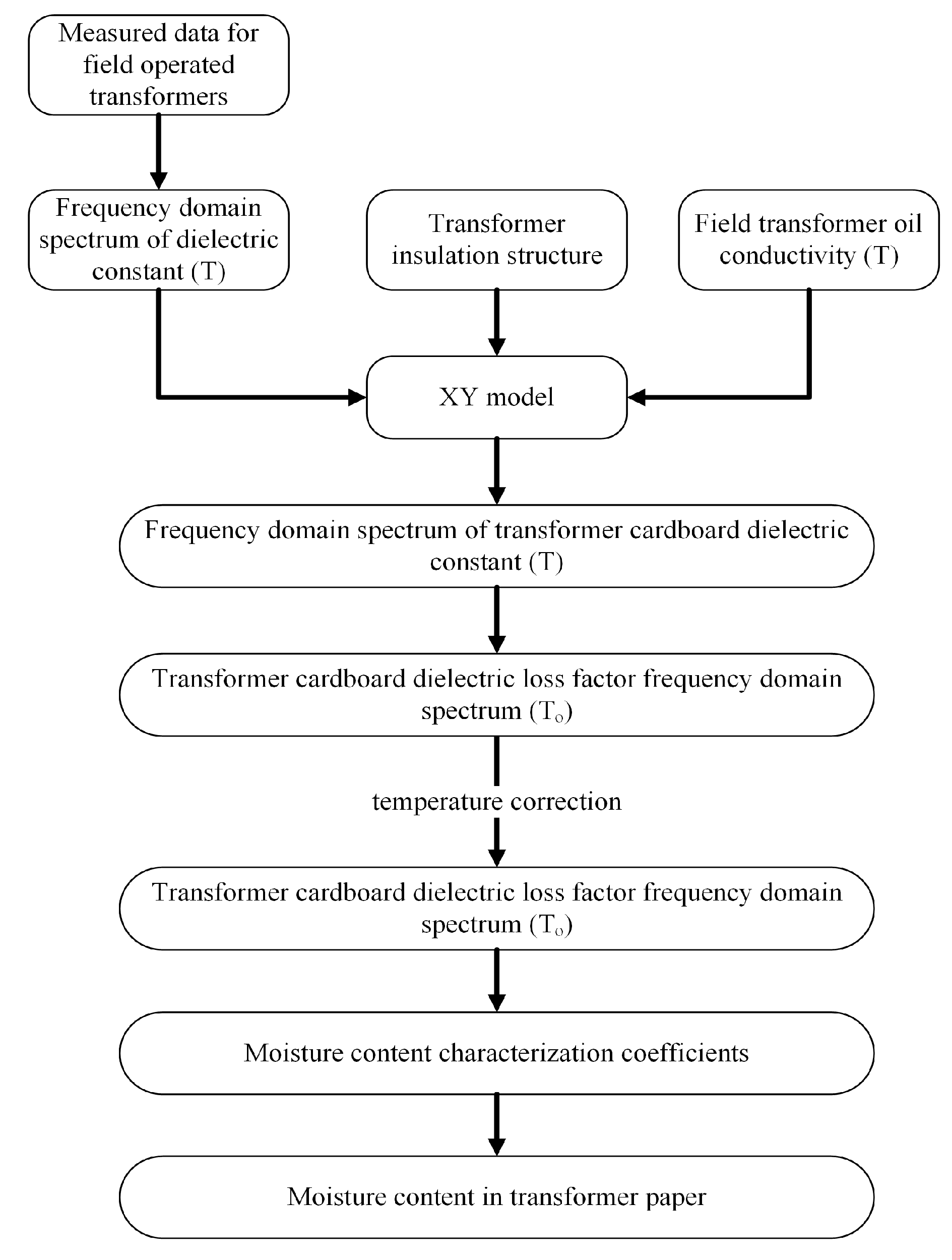
5.4. Moisture Assessment of On-Site Transformers
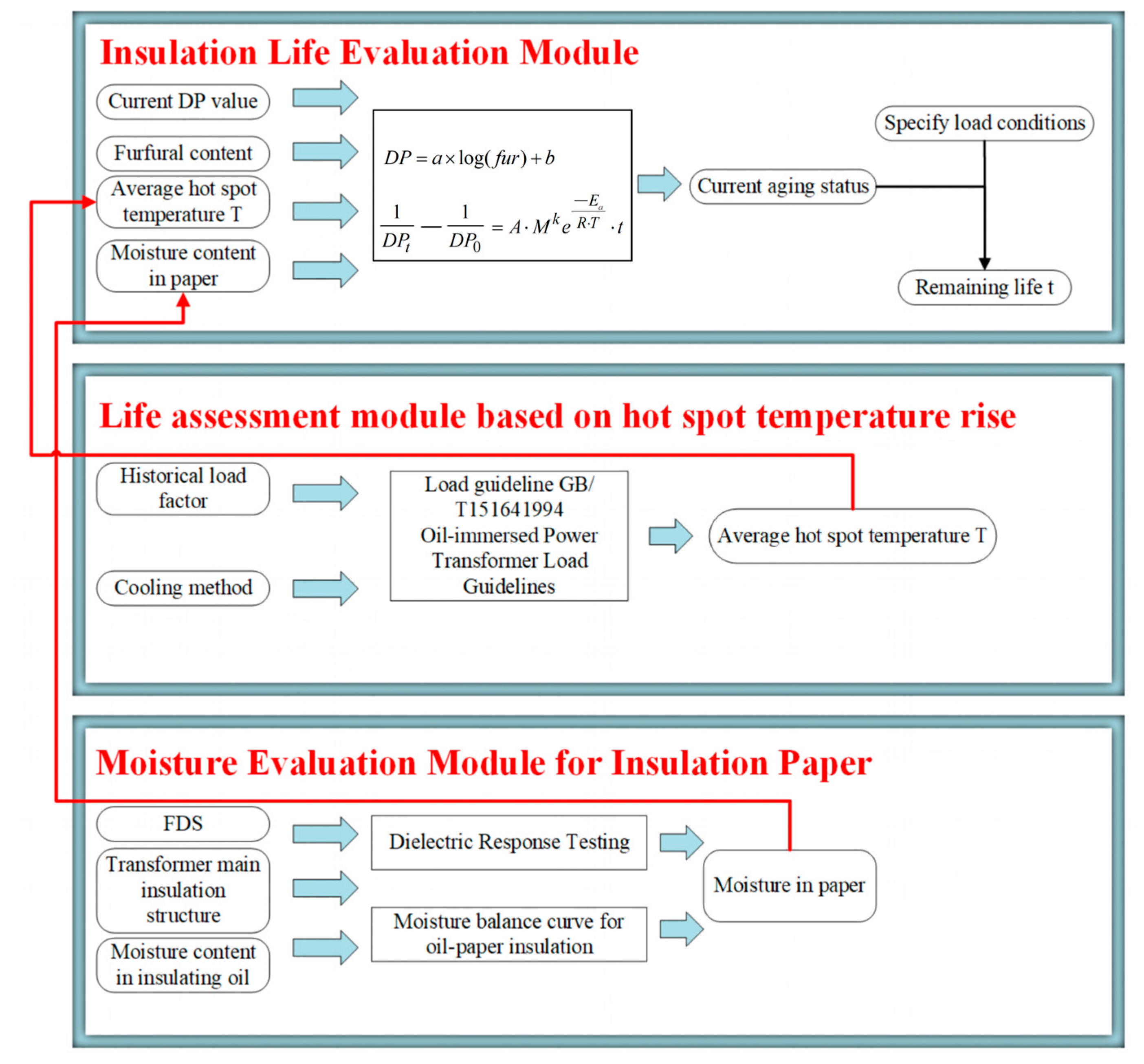
6. Life Evaluation of On-Site Transformers under the Synergistic Effect of Multiple Factors
6.1. Insulation Life Assessment Model Considering the Effects of Moisture and Temperature
6.2. Example Validation I
6.3. Example Validation II
7. Conclusions
- Based on the experimental data, the relationship between furfural content in oil and the polymerization degree of insulating paper was fitted, and a method for assessing the aging state of oil-paper insulation by furfural content in oil was proposed.
- The FDS tests were conducted in the laboratory on oil-immersed insulating papers at different moisture contents. Then, the influence of the moisture content of the insulating paper on the FDS curve was analyzed, and the characteristic parameters were extracted to assess the moisture content of the paper quantitatively.
- The time-temperature-moisture superposition method was introduced to improve oil-paper insulation’s accelerated thermal aging life prediction model. An on-site transformer life assessment method was established based on the moisture content of insulating paper, transformer load under different oil circulation cooling modes, and the time-temperature-moisture superposition life evaluation model. This method can effectively estimate the transformer insulation life with little amount of transformer insulation information. After the on-site transformer example verification, it was shown that the proposed life assessment method has high feasibility and accuracy, which makes it suitable for practical application.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jurgensen, J.H.; Nordstrom, L.; Hilber, P. Estimation of Individual Failure Rates for Power System Components Based on Risk Functions. IEEE Trans. Power Del. 2019, 34, 1599–1607. [Google Scholar] [CrossRef]
- Cheng, L.; Yu, T.; Wang, G.; Yang, B.; Zhou, L. Hot Spot Temperature and Grey Target Theory-Based Dynamic Modelling for Reliability Assessment of Transformer Oil-Paper Insulation Systems: A Practical Case Study. Energies 2018, 11, 249. [Google Scholar] [CrossRef]
- McNutt, W.J. Insulation Thermal Life Considerations for Transformer Loading Guides. IEEE Trans. Power Del. 1992, 7, 392–401. [Google Scholar] [CrossRef]
- Song, R.; Chen, W.; Yang, D.; Shi, H.; Zhang, R.; Wang, Z. Aging assessment of oil–paper insulation based on visional recognition of the dimensional expanded Raman spectra. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Jin, L.; Kim, D.; Abu-Siada, A.; Kumar, S. Oil-Immersed Power Transformer Condition Monitoring Methodologies: A Review. Energies 2022, 15, 3379. [Google Scholar] [CrossRef]
- Islam, M.M.; Lee, G.; Hettiwatte, S.N. A Review of Condition Monitoring Techniques and Diagnostic Tests for Lifetime Estimation of Power Transformers. Electr. Eng. 2018, 100, 581–605. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Li, S.; Zheng, H.; Liu, J. A Molecular Dynamics Study of the Generation of Ethanol for Insulating Paper Pyrolysis. Energies 2020, 13, 265. [Google Scholar] [CrossRef]
- Yang, Q.; Su, P.; Chen, Y. Comparison of Impulse Wave and Sweep Frequency Response Analysis Methods for Diagnosis of Transformer Winding Faults. Energies 2017, 10, 431. [Google Scholar] [CrossRef]
- Huang, W.; Shao, C.; Dong, M.; Hu, B.; Zhang, W.; Sun, Y.; Xie, K.; Li, W. Modeling the Aging-Dependent Reliability of Transformers Considering the Individualized Aging Threshold and Lifetime. IEEE Trans. Power Del. 2022, 37, 4631–4645. [Google Scholar] [CrossRef]
- Liao, R.; Sang, F.; Liu, G.; Yang, L. Study on Neutral Acid and Water Dissolved in Oil for Different Types of Oil-paper Insulation Compositions of Transformers in Accelerated Ageing Tests. Proc. CSEE 2010, 30, 125–131. [Google Scholar]
- Sedighi, A.R.; Kafiri, A.; Sehhati, M.R.; Behdad, F. Life Estimation of Distribution Transformers Using Thermography: A Case Study. Meas. J. Int. Meas. Confed. 2020, 149, 106994. [Google Scholar] [CrossRef]
- Zhang, E.; Liu, J.; Zhang, C.; Zheng, P.; Nakanishi, Y.; Wu, T. State-of-Art Review on Chemical Indicators for Monitoring the Aging Status of Oil-Immersed Transformer Paper Insulation. Energies 2023, 16, 1396. [Google Scholar] [CrossRef]
- Ariannik, M.; Razi-Kazemi, A.A.; Lehtonen, M. An Approach on Lifetime Estimation of Distribution Transformers Based on Degree of Polymerization. Reliab. Eng. Syst. Saf. 2020, 198, 106881–106889. [Google Scholar] [CrossRef]
- Heywood, R.J.; Stevens, G.C.; Ferguson, C.; Emsley, A.M. Life Assessment of Cable Paper Using Slow Thermal Ramp Methods. Thermochim. Acta 1999, 332, 189–195. [Google Scholar] [CrossRef]
- Zou, X.; Uesaka, T.; Gurnagul, N. Prediction of Paper Permanence by Accelerated Aging I. Kinetic Analysis of the Aging Process. Cellulose 1996, 3, 243–267. [Google Scholar] [CrossRef]
- Heywood, R.J.; Xiao, X.; Ali, M.; Emsley, A.M. Degradation of Cellulosic Insulation in Power Transformers. Part 3: Effects of Oxygen and Water on Ageing in Oil. IEE Proc. Sci. Meas. Technol. 2000, 147, 115–119. [Google Scholar]
- Emsley, A.M.; Ali, M.; Xiao, X.; Heywood, R.J. Degradation of Cellulosic Insulation in Power Transformers. Part 4: Effects of Ageing on the Tensile Strength of Paper. IEE Proc. Sci. Meas. Technol. 2000, 147, 285–290. [Google Scholar] [CrossRef]
- Emsley, A.M. The Kinetics and Mechanisms of Degradation of Cellulosic Insulation in Power Transformers. Polym. Degrad. Stab. 1994, 44, 343–349. [Google Scholar] [CrossRef]
- Fan, X.; Yang, S.; Lai, B.; Liu, J.; Zhang, Y.; Wang, Z. Normalization for FDS of Transformer Insulation Considering the Synergistic Effect Generated by Temperature and Moisture. IEEE Access 2020, 8, 202013–202021. [Google Scholar] [CrossRef]
- Fofana, I.; Borsi, H.; Gockenbach, E. Results on Aging of Cellulose Paper under Selective Conditions. In Proceedings of the CEIDP, Kitchener, ON, Canada, 14–17 October 2001; pp. 205–208. [Google Scholar]
- Stevens, G.C.; Emsley, A.M. Review of Chemical Indicators of Degradation of Cellulosic Electrical Paper Insulation in Oil-Filled Transformers. IEE Proc. Sci. Meas. Technol. 1994, 141, 324–334. [Google Scholar]
- Vasovic, V.; Lukic, J.; Mihajlovic, D.; Pejovic, B.; Radakovic, Z.; Radoman, U.; Orlovic, A. Aging of Transformer Insulation—Experimental Transformers and Laboratory Models with Different Moisture Contents: Part I—DP and Furans Aging Profiles. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1840–1846. [Google Scholar] [CrossRef]
- Medina, R.D.; Romero, A.A.; Mombello, E.E.; Rattá, G. Assessing Degradation of Power Transformer Solid Insulation Considering Thermal Stress and Moisture Variation. Electr. Power Syst. Res. 2017, 151, 1–11. [Google Scholar] [CrossRef]
- Saleh, N.; Azis, N.; Jasni, J.; Ab Kadir, M.Z.A.; Talib, M.A. Paper Lifetime Mathematical Modelling Based on Multi Pre-Exponential Factors for Oil-Immersed Transformer. Pertanika J. Sci. Technol. 2022, 30, 1115–1133. [Google Scholar] [CrossRef]
- Vasovic, V.; Lukic, J.; Mihajlovic, D.; Pejovic, B.; Milovanovic, M.; Radoman, U.; Radakovic, Z. Aging of Transformer Insulation of Experimental Transformers and Laboratory Models with Different Moisture Contents: Part II—Moisture Distribution and Aging Kinetics. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1847–1852. [Google Scholar] [CrossRef]
- Ariannik, M.; Razi-Kazemi, A.A.; Lehtonen, M. Effect of Cumulative Moisture Content on Degradation of Transformer Paper Insulation. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 611–618. [Google Scholar] [CrossRef]
- Srinivasan, M.; Krishnan, A. Prediction of Transformer Insulation Life with an Effect of Environmental Variables. Int. J. Comput. Appl. 2012, 55, 43–48. [Google Scholar] [CrossRef]
- Teymouri, A.; Vahidi, B. Estimation of Power Transformer Remaining Life from Activation Energy and Pre-Exponential Factor in the Arrhenius Equation. Cellulose 2019, 26, 9709–9720. [Google Scholar] [CrossRef]
- Fan, X.; Liu, J.; Goh, H.H.; Zhang, Y.; Zhang, C.; Rahman, S. Acquisition of FDS for Oil-Immersed Insulation at Transformer Hotspot Region Based on Multiconstraint NSGA Model. IEEE Trans. Ind. Electron. 2022, 69, 13625–13635. [Google Scholar] [CrossRef]
- Fan, X.; Liu, J.; Lai, B.; Zhang, Y.; Zhang, C. FDS Measurement-Based Moisture Estimation Model for Transformer Oil-Paper Insulation Including the Aging Effect. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Hernandez, G.; Ramirez, A. Dielectric Response Model for Transformer Insulation Using Frequency Domain Spectroscopy and Vector Fitting. Energies 2022, 15, 2655. [Google Scholar] [CrossRef]
- Fan, X.; Liu, J.; Zhang, Y.; Ding, Z.; Wang, Q. Polarization Loss Analysis and Ageing Characterisation of Transformer Oil-immersed Insulation by Using Decoupled Frequency Domain Spectroscopy. High Volt. 2022, 7, 575–585. [Google Scholar] [CrossRef]
- Martin, D.; Zare, F.; Caldwell, G.; McPherson, L. Calculating the Residual Life of Insulation in Transformers Connected to Solar Farms and Operated at High Load. IEEE Electr. Insul. Mag. 2020, 36, 10–20. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, J.; Wang, L.; Yuan, S.; Huang, L.; Wang, D.; Guo, L. A Method for Hot-Spot Temperature Prediction and Thermal Capacity Estimation for Traction Transformers in High-Speed Railway Based on Genetic Programming. IEEE Trans. Transport. Electrific. 2019, 5, 1319–1328. [Google Scholar] [CrossRef]
- IEEE Std C57.91™-2011; IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators. IEEE: New York, NY, USA, 2011.
- Su, Z.; Zhang, Y.; Du, Y.; Su, Y.; Deng, J.; Goh, H.H.; Yin, J.; Wang, G. An Enhanced X Model of Oil-Impregnated Paper Bushings Including Axial and Radial Nonuniform Thermal Aging. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 825–833. [Google Scholar] [CrossRef]
- Lin, Y.; Wei, C.; Tao, F.; Li, J. Aging Assessment of Oil-Paper Insulation of Power Equipment With Furfural Analysis Based on Furfural Generation and Partitioning. IEEE Trans. Power Del. 2019, 34, 1626–1633. [Google Scholar] [CrossRef]
- Yang, L. Study on Aging Characteristics of Oil-Paper in Transformer and Its Lifetime Estimation Method. Ph.D. Thesis, Chongqing University, Chongqing, China, 2009. [Google Scholar]
- Du, Y. Assessment of Moisture Status and Thermal Aging in Oil-Impregnated Paper Condenser Bushings Based on Frequency Domain Spectroscopy. Master’s Thesis, Chongqing University, Chongqing, China, 2017. [Google Scholar]
- GB/T 15164-1994; Loading Guide for Oil-Immersed Power Transformers. IEC Publishing: Geneva, Switzerland, 1994.
- Xiao, R. Temperature Field Simulation Modeling and Rapid Prediction Method of Real-time Temperature of Converter Transformer. Master’s Thesis, Chongqing University, Chongqing, China, 2022. [Google Scholar]
- Wang, Y.; Gao, J.; Liao, R.; Zhang, Y.; Hao, J.; Liu, J.; Ma, Z. Investigation of characteristic parameters for condition evaluation of transformer oil-paper insulation using frequency domain spectroscopy. Int. Trans. Electr. Energy Syst. 2015, 25, 2921–2932. [Google Scholar] [CrossRef]
- Fan, X.; Liang, F.; Luo, H.; Li, C.; Liu, J.; He, J. Adaptive-Optimization-Based Digital Simulation Database for Nonuniform Aging Diagnosis of Transformer Insulation System. IEEE Trans. Ind. Electron. 2023. [CrossRef]
- Liu, J.; Sun, T.; Fan, X.; Zhang, Y.; Lai, B. A Modified Simulation Model for Predicting the FDS of Transformer Oil-Paper Insulation Under Nonuniform Aging. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Martins, M. Study of Moisture Equilibrium in Oil-Paper System with Temperature Variation. In Proceedings of the 7th International Conference on Properties and Applications of Dielectric Materials, Nagoya, Japan, 1–5 June 2003; Volume 3, pp. 1124–1129. [Google Scholar]
- Yang, L.; Deng, B.; Liao, R.; Sun, C.; Pu, J. Improvement of Lifetime Model on Thermal Aging of Oil-paper Insulation by Time-temperature-moisture Superposition Method. Proc. Chin. Soc. Elec. Eng. 2011, 31, 196–203. [Google Scholar]
- Yang, L.; Liao, R.; Sun, C.; Sun, H. Influence of Natural Ester on Thermal Aging Characteristics of Oil-Paper in Power Transformers. Eur. Trans. Electr. Power. 2010, 20, 1223–1236. [Google Scholar] [CrossRef]


| Confidence Level (Math.) | Model Parameter | Sample Size (Statistics) | R2 | |
|---|---|---|---|---|
| a | b | |||
| 100% | −115.82 | 567.85 | 21 | 0.92 |
| 95% | −135.50 | 512.45 | 21 | / |
| 95% | −96.05 | 623.25 | 21 | / |
| Material | Components | Density (kg/m3) | Specific Heat Capacity (J/kg·K) | Thermal Conductivity (W/m·K) |
|---|---|---|---|---|
| Copper | Transformer winding | 8900 | 385 | 397 |
| Steel | Transformer core | 7550 | 450 | 52 |
| Epoxy resin | Insulation layer | 930 | 1340 | 0.19 |
| Mineral oil | Insulation oil | 878 | 1881 | 0.13 |
| Air | Outside Air | 1.18 | 1006.3 | 0.026 |
| Parameters | Meaning | Meaning Definition |
|---|---|---|
| ε″r (f = 100) | The imaginary part of complex relative permittivity at f = 100 Hz | Moisture Content Characteristics |
| ε″r (f = 101) | The imaginary part of complex relative permittivity at f = 101 Hz | |
| ε″r (f = 102) | The imaginary part of complex relative permittivity at f = 102 Hz |
| Parameters | Meaning | Meaning Definition |
|---|---|---|
| tanδ (f = 100) | Value of dielectric loss factor at f = 10 Hz0 | Moisture Content Characteristics |
| tanδ (f = 101) tanδ (f = 102) | Value of dielectric loss factor at f = 10 Hz1 Value of dielectric loss factor at f = 10 Hz2 |
| Frequency | Fitting Formula | The Goodness-of-Fit R2 |
|---|---|---|
| 100 | ε″r = 1.67 × 10−3 + 22.50 × 10−4 exp (1.32 × Km.c.) | 0.99 |
| 101 | ε″r = 4.37 × 10−3 + 6.17 × 10−4 exp (1.12 × Km.c.) | 0.99 |
| 102 | ε″r = 7.21 × 10−3 + 3.73 × 10−4 exp (0.72 × Km.c.) | 0.99 |
| Frequency | Fitting Formula | The Goodness-of-Fit R2 |
|---|---|---|
| 100 | tanδ = −5.74 × 10−3 + 28.90 × 10−4 exp (1.26 × Km.c.) | 0.99 |
| 101 | tanδ = 35.64 × 10−3 + 5.24 × 10−5 exp (1.36 × Km.c.) | 0.99 |
| 102 | tanδ = 2.07 × 10−3 + 0.75 × 10−5 exp (1.46 × Km.c.) | 0.99 |
| Moisture Content (%) | Temperature (°C) | αT,M | tDP=400 (Days) |
|---|---|---|---|
| 0.2 | 65 | 0.05 | 28,680.0 |
| 75 | 0.13 | 11,582.0 | |
| 85 | 0.32 | 4705.3 | |
| 95 | 0.74 | 2034.7 | |
| 105 | 1.63 | 923.7 | |
| 2 | 65 | 0.31 | 4795.2 |
| 75 | 0.80 | 1890.7 | |
| 85 | 1.92 | 785.4 | |
| 95 | 4.40 | 342.2 | |
| 105 | 9.66 | 155.8 |
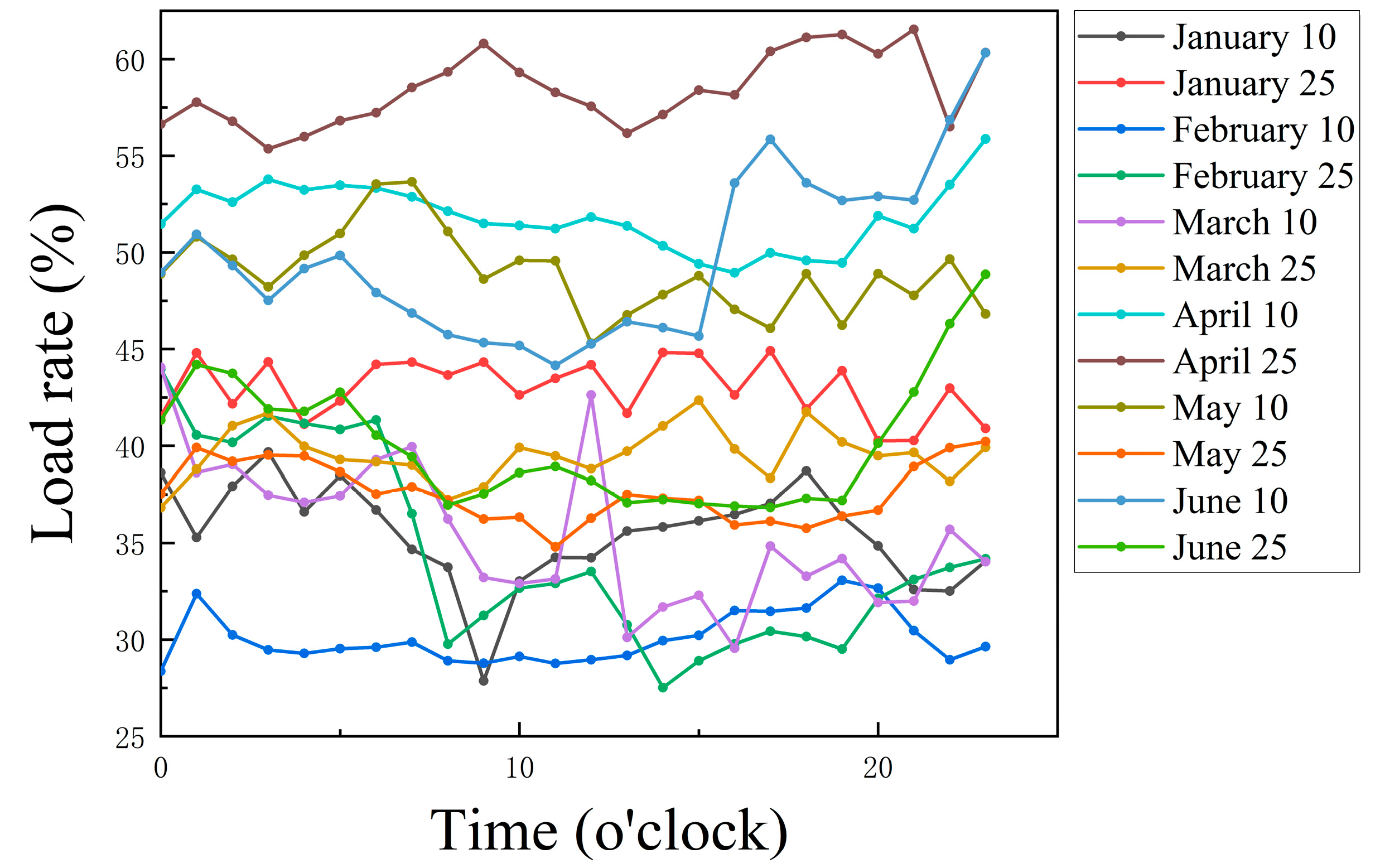
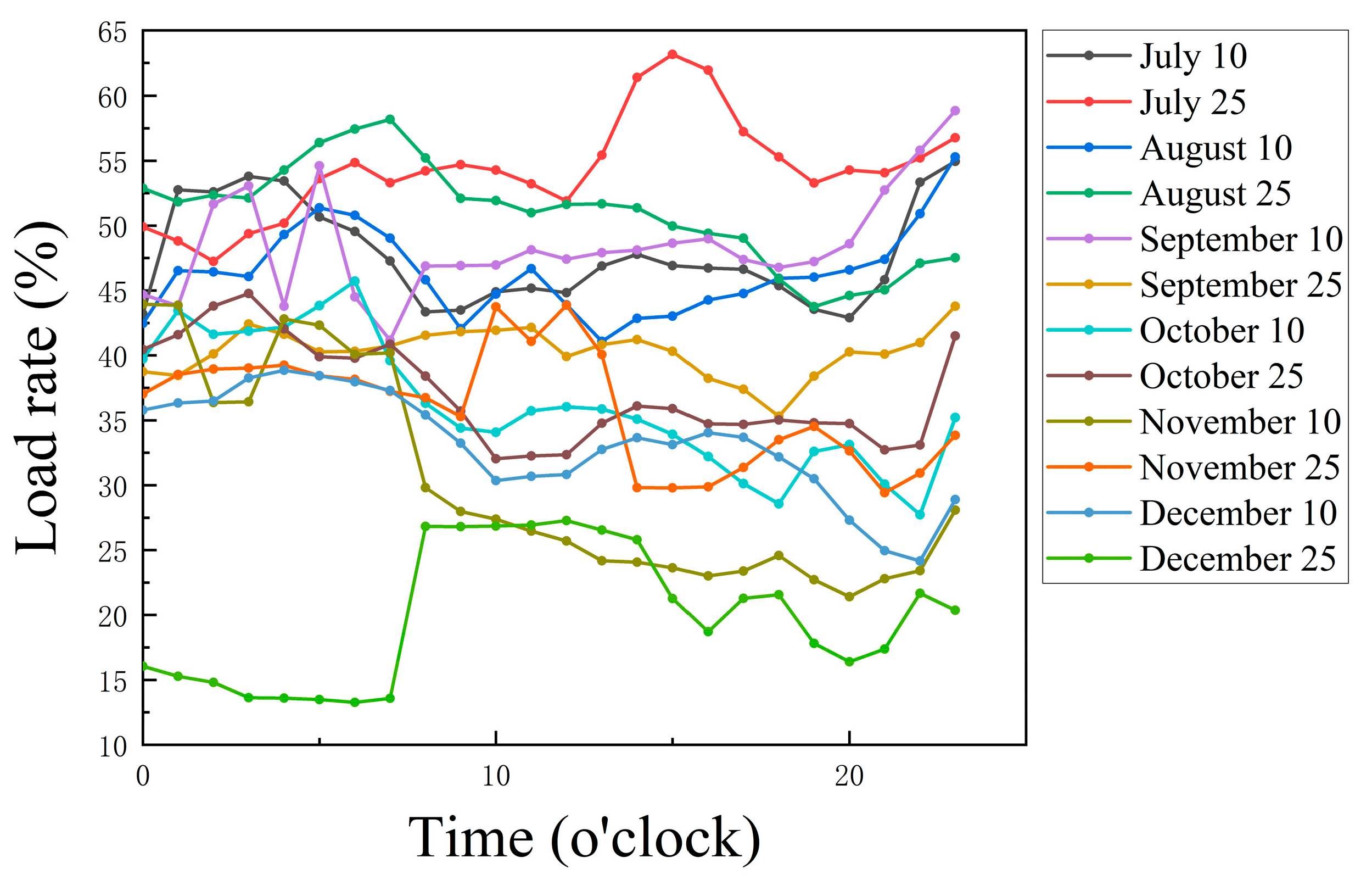
| August and December Load Factor for a Transformer | |||||||
|---|---|---|---|---|---|---|---|
| Dates | Load Factor | Dates | Load Factor | Dates | Load Factor | Dates | Load Factor |
| 1 August | 67.56 | 08.09 | 66.18 | 08.17 | 74.10 | 08.25 | 62.18 |
| 2 August | 63.04 | 08.10 | 68.50 | 08.18 | 72.38 | 08.26 | 71.43 |
| 3 August | 67.07 | 08.11 | 68.61 | 08.19 | 69.75 | 08.27 | 70.81 |
| 4 August | 60.18 | 08.12 | 64.35 | 08.20 | 70.91 | 08.28 | 67.70 |
| 5 August | 63.36 | 08.13 | 67.93 | 08.21 | 61.73 | 08.29 | 65.48 |
| 6 August | 69.83 | 08.14 | 65.11 | 08.22 | 64.90 | 08.30 | 69.07 |
| 7 August | 62.48 | 08.15 | 64.06 | 08.23 | 61.17 | 08.31 | 63.26 |
| 8 August | 54.34 | 08.16 | 67.63 | 08.24 | 50.94 | / | / |
| 1 December | 50.18 | 12.09 | 47.04 | 12.17 | 52.88 | 12.25 | 55.48 |
| 2 December | 48.78 | 12.10 | 55.27 | 12.18 | 55.44 | 12.26 | 50.80 |
| 3 December | 46.93 | 12.11 | 46.47 | 12.19 | 52.78 | 12.27 | 49.95 |
| 4 December | 51.77 | 12.12 | 53.60 | 12.20 | 54.23 | 12.28 | 56.03 |
| 12 December | 45.63 | 12.13 | 46.48 | 12.21 | 53.61 | 12.29 | 56.96 |
| 6 December | 47.68 | 12.14 | 54.53 | 12.22 | 56.10 | 12.30 | 58.69 |
| 7 December | 53.23 | 12.15 | 57.12 | 12.23 | 52.86 | 12.31 | 62.90 |
| 8 December | 51.93 | 12.16 | 56.22 | 12.24 | 54.34 | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Fang, Y.; Cheng, H.; Sun, Y.; Li, B.; Li, K.; Zhao, W.; Sun, Z.; Zhang, Y. Innovative Transformer Life Assessment Considering Moisture and Oil Circulation. Energies 2024, 17, 429. https://doi.org/10.3390/en17020429
Liang Z, Fang Y, Cheng H, Sun Y, Li B, Li K, Zhao W, Sun Z, Zhang Y. Innovative Transformer Life Assessment Considering Moisture and Oil Circulation. Energies. 2024; 17(2):429. https://doi.org/10.3390/en17020429
Chicago/Turabian StyleLiang, Zhengping, Yan Fang, Hao Cheng, Yongbin Sun, Bo Li, Kai Li, Wenxuan Zhao, Zhongxu Sun, and Yiyi Zhang. 2024. "Innovative Transformer Life Assessment Considering Moisture and Oil Circulation" Energies 17, no. 2: 429. https://doi.org/10.3390/en17020429
APA StyleLiang, Z., Fang, Y., Cheng, H., Sun, Y., Li, B., Li, K., Zhao, W., Sun, Z., & Zhang, Y. (2024). Innovative Transformer Life Assessment Considering Moisture and Oil Circulation. Energies, 17(2), 429. https://doi.org/10.3390/en17020429








