Implementation and Adaptability Analysis of Numerical Simulation for Shale Oil CO2 Huff and Puff
Abstract
1. Introduction
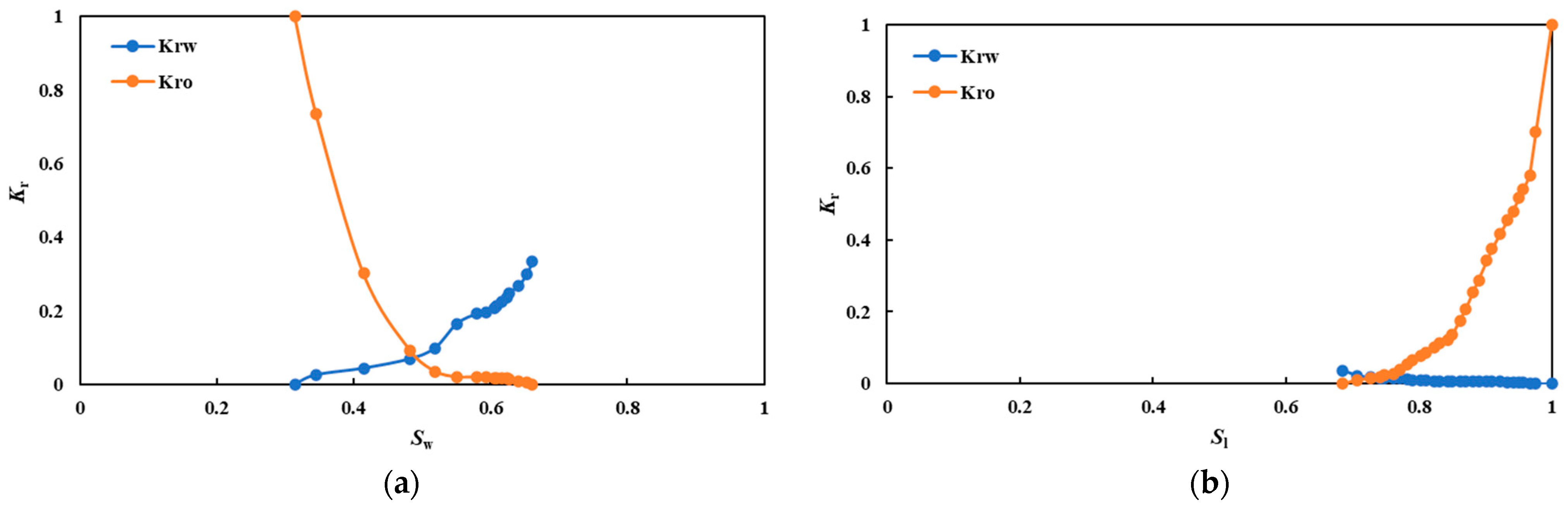
2. Establishment of a Numerical Model for Shale Oil Fracturing Horizontal Wells
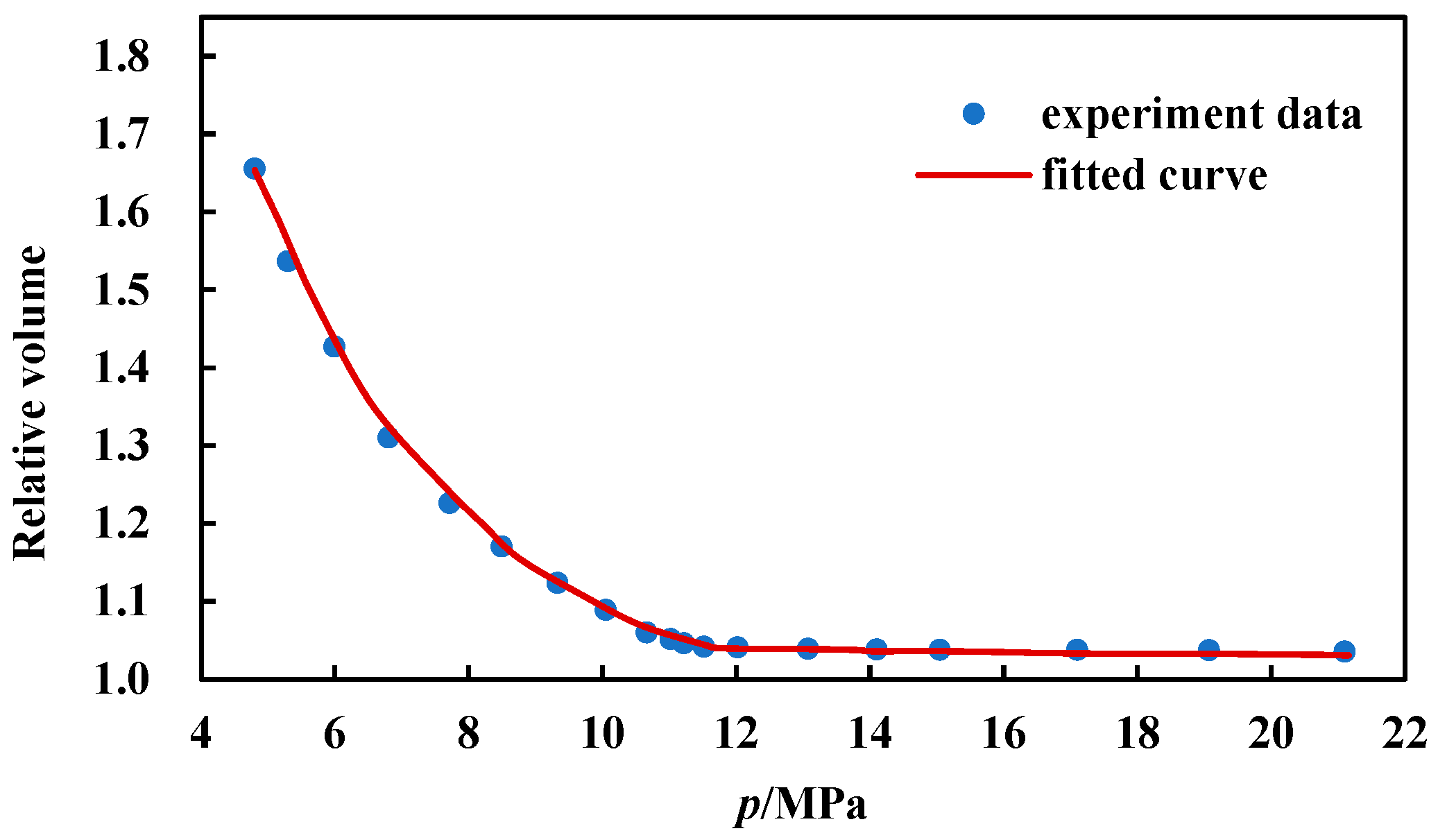
3. A Fluid Model Considering the Nanoconfinement Effect
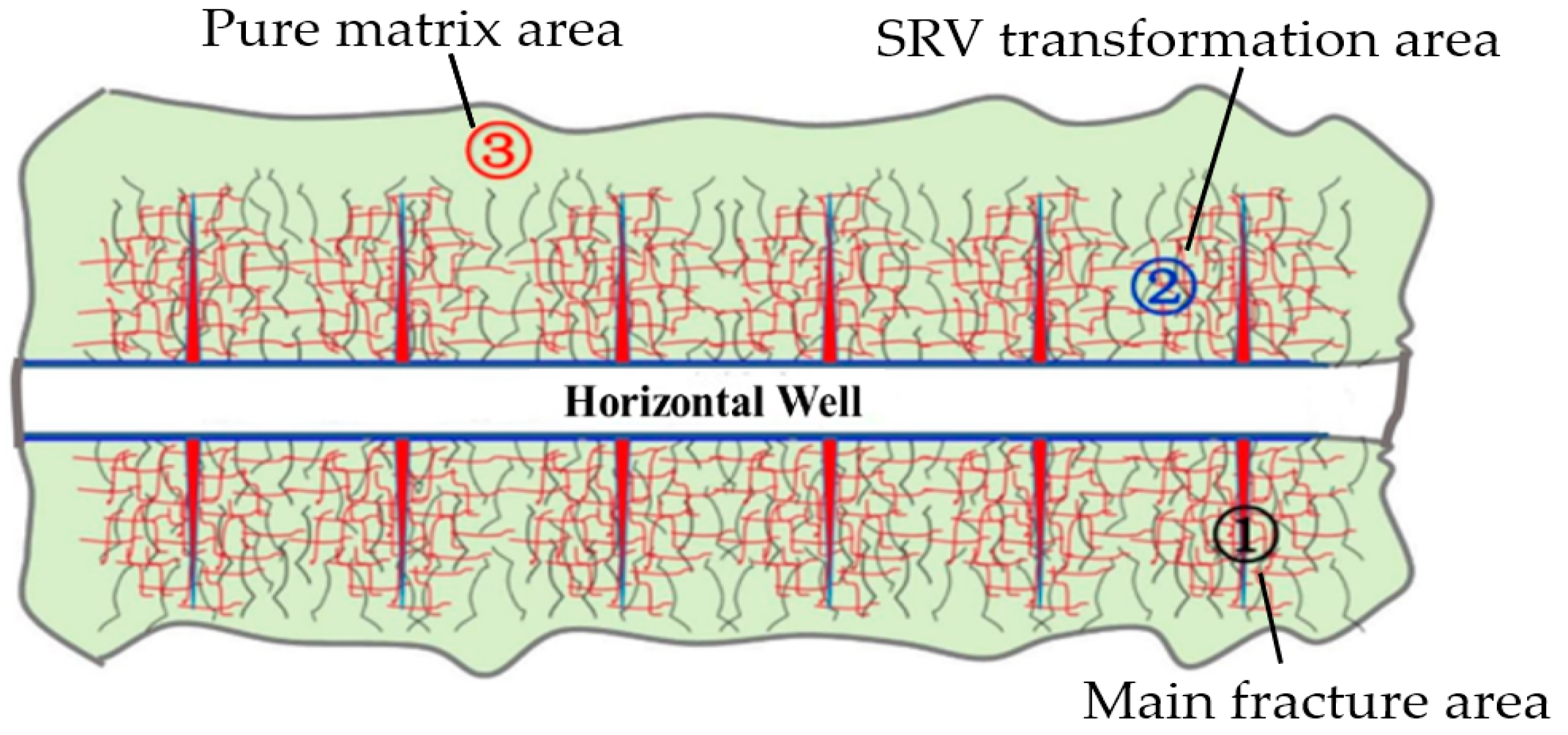
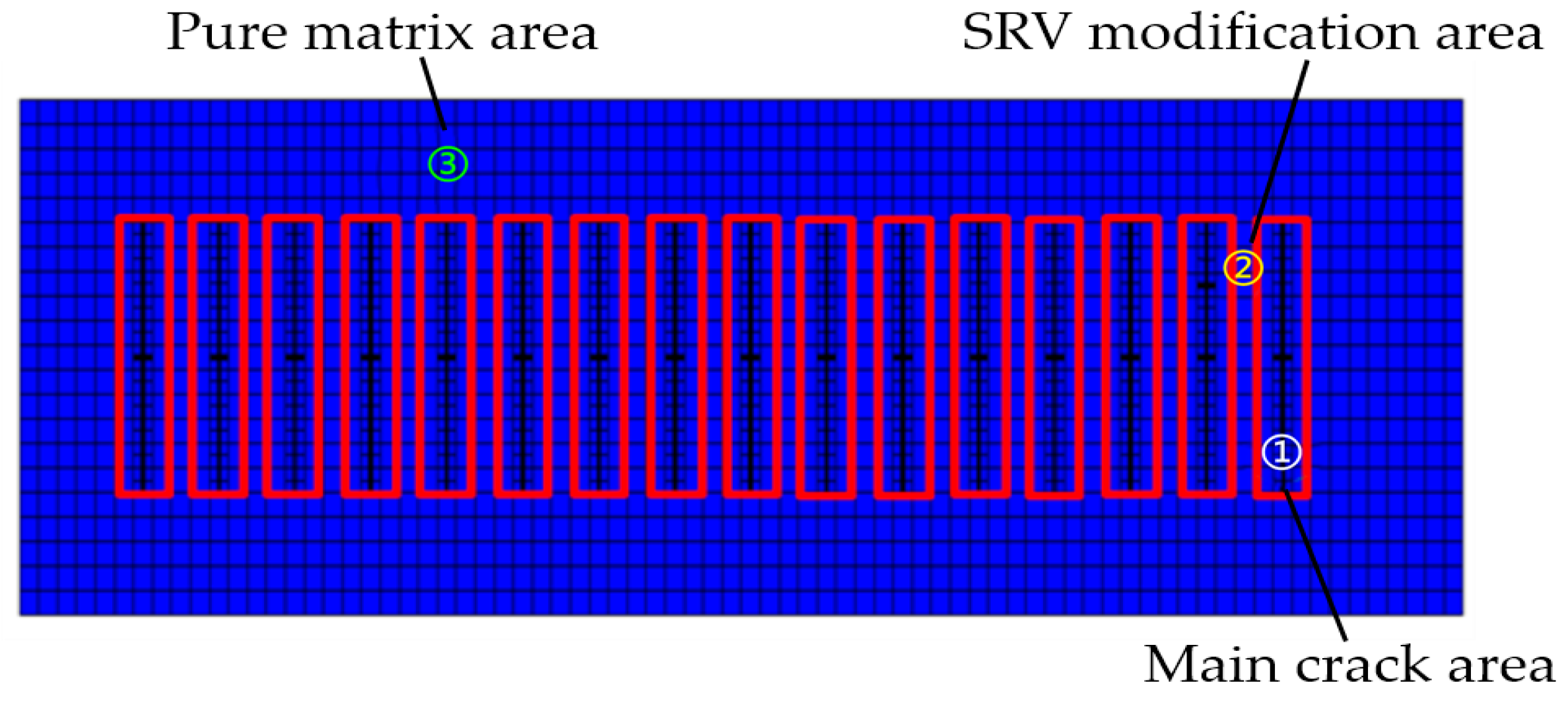
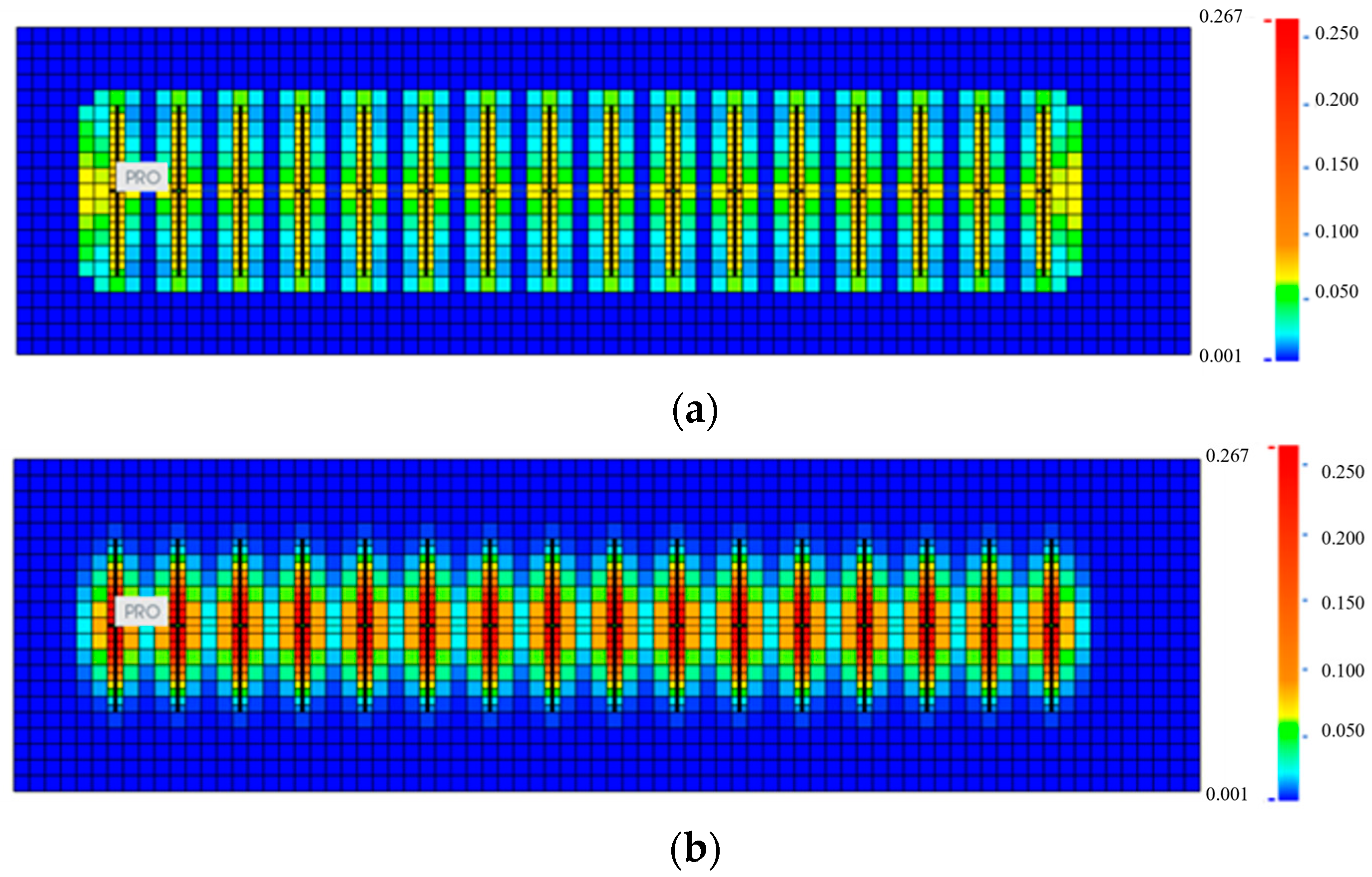
4. SRV Regional Fracture Network Model for Shale Oil Horizontal Wells
- (1)
- Construction of a matrix and natural fracture system
- (2)
- Construction of a hydraulic fracturing system
- (3)
- Simulation of SRV fracture network
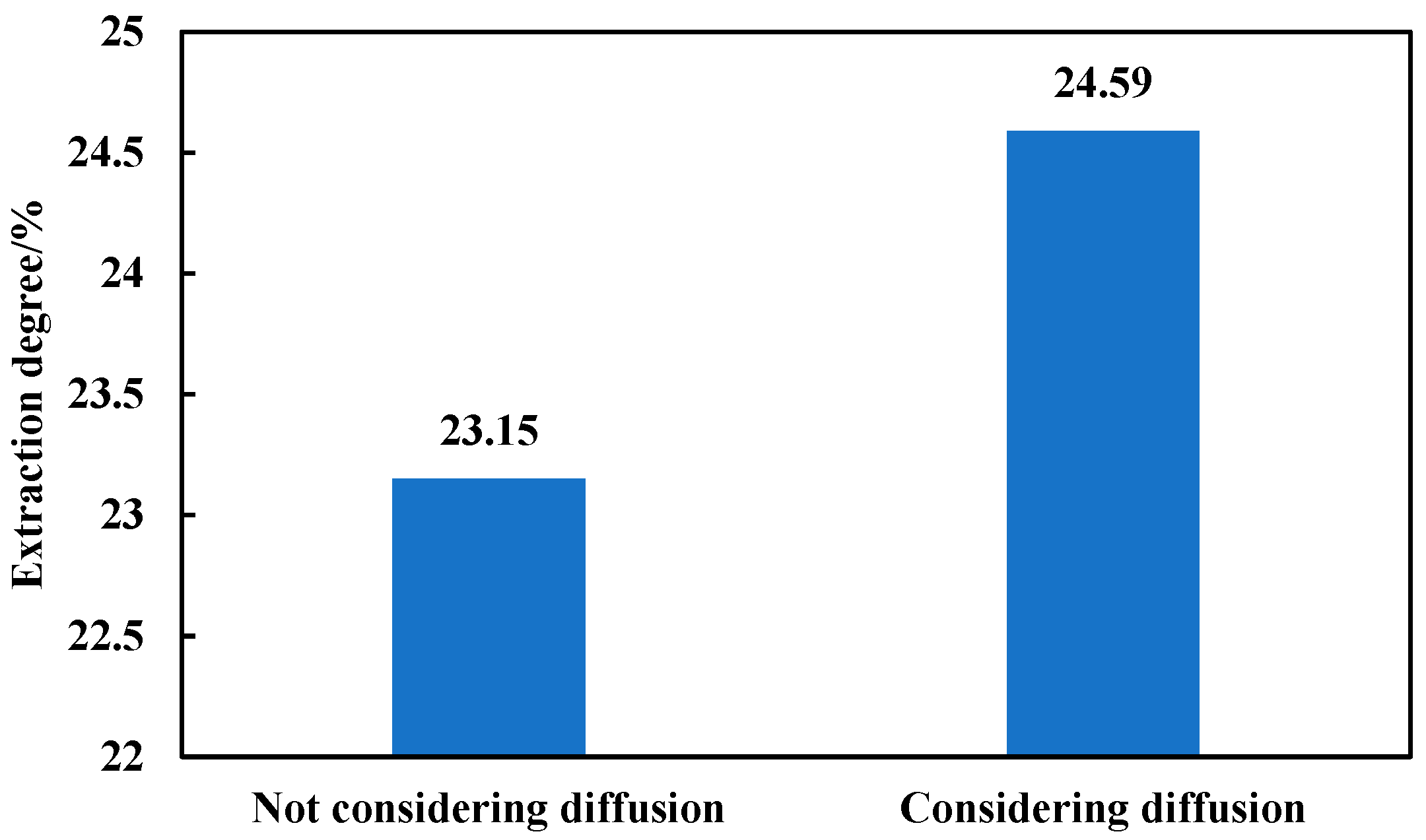
5. Considering the CO2 Diffusion Effect
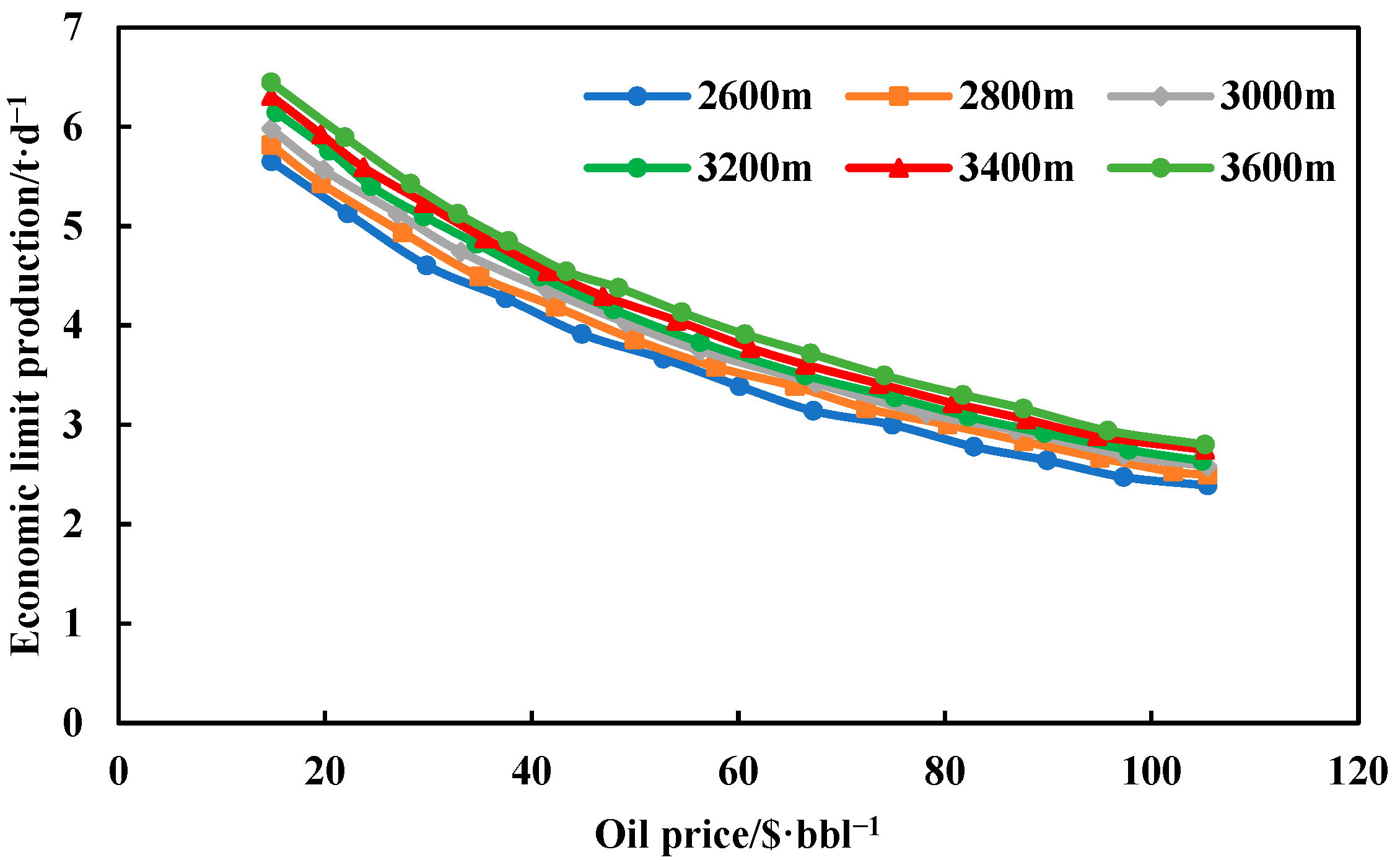
6. Adaptability Analysis of Shale Oil CO2 Huff and Puff
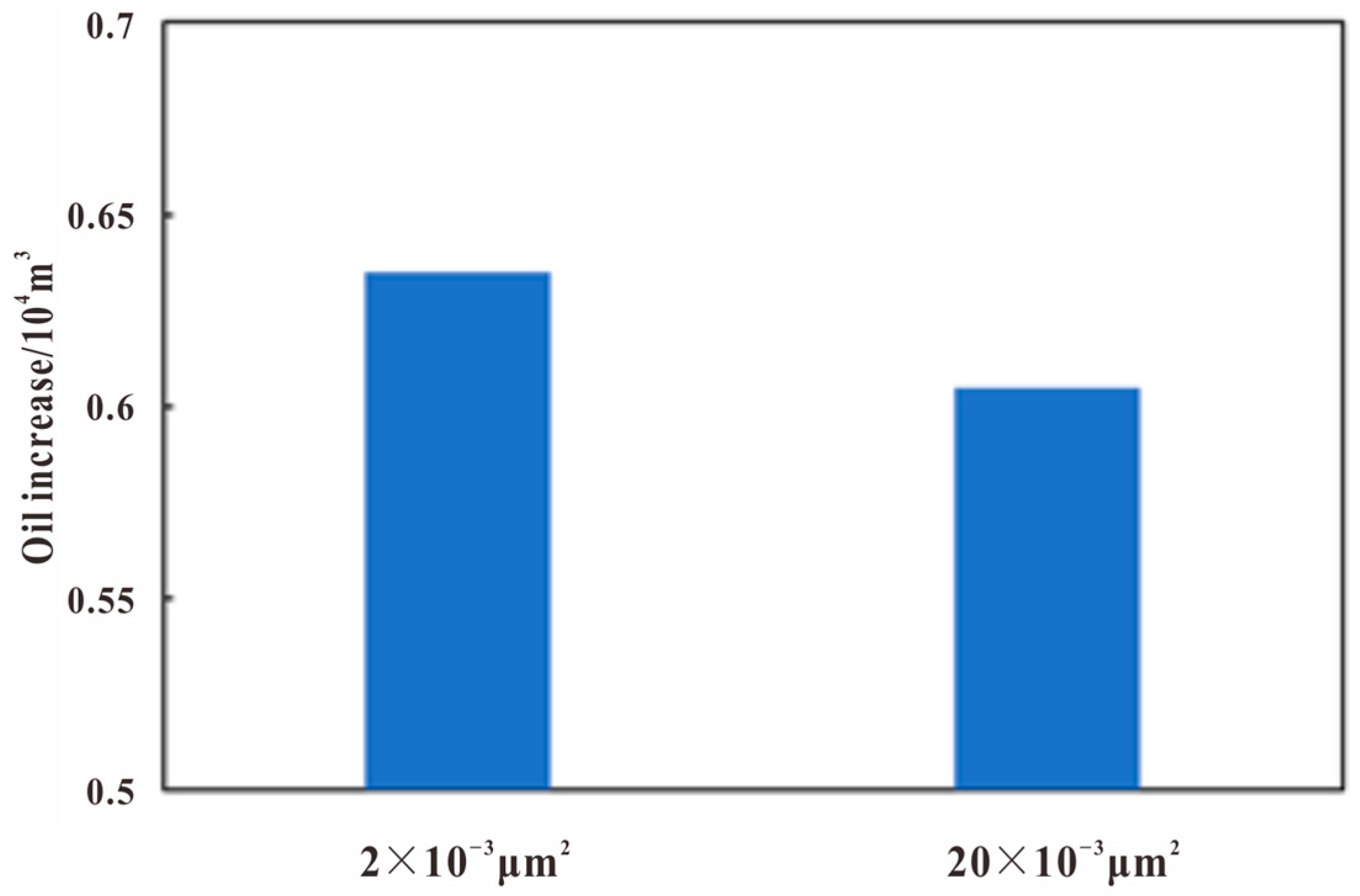
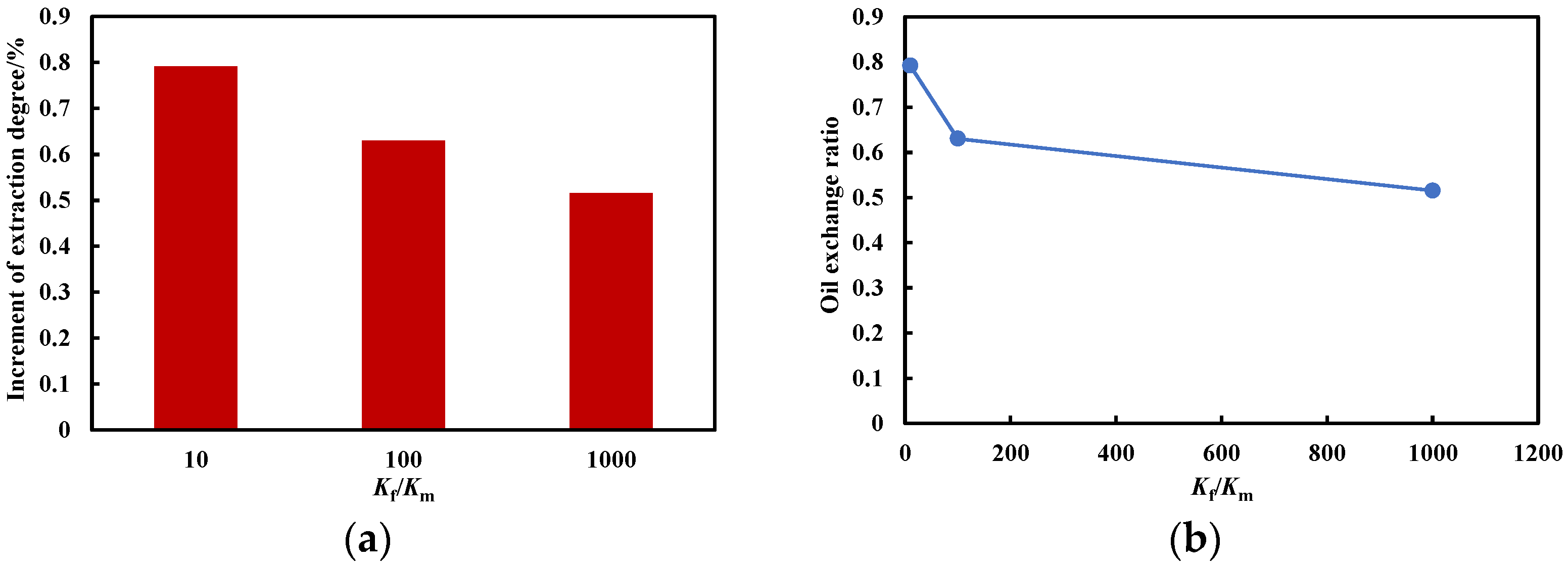
7. Adaptability Analysis of Kf/Km
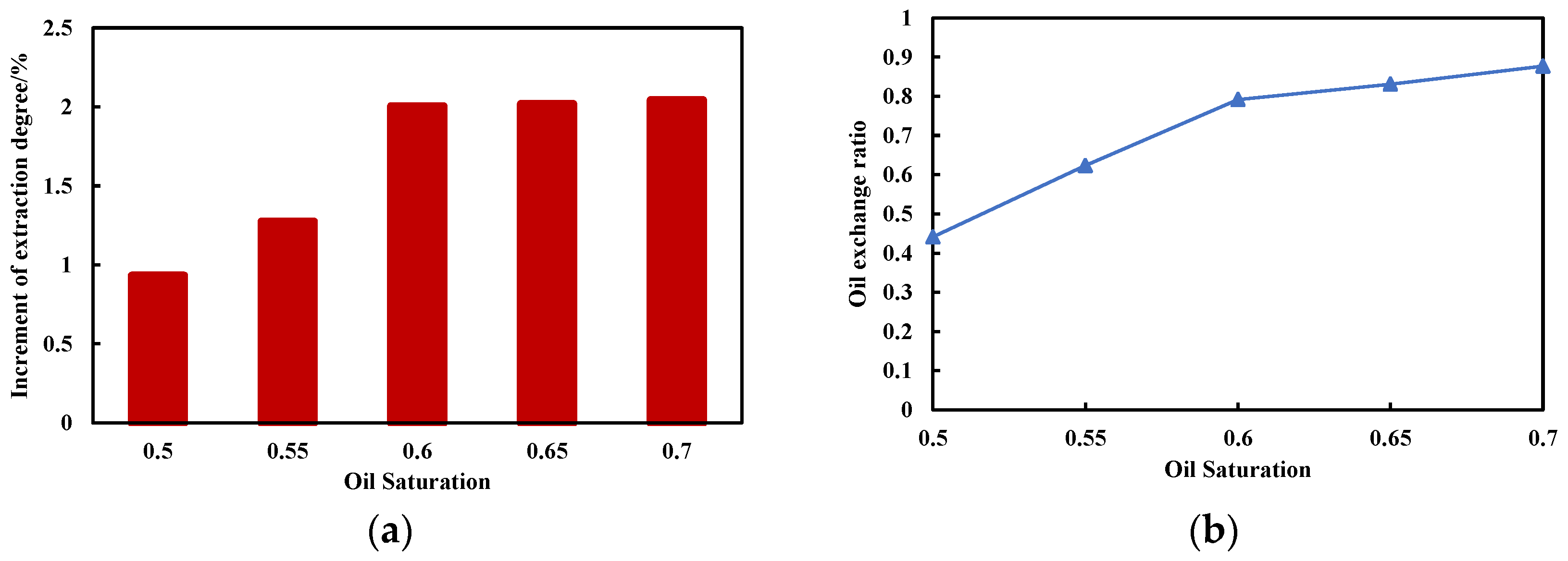
8. Adaptability Analysis of Oil Saturation
9. Kf/Km—Oil Saturation Chart Determination
10. Conclusions
- (1)
- By correcting the critical parameter of the average pore throat radius and using the fluid p–T phase diagram shift to reflect the nanoconfinement effect, it was found that the corrected p–T phase diagram shifts upwards, causing an increase in bubble point pressure, and thus affecting the properties of each component in crude oil.
- (2)
- By comparing the cases of CO2 diffusion coefficient consideration and non-consideration, it was found that during the injection and shut-in stages, the CO2 content and recovery degree in the oil phase of the matrix corresponding to CO2 diffusion were high.
- (3)
- Taking the incremental recovery rate and oil change rate as references, the development effect of CO2 huff and puff under the coupling effect of Kf/Km and oil saturation was explored, and K–So charts under different Kf/Km and oil saturation values were obtained. The chart results show that when Kf/Km is 1000 and the increases in the CO2 recovery rate reach 1.5% and 2%, the lower limits of oil saturation are 0.54 and 0.57%, respectively. When the oil saturation is 0.5 and the CO2 huff and puff oil change rate reaches 0.3, the lower limit of Kf/Km is 700. Finally, when the oil saturation is 0.548 and the CO2 huff and puff oil change rate reaches 0.6, the lower limit of Kf/Km is 10.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Li, K.; Ma, Q.; Fan, J. Position and prospect of CCUS technology development under carbon neutrality. China Popul. Resour. Environ. 2021, 31, 29–33. [Google Scholar]
- Hu, Y.; Hao, M.; Chen, G.; Sun, R.; Li, S. Technology and practice of CO2 flooding and storage in China. Pet. Explor. Dev. 2019, 46, 716–727. [Google Scholar] [CrossRef]
- Yang, Y. Research and practice of CO2 flooding technology for ultra-low permeability reservoirs in Shengli Oilfield. Pet. Geol. Recovery Effic. 2020, 27, 11–19. [Google Scholar]
- Li, D.; Saraji, S.; Jiao, Z.; Zhang, Y. CO2 injection strategies for enhanced oil recovery and geological sequestration in a tight reservoir: An experimental study. Fuel 2021, 284, 119013. [Google Scholar] [CrossRef]
- Huang, X.; Gu, L.; Li, S.; Du, Y.; Liu, Y. Absolute adsorption of light hydrocarbons on organic–rich shale: An efficient determination method. Fuel 2022, 308, 121998. [Google Scholar] [CrossRef]
- Zeng, T.; Miller, C.S.; Mohanty, K.K. Combination of a chemical blend with CO2 huff-n-puff for enhanced oil recovery in oil shales. J. Pet. Sci. Eng. 2020, 194, 107546. [Google Scholar] [CrossRef]
- Zhao, P.; Gray, K.E. Finite discrete-element modeling of multifracture propagation in fractured reservoirs. J. Pet. Sci. Eng. 2021, 208, 109229. [Google Scholar] [CrossRef]
- Wang, H. Hydraulic fracture propagation in natural fractured reservoirs complex fracture or fracture networks. J. Nat. Gas Sci. Eng. 2019, 68, 102911. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E. Modeling hydraulic fracture propagation and proppant transport in a two-layer formation with stress drop. Eng. Fract. Mech. 2018, 199, 705–720. [Google Scholar] [CrossRef]
- Deng, B.; Yin, G.; Li, M.; Zhang, D.; Lu, J.; Liu, Y.; Chen, J. Feature of fractures induced by hydrofracturing treatment using water and L-CO2 as fracturing fluids in laboratory experiments. Fuel 2018, 226, 35–46. [Google Scholar] [CrossRef]
- Jin, L.; Hawthorne, S.; Sorensen, J.; Pekot, L.; Kurz, B.; Smith, S.; Heebink, L.; Bosshart, N.; Torres, J.; Dalkhaa, C.; et al. Extraction of oil from the Bakken shales with supercritical CO2. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017. [Google Scholar]
- Tovar, F.D.; Barrufet, M.A.; Schechter, D.S. Gas injection for EOR in organic rich shale. part i: Operational philosophy. In Proceedings of the SPE Improved Oil Recovery Conference, Oklahoma City, OK, USA, 14–18 April 2018. [Google Scholar]
- Gamadi, T.D.; Elldakli, F.; Sheng, J.J. Compositional simulation evaluation of EOR potential in shale oil reservoirs by cyclic natural gas injection. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, OnePetro, Denver, CO, USA, 25–27 August 2014. [Google Scholar]
- Chen, C.; Balhoff, M.; Mohanty, K.K. Effect of reservoir heterogeneity on primary recovery and CO2 huff-n-puff recovery in shale-oil reservoirs. SPE Reserv. Eval. Eng. 2014, 17, 404–413. [Google Scholar] [CrossRef]
- Orozco, D.; Fragoso, A.; Selvan, K.; Noble, G.; Aguilera, R. Eagle ford huff-n-puff gas-injection pilot: Comparison of reservoir-simulation, material balance, and real performance of the pilot well. SPE Reserv. Eval. Eng. 2020, 23, 247–260. [Google Scholar] [CrossRef]
- Lu, J.; Wang, X.; He, Y.; Yang, C.; Deng, N. Diagenesis and pore evolution of tight sandstone of Chang 7 oil-bearing formation in Fuxian area, Ordos Basin. J. Northeast Pet. Univ. 2017, 41, 9–20. [Google Scholar]
- Li, Z.; Qu, X.; Liu, W.; Lei, Q.; Sun, H.; He, Y. Discussion on reasonable development mode of tight oil in Chang 7 member of Ordos Basin. Pet. Explor. Dev. 2015, 42, 217–221. [Google Scholar] [CrossRef]
- Li, Y.; Shang, Y.; Yang, P. Modeling fracture connectivity in naturally fractured reservoirs: A case study in the Yanchang Formation, Ordos Basin, China. Fuel 2018, 211, 789–796. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, L.; Fan, K. Current status and progress in research on fracture prediction of low permeability reservoirs in oil and gas basins. Geol. Rev. 2006, 52, 777–782. [Google Scholar]
- Nojabaei, B.; John, R.T.; Chu, L. Effect of capillary pressure on fluid density and phase behavior in tight rocks and shales. In Proceedings of the SPE 159258, SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar]
- Barsotti, E.; Tan, S.P.; Saraji, S.; Piri, M.; Chen, J.H. A review on capillary condensation in nanoporous media: Implications for hydrocarbon recovery from tight reservoirs. Fuel 2016, 184, 344–361. [Google Scholar] [CrossRef]
- Pitakbunkate, T.; Balbuena, P.B.; Moridis, G.J.; Blasingame, T.A. Effect of confinement on pressure/volume/temperature properties of hydrocarbons in shale reservoirs. SPE J. 2016, 21, 621–634. [Google Scholar] [CrossRef]
- Li, L.; Su, Y.; Sheng, J.J.; Hao, Y.; Wang, W.; Lv, Y.; Zhao, Q.; Wang, H. Experimental and numerical study on CO2 sweep volume during CO2 huff-n-puff enhanced oil recovery process in shale oil reservoirs. Energy Fuels 2019, 33, 4017–4032. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, K.S. Investigation of asphaltene-derived formation damage and nano-confinement on the performance of CO2 huff-n-puff in shale oil reservoirs. J. Pet. Sci. Eng. 2019, 182, 106–304. [Google Scholar] [CrossRef]
- Zarragoicoechea, G.J.; Kuz, V.A. Critical shift of a confined fluid in a nanopore. Fluid Phase Equilibria 2004, 220, 7–9. [Google Scholar] [CrossRef]
- Fu, J.; Guo, W.; Li, S.; Liu, X.; Cheng, D.; Zhou, X. Characteristics and exploration potential of multi type Shale oil in Chang 7 Member of Ordos Basin. Nat. Gas Geosci. 2021, 32, 1749–1761. [Google Scholar]
- Zhang, L.; Liu, S.; Yong, R.; Li, B.; Zhao, Y.L. Numerical simulation of staged fracturing horizontal wells in tight reservoirs based on EDFM. J. Southwest Pet. Univ. 2019, 41, 1–11. [Google Scholar]
- Zhu, D.; Hu, Y.; Cui, M.; Chen, Y.; Liang, C.; Cai, W.; He, Y.; Wang, X.; Chen, H.; Li, X. Coupling local grid refinement with embedded discrete fracture model to predict the production capacity of fracturing renovation wells. Pet. Explor. Dev. 2020, 47, 341–348. [Google Scholar] [CrossRef]
- Zhang, D. Research on the method for determining the economic limit production of CO2 flooding. China Sci. Technol. Inf. 2016, 8, 122–123. [Google Scholar]
- Yuan, Z.; Yang, S.; Zhang, Z.; Wang, M.; Zhang, X. Adaptability evaluation and law simulation of CO2 injection huff and puff in ultra-low permeability reservoirs. Unconv. Oil Gas 2022, 9, 85–92. [Google Scholar]
- Ding, Z.; Dong, P.; Yang, X.; Ding, D.; Zuo, W.; Pan, H. Numerical simulation of CO2 miscible flooding in fractured reservoirs considering Molecular diffusion. Block Oil Gas Field 2015, 22, 245–250. [Google Scholar]
- Jiang, J.; Liu, Q.; Wang, J. Calculation method of effective action radius of carbon dioxide huff and puff in tight reservoir. Sci. Technol. Eng. 2020, 20, 2216–2222. [Google Scholar]
- Luo, Y.; Sun, L.; Wu, Z.; Zhao, X.; Xiao, H. A CO2 huff and puff productivity prediction model for horizontal wells in tight reservoirs based on diffusion coefficient changes. Sci. Technol. Eng. 2021, 21, 3588–3594. [Google Scholar]
- Li, D.; Hou, J.; Zhao, F.; Wang, S.; Yue, X. Study on molecular diffusion coefficient and solubility of carbon dioxide in crude oil. Oilfield Chem. 2009, 26, 405–408. [Google Scholar]
- Du, F.; Nojabaei, B. Estimating diffusion coefficients of shale oil, gas, and condensate with nano-confinement effect. J. Pet. Sci. Eng. 2020, 193, 107–362. [Google Scholar] [CrossRef]
- Han, W. Study on CO2 Huff and Puff Effect of Fractured Horizontal Wells in Tight Oil Reservoir. Master’s Thesis, China University of Petroleum, Beijing, China, 2018. [Google Scholar]
- Yang, X. Optimization of Numerical Simulation Parameters of Shale Oil CO2 Huff and Puff. Master’s Thesis, China University of Petroleum, Beijing, China, 2021. [Google Scholar]





| Parameter | Basic Value |
|---|---|
| Matrix permeability/10−3 μm2 | 0.02 |
| Oil saturation | 0.6 |
| Kf/Km | 10 |
| Horizontal well section length/m | 1200 |
| Reservoir thickness/m | 12 |
| Soaking time/d | 30 |
| Artificial crack half-length/m | 100 |
| Original Component | Mole Fraction/% | Pseudo-Component | Mole Fraction/% |
|---|---|---|---|
| CO2 | 0.11 | CO2 | 0.11 |
| N2 | 1.37 | N2~CH4 | 28.69 |
| CH4 | 27.32 | ||
| C2H6 | 8.66 | C2H6~nC6 | 32.10 |
| C3H8 | 10.05 | ||
| iC4 | 1.64 | ||
| nC4 | 4.45 | ||
| iC5 | 1.56 | ||
| nC5 | 2.22 | ||
| nC6 | 3.52 | ||
| nC7 | 4.62 | nC7~nC10 | 14.76 |
| nC8 | 3.93 | ||
| nC9 | 3.41 | ||
| nC10 | 2.80 | ||
| C11-C14 | 8.91 | C11~C21 | 17.39 |
| C15-C18 | 5.65 | ||
| C19-C21 | 2.83 | ||
| C22-C25 | 2.54 | C22~C30 | 4.46 |
| C26-C30 | 1.91 | ||
| C31+ | 2.49 | C31+ | 2.49 |
| Component | CO2 | N2~CH4 | C2H6~nC6 | nC7~nC10 | C11~C21 | C22~C30 | C31+ |
|---|---|---|---|---|---|---|---|
| pcb/atm | 72.80 | 44.86 | 39.90 | 25.05 | 15.41 | 9.33 | 6.95 |
| Tcb/K | 304.20 | 187.38 | 395.70 | 576.47 | 791.97 | 915.44 | 1121.75 |
| Component | CO2 | N2~CH4 | C2H6~nC6 | nC7~nC10 | C11~C21 | C22~C30 | C31+ |
|---|---|---|---|---|---|---|---|
| pcb/atm | 72.60 | 44.66 | 39.67 | 24.86 | 15.25 | 9.21 | 6.84 |
| Tcb/K | 302.88 | 186.57 | 393.41 | 572.06 | 784.07 | 904.13 | 1105.41 |
| Pressure/MPa | Temperature/°C | Permeability/10−3 μm2 | Diffusion Coefficient/10−9 m2·s−1 | |
|---|---|---|---|---|
| Tight oil | 6.5~30 | 70~150 | / | 0.0246~2.8274 |
| 15~30 | 20~80 | / | 0.2~5.45 | |
| 20 | 60 | 0.08 | 500 |
| Kf/Km | Increment of Extraction Degree/% | Oil Exchange Ratio |
|---|---|---|
| 10 | 2.2032 | 0.7919 |
| 100 | 2.1103 | 0.6302 |
| 1000 | 2.0132 | 0.5153 |
| Oil Saturation | Increment of Extraction Degree/% | Oil Exchange Ratio |
|---|---|---|
| 0.5 | 0.9311 | 0.4413 |
| 0.55 | 1.2732 | 0.6236 |
| 0.6 | 2.0024 | 0.7919 |
| 0.65 | 2.0165 | 0.8309 |
| 0.7 | 2.0413 | 0.8771 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Wang, Y.; Huang, S.; Liu, M.; Yang, C. Implementation and Adaptability Analysis of Numerical Simulation for Shale Oil CO2 Huff and Puff. Energies 2024, 17, 454. https://doi.org/10.3390/en17020454
Zhao F, Wang Y, Huang S, Liu M, Yang C. Implementation and Adaptability Analysis of Numerical Simulation for Shale Oil CO2 Huff and Puff. Energies. 2024; 17(2):454. https://doi.org/10.3390/en17020454
Chicago/Turabian StyleZhao, Fenglan, Yu Wang, Shijun Huang, Miaomiao Liu, and Changhe Yang. 2024. "Implementation and Adaptability Analysis of Numerical Simulation for Shale Oil CO2 Huff and Puff" Energies 17, no. 2: 454. https://doi.org/10.3390/en17020454
APA StyleZhao, F., Wang, Y., Huang, S., Liu, M., & Yang, C. (2024). Implementation and Adaptability Analysis of Numerical Simulation for Shale Oil CO2 Huff and Puff. Energies, 17(2), 454. https://doi.org/10.3390/en17020454






