The Kinetics of Semi-Coke CO2 Gasification Based on Pore Fractal Growth
Abstract
1. Establishment of the Pore Fractal Growth Model during Carbon Gasification
1.1. The Hypothesis of Fractal Growth
1.2. Fractal Dimension, Surface Area and Pore Volume of Porous Carbon
2. Experiment
2.1. Preparation of Porous Carbon with Different Degrees of Gasification
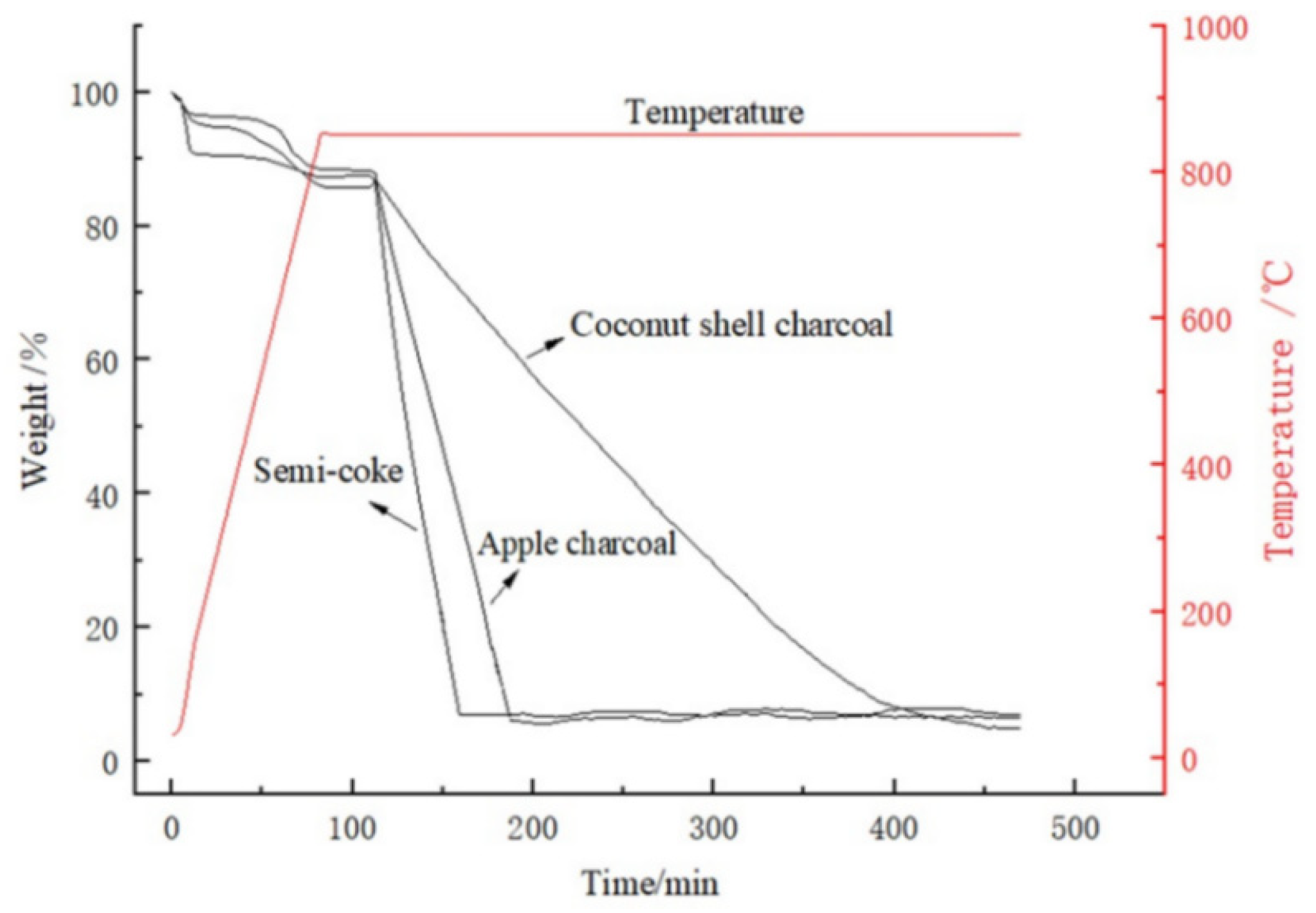
2.2. Thermogravimetric Experiment
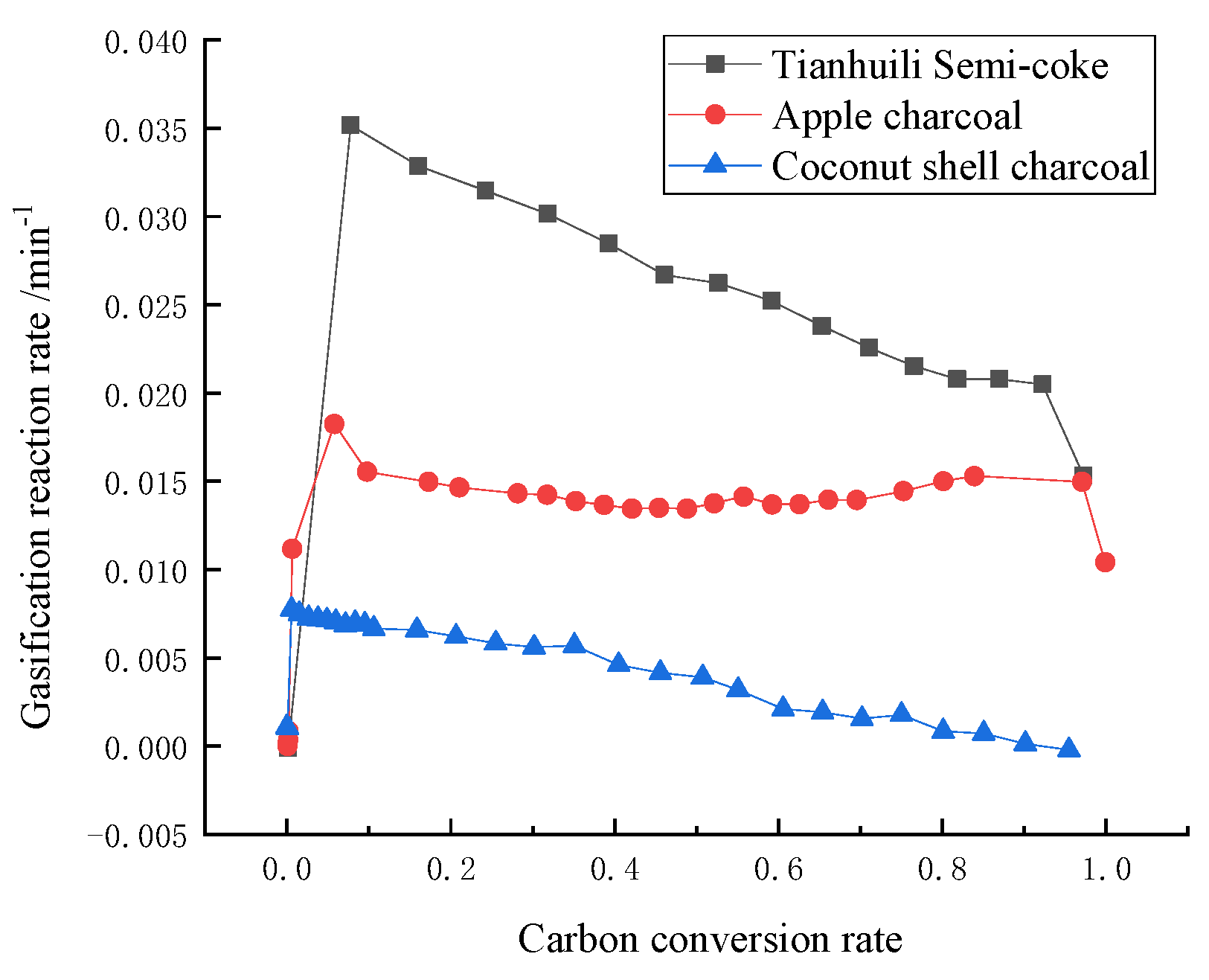
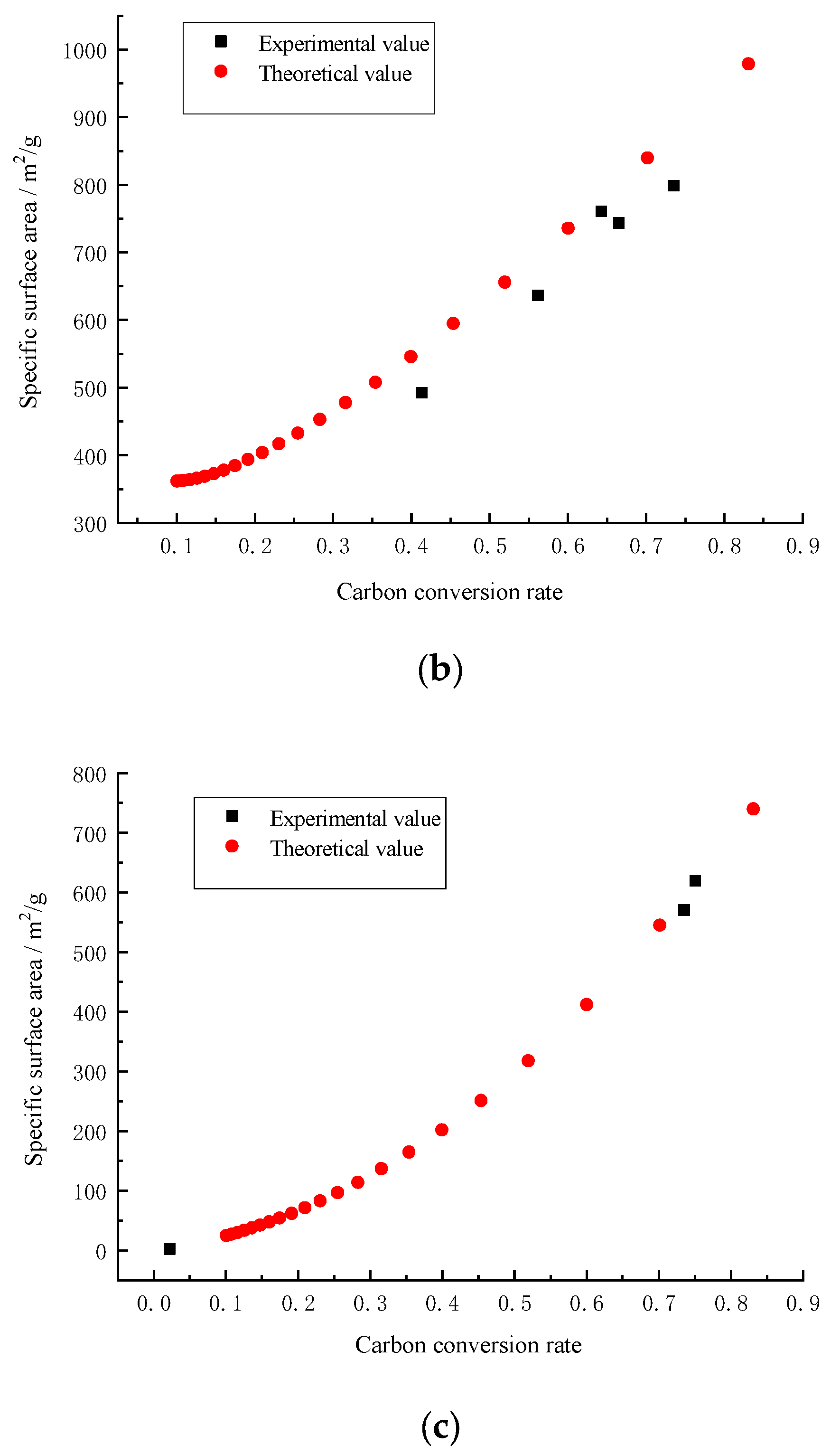
3. Results and Discussion
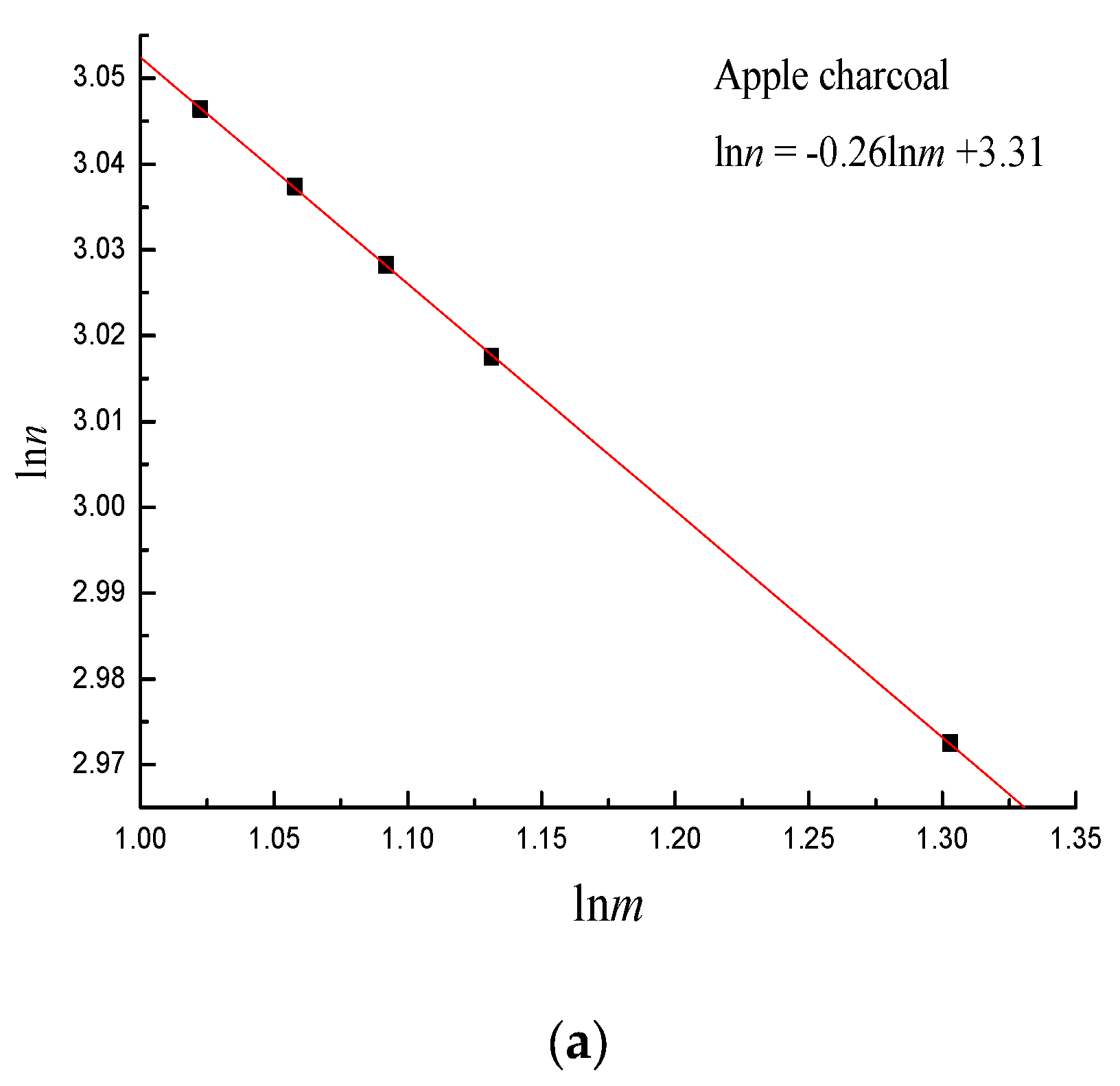
4. Establishment of Pore Fractal Growth Kinetics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yi, W.; Wang, X.; Zeng, K.; Yang, H.; Shao, J.; Zhang, S.; Watkinson, A.P.; Chen, H. An improved gasification kinetic model for biochar with high alkali and alkaline earth metals content. Fuel 2023, 342, 127849. [Google Scholar] [CrossRef]
- Lampropoulos, A.; Varvoutis, G.; Montes-Morán, M.A.; Menéndez, J.A.; Konsolakis, M.; Marnellos, G.E. Detailed kinetic analysis and modelling of the dry gasification reaction of olive kernel and lignite coal chars. Int. J. Hydrogen Energy 2023, 48, 11970–11983. [Google Scholar]
- Xu, T.; Wu, Y.P.; Bhattacharya, S. Gasification kinetic modelling of Victorian brown coal chars and validity for entrained flow gasification in CO2. Int. J. Min. Sci. Technol. 2021, 31, 473–481. [Google Scholar] [CrossRef]
- Betancur, M.; Arenas, C.N.; Martínez, J.D.; Navarro, M.V.; Murillo, R. CO2 gasification of char derived from waste tire pyrolysis: Kinetic models comparison. Fuel 2020, 273, 117745. [Google Scholar]
- Guo, Y.; Zhao, Y.; Gao, D.; Liu, P.; Meng, S.; Sun, S. Kinetics of steam gasification of in-situ chars in a micro fluidized bed. Int. J. Hydrogen Energy 2016, 41, 15187–15198. [Google Scholar] [CrossRef]
- Tanner, J.; Bhattacharya, S. Kinetics of CO2 and steam gasification of Victorian brown coal chars. Chem. Eng. J. 2016, 285, 331–340. [Google Scholar] [CrossRef]
- Alvarez, J.; Lopez, G.; Amutio, M.; Bilbao, J.; Olazar, M. Evolution of biomass char features and their role in the reactivity during steam gasification in a conical spouted bed reactor. Energy Convers. Manag. 2019, 181, 214–222. [Google Scholar]
- Cai, W.; Liu, P.; Chen, B.; Xu, H.; Liu, Z.; Zhou, Q. Plastic waste fuelled solid oxide fuel cell system for power and carbon nanotube CO generation. Int. J. Hydrogen Energy 2019, 44, 1867–1876. [Google Scholar] [CrossRef]
- Lahijani, P.; Zainal, Z.A.; Mohammadi, M.; Mohamed, A.R. Conversion of the greenhouse gas CO2 to the fuel gas CO via the boudouard reaction: A review. Renew. Sustain. Energy Rev. 2015, 41, 615–632. [Google Scholar]
- Kim, Y.T.; Seo, D.K.; Hwang, J. Study of the effect of coal type and particle size on char-CO2 gasification via gas analysis. Energy Fuels 2011, 25, 5044–5054. [Google Scholar] [CrossRef]
- Shurtz, R.C.; Fletcher, T.H. Coal char-CO2 gasification measurements and modeling in a pressurized flat-flame burner. Energy Fuels 2013, 27, 3022–3038. [Google Scholar]
- Xu, K.; Hu, S.; Su, S.; Xu, C.; Sun, L.; Shuai, C.; Jiang, L.; Xiang, J. Study on char surface active sites and their relationship to gasification reactivity. Energy Fuels 2012, 27, 118–125. [Google Scholar]
- Duman, G.; Uddin, M.A.; Yanik, J. The effect of char properties on gasification reactivity. Fuel Process. Technol. 2014, 118, 75–81. [Google Scholar] [CrossRef]
- Alvarez, J.; Lopez, G.; Amutio, M.; Bilbao, J.; Olazar, M. Kinetic Study of Carbon Dioxide Gasification of Rice Husk Fast Pyrolysis Char. Energy Fuels 2015, 29, 3198–3207. [Google Scholar] [CrossRef]
- Hurt, R.H.; Sarofim, A.F.; Longwell, J.P. The role of microporous surface area in the gasification of chars from a sub-bituminous coal. Fuel 1991, 70, 1079–1082. [Google Scholar] [CrossRef]
- Keown, D.M.; Hayashi, J.I.; Li, C.Z. Drastic changes in biomass char structure and reactivity upon contact with steam. Fuel 2008, 87, 1127–1132. [Google Scholar] [CrossRef]
- Rafsanjani, H.H.; Jamshidi, E.; Rostam-Abadi, M. A new mathematical solution for predicting char activation reactions. Carbon 2002, 40, 1167–1171. [Google Scholar] [CrossRef]
- Feng, B.; Bhatia, S.K. Variation of the Pore Structure of Coal Chars During Gasification. Carbon 2003, 41, 507–523. [Google Scholar] [CrossRef]
- Liu, G.; Benyon, P.; Benfell, K.E.; Bryant, G.W.; Tate, A.G.; Boyd, R.K. The Porous Structure of Bituminous Coal Chars and its Influence on Combustion and Gasification Under Chemically Controlled Conditions. Fuel 2000, 79, 617–626. [Google Scholar] [CrossRef]
- Karouki, E.; Sfakiotakis, S. Gasification of waste biomass chars by carbon dioxide via thermogravimetry. Part I: Effect of mineral matter. Fuel 2011, 90, 1120–1127. [Google Scholar]
- Wu, S.; Gu, J.; Li, L.; Wu, Y.; Gao, J. The reactivity and kinetics of Yanzhou coal chars from elevated pyrolysis temperatures during gasification in steam at 900–1200 °C. Process Saf. Environ. Prot. 2006, 84, 420–428. [Google Scholar]
- Wang, G.; Zhang, J.; Shao, J.; Liu, Z.; Wang, H.; Li, X.; Zhang, P.; Geng, W.; Zhang, G. Experimental and modeling studies on CO2 gasification of biomass chars. Energy 2016, 114, 143–154. [Google Scholar] [CrossRef]
- Cortazar, M.; Lopez, G.; Alvarez, J.; Arregi, A.; Amutio, M.; Bilbao, J.; Olazar, M. Experimental study and modeling of biomass char gasification kinetics in a novel thermogravimetric flow reactor. Chem. Eng. J. 2020, 369, 125200. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Perlmutter, D.D. A random pore model for fluid-solid reactions: I.isothermal, kinetic control. AIChE J. 1980, 26, 379–386. [Google Scholar]
- Dutta, S.; Wen, C.Y.; Belt, R.J. Reactivity of coal and char 1: In carbon dioxide atmosphere. Ind. Eng. Chem. Process Des. Dev. 1977, 161, 20–30. [Google Scholar] [CrossRef]
- Zhu, J.L.; Tang, H.P.; Xi, Z.P.; Dix, B. Fractal analysis of pore structure and its application for prediction of permeability and porosity. Rare Met. Mater. Eng. 2009, 38, 2106–2110. [Google Scholar]
- Yang, D.K.; Wang, K.; Wang, J.F. Correlation analysis of surface fractal dimension and pore properties of zeolite molecular sieve. Ind. Catal. 2014, 22, 443–446. [Google Scholar]
- Chen, X.D.; Zhou, J.K.; Ding, N. Fractal characterization of pore system evolution in cementitious materials. KSCE J. Civ. Eng. 2015, 19, 719–724. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Li, K.; Zhou, L. Fractal surface and fractal adsorption model of sediment. J. Hydraul. Eng. 2003, 3, 14–18. [Google Scholar]
- Zhao, Z.G. Surface fractal analysis of mesoporous adsorbent. Acta Chim. Sin. 2004, 62, 219–223. [Google Scholar]
- Ren, A.L.; Wang, Q.S.; Guo, B. Structure characterization and surface fractal analysis of sludge activated carbon. Acta Chim. Sin. 2006, 64, 1068–1072. [Google Scholar]
- Zhuang, Q.; Li, T.H.; Chen, Q.X.; Li, F.J.; Cheng, Y.L. Fractal theory and its application in the study of activated carbon. Carbon Tech. 2009, 28, 36–40. [Google Scholar]
- Passe-Coutrin, N.; Altenor, S.; Cossement, D.; Jean-Marius, C.; Gaspard, S. Comparison of parameters calculated from the BET and Freundlich isotherms obtained by nitrogen adsorption on activated carbons: A new method for calculating the specific surface area. Microporous Mesoporous Mater. 2008, 111, 517–522. [Google Scholar] [CrossRef]
- Zhang, J.Z. Fractal[M]; Tsinghua University Press: Beijing, China, 2011; pp. 369–376. [Google Scholar]
- Wang, J.Z.; Zhou, A.N.; Liu, G.Y.; Song, Z.X.; Ma, C.; Wang, D. Study on fractal model of activated carbon for pore formation. Carbon Lett. 2022, 32, 863–873. [Google Scholar] [CrossRef]
- Liu, H.; Luo, C.H.; Kaneko, M.; Kato, S.; Kojima, T. Unification of gasification kinetics of char in CO2 at elevated temperatures with a modified random pore model. Energy Fuels 2003, 17, 961–970. [Google Scholar] [CrossRef]
- Ahmed, I.I.; Gupta, A.K. Kinetics of woodchips char gasification with steam and carbon dioxide. Appl. Energy 2011, 88, 1613–1619. [Google Scholar]
- Seo, D.K.; Lee, S.K.; Kang, M.W.; Hwang, J.; Yu, T.U. Gasification reactivity of biomass chars with CO2. Biomass Bioenergy 2010, 34, 1946–1953. [Google Scholar] [CrossRef]
- Struis RP, W.J.; Scala, C.V.; Stucki, S.; Prins, R. Gasification reactivity of charcoal with CO2. Part I: Conversion and structural phenomena. Chem. Eng. Sci. 2002, 57, 3581–3592. [Google Scholar]
- Morimoto, T.; Ochiai, T.; Wasaka, S.; Oda, H. Modeling on pore variation of coal chars during CO2 gasification associated with their submicropores and closed pores. Energy Fuels 2006, 20, 353–358. [Google Scholar]

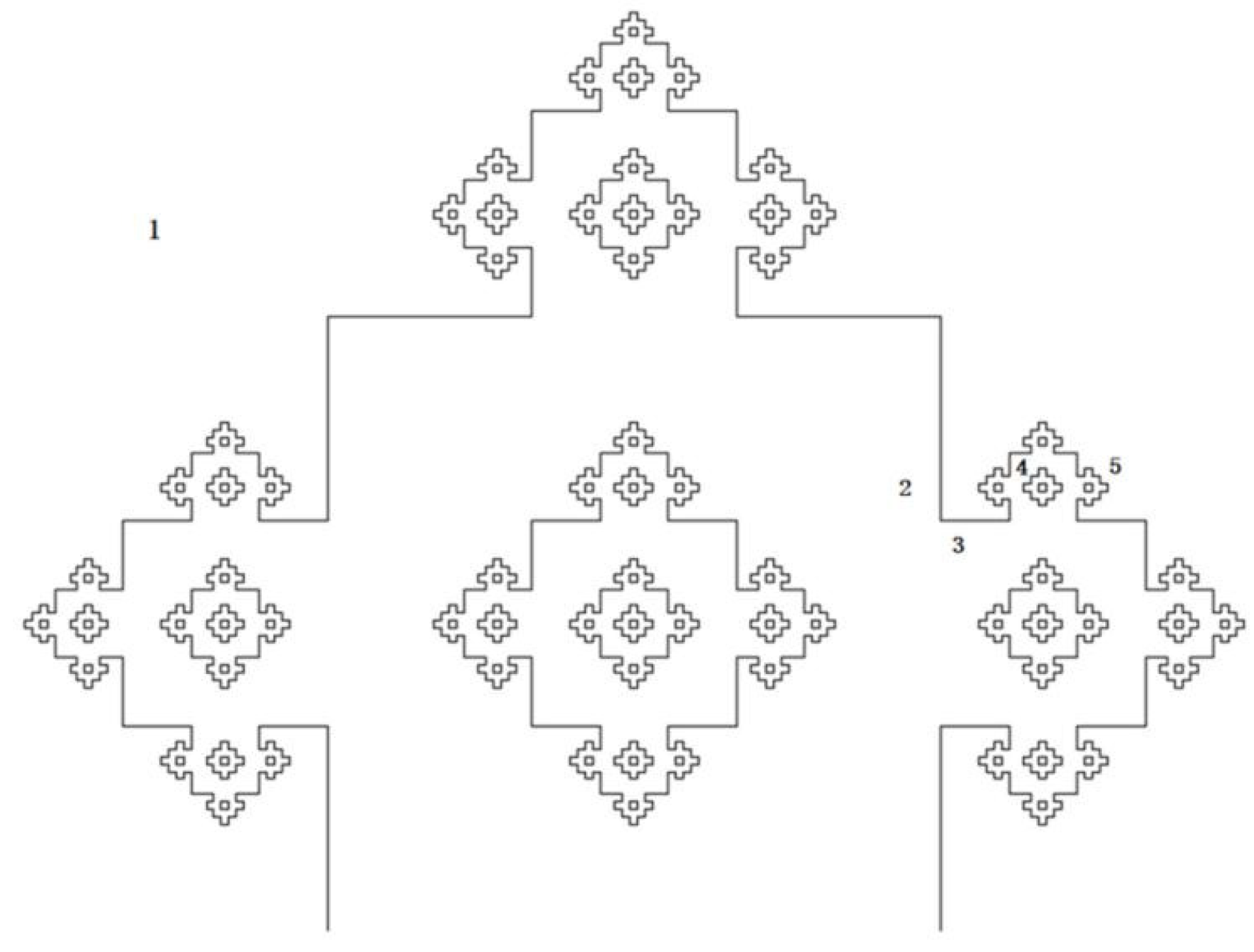


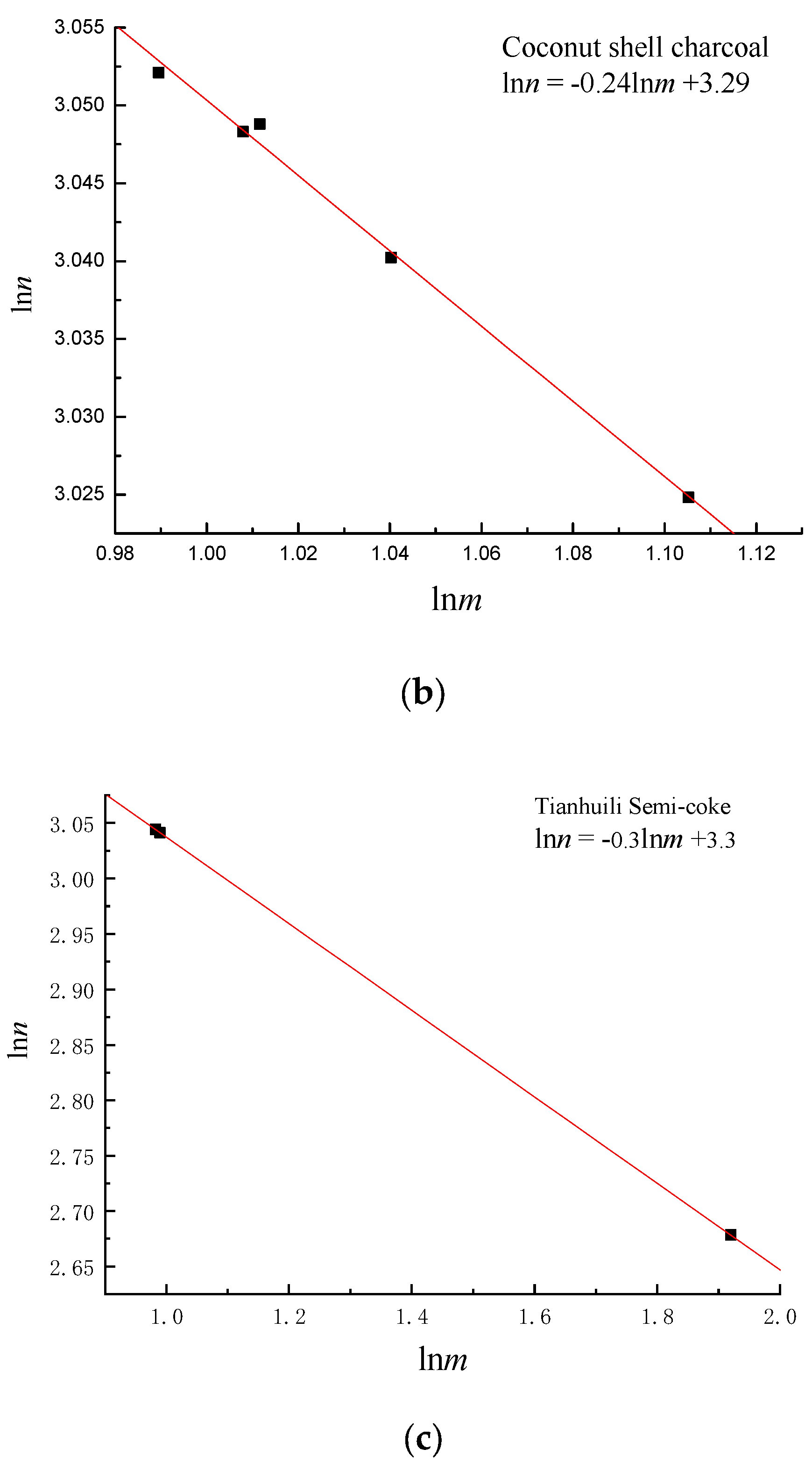
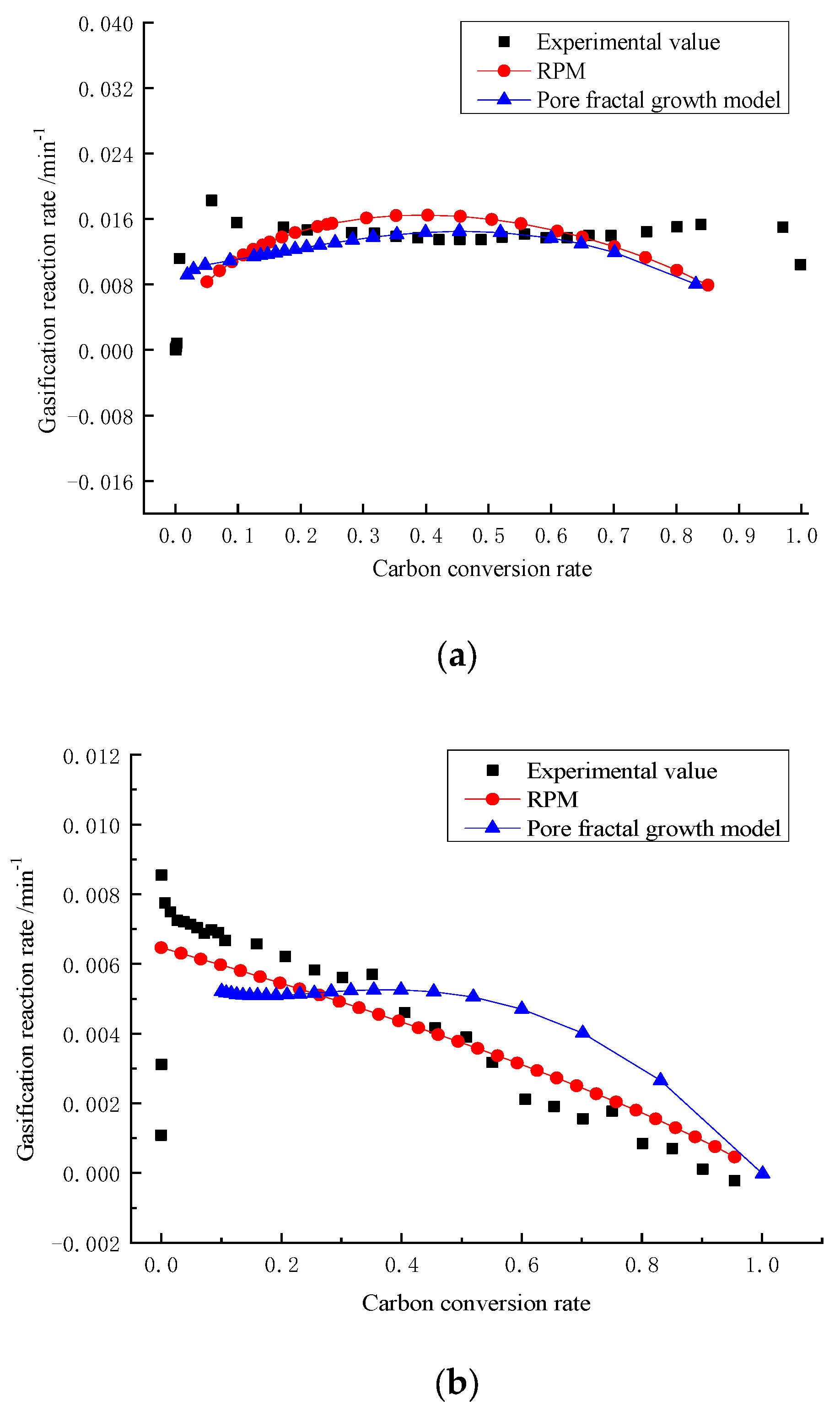
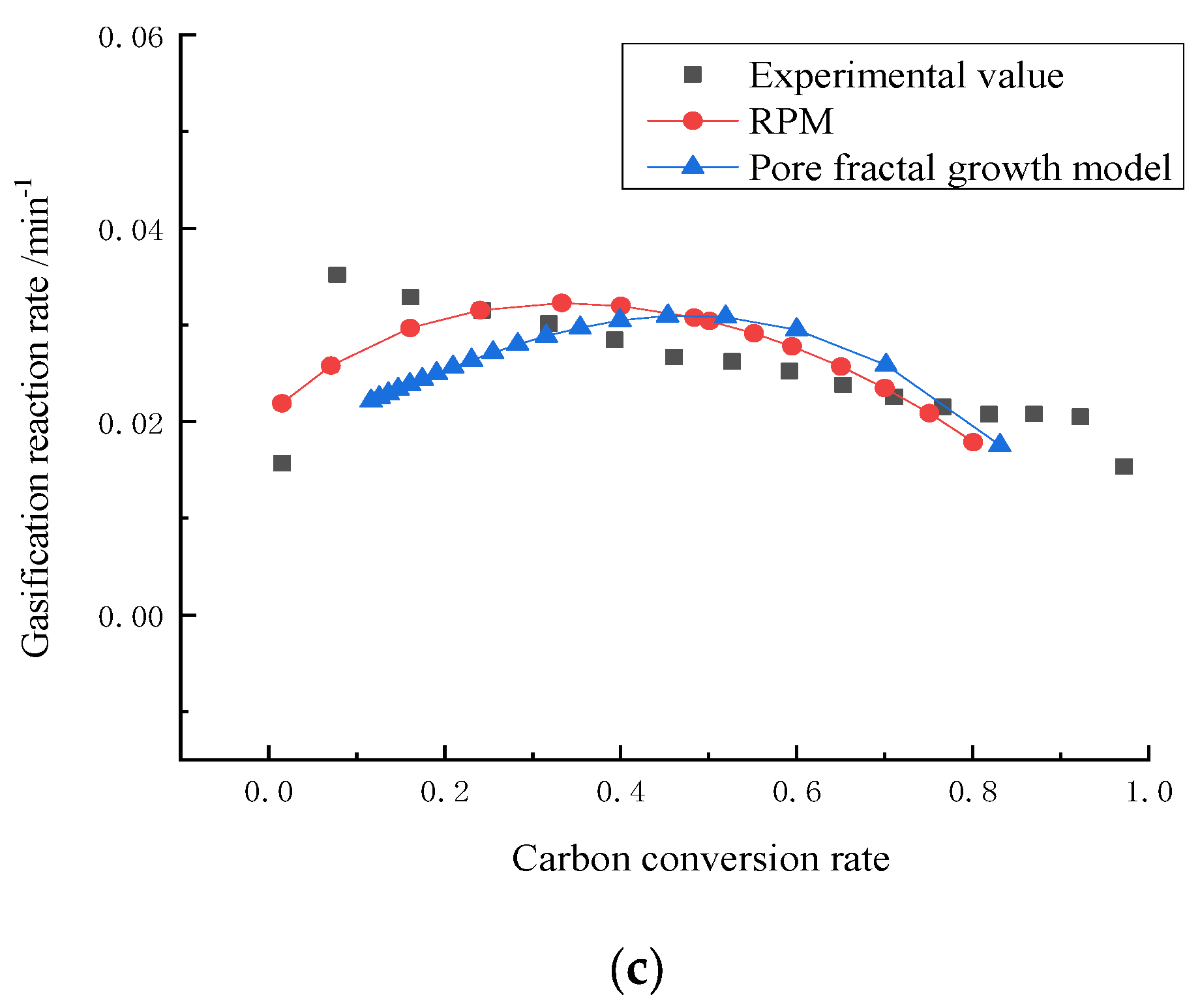
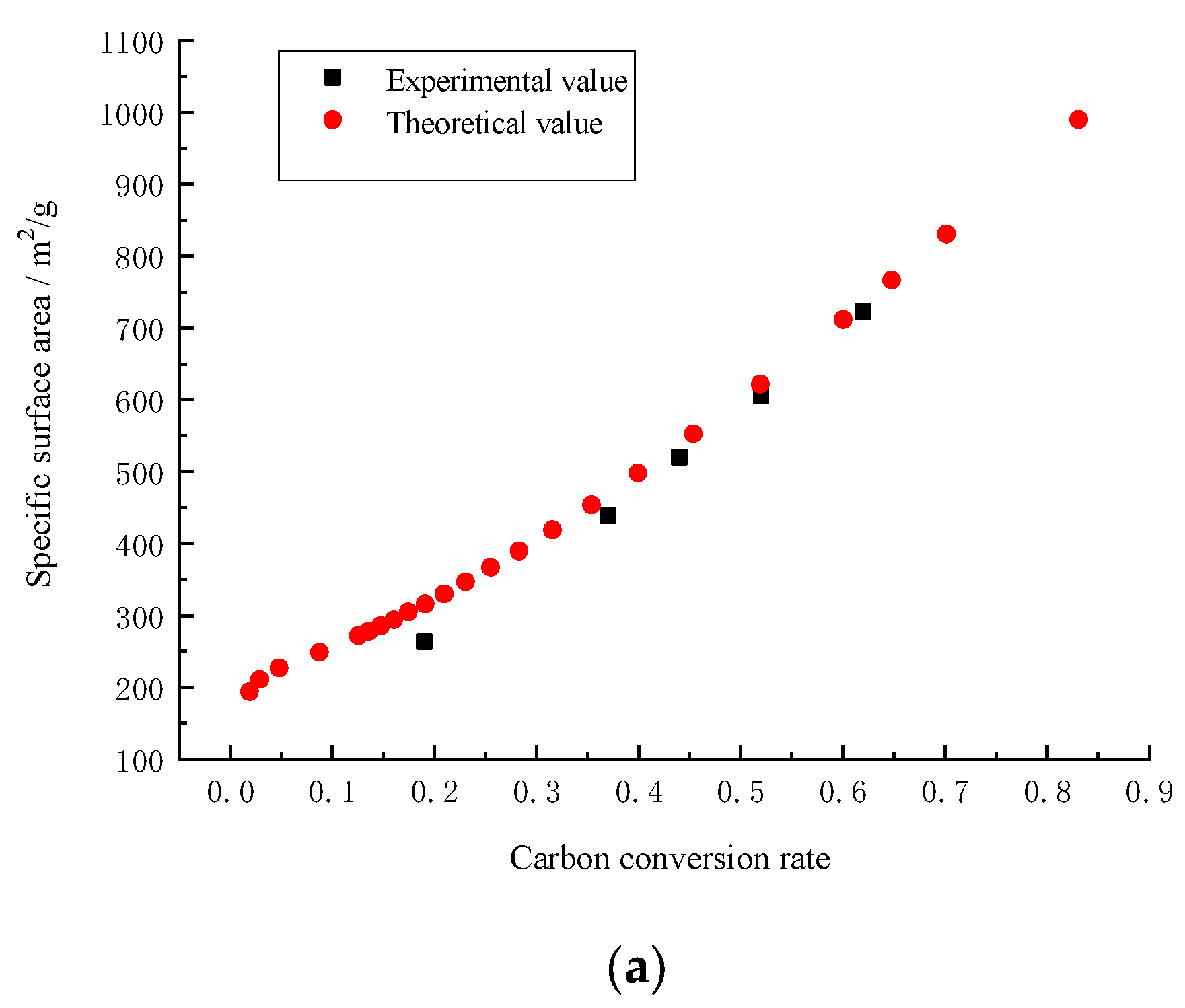
| Degree | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|
| Side length | 1 | 1/3 | (1/3)2 | (1/3)3 | (1/3)n−1 |
| Single area | 0 | (1/3)2 | (1/3)2×2 | (1/3)2×3 | (1/3)2×(n−1) |
| Number of new pores | 0 | 6 | 13 × 6 | 132 × 6 | 13n−2 × 6 |
| Number of new surfaces | 0 | 5 × 6 | 13 × 5 × 6 | 132 × 5 × 6 | (1/3)n−2 × 5 × 6 |
| New area | 0 | 5 × 6 × (1/3)2 | 13 × 5 × 6 × (1/3)2×2 − 5 × 6 × (1/3)2×2 | 132 × 5 × 6 × (1/3)2×3 − 13 × 5 × 6 × (1/3)2×3 | …… |
| Total number of pores | 0 | 6 | 6 × 33 + 13 × 6 | 6 × 33×2 + 13 × 6 × 33 + 132 × 6 | …… |
| Total pore volume | 0 | 6 × (1/3)3 | (6 × 33 + 13 × 6) × (1/3)3 × 2 | (6 × 33×2 + 13 × 6 × 33 + 132 × 6) × (1/3)3×3 | …… |
| Sample | Volatile Matter (wt.%) | Fixed Carbon (wt.%) | Ash (wt.%) |
|---|---|---|---|
| Tianhuili semi-coke | 12.54 | 69.26 | 5.71 |
| Apple charcoal | 9.48 | 78.65 | 5.11 |
| Coconut shell charcoal | 4.89 | 76.27 | 6.42 |
| Raw Material | Heating Rate | Carbonization Temperature | Carbonization Time | Gasification Temperature | Gasification Time/min |
|---|---|---|---|---|---|
| Tianhuili semi-coke | 10 °C/min | 600 °C | 60 min | 850 °C | (0, 60, 120, 180, 240) |
| Coconut shell charcoal | 10 °C/min | 600 °C | 60 min | 850 °C | (0, 60, 90, 120, 180) |
| Apple charcoal | 10 °C/min | 600 °C | 60 min | 850 °C | (0, 30, 60, 90, 120) |
| Purge gas | Before reaching the gasification temperature of 850 °C, nitrogen was injected as a protective gas; after reaching 850 °C, the reactant gas CO2 was injected. After the gasification process, the gas was switched to N2 at room temperature for protection. | ||||
| Raw Material | Specific Surface Area/ SSSA/m2/g | Pore Volume V/mL/g | Carbon Conversion Rate x | Fractal Dimension/D | Reaction Step Length/m | Reaction Degree/n | S n |
|---|---|---|---|---|---|---|---|
| Apple charcoal-0 | 263.89 | 0.133 | 0.19 | 2.7804 | 3.68 | 19.54 | 1.25 × 1011 |
| Apple charcoal-30 | 439.55 | 0.262 | 0.37 | 2.8103 | 3.10 | 20.44 | 2.11 × 1011 |
| Apple charcoal-60 | 520.49 | 0.315 | 0.44 | 2.8186 | 2.98 | 20.66 | 2.50 × 1011 |
| Apple charcoal-90 | 606.19 | 0.370 | 0.52 | 2.8262 | 2.88 | 20.85 | 2.90 × 1011 |
| Apple charcoal-120 | 723.37 | 0.440 | 0.62 | 2.8348 | 2.78 | 21.04 | 3.48 × 1011 |
| Coconut shell charcoal-0 | 492.62 | 0.295 | 0.41 | 2.8158 | 3.02 | 20.59 | 2.35 × 1011 |
| Coconut shell charcoal-60 | 636.49 | 0.401 | 0.56 | 2.8301 | 2.83 | 20.91 | 3.02 × 1011 |
| Coconut shell charcoal-80 | 760.81 | 0.459 | 0.64 | 2.8375 | 2.75 | 21.09 | 3.66 × 1011 |
| Coconut shell charcoal-120 | 743.28 | 0.475 | 0.67 | 2.8383 | 2.74 | 21.08 | 3.58 × 1011 |
| Coconut shell charcoal-180 | 798.84 | 0.525 | 0.74 | 2.8431 | 2.69 | 21.16 | 3.81 × 1011 |
| Tianhuili Semi-coke-0 | 2.58 | 0.016 | 0.02 | 2.6582 | 6.82 | 14.56 | 1.23× 109 |
| Tianhuili Semi-coke-60 | 570.50 | 0.525 | 0.74 | 2.8414 | 2.69 | 20.93 | 2.73 × 1011 |
| Tianhuili Semi-coke-120 | 619.26 | 0.536 | 0.75 | 2.8437 | 2.67 | 20.99 | 2.95 × 1011 |
| Tianhuili Semi-coke-180 | 602.41 | 0.510 | 0.71 | 2.8407 | 2.70 | 20.96 | 2.89 × 106 |
| Tianhuili Semi-coke-240 | Complete gasification | ||||||
| Raw Material—Gasification Time | Pore Volume mL/g | Carbon Conversion Rate x | dx/dt | S*(1 − x) | K |
|---|---|---|---|---|---|
| Apple charcoal-0 | 0.133 | 0.19 | 0.015 | 214.92 | 6.98 × 10−5 |
| Apple charcoal-30 | 0.262 | 0.37 | 0.0136 | 278.44 | 4.88 × 10−5 |
| Apple charcoal-60 | 0.315 | 0.44 | 0.0136 | 290.93 | 4.67 × 10−5 |
| Apple charcoal-90 | 0.37 | 0.52 | 0.0134 | 291.72 | 4.59 × 10−5 |
| Apple charcoal-120 | 0.44 | 0.62 | 0.0136 | 277.6 | 4.90 × 10−5 |
| Coconut shell charcoal-0 | 0.295 | 0.41 | 0.0047 | 289.09 | 1.63 × 10−5 |
| Coconut shell charcoal-60 | 0.401 | 0.56 | 0.0025 | 278.93 | 8.96 × 10−6 |
| Coconut shell charcoal-80 | 0.459 | 0.64 | 0.00184 | 271.72 | 6.77 × 10−6 |
| Coconut shell charcoal-120 | 0.475 | 0.67 | 0.00167 | 248.8 | 6.71 × 10−6 |
| Coconut shell charcoal-180 | 0.525 | 0.74 | 0.00149 | 211.46 | 7.05 × 10−6 |
| Tianhuili Semi-coke-0 | 0.016 | 0.02 | 0.009 | 2.52 | 3.57 × 10−3 |
| Tianhuili Semi-coke-60 | 0.525 | 0.74 | 0.026 | 151.01 | 1.72 × 10−4 |
| Tianhuili Semi-coke-120 | 0.536 | 0.75 | 0.0215 | 154.38 | 1.39 × 10−4 |
| Tianhuili Semi-coke-180 | 0.51 | 0.71 | 0.0136 | 172.12 | 7.90 × 10−5 |
| Tianhuili Semi-coke-240 | Complete gasification | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhou, A.; Song, Z.; Liu, G.; Qin, S.; Wang, J. The Kinetics of Semi-Coke CO2 Gasification Based on Pore Fractal Growth. Energies 2024, 17, 483. https://doi.org/10.3390/en17020483
Wang J, Zhou A, Song Z, Liu G, Qin S, Wang J. The Kinetics of Semi-Coke CO2 Gasification Based on Pore Fractal Growth. Energies. 2024; 17(2):483. https://doi.org/10.3390/en17020483
Chicago/Turabian StyleWang, Junzhe, Anning Zhou, Zongxing Song, Guoyang Liu, Sicheng Qin, and Jing Wang. 2024. "The Kinetics of Semi-Coke CO2 Gasification Based on Pore Fractal Growth" Energies 17, no. 2: 483. https://doi.org/10.3390/en17020483
APA StyleWang, J., Zhou, A., Song, Z., Liu, G., Qin, S., & Wang, J. (2024). The Kinetics of Semi-Coke CO2 Gasification Based on Pore Fractal Growth. Energies, 17(2), 483. https://doi.org/10.3390/en17020483




