Numerical Study of H2 Production and Thermal Stress for Solid Oxide Electrolysis Cells with Various Ribs/Channels
Abstract
1. Introduction
2. Model Development
- (1)
- All gases are ideal and incompressible in laminar flow.
- (2)
- The porous electrode is homogeneous.
- (3)
- The anode, electrolyte layer and cathode are isotropic and linear elastic, which conform to the isotropic Hooke’s law.
- (4)
- The thermophysical properties (e.g., elastic modulus, coefficient of thermal expansion, and Poisson ratio) of all SOEC components do not change with the local temperature (i.e., evaluated at a constant temperature of 800 °C).
- (5)
- The interface between the anode, cathode, and electrolyte layer is continuous, allowing for free deformation without any fractures.
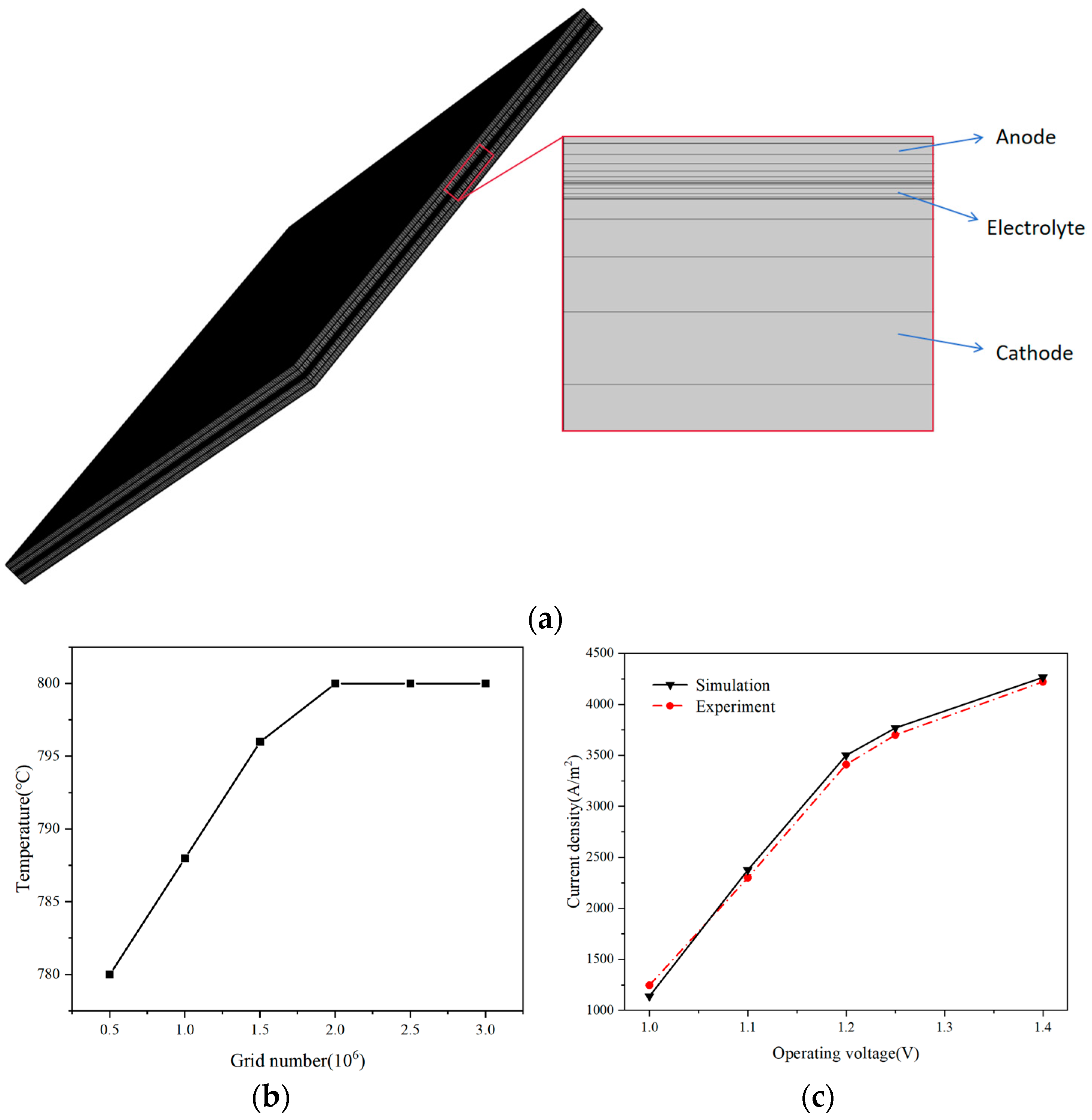
2.1. Full-Scale Stack Geometric Parameters and Modeling Methods
2.2. Governing Equations
2.2.1. Electrochemical Reactions
2.2.2. Gas Flow and Momentum Equations
2.2.3. Gas Transport Equations
2.2.4. Heat Transfer Equation
2.2.5. Thermal Stress–Strain Equation
2.3. Boundary Conditions and Parameters
2.4. Model Validation
3. Results and Discussion
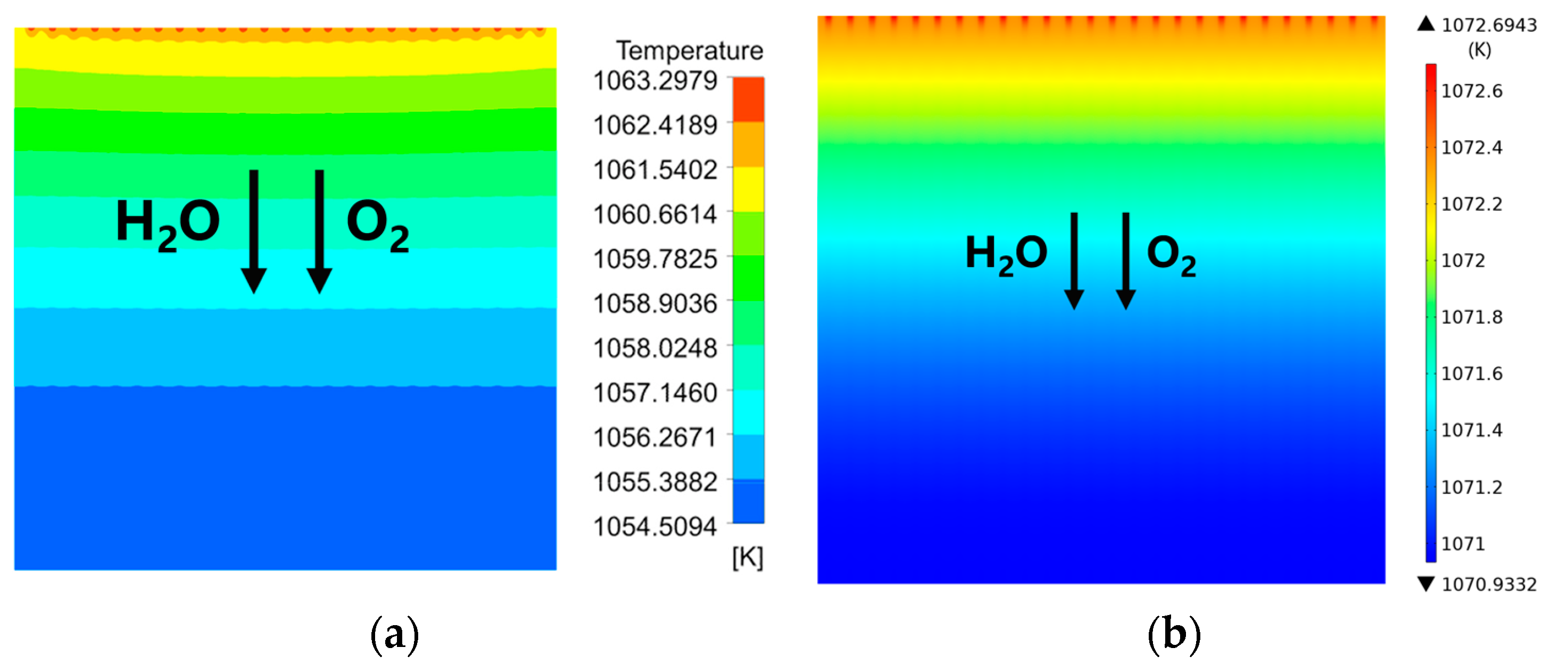
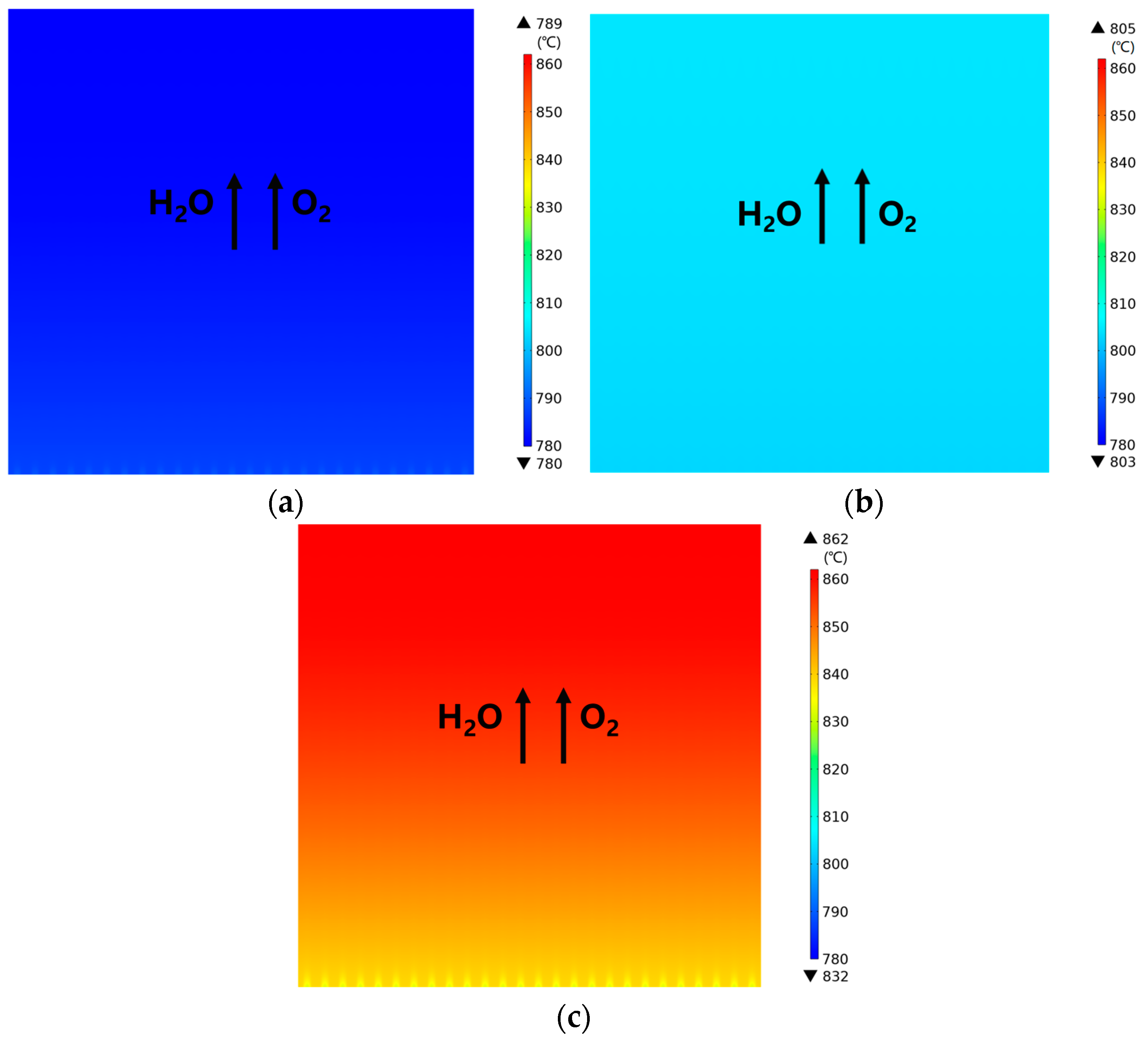
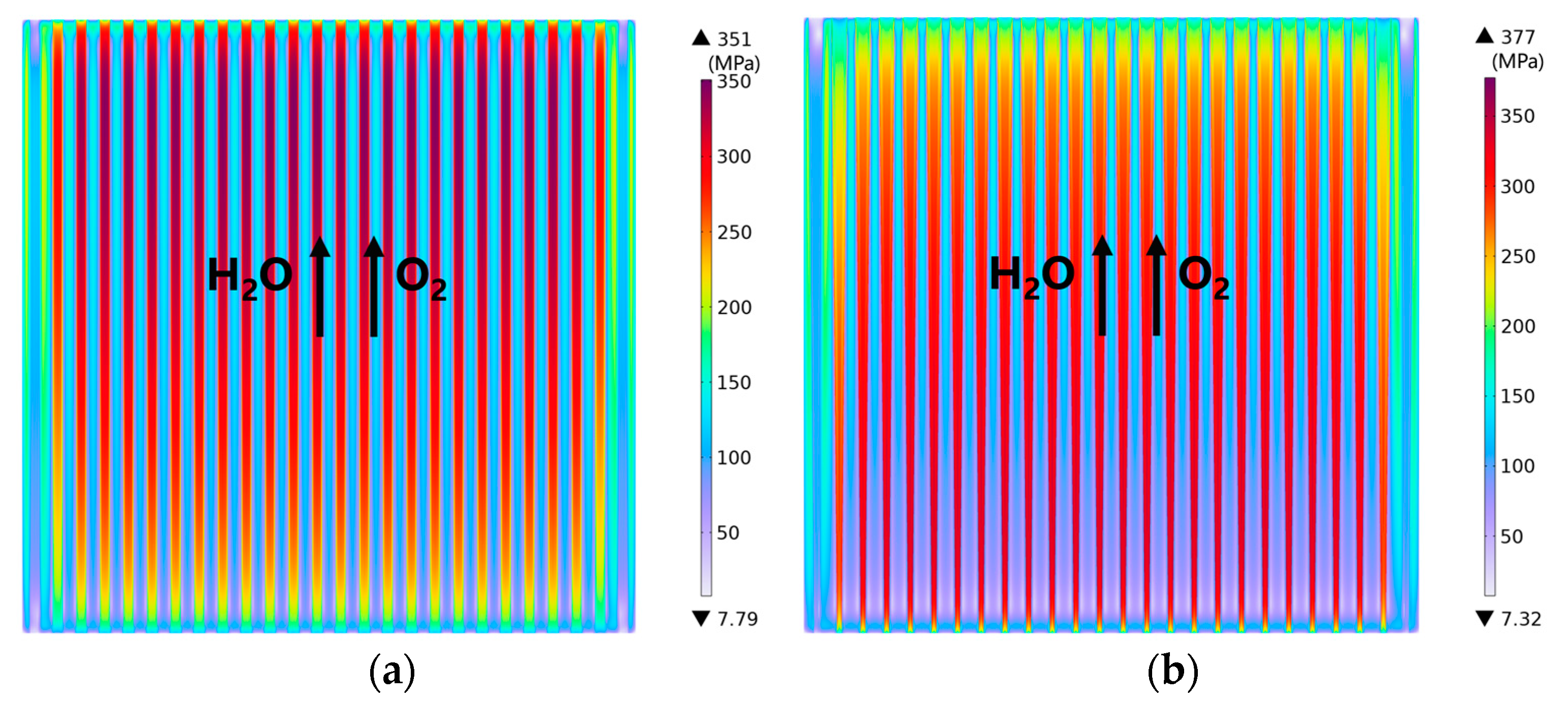
3.1. Predicted Performance for the Base-Case (i.e., Rib/Channel Width Ratio = 1)
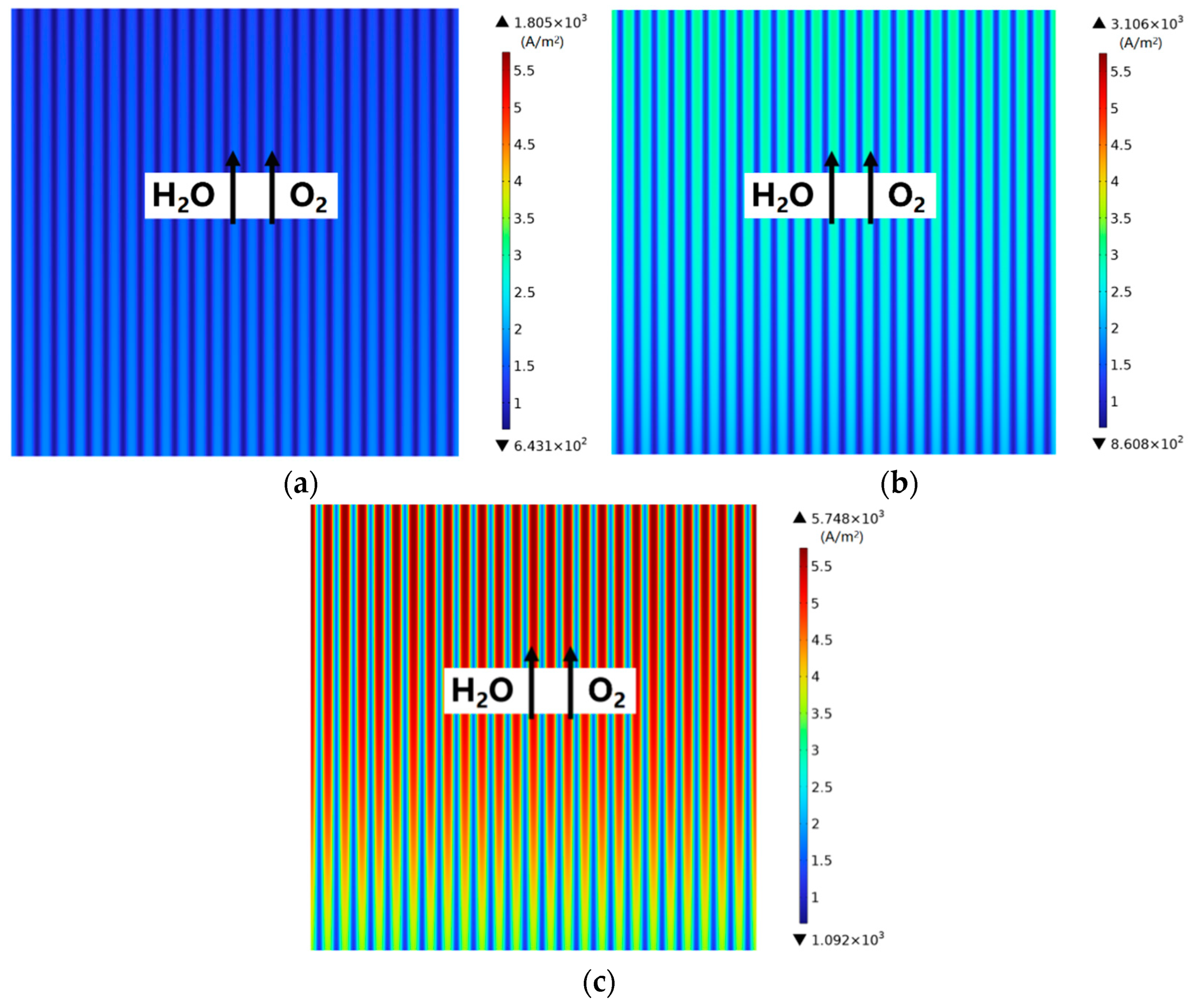
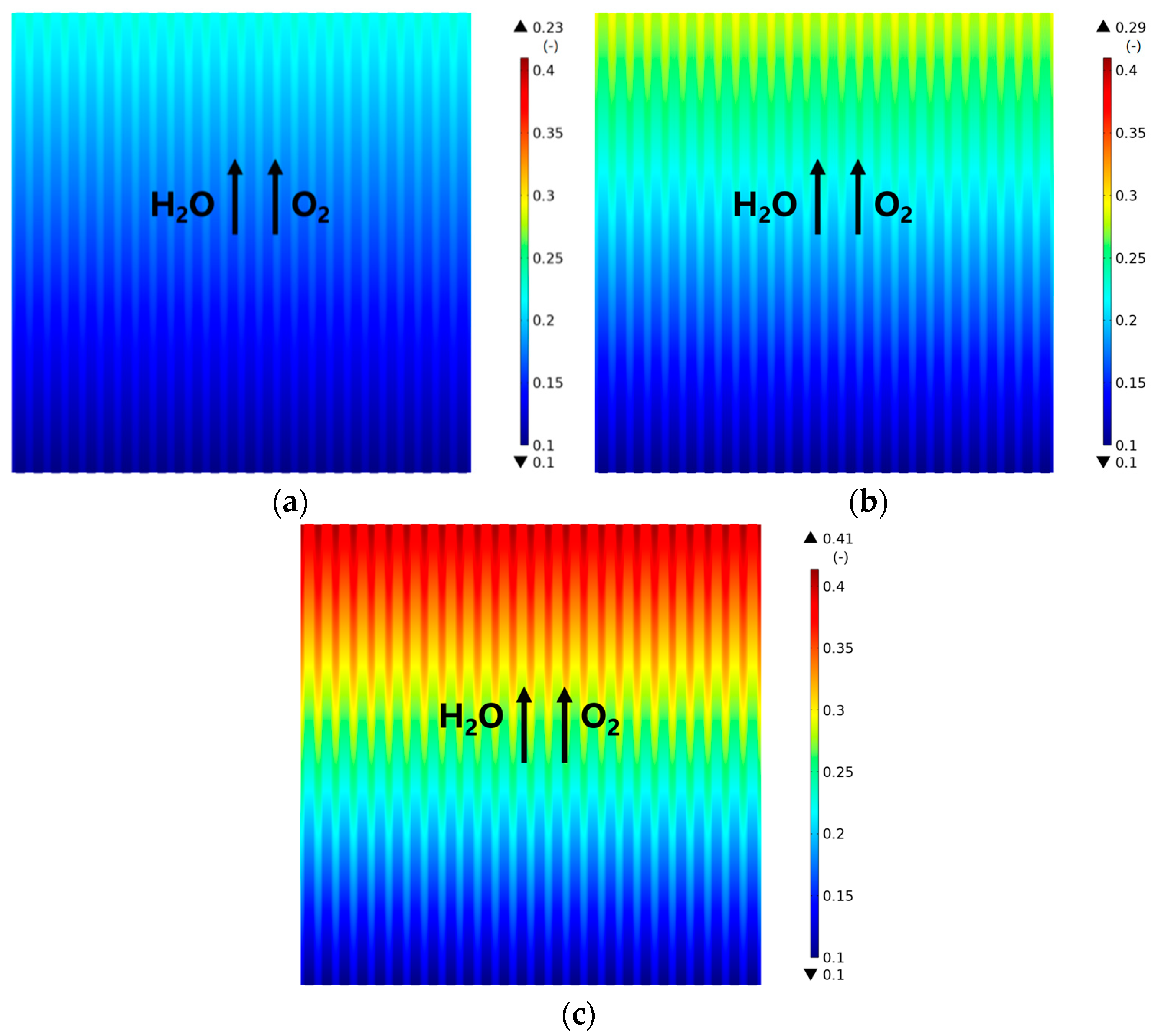
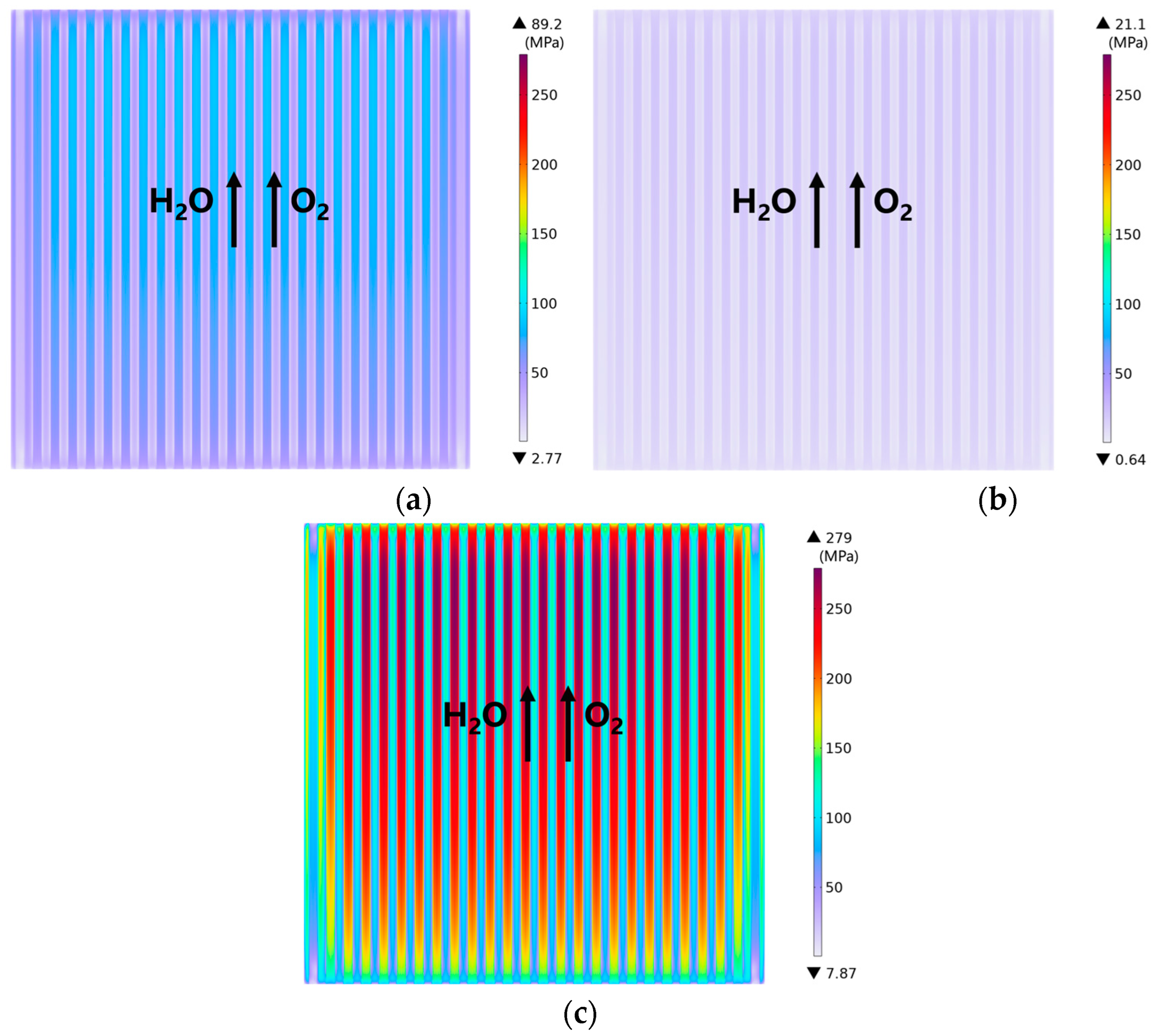
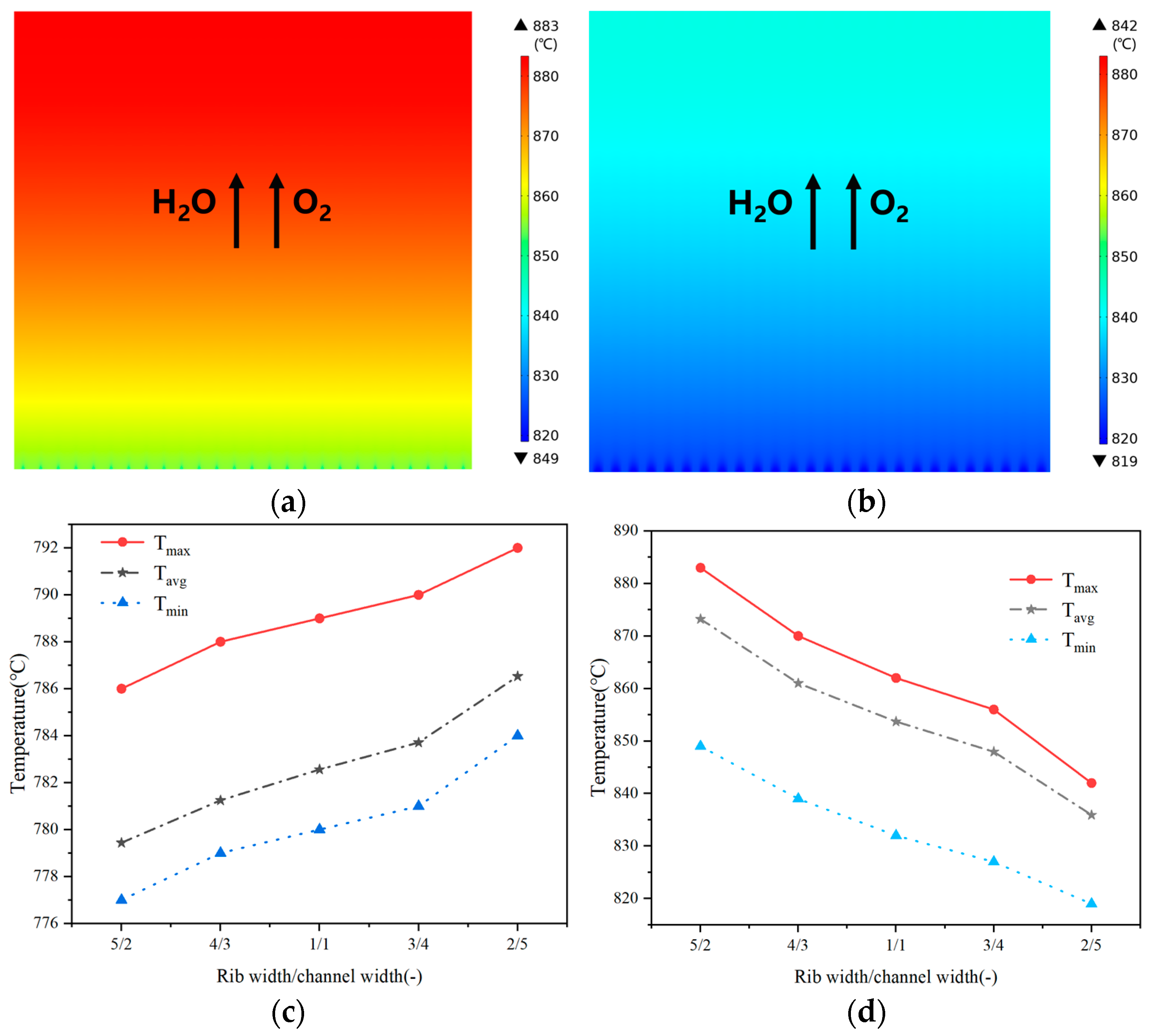
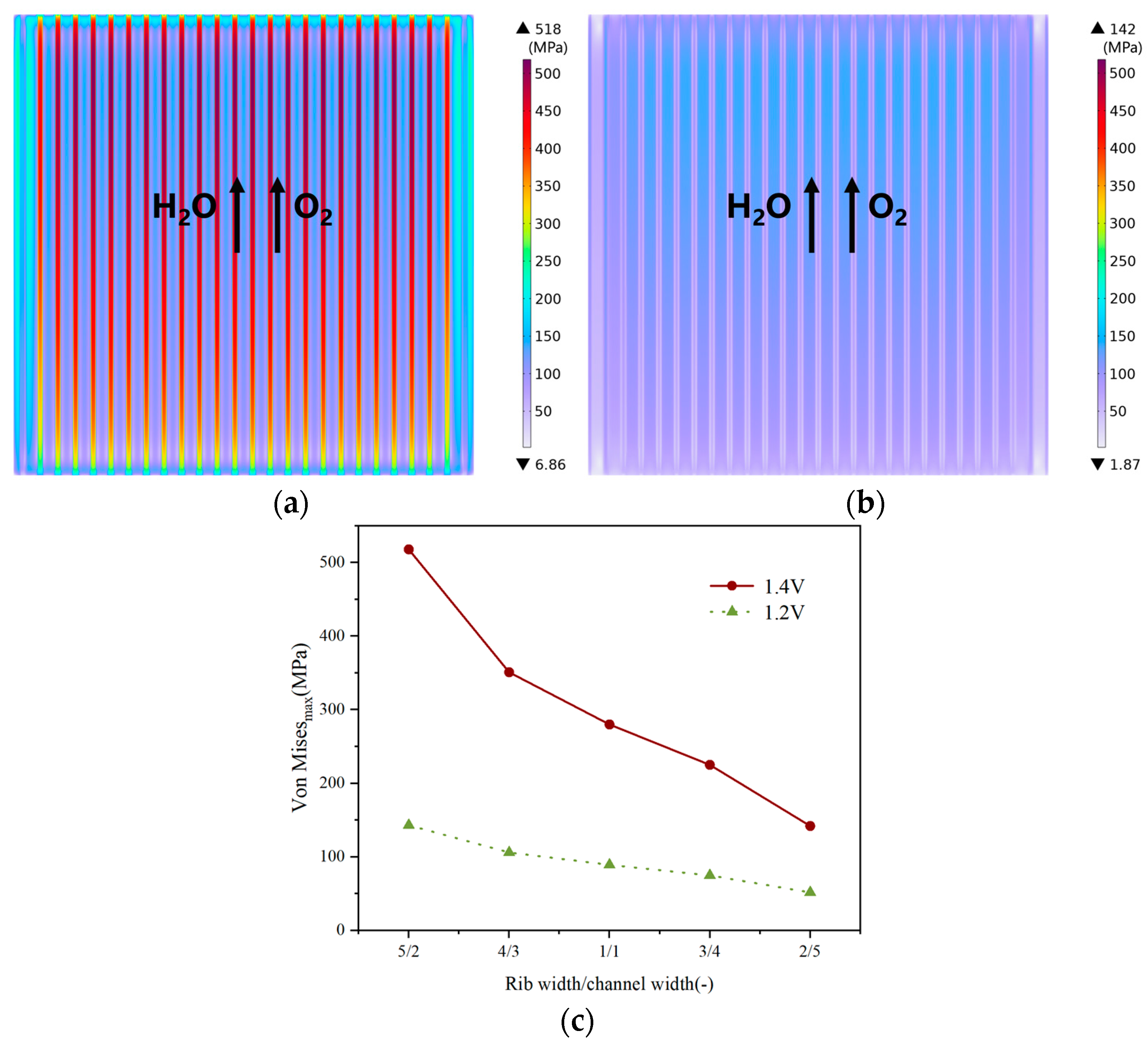
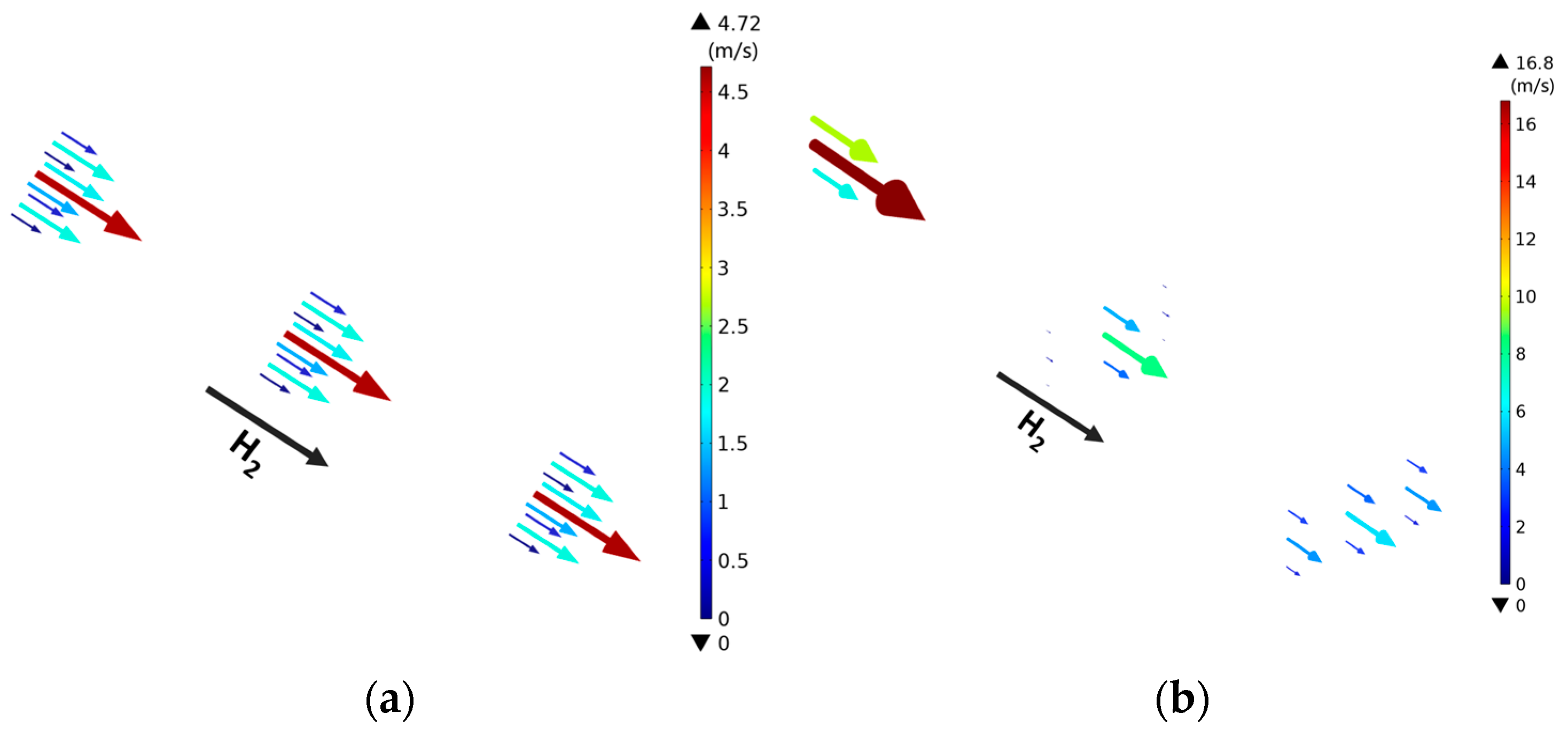
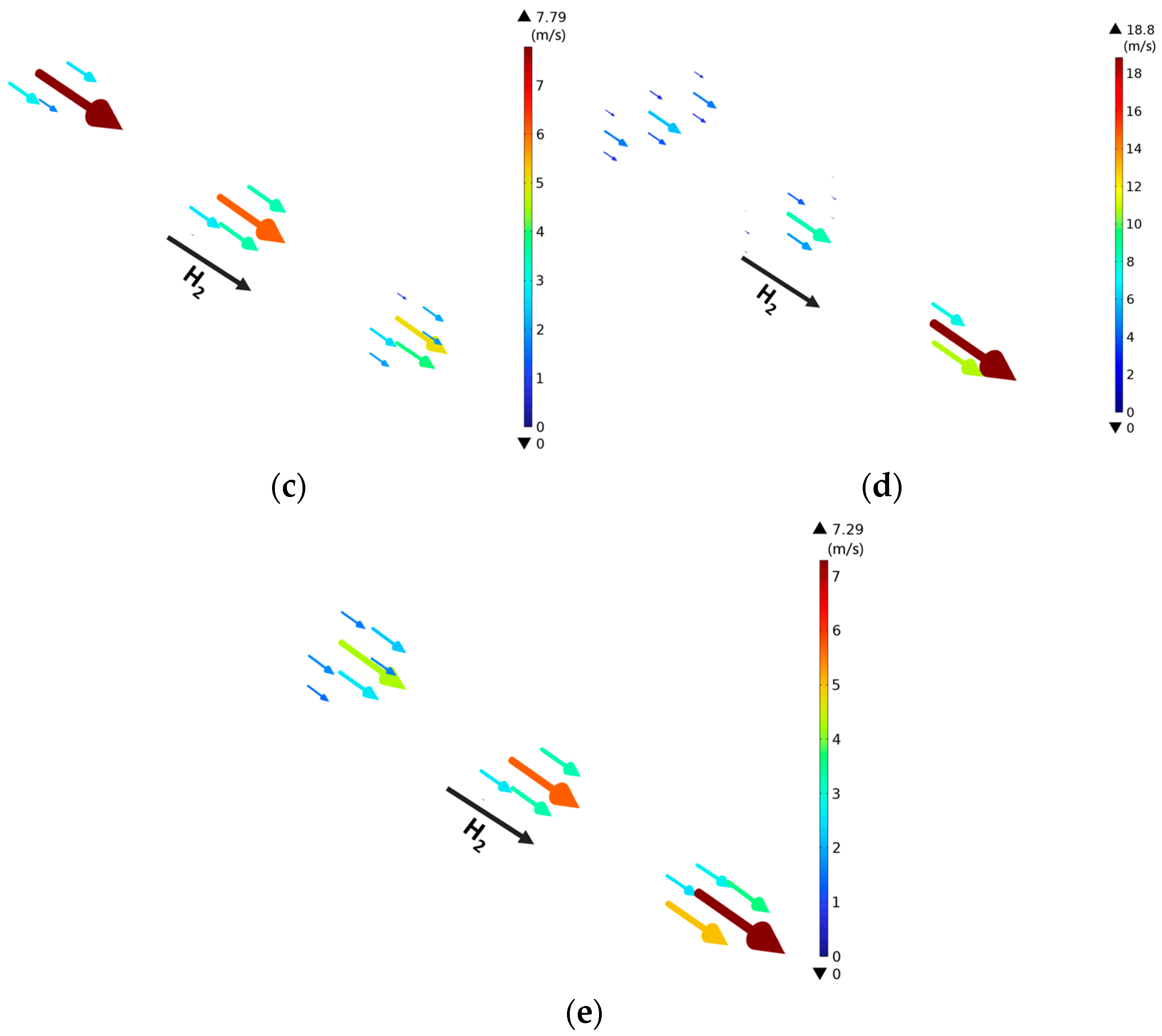
3.2. Effect of Rib/Channel Width Ratio
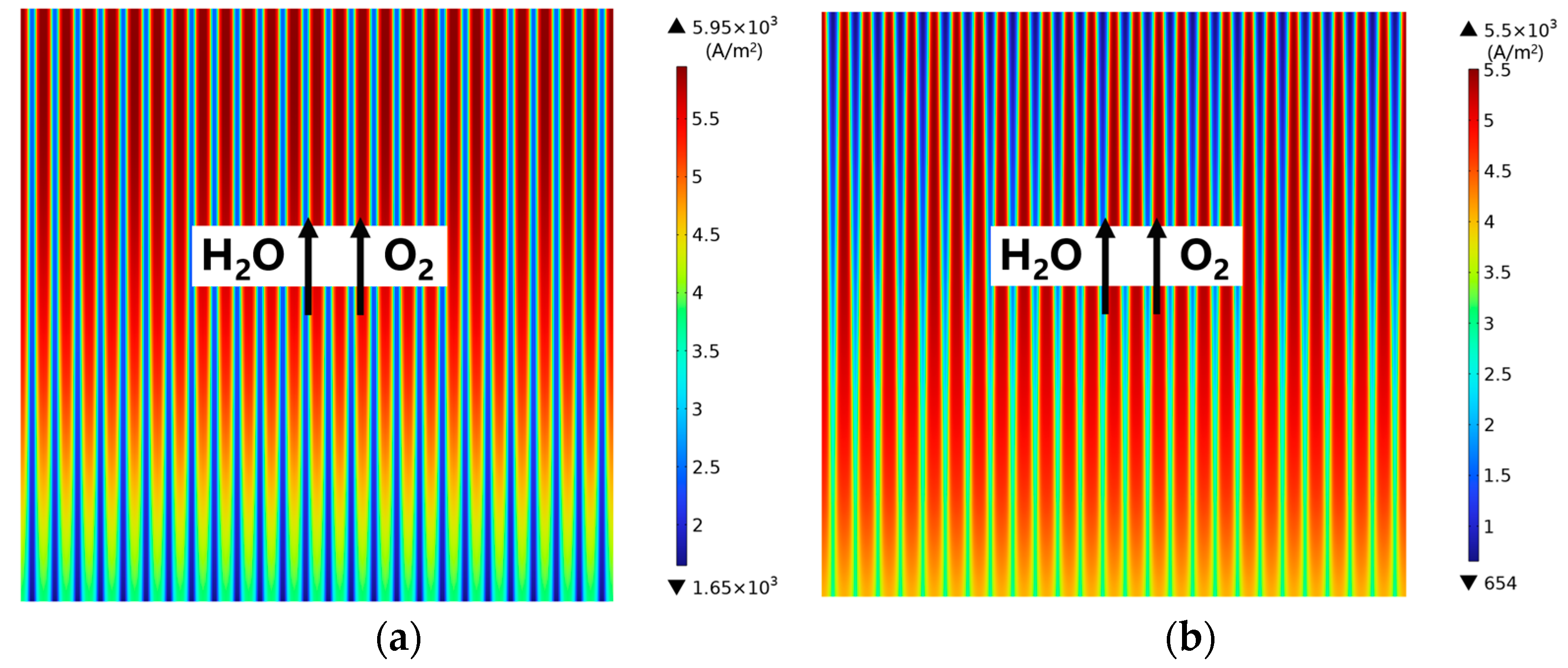
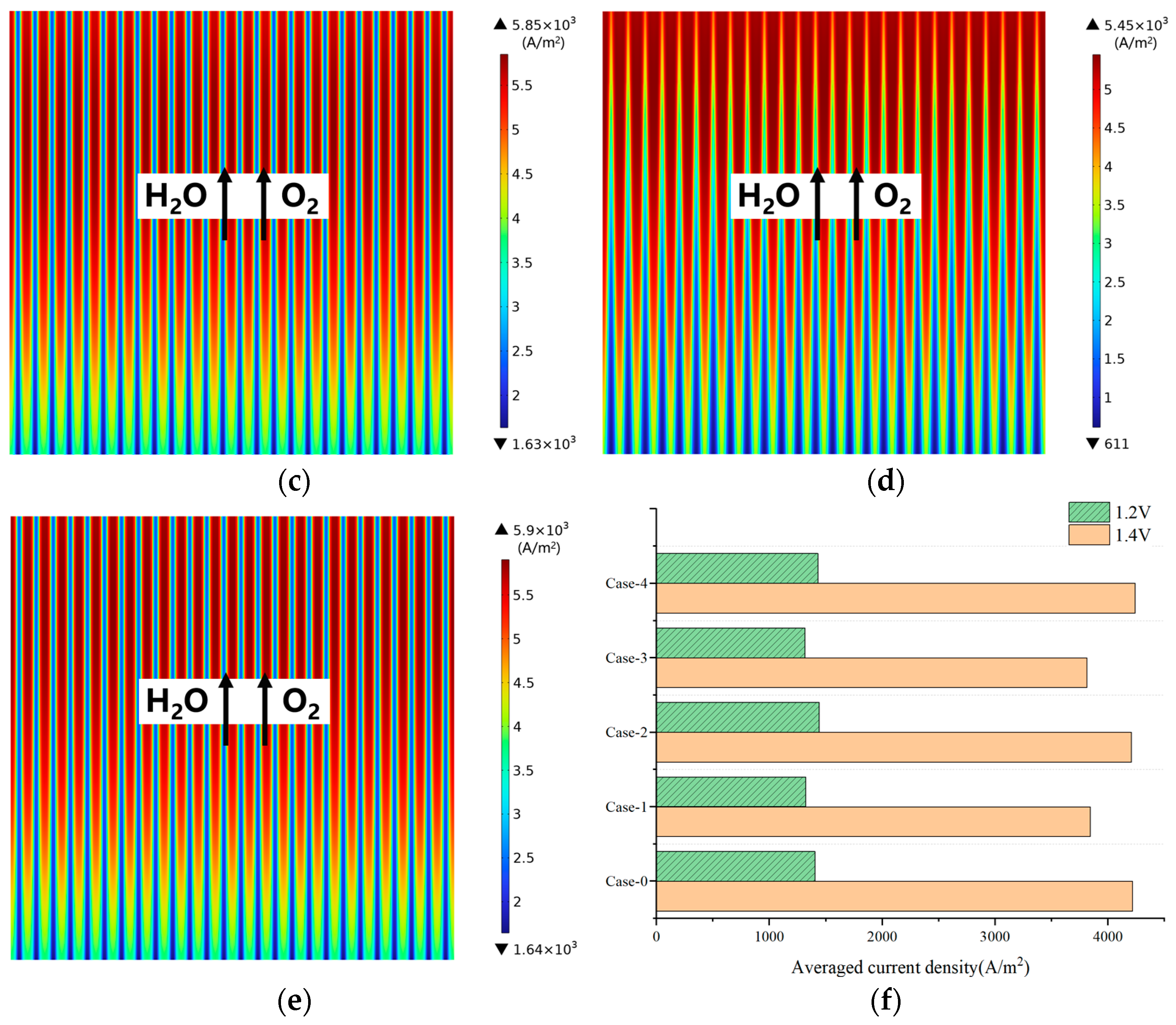
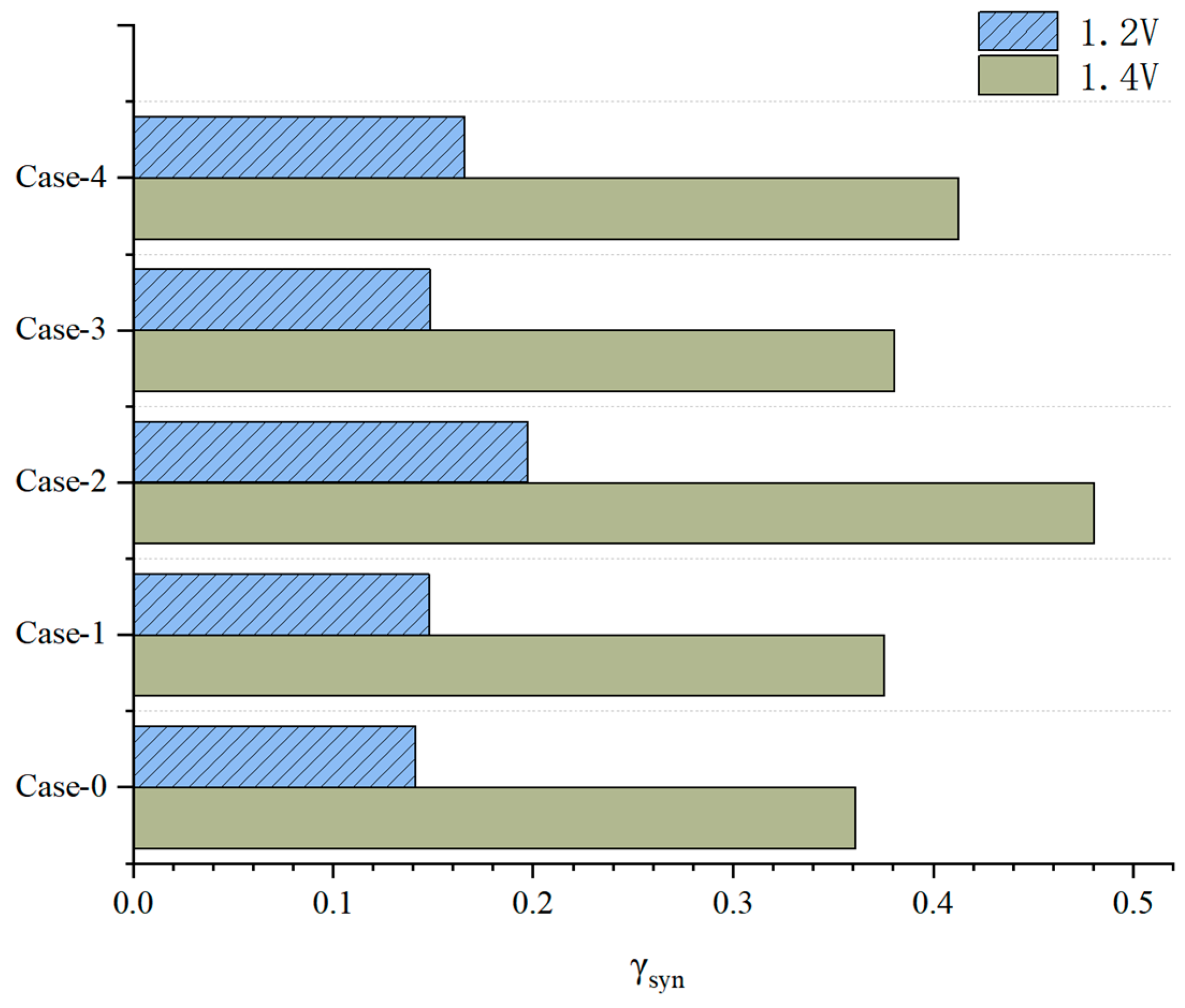
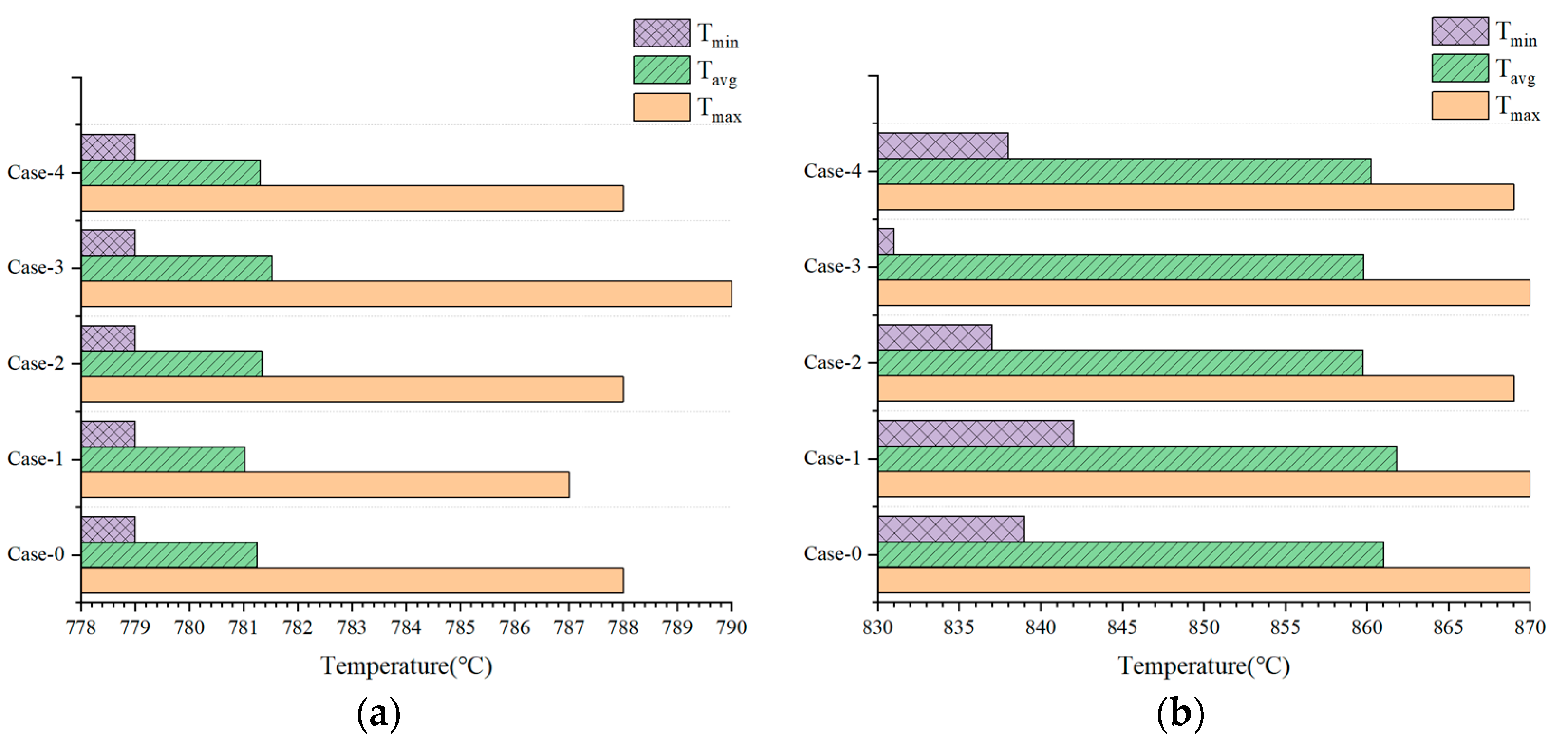
3.3. Effect of Gradient Configuration and Geometry Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, S.; Liu, Q.; Sun, J.; Jin, H. A review on the utilization of hybrid renewable energy. Renew. Sustain. Energy Rev. 2018, 91, 1121–1147. [Google Scholar] [CrossRef]
- Yang, Y.; Bremner, S.; Menictas, C.; Kay, M. Battery energy storage system size determination in renewable energy systems: A review. Renew. Sustain. Energy Rev. 2018, 91, 109–125. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, X.; Shi, Y.; Ghoniem, A.F.; Cai, N. Exergy analysis of an integrated solid oxide electrolysis cell-methanation reactor for renewable energy storage. Appl. Energy 2018, 215, 371–383. [Google Scholar] [CrossRef]
- Jensen, S.H.; Graves, C.; Mogensen, M.; Wendel, C.; Braun, R.; Hughes, G. Large-scale electricity storage utilizing reversible solid oxide cells combined with underground storage of CO2 and CH4. Energy Environ. Sci. 2015, 8, 2471–2479. [Google Scholar] [CrossRef]
- Zhang, X.; Song, Y.; Wang, G.; Bao, X. Co-electrolysis of CO2 and H2O in high-temperature solid oxide electrolysis cells: Recent advance in cathodes. J. Energy Chem. 2017, 26, 839–853. [Google Scholar] [CrossRef]
- Udagawa, J.; Aguiar, P.; Brandon, N. Hydrogen production through steam electrolysis: Control strategies for a cathode-supported intermediate temperature solid oxide electrolysis cell. J. Power Sources 2008, 180, 354–364. [Google Scholar] [CrossRef]
- Cai, Q.; Adjiman, C.S.; Brandon, N.P. Optimal control strategies for hydrogen production when coupling solid oxide electrolysers with intermittent renewable energies. J. Power Sources 2014, 268, 212–224. [Google Scholar] [CrossRef]
- Kornely, M.; Leonide, A.; Weber, A.; Ivers-Tiffée, E. Performance limiting factors in anode-supported cells originating from metallic interconnector design. J. Power Sources 2011, 196, 7209–7216. [Google Scholar] [CrossRef]
- Jiang, S.; Love, J.; Apateanu, L. Effect of contact between electrode and current collector on the performance of solid oxide fuel cells. Solid. State Ionics 2003, 160, 15–26. [Google Scholar] [CrossRef]
- Ferguson, J.R.; Fiard, J.M.; Herbin, R. Three-dimensional numerical simulation for various geometries of solid oxide fuel cells. J. Power Sources 1996, 58, 109–122. [Google Scholar] [CrossRef]
- Tanner, C.W.; Virkar, A.V. A simple model for interconnect design of planar solid oxide fuel cells. J. Power Sources 2003, 113, 44–56. [Google Scholar] [CrossRef]
- Lin, Z.; Stevenson, J.; Khaleel, M. The effect of interconnect rib size on the fuel cell concentration polarization in planar SOFCs. J. Power Sources 2003, 117, 92–97. [Google Scholar] [CrossRef]
- Jeon, D.H.; Nam, J.H.; Kim, C.-J. Microstructural optimization of anode-supported solid oxide fuel cells by a comprehensive microscale model. J. Electrochem. Soc. 2006, 153, A406. [Google Scholar] [CrossRef]
- Liu, S.; Song, C.; Lin, Z. The effects of the interconnect rib contact resistance on the performance of planar solid oxide fuel cell stack and the rib design optimization. J. Power Sources 2008, 183, 214–225. [Google Scholar] [CrossRef]
- Liu, S.; Kong, W.; Lin, Z. Three-dimensional modeling of planar solid oxide fuel cells and the rib design optimization. J. Power Sources 2009, 194, 854–863. [Google Scholar] [CrossRef]
- Kong, W.; Li, J.; Liu, S.; Lin, Z. The influence of interconnect ribs on the performance of planar solid oxide fuel cell and formulae for optimal rib sizes. J. Power Sources 2012, 204, 106–115. [Google Scholar] [CrossRef]
- Kong, W.; Gao, X.; Liu, S.; Su, S.; Chen, D. Optimization of the interconnect ribs for a cathode-supported solid oxide fuel cell. Energies 2014, 7, 295–313. [Google Scholar] [CrossRef]
- Sun, Q.; Ni, M. Three-dimensional Modeling of internal reforming SOFC with a focus on the interconnect size effect. ECS Trans. 2015, 68, 2317–2338. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, Q.; Zhang, W.; Chen, D. Optimization of distributed cylindrical interconnect ribs for anode-and cathode-supported solid oxide fuel cell. Int. J. Electrochem. Soc. 2015, 10, 7521–7534. [Google Scholar] [CrossRef]
- Kong, W.; Han, Z.; Lu, S.; Gao, X.; Wang, X. A novel interconnector design of SOFC. Int. J. Hydrogen Energy 2020, 45, 20329–20338. [Google Scholar] [CrossRef]
- Fu, Q.; Li, Z.; Wei, W.; Liu, F.; Xu, X.; Liu, Z. Performance enhancement of a beam and slot interconnector for anode-supported SOFC stack. Energy Convers. Manag. 2021, 241, 114277. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Mukhopadhyay, J.; Biswas, N.; Basu, R.N.; Das, P.K. Performance evaluation of different bipolar plate designs of 3D planar anode-supported SOFCs. Int. J. Heat Mass. Trans. 2018, 123, 382–396. [Google Scholar] [CrossRef]
- Wang, Y.; Du, Y.; Ni, M.; Zhan, R.; Du, Q.; Jiao, K. Three-dimensional modeling of flow field optimization for co-electrolysis solid oxide electrolysis cell. Appl. Therm. Eng. 2020, 172, 114959. [Google Scholar] [CrossRef]
- Guo, M.; He, Q.; Cheng, C.; Zhao, D.; Ni, M. New interconnector designs for electrical performance enhancement of solid oxide fuel cells: A 3D modelling study. J. Power Sources 2022, 533, 231373. [Google Scholar] [CrossRef]
- Costamagna, P.; Honegger, K. Modeling of solid oxide heat exchanger integrated stacks and simulation at high fuel utilization. J. Electrochem. Soc. 1998, 145, 3995. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, X.; Li, G. Comparative performance investigation of different gas flow configurations for a planar solid oxide electrolyzer cell. Int. J. Hydrogen Energy 2017, 42, 10785–10801. [Google Scholar] [CrossRef]
- Luo, Y.; Shi, Y.; Li, W.; Cai, N. Dynamic electro-thermal modeling of co-electrolysis of steam and carbon dioxide in a tubular solid oxide electrolysis cell. Energy 2015, 89, 637–647. [Google Scholar] [CrossRef]
- Zeng, Y.; Fan, P.; Zhang, X.; Fu, C.; Li, J.; Li, G. Sensitivity analysis for a planar SOFC: Size effects of the porous gas diffusion layer underneath the channel rib. Fuel Cells 2014, 14, 123–134. [Google Scholar] [CrossRef]
- Zheng, J.; Xiao, L.; Wu, M.; Lang, S.; Zhang, Z.; Yuan, J. Numerical analysis of thermal stress for a stack of planar solid oxide fuel cells. Energies 2022, 15, 343. [Google Scholar] [CrossRef]
- Cui, D.; Cheng, M. Thermal stress modeling of anode supported micro-tubular solid oxide fuel cell. J. Power Sources 2009, 192, 400–407. [Google Scholar] [CrossRef]
- Pianko-Oprych, P.; Zinko, T.; Jaworski, Z. A numerical investigation of the thermal stresses of a planar solid oxide fuel cell. Materials 2016, 9, 814. [Google Scholar] [CrossRef] [PubMed]
- Gross-Barsnick, S.-M.; Babelot, C.; Federmann, D.; Pabst, U. Optimization of tensile strength measurements on glass-ceramic sealant used for SOFC stacks. ECS Trans. 2015, 68, 2573. [Google Scholar] [CrossRef]
- Qu, Z.; Aravind, P.; Boksteen, S.; Dekker, N.; Janssen, A.; Woudstra, N. Three-dimensional computational fluid dynamics modeling of anode-supported planar SOFC. Int. J. Hydrogen Energy 2011, 36, 10209–10220. [Google Scholar] [CrossRef]
- Guo, M.; Zhao, D.; Xu, Q.; Li, Z.; Xu, H.; Ni, M. New interconnector design optimization to balance electrical and mechanical performance of solid oxide fuel cell stack. Int. J. Hydrogen Energy 2023, 48, 3107–3121. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Cell width | 91 mm |
| Cell length | 91 mm |
| Channel height | 1 mm |
| Channel width | 1.75 mm |
| Rib width | 1.75 mm |
| Number of channels | 26 |
| Cathode thickness | 410 μm |
| Electrolyte layer thickness | 10 μm |
| Anode thickness | 25 μm |
| γ/A∙m−2 | Eact/J∙mol−1 | |
|---|---|---|
| Cathode | 1.34 × 1010 | 1.0 × 105 |
| Anode | 2.05 × 108 | 1.2 × 105 |
| Parameter | Cathode | Electrolyte | Anode | Inter-Connector |
|---|---|---|---|---|
| Material | Ni-YSZ | YSZ | LSM | stainless steel |
| Density, kg/m3 | 7740 | 6000 | 5300 | 7700 |
| Specific heat capacity (W·kg−1·K−1) | 595 | 400 | 607 | 600 |
| Thermal conductivity (W−1·m·K−1) | 6.23 | 2.7 | 10 | 44.5 |
| Electronic/ionic conductivity (1/Ω·m) | 769,000 | |||
| CTE, (1/K) | 12.2 | 10.3 | 11.7 | 15.5 |
| Young modulus (GPa) | 57 | 185 | 35 | 214 |
| Poisson’s ratio | 0.28 | 0.32 | 0.25 | 0.3 |
| Boundary Conditions | ||||
|---|---|---|---|---|
| Momentum | Thermal | Species | Electric Potential | |
| Top IC wall | Stationary wall with no slip for velocity | Symmetry | Zero diffusive flux | Φtop = Vcell |
| Bottom IC wall | Stationary wall with no slip for velocity | Symmetry | Zero diffusive flux | Φbottem = 0 |
| Air inlet | 0.33 L/min | 800 °C | 21% O2 + 79% N2 | Insulation |
| Air outlet | Pressure condition | Convection | Convection | Insulation |
| Fuel inlet | 0.217 L/min | 800 °C | 90% H2O + 10% H2 | Insulation |
| Fuel outlet | Pressure condition | Convection | Convection | Insulation |
| Side walls | Stationary wall with no slip for velocity | Insulation | Zero diffusive flux | Insulation |
| Rib/Channel Width Ratio | Rib Width | Channel Width |
|---|---|---|
| 5:2 | 2.5 mm | 1 mm |
| 4:3 | 2 mm | 1.5 mm |
| 1:1 (base-case) | 1.75 mm | 1.75 mm |
| 3:4 | 1.5 mm | 2 mm |
| 2:5 | 1 mm | 2.5 mm |
| Cases | Ribs | Cross-Section Parameters of Channel Inlet | Cross-Section Parameters of Channel Outlet |
|---|---|---|---|
| Case-0 | Traditionally straight and parallel channel |  |  |
| Case-1 | Gradient channel expanding in width direction | 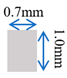 | 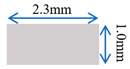 |
| Case-2 | Gradient channel expanding in thickness direction | 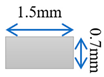 | 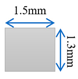 |
| Case-3 | Gradient channel shrinking in width direction | 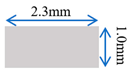 | 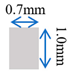 |
| Case-4 | Gradient channel shrinking in thickness direction | 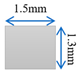 | 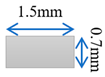 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Xiao, L.; Wang, H.; Ou, D.; Yuan, J. Numerical Study of H2 Production and Thermal Stress for Solid Oxide Electrolysis Cells with Various Ribs/Channels. Energies 2024, 17, 510. https://doi.org/10.3390/en17020510
Liu Y, Xiao L, Wang H, Ou D, Yuan J. Numerical Study of H2 Production and Thermal Stress for Solid Oxide Electrolysis Cells with Various Ribs/Channels. Energies. 2024; 17(2):510. https://doi.org/10.3390/en17020510
Chicago/Turabian StyleLiu, Yingqi, Liusheng Xiao, Hao Wang, Dingrong Ou, and Jinliang Yuan. 2024. "Numerical Study of H2 Production and Thermal Stress for Solid Oxide Electrolysis Cells with Various Ribs/Channels" Energies 17, no. 2: 510. https://doi.org/10.3390/en17020510
APA StyleLiu, Y., Xiao, L., Wang, H., Ou, D., & Yuan, J. (2024). Numerical Study of H2 Production and Thermal Stress for Solid Oxide Electrolysis Cells with Various Ribs/Channels. Energies, 17(2), 510. https://doi.org/10.3390/en17020510







