Research on Electric Hydrogen Hybrid Storage Operation Strategy for Wind Power Fluctuation Suppression

Abstract

Due to real-time fluctuations in wind farm output, large-scale renewable energy (RE) generation poses significant challenges to power system stability. To address this issue, this paper proposes a deep reinforcement learning (DRL)-based electric hydrogen hybrid storage (EHHS) strategy to mitigate wind power fluctuations (WPFs). First, a wavelet packet power decomposition algorithm based on variable frequency entropy improvement is proposed. This algorithm characterizes the energy characteristics of the original wind power in different frequency bands. Second, to minimize WPF and the comprehensive operating cost of EHHS, an optimization model for suppressing wind power in the integrated power and hydrogen system (IPHS) is constructed. Next, considering the real-time and stochastic characteristics of wind power, the wind power smoothing model is transformed into a Markov decision process. A modified proximal policy optimization (MPPO) based on wind power deviation is proposed for training and solving. Based on the DRL agent’s real-time perception of wind power energy characteristics and the IPHS operation status, a WPF smoothing strategy is formulated. Finally, a numerical analysis based on a specific wind farm is conducted. The simulation results based on MATLAB R2021b show that the proposed strategy effectively suppresses WPF and demonstrates excellent convergence stability. The comprehensive performance of the MPPO is improved by 21.25% compared with the proximal policy optimization (PPO) and 42.52% compared with MPPO.

1. Introduction

Due to the increasing scarcity of fossil fuels and the global need for production and carbon reduction, the installed capacity of renewable energy (RE) generation is rapidly developing throughout the world. From 2013 to 2023, the combined renewable electricity and biofuels primary energy input consumption worldwide increased from 52.93 exajoules to 90.23 exajoules, with an average growth rate of 5.5% [1]. Furthermore, the average rate of increase in wind and solar installed capacity to 2035 is supposed as 450–600 GW per year—around 1.9 to 2.5 times faster than the highest rate in the past [2]. The proportion of non-fossil energy supply, dominated by RE, in China is expected to reach 60% by 2050 [3]. To accommodate a high proportion of RE, measures must be taken to address the impact of its integration [4].

Unlike traditional power sources, renewable energy (RE) sources such as wind and solar power have significant intermittency and output fluctuations, weak support from power generation equipment, and low anti-interference ability [5]. These negative characteristics hinder achieving electricity balance in the power system [6]. Additionally, the integration of RE generation has introduced a large number of power electronic devices, such as inverters and DC converters, causing issues like transient overvoltage and broadband oscillations, which seriously impact power system stability. Therefore, it is urgent to introduce flexible resources to promote the consumption of a high proportion of RE and mitigate its adverse effects [7].

Hydrogen is a clean secondary energy source with high calorific value and diverse sources [8]. Compared to electrochemical energy storage (EES), hydrogen has a longer storage and discharge cycle and a larger storage capacity. The electrolysis-hydrogen storage-gas power generation cycle allows the coupling of electricity and hydrogen to balance electricity consumption effectively [9]. It can supply power to nearby loads and provide frequency and voltage support for the power grid [10].

This paper applies an electric hydrogen hybrid storage (EHHS) system to smooth wind power fluctuations. Many studies have examined the smoothing effect of hybrid energy storage systems composed of EES and supercapacitors on new energy generation. Although the stabilizing effect of EHHS on voltage and the reducing effect on net load fluctuations have been studied [11], further research on the power coordination and allocation strategy is necessary considering the particularity of the operating points between EES and the hydrogen system [12].

This paper aims to use improved wavelet characterization theory and deep reinforcement learning (DRL) technology to suppress the fluctuation of wind power based on EHHS. Common smoothing methods include wavelet transform and model predictive control. References [13,14,15] propose decoupling wind power and hybrid energy storage (HES) power using wavelet transform or low-pass filtering. For more robust battery output processing, reference [16] used adaptive variational mode decomposition to extract frequencies from different wind scenarios, enabling effective determination of the pre-scheduled power of the HES. Additionally, the PI controller adjustment strategy proposed in reference [17] for HES can effectively control the exchange of active and reactive power between wind farms and the power grid, thereby smoothing wind power fluctuations. Moreover, scholars have used predictive control algorithms to smooth wind power [18,19,20,21,22,23,24,25]. The basic idea is to optimize the charging and discharging behavior of HES through controlling the state of charge (SOC) of the battery, thereby smoothing wind power and improving battery life. Stochastic predictive control [22,24] and intelligent predictive control algorithms [20,25] can provide more precise predictions and management of wind power uncertainty. However, research on stabilizing RE sources with HES mainly focuses on EES and supercapacitors, with relatively little complementary research on EES and hydrogen energy system. For example, the literature [26] studied the interaction between wind power and hydrogen energy systems but did not include EES, resulting in a lack of consideration for the volatility of hydrogen energy storage. Consequently, it could not achieve optimal power flow management between wind power, hydrogen energy, and EES.

However, conventional predictive control algorithms generally require prior accurate predictions, as referenced in [27,28], which are difficult to achieve in real operating scenarios of wind farms. Moreover, methods like model predictive control (MPC) and fuzzy control have complex application rules, poor scalability, and limited generalization performance. Therefore, this paper applies improved wavelet characterization theory and DRL to the allocation of EHHS power. Scholars have applied DRL to study collaborative control between wind turbines and HES [29,30,31]. These studies have shown that DRL strategies can effectively manage the nonlinearity and randomness of wind power, maximizing rewards or achieving specific goals. However, DRL has not yet been applied for control in wind EHHS systems. This paper combines the complementary characteristics of EES and hydrogen energy over different time periods to study the real-time perception and power smoothing effects of DRL in this new energy storage system.

The major contribution of this article can be concluded as:

(1)

DRL algorithm is utilized for research on smoothing on-grid WPF. Fast perception of EHHS status and formulation of charging and discharging operation strategies through DRL intelligent agents significantly suppress the on-grid WPF.

(2)

A wavelet packet power decomposition algorithm based on variable frequency entropy improvement is proposed. This algorithm addresses the drawback of the wavelet packet decomposition (WPD) algorithm that requires precise input conditions and manual setting of response time boundary points for different energy storage components.

(3)

A modified proximal policy optimization (MPPO) based on wind power deviation is proposed for training and solving the unique challenges of WPF. By dynamically adjusting the clipping rate based on real-time WPF, the training efficiency and stability of the algorithm are balanced, and the overall performance of the model is improved.

The remainder of this paper is as follows. Section 2 introduces the energy flow architecture and information exchange forms of EHHS. Section 3 establishes the power allocation strategy and smoothing effect optimization function of EHHS. Section 4 explains the optimization method of the wind power stabilization strategy using the MPPO algorithm. Section 5 illustrates the improvement effects of the proposed MPPO and the advantages of EHHS through case studies. Finally, Section 6 presents the conclusions.

2. Architecture of Electric Hydrogen Hybrid Storage System

The architecture of EHHS is shown in Figure 1. It illustrates the information exchange between wind farms and the grid, including actual on-grid power transmission, maximum wind power fluctuation, and wind power prediction. The power allocation controller manages the output strategy of EHHS. First, the controller uses an improved wavelet transform method to decompose the original wind power and obtain the direct on-grid power and fluctuation smoothing scale for EHHS. Simultaneously, the EES and HES provide real-time SOC and SOH information to the controller. After optimization using the DRL algorithm, the charging/discharging strategy is sent back to the energy storage system, which then interacts with the power grid through a power converter.

3. Wind Power Fluctuation Suppression Strategy of EHHS

The proposed EHHS wind power fluctuation suppression strategy is shown in Figure 2. First, an improved WPD algorithm is used to decompose the real-time output of wind turbines and characterize wind power in different frequency bands. Second, the state parameters (SOC, SOH, etc.) of EHHS are combined with the WPD results to form a deep reinforcement learning proximal policy optimization (PPO) agent. Using the Actor network, the agent interacts with the environment and accumulates training samples. Then, an improved PPO algorithm based on power deviation is proposed for optimization training, learning the optimal mapping relationship between environmental states and action strategies. Finally, the trained PPO agent is deployed online to smooth real-time fluctuations in wind power.

3.1. Wavelet Packet Power Decomposition Algorithm Based on Frequency Conversion Entropy Improvement

3.1.1. Traditional Wavelet Packet Decomposition Algorithm

The WPD algorithm decomposes the original wind power into low-frequency and high-frequency signals. Compared with traditional wavelet decomposition, WPD offers higher frequency decomposition rates and better time resolution. The algorithm decomposes the original signal through x layers, maps it to 2^x wavelet packet spaces, and then reconstructs the 2^x components of the x-th layer.

$$\left\{\begin{array}{l}{\alpha }_n^{k,2x}={\displaystyle \sum _{i=1}^x{u}_{i-2n}{\alpha }_i^{k+1,x}}\\ {\alpha }_n^{k,2x+1}={\displaystyle \sum _{i=1}^x{v}_{i-2n}{\alpha }_i^{k+1,x}}\end{array}\right.$$

(1)

where n denotes the number of signals obtained from wavelet decomposition, $n=1,2,\dots ,2^x$; ${\alpha }^{k,2x},{\alpha }^{k,2x+1}$ denote the low-frequency and high-frequency coefficients, $u_{i-2n},v_{i-2n}$ denote the decompose coefficients for low-pass and high-pass filters. The reconstruction algorithm is:

$${\alpha }_n^{j+1}={\displaystyle \sum _{i=1}^x\left(u_{n-2i}{\alpha }_i^{j,2x}+v_{n-2i}{\alpha }_i^{2x+2}\right)}$$

(2)

The wavelet packet algorithm is first used to decompose and obtain the wind power output power. The xth-layer 0-node power component is taken as the grid reference power, and the others are taken as the EHHS reference power. Based on the analysis of the EHHS operating characteristics, the power component frequency division point i is determined, leading to the final EHHS power command. The power commands for EES and HES are detailed below:

$$\left\{\begin{array}{l}{P}_{\mathrm{EES}}\left(t\right)={\displaystyle \sum _1^i{S}_{x,i}}\\ P_{\mathrm{HS}}\left(t\right)={\displaystyle \sum _{i+1}^{2^x}{S}_{x,i}}\end{array}\right.$$

(3)

where $P_{\mathrm{EES}}\left(t\right),P_{\mathrm{HS}}\left(t\right)$ denote the power commands for EES and HES at time t, respectively; when both values are negative, it indicates that EES and the fuel cell are discharging; when both are positive, it indicates that EES is charging, and the electrolytic cell is absorbing power.

3.1.2. Variable Frequency Entropy Strategy Based on WPD

Although the WPD algorithm offers high time and frequency resolution, its application is limited because it generally requires precise input conditions and manual setting of response time boundary points for different energy storage components. To address the drawbacks of the WPD algorithm, this paper employs a frequency conversion entropy strategy based on the WPD. By combining this with the specific characteristics of EHHS, the approach optimizes the time and frequency boundary points, leading to the optimal and most economical power allocation strategy for EHHS.

Based on the WPD algorithm, the n-th node coefficient is set as $B_{j,n}=\left\{B_{j,n}\left(x\right),x=1,2,\dots ,N\right\}$ and the sampling interval is t. The reconstructed trajectory matrix is obtained as follows:

$${\left[A_{j,n}\right]}_{L\cdot M}=\left[\begin{array}{cccc}{\alpha }_{j,n}\left(1\right)& {\alpha }_{j,n}\left(1+t\right)& \cdots & {\alpha }_{j,n}\left(1+\left(M-1\right)t\right)\\ {\alpha }_{j,n}\left(2\right)& {\alpha }_{j,n}\left(2+t\right)& \cdots & {\alpha }_{j,n}\left(2+\left(M-1\right)t\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\alpha }_{j,n}\left(L\right)& {\alpha }_{j,n}\left(L+t\right)& \cdots & {\alpha }_{j,n}\left(L+\left(M-1\right)t\right)\end{array}\right]$$

(4)

where L denotes the sliding window length when performing sliding average filtering on the original wind power.

The singular values of wavelet decomposition can be obtained from Equation (4), ${\lambda }_{j,n}^x\left[1\le x\le \left(m+1\right)t\right]$, which can reflect the proportion of energy. Assuming that the signal energy obtained from each order of WPD is $E_k$, the total energy is:

$$E_k=\left|-{\displaystyle \sum _{x=1}^N{\lambda }_{j,n}^x\ln \left({\lambda }_{j,n}^x\right)}\right|$$

(5)

After normalizing Equation (5), the entropy value, $P_k$, can be obtained as follows:

$$P_k={\displaystyle \frac{E_k}{E_0}}={\displaystyle \frac{\left|-{\displaystyle \sum _{x=1}^N{\lambda }_{j,n}^x\ln \left({\lambda }_{j,n}^x\right)}\right|}{\sqrt{{\displaystyle \sum _{n=1}^{2^x}{E}_n^2}}}}$$

(6)

The corresponding entropy spectrum can be obtained as follows:

$$H_{j,n}\left({\lambda }_{j,n}^x\right)={\left[P_k\right]}_{L\cdot M}$$

(7)

Take the order with the fastest decrease in normalized entropy value in the entropy spectrum as the boundary point D. Based on this principle, the power command for EHHS, derived from the improved wavelet packet algorithm, is as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{EES}}^H\left(t\right)={\displaystyle \sum _1^D{S}_{x\prime ,D}}\\ P_{\mathrm{HS}}^H\left(t\right)={\displaystyle \sum _{D+1}^{2^{x\prime }}{S}_{x\prime ,D}}\end{array}\right.$$

(8)

where x′ is the number of WPD layers determined based on entropy changes.

3.2. Modeling of Wind Power Fluctuation Suppression

3.2.1. Objective Function

In this section, the objective functions are categorized into two types of assessment: stabilization effect and operational cost.

A

The optimal effect of WPF suppression

Generally, the system’s ability to withstand fluctuations in wind power is determined via its frequency regulation capability:

$$\left|P_{\mathrm{G}}\left(t\right)-P_{\mathrm{G}}\left(t-1\right)\right|\le \Delta P_{\mathrm{WT}}$$

(9)

where $\Delta P_{\mathrm{WT}}$ denotes the tolerable WPF.

This paper evaluates the degree of WPF through measuring the total amplitude that exceeds the limit. One of the objective functions is to minimize this fluctuation.

$$\Delta Y={\displaystyle \sum _{t=1}^{T/\Delta t}\left[\left|P\left(t\right)-P\left(t-1\right)\right|-\Delta P_{\mathrm{WT}}\right]}$$

(10)

where T denotes the sampling period.

B

The optimal operating cost of EHHS

The operating costs of EHHS encompass those of both HES and EES, as indicated by the following equation:

$$C_{\mathrm{HS}}+C_{\mathrm{EES}}=\left(C_{\mathrm{HS},om}+C_{\mathrm{EES},om}\right)+\left(C_{\mathrm{HS},loss}+C_{\mathrm{EES},loss}\right)$$

(11)

where $C_{\mathrm{HS}},C_{\mathrm{EES}}$ are the costs of HES and EES, respectively. The subscripts om, loss, respectively, represent operation and consumption.

The operation and maintenance costs of HES and EES are detailed below:

$$C_{\mathrm{HS},om}={\displaystyle \sum _{t=1}^T\left({\displaystyle \sum _{i=1}^{N_{\mathrm{PE}}}\frac{{\sigma }_{\mathrm{PE},i,t}{C}_{\mathrm{PE},i,inv}}{T_{\mathrm{PE},i,l}}+{\displaystyle \sum _{i=1}^{N_{\mathrm{FC}}}\frac{{\sigma }_{\mathrm{FC},i,inv}}{T_{\mathrm{FC},i,l}}}}\right)}$$

(12)

$$C_{\mathrm{EES},om}={\gamma }_{\mathrm{EES},om}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_{\mathrm{EES}}}\left(P_{\mathrm{EES},i,t}^{dis}+P_{\mathrm{EES},i,t}^{cha}\right)}}$$

(13)

where ${\sigma }_{\mathrm{PE},i,t},{\sigma }_{\mathrm{FC},i,t}$ denote the 0–1 state variable of i-th Proton exchange membrane electrolyser (PEMEL) or Proton exchange membrane fuel cell (PEMFC), 0 indicates startup, 1 indicates shutdown. The subscript inv represents the construction cost; $T_{\mathrm{PE},i,l},T_{\mathrm{FC},i,l}$ denote the maximum operating time; ${\gamma }_{\mathrm{EES},om}$ denotes the cost coefficient of EES charging and discharging; N denotes the number of device; $P_{\mathrm{EES},i,t}^{dis},P_{\mathrm{EES},i,t}^{cha}$ denote the discharge and charging power of the i-th battery at time t.

There is energy conversion loss in the energy storage process. The cost associated with these losses for HES and EES is considered as follows:

$$C_{\mathrm{HS},loss}={\gamma }_d{\displaystyle \sum _{t=1}^T\left[{\displaystyle \sum _{i=1}^{N_{\mathrm{PE}}}{P}_{i,t}^{\mathrm{PE}}\left(1-{\eta }_{\mathrm{PE},i,t}\right)+{\displaystyle \sum _{i=1}^{N_{\mathrm{FC}}}{P}_{i,t}^{\mathrm{FC}}\left(1-{\eta }_{\mathrm{FC},i}\right)}}\right]}$$

(14)

$$C_{\mathrm{EES},loss}={\gamma }_d{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_{\mathrm{EES}}}\left[P_{\mathrm{EES},i,t}^{dis}\left(1-{\eta }_{\mathrm{EES},i,dis}\right)+P_{\mathrm{EES},i,t}^{cha}\left(1-{\eta }_{\mathrm{EES},i,cha}\right)\right]}}$$

(15)

where ${\gamma }_d$ denotes the transmission and distribution tariff; $\eta$ denotes the operating efficiency.

Restraints

A

Power balance

$$P_{\mathrm{WT}}\left(t\right)+P_{\mathrm{EES}}\left(t\right)=P_{\mathrm{load}}\left(t\right)+P_{\mathrm{PE}}\left(t\right)$$

(16)

where $P_{\mathrm{load}}\left(t\right)$ denotes the fluctuating load; $P_{\mathrm{PE}}\left(t\right)$ denotes the electrolytic cell power.

B

Unit time exchange power of EES

$$\left\{\begin{array}{l}0<P_{cha}\left(t\right)<P_{cha}^{\max },P_{dis}\left(t\right)=0\\ 0<P_{dis}\left(t\right)<P_{dis}^{\max },P_{cha}\left(t\right)=0\end{array}\right.$$

(17)

where $P_{cha}^{\max },P_{dis}^{\max }$ denote the upper limits of real-time charging and discharging power for EES.

C

Electrolytic cell operation

When the operating power of the electrolytic cell falls below a certain threshold, there is a risk that the hydrogen–oxygen mixture may exceed the explosive limit. The hydrogen production capacity of the electrolytic cell can be expressed in the following equation:

$$\left\{\begin{array}{l}{P}_{\mathrm{PE}}^{\min }<P_{\mathrm{PE}}\left(t\right)<P_{\mathrm{PE}}^{\max },P_{\mathrm{H}}\left(t\right)={\eta }_{\mathrm{PE}}{P}_{\mathrm{PE}}\left(t\right)\\ P_{\mathrm{PE}}\left(t\right)=0,P_{\mathrm{H}}=0\end{array}\right.$$

(18)

where $P_{\mathrm{PE}}^{\min },P_{\mathrm{PE}}^{\max }$ denote the lower and upper ranges of the operating power of the electrolytic cell; $P_{\mathrm{H}}\left(t\right)$ denotes the hydrogen production; ${\eta }_{\mathrm{PE}}$ denotes the efficiency of hydrogen production.

D

Hydrogen storage status

$${\mathrm{SOH}}_{\min }\le \mathrm{SOH}\left(t\right)\le {\mathrm{SOH}}_{\max }$$

(19)

where $\mathrm{SOH}\left(t\right)$ denotes the status for hydrogen storage tanks.

E

Upper and lower limits of SOC for EES

$${\mathrm{SOC}}_{\min }\le \mathrm{SOC}\left(t\right)\le {\mathrm{SOC}}_{\max }$$

(20)

where $\mathrm{SOC}\left(t\right)$ denotes the status of EES batteries.

3.2.2. WPF Suppression Strategy Based on Markov Decision Process

To mitigate the impact of power generation volatility in renewable energy systems on wind power smoothing algorithms, this section converts the model into a Markov Decision Process (MDP) and trains it, using a MPPO algorithm with deep reinforcement learning.

As a deep reinforcement learning algorithm based on the Actor–Critic architecture, PPO agents observe states of the IPHS, $s_t$, and make real-time decision actions, $a_t$, based on the Actor network. After executing the actions $a_t$, the agents will receive immediate rewards, $r_t$. Repeat the above interaction to continuously accumulate samples and update the parameters of the agent network, ultimately achieving the mapping between environmental state and optimal action.

A

States

The state represents the agent’s perception of real-time environmental information to assist in decision-making. In this paper, the environmental state includes original wind power and high- and low-frequency components obtained by WPD, SOC, and SOH:

$$s_t=\left\{P_{\mathrm{WT},t}^{\prime },F_{\mathrm{WT},t}^{\prime },SO{C}_{\mathrm{EES},t},SO{H}_{\mathrm{HS},t}\right\}$$

(21)

where $P_{\mathrm{WT},t}^{\prime },F_{\mathrm{WT},t}^{\prime }$ denote the original wind power and high- and low-frequency components obtained from WPD, respectively.

B

Actions

Based on environmental information, the agent selects an action from the action set [32]. For EHHS, its operating space consists of the outputs of EES and HES.

$$a_t=\left\{P_{\mathrm{EES},t},P_{\mathrm{HS},t}\right\}$$

(22)

C

Rewards

Rewards are real-time feedback from the environment following the execution of an action, used to guide the agent toward better decision-making. In this paper, the reward comprises the cost of EHHS and a penalty for exceeding the WPD limits:

$$r_t=r_t^{\mathrm{EHHS}}+r_t^{\mathrm{PU}}$$

(23)

$$r_t^{\mathrm{EHHS}}=-C_{\mathrm{EES},t}-C_{\mathrm{HS},t}$$

(24)

$$r_t^{\mathrm{PU}}=\left\{\begin{array}{l}-{\lambda }_{\mathrm{WT}}\left|P_{\mathrm{WT},t}-P_{\mathrm{WT},t-1}\right|,\left|P_{\mathrm{WT},t}-P_{\mathrm{WT},t-1}\right|<\Delta P_{\mathrm{WT}}^F\\ -500,\left|P_{\mathrm{WT},t}-P_{\mathrm{WT},t-1}\right|\ge \Delta P_{\mathrm{WT}}^F\end{array}\right.$$

(25)

where $r_t^{\mathrm{EHHS}},r_t^{\mathrm{PU}}$ denote the cost of EHHS and the penalty, respectively; $C_{\mathrm{EES},t},C_{\mathrm{HS},t}$ denote the cost of EES and HES; ${\lambda }_{\mathrm{WT}}$ denotes the penalty coefficient; $\Delta P_{\mathrm{WT}}^F$ denotes the WPD limit.

4. Solution Based on the MPPO Algorithm

4.1. Basic Principles of PPO Algorithm

In the PPO algorithm, the advantage function at time t, $A_t\left(a,s\right)$, can be expressed as follows:

$$A_t\left(a,s\right)=-V_{\Psi }\left(s_t\right)+r_t+\beta r_{t+1}+\dots +{\beta }^{K-t+1}{r}_{K-1}+{\beta }^{K-t}{V}_{\Psi }\left(s_K\right)$$

(26)

where $V_{\Psi }\left(s_t\right)$ denotes the state value function; $\beta$ denotes the depreciation rate; K denotes the step length.

According to Equation (26), the training objective F is to obtain the agent network parameters that can maximize the expected advantage function:

$$\begin{array}{ll}F& =\underset{\theta }{\max }{ℂ}_t\left[{\displaystyle \frac{{\pi }_{{\theta }^{k+1}}\left(a\left|s\right.\right)}{{\pi }_{{\theta }^k}\left(a\left|s\right.\right)}}{A}_t\left(a,s\right)\right]\\ & =\underset{\theta }{\max }{ℂ}_t\left[{\tau }_t{A}_t\left(a,s\right)\right]\end{array}$$

(27)

where ${\pi }_{{\theta }^k}$ denotes the function of strategy; ${\tau }_t$ denotes the ratio of old to new strategies.

In order to ensure training stability, ${\tau }_t$ has been limited to ensure that its value is within $\left[1-\epsilon ,1+\epsilon \right]$. The objective function can be modified to the following:

$$F_{\mathrm{clip}}=\max {ℂ}_t\left[\min \left({\tau }_t{A}_t,\mathrm{clip}\left({\tau }_t\right)A_t\right)\right]$$

(28)

$$\mathrm{clip}\left({\tau }_t\right)=\left\{\begin{array}{ll}1-\epsilon & {\tau }_t<1-\epsilon \\ {\tau }_t& 1-\epsilon \le {\tau }_t\le 1-\epsilon \\ 1+\epsilon & {\tau }_t>1+\epsilon \end{array}\right.$$

(29)

where $\epsilon$ denotes the clipping rate.

4.2. Adaptive Clipping Rate Mechanism Based on Power Fluctuations

The proposed MPPO algorithm aims to dynamically adjust the clipping rate based on sample quality, balancing training speed, and algorithm stability for varying samples.

A heuristic search algorithm is employed for the optimization strategy. In the algorithm, the crossover factor (CR) significantly impacts performance. A small CR value can reduce population diversity and result in local optima. Conversely, a large value can decrease the search accuracy. Therefore, this paper proposes an improved differential evolution algorithm that accounts for wind power deviation.

$$CR=\left\{\begin{array}{l}0.5\Delta P_t^2/\xi +0.2,\Delta P_t^2\le \xi \\ rand(0.1,0.5),\Delta P_t^2>\xi \end{array}\right.$$

(30)

$$\Delta P_t^2={{\displaystyle \sum _{i=1}^N\left(\frac{P_{i,t}-P_i^r}{P_i^{\max }-P_i^{\min }}\right)}}^2$$

(31)

where $\Delta P_t^2$ denotes the sum of squares of wind power deviation at time t; $\xi$ denotes the threshold; rand denotes random number generation function.

Equation (30) shows that when the power deviation is small, the value of the cross factor CR is small to improve the search accuracy and convergence speed. When the power deviation is large, CR becomes a random number within the range of (0.1, 0.5) to ensure the richness of the population.

Notably, a large time difference error (TD-error) suggests that the current strategy is ineffective, necessitating a larger clipping rate, whereas a small TD-error implies that the strategy is effective, requiring a reduction in clipping rate to maintain convergence stability. The dynamic clipping rate is calculated as follows:

$$\epsilon =\left\{\begin{array}{ll}{\epsilon }_{\max }& {\delta }_t\ge \overline{{\delta }_t}\\ {\epsilon }_{\min }& {\delta }_t<\overline{{\delta }_t}\end{array}\right.$$

(32)

where ${\epsilon }_{\max },{\epsilon }_{\min }$ denote the maximum and minimum clipping rate; ${\delta }_t$ denotes the time difference error; $\overline{{\delta }_t}$ denotes the mean error.

4.3. The Training Process of the Improved PPO Algorithm

Figure 3 illustrates the training process of the improved PPO algorithm. Initially, the training environment is set up, followed by the decomposition of real-time wind turbine output using the enhanced WPD, which characterizes wind power energy across different frequency bands. The real-time status is observed and the action decisions are made. Secondly, the reward, $r_t$, is calculated and the sample, $\left(s_t,a_t,r_t,s_{t+1}\right)$, is stored in the experience pool. Next, the real-time WPF is calculated and the clipping rate, $\epsilon$, is dynamically adjusted, and the parameters of the agent network are updated. These steps are repeated until the maximum number of training rounds is reached, after which the trained agent is finalized.

5. Case Study

5.1. Configuration and Parameter Setting of IPHS

This paper uses actual wind power data from a city in northwest China in 2020 and is configured with EES and HES [33]. The total installed capacity in the region is 2800 MW, comprising 1700 MW from thermal units and 1100 MW from wind units. Each wind power unit has a capacity of 5 MW. The total capacity of the HES is set at 5% to 10% of the total capacity. The charging and discharging duration for HES is assumed to be 10 h. The general cost coefficients of EES and HES are 0.005 CNY/kWh and 0.02 CNY/kWh, respectively. The WPF penalty coefficient, ${\lambda }^{\mathrm{W}}$, is set at 1 CNY/MW. The capacity configuration of EHHS is detailed in

Table 1. The capacity configuration of EHHS.

Device	Capacity
EES power/MW	60
EES capacity/MWh	150
Electrolytic cell power/MW	50
HES capacity/m3	2100
Fuel cell power/MW	50

.

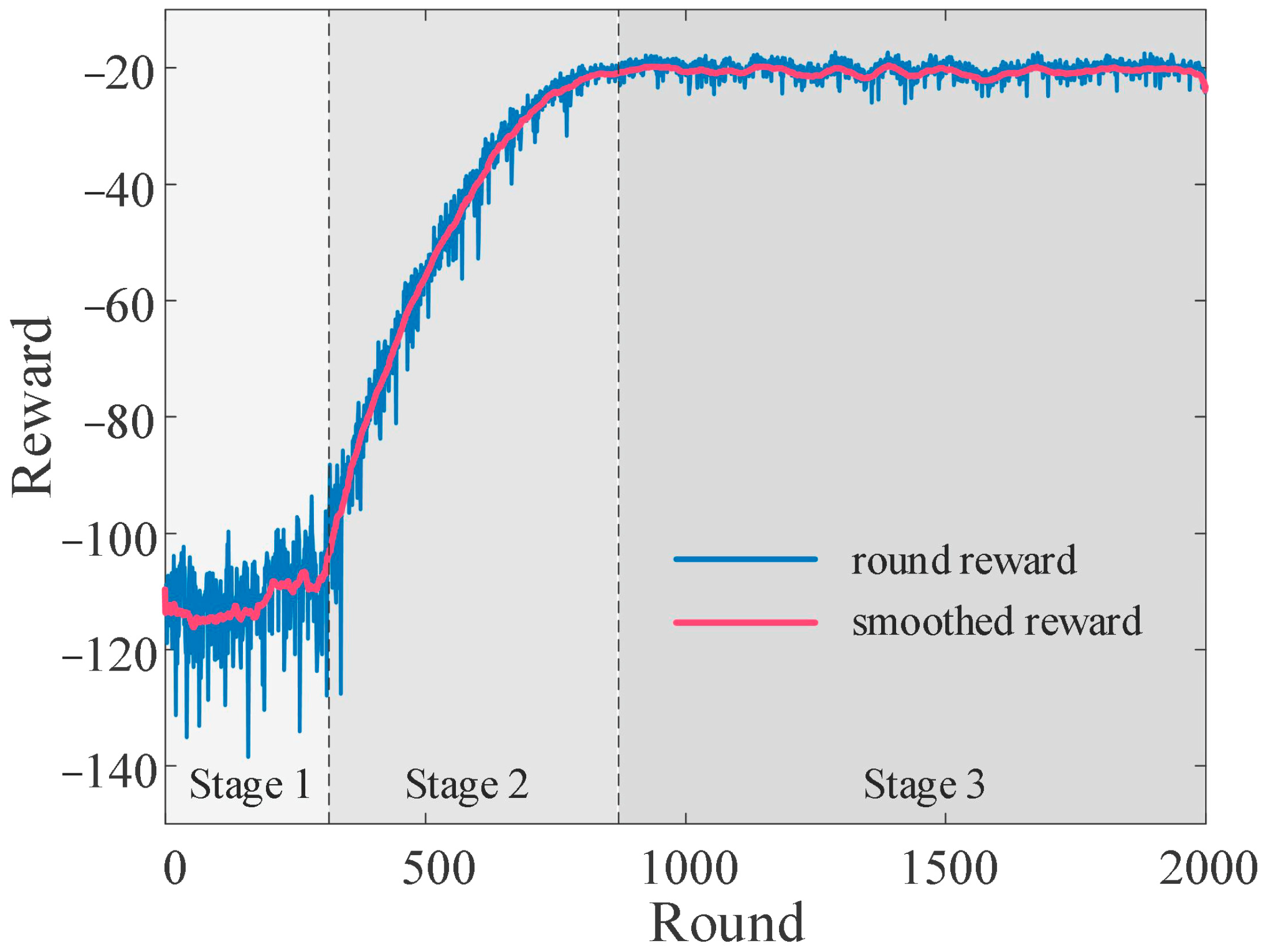
5.2. Analysis of Training Process

Assuming a discount rate of 0.95, an experience pool capacity of 8000, a mini-batch size of 128, and clipping rates of 0.3 and 0.1 for the maximum and minimum, respectively, the offline training reward curve of the agent is shown in Figure 4. The smoothed reward is added as the auxiliary line to better showcase the overall trend in the reward curve.

Figure 4 illustrates that the reward curve for the agent shows a significant upward trend in fluctuation. In the first stage, the agent continuously explores the training environment and obtains low and fluctuating reward values, with an average of −110.23, indicating a risk of exceeding the on-grid power limit. However, due to the PPO improvement mechanism proposed in this paper, which adapts the clipping rate based on the WPF limit, the efficiency of network parameter updates improved early in the training process, resulting in a notable increase in the reward curve between rounds 340 and 850. In the later stage of training (Stage 3), the model employed a smaller clipping rate to maintain convergence stability, resulting in the reward value converging to approximately −20.20. This demonstrates that the agent had effectively learned the optimal mapping between environmental state and action decisions.

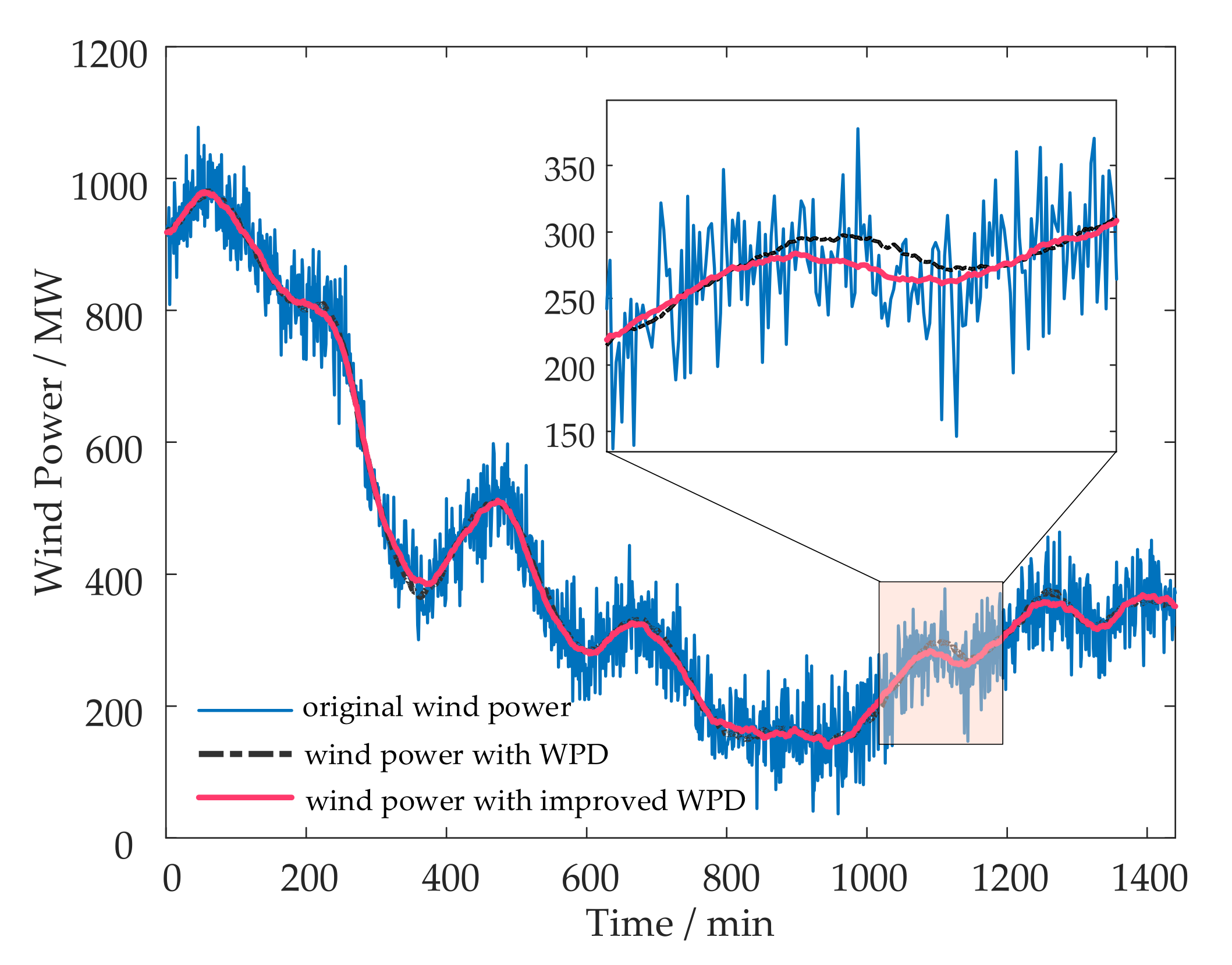
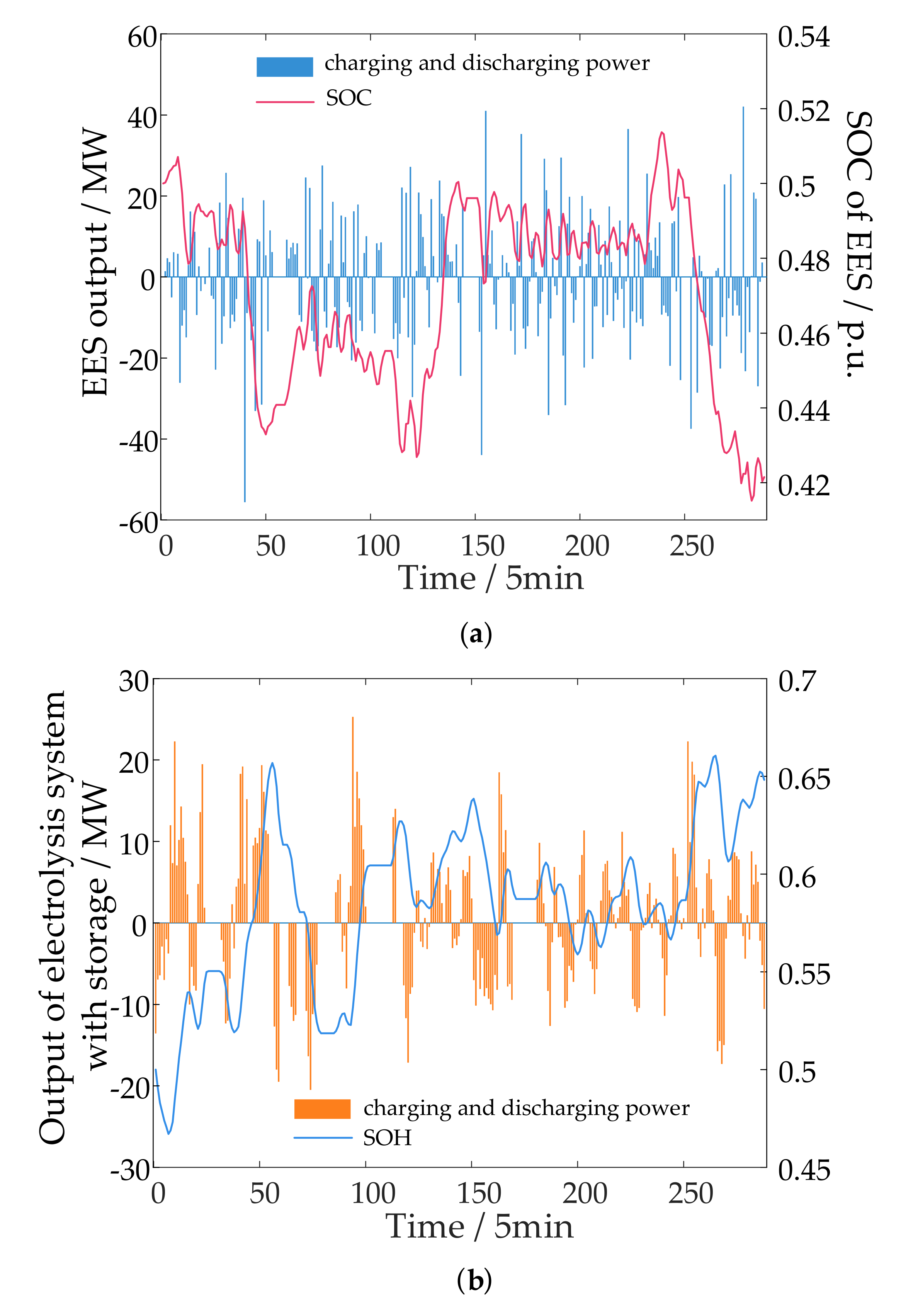
5.3. WPF Suppression Model Application and Results Analysis

The comparison of the on-grid wind power and fluctuation before and after suppression is shown in Figure 5 and Figure 6, respectively.

The results show that the proposed modified WPD algorithm can better characterize wind power, which is helpful for power scheduling and utilization. In addition, as shown in Figure 6, there is a significant problem of the WPF limit being exceeded before suppression, especially around 3:15 am, when the power fluctuation reached 75.17 MW, exceeding the threshold by 36.67% (Figure 6 is an analysis chart for 24 h, a day and a night). The average fluctuation of wind power throughout the day before suppression reached as high as 20.11 MW, which posed a significant challenge to the stable operation of the power grid. On the contrary, the proposed algorithm effectively reduces the fluctuation amplitude to an average of 5.74 MW, representing a 71.46% reduction compared with before. Furthermore, based on the proposed method, the scenarios of short-term severe fluctuations in wind power were significantly reduced, markedly enhancing the power grid’s ability to accommodate wind energy.

By conducting online testing on the offline trained agent, the agent can formulate an EHHS operation strategy online, which is shown in Figure 7. Comparing Figure 7a,b, it can be seen that the operation strategy of EES is more flexible and can quickly adjust the charging and discharging power to mainly absorb the low-frequency components of wind power fluctuations. On the contrary, due to physical characteristics, the charging and discharging strategies of an electrolysis system with storage tend to be more conservative. The proposed method can effectively mitigate wind power grid fluctuations by coordinating the implementation and operation strategies of EHHS. In addition, the SOC curve of EES indicates that it mostly operates in a shallow charging and discharging state, which helps extend its service life. The SOH of HES generally ranged between 0.5 and 0.7, with sufficient power and capacity space to smooth out fluctuations.

5.4. Comparison of Different Algorithms

Finally, to validate the superiority of the proposed MPPO algorithm, Deep Deterministic Policy Gradient (DDPG) and PPO algorithms were used as control benchmarks for testing. The training reward curves for different DRL algorithms are shown in Figure 8. The result shows that the DDPG algorithm achieved convergence in about 600 rounds, but its stability was poor in the later stage, with an average reward of only −35.14. Although the PPO algorithm converged more slowly than the DDPG, it effectively mitigated instability during training by limiting the update step size. The reward value remained relatively stable in later stages, approximately −25.65. The proposed MPPO algorithm combined the PPO’s stability with dynamic clipping rate adjustments based on WPF to enhance early training efficiency and ensure stability in later stages. The reward value at the late stage of training of the MPPO algorithm was −20.20. The reward value increased by 21.25% from −25.65 to −20.20 compared with the conventional PPO algorithm, demonstrating the effectiveness and superiority of the proposed mechanism in WPF suppression.

The system costs and on-grid power fluctuations using different DRL algorithms are shown in

Table 2. The results using different DRL algorithms.

Device	DDPG	PPO	MPPO
Cost of EES/CNY	1749.31	1387.16	1295.33
Cost of HES/CNY	4127.88	3512.28	2869.12
Average of on-grid power fluctuations/MW	9.52	6.90	5.74

.

According to Table 2, the proposed MPPO algorithm significantly outperformed in terms of cost and mean on-grid power. The proposed method utilized a WPD algorithm enhanced via frequency conversion entropy to characterize the energy features of the original wind power, optimizing the comprehensive costs of EES and HES. The MPPO algorithm was also used to achieve efficient management and scheduling of EES and HES. Compared with the PPO, the cost of EES and HES was reduced by 6.62% and 18.31%, respectively. Regarding on-grid power fluctuations, the MPPO algorithm dynamically adjusted strategy parameters based on real-time fluctuations, enabling a rapid response to WPF. The average of on-grid power fluctuations is 5.74 MW, approximately 16.81% lower than the PPO, significantly enhancing the stability and reliability of on-grid wind power. It can be seen from Table 2 that the three DRL algorithms have different effects on the suppression of WPF. The PPO represented the policy using a probability distribution and achieved policy updates through limiting the magnitude of changes between the new and old policies, thus obtaining more stable results in case experiments. The DDPG algorithm directly outputted actions instead of a probability distribution of actions. In some cases, DDPG adopted more aggressive policy updates, leading to greater fluctuations in wind power. The proposed MPPO algorithm dynamically adjusted strategy parameters based on real-time fluctuations, enabling a rapid response to WPF and achieving excellent results in various indicators.

6. Conclusions

This paper proposes an EHHS strategy based on a MPPO algorithm to mitigate real-time fluctuations of wind power. A WPD enhanced via frequency conversion entropy was employed to characterize the energy features of wind power across different frequency bands, while an MPPO algorithm based on wind power deviation was introduced to develop WPF suppression strategies.

We conducted a numerical simulation based on a wind farm and obtained the following conclusions:

(1)

This paper explores the energy flow and complementary characteristics of EHHS based on a DRL algorithm, achieving real-time perception of system status. By formulating power charging and discharging strategies for EES and HES, WPF is effectively mitigated and the overall system cost is reduced.

(2)

The proposed modified WPD algorithm can accurately characterize the wind power, thereby formulating high- and low-frequency power allocation plans. The average on-grid WPF was only 5.74 MW, a decrease of 71.46% compared with before suppression.

(3)

Compared with other DRL algorithms, the proposed MPPO algorithm can dynamically adjust the clipping rate based on WPF during the training process, effectively balancing the training efficiency and convergence stability. Compared with the conventional PPO algorithm, the MPPO algorithm increased the training reward value by 21.25% and reduced the on-grid WPF by 16.81%.

Future work will involve integrating long-term forecasting, mid-term scheduling, and short-term real-time control to enhance and optimize EHHS charging and discharging strategies, aiming for coordinated scheduling across multiple time scales. Additionally, conducting empirical research based on a Hardware-in-the-Loop platform is also a direction for our next steps.