Method for Calculating Heat Transfer in a Heat Accumulator Using a Phase Change Material with Intensification Due to Longitudinal Fins
Abstract
1. Introduction
2. Materials and Methods
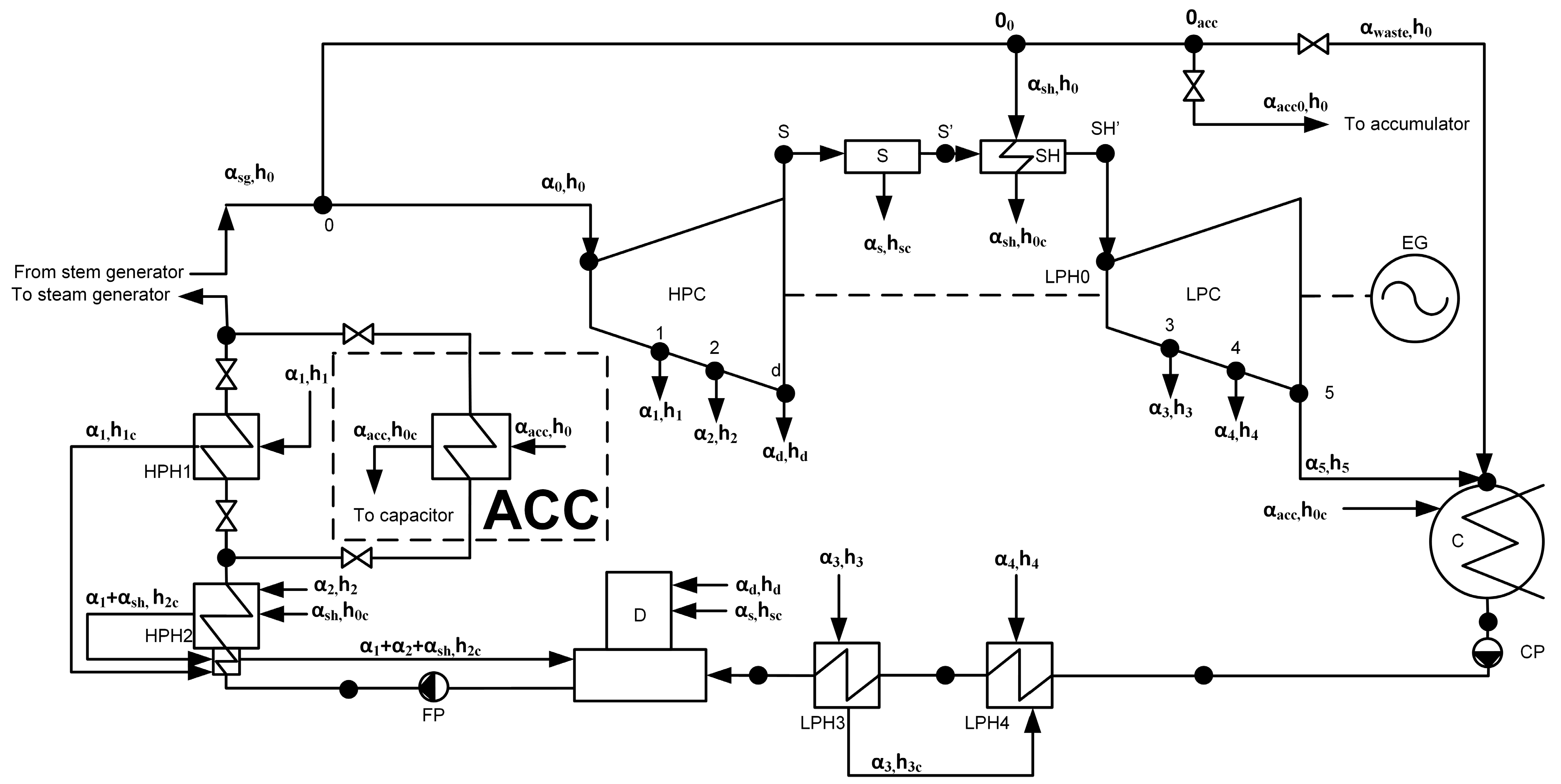
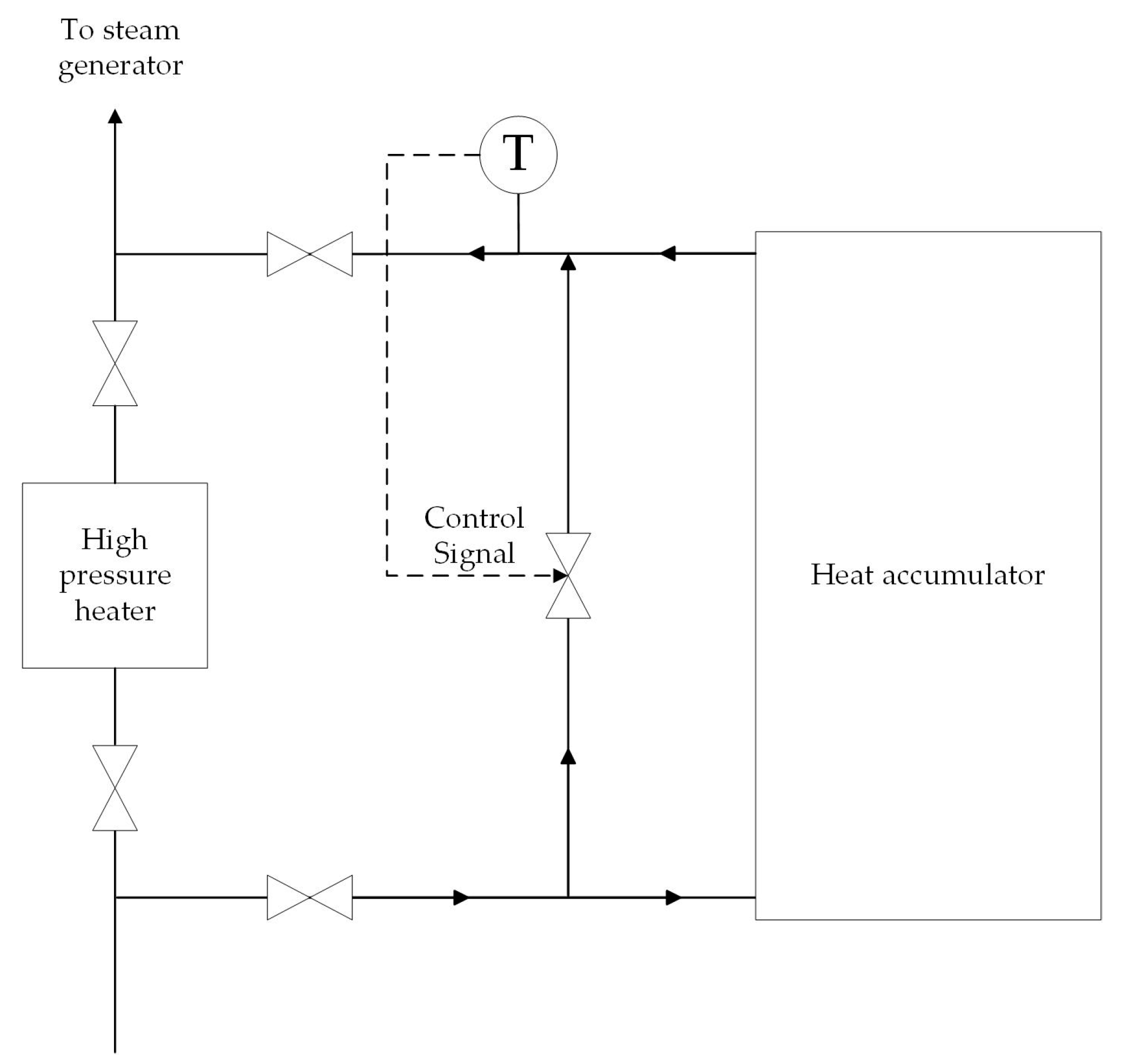
2.1. Method of Application of the Heat Accumulator with a PCM at a Low-Power Nuclear Power Plant
2.2. Topological Optimization
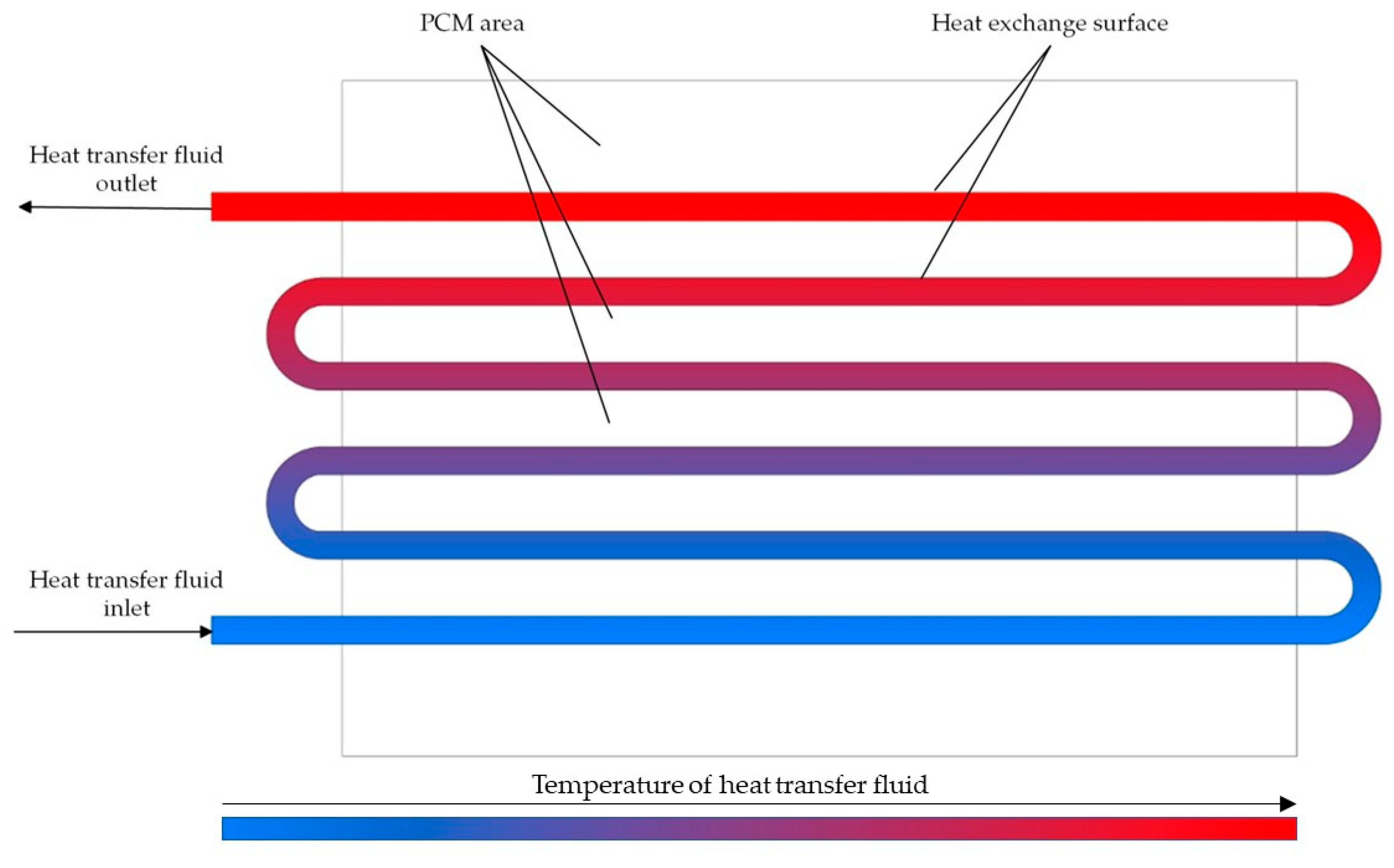
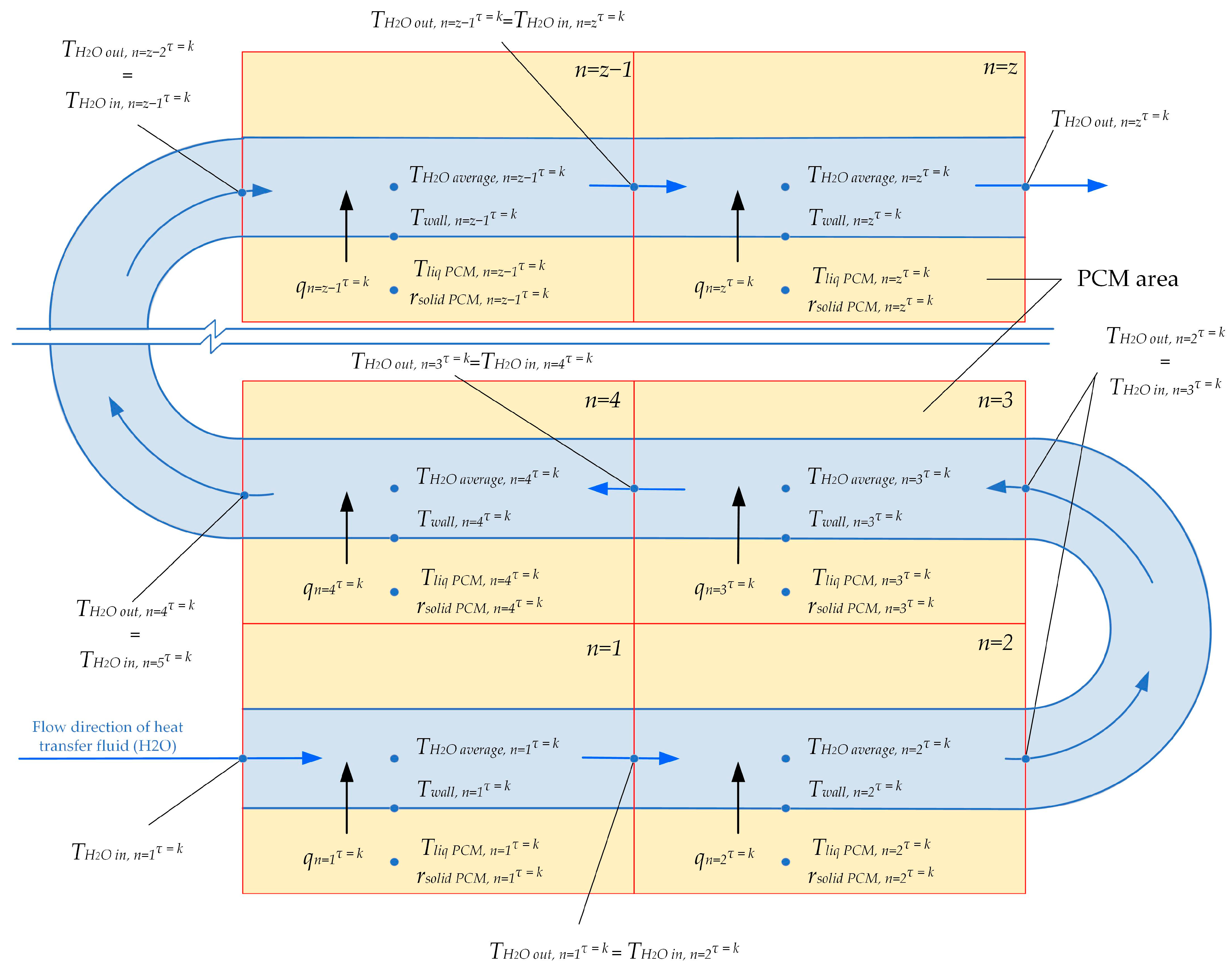
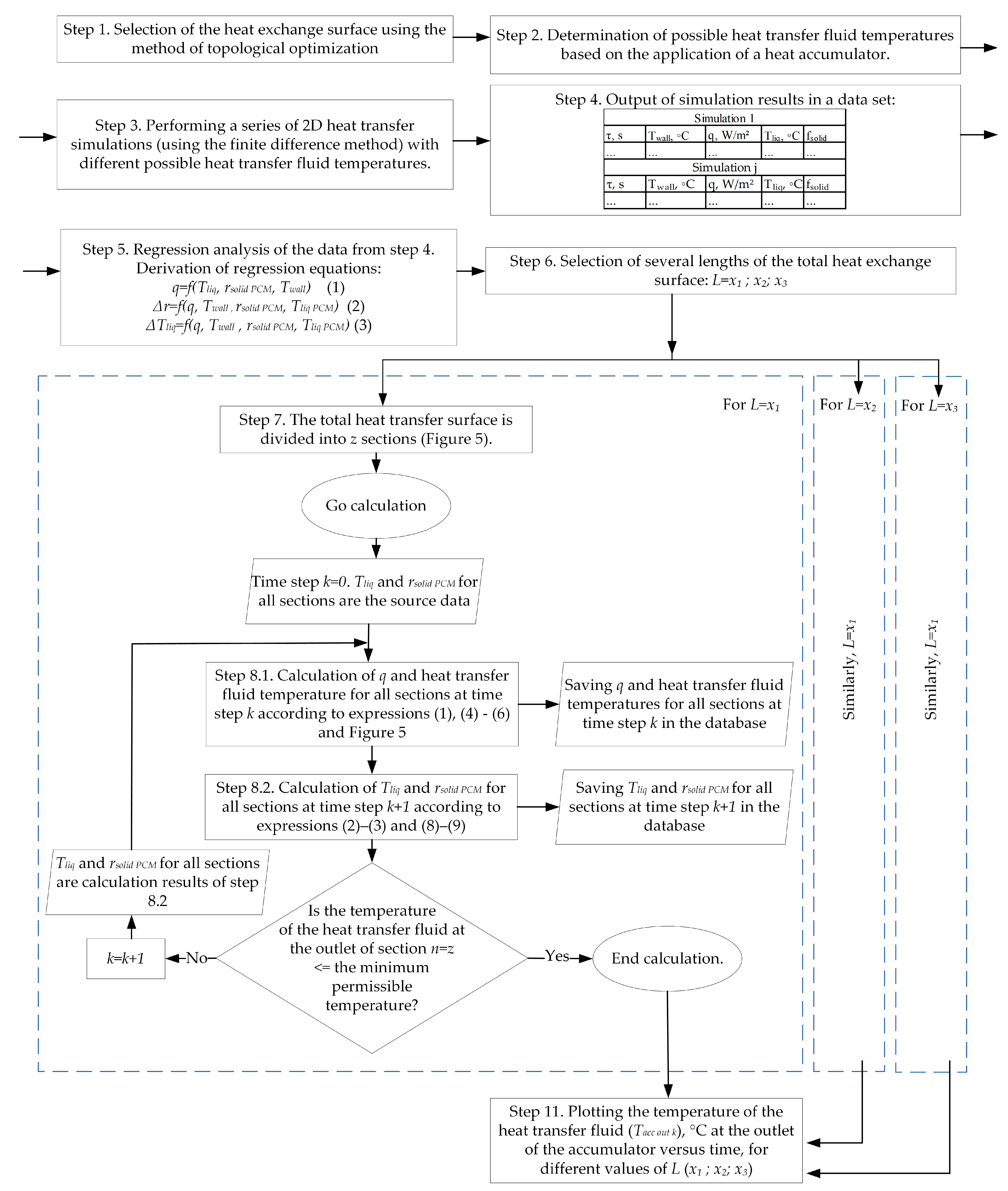
2.3. Method for Calculating Heat Transfer Across the Entire Heat Exchange Surface of a Heat Accumulator Using a PCM
2.4. Simulation in ANSYS FLUENT
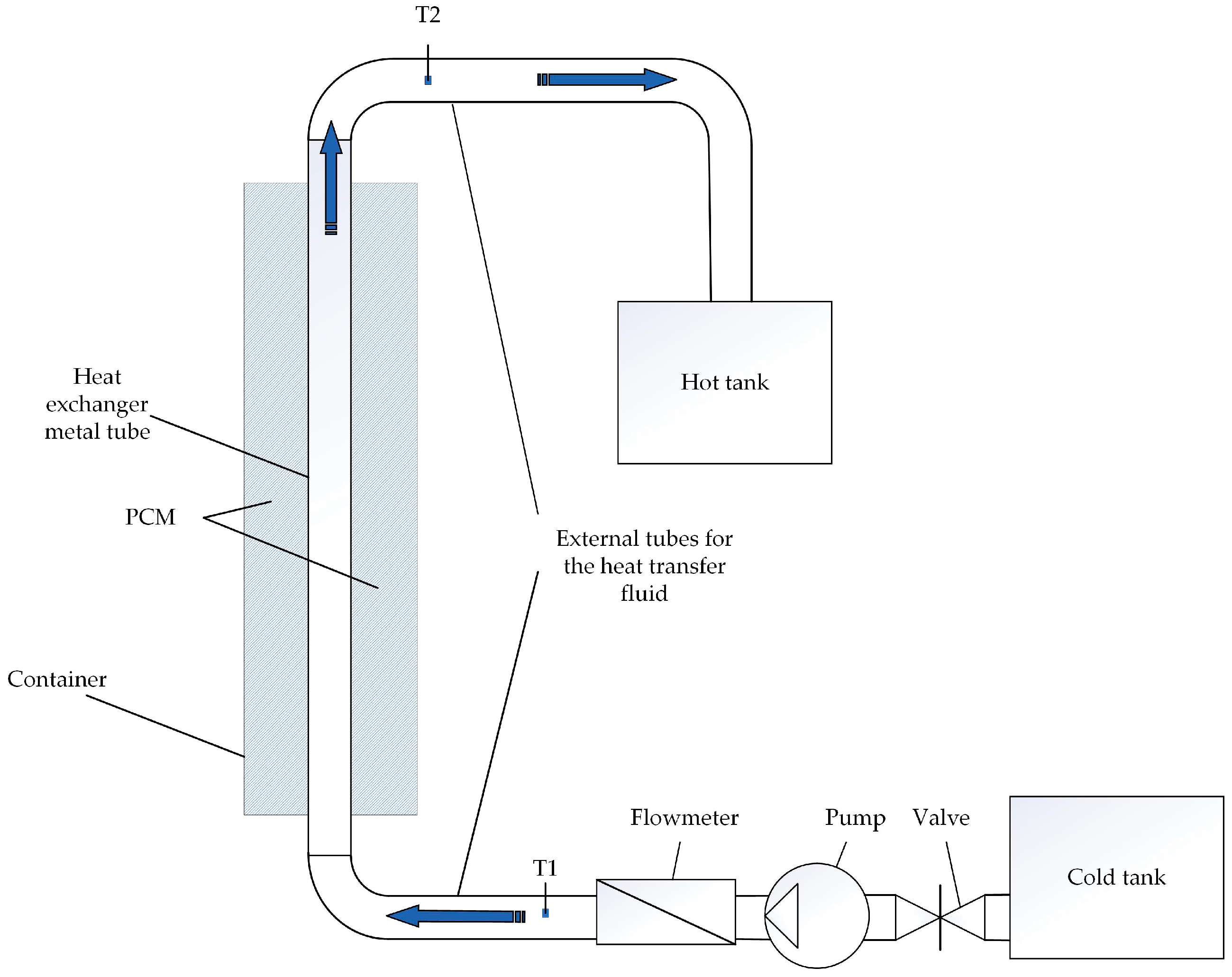
2.5. Experimental Verification of the ANSYS FLUENT Model and Verification of the Received Regression Dependencies
3. Results
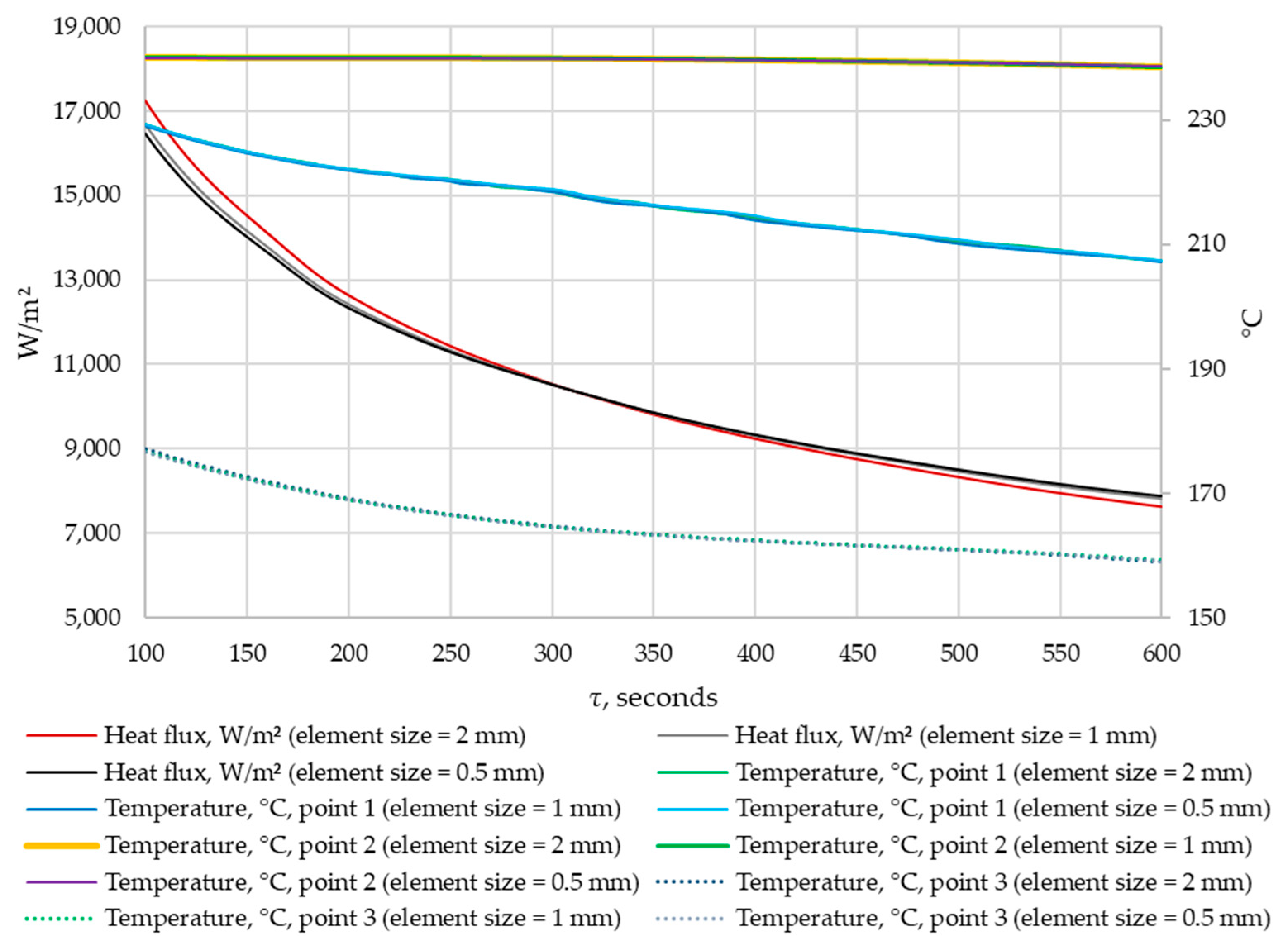
3.1. Grid-Independence Study
3.2. The Results of the Experimental Verification of the ANSYS FLUENT Model
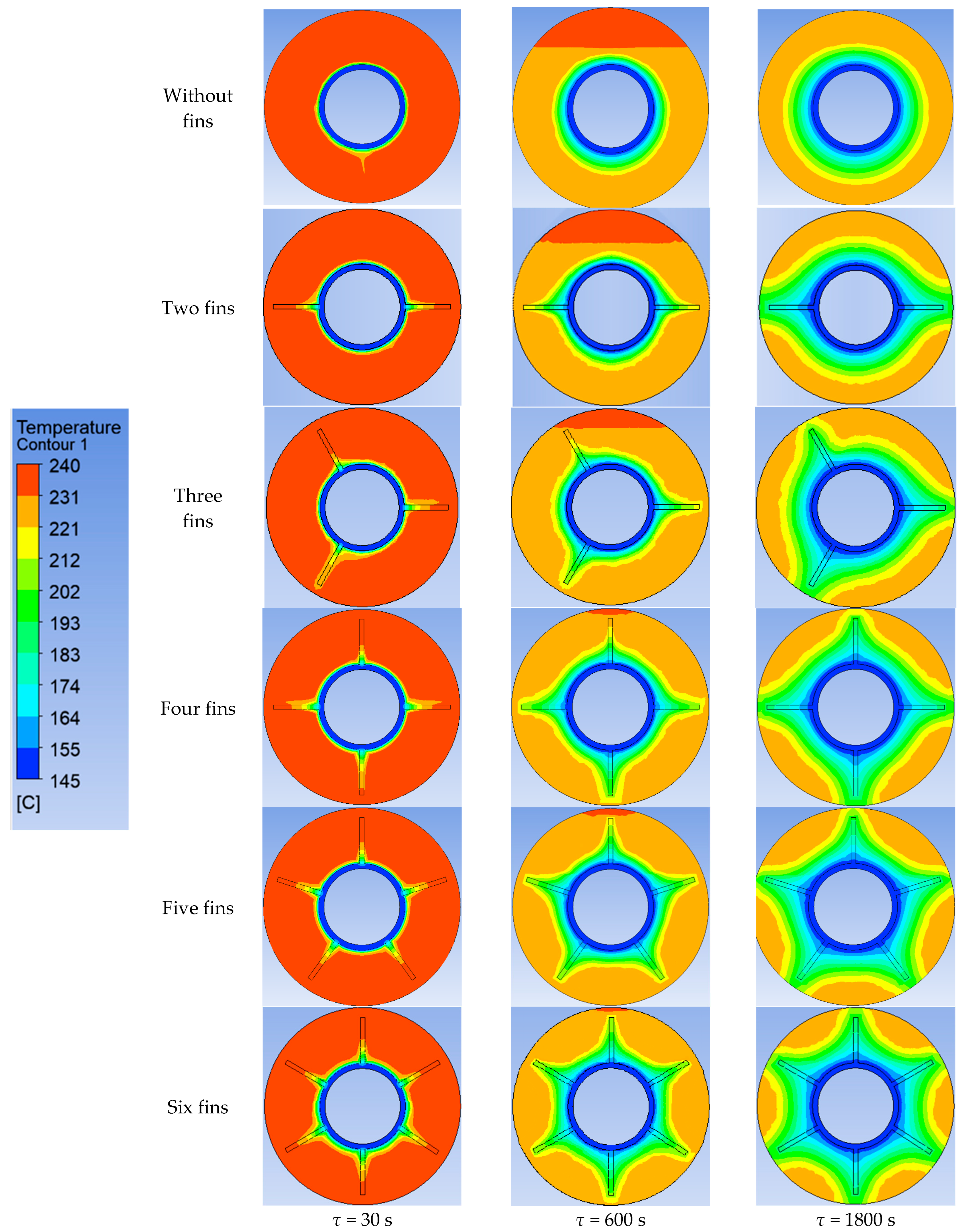
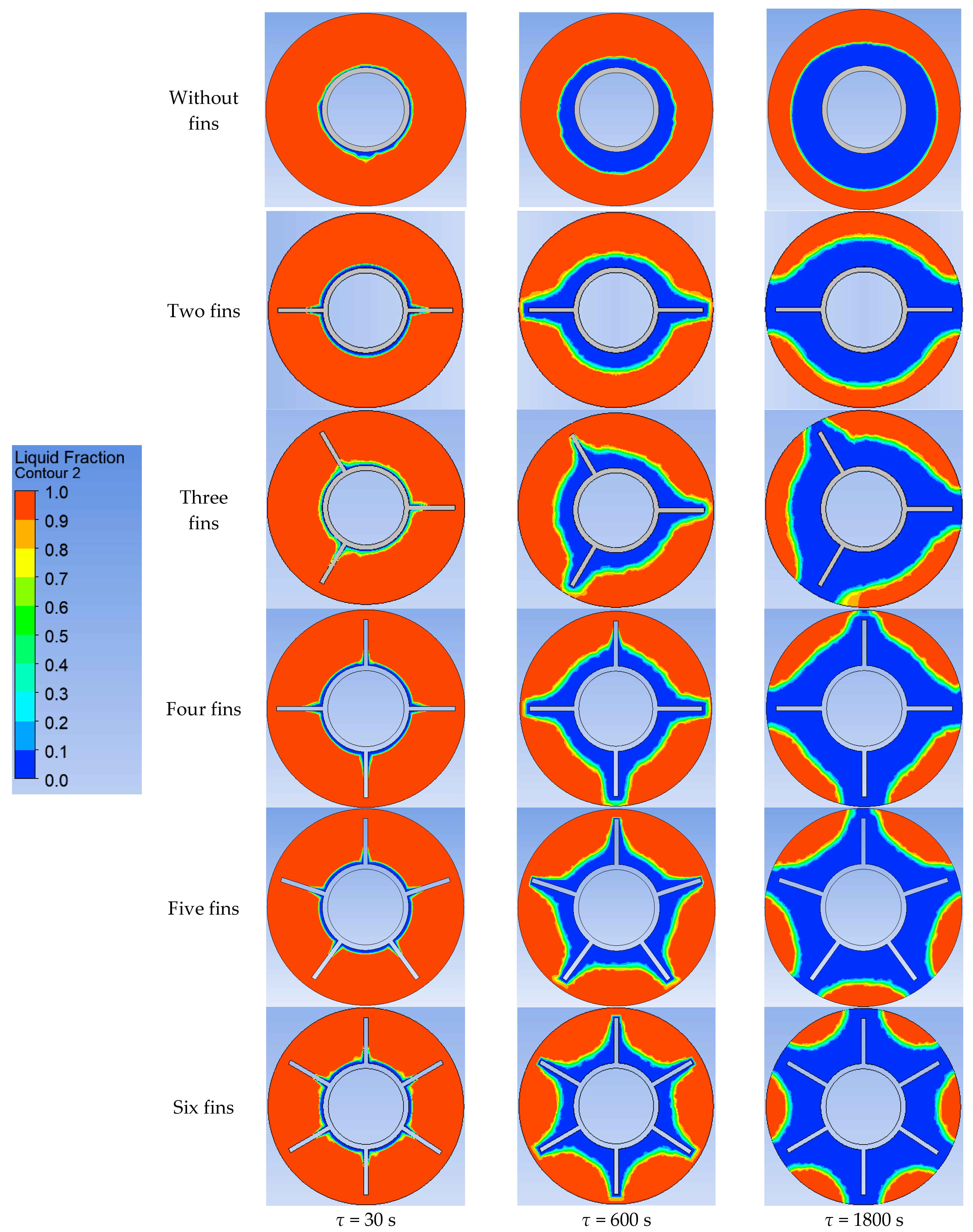
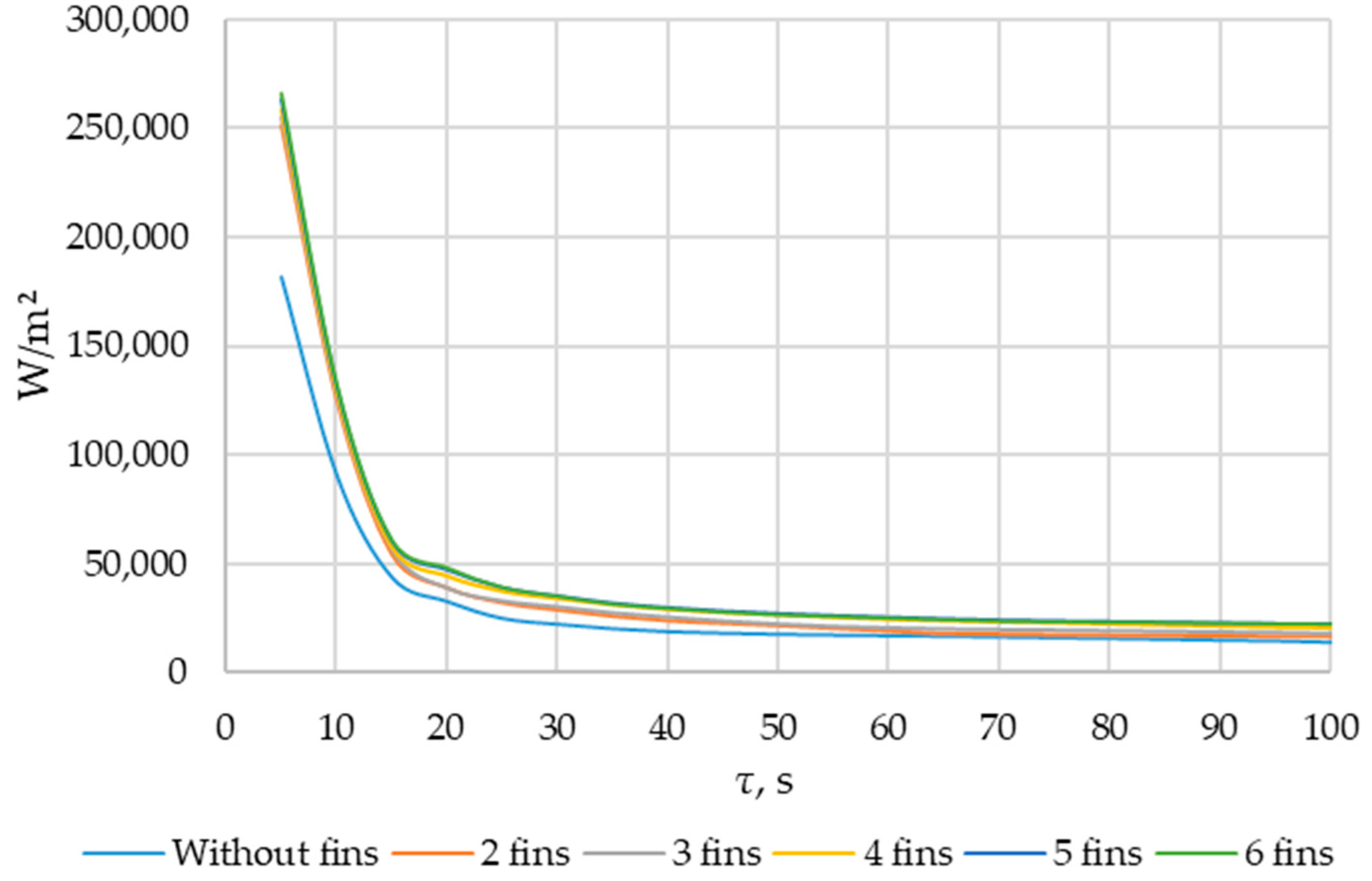
3.3. Results of Topological Optimization of Heat Transfer Surface
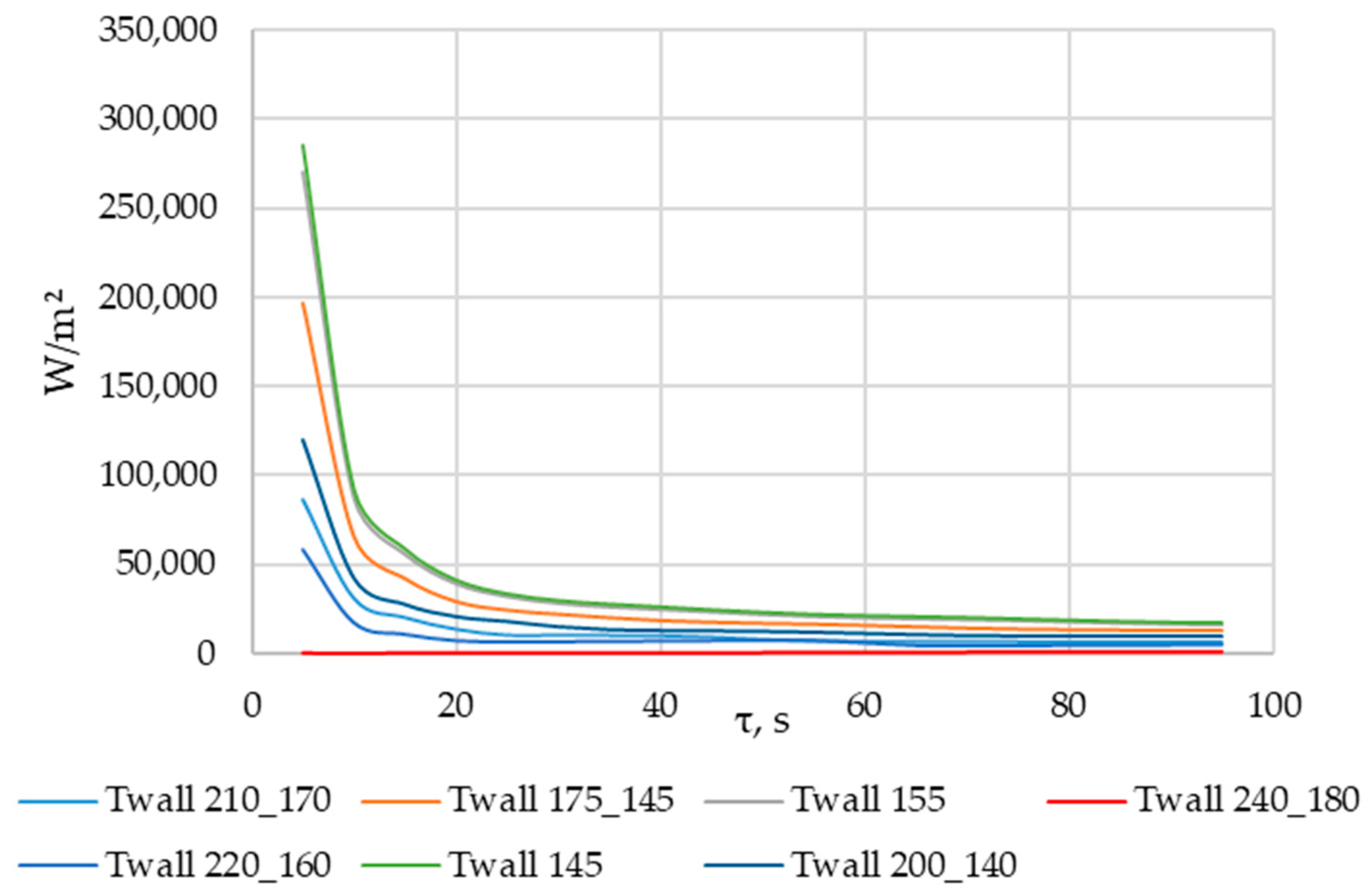
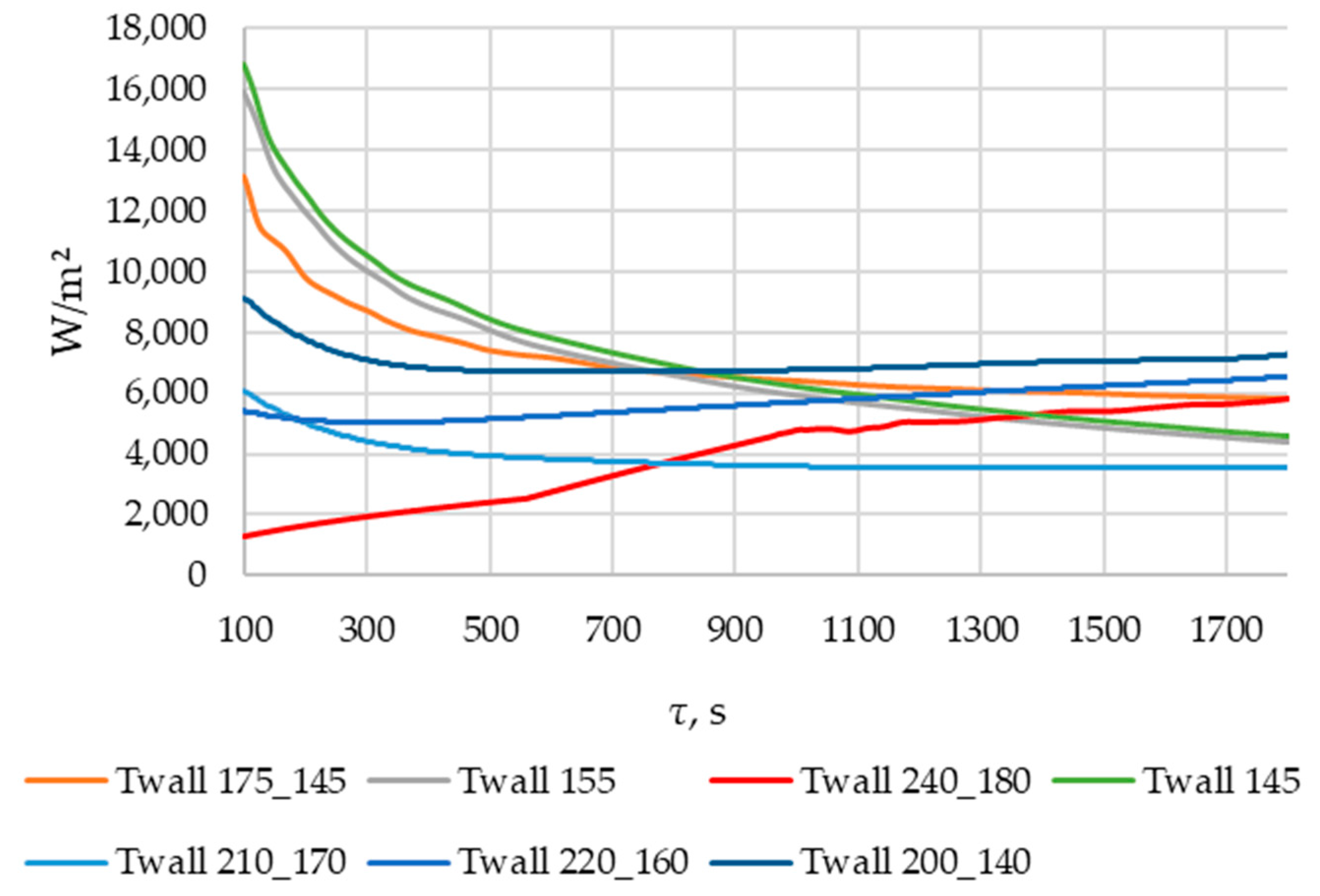
3.4. ANSYS Simulation of Heat Transfer at Different Tube Wall Temperature Conditions
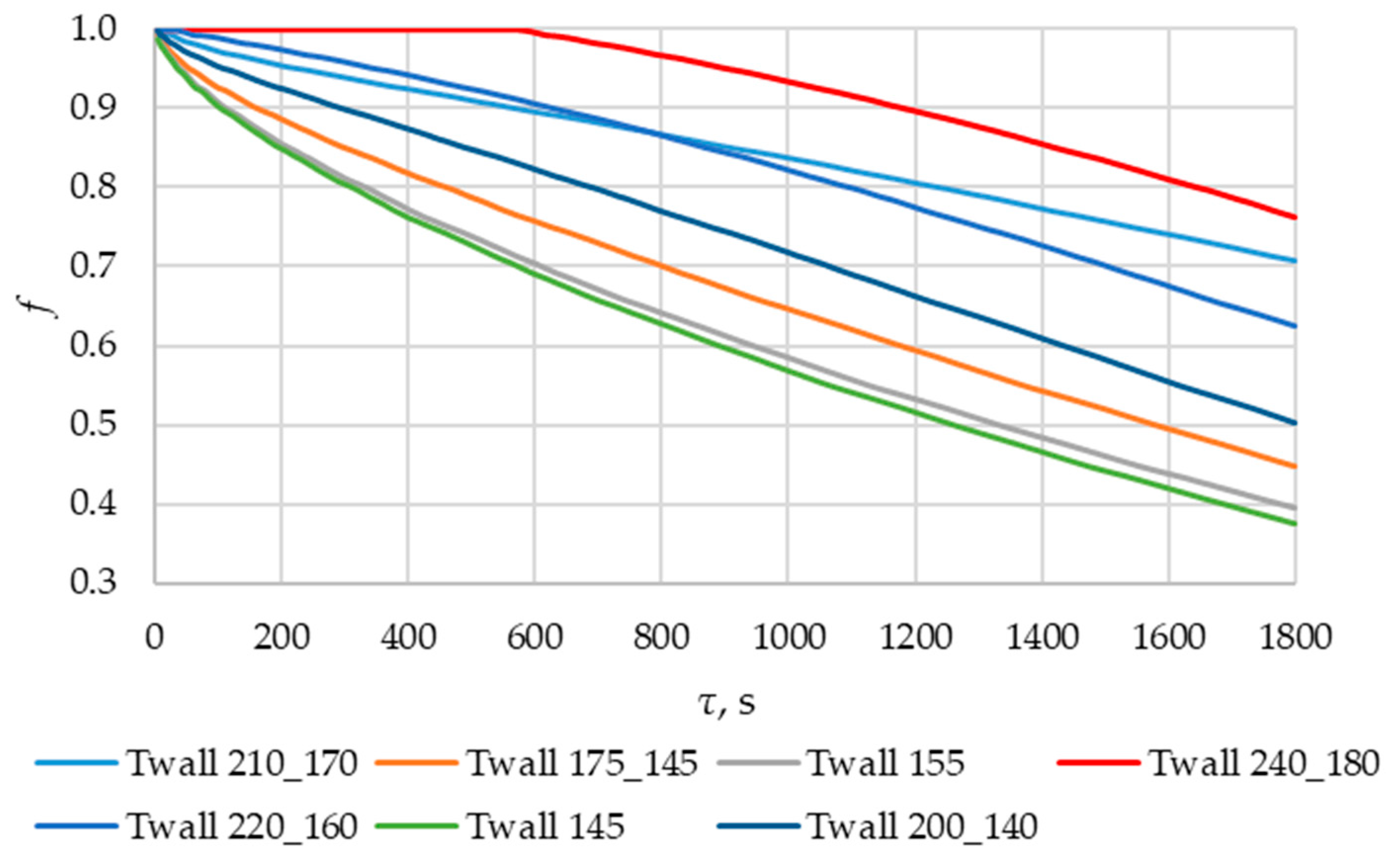
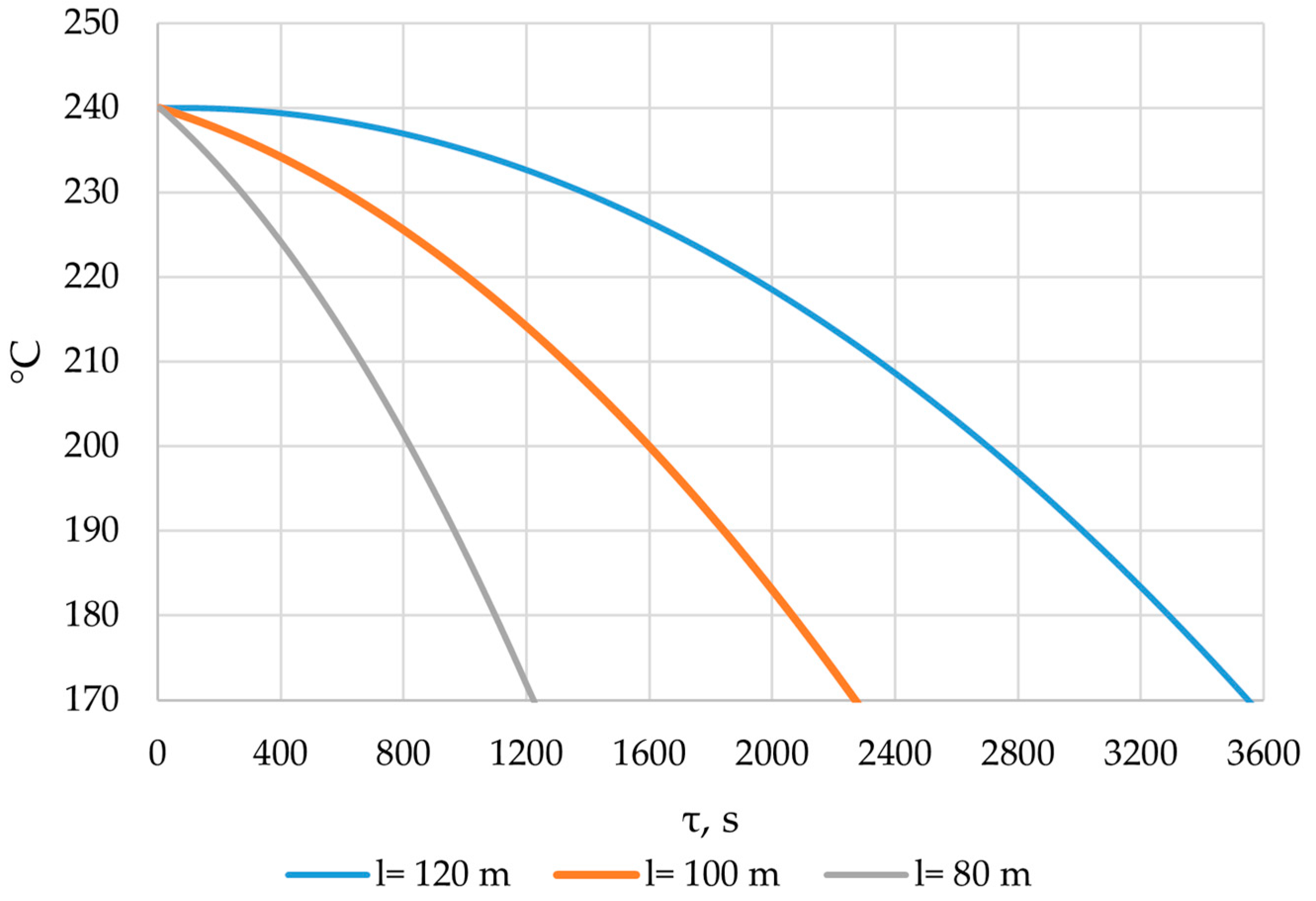
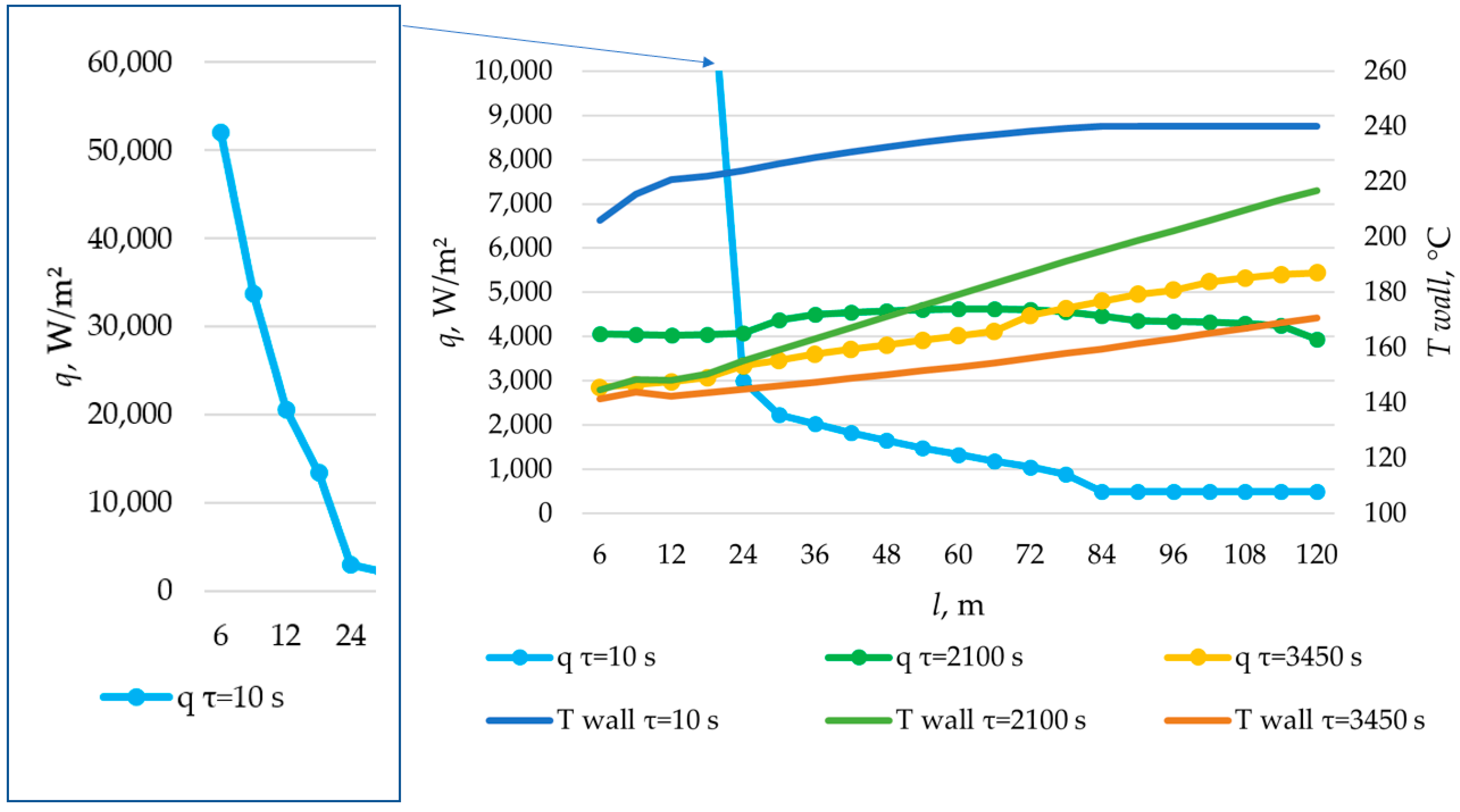
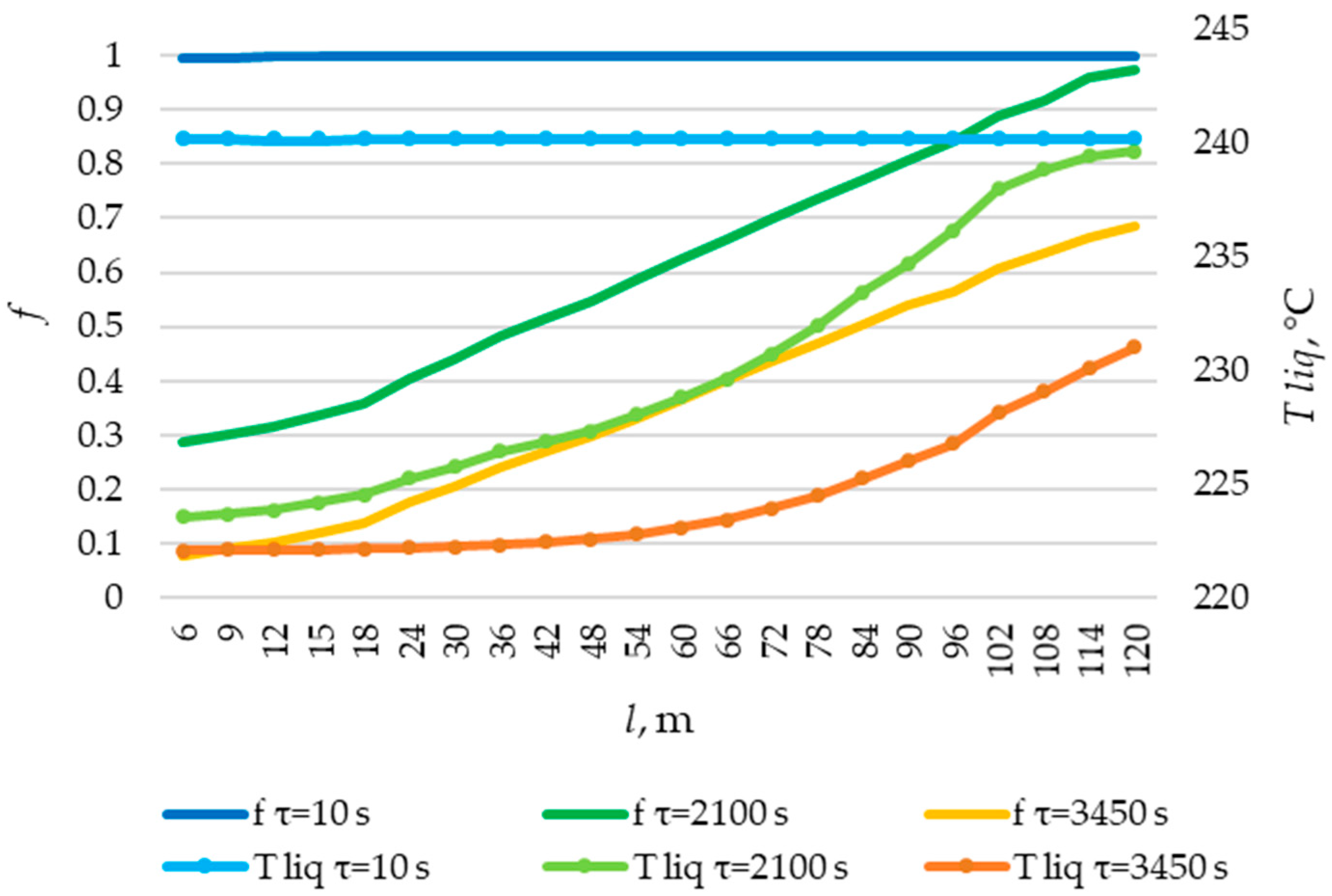
3.5. Calculation of Heat Transfer Across the Entire Heat Transfer Surface
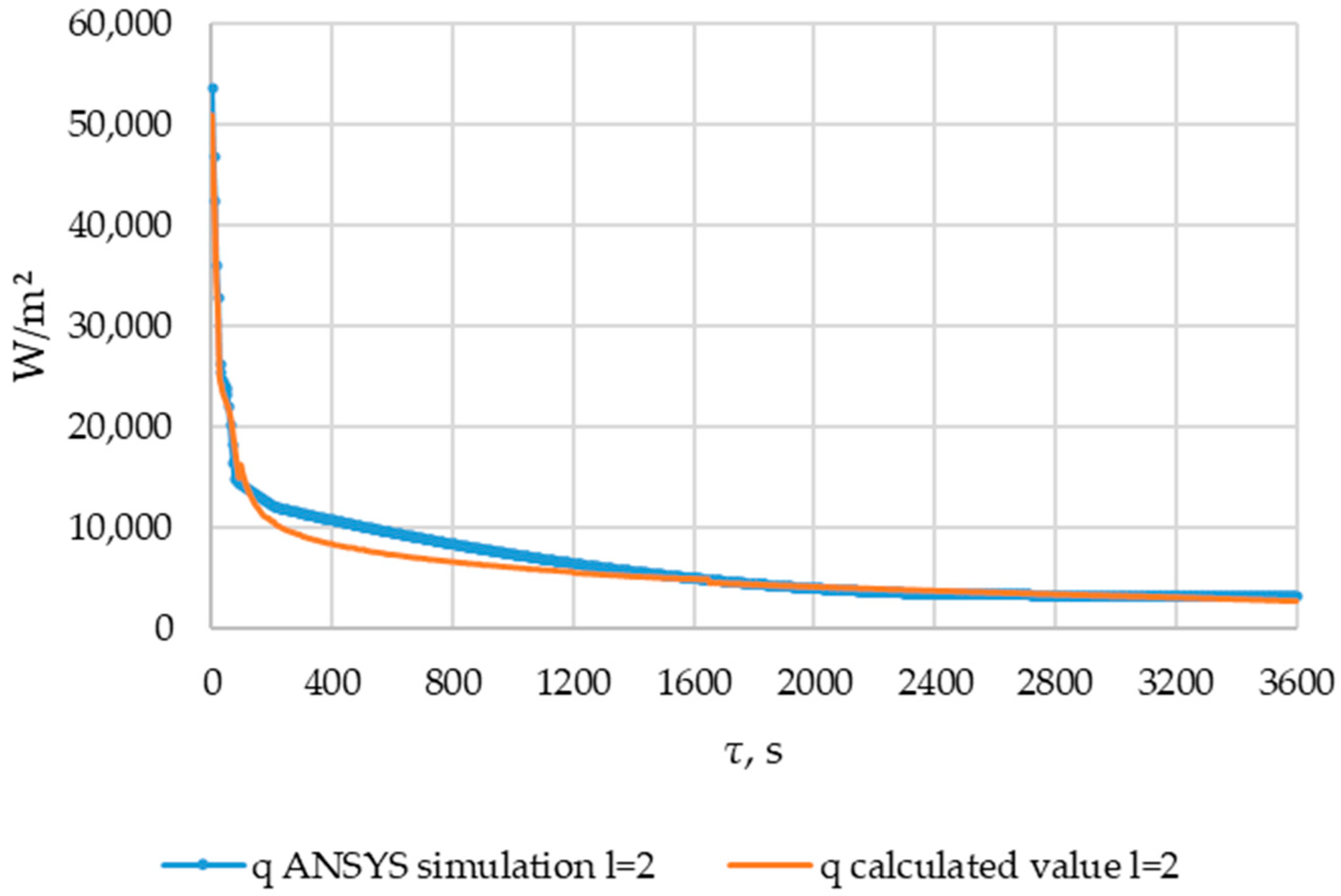
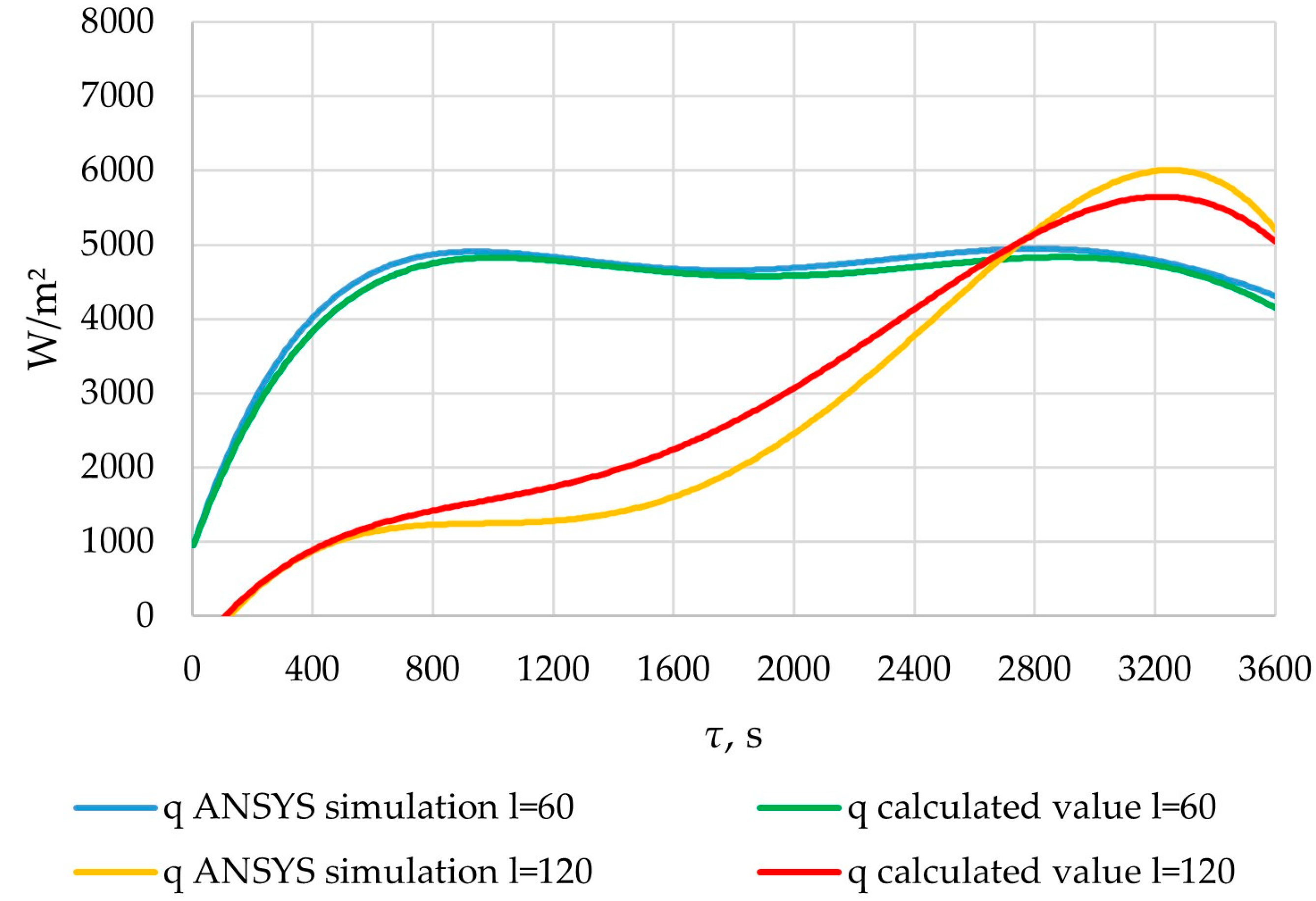
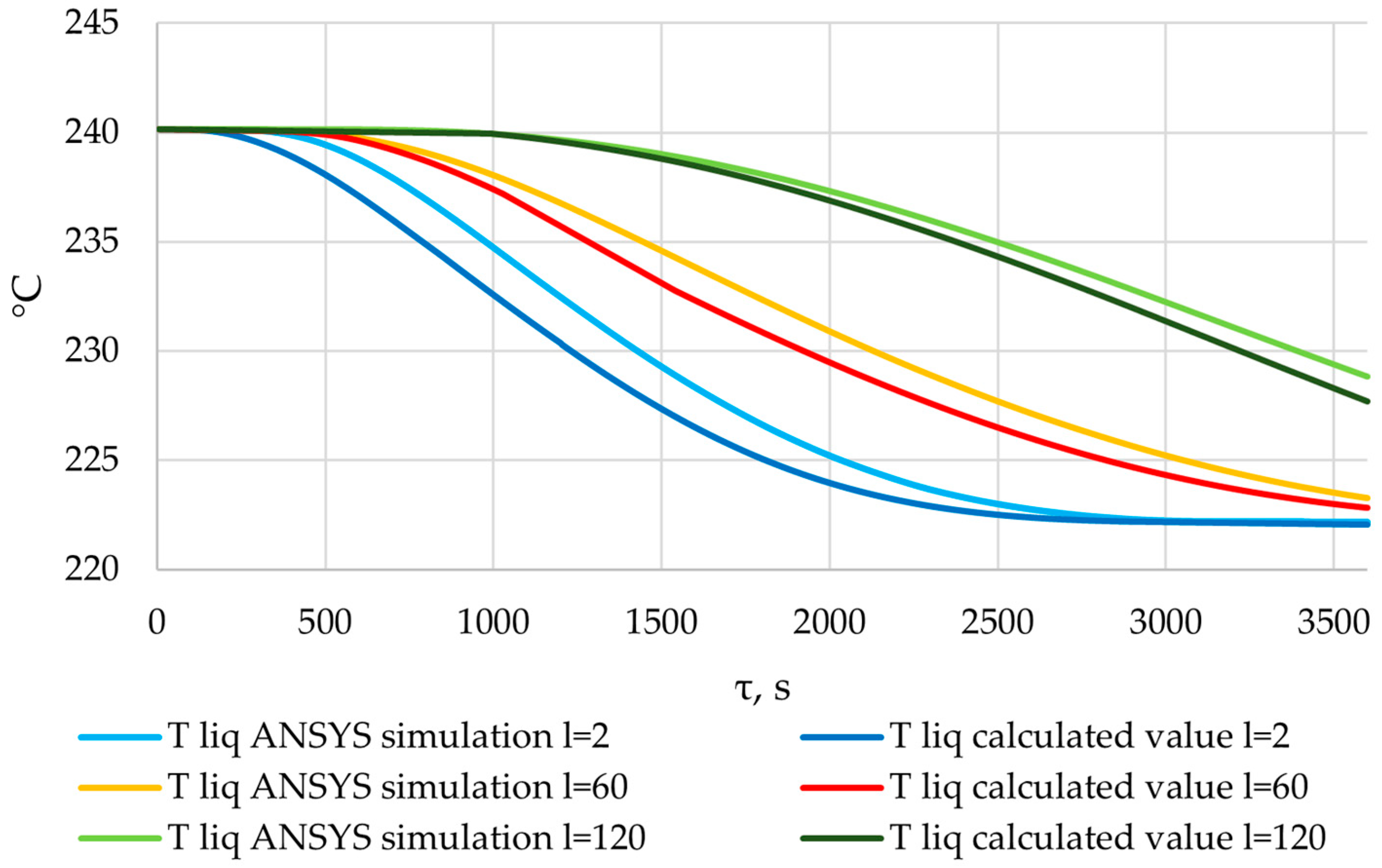
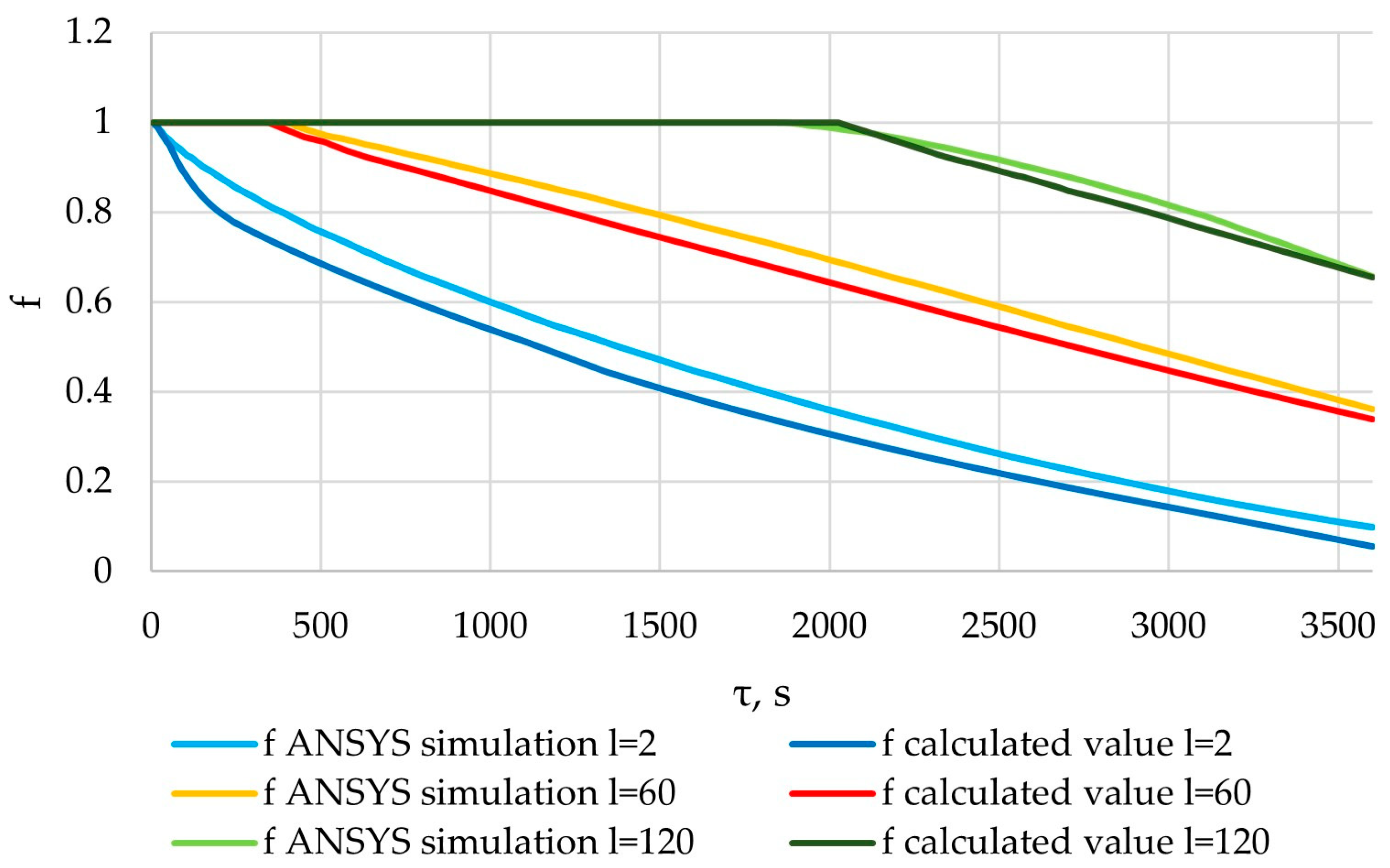
3.6. Checking the Received Dependencies
4. Discussion
5. Conclusions
- Heat transfer over the entire coil heat exchange surface in a heat accumulator with a PCM is calculated at discrete sections at each time step, taking into account the parameters and state of the heat transfer fluid in those sections and the parameters and condition of the PCM surrounding those sections;
- The heat flux density at each time step for each discrete section is determined by the dependence: q = f(Tliq, rsolid PCM, Twall);
- The surface temperature of the wall at each discrete section, from the side of the heat transfer fluid, is determined by a method of iterative calculation that takes into account heat transfer between the fluid and the wall: q = f(Tliq, rsolid PCM, Twall) = αH2O(Twall-Taverage);
- The change in the solid phase of the PCM Δrsolid PCM and the temperature of the liquid region of the PCM ΔTliq between time steps around each discrete section of the heat exchange surface is determined by the following expressions: Δr = f(q, Twall, rsolid PCM, Tliq PCM) and ΔTliq = f(q, Twall, rsolid PCM, Tliq PCM);
- The expressions q = f(Tliq, rsolid PCM, Twall), Δr = f(q, Twall, rsolid PCM, Tliq PCM), and ΔTliq = f(q, Twall, rsolid PCM, Tliq PCM) can be determined based on the results of a series of experiments or simulations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gendler, S.G.; Fazylov, I.R. Application efficiency of closed gathering system toward microclimate normalization in operating galleries in oil mines. Min. Inf. Anal. Bull. 2021, 9, 65–78. (In Russian) [Google Scholar] [CrossRef]
- Blinov, P.A.; Sadykov, M.I.; Gorelikov, V.G.; Nikishin, V.V. Development and research of backfill compounds with improved elastic and strength properties for oil and gas well lining. J. Min. Inst. 2024, 268, 588–598. [Google Scholar]
- Myakotnykh, A.A.; Ivanova, P.V.; Ivanov, S.L. Criteria and technological requirements for creation of a bridge platform to extract peat raw materials for climate-neutral geotechnology. Russ. Min. Ind. 2024, 4, 116–120. (In Russian) [Google Scholar] [CrossRef]
- Zhukovskiy, Y.; Koshenkova, A.; Vorobeva, V.; Rasputin, D.; Pozdnyakov, R. Assessment of the impact of technological development and scenario forecasting of the sustainable development of the fuel and energy complex. Energies 2023, 16, 3185. [Google Scholar] [CrossRef]
- Gendler, S.; Prokhorova, E. Risk-Based Methodology for Determining Priority Directions for Improving Occupational Safety in the Mining Industry of the Arctic Zone. Resources 2021, 10, 20. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.; Tsvetkov, P.; Buldysko, A.; Malkova, Y.; Stoianova, A.; Koshenkova, A. Scenario modeling of sustainable development of energy supply in the Arctic. Resources 2021, 10, 124. [Google Scholar] [CrossRef]
- Nazarychev, A.N.; Dyachenok, G.V.; Sychev, Y.A. A reliability study of the traction drive system in haul trucks based on failure analysis of their functional parts. J. Min. Inst. 2023, 261, 363–373. [Google Scholar]
- Shklyarskiy, Y.E.; Skamyin, A.N.; Carrizosa, M.J. Energy efficiency in the mineral resources and raw materials complex. J. Min. Inst. 2023, 261, 323–324. [Google Scholar]
- Nevskaya, M.; Shabalova, A.; Kosovtseva, T.; Nikolaychuk, L. Applications of simulation modeling in mining project risk management: Criteria, algorithm, evaluation. J. Infrastruct. Policy Dev. 2024, 8, 5375. [Google Scholar] [CrossRef]
- Sychev, Y.; Nazarychev, A.N.; Dyachenok, G.V. Improving the Labor Safety of Mining Dump Truck Drivers by Reducing the Risk of Failure of the Functional Units of the Traction Electric Drive under Operating Conditions. Bezop. Tr. Promyshlennosti Occup. Saf. Ind. 2023, 9, 52–58. (In Russian) [Google Scholar] [CrossRef]
- Abramovich, B.N.; Bogdanov, I.A. Improving the efficiency of autonomous electrical complexes of oil and gas enterprises. J. Min. Inst. 2021, 249, 408–416. [Google Scholar] [CrossRef]
- Korolev, N.A.; Zhukovskiy, Y.L.; Buldysko, A.D.; Baranov, G.D.; Chen, P. Energy resource evaluation from technical diagnostics of electromechanical devices in minerals sector. Min. Inf. Anal. Bull. 2024, 5, 158–181. (In Russian) [Google Scholar] [CrossRef]
- Lebedev, A.; Cherepovitsyn, A. Waste Management during the Production Drilling Stage in the Oil and Gas Sector: A Feasibility Study. Resources 2024, 13, 26. [Google Scholar] [CrossRef]
- Nepsha, F.S.; Varnavskiy, K.A.; Voronin, V.A.; Zaslavskiy, I.S.; Liven, A.S. Integration of renewable energy at coal mining enterprises: Problems and prospects. Min. Inst. 2023, 261, 455–469. [Google Scholar]
- Shpenst, V.A.; Belsky, A.A.; Orel, E.A. Improving the efficiency of autonomous electrical complex with renewable energy sources by means of adaptive regulation of its operating modes. J. Min. Inst. 2023, 261, 479–492. [Google Scholar]
- Shklyarskiy, Y.; Andreeva, I.; Sutikno, T.; Jopri, M.H. Energy management in hybrid complexes based on wind generation and hydrogen storage. Bull. Electr. Eng. Inform. 2024, 13, 1483–1494. [Google Scholar] [CrossRef]
- Shpenst, V.A.; Orel, E.A. Improving the Reliability of DC-DC Power Supply by Reserving Feedback Signals. Energ. Proc. CIS High. Educ. Inst. Power Eng. Assoc. 2021, 64, 408–420. [Google Scholar] [CrossRef]
- Skamyin, A.; Shklyarskiy, Y.; Gurevich, I. Influence of Background Voltage Distortion on Operation of Passive Harmonic Compensation Devices. Energies 2024, 17, 1342. [Google Scholar] [CrossRef]
- Belsky, A.; Glukhanich, D.; Sutikno, T.; Jopri, M.H. Estimation of hourly solar irradiation on tilted surfaces. Bull. Electr. Eng. Inform. 2023, 12, 3202–3214. [Google Scholar] [CrossRef]
- Belsky, A.A.; Glukhanich, D.Y. Standalone power system with photovoltaic and thermoelectric installations for power supply of remote monitoring and control stations for oil pipelines. Renew. Energy Focus 2023, 47, 100493. [Google Scholar] [CrossRef]
- Zhan, L.; Bo, Y.; Lin, T.; Fan, Z. Development and outlook of advanced nuclear energy technology. Energy Strategy Rev. 2021, 34, 100630. [Google Scholar] [CrossRef]
- Rogalev, N.; Rogalev, A.; Kindra, V.; Zlyvko, O.; Osipov, S. An Overview of Small Nuclear Power Plants for Clean Energy Production: Comparative Analysis of Distributed Generation Technologies and Future Perspectives. Energies 2023, 16, 4899. [Google Scholar] [CrossRef]
- Krūmiņš, J.; Kļaviņš, M. Investigating the potential of nuclear energy in achieving a carbon-free energy future. Energies 2023, 16, 3612. [Google Scholar] [CrossRef]
- Bhowmik, P.K.; Sabharwall, P.; Johnson, J.T.; Retamales, M.E.T.; Wang, C.; O’Brien, J.E.; Lietwiler, C.; Wu, Q. Scaling methodologies and similarity analysis for thermal hydraulics test facility development for water-cooled small modular reactor. Nucl. Eng. Des. 2024, 424, 113235. [Google Scholar] [CrossRef]
- Rahmanta, M.A.; Harto, A.W.; Agung, A.; Ridwan, M.K. Nuclear Power Plant to Support Indonesia’s Net Zero Emissions: A Case Study of Small Modular Reactor Technology Selection Using Technology Readiness Level and Levelized Cost of Electricity Comparing Method. Energies 2023, 16, 3752. [Google Scholar] [CrossRef]
- Petrunin, V.V.; Fadeev, Y.P.; Pakhomov, A.N.; Veshnyakov, K.B.; Polunichev, V.I.; Shamanin, I.E. Conceptual Design of Small NPP with RITM-200 Reactor. Energy 2019, 125, 365–369. [Google Scholar] [CrossRef]
- Peakman, A.; Merk, B.; Hesketh, K. The potential of pressurised water reactors to provide flexible response in future electricity grids. Energies 2020, 13, 941. [Google Scholar] [CrossRef]
- Gitelman, L.; Kozhevnikov, M.; Visotskaya, Y. Diversification as a method of ensuring the sustainability of energy supply within the energy transition. Resources 2023, 12, 19. [Google Scholar] [CrossRef]
- Aminov, R.Z.; Garievskii, M.V.; Anoshin, D.M. Development of Design Solutions for a Latent Heat Thermal Energy Storage under Conditions of Its Operation in a Single Energy Complex with an NPP. Therm. Eng. 2024, 71, 203–214. [Google Scholar] [CrossRef]
- Ali, M.; Alkaabi, A.K.; Lee, J.I. CFD simulation of an integrated PCM-based thermal energy storage within a nuclear power plant connected to a grid with constant or variable power demand. Nucl. Eng. Des. 2022, 394, 111819. [Google Scholar] [CrossRef]
- Alameri, S.A.; King, J.C.; Alkaabi, A.K.; Addad, Y. Prismatic-core advanced high temperature reactor and thermal energy storage coupled system–A preliminary design. Nucl. Eng. Technol. 2020, 52, 248–257. [Google Scholar] [CrossRef]
- Ali, M.; Alkaabi, A.K.; Alameri, S.A.; Addad, Y. Overall efficiency analysis of an innovative load-following nuclear power plant-thermal energy storage coupled cycle. Int. J. Exergy 2021, 36, 98–122. [Google Scholar] [CrossRef]
- Ali, M.; Alkaabi, A.K.; Addad, Y. Numerical investigation of a vertical triplex-tube latent heat storage/exchanger to achieve flexible operation of nuclear power plants. Int. J. Energy Res. 2022, 46, 2970–2987. [Google Scholar] [CrossRef]
- Aminov, R.Z.; Anoshin, D.M.; Garievsky, M.V. Numerical modeling of discharge modes and evaluation of the major characteristics of latent heat thermal energy storage at a nuclear power plant. J. Energy Storage 2024, 99, 113209. [Google Scholar] [CrossRef]
- Aminov, R.Z. Application of multifunctional systems with latent heat thermal energy storages: A way to improve NPP safety and efficiency. Therm. Eng. 2022, 69, 555–562. [Google Scholar] [CrossRef]
- Bocharov, G.S.; Dedov, A.V.; Eletskii, A.V.; Vagin, A.O.; Zacharenkov, A.V.; Zverev, M.A. Thermal Balance of a Water Thermal Accumulator Based on Phase Change Materials. J. Compos. Sci. 2023, 7, 399. [Google Scholar] [CrossRef]
- Xu, X.; Chang, C.; Guo, X.; Zhao, M. Experimental and Numerical Study of the Ice Storage Process and Material Properties of Ice Storage Coils. Energies 2023, 16, 5511. [Google Scholar] [CrossRef]
- Nascimento Porto, T.; Delgado, J.M.P.Q.; Guimarães, A.S.; Fernandes Magalhães, H.L.; Moreira, G.; Brito Correia, B.; Freire de Andrade, T.; Barbosa de Lima, A.G. Phase change material melting process in a thermal energy storage system for applications in buildings. Energies 2020, 13, 3254. [Google Scholar] [CrossRef]
- Porto, T.R.; Lima, J.A.; Andrade, T.H.; Delgado, J.M.; Lima, A.G. 3D Numerical Analysis of a Phase Change Material Solidification Process Applied to a Latent Thermal Energy Storage System. Energies 2023, 16, 3013. [Google Scholar] [CrossRef]
- Huang, Y.; Stonehouse, A.; Abeykoon, C. Encapsulation methods for phase change materials—A critical review. Int. J. Heat Mass Transf. 2023, 200, 123458. [Google Scholar] [CrossRef]
- Wang, G.; Tang, Z.; Gao, Y.; Liu, P.; Li, Y.; Li, A.; Chen, X. Phase change thermal storage materials for interdisciplinary applications. Chem. Rev. 2023, 123, 6953–7024. [Google Scholar] [CrossRef] [PubMed]
- Masood, U.; Haggag, M.; Hassan, A.; Laghari, M. A Review of Phase Change Materials as a Heat Storage Medium for Cooling Applications in the Built Environment. Buildings 2023, 13, 1595. [Google Scholar] [CrossRef]
- Shmyhol, D.; Rimár, M.; Fedak, M.; Krenický, T.; Lopušniak, M.; Polivka, N. Techniques for Enhancing Thermal Conductivity and Heat Transfer in Phase Change Materials in Hybrid Phase Change Material–Water Storage Tanks. Appl. Sci. 2024, 14, 3732. [Google Scholar] [CrossRef]
- Powała, K.; Obraniak, A.; Heim, D.; Mrowiec, A. Macroencapsulation of paraffin in a polymer–gypsum composite using granulation technique. Materials 2022, 15, 3783. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Lu, Y.; Yang, Y.; Wu, Y.; Zheng, K.; Li, L. Research on Thermal Adaptability of Flexible Operation in Different Types of Coal-Fired Power Units. Energies 2024, 17, 2185. [Google Scholar] [CrossRef]
- Wu, S.; Yan, T.; Kuai, Z.; Pan, W. Thermal conductivity enhancement on phase change materials for thermal energy storage: A review. Energy Storage Mater. 2020, 25, 251–295. [Google Scholar] [CrossRef]
- Yu, K.; Jia, M.; Yang, Y.; Liu, Y. A clean strategy of concrete curing in cold climate: Solar thermal energy storage based on phase change material. Appl. Energy 2023, 331, 120375. [Google Scholar] [CrossRef]
- Khan, M.I.; Asfand, F.; Al-Ghamdi, S.G. Progress in research and development of phase change materials for thermal energy storage in concentrated solar power. Appl. Therm. Eng. 2023, 219, 119546. [Google Scholar] [CrossRef]
- Goel, V.; Saxena, A.; Kumar, M.; Thakur, A.; Sharma, A.; Bianco, V. Potential of phase change materials and their effective use in solar thermal applications: A critical review. Appl. Therm. Eng. 2023, 219, 119417. [Google Scholar] [CrossRef]
- Rashid, F.L.; Al-Obaidi, M.A.; Dulaimi, A.; Bahlol, H.Y.; Hasan, A. Recent advances, development, and impact of using phase change materials as thermal energy storage in different solar energy systems: A review. Designs 2023, 7, 66. [Google Scholar] [CrossRef]
- Musiał, M.; Lichołai, L.; Pękala, A. Analysis of the Thermal Performance of Isothermal Composite Heat Accumulators Containing Organic Phase-Change Material. Energies 2023, 16, 1409. [Google Scholar] [CrossRef]
- Bykowa, E.; Skachkova, M.; Raguzin, I.; Dyachkova, I.; Boltov, M. Automation of Negative Infrastructural Externalities As-sessment Methods to Determine the Cost of Land Resources Based on the Development of a “Thin Client” Model. Sustainability 2022, 14, 9383. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Z. A cross-scale ‘material-component-system’ framework for transition towards zero-carbon buildings and districts with low, medium and high-temperature phase change materials. Sustain. Cities Soc. 2023, 89, 104378. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, Y. Energy, exergy and economic analysis of ceramic foam-enhanced molten salt as phase change material for medium-and high-temperature thermal energy storage. Energy 2023, 262, 125462. [Google Scholar] [CrossRef]
- Radomska, E.; Mika, L.; Sztekler, K.; Lis, L. The impact of heat exchangers’ constructions on the melting and solidification time of phase change materials. Energies 2020, 13, 4840. [Google Scholar] [CrossRef]
- Ma, F.; Zhu, T.; Zhang, Y.; Lu, X.; Zhang, W.; Ma, F. A review on heat transfer enhancement of phase change materials using fin tubes. Energies 2023, 16, 545. [Google Scholar] [CrossRef]
- Hosseinpour, A.; Pourfallah, M.; Gholinia, M. Analysis of phase change material (PCM) melting utilizing environmentally friendly nanofluids in a double tube with spiral fins: A numerical study. Int. J. Thermofluids 2024, 22, 100620. [Google Scholar] [CrossRef]
- Taghavi, M.; Poikelispää, M.; Agrawal, V.; Syrjälä, S.; Joronen, T. Numerical investigation of a plate heat exchanger thermal energy storage system with phase change material. J. Energy Storage 2023, 61, 106785. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, G.; Wu, Y.; Yang, J.; Sui, Y.; Zhao, X. Energy storage potential analysis of phase change material (PCM) energy storage units based on tunnel lining ground heat exchangers. Appl. Therm. Eng. 2023, 235, 121403. [Google Scholar] [CrossRef]
- Moghadam, F.N.; Izadpanah, E.; Shekari, Y.; Amini, Y. Experimental evaluation of shell geometry impact on thermal and exergy performance in helical coiled tube heat exchanger with phase change material. J. Energy Storage 2024, 83, 110790. [Google Scholar] [CrossRef]
- Wang, Y.; Alvarado, J.L.; Terrell, W., Jr. Thermal performance of microencapsulated phase change material slurry in helical coils with reversed loops and wire coil inserts. Exp. Heat Transf. 2023, 36, 984–1011. [Google Scholar] [CrossRef]
- Sheikh, M.I.A.R.; Ahammed, M.E.; Gumtapure, V. Thermal behavior of composite phase change material of polyethylene in a shell and coil-based thermal energy storage: Numerical analysis. J. Energy Storage 2023, 74, 109438. [Google Scholar] [CrossRef]
- Shank, K.; Bernat, J.; Justice, Q.; Niksiar, P.; Tiari, S. Experimental study of a latent heat thermal energy storage system assisted by variable-length radial fins. J. Energy Storage 2023, 68, 107692. [Google Scholar] [CrossRef]
- Hosseini, A.; Banakar, A.; Gorjian, S.; Jafari, A. Experimental and numerical investigation of the melting behavior of a phase change material in a horizontal latent heat accumulator with longitudinal and annular fins. J. Energy Storage 2024, 82, 110563. [Google Scholar] [CrossRef]
- Zhang, W.; Pan, L.; Ding, D.; Zhang, R.; Bai, J.; Du, Q. Progress in the Study of Enhanced Heat Exchange in Phase Change Heat Storage Devices. ACS Omega 2023, 8, 22331–22344. [Google Scholar] [CrossRef]
- Dagdevir, T.; Ding, Y. Numerical investigation of battery thermal management by using helical fin and composite phase change material. J. Energy Storage 2024, 75, 109674. [Google Scholar] [CrossRef]
- Zhang, N.; Cao, X.; Fan, X.; Chen, L.; Qu, Y. Thermal storage performance of latent heat thermal energy storage device with helical fin under realistic working conditions. Appl. Therm. Eng. 2024, 236, 121668. [Google Scholar] [CrossRef]
- Palmer, B.; Arshad, A.; Yang, Y.; Wen, C. Energy storage performance improvement of phase change materials-based triplex-tube heat exchanger (TTHX) using liquid–solid interface-informed fin configurations. Appl. Energy 2023, 333, 120576. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; Ge, R. Comparative investigation of charging performance in shell and tube device containing molten salt based phase change materials for thermal energy storage. Case Stud. Therm. Eng. 2023, 43, 102804. [Google Scholar] [CrossRef]
- Qasem, N.A.; Belazreg, A.; Khetib, Y.; Abderrahmane, A.; Homod, R.Z.; Younis, O.; Rawa, M. Effect of novel fin distribution on the melting process of thermal storage units. Appl. Therm. Eng. 2024, 243, 122547. [Google Scholar] [CrossRef]
- Guo, X.; Han, X.; Lin, J.; Liu, S.; Han, Z. Effect of eccentricity and V-shaped fins on the heat transfer performance of a phase change heat storage system. J. Energy Storage 2023, 73, 108833. [Google Scholar] [CrossRef]
- İzgi, B.; Demirağ, H.Z. Multi-objective optimization of fin shape in a cylindrical encapsulated phase change material for thermal energy storage applications. Appl. Therm. Eng. 2023, 231, 120921. [Google Scholar] [CrossRef]
- Cai, L.; Mi, S.; Luo, C. Study on enhanced heat transfer of a phase change material slurry in transverse corrugated tubes. Appl. Therm. Eng. 2023, 226, 120293. [Google Scholar] [CrossRef]
- Belhadad, T.; Kanna, A.; Samaouali, A.; Kadiri, I. CFD Investigation of Fin Design Influence on Phase Change Material Melting for Solar Thermal Energy Storage. e-Prime-Adv. Electr. Eng. Electron. Energy 2023, 6, 100306. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.X.; Zhang, M.; Zhao, X.; Li, T. Enhanced thermal performance of shell and tube phase change heat accumulator with novel biomimetic spider web fins. Appl. Therm. Eng. 2023, 233, 121224. [Google Scholar] [CrossRef]
- Rogowski, M.; Andrzejczyk, R. Recent advances of selected passive heat transfer intensification methods for phase change material-based latent heat energy storage units: A review. Int. Commun. Heat Mass Transf. 2023, 144, 106795. [Google Scholar] [CrossRef]
- Urschitz, G.; Walter, H.; Brier, J. Experimental investigation on bimetallic tube compositions for the use in latent heat thermal energy storage units. Energy Convers. Manag. 2016, 125, 368–378. [Google Scholar] [CrossRef]
- Negi, A.; Ranakoti, L.; Bhandari, P.; Khargotra, R.; Singh, T. Thermo-physical characteristics and storage material compatibility in nano-enhanced phase change materials for solar distillation applications: A critical assessment. Sol. Energy Mater. Sol. Cells 2024, 271, 112870. [Google Scholar] [CrossRef]
- Riahi, S.; Evans, M.; Belusko, M.; Liu, M.; Bruno, F. Orientation impact on structural integrity of a shell and tube latent heat thermal energy storage system. J. Energy Storage 2022, 52, 104829. [Google Scholar] [CrossRef]
- Dal Magro, F.; Benasciutti, D.; Nardin, G. Thermal stress analysis of PCM containers for temperature smoothing of waste gas. Appl. Therm. Eng. 2016, 106, 1010–1022. [Google Scholar] [CrossRef]
- Beck, A.; Koller, M.; Walter, H.; Hameter, M. Transient numerical analysis of different finned tube designs for use in latent heat thermal energy storage devices. Energy Sustain. 2015, 56857, V002T13A004. [Google Scholar] [CrossRef]
- Wołoszyn, J.; Szopa, K. A combined heat transfer enhancement technique for shell-and-tube latent heat thermal energy storage. Renew. Energy 2023, 202, 1342–1356. [Google Scholar] [CrossRef]
- Al-Salami, H.A.; Dhaidan, N.S.; Abbas, H.H.; Al-Mousawi, F.N.; Homod, R.Z. Review of PCM charging in latent heat thermal energy storage systems with fins. Therm. Sci. Eng. Prog. 2024, 51, 102640. [Google Scholar] [CrossRef]
- Kirincic, M.; Trp, A.; Lenic, K.; Batista, J. Latent thermal energy storage performance enhancement through optimization of geometry parameters. Appl. Energy 2024, 365, 123255. [Google Scholar] [CrossRef]
- Karimi, A.R.; Siavashi, M.; Keshtkaran, A.H.; Tousi, R. Impact of using different numbers of fins on heat transfer augmentation in a phase-change material helical coil latent energy storage system. Int. Commun. Heat Mass Transf. 2024, 156, 107608. [Google Scholar] [CrossRef]
- Khedher, N.B.; Hosseinzadeh, K.; Abed, A.M.; Khosravi, K.; Mahdi, J.M.; Sultan, H.S.; Talebizadehsardari, P. Accelerated charging of PCM in coil heat exchangers via central return tube and inlet positioning: A 3D analysis. Int. Commun. Heat Mass Transf. 2024, 152, 107275. [Google Scholar] [CrossRef]
- Miao, X.; Riaz, F.; Alotaibi, B.; Agrawal, M.K.; Abuhussain, M.; Alsenani, T.R.; Lin, Q. Performance enhancement of latent heat thermal energy storage system by using spiral fins in phase change material solidification process. Process Saf. Environ. Prot. 2023, 176, 568–579. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; Ge, R. Comparison of performance enhancement in a shell and tube based latent heat thermal energy storage device containing different structured fins. Renew. Energy 2023, 206, 994–1006. [Google Scholar] [CrossRef]
- Palaev, A.G.; Krasnikov, A.A. Ultrasonic treatment of a welded joint from the external, internal and two sides on reducing residual welding stresses. Int. J. Eng. 2024, 37, 2171–2180. [Google Scholar] [CrossRef]
- Choure, B.K.; Alam, T.; Kumar, R. A review on heat transfer enhancement techniques for PCM based thermal energy storage system. J. Energy Storage 2023, 72, 108161. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y.; Zeng, L.; Cui, W.; Xie, J. A novel topology optimization of fin structure in shell-tube phase change accumulator considering the double objective functions and natural convection. J. Energy Storage 2024, 80, 110327. [Google Scholar] [CrossRef]
- Diaconu, B.M.; Cruceru, M.; Anghelescu, L. Phase Change Materials—Applications and Systems Designs: A Literature Review. Designs 2022, 6, 117. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Li, Y.; Guo, J.; Huang, X.; Yang, X.; He, Y.L. Design and evaluation of metal foam horizontal tube-and-shell phase change accumulator: Optimal position distribution of heating tubes. Int. J. Heat Fluid Flow 2024, 107, 109367. [Google Scholar] [CrossRef]
- Laing, D.; Bauer, T.; Breidenbach, N.; Hachmann, B.; Johnson, M. Development of high temperature phase-change-material storages. Appl. Energy 2013, 109, 497–504. [Google Scholar] [CrossRef]
- Łach, Ł.; Svyetlichnyy, D. 3D Model of Heat Flow during Diffusional Phase Transformations. Materials 2023, 16, 4865. [Google Scholar] [CrossRef]
- Huang, R.; Mahvi, A.; Odukomaiya, W.; Goyal, A.; Woods, J. Reduced-order modeling method for phase-change thermal energy storage heat exchangers. Energy Convers. Manag. 2022, 263, 115692. [Google Scholar] [CrossRef]
- Zhang, Q.; Sazon TA, S.; Fadnes, F.S.; Peng, X.; Ahmed, N.; Nikpey, H.; Assadi, M. Design optimization of the cooling systems with PCM-to-air heat exchanger for the energy saving of the residential buildings. Energy Convers. Manag. X 2024, 23, 100630. [Google Scholar] [CrossRef]
- Lebedev, V.; Deev, A. Heat Storage as a Way to Increase Energy Efficiency and Flexibility of NPP in Isolated Power System. Appl. Sci. 2023, 13, 13130. [Google Scholar] [CrossRef]
- Bose, J.R.; Manova, S.; Angeline, A.A.; Asirvatham, L.G.; Gautam, S. Numerical study on the heat transfer characteristics of Cu-water and TiO2-Water nanofluid in a circular horizontal tube. Energies 2023, 16, 1449. [Google Scholar] [CrossRef]
- Arsenyeva, O.; Tovazhnyanskyy, L.; Kapustenko, P.; Klemeš, J.J.; Varbanov, P.S. Review of developments in plate heat exchanger heat transfer enhancement for single-phase applications in process industries. Energies 2023, 16, 4976. [Google Scholar] [CrossRef]
- Rosa, N.; Soares, N.; Costa, J.; Lopes, A.G. Validation of a Simplified Numerical Model for Predicting Solid–Liquid Phase Change with Natural Convection in Ansys CFX. Inventions 2023, 8, 93. [Google Scholar] [CrossRef]
- Erdoğan, A.; Çakmak, G. Investigation of numerical and experimental assessment of melting behavior of phase change material in U tube heat exchanger. Case Stud. Therm. Eng. 2023, 49, 103206. [Google Scholar] [CrossRef]
- Zaib, A.; Mazhar, A.R.; Aziz, S.; Talha, T.; Jung, D.W. Heat Transfer Augmentation Using Duplex and Triplex Tube Phase Change Material (PCM) Heat Exchanger Configurations. Energies 2023, 16, 4037. [Google Scholar] [CrossRef]
- Şimşek, F.; Demirci, H. Investigation of the use of new fin on the melting time of the phase change material stored in the heat exchanger by computational fluid dynamics analysis. J. Build. Eng. 2024, 91, 109505. [Google Scholar] [CrossRef]
- Abd El-Hamid, M.; Wei, G. Effect of varying the thermophysical properties of phase change material on the performance of photovoltaic/thermal-PCM hybrid module numerically. J. Energy Storage 2024, 86, 111326. [Google Scholar] [CrossRef]
- Shaban, M.; Khan, T.I.; Anwar, M.; Alzaid, M.; Alanazi, R. Effect of Asymmetric Fins on Thermal Performance of Phase Change Material-Based Thermal Energy Storage Unit. Materials 2023, 16, 2567. [Google Scholar] [CrossRef]
- Kos, Z.; Babii, I.; Grynyova, I.; Nikiforov, O. Ensuring the Energy Efficiency of Buildings through the Simulation of Structural, Organizational, and Technological Solutions for Facade Insulation. Appl. Sci. 2024, 14, 801. [Google Scholar] [CrossRef]
- Tian, Z.; Liao, Z.; Xu, C.; Jiang, K.; Du, X. Experimental and numerical investigation of the melting process of solar salt in a spherical capsule. J. Energy Storage 2023, 74, 109388. [Google Scholar] [CrossRef]
- Vogel, J.; Keller, M.; Johnson, M. Numerical modeling of large-scale finned tube latent thermal energy storage systems. J. Energy Storage 2020, 29, 101389. [Google Scholar] [CrossRef]
- Scharinger-Urschitz, G.; Walter, H.; Haider, M. Heat transfer in latent high-temperature thermal energy storage systems—Experimental investigation. Energies 2019, 12, 1264. [Google Scholar] [CrossRef]

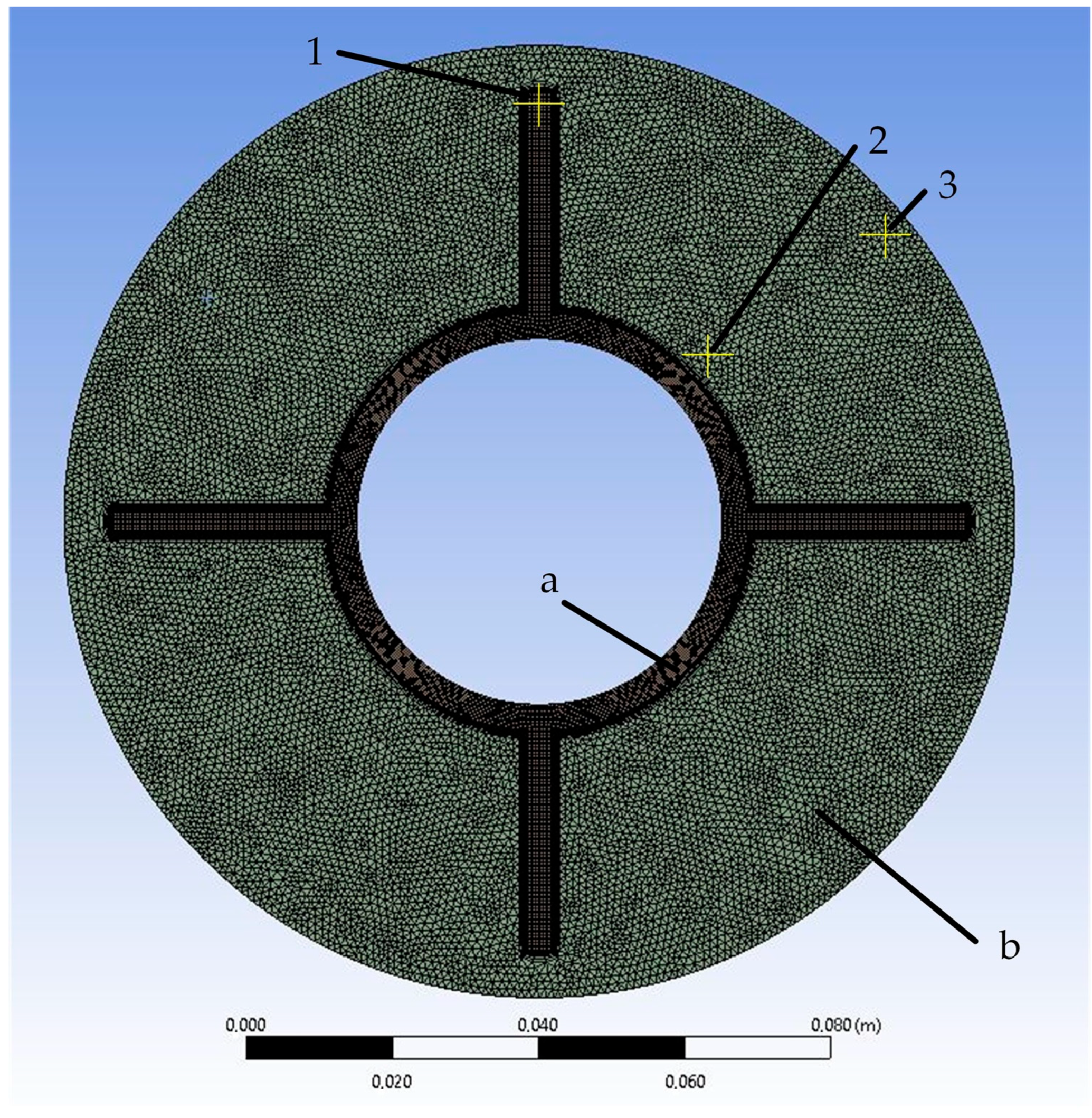


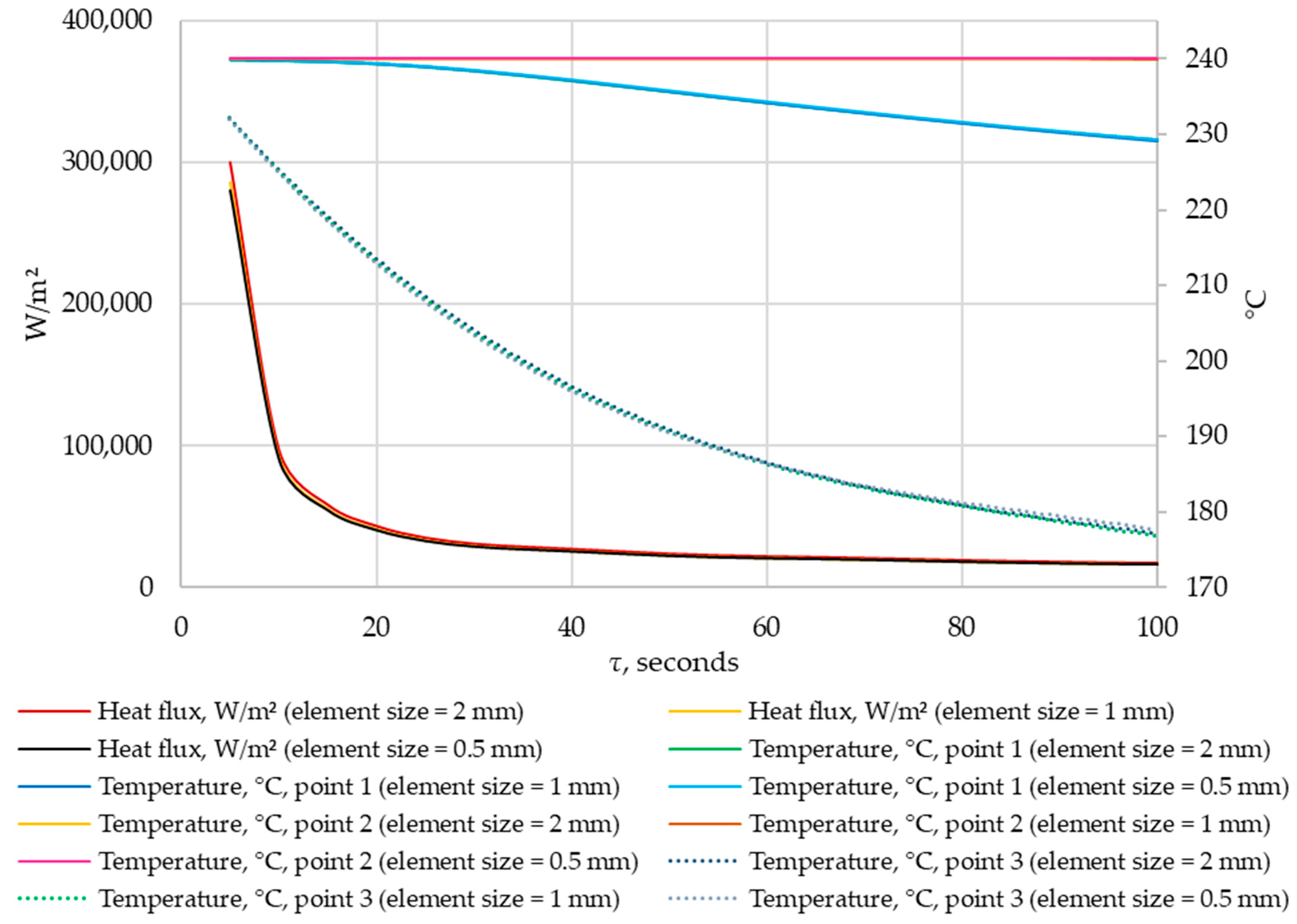



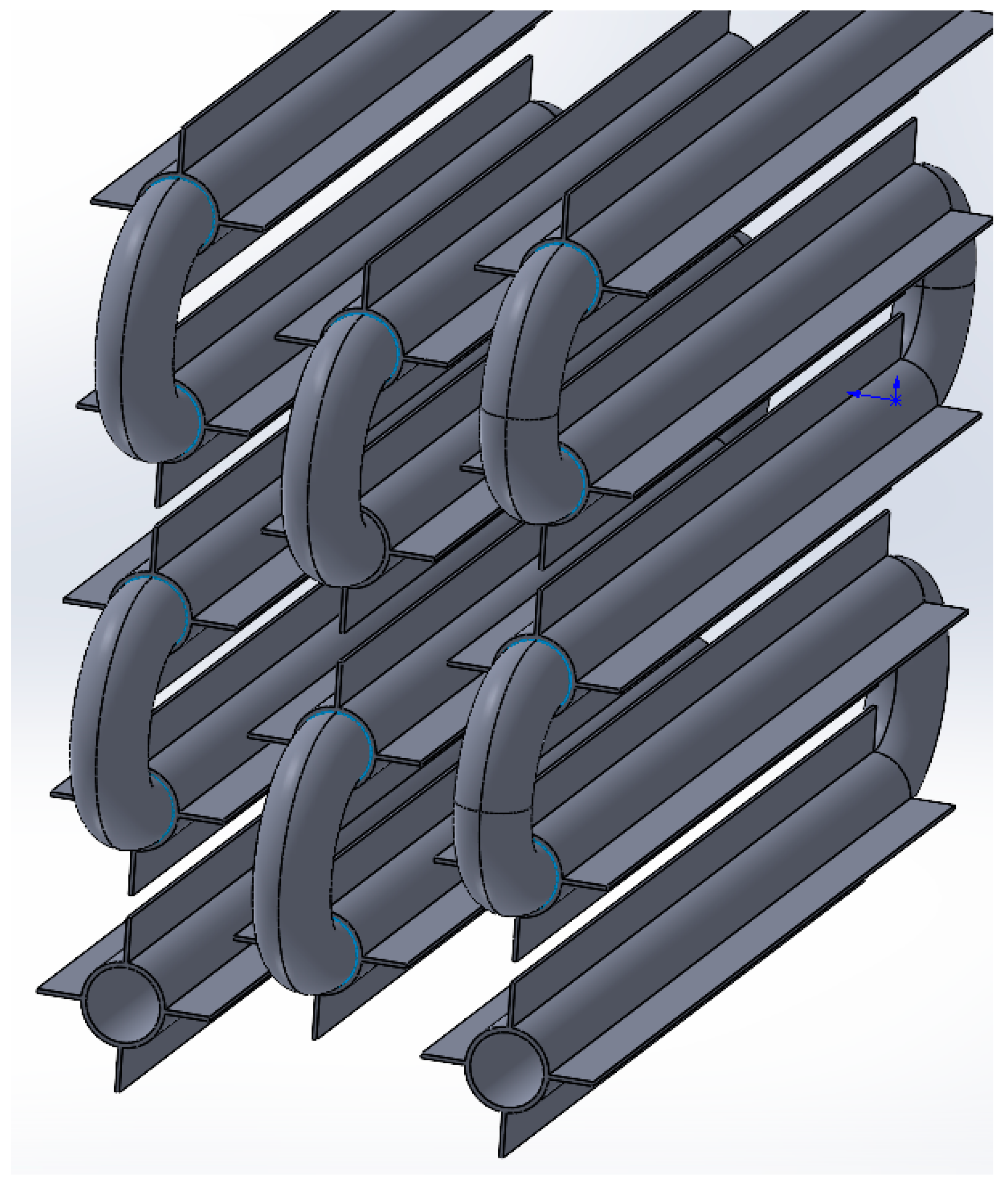
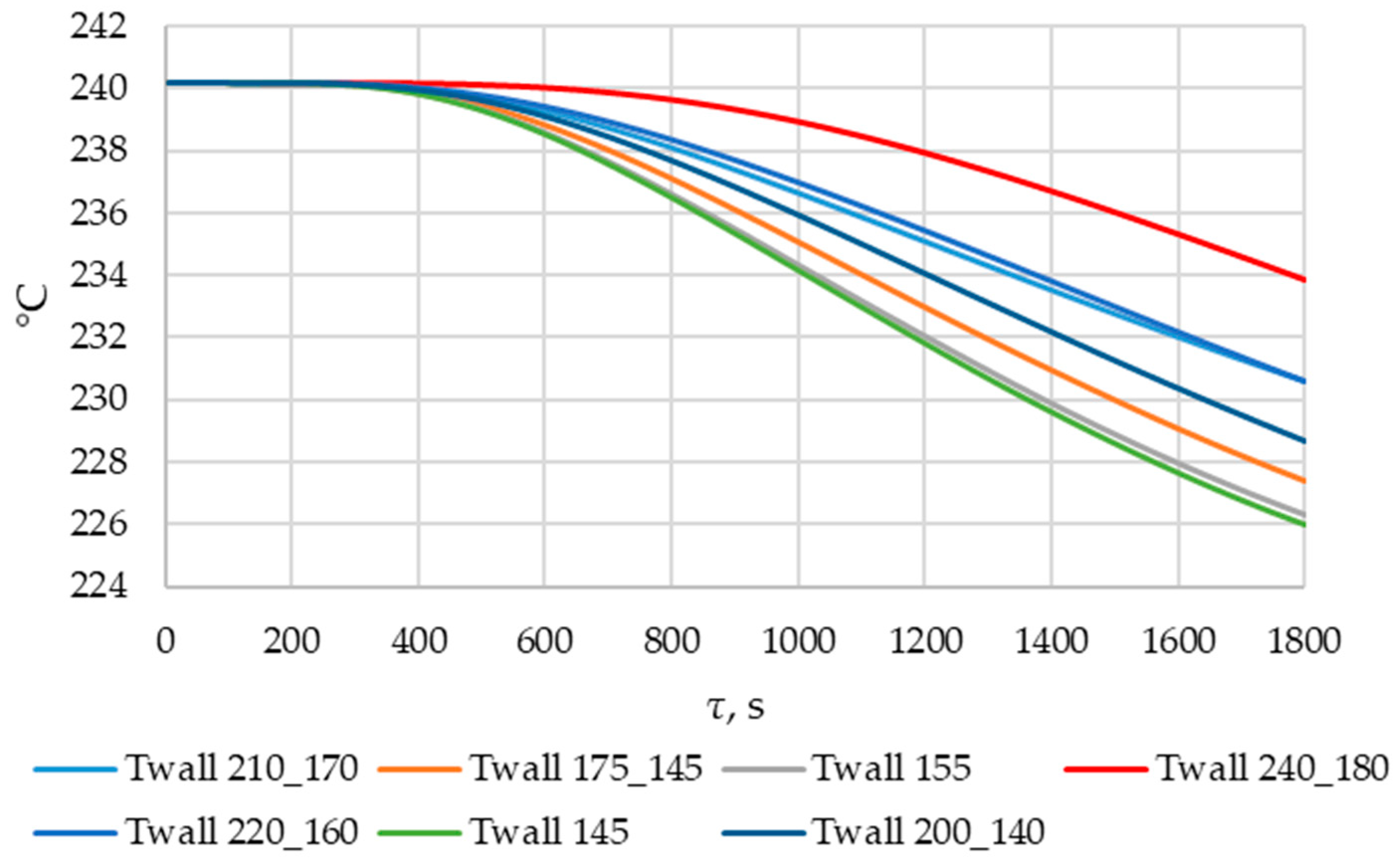
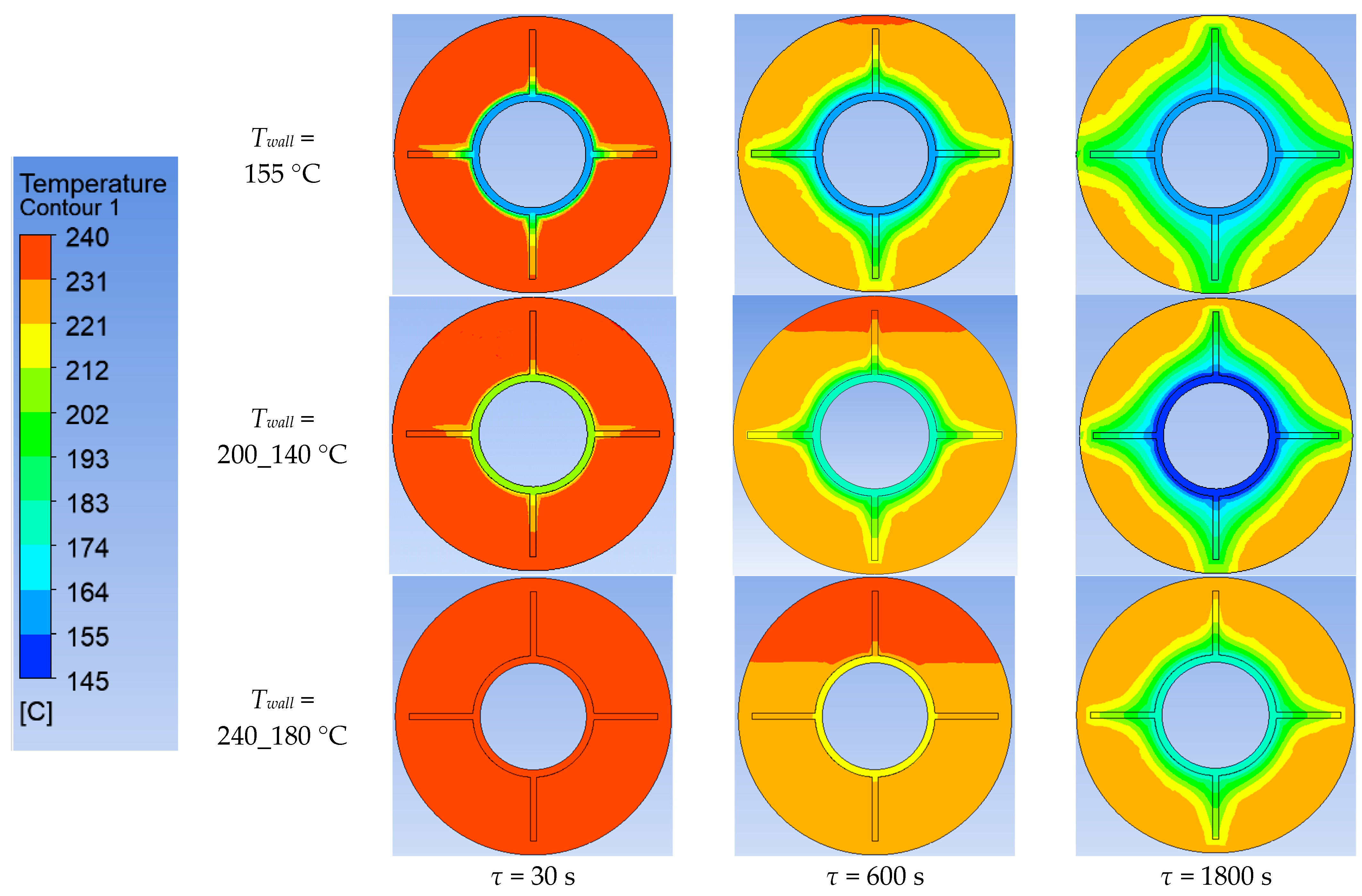
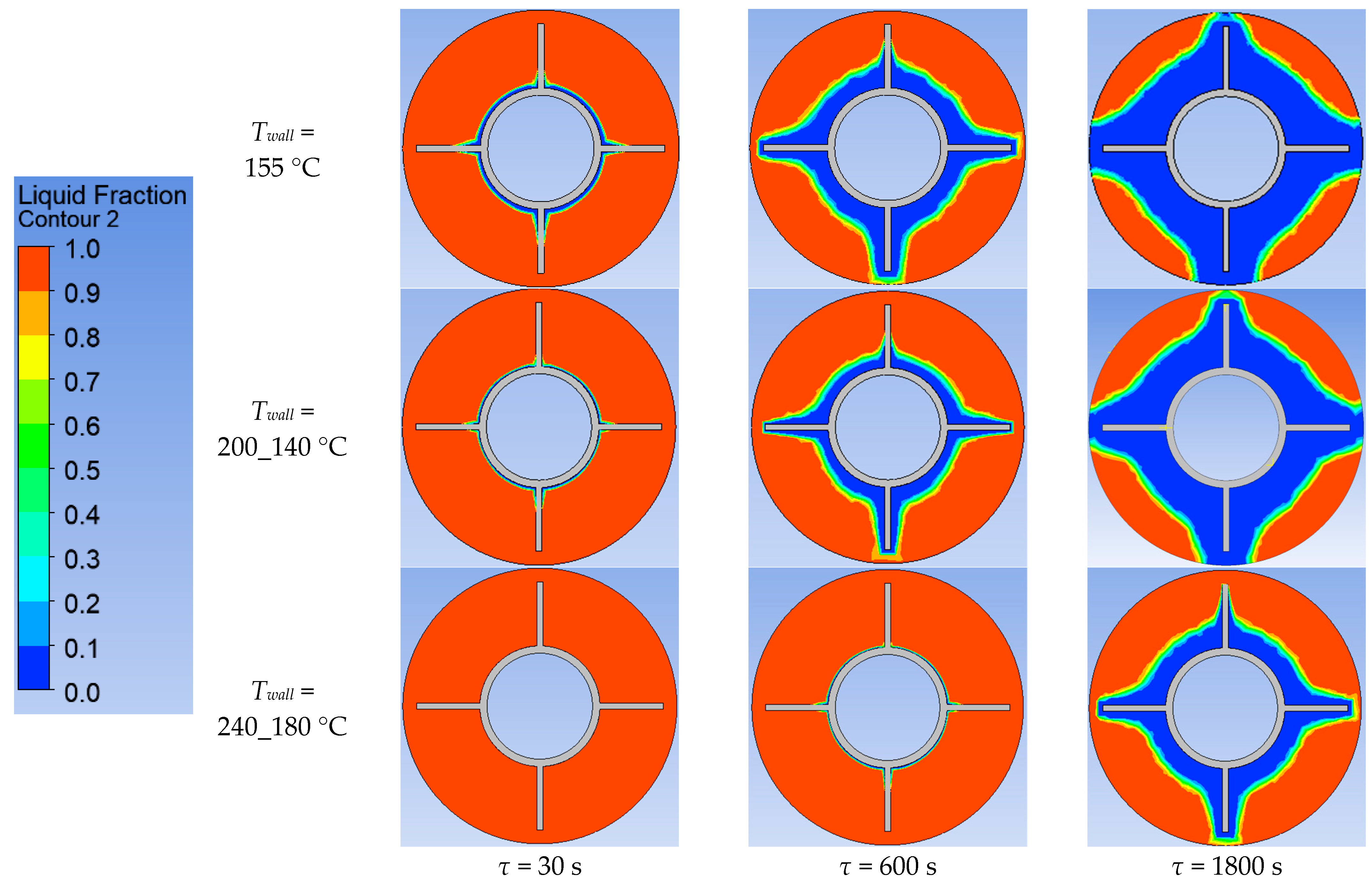
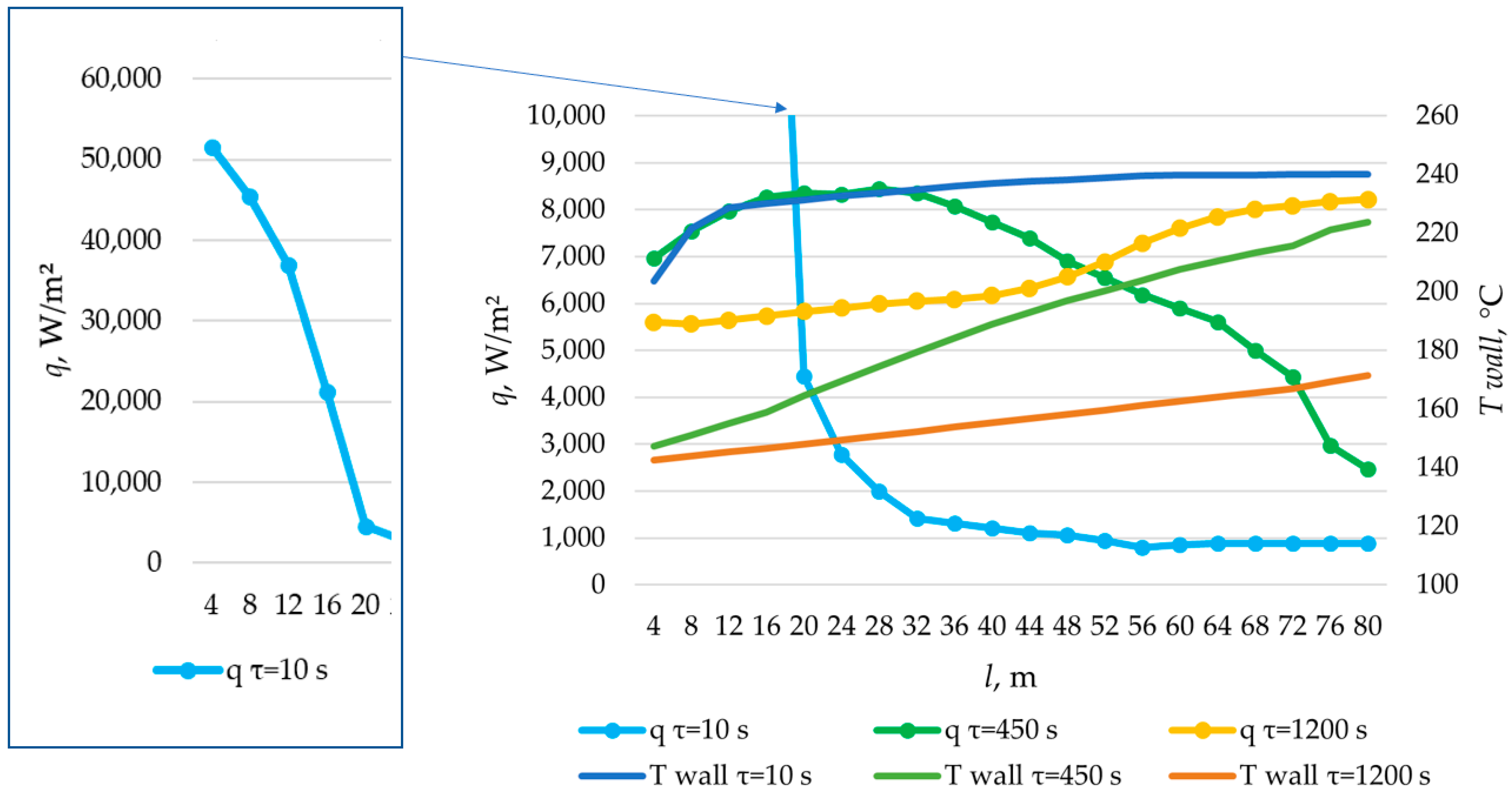
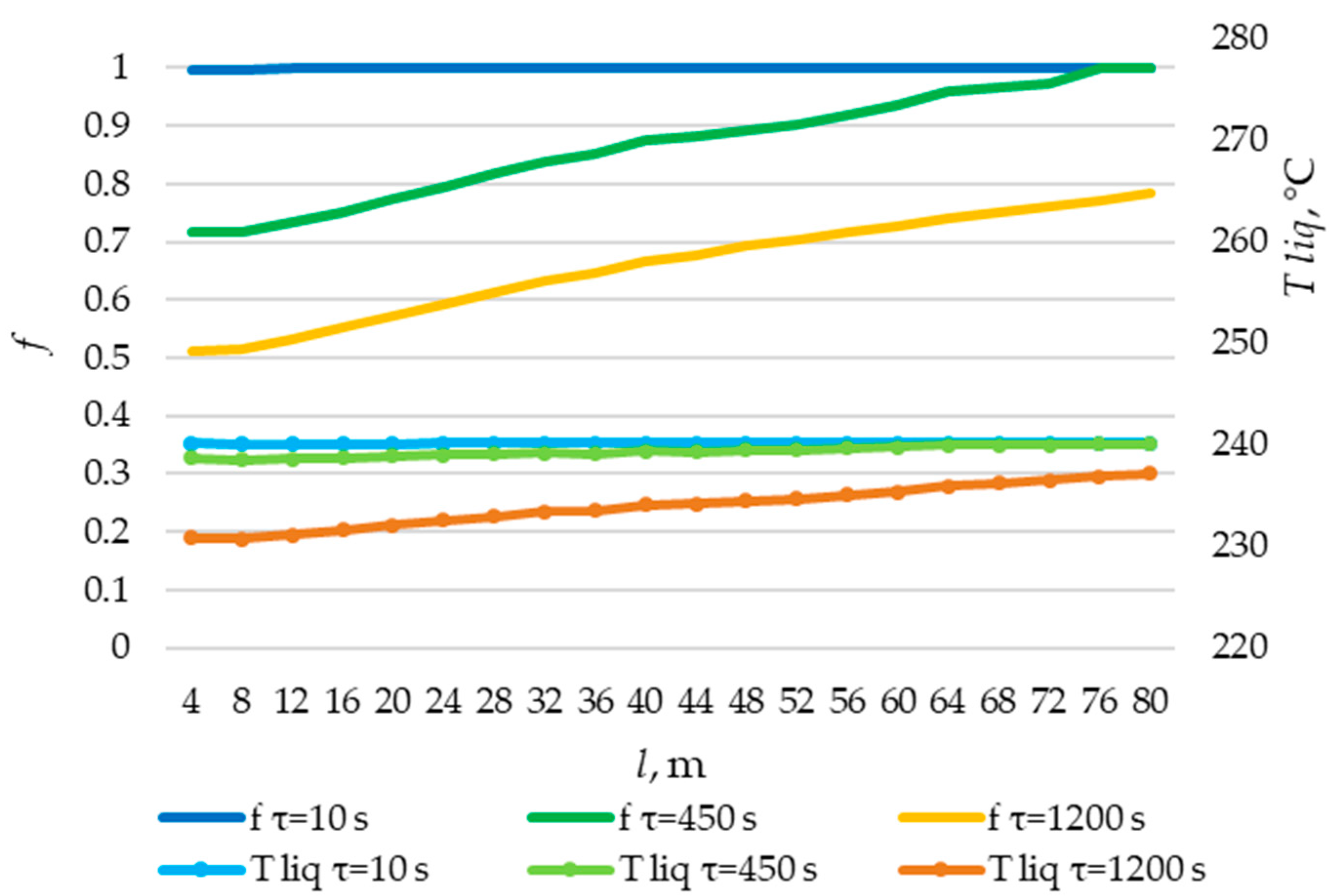
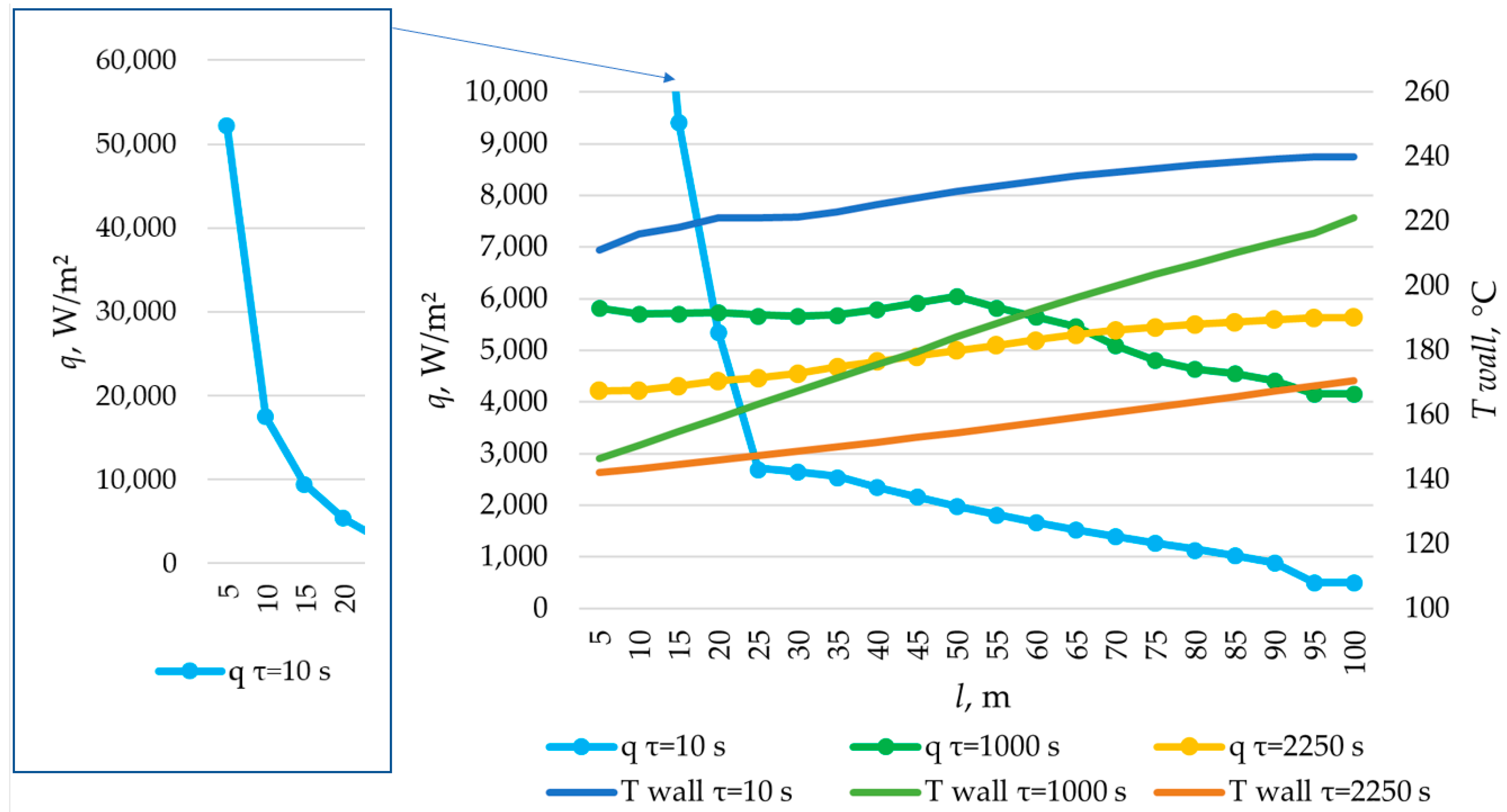
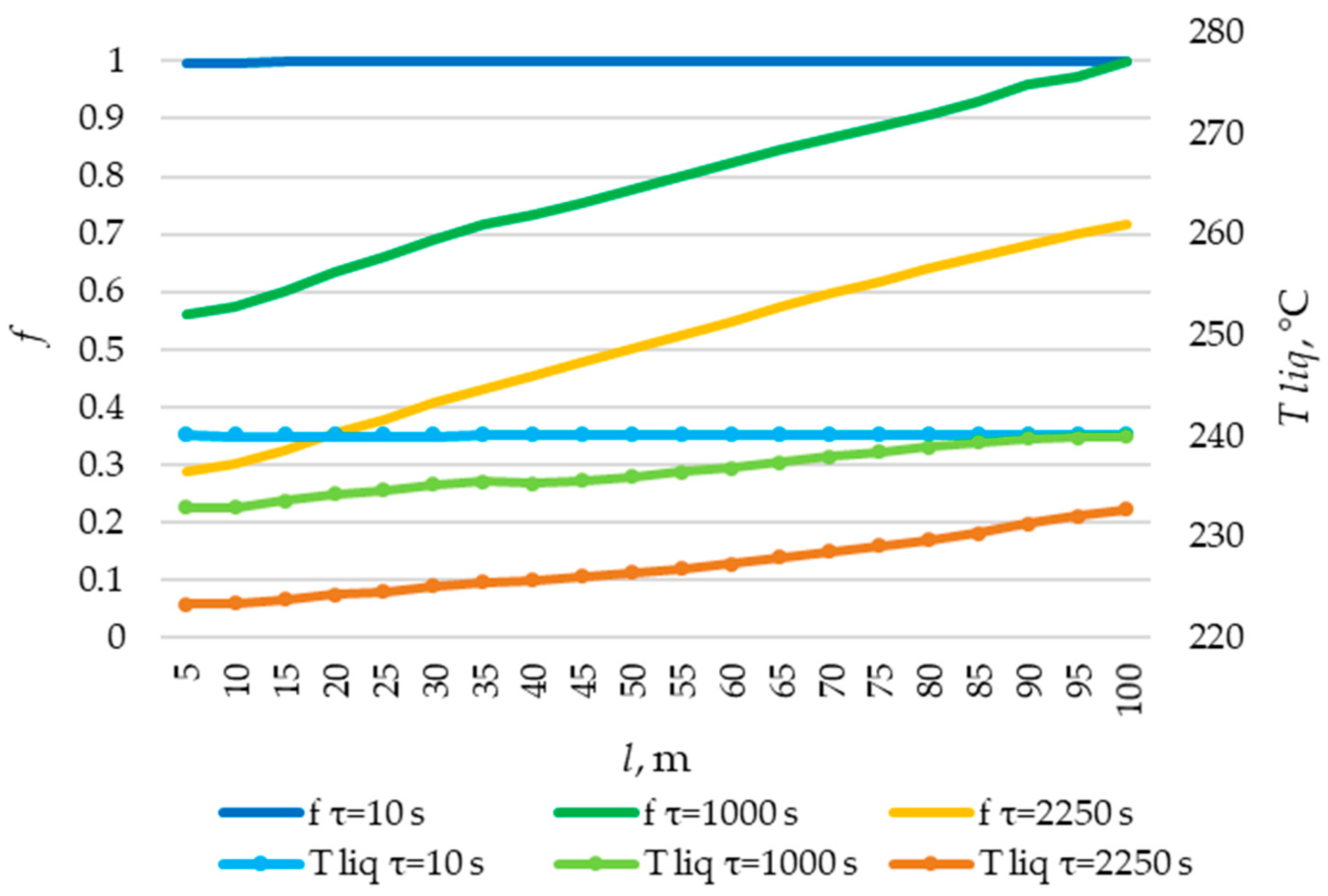
| Structure (Mass. KNO3/NaNO3) | Melting Point, °C | Melting Heat, kJ/kg | Heat Capacity, kJ/(kg·K) | Thermal Conductivity, W/(m·K) | Density, kg/m3 |
|---|---|---|---|---|---|
| 55/45 | 222 | 105.3 | 1.5 | 0.52 | 1752 |
| Simulation Number | Twall, °C |
|---|---|
| 1 | 145 = const |
| 2 | 155 = const |
| 3 | 175_145 * |
| 4 | 200_140 * |
| 5 | 210_170 * |
| 6 | 220_160 * |
| 7 | 240_180 * |
| Melting Point, °C | Melting Heat, kJ/kg | Heat Capacity, kJ/(kg·K) | Thermal Conductivity, W/(m·K) | Density, kg/m3 |
|---|---|---|---|---|
| 60 | 198 | 2.5 | 0.24 | 800 |
| № | Heat Flux Density, W/m2 | Duration of the Heat Exchange Process, Seconds | PCM, Melting Point | Tpcm, °C | THTF, °C | Heat Transfer Coefficient, W/(m2∙K) | Heat Exchange Surface | Reference |
|---|---|---|---|---|---|---|---|---|
| 1 | 130,000… 5000 | 1800 | Solar salt, 222 °C | 240 | 145 | 1368… 53 | Tube with 4 longitudinal fins | Current research |
| 2 | 18,500… 2500 | 1200 | Solar salt, 222 °C | 217 | 270 | 347… 47 | Spherical capsule | [108] |
| 3 | 30,000… 13,000 | 1800 | Solar salt, 222 °C | 225 | 190 (start) 180 (end) | 855… 285 | Tube with radial plate fins | [109] |
| 4 | 60,000… 24,000 | 1800 | NaNO3, 306 °C | 335 | 276 | 1500… 400 | Tube with complex structure of longitudinal fins | [110] |
| Variables | F | l = 2 m | l = 60 m | l = 120 m |
|---|---|---|---|---|
| q | Fcalc | 289.32 | 194.94 | 455.16 |
| Ftable | 1.89 | 1.89 | 1.89 | |
| f | Fcalc | 1439.01 | 2376.09 | 4174.06 |
| Ftable | 2.62 | 2.62 | 2.62 | |
| Tliq | Fcalc | 1975.92 | 2957.12 | 221.32 |
| Ftable | 1.89 | 1.89 | 1.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lebedev, V.; Deev, A.; Deev, K. Method for Calculating Heat Transfer in a Heat Accumulator Using a Phase Change Material with Intensification Due to Longitudinal Fins. Energies 2024, 17, 5281. https://doi.org/10.3390/en17215281
Lebedev V, Deev A, Deev K. Method for Calculating Heat Transfer in a Heat Accumulator Using a Phase Change Material with Intensification Due to Longitudinal Fins. Energies. 2024; 17(21):5281. https://doi.org/10.3390/en17215281
Chicago/Turabian StyleLebedev, Vladimir, Andrey Deev, and Konstantin Deev. 2024. "Method for Calculating Heat Transfer in a Heat Accumulator Using a Phase Change Material with Intensification Due to Longitudinal Fins" Energies 17, no. 21: 5281. https://doi.org/10.3390/en17215281
APA StyleLebedev, V., Deev, A., & Deev, K. (2024). Method for Calculating Heat Transfer in a Heat Accumulator Using a Phase Change Material with Intensification Due to Longitudinal Fins. Energies, 17(21), 5281. https://doi.org/10.3390/en17215281





