Hardware-in-the-Loop Implementation of an Optimized Energy Management Strategy for Range-Extended Electric Trucks
Abstract
:1. Introduction
2. System Description and Modeling
2.1. Road Load and Powertrain Components Modeling
2.2. Backward-Looking Simulator for Dynamic Programming Solution
2.3. Forward-Looking Simulator for Online Control Implementation
2.4. Hardware-in-the-Loop Simulation Setup
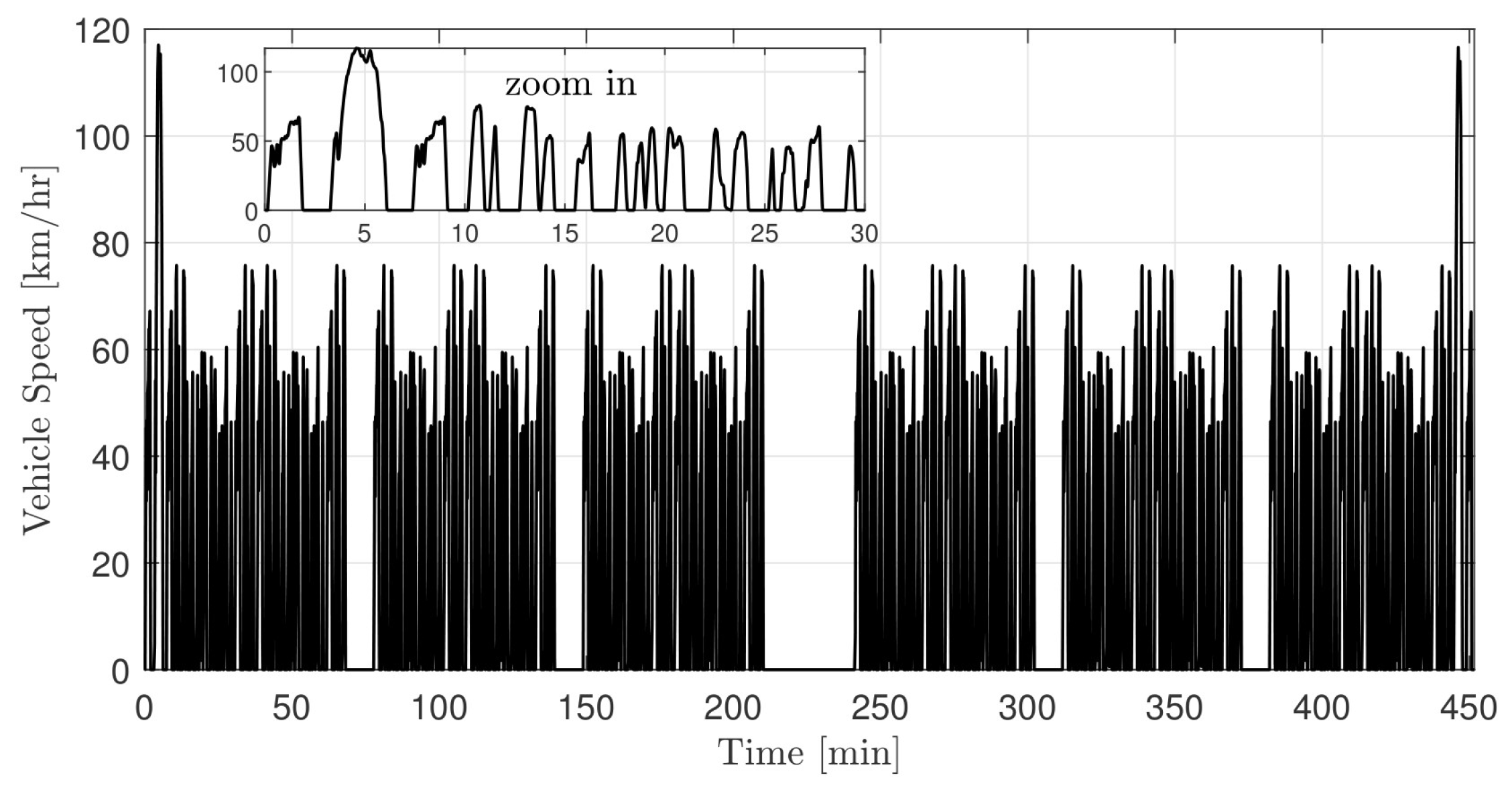
2.5. Representative Pick-Up and Delivery Drive Cycle Description
3. Optimal Energy Management Strategy Using Dynamic Programming
4. Online Implementable Energy Management Strategies
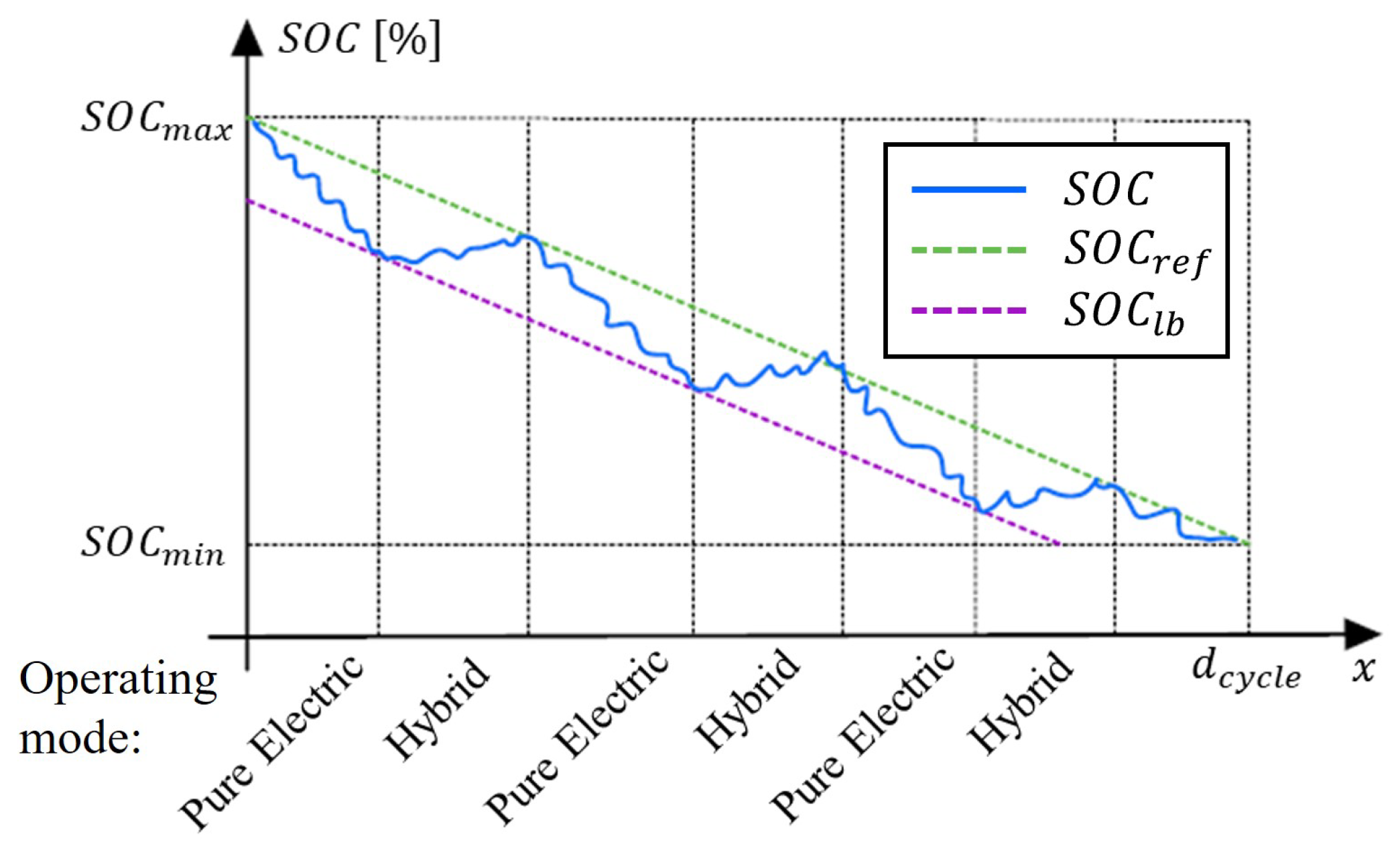
4.1. Charge-Depleting–Charge-Sustaining Strategy
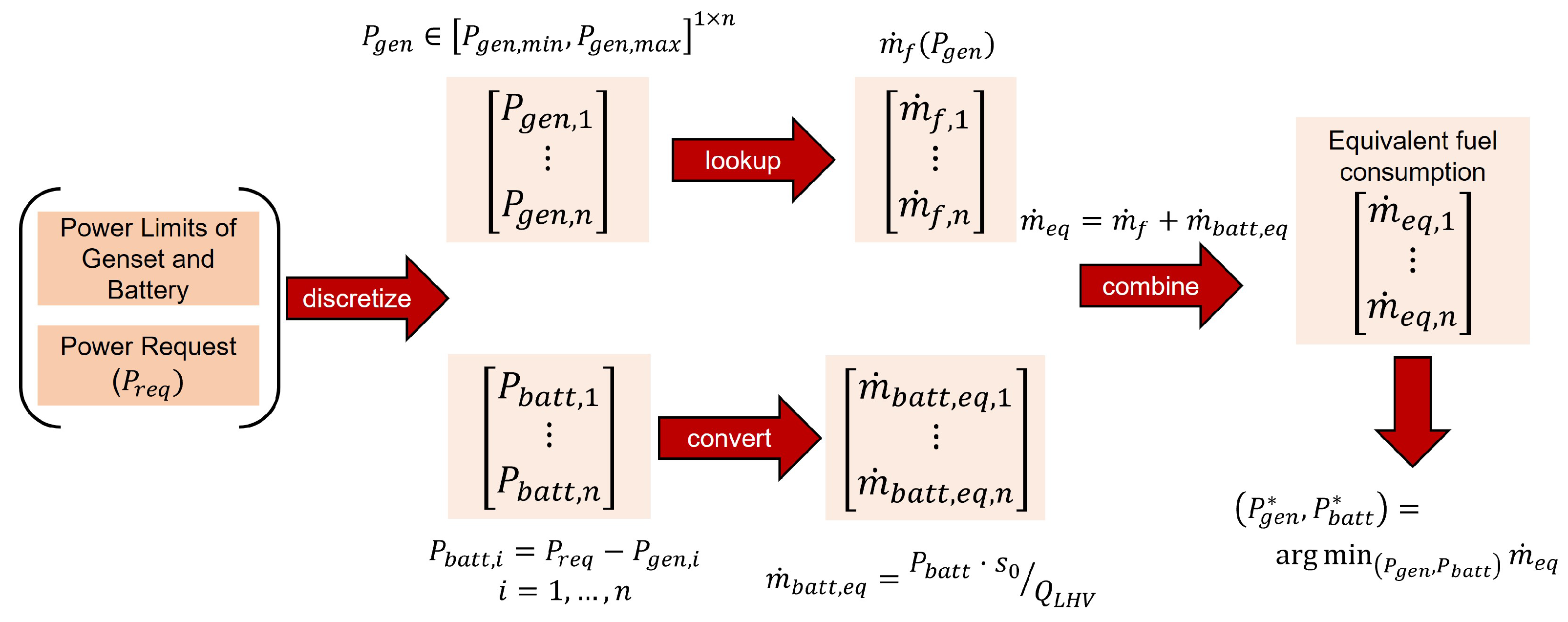
4.2. Hierarchical Energy Management Strategy
5. Results and Discussion
5.1. Dynamic Programming Simulation Results
5.2. Model-in-the-Loop Simulation Results
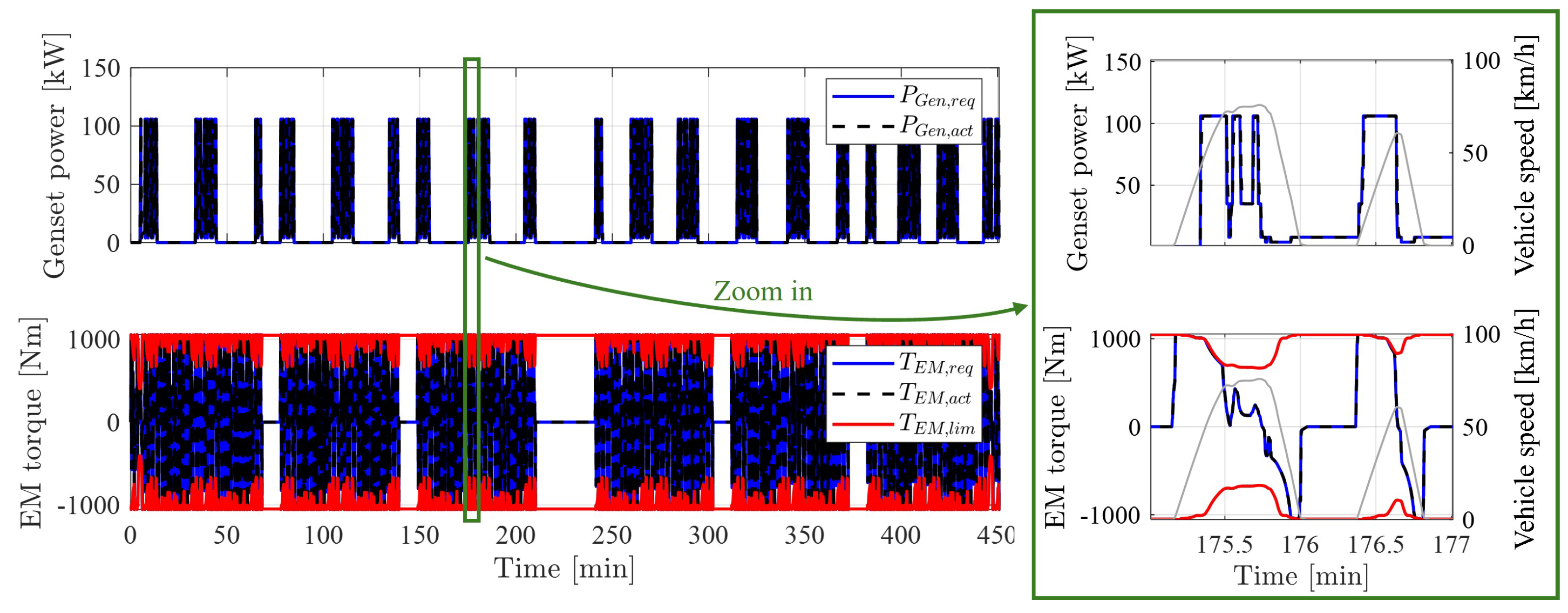
5.3. Hardware-in-the-Loop Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Delgado, O.; Rodríguez, F. CO2 Emissions and Fuel Consumption Standards for Heavy-Duty Vehicles in the European Union-International Council on Clean Transportation. 2018. Available online: https://trid.trb.org/View/1513348 (accessed on 15 July 2024).
- Rizzoni, G.; Ahmed, Q.; Arasu, M.; Oruganti, P.S. Transformational Technologies Reshaping Transportation—An Academia Perspective (L. Ray Buckendale 2019 Lecture); SAE Technical Paper 2019-01-2620; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Alternative Fuels Data Center: Hybrid Electric Vehicles. Available online: https://afdc.energy.gov/vehicles/electric-basics-hev (accessed on 15 July 2024).
- Nykvist, B.R.; Olsson, O. The feasibility of heavy battery electric trucks. Joule 2021, 5, 901–913. [Google Scholar] [CrossRef]
- Sugihara, C.; Hardman, S.; Kurani, K. Social, technological, and economic barriers to heavy-duty truck electrification. Res. Transp. Bus. Manag. 2023, 51, 101064. [Google Scholar] [CrossRef]
- Cunanan, C.; Tran, M.K.; Lee, Y.; Kwok, S.; Leung, V.; Fowler, M. A Review of Heavy-Duty Vehicle Powertrain Technologies: Diesel Engine Vehicles, Battery Electric Vehicles, and Hydrogen Fuel Cell Electric Vehicles. Clean Technol. 2021, 3, 474–489. [Google Scholar] [CrossRef]
- Impullitti, J.; Kosowski, M. Plug-In Hybrid Medium-Duty Truck Demonstration and Evaluation Prepared for: California Energy Commission; South Coast Air Quality Management District: Diamond Bar, CA, USA, 2020.
- Moriarty, K. Clean Cities Guide to Alternative Fuel and Advanced Medium-and Heavy-Duty Vehicles; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2013.
- Xiao, B.; Ruan, J.; Yang, W.; Walker, P.D.; Zhang, N. A review of pivotal energy management strategies for extended range electric vehicles. Renew. Sustain. Energy Rev. 2021, 149, 111194. [Google Scholar] [CrossRef]
- Zhao, T.; Ahmed, Q.; Rizzoni, G. Influence of Battery Charging Current Limit on the Design of Range Extender Hybrid Electric Trucks. In Proceedings of the 2018 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Duran, A.; Li, K.; Kresse, J.; Kelly, K. Development of 80- and 100- Mile Work Day Cycles Representative of Commercial Pickup and Delivery Operation; SAE Technical Papers; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018; pp. 10–12. [CrossRef]
- Yang, C.; Sun, T.; Wang, W.; Li, Y.; Zhang, Y.; Zha, M. Regenerative braking system development and perspectives for electric vehicles: An overview. Renew. Sustain. Energy Rev. 2024, 198, 114389. [Google Scholar] [CrossRef]
- Hunter, C.; Penev, M.; Reznicek, E.; Lustbader, J.; Birky, A.; Zhang, C. Spatial and Temporal Analysis of the Total Cost of Ownership for Class 8 Tractors and Class 4 Parcel Delivery Trucks; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018.
- Tran, D.D.; Vafaeipour, M.; Baghdadi, M.E.; Barrero, R.; Mierlo, J.V.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Panday, A.; Bansal, H.O. A review of optimal energy management strategies for hybrid electric vehicle. Int. J. Veh. Technol. 2014, 2014, 160510. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, X.; Liu, Q.; Li, S.; Xu, Y. Review article: A comprehensive review of energy management strategies for hybrid electric vehicles. Mech. Sci. 2022, 13, 147–188. [Google Scholar] [CrossRef]
- Villani, M.; Shiledar, A.; Ahmed, Q.; Rizzoni, G. Design of a Hierarchical Energy Management Strategy for a Range-Extender Electric Delivery Truck. In Proceedings of the 2021 European Control Conference, ECC 2021, Delft, The Netherlands, 29 June 2021–2 July 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 892–898. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming and Lagrange Multipliers. Proc. Natl. Acad. Sci. USA 1956, 42, 767–769. [Google Scholar] [CrossRef]
- Paganelli, G.; Guerra, T.M.; Delprat, S.; Santin, J.J.; Delhom, M.; Combes, E. Simulation and assessment of power control strategies for a parallel hybrid car. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2000, 214, 705–717. [Google Scholar] [CrossRef]
- Stockar, S.; Marano, V.; Canova, M.; Rizzoni, G.; Guzzella, L. Energy-optimal control of plug-in hybrid electric vehicles for real-world driving cycles. IEEE Trans. Veh. Technol. 2011, 60, 2949–2962. [Google Scholar] [CrossRef]
- Tribioli, L.; Barbieri, M.; Capata, R.; Sciubba, E.; Jannelli, E.; Bella, G. A real time energy management strategy for plug-in hybrid electric vehicles based on optimal control theory. Energy Procedia 2014, 45, 949–958. [Google Scholar] [CrossRef]
- Padmarajan, B.V.; McGordon, A.; Jennings, P.A. Blended Rule-Based Energy Management for PHEV: System Structure and Strategy. IEEE Trans. Veh. Technol. 2016, 65, 8757–8762. [Google Scholar] [CrossRef]
- Lei, Z.; Qin, D.; Zhao, P.; Li, J.; Liu, Y.; Chen, Z. A real-time blended energy management strategy of plug-in hybrid electric vehicles considering driving conditions. J. Clean. Prod. 2020, 252, 119735. [Google Scholar] [CrossRef]
- Yao, D.; Lu, X.; Chao, X.; Zhang, Y.; Shen, J.; Zeng, F.; Zhang, Z.; Wu, F. Adaptive Equivalent Fuel Consumption Minimization Based Energy Management Strategy for Extended-Range Electric Vehicle. Sustainability 2023, 15, 4607. [Google Scholar] [CrossRef]
- Xi, L.; Zhang, X.; Sun, C.; Wang, Z.; Hou, X.; Zhang, J. Intelligent Energy Management Control for Extended Range Electric Vehicles Based on Dynamic Programming and Neural Network. Energies 2017, 10, 1871. [Google Scholar] [CrossRef]
- Lin, W.; Zhao, H.; Zhang, B.; Wang, Y.; Xiao, Y.; Xu, K.; Zhao, R.; Lin, W.; Zhao, H.; Zhang, B.; et al. Predictive Energy Management Predictive Energy Management Strategy for Range-Extended Electric Vehicles Based on ITS Information and Start-Stop Optimization with Vehicle Velocity Forecast. Energies 2022, 15, 7774. [Google Scholar] [CrossRef]
- Llorente, R.M. Embedded Control System Development Process: Model-Based Design and Architecture Basics. In Practical Control of Electric Machines: Model-Based Design and Simulation; Advances in Industrial Control; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–26. [Google Scholar] [CrossRef]
- Board, T.R.; Council, N.R. Technologies and Approaches to Reducing the Fuel Consumption of Medium- and Heavy-Duty Vehicles; National Academies Press: Washington, DC, USA, 2010; pp. 1–250. [Google Scholar] [CrossRef]
- Shokry, H.; Hinchey, M. Model-based verification of embedded software. Computer 2009, 42, 53–59. [Google Scholar] [CrossRef]
- Krizan, J.; Ertl, L.; Bradac, M.; Jasansky, M.; Andreev, A. Automatic code generation from Matlab/Simulink for critical applications. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Toronto, ON, Canada, 4–7 May 2014; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Villani, M.; Shiledar, A.; D’Arpino, M.; Rizzoni, G. Battery Selection and Optimal Energy Management for a Range-Extended Electric Delivery Truck. SAE Int. J. Adv. Curr. Pract. Mobil. 2022, 5, 1282–1291. [Google Scholar] [CrossRef]
- Sundström, O.; Guzzella, L. A generic dynamic programming Matlab function. In Proceedings of the IEEE International Conference on Control Applications, St. Petersburg, Russia, 8–10 July 2009; pp. 1625–1630. [Google Scholar] [CrossRef]
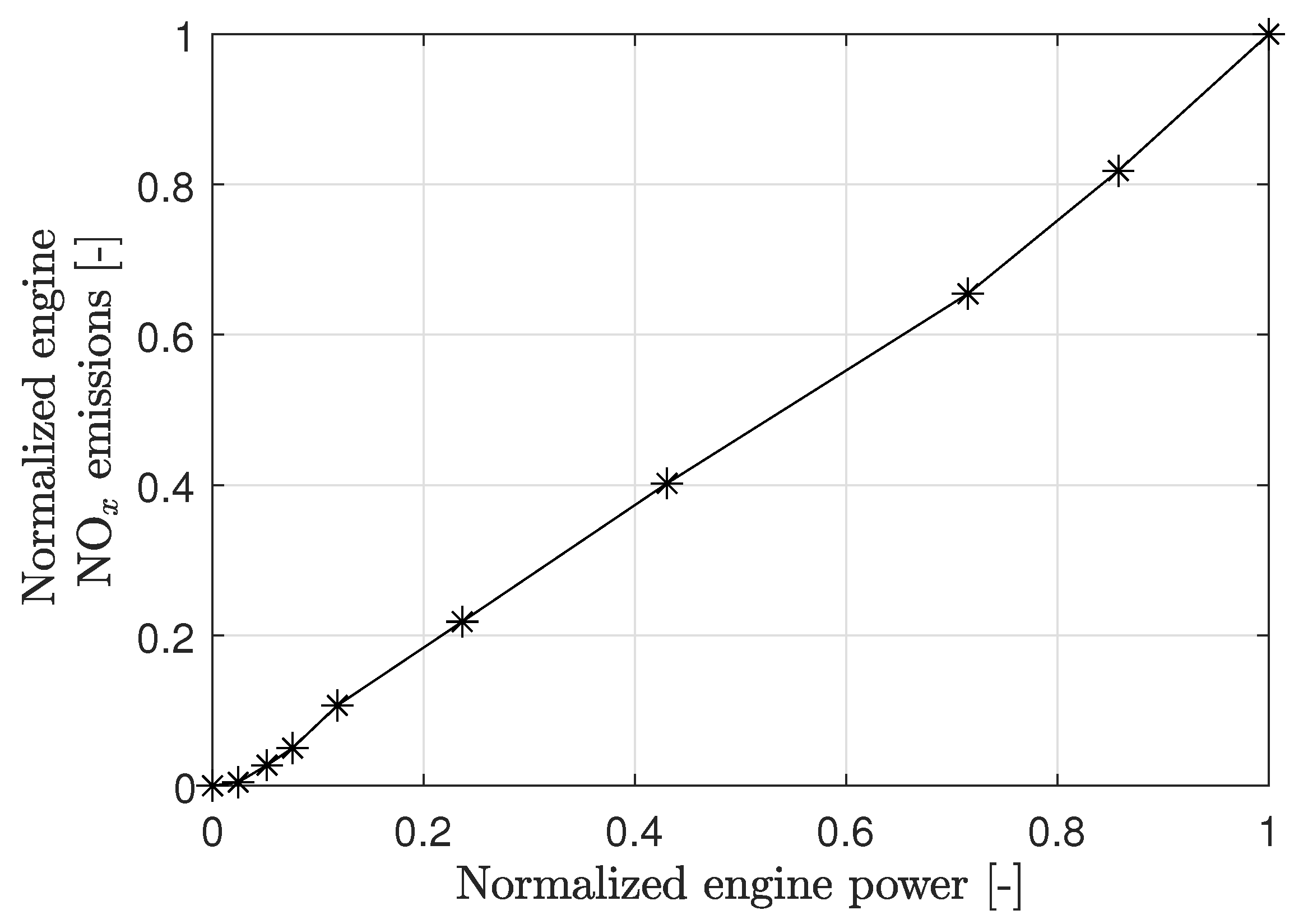
- International Council on Clean Transportation. U.S. Heavy-Duty Vehicle NOx Standards: Updates to Emission Limits, Testing Requirements, and Compliance Procedures; International Council on Clean Transportation: San Francisco, CA, USA, 2023. [Google Scholar]
- Villani, M.; Shiledar, A.; Zhao, T.; Lana, C.; Le, D.; Ahmed, Q.; Rizzoni, G. Optimal Energy Management Strategy for Energy Efficiency Improvement and Pollutant Emissions Mitigation in a Range-Extender Electric Vehicle. In Proceedings of the 15th International Conference on Engines & Vehicles, Capri, Italy, 12–16 September 2021. [Google Scholar] [CrossRef]
- Gonder, J.; Markel, T. Energy management strategies for plug-in hybrid electric vehicles. In Proceedings of the SAE World Congress & Exhibition, Detroit, MI, USA, 16–19 April 2007. [Google Scholar] [CrossRef]
- Jeffers, M.A.; Miller, E.; Kelly, K.; Kresse, J.; Li, K.; Dalton, J.; Kader, M.; Frazier, C. Development and Demonstration of a Class 6 Range-Extended Electric Vehicle for Commercial Pickup and Delivery Operation. In Proceedings of the WCX 2020 World Congress Experience, Detroit, MC, USA, 21–23 April 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Rodrigues, M.; King, S.; Scott, D.; Wang, D. Advanced energy management strategies for range extended electric vehicle. In Proceedings of the Symposium on International Automotive Technology 2015, Pune, India, 21–24 January 2015. [Google Scholar] [CrossRef]
- Paganelli, G.; Delprat, S.; Guerra, T.M.; Rimaux, J.; Santin, J.J. Equivalent consumption minimization strategy for parallel hybrid powertrains. IEEE Veh. Technol. Conf. 2002, 4, 2076–2081. [Google Scholar] [CrossRef]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal control of parallel hybrid electric vehicles. IEEE Trans. Control. Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]













| Parameter | Value |
|---|---|
| Mass [kg] | 8890 |
| Rolling resistance coefficient [-] | 0.0072 |
| Wheel radius [m] | 0.4191 |
| Frontal area [m2] | 5.41 |
| Aerodynamic drag coefficient [-] | 0.622 |
| Genset peak power [kW] | 148.5 |
| Electric motor peak power [kW] | 245 |
| Battery pack energy [kWh] | 74 |
| Software/Hardware | Description |
|---|---|
| MATLAB® R2020b/Simulink® 10.2 | Automatic C code generation |
| Post-processing of HIL results | |
| dSPACE® ControlDesk R2021-B | To set up and monitor the real-time HIL experiment |
| dSPACE® Scalexio Midsize HIL system | DS1006 processor board for running complex plant model |
| DS2211 HIL I/O board for CAN communication | |
| SpeedGoat® Real-time Target Machine Baseline | Target machine for controller code execution |
| IO613 board for CAN communication | |
| Communication Protocols | High-speed CAN |
| Custom database file for CAN messages | |
| Baud Rate 500 Kbit/s |
| Parameter | Value |
|---|---|
| Duration | 450 min |
| Distance covered | 148 km |
| Maximum speed | 116 km/h |
| Average speed | 40 km/h |
| Maximum acc. | 1.15 m/s2 |
| Maximum decel. | 1.90 m/s2 |
| Fuel Penalty [g] | Fuel Used [kg] | Genset Starts [-] | Emissions [g/bhp-h] |
|---|---|---|---|
| 0 | 14.5 | 546 | 0.08 |
| 5 | 14.8 | 121 | 0.08 |
| 10 | 15.3 | 50 | 0.08 |
| 20 | 15.7 | 23 | 0.08 |
| 30 | 16.0 | 11 | 0.12 |
| 40 | 16.0 | 10 | 0.12 |
| 50 | 16.1 | 8 | 0.13 |
| EMS | Fuel Consumption [kg] (Improvement over Baseline) | Genset Starts [-] | Emissions [g/bhp-h] |
|---|---|---|---|
| CD–CS (baseline, MIL) | 17.2 | 21 | 0.08 |
| DP (benchmark) | 15.7 (−8.7%) | 23 | 0.08 |
| H–EMS (MIL) | 16.0 (−7.0%) | 19 | 0.08 |
| EMS | Fuel Consumption [kg] | Genset Starts [-] | Emissions [g/bhp-h] |
|---|---|---|---|
| H–EMS (MIL) | 16.0 | 19 | 0.08 |
| H–EMS (HIL) | 16.3 (+1.8%) | 19 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiledar, A.; Villani, M.; Rizzoni, G. Hardware-in-the-Loop Implementation of an Optimized Energy Management Strategy for Range-Extended Electric Trucks. Energies 2024, 17, 5294. https://doi.org/10.3390/en17215294
Shiledar A, Villani M, Rizzoni G. Hardware-in-the-Loop Implementation of an Optimized Energy Management Strategy for Range-Extended Electric Trucks. Energies. 2024; 17(21):5294. https://doi.org/10.3390/en17215294
Chicago/Turabian StyleShiledar, Ankur, Manfredi Villani, and Giorgio Rizzoni. 2024. "Hardware-in-the-Loop Implementation of an Optimized Energy Management Strategy for Range-Extended Electric Trucks" Energies 17, no. 21: 5294. https://doi.org/10.3390/en17215294
APA StyleShiledar, A., Villani, M., & Rizzoni, G. (2024). Hardware-in-the-Loop Implementation of an Optimized Energy Management Strategy for Range-Extended Electric Trucks. Energies, 17(21), 5294. https://doi.org/10.3390/en17215294








