Anisotropy of Reynolds Stresses and Their Dissipation Rates in Lean H₂-Air Premixed Flames in Different Combustion Regimes

Abstract

The interrelation between Reynolds stresses and their dissipation rate tensors for different Karlovitz number values was analysed using a direct numerical simulation (DNS) database of turbulent statistically planar premixed H₂-air flames with an equivalence ratio of 0.7. It was found that a significant enhancement of Reynolds stresses and dissipation rates takes place as a result of turbulence generation due to thermal expansion for small and moderate Karlovitz number values. However, both Reynolds stresses and dissipation rates decrease monotonically within the flame brush for large Karlovitz number values, as the flame-generated turbulence becomes overridden by the strong isotropic turbulence. Although there are similarities between the anisotropies of Reynolds stress and its dissipation rate tensors within the flame brush, the anisotropy tensors of these quantities are found to be non-linearly related. The predictions of three different models for the dissipation rate tensor were compared to the results computed from DNS data. It was found that the model relying upon isotropy and a linear dependence between the Reynolds stress and its dissipation rates does not correctly capture the turbulence characteristics within the flame brush for small and moderate Karlovitz number values. In contrast, the models that incorporate the dependence of the invariants of the anisotropy tensor of Reynolds stresses were found to capture the components of dissipation rate tensor for all Karlovitz number conditions.

1. Introduction

Modelling of turbulent flows poses a major challenge in computational fluid dynamics (CFD) simulations. This challenge is exacerbated further in simulations of turbulent premixed flames. In premixed flames, this challenge arises owing to thermal expansion effects which are manifested by density change and normal flame acceleration. Several previous analytical [1,2,3,4], experimental [5,6,7,8,9] and computational [10,11,12,13,14] analyses showed that thermal expansion in premixed turbulent combustion affects the turbulent fluid motion. This has implications for premixed combustion modelling. An overview of the effects of thermal expansion on the various aspects of premixed turbulent combustion is provided in a recent review [14] and references therein.

The Reynolds Averaged Navier–Stokes (RANS) methodology is still the most commonly used simulation tool for industrial applications. Accurate closures of turbulent kinetic energy and dissipation rates play crucial roles in the fidelity of RANS simulations. Moreover, second-moment closure is a well-established methodology in premixed combustion modelling [15,16,17,18,19]. The anisotropy of Reynolds stresses plays a pivotal role in the closure of the pressure strain term in the Reynolds stress transport equation (e.g., return to isotropy) [16]. This aspect was recognised by Tian and Lindstedt [19] who analysed the second-moment closure of premixed turbulent flames in the flamelet regime. It has been found that second-moment closure provides better predictions of turbulence quantities in complex flow configurations (e.g., gas turbine combustors [20]; large-scale explosions and accidents where H₂ is also involved [21]; impinging jets [22]) than eddy viscosity models when large eddy simulation (LES) is too expensive in comparison to RANS.

Improving fundamental understanding of the anisotropy of Reynolds stress and its dissipation rates, along with its modelling, can offer increased accuracy in the prediction of turbulent kinetic energy and viscous dissipation rate [19]. Both turbulent kinetic energy and viscous dissipation rate are often needed as input parameters for combustion models (e.g., flame surface density-based [23] and scalar dissipation rate-based [24] closures). Thus, accurate estimations of turbulent kinetic energy and its dissipation rate can, in turn, improve the fidelity of RANS simulations of turbulent premixed flames.

It was demonstrated in previous analyses [14] that the thermal expansion preferentially affects the Reynolds stress components in the direction of the mean flame propagation. However, this effect weakens with increasing Karlovitz number. The effects of thermal expansion on the dissipation rate of Reynolds stress within the turbulent premixed flame brush and its Karlovitz number dependence are yet to be analysed in detail. The thermal expansion effects in premixed flames induce a significant amount of anisotropy in the sub-grid stresses [14], which can be demonstrated using the Lumley triangle [25]. Moreover, a multiscale analysis by Klein et al. [16] revealed that the anisotropies of Reynolds stress and dissipation rate tensors are qualitatively similar using Lumley triangles. However, none of these papers dealt with the anisotropy of dissipation rate tensor and its correlation with Reynolds stresses and the modelling of dissipation rate tensor in the context of RANS simulations. Recently, Ahmed et al. [26] analysed the relation between the anisotropies of Reynolds stresses and viscous dissipation rate, and the modelling of viscous dissipation rate tensor components during a premixed flame–wall interaction using a direct numerical simulation (DNS) database with unity Lewis number.

It was demonstrated previously [14] that the anisotropy of sub-grid stresses increases with a decrease in the effective Lewis number. Thus, it is necessary to understand the statistical behaviour of anisotropies of Reynolds stresses and their dissipation rates for lean H₂-air premixed turbulent flames with an effective Lewis number smaller than unity. This information is fundamental to the design process of the next generation combustors, which are to be operated using carbon-free high hydrogen content fuels. Therefore, the present paper concentrates on the statistical behaviours of the Reynolds stress components ($\widetilde{u_i^{″}{u}_j^{″}}$) and their dissipation rates (i.e., ${\tilde{\epsilon }}_{ij}=2\overline{\mu \left(\partial u_i^{″}/\partial x_k\right)(\partial u_j^{″}/\partial x_k})/\overline{\rho }$, where $u_i$ is the ith component of velocity and $\overline{q},\tilde{q}=\overline{\rho q}/\overline{\rho }$ and $q^{″}=q-\tilde{q}$ denote the Reynolds average, Favre average and Favre fluctuation of a general variable $q$, respectively. Here $\rho$ and $\mu$ denote the gas density and viscosity, respectively, along with their interdependence.

Most previous analyses [10,11,12,13] on the closure of turbulence in premixed combustion focussed on the modelling of Reynolds stress $\widetilde{u_i^{″}{u}_j^{″}}$ and turbulent kinetic energy $\tilde{k}=\widetilde{u_j^{″}{u}_i^{″}}/2$ mostly for hydrocarbon-air flames. However, to date, relatively limited attention has been devoted to the analysis of the interrelation between Reynolds stress and their dissipation rate components (i.e., $\widetilde{u_i^{″}{u}_j″}$ and ${\tilde{\epsilon }}_{ij}$) in premixed turbulent lean H₂-air flames under different regimes of turbulent premixed combustion. Thus, the main objective of the present study is to consider the statistical behaviours of $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$ within the flame brush for turbulent statistically planar H₂-air premixed flames for an equivalence ratio of $\varphi =0.7$ for different Karlovitz number values, $Ka$. In particular, the analysis aims to: (a) compare the anisotropies of $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$, and interrelations between them within the flame brush for different Karlovitz number values; and (b) provide physical explanations for the observed behaviour in (a) and their modelling implications.

To meet these objectives, this paper will analyse the anisotropy of $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$ tensors based on DNS data of turbulent statistically planar H₂-air premixed flames for an equivalence ratio of $\varphi =0.7$ for different Karlovitz number values, $Ka$. This information will be used to assess and explain the performance of existing ${\tilde{\epsilon }}_{ij}$ models, which were proposed previously for non-reacting flows, in the context of RANS modelling of premixed turbulent combustion.

2. Mathematical Background

One of the ways to characterise $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$ is to analyse the anisotropy associated with these tensors (known as anisotropy tensors), which are expressed as [25,26,27,28]:

$$b_{ij}=\widetilde{u_i^{″}{u}_j^{″}}/2\tilde{k}-{\delta }_{ij}/3;d_{ij}={\tilde{\epsilon }}_{ij}/2\tilde{\epsilon }-{\delta }_{ij}/3$$

(1)

where $\tilde{k}=\widetilde{u_i^{″}{u}_i^{″}}/2$ and $\tilde{\epsilon }=\overline{\mu \left(\partial u_i^{″}/\partial x_k\right)(\partial u_i^{″}/\partial x_k})/\overline{\rho }={\tilde{\epsilon }}_{ii}/2$ are the turbulent kinetic energy and its dissipation rate, respectively. The first invariants of these tensors are identically zero as they are trace-free (i.e., $b_{ii}=d_{ii}=0$) but their second (i.e., $I{I}_b$ and $I{I}_d$) and third invariants (i.e., $II{I}_b$ and $II{I}_d$) are given as [25,26,27,28]:

$$I{I}_b=-b_{ij}{b}_{ji}/2;I{I}_d=-d_{ij}{d}_{ji}/2$$

(2)

$$II{I}_b=b_{ij}{b}_{jk}{b}_{ki}/3\mathrm{and}II{I}_d=d_{ij}{d}_{jk}{d}_{ki}/3$$

(3)

The invariants given by Equations (2) and (3) appear in the characteristic equations of $b_{ij}$ and $d_{ij}$ tensors and, therefore, in turn influence the eigenvalues of anisotropy tensors. Based on the eigenvalues of the anisotropy tensors, the following boundaries of the realisable states of turbulence can be achieved [25,26,27,28]:

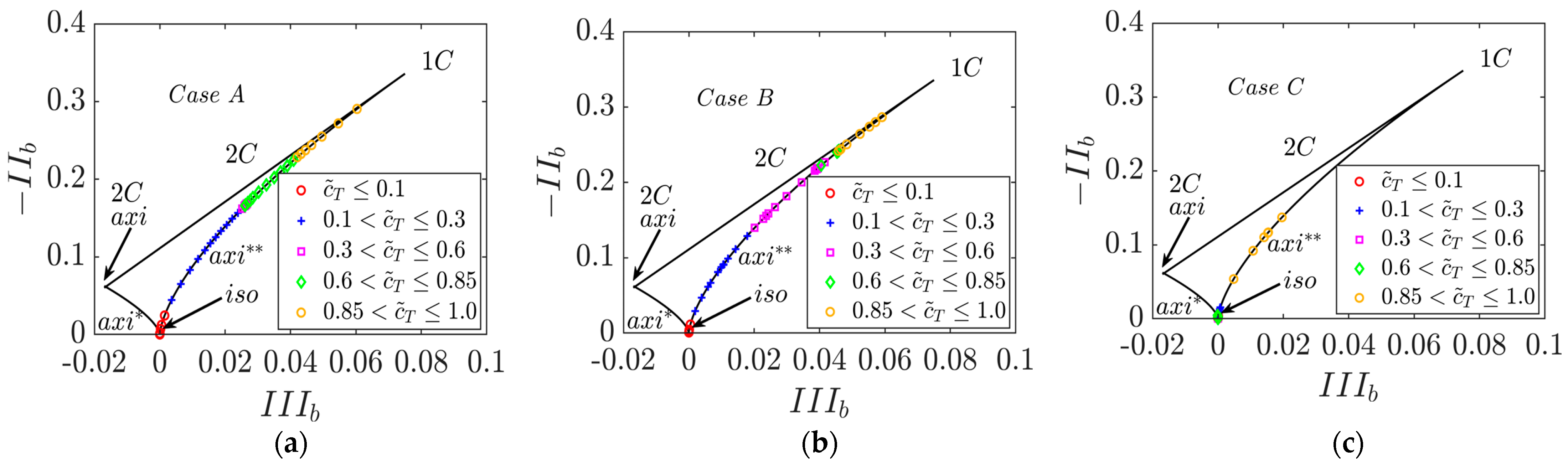
• One component (1C) limit: Under this condition, only one of the eigenvalues of either $\widetilde{u_i^{″}{u}_j^{″}}$ or ${\tilde{\epsilon }}_{ij}$ assumes non-zero values. The corresponding eigenvalues of anisotropy tensor can be expressed as: $\left\{{\lambda }_1,{\lambda }_2,{\lambda }_3\right\}=\{2/3,-1/3,-1/3\}$.
• Two-component (2C) axisymmetric limit: As the name suggests, two eigenvalues of either $\widetilde{u_i^{″}{u}_j^{″}}$ or ${\tilde{\epsilon }}_{ij}$ are non-zero for this limit. The corresponding eigenvalues of the anisotropy tensor are given by $\left\{{\lambda }_1,{\lambda }_2,{\lambda }_3\right\}=\{1/6,1/6,-1/3\}$.
• Three-component (3C) isotropy limit: All three eigenvalues of either $\widetilde{u_i^{″}{u}_j^{″}}$ or ${\tilde{\epsilon }}_{ij}$ are non-zero and equal. The eigenvalues of the anisotropy tensor are $\left\{{\lambda }_1,{\lambda }_2,{\lambda }_3\right\}=\{0,0,0\}$.

These limits are used to create the borders of the Lumley triangle in the following manner [28,29,30]:

‑

A two-component limit that translates to ellipse-like (pancake) turbulence structures with ${\lambda }_1>{\lambda }_2$ and ${\lambda }_3$ = 0.

‑

An axisymmetric expansion where rod-like turbulence structures are obtained with ${\lambda }_1>{\lambda }_2{=\lambda }_3$.

‑

Axisymmetric compression where disc-like turbulence structures with ${\lambda }_1={\lambda }_2{>\lambda }_3$ are obtained.

All the realisable points reside within the Lumley triangle defined by the borders and vertices mentioned above.

Hanjalic and Launder [29] proposed a model for ${\tilde{\epsilon }}_{ij}$ for non-reacting turbulent flows:

$${\tilde{\epsilon }}_{ij}=f{\tilde{\epsilon }}_{ij}^a+\left(1-f\right)2{\delta }_{ij}\tilde{\epsilon }/3$$

(4)

Here, ${\tilde{\epsilon }}_{ij}^a=(\widetilde{u_i^{″}{u}_j^{″}}/\tilde{k})\tilde{\epsilon }$, $f={\left(1+R{e}_t/10\right)}^{-1}$ is a bridging function, where $R{e}_t={\rho }_0{\tilde{k}}^2/{\mu }_0\tilde{\epsilon }$ is the turbulent Reynolds number, with ${\rho }_0$ and ${\mu }_0$ being the unburned gas density and unburned gas viscosity, respectively. Antonia et al. [27] proposed an alternative model for ${\tilde{\epsilon }}_{ij}$:

$${\tilde{\epsilon }}_{ij}=f_b{\tilde{\epsilon }}_{ij}^a+\left(1-f_b\right){\tilde{\epsilon }}_{ij}^b$$

(5)

In Equation (5), $f_b=\mathrm{e}\mathrm{x}\mathrm{p} (-20A_b^2)$ is a bridging function where $A_b$ is given by: $A_b=1+9(I{I}_b+3II{I}_b)$ [25,27,28]. Two modelling options exist for ${\tilde{\epsilon }}_{ij}^b$ [27,30,31]:

$${\tilde{\epsilon }}_{ij}^b=2\tilde{\epsilon }(10R{e}_t^{-0.5}{b}_{ij}+{\delta }_{ij}/3)$$

(6a)

$${\tilde{\epsilon }}_{ij}^b=2\tilde{\epsilon }(b_{ij}-2\alpha [\left(2I{I}_b+1/3\right)b_{ij}+\left(b_{ik}{b}_{kj}+2I{I}_b{\delta }_{ij}/3\right)]+{\delta }_{ij}/3)$$

(6b)

Here, $\alpha ~O\left(1\right)$ is a model parameter unity and is assumed to be 1.0 in this analysis. The models expressed as Equation (4), Equation (5) with Equation (6a) and Equation (5) with Equation (6b) will henceforth be referred to as Model 1, Model 2 and Model 3, respectively. It was demonstrated previously [27] that Model 2 and Model 3 are more successful in predicting anisotropic turbulence than Model 1 for non-reacting turbulent flows. The performance of these models in different regimes of premixed combustion will be demonstrated in Section 4 of this paper.

3. Numerical Implementation

3.1. Direct Numerical Simulation Configuration

A direct numerical simulation (DNS) database [32] of statistically planar H₂-air flames with an equivalence ratio of 0.7 has been considered for this analysis. According to the linear stability analysis, a positive value of the nondimensional wave number $k_n$ for the cellular thermodiffusive instability suggests a stabilising effect, whereas the flames become unconditionally unstable for a negative value of $k_n$ [33]. The effective Lewis number $L{e}_{eff}$ of H₂-air premixed flame with $\varphi =0.7$ is close to 0.5 [34], for which the value of $k_n$ is close to zero, which suggests that the thermodiffiusive instability effects are weak for $\varphi =0.7$ H₂-air premixed flames. Klein et al. [35] demonstrated that the ratio of the normalised turbulent burning velocity $S_T/S_L$ and the normalised flame surface area $A_T/A_L$ (where subscripts T and L are used for turbulent and laminar flames) remains close to unity for the flames in this database, which is qualitatively similar to previous findings for unity Lewis number flames [36].

A well-validated compressible DNS code, which solves the standard governing equations of mass, momentum, energy, and species mass fractions, is used for these simulations [32]. A chemical mechanism [37] involving 9 species and 19 chemical reactions is used for H₂-air combustion. A mixture averaged transport is adopted for the evaluation of transport coefficients (e.g., viscosity, diffusivity and thermal conductivity). Moreover, all the transport coefficients and specific heats are taken to be temperature dependent. For these simulations, the unburned gas temperature $T_0$ is 300 K and the pressure is taken to be atmospheric. These conditions give rise to an unstretched laminar burning velocity $S_L=135.62 \mathrm{c}\mathrm{m}/\mathrm{s}$ for $\varphi =0.7$. The simulation domain is taken to be a rectangular parallelopiped with the long direction aligning with the mean direction of flame propagation. The boundaries aligning with the direction of mean flame propagation are considered as turbulent inflow and partially non-reflecting outflow, respectively. The non-periodic boundaries are specified using an improved version of the Navier–Stokes Characteristic Boundary Conditions (NSCBC) [38]. A solenoidal homogeneous, isotropic turbulence field is injected through the inlet. As the simulation progresses, the mean inlet velocity has been dynamically updated to match the turbulent burning velocity during the simulation. An eighth order finite difference scheme is used for spatial discretisation for the internal grid points, but the order of spatial differentiation decreases gradually to a one-sided fourth order scheme at the non-periodic boundaries. An explicit fourth order Runge–Kutta scheme is for the purpose of time-advancement.

3.2. Simulation Parameters

The normalised root-mean-square turbulent velocity fluctuation $u^{\prime }/S_L$, the most energetic length scale to flame thickness ratio $l_T/{\delta }_{th}$ at the inlet and the corresponding Damköhler number $Da=l_T{S}_L/u^{\prime }{\delta }_{th}$, Karlovitz number $Ka={{\left({{\rho }_{0}S}_L{\delta }_{th}/{\mu }_0\right)}^{0.5}\left(u\prime /S_L\right)}^{1.5}{\left(l_T/{\delta }_{th}\right)}^{-0.5}$ and turbulent Reynolds number $R{e}_t={\rho }_0{u}^{″}{l}_T/{\mu }_0$ for all cases considered here are provided in

Table 1. List of inflow turbulence parameters. The values of $R{e}_t,Da$ and $Ka$ shown in parentheses are based on $L_{11}/{\delta }_{th}$ and the values without parentheses are based on $l_T/{\delta }_{th}$.

Case	${\mathit{u}}^{\mathbf{\prime }}/{\mathit{S}}_{\mathit{L}}$	${\mathit{l}}_{\mathit{T}}/{\mathit{\delta }}_{\mathit{t}\mathit{h}}$	${\mathit{L}}_{11}/{\mathit{\delta }}_{\mathit{t}\mathit{h}}$	$\mathit{R}{\mathit{e}}_{\mathit{t}}$	Da	Ka
A	0.7	14.0	5.6	227 (91)	20.0 (8.0)	0.75 (1.19)
B	5.0	14.0	5.6	1623 (649)	2.8 (1.12)	14.4 (22.75)
C	14.0	4.0	1.6	1298 (519)	0.29 (0.12)	126 (199.0)

. The definition of $Ka$ is based on inertial scaling. It is debatable whether the inertial scaling is valid for these flames, but this definition is used as it is widely used in the literature [39]. Here, $l_T$ is the most energetic length scale; ${\delta }_{th}=(T_{ad}-T_0)/{\max \left|\nabla T\right|}_L$ is the laminar thermal flame thickness. Among the cases listed in Table 1, cases A, B and C fall nominally in the corrugated flamelets regime ($Ka<1$), thin reaction zones regime ($1<Ka<100$) and broken reaction zones regime ($Ka>100$), respectively, according to the Borghi–Peters diagram [39]. These three cases provide a sufficiently wide spread of Karlovitz number, which enables us to compare the statistical behaviours of $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$, and the interrelations between them for different premixed combustion regimes.

In cases A and B, the domain size is $20 \mathrm{mm}\times 10 \mathrm{mm}\times 10 \mathrm{mm}$, whereas the domain size of $8 \mathrm{mm}\times 2 \mathrm{mm}\times 2 \mathrm{mm}$ is used in case C. A uniform cartesian grid of $512\times 256\times 256$ is used for cases A and B, whereas $1280\times 320\times 320$ is used for case C, which ensures 10 grid points within ${\delta }_{th}$ and more than 1 grid point inside the Kolmogorov length scale. The longitudinal integral scale $L_{11}$ for the cases considered here is 2.5 times smaller than most energetic scale $l_T$, which leads to an increase (decrease) in $Ka$ ($Da$) by a factor 1.6 (2.5) if $L_{11}$ is used instead of $l_T$ in their definitions. For the sake of completeness, the values of $L_{11}/{\delta }_{th}$ and the values of $R{e}_t,Da$ and $Ka$ based on $L_{11}/{\delta }_{th}$ are also shown in Table 1. This further suggests that the simulation domain size is $10L_{11}\times 5L_{11}\times 5L_{11}$ in cases A and B and $8L_{11}\times 4L_{11}\times 4L_{11}$ in case C. Thus, the domain size accommodates a sufficient number of turbulent eddies. This domain size is comparable to several previous studies [10,11,12,40,41,42,43,44,45], which contributed significantly to fundamental understanding and modelling of premixed turbulent combustion. The simulation times for cases A–C correspond to $\left\{\mathrm{1.0,6.8,6.7}\right\}{l}_T/u\prime$) or $\left\{\mathrm{2.5,17,16.75}\right\}{L}_{11}/u\prime$, respectively. By the time the simulation is completed, the flame surface area and turbulent burning velocity reached a quasi-stationary state; related information is provided elsewhere [32].

4. Results and Discussion

4.1. Flame Morphology

The distributions of non-dimensional temperature $c_T=(T-T_0)/(T_{ad}-T_0)$ in the central mid-plane for cases A–C are shown in Figure 1a–c. Figure 1a shows that the isosurfaces of $c_T$ are parallel to each other in case A, which is expected in the flames within the corrugated flamelet regime where turbulent eddies cannot enter into the flame. By contrast, the isosurfaces of $c_T$ are not parallel in case C and the isosurfaces representing the preheat zone in this case are found to be more wrinkled than the isosurfaces representing the reaction zone. This implies that small turbulent eddies penetrate the preheat zone in case C, as expected for large Karlovitz number (i.e., ${\delta }_{th}\gg \eta$) Flames. The non-dimensional temperature $c_T$ distribution of case B shows some attributes of case C because ${\delta }_{th}>\eta$ is also valid for case B. The behaviour of case B is intermediate between cases A and C. A detailed discussion of $c_T$ distribution in these flames has been provided elsewhere [32], which is not repeated here for the sake of brevity.

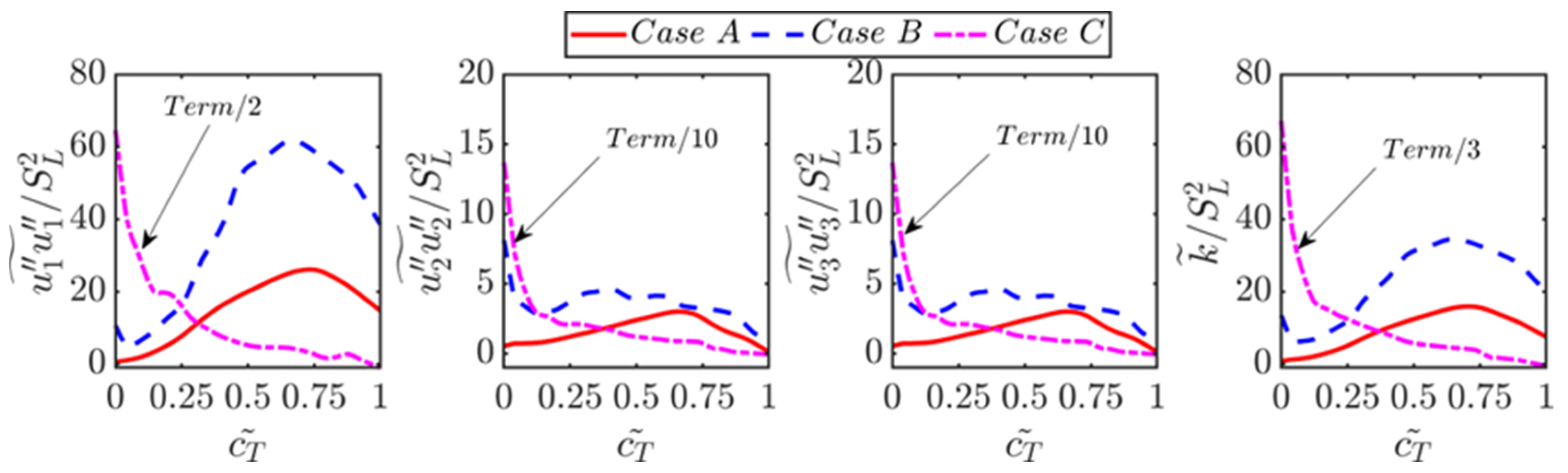
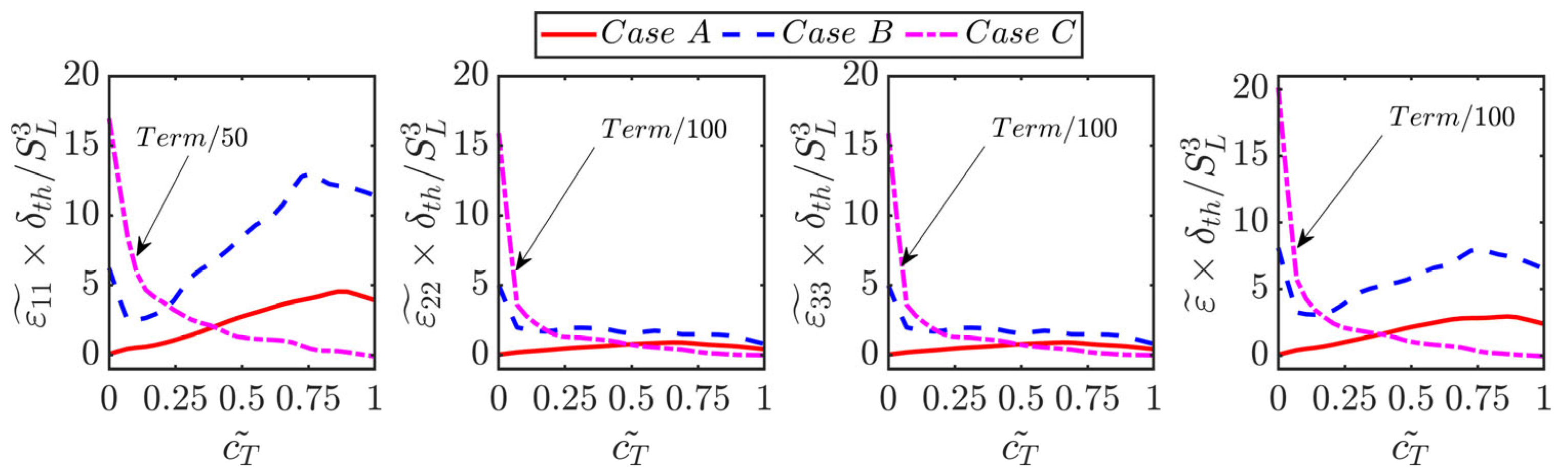
4.2. Variations of Reynolds Stresses and Its Dissipation Rates

The variations of $\widetilde{u_1^{″}{u}_1^{″}}/S_L^2,$ $\widetilde{u_2^{″}{u}_2^{″}}/S_L^2$, $\widetilde{u_3^{″}{u}_3^{″}}/S_L^2$ and $\tilde{k}/S_L^2$ with ${\tilde{c}}_T$ for cases A, B and C are shown in Figure 2. Note that $\widetilde{u_1^{″}{u}_1^{″}},$ $\widetilde{u_2^{″}{u}_2^{″}}$ and $\widetilde{u_3^{″}{u}_3^{″}}$ are the only non-zero Reynolds stress components and thus are shown here. At the upstream of the turbulent flame brush (${\tilde{c}}_T=0),$ the magnitudes of Reynolds stresses increase from case A to case C, as expected. Their subsequent variations throughout the flame brush, however, show significant differences. For cases A and B, all of $\widetilde{u_1^{″}{u}_1^{″}},$ $\widetilde{u_2^{″}{u}_2^{″}}$ and $\widetilde{u_3^{″}{u}_3^{″}}$ (with some initial drop for case B only) increase as the flow goes through the flame brush due to turbulence generation by thermal expansion, followed by a decrease towards the burned gas side. For case C, however, all of $\widetilde{u_1^{″}{u}_1^{″}},$ $\widetilde{u_2^{″}{u}_2^{″}}$ and $\widetilde{u_3^{″}{u}_3^{″}}$ decay monotonically from the leading edge to the end of the flame brush. This implies that the effect of heat release and associated turbulence generation becomes attenuated at higher level of turbulence. The augmentation of $\widetilde{u_1^{″}{u}_1^{″}}/S_L^2,$ $\widetilde{u_2^{″}{u}_2^{″}}/S_L^2$, $\widetilde{u_3^{″}{u}_3^{″}}/S_L^2$ and $\tilde{k}/S_L^2$ within the flame brush in cases A and B is qualitatively similar to the previous simple chemistry findings by Chakraborty et al. [46] for premixed turbulent flames with $L{e}_{eff}\ll 1$. Chakraborty et al. [46] also provided the physical explanations for the effects of $L{e}_{eff}$ on the turbulent kinetic energy transport in premixed turbulent flames.

In this configuration, $x_2$ and $x_3$ directions are statistically equivalent to each other and thus $\widetilde{u_2^{″}{u}_2^{″}}$ and $\widetilde{u_3^{″}{u}_3^{″}}$ assume almost identical values with their magnitudes being smaller than $\widetilde{u_1^{″}{u}_1^{″}}$ for all cases considered, since the effect of heat release is mainly in the $x_1$ direction. Thus, $\widetilde{u_1^{″}{u}_1^{″}}/2$ is the dominant contributor to $\tilde{k}=\widetilde{u_i^{″}{u}_i^{″}}/2$. Since such effect is overridden by the strong turbulence, the three stress curves are similar in case C.

The variations of $\{{\tilde{\epsilon }}_{11},$ ${\tilde{\epsilon }}_{22}$, ${\tilde{\epsilon }}_{33},\tilde{\epsilon }\}\times {\delta }_{th}/S_L^3$ with ${\tilde{c}}_T$ for cases A, B and C are shown in Figure 3. Similar to Reynolds stress components, ${\tilde{\epsilon }}_{11}$ assumes greater magnitudes than ${\tilde{\epsilon }}_{22}$ and ${\tilde{\epsilon }}_{33}$. Thus, ${\tilde{\epsilon }}_{11}/2$ remains the major contributor to $\tilde{\epsilon }$ for all cases considered. Similar to Reynolds stress component variations within the flame brush, ${\tilde{\epsilon }}_{11},$ ${\tilde{\epsilon }}_{22}$, and ${\tilde{\epsilon }}_{33}$ for cases A and B increase and decrease through the flame brush, while for case C they decrease monotonically.

The differences in magnitudes of $\widetilde{u_1^{″}{u}_1^{″}},$ $\widetilde{u_2^{″}{u}_2^{″}}$ and $\widetilde{u_3^{″}{u}_3^{″}}$ in Figure 2 and ${\tilde{\epsilon }}_{11},$ ${\tilde{\epsilon }}_{22}$ and ${\tilde{\epsilon }}_{33}$ in Figure 3 imply that the Reynolds stress and dissipation tensors exhibit a significant level of anisotropy. This has implications for the turbulent flow structure and the modelling of dissipation rate tensor ${\tilde{\epsilon }}_{ij}$. The anisotropy states of Reynolds stresses are usually characterised by the plots of $-I{I}_b$ versus $II{I}_b$ in the form of the Lumley triangle, as shown in Figure 4a–c for cases A–C, respectively, with data points color-coded for different ranges of ${\tilde{c}}_T$. Similarly, the corresponding Lumley triangles for the dissipation rate tensor are shown in Figure 5a–c for cases A–C, respectively, at different ranges of ${\tilde{c}}_T$. Since the incoming turbulence is isotropic, the flow starts from (0,0) in the diagram and moves along a trajectory. For all cases, both $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$ tensors follow a predominantly two-component axisymmetric expansion state (i.e., $\widetilde{u_1^{″}{u}_1^{″}}>\widetilde{{(u}_2^{″}{u}_2^{″}}+\widetilde{u_3^{″}{u}_3^{″}})$ and ${\tilde{\epsilon }}_{11}>({\tilde{\epsilon }}_{22}+{\tilde{\epsilon }}_{33})$) with an increase in ${\tilde{c}}_T$ and the anisotropy state tends towards the one-component side of the two-component axisymmetric expansion branch. The level of anisotropy at the end of the flame brush is the strongest for case A and the weakest for case C, that is, the terminal data points at the burned gas side of the flame brush are significantly closer to the origin for case C. This suggests that the dominant effect of heat release and the associated flame-generated turbulence induce turbulence anisotropy within the flame brush.

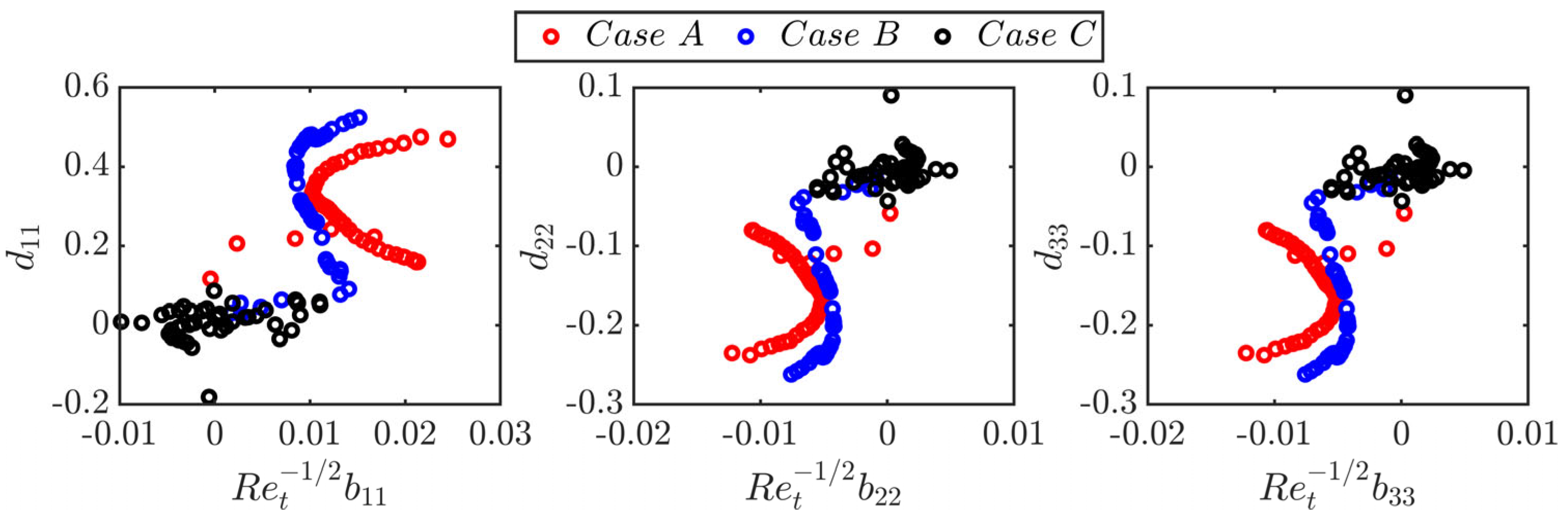
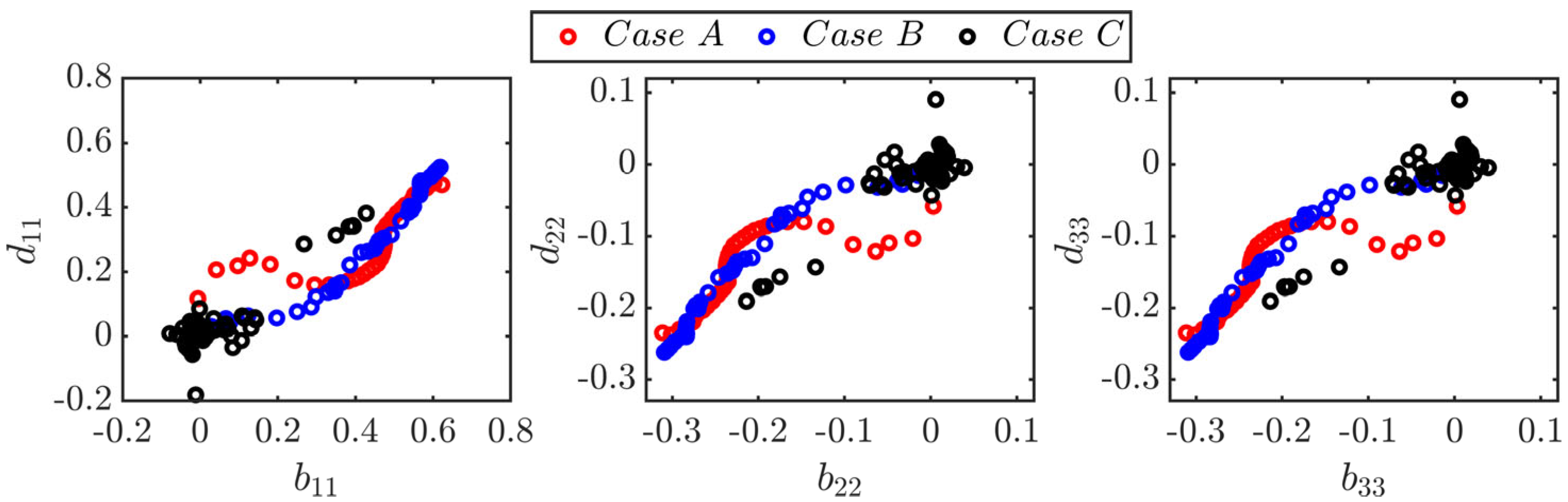
4.3. Interrelation Between $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$ Tensors

The qualitative similarities of anisotropy behaviours between $\widetilde{u_i^{″}{u}_j^{″}}$ and ${\tilde{\epsilon }}_{ij}$ tensors motivate the exploration of the relationship between $b_{ij}$ and $d_{ij}$. Lumley [47] suggested $d_{ij}/b_{ij}~\left({\lambda }_T/u^{\prime }\right)/(l/u^{\prime })~R{e}_t^{-0.5}$, with ${\lambda }_T$ and $l$ being the Taylor microscale and local integral length scale, respectively. The variations of $d_{ij}$ with ${R{e}_t^{-0.5}b}_{ij}$ for $0.1<{\tilde{c}}_T<0.9$ for cases A–C are shown in Figure 6, indicating that $d_{ij}$ and ${R{e}_t^{-0.5}b}_{ij}$ are non-linearly interrelated. Moreover, the variation between $d_{ij}$ and $b_{ij}$ is also found to be non-linear for all cases considered here, as shown in Figure 7. These behaviours are qualitatively similar to previous findings [27,48] for non-reacting flows.

4.4. Performance Assessment of ${\tilde{\epsilon }}_{ij}$ Models

The predictions of $\left\{{\tilde{\epsilon }}_{11},{\tilde{\epsilon }}_{22},{\tilde{\epsilon }}_{33}\right\}\times {\delta }_{th}/S_L^3$ according to Equations (4) and (5) with Equations (6a) and (5) with Equation (6b), (i.e., Model 1, Model 2 and Model 3, respectively) are shown along with the values directly computed from DNS data in Figure 8a–c for cases A–C, respectively. It is evident that Model 1 significantly underpredicts ${\tilde{\epsilon }}_{11}$, and overpredicts ${\tilde{\epsilon }}_{22}$ and ${\tilde{\epsilon }}_{33}$ in cases A and B. On the other hand, both Models 2 and 3 predict ${\tilde{\epsilon }}_{11},{\tilde{\epsilon }}_{22}$ and ${\tilde{\epsilon }}_{33}$ accurately, with some discrepancies on the product side of the flame brush. In case C, since the flame-induced anisotropy is minimal, all three models capture the DNS results accurately throughout the flame brush.

These results suggest that Model 1 is subjected to larger errors as flame-generated anisotropy increases. This is a consequence of the fact that Equation (4) considers a linear relation between $b_{ij}$ and $d_{ij}$ in the ${\tilde{\epsilon }}_a$ expression and the second term on the right-hand side also includes the isotropic distribution of dissipation rate tensor. Therefore, Model 1 yields a larger level of errors for cases A and B where the anisotropy level is significant. In case C, the level of anisotropy is much weaker and ${\tilde{\epsilon }}_a$ becomes close to $2\tilde{\epsilon }/3$ because $\widetilde{u_i^{″}{u}_{j=i}^{″}}/\tilde{k}\approx 2/3$, hence ${\tilde{\epsilon }}_{11}\approx {\tilde{\epsilon }}_{22}\approx {\tilde{\epsilon }}_{33}\approx 2\tilde{\epsilon }/3$ is obtained irrespective of the expression of $f$. In contrast, the superior performance of Models 2 and 3 is achieved by accounting for the departure from isotropy through the involvement of $A_b$ in $f_b$, because $A_b=1+9(I{I}_b+3II{I}_b)$ addresses the departure from the 2-component limit (where $A_b=0$). The Model 3 expression (i.e., Equations (5) and (6b)) includes $I{I}_b$ and $II{I}_b$ and thus not only accounts for the local anisotropic behaviour but also satisfies the following conditions: (a) the symmetry with respect to $i$ and $j$; (b) $d_{ii}=0$; (c) in the homogeneous two-component limit yields ($d_{m^{*}{m}^{*}}=b_{m^{*}{m}^{*}}=-1/3$ where * indicates no summation) [27]. Thus, Model 3 is considered the best choice for modelling dissipation rate (i.e., $\tilde{\epsilon }\approx {\tilde{\epsilon }}_{ii}/2$) and the components of ${\tilde{\epsilon }}_{ij}$ within the flame brush for all premixed turbulent combustion regimes. Although Model 2 and Model 3 were proposed for non-reacting flows [27,30,31], their satisfactory performances in cases A–C seem to suggest that implicit thermal expansion effects in the invariants is sufficient to capture the anisotropies of the dissipation rate tensor in premixed turbulent combustion. The current detailed chemistry DNS findings for cases A and B are qualitatively similar to the single-step chemistry DNS results by Ahmed et al. [26] for stoichiometric methane-air flames representative of the flamelets regime of combustion before interacting with the wall.

5. Conclusions

A DNS database of statistically planar premixed turbulent H₂-air flames with an equivalence ratio of 0.7 was utilised to analyse the interrelation between anisotropies of Reynolds stresses and viscous dissipation rate tensors for different Karlovitz numbers. The main findings can be summarised in the following manner.

• It was found that the normal flame acceleration arising from thermal expansion and associated flame-generated turbulence leads to a significant amount of augmentation of Reynolds stress and viscous dissipation rate tensors within the flame brush for small and moderate Karlovitz number values. In contrast, the components of Reynolds stress and dissipation rate tensors show a monotonic decay from the reactant side of the flame brush for large Karlovitz number values. It was found that the extent of anisotropy increases within the flame brush where the thermal expansion effects are strong for small and moderate Karlovitz number values.
• In spite of the superficial similarities between Reynolds stresses and viscous dissipation rate tensors, their anisotropies do not follow a linear relation according to Lumley’s scaling [47]. Therefore, the model based on this assumption is not successful in capturing the viscous dissipation rate components obtained from DNS data for small and moderate Karlovitz number values. Instead, the models which incorporate the statistical variations of the invariants of the anisotropy tensor of Reynolds stresses were found to predict the components of ${\tilde{\epsilon }}_{ij}$ for small and moderate Karlovitz number values. However, all the models provide satisfactory performance for large Karlovitz number values because the anisotropy effects are weak under that condition.

The accurate predictions of ${\tilde{\epsilon }}_{ij}$ can lead to an improvement in the fidelity of RANS simulations of premixed combustion as $\tilde{\epsilon }$ is often used as an input parameter for combustion models. Finally, the model identified to provide satisfactory performance based on a priori DNS analysis needs to be implemented in RANS of turbulent premixed combustion in a configuration where the experimental data are available for comparison purposes. This will form the basis of future investigations.