Anisotropy of Reynolds Stresses and Their Dissipation Rates in Lean H2-Air Premixed Flames in Different Combustion Regimes
Abstract
:1. Introduction
2. Mathematical Background
- One component (1C) limit: Under this condition, only one of the eigenvalues of either or assumes non-zero values. The corresponding eigenvalues of anisotropy tensor can be expressed as: .
- Two-component (2C) axisymmetric limit: As the name suggests, two eigenvalues of either or are non-zero for this limit. The corresponding eigenvalues of the anisotropy tensor are given by .
- Three-component (3C) isotropy limit: All three eigenvalues of either or are non-zero and equal. The eigenvalues of the anisotropy tensor are .
- ‑
- A two-component limit that translates to ellipse-like (pancake) turbulence structures with and = 0.
- ‑
- An axisymmetric expansion where rod-like turbulence structures are obtained with .
- ‑
- Axisymmetric compression where disc-like turbulence structures with are obtained.
3. Numerical Implementation
3.1. Direct Numerical Simulation Configuration
3.2. Simulation Parameters
4. Results and Discussion
4.1. Flame Morphology
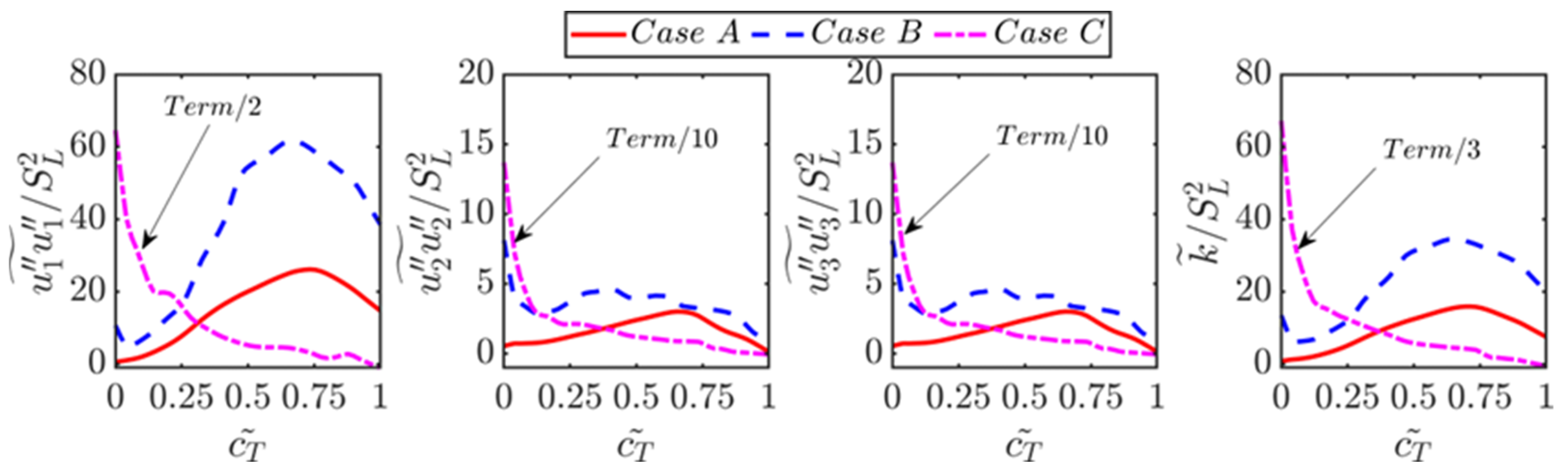
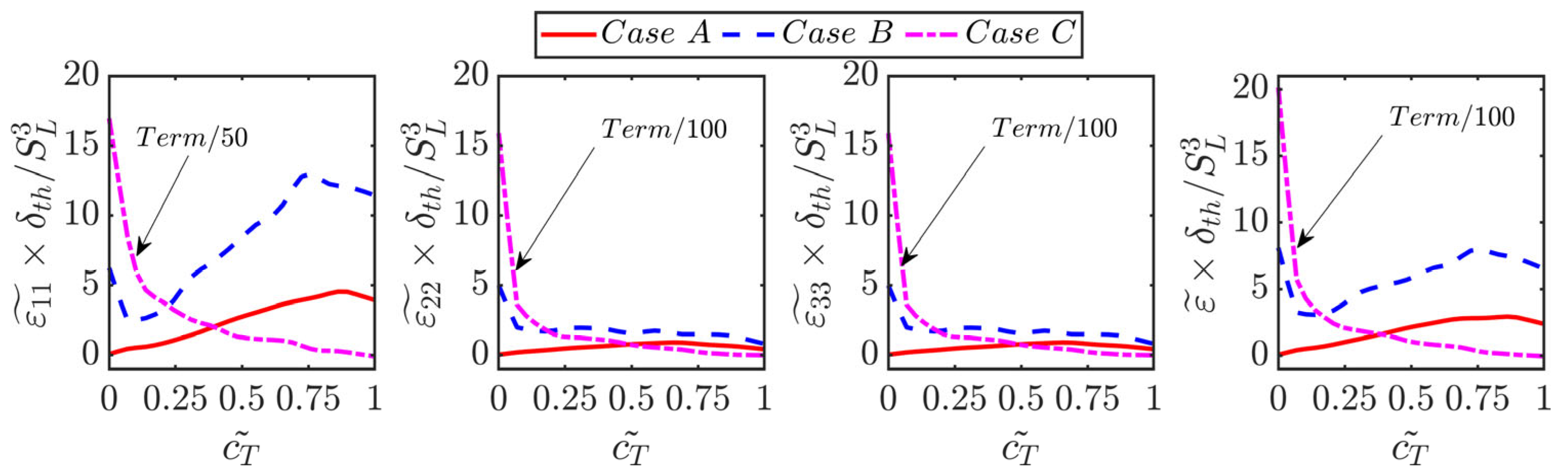
4.2. Variations of Reynolds Stresses and Its Dissipation Rates
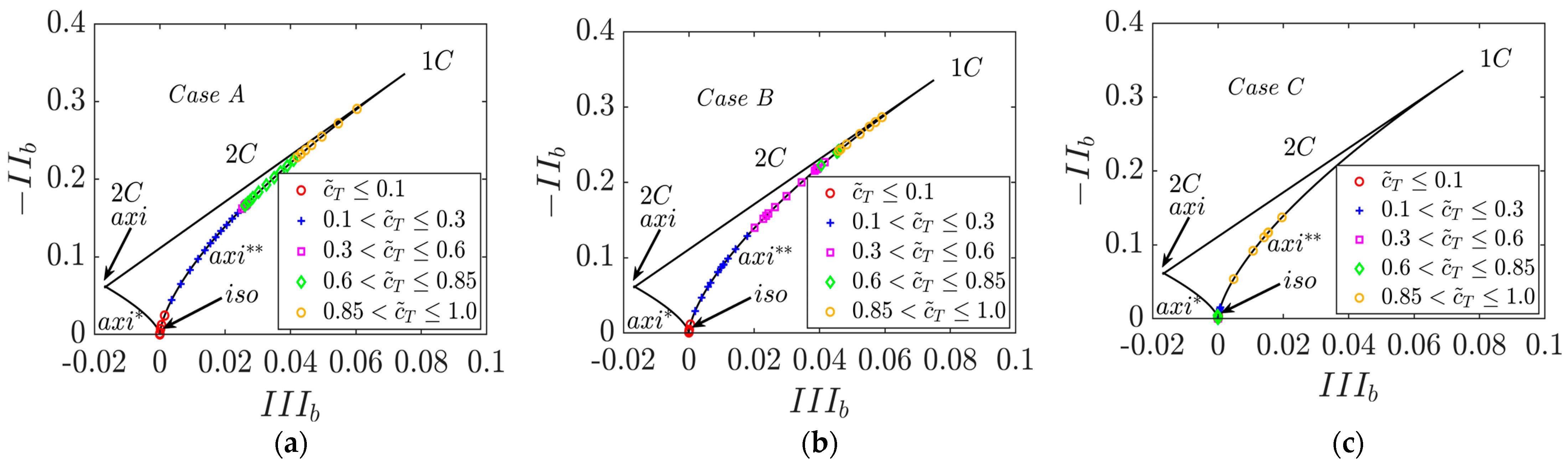
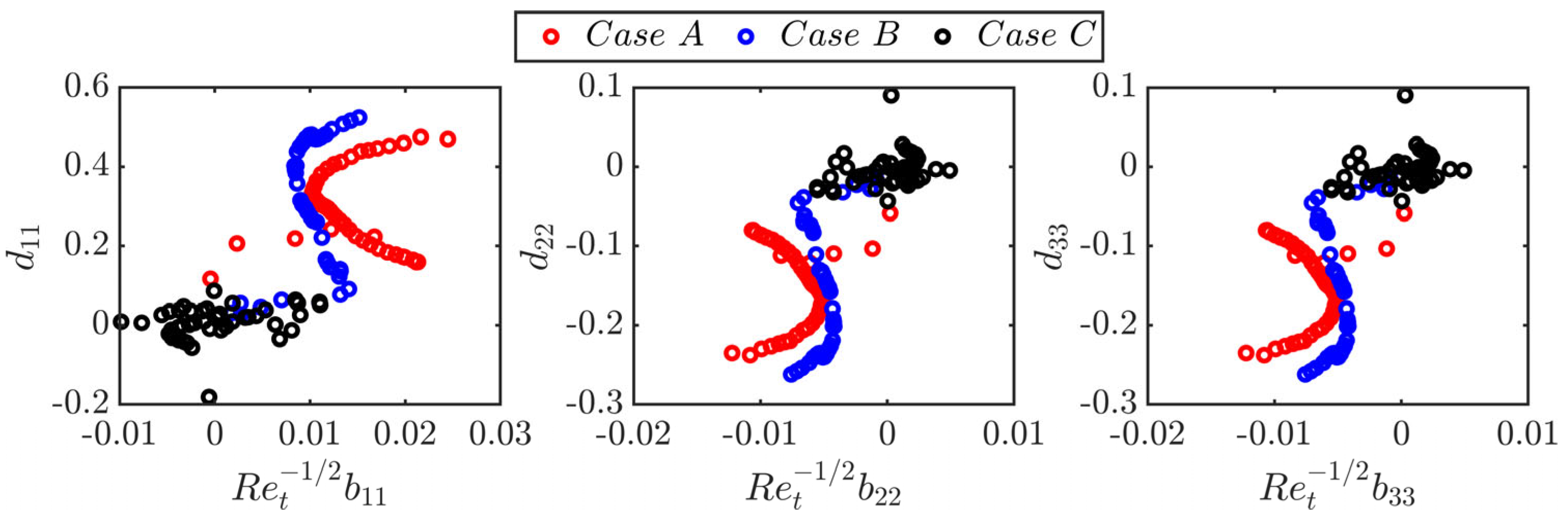
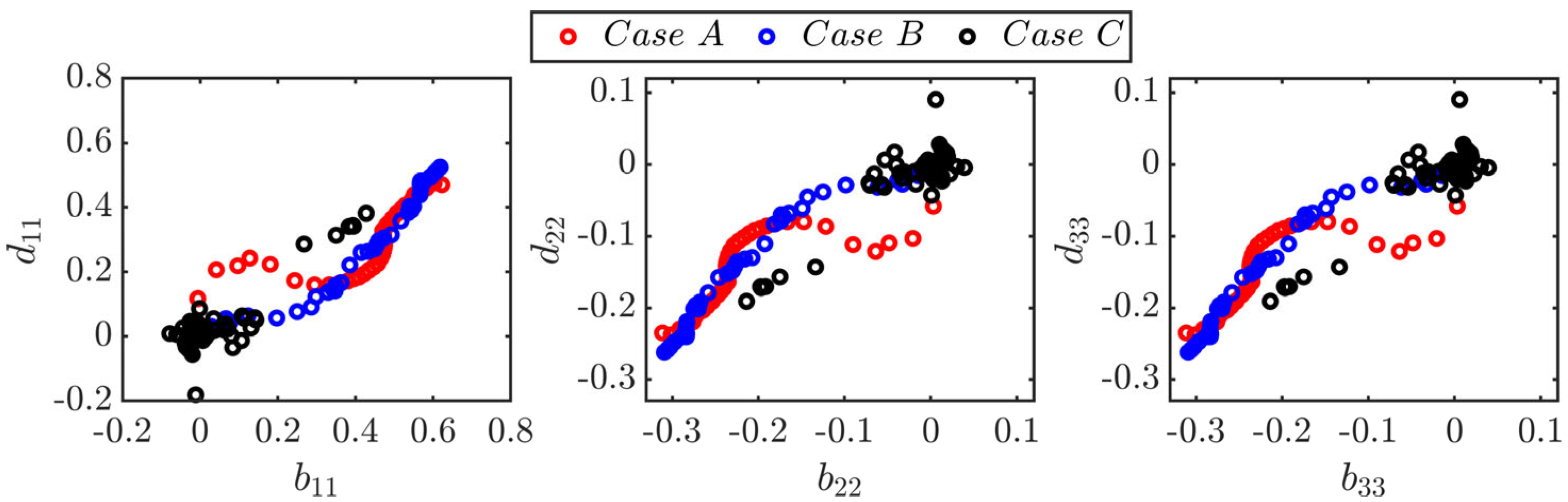
4.3. Interrelation Between and Tensors
4.4. Performance Assessment of Models
5. Conclusions
- It was found that the normal flame acceleration arising from thermal expansion and associated flame-generated turbulence leads to a significant amount of augmentation of Reynolds stress and viscous dissipation rate tensors within the flame brush for small and moderate Karlovitz number values. In contrast, the components of Reynolds stress and dissipation rate tensors show a monotonic decay from the reactant side of the flame brush for large Karlovitz number values. It was found that the extent of anisotropy increases within the flame brush where the thermal expansion effects are strong for small and moderate Karlovitz number values.
- In spite of the superficial similarities between Reynolds stresses and viscous dissipation rate tensors, their anisotropies do not follow a linear relation according to Lumley’s scaling [47]. Therefore, the model based on this assumption is not successful in capturing the viscous dissipation rate components obtained from DNS data for small and moderate Karlovitz number values. Instead, the models which incorporate the statistical variations of the invariants of the anisotropy tensor of Reynolds stresses were found to predict the components of for small and moderate Karlovitz number values. However, all the models provide satisfactory performance for large Karlovitz number values because the anisotropy effects are weak under that condition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karlovitz, B.; Denniston, D.W., Jr.; Knapschaefer, D.H.; Wells, F.E. Studies on turbulent flames. Proc. Combust. Inst. 1953, 4, 613–620. [Google Scholar] [CrossRef]
- Bray, K.N.C.; Libby, P.A. Interaction effects in turbulent premixed flames. Phys. Fluids A 1976, 19, 1687–1701. [Google Scholar] [CrossRef]
- Bray, K.N.C.; Libby, P.A.; Masuya, G.; Moss, J.B. Turbulence production in premixed turbulent flames. Combust. Sci. Technol. 1980, 25, 127–140. [Google Scholar] [CrossRef]
- Strahle, W.C. Velocity-pressure gradient correlation in turbulent reactive flows. Combust. Sci. Technol. 1983, 32, 289–305. [Google Scholar] [CrossRef]
- Borghi, R.; Escudie, D. Assessment of a theoretical model of turbulent combustion by comparison with a simple experiment. Combust. Flame 1984, 56, 149–164. [Google Scholar] [CrossRef]
- Moreau, P.; Boutier, A. Laser velocimeter measurements in a turbulent flame. Proc. Combust. Inst. 1977, 16, 1747–1756. [Google Scholar] [CrossRef]
- Moss, J.B. Simultaneous measurements of concentration and velocity in an open premixed flame. Combust. Sci. Technol. 1980, 22, 119–129. [Google Scholar] [CrossRef]
- Shepherd, I.G.; Moss, J.B.; Bray, K.N.C. Turbulent transport in a confined premixed flame. Proc. Combust. Inst. 1982, 19, 423–431. [Google Scholar] [CrossRef]
- Chomiak, J.; Nisbet, J. Modelling variable density effects in turbulent flames. Combust. Flame 1995, 102, 371–386. [Google Scholar] [CrossRef]
- Rutland, C.J.; Cant, R.S. Turbulent transport in premixed flames. In Proceedings of the 1994 Summer Program; Centre for Turbulence Research, Stanford University/NASA Ames: Stanford, CA, USA, 1994; pp. 75–94. [Google Scholar]
- Zhang, S.; Rutland, C.J. Premixed flame effects on turbulence and pressure-related terms. Combust. Flame 1995, 102, 447–461. [Google Scholar] [CrossRef]
- Nishiki, S.; Hasegawa, T.; Borghi, R.; Himeno, R. Modelling of flame generated turbulence based on Direct Numerical Simulation databases. Proc. Combust. Inst. 2002, 29, 2017–2022. [Google Scholar] [CrossRef]
- Klein, M.; Trummler, T.; Urban, N.; Chakraborty, N. Multiscale analysis of anisotropy of Reynolds Stresses, sub-grid stresses and dissipation in statistically planar turbulent premixed flames. App. Sci. 2022, 12, 2275. [Google Scholar] [CrossRef]
- Chakraborty, N. Influence of thermal expansion on fluid dynamics of turbulent premixed combustion and its modelling implications. Flow Turb. Combust. 2021, 106, 753–806. [Google Scholar] [CrossRef]
- Bradley, D.; Gaskell, P.H.; Gu, X.J. Application of a Reynolds stress, stretched flamelet, mathematical model to computations of turbulent burning velocities and comparison with experiments. Combust. Flame 1994, 96, 221–248. [Google Scholar] [CrossRef]
- Bailly, P.; Champion, M.; Garréton, D. Counter-gradient diffusion in a confined turbulent premixed flame. Phys. Fluids 1997, 9, 766–775. [Google Scholar] [CrossRef]
- Lindstedt, R.P.; Váos, E.M. Second moment modeling of premixed turbulent flames stabilized in impinging jet geometries. Proc. Combust. Inst. 1998, 27, 957–962. [Google Scholar] [CrossRef]
- Robin, V.; Champion, M.; Mura, A. A second-order model for turbulent reactive flows with variable equivalence ratio. Combust. Sci. Technol. 2008, 180, 1709–1734. [Google Scholar] [CrossRef]
- Tian, L.; Lindstedt, R.P. The impact of dilatation, scrambling, and pressure transport in turbulent premixed flames. Combust. Theor. Modell. 2017, 21, 1114–1147. [Google Scholar] [CrossRef]
- Jiang, L.-Y. RANS Modelling of Turbulence in Combustors. Turbulence Modelling Approaches-Current State, Development Prospects, Applications; InTech: London, UK, 2017. [Google Scholar] [CrossRef]
- Terada, A.; Kamiji, Y.; Hino, R.; Matsumoto, M.; Sugiyama, H.; Kadowaki, S. Development of hydrogen behavior simulation code system Outline of code system and validation using existing data. In Proceedings of the 23rd International Conference on Nuclear Engineering (ICONE-23), Chiba, Japan, 17–21 May 2015; p. 3737. [Google Scholar]
- Lindstedt, R.P.; Luff, D.S.; Whitelaw, J.H. Velocity and strain-rate characteristics of opposed isothermal flows. Flow Turb. Combust. 2005, 74, 169–194. [Google Scholar] [CrossRef]
- Bray, K.N.C.; Libby, P.A. Passage times and flamelet crossing frequencies in premixed turbulent combustion. Combust. Sci. Technol. 1986, 47, 253–274. [Google Scholar] [CrossRef]
- Kolla, H.; Rogerson, J.W.; Chakraborty, N.; Swaminathan, N. Scalar dissipation rate modeling and its validation. Combust. Sci. Technol. 2009, 181, 518–535. [Google Scholar] [CrossRef]
- Leschziner, M. Statistical Turbulence Modelling for Fluid Dynamics-Demystified: An Introductory Text for Graduate Engineering Students, 1st ed.; Imperial College Press: London, UK, 2015. [Google Scholar]
- Ahmed, U.; Ghai, S.K.; Chakraborty, N. Relations between Reynolds stresses and their dissipation rates during premixed flame-wall interaction within turbulent boundary layers. Phys. Fluids 2024, 36, 045120. [Google Scholar] [CrossRef]
- Antonia, R.A.; Dejinidi, R.; Spalart, P.R. Anisotropy of the dissipation tensor in a turbulent boundary layer. Phys. Fluids 1994, 6, 2475–2479. [Google Scholar] [CrossRef]
- Lumley, J.L.; Newman, G.R. The return to isotropy of homogeneous turbulence. J. Fluid Mech. 1977, 82, 161–178. [Google Scholar] [CrossRef]
- Hanjalic, K.; Launder, B.E. Contribution towards a Reynolds-stress closure for low-Reynolds-number turbulence. J. Fluid Mech. 1976, 74, 593–610. [Google Scholar] [CrossRef]
- Launder, B.E.; Tselepidakis, D.P. Contribution to the modelling of near-wall turbulence. In Turbulent Shear Flows; Durst, F., Friedrich, R., Launder, B.E., Schmidt, F.W., Schumann, U., Whitelaw, J.H., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 81–96. [Google Scholar]
- Hallback, M.; Groth, J.; Johansson, A.V. An algebraic model for nonisotropic turbulent dissipation rate in Reynolds stress closures. Phys. Fluids A 1990, 2, 1859–1866. [Google Scholar] [CrossRef]
- Im, H.G.; Arias, P.G.; Chaudhuri, S.; Uranakara, H.A. Direct numerical simulations of statistically stationary turbulent premixed flames. Combust. Sci. Technol. 2016, 188, 1182–1198. [Google Scholar] [CrossRef]
- Pelce, P.; Clavin, P. Influence of hydrodynamics and diffusion upon the stability limits of laminar premixed flames. J. Fluid Mech. 1982, 124, 219–237. [Google Scholar] [CrossRef]
- Bechtold, J.K.; Matalon, M. The dependence of the Markstein length on stoichiometry. Combust. Flame 2001, 127, 1906–1913. [Google Scholar] [CrossRef]
- Klein, M.; Herbert, A.; Kosaka, H.; Böhm, B.; Dreizler, A.; Chakraborty, N.; Papapostolou, V.; Im, H.G.; Hasslberger, J. Evaluation of flame area based on detailed chemistry DNS of premixed turbulent hydrogen-air flames in different regimes of combustion. Flow Turb. Combust. 2019, 104, 403–419. [Google Scholar] [CrossRef]
- Chakraborty, N.; Alwazzan, D.; Klein, M.; Cant, R.S. On the validity of Damköhler″s first hypothesis in turbulent Bunsen burner flames: A computational analysis. Proc. Combust. Inst. 2019, 37, 2231–2239. [Google Scholar] [CrossRef]
- Burke, M.P.; Chaos, M.; Ju, Y.; Dryer, F.L.; Klippenstein, S.J. Comprehensive H2-O2 kinetic model for high-pressure combustion. Int. J. Chem. Kin 2012, 44, 444–474. [Google Scholar] [CrossRef]
- Yoo, C.S.; Im, H.G. Characteristic boundary conditions for simulations of compressible reacting flows with multi-dimensional, viscous and reaction effects. Combust. Theor. Model. 2007, 11, 259–286. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Veynante, D.; Trouvé, A.; Bray, K.N.C.; Mantel, T. Gradient and counter-gradient turbulent scalar transport in turbulent premixed flames. J. Fluid Mech. 1997, 332, 263–293. [Google Scholar] [CrossRef]
- Nishiki, S.; Hasegawa, T.; Borghi, R.; Himeno, R. Modelling of turbulent scalar flux in turbulent premixed flames based on DNS database. Combust. Theory Model. 2006, 10, 39–55. [Google Scholar] [CrossRef]
- Grout, R.W. An age extended progress variable for conditioning reaction rates. Phys. Fluids 2007, 19, 105107. [Google Scholar] [CrossRef]
- Swaminathan, N.; Xu, G.; Dowling, A.P.; Balachandran, R. Heat release rate correlation and combustion noise in premixed flames. J. Fluid Mech. 2011, 681, 80–115. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Nishiki, S.; Hasegawa, T. A direct numerical simulation study of vorticity transformation in weakly turbulent premixed flames. Phys. Fluids 2014, 26, 105104. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Chomiak, J.; Nishiki, S.; Hasegawa, T. Unburned mixture fingers in premixed turbulent flames. Proc. Combust. Inst. 2015, 35, 1401–1408. [Google Scholar] [CrossRef]
- Chakraborty, N.; Katragadda, M.; Cant, R.S. Effects of Lewis number on turbulent kinetic energy transport in turbulent premixed combustion. Phys. Fluids 2011, 23, 075109. [Google Scholar] [CrossRef]
- Lumley, J.L. Introduction to Prediction Methods for Turbulent Flow; Lecture Series; Von Karman Institute: Sint-Genesius-Rode, Belgium, 1975. [Google Scholar]
- Mansour, N.N.; Kim, J.; Moin, P. Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 1988, 194, 15–44. [Google Scholar] [CrossRef]



| Case | Da | Ka | ||||
|---|---|---|---|---|---|---|
| A | 0.7 | 14.0 | 5.6 | 227 (91) | 20.0 (8.0) | 0.75 (1.19) |
| B | 5.0 | 14.0 | 5.6 | 1623 (649) | 2.8 (1.12) | 14.4 (22.75) |
| C | 14.0 | 4.0 | 1.6 | 1298 (519) | 0.29 (0.12) | 126 (199.0) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, N.; Ghai, S.K.; Im, H.G. Anisotropy of Reynolds Stresses and Their Dissipation Rates in Lean H2-Air Premixed Flames in Different Combustion Regimes. Energies 2024, 17, 5325. https://doi.org/10.3390/en17215325
Chakraborty N, Ghai SK, Im HG. Anisotropy of Reynolds Stresses and Their Dissipation Rates in Lean H2-Air Premixed Flames in Different Combustion Regimes. Energies. 2024; 17(21):5325. https://doi.org/10.3390/en17215325
Chicago/Turabian StyleChakraborty, Nilanjan, Sanjeev Kumar Ghai, and Hong G. Im. 2024. "Anisotropy of Reynolds Stresses and Their Dissipation Rates in Lean H2-Air Premixed Flames in Different Combustion Regimes" Energies 17, no. 21: 5325. https://doi.org/10.3390/en17215325
APA StyleChakraborty, N., Ghai, S. K., & Im, H. G. (2024). Anisotropy of Reynolds Stresses and Their Dissipation Rates in Lean H2-Air Premixed Flames in Different Combustion Regimes. Energies, 17(21), 5325. https://doi.org/10.3390/en17215325







