Advancements in Key Technologies for Vibration Isolators Utilizing Electromagnetic Levitation
Abstract
:1. Introduction
2. Passive Isolators
2.1. Permanent Magnet Springs
2.1.1. Single-Pair Permanent Magnet Springs
2.1.2. Multiple-Pair Permanent Magnet Springs
2.1.3. Specially Shaped Permanent Magnet Springs
2.2. Planar Isolators
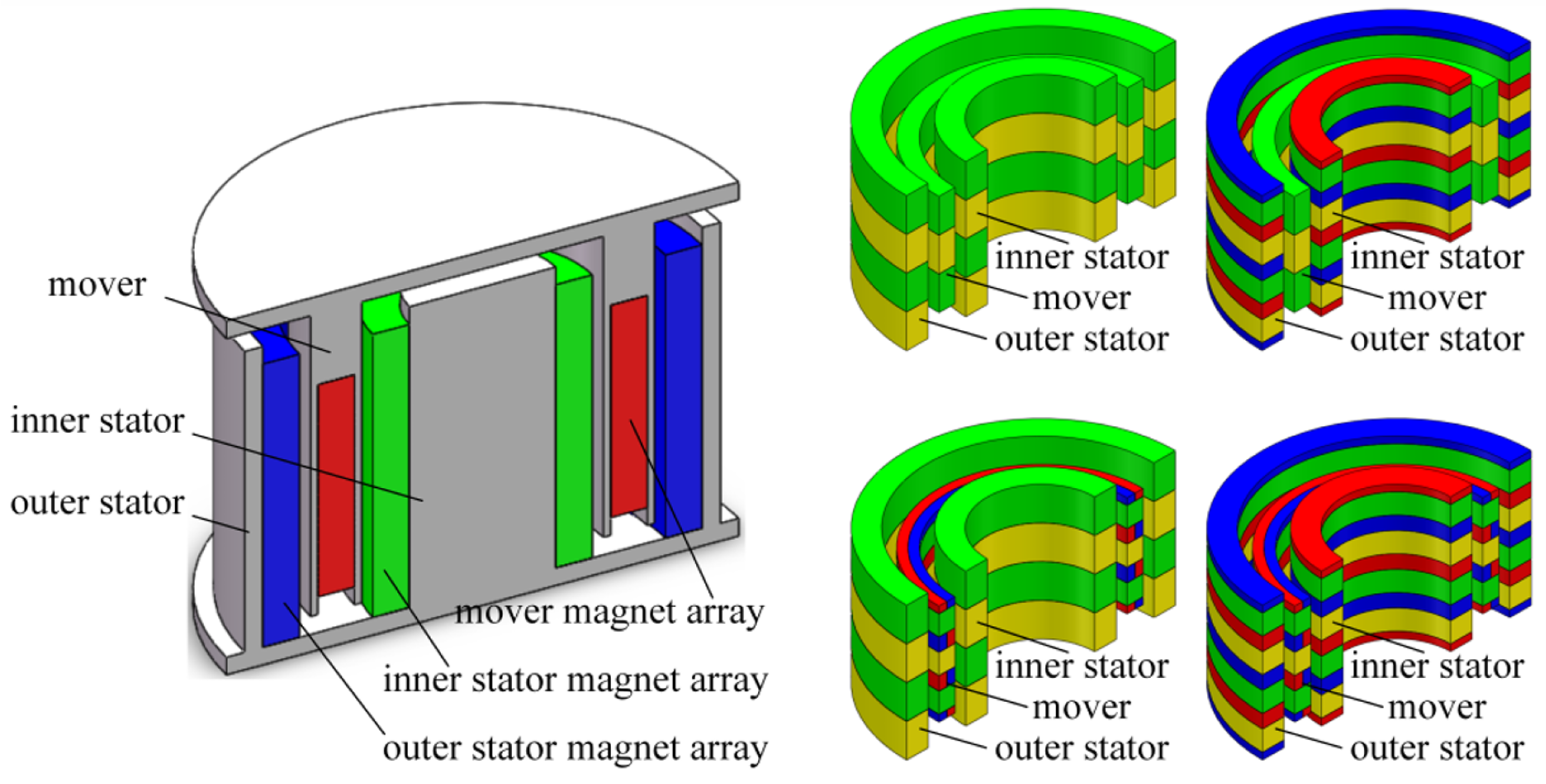
2.3. Permanent Magnet Array Isolators
2.3.1. Horizontal Air Gap Permanent Magnet Isolators
2.3.2. Vertical Air Gap Permanent Magnet Isolators
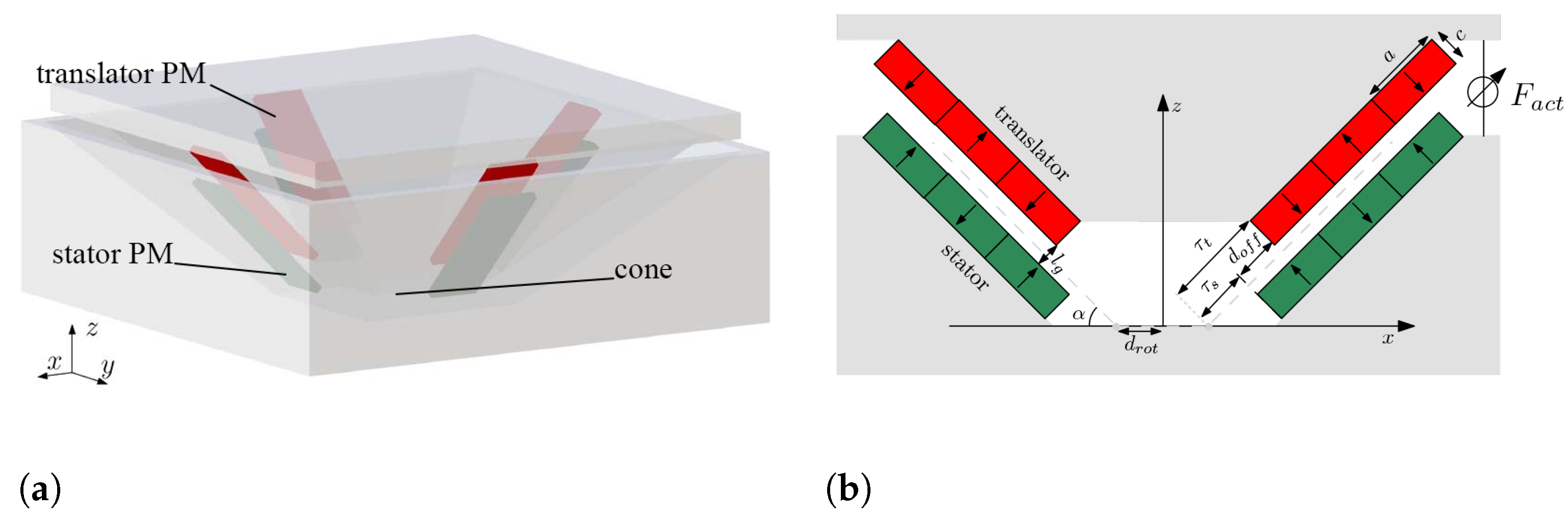
2.3.3. Inclined Air-Gap Permanent Magnet Isolators
2.4. Impact of Isolator Arrangement
2.5. Analytical Methods for Passive Isolators
2.5.1. Equivalent Magnetic Charge Method
2.5.2. Equivalent Current Method
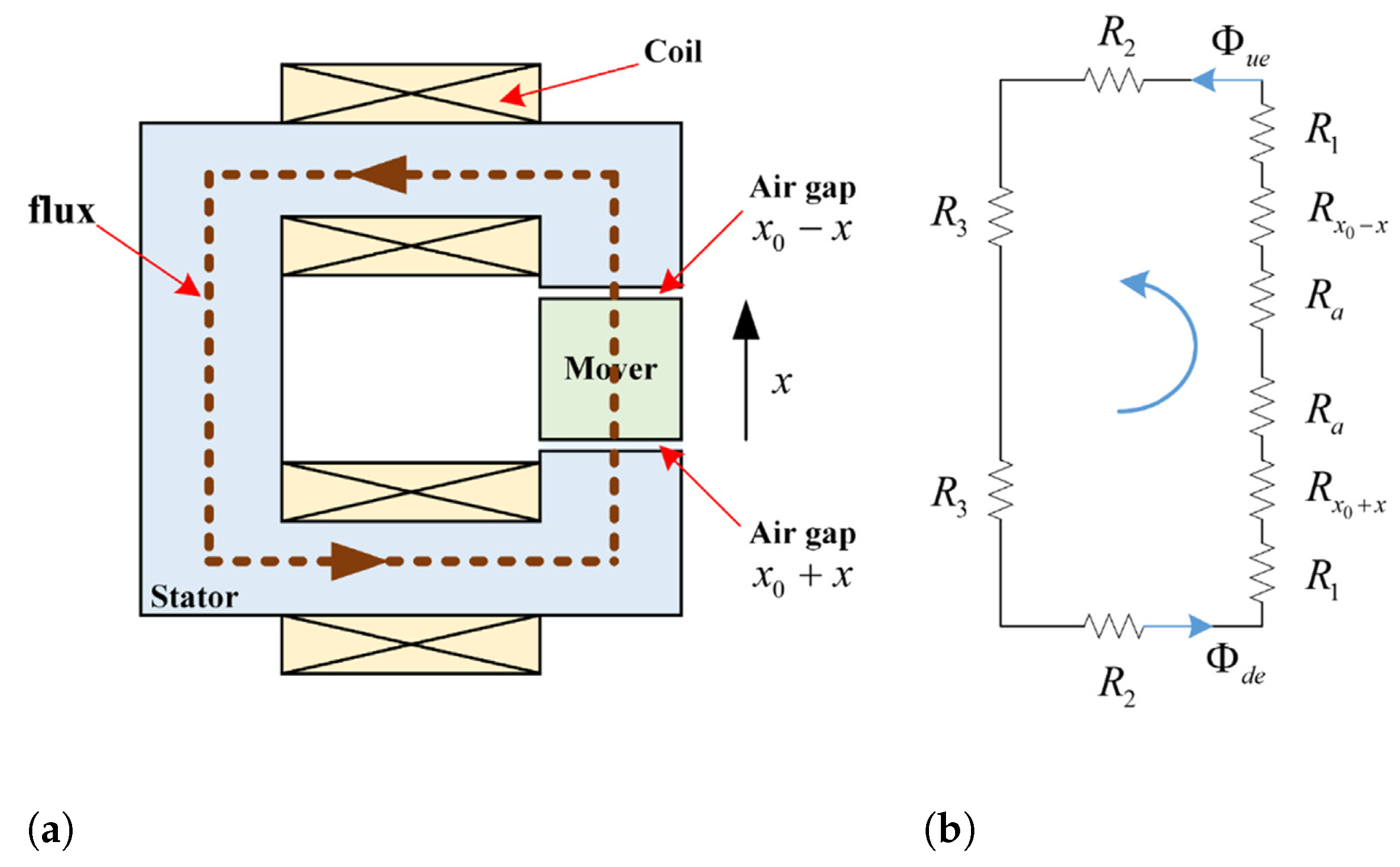
2.5.3. Equivalent Magnetic Circuit Method
2.5.4. Semi-Analytical Method
3. Active Isolators
3.1. Electromagnet Actuators
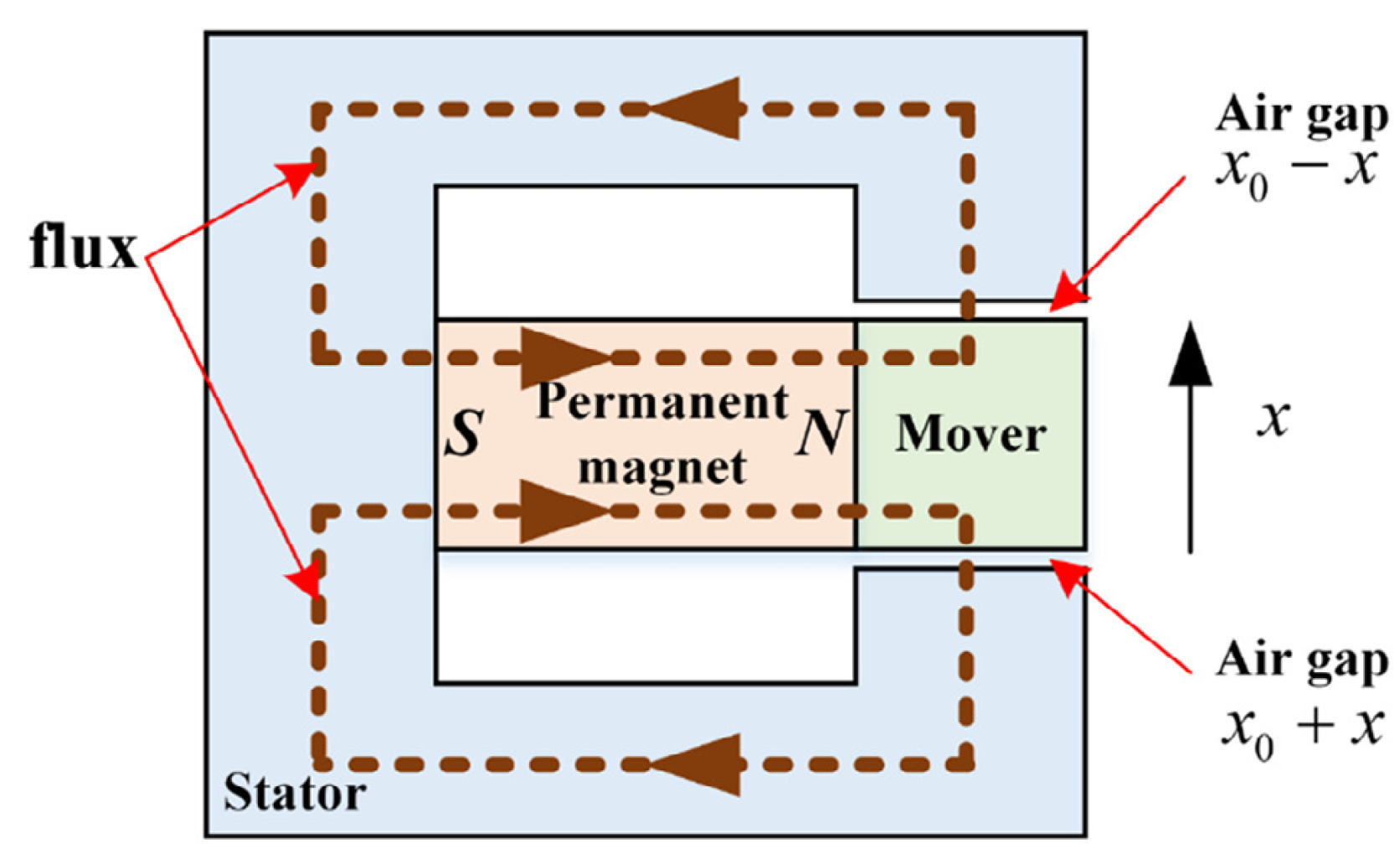
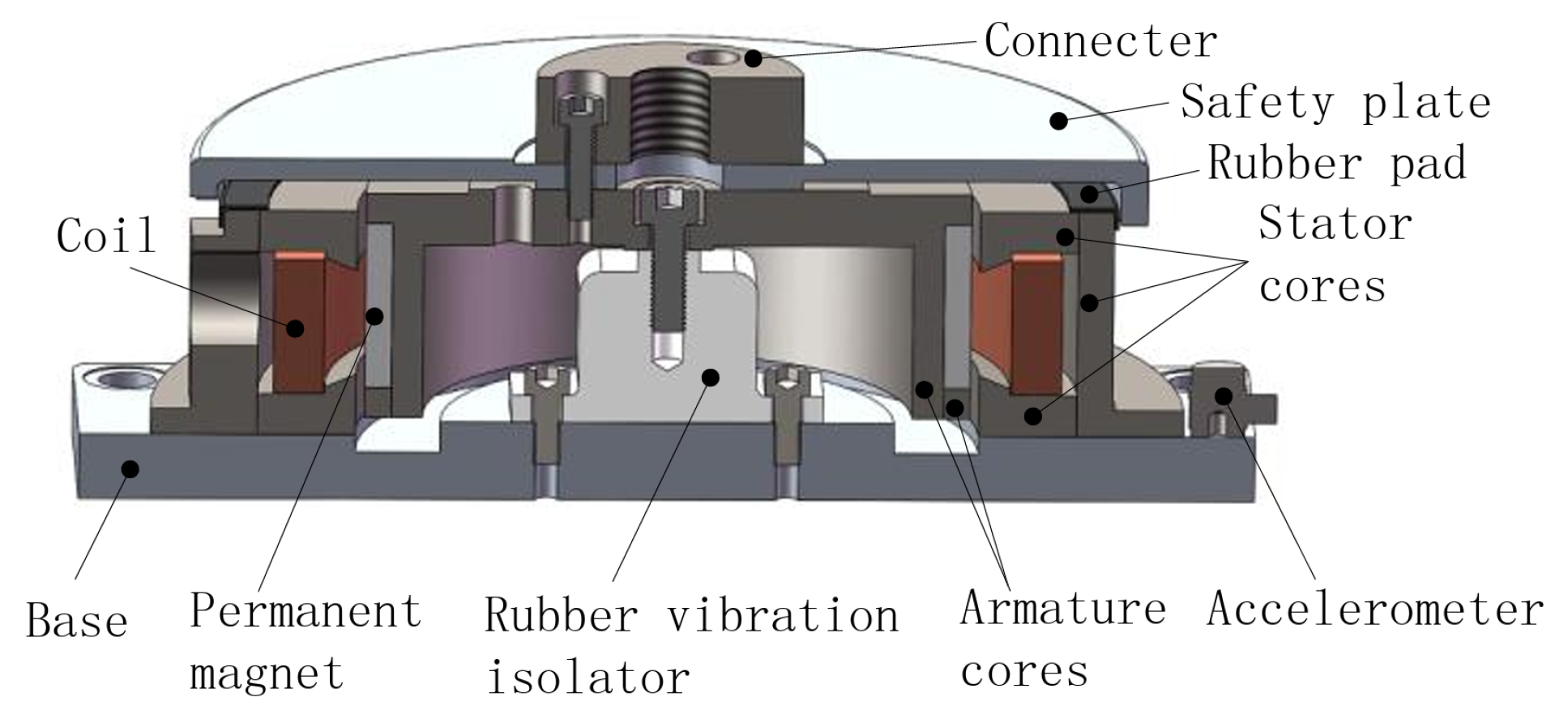
3.1.1. E-Shaped Electromagnet Actuators
Unilateral E-Shaped Electromagnet Actuators
Bilateral E-Shaped Electromagnet Actuators
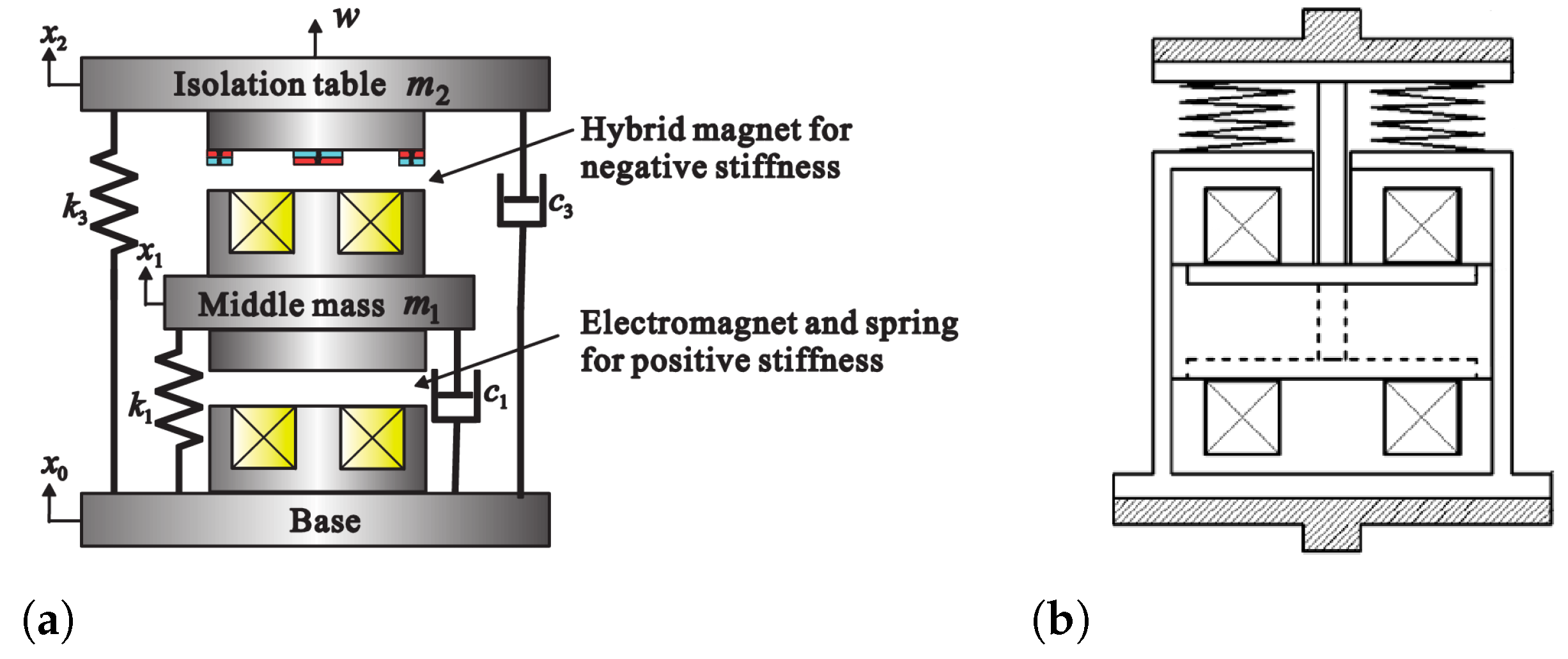
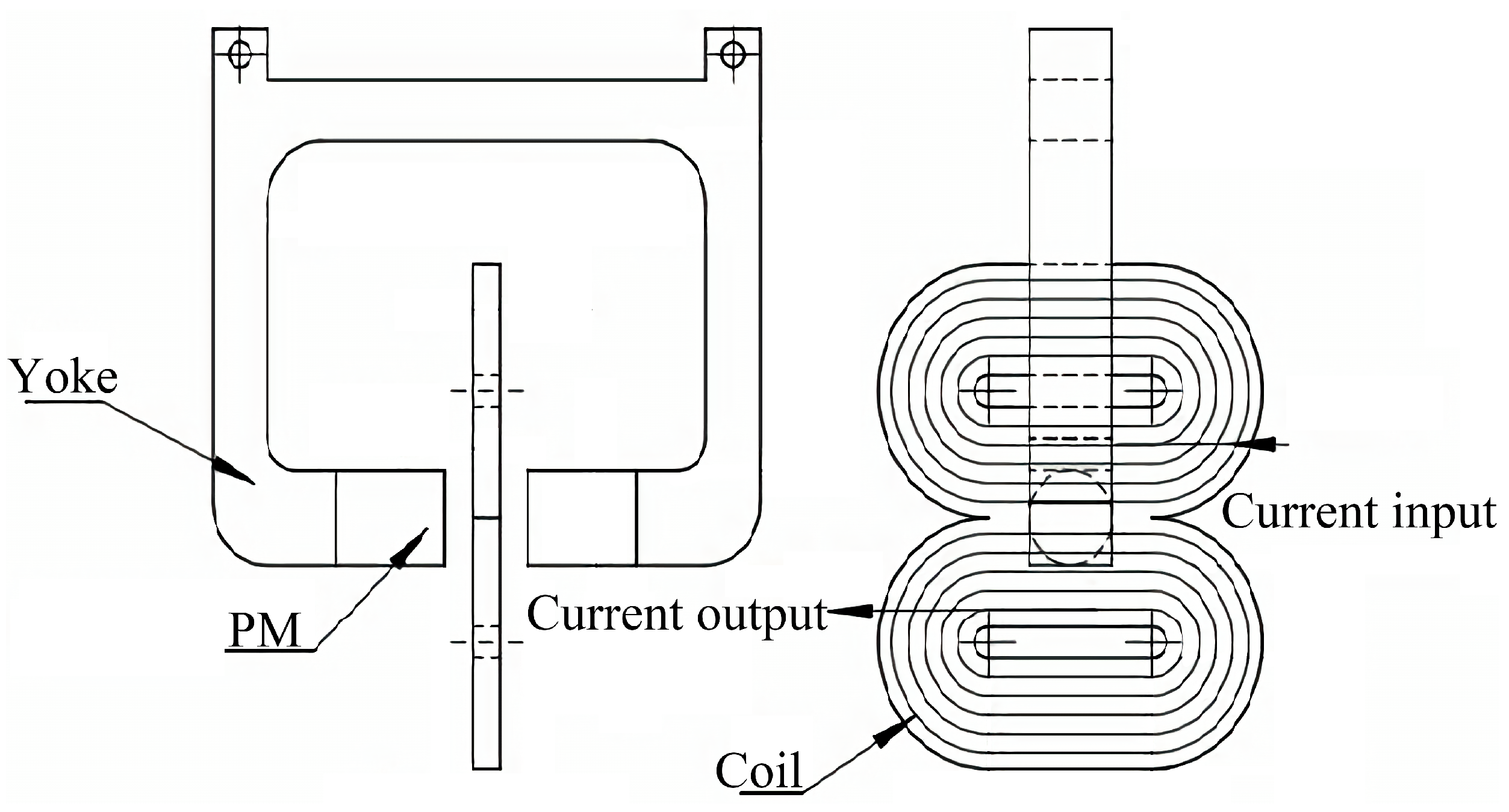
3.1.2. U-Shaped Electromagnet Actuators
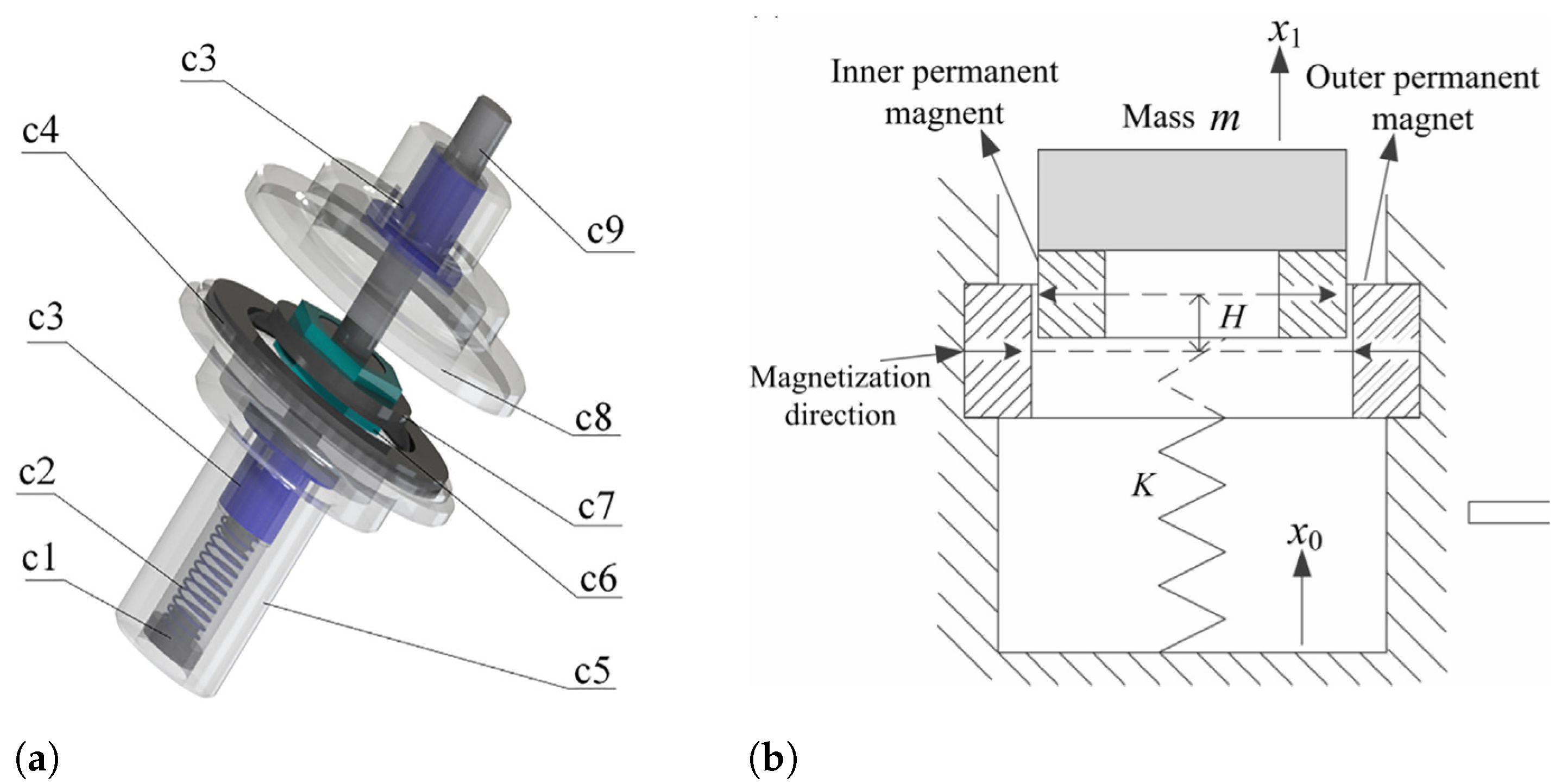
3.1.3. Cylindrical Electromagnet Actuators
3.1.4. Specially Shaped Electromagnet Actuators
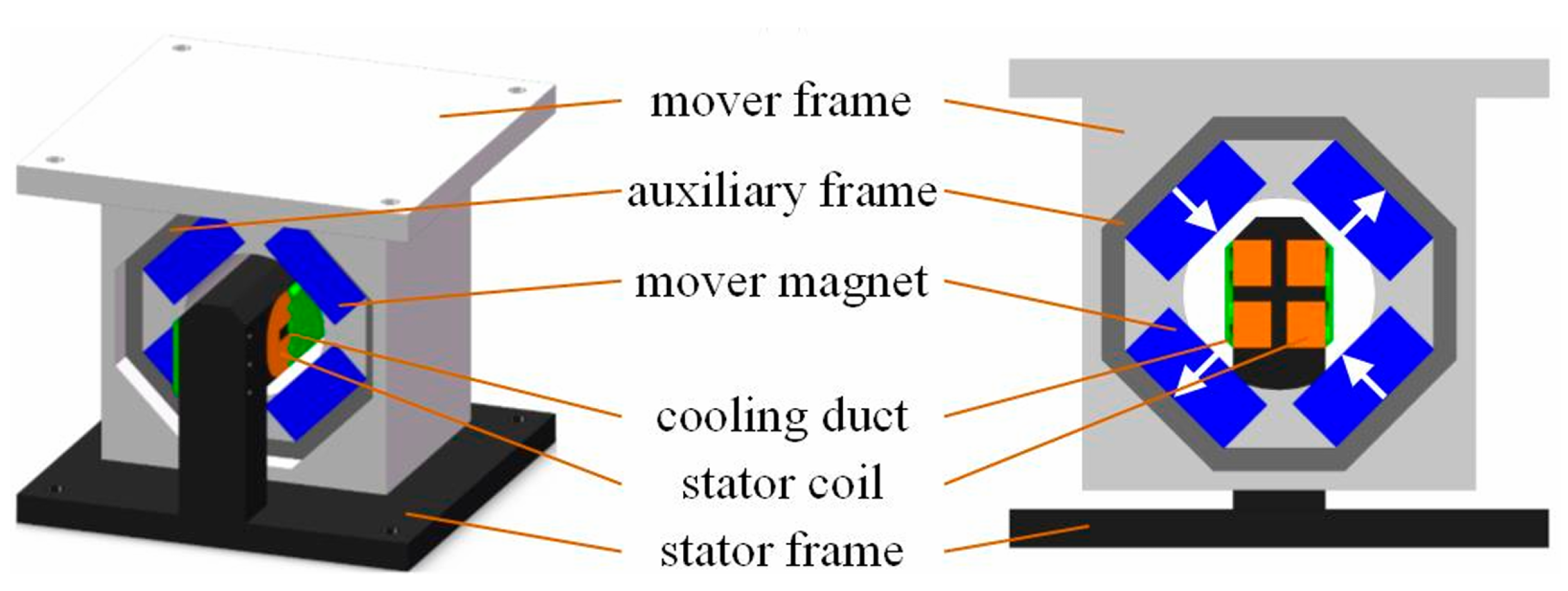
3.2. Linear Motors
3.2.1. Traditional Dual-Sided Voice Coil Motors
3.2.2. Special Voice Coil Motors
3.2.3. Other Configurations
3.3. Rotary Platforms
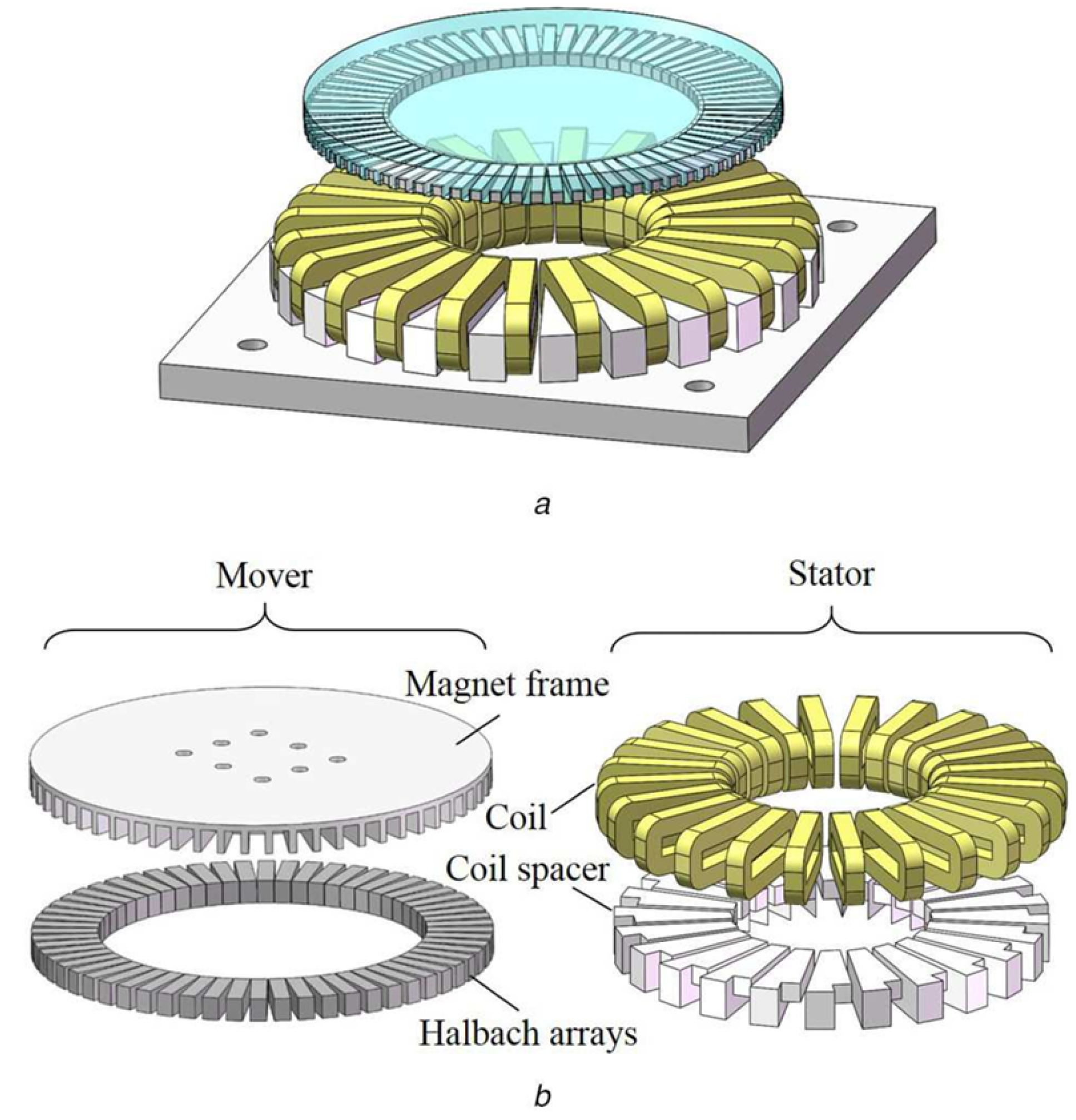
3.4. Planar Motors
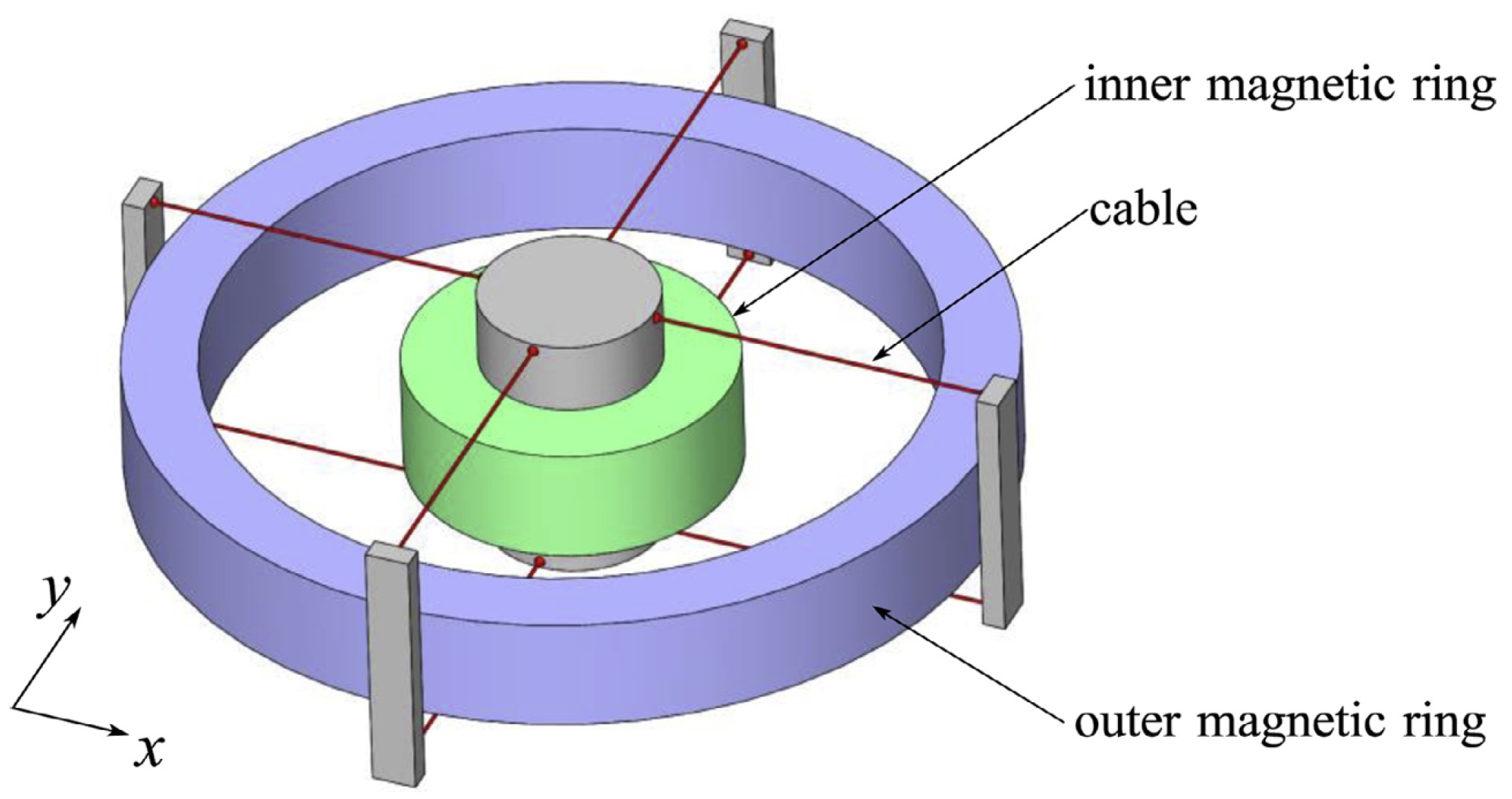
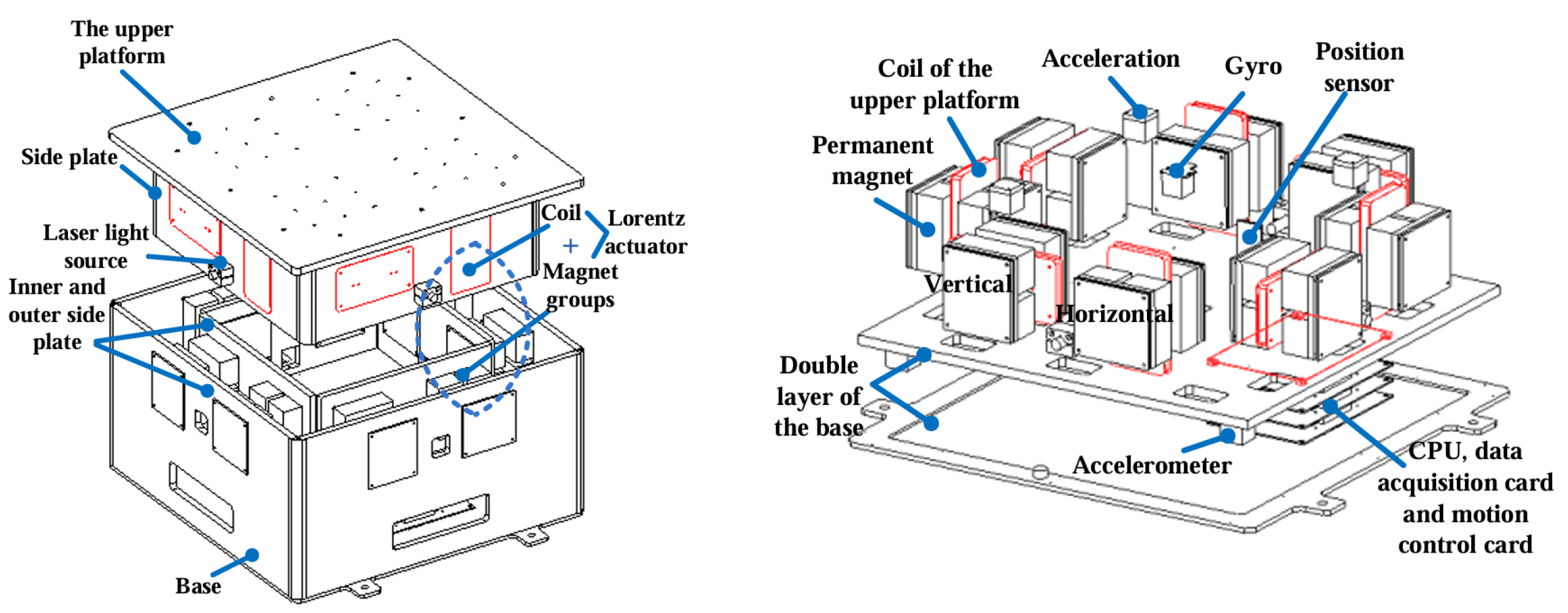
3.5. Multi-Degree-of-Freedom Actuators
3.5.1. Single-Degree-of-Freedom Superposition
3.5.2. Multi-Degree-of-Freedom Superposition
4. Summary
4.1. Passive Isolators
4.2. Active Isolators
5. Challenges and Developments
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PM | permanent magnet |
| PMS | permanent magnet spring |
| MS | magnet spring |
| PS | positive stiffness |
| NS | negative stiffness |
| QZS | quasi-zero stiffness |
| HSLD | high static low dynamic |
| DOF | degree-of-freedom |
| FEM | finite element method |
References
- Li, Z.; Li, D.; Lu, Y.; Tang, C. Analysis on Vibration Control of a Large-Span Pedestrian Suspension Bridge Based on a Multiple Tuned Mass Damper System. Noise Vib. Worldw. 2019, 50, 56–63. [Google Scholar] [CrossRef]
- Jiang, L.; Cheng, R.; Zhang, H.; Ma, K. Human-Induced-Vibration Response Analysis and Comfort Evaluation Method of Large-Span Steel Vierendeel Sandwich Plate. Buildings 2022, 12, 1228. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.J.; Oseth, O.; Rønnquist, A. Wind Deflection Analysis of Railway Catenary Under Crosswind Based on Nonlinear Finite Element Model and Wind Tunnel Test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Tsunashima, H.; Hirose, R. Condition Monitoring of Railway Track from Car-Body Vibration Using Time-Frequency Analysis. Veh. Syst. Dyn. 2022, 60, 1170–1187. [Google Scholar] [CrossRef]
- Azhar, A.S.; Kudus, S.A.; Jamadin, A.; Mustaffa, N.K.; Sugiura, K. Recent Vibration-Based Structural Health Monitoring on Steel Bridges: Systematic Literature Review. Ain Shams Eng. J. 2024, 15, 102501. [Google Scholar] [CrossRef]
- Tao, Y.; Rui, X.T.; Zhang, J.S.; Yang, F.F. Simulation of vibration characteristics of IMU with controllable magnetorheological isolation system. Multibody Syst. Dyn. 2020, 59, 1–20. [Google Scholar] [CrossRef]
- Hol, S.A.J.; Lomonova, E.; Vandenput, A.J.A. Design of a magnetic gravity compensation system. Precis. Eng. 2006, 30, 265–273. [Google Scholar] [CrossRef]
- Choi, Y.M.; Lee, M.G.; Gweon, D.G.; Jeong, J. A new magnetic bearing using Halbach magnet arrays for a magnetic levitation stage. Rev. Sci. Instrum. 2009, 80, 045106. [Google Scholar] [CrossRef]
- Yang, P. Research on Six-Degree-of-Freedom Microgravity Simulation Experimental Platform. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2014. [Google Scholar]
- Luo, H.T.; Fan, C.H.; Li, Y.X.; Li, Y.X.; Liu, G.M.; Yu, C.S. Design and experiment of micro-vibration isolation system for optical satellite. Eur. J. Mech. A-Solids 2023, 97, 13. [Google Scholar] [CrossRef]
- Yang, P.; Wu, H.T.; Yang, X.L.; Chen, B. Research on Six-Degree-of-Freedom Microgravity Simulation Platform. J. Mech. Des. Manuf. 2015, 3, 5–9. [Google Scholar]
- Zuo, B.; Liu, J.G.; Li, Y.M. Dynamics Modeling of Parallel Active Vibration Isolation System for Space Station Scientific Experiment Platform. J. Mech. Des. Manuf. 2014, 3, 199–203. [Google Scholar]
- Li, H.Y.; Cheng, Z.; Zhao, D.N.; Wang, H.W.; Li, D.Y.; Zhang, J.B.; Song, X.D.; Zhao, L.N. Research on Multi-Degree-of-Freedom Microgravity Simulation Deployment Test System Based on Suspension and Air-Floating Methods. J. Eng. Des. 2020, 27, 508–515. [Google Scholar]
- Zhang, H.; Kou, B.Q.; Zhou, Y.H.; Liu, Y.J.; Ge, Q.W.; Shao, Y. Modeling and Analysis of a Large-Load Magnetic Levitation Gravity Compensator. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
- Zhang, H.; Kou, B.Q.; Jin, Y.X.; Zhang, H.L.; Zhou, Y.H. Analysis and Optimization of an Electromagnetic Actuator with Passive Gravity Compensation. In Proceedings of the 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016. [Google Scholar]
- Zhang, H.; Kou, B.Q.; Jin, Y.X.; Zhang, H.L. Modeling and Analysis of a New Cylindrical Magnetic Levitation Gravity Compensator with Low Stiffness for the 6-DOF Fine Stage. IEEE Trans. Ind. Electron. 2015, 62, 3629–3639. [Google Scholar] [CrossRef]
- Janssen, J.L.G.; Paulides, J.J.H.; Lomonova, E.A.; Delinchant, B.; Yonnet, J.P. Design study on a magnetic gravity compensator with unequal magnet arrays. Mechatronics 2013, 23, 197–203. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.X.; Wang, K.; Xu, D.L.; Wen, G.L. Design and experimental study of a compact quasi-zero-stiffness isolator using wave springs. Sci. China Technol. Sci. 2021, 64, 2255–2271. [Google Scholar] [CrossRef]
- He, W.F.; Qiao, J.B.; Xu, H.; Huang, J.L. Experiment investigation and dynamic responses of three-dimensional isolation system with high-static-low-dynamic stiffness. Soil Dyn. Earthq. Eng. 2023, 165, 107679. [Google Scholar] [CrossRef]
- Liu, Y.J.; Liu, J.; Pan, G.; Huang, Q.G. Modeling and analysis of a metal rubber vibration isolation system considering the nonlinear stiffness characteristics. Rev. Sci. Instrum. 2023, 94, 015105. [Google Scholar] [CrossRef]
- Lin, D.Z.; Yang, F.; Gong, D.; Li, R.H. A new vibration isolator integrating tunable stiffness-damping and active driving properties based on radial-chains magnetorheological elastomer. Mech. Syst. Signal Process. 2023, 183, 109633. [Google Scholar] [CrossRef]
- Yuan, S.J.; Sun, Y.; Wang, M.; Ding, J.H.; Zhao, J.L.; Huang, Y.N.; Peng, Y.; Xie, S.R.; Luo, J.; Pu, H.Y.; et al. Tunable negative stiffness spring using Maxwell normal stress. Int. J. Mech. Sci. 2021, 193, 106127. [Google Scholar] [CrossRef]
- Tang, J.; Yang, Y.; Li, Y.H.; Cao, D.Q. A 6-DOF micro-vibration isolation platform based on the quasi-zero-stiffness isolator. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2021, 235, 6019–6035. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, Y.; Xu, D.F.; Hu, J.C.; Min, W.; Pang, L.C.l. A negative stiffness vibration isolator using magnetic spring combined with rubber membrane. J. Mech. Sci. Technol. 2013, 27, 813–824. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Q.; Xu, D.F.; Zhang, M. Modeling of Axial Magnetic Force and Stiffness of Ring-Shaped Permanent-Magnet Passive Vibration Isolator and Its Vibration Isolating Experiment. IEEE Trans. Magn. 2012, 48, 2228–2238. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Q.; Xu, D.F.; Hu, C.X.; Zhang, M. Modeling and analysis of a negative stiffness magnetic suspension vibration isolator with experimental investigations. Rev. Sci. Instrum. 2012, 83, 095108. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Xu, D.F.; Hu, J.C.; Hao, L. A Low Frequency Permanent Magnet Passive Vibration Isolator. Adv. Mater. Res. 2012, 586, 328–336. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.X.; Xu, D.L.; Ouyang, H.J. Design and experimental investigation of ultra-low frequency vibration isolation during neonatal transport. Mech. Syst. Signal Process. 2020, 139, 106633. [Google Scholar] [CrossRef]
- Zhou, J.X.; Wang, K.; Xu, D.L.; Ouyang, H.J.; Fu, Y.M. Vibration isolation in neonatal transport by using a quasi-zero-stiffness isolator. J. Vib. Control 2018, 24, 3278–3291. [Google Scholar] [CrossRef]
- Zheng, Y.S.; Zhang, X.N.; Luo, Y.J.; Yan, B.; Ma, C.C. Design and experiment of a high-static-low-dynamic stiffness isolator using a negative stiffness magnetic spring. J. Sound Vib. 2016, 360, 31–52. [Google Scholar] [CrossRef]
- Wang, S.; Xin, W.P.; Ning, Y.H.; Li, B.; Hu, Y. Design, Experiment, and Improvement of a Quasi-Zero-Stiffness Vibration Isolation System. Appl. Sci. 2020, 10, 2273. [Google Scholar] [CrossRef]
- Dong, G.X.; Ma, C.C.; Zhang, F.; Luo, Y.J.; Bi, C.X. Non-resonant response of the novel airborne photoelectric quasi-zero stiffness platform with friction damping. Int. J. Appl. Electrom. 2020, 64, 315–324. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Chen, S.H.; Xia, D.; He, J.J.; Zhang, P. The design of negative stiffness spring for precision vibration isolation using axially magnetized permanent magnet rings. J. Vib. Control 2019, 25, 2667–2677. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Bardaweel, H. Design guidelines and parametric study of nonlinear magnetic springs for vibration systems. In Proceedings of the Energy Harvesting and Storage: Materials, Devices, and Applications X, Online, 27 April–8 May 2020; Volume 11387. [Google Scholar]
- Mofidian, S.M.M.; Bardaweel, H. Displacement transmissibility evaluation of vibration isolation system employing nonlinear-damping and nonlinear-stiffness elements. J. Vib. Control 2018, 24, 4247–4259. [Google Scholar] [CrossRef]
- Kamaruzaman, N.A.; Robertson, W.S.P.; Ghayesh, M.H.; Cazzolato, B.S.; Zander, A.C. Improving Passive Stability of a Planar Quasi-zero Stiffness Magnetic Levitation System via Lever Arm. In Proceedings of the 2018 IEEE International Magnetic Conference (Intermag), Singapore, 23–27 April 2018. [Google Scholar]
- Zhu, T.; Cazzolato, B.; Robertson, W.S.P.; Zander, A. Vibration isolation using six degree-of-freedom quasi-zero stiffness magnetic levitation. J. Sound Vib. 2015, 358, 48–73. [Google Scholar] [CrossRef]
- Dong, G.X.; Zhang, X.N.; Luo, Y.J.; Zhang, Y.H. Investigation on the design of magnetic spring-beam vibration isolator with negative stiffness characteristic. Int. J. Appl. Electrom. 2016, 52, 1321–1329. [Google Scholar] [CrossRef]
- Sun, X.T.; Wang, F.; Xu, J. Analysis, design and experiment of continuous isolation structure with Local Quasi-Zero-Stiffness property by magnetic interaction. Int. J. Non-Linear Mech. 2019, 116, 289–301. [Google Scholar] [CrossRef]
- Dong, G.X.; Zhang, X.N.; Xie, S.L.; Yan, B.; Luo, Y.J. Simulated and experimental studies on a high-static-low-dynamic stiffness isolator using magnetic negative stiffness spring. Mech. Syst. Signal Process. 2017, 86, 188–203. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.Y.; Zhao, C.X.; Wu, C.Y.; Wang, K.; Wang, P.F. A vari-stiffness nonlinear isolator with magnetic effects: Theoretical modeling and experimental verification. Int. J. Mech. Sci. 2018, 148, 745–755. [Google Scholar] [CrossRef]
- Shin, K. On the Performance of a Single Degree-of-Freedom High-Static-Low-Dynamic Stiffness Magnetic Vibration Isolator. Int. J. Precis. Eng. Manuf. 2014, 15, 439–445. [Google Scholar] [CrossRef]
- Li, H.; Zhang, J. Design and analysis of a magnetic QZS vibration isolator. In Proceedings of the Mechanical Engineering, Materials Science and Civil Engineering II, Beijing, China, 25–26 October 2013; Volume 470, pp. 484–488. [Google Scholar]
- Zhang, F.; Shao, S.B.; Tian, Z.; Xu, M.L.; Xie, S.L. Active-passive hybrid vibration isolation with magnetic negative stiffness isolator based on Maxwell normal stress. Mech. Syst. Signal Process. 2019, 123, 244–263. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, M.L.; Shao, S.B.; Xie, S.L. A new high-static-low-dynamic stiffness vibration isolator based on magnetic negative stiffness mechanism employing variable reluctance stress. J. Sound Vib. 2020, 476, 115322. [Google Scholar] [CrossRef]
- Zheng, Y.S.; Zhang, X.N.; Ma, C.C.; Zhang, Z.F.; Zhang, S. An ultra-low frequency pendulum isolator using a negative stiffness magnetic spring. Int. J. Appl. Electrom. 2016, 52, 1313–1320. [Google Scholar] [CrossRef]
- Liu, C.R.; Zhao, R.; Yu, K.P.; Liao, B.P. In-plane quasi-zero-stiffness vibration isolator using magnetic interaction and cables: Theoretical and experimental study. Appl. Math. Model. 2021, 96, 497–522. [Google Scholar] [CrossRef]
- Zhou, Y.H. Fundamental Research on Low-Stiffness Passive Magnetic Levitation Vibration Isolation Unit. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Kou, B.; Zhou, Y.; Yang, X.; Xing, F.; Zhang, H. Electromagnetic and Mechanical Characteristics Analysis of a Flat-Type Vertical-Gap Passive Magnetic Levitation Vibration Isolator. Shock Vib. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Li, Q.; Li, S.; Li, F.X.; Xu, D.F.; He, Z.Y. Analysis and Experiment of Vibration Isolation Performance of a Magnetic Levitation Vibration Isolator with Rectangular Permanent Magnets. J. Vib. Eng. Technol. 2020, 8, 751–760. [Google Scholar] [CrossRef]
- Hsieh, W.H.; Zhou, Y.; Kou, B.; Luo, J.; Zhang, H. Research on typical topologies of a tubular horizontal-gap passive magnetic levitation vibration isolator. MATEC Web Conf. 2017, 119, 01013. [Google Scholar]
- Zhang, H. Fundamental Research on Multi-Degree-of-Freedom Magnetic Levitation Micro-Motion Platform. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]
- Li, J.Z.; Liu, Q.; Wang, L.; Wang, S.T.; Wang, J. Considering Operating Point Variation in 3-D Analytical Charge Model Used for Design of Low-Stiffness Permanent Magnet Vibration Isolator. IEEE Trans. Ind. Electron. 2020, 67, 6732–6741. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Kou, B.Q.; Wang, L.Q.; Xing, F. Modeling and Analysis of a Maglev Vibration Isolation Unit Using Rectangle Halbach Permanent Magnet Array. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 1711–1714. [Google Scholar]
- Li, J.Z.; Wang, L.; Liu, Q.; Wang, S.T.; Zhang, Z. Low stiffness magnetic vibration isolator based on Halbach permanent magnet array. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 5543–5547. [Google Scholar]
- Shan, J.Z.; Shi, Z.G.; Gong, N.; Shi, W.X. Performance improvement of base isolation systems by incorporating eddy current damping and magnetic spring under earthquakes. Struct. Control Health Monit. 2020, 27, 6. [Google Scholar] [CrossRef]
- van Casteren, D.T.E.H.; Paulides, J.J.H.; Janssen, J.L.G.; Lomonova, E.A. Analytical Force, Stiffness, and Resonance Frequency Calculations of a Magnetic Vibration Isolator for a Microbalance. IEEE Trans. Ind. Appl. 2015, 51, 204–210. [Google Scholar] [CrossRef]
- van Casteren, D.T.E.H.; Paulides, J.J.H.; Janssen, J.L.G.; Lomonova, E.A. Analytical Stiffness Calculations of a Cone-Shaped Magnetic Vibration Isolator for a Micro Balance. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2013; pp. 1184–1190. [Google Scholar]
- Zhou, Y.H. Fundamental Research on Active-Passive Hybrid Magnetic Levitation Vibration Isolation Platform. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Fang, H.N. Research on the Arrangement Scheme of Magnetic Levitation Isolator for Multi-Degree-of-Freedom Vibration Isolation System. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2013. [Google Scholar]
- Yang, B.B.; Hu, Y.F.; Fang, H.N.; Song, C.S. Research on arrangement scheme of magnetic suspension isolator for multi-degree freedom vibration isolation system. J. Ind. Inf. Integr. 2017, 6, 47–55. [Google Scholar] [CrossRef]
- Ning, X.G.; Zhang, Q.H.; Zhang, Z.X. Structural Design of a Gas-Magnetic Hybrid Vibration Isolation Device. J. Mech. 2019, 46, 76–80. [Google Scholar]
- Yonnet, J. 3D analytical calculation of the forces exerted between two cuboidal magnets. IEEE Trans. Magn. 1984, 20, 1962–1964. [Google Scholar]
- Robertson, W.S.; Kidner, M.R.F.; Cazzolato, B.S.; Zander, A.C. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation. J. Sound Vib. 2009, 326, 88–103. [Google Scholar] [CrossRef]
- Charpentier, J.F.; Lemarquand, G. Calculation of ironless permanent magnet couplings using semi-numerical magnetic pole theory method. Compel 2001, 20, 72–89. [Google Scholar] [CrossRef]
- Allag, H.; Yonnet, J.P.; Latreche, M.E.H. 3D Analytical Calculation of Forces between Linear Halbach-Type Permanent-Magnet Arrays. In Proceedings of the 8th International Symposium on Advanced Electromechanical Motion Systems (ELECTROMOTION 2009)/EPE Chapter Electric Drives Joint Symposium, Lille, France, 1–3 July 2009. [Google Scholar]
- Allag, H.; Yonnet, J.P. 3-D Analytical Calculation of the Torque and Force Exerted Between Two Cuboidal Magnets. IEEE Trans. Magn. 2009, 45, 3969–3972. [Google Scholar] [CrossRef]
- Allag, H.; Yonnet, J.P.; Latreche, M.E.H. Analytical calculation of the torque exerted between two perpendicularly magnetized magnets. J. Appl. Phys. 2011, 109, 07E701. [Google Scholar] [CrossRef]
- Rovers, J.M.M.; Jansen, J.W.; Lomonova, E.A.; Ronde, M.J.C. Calculation of the Static Forces Among the Permanent Magnets in a Halbach Array. IEEE Trans. Magn. 2009, 45, 4372–4375. [Google Scholar] [CrossRef]
- Janssen, J.L.G.; Paulides, J.J.H.; Compter, J.C.; Lomonova, E.A. Three-Dimensional Analytical Calculation of the Torque Between Permanent Magnets in Magnetic Bearings. IEEE Trans. Magn. 2010, 46, 1748–1751. [Google Scholar] [CrossRef]
- Janssen, J.L.G.; Paulides, J.J.H.; Lomonova, E.A. 3-D Analytical Calculation of the Torque Between Perpendicular Magnetized Magnets in Magnetic Suspensions. IEEE Trans. Magn. 2011, 47, 4286–4289. [Google Scholar] [CrossRef]
- Janssen, J.L.G. Extended Analytical Charge Modeling for Permanent Magnet Based Devices: Practical Application to the Interactions in a Vibration Isolation System. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2011. [Google Scholar]
- Kremers, M.F.J.; Paulides, J.J.H.; Ilhan, E.; Janssen, J.L.G.; Lomonova, E.A. Relative Permeability in a 3D Analytical Surface Charge Model of Permanent Magnets. IEEE Trans. Magn. 2013, 49, 2299–2302. [Google Scholar] [CrossRef]
- Tang, W.B.; Xiao, L.Y.; Xia, D.; Yang, W.H.; Wang, Z. 2-D and 3-D Analytical Calculation of the Magnetic Field and Levitation Force Between Two Halbach Permanent Magnet Arrays. IEEE Trans. Magn. 2021, 57, 8300208. [Google Scholar] [CrossRef]
- Bao, Y.Y.; Zheng, J.; Sun, R.X.; Deng, Z.G. Magnetic force characteristics enhancement by a novel permanent magnetic levitation (PML) analysis method for hybrid maglev. J. Magn. Magn. Mater. 2021, 529, 167888. [Google Scholar] [CrossRef]
- Jansen, J.W.; Janssen, J.L.G.; Rovers, J.M.M.; Paulides, J.J.H.; Lomonova, E.A. (Semi) Analytical Models for the Design of High-Precision Permanent Magnet Actuators. Int. Compumag Soc. Newsl. 2009, 16, 4–17. [Google Scholar]
- Elies, P.; Lemarquand, G. Comparison of the torque of flat airgap synchronous couplings versus the magnetization direction of the magnets. IEEE Trans. Magn. 1999, 35, 548–556. [Google Scholar] [CrossRef]
- Elies, P.; Lemarquand, G. Analytical optimization of the torque of a permanent-magnet coaxial synchronous coupling. IEEE Trans. Magn. 1998, 34, 2267–2273. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Deptula, A.; Urbanowicz, K.; Skackauskas, P.; Deptula, A.M.; Danilevicius, A.; Sukevicius, S.; Lapka, M. Research of Vibration Effects on a Hydraulic Valve in the Pressure Pulsation Spectrum Analysis. J. Mar. Sci. Eng. 2023, 11, 301. [Google Scholar] [CrossRef]
- Yang, J.; Xiong, Y.P.; Xing, J.T. Dynamics and power flow behaviour of a nonlinear vibration isolation system with a negative stiffness mechanism. J. Sound Vib. 2013, 332, 167–183. [Google Scholar] [CrossRef]
- Sun, X.; Jing, X.; Xu, J.; Cheng, L. Vibration isolation via a scissor-like structured platform. J. Sound Vib. 2014, 333, 2404–2420. [Google Scholar] [CrossRef]
- Zhang, B.; Dong, W.H.; Li, X.L.; Long, Z.Q. Design of Active-Passive Composite Vibration Isolation System of Magnetic Levitation and Spring Based on Fuzzy PID Control. In Proceedings of the Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 2381–2386. [Google Scholar]
- Raab, M.; Hutter, M.; Kazi, A.; Schinkoethe, W.; Gundelsweiler, B. Magnetically Levitated Linear Drive Using an Active Gravity Compensation Based on Hybrid Shape Memory Actuators. IEEE/ASME Trans. Mechatron. 2021, 26, 1380–1391. [Google Scholar] [CrossRef]
- Hoque, M.E.; Mizuno, T.; Ishino, Y.; Takasaki, M. A modified zero-power control and its application to vibration isolation system. J. Vib. Control 2012, 18, 1788–1797. [Google Scholar] [CrossRef]
- Mizuno, T.; Namai, M.; Takasaki, M.; Ishino, Y. Proposal of Magnetic Suspension with Elastic Ferromagnetic Substance for Vibration Isolation System. In Proceedings of the CACS International Automatic Control Conference (CACS), Pingtung, Taiwan, 12–15 November 2017. [Google Scholar]
- Shahadat, M.M.Z.; Mizuno, T.; Takasaki, M.; Ishino, Y. Parallel-Mechanism Based Vibration Isolation System Using Displacement Cancellation Control. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015. [Google Scholar]
- Hoque, M.E.; Mizuno, T.; Ishino, Y.; Takasaki, M. A three-axis vibration isolation system using modified zero-power controller with parallel mechanism technique. Mechatronics 2011, 21, 1055–1062. [Google Scholar] [CrossRef]
- Hoque, M.E.; Mizuno, T.; Kishita, D.; Takasaki, M.; Ishino, Y. Development of an Active Vibration Isolation System Using Linearized Zero-Power Control with Weight Support Springs. J. Vib. Acoust. 2010, 132, 041006. [Google Scholar] [CrossRef]
- Yu, X.W.; Liu, D.Z.; Wang, D.; Li, Y.; Yang, H. Optimal Design of Electromagnetic Actuators in Hybrid Vibration Isolation Systems. J. Nav. Eng. Univ. 2010, 22, 1–4. [Google Scholar]
- Sun, L.F. Design and Vibration Isolation Characteristics of Metal Mesh-Magnetic Levitation Isolator. Master’s Thesis, North University of China, Taiyuan, China, 2011. [Google Scholar]
- Duan, X.S. Dynamic Modeling and Self-Convergent Control of Magnetic Levitation Vibration Isolator. Master’s Thesis, University of Science and Technology of China, Hefei, China, 2010. [Google Scholar]
- Yang, Z.G.; Kong, X.R.; Xing, S.R. Exploration of Magnetic Suspension Technology used for Spacecraft Micro-vibration Isolation. In Proceedings of the 2014 International Conference on Mechatronics and Control (ICMC), Jinzhou, China, 3–5 July 2014; pp. 1545–1549. [Google Scholar]
- Meng, K.; Sun, Y.; Pu, H.Y.; Luo, J.; Yuan, S.J.; Zhao, J.L.; Xie, S.R.; Peng, Y. Development of Vibration Isolator with Controllable Stiffness Using Permanent Magnets and Coils. J. Vib. Acoust. 2019, 141, 1. [Google Scholar] [CrossRef]
- Chen, F. Vibration suppression with electromagnetic hybrid vibration isolators. In Proceedings of the 9th International Conference on Mechatronics and Manufacturing (ICMM 2018), Phuket, Thailand, 27–29 January 2018; p. 361. [Google Scholar]
- Su, P.; Wu, J.C.; Liu, S.Y.; Jiang, J. Study on the dynamics of two-degree-of-freedom system with variable stiffness magnetic isolator. J. Vibroeng. 2018, 20, 116–126. [Google Scholar] [CrossRef]
- Su, P.; Wu, J.C.; Liu, S.Y.; Fang, Y. A study of a nonlinear magnetic vibration isolator with quasi-zero-stiffness. J. Vibroeng. 2018, 20, 310–320. [Google Scholar] [CrossRef]
- Ma, J.G.; Shuai, C.G.; Li, Y. Mechanical Characteristics and Active Vibration Isolation Experimental Study of Magnetic Levitation-Airbag Hybrid Vibration Isolator. J. Vib. Shock 2018, 37, 198–204. [Google Scholar]
- Zhou, N.; Liu, K. A tunable high-static-low-dynamic stiffness vibration isolator. J. Sound Vib. 2010, 329, 1254–1273. [Google Scholar] [CrossRef]
- Ledezma-Ramirez, D.F.; Ferguson, N.S.; Brennan, M.J. An experimental switchable stiffness device for shock isolation. J. Sound Vib. 2012, 331, 4987–5001. [Google Scholar] [CrossRef]
- Su, K.H.; Pan, W.H. Design of Adaptive Fuzzy Magnetic Suspension Vibrator for Foot Robot. In Proceedings of the 2015 International Conference on Fuzzy Theory and Its Applications (iFUZZY), Yilan, Taiwan, 18–20 November 2015; pp. 127–132. [Google Scholar]
- Zhang, B.; Teng, Y.T.; Xing, L.L.; Wu, Q.; Cheng, L.N.; Zhang, T. The simulation of reference corner cube vibration isolation system of laser interference absolute gravimeter. Chin. J. Geophys. 2017, 60, 4221–4230. [Google Scholar]
- Jiang, Y.L.; Song, C.S.; Ding, C.M.; Xu, B.H. Design of magnetic-air hybrid quasi-zero stiffness vibration isolation system. J. Sound Vib. 2020, 477, 115346. [Google Scholar] [CrossRef]
- Xu, J.W.; Yang, X.F.; Li, W.; Zheng, J.Y.; Wang, Y.Q.; Fan, M.B. Research on semi-active vibration isolation system based on electromagnetic spring. Mech. Ind. 2020, 21, 101. [Google Scholar] [CrossRef]
- Chen, S.Q.; Wang, Y. Experimental study on active vibration isolation control based on magnetic suspension isolator. J. Southeast Univ. (Nat. Sci. Ed.) 2010, 40, 61–66. [Google Scholar]
- Chang, K.N.; Huang, K.Y. Development and Performance Study of A Magnetic-Aerostatic Vibration Isolation Platform. Proc. SPIE 2012, 8341, 62. [Google Scholar]
- Mofidian, S.M.M.; Bardaweel, H. Theoretical study and experimental identification of elastic-magnetic vibration isolation system. J. Intell. Mater. Syst. Struct. 2018, 29, 3550–3561. [Google Scholar] [CrossRef]
- Wu, Q.Q.; Yue, H.H.; Liu, R.Q.; Ding, L.; Deng, Z.Q. Parametric Design and Multiobjective Optimization of Maglev Actuators for Active Vibration Isolation System. Adv. Mech. Eng. 2014, 6, 215358. [Google Scholar] [CrossRef]
- Wu, Q.Q.; Liu, R.Q.; Yue, H.H.; Deng, Z.Q.; Guo, H.W. Design and Optimization of Magnetic Levitation Actuators for Active Vibration Isolation System. Adv. Mater. Res. 2013, 774–776, 168–171. [Google Scholar] [CrossRef]
- Kremers, M.F.J.; Paulides, J.J.H.; Janssen, J.L.G.; Lomonova, E.A. Design Considerations for Coreless Linear Actuators. IEEE Trans. Magn. 2013, 49, 2271–2274. [Google Scholar] [CrossRef]
- Janssen, J.L.G.; Paulides, J.; Encica, L.; Lomonova, E.A. High-performance moving-coil actuators with double-sided PM arrays: A design comparison. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2010. [Google Scholar]
- Kim, J.Y.; Ahn, D. Analysis of High Force Voice Coil Motors for Magnetic Levitation. Actuators 2020, 9, 133. [Google Scholar] [CrossRef]
- Lahdo, M.; Kovalev, S.; Strohla, T. Design and Analysis of a Linear Actuator for Contactless Positioning Systems. In Proceedings of the 2017 IEEE First Ukraine Conference on Electrical and Computer Engineering (Ukrcon), Kyiv, Ukraine, 29 May–2 June 2017; pp. 421–426. [Google Scholar]
- Ito, S.; Neyer, D.; Pirker, S.; Steininger, J.; Schitter, G. Atomic Force Microscopy Using Voice Coil Actuators for Vibration Isolation. In Proceedings of the 2015 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; pp. 470–475. [Google Scholar]
- Hong, D.P.; Hwang, H.Y.; Lee, M.Y.; Jo, Y.K.; Vu, D.T.; Lee, D.Y. New Electro-Magnetic Actuator for Active Vibration Isolators. Int. J. Precis. Eng. Manuf. 2015, 16, 209–212. [Google Scholar] [CrossRef]
- Zhou, Y.; Kou, B.; Zhang, H.; Zhang, L.; Wang, L.K. Design, Analysis and Test of a Hyperbolic Magnetic Field Voice Coil Actuator for Magnetic Levitation Fine Positioning Stage. Energies 2019, 12, 1830. [Google Scholar] [CrossRef]
- Zhou, Y.; Kou, B.; Zhang, H.; Luo, J.; Gan, L. Force Characteristic Analysis of a Linear Magnetic Bearing With Rhombus Magnet Array for Magnetic Levitation Positioning System. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Chen, C.H. Research on Dynamics and Control System of Magnetic Suspension Microgravity Vibration Isolation System. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2019. [Google Scholar]
- Zhao, Y.M.; Cui, J.N.; Zou, L.M.; Cheng, Z.Y.; Lu, Y.S. High linearity electromagnetic actuator using double closed rectangular magnetic circuits for active vibration isolation. In Proceedings of the 2019 14th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Changsha, China, 1–3 November 2019; pp. 58–64. [Google Scholar]
- Meng, K.; Gu, Y.; Ma, J.H.; Liu, X.D.; Geng, X.Q.; Liu, Y.X.; Liu, X.H.; Zhang, H.M.; Shao, F.X. Controllable electromagnetic negative stiffness spring for vibration isolator: Design, analyses and experimental verification. Int. J. Appl. Electromagn. 2021, 65, 781–802. [Google Scholar] [CrossRef]
- Zheng, T.; Lu, X.; Xu, F.Q.; Xu, X.Z. Optimisation method of magnetic levitation actuator for rotary table. IET Electr. Power Appl. 2020, 14, 893–900. [Google Scholar] [CrossRef]
- Dyck, M.; Lu, X.D.; Altintas, Y. Magnetically Levitated Rotary Table With Six Degrees of Freedom. IEEE/ASME Trans. Mechatron. 2017, 22, 530–540. [Google Scholar] [CrossRef]
- Wang, W.R.; Yang, G.J.; Yan, J.H.; Ge, H.L.; Zhi, P.F. Magnetic levitation planar motor and its adaptive contraction backstepping control for logistics system. Adv. Mech. Eng. 2021, 13, 168781402110047. [Google Scholar] [CrossRef]
- Sun, H.B.; Cheng, R.; Yang, K.M.; Zhu, Y.; Lu, S. Torque ripple error compensation of high-dynamic coil array commutation algorithm for magnetic levitation planar motor. IET Electr. Power Appl. 2020, 14, 809–817. [Google Scholar] [CrossRef]
- Zhang, S.G.; Dang, X.P.; Wang, K.; Huang, J.T.; Yang, J.X.; Zhang, G.H. An Analytical Approach to Determine Coil Thickness for Magnetically Levitated Planar Motors. IEEE/ASME Trans. Mechatron. 2017, 22, 572–580. [Google Scholar] [CrossRef]
- Zhu, H.; Pang, C.K.; Teo, T.J.; Marek, L.T. Modeling and Design of a Size and Mass Reduced Magnetically Levitated Planar Positioner. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2366–2371. [Google Scholar]
- Lei, J. Research on Structural Dynamic Characteristics of Lorentz Planar Motor. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2010. [Google Scholar]
- Gong, Z.P.; Ding, L.; Gao, H.B.; Yue, H.H.; Liu, R.Q.; Deng, Z.Q. Design and Control of a Novel Six-DOF Maglev Platform For Positioning and Vibration Isolation. In Proceedings of the 2017 2nd International Conference on Advanced Robotics and Mechatronics (ICARM), Tai’an, China, 27–31 August 2017; pp. 155–160. [Google Scholar]
- Gong, Z.P.; Ding, L.; Yue, H.H.; Gao, H.B.; Liu, R.Q.; Deng, Z.Q.; Lu, Y.F. System integration and control design of a maglev platform for space vibration isolation. J. Vib. Control 2019, 25, 1720–1736. [Google Scholar] [CrossRef]
- Wu, Q.Q. Research on Six-Degree-of-Freedom Magnetic Suspension Vibration Isolation System and Its Mechanical Characteristics. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Sundaravadivu, K.; Ramadevi, C.; Vishnupriya, R. Design of Optimal Controller for Magnetic Levitation System Using Brownian Bat Algorithm. In Artificial Intelligence and Evolutionary Computations in Engineering Systems; ICAIECES 2015; Springer: New Delhi, India, 2016; pp. 1321–1329. [Google Scholar]
- Ding, C.; Damen, A.A.H.; van den Bosch, P.P.J.; Janssen, J.L.G. Vibration Isolation of an Electromagnetic Actuator with Passive Gravity Compensation. In Proceedings of the International Conference on Computer Automation (ICCA), Xiamen, China, 9–11 June 2010; pp. 85–89. [Google Scholar]
- Wu, Q.Q.; Cui, N.; Zhao, S.F.; Zhang, H.B.; Liu, B.L. Modeling and Control of a Six Degrees of Freedom Maglev Vibration Isolation System. Sensors 2019, 19, 3608. [Google Scholar] [CrossRef]
- Chen, C.H.; Hu, Y.F.; Wu, H.C.; Song, C.S. Parametric design and experiment of maglev actuators for microgravity vibration isolation system. Int. J. Appl. Electromagn. 2018, 58, 319–335. [Google Scholar] [CrossRef]
- Guo, Z.X.; Zhang, Y.; Hu, Q. Integrated vibration isolation and attitude control for spacecraft with uncertain or unknown payload inertia parameters. Acta Astronaut. 2018, 151, 107–119. [Google Scholar] [CrossRef]
- Liu, R.Q.; Yang, F.; Mu, X.K.; Yue, H.H.; Zhu, C.X. Research on the 2-degree-of-freedom electromagnetic actuator in space. Adv. Mech. Eng. 2018, 10, 168781401775026. [Google Scholar] [CrossRef]
- Li, S.Z. Research on Six-Dimensional Vibration Isolation System Based on Two-Degree-of-Freedom Electromagnetic Actuator. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Bozkurt, A.F.; Guney, O.F.; Erkan, K. Multi Degrees of Freedom Robust Magnetic Levitation Control of a Flexible Transport Mover with Disturbance Observer and State Feedback Control. Control Eng. Appl. Inf. 2018, 20, 50–59. [Google Scholar]
- Takahashi, M. Design Concept and Structural Configuration of Magnetic Levitation Stage with Z-Assist System. Int. J. Autom. Technol. 2021, 15, 706–714. [Google Scholar] [CrossRef]
- Zhu, H.; Teo, T.J.; Pang, C.K. Magnetically Levitated Parallel Actuated Dual-Stage (Maglev-PAD) System for Six-Axis Precision Positioning. IEEE/ASME Trans. Mechatron. 2019, 24, 1829–1838. [Google Scholar] [CrossRef]
- Schaeffel, C.; Katzschmann, M.; Mohr, H.U.; Gloess, R.; Rudolf, C.; Mock, C.; Walenda, C. 6D planar magnetic levitation system—PIMag 6D. Mech. Eng. J. 2016, 3, 15-00111. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Kim, W.J. Two-Phase Lorentz Coils and Linear Halbach Array for Multiaxis Precision-Positioning Stages with Magnetic Levitation. IEEE/ASME Trans. Mechatron. 2017, 22, 2662–2672. [Google Scholar] [CrossRef]
- Lahdo, M.; Kovalev, S.; Strohla, T. A Lorentz Actuator for High-Precision Magnetically Levitated Planar Systems. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 264–269. [Google Scholar]
- Lahdo, M.; Strohla, T.; Kovalev, S. Magnetically Levitated Planar Positioning Systems Based on Lorentz Forces. In Proceedings of the 2017 11th International Symposium on Linear Drives for Industry Applications (LDIA), Osaka, Japan, 6–8 September 2017. [Google Scholar]
- Liu, C.N.; Lai, S.K.; Ni, Y.Q.; Chen, L. Dynamic modelling and analysis of a physics-driven strategy for vibration control of railway vehicles. Veh. Syst. Dyn. 2024, in press. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.N.; Chen, L.; Zhang, X.L. Phase deviation of semi-active suspension control and its compensation with inertial suspension. Acta Mech. Sin. 2024, 40, 523367. [Google Scholar] [CrossRef]
- Wu, D.; Zheng, S.; He, P.; Zhang, Z. Optimization of the on/off status configuration of control units in an active vibration isolation system-experiment. Smart Mater. Struct. 2024, 33, 065021. [Google Scholar] [CrossRef]
- Zhu, Z.J.; Xiao, Y.; Zhou, M.R.; Li, Y.Q.; Yu, D.L. Active Composite Control of Disturbance Compensation for Vibration Isolation System with Uncertainty. Actuators 2024, 13, 334. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, Y.; Zhang, H.; Zhang, L.; Cai, H. Advancements in Key Technologies for Vibration Isolators Utilizing Electromagnetic Levitation. Energies 2024, 17, 5343. https://doi.org/10.3390/en17215343
Lou Y, Zhang H, Zhang L, Cai H. Advancements in Key Technologies for Vibration Isolators Utilizing Electromagnetic Levitation. Energies. 2024; 17(21):5343. https://doi.org/10.3390/en17215343
Chicago/Turabian StyleLou, Yuexuan, He Zhang, Lu Zhang, and Haoran Cai. 2024. "Advancements in Key Technologies for Vibration Isolators Utilizing Electromagnetic Levitation" Energies 17, no. 21: 5343. https://doi.org/10.3390/en17215343
APA StyleLou, Y., Zhang, H., Zhang, L., & Cai, H. (2024). Advancements in Key Technologies for Vibration Isolators Utilizing Electromagnetic Levitation. Energies, 17(21), 5343. https://doi.org/10.3390/en17215343







