Simulation of Dynamic Characteristics of Supercritical Boiler Based on Coupling Model of Combustion and Hydrodynamics
Abstract
1. Introduction
2. Research Focus
3. Model Development and Validation
3.1. Model Development
- The coal type is fixed;
- Radiative heat transfer in the furnace occurs only between adjacent layers;
- The axial heat conduction of the tube wall is neglected.
3.2. Model Validation
4. Results and Discussion
4.1. Spatial Distribution of Thermodynamic Parameters
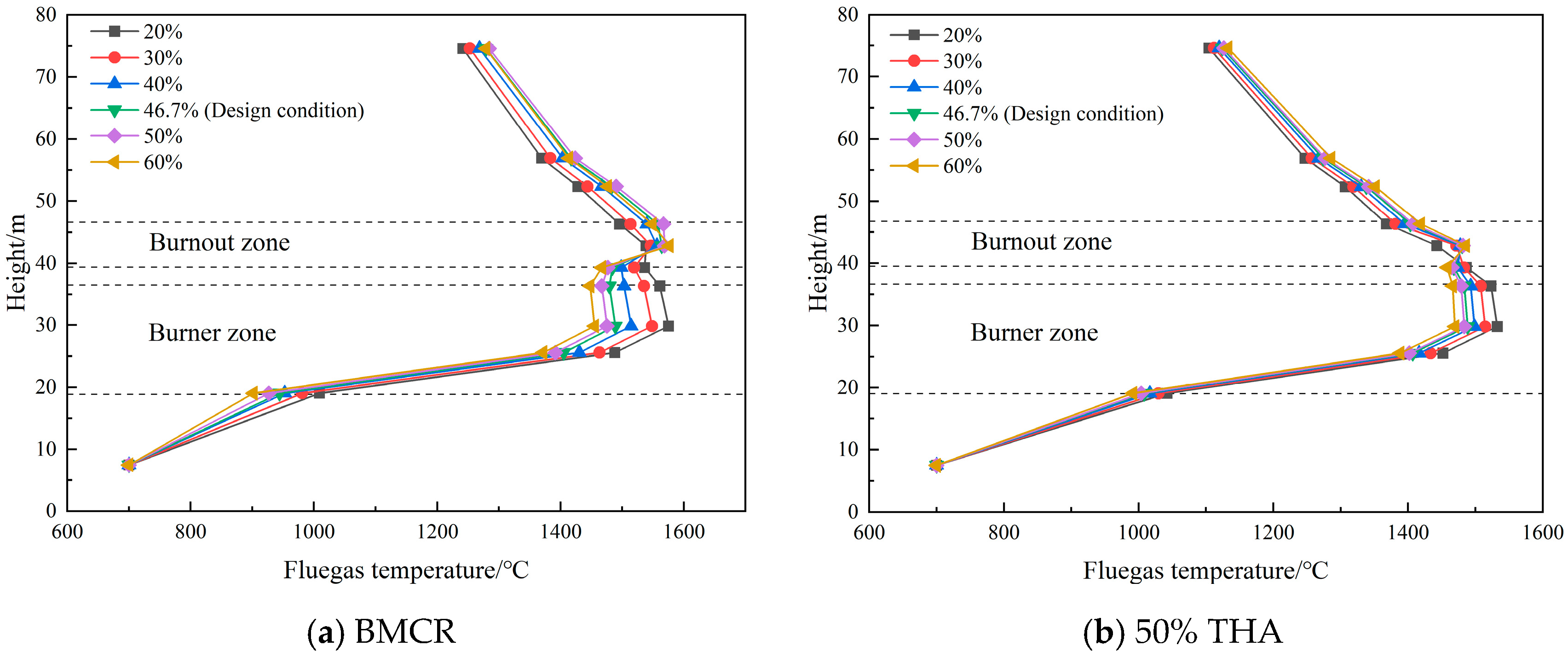
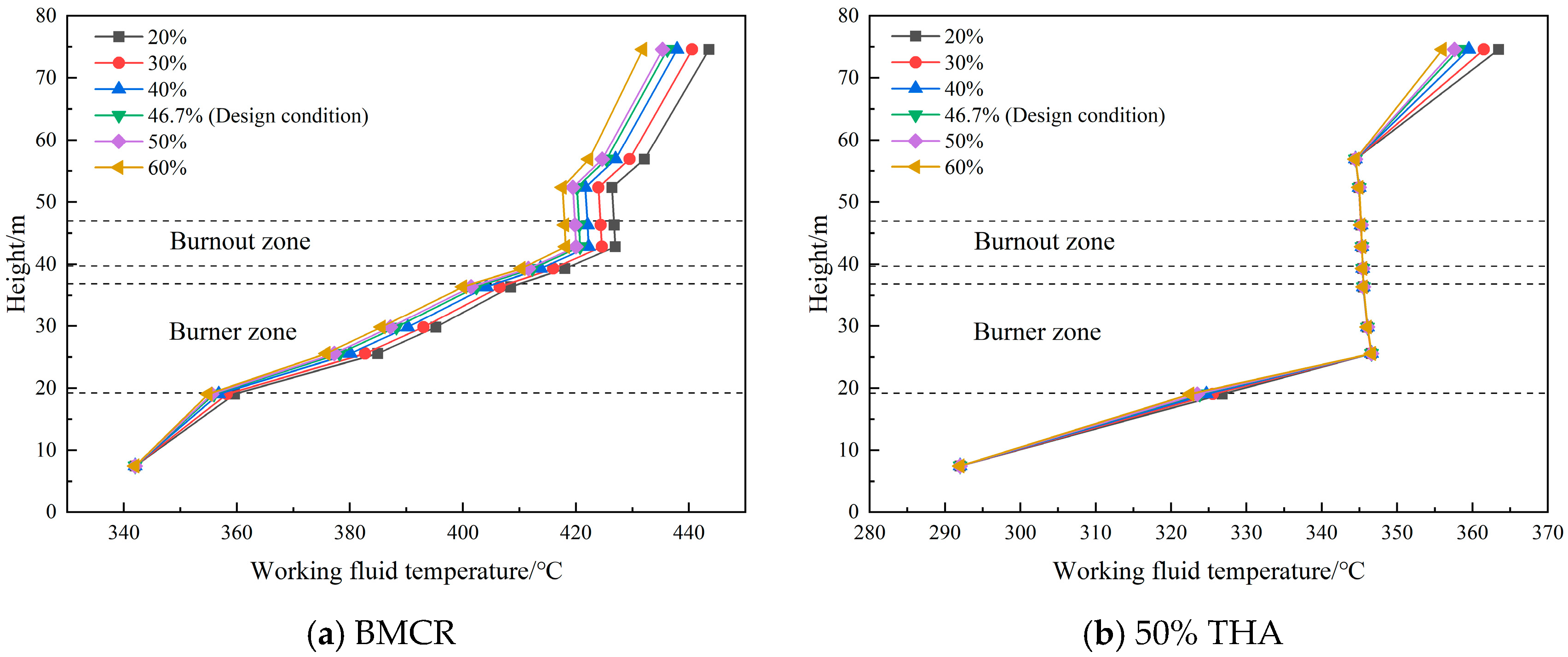
4.1.1. Different OFA Ratios
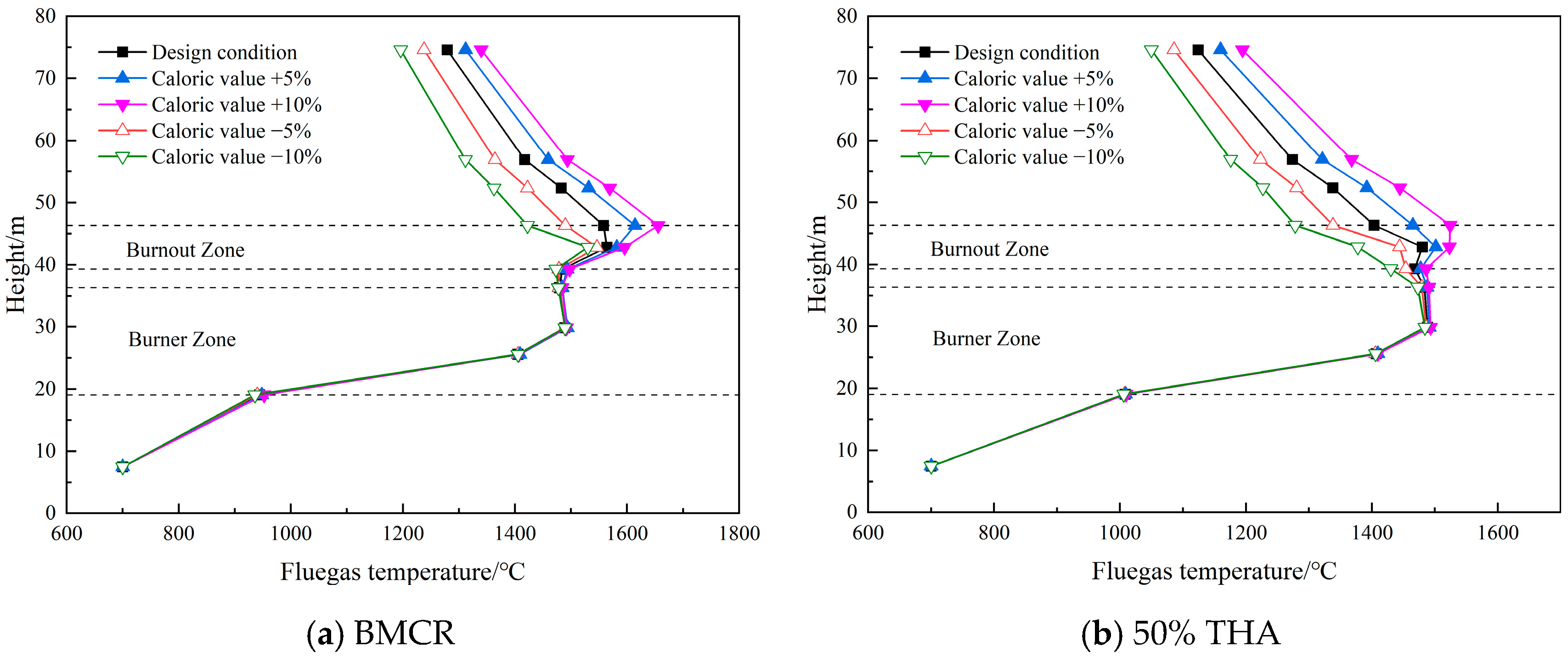
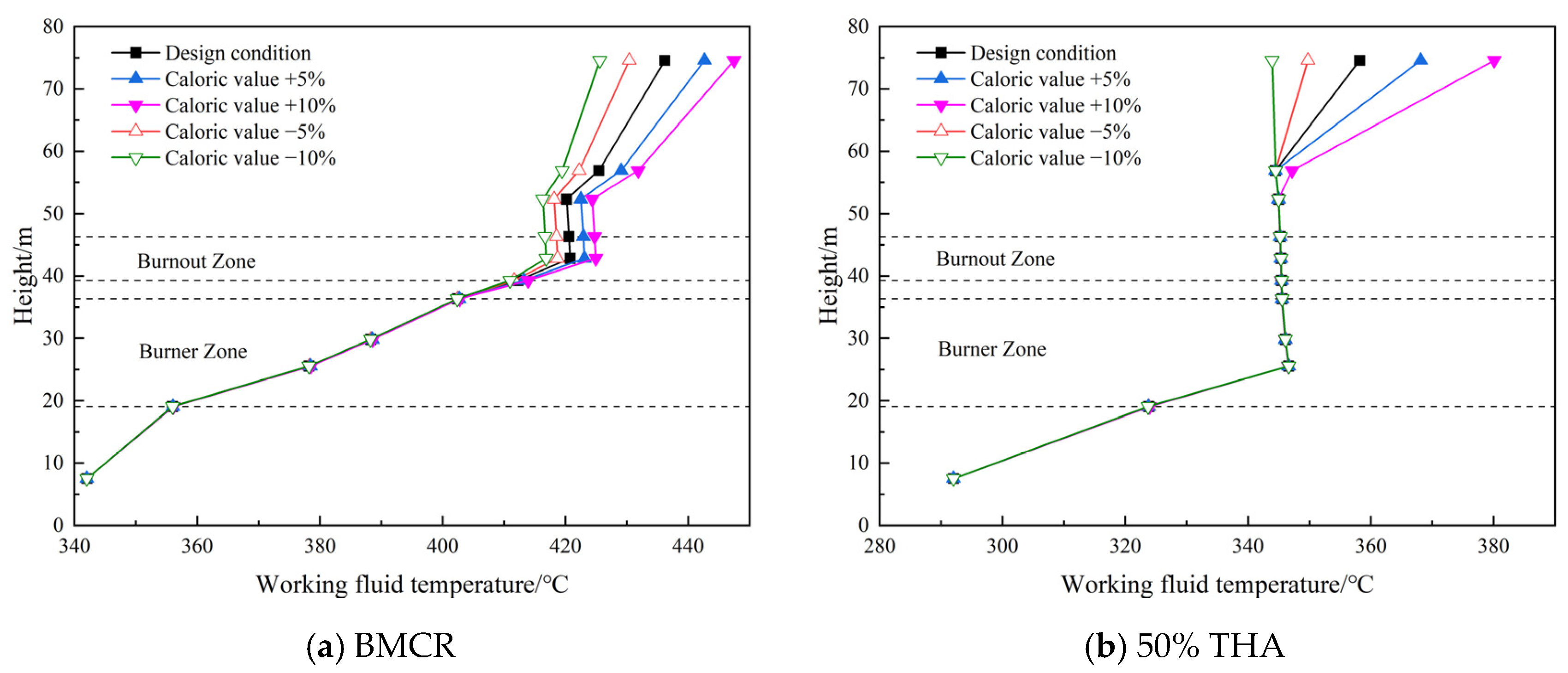
4.1.2. Different Coal Calorific Values
4.2. Dynamic Characteristics of Thermodynamic Parameters
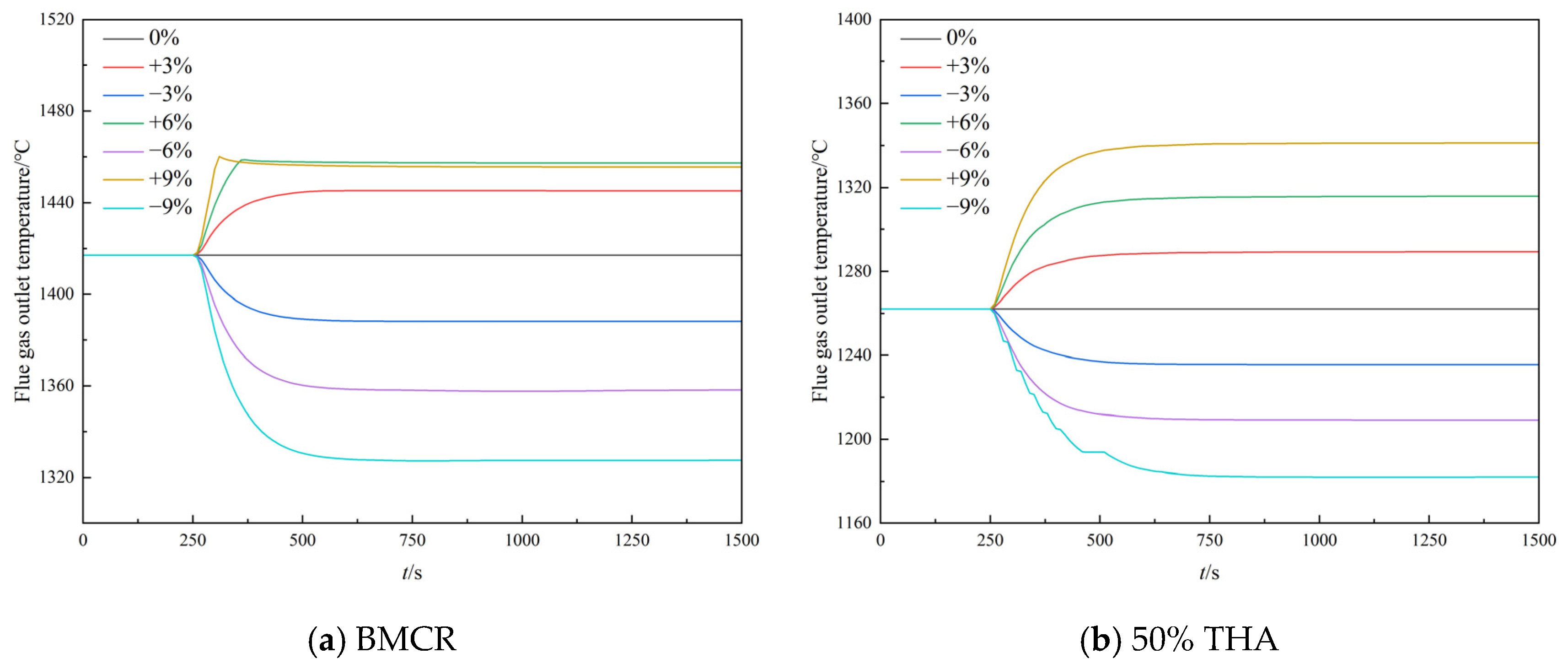
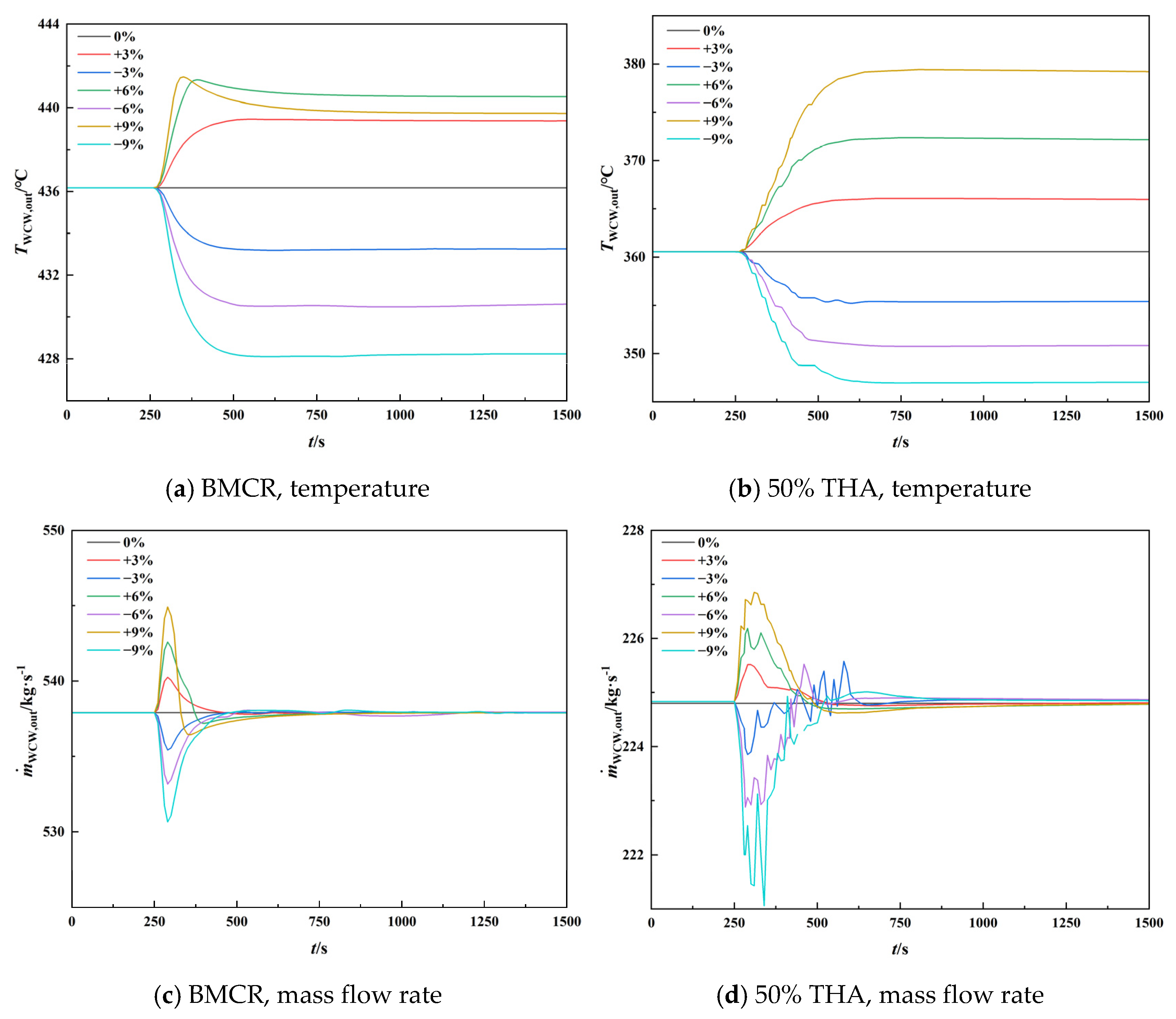
4.2.1. Step Disturbance of Coal Feeding Rate
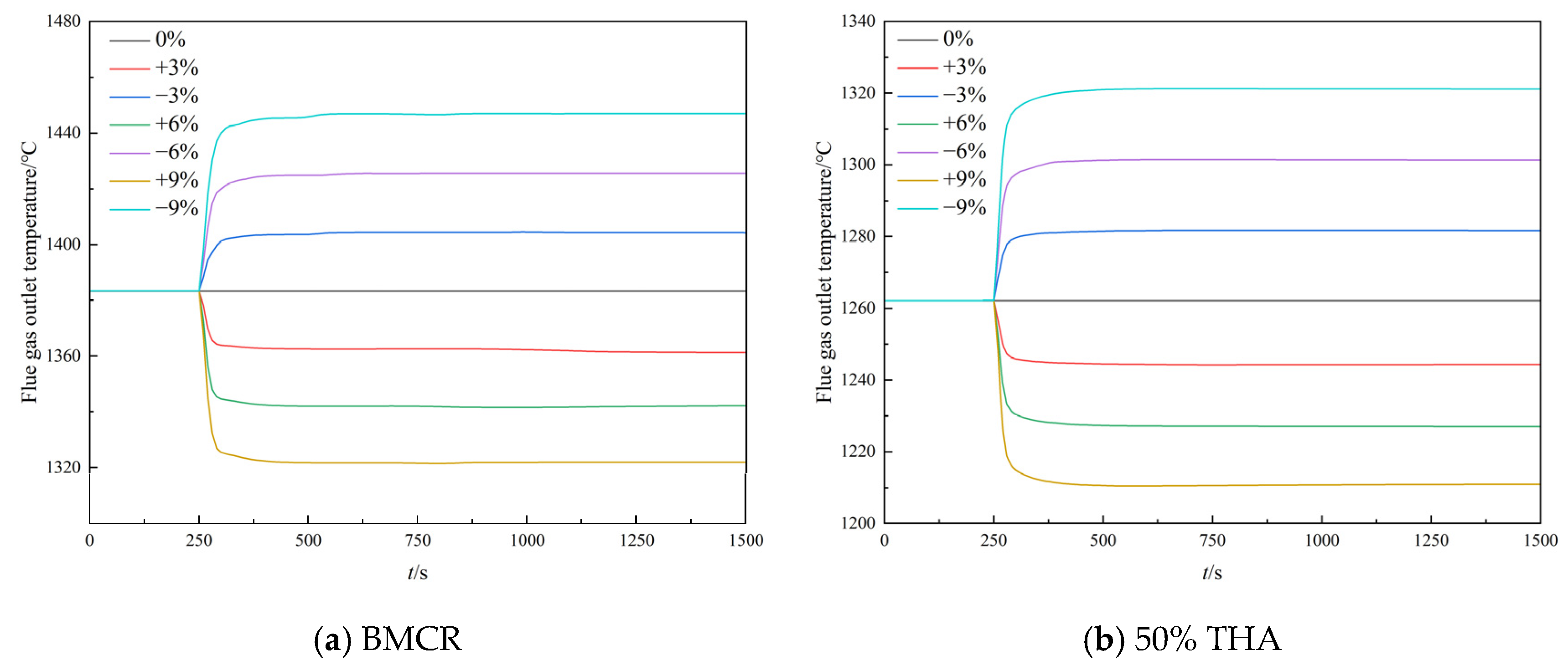
4.2.2. Step Disturbance of Air Flow Rate
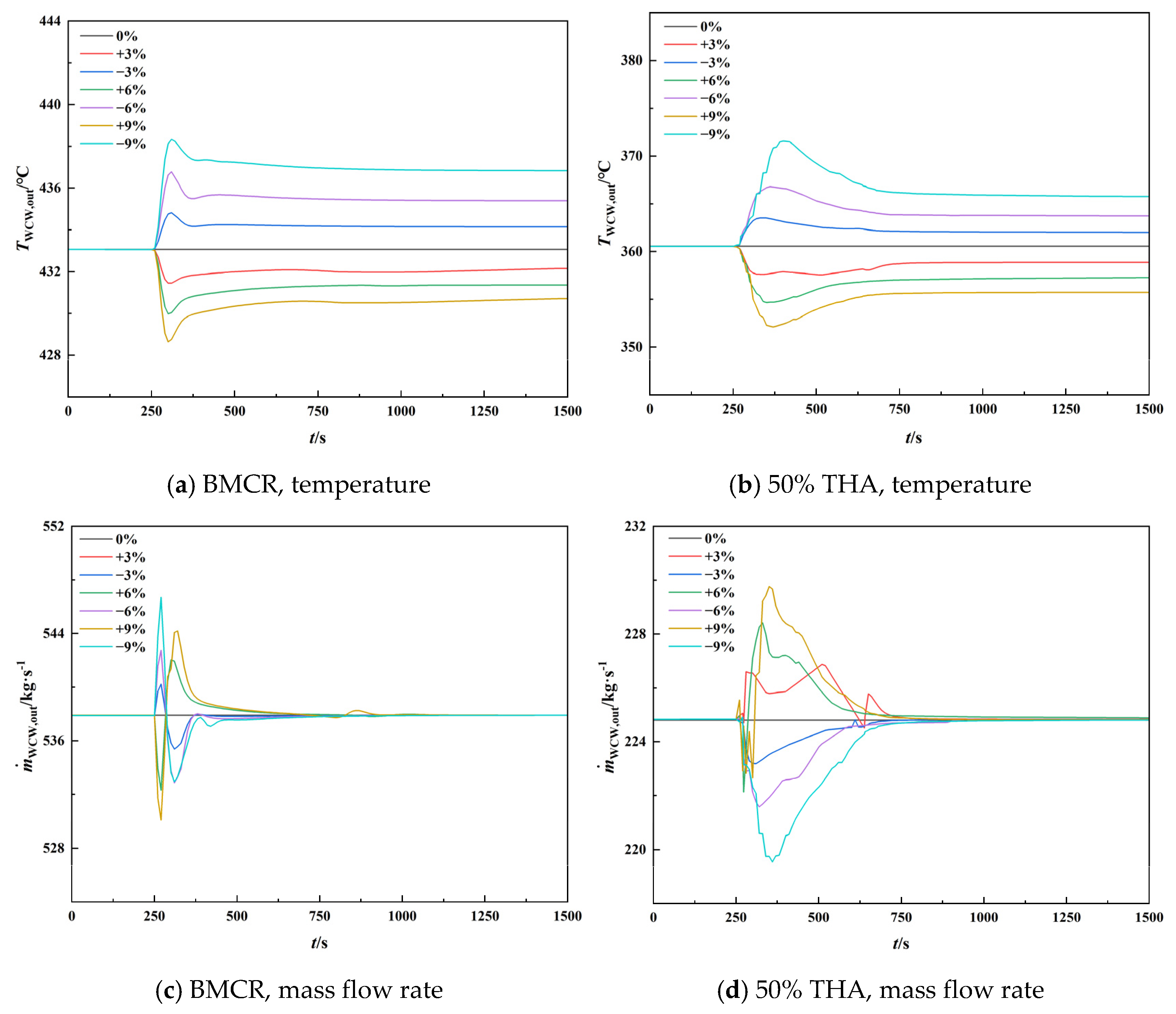
4.2.3. Step Disturbance of Feedwater Flow Rate
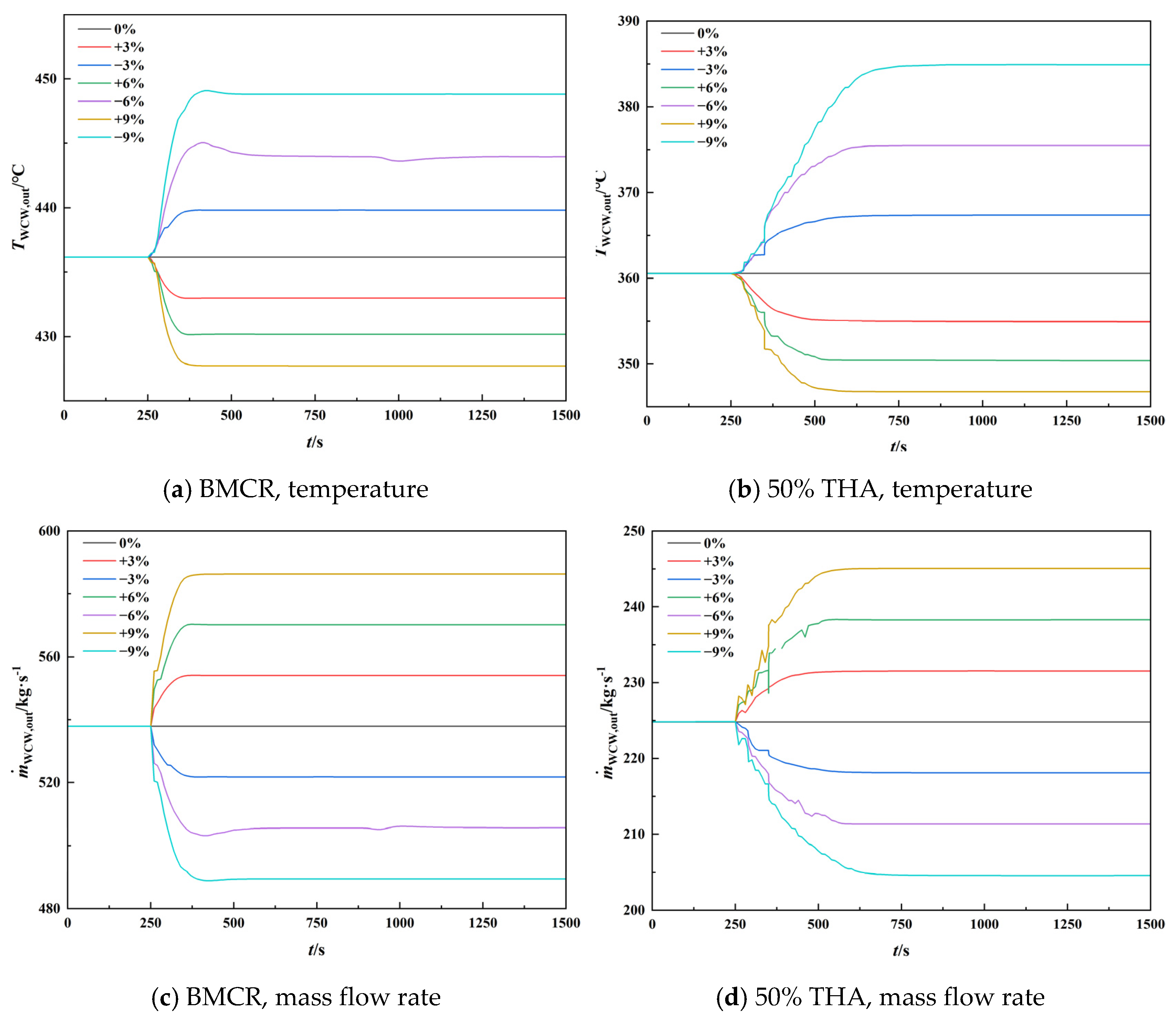
4.2.4. Step Disturbance of Feedwater Temperature
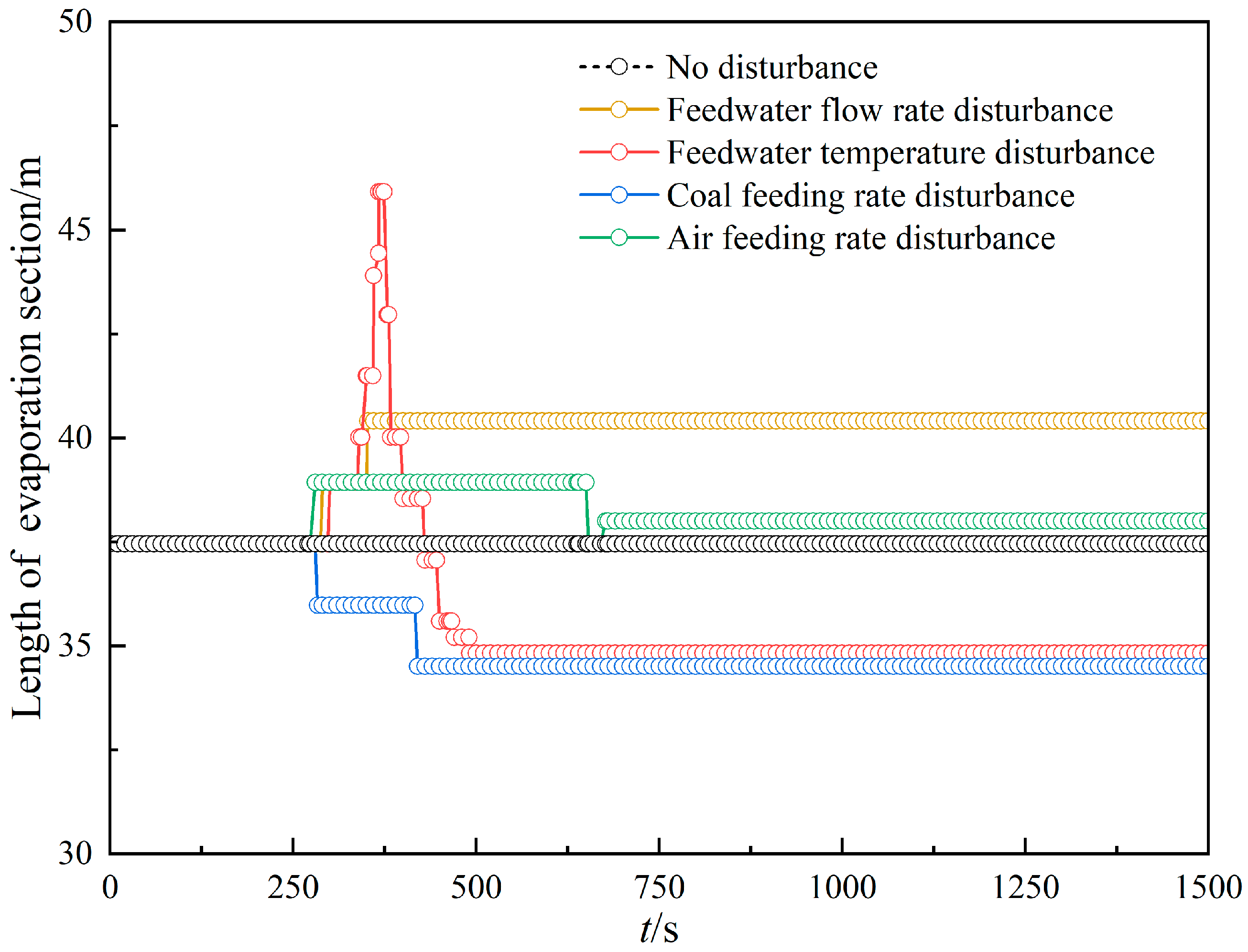
4.2.5. Comparison of the PTP Position for Different Working Conditions
5. Conclusions
- The OFA ratio has a great influence on the temperature distribution in the furnace. The lower the OFA ratio, the higher the flue gas temperature in the burner zone and the lower the temperature at the furnace exit. Meanwhile, the lower the OFA ratio, the higher the fluid temperature and the shorter the length of the evaporation section. The temperature difference in the WCW outlet fluid at the 20% and 60% OFA ratios is 11.7 °C under the BMCR condition and 7.4 °C under the 50% THA condition.
- The change in the coal calorific value has a limited influence on the temperature of the burner area, and the difference in the temperature is mainly reflected in the area above the combustion zone. Under the BMCR and 50% THA conditions, when the coal caloric value increases by 5%, the flue gas outlet temperature increases by 32.7 °C and 35.4 °C, and the fluid outlet temperature increases by 6.5 °C and 9.9 °C, respectively. Meanwhile, an increase in the coal calorific value results in a decrease in the dryout point height and a decrease in the length of the evaporation section.
- The changes in the length of the evaporation section are −2.95 m, 2.95 m, −2.62 m, and 0.54 m when the coal feeding rate, feedwater flow rate, feedwater temperature, and air supply rate are suddenly increased by 5%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohamed, O.; Khalil, A.; Wang, J. Modeling and Control of Supercritical and Ultra-Supercritical Power Plants: A Review. Energies 2020, 13, 2935. [Google Scholar] [CrossRef]
- Avagianos, I.; Rakopoulos, D.; Karellas, S.; Kakaras, E. Review of Process Modeling of Solid-Fuel Thermal Power Plants for Flexible and Off-Design Operation. Energies 2020, 13, 6587. [Google Scholar] [CrossRef]
- Kruger, M.; Muslubas, S.; Loeper, T.; Klasing, F.; Knodler, P.; Mielke, C. Potentials of Thermal Energy Storage Integrated into Steam Power Plants. Energies 2020, 13, 2226. [Google Scholar] [CrossRef]
- Yin, J.; Liu, M.; Zhao, Y.; Wang, C.; Yan, J. Dynamic performance and control strategy modification for coal-fired power unit under coal quality variation. Energy 2021, 223, 120077. [Google Scholar] [CrossRef]
- Oko, E.; Wang, M. Dynamic modelling, validation and analysis of coal-fired subcritical power plant. Fuel 2014, 135, 292–300. [Google Scholar] [CrossRef]
- Mahmoudi, F.; Najafabadi, T.A.; Moarefianpour, A. Developing an operating instruction to attenuate pressure stress during fuel shortage events of a power boiler based on dynamic modelling. Appl. Therm. Eng. 2022, 200, 117565. [Google Scholar] [CrossRef]
- Zima, W.; Grądziel, S.; Cebula, A.; Rerak, M.; Kozak-Jagieła, E.; Pilarczyk, M. Mathematical model of a power boiler operation under rapid thermal load changes. Energy 2023, 263, 125836. [Google Scholar] [CrossRef]
- Liu, K.; Wang, C.; Wang, L.; Liu, B.; Ye, M.; Guo, Y.; Che, D. Dynamic performance analysis and control strategy optimization for supercritical coal-fired boiler: A dynamic simulation. Energy 2023, 282, 128712. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Liu, X. Heat transfer calculation methods in three-dimensional CFD model for pulverized coal-fired boilers. Appl. Therm. Eng. 2020, 166, 114633. [Google Scholar] [CrossRef]
- Li, X.; Zeng, L.; Zhang, N.; Chen, Z.; Li, Z.; Qin, Y. Effects of the air-staging degree on performances of a supercritical down-fired boiler at low loads: Air/particle flow, combustion, water wall temperature, energy conversion and NO emissions. Fuel 2022, 308, 121896. [Google Scholar] [CrossRef]
- Gu, M.; Wang, M.; Chen, X.; Wang, J.; Lin, Y.; Chu, H. Numerical study on the effect of separated over-fire air ratio on combustion characteristics and NOx emission in a 1000 MW supercritical CO2 boiler. Energy 2019, 175, 593–603. [Google Scholar] [CrossRef]
- Gu, Y.; Zhao, W.; Wu, Z. Online adaptive least squares support vector machine and its application in utility boiler combustion optimization systems. J. Process Control 2011, 21, 1040–1048. [Google Scholar] [CrossRef]
- Tan, P.; He, B.; Zhang, C.; Rao, D.; Li, S.; Fang, Q.; Chen, G. Dynamic modeling of NOX emission in a 660 MW coal-fired boiler with long short-term memory. Energy 2019, 176, 429–436. [Google Scholar] [CrossRef]
- Xu, L.; Yuan, J.; Wang, J. Dynamic modeling and solution algorithm of the evaporation system for the ultra-supercritical power plant. Int. J. Heat Mass Transf. 2017, 105, 589–596. [Google Scholar] [CrossRef]
- Zima, W.; Nowak-Ocłoń, M.; Ocłoń, P. Simulation of fluid heating in combustion chamber waterwalls of boilers for supercritical steam parameters. Energy 2015, 92, 117–127. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S. Dynamic simulation of the water-steam flow in a supercritical once-through boiler. J. Mech. Sci. Technol. 2017, 31, 4965–4975. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Liu, B.; Liu, K.; Han, Y.; Wang, L.; Che, D. Dynamic analysis for ultra-supercritical boiler water wall considering uneven heat flux distribution and combustion instability. Int. J. Heat Mass Transf. 2025, 236, 126269. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, W.; Xu, W. A study of the hydrodynamic characteristics of a vertical water wall in a 2953t/h ultra-supercritical pressure boiler. Int. J. Heat Mass Transf. 2015, 86, 404–414. [Google Scholar] [CrossRef]
- Zhu, H.; Tan, P.; He, Z.; Ma, L.; Zhang, C.; Fang, Q.; Chen, G. Revealing steam temperature characteristics for a double-reheat unit under coal calorific value variation. Energy 2023, 283, 128530. [Google Scholar] [CrossRef]
- Müller-Steinhagen, H.; Heck, K. A simple friction pressure-drop correlation for 2-phase flow in pipes. Chem. Eng. Process.-Process Intensif. 1986, 20, 297–308. [Google Scholar] [CrossRef]
- Colebrook, C.F.; White, C.M. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Gnielinski, V. New Equations for Heat and Mass Transfer in Turbulent Pipe and Channel Flows. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Steiner, D.; Taborek, J. Flow Boiling Heat Transfer in Vertical Tubes Correlated by an Asymptotic Model. Heat Transf. Eng. 1992, 13, 43–69. [Google Scholar] [CrossRef]
- Filonenko, G.K. Hydraulic resistance in pipes. Teploenergetika 1954, 1, 40–44. [Google Scholar]
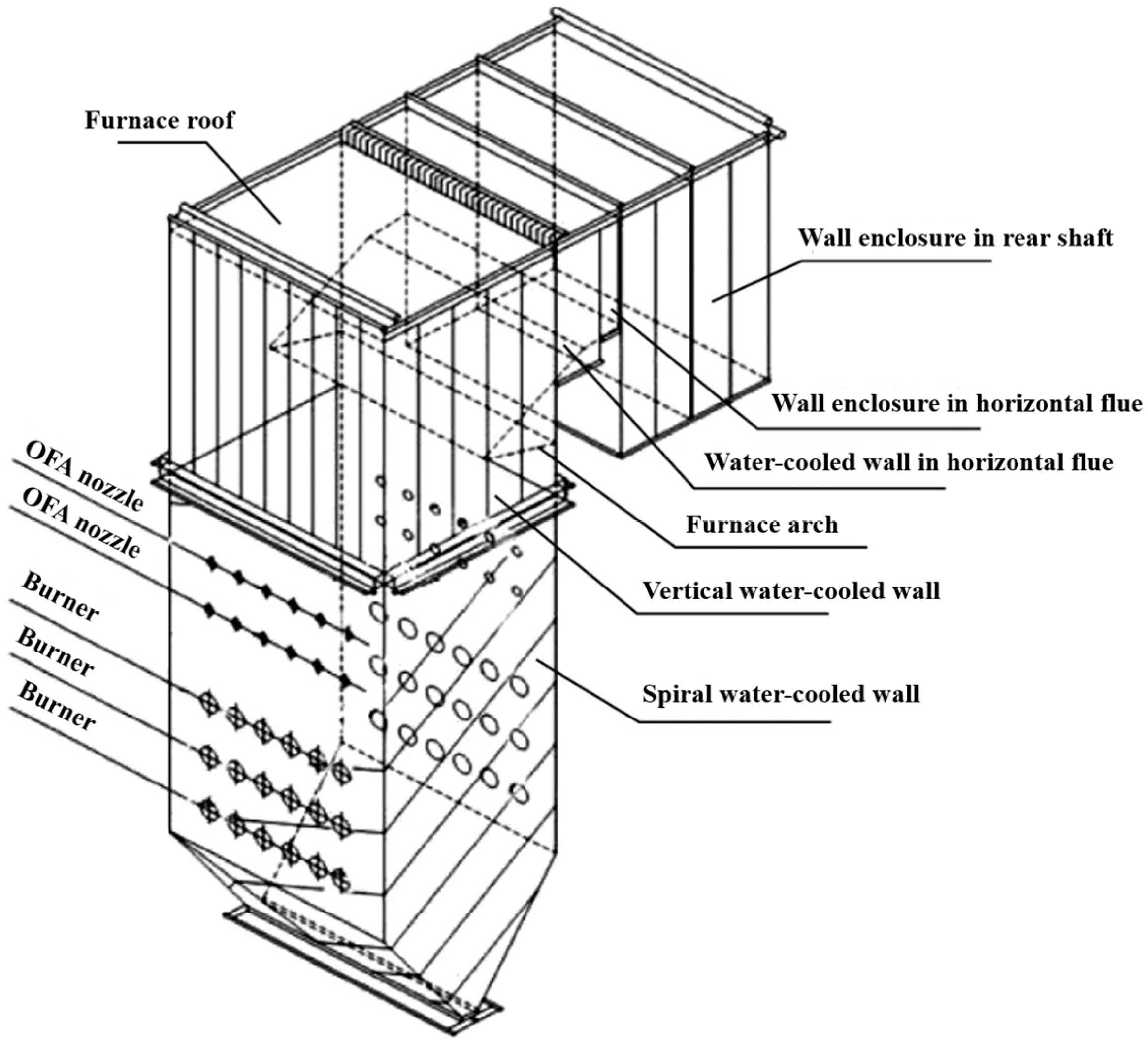
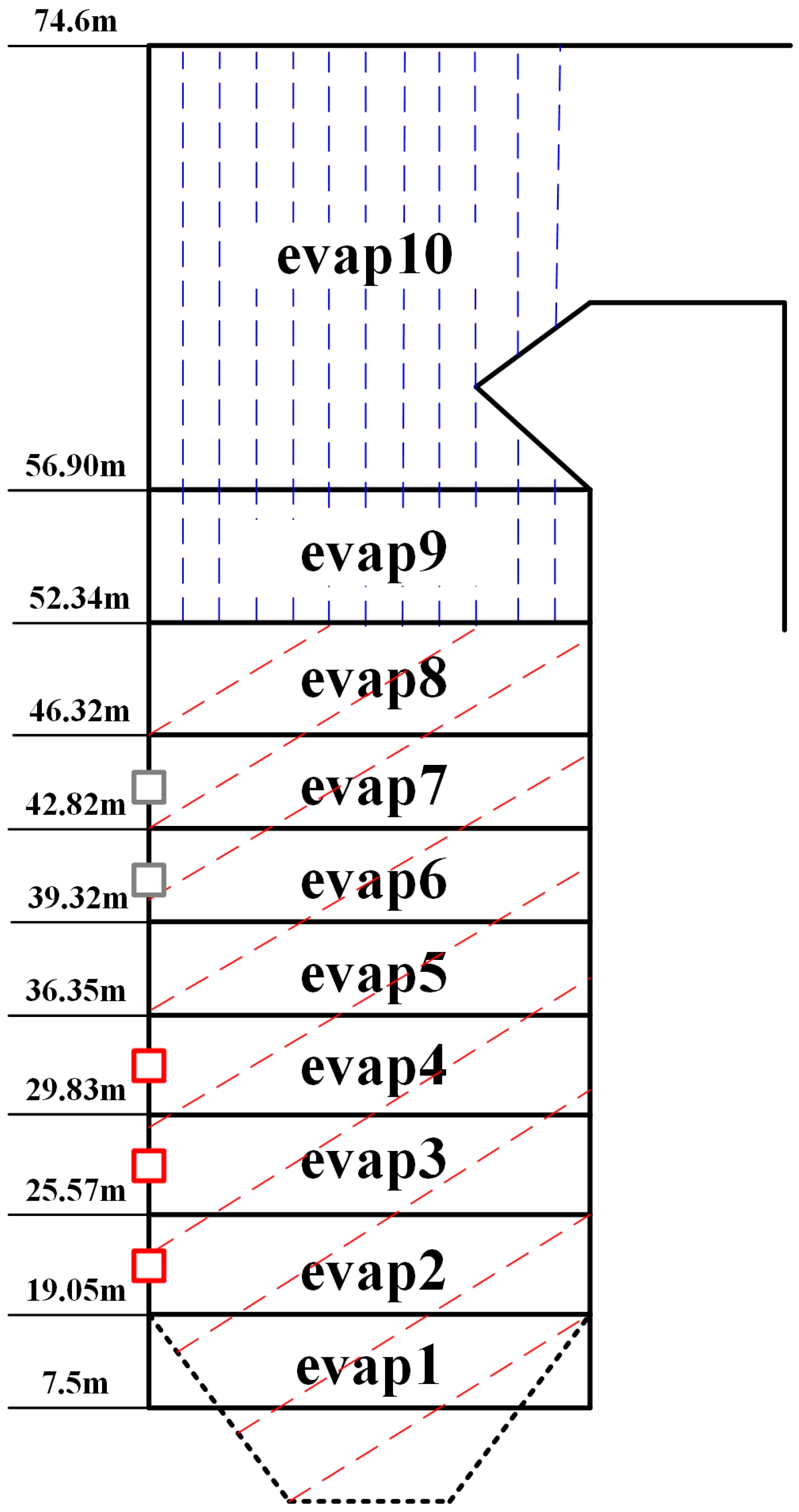

| Items | BMCR | THA | 75% THA | 50% THA |
|---|---|---|---|---|
| Feedwater flow rate/t·h−1 | 2104.9 | 1842.8 | 1337.8 | 879.8 |
| Feedwater temperature/°C | 342.0 | 330 | 310 | 290.0 |
| Feedwater pressure/MPa | 33.3 | 32.2 | 23.8 | 15.9 |
| Coal feeding rate/t·h−1 | 310.8 | 282.42 | 215.41 | 150.1 |
| Total air flow rate/kg·s−1 | 601.7 | 541.6 | 424.1 | 321.5 |
| Separator pressure/MPa | 31.8 | 31.0 | 22.9 | 15.3 |
| Separator temperature/°C | 438 | 436 | 411 | 358 |
| Component Analysis | LHV/ MJ·kg−1 | ||||||
|---|---|---|---|---|---|---|---|
| Car/% | Har/% | Oar/% | Nar/% | Sar/% | Mar/% | Aar/% | |
| 48.63 | 3.27 | 9.07 | 0.84 | 0.75 | 11.4 | 26.04 | 18.52 |
| Working Conditions | Design Value/°C | Simulated Results/°C | Relative Error/% |
|---|---|---|---|
| BMCR | 438 | 438.4 | 0.09% |
| THA | 436 | 427.4 | 1.97% |
| 75% THA | 411 | 399.1 | 2.90% |
| 50% THA | 358 | 358.2 | 0.05% |
| OFA Ratio | 20% | 30% | 40% | 46.7% | 50% | 60% |
|---|---|---|---|---|---|---|
| Boiling point height/m | 22.59 | 23.13 | 23.13 | 23.67 | 23.67 | 23.67 |
| Dryout point height/m | 57.64 | 59.11 | 59.11 | 62.06 | 62.06 | 62.0 |
| Length of evaporation section/m | 35.01 | 35.9 | 35.98 | 38.39 | 38.39 | 38.39 |
| Coal Calorific Value | −10% | −5% | 0% | +5% | +10% |
|---|---|---|---|---|---|
| Boiling point height/m | 23.67 | 23.67 | 23.67 | 23.67 | 23.67 |
| Dryout point height/m | 73.86 | 67.96 | 62.06 | 57.63 | 55.19 |
| Length of evaporation section/m | 50.19 | 44.29 | 38.39 | 33.97 | 31.51 |
| Coal Feeding Rate | −9% | −6% | −3% | 0% | +3% | +6% | +9% |
|---|---|---|---|---|---|---|---|
| Boiling point height/m | 23.13 | 23.13 | 23.13 | 23.13 | 23.13 | 23.13 | 23.13 |
| Dryout point height/m | 70.91 | 66.49 | 63.54 | 60.59 | 57.64 | 56.33 | 55.19 |
| Length of evaporation section/m | 47.78 | 43.36 | 40.41 | 37.46 | 34.51 | 33.2 | 32.06 |
| Air Flow Rate | −9% | −6% | −3% | 0% | +3% | +6% | +9% |
|---|---|---|---|---|---|---|---|
| Boiling point height/m | 23.67 | 23.67 | 23.13 | 23.13 | 22.59 | 22.59 | 22.59 |
| Dryout point height/m | 59.11 | 59.11 | 60.59 | 60.59 | 60.59 | 62.06 | 62.06 |
| Length of evaporation section/m | 35.44 | 35.44 | 37.46 | 37.46 | 38 | 39.48 | 39.48 |
| Feedwater Flow Rate | −9% | −6% | −3% | 0% | +3% | +6% | +9% |
|---|---|---|---|---|---|---|---|
| Boiling point height/m | 22.04 | 22.59 | 22.59 | 23.13 | 23.13 | 23.67 | 24.22 |
| Dryout point height/m | 37.53 | 54.43 | 65.71 | 60.59 | 63.54 | 67.96 | 70.92 |
| Length of evaporation section/m | 15.49 | 31.84 | 34.12 | 37.46 | 40.41 | 44.29 | 46.7 |
| Feedwater Temperature | −9% | −6% | −3% | 0% | +3% | +6% | +9% |
|---|---|---|---|---|---|---|---|
| Boiling point height/m | 27.17 | 25.75 | 24.21 | 23.13 | 21.5 | 20.41 | 19.05 |
| Dryout point height/m | 72.39 | 67.96 | 65.01 | 60.59 | 56.33 | 53.67 | 37.53 |
| Length of evaporation section/m | 45.22 | 42.21 | 40.8 | 37.46 | 34.83 | 33.26 | 18.48 |
| Pre-Disturbance | Coal Feeding Rate Disturbance | Feedwater Flow Rate Disturbance | Feedwater Temperature Disturbance | Air Feeding Rate Disturbance | |
|---|---|---|---|---|---|
| Boiling point height/m | 23.13 | 23.13 | 23.13 | 21.5 | 22.59 |
| Dryout point height/m | 60.59 | 57.64 | 63.54 | 56.33 | 60.59 |
| Length of evaporation section/m | 37.46 | 34.51 | 40.41 | 34.84 | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Wang, C.; Liu, K.; Zhang, L.; Zhu, Y.; Wang, Y.; Wang, L.; Che, D. Simulation of Dynamic Characteristics of Supercritical Boiler Based on Coupling Model of Combustion and Hydrodynamics. Energies 2024, 17, 5349. https://doi.org/10.3390/en17215349
Han Y, Wang C, Liu K, Zhang L, Zhu Y, Wang Y, Wang L, Che D. Simulation of Dynamic Characteristics of Supercritical Boiler Based on Coupling Model of Combustion and Hydrodynamics. Energies. 2024; 17(21):5349. https://doi.org/10.3390/en17215349
Chicago/Turabian StyleHan, Yuan, Chao Wang, Kairui Liu, Linxi Zhang, Yujie Zhu, Yankai Wang, Limin Wang, and Defu Che. 2024. "Simulation of Dynamic Characteristics of Supercritical Boiler Based on Coupling Model of Combustion and Hydrodynamics" Energies 17, no. 21: 5349. https://doi.org/10.3390/en17215349
APA StyleHan, Y., Wang, C., Liu, K., Zhang, L., Zhu, Y., Wang, Y., Wang, L., & Che, D. (2024). Simulation of Dynamic Characteristics of Supercritical Boiler Based on Coupling Model of Combustion and Hydrodynamics. Energies, 17(21), 5349. https://doi.org/10.3390/en17215349





