Electricity Bill Savings from Reduced Household Energy Consumption in Apartment Complexes
Abstract
:1. Introduction
2. Electricity Bills of Households in Apartment Complexes
2.1. Bills by the Single Contract (SC)
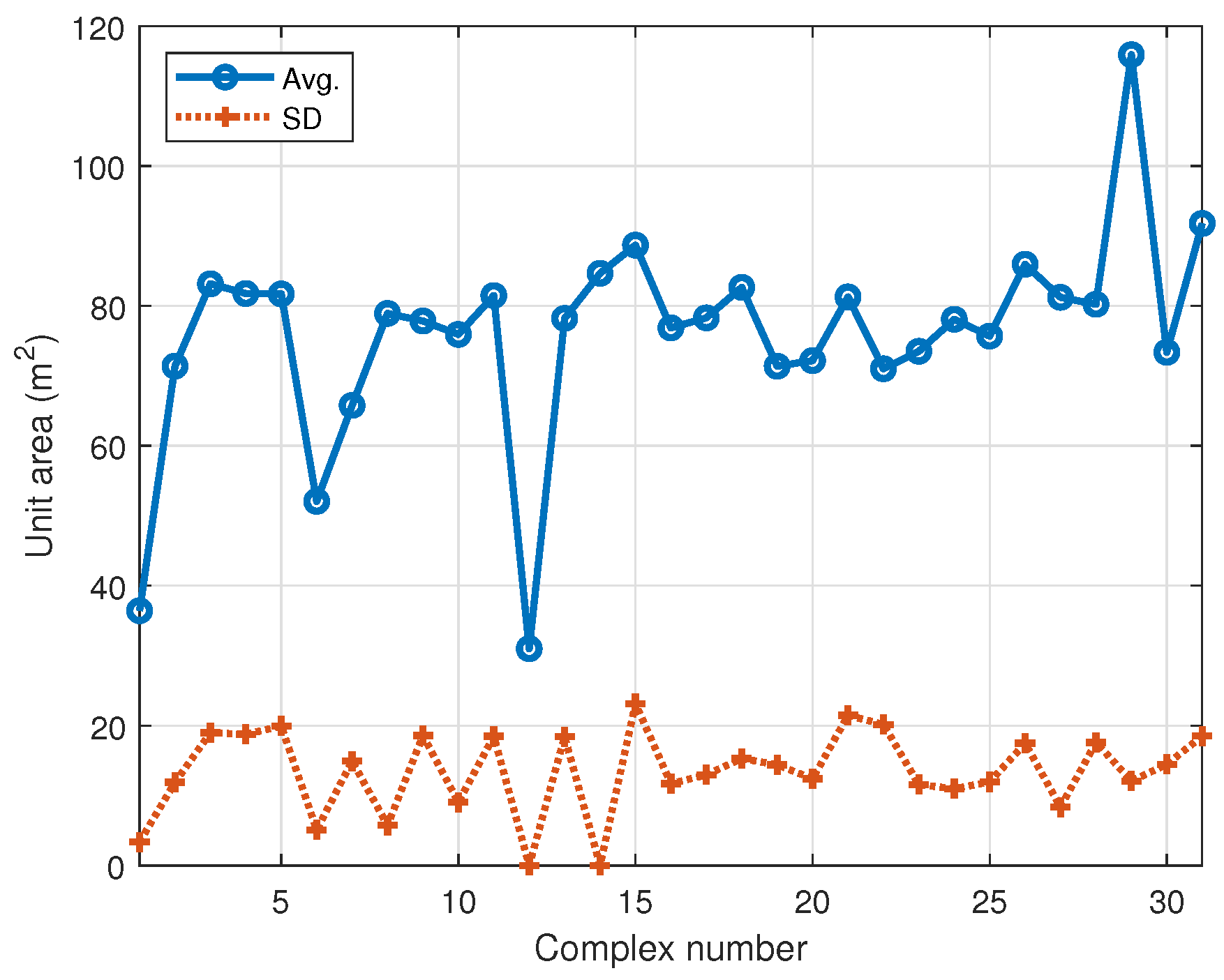
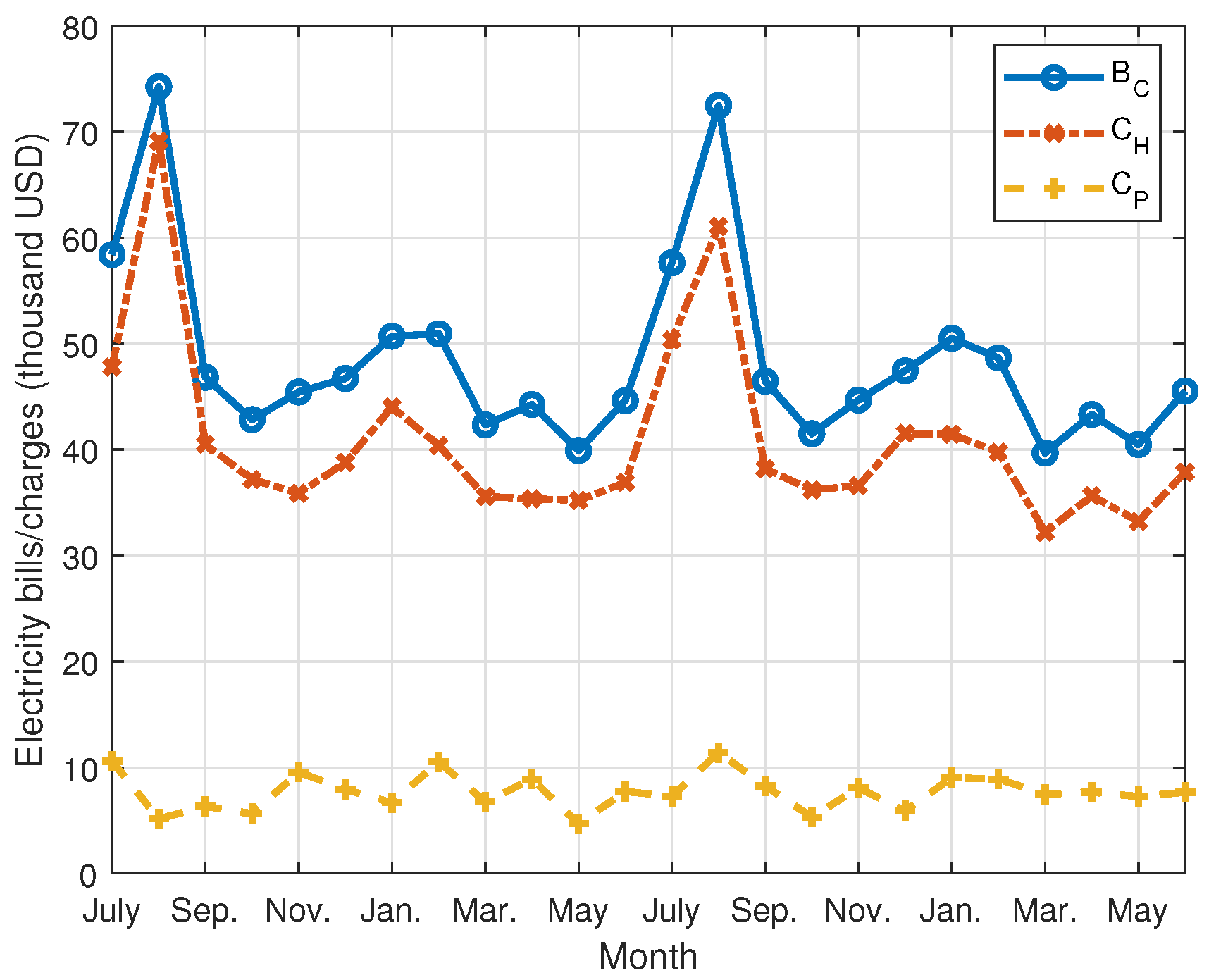
2.2. Apartment Complexes Used for the Electricity Bill Analysis
3. Bill Savings by Reducing Electricity Usage
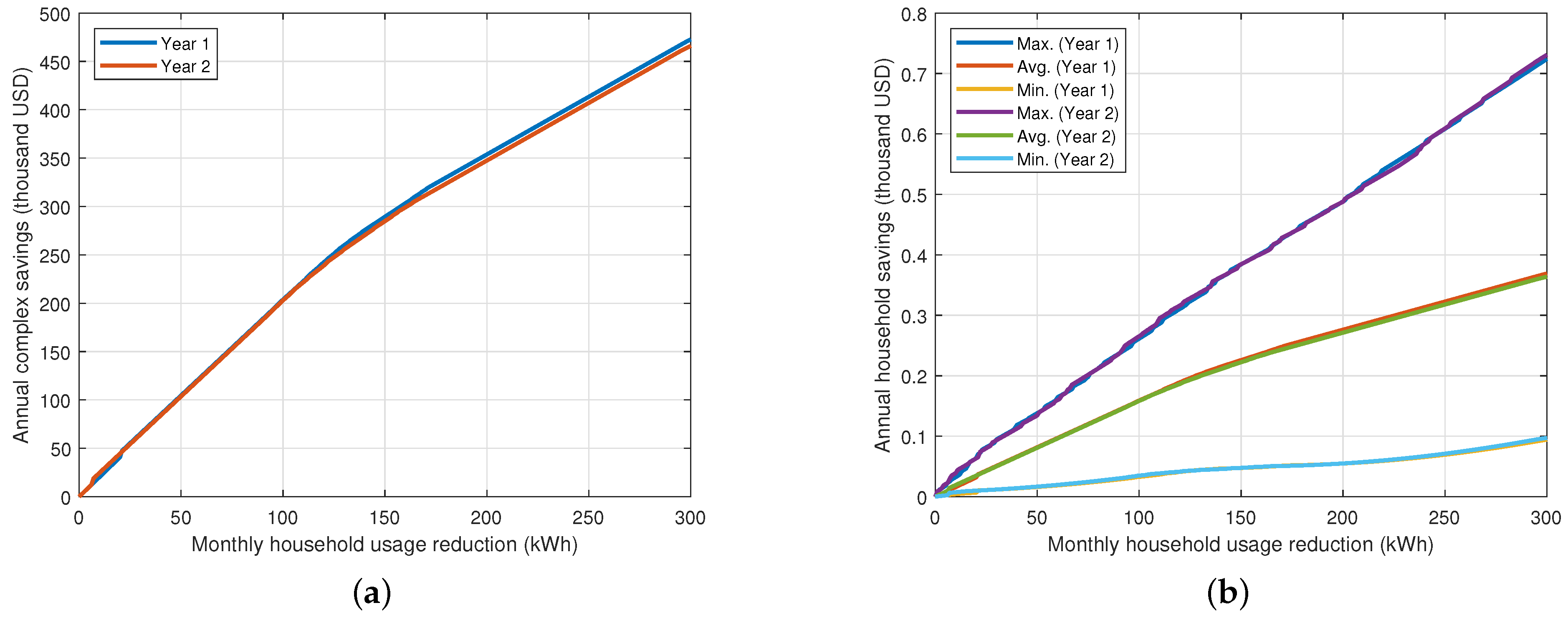
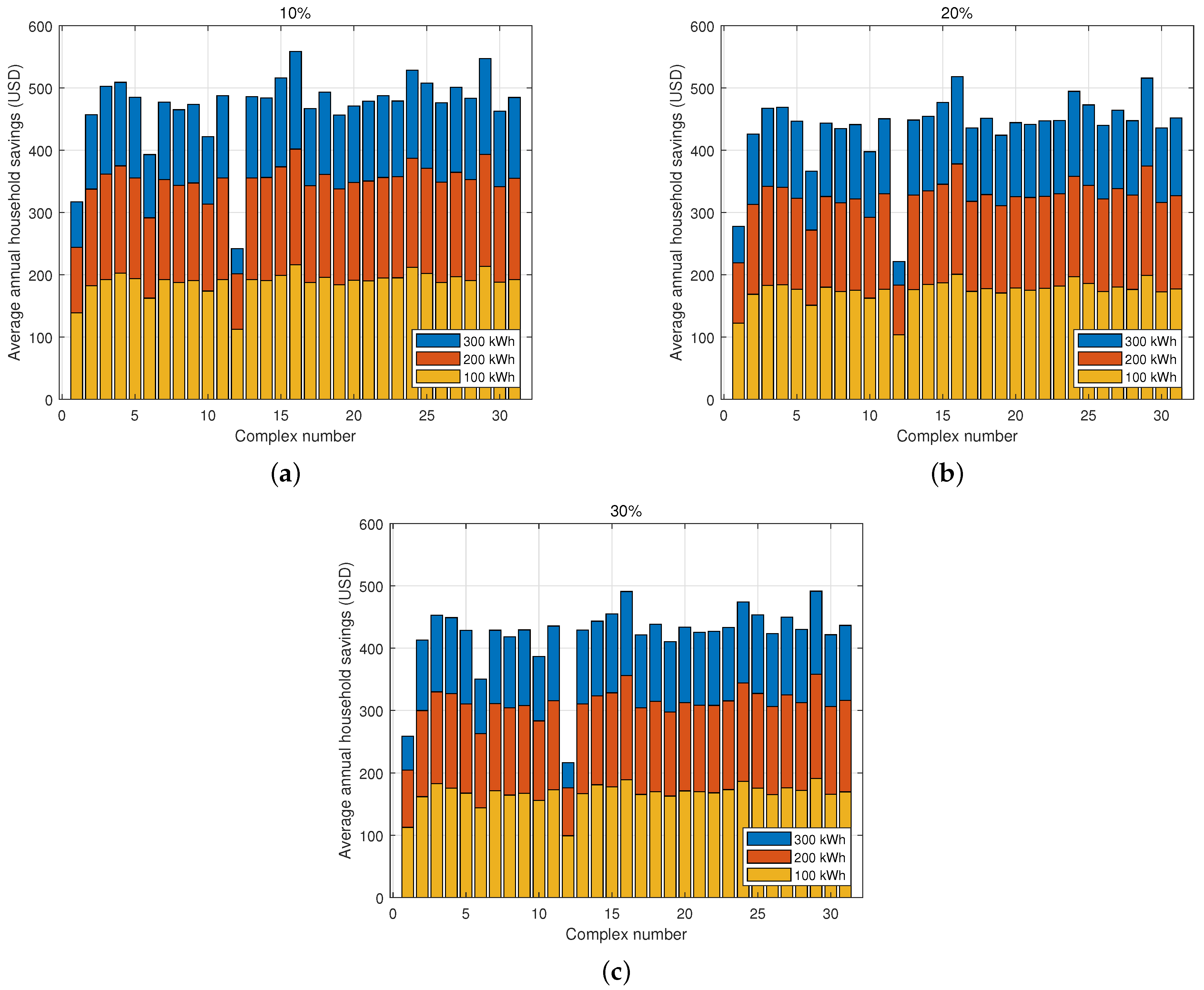
3.1. Electricity Usage Reduction by All Households
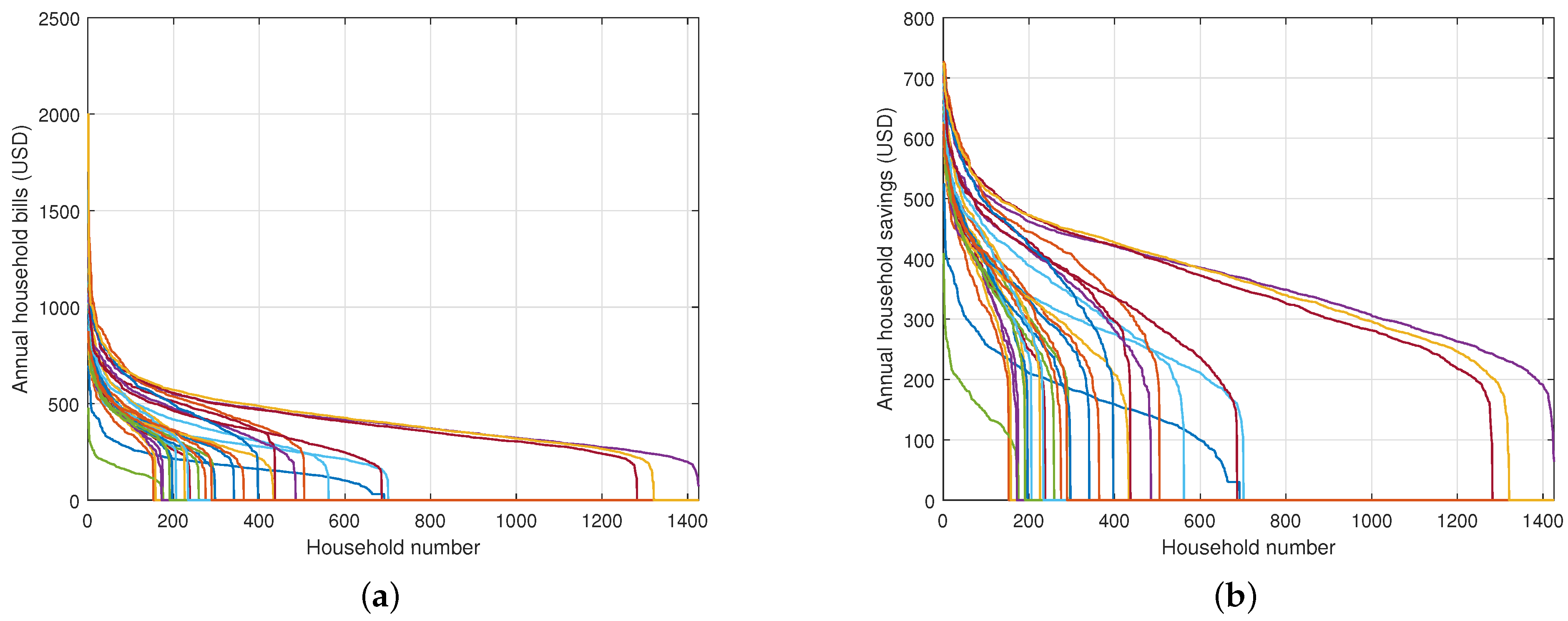
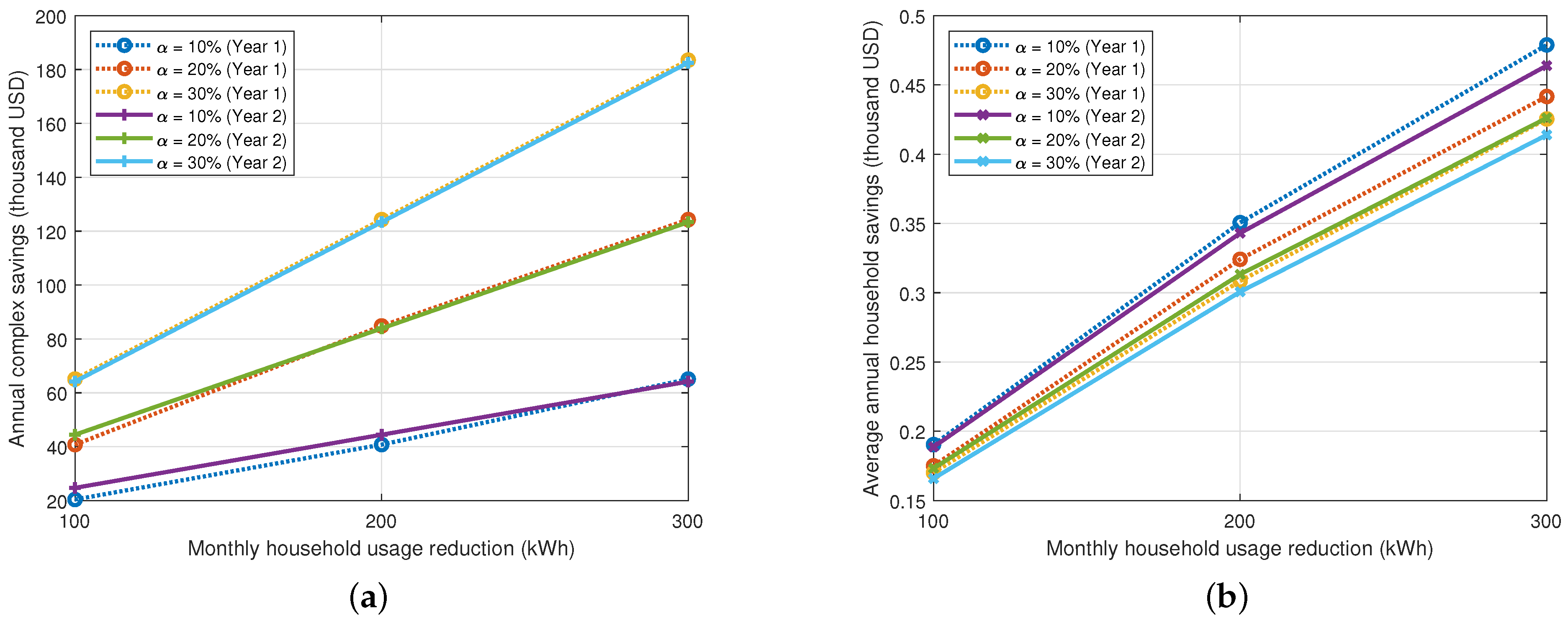
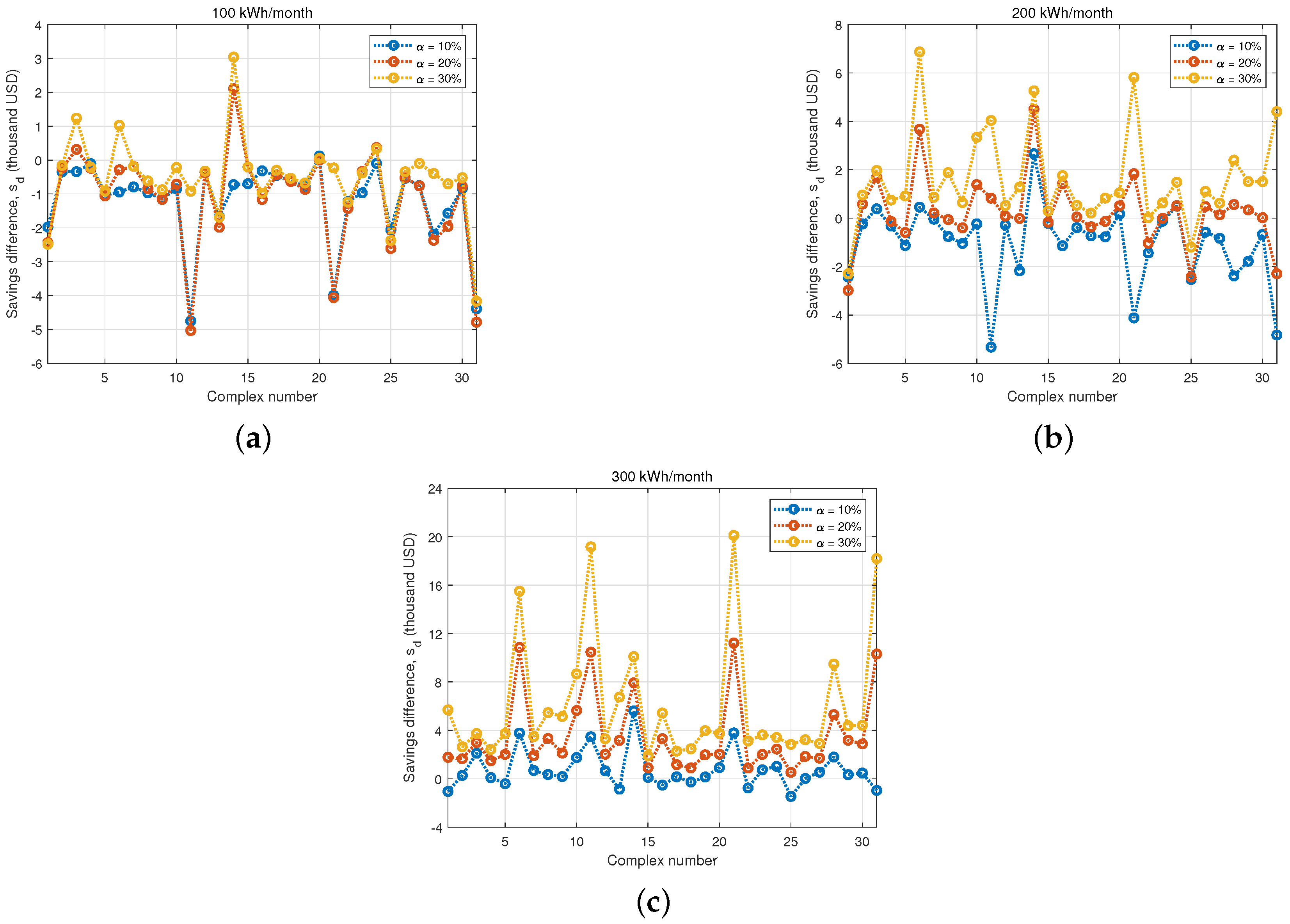
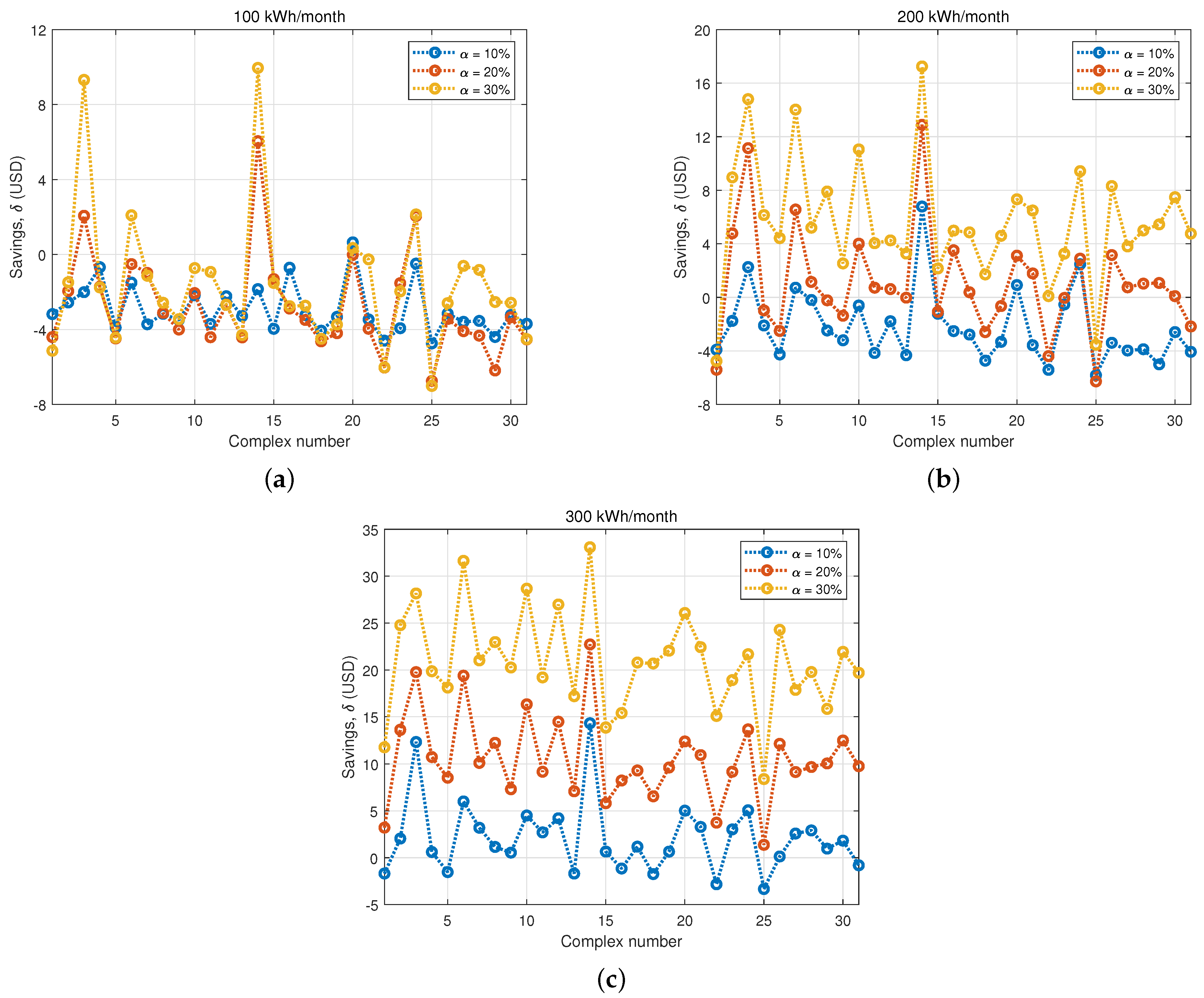
3.2. Electricity Usage Reduction by Selected Households
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMI | advanced metering infrastructure |
| GC | general contract |
| HV | high voltage |
| KEPCO | Korea Electric Power Corporation |
| KMA | Korea Meteorological Administration |
| LV | low voltage |
| PV | photovoltaic |
| SC | single contract |
| TOU | time of use |
Appendix A. Photovoltaic (PV) Solar Energy Generation
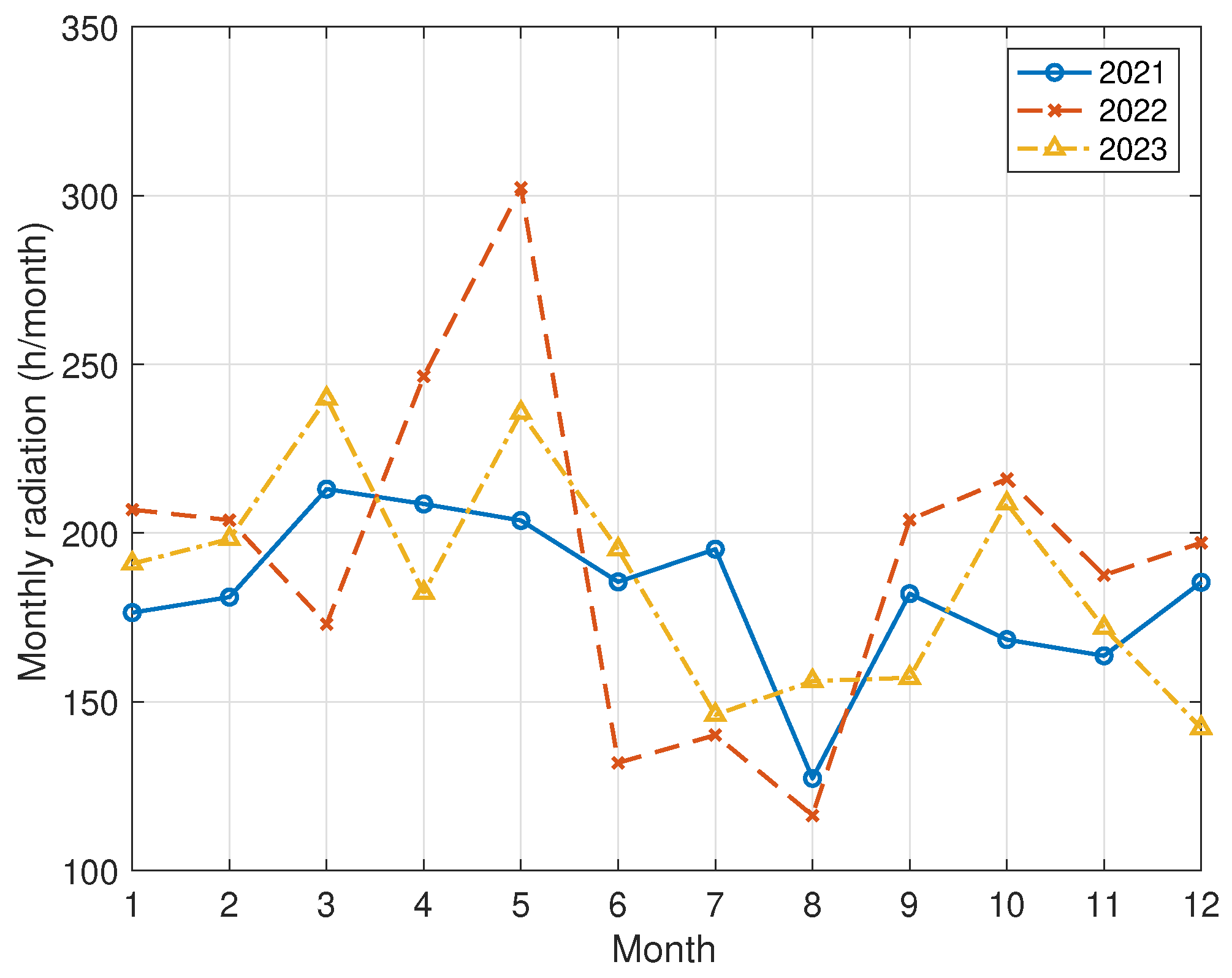
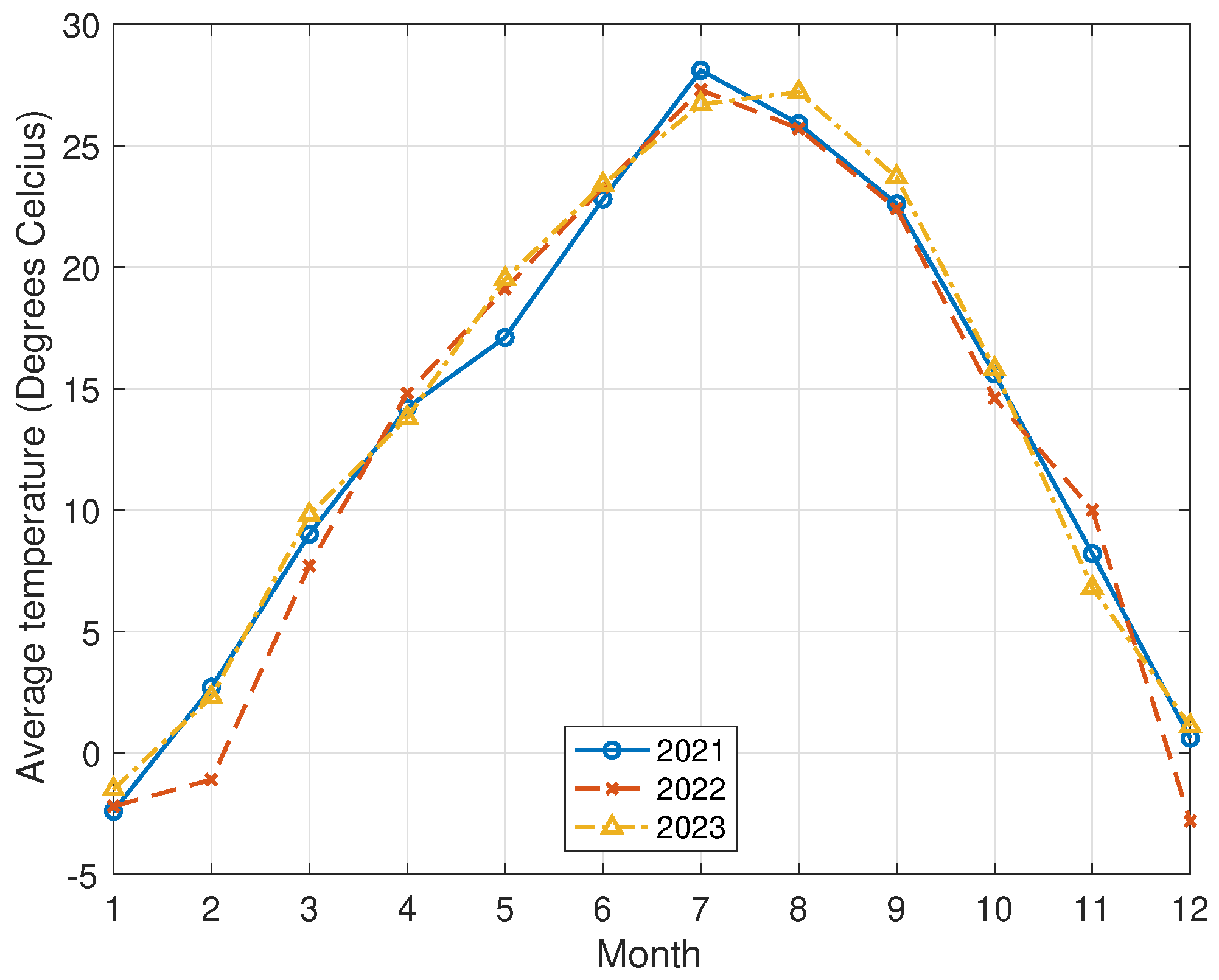
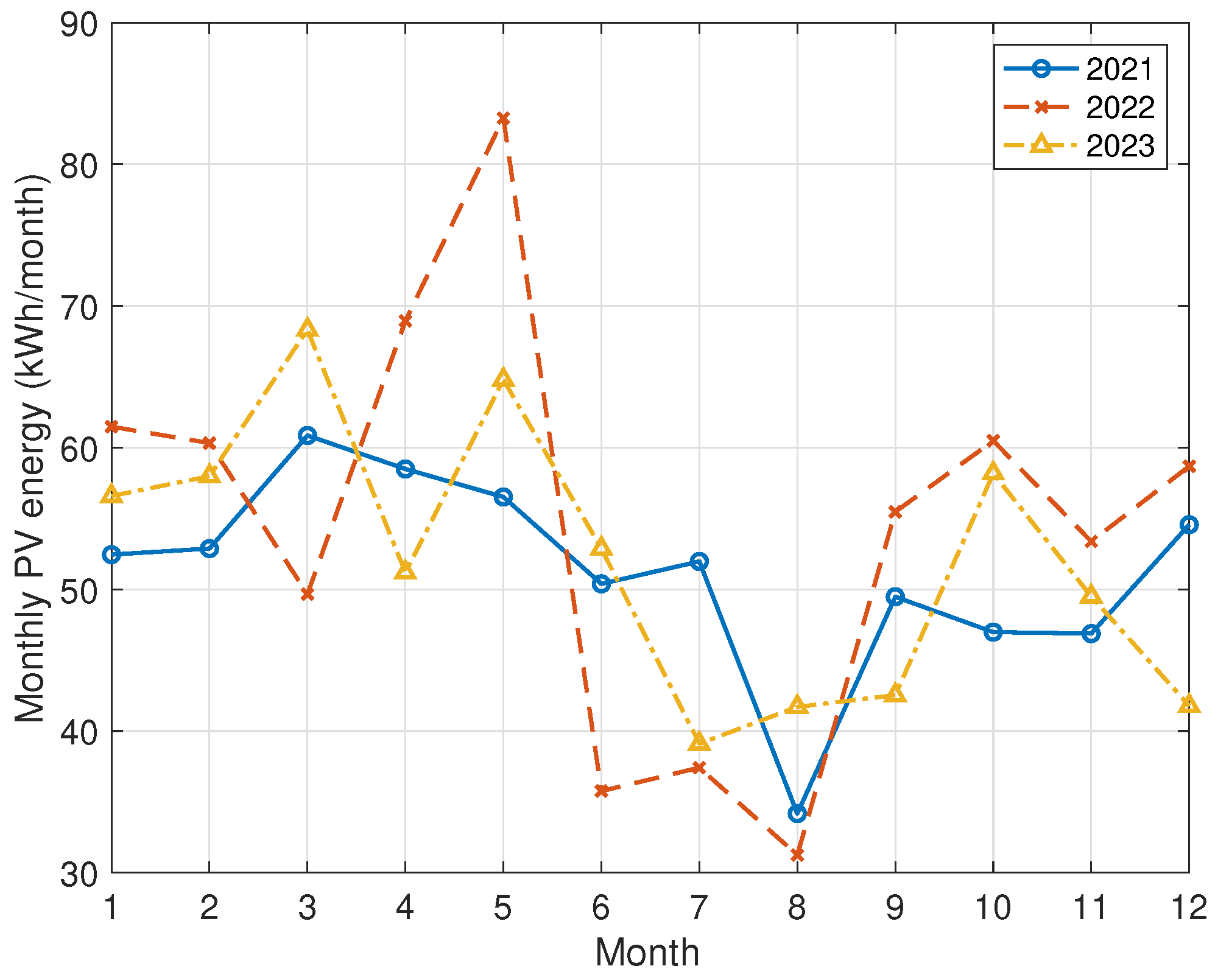
References
- Kim, D.S.; Jung, W.; Chung, B.J. Analysis of the electricity supply contracts for medium-voltage apartments in the Republic of Korea. Energies 2021, 14, 293. [Google Scholar] [CrossRef]
- Chung, Y.M.; Kang, S.; Jung, J.; Chung, B.J.; Kim, D.S. Residential electricity rate plans and their selections based on statistical learning. IEEE Access 2022, 10, 74012–74022. [Google Scholar] [CrossRef]
- Zhou, S.; Matisoff, D. Advanced metering infrastructure deployment in the United States: The impact of polycentric governance and contextual changes. Rev. Policy Res. 2016, 33, 646–665. [Google Scholar] [CrossRef]
- DOE. AMI and Customer Systems: Results from the SGIG Program; DOE: Washington, DC, USA, 2016. [Google Scholar]
- World Bank Group. Survey of International Experience in Advanced Metering Infrastructure and Its Implementation; World Bank Group: Washington, DC, USA, 2018. [Google Scholar]
- IRENA. Time-of-Use Tariffs: Innovation Landscape Brief; IRENA: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Barjaková, M.; Belton, C.A.; Purcell, K.; Lunn, P.D. Effective communication of time–of–use electricity tariffs: Plain and simple. Util. Policy 2024, 90, 101798. [Google Scholar] [CrossRef]
- Chen, Y.T. The factors affecting electricity consumption and the consumption characteristics in the residential sector—A case example of Taiwan. Sustainability 2017, 9, 1484. [Google Scholar] [CrossRef]
- Statistics Korea. 2023 Population and Housing Census (Register-Based Census); Statistics Korea: Daejon, Republic of Korea, 2024. [Google Scholar]
- KEPCO. Electricity Rate System; KEPCO: Naju, Republic of Korea, 2024. [Google Scholar]
- KEPCO. Basic Terms of Supply; KEPCO: Naju, Republic of Korea, 2024. [Google Scholar]
- Fajardy, M.; Reiner, D.M. An Overview of the Electrification of Residential and Commercial Heating and Cooling and Prospects for Decarbonisation; Univeristy of Cambridge: Cambridge, UK, 2020. [Google Scholar]
- Deason, J.; Borgeson, M. Electrification of buildings: Potential, challenges, and outlook. Curr. Sustain. Energy Rep. 2019, 6, 131–139. [Google Scholar] [CrossRef]
- Lu, S.; Ren, J. A comprehensive review on energy poverty: Definition, measurement, socioeconomic impact and its alleviation for carbon neutrality. In Environment, Development and Sustainability; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Murshed, M. A regional appraisal of electricity accessibility determinants: The relevance of international remittances, clean energy, income inequality, and institutional quality. Environ. Sci. Pollut. Res. 2023, 30, 51228–51244. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Chai, L.; Feng, X.; Wei, Y.; Zhang, H. Research on the driving factors and policy guidance for a reduction in electricity consumption by urban residents. Energies 2024, 17, 5122. [Google Scholar] [CrossRef]
- Mehdipour Pirbazari, A.; Farmanbar, M.; Chakravorty, A.; Rong, C. Short-term load forecasting using smart meter data: A generalization analysis. Processes 2020, 8, 484. [Google Scholar] [CrossRef]
- Shu, C.; Xu, F.; Xiang, N. Research on determinants of urban residential electricity conservation behaviors based on intervention experiment—The evidence from household survey of 4 megacities in China. In Proceedings of the 2020 International Conference on Resource Sustainability: Sustainable Urbanisation in the BRI Era, Singapore, 13–15 December 2020; pp. 205–215. [Google Scholar]
- Sun, Y.; Yuan, Z.; Sun, K.; Wang, B. Electricity-saving potential of residential buildings: Empirical evidence from resident habits. Energy Effic. 2023, 16, 90. [Google Scholar] [CrossRef]
- Chung, Y.M.; Chung, B.J.; Kim, D.S. Analysis of residential electricity usage characteristics and the effects of shifting home appliance usage time under a time-of-use rate plan. Energies 2023, 16, 6602. [Google Scholar] [CrossRef]
- Yu, T.; Kim, D.S.; Son, S.Y. Optimization of scheduling for home appliances in conjunction with renewable and energy storage resources. Int. J. Smart Home 2012, 7, 261–272. [Google Scholar]
- KEPCO. Past Electricity Rate Table (In Korean). Available online: https://online.kepco.co.kr/PRM025D00 (accessed on 24 October 2024).
- Evans, D. Simplified method for predicting photovoltaic array output. Sol. Energy 1981, 27, 555–560. [Google Scholar] [CrossRef]
- Zondag, H. Flat-plate PV-thermal collectors and systems: A review. Renew. Sustain. Energy Rev. 2008, 12, 891–959. [Google Scholar] [CrossRef]
- Dubey, S.; Sarvaiya, J.N.; Seshadri, B. Temperature dependent photovoltaic (PV) efficiency and its effect on PV production in the world—A review. Energy Procedia 2013, 33, 311–321. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, E.; Han, J.; Lee, J. Digitally controlled temperature-compensated crystal oscillator in developing low-cost radio frequency modules. Int. J. Inform. 2015, 18, 3157–3166. [Google Scholar]



| Base Rate (USD) | Usage Rate (USD/kWh) | ||||
|---|---|---|---|---|---|
| 0.539 | 0.930 | 4.474 | 0.078 | 0.128 | 0.179 |
| (730) | (1260) | (6060) | (105.0) | (174.0) | (242.3) |
| Complex | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 691 | 152 | 190 | 174 | 295 | 700 | 237 | 340 | 363 | 432 | 1426 |
| Area () | 33–40 | 60–85 | 59–115 | 60–115 | 59–114 | 49–60 | 33–84 | 73–85 | 59–109 | 69–85 | 60–115 |
| Complex | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| N | 175 | 561 | 436 | 196 | 504 | 158 | 171 | 258 | 205 | 1281 | 296 |
| Area () | 31 | 59–115 | 85 | 60–127 | 60–85 | 60–102 | 60–115 | 60–114 | 60–85 | 60–115 | 56–121 |
| Complex | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
| N | 274 | 223 | 482 | 190 | 233 | 685 | 396 | 288 | 1320 | ||
| Area () | 60–84 | 60–124 | 59–84 | 60–115 | 60–85 | 28–119 | 108–134 | 60–105 | 72–127 |
| Usage Reduction | 100 kWh | 200 kWh | 300 kWh |
|---|---|---|---|
| Savings with usage reduction when = 10% | 24,695 (Complex 21, Year 2) | 45,530 (Complex 11, Year 1) | 73,220 (Complex 11, Year 1) |
| Savings with usage reduction when = 20% | 45,371 (Complex 11, Year 1) | 94,956 (Complex 11, Year 1) | 138,889 (Complex 11, Year 1) |
| Savings with usage reduction when = 30% | 73,066 (Complex 11, Year 1) | 139,043 (Complex 11, Year 1) | 205,570 (Complex 11, Year 1) |
| Usage Reduction | 100 kWh | 200 kWh | 300 kWh |
|---|---|---|---|
| Savings with usage reduction when = 10% | 216 (Complex 16, Year 1) | 402 (Complex 16, Year 1) | 559 (Complex 16, Year 1) |
| Savings with usage reduction when = 20% | 201 (Complex 16, Year 1) | 378 (Complex 16, Year 1) | 518 (Complex 16, Year 1) |
| Savings with usage reduction when = 30% | 194 (Complex 16, Year 2) | 358 (Complex 29, Year 1) | 491 (Complex 16, Year 1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, Y.M.; Chung, B.J.; Kim, D.S. Electricity Bill Savings from Reduced Household Energy Consumption in Apartment Complexes. Energies 2024, 17, 5488. https://doi.org/10.3390/en17215488
Chung YM, Chung BJ, Kim DS. Electricity Bill Savings from Reduced Household Energy Consumption in Apartment Complexes. Energies. 2024; 17(21):5488. https://doi.org/10.3390/en17215488
Chicago/Turabian StyleChung, Young Mo, Beom Jin Chung, and Dong Sik Kim. 2024. "Electricity Bill Savings from Reduced Household Energy Consumption in Apartment Complexes" Energies 17, no. 21: 5488. https://doi.org/10.3390/en17215488
APA StyleChung, Y. M., Chung, B. J., & Kim, D. S. (2024). Electricity Bill Savings from Reduced Household Energy Consumption in Apartment Complexes. Energies, 17(21), 5488. https://doi.org/10.3390/en17215488







