Low-Carbon Optimization Scheduling of Integrated Energy Systems Based on Bilateral Demand Response and Two-Level Stackelberg Game
Abstract
1. Introduction
2. Energy Flow and Device Model
2.1. IES Energy Flow
2.2. Device Model
2.2.1. CCS-P2G-CHP Model
2.2.2. IDR Model
2.2.3. Garbage Incineration Device Model
2.2.4. ESS
3. A Multi-Agent Optimization Model Considering Bilateral IDR Trading Mechanism
3.1. Bilateral IDR Trading Mechanism
3.2. IES Model
3.2.1. IES Objective Function
- (1)
- The operating cost of CCS-P2G-CHP unit
- (2)
- External interaction costs
- (3)
- Ladder-type carbon trading cost
- (4)
- IDR cost
3.2.2. IES Constraint Condition
3.2.3. Uncertainty Model of WT Output
3.3. LA Model
3.3.1. LA Objective Function
3.3.2. LA Constraint Condition
3.4. User Model
3.4.1. User Objective Function
3.4.2. User Constraint Conditions
4. A Two-Level Stackelberg Game Model
A Two-Level Stackelberg Game
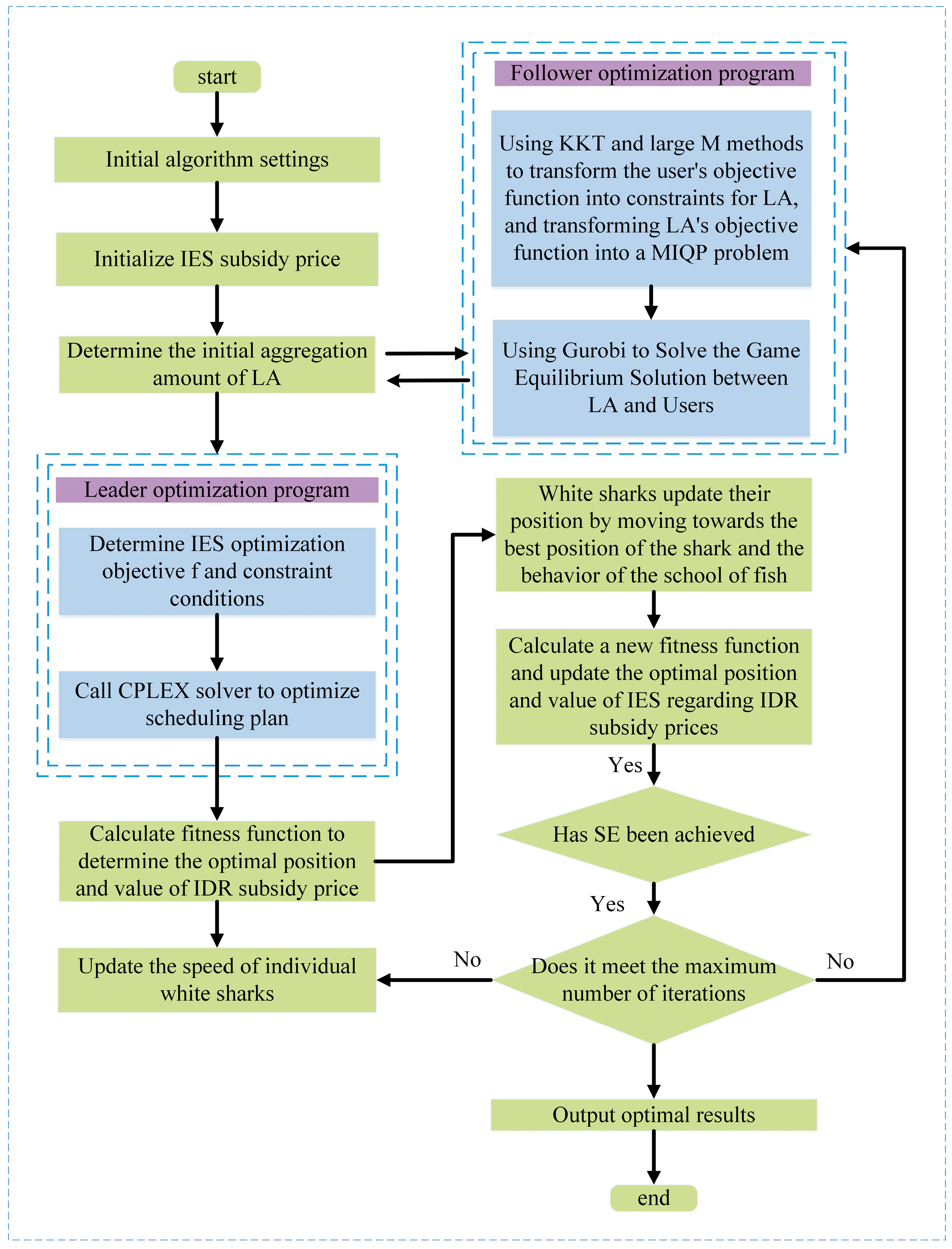
5. Solving Game Models
5.1. KKT Conversion
5.2. Linear Transformation
5.3. Solving Process
6. Example Analysis
6.1. Parameter Settings
6.2. Comparative Analysis of Economic and Environmental Benefits
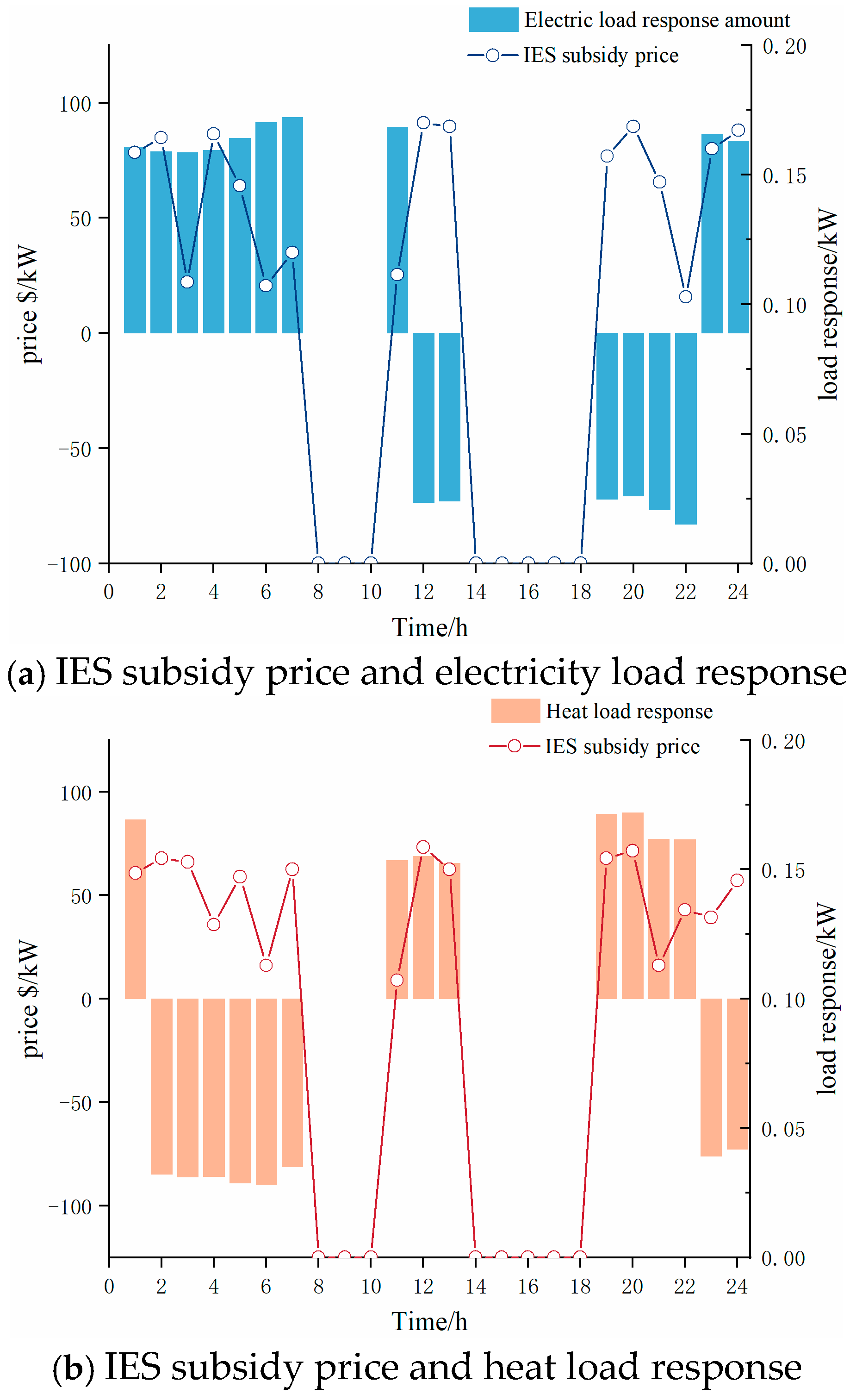
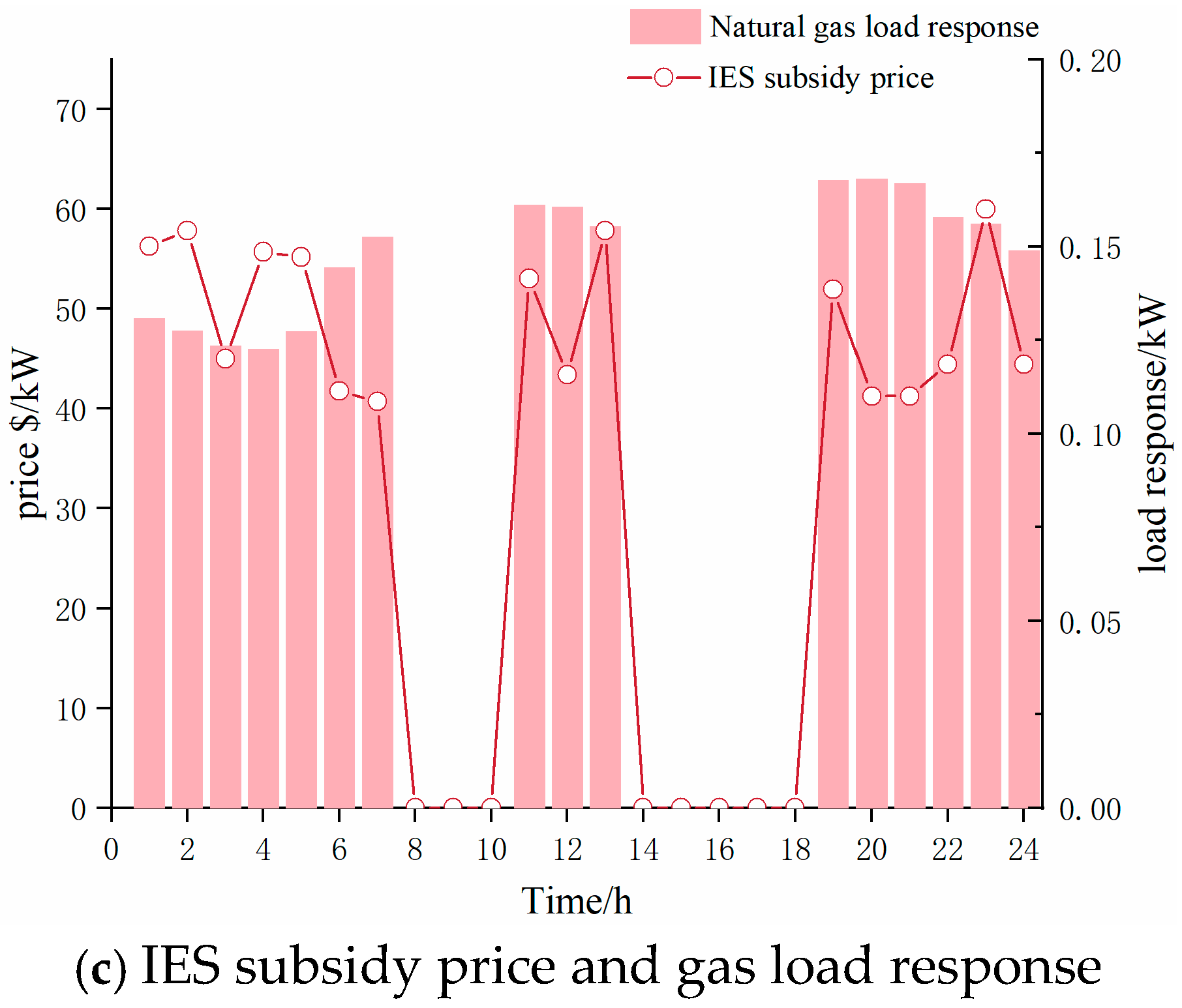
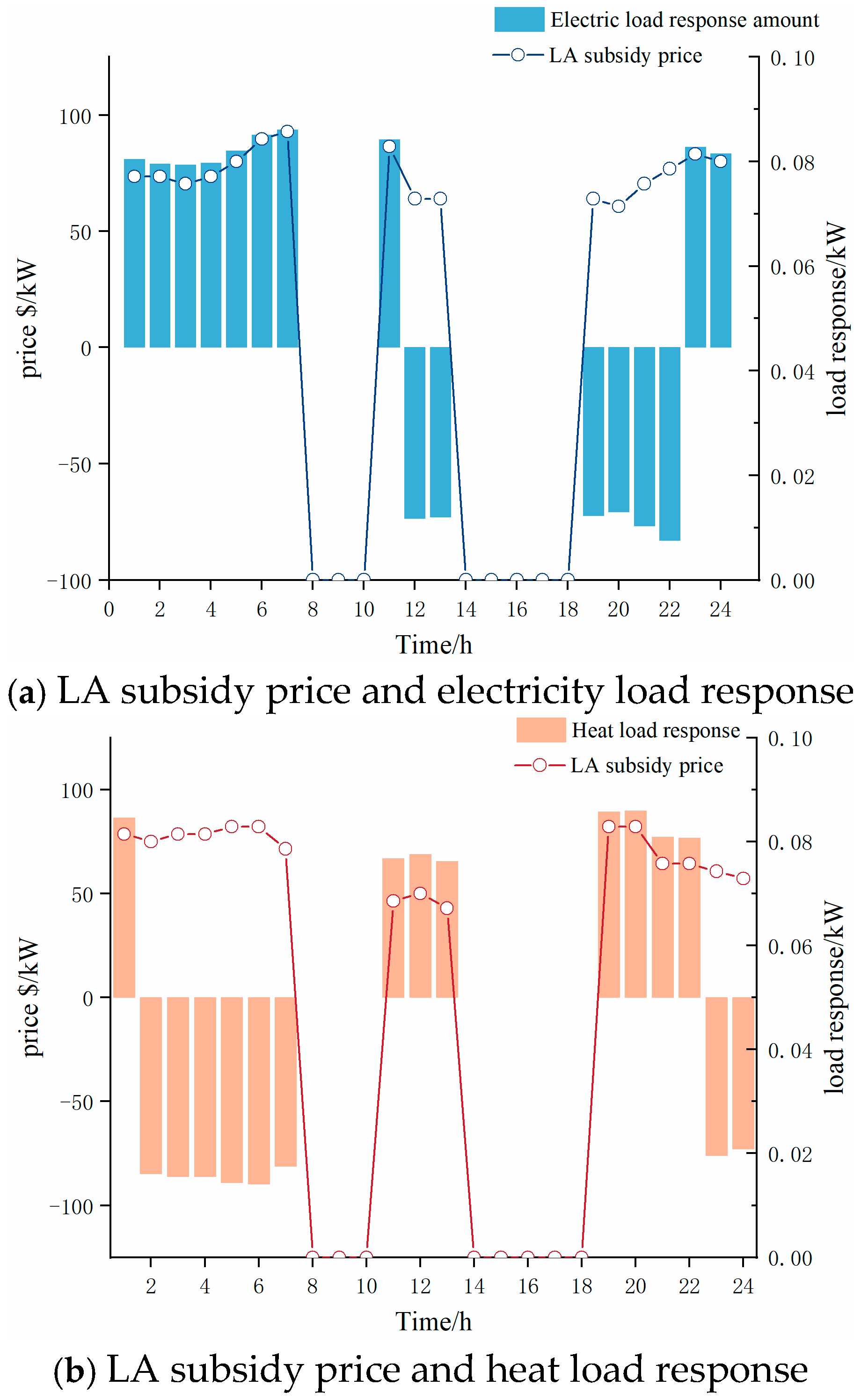
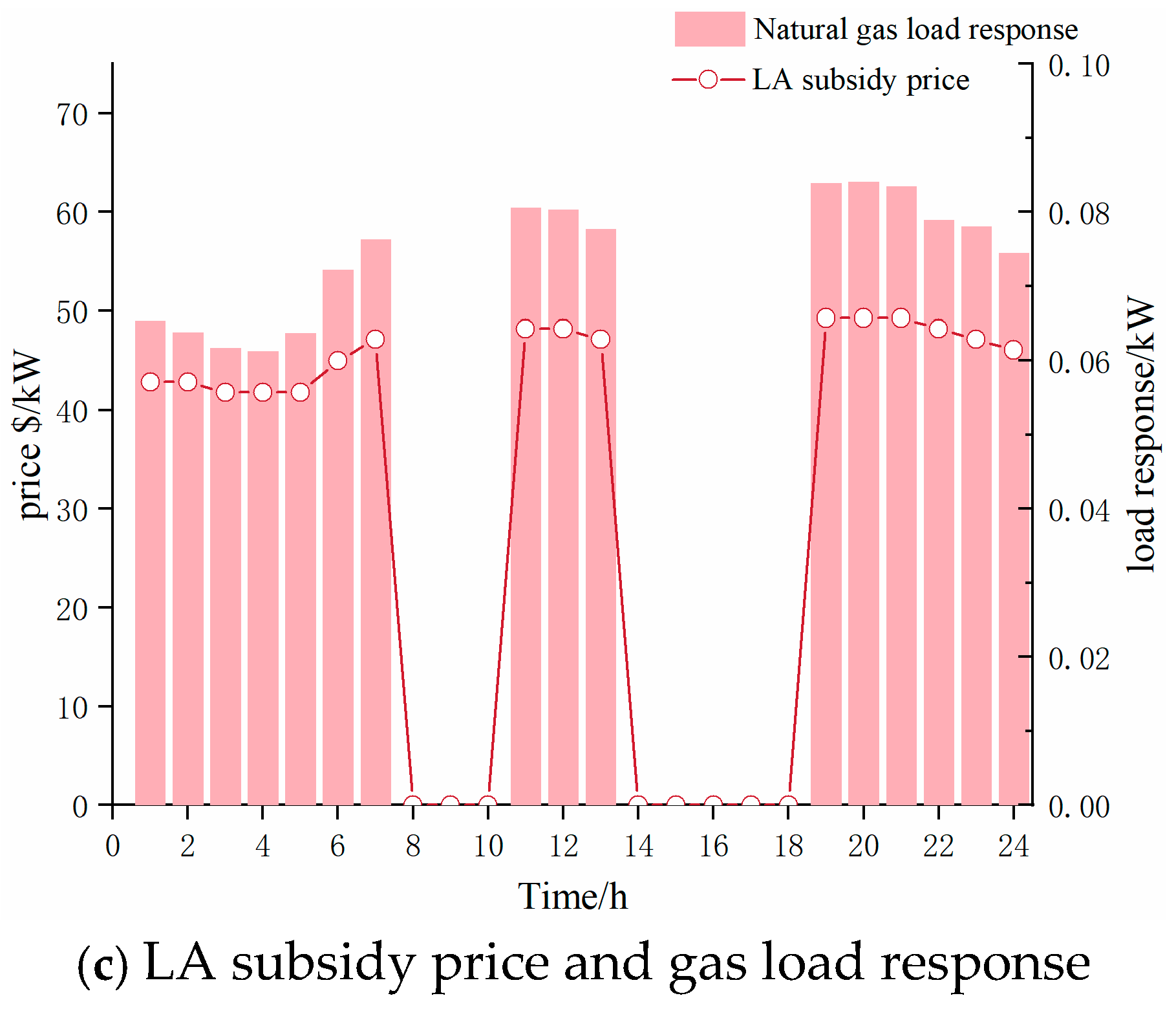
6.3. IDR Subsidy Prices and Response Amount
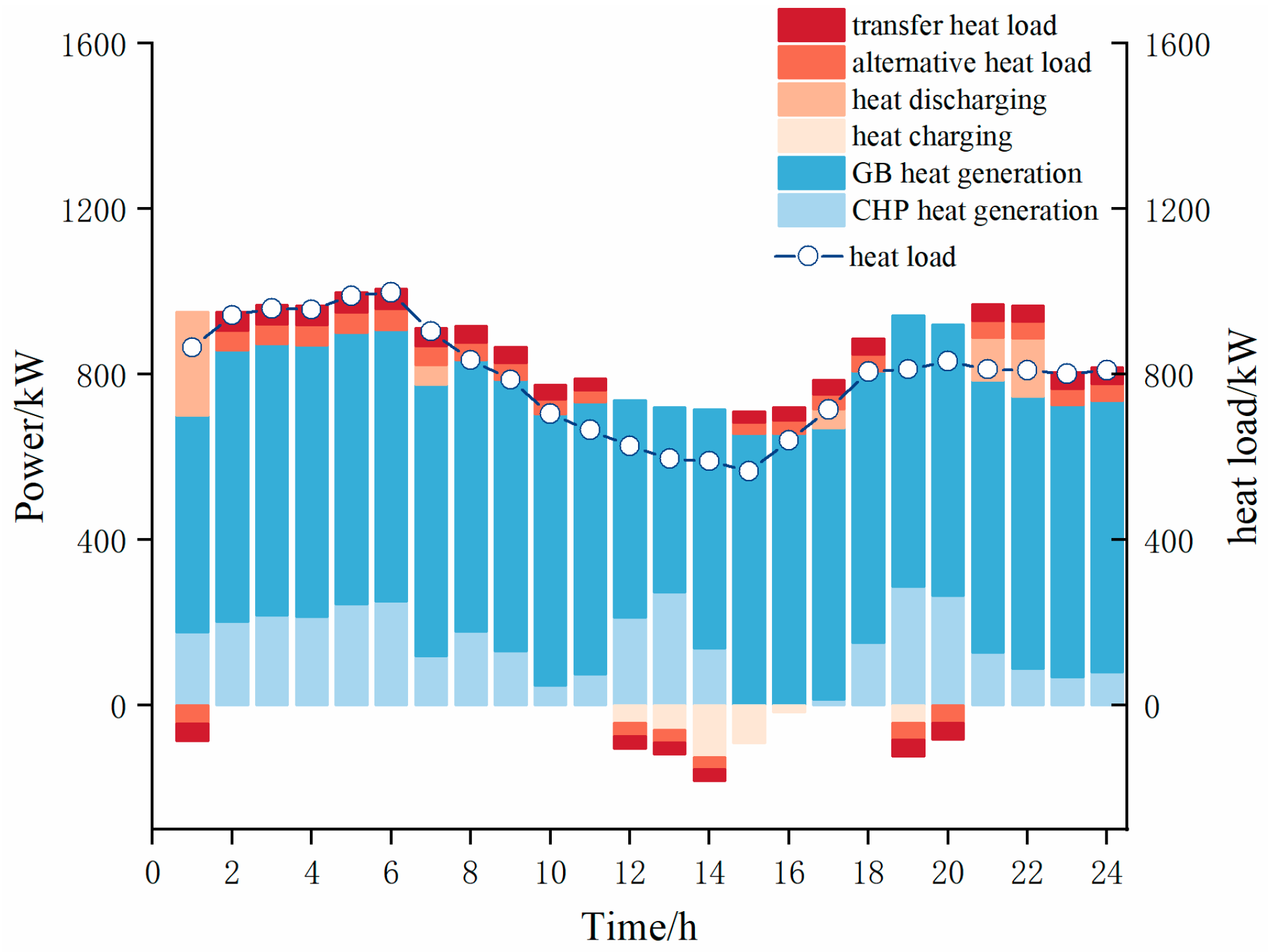
6.4. Scheduling Results
6.5. Sensitivity Analysis of Ladder-Type Carbon Trading Parameters
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IDR | Integrated demand response |
| IES | Integrated energy system |
| LA | Load aggregator |
| DSO | Distribution system operator |
| UA | User aggregators |
| CCS | Carbon capture systems |
| P2G | Power to gas |
| CHP | Combined heat and power |
| WT | Wind turbine |
| KKT | Karush–Kuhn–Tucke |
| WSO | White Shark Optimization |
| GBs | Gas boilers |
| GT | Gas turbine |
| WHB | Waste heat boiler |
| Variables | |
| Generated power via GT (kW) | |
| Natural gas consumption of GT (kg) | |
| Generated heat power via GT (kW) | |
| Natural gas consumption of GB (kg) | |
| Electrical power consumption of CCS (kW) | |
| Carbon dioxide required by P2G (kg) | |
| Natural gas generated by P2G | |
| Electrical power consumption of P2G (kW); | |
| Translatable load (kW) | |
| Alternative load (kW) | |
| Fixed load (kW) | |
| Generated power via garbage incineration device (kW) | |
| Energy consumption of the flue gas treatment system (kW) | |
| Power of charging and discharging energy (kW) | |
| Operating cost of IES (USD) | |
| Operating cost of CCS-P2G-CHP unit (USD) | |
| External interaction costs (USD) | |
| ladder-type carbon trading cost (USD) | |
| IDR cost (USD) | |
| DR subsidy price provided by IES to LA (USD) | |
| DR resources aggregated by LA (kW) | |
| Utility function of LA (USD) | |
| IDR subsidy cost provided by IES to LA (USD) | |
| Subsidy prices provided by LA to users (USD) | |
| DR resources provided by user (kW) | |
| Parameters | |
| Power generation efficiency of CHP | |
| Combustion heat value of natural gas | |
| Upper/lower limits of GT power generation (kW). | |
| Minimum/maximum power generation via CHP at time t (kW). | |
| Thermoelectric conversion coefficients | |
| The linear supply slope of the CHP thermoelectric power | |
| Heat production efficiency | |
| Lower/upper limit of CCS power consumption (kW). | |
| Lower/upper limit of P2G power consumption (kW). | |
| Energy conversion coefficient for capturing carbon dioxide consumption | |
| Flue gas flowing into the reaction tower and storage tank | |
| Flue gas generated per unit of electrical energy | |
| Energy consumption coefficient of the flue gas treatment system | |
| Energy loss coefficient | |
| Minimum/maximum remaining capacity (kW). | |
| Upper limit of energy power for charging/discharging (kW). | |
| Operating cost coefficient of the CCS-P2G-CHP coupling system | |
| Operating and maintenance cost coefficients of P2G and CCS | |
| Purchase price and amount of natural gas (USD) | |
| Purchase price and amount of electricity (USD) | |
| Carbon emission quota of IES | |
| Carbon dioxide emission coefficients of CHP units, GB, and garbage incineration devices | |
| Carbon trading base price | |
| Interval length of carbon emissions | |
| Price increase rate | |
| Upper limits of the DR aggregated by LA | |
| Minimum and maximum DR subsidy prices provided by IES (USD) | |
| Maximum allowable deviation of WT | |
| Proportional deviation of WT output | |
| Uncertainty of the model | |
| Dual variable | |
| 0–1 variable | |
| Combustion heat value of natural gas | |
| Upper/lower limits of GT power generation (kW) | |
| Minimum/maximum power generation via CHP at time t (kW) | |
| Upper limit of energy power for charging/discharging (kW) | |
| Operating cost coefficient of the CCS-P2G-CHP coupling system |
Appendix A

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.35 | 0.425 | ||
| 35 | 0.55 | ||
| 50 | 0.65 | ||
| 500 | 18.20 | ||
| 0.15 | 0.25 | ||
| 0.2 | 5 | ||
| 0.85 | 0.25 | ||
| 0.9 | 0.013 | ||
| 0.55 | 0.004 | ||
| 0.2 | 0.039 | ||
| 0.6 | 0.15 | ||
| 0.96 | 0.2 | ||
| 0.513 | 0.15 | ||
| 0.02 | 0.2 | ||
| 0.02 | 9.8 | ||
| 0.95 | 0.76 | ||
| 50 | 0.3 | ||
| 500 | 0.02 | ||
| 100 | 0.9 | ||
| 100 | 100 | ||
| 50 | 100 | ||
| 500 | 150 | ||
| 39 |
| Carbon Trading Base Price | IES Total Cost | Electricity Purchase Cost | Gas Purchase Cost | Carbon Trading Cost |
|---|---|---|---|---|
| 0.1 | 3300.92 | 317.47 | 1897.33 | 503.47 |
| 0.15 | 3522.68 | 363.46 | 1881.43 | 726.78 |
| 0.2 | 3735.13 | 473.78 | 1846.14 | 903.66 |
| 0.25 | 3798.30 | 488.27 | 1768.65 | 1043.01 |
| 0.3 | 4119.60 | 557.69 | 1822.28 | 1281.18 |
| 0.35 | 4326.40 | 579.26 | 1817.22 | 1478.59 |
| 0.40 | 4517.19 | 584.36 | 1814.56 | 1685.03 |
| Price Growth Rate | IES Total Cost | Electricity Purchase Cost | Gas Purchase Cost | Carbon Trading Cost |
|---|---|---|---|---|
| 0.1 | 3705.63 | 393.83 | 1877.20 | 886.93 |
| 0.15 | 3791.90 | 474.07 | 1852.38 | 941.87 |
| 0.2 | 3873.94 | 523.42 | 1839.00 | 1002.64 |
| 0.25 | 3809.00 | 489.64 | 1773.63 | 1045.95 |
| 0.4 | 4159.84 | 583.29 | 1820.58 | 1322.42 |
| 0.6 | 4460.98 | 611.81 | 1813.47 | 1647.85 |
| 0.80 | 4775.20 | 659.72 | 1804.20 | 1945.57 |
References
- Liang, T.; Zhang, X.; Tan, J.; Jing, Y.; Lv, L. Deep reinforcement learning-based optimal scheduling of integrated energy systems for electricity, heat, and hydrogen storage. Electr. Power Syst. Res. 2024, 233, 110480. [Google Scholar] [CrossRef]
- Wang, C.; Chen, S.; Zhao, J.; Zhou, Y.; Wei, Z.; Zheng, S. Coordinated scheduling of integrated electricity, heat, and hydrogen systems considering energy storage in heat and hydrogen pipelines. J. Energy Storage 2024, 85, 111034. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, X. Flexible resource optimization allocation of park electric heating integrated energy system considering demand response. Mod. Electr. Power 2023, 1–11. [Google Scholar] [CrossRef]
- Mo, J.; Yan, G.; Song, N.; Yuan, M. A review of research on optimization and scheduling of electric heating integrated energy systems based on demand response. Adv. Eng. Sci. 2023, 1–16. [Google Scholar] [CrossRef]
- Nawaz, A.; Zhou, M.; Wu, J.; Long, C. A comprehensive review on energy management, demand response, and coordination schemes utilization in multi-microgrids network. Appl. Energy 2022, 323, 119596. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Z. Low carbon economic scheduling model for a park integrated energy system considering integrated demand response, ladder-type carbon trading and fine utilization of hydrogen. Energy 2024, 290, 130311. [Google Scholar] [CrossRef]
- Zhang, G.; Niu, Y.; Xie, T.; Zhang, K. Multi-level distributed demand response study for a multi-park integrated energy system. Energy Rep. 2023, 9, 2676–2689. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, J.; Yu, P.; Tinajero, G.D.; Guan, Y.; Yan, Q.; Zhang, X.; Guo, H. Dual-Stackelberg game-based trading in community integrated energy system considering uncertain demand response and carbon trading. Sustain. Cities Society 2024, 101, 105088. [Google Scholar] [CrossRef]
- Tan, M.; Wang, L.; Jiang, C.; Liu, H.; Wu, L.; Tang, J. A Double Layer Optimization Model for Demand Response Considering the Adjustment Potential of Load Aggregators. Electr. Power 2022, 55, 32–44. [Google Scholar]
- Jangid, B.; Mathuria, P.; Gupta, V. A hierarchical scheduling framework for DSO and shiftable load aggregator. Electr. Power Syst. Res. 2023, 225, 109861. [Google Scholar] [CrossRef]
- Yan, H.; Hou, H.; Deng, M.; Si, L.; Wang, X.; Hu, E.; Zhou, R. Stackelberg game theory based model to guide users’ energy use behavior, with the consideration of flexible resources and consumer psychology, for an integrated energy system. Energy 2024, 288, 129806. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y.; Zhao, X.; Xu, N.; Li, C.; Xue, W. Dual layer optimization scheduling strategy for regional integrated energy systems considering demand response. Electr. Power 2021, 54, 141–150. [Google Scholar]
- Li, Z.; Liu, Q.; Guo, W. Stackelberg Game Strategy Between Integrated Energy Microgrid Operators and Load Aggregators Considering Users Energy Consumption Behavior. South. Power Syst. Technol. 2022, 16, 35–46. [Google Scholar]
- Najafi, A.; Jasiński, M.; Leonowicz, Z. A hybrid distributed framework for optimal coordination of electric vehicle aggregators problem. Energy 2022, 249, 123674. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Tan, Z. Optimization of dual layer master-slave game operation in comprehensive energy systems considering load aggregators. Renew. Energy Resour. 2023, 41, 1554–1562. [Google Scholar]
- Li, S.; Zhang, L.; Nie, L.; Wang, J. Trading strategy and benefit optimization of load aggregators in integrated energy systems considering integrated demand response: A hierarchical Stackelberg game. Energy 2022, 249, 123678. [Google Scholar] [CrossRef]
- Li, J.; Ai, Q.; Yin, S.; Hao, R. An aggregator-oriented hierarchical market mechanism for multi-type ancillary service provision based on the two-loop Stackelberg game. Appl. Energy 2022, 323, 119644. [Google Scholar] [CrossRef]
- Soepyan, F.B.; Habib, M.; Zhang, Z.; Nemetz, L.R.; Haque, M.E.; Esquino, A.M.; Rivero, J.R.; Bhattacharyya, D.; Lipscomb, G.G.; Matuszewski, M.S.; et al. Optimization of a Natural Gas Power Plant with Membrane and Solid Sorbent Carbon Capture Systems. Carbon Capture Sci. Technol. 2024, 10, 100165. [Google Scholar] [CrossRef]
- Park, J.; Kang, S.; Kim, S.; Kim, H.; Cho, H.S.; Lee, J.H. Enhancing the economic viability and reliability of renewables based electricity supply through Power-to-Gas-to-Power with green hydrogen. Energy Convers. Manag. 2024, 310, 118485. [Google Scholar] [CrossRef]
- Chen, M.; Lu, H.; Chang, X.; Liao, H. An optimization on an integrated energy system of combined heat and power, carbon capture system and power to gas by considering flexible load. Energy 2023, 273, 127203. [Google Scholar] [CrossRef]
- Liang, N.; He, X.; Tan, J.; Pan, Z.; Zheng, F. Stackelberg game-based optimal scheduling for multi-community integrated energy systems considering energy interaction and carbon trading. Int. J. Electr. Power Energy Syst. 2023, 153, 109360. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Qu, Y. Optimization and scheduling of integrated energy systems for electricity to gas and carbon cycling based on a tiered carbon trading mechanism and refinement. Mod. Electr. Power 2023, 1–9, 335–343. [Google Scholar]
- Chen, H.; Guo, S.; Song, X.; He, T. Design and evaluation of a municipal solid waste incineration power plant integrating with absorption heat pump. Energy 2024, 294, 131007. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Y.; Liu, W.; Zhang, X.; Wang, X. Two stage scheduling strategy for high-speed railway stations considering temperature control load in green electricity trading scenarios. Acta Energiae Solaris Sin. 2024, 1–10. [Google Scholar] [CrossRef]
- Chen, Z.; Dong, Y.; Teng, M. Hybrid Generation of wind-solar-pumped storage thermal systems considering wind-solar uncertainties. China Rural Water Hydropower 2024, 08, 208–215. [Google Scholar]
- Li, W.; Zou, Y.; Yang, H.; Fu, X.; Li, Z. Two stage stochastic Energy scheduling for multi energy rural microgrids with irrigation systems and biomass fermentation. IEEE Trans. Smart Grid, 2024; early access. [Google Scholar]
- Dong, Y.; Zhang, H.; Ma, P.; Wang, C.; Zhou, X. A hybrid robust-interval optimization approach for integrated energy systems planning under uncertainties. Energy 2023, 274, 127267. [Google Scholar] [CrossRef]
- Zhou, K.; Fei, Z.; Rong, H. Hybrid robust decentralized optimization of emission-aware multi-energy microgrids considering multiple uncertainties. Energy 2023, 265, 126405. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, X.; Zhang, H.; Zhao, C.; Xu, Y. Optimal configuration of integrated energy station using adaptive operation mode of combined heat and power units. Int. J. Electrical Power and Energy Systems 2023, 152, 109171. [Google Scholar] [CrossRef]
- Ma, B.; Yang, L.; Chen, C.; Wang, Y.; Wang, B. Collaborative optimization strategy for integrated energy systems considering demand response. Renew. Energy Resour. 2023, 41, 676–684. [Google Scholar]
- Wang, N.; Jin, Q.; Wang, S.; Gao, Y. A low-carbon co integration optimization model considering the combined operation of waste incineration power plants and electricity to gas conversion. Chin. J. Electr. Eng. 2023, 1–10. [Google Scholar]
- Zheng, W.; Xu, Z.; Shao, Z.; Li, J.; Lei, K.; Li, J. Optimal dispatch of nearly-zero carbon integrated energy system considering waste incineration plant-carbon capture system and market mechanisms. Int. J. Hydrogen Energy 2023, 48, 27013–27031. [Google Scholar] [CrossRef]
- Yan, N.; Li, X.; Wu, Z.; Shao, J.; Guerrero, J.M. Low-Carbon economic scheduling with Demand-Side response uncertainty in regional integrated energy system. Int. J. Electr. Power Energy Syst. 2024, 156, 109691. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, J.; Wang, H.; Zhao, W.; Yang, L. Optimization scheduling of integrated energy systems considering carbon capture and electricity to gas conversion. Electr. Power Autom. Equip. 2023, 43, 127–134. [Google Scholar]
- Wu, Q.; Li, C. Economy-environment-energy benefit analysis for green hydrogen based integrated energy system operation under carbon trading with a robust optimization model. J. Energy Storage 2022, 55, 105560. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. Incentive-based demand response considering hierarchical electricity market: A Stackelberg game approach. Appl. Energy 2017, 203, 267–279. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, H.; Sun, S.; Mi, L. Double layer optimization scheduling of multi microgrid systems considering demand response and shared energy storage. Electr. Power Autom. Equip. 2023, 43, 18–26. [Google Scholar]
- Zhang, Y.; Zhao, H.; Li, B.; Wang, X. Research on dynamic pricing and operation optimization strategy of integrated energy system based on Stackelberg game. Int. J. Electr. Power Energy Syst. 2022, 143, 108446. [Google Scholar] [CrossRef]
- Li, H.; Cui, S.; Fan, W. Low carbon economic scheduling of integrated energy systems based on improved white shark algorithm. Electr. Meas. Instrum. 2023, 6, 1–11. [Google Scholar]
- Xie, C.; Wang, B.; Zhao, S.; Tan, J.; Huang, J.; Xie, Z. Solving Electricity Market Equilibrium Based on Double Layer Particle Swarm Optimization Algorithm. Power Syst. Technol. 2018, 42, 1170–1177. [Google Scholar]
- Chen, J.; Hu, Z.; Chen, J.; Chen, Y.; Gao, M.; Lin, M. Optimization and scheduling of integrated energy systems considering stepped carbon trading and flexible supply-demand dual response. High Volt. Eng. 2021, 47, 3094–3106. [Google Scholar]
- Liu, W.; Yao, Q.; Wang, Y.; Chen, L.; Lu, Y. A master-slave game power planning model based on a stepped demand response mechanism for supply and demand. Autom. Electr. Power Syst. 2022, 46, 54–63. [Google Scholar]



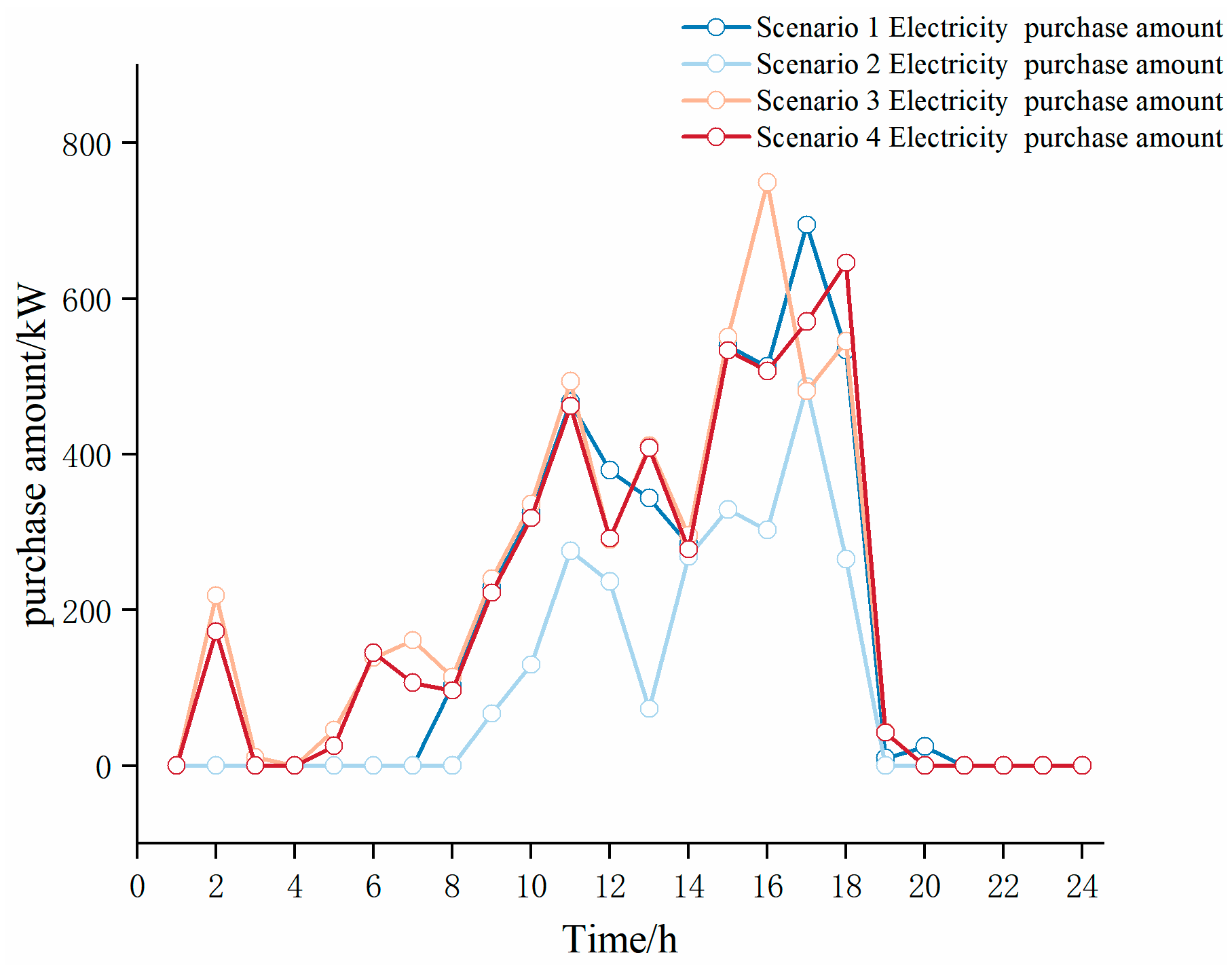
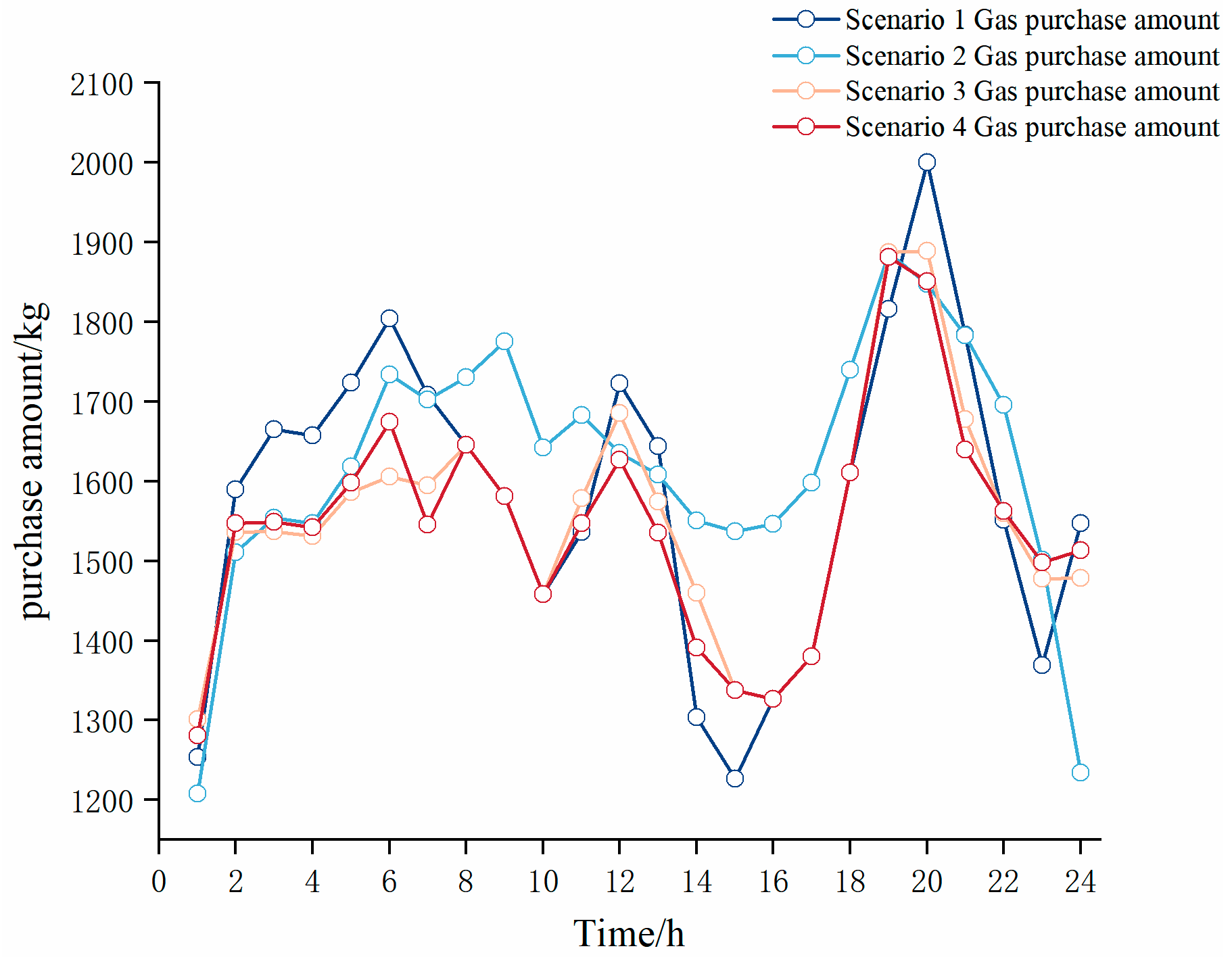

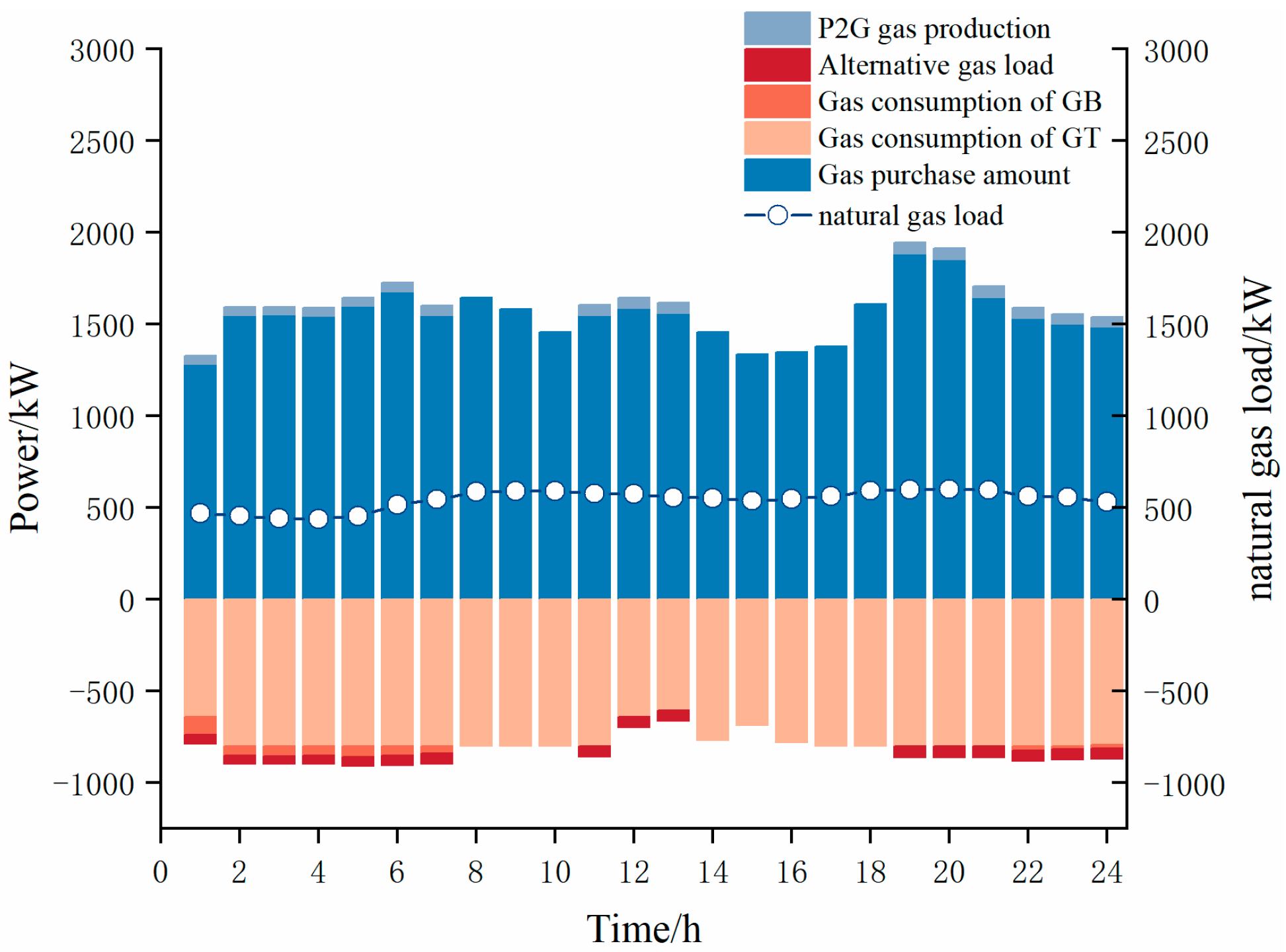
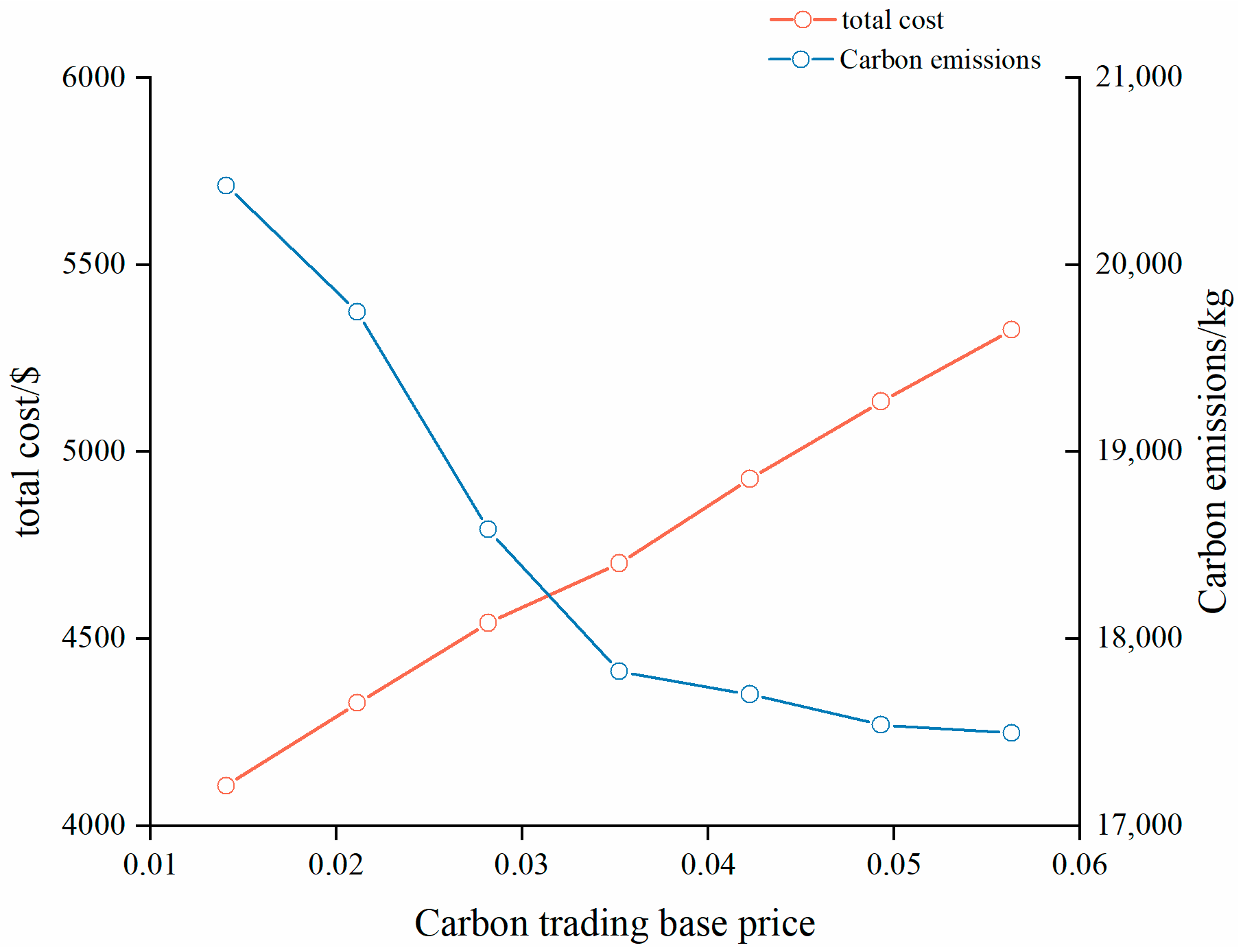

| Scenario | Total Cost/USD | CHP Cost/USD | Electricity Purchase Cost/USD | Gas Purchase Cost/USD | Carbon Trading Cost/USD | Carbon Emissions/kg | IDR Cost/USD | LA Benefits/USD | User Benefits/USD |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4118.91 | 28.17 | 500.58 | 1863.28 | 1278.30 | 20,558.56 | 448.57 | 219.99 | 82.45 |
| 2 | 4174.54 | 66.26 | 274.75 | 1910.74 | - | 21,171.95 | 424.10 | 204.25 | 77.32 |
| 3 | 3950.52 | 21.87 | 541.11 | 1861.64 | 1087.11 | 17,857.54 | 438.78 | 168.74 | 59.50 |
| 4 | 3798.30 | 22.70 | 488.27 | 1768.65 | 1043.01 | 17,826.22 | 475.68 | 223.35 | 91.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Wu, Q.; Guo, H.; Bai, J. Low-Carbon Optimization Scheduling of Integrated Energy Systems Based on Bilateral Demand Response and Two-Level Stackelberg Game. Energies 2024, 17, 5491. https://doi.org/10.3390/en17215491
Pan H, Wu Q, Guo H, Bai J. Low-Carbon Optimization Scheduling of Integrated Energy Systems Based on Bilateral Demand Response and Two-Level Stackelberg Game. Energies. 2024; 17(21):5491. https://doi.org/10.3390/en17215491
Chicago/Turabian StylePan, Hua, Qunli Wu, Huiling Guo, and Jiayi Bai. 2024. "Low-Carbon Optimization Scheduling of Integrated Energy Systems Based on Bilateral Demand Response and Two-Level Stackelberg Game" Energies 17, no. 21: 5491. https://doi.org/10.3390/en17215491
APA StylePan, H., Wu, Q., Guo, H., & Bai, J. (2024). Low-Carbon Optimization Scheduling of Integrated Energy Systems Based on Bilateral Demand Response and Two-Level Stackelberg Game. Energies, 17(21), 5491. https://doi.org/10.3390/en17215491





