Maximum Energy Density for Evaluation of the Dynamic Accuracy of LVDT Sensors Applied in the Energy Industry
Abstract
1. Introduction
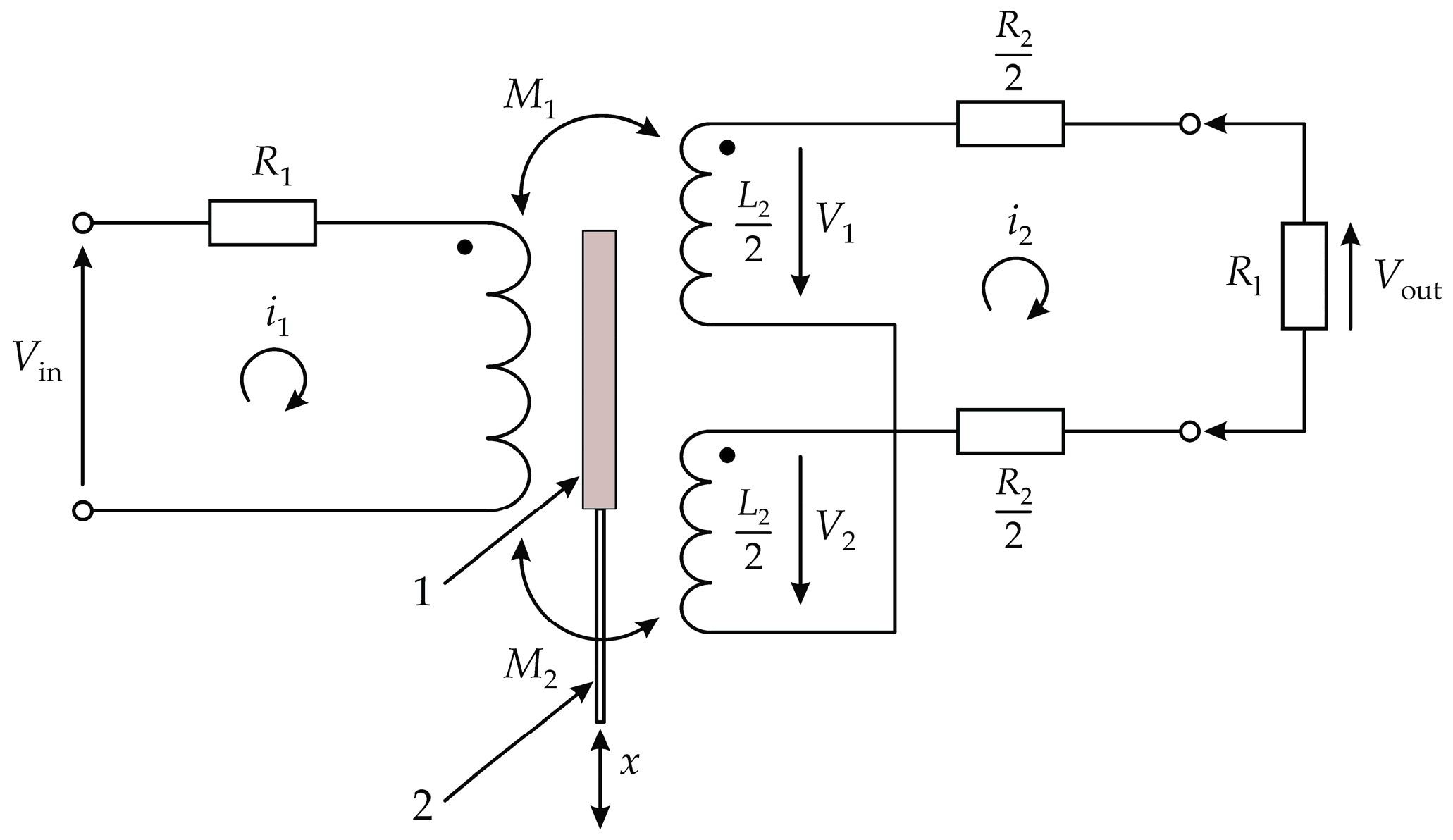
2. Materials and Methods
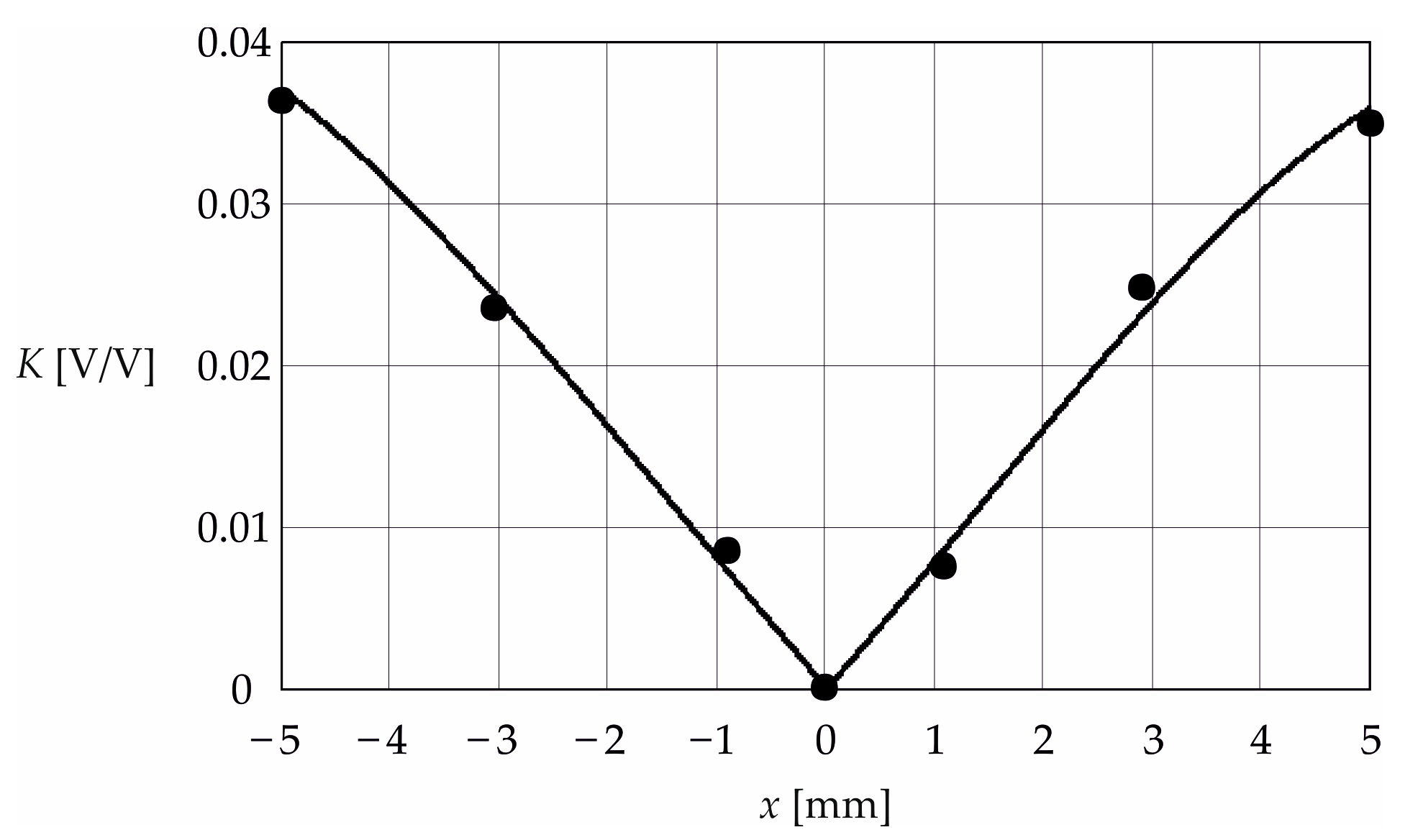
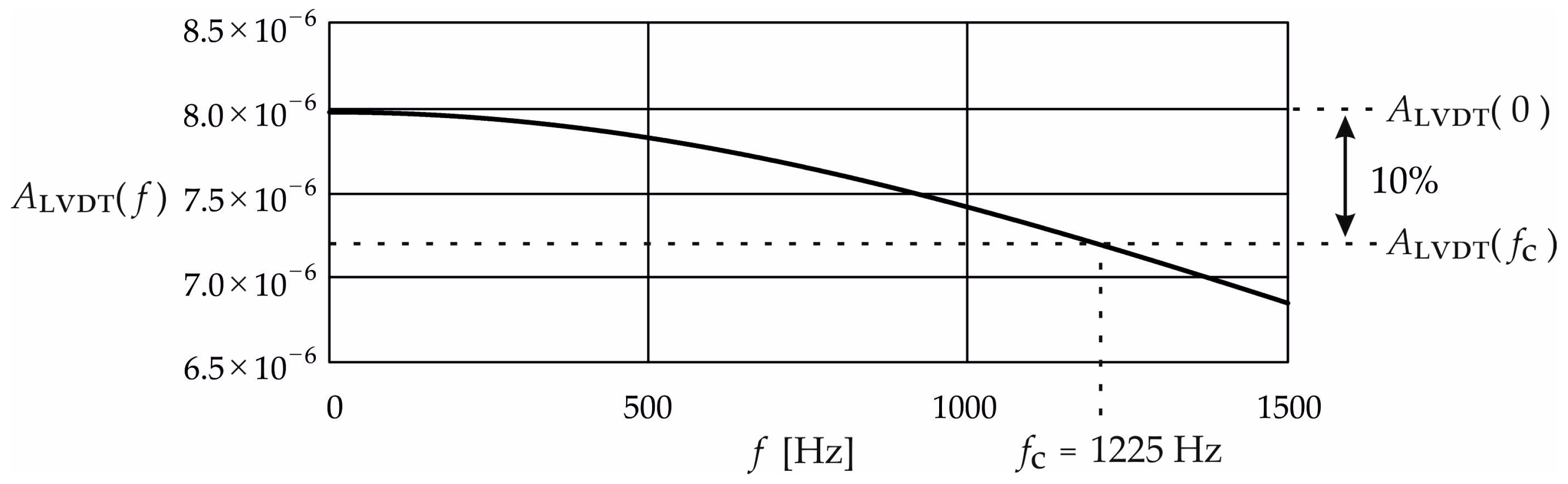
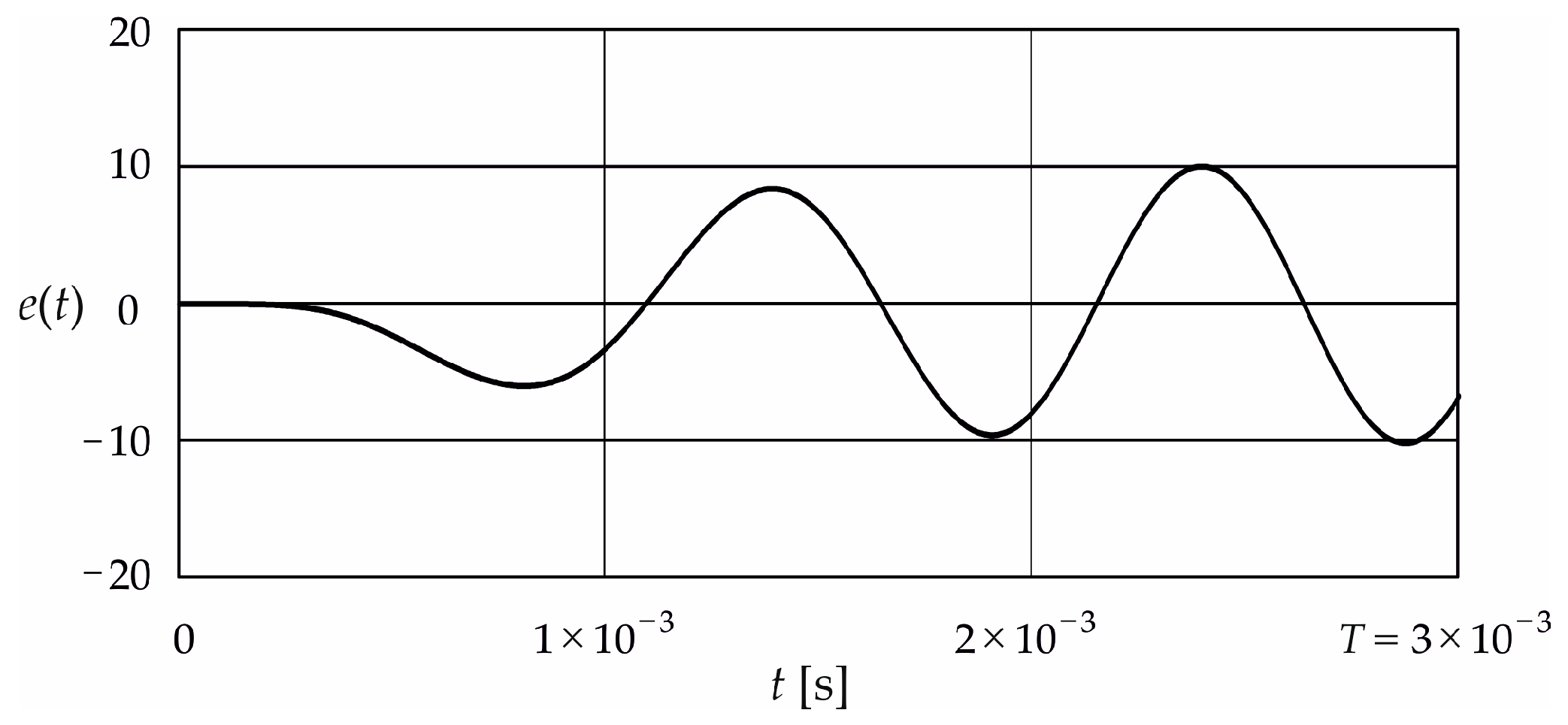
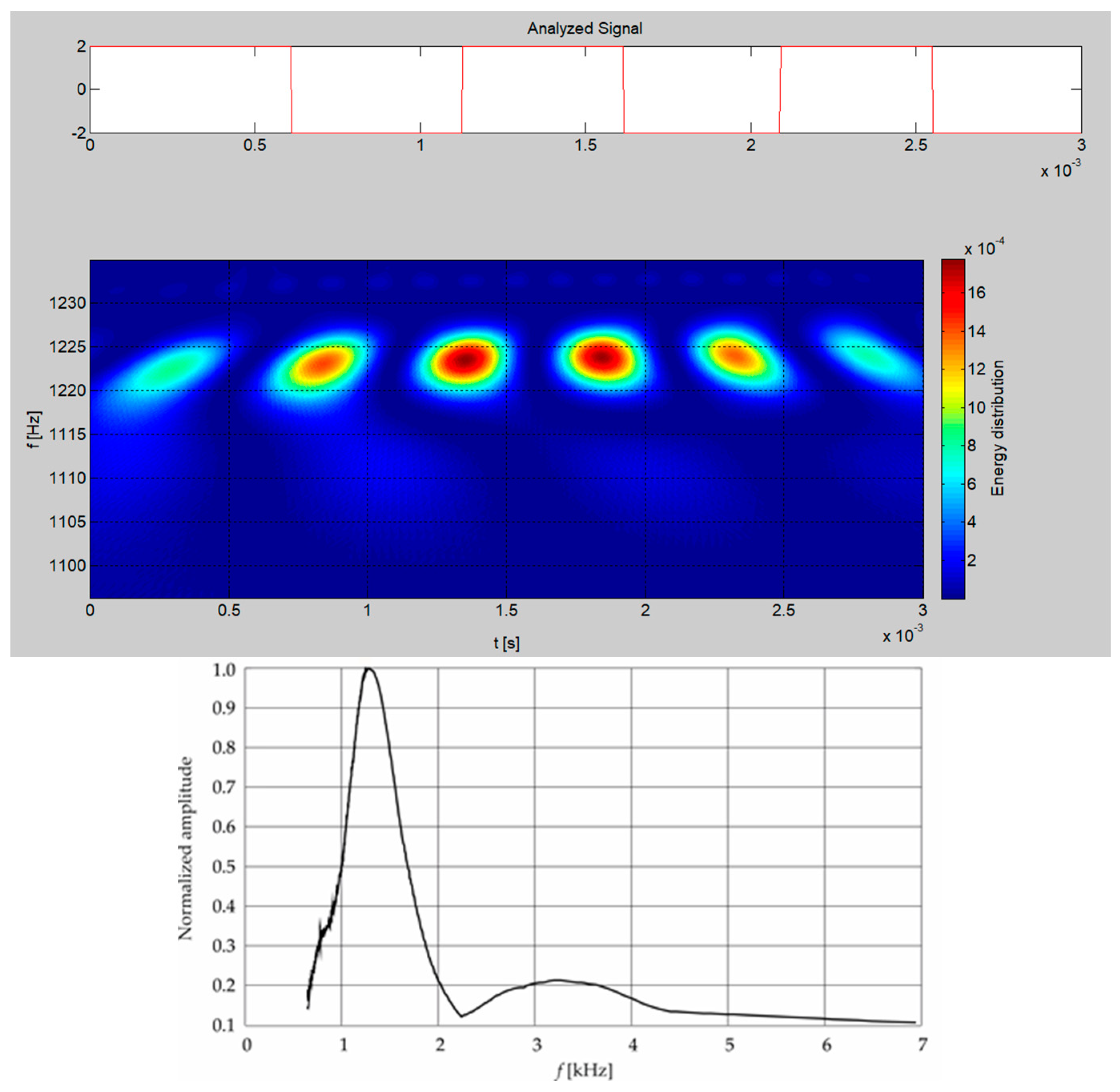
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jefriyanto, W.; Saka, B.G.M.; Pineng, M.; Djamal, M. Development of LVDT (Linear Variable Differential Transformer) sensor as land displacement sensor. J. Phys. Conf. Ser. 2020, 1528, 012041. [Google Scholar] [CrossRef]
- Tomczyk, K. Uncertainties in determining the upper bound of dynamic error for the LVDT sensor. Measurement 2024, 235, 114950. [Google Scholar] [CrossRef]
- Masi, A.; Danzeca, S.; Losito, R.; Peronnard, P.; Secondo, R.; Spiezia, G. A high precision radiation-tolerant LVDT conditioning module. Nucl. Instrum. Meth. A 2014, 745, 73–81. [Google Scholar] [CrossRef]
- Petchmaneelumka, W.; Songsuwankit, K.; Riewruja, V. Accurate LVDT signal converter. Int. J. Electr. Eng. 2016, 11, 340–347. [Google Scholar] [CrossRef]
- Wang, Y.; Egner, F.S.; Willems, T.; Naets, F.; Kirchner, M. Using multi-sine excitation and rigid body motion compensation in randomly sampled camera-based experimental modal analysis to improve SNR. Mech. Syst. Signal Process. 2023, 204, 110763. [Google Scholar] [CrossRef]
- Oliva-Gonzalez, L.J.; Martínez-Guerra, R. State estimation-based parameter identification for a class of nonlinear fractional-order systems. Nonlinear Dyn. 2024, 112, 6379–6402. [Google Scholar] [CrossRef]
- Xiao, F.; Zhu, W.; Meng, X.; Chen, G.S. Parameter Identification of Structures with Different Connections Using Static Responses. Appl. Sci. 2022, 12, 5896. [Google Scholar] [CrossRef]
- Kurtulbaş, E.; Ciğeroğlu, Z.; Şahin, S.; El Messaoudi, N.; Mehmeti, V. Monte Carlo, molecular dynamic, and experimental studies of the removal of malachite green using g-C3N4/ZnO/Chitosan nanocomposite in the presence of a deep eutectic solvent. Int. J. Biol. Macromol. 2024, 274, 133378. [Google Scholar] [CrossRef]
- Rubio, J.d.J. Stability Analysis of the Modified Levenberg–Marquardt Algorithm for the Artificial Neural Network Training. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3510–3524. [Google Scholar] [CrossRef]
- Božić, D.; Runje, B.; Razumić, A. Risk Assessment for Linear Regression Models in Metrology. Appl. Sci. 2024, 14, 2605. [Google Scholar] [CrossRef]
- Tomczyk, K.; Layer, E. Energy density for signals maximizing the integral-square error. Measurement 2016, 90, 224–232. [Google Scholar] [CrossRef]
- Yang, H.; Jing, X.; Yin, Z.; Chen, S.; Wang, C. A Method to Obtain the Transducers Impulse Response (TIR) in Photoacoustic Imaging. Appl. Sci. 2024, 14, 920. [Google Scholar] [CrossRef]
- Layer, E. Modelling of Simplified Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 978-3-540-43762-8. [Google Scholar]
- Tomczyk, K. Monte Carlo-Based Procedure for Determining the Maximum Energy at the Output of Accelerometers. Energies 2020, 13, 1552. [Google Scholar] [CrossRef]
- Beşkirli, M.; Kiran, M.S. Optimization of Butterworth and Bessel Filter Parameters with Improved Tree-Seed Algorithm. Biomimetics 2023, 8, 540. [Google Scholar] [CrossRef] [PubMed]
- Mei, A. The Design and Simulation of a Fifth-order Chebyshev Low-Pass Filter. J. Phys. Conf. Ser. 2022, 2386, 012066. [Google Scholar] [CrossRef]
- Nikitin, Y.; Božek, P.; Peterka, J. Logical–Linguistic Model of Diagnostics of Electric Drives with Sensors Support. Sensors 2020, 20, 4429. [Google Scholar] [CrossRef]
- Honig, M.; Steiglitz, K. Maximizing the output energy of a linear channel with a time- and amplitude-limited input. IEEE Trans. Inf. Theory 1992, 38, 1041–1052. [Google Scholar] [CrossRef][Green Version]
- Elia, M.; Taricco, G.; Viterbo, E. Optimal energy transfer in band-limited communication channels. IEEE Trans. Inf. Theory 1999, 45, 2020–2029. [Google Scholar] [CrossRef][Green Version]
- Tomczyk, K.; Kowalczyk, M. Accuracy Assessment of Charge-Mode Accelerometers Using Multivariate Regression of the Upper Bound of the Dynamic Error. Energies 2023, 16, 7784. [Google Scholar] [CrossRef]
- Huang, J.; Glæsner, N.; Triolo, J.M.; Bekiaris, G.; Bruun, S.; Liu, F. Application of Fourier transform mid-infrared photoacoustic spectroscopy for rapid assessment of phosphorus availability in digestates and digestate-amended. Sci. Total Environ. 2022, 832, 155040. [Google Scholar] [CrossRef]
- Kumar, B.; Bag, S. Phase transformation effect in distortion and residual stress of thin-sheet laser welded Ti-alloy. Opt. Lasers Eng. 2019, 122, 209–224. [Google Scholar] [CrossRef]
- Wu, R.-C.; Huang, L.-J. Non-Distorted Optimization Spectrum Analysis. Energies 2018, 11, 1841. [Google Scholar] [CrossRef]
- Dichev, D.; Koev, H.; Bakalova, T.; Louda, P. A Model of the Dynamic Error as a Measurement Result of Instruments Defining the Parameters of Moving Objects. Meas. Sci. Rev. 2014, 14, 183–189. [Google Scholar] [CrossRef]
- Dichev, D.; Diakov, D.; Zhelezarov, I.; Valkov, S.; Ormanova, M.; Dicheva, R.; Kupriyanov, O. A Method for Correction of Dynamic Errors When Measuring Flat Surfaces. Sensors 2024, 24, 5154. [Google Scholar] [CrossRef] [PubMed]
- Tomczyk, K.; Beńko, P. Analysis of the Upper Bound of Dynamic Error Obtained during Temperature Measurements. Energies 2022, 15, 7300. [Google Scholar] [CrossRef]
- Dudzik, M.; Tomczyk, K.; Jagiello, A.S. Analysis of the error generated by the voltage output accelerometer using the optimal structure of an artificial neural network. In Proceedings of the 2018 19th International Conference on Research and Education in Mechatronics, REM 2018, Delft, The Netherlands, 7–8 June 2018. [Google Scholar] [CrossRef]
- Bialasiewicz, J.T. Wavelet-based approach to evaluation of signal integrity. IEEE Trans. Ind. Electron. 2013, 60, 4590–4598. [Google Scholar] [CrossRef]
- Huang, M.-C. Wave parameters and functions in wavelet analysis. Ocean Eng. 2004, 31, 111–125. [Google Scholar] [CrossRef]
- Datasheet for Portable Calibrator; 9110D Series; The Modal Shop: Cincinnati, OH, USA, 2023; Available online: https://www.modalshop.com/docs/themodalshoplibraries/datasheets/9110d-portable-vibration-calibrator-datasheet-ds-0103.pdf?sfvrsn=202f7b45_7 (accessed on 22 October 2024).
- Datasheet of the LVDT Sensor; DTA-xG8; Micro Epsilon: Birkenhead, UK; Available online: http://www.micro-epsilon.pl/download/indusensor-lvdt_dta_g8.pdf (accessed on 10 September 2024).
- Ostertagová, E. Modelling using Polynomial Regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, R. Wavelet transform-based multipitch estimation in polyphonic music. Heliyon 2020, 6, e03243. [Google Scholar] [CrossRef]


[mm] | [mH] | [mH] | [mH] | [mH] | |||
|---|---|---|---|---|---|---|---|
| 64 | 62 | 407 | 5.13 | 3.88 | 6.51 | 9.27 | |
| 75 | 69 | 371 | 5.18 | 3.76 | 6.69 | 8.85 | |
| 99 | 80 | 323 | 5.98 | 4.68 | 7.53 | 8.52 | |
| 0 | 103 | 98 | 206 | 6.08 | 4.06 | 8.02 | 8.03 |
| 1 | 97 | 92 | 295 | 5.92 | 4.76 | 7.32 | 8.34 |
| 3 | 79 | 72 | 389 | 5.19 | 4.12 | 6.76 | 8.98 |
| 5 | 69 | 66 | 396 | 5.01 | 3.96 | 6.39 | 9.31 |
| 0 | 1 | 3 | 5 | ||||
|---|---|---|---|---|---|---|---|
| 0.0372 | 0.0212 | 0.0084 | 0.0078 | 0.0253 | 0.0358 |
| Type of filter | x = 0 mm | x = 1 mm | x = 3 mm | x = 5 mm |
| [Hz] | 1232 | 1241 | 1225 | 1002 |
| Butterworth | ||||
| Bessel | ||||
| Chebyshev |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomczyk, K.; Beńko, P.; Ostrowska, K. Maximum Energy Density for Evaluation of the Dynamic Accuracy of LVDT Sensors Applied in the Energy Industry. Energies 2024, 17, 5525. https://doi.org/10.3390/en17225525
Tomczyk K, Beńko P, Ostrowska K. Maximum Energy Density for Evaluation of the Dynamic Accuracy of LVDT Sensors Applied in the Energy Industry. Energies. 2024; 17(22):5525. https://doi.org/10.3390/en17225525
Chicago/Turabian StyleTomczyk, Krzysztof, Piotr Beńko, and Ksenia Ostrowska. 2024. "Maximum Energy Density for Evaluation of the Dynamic Accuracy of LVDT Sensors Applied in the Energy Industry" Energies 17, no. 22: 5525. https://doi.org/10.3390/en17225525
APA StyleTomczyk, K., Beńko, P., & Ostrowska, K. (2024). Maximum Energy Density for Evaluation of the Dynamic Accuracy of LVDT Sensors Applied in the Energy Industry. Energies, 17(22), 5525. https://doi.org/10.3390/en17225525








