A Comparison of the Energy Expenditure in Different Storage Tank Geometries to Maintain H2 in the Liquid State
Abstract
:1. Introduction
1.1. Importance of Hydrogen
1.2. Energy Content
1.3. Safety Questions
1.4. Storage Methods
1.4.1. Storage—Gaseous State
1.4.2. Storage—Liquid State
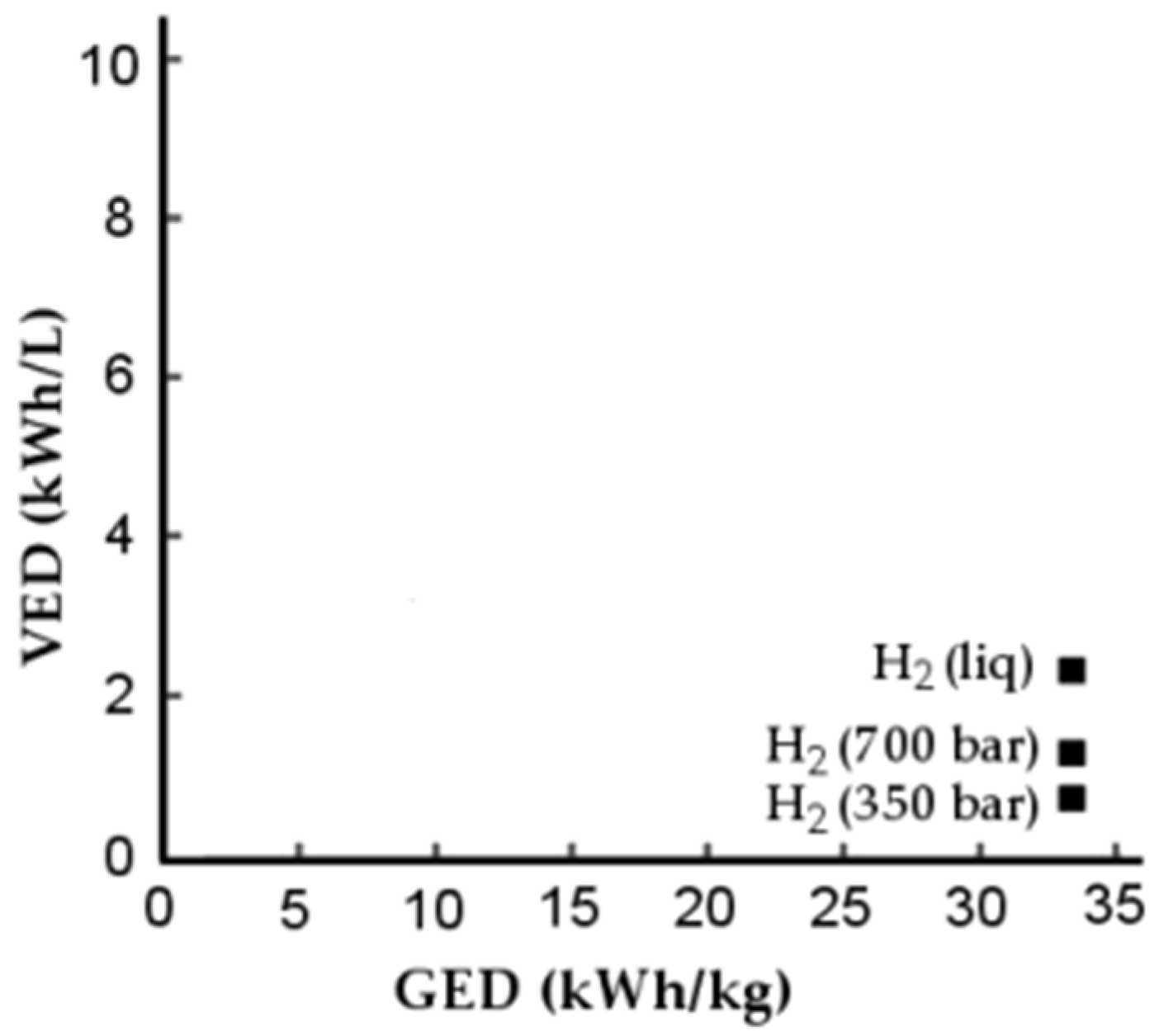
1.5. VED and GED
2. Methodology
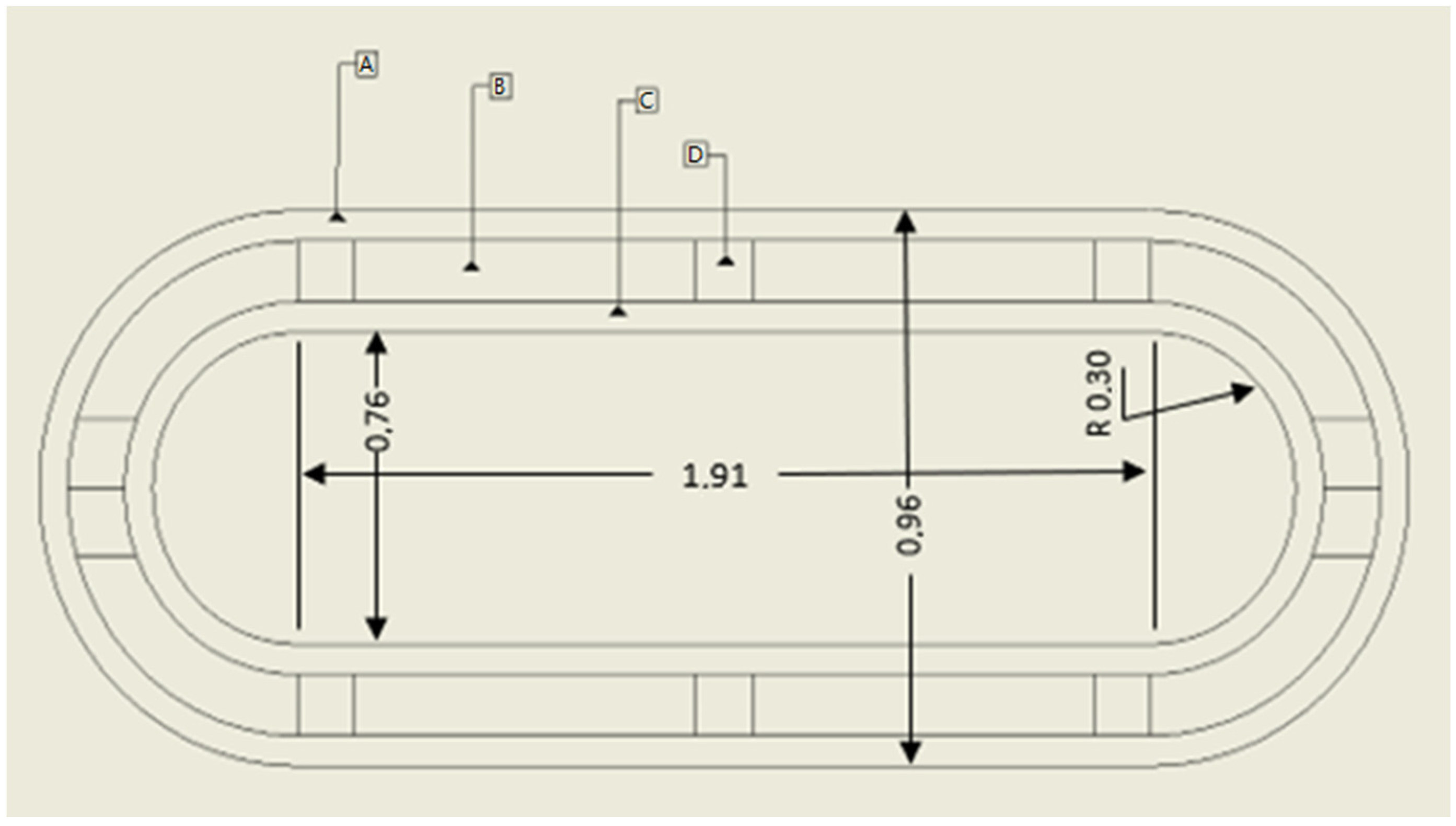
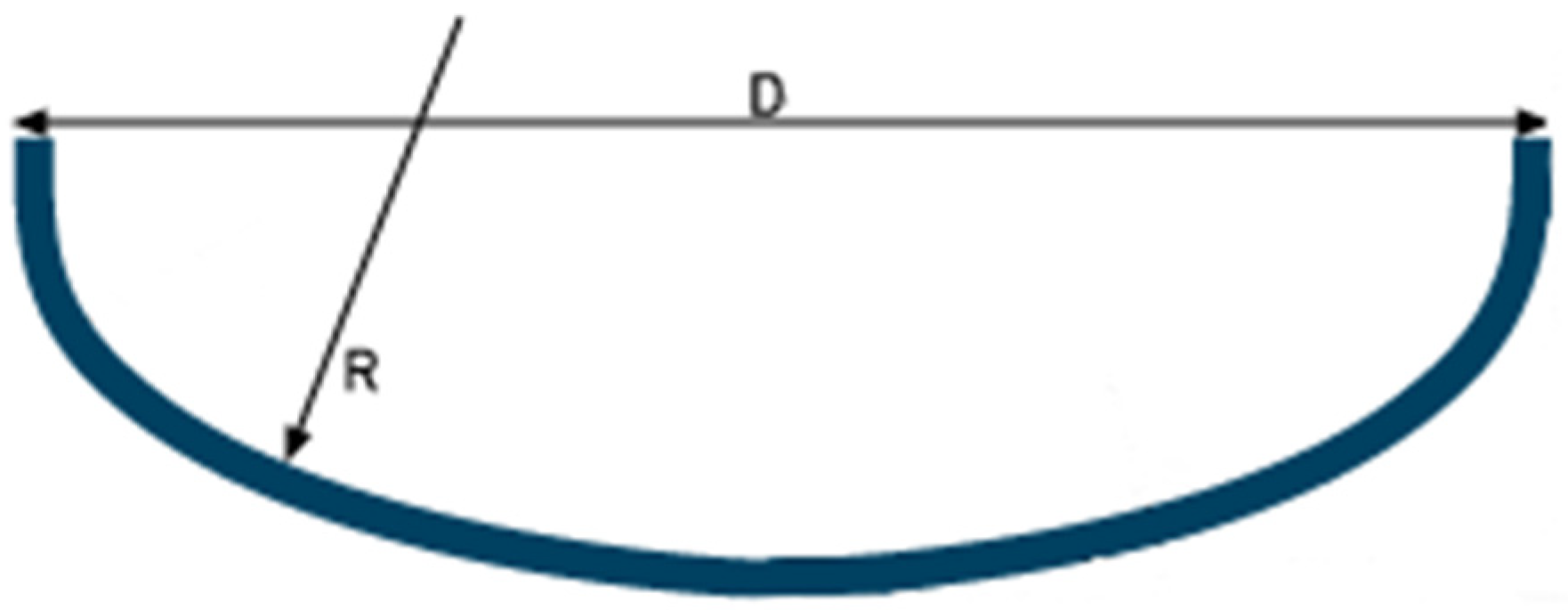
2.1. Geometry
2.2. Materials
2.3. Summary of Characteristics of the Containers Studied
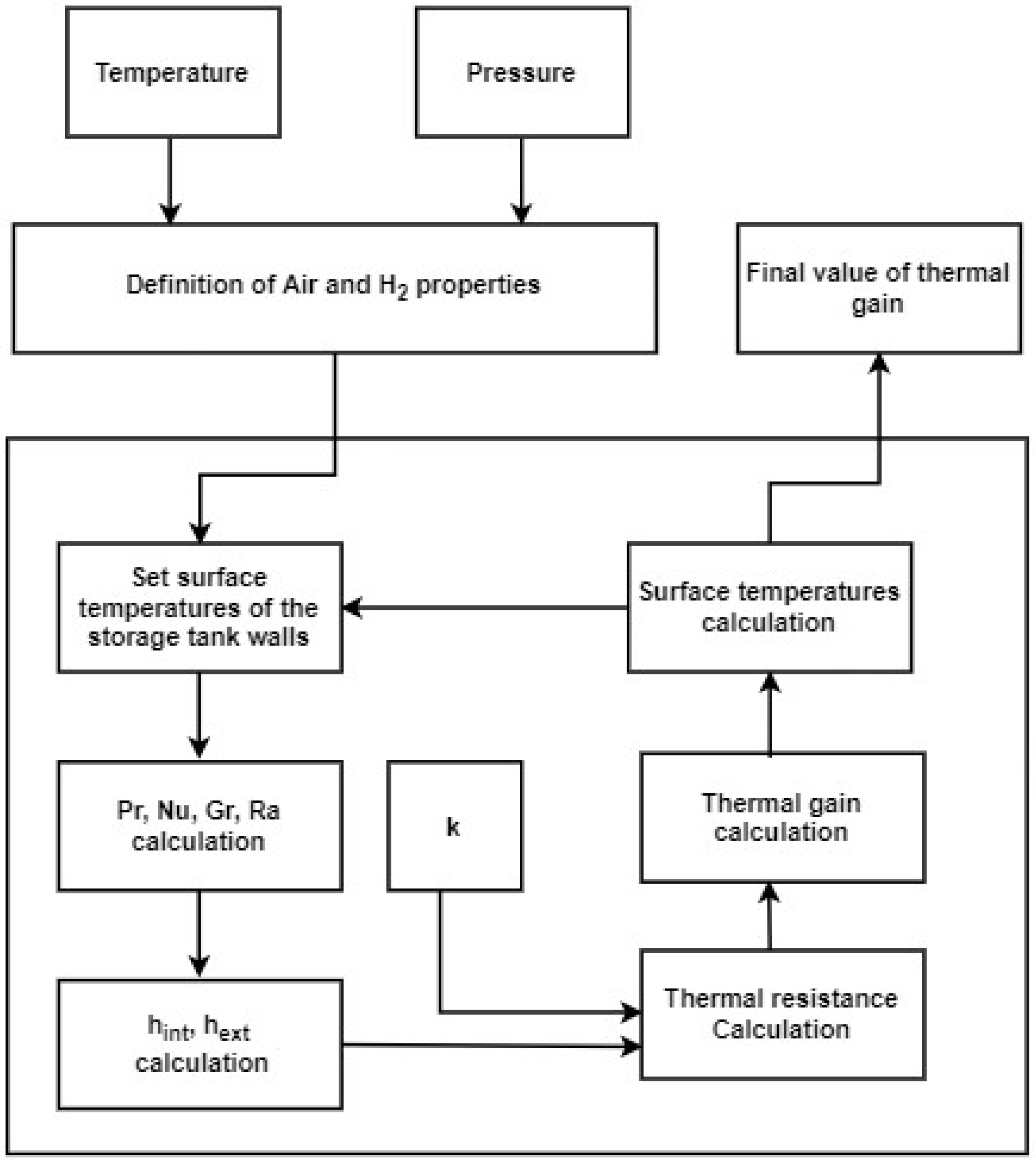
3. Method for the Evaluation of Thermal Gain
4. Cooling System
4.1. Simplified Scheme
4.2. Levels of Temperature and Refrigerants
- 308 K down to 263 K—tetrafluorotane (R-134a).
- 263 K down to 183 K—ethane (R-170).
- 183 K down to 115 K—methane (R-50).
- 115 K a 75 K—nitrogen (R-728).
- 75 K a 22 K—hydrogen (R-702p).
4.3. Refrigeration Cycle Characteristics
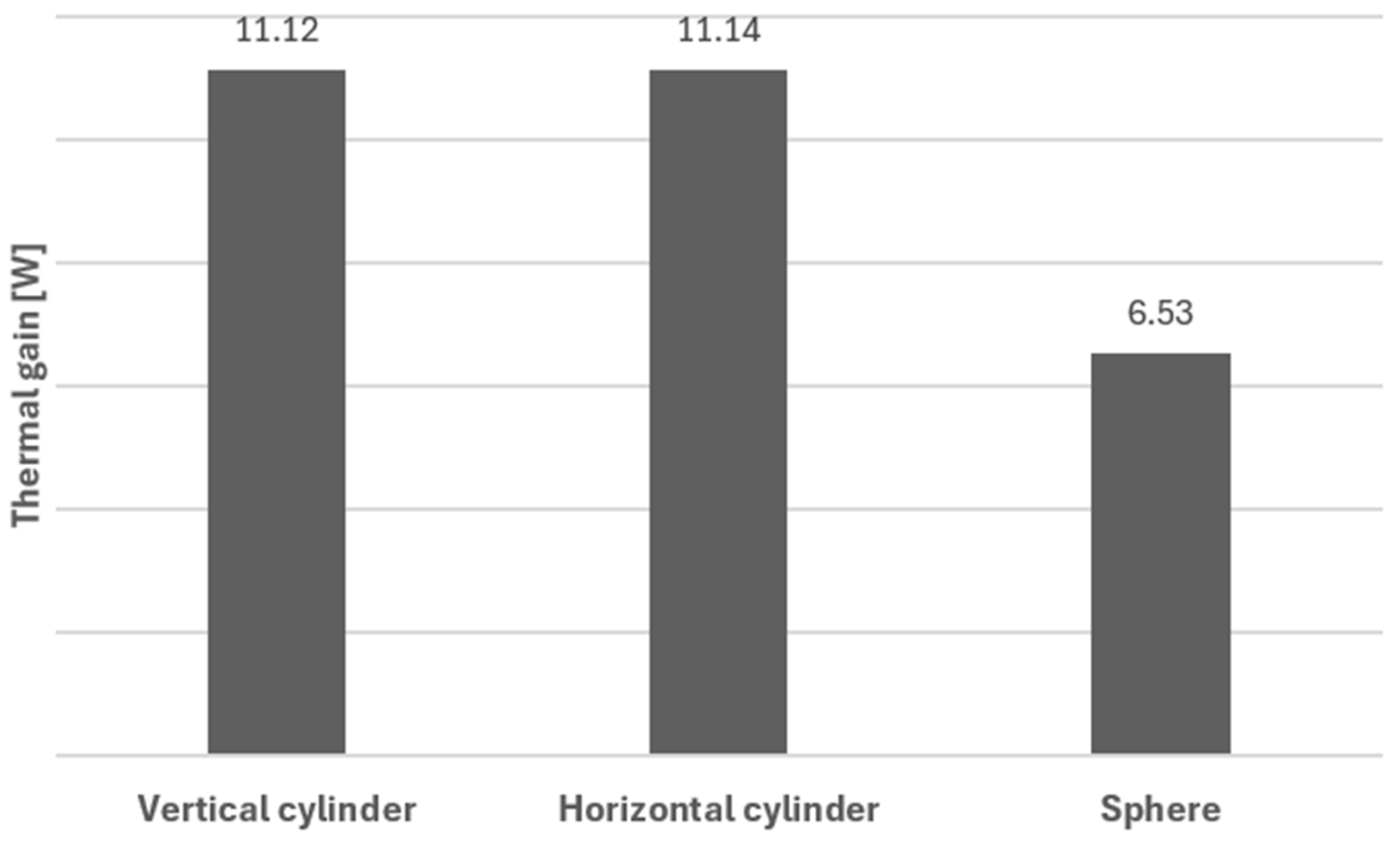
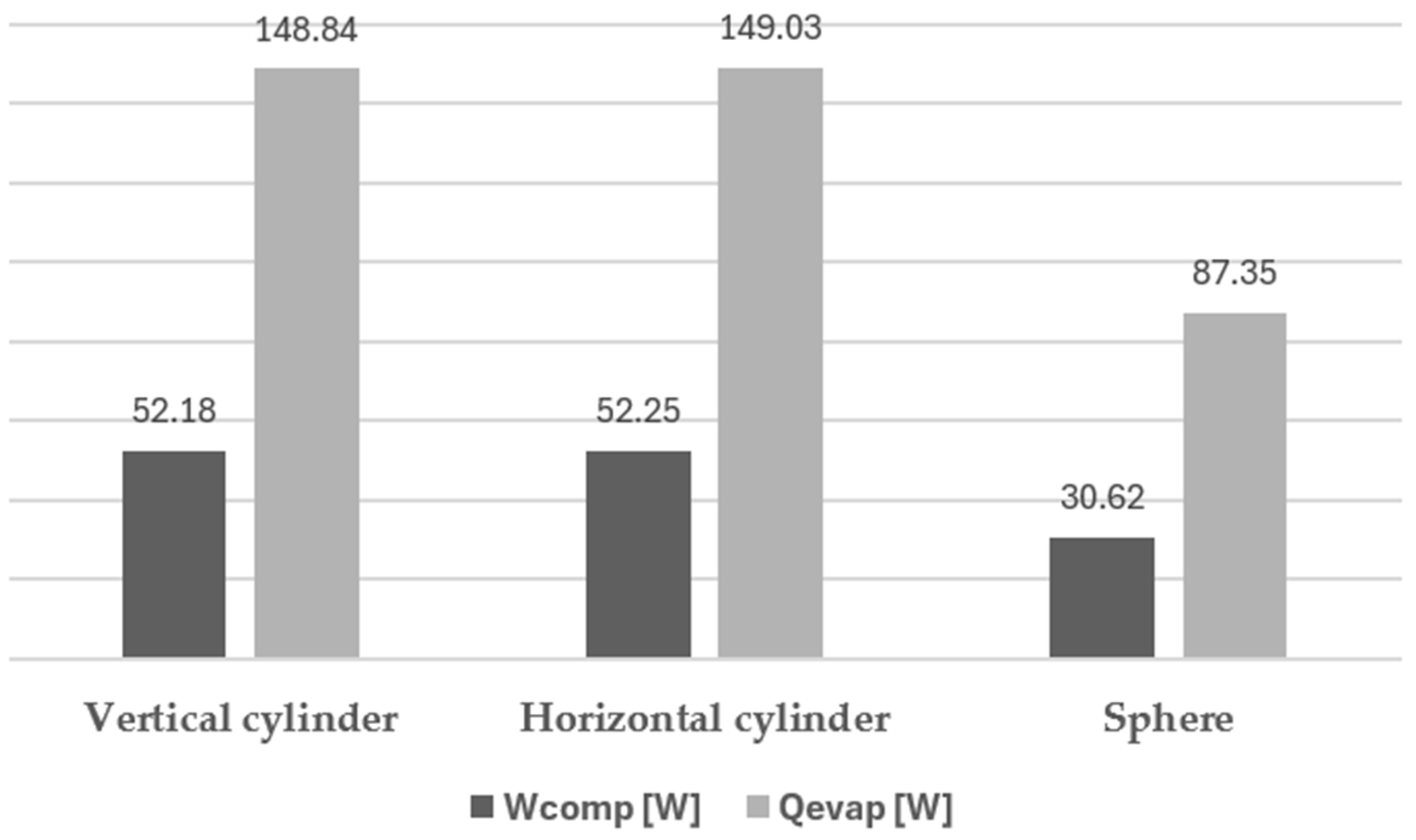
5. Results and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| COP | Coefficient of performance | Qevap | Evaporator heat gain [W] |
| cp | Specific heat at constant pressure (J∙kg−1∙K−1) | Ra | Rayleigh number |
| D | Diameter [m] | Rconv | Rconv Convective thermal resistance [K.W−1] |
| einner wall | Storage tank inner wall thickness [m] | rend caps | End caps radius [m] |
| ELH2,stored | Hydrogen energy stored [J] | Riso | Riso Conduction thermal resistance [K.W−1] |
| eouter wall | Storage tank outer wall thickness [m] | rtank | Storage tank radius [m] |
| Ew,ev | Weekly hydrogen energy loss [J] | T | Temperature [K] |
| GED | Gravimetric energy density [J∙Kg−1] | Tamb | Ambient temperature [K] |
| Gr | Grashof number | TEC | Coefficients of thermal expansion [K−1] |
| HHV | Higher heating value [J∙Kg−1] | VED | Volumetric energy density [J∙m−3] |
| k | Thermal conductivity [W∙m−1∙K−1] | Vtank | Storage tank radius [m3] |
| L | Length [m] | Wcomp | Compressor work [W] |
| Ltank | Tank length [m] | α | Thermal diffusivity [m2∙s−1] |
| Nu | Nusselt number | β | Thermal expansion coefficient [K−1] |
| P | Pressure [Pa] | σced | Yield stress [MPa] |
| Pr | Prandtl number | μ | Dynamic viscosity [N∙s∙m−2] |
| QCT | Thermal gain [W] | ν | Kinematic viscosity [m2∙s−1] |
| Qcond | Condenser heat power [W] | ρ | Density [kg∙m−3] |
References
- Goldemberg, J. The Promise of Clean Energy. Energy Policy 2006, 34, 2185–2190. [Google Scholar] [CrossRef]
- European Commission. 2030 Climate Targets. 2023. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2030-climate-targets_en (accessed on 13 March 2024).
- Shafiee, S.; Topal, E. When Will Fossil Fuel Reserves Be Diminished? Energy Policy 2009, 37, 181–189. [Google Scholar] [CrossRef]
- Radetzki, M. Fossil fuels will not run out. Miner. Energy—Raw Mater. Rep. 1996, 12, 26–30. [Google Scholar] [CrossRef]
- Mandal, T.; Gregory, D.H. Hydrogen: Future energy vector for sustainable development. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 203–210, 539. [Google Scholar] [CrossRef]
- Kovács, K.L.; Maróti, G.; Rákhely, G. A novel approach for biohydrogen production. Int. J. Hydrogen Energy 2006, 31, 1460–1468. [Google Scholar] [CrossRef]
- Kottenstette, R.; Cotrell, J. Hydrogen storage in wind turbine towers. Int. J. Hydrogen Energy 2004, 29, 1277–1288. [Google Scholar] [CrossRef]
- Balat, M.; Balat, M. Political, economic and environmental impacts of biomass-based hydrogen. Int. J. Hydrogen Energy 2009, 34, 3589–3603. [Google Scholar] [CrossRef]
- Balat, H.; Kırtay, E. Hydrogen from biomass–present scenario and future prospects. Int. J. Hydrogen Energy 2010, 35, 7416–7426. [Google Scholar] [CrossRef]
- Calise, F.; D’Accadia, M.D.; Santarelli, M.; Lanzini, A.; Ferrero, D. Solar Hydrogen Productions. Processes, Systems anda Technologies; Academic Press: San Diego, CA, USA, 2019. [Google Scholar]
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Barbir, F.; Veziroğlu, T.N. Effective costs of the future energy systems. Int. J. Hydrogen Energy 1992, 17, 299–308. [Google Scholar] [CrossRef]
- Nicoletti, G.; Arcuri, N.; Nicoletti, G.; Bruno, R. A technical and environmental comparison between hydrogen and some fossil fuels. Energy Convers. Manag. 2015, 89, 205–213. [Google Scholar] [CrossRef]
- Fischer, M. Safety aspects of hydrogen combustion in hydrogen energy systems. Int. J. Hydrogen Energy 1986, 11, 593–601. [Google Scholar] [CrossRef]
- Hoagland, W. Safe Handling of Hydrogen. In Hydrogen Science and Engineering: Materials, Processes, Systems and Technology; Stolten, P., Emonts, B., Eds.; Wiley: Hoboken, NJ, USA, 2016; ISBN 9783527674268. [Google Scholar] [CrossRef]
- Mckinley, K.R.; Browne, S.H.; Richard Neill, D.; Seki, A.; Takahashi, P.K. Hydrogen Fuel from Renewable Resources. Energy Sources 1990, 12, 105–110. [Google Scholar] [CrossRef]
- Najjar, Y.S. Hydrogen safety: The road toward green technology. Int. J. Hydrogen Energy 2013, 38, 10716–10728. [Google Scholar] [CrossRef]
- Yartys, V.A.; Lototsky, M.V.; Veziroglu, S.V.; Yu, T.N.; Zaginaichenko, S.; Schur, D.V.; Shpak, A.P. Hydrogen Materials Science and Chemistry of Carbon Nanomaterials; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Zhang, Y.; Shi, J.; Han, G.; Li, M.; Ji, Q.; Ma, D.; Liu, Z. Chemical vapor deposition of monolayer WS2 nanosheets on Au foils toward direct application in hydrogen evolution. Nano Res. 2015, 8, 2881–2890. [Google Scholar] [CrossRef]
- Lim, K.L.; Kazemian, H.; Yaakob, Z.; Daud, W.R.W.; Cunningham, M. Solid-state Materials and Methods for Hydrogen Storage: A Critical Review. Chem. Eng. Technol. 2010, 33, 213–226. [Google Scholar] [CrossRef]
- Moseley, P.T.; Garche, J. (Eds.) Electrochemical Energy Storage for Renewable Sources and Grid Balancing; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Andersson, J.; Grönkvist, S. Large-scale storage of hydrogen. Int. J. Hydrogen Energy 2019, 44, 11901–11919. [Google Scholar] [CrossRef]
- Züttel, A. Hydrogen storage methods. Naturwissenschaften 2004, 91, 157–172. [Google Scholar] [CrossRef]
- Lototsky, M.V.; Yartys, V.A.; Zavaliy, I.Y. Vanadium-based BCC alloys: Phase-structural characteristics and hydrogen sorption properties. J. Alloys Compd. 2005, 404, 421–426. [Google Scholar] [CrossRef]
- Valenti, G. 2—Hydrogen liquefaction and liquid hydrogen storage. In Compendium of Hydrogen Energy; Ram, B., Gupta, A., Basile, T., Nejat, V., Eds.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2016; pp. 27–51. ISBN 9781782423621. [Google Scholar] [CrossRef]
- Notardonato, W.U.; Swanger, A.M.; Fesmire, J.E.; Jumper, K.M.; Johnson, W.L.; Tomsik, T.M. Zero boil-off methods for large-scale liquid hydrogen tanks using integrated refrigeration and storage. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Philadelphia, PA, USA, 2017; Volume 278, p. 012012. [Google Scholar]
- Pinto, G.; Monteiro, J.; Baptista, A.; Ribeiro, L.; Leite, J. Study of the Permeation Flowrate of an Innovative Way to Store Hydrogen in Vehicles. Energies 2021, 14, 6299. [Google Scholar] [CrossRef]
- VMolkov, M.; Dadashzadeh, S.; Kashkarov, D.M. Performance of hydrogen storage tank with TPRD in an engulfing fire. Int. J. Hydrogen Energy 2021, 46, 36581–36597. [Google Scholar] [CrossRef]
- Mital, S.K.; Gyekenyesi, J.Z.; Arnold, S.M.; Sullivan, R.M.; Manderscheid, J.M.; Murthy, P.L. Review of Current State of the Art and Key Design Issues with Potential Solutions for Liquid Hydrogen Cryogenic Storage Tank Structures for Aircraft Applications. 2006. NASA/TM-2006-214346. Available online: https://ntrs.nasa.gov/citations/20060056194 (accessed on 13 March 2024).
- Winnefeld, C.; Kadyk, T.; Bensmann, B.; Krewer, U.; Hanke-Rauschenbach, R. Modelling and Designing Cryogenic Hydrogen Tanks for Future Aircraft Applications. Energies 2018, 11, 105. [Google Scholar] [CrossRef]
- Coutinho, B. Armazenamento de Hidrogénio no Estado Líquido. Master’s Thesis, ISEP, Polytechnic of Porto, Porto, Portugal, 2023. [Google Scholar]
- Baptista, A.; Pinho, C.; Pinto, G.; Ribeiro, L.; Monteiro, J.; Santos, T. Assessment of an Innovative Way to Store Hydrogen in Vehicles. Energies 2019, 12, 1762. [Google Scholar] [CrossRef]
- Alkhaledi, A.N.; Sampath, S.; Pilidis, P. A hydrogen fuelled LH2 tanker ship design. Ships Offshore Struct. 2022, 17, 1555–1564. [Google Scholar] [CrossRef]
- Haynes, W.M. (Ed.) CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- JHutchins, E. Marschall. Int. J. Heat MassTransfer 1989, 32, 2047e2053. [Google Scholar]
- Kanoǧlu, M. Exergy analysis of multistage cascade refrigeration cycle used for natural gas liquefaction. Int. J. Energy Res. 2002, 26, 763–774. [Google Scholar] [CrossRef]
- Stolzenburg, K.; Berstad, D.; Decker, L.; Elliott, A.; Haberstroh, C.; Hatto, C.; Walnum, H.T. Efficient liquefaction of hydrogen: Results of the IDEALHY project. In Proceedings of the XXth Energie—Symposium, Stralsund, Germany, 7–9 November 2013; pp. 7–9. [Google Scholar]




| Fuel | HHV (J∙kg−1) | HHV (J∙m−3) |
|---|---|---|
| Liquid state | ||
| Methanol | 22.3 | 18.10 |
| Ethanol | 29.9 | 23.60 |
| Fuel oil | 45.5 | 38.65 |
| Gasoline for aviation | 46.5 | 35.30 |
| Gasoline | 47.4 | 34.85 |
| LH2 | 141.9 | 10.10 |
| Gaseous state | ||
| Natural gas | 50 | 0.04 |
| GH2 | 141.9 | 0.013 |
| Properties | Fuel | |||
|---|---|---|---|---|
| Hydrogen | Methane | Propane | Gasoline | |
| Density, PTN (kg∙m−3) | 0.084 | 0.65 | 2.01 | 4.40 |
| Flammability range in air, PTN (% v/v) | 4.0–77 | 4.4–16.5 | 1.7–10.9 | 1.0–7.6 |
| Ignition temperature (°C) | 560 | 540 | 487 | 228–471 |
| Minimum ignition energy in air (MJ) | 0.02 | 0.3 | 0.26 | 0.24 |
| Diffusion coefficient in air (cm2∙s−1) | 0.61 | 0.16 | 0.12 | 0.05 |
| Specific heat at constant pressure (J∙kg−1∙K−1) | 14.89 | 2.22 | 1.67 | 1.2 |
| Material/System | k (W∙m−1∙K−1) | Density (kg∙m−3) |
|---|---|---|
| Multilayer vacuum insulation (MLI) | 10−5–10−8 | - |
| Microspheres in vacuum | 10−6–10−7 | - |
| Rohacell® foam | 35 × 10−3–5 × 10−3 | 35.24 |
| Airgel | 10−2–10−7 | 100–500 |
| Pearlite | 10−5–10−6 | 128 |
| Polyurethane foam | 10−2–10−4 | 32–64 |
| Polyamide | 3.5 × 10−1 | 1430 |
| Material/System | Dimension | Unit |
|---|---|---|
| rtank | 0.382 | m |
| Ltank | 1.913 | m |
| Vtank | 1 | m3 |
| einner wall | 10 | mm |
| Insulation thickness | 10/20/30/40/50 | mm |
| eouter wall | 10 | mm |
| Number of supporting rods | 8 | |
| rend caps | 0.306 | m |
| Material/System | Dimension | Unit |
|---|---|---|
| rtank | 0.620 | m |
| Vtank | 1 | m3 |
| einner wall | 10 | mm |
| Insulation thickness | 10/20/30/40/50 | mm |
| eouter wall | 10 | mm |
| No. of supporting rods | 8 |
| Material | k [W∙m−1∙K−1] | ρ [kg∙m−3] | σced [MPa] |
|---|---|---|---|
| Al 2219 | 171 | 2825 | 172 |
| 4301 Cr-Ni | 15 | 7900 | 270 |
| Material/System | k (W∙m−1∙K−1) | ρ (kg∙m−3) |
|---|---|---|
| Multilayer vacuum insulation (MLI) | 10−5–10−8 | - |
| Microspheres in vacuum | 10−6–10−7 | - |
| Rohacell® foam | 35 × 10−3–5 × 10−3 | 35.24 |
| Airgel | 10−2–10−7 | 100–500 |
| Pearlite | 10−5–10−6 | 128 |
| Polyurethane foam | 10−2–10−4 | 32–64 |
| Polyamide | 3.5 × 10−1 | 1430 |
| Sub-Cycle | Stage | Level of Evaporation | Level of Condensation | ||
|---|---|---|---|---|---|
| T [K] | P [MPa] | T [K] | P [MPa] | ||
| R-702p (Hydrogen) | 1st | 18.0 | 0.05 | 25.7 | 0.36 |
| R-728 (Nitrogen) | 1st | 70.0 | 0.04 | 79.0 | 0.12 |
| 2nd | 79.0 | 0.12 | 90.0 | 0.36 | |
| R-50 (Methane) | 1st | 110.0 | 0.09 | 123.0 | 0.22 |
| 2nd | 123.0 | 0.22 | 137.0 | 0.56 | |
| 3rd | 137.0 | 0.56 | 159.0 | 1.40 | |
| R-170 (Ethano) | 1st | 178.0 | 0.07 | 197.0 | 0.18 |
| 2nd | 197.0 | 0.18 | 219.0 | 0.44 | |
| 3rd | 219.0 | 0.44 | 248.0 | 1.10 | |
| R-134a (Tetrafluorotane) | 1st | 264.0 | 0.21 | 284.0 | 0.42 |
| 2nd | 284.0 | 0.42 | 306.0 | 0.84 | |
| Parameters | Units | |
|---|---|---|
| Wcomp | 0.0175 | kW |
| Qevap | 0.123 | kW |
| Wcomp/Qevap | 0.142 | - |
| COP | 7.03 | - |
| Parameter | Vertical Cylinder | Horizontal Cylinder | Sphere |
|---|---|---|---|
| Ew,ev [J] | 1.79 × 109 | 1.79 × 109 | 1.05 × 109 |
| E LH2,stored [J] | 8.15 × 109 | 8.15 × 109 | 8.15 × 109 |
| Sub-Cycle | Stage | Level of Evaporation | Level of Condensation | Qevap/QCT | Qcondenser/QCT | ||
|---|---|---|---|---|---|---|---|
| T [K] | P [MPa] | T [K] | P [MPa] | - | - | ||
| R-702p (Hydrogen) | 1st | 18.0 | 0.05 | 25.7 | 0.36 | 1 | 1.79 |
| R-728 (Nitrogen) | 1st | 70.0 | 0.04 | 79.0 | 0.12 | 1.79 | 2.07 |
| 2nd | 79.0 | 0.12 | 90.0 | 0.36 | 2.07 | 2.34 | |
| R-50 (Methane) | 1st | 110.0 | 0.09 | 123.0 | 0.22 | 2.34 | 2.65 |
| 2nd | 123.0 | 0.22 | 137.0 | 0.56 | 2.65 | 2.71 | |
| 3rd | 137.0 | 0.56 | 159.0 | 1.40 | 2.71 | 3.41 | |
| R-170 (Ethano) | 1st | 178.0 | 0.07 | 197.0 | 0.18 | 3.41 | 3.75 |
| 2nd | 197.0 | 0.18 | 219.0 | 0.44 | 3.75 | 4.20 | |
| 3rd | 219.0 | 0.44 | 248.0 | 1.10 | 4.20 | 4.77 | |
| R-134a (Tetrafluorotane) | 1st | 264.0 | 0.21 | 284.0 | 0.42 | 4.77 | 5.13 |
| 2nd | 284.0 | 0.42 | 306.0 | 0.84 | 5.13 | 5.69 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteiro, J.; Ribeiro, L.; Pinto, G.F.; Cavadas, A.; Coutinho, B.; Baptista, A. A Comparison of the Energy Expenditure in Different Storage Tank Geometries to Maintain H2 in the Liquid State. Energies 2024, 17, 5557. https://doi.org/10.3390/en17225557
Monteiro J, Ribeiro L, Pinto GF, Cavadas A, Coutinho B, Baptista A. A Comparison of the Energy Expenditure in Different Storage Tank Geometries to Maintain H2 in the Liquid State. Energies. 2024; 17(22):5557. https://doi.org/10.3390/en17225557
Chicago/Turabian StyleMonteiro, Joaquim, Leonardo Ribeiro, Gustavo F. Pinto, Adélio Cavadas, Beatriz Coutinho, and Andresa Baptista. 2024. "A Comparison of the Energy Expenditure in Different Storage Tank Geometries to Maintain H2 in the Liquid State" Energies 17, no. 22: 5557. https://doi.org/10.3390/en17225557
APA StyleMonteiro, J., Ribeiro, L., Pinto, G. F., Cavadas, A., Coutinho, B., & Baptista, A. (2024). A Comparison of the Energy Expenditure in Different Storage Tank Geometries to Maintain H2 in the Liquid State. Energies, 17(22), 5557. https://doi.org/10.3390/en17225557








