The Effect of Carbon Nanotubes on the Viscosity and Surface Tension of Heat Transfer Fluids—A Review Paper
Abstract
:1. Introduction
2. Theoretical Background of Surface Tension and Viscosity
2.1. Surface Tension
- The liquid molecular structure’s nature: Water and other liquids with strong intermolecular interactions, like hydrogen bonds, typically have higher surface tensions. Surface tension is lower in non-polar liquids with fewer intermolecular interactions.
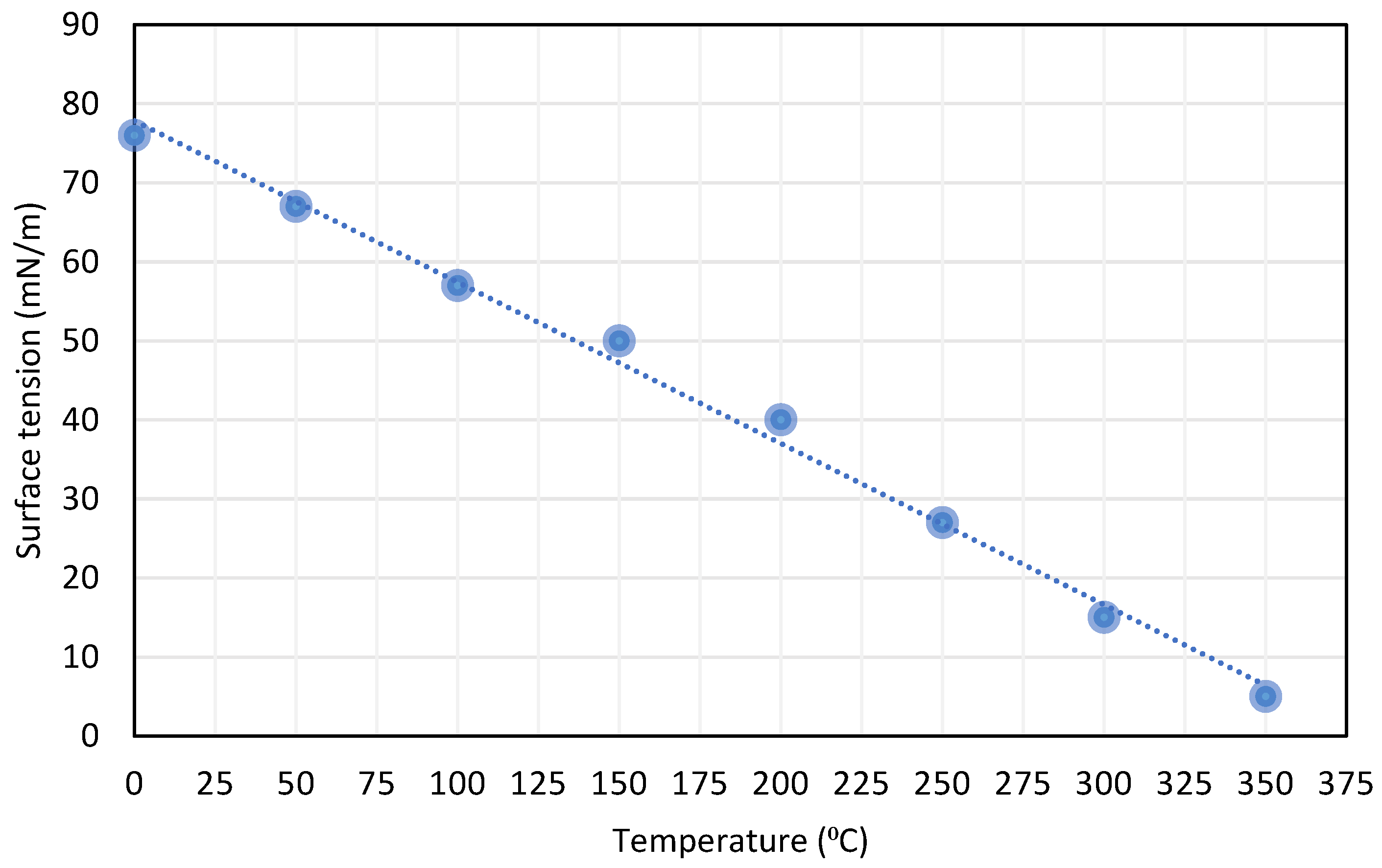
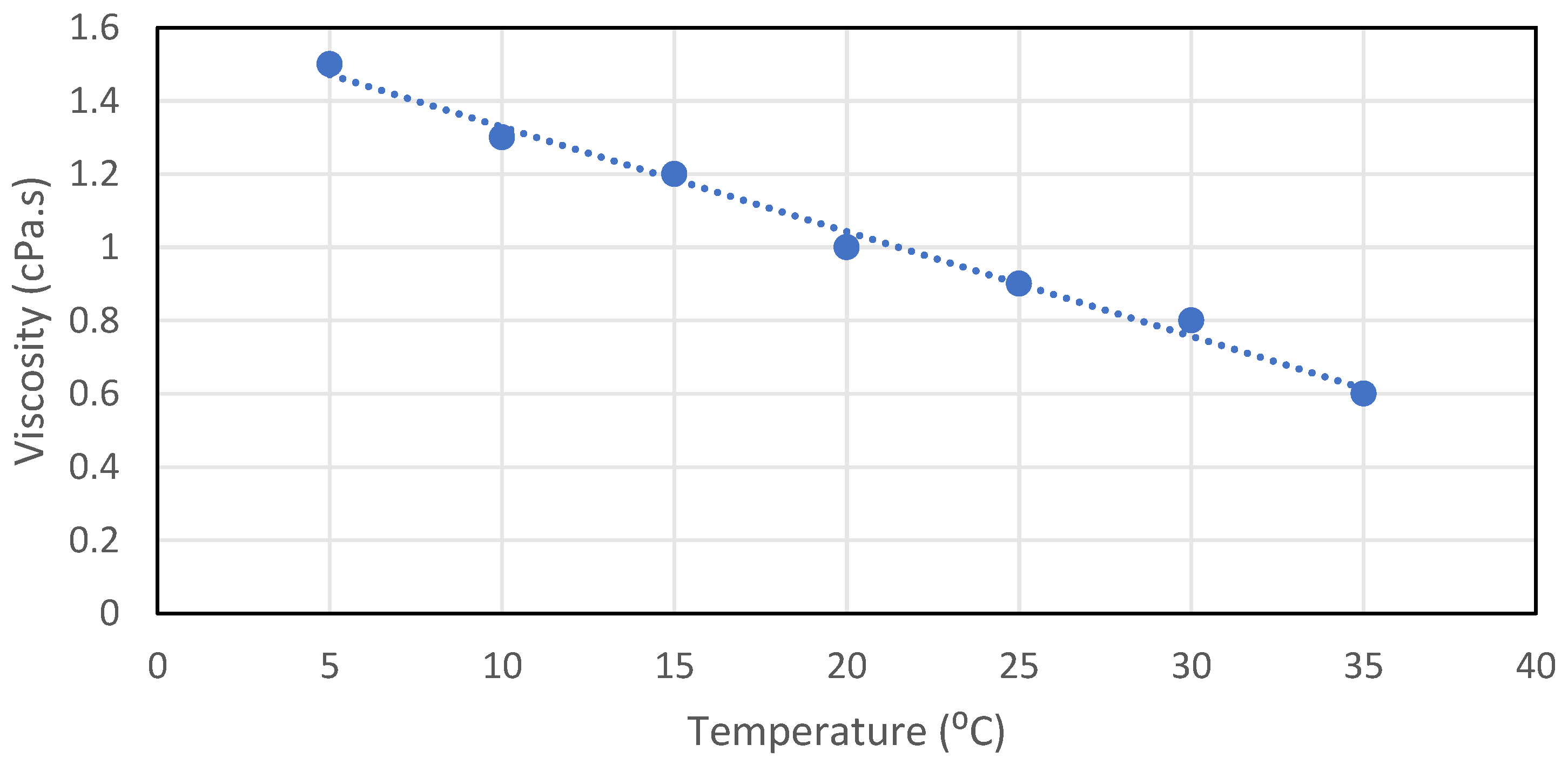
- Temperature: Molecules increase kinetic energy as the temperature rises, lowering the cohesive forces at the liquid’s surface. Tension typically falls as temperature rises.
2.2. Vescosity
- Newtonian fluids are those that respond to shear forces by moving the liquid in a straight-line fashion.
- Non-Newtonian fluids, on the other hand, obey a separate set of laws. The viscosity of shear-thinning fluids decreases as the pressure or force increases. Thixotropic fluids’ viscosity changes with time. Gels like ketchup, for example, are stable at repose but become fluids when disturbed.
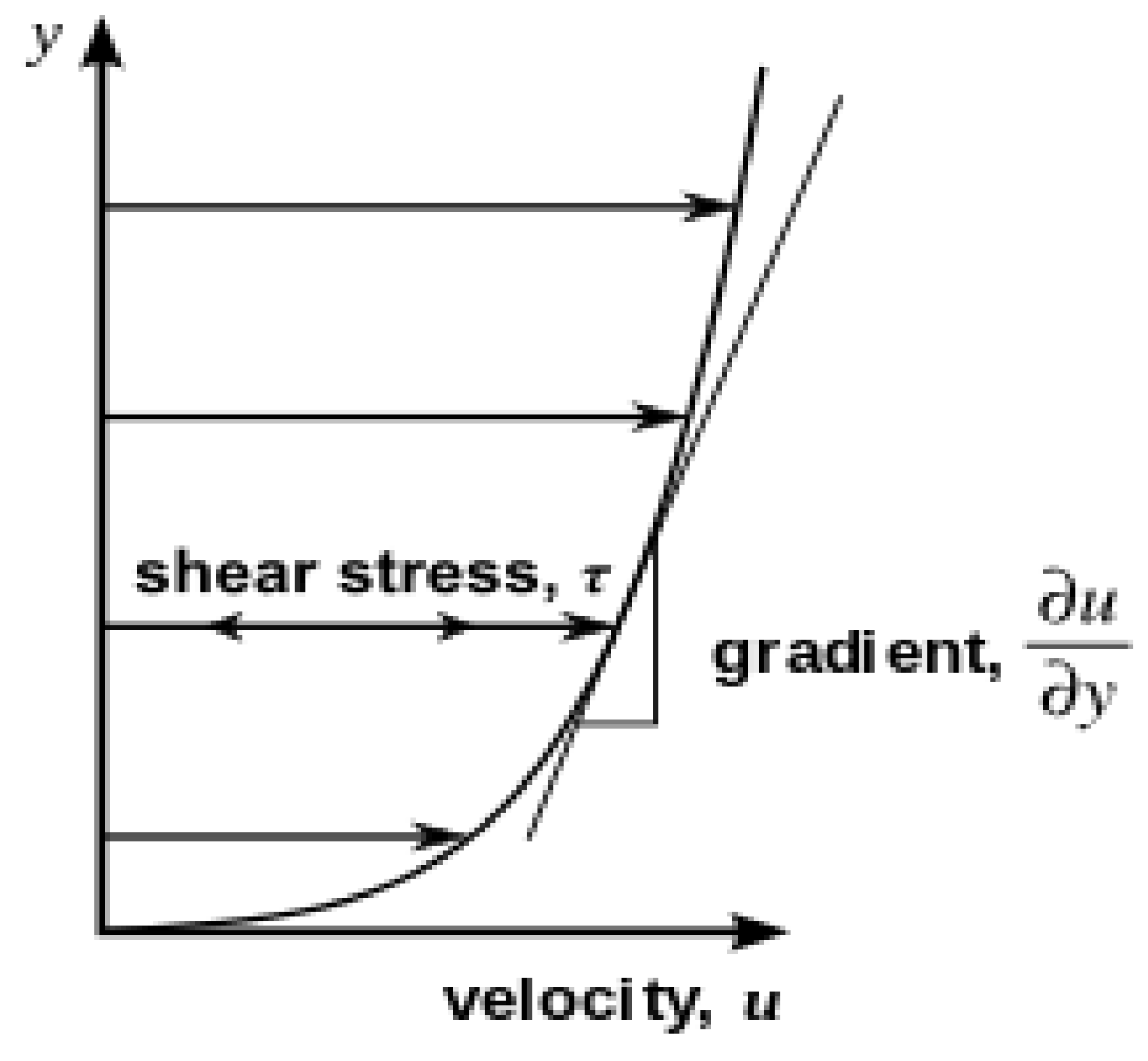
- The term viscosity is divided into two types: dynamic and kinematic viscosity. Materials science and engineering are interested in dynamic viscosity (forces or stresses involved in the deformation of a material). In a fluid such as water, the stresses caused by shearing the fluids do not depend on the distance sheared; rather, they depend on the fluid itself. This is what we mean by dynamic viscosity, and it can be presented by the following equation, named Newton’s Law of Viscosity [37].where du/dy is the rate of shear deformation, F is the shear force (N), A is the unit area (m2), µ is the dynamic viscosity (kg/m/s) or (Pa·s(, u is the velocity (m/s), and y is the separation distance (m). Figure 4 below shows the parallel flow corresponding to the shear stress proportional to the velocity gradient of the fluid’s shear rate deformation, dividing the force by the unit area to obtain τ (N/m2) as follows [38]:
3. Results and Discussion
3.1. Factors Affecting Surface Tension
3.1.1. Temperature
3.1.2. Concentration
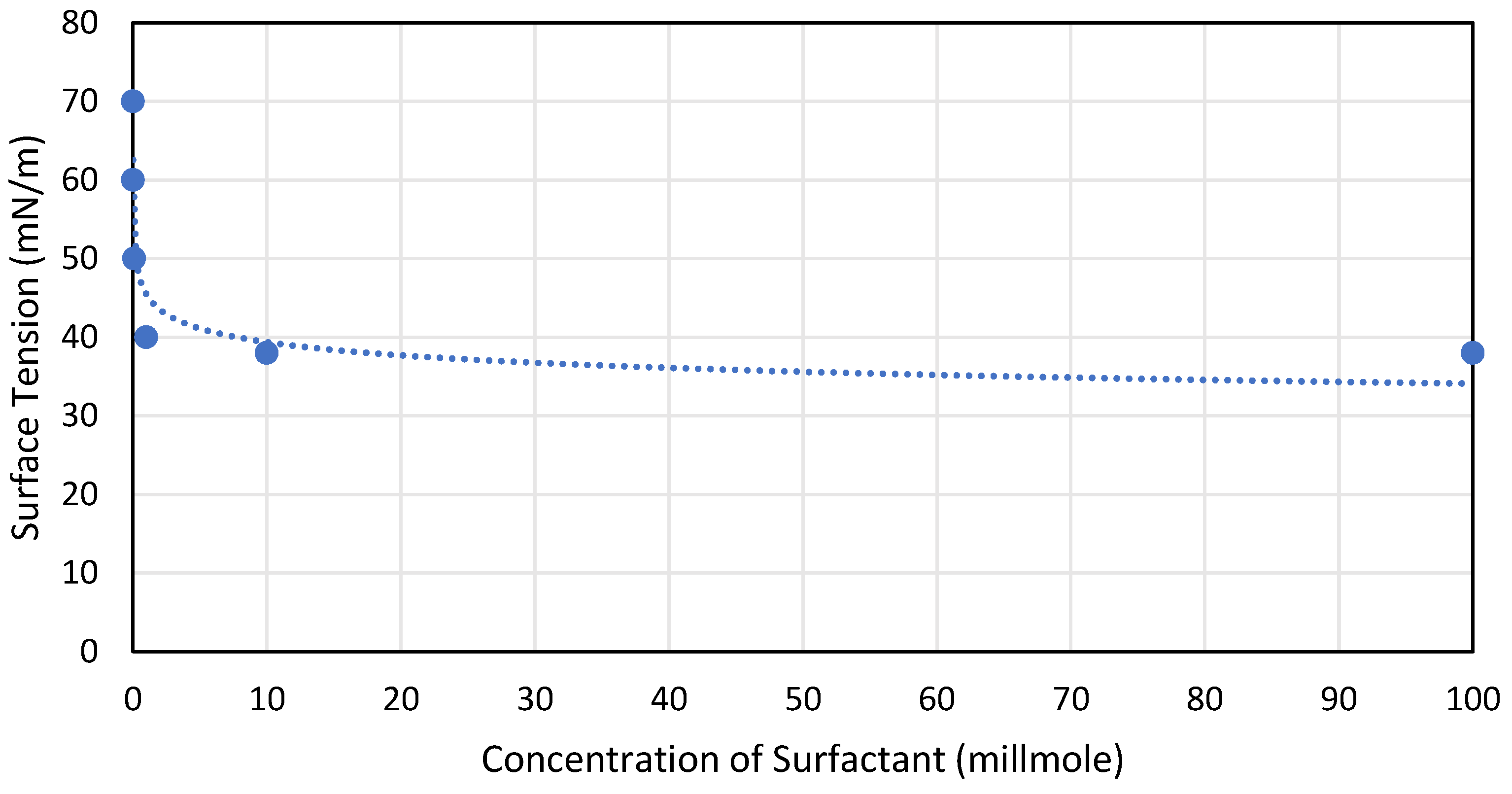
3.1.3. Surfactant
- ➢
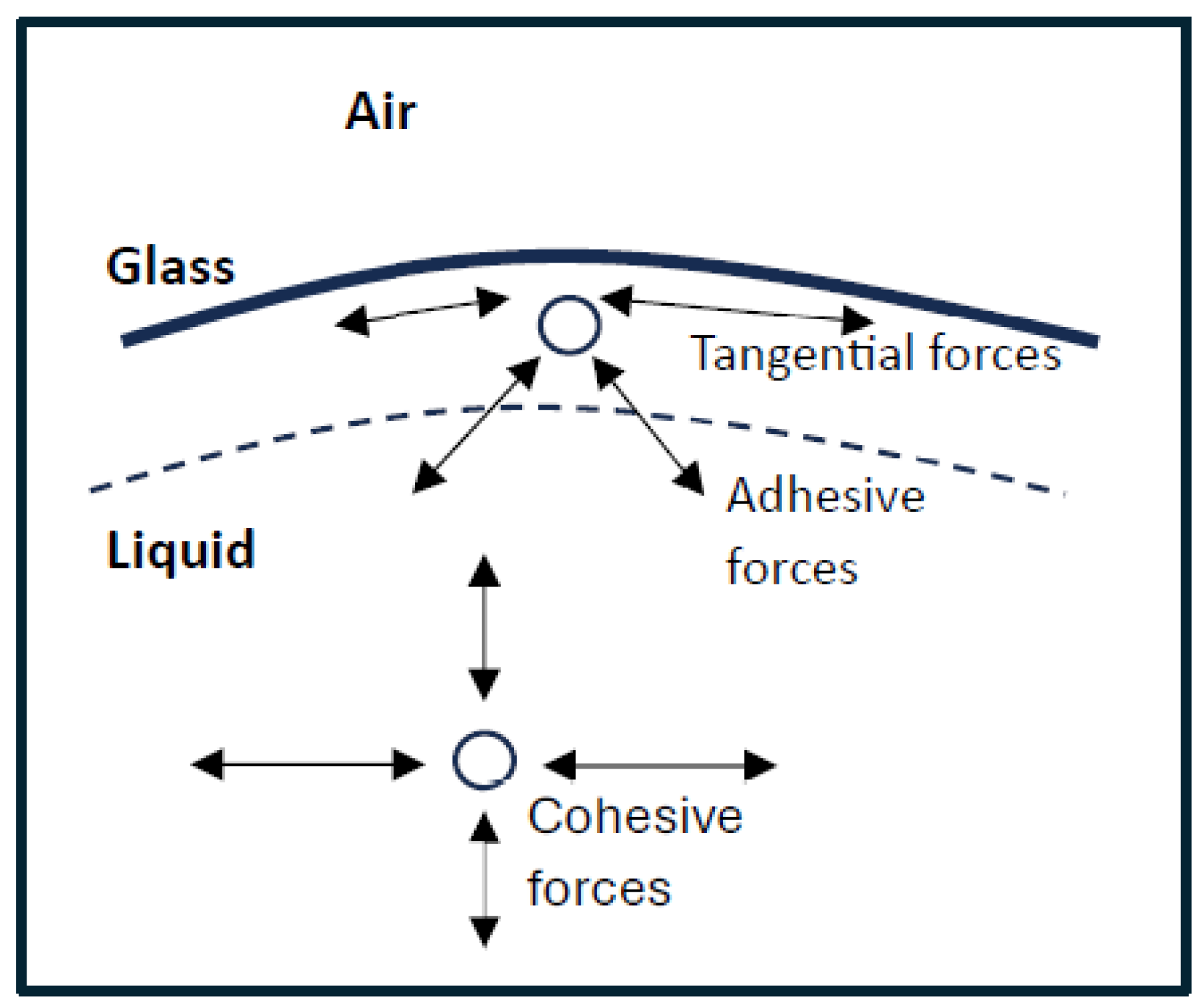
- Forces’ interactions with molecules: Strong cohesive forces, like hydrogen bonds and van der Waals forces, between molecules in a liquid increase surface tension.Adhesive forces between the liquid and the container of glass might affect the apparent surface tension of the liquid when it comes to capillary action, as an example.
- ➢
- Dissolved gases: A liquid’s surface tension can be affected by the type and quantity of present gases dissolved in it [48].
- ➢
- External pressure: surface tension is normally insensitive to changes in external high pressure can affect the surface tension noticeably. Vapor pressure of the liquid in volatile liquids tends to have higher vapor pressures because of their greater propensity to escape into the gas phase. This means that higher vapor pressure can decrease surface tension [49].
- ➢
- Area of surface: Surface area can also affect surface tension. Based on the Laplace differential pressure between the inside and the outside of a curved surface that forms the boundary between two fluid regions. The pressure difference resulted from surface tension as an interface between liquid and air, or immiscible liquids’ surface curvatures in liquid droplets will affect surface tension; nevertheless, this is more of an issue to be considered rather than having a direct impact on the underlying surface tension, on the understanding of phenomena such as capillarity [4,50].
- ➢
- Electric field influence: The surface tension of a liquid can be altered by the application of an electric field. This is especially important in electro-wetting, where an electric field alters a droplet’s surface tension on a surface [52].
- ➢
- Temperature gradients: Temperature gradients are called the Marangoni Effect, which means differences in surface tension can induce fluid motion, or Marangoni flow when there is a temperature gradient across a liquid’s surface [46].
4. Future Research Prospectives
CNT–Water Suspension Viscosity
- ➢
- CNT Addition Effect on Viscosity:
- ➢
- CNTs’ large aspect ratio:
- ➢
- Dispersion Quality:
- ➢
- Functionalization:
- ➢
- Temperature increases the effect on the viscosity of CNT Nanofluids:
- ➢
- CNT–Water Nanofluid Surface Tension:
5. Conclusions
- ➢
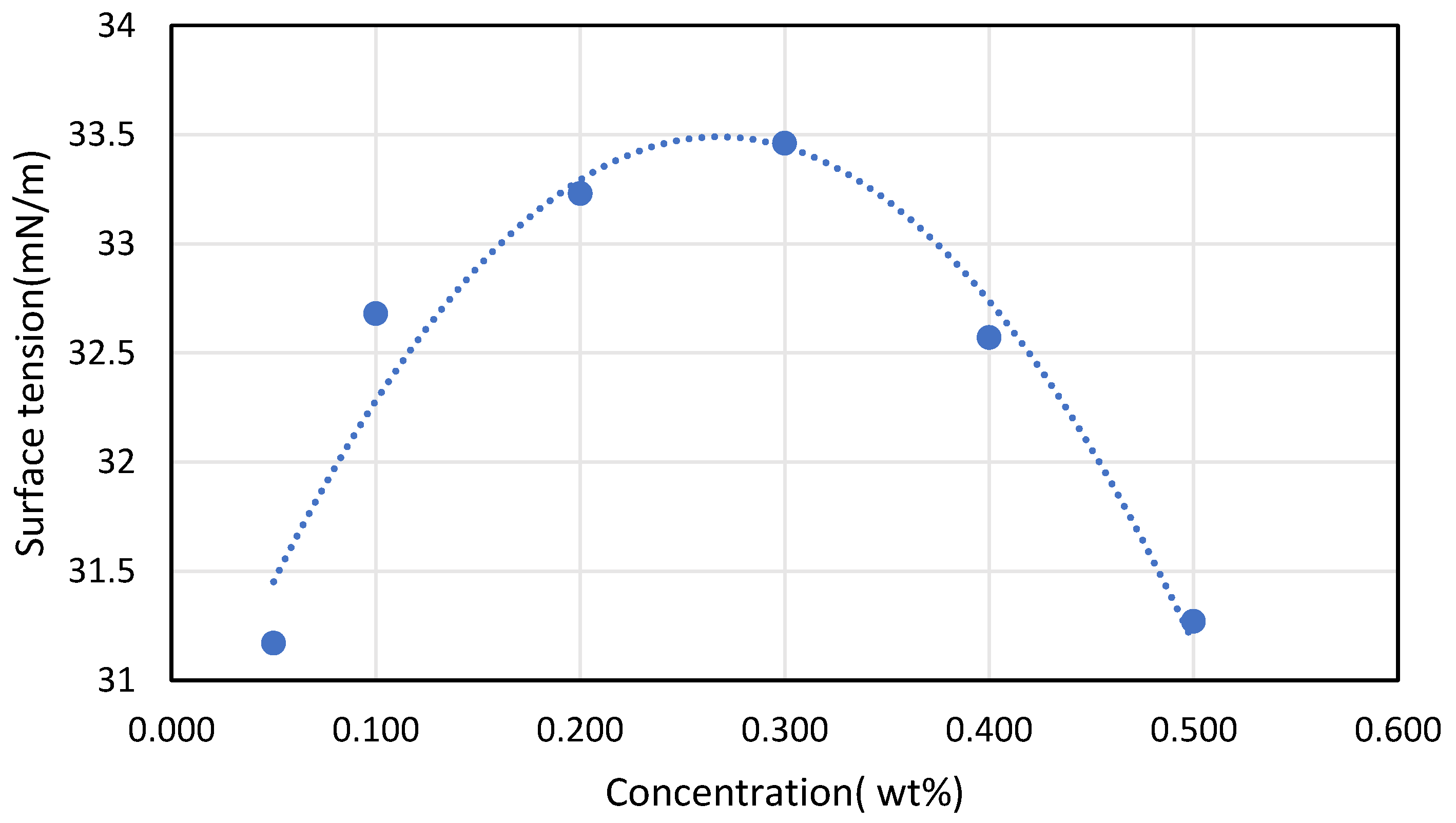
- There is an optimal concentration for surface tension, beyond which the surface tension will fall. As the concentration of CNT in nanofluids increases, the interaction and entanglement of CNTs within the fluids causes an increase in suspension viscosity. The most reasonable answer was this one. While some answers were contradicted and distinct, they lacked logical support.
- ➢
- Because the forces or bonds between molecules drop as kinetic energy increases, increasing temperature lowers viscosity and surface tension.
- ➢
- The use of surfactants during the creation of nanofluids typically results in a drop in surface tension since the molecules’ forces are reduced because of the surfactants. Simultaneously, the type and concentration of surfactant also affect the nanofluid’s viscosity.
- ➢
- Certain other elements, such as surface area, stresses, and gas present, influence surface tension but not viscosity.
- ➢
- There is no known influence of other parameters on surface tension, such as aspect ratio, dispersion quality, and functionalization.
- ➢
- Certain articles mentioned a relationship between viscosity and surface tension. These relationships were complex and susceptible to many experimental setups, though. Functional groups of nanotubes, which may change the surface chemistry of CNTs and their interactions with surrounding fluids, were one of the influencing elements. These groups can also modify the viscosity of nanofluids.
- ➢
- Hydrophilic functional groups can promote dispersion in water-based nanofluids in two distinct ways, which may result in a possible reduction in viscosity. On the other hand, adding hydrophobic groups might cause them to aggregate and increase viscosity. The impact is continuous with respect to the distribution and density of functional groups, highlighting the significance of investigating CNT properties.
- ➢
- Adding CNTs can change surface properties and interrupt hydrogen bonding in water, affecting surface tension. The presence of CNTs in the fluids can affect viscosity, especially if they become entangled or form aggregates.
- ➢
- To comprehend the relationship between surface tension and viscosity in CNT water fluids, experimental studies are recommended in this context.
- ➢
- Surface tension affects how the fluid wets a surface or moves through capillary spaces. Higher surface tension can cause a higher resistance to movement, but this must be balanced with the viscosity, as higher viscosity will further resist flow.
- ➢
- CNT nanofluids might sometimes exhibit shear-thinning behavior, where viscosity decreases with increasing shear rate. Surface tension can influence how the fluid spreads under these conditions, particularly in microfluidics or porous media.
- ➢
- Surface tension can affect nanoparticle suspension stability leading to agglomeration if surface tension is too high, increasing viscosity and leading to inconsistent behavior.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CNT | Carbon nano tubes |
| SWCNT | Single walled carbon nano tuvbes |
| MWCNT | Multi walled carbon nano tubes |
List of Symboles
| ø | Concentration of CNT | % |
| μ | Dynamic viscosity | cPa·s |
| γ | Surface tension | N/m |
| τ | Sheer stress | N/m2 |
| W | Work | N·m |
| L | Length | m |
| F | Force | |
| m | Mass | g |
| g | Gravitation acceleration | m/s2 |
| V | substance’s molar volume, | mL/mole |
| Tc | critical temperature | °C |
| K | Thermal conductivity | W/m·K |
| Cp | Specific heat | j/g·°C |
| ρ | Density | g/L |
| µ0 | Solvant viscosity | cPa·s |
| ϻeff | Suspension effective | cPa·s |
| h | Heat transfere coefficient | W/m2·K |
| δ and β | Constants | none dimensional |
| Tm | Melting temperature | K |
| T | Fluid’s temperature | K |
| B | coefficient of the particle shape | none dimensional |
| ν | kinematic viscosity | m2/s |
| A | Unit area | m2 |
| du/dy | Rate of shear deformation | N/m·kg·s |
References
- Gregersen, E. Viscosity. Encyclopedia Britannica. Available online: https://www.britannica.com/science/viscosity (accessed on 25 June 2024).
- Casaos, A. The Viscosity of Dilute Carbon Nanotube and Graphine Oxide Nanofluids. Phys. Chem. 2020, 22, 11474–11484. [Google Scholar]
- Khoswan, I.; Nassar, H.; Assali, M.; AbuSafa, A.; Sawalha, S.; Hilal, H.S. Why carbon nanotubes improve aqueous nanofluid thermal conductivity: A qualitative model critical review. Processes 2024, 12, 834. [Google Scholar] [CrossRef]
- Ahmari, H.; Amiri, M.C. On the Relationship between Surface Tension and Viscosity of Fluids. Chem. Eng. Res. Bull. 2015, 18, 18–22. [Google Scholar] [CrossRef]
- Bashirnezhad, K.; Bazri, S.; Safaei, M.R.; Goodarzi, M.; Dahari, M.; Mahian, O.; Dalkılıça, A.S.; Wongwises, S. Viscosity of Nanofluids: A Review of Recent Experimental Studies. Int. Commun. Heat Mass Transf. 2016, 73, 114–123. [Google Scholar] [CrossRef]
- Cham sa-ard, W.; Fawcett, D.; Fung, C.C.; Chapman, P.; Rattan, S.; Poinern, G.E.J. Synthesis, Characterisation and Thermo-Physical Properties of Highly Stable Graphene Oxide-Based Aqueous Nanofluids for Potential Low-Temperature Direct Absorption Solar Applications. Sci. Rep. 2021, 11, 16549. [Google Scholar] [CrossRef]
- Yang, H.; Neal, L.; Flores, E.E.; Adronov, A.; Kim, N.Y. Role and Impact of Surfactants in Carbon Nanotube Dispersions and Sorting. J. Surfactants Deterg. 2023, 26, 607–622. [Google Scholar] [CrossRef]
- Almanassra, I.W.; Manasrah, A.D.; Al-Mubaiyedh, U.A.; Al-Ansari, T.; Malaibari, Z.O.; Atieh, M.A. An Experimental Study on Stability and Thermal Conductivity of Water/CNTs Nanofluids Using Different Surfactants: A Comparison Study. J. Mol. Liq. 2020, 304, 111025. [Google Scholar] [CrossRef]
- Gao, T.; Li, C.; Zhang, Y.; Yang, M.; Jia, D.; Jin, T.; Hou, Y.; Li, R. Dispersing Mechanism and Tribological Performance of Vegetable Oil-Based CNT Nanofluids with Different Surfactants. Tribol. Int. 2019, 131, 51–63. [Google Scholar] [CrossRef]
- Wang, J.; Li, G.; Li, T.; Zeng, M.; Sundén, B. Effect of Various Surfactants on Stability and Thermophysical Properties of Nanofluids. J. Therm. Anal. Calorim. 2021, 143, 4057–4070. [Google Scholar] [CrossRef]
- Kalsi, S.; Kumar, S.; Kumar, A.; Alam, T.; Dobrotă, D. Thermophysical Properties of Nanofluids and Their Potential Applications in Heat Transfer Enhancement: A Review. Arab. J. Chem. 2023, 16, 105272. [Google Scholar] [CrossRef]
- Su, G.; Yang, L.; Liu, S.; Song, J.; Jiang, W.; Jin, X. Review on Factors Affecting Nanofluids Surface Tension and Mechanism Analysis. J. Mol. Liq. 2024, 407, 125159. [Google Scholar] [CrossRef]
- Bhuiyan, M.H.U.; Saidur, R.; Amalina, M.A.; Mostafizur, R.M.; Islam, A. Effect of Nanoparticles Concentration and Their Sizes on Surface. Procedia Eng. 2015, 105, 431–437. [Google Scholar] [CrossRef]
- Emelyanenko, A.M.; Boinovich, L.B. Effect of Dispersed Particles on Surface Tension, Wetting, and Spreading of Nanofluids. Curr. Opin. Colloid Interface Sci. 2023, 68, 101762. [Google Scholar] [CrossRef]
- Rashid, F.L.; Mohammed, H.I.; Dulaimi, A.; Al-Obaidi, M.A.; Talebizadehsardari, P.; Ahmad, S.; Ameen, A. Analysis of Heat Transfer in Various Cavity Geometries with and without Nano-Enhanced Phase Change Material: A Review. Energy Rep. 2023, 10, 3757–3779. [Google Scholar] [CrossRef]
- Gad, M.S.; Ağbulut, Ü.; Afzal, A.; Panchal, H.; Jayaraj, S.; Qasem, N.A.A.; El-Shafay, A.S. A Comprehensive Review on the Usage of the Nano-Sized Particles along with Diesel/Biofuel Blends and Their Impacts on Engine Behaviors. Fuel 2023, 339, 127364. [Google Scholar] [CrossRef]
- Rashidi, S.; Karimi, N.; Li, G.; Sundén, B. Progress in Phase Change Nano-Emulsions for Energy Applications—A Concise Review. J. Mol. Liq. 2023, 387, 122547. [Google Scholar] [CrossRef]
- Lu, G.; Wang, X.-D.; Duan, Y.-Y. A Critical Review of Dynamic Wetting by Complex Fluids: From Newtonian Fluids to Non-Newtonian Fluids and Nanofluids. Adv. Colloid Interface Sci. 2016, 236, 43–62. [Google Scholar] [CrossRef]
- Peer-Reviewed Journal Articles and Book Chapters. Available online: https://www.sciencedirect.com (accessed on 25 June 2024).
- Berry, M.V. The Molecular Mechanism of Surface Tension. Phys. Educ. 1971, 6, 79–84. [Google Scholar] [CrossRef]
- American Chemistry Socity. Chimestry for life. The Water Molecule and Dissolving. Surface Tension. Chapter 5. Lesson 5.2. Available online: https://www.acs.org/middleschoolchemistry/lessonplans/chapter5/lesson2.html (accessed on 20 October 2024).
- Halliday, D.; Kenneth, R.R.; Krane, S. Physics; John Willy & Sons: Hoboken, NJ, USA, 2010; p. 342. [Google Scholar]
- Ahadian, S.E. Determination of Surface Tension and Viscosity of Liquids by Aid of the Capillary Rise Precedure Using Artificial Neural Network (ANN). Iran J. Chem. Eng. 2008, 27, 7–15. [Google Scholar]
- Urone, P.P.; Hinrichs, R. Cohesion and Adhesion in Liquids: Surface Tension and Capillary Action. Available online: https://openstax.org/books/college-physics-2e/pages/11-8-cohesion-and-adhesion-in-liquids-surface-tension-and-capillary-action#eip-id2439890 (accessed on 13 October 2024).
- Butt, H.J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces; Wiley-VCH Verlag GmbH & Co. KGaA: Hoboken, NJ, USA, 2003. [Google Scholar]
- White, H.E. Modern Coledge Physics; D. Van Nostrand Company: New York, NY, USA, 1948. [Google Scholar]
- Kerker, M. Colloid and Interface Science: Adsorption, Catalysis, Solid Surfaces, Wetting, Surface Tension; Academic Press: Cambridge, MA, USA, 1976; Volume 3, pp. 12–30. [Google Scholar]
- Rudolfhellmuth File:Surface Growing.Png. Available online: https://commons.wikimedia.org/w/index.php?curid=30083123 (accessed on 16 October 2024).
- Sears, F. University Physics; Addison Wesley: London, UK, 1955. [Google Scholar]
- Hahn, K. Illustrative Diagram of Surface Tension Forces on a Needle Floating on the Surface of Wate. 2007. Available online: https://commons.wikimedia.org/wiki/File:SurftensionDiagram.png (accessed on 20 June 2024).
- Li, H.; Li, Z.; Qiu, L.; Dong, S.; Ouyang, J.; Dong, X.; Han, B. Rheological Behaviors and Viscosity Prediction Model of Cementitious Composites with Various Carbon Nanotubes. Constr. Build. Mater. 2023, 379, 131214. [Google Scholar] [CrossRef]
- Fuchs, J. Is It Viscosity or Is It Surface Tension? Available online: https://techblog.ctgclean.com/2015/02/visicosity/ (accessed on 15 October 2024).
- Cavendish, M. Growing Up with Science; Marshall Cavendish: Singapore, 2006. [Google Scholar]
- Martin, E. A Study of Laminar Compressible Viscous Pipe Flow Accelerated by an Axial Body Force, with Application to Magnetogasdynamics; NASA: Washington, DC, USA, 1961; p. 7.
- Balescu, R. Equilibrium and Non-Equilibrium Statistical Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics: Volume 6, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1987; pp. 9–18. ISBN 9780750627672. [Google Scholar]
- Kamal, M.R.; Mutel, A. Rheological Properties of Suspensions in Newtonian and Non-Newtonian Fluids. J. Polym. Eng. 1985, 5, 293–382. [Google Scholar] [CrossRef]
- White, F. Fluid Mechanics: Solutions Manual; McGraw-Hill Publishing: London, UK, 2003; ISBN 9780072402209. [Google Scholar]
- Hinze, J.O. Turbulent Flow Regions with Shear Stress and Mean Velocity Gradient of Opposite Sign. Appl. Sci. Res. 1970, 22, 163–175. [Google Scholar] [CrossRef]
- Byron, W.E.S.; Lightfoot, E.N.R. Transport Phenomena; John Wiley & Sons: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Ghosh, S.; Ray, A.; Pramanik, N. Self-Assembly of Surfactants: An Overview on General Aspects of Amphiphiles. Biophys. Chem. 2020, 265, 106429. [Google Scholar] [CrossRef]
- Klein, H.J. (Ed.) An Introduction to Surface Tension; Nova Science Publishers: Hauppauge, NY, USA, 2020. [Google Scholar]
- Eras-Muñoz, E.; Farré, A.; Sánchez, A.; Font, X.; Gea, T. Microbial Biosurfactants: A Review of Recent Environmental Applications. Bioengineered 2022, 13, 12365–12391. [Google Scholar] [CrossRef]
- El Haber, M.; Ferronato, C.; Giroir-Fendler, A.; Fine, L.; Nozière, B. Salting out, Non-Ideality and Synergism Enhance Surfactant Efficiency in Atmospheric Aerosols. Sci. Rep. 2023, 13, 20672. [Google Scholar] [CrossRef]
- Soleimani, H. Synthesis of Carbon Nanotubes for Oil-Water Interfacial Tension Reduction. Oil Gas Res. 2015, 1, 104. [Google Scholar] [CrossRef]
- Berrada, N.; Hamze, S.; Desforges, A.; Ghanbaja, J.; Al, J.G. Surface Tension of Functionalized MWCNT Based Nanofluids in Water and Commercial Polyproplene-Glycol Mixture. J. Mol. Liq. 2019, 293, 293111473. [Google Scholar] [CrossRef]
- Varghese, N.; Sykes, T.C.; Quetzeri-Santiago, M.A.; Castrejón-Pita, A.A.; Castrejón-Pita, J.R. Effect of Surfactants on the Splashing Dynamics of Drops Impacting Smooth Substrates. Langmuir 2024, 40, 8781–8790. [Google Scholar] [CrossRef]
- Lee, J.I.; Yim, B.S.; Kim, J.M. Effect of Dissolved-Gas Concentration on Bulk Nanobubbles Generation Using Ultrasonication. Sci. Rep. 2020, 10, 18816. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Lippmann, D.Z.; Curl, R.F., Jr.; Huggins, C.M.; Petersen, D.E. The Volumetric and Thermodynamic Properties of Fluids. II. Compressibility Factor, Vapor Pressure and Entropy of Vaporization. Chem. Soc. 1955, 77, 433–3440. [Google Scholar] [CrossRef]
- Sedev, R. Physical Properties: Surface Tension and Capillarity. In Encyclopedia of Physical Organic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Atia, A.; Radwan, N.R.E. Adsorption of Different Surfactants on Kaolinite. Adsorpt. Sci. Technol. 1997, 15, 619–626. [Google Scholar] [CrossRef]
- Mel’nikovskii, L.A.; Kriminskii, S.A. Effect of an Electric Field on the Surface Tension of a Liquid at Low Temperatures. Fluids 1997, 84, 578–579. [Google Scholar] [CrossRef]
- Saeed, M.; Alqaed, J. The Effect of Ghraphene Nano-Powder on the Viscosity of Water: An Experimental Study and Artificial Neural Network Modeling. Nanochnol. Rev. 2022, 11, 2768–2785. [Google Scholar]
- Hasan, M. The Computation of Three Dimensional Systems with Various turbulence Model Variations. Heat Mass Transf. 1996, 31, 451–461. [Google Scholar] [CrossRef]
- Vakili-Nezhaad, G.; Dorany, A. Investigation of the Effect of Multiwalled Carbon Nanotubes on the Viscosity Index of Lube Oil Cuts. Chem. Eng. Commun. 2009, 196, 997–1007. [Google Scholar] [CrossRef]
- Saidur, H. A Review on Applications and Challenges of Nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Alshqirate, A.A.; Al Hammad, M.; Tarawneh, M. Parameters Affecting Heat Transfer During condensation inside Micropipes: Surface tension Effect. Paper II. Exp. Heat Transf. 2015, 28, 405–416. [Google Scholar] [CrossRef]
- Lu, G.; Duan, Y.-Y.; Wang, X.-D. Surface tension, viscosity, and rheology of water-based nanofluids: A microscopic interpretation on the molecular level. J. Nanopart. Res. 2014, 16, 2564. [Google Scholar] [CrossRef]
- Wei, R.; Chen, J.-H.; Huizinga, J.D. On the relationship between viscosity and surface tension. J. Emerg. Investig. 2014. Available online: https://emerginginvestigators.org/articles/on-the-relationship-between-viscosity-and-surface-tension/pdf (accessed on 1 October 2024). [CrossRef]
- Liñeira del Río, J.M.; Alba, A.; Guimarey, M.J.G.; Prado, J.I.; Amigo, A.; Fernández, J. Surface Tension, Wettability and Tribological Properties of a Low Viscosity Oil Using CaCO3 and CeF3 Nanoparticles as Additives. J. Mol. Liq. 2023, 391, 123188. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Shadanfar, E.K. Air Dehumidification Using Various TEG Based Nano Solvents in Hollow Fiber Membrane Contactors. Heat Mass Transfer 2021, 57, 1623–1631. [Google Scholar] [CrossRef]
- Li, S.; Yan, J.; Zhang, Y.; Qin, Y.; Zhang, Y.; Du, S. Comparative Investigation of Carbon Nanotubes Dispersion Using Surfactants: A Molecular Dynamics Simulation and Experimental Study. J. Mol. Liq. 2023, 377, 121569. [Google Scholar] [CrossRef]
- Mahyari, A.A.; Karimipour, A.; Afrand, M. Effects of Dispersed Added Graphene Oxide-Silicon Carbide Nanoparticles to Present a Statistical Formulation for the Mixture Thermal Properties. Phys. A Stat. Mech. Its Appl. 2019, 521, 98–112. [Google Scholar] [CrossRef]
- Taghizadeh, A.; Taghizadeh, M.; Azimi, M.; Alsagri, A.S.; Alrobaian, A.A.; Afrand, M. Influence of Cerium Oxide Nanoparticles on Thermal Conductivity of Antifreeze: Preparation and Stability of Nanofluid Using Surfactant. J. Therm. Anal. Calorim. 2020, 139, 225–236. [Google Scholar] [CrossRef]
- Fedele, L.; Colla, L.; Bobbo, S.; Barison, S.; Agresti, F. Experimental Stability Analysis of Different Water-Based Nanofluids. Nanoscale Res. Lett. 2011, 6, 300. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H.; Chen, L.; Li, Y. Investigation of Thermal Conductivity and Viscosity of Ethylene Glycol Based ZnO Nanofluid. Thermochim. Acta 2009, 491, 92–96. [Google Scholar] [CrossRef]
- Wei, L.W.X. Synthesis and Thermal Conductivity of Microfluidic Copper Nanofluids. Particuology 2010, 8, 262–271. [Google Scholar] [CrossRef]
- Chamsa-Ard, W.; Brundavanam, S.; Fung, C.C.; Fawcett, D.; Poinern, G. Nanofluid Types, Their Synthesis, Properties and Incorporation in Direct Solar Thermal Collectors: A Review. Nanomater 2017, 7, 131. [Google Scholar] [CrossRef]
- Liu, W.; Malekahmadi, O.; Bagherzadeh, S.A.; Ghashang, M.; Karimipour, A.; Hasani, S.; Tlili, I.; Goodarzi, M. A Novel Comprehensive Experimental Study Concerned Graphene Oxide Nanoparticles Dispersed in Water: Synthesise, Characterisation, Thermal Conductivity Measurement and Present a New Approach of RLSF Neural Networ. Int. Commun Heat Mass Transf. 2019, 109, 104333. [Google Scholar] [CrossRef]
- Murshed, S.M.; Leong, K.C.; Yang, C. Thermophysical and Electrokinetic Properties of Nanofluids: A Critical Review. Appl. Therm. Eng. 2008, 28, 2109–2125. [Google Scholar] [CrossRef]
- Yazdanifard, F.; Ameri, M.; Ebrahimnia-Bajestan, E. Performance of Nanofluid-Based Photovoltaic/Thermal Systems: A Review. Renew. Sustain. Energy Rev. 2017, 76, 323–352. [Google Scholar] [CrossRef]
- Said, Z.; Sajid, M.; Alim, M.; Saidur, R.; Rahim, N. Experimental Investigation of the Thermophysical Properties of AL2O3-Nanofluid and Its Effect on a Flat Plate Solar Collector. Int. Commun. Heat Mass Transf. 2013, 48, 99–107. [Google Scholar] [CrossRef]
- Al-Shamani, A.; Sopian, K.; Mat, S.; Hasan, H.A.; Abed, A.; Ruslan, M.H. Experimental Studies of Rectangular Tube Absorber Photovoltaic Thermal Collector with Various Types of Nanofluids under the Tropical Climate Conditions. Energy Convers. Manag. 2016, 124, 528–542. [Google Scholar] [CrossRef]
- Mishra, P.C.; Mukherjee, S.; Nayak, S.K.; Panda, A. A brief review on viscosity of nanofluids. Int. Nano Lett. 2014, 4, 109–120. [Google Scholar] [CrossRef]
- Verma, S.; Tiwari, A.; Tiwari, S.; Chauhan, D.S. Performance analysis of hybrid nanofluids in flat plate solar collector as an advanced working fluid. Sol. Energy 2018, 167, 231–241. [Google Scholar] [CrossRef]
- Iranmanesh, S.; Ong, H.C.; Ang, B.C.; Sadeghinezhad, E.; Esmaeilzadeh, A.; Mehrali, M. Thermal Performance Enhancement of an Evacuated Tube Solar Collector Using Graphene Nanoplatelets Nanofluid. J. Clean. Prod. 2017, 162, 121–129. [Google Scholar] [CrossRef]
- Konijn, B.J.; Sanderink, O.B.J.; Kruyt, N.P. Experimental Study of the Viscosity of Suspensions: Effect of Solid Fraction, Particle Size and Suspending Liquid. Powder Technol. 2014, 266, 61–69. [Google Scholar] [CrossRef]
- Choudhary, M.; Sharma, A.; Aravind Raj, S.; Sultan, M.T.H.; Hui, D.; Shah, A.U.M. Contemporary Review on Carbon Nanotube (CNT) Composites and Their Impact on Multifarious Applications. Nanotechnol. Rev. 2022, 11, 2632–2660. [Google Scholar] [CrossRef]
- Salah, L.S.; Ouslimani, N.; Bousba, D.; Huynen, I.; Danlée, Y.; Aksas, H. Carbon Nanotubes (CNTs) from Synthesis to Functionalized (CNTs) Using Conventional and New Chemical Approaches. J. Nanomater. 2021, 2021, 4972770. [Google Scholar] [CrossRef]
- Kharlamova, M.; Paukov, M.; Burdanova, M. Nanotube Functionalization: Investigation, Methods and Demonstrated Applications. Materials 2022, 15, 5386. [Google Scholar] [CrossRef]
- Abdullah, N.N.; Ibrahim, H.A. Experimental Measurements of Viscosity and Thermal Conductivity of Single Layer Graphene Based DI-Water Nanofluid. J. Eng. 2017, 23, 142–161. [Google Scholar] [CrossRef]
- Kumar, R.; Milanova, D. Effect of Surface Tension on Nanotube Nanofluids. Appl. Phys. Lett. 2009, 94, 073107. [Google Scholar] [CrossRef]
- Ahammed, N.; Asirvatham, L.G.; Wongwises, S. Effect of Volume Concentration and Temperature on Viscosity and Surface Tension of Graphene–Water Nanofluid for Heat Transfer Applications. J. Therm. Anal. Calorim. 2016, 123, 1399–1409. [Google Scholar] [CrossRef]
- Wasankara, V.K.; Pachgharea, P.R. Effect of Surface Tension on the Thermal Performance of Pulsating Heat Pipe: A Review. Int. J. Res. Eng. 2020, 10, 29–34. [Google Scholar]
- Ajeena, A.M.; Víg, P.; Farkas, I. A Comprehensive Analysis of Nanofluids and Their Practical Applications for Flat Plate Solar Collectors: Fundamentals, Thermophysical Properties, Stability, and Difficulties. Energy Rep. 2022, 8, 4461–4490. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H. A Review on Nanofluids: Preparation, Stability Mechanisms, and Applications. J. Nanomater. 2012, 2012, 435873. [Google Scholar] [CrossRef]



| Liquid | Surface Tension γ (N/m) | Ref. |
|---|---|---|
| Water at 0 °C | 0.0756 | [26] |
| Water at 20 °C | 0.0728 | [26] |
| Water at 100 °C | 0.0589 | [26] |
| Soapy water (typical) | 0.0370 | [26] |
| Ethyl alcohol | 0.0223 | [32] |
| Mercury | 0.465 | [26] |
| Olive oil | 0.032 | [26] |
| Tissue fluids (typical) | 0.050 | [26] |
| Blood, whole at 37 °C | 0.058 | [26] |
| Blood plasma at 37 °C | 0.073 | [26] |
| Gold at 1070 °C | 1.000 | [26] |
| Benzene | 0.0282 | [32] |
| Oxygen at −193 °C | 0.0157 | [26] |
| Helium at −269 °C | 0.00012 | [26] |
| Author | Findings |
|---|---|
| [46] | A decrease in surface tension with temperature for nanofluids was examined, and an opposite tendency regarding surface tension was obtained regarding surface tension with MWCNT concentration, the same for distilled water, but an increase was observed with Tyfocor anti frees as a base fluid instead of water. |
| [52] | Showed that the nanoparticle wettability is responsible for the modified surface tension. Because hydrophobic nanoparticles always tend to be on the free surface as they behave like surfactants and reduce surface tension. |
| [53] | Found a simple correlation that can predict the rheological behavior of graphene/water nanofluids and compared it to the experimental results which confine |
| [31] | Found that experimental results suggested adding CNTs to cementitious composites reduces the flow index while increasing the critical shear rate. CNTs with sub-micrometer lengths and tiny diameters provide high-yield stresses and low viscosities to cementitious composites. |
| [54] | Presented in his paper that the concentration increment of CNT will increase the viscosity as can be seen in Figure 8 Below. This makes sense as more particles are closing the gap between the molecules of the base fluids making them move tightly. |
| [55] | Presented that the relative viscosity (ηr) is a function of concentration (C) of MW CNTs at 5 different temperature settings. The fitting line was calculated with the Maron–Pierce model, and the relation was directly proportional. |
| [56] | Mentioned in his paper that the nanofluids have good properties such as high thermal conductivity and low viscosity with high photo-thermal properties that are attractive for thermal applications. This contradicts all the literature that says that the CNT increases the viscosity. |
| [56] | Mentioned that the nanofluids have a reduced pumping power as compared to pure liquid to achieve equivalent heat transfer intensification. |
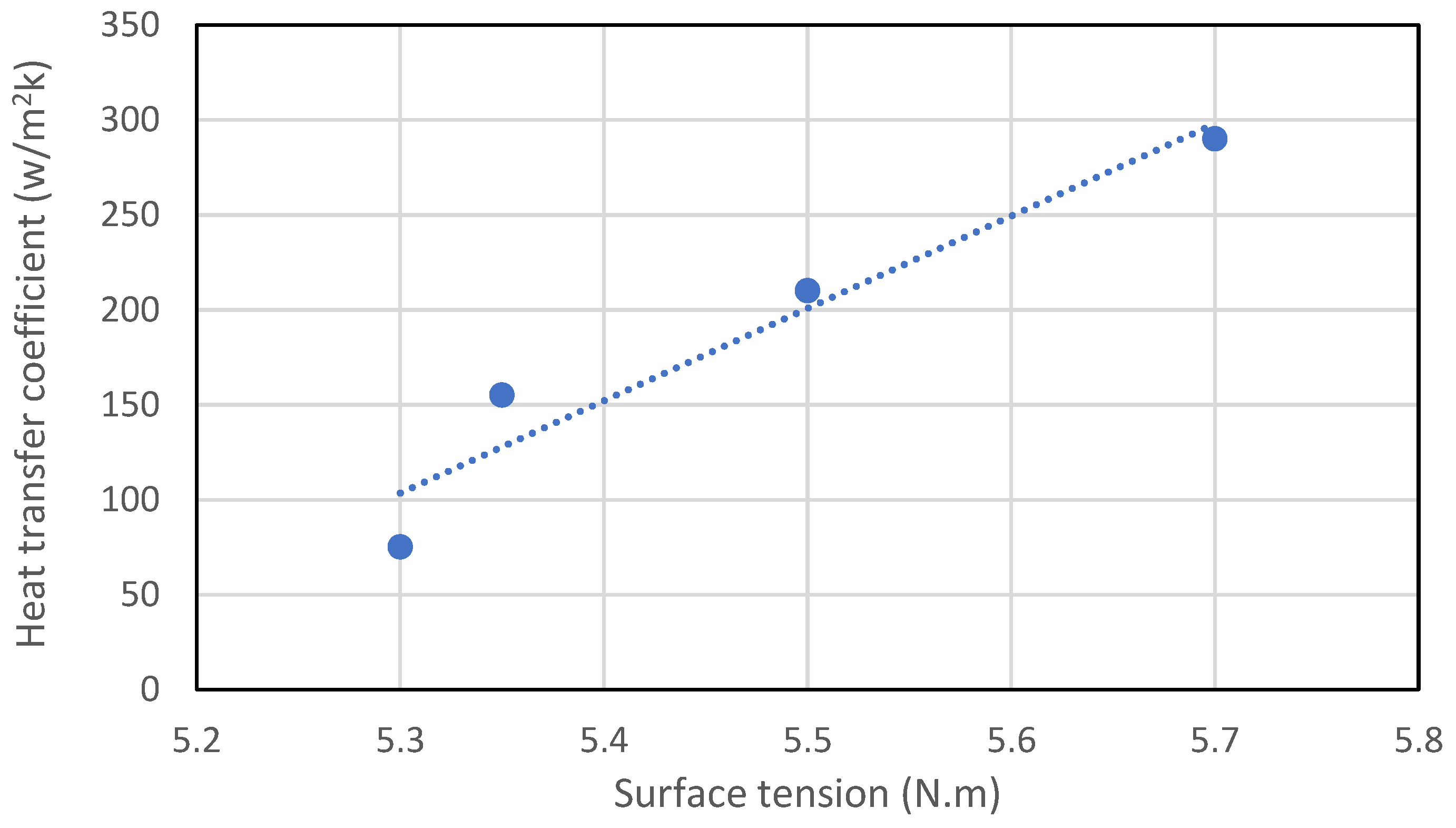
| [57] | Shows that the surface tension relation with the heat transfer coefficient, which is linearly increasing, as in Figure 9. |
| [58] | Explores the properties of both viscosity and surface tension, he also highlighted the distinctions and occasional interactions between them. |
| [59] | Experienced the theoretical and experimental underpinning and observations of the relationship—or lack thereof—between the two properties. |
| [60] | In this book chapterthe auther discussed both surface tension and viscosity in depth, including their definitions, significance, and interactions. |
| [61] | This author discussed the nuances of viscosity and all fluid properties without establishing a strict connection to surface tension. |
| [62] | This author reviewed and discussed theoretical models and experiments regarding fluid properties, providing the complexities of the relationship between surface tension and viscosity. |
| Item No. | Findings |
|---|---|
| 1 | CNT Characteristics on Surface Tension and Viscosity
|
| 2 | Temperature Effects on Surface Tension and Viscosity
|
| 3 | Impact of Concentration on Surface Tension-Viscosity Relationship
|
| 4 | Interrelation Between Surface Tension and Viscosity in Dynamic Conditions
|
| 5 | Numerical and Computational Modeling
|
| 6 | Experimental Techniques for Simultaneous Measurement
|
| 7 | Applications and Industry-Specific Research
|
| 8 | Environmental and Economic Considerations
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoswan, I.; Abusafa, A.; Odeh, S. The Effect of Carbon Nanotubes on the Viscosity and Surface Tension of Heat Transfer Fluids—A Review Paper. Energies 2024, 17, 5584. https://doi.org/10.3390/en17225584
Khoswan I, Abusafa A, Odeh S. The Effect of Carbon Nanotubes on the Viscosity and Surface Tension of Heat Transfer Fluids—A Review Paper. Energies. 2024; 17(22):5584. https://doi.org/10.3390/en17225584
Chicago/Turabian StyleKhoswan, Ibrahim, Abdelrahim Abusafa, and Saad Odeh. 2024. "The Effect of Carbon Nanotubes on the Viscosity and Surface Tension of Heat Transfer Fluids—A Review Paper" Energies 17, no. 22: 5584. https://doi.org/10.3390/en17225584
APA StyleKhoswan, I., Abusafa, A., & Odeh, S. (2024). The Effect of Carbon Nanotubes on the Viscosity and Surface Tension of Heat Transfer Fluids—A Review Paper. Energies, 17(22), 5584. https://doi.org/10.3390/en17225584